Пространственные фермы. Теория расчета, примеры и задачи. Подольский И.С. 1931 | Библиотека: книги по архитектуре и строительству
| Пространственные фермы. Теория расчета, примеры и задачи |
| Подольский И.С. |
| Государственное издательство. Москва-Ленинград. 1931 |
| 348 страниц |
Содержание:
Предисловие
Часть I. Теория расчета пространственных ферм
Глава I. Основные условия устройства пространственных ферм
§ 1. Общие понятия о пространственных фермах
§ 2. Образование простейших пространственных ферм
§ 3. Преобразование простейших ферм. Сложные системы
§ 4. Сетчатые системы
§ 5. Балочно-сферические покрытия
§ 6. Классификация пространственных ферм
§ 7. Устройство опор пространственных ферм
§ 8. Условия статической определимости пространственных ферм
Глава II. Статическое равновесие сил в пространстве
Статическое равновесие сил в пространстве
§ 9. Сложение и разложение сил в пространстве
§ 10. Разложение силы на три направления в пространстве
§ 11. Нулевая нагрузка и нулевые усилия
§ 12. Разложение силы на шесть направлений в пространстве
§ 13. Исследование геометрической неизменяемости пространственных систем
Глава III. Расчет статически определимых пространственных систем
§ 14. Общие основания расчета ферм
§ 15. Расчет пространственных ферм по способу непосредственного разложения узловой нагрузки
§ 16. Расчет пространственных систем путем разложения ни на плоские фермы
§ 17. Расчет пространственных ферм по способу замены стержней
§ 18. Заключения о способах расчета пространственных ферм
§ 19. Расчет опорного кольца и условия правильного расположения подвижных опор
§ 20. Элементы расчета пространственных покрытий
Глава IV, Расчет пространственных стропильных систем
§ 21. Расчет балочно-сферического покрытия
 Расчет пирамидальных покрытий
Расчет пирамидальных покрытий§ 23. Расчет цилиндрического сетчатого покрытия
§ 24. Зубчатые пространственные стропила
Глава V. Расчет металлических пилонов и башен
§ 25. Пилоны раскосной системы
§ 26. Пилоны сетчатой системы (гиперболоиды)
Глава VI. Расчет статически неопределимых пространственных ферм
§ 27. Общие основания расчета статически неопределимых пространственных ферм
§ 28. Расчет статически неопределимой пространственной фермы с одним лишним стержнем
§ 29. Расчет статически неопределимых пространственных ферм со многими лишними стержнями
§ 30. Примеры расчета статически неопределимых пространственных ферм
§ 31. Влияние температуры на усилия в пространственных фермах
§ 32. Определение усилий от действия температуры в статически неопределимых пространственных фермах
Глава VII. Пространственные фермы аэропланов
§ 33. Общие схемы пространственных ферм аэропланов
§ 31 Необходимость расчета аэропланной фермы как пространственной системы
§ 35.
 Расчет статически неопределимой, пространственной фермы аэроплана
Расчет статически неопределимой, пространственной фермы аэроплана§ 36. Расчет пространственной фермы аэроплана рамной конструкции (без тросов)
§ 37. Метод расчета пространственной фермы крыла аэроплана
§ 38. Расчет фермы фюзеляжа на кручение
Часть II. Задачи и упражнения по расчету пространственных ферм
1. Задачи и упражнения к первой главе
2. Контрольные задачи к первой главе
3. Задачи и упражнения ко второй главе
4. Применение метода нулевой нагрузки
5. Разложение сил на шесть направлений в пространстве
6. Определение геометрической неизменяемости пространственной системы по способу нулевых усилий
7. Контрольные задачи ко второй главе
9. Непосредственное разложение узловой нагрузки
10. Разложение пространственных ферм на плоские системы
11. Способ замены стержней
12. Расчет опорного кольца
13. Контрольные задачи к третьей главе
14. Задачи и упражнения к четвертой главе
15.
 Контрольные задачи к четвертой главе
Контрольные задачи к четвертой главе16. Контрольные задачи к пятой главе
17. Задачи и упражнения к шестой главе
18. Контрольные задачи к шестой главе
Литература о пространственных фермах
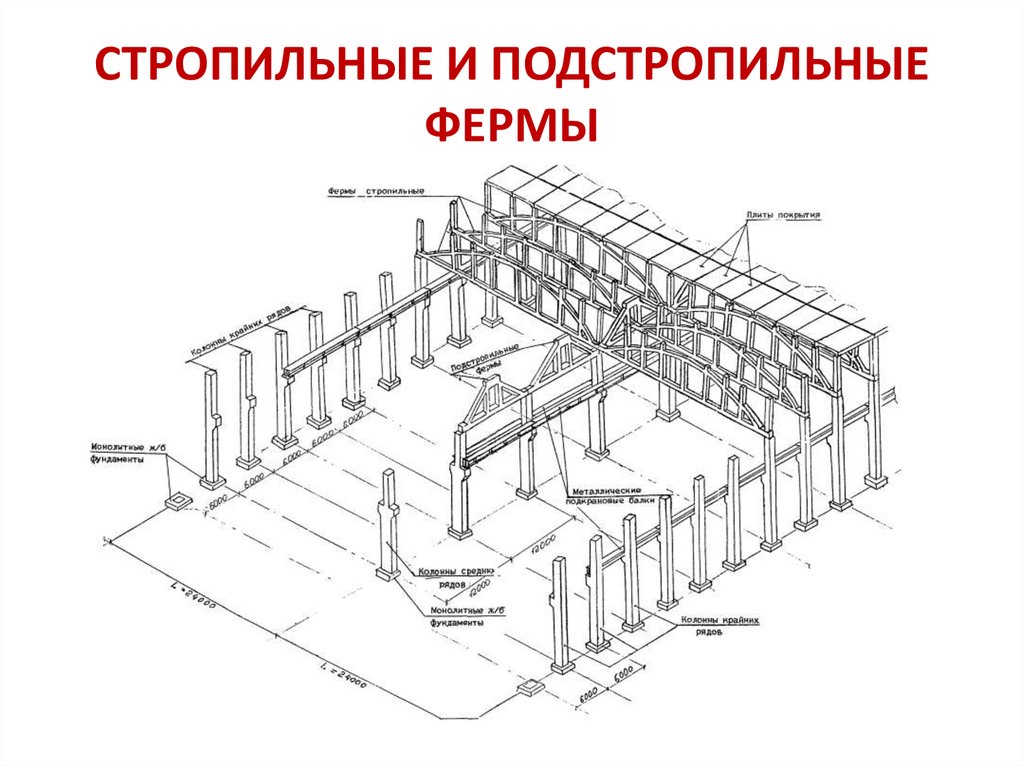
Пространственные фермы применяются для устройства купольных и шатровых покрытий в разных общественных зданиях крупных размеров, например: банки, цирки, выставочные павильоны, машинные здания, фабричные и заводские корпуса, а также в мостах, кранах, газгольдерах, башнях, маяках, кессонах и павильонах.
Летательные аппараты — аэропланы и дирижабли — тоже представляют пространственные стержневые системы или фермы. Сюда же относятся радиомачты и причальные мачты для дирижаблей.
Главная цель устройства какой-либо пространственной фермы заключается в том, чтобы получить конструкцию, свободную от внутренних стержней, а также чтобы придать всему сооружению легкую, изящную и рациональную форму.
В некоторых случаях, например в купольном покрытии, требуется еще устройство верхнего освещения (световой фонарь).
Но чтобы суметь выбрать или спроектировать наиболее рациональную в конструктивном отношении какую-либо пространственную ферму, чтобы получить систему жесткую, геометрически-неизменяемую и в то же время статически определимую, а также чтобы избежать излишней затраты материала и получить конструкцию наименьшего веса, — для всего этого необходимо знать основные условия устройства пространственных ферм и приемы расчета их, т. е. определение усилий во всех элементах пространственной системы.
Для того чтобы приобрести некоторый навык в расчете пространственных ферм, необходима также и практическая работа, заключающаяся в решении разного рода задач и в выполнении разных упражнений, начиная с самых простых, элементарных, и переходя затем к более сложным.
Изучение пространственных ферм кроме практической цели имеет также большое образовательное значение для каждого инженера, так как дает понятие о распределении усилий в стержнях, расположенных не в плоскости, а в пространстве, а также позволяет ознакомиться с применением законов статики к равновесию сил, расположенных в пространстве, и тем способствует развитию образного мышления о пространственных конструкциях, выражаемых всегда чертежами на плоскости.
Эта способность умозрительного представления «пространства» достигается также не сразу, а только после многих упражнений по расчету пространственных ферм.
Для этой цели в курсе приведено достаточное количество (всего около 200) примеров и задач с соответствующими подробными решениями.
Все эти примеры могут служить материалом для самостоятельной или лабораторно-групповой проработки курса. Однако некоторые, так называемые «контрольные задачи», приведены в курсе без соответствующих решений, чтобы дать возможность учащимся самостоятельно попробовать свои силы и доказать свое знакомство с курсом. Трудность решения этих контрольных задач не более трудности подобных задач с приведенными решениями их.
Теория расчета пространственных ферм изложена в курсе с достаточной полнотой, причем, так как настоящий курс служит учебным руководством в Военной воздушной академии, то заключительная глава курса посвящена расчету пространственных ферм аэропланов.
Оригинальную часть настоящего труда представляет расчет сетчатых гиперболоидов (§ 26).
Проф. И. Подольский. Москва, 1930 г.
Конструкции зданий и сооружений
Подольский И.С.
Скачать книгу: Пространственные фермы. Теория расчета, примеры и задачи. Подольский И.С. 1931
7.3 Особенности расчета пространственных ферм
Плоская ферма не устойчива, поэтому в металлоконструкциях не применяется, а используются исключительно пространственные фермы.
Простейшая пространственная ферма представляет собой элементарный тетраэдр, составленный из 6 стержней, и имеет 4 узла.
Рисунок 18 – Тетраэдр
Этот элементарный тетраэдр может быть развит в ферму любых размеров путем последовательного присоединения новых узлов с помощью 3-х стержней (рис 19).
Рисунок 19 – Простейшая пространственная ферма
Образованные таким
образом фермы получили название
простейшие. Фермы, полученные любым
другим способом, называют сложные.
Фермы, полученные любым
другим способом, называют сложные.
В простейших фермах существует однозначная зависимость между числом узлов и числом стержней. Эту зависимость можно получить путем следующих рассуждений. Пусть ферма имеет «n» стержней и «m» узлов. Это означает, что до элементарного тетраэдра было присоединено (m-4) узла, на это было затрачено 3(m-4) стержней. Если к этому числу добавить 6 стержней элементарного тетраэдра, то получим общее число стержней в ферме:
;
| . | (6) |
Можно легко показать, что если это условие выполнено, то ферма будет геометрически не изменяемой и статически определимой.
Для определения
усилия в стержнях пространственных
ферм можно применять те же аналитические
методы, что и для плоских ферм (то есть
метод вырезания узлов и метод сквозного
сечения). Однако при этом необходимо
записывать и решать 6 уравнений статики:
Однако при этом необходимо
записывать и решать 6 уравнений статики:
(7) |
Однако такой метод отличается громоздкостью и трудоемкостью, поэтому на практике был предложен и широко применяется более простой метод — метод разделения пространственной фермы на плоские.
Общие рекомендации по этому методу следующие:
1 Из пространственной фермы мысленно выделяются плоские фермы обычно грани.
2 Используя конкретные конструктивные особенности и особенности нагружения пространственной фермы выделяют части общих нагрузок которые прикладывают к выделенным плоским фермам.
3 Далее применяют хорошо разработанные методы расчета плоских ферм.
При таком подходе
все упрощения должны быть выполнены
так, чтобы погрешность расчета увеличивала
запас надежности конструкции.
Список литературы: [1] с.18…24, 31…36; [8] с.21…24; [10] с.146…150, [12] с.150…178.
Вопросы для самопроверки
Дайте определение расчетной схемы «ферма».
На каких допущениях базируется теория расчета ферм?
Какие типы стержней может содержит ферма? Покажите на примере.
Что такое узлы и панели? Покажите на примере.
Классификация ферм.
Отличие балочной фермы от консольной. Покажите на примере.
Приведите пример шпренгельной фермы. С какой целью вводятся дополнительные стержни?
Приведите пример фермы с ломаными поясами.
Какие методы определения усилий в стержнях ферм вы знаете?
Графические методы определения усилий в стержнях ферм (метод Кульмана и метод Максвелла-Кремоны).
 Их достоинства и недостатки.
Их достоинства и недостатки.Аналитические методы определения усилий в стержнях ферм (метод вырезания узлов и метод сквозного сечения).
Достоинства метода сквозного сечения перед методом вырезания узлов.
Сколько уравнений статики можно составить для плоской фермы?
Сколько уравнений статики можно составить для пространственной фермы?
Приведите пример простейшей пространственной фермы.
Способы определения усилий в стержнях пространственных ферм.
Приведите пример пространственной фермы.
Чем ферма отличается от рамы?
Какие усилия действуют в стержнях ферм?
Можно ли рассчитывать ферму по расчетной схеме «рама»?
Пространственные фермы – гражданское строительство X
Пространственные фермы из-за их формы, расположения элементов или приложенной нагрузки не могут быть подразделены на плоские фермы для целей анализа и поэтому должны анализироваться как трехмерные конструкции, подверженные трехмерные силовые системы.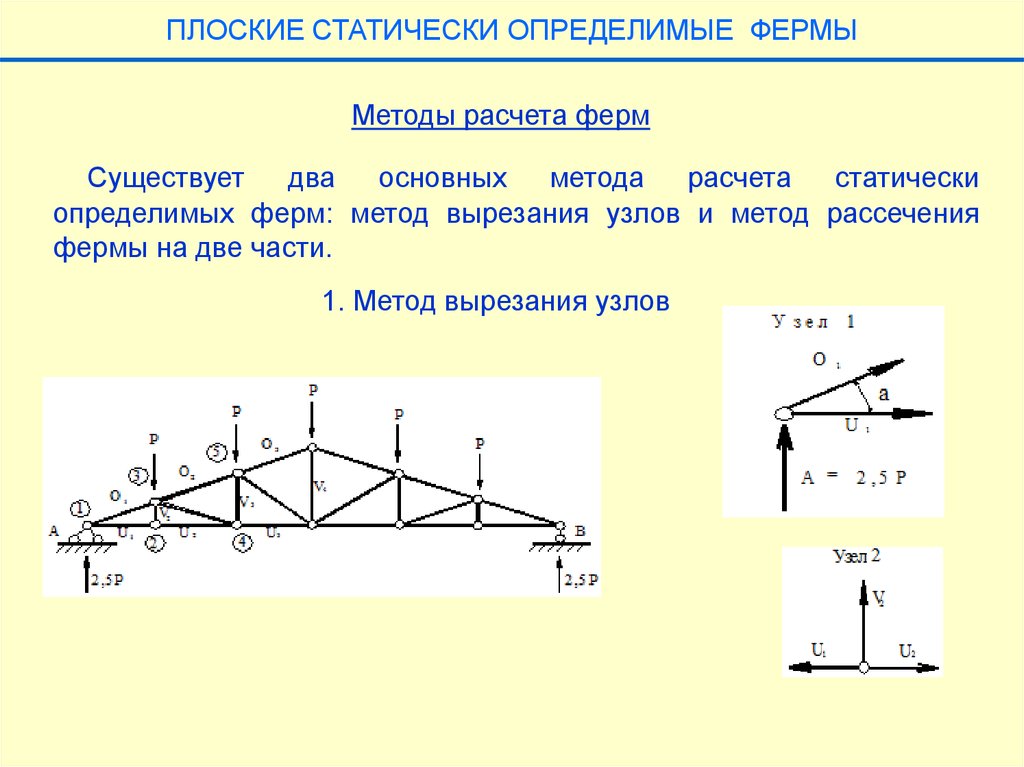 Как указано в разделе 4.1, для упрощения расчета пространственных ферм предполагается, что элементы фермы соединены на своих концах безфрикционными шаровыми шарнирами, все внешние нагрузки и реакции приложены только в узлах, а центральная ось каждого члена совпадает с линией, соединяющей центры соседних суставов. Из-за этих упрощающих допущений элементы пространственных ферм можно рассматривать как элементы осевых сил.
Как указано в разделе 4.1, для упрощения расчета пространственных ферм предполагается, что элементы фермы соединены на своих концах безфрикционными шаровыми шарнирами, все внешние нагрузки и реакции приложены только в узлах, а центральная ось каждого члена совпадает с линией, соединяющей центры соседних суставов. Из-за этих упрощающих допущений элементы пространственных ферм можно рассматривать как элементы осевых сил.
Простейшая внутренне устойчивая (или жесткая) пространственная ферма может быть образована путем соединения шести элементов на концах четырьмя шаровыми соединениями в виде тетраэдра, как показано на рис. 4.28 (а). Эту четырехгранную ферму можно рассматривать как основной элемент пространственной фермы. Следует понимать, что эта базовая пространственная ферма внутренне устойчива в том смысле, что она представляет собой трехмерное жесткое тело, которое не изменит своей формы под действием общей трехмерной нагрузки, приложенной к ее соединениям. Базовую ферму ABCD на рис. 4.28 (а) можно увеличить, прикрепив три новых элемента BE, CE и DE к трем существующим узлам B, C и D и соединив их, чтобы сформировать новый узел E. , как показано на рис. 4.28(b). Пока новый стык E не лежит в плоскости, содержащей существующие стыки B;C,
4.28 (а) можно увеличить, прикрепив три новых элемента BE, CE и DE к трем существующим узлам B, C и D и соединив их, чтобы сформировать новый узел E. , как показано на рис. 4.28(b). Пока новый стык E не лежит в плоскости, содержащей существующие стыки B;C,
и D, новая увеличенная ферма будет устойчивой внутри. Ферму можно дополнительно увеличить, повторив ту же процедуру (как показано на рис. 4.28 (с)) столько раз, сколько необходимо. Фермы, построенные по этой методике, называются простыми пространственными фермами.
Простая пространственная ферма образована путем увеличения основного элемента тетраэдра, содержащего шесть элементов и четыре соединения, путем добавления трех дополнительных элементов для каждого дополнительного соединения, поэтому общее количество элементов m в простой пространственной ферме равно
m = 6 + 3 (j-4) = 3j – 6 [уравнение 4.5]
, где j = общее количество соединений (включая соединения с опорами).
Типы опор, обычно используемые для пространственных ферм, изображены на рис. 4.29. Количество и направления сил реакции, которые опора может оказывать на ферму, зависят от количества и направлений перемещений, которые она предотвращает.
4.29. Количество и направления сил реакции, которые опора может оказывать на ферму, зависят от количества и направлений перемещений, которые она предотвращает.
Как было предложено в разделе 3.1, чтобы внутренне устойчивая космическая конструкция находилась в равновесии под действием общей системы трехмерных сил, она должна поддерживаться не менее чем шестью реакциями, удовлетворяющими шести уравнениям равновесия (уравнение (3.1) ):
Поскольку имеется только шесть уравнений равновесия, их нельзя использовать для определения более шести реакций. Таким образом, внутренне устойчивая пространственная структура, статически определенная внешне, должна поддерживаться ровно шестью реакциями. Если пространственная конструкция поддерживается более чем шестью реакциями, то все реакции не могут быть определены из шести уравнений равновесия, и такая структура называется внешне статически неопределимой. И наоборот, если пространственная конструкция поддерживается менее чем шестью реакциями, то реакций недостаточно для предотвращения всех возможных перемещений конструкции в трехмерном пространстве, и такая конструкция называется внешне статически неустойчивой.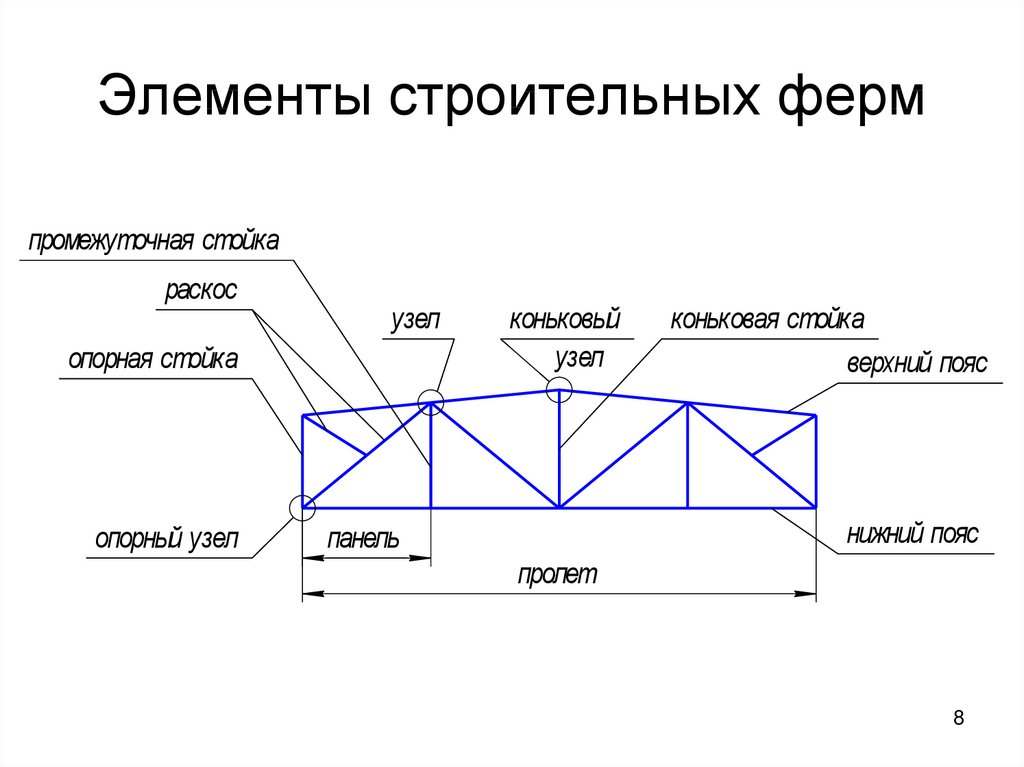 Таким образом, если
Таким образом, если
Как и в случае плоских конструкций, рассмотренных в предыдущей главе, условия статической определенности и неопределенности, указанные в уравнении. (4.6), необходимы, но недостаточны. Для того чтобы пространственная конструкция была геометрически устойчивой внешне, реакции должны быть правильно организованы, чтобы они могли предотвратить перемещения в направлениях, а также повороты вокруг каждой из трех координатных осей. Например, если бы линии действия всех реакций пространственной конструкции были либо параллельны, либо пересекали общую ось, то конструкция была бы геометрически неустойчивой.
Если пространственная ферма состоит из m элементов и опирается на r внешних реакций, то для ее расчета необходимо определить всего m þ r неизвестных сил. Поскольку ферма находится в равновесии, каждое ее соединение также должно находиться в равновесии. В каждом стыке внутренние и внешние силы образуют трехмерную параллельную систему сил, которая должна удовлетворять трем уравнениям равновесия: Fx = 0, Fy = 0 и Fz = 0.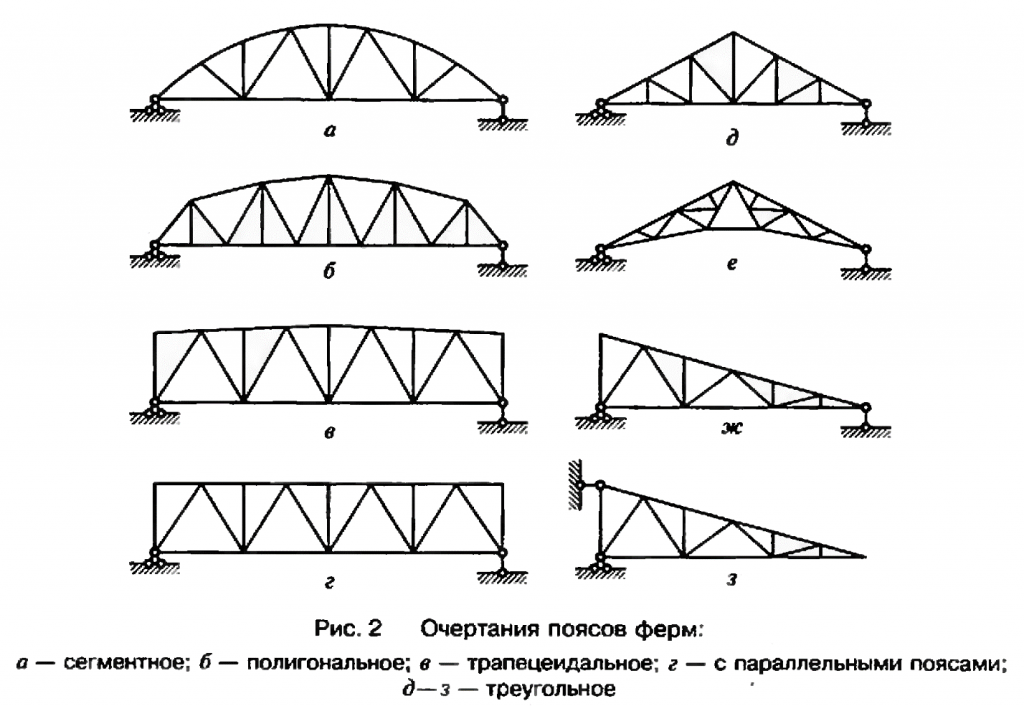 Следовательно, если ферма содержит j суставов, общее количество доступных уравнений равновесия равно 3j. Если m + r = 3j, то все неизвестные могут быть определены путем решения 3j уравнений равновесия, и ферма статически определима.
Следовательно, если ферма содержит j суставов, общее количество доступных уравнений равновесия равно 3j. Если m + r = 3j, то все неизвестные могут быть определены путем решения 3j уравнений равновесия, и ферма статически определима.
Космические фермы, содержащие больше неизвестных, чем имеется в уравнениях равновесия (m+r>3j), являются статически неопределимыми, а те, в которых неизвестных меньше, чем в уравнениях равновесия (m+r<3j), статически неустойчивы. Таким образом, условия статической неустойчивости, определенности и неопределенности пространственных ферм можно резюмировать следующим образом:
(4.7), чтобы быть справедливым, ферма должна быть устойчивой и действовать как единое твердое тело при общей трехмерной системе нагрузок при прикреплении к опорам.
Два метода расчета плоских ферм, рассмотренные в разделах 4.5 и 4.6, могут быть распространены на анализ пространственных ферм. Метод соединений по существу остается тем же, за исключением того, что три уравнения равновесия (— Fx = 0, — Fy = 0 и — Fz = 0) теперь должны удовлетворяться в каждом стыке пространственной фермы. Поскольку три уравнения равновесия нельзя использовать для определения более трех неизвестных сил, анализ начинают с соединения, на которое действует не более трех неизвестных сил (которые не должны быть компланарными). Три неизвестных определяются путем применения трех уравнений равновесия. Затем мы переходим от соединения к соединению, вычисляя три или меньше неизвестных сил в каждом последующем соединении, пока не будут определены все желаемые силы.
Поскольку три уравнения равновесия нельзя использовать для определения более трех неизвестных сил, анализ начинают с соединения, на которое действует не более трех неизвестных сил (которые не должны быть компланарными). Три неизвестных определяются путем применения трех уравнений равновесия. Затем мы переходим от соединения к соединению, вычисляя три или меньше неизвестных сил в каждом последующем соединении, пока не будут определены все желаемые силы.
Так как трудно визуализировать ориентацию наклонных стержней в трехмерном пространстве, обычно удобно выражать прямоугольные составляющие сил в таких стержнях через проекции длин стержней в x; y и z направления. Рассмотрим элемент AB пространственной фермы, как показано на рис. 4.30. Проекции его длины LAB на x; направления y и z равны xAB; yAB и zAB соответственно, как показано, с
1. Если все элементы, соединенные с соединением, кроме одного, лежат в одной плоскости и к соединению не приложены никакие внешние нагрузки или реакции, то сила в элементе, который не лежит в одной плоскости, равна нулю.
2. Если все элементы, соединенные с соединением, кроме двух, имеют нулевую силу и к соединению не приложены никакие внешние нагрузки или реакции, то, если два оставшихся элемента не лежат на одной прямой, сила в каждом из них также равна нулю.
Первый тип расположения показан на рис. 4.31(а). Он состоит из четырех стержней AB, AC, AD и AE, соединенных с шарниром A. Из них AB, AC и AD лежат в плоскости xz, а стержень AE — нет. Обратите внимание, что к соединению A не приложены никакие внешние нагрузки или реакции. Должно быть очевидно, что для удовлетворения уравнения равновесия – Fy = 0 компонент y FAE должен быть равен нулю, и, следовательно, – AE = 0,9.0003
Второй тип расположения показан на рис. 4.31(b). Он состоит из четырех элементов AB, AC, AD и AE, соединенных с соединением A, из которых AD и AE являются элементами с нулевой силой, как показано. Обратите внимание, что к соединению не применяются никакие внешние нагрузки или реакции. Выбирая ориентацию оси x в направлении стержня AB, мы можем видеть, что уравнения равновесия — Fy = 0 и — Fz = 0 могут удовлетворяться, только если FAC = 0. Поскольку x-компонента FAC равна нулю, уравнение ˆ’Fx = 0 выполняется только в том случае, если FAB также равен нулю.
Поскольку x-компонента FAC равна нулю, уравнение ˆ’Fx = 0 выполняется только в том случае, если FAB также равен нулю.
Как и в случае с плоскими фермами, метод сечений может применяться для определения усилий в отдельных элементах пространственных ферм. Воображаемое сечение проходит через ферму, разрезая элементы, силы которых желательны. Затем рассчитываются желаемые усилия на стержень путем применения шести уравнений равновесия (уравнение (3.1)) к одной из двух частей фермы. Из шести уравнений равновесия можно определить не более шести неизвестных сил, поэтому обычно выбирают сечение, которое не проходит более чем через шесть элементов с неизвестными силами.
Из-за значительных вычислительных затрат анализ космических ферм сегодня выполняется на компьютерах. Однако важно проанализировать хотя бы несколько относительно небольших пространственных ферм вручную, чтобы получить представление об основных понятиях, связанных с анализом таких конструкций.
Определите реакции на опорах и усилие в каждом элементе пространственной фермы, показанной на рис. 4.32(а).
4.32(а).
Решение
Статическая определенность Ферма содержит 9членов и 5 суставов и поддерживается 6 реакциями. Поскольку m+r=3j, а реакции и элементы фермы правильно расположены, она статически определима.
Проекции элементов Проекции элементов фермы в x; Направления y и z, полученные из рис. 4.32(a), а также их длины, вычисленные по этим проекциям, приведены в таблице 4.1.
Элементы с нулевой силой Из рис. 4.32(а) видно, что в стыке D соединены три элемента, AD;CD и DE. Из этих элементов AD и CD лежат в одной плоскости ðxzÃ, а DE — нет. Поскольку к соединению не применяются никакие внешние нагрузки или реакции, элемент DE является элементом с нулевой силой.
3D калькулятор ферм — Краткое руководство
Опубликовано: 23 сентября 2022 г.
|
Учебник
Добро пожаловать в это краткое руководство по использованию 3D-калькулятора ферм. Чтобы как можно быстрее приступить к работе, прочтите это руководство или посмотрите пошаговое видео ниже. Если вы уже использовали набор инструментов для 2D-анализа фермы, хорошая новость заключается в том, что 3D-версия работает точно так же . Если вы совершенно не знакомы с обоими, к концу этого урока вы должны научиться анализировать свои собственные структуры. Мы будем работать над решением образца структуры, доступ к данным для которого можно получить, нажав кнопку Example Data под окном просмотра 3D (на странице решателя).
Чтобы как можно быстрее приступить к работе, прочтите это руководство или посмотрите пошаговое видео ниже. Если вы уже использовали набор инструментов для 2D-анализа фермы, хорошая новость заключается в том, что 3D-версия работает точно так же . Если вы совершенно не знакомы с обоими, к концу этого урока вы должны научиться анализировать свои собственные структуры. Мы будем работать над решением образца структуры, доступ к данным для которого можно получить, нажав кнопку Example Data под окном просмотра 3D (на странице решателя).
Если вас больше интересует, как выполнять базовые структурные расчеты, взгляните на этот курс по трехмерному анализу пространственной рамы. Этот набор онлайн-инструментов основан на калькуляторе расчета ферм, который мы создали в этом курсе.
Воспроизвести видео о 3D калькуляторе ферм TN_1000 | DegreeTutors.com
Предыдущий
Следующий
🛠 У нас также есть бесплатный 2D-калькулятор ферм для более простых конструкций — проверьте его здесь.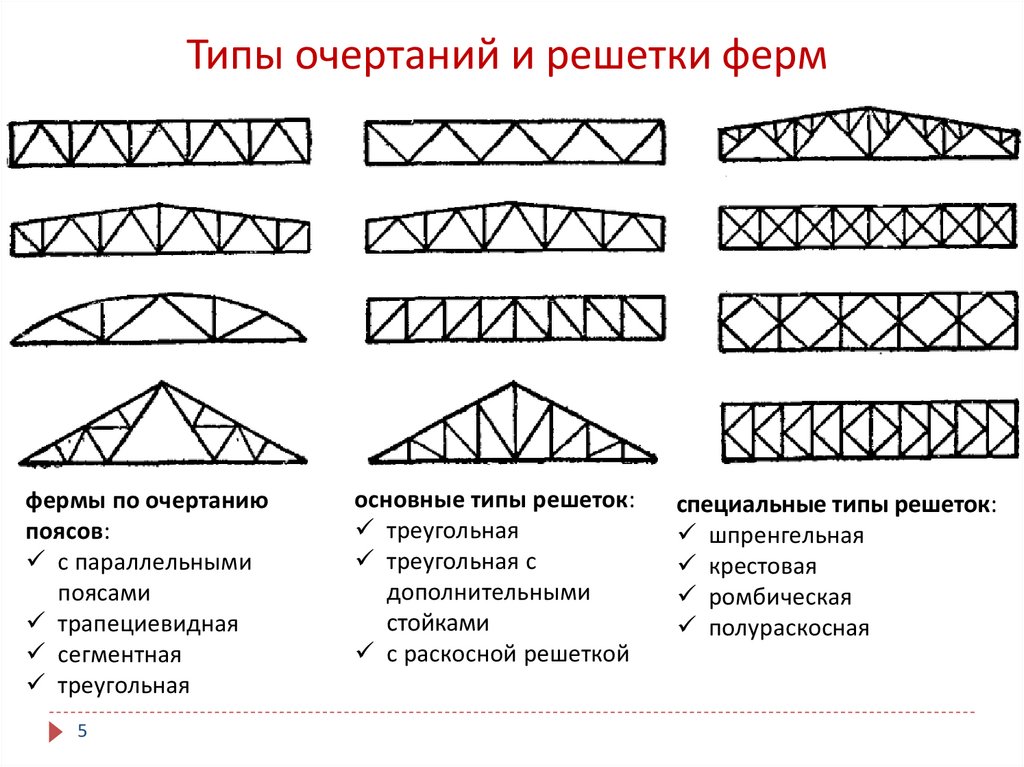
Если вы только изучаете анализ ферм, используя метод секций или метод соединений , сначала перейдите сюда — это отличный способ создать примеры вопросов для себя, чтобы решить и улучшить свои навыки ручного анализа.
Шаг 1. Определение конструкции
Структура, которую мы собираемся смоделировать, представляет собой решетчатую башню, основанную на типе конструкции, поддерживающей линии электропередач. Он подходит для этого анализа, потому что это, по сути, трехмерная ферма — предполагается, что все элементы нагружены в осевом направлении. Этот решатель работает только с конструкциями, состоящими из элементов, нагруженных в осевом направлении, без изгиба или сдвига (пока!).
Рис. 1. Анализируемая трехмерная ферма или «пространственная рама» . Как упоминалось выше, данные для этой структуры уже сгенерированы и находятся в свободном доступе, поэтому вы можете следовать этому руководству. Но когда вы выйдете за пределы этого руководства, вы быстро обнаружите, что создание данных для любой значительной трехмерной структуры становится огромным узким местом. Просто очень много времени требуется, чтобы вручную определить координаты всех узлов, а затем определить элементы, которые соединяются между этими узлами.
Просто очень много времени требуется, чтобы вручную определить координаты всех узлов, а затем определить элементы, которые соединяются между этими узлами.
Итак, Я создал файл моделирования шаблона Blender с некоторыми пользовательскими сценариями . Вы можете использовать этот файл для моделирования своей конструкции и легко генерировать данные об узлах, элементах, ограничениях и силах для вашей конструкции. Сгенерированные данные могут быть напрямую скопированы в поля ввода данных решателя. Вы можете получить доступ к файлу шаблона, нажав кнопку Modeling Template рядом с кнопкой Example Data на странице решателя. Я не буду освещать это в этой статье, но вы можете посмотреть видеоурок выше, чтобы увидеть, как используется файл шаблона, рис. 2.
Рис. 2а. Шаблон моделирования Blender можно использовать для создания структурных моделей. Рис. 2b. Данные, экспортированные из шаблона моделирования, можно использовать непосредственно в наборе инструментов анализа ферм.
Узлы
Начнем с определения положения каждого узла в структуре. Это делается путем указания координат x, y и z. Информацию об узлах можно копировать и вставлять непосредственно из таблицы выборочных данных. Обязательно скопируйте только данные, содержащиеся в зеленых ячейках на листе Google, рис. 3.
Рис. 3. Копирование информации об узле из таблицы выборочных данных в поле ввода данных.Вы можете вводить данные вручную в поля ввода данных в решателе, но обычно гораздо удобнее собирать данные в электронной таблице и просто копировать и вставлять их в решатель. Обратите внимание, что первый столбец чисел — это последовательные номера узлов. Как только информация об узлах будет вставлена, узлы появятся в окне 3D-просмотра, рис. 4.
Обратите внимание, что для создания изображения на рис. 4 я изменил окно 3D-просмотра на перспективная проекция (по умолчанию орфографическая) и увеличен параметр масштаба для улучшения видимости.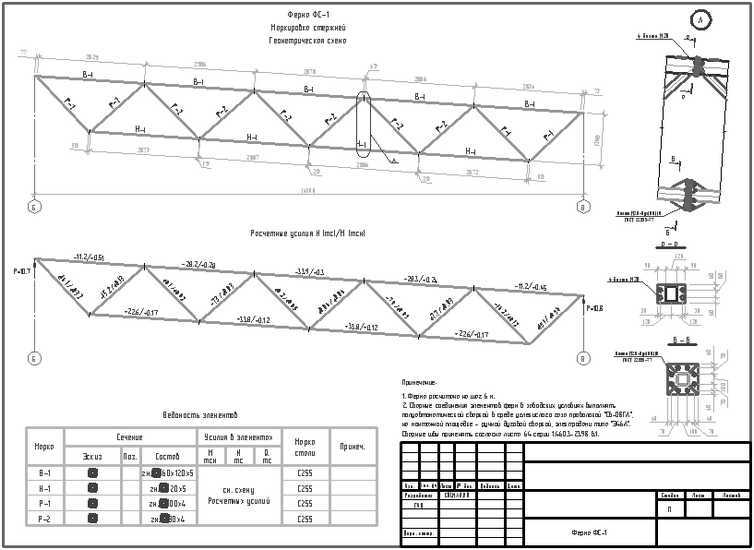 Я также отключил « Сбросить окно просмотра при обновлении », чтобы остановить сброс точки обзора при изменении параметров окна просмотра. Доступ ко всем этим параметрам осуществляется с правой панели управления.
Я также отключил « Сбросить окно просмотра при обновлении », чтобы остановить сброс точки обзора при изменении параметров окна просмотра. Доступ ко всем этим параметрам осуществляется с правой панели управления.
членов/элементов
Далее добавляется информация об элементе. Опять же, каждый элемент определяется в новой строке с полным определением, состоящим из:
- Номер элемента
- Номер узла в конце i (со ссылкой на номера узлов, установленные в предыдущем поле ввода данных)
- Номер узла в конце j (ссылаясь на номера узлов, установленные в предыдущем поле ввода данных)
- Модуль материала (Юнга)
- Площадь поперечного сечения
- Предел текучести
- Собственный вес
После вставки данных элемента окно 3D-просмотра обновляется соответствующим образом, рис. 5.
5.
Шаг 2. Определение опор/ограничителей
Информация об ограничениях добавляется в третье поле ввода данных. Чтобы определить ограничение, мы просто указываем номер узла и вводим TRUE или FALSE , чтобы указать ограничение в соответствующем глобальном направлении x, y или z. Опять же, я рекомендую вести запись в отдельном файле Excel и копировать и вставлять туда. Окно 3D-просмотра будет обновляться при добавлении каждого полного определения ограничения, рис. 6.9.0003 Рис. 6. Ограничения полного штифта (x, y и z), заданные для узлов 1, 4, 51 и 52.
Шаг 3. Определение приложенных усилий сначала номер соответствующего узла, за которым следуют компоненты силы x, y и z, приложенные к этому узлу. Итак, в этом случае мы прикладываем силу 5 кН в отрицательном направлении по оси Y к указанным узлам. Силы появятся в окне 3D-просмотра по мере их добавления в поле ввода данных.
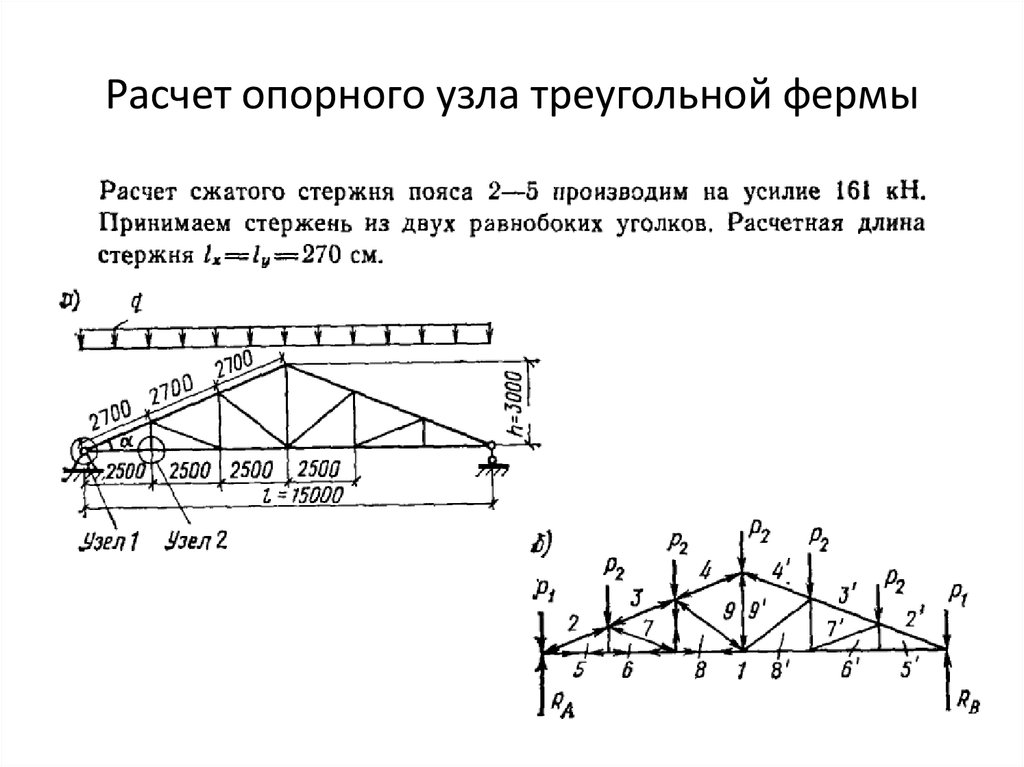 Видимость силы можно включать и выключать в окне 3D-просмотра из Общие секция панели управления справа от видового экрана.
Видимость силы можно включать и выключать в окне 3D-просмотра из Общие секция панели управления справа от видового экрана.Помимо указания точечных нагрузок на любой узел, мы также можем включать и выключать собственный вес. Это дополнительно добавит к конструкции силу собственного веса, чтобы возвращаемые результаты отражали влияние собственного веса.
Просмотр результатов 3D-калькулятора ферм
После того, как все данные будут введены, вы можете нажать кнопку РЕШИТЬ , чтобы отправить свой анализ. Ваши результаты должны быть возвращены немедленно, хотя может быть небольшая задержка, если одновременно отправляется много запросов. Когда ваша работа будет завершена и результаты будут возвращены, появится несколько разных таблиц результатов. Вы также сможете просматривать данные результатов в окне 3D-просмотра. Лучшее, что можно сделать на этом этапе, — это просто покопаться в себе и включить и выключить что-то, чтобы лучше понять, как отображаются результаты. Но я кратко расскажу о ваших вариантах ниже. Обратите внимание, что как только вы отправите задание, блок ввода данных рухнет, а не исчез. Вы можете вернуть его обратно (вместе со своими входными данными), развернув панель ввода данных.
Но я кратко расскажу о ваших вариантах ниже. Обратите внимание, что как только вы отправите задание, блок ввода данных рухнет, а не исчез. Вы можете вернуть его обратно (вместе со своими входными данными), развернув панель ввода данных.
Отчет об анализе
Первое, что нужно просмотреть, — это сводка отчета об анализе, рис. 7. Он дает общий обзор того, как прошел ваш анализ. Вы можете читать подробности построчно, но заголовок , вы должны увидеть полный список зеленых галочек . Если есть какие-то красные индикаторы ошибок, значит что-то пошло не так. Если что-то пойдет не так, вы, скорее всего, не получите отчет о результатах. Но если вы это сделаете, вы должны игнорировать их и выяснить, что могло привести к провалу вашего анализа. Это может быть связано с тем, как вы определили свою структуру.
Рис. 7. Отчет об анализе. Обратите особое внимание на пункты с 8 по 12. Проверки 8, 9 и 10 оценивают равновесие сил в направлениях x, y и z и сообщают о разнице между приложенными силами и реакциями. Теоретически это число должно быть равно нулю, хотя обычно оно очень мало из-за того, как малые числа обрабатываются в языках программирования.
Теоретически это число должно быть равно нулю, хотя обычно оно очень мало из-за того, как малые числа обрабатываются в языках программирования.
Проверка 11 вычисляет максимальное узловое отклонение как долю наибольшего межузлового расстояния в конструкции. Это дает представление о том, являются ли расчетные отклонения слишком большими. Очень большие отклонения по сравнению с масштабом конструкции предполагают, что конструкция и/или нагрузка заслуживают дальнейшего изучения, поскольку может возникнуть геометрическая нелинейность (мы подробно обсуждаем это в этом курсе). Инструментарий выдаст предупреждение, если отклонение превысит 10% от максимального межузлового расстояния, но этот предел сам по себе является произвольным. Вы должны использовать собственное инженерное суждение для оценки приемлемости прогибов.
Проверка 12 показывает, не превысили ли какие-либо элементы заданный предел текучести. Чтобы результаты калькулятора ферм были действительными, все элементы должны оставаться в пределах своего диапазона упругости. В противном случае нелинейность материала приведет к неточным результатам калькулятора. Это одна из самых простых вещей, которую легко упустить из виду при простом анализе фермы, поэтому следите за красным предупреждающим знаком.
В противном случае нелинейность материала приведет к неточным результатам калькулятора. Это одна из самых простых вещей, которую легко упустить из виду при простом анализе фермы, поэтому следите за красным предупреждающим знаком.
Табличные данные
Реакции, осевые силы и узловые смещения представлены в трех таблицах под аналитическим отчетом, рис. 8. Если вы являетесь участником DegreeTutors и вошли в систему, вы можете загрузить данные из каждой таблицы в формате файла csv . Функциональность таблицы довольно интуитивно понятна, поэтому я не буду подробно описывать здесь каждую функциональность по отдельности.
Рис. 8. Таблицы данных реакций, осевых сил и узловых перемещений.Просмотр результатов в 3D-окне
Лучший способ быстро понять, как конструкция реагирует на приложенные нагрузки, — просмотреть результаты в 3D-окне. Чтобы получить наилучший обзор 3D-окна и его функций визуализации данных, вам следует посмотреть видеоролик о начале работы. Кроме того, просто поэкспериментируйте с панелью управления справа. Вы довольно быстро разберетесь, что делает каждый переключатель и виджет, но здесь я кратко опишу функциональность.
Кроме того, просто поэкспериментируйте с панелью управления справа. Вы довольно быстро разберетесь, что делает каждый переключатель и виджет, но здесь я кратко опишу функциональность.
Осевые силы и реакции
Представление осевых сил можно включать и выключать в разделе Осевые силы панели управления. Цвет стержней указывает величину осевой силы и соответствует цветовой шкале под окном 3D-просмотра. Вы можете просмотреть элементы, окрашенные по непрерывной шкале или по двоичной шкале, которая просто указывает на растяжение (синий цвет) и сжатие (красный цвет). В разделе Axial Forces панели управления вы также можете включать и выключать метки сил.
Реакции поддержки можно включать и выключать в разделе Реакции панели управления. Включение реакций заменит опоры стрелками силы реакции, указывающими направление сил реакции. Величина указывается с аннотацией.
Рис. 9. Осевые силы и реакции в трехмерном виде.Изогнутая форма и узловые смещения
Можно включать и выключать изогнутую форму конструкции, а также аннотации, показывающие узловые смещения в направлениях x, y и z.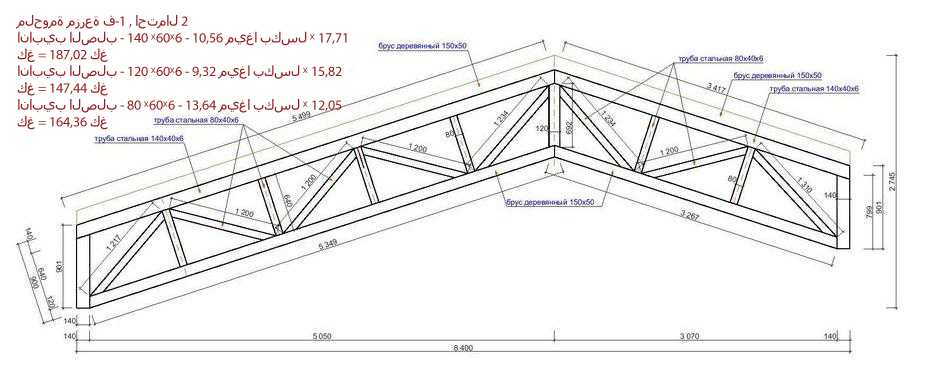 Как и аннотации осевой силы, эти метки могут быть довольно плотными, если рассматривать их по всей конструкции. Таким образом, лучше увеличить интересующую область, прежде чем включать метки. Отклонение можно масштабировать с помощью ползунка в Прогиб секции панели управления. Это облегчает определение качественной изогнутой формы, когда отклонения слишком малы, чтобы их можно было воспринять в масштабе конструкции.
Как и аннотации осевой силы, эти метки могут быть довольно плотными, если рассматривать их по всей конструкции. Таким образом, лучше увеличить интересующую область, прежде чем включать метки. Отклонение можно масштабировать с помощью ползунка в Прогиб секции панели управления. Это облегчает определение качественной изогнутой формы, когда отклонения слишком малы, чтобы их можно было воспринять в масштабе конструкции.
Завершение
Это более или менее все, что вам нужно знать, чтобы приступить к работе с этим набором инструментов для трехмерного анализа ферм. Остальные параметры на панели управления говорят сами за себя, поэтому, как я уже сказал выше, просто поэкспериментируйте с ними, и вы освоитесь. Я надеюсь, что студенты, в частности, найдут этот набор инструментов полезным для быстрого создания данных анализа трехмерных шарнирно-соединенных конструкций в рамках студенческих проектных проектов.
Как вы увидите, если вы посмотрите обучающее видео в верхней части этого поста, набор инструментов станет намного более мощным, когда вы объедините его с Blender для создания моделей конструкций.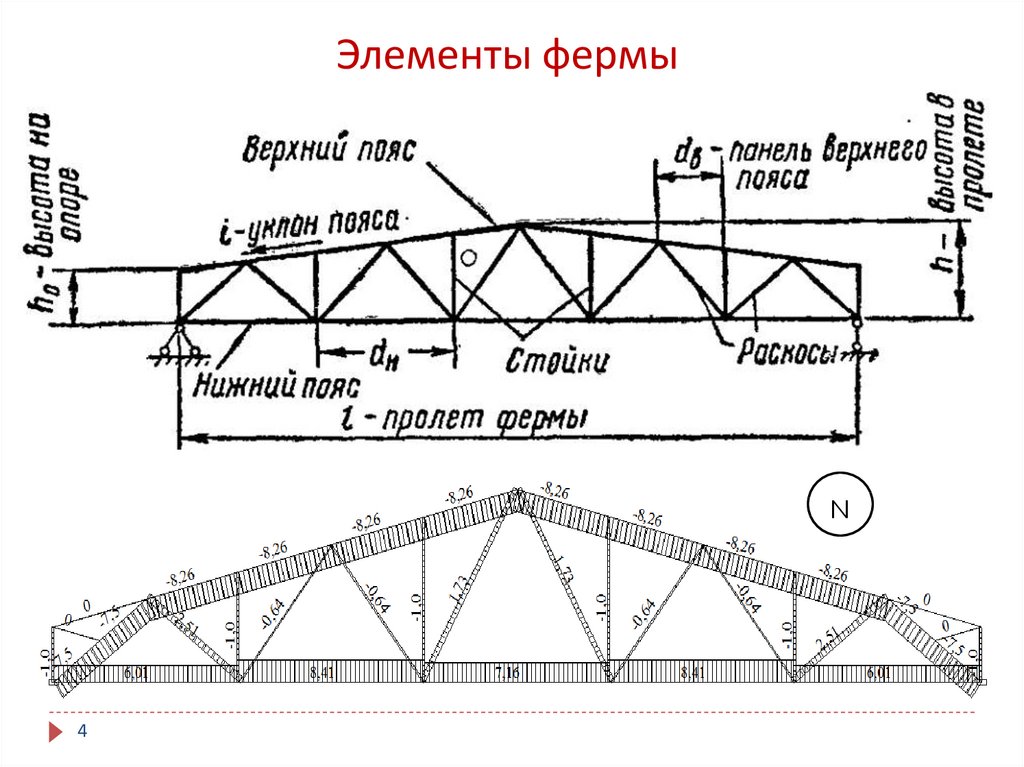 Моделируя в Blender и используя экспортированные данные для ввода в набор инструментов для анализа, вы можете быстро повторять проекты и исследовать, как различные конфигурации реагируют на нагрузку. Если вы еще не знакомы с Blender, я не могу убедить вас попробовать — вы будете поражены тем, насколько легко разрабатывать сложные трехмерные структурные модели, используя всего несколько команд.
Моделируя в Blender и используя экспортированные данные для ввода в набор инструментов для анализа, вы можете быстро повторять проекты и исследовать, как различные конфигурации реагируют на нагрузку. Если вы еще не знакомы с Blender, я не могу убедить вас попробовать — вы будете поражены тем, насколько легко разрабатывать сложные трехмерные структурные модели, используя всего несколько команд.
Пока это все. Я надеюсь, что вы найдете этот набор инструментов для анализа ферм полезным — если вы это сделаете, расскажите кому-нибудь еще, кому он также может быть полезен.
Линкедин Твиттер YouTube
Автор
Доктор Шон Кэрролл
Бакалавр искусств (с отличием), MSc, PhD, CEng MIEI, FHEA
Привет, я Шон, основатель DegreeTutors.com. Я надеюсь, что вы нашли этот урок полезным. Проработав 10 лет в качестве преподавателя в университете по проектированию конструкций, я создала DegreeTutors.com, чтобы помочь большему количеству людей понять инженерное дело и получить от его изучения такое же удовольствие, как и я.