Пример расчета металлической балки в ручную: Расчёт металлической балки онлайн (калькулятор)

Содержание

какова максимальная длина и толщина, как рассчитать (пример сбора нагрузок, определения внутренних усилий, предельного прогиба, подбора высоты и ширины, шага)?

Конструктивный раздел рабочего проекта жилого или общественного здания является важной частью комплекта технической документации.

Инженер разрабатывает комплекс решений, выполнение которых гарантирует безопасную эксплуатацию объекта.

Перед разработкой чертежей несущих элементов здания требуется провести общий и локальный расчёт каждого из них с подбором оптимальных сечений.

Проектировщики уделяют повышенное внимание конструктивным решениям перекрытий, и, при необходимости, добавляет в конструкцию балки, повышающие прочность и компенсирующие прогибы конструкции.

О расчете балок перекрытия поговорим в статье.

Содержание

1 Для чего требуется?
2 Исходные данные
3 Как рассчитать?
- 3.1 Сбор нагрузок
- 3.2 Определение внутренних усилий
- 3.3 Подбор высоты и ширины
- 3. 4 Подбор шага
- 3.5 Определение предельного прогиба
4 Классические ошибки
5 Заключение

Для чего требуется?

Балки перекрытия – это горизонтальные линейные несущие элементы здания, расположенные в пролёте между вертикальными конструкциями. Работают на изгиб под действием постоянных и временных нагрузок.

Расчёт балок перекрытия является неотъемлемым этапом разработки раздела проекта «Конструктивные решения», и он выполняется по следующим причинам:

Подбор оптимального поперечного сечения элемента, воспринимающего внутренние усилия, которые образуются под действием внешних сил.
Определение шага балок и их количества, исходя из условий предельного равновесия перекрытия и объёмно-планировочных ограничений помещения.
В случае конструирования железобетонного перекрытия – определение минимального процента армирования в зонах повышенных напряжений, в соответствии со значениями эпюр момента и поперечной силы.
Назначение минимального запаса прочности и устойчивости в случае непредвиденного увеличения эксплуатационных нагрузок.

При корректном расчёте балочных конструкций, по завершении монтажных работ и приложения всех расчётных нагрузок, перекрытие не разрушается, а его деформации остаются в пределах нормативных значений.

Исходные данные

Расчёт балок проводится в два этапа – определение внутренних усилий в стержневом элементе и подбор сечений конструкции для последующего конструирования. Для выполнения первой части расчёта потребуются следующие исходные данные:

длина пролёта, вдоль которого располагается стержневой элемент;
характер опирания балки на вертикальную конструкцию – шарнирное, либо жёсткое защемление;
вес вышележащих конструкций перекрытия и полов – постоянные нагрузки;
временная нагрузка, равномерно распределённая по площади, принимаемая по СНиП, исходя из эксплуатационных характеристик помещения;

штамповые нагрузки, при наличии технологических особенностей при эксплуатации.

Когда усилия известны, инженер начинает подбор ширины и высоты, а, при необходимости, конструирование элемента. Для этого также потребуются некоторые данные:

материал стержневого элемента – как правило, железобетон, металлический профиль или деревянный брус;
архитектурные ограничения, например, предельная высота балки;
жёсткость материала – класс железобетона, марка стали, порода дерева и т. д.;
дополнительные ограничения, связанные с особенностями эксплуатации здания – наличие инженерных коммуникаций под потолком.

Подбор сечения сводится к назначению его габаритов в произвольном порядке с последующей проверкой условий прочности и устойчивости.

Как рассчитать?

Все балки перекрытий, вне зависимости от их количества, материала, высоты и условий работы, рассчитываются в строгом соответствии с определённым алгоритмом.

Сбор нагрузок

Большинство нагрузок, прикладываемых к перекрытию, являются равномерно распределёнными по площади, и их необходимо привести к линейным значениям.

Чтобы собрать все нагрузки на балку, необходимо выполнить следующие шаги:

Определить величину промежуточного пролёта между стержнями.
Выделить в перекрытии расчётную полосу. Ширина этого гипотетического элемента составляет ½ пролёта между стержневыми элементами, отложенную в каждую сторону от центральной оси рассматриваемой балки.
Вычислить массу расчётной полосы перекрытия, путём умножения её объёма на плотность материала.
Таким же образом определить загружение от веса полов.
Привести временную эксплуатационную нагрузку из распределённой по площади на стержневой элемент.
Добавить особые штамповые, либо точечные загружения при наличии специальных условий эксплуатации.

Если речь идёт о плите покрытия, то в качестве временной нагрузки принимается нормативный вес снегового покрова для конкретного региона страны. Например, в Москве этот показатель составляет 180 кг/м2.

Пример: если стержни уложены в пролёте 6 м, а расстояние между ними составляет 2 м, перекрытие – монолитная железобетонная плита толщиной 180 мм, вес полов 150 кг/м2, а временная нагрузка в жилом здании – 100 кг/м2, на стержневой элемент собираются следующие загружения:

масса участка плиты: 6 м х 2 м х 0,18 м х 2500 кг/м3 (r – плотность железобетона) = 5400 кг;
масса полов: 150 кг/м2 х 6 м х 2 м = 1800 кг;
временная нагрузка: 100 кг/м2 х 6 м х 2 м = 1200 кг;
суммарная нагрузка на деталь составит: 5400 кг + 1800 кг + 1200 кг = 8400 кг;
учитывая, что стержневой элемент имеет длину 6 м, то прикладываемая равномерно распределённая нагрузка q = 8400 кг / 6 м = 1400 кг/м, или 14 кН/м.

В зависимости от условий работы, назначается повышающий коэффициент, принимаемый по СНиП – от 1,05 до 1,2.

Определение внутренних усилий

Когда известны все нагрузки, длина и характер защемления, проектировщик определяет внутренние усилия в стержневом элементе:

Изгибающий момент, являющийся основной характеристикой изгибаемого элемента, определяется по формуле M = ql2 / 8, при стандартном опирании детали на вертикальные опоры. l – длина пролёта. Таким образом, M = 14 кН/м * 62 / 8 = 63 кН*м. Максимальное значение момента оказывается в центре полёта.
Поперечное усилие Q, называется также перерезывающей силой, которая имеет предельную величину около опор. Q = ql / 2 = 14 кН/м * 6 / 2 = 42 кН.

Исходя из полученных значений, инженер строит 2 эпюры с графическим отображением данных усилий.

Подбор высоты и ширины

Определив значения внутренних усилий и владея информацией о материале конструкции, инженер начинает подбор поперечного сечения.

Исходя из объёмно-планировочных показателей и опыта в проектировании, инженер самостоятельно назначает предварительное сечение, например, h = 45 cм, b = 20 cм, где h – высота, b – ширина.

Высота железобетонной балки складывается из двух величин: h = h0 + a, где h0 – рабочая высота от центра растянутой арматуры в нижней зоне до верхней кромки, а – величина защитного слоя бетона от грани арматуры до низа элемента + 1/2 диаметра рабочего стержня. Принимая a = 5 см, можно определить h0 = 45 см – 5 см = 40 см.

Далее проверяются условия равновесия по двум формулам: Rs As = Rbbx и M = Rbbx (h0 – x/2), где Rs и Rb – расчётные сопротивления арматуры и бетона, соответственно, зависящие от классов материалов, х – высота сжатой зоны бетона. Чаще всего, в конструкцию закладывают арматурную сталь А500s, а бетон для перекрытий принимается класса В25. Таким образом, в соответствии со СНиП, Rs = 43,5 кН/см2, а Rb = 1,45 кН/см2.

Высота сжатой зоны составляет х = Rs Аs / gb1 Rbb, где As – площадь рабочей арматуры, gb1 – коэффициент условий работы бетона, принимаемый в стандартных конструкциях 0,9.

Площадь рабочей арматуры Аs = gb1Rbbeh0/Rs, где e – относительная высота сжатой зоны бетона, определяемая по формуле e = (1 – (1 – 2am)1/2), а безразмерная величина am = M / (gb1 Rbbh02) = 6300 кНсм / (0,9 * 1,45 * 20 * 1600) = 0,15. e = (1 – (1 – 2 * 0,15) 1/2) = 1 – 0,837 = 0,163. Таким образом, в конкретно взятом примере, Аs = 0,9 * 1,45 * 20 * 0,163 * 40 /43,5 = 3,91 см2.

По факту принимается арматура большего сечения, чем показал расчёт. 2d16 имеют площадь 4,02 см2. Высота сжатой зоны, исходя из 1 условия предельного равновесия, составит х = 43,5 * 4,02 / (0,9 * 1,45 * 20) = 6,7 см.

Предельно допустимый момент, который может воспринять сечение, выводится из 2 условия предельного равновесия и составляет M = gb1 Rbbx(h0 – x/2) = 0,9 * 1,45 * 20 * 6,7 * (40 – 6,7/2) = 6409 кНсм < M = 6300 кНсм. В данном примере условие прочности полностью выполняется.

Если прочность и устойчивость конструкции не обеспечивается, проектировщик должен вернуться к началу алгоритма и назначить другие габариты сечения, а затем провести проверку ещё раз.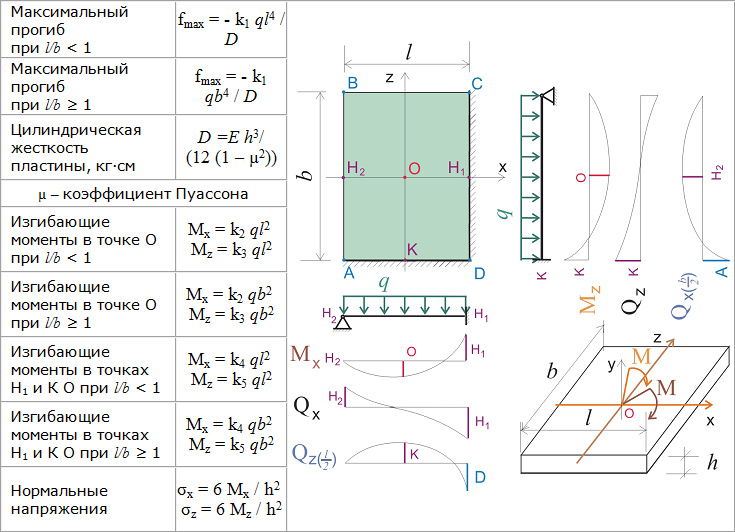

Подбор шага

Если высота и ширина подобраны верно, необходимо определить количество элементов в перекрытии, которое зависит от следующих критериев:

Объёмно-планировочные решения помещения.
Если подобранное сечение детали, удовлетворяющее условиям прочности и устойчивости, значительно сокращает высоту комнаты в чистоте, то проектировщику придётся уменьшать сечение, добавляя количество деталей с более частым шагом.
Шаг и количество балок должны быть подобраны таким образом, чтобы свободный пролёт плиты между ними обеспечивал условиям предельного равновесия. Для расчёта конструктивного элемента необходимо принять расчётную полосу шириной 1 м, собрать на неё нагрузки и полностью повторить алгоритм.

При корректно подобранном шаге, удовлетворяющим условиям равновесия, эксплуатации перекрытия обеспечит полную безопасность людей, пребывающих в здании.

Определение предельного прогиба

Помимо прочности, балочная система должна отвечать условиям предельных деформаций.

Если линейный элемент имеет вертикальные перемещения под действием суммарной нагрузки, не превышающие нормативных значений, то сечение подобрано верно.

Алгоритм выглядит следующим образом:

Определяется фактический прогиб конструкции по формуле f = 5/384 * qnl4/EI, где qn – суммарная нагрузка, l – величина пролёта, Е – модуль упругости материала, принимаемый по таблице СНиП (для бетона класса В25 он составляет 30000 кгс/см2), I – момент инерции сечения.
I – это переменная величина, которая зависит от формы сечения. В случае, с прямоугольником I = bh4/12, а в конкретном примере I = 20 * 91125 / 12 = 151875 см4.
Реальный прогиб составит f = 5/384 * 6300 * 6004 / 30000 * 151875 = 2,3 см.
Полученное значение сравнивается с предельно допустимой нормативной величиной, которая для стандартных стержней в жилых и общественных зданиях составляет 1/250l, а в случае пролёта 6 м = 600 см, 1/1250 *600 = 2,4 см. То есть, конструкция удовлетворяет условиям предельных деформаций.

В случае, когда данное условие не выполняется, проектировщику необходимо принимать другой класс бетона, уменьшать шаг или изменять габариты сечения.

Классические ошибки

Инженеры, не имеющие должного опыта, часто допускают некоторые ошибки при расчёте балок, а именно:

Слишком малое сечение, даже если оно и проходит по условиям прочности, может прогнуться больше нормативных значений, из-за чего перекрытие перестанет удовлетворять эксплуатационным требованиям.
Наоборот, слишком большое сечение приведёт к перерасходу материалов и повышенным затратам при строительстве.

Неверно выбранное защемление балки повлияет на результат расчёта.
При расчёте необходимо приводить все единицы к единому модулю, а, в противном случае, результат окажется далёким от истины.

Чтобы не совершать типичные ошибки, следует выполнять расчёт в соответствии с алгоритмом и фиксировать все промежуточные результаты. После выполнения расчёта следует несколько раз проверить результат. Если возникают сомнения, лучше сравнить подобранное сечение балки с аналогичными примерами.

Заключение

Расчёт балок перекрытия – кропотливый процесс, требующий повышенного внимания, знаний формул и алгоритма. Перед началом выполнения чертежа нужно определить 4 главных параметра – нагрузки на балку, оптимальное сечение элемента, шаг стержней в перекрытии и фактический прогиб конструкции.

стальных балок-примеры-расчета — Google

AlleBilderVideosNewsMapsShoppingBücher

suchoptionen

= wl ² /8 = 20 x 90 0 2 .
= wl/2 = 20 x 6 / 2 = 60 кН.
b/T = 100 / 16 = 6,25 < 9ε = 9 – Фланец пластиковый.
d/t = 428 / 10 = 42,8 < 80ε = 80 – Сеть пластиковая.
Следовательно, секция пластиковая.
λ _LT = uvλ√(β _w ) = 0,9 х 0,919 х 138,568 х √(1) = 114,6.
Из таблицы 16 для λ _LT = 114,6 ; P _B = 102 Н/мм ²

Стальной дизайн луча. — Steel Beam Calculator

www.steelbeamcalculator.co.uk › en-gb › eurocode

3 Пример третий. Расчет стальных балок для стальных балок, поддерживающих наружную полую стену. Созданные калькулятором отчеты показывают изгиб, …

Расчет конструкции стальной балки для начинающих — инженер-строитель

www.youtube.com › смотреть

23.11.2020 · Пример простой конструкции стальной балки, выполненной в качестве практики инженерия. Причина, по которой я не…
Дауэр: 10:36
Прислан: 23.11.2020

Как сделать расчет стальной балки — YouTube

www.youtube.com › смотрите

05.08.2021 · Если вам понравилось видео, почему бы вам не купить нам кофе https://www.buymeacoffee.com/SECalcsIn …
Дауэр: 11:32
Прислан: 05.08.2021

Ähnliche Fragen

Как рассчитать сталь для балок?

Как рассчитать необходимый размер балки?

Как рассчитать балки?

Как рассчитать прочность балки?

Как сделать расчет стальной балки — Часть 1 — Нагрузки — YouTube

www. youtube.com. Конструкция стальной балки Пошаговое объяснение с примерами…

www.youtube.com › смотреть

22.11.2017 · http://www.theopeneducator.com/https://www.youtube.com/theopeneducator.
Dauer: 11:13
Прислан: 22.11.2017

Проектирование стальных балок – пошаговое руководство – Основы конструкций

www.structuralbasics.com › Steel-beam-design

Расчет характеристических нагрузок, действующих на балку · Комбинации нагрузок · Определение свойств стальной балки · Классификация поперечного сечения · Проверка на изгиб …

[PDF] Steel-Beam-Calculation-Example-Report.pdf

beamcalc.co.uk › wp-content › uploads › 2019/07 › Steel-Beam-Calc…

31.07.2019 · при заказе балок. Вся конструкционная сталь, указанная в наших таблицах расчетов, относится к классу S355, если не указано иное в расчетах.

Пример проектирования стальных балок в соответствии с Еврокодом 3 — Structville

structville. com › Балки

14.02.2020 · Пример проектирования стальных балок в соответствии с Еврокодом 3 · Введение сечение балки, подверженное …

Решенный пример расчета стальных балок согласно BS 5950 — 1

structville.com › Стальные конструкции

16.02.2020 · Универсальные секции балок обычно используются в зданиях для несущей нагрузки. Нагрузки на балки могут включать нагрузку от перекрытия, стен, здания …

Ähnlichesuchanfragen

Расчет стальной балки Рабочий пример

Расчет стальной балки пример PDF

Формула расчета балки

Расчет стальной конструкции PDF Пример проекта

Стальная балка какого размера для поддержки балок перекрытия

Конструкционная открытая стальная балка и колонна Уравнения для анализа пер. Руководство ASIC 9-го издания

Уравнения для расчета открытой стальной балки и колонны пер. ASIC 9 -е издание Руководство

Правила и калькуляторов пучка

Площадь момента инерционных уравнений и калькуляторов

Открытый калькулятор:
Стальные и колонны.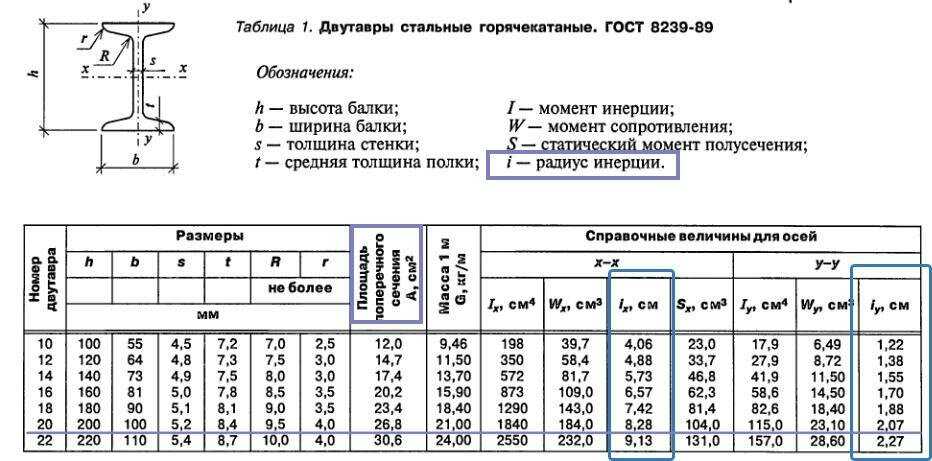

Калькулятор определит нагрузку на колонну и приложенное напряжение для широких, узких и других профилей полки AISC.
«P» — осевая нагрузка, приложенная к элементу, которая может быть как сжимающей, так и растягивающей.
Условные обозначения: + = сжатие, — = растяжение
«Mx» — изгибающий момент, приложенный относительно оси X (большой оси) элемента.
Примечание: ввод значения ДОЛЖЕН БЫТЬ положительным (+).
«My» — приложенный изгибающий момент относительно оси Y (малой оси) стержня.
Примечание: ввод значения ДОЛЖЕН БЫТЬ положительным (+).
«Kx» — коэффициент эффективной длины относительно оси X (большой оси) для сжимаемого элемента, нагруженного в осевом направлении. Типичные значения следующие:
Конечные условия столбца Значение «Kx»
(снизу вверх) (рекомендуется)
Фиксированный-Фиксированный 0,65
Фиксированный-Фиксированный 0,80
Фиксированный-Подвижный 1,2
Закрепленный-Закрепленный 1,0
Закрепленный-Свободный 2,004
Закрепленный-Подвижный 9. 0 где:
Фиксированный конец обозначает фиксированное вращение и фиксированное смещение.
Закрепленный конец означает отсутствие вращения и фиксированное смещение.
Конец ползунка обозначает фиксированное вращение и свободное перемещение.
Свободный конец означает свободное вращение и перемещение.
«Ky» — коэффициент эффективной длины относительно оси Y (малой оси) для сжимаемого элемента, нагруженного в осевом направлении. Типичные значения следующие:
Конечные условия столбца Значение «Ky»
(снизу вверх) (рекомендуется)
Фиксированный-Фиксированный 0,65
Фиксированный-Фиксированный 0,80
Фиксированный-Подвижный 1,2
Закрепленный-Закрепленный 1,0
Закрепленный-Свободный 2,00 4
Закрепленный-Подвижный где:
Фиксированный конец обозначает фиксированное вращение и фиксированное смещение.
Закрепленный конец означает отсутствие вращения и фиксированное смещение.
Конец ползунка обозначает фиксированное вращение и свободное перемещение.
Свободный конец означает свободное вращение и перемещение.
‘Lx’ — фактическая длина элемента без раскосов для потери устойчивости колонного типа (осевое сжатие) вокруг оси X (большой оси).
Примечание: для входных значений Lx <=1,0' эта программа
будет использовать значение =1,0′.
‘Ly’ — фактическая длина элемента без связей для потери устойчивости столбчатого типа (осевое сжатие) вокруг оси Y (малой оси).
Примечание: для входных значений Ly <=1,0' эта программа
будет использовать значение =1,0′.
«Lb» — фактическая длина полки элемента без раскрепления для изгиба по оси X
(большая ось). «Свободная длина» может быть более конкретно определена как расстояние между поперечными сечениями, закрепленными против скручивания или бокового смещения сжимаемой полки.
Примечания:
1. В большинстве случаев «Lb» равно «Ly».
2. Для консолей, раскрепленных от скручивания только
на опоре, ‘Lb’ можно условно принять за фактическую длину
. 2 <= 2,3
где:
Mx1 = меньший изгибающий момент по оси X (большая ось) на любом из концов свободной длины
Mx2 = больший изгибающий момент по оси X (большая ось) на любом из концов свободной длины
Mx1/ Mx2 = положительный для изгиба с обратной кривизной (оба имеют одинаковые знаки)
= отрицательный для изгиба с одинарной кривизной (оба имеют противоположные знаки)
Примечания:
1. Когда изгибающий момент в любой точке в пределах свободной длины больше, чем в обоих
концы этой длины, затем используйте ‘Cb’ = 1,0.
2. При вычислении Fbx для использования в AISC Eqn. h2-1:
а. Для кадров с боковым смещением (совместное перемещение) вычислите «Cb», используя приведенное выше уравнение.
б. Для рам без бокового смещения (укрепленных против совместного перемещения) используйте ‘Cb’ = 1,0.
3. Для консольных балок ‘Cb’ можно условно принять равным 1,0.
«Cmx» — это коэффициент, применяемый к члену изгиба оси X (большая ось) в уравнении взаимодействия (h2-1) и зависящий от кривизны колонны, вызванной приложенными моментами. Значение коэффициента ‘Cmx’ определяется следующим образом:
Категория A:
Для сжатых элементов в рамах, подверженных совместному перемещению (боковому перемещению), Cmx = 0,85.
Категория B:
Для сжимаемых элементов, стесненных вращением, в рамах, раскрепленных поступательным движением шарнира
(без бокового смещения) и не подвергающихся поперечной нагрузке между их опорами
в плоскости изгиба, Cmx =0,6-0,4*(Mx1/Mx2)
, где :
Mx1 = меньший изгибающий момент по оси X (большая ось) на любом из концов свободной длины
Mx2 = больший изгибающий момент по оси X (большая ось) на любом из концов свободной длины
Mx1/Mx2 = положительное значение для изгиба с обратной кривизной (оба имеют одинаковые знаки)
= отрицательное значение для изгиба с одинарным изгибом (оба имеют противоположные знаки) и с учетом поперечной нагрузки между их опорами
в плоскости изгиба допускаются следующие значения Cmx:
1. Для элементов, концы которых закреплены от вращения в плоскости изгиба, Cmx = 0,85.
2. Для элементов, концы которых не закреплены от поворота в плоскости изгиба, Cmx = 1,0.
«Cmy» — это коэффициент, применяемый к члену изгиба по оси Y (малой оси) в уравнении взаимодействия (h2-1) и зависящий от кривизны колонны, вызванной приложенными моментами. Значение коэффициента «Cmy» определяется следующим образом:
Категория A:
Для сжатых элементов в рамах, подлежащих совместному переносу (боковому перемещению), Cmy = 0,85.
Категория B:
Для сжимаемых элементов с ограничением вращения в рамах, закрепленных на стыке
поступательное движение (без бокового смещения) и не подвергающееся поперечной нагрузке между их опорами
в плоскости изгиба, Cmy =0,6-0,4*(My1/My2)
где:
My1 = меньший изгибающий момент по оси Y (малая ось) при любой из концов незакрепленного участка
My2 = большая ось Y (малая ось) изгибающий момент на любом из концов незакрепленного участка
My1/My2 = положительный для изгиба с обратной кривизной (оба имеют одинаковые знаки)
= отрицательный для одиночный изгиб кривизны (оба имеют противоположные знаки)
Категория C:
Для деформируемых на сжатие элементов в рамах, закрепленных на соединении
поступательного движения (без бокового смещения) и подвергающихся поперечной нагрузке между их опорами
в плоскости изгиба, допускаются следующие значения «Cmy»:
1. Для элементы, концы которых защемлены от поворота в плоскости изгиба, Cmy = 0,85.
2. Для элементов, концы которых не закреплены от поворота в плоскости изгиба, Cmy = 1,0.
«ASIF» — это коэффициент увеличения допустимого напряжения, который применяется ко всем допустимым напряжениям и напряжениям потери устойчивости столбца Эйлера, используемым при расчете коэффициента напряжения.
Примечание: например, значение 1,333 может использоваться для
«ASIF» для комбинаций нагрузок, включающих ветровую или сейсмическую нагрузку.
В противном случае используйте 1.0.
коэффициент гибкости элементов, подвергающихся осевой сжимающей нагрузке.
Примечание: «Lx» преобразуется из футов в
дюймы при вычислении выражения.
Выражение «Ky*Ly/ry» представляет собой эффективный коэффициент гибкости для элементов, подвергающихся осевой сжимающей нагрузке.
Примечание: «Ly» преобразуется из футов в дюймы за 92*E/Fy)
где:
E = модуль упругости для стали = 29 000 тысяч фунтов на квадратный дюйм
‘fa’ — фактическое напряжение сжатия для сжимаемого элемента с осевой нагрузкой, которое рассчитывается следующим образом:
fa = P/A
‘ft’ — допустимое растягивающее напряжение для нагруженного в осевом направлении элемента, рассчитываемое следующим образом:
ft = P/A
‘Fa’ — допустимое напряжение сжатия для сжимающего элемента, нагруженного в осевом направлении, и рассчитывается следующим образом:
Для: K*L*12/r <= Cc = SQRT(2*p^2*E/Fy) 92)
Примечание: большее значение Kx*Lx*12/rx или Ky*Ly*12/ry должно использоваться в приведенных выше уравнениях
для определения «Fa».
«Ft» — допустимое напряжение растяжения для аксиально нагруженного растянутого элемента и рассчитывается следующим образом:
Ft = 0,60*Fy рассчитывается следующим образом:
Па = Fa*A
«S.R.» — коэффициент напряжения для элемента, который рассчитывается следующим образом:
Для элементов с комбинированным осевым сжатием и изгибом, когда fa/Fa > 0,15 по уравнению. h2-1:
С.Р. = fa/(ASIF*Fa) + Cmx*fbx/((1-fa/(ASIF*F’ex))*(ASIF*Fbx)) + Cmy*fby/((1-fa/(ASIF*F’ ey))*(ASIF*Fby)) <= 1,0
и по уравнению. h2-2:
С.Р. = fa/(ASIF*0,60*Fy) + fbx/(ASIF*Fbx) + fby/(ASIF*Fby) <= 1,0
h2-1 или уравнение h2-2
Для элементов с комбинированным осевым сжатием и изгибом, когда fa/Fa <= 0,15 по уравнению. h2-3:
СР = fa/(ASIF*Fa) + fbx/(ASIF*Fbx) + fby/(ASIF*Fby) <= 1,0
Для элементов с комбинированным осевым растяжением и изгибом:
S.R. = ft/(ASIF*Ft) + fbx/(ASIF*Fbx) + fby/(ASIF*Fby) <= 1,0
Примечание: в этом случае необходимо также проверить коэффициент напряжения, рассчитанный только из сжимающего напряжения изгиба. .
‘Lc’ — максимальная длина сжатой полки без связей, при которой допустимое напряжение изгиба по оси X (большая ось) может приниматься равным 0,66*Fy, или по формуле кода AISC. F1-3, если применимо.
Lc = меньше из: 76*bf/SQRT(Fy) или 20000/((d/Af)*Fy) оси) напряжение изгиба может быть принято равным 0,60*Fy, когда Cb = 1.
Значение ‘Lb’ преобразуется при оценке из
футов в дюймы.
fbx = Mx*12/Sx
«Fbx» — допустимое напряжение изгиба по оси X (большая ось), которое рассчитывается следующим образом:
Для сжатия или растяжения вследствие изгиба
, когда bf/(2*tf) <= 65/SQRT(Fy) и d/tw соблюдены компактные критерии,
и Lb <= Lc:
Fbx = 0,66*Fy (уравнение F1-1)
, когда 65 /SQRT(Fy) < bf/(2*tf) <= 95/SQRT(Fy)
и Lb <= Lc:
Fbx = Fy*(0,79-0,002*bf/(2*tf)*SQRT(Fy) ) (Уравнение F1-3)
, когда bf/(2*tf) > 95/SQRT(Fy) и Lb <= Lc:
Fbx = 0,60*Fy (Уравнение F1-5)
Для растяжения из-за изгиба,
, когда критерий компактности не соблюдается,
Fbx = 0,60*Fy
Для сжатия из-за изгиба, а элемент компактен или не
2) <= 0,60*Fy (уравнение F1-7)
и для ЛЮБОГО значения Lb*12/rt:
Fbx = 12000*Cb/(Lb*12*d/Af) <= 0,60*Fy (уравнение.