Пример расчета стропильной фермы — Подбор сечений элементов ферм — Фермы
Пример. Расчет стропильной фермы. Требуется рассчитать и подобрать сечения элементов стропильной фермы промышленного здания. На ферме посередине пролета расположен фонарь высотой 4 м.
Пролет фермы L = 24 м; расстояние между фермами b = 6 м; панель фермы d = 3 м. Кровля теплая по крупнопанельным железобетонным плитам размером 6 X 1,6 м. Снеговой район III. Материал фермы сталь марки Ст. 3. Коэффициент условий работы для сжатых элементов фермы m = 0,95, для растянутых m = 1.
1) Расчетные нагрузки. Определение расчетных нагрузок приведено в таблице.
Таблица Определение расчетных нагрузок.
Таблица Расчет узловых нагрузок.
Собственный вес стальных конструкций ориентировочно принят в соответствии с таблицей Ориентировочные веса стального каркаса промышленных зданий в кг на 1м2 здания: фермы — 25 кг/м2, фонарь — 10 кг/м2, связи — 2 кг/м2.
Снеговая нагрузка для III района 100 кг/м2; нагрузка от снега вне фонаря вследствие возможных заносов принята с коэффициентом с = 1,4 (смотрите Требования, предъявляемые к стальным конструкциям).
Суммарная расчетная равномерно распределенная нагрузка:
на фонаре q1 = 350 + 140 = 490 кг/м2;
на ферме q2 = 350 + 200 = 550 кг/м2.
2) Узловые нагрузки. Вычисление узловых нагрузок приведено в таблице.
Узловые нагрузки Р1, Р2, Р3 и Р4 получены как произведение из равномерно распределенной нагрузки на соответствующие грузовые площади. К нагрузке Р3 добавлена нагрузка G1 складывающаяся из веса бортовой плитки 135 кг/м и веса остекленных поверхностей фонаря высотой 3 м, принимаемого равным 35 кг/м2.
Местная нагрузка Рм, показанная пунктиром на фигуре, возникает вследствие опирания железобетонных плит шириной 1,5 м в середине панели и вызывает изгиб верхнего пояса. Ее величина уже учтена при вычислении узловых нагрузок Р 1 — Р4.
К примеру расчета стропильной фермы
3) Определение усилий. Определение усилий в элементах фермы производим графическим путем, строя диаграмму Кремоны-Максвелла. Найденные величины расчетных усилий записываем в таблице. Верхний пояс подвергается, кроме сжатия, также и местному изгибу.
Таблица Даннные для расчета.
Примечание. Расчетные напряжения в сжатых элементах фермы определены с учетом коэффициента условий работы (m — 0,95) с целью сопоставления во всех случаях с расчетным сопротивлением.
Момент от местной нагрузки равен (смотрите Определение усилий в элементах ферм):
в первой панели
во второй панели
4) Подбор сечений. Подбор сечений начинаем с самого нагруженного элемента верхнего пояса, имеющего N = — 68,4 т и М2 = 3,3 тм. Намечаем сечение из двух равнобоких уголков 150 X 14, для которого по таблицам сортамента находим геометрические характеристики: F = 2 * 40,4 = 80,8 см
Гибкость: λх = lx/rx = 300/4,6 = 65; λy = 150/6,6 = 23. По табл. 1 приложения II находим: φх = 0,83; φу = 0,96. Эксцентриситет е = 330mсм/68,4m = 4,84см. Расчетный эксцентриситет (смотрите формулу (18.II))
Здесь коэффициент η = 1,3 взят по табл. 4 приложения II. Так как е1 < 4, то проверку сечения производим по формуле (17. II), определив предварительно φвн по табл. 2 приложения II в зависимости от e1 = 1,4 и = 65 (интерполяцией между четырьмя ближайшими значениями е 1 и λ): φвн = 0,45.
Проверка напряжения
Проверку напряжения в плоскости, перпендикулярной плоскости действия момента, производим но формуле (28.VIII), для чего предварительно определяем коэффициент с по формуле (29.VIII)
Напряжение
Производим для подобранного сечения проверку элемента верхнего пояса В4. Усилие в элементе N = — 72,5 т, изгибающий момент отсутствует. Сечение из двух уголков 150 X 14. Гибкость
Коэффициенты: φх = 0,83; φу= 0,68.
Напряжение
Сохраняем принятое сечение пояса по конструктивным соображениям. Первая панель верхнего пояса подвергается только местному изгибу, вследствие чего сечение ее не должно определять выбора профилей уголков пояса, предназначенных в основном для работы на сжатие.
Поэтому, оставляя в первой панели те же два уголка 150 X 14, усилием их вертикальным листом 200 X 12, расположенным между уголками, и проверяем полученное сечение на изгиб.
Определяем положение центра тяжести сечения:
где z0 и zл — расстояния до центров тяжести уголков и листа от верхней, кромки уголков;
Момент инерции
Момент сопротивления
Наибольшее растягивающее напряжение
Расчетные данные подобранного сечения верхнего пояса вписываем в таблице выше.
Далее подбираем сечение нижнего пояса из уголков 130 X 90 X 8 и определяем расчетное напряжение
После этого устанавливаем минимальные уголки для средних наименее нагруженных раскосов; для сжатого элемента Д3 эти уголки определяются требованиями предельной гибкости (для раскосов λпр = 150, смотрите таблицу Предельная гибкость λ сжатых и растянутых элементов).
Для этого находим необходимые минимальные радиусы инерции (учитывая, что l x = 0,8l):
Равнобокие уголки, наиболее соответствующие полученным радиусам инерции, определяем по табл. 1 приложения III. Можно также использовать, данные табл. 32 для равнобоких уголков:
Этим данным наиболее близко отвечают уголки 75 X 6, имеющие rx = 2,31 см и ry — 3,52 см.
Соответственные значения гибкости будут равны:
Эти уголки и приняты для средних раскосов фермы и занесены в таблице выше. Хотя раскос Д4 растянут, но, как указывалось выше, в результате возможной несимметричной нагрузки средние раскосы могут испытывать незначительное сжатие, т. е. изменить знак усилия. Поэтому они всегда проверяются на предельную гибкость.
Первый раскос имеет большое усилие, но меньше, чем нижний пояс; однако вследствие того, что он сжат, профиль нижнего пояса из уголков 130 X 90 X 8 для него недостаточен. Приходится вводить еще один, четвертый, профиль — уголок 150 X 100 X 10.
Наконец, для растянутого раскоса Д2 получаются уголки 65 X 6. Эти же уголки используем для стоек (чтобы не вводить нового профиля). Проверка напряжений, приведенная в таблице выше, показывает, что отсутствуют как перенапряжения в элементах ферм, так и превышения предельных гибкостей.
«Проектирование стальных конструкций»,
К.К.Муханов
При подборе сечений элементов ферм необходимо стремиться к возможно меньшему числу различных номеров и калибров уголковых профилей в целях упрощения прокатки и удешевления транспортировки металла (поскольку прокатка на заводах специализирована по профилям). Обычно удается рационально подобрать сечения элементов стропильных ферм, применяя уголки в пределах 5 — 6 различных калибров сортамента. Подбор сечений начинается со сжатого…
В критическом состоянии потеря устойчивости сжатого стержня возможна в любом направлении. Рассмотрим два главных направления — в плоскости фермы и из плоскости фермы. Возможная деформация верхнего пояса фермы при потере устойчивости в плоскости фермы может произойти так, как показано на фигуре, а, т. е. между узлами фермы. Такая форма деформации соответствует основному случаю продольного изгиба…Выбор типа уголков для верхнего сжатого пояса стропильных ферм производится с учетом минимального расхода металла, обеспечения равноустойчивости пояса во всех направлениях, а также создания необходимой для удобства транспортировки и монтажа жесткости из плоскости фермы. Так как расчетные длины пояса в плоскости и из плоскости фермы во многих случаях значительно отличаются друг от друга (lу =…
3.19. Пример расчета статически определимой фермы
Определить усилия во всех стержнях статически определимой фермы (рис. 3.72):
Рис. 3.72
1). Кинематический анализ:
А. W=З×D−З×П−2×Ш− С =3×13−3×0−2×18−3=0,
Система может быть неизменяемой;
Б. Структурный анализ:
Очевидно, что мы имеем дело с неизменяемой системой (см. табл.2.1).
2). Определение опорных реакций:
m1 = Р1×3 + Р2× 4 + Р3×6 + Р4×8 + Р5×12 − y8× 16 = 0;
откуда y8 = 56 кН.
m8 = y1×16 + Р1× 3 − Р2×4 + Р3×6 − Р4×8 − P5×4 = 0;
откуда y1=3.44 кН.
xi = x 1+ Р1 + Р3= 0; откуда x1=− Р1 − Р3= −4 кН.
Проверка:
yi = 3.44 −Р2 − Р4− P5 + 7.56 = 0.
3). Определение усилий во всех стержнях:
Отметим нулевые стержни (2-3) и (7-6): N2-3= 0, N7-6 =0.
Для определения усилий в остальных стержнях воспользуемся методом вырезания узлов. Отметим, что начинать следует с узлов, в которых сходятся не более двух стержней с неизвестными усилиями.
Узел 1:
Рис. 3.73
Далее переходим к узлу 2:
Рис. 3.74
Затем имеем возможность рассмотреть узел 3:
(ось перпендикулярна направлению 1−3−5)
Рис. 3.75
Таким образом могут быть определены усилия во всех стержнях фермы. Окончательные результаты расчета изображены на рис. 3.76.
Рис. 3.76
Выборочная проверка правильности определения усилий заключается в рассмотрении того узла, равновесие которого не было использовано при определении усилий (например узел 4):
Рис. 3.77
3.20. Расчет ферм на внеузловую нагрузку
При возведении покрытия на практике иногда невозможно избежать внеузлового нагружения фермы (например при недостатке или отсутствии плит с шириной, равной длине панели фермы и т.п.). При этом в элементах фермы, непосредственно подверженных действию этой нагрузки, помимо продольных сил «N», возникают изгибающий момент «М» и поперечная сила «Q»(рис.3.78).
Рис. 3.78
В стержнях верхнего пояса «СD» и «DВ» возникают внутренние усилия «М» и «Q», приближенно соответствующие простым балкам на двух шарнирных опорах (индекс «о»).
В таких случаях расчет ведут в следующей последовательности:
1). Производится расчет каждого элемента, загруженного внеузловой нагрузкой, как для простой однопролетной балки.
2). Заданная ферма загружается узловой нагрузкой (рис.3.79), по величине равной полученным значениям опорных реакций от внеузловой нагрузки в простых балках, и производится обычный расчет фермы (определяются продольные усилия).
Рис. 3.79
3). В стержнях, подверженных действию внеузловой нагрузки, сечение подбирается по известной из курса «Сопротивление материалов» формуле:
= N/А ± М/WR;
Во всех других элементах фермы, подбор сечений производится по упомянутой ранее формуле:
= N/АR
Заметим, что для сжатых и сжато-изогнутых элементов фермы необходимо провести дополнительный расчет на устойчивость.
Внеузловая нагрузка на фермы является экономически невыгодной (перерасход материала), поэтому на практике для уменьшения длины панели применяют либо составные, либо шпренгельные фермы.
studfiles.net
Основы расчёта ферм: ручной и машинный счёт
 Фермами называют плоские и пространственные стержневые конструкции с шарнирными соединениями элементов, загружаемые исключительно в узлах. Шарнир допускает вращение, поэтому считается, что стержни под нагрузкой работают только на центральное растяжение-сжатие. Фермы позволяют значительно сэкономить материал при перекрытии больших пролётов.
Фермами называют плоские и пространственные стержневые конструкции с шарнирными соединениями элементов, загружаемые исключительно в узлах. Шарнир допускает вращение, поэтому считается, что стержни под нагрузкой работают только на центральное растяжение-сжатие. Фермы позволяют значительно сэкономить материал при перекрытии больших пролётов.
Рисунок 1
Фермы классифицируются:
- по очертанию внешнего контура;
- по виду решётки;
- по способу опирания;
- по назначению;
- по уровню проезда транспорта.
Также выделяют простейшие и сложные фермы. Простейшими называют фермы, образованные последовательным присоединением шарнирного треугольника. Такие конструкции отличаются геометрической неизменяемостью, статической определимостью. Фермы со сложной структурой, как правило, статически неопределимы.
Для успешного расчёта необходимо знать виды связей и уметь определять реакции опор. Эти задачи подробно рассматриваются в курсе теоретической механики. Разницу между нагрузкой и внутренним усилием, а также первичные навыки определения последних дают в курсе сопротивления материалов.
Рассмотрим основные методы расчёта статически определимых плоских ферм.
Способ проекций
На рис. 2 симметричная шарнирно-опёртая раскосная ферма пролётом L = 30 м, состоящая из шести панелей 5 на 5 метров. К верхнему поясу приложены единичные нагрузки P = 10 кН. Определим продольные усилия в стержнях фермы. Собственным весом элементов пренебрегаем.
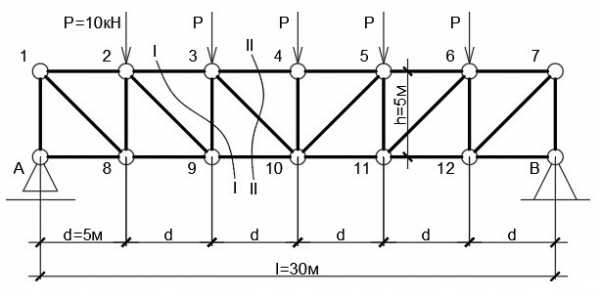
Рисунок 2
Опорные реакции определяются путём приведения фермы к балке на двух шарнирных опорах. Величина реакций составит R (A) = R (B) = ∑P/2 = 25 кН. Строим балочную эпюру моментов, а на её основе — балочную эпюру поперечных усилий (она понадобится для проверки). За положительное направление принимаем то, что будет закручивать среднюю линию балки по часовой стрелке.
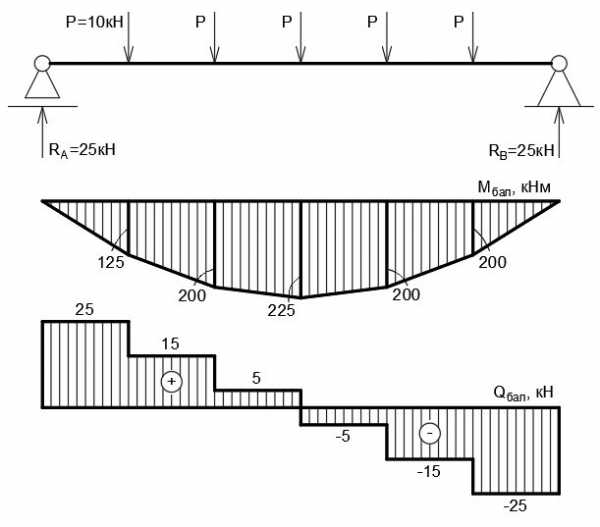
Рисунок 3
Метод вырезания узла
Метод вырезания узла заключается в отсечении отдельно взятого узла конструкции с обязательной заменой разрезаемых стержней внутренними усилиями с последующим составлением уравнений равновесия. Суммы проекций сил на оси координат должны равняться нулю. Прикладываемые усилия изначально предполагаются растягивающими, то есть направленными от узла. Истинное направление внутренних усилий определится в ходе расчёта и обозначится его знаком.
Рационально начинать с узла, в котором сходится не более двух стержней. Составим уравнения равновесия для опоры, А (рис. 4).
∑ F (y) = 0: R (A) + N (A-1) = 0
∑ F (x) = 0: N (A-8) = 0
Очевидно, что N (A-1) = -25кН. Знак «минус» означает сжатие, усилие направлено в узел (мы отразим это на финальной эпюре).
Условие равновесия для узла 1:
∑ F (y) = 0: -N (A-1) — N (1−8)∙cos45° = 0
∑ F (x) = 0: N (1−2) + N (1−8)∙sin45° = 0
Из первого выражения получаем N (1−8) = —N (A-1)/cos45° = 25кН/0,707 = 35,4 кН. Значение положительное, раскос испытывает растяжение. N (1−2) = -25 кН, верхний пояс сжимается. По этому принципу можно рассчитать всю конструкцию (рис. 4).
Рисунок 4
Метод сечений
Ферму мысленно разделяют сечением, проходящим как минимум по трём стержням, два из которых параллельны друг другу. Затем рассматривают равновесие одной из частей конструкции. Сечение подбирают таким образом, чтобы сумма проекций сил содержала одну неизвестную величину.
Проведём сечение I-I (рис. 5) и отбросим правую часть. Заменим стержни растягивающими усилиями. Просуммируем силы по осям:
∑ F(y) = 0: R(A) — P + N(9−3)
N(9−3) = P — R(A) = 10 кН — 25 кН = -15 кН
Стойка 9−3 сжимается.
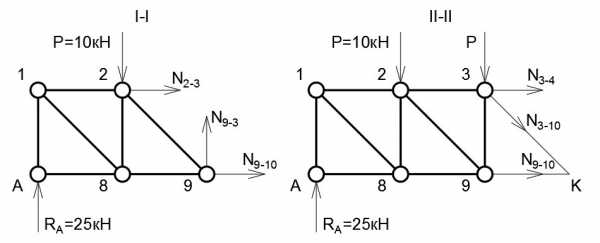
Рисунок 5
Способ проекций удобно применять в расчётах ферм с параллельными поясами, загруженными вертикальной нагрузкой. В этом случае не придётся вычислять углы наклона усилий к ортогональным осям координат. Последовательно вырезая узлы и проводя сечения, мы получим значения усилий во всех частях конструкции. Недостатком способа проекций является то, что ошибочный результат на ранних этапах расчёта повлечёт за собой ошибки во всех дальнейших вычислениях.
Способ моментной точки
Способ моментной точки требует составлять уравнение моментов относительно точки пересечения двух неизвестных сил. Как и в методе сечений, три стержня (один из которых не пересекается с остальными) разрезаются и заменяются растягивающими усилиями.
Рассмотрим сечение II-II (рис. 5). Стержни 3−4 и 3−10 пересекаются в узле 3, стержни 3−10 и 9−10 пересекаются в узле 10 (точка K). Составим уравнения моментов. Суммы моментов относительно точек пересечения будут равняться нулю. Положительным принимаем момент, вращающий конструкцию по часовой стрелке.
∑ m(3) = 0: 2d∙R(A) — d∙P — h∙N(9−10) = 0
∑ m(K) = 0: 3d∙R(A) — 2d∙P — d∙P + h∙N(3−4) = 0
Из уравнений выражаем неизвестные:
N(9−10) = (2d∙R(A) — d∙P)/h = (2∙5м∙25кН — 5м∙10кН)/5м = 40 кН (растяжение)
N(3−4) = (-3d∙R(A) + 2d∙P + d∙P)/h = (-3∙5м∙25кН + 2∙5м∙10кН + 5м∙10кН)/5м = -45 кН (сжатие)
Способ моментной точки позволяет определить внутренние усилия независимо друг от друга, поэтому влияние одного ошибочного результата на качество последующих вычислений исключено. Данным способом можно воспользоваться в расчёте некоторых сложных статически определимых ферм (рис. 6).
Рисунок 6
Требуется определить усилие в верхнем поясе 7−9. Известны размеры d и h, нагрузка P. Реакции опор R(A) = R(B) = 4,5P. Проведём сечение I-I и просуммируем моменты относительно точки 10. Усилия от раскосов и нижнего пояса не попадут в уравнение равновесия, так как сходятся в точке 10. Так мы избавляемся от пяти из шести неизвестных:
∑ m(10) = 0: 4d∙R(A) — d∙P∙(4+3+2+1) + h∙O(7−9) = 0
O(7−9) = -8d∙P/h
Аналогично можно рассчитать остальные стержни верхнего пояса.
Признаки нулевого стержня
Нулевым называют стержень, в котором усилие равно нулю. Выделяют ряд частных случаев, в которых гарантированно встречается нулевой стержень.
- Равновесие ненагруженного узла, состоящего из двух стержней, возможно только в том случае, если оба стержня нулевые.
- В ненагруженном узле из трёх стержней одиночный (не лежащий на одной прямой с остальными двумя) стержень будет нулевым.
Рисунок 7
- В трехстержневом узле без нагрузки усилие в одиночном стержне будет равно по модулю и обратно по направлению приложенной нагрузке. При этом усилия в стержнях, лежащих на одной прямой, будут равны друг другу, и определятся расчётом N(3) = -P, N(1) = N(2).
- Трехстержневой узел с одиночным стержнем и нагрузкой, приложенной в произвольном направлении. Нагрузка P раскладывается на составляющие P’ и P» по правилу треугольника параллельно осям элементов. Тогда N(1) = N(2) + P’, N(3) = -P».
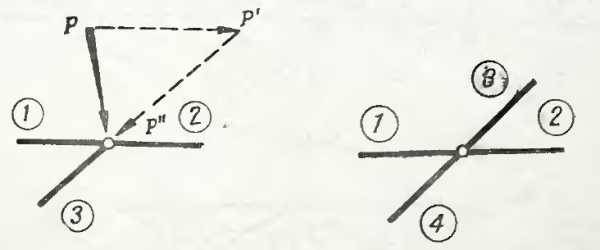
Рисунок 8
- В ненагруженном узле из четырёх стержней, оси которых направлены по двум прямым, усилия будут попарно равны N(1) = N(2), N(3) = N(4).
Пользуясь методом вырезания узлов и зная правила нулевого стержня, можно проводить проверку расчётов, проведённых другими методами.
Расчёт ферм на персональном компьютере
Современные вычислительные комплексы основаны на методе конечного элемента. С их помощью осуществляют расчёты ферм любого очертания и геометрической сложности. Профессиональные программные пакеты Stark ES, SCAD Office, ПК Лира обладают широким функционалом и, к сожалению, высокой стоимостью, а также требуют глубокого понимания теории упругости и строительной механики. Для учебных целей и подойдут бесплатные аналоги, например Полюс 2.1.1.
В Полюсе можно рассчитывать плоские статически определимые и неопределимые стержневые конструкции (балки, фермы, рамы) на силовое воздействие, определять перемещения и температурное воздействие. Перед нами эпюра продольных усилий для фермы, изображённой на рис. 2. Ординаты графика совпадают с полученными вручную результатами.
Рисунок 9
Порядок работы в программе Полюс
- На панели инструментов (слева) выбираем элемент «опора». Размещаем помещаем элементы на свободное поле кликом левой кнопки мыши. Чтобы указать точные координаты опор, переходим в режим редактирования, нажав на значок курсора на панели инструментов.
- Двойной клик по опоре. Во всплывающем окне «свойства узла» задаём точные координаты в метрах. Положительное направление осей координат — вправо и вверх соответственно. Если узел не будет использоваться в качестве опоры, установите флажок «не связан с землёй». Здесь же можно задать приходящие в опору нагрузки в виде точечной силы или момента, а также перемещения. Правило знаков такое же. Удобно разместить крайнюю левую опору в начале координат (точка 0, 0).
- Далее размещаем узлы фермы. Выбираем элемент «свободный узел», кликаем по свободному полю, точные координаты прописываем для каждого узла в отдельности.
- На панели инструментов выбираем «стержень». Кликаем на начальном узле, отпускаем кнопку мышки. Затем кликаем на конечном узле. По умолчанию стержень имеет шарниры на двух концах и единичную жёсткость. Переходим в режим редактирования, двойным кликом по стержню открываем всплывающее окно, при необходимости изменяем граничные условия стержня (жёсткая связь, шарнир, подвижный шарнир для опорного конца) и его характеристики.
- Для загружения ферм используем инструмент «сила», нагрузка прикладывается в узлах. Для сил, прикладываемых не строго вертикально или горизонтально, устанавливаем параметр «под углом», после чего вводим угол наклона к горизонтали. Альтернативно можно сразу ввести значение проекций силы на ортогональные оси.
- Программа считает результат автоматически. На панели задач (вверху) можно переключать режимы отображения внутренних усилий (M, Q, N), а также опорных реакций (R). Результатом будет эпюра внутренних усилий в заданной конструкции.
В качестве примера рассчитаем сложную раскосную ферму, рассмотренную в методе моментной точки (рис. 6). Примем размеры и нагрузки: d = 3м, h = 6м, P = 100Н. По выведенной ранее формуле значение усилия в верхнем поясе фермы будет равно:
O(7−9) = -8d∙P/h = -8∙3м∙100Н/6м = -400 Н (сжатие)
Эпюра продольных усилий, полученная в Полюсе:
Рисунок 10
Значения совпадают, конструкция смоделирована верно.
Список литературы
- Дарков А. В., Шапошников Н. Н. — Строительная механика: учебник для строительных специализированных вузов — М.: Высшая школа, 1986.
- Рабинович И. М. — Основы строительной механики стержневых систем — М.: 1960.
planken.guru
3. Пример расчета фермы
Задание.Для фермы показанной на рисунке требуется:
а) определить аналитически усилия в стержнях заданной панели, включая правую стойку;
б) построить линии влияния усилий в тех же стержнях;
в) по линиям влияния подсчитать значения усилий от заданной нагрузки и сравнить их со значениями, полученными аналитически.
3.1. Исходные данные для расчета фермы.
ℓ = 24 м; P= 2 кН; № панели 2;h= 6 м.
d = ℓ/6 = 24 / 6 = 4 м
Рисунок 7 Заданная ферма
3.1.1 Определение реакций: RA = RB = 2,5·P = 2,5·2 = 5 кН.
3.1.2 Определение усилий в стержнях 2-й панели
Сечение 1-1
Рисунок 8 Определение усилий в стержнях 2-й панели
Усилие в стержне U2:
Σ =
0;RA ·d
– U2·hU=0;
=
0;RA ·d
– U2·hU=0;
U2 = RA ·d /hU= 5· 4 / 4,5 = 4,444 кН
Усилие в стержне O2:
tg α = h / 4d = 6 / 4 · 4 = 0,375; => α = 20,56°; => Sin α = 0,351
hO = 4·d · Sin α = 4·4·0,351 = 5,616 м
Σ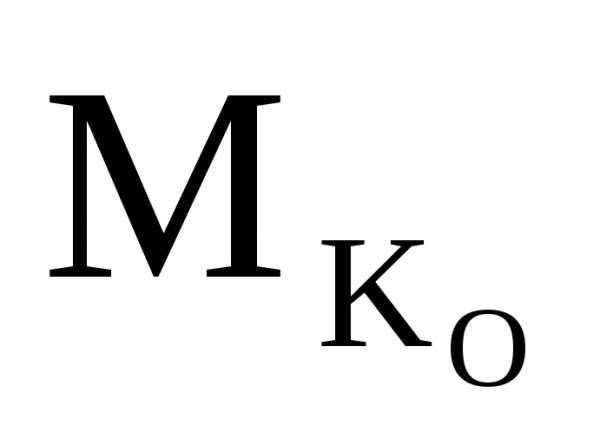 =
0; RA ·2·d – P·d + O2 ·hO =0;
=
0; RA ·2·d – P·d + O2 ·hO =0;
O2 = (P·d — RA ·2·d) /hO= (2·4 — 5·2·4 )/ 5,616 =-5,698 кН
Усилие в стержне D2:
tg β = hU / d = 4,5 / 4 = 1,125; => β = 48,37°; => Sin β = 0,747
hD = 4·d · Sin β = 4·4·0,747 = 11,952 м
Σ =
0; -RA ·2·d + P·3·d + D2 ·hD =0;
=
0; -RA ·2·d + P·3·d + D2 ·hD =0;
D2 = (RA ·2·d — P·3·d) / hD = (5·2·4 — 2·3·4)/ 11,952 = 1,339 кН
Сечение 2-2
Рисунок 9 Определение усилий в стойке V2
Усилие в стержне V2:
Σ =
0; -RA ·2·d
+ P·3·d
— V2·4·d
=0;
=
0; -RA ·2·d
+ P·3·d
— V2·4·d
=0;
V2 = (P·3·d — RA ·2·d) /4·d= (2·3·4 — 5·2·4)/ 4·4 = -1,0 кН
Дополнительно покажем: определение усилия D3 методом проекций (т.к. моментная точка находится в бесконечности).
3.1.3 Определение усилия в раскосе 3-й панели D3
tg γ = h / d = 6 / 4 = 1,5; => γ = 56,31°; => Sin γ = 0,832
ΣY = 0; RA — P – P — D3 · Sin γ =0;
D3 = (RA — 2·P) / Sin γ = (5-2·2)/ 0,832 = 1,202 кН
Сечение 3-3
Рисунок 10 Определение усилия в стержне 3-й панели (D3)
А также: покажем определение усилия V3 методом вырезания узлов
3.1.4 Определение усилия в стойке V3
Сечение 4-4
Рисунок 11 Определение усилия в стойке V3
ΣY= 0
V3= -P= -2 кН
3 .2.
Построение линий влияния усилий в
стержнях фермы
.2.
Построение линий влияния усилий в
стержнях фермы
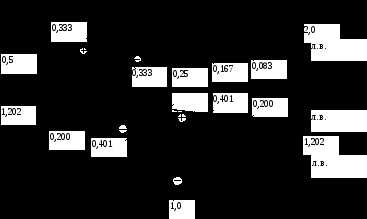
Рисунок 12 Построение линий влияния усилий в стержнях фермы
Сечение 1-1
Построение л.в. 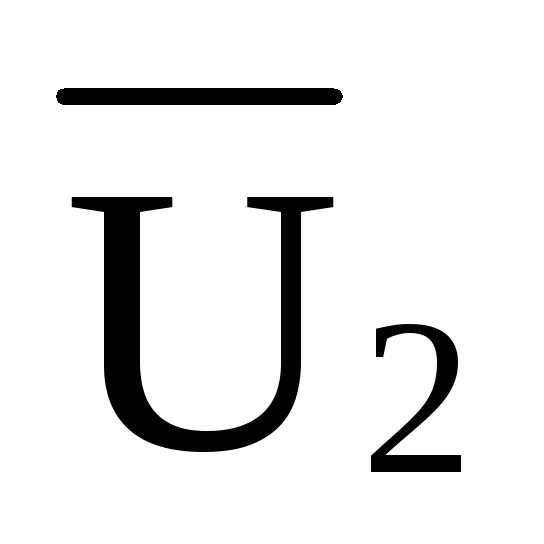
Груз слева Груз справа
Рассматриваем правую часть Рассматриваем левую часть
Σ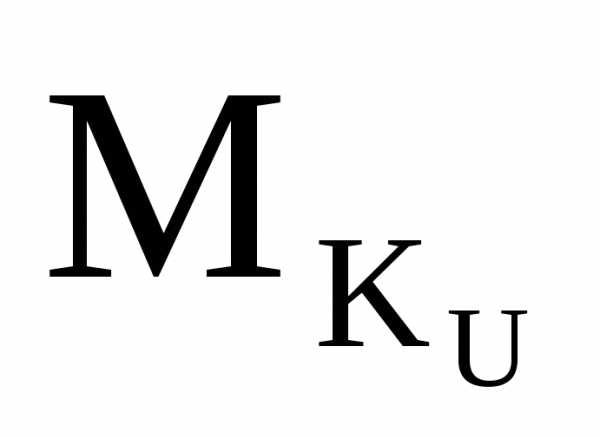 =
0 Σ
=
0 Σ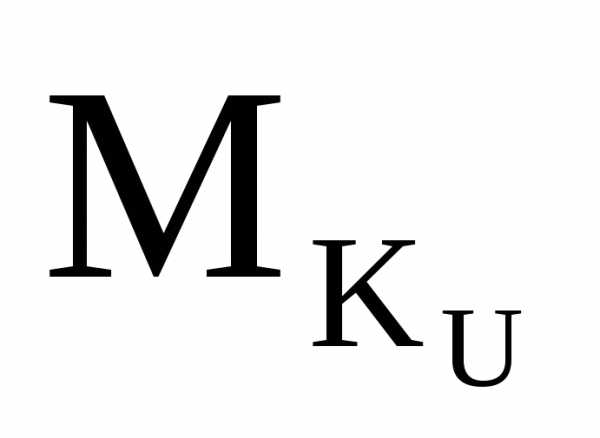 =
0
=
0
— 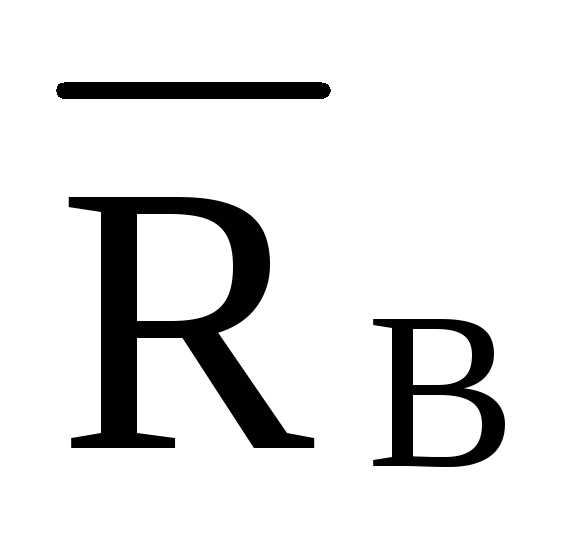 ·5·d
+
·5·d
+ 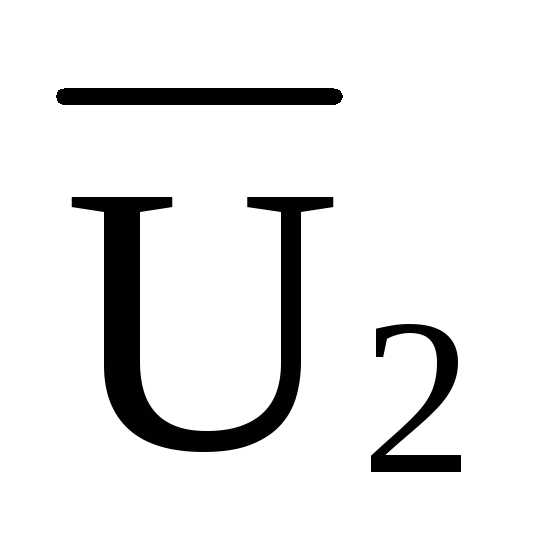 ·
hu =0
·
hu =0 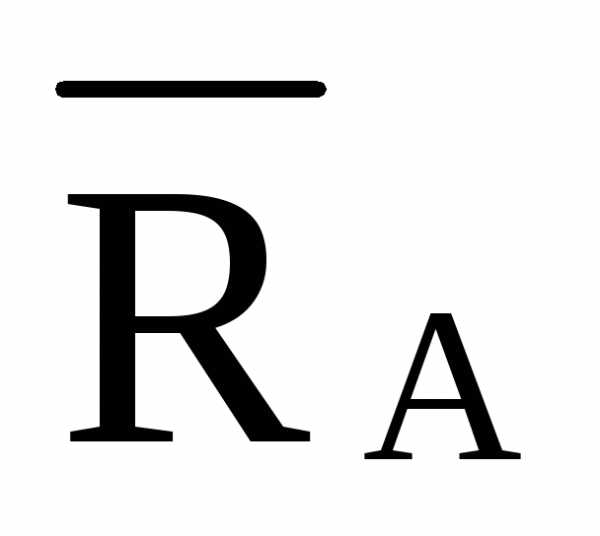 ·d
—
·d
—  ·
hu =0
·
hu =0
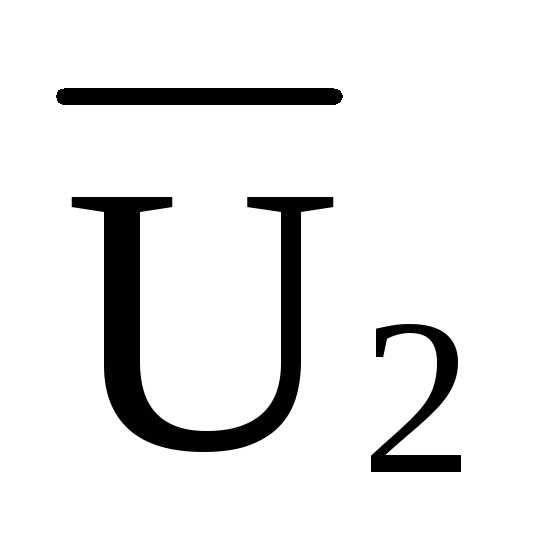 =
= ·5·d
/hu=
·5·d
/hu= ·5·4
/4,5=
·5·4
/4,5=  =
=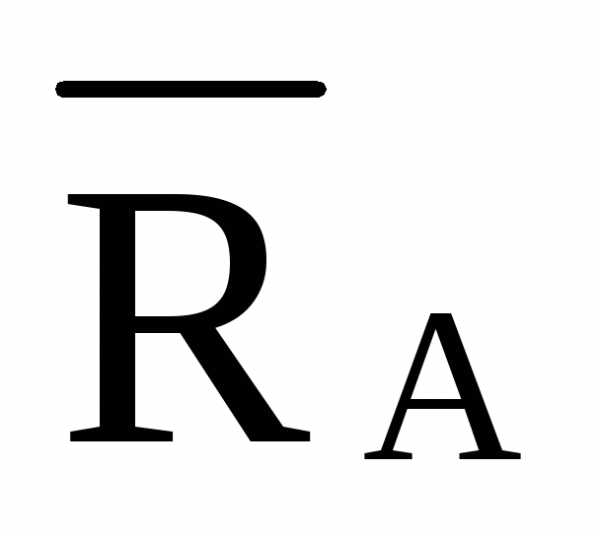 ·d
/hu=
·d
/hu= ·4
/4,5=
·4
/4,5=
=4,444·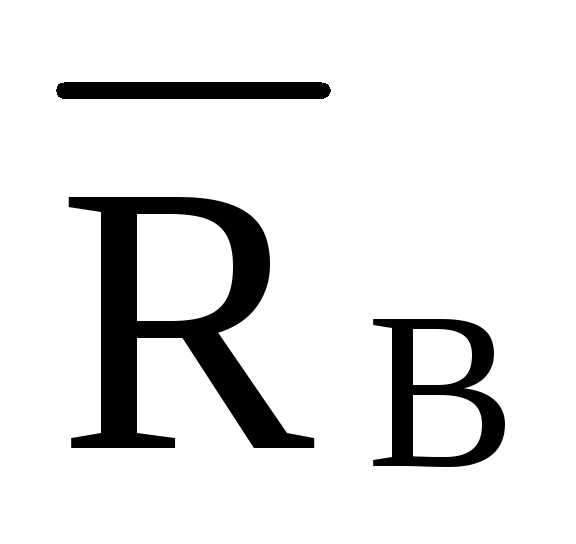 =0,889·
=0,889·
л.в.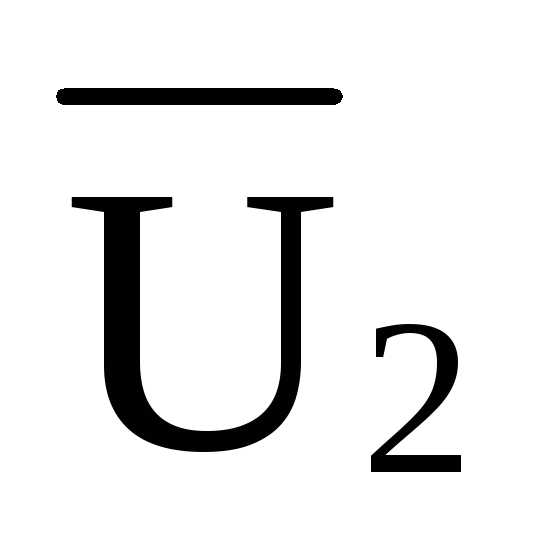 =4,444·л.в.
=4,444·л.в.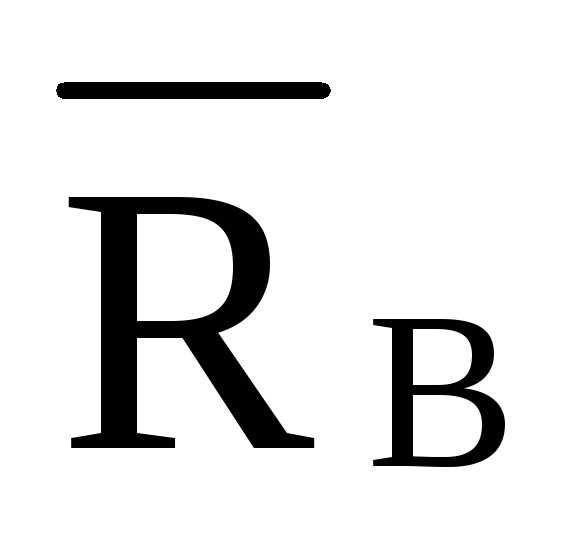 л.в.
л.в.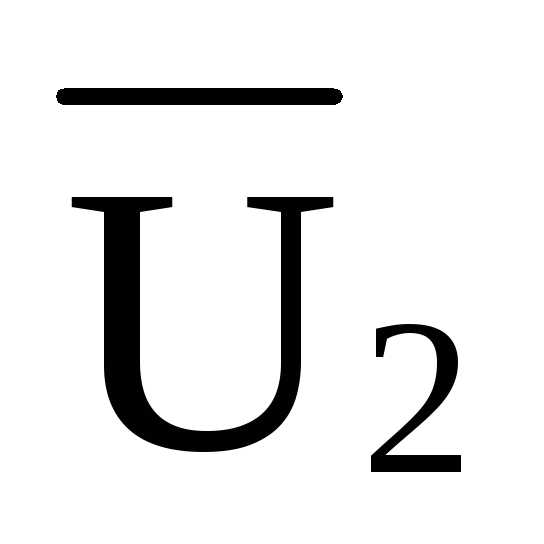 =0,889·л.в.
=0,889·л.в. 
Построение л.в. 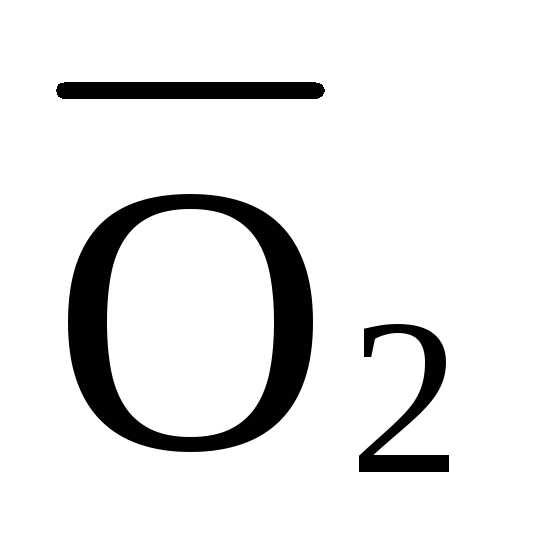
Груз слева Груз справа
Рассматриваем правую часть Рассматриваем левую часть
Σ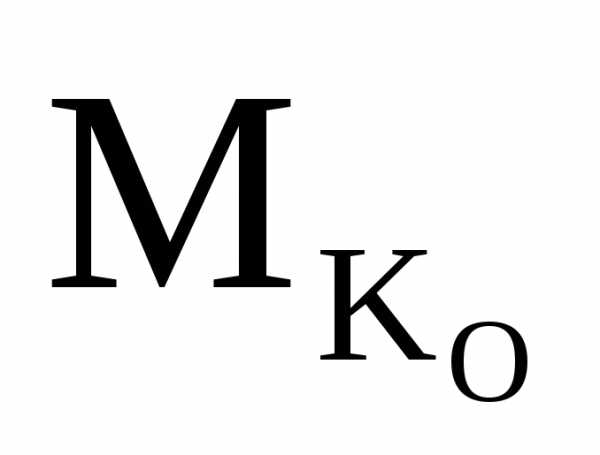 =
0 Σ
=
0 Σ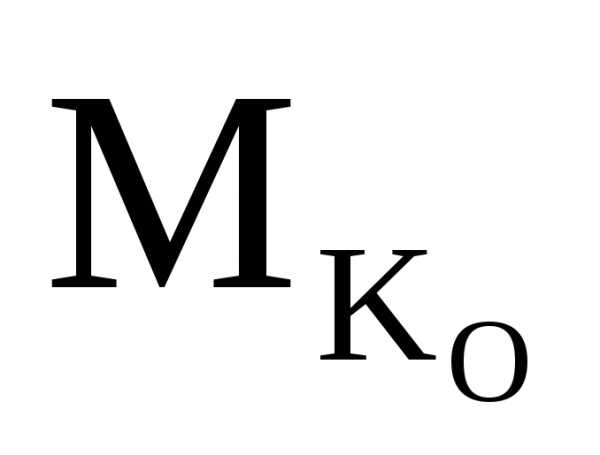 =
0
=
0
—  ·4·d
—
·4·d
—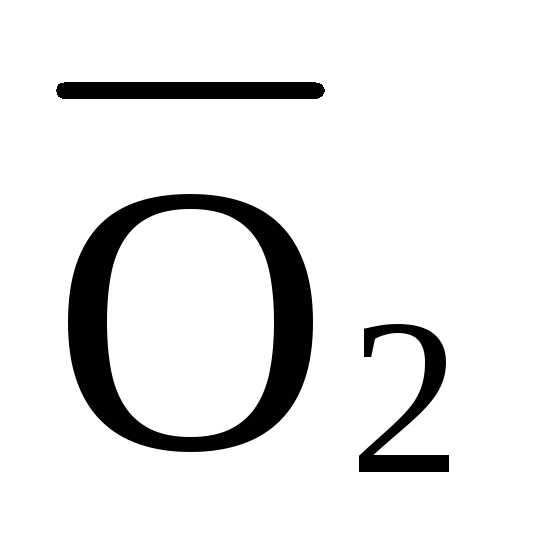 ·
ho =0
·
ho =0 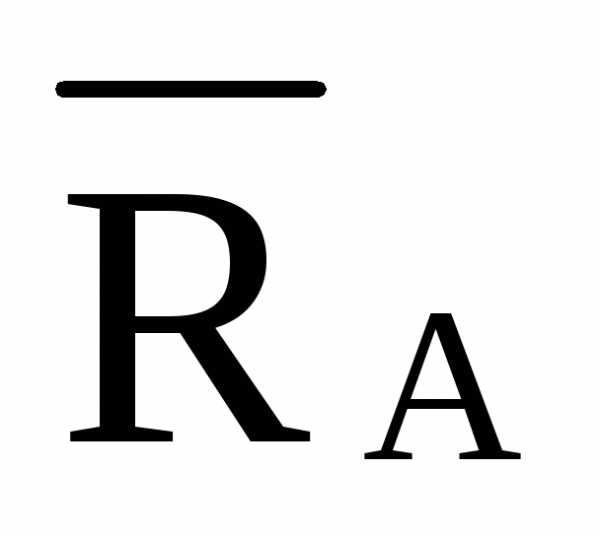 ·2·d
+
·2·d
+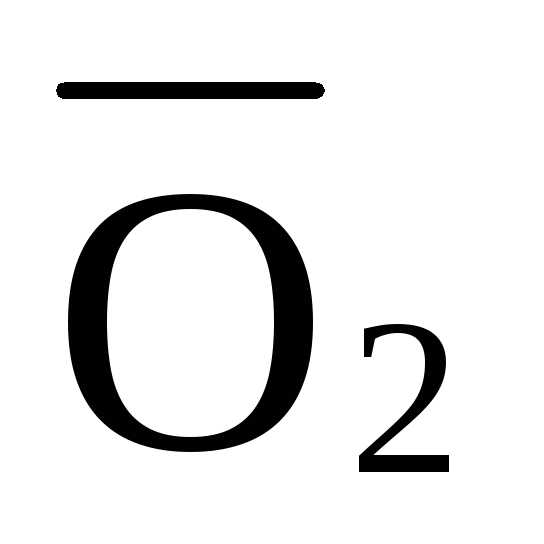 ·
ho =0
·
ho =0
 =-
=-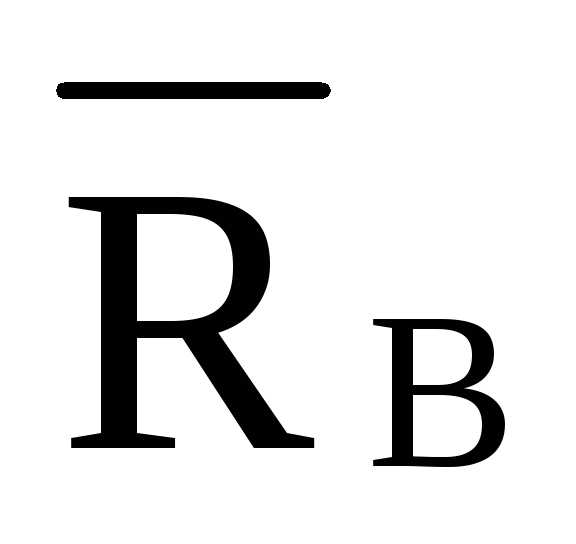 ·4·d
/ho=-
·4·d
/ho=-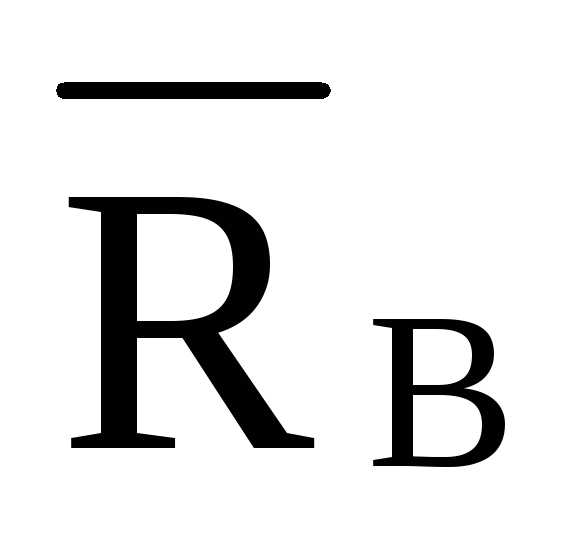 ·4·4
/5,616=
·4·4
/5,616= 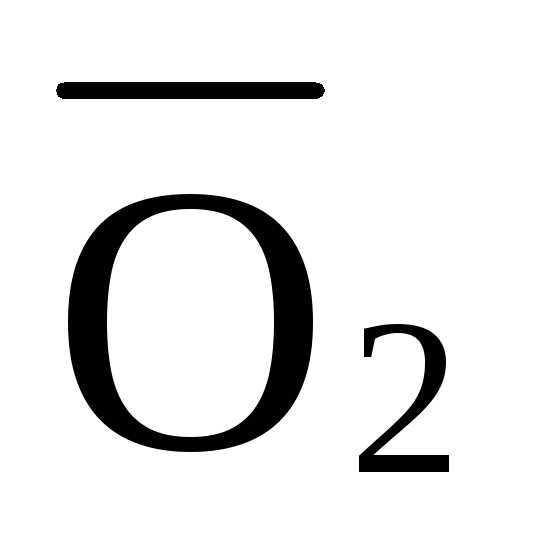 =-
=-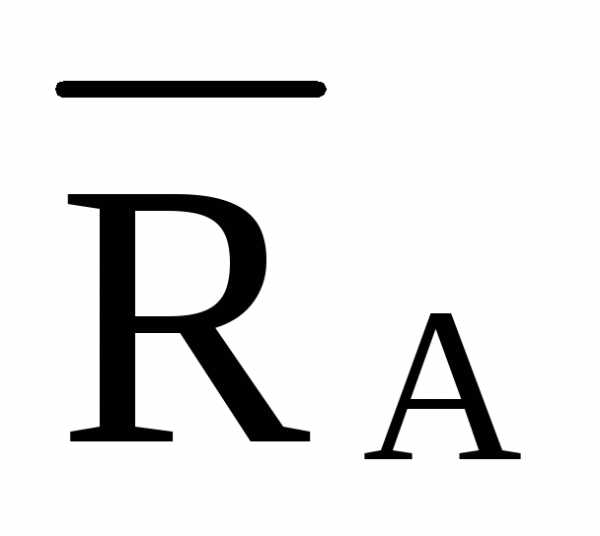 ·2·d
/ho=-
·2·d
/ho=-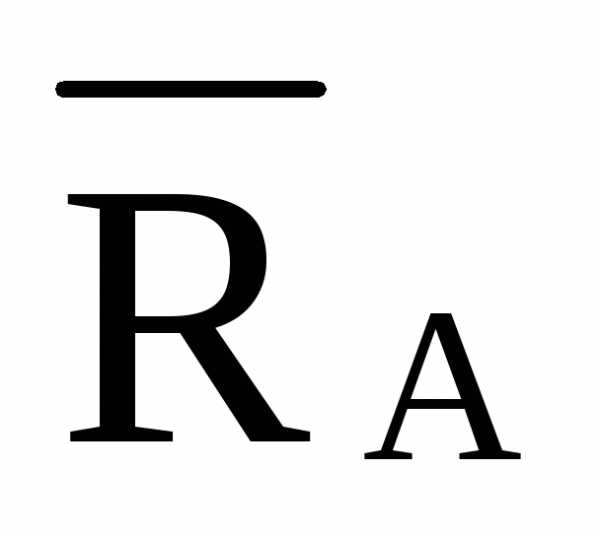 ·2·4
/5,616==-2,849·
·2·4
/5,616==-2,849· =-1,425·
=-1,425·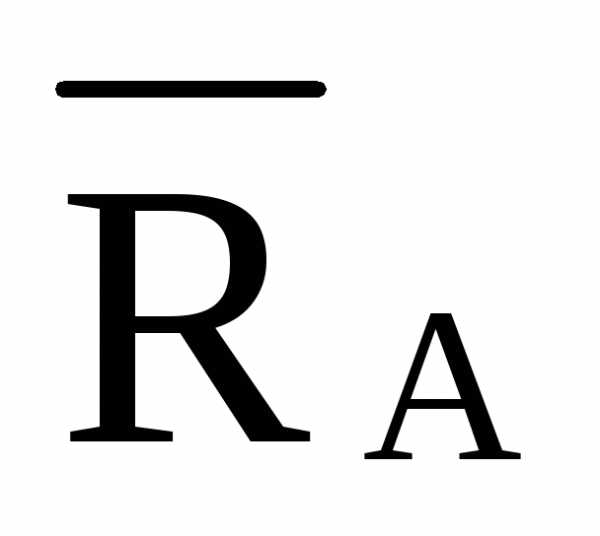
л.в.  =-2,849·л.в.
=-2,849·л.в.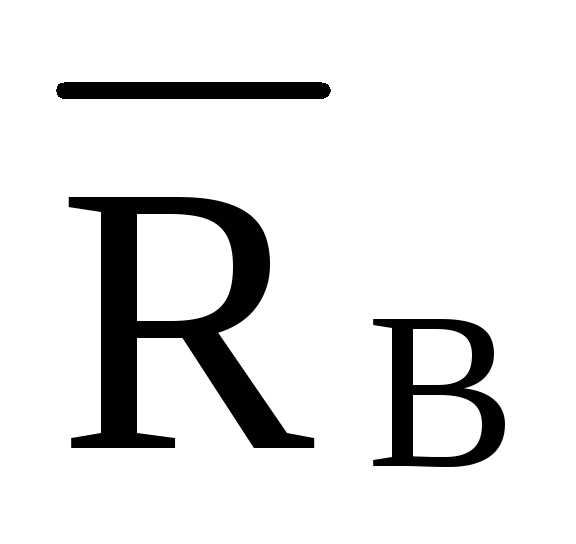 л.в.
л.в. 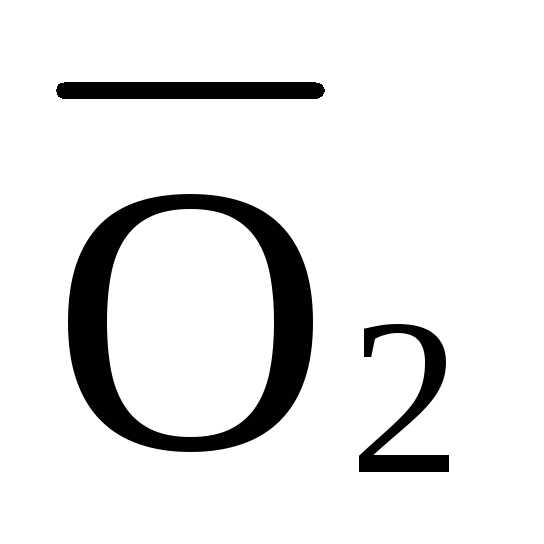 =-1,425·л.в.
=-1,425·л.в. 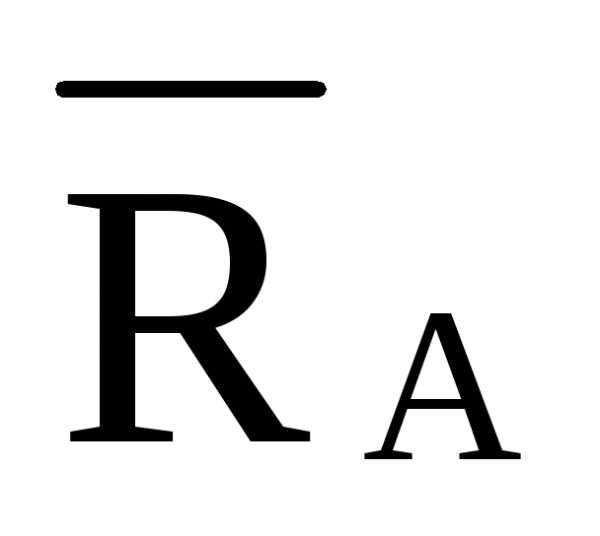
Построение л.в. 
Груз слева Груз справа
Рассматриваем правую часть Рассматриваем левую часть
Σ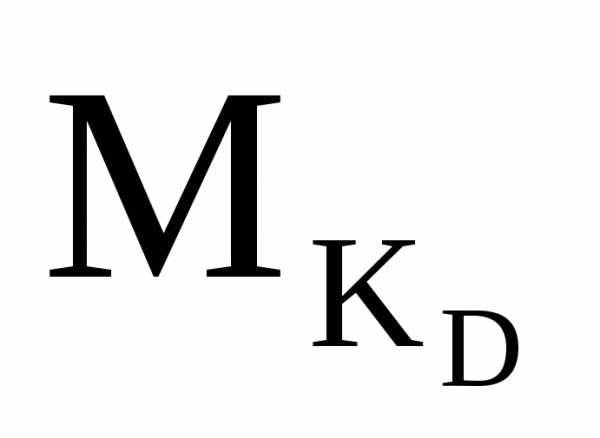 =
0 Σ
=
0 Σ =
0
=
0
— 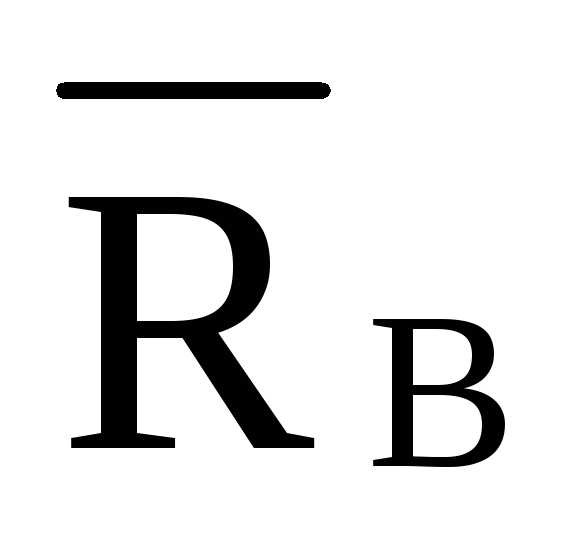 ·8·d
—
·8·d
— 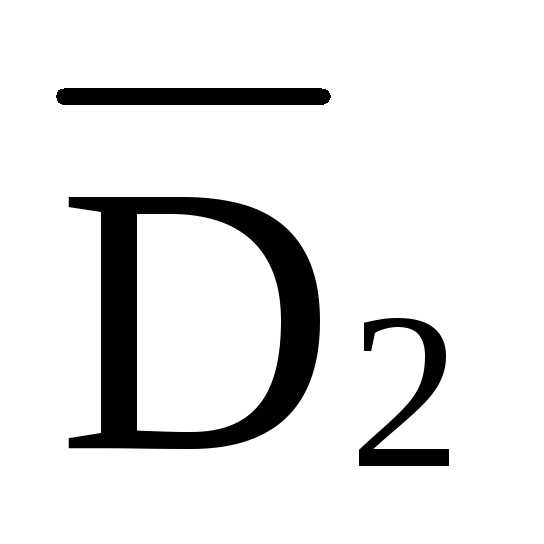 ·
hD =0 —
·
hD =0 —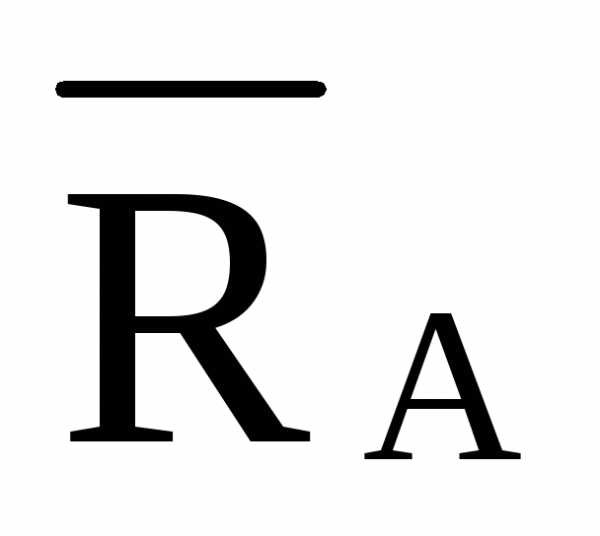 ·2·d
+
·2·d
+  ·
hD =0
·
hD =0
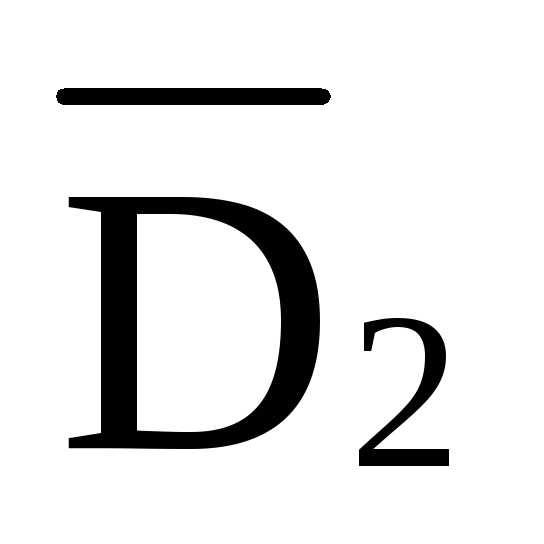 =-
=-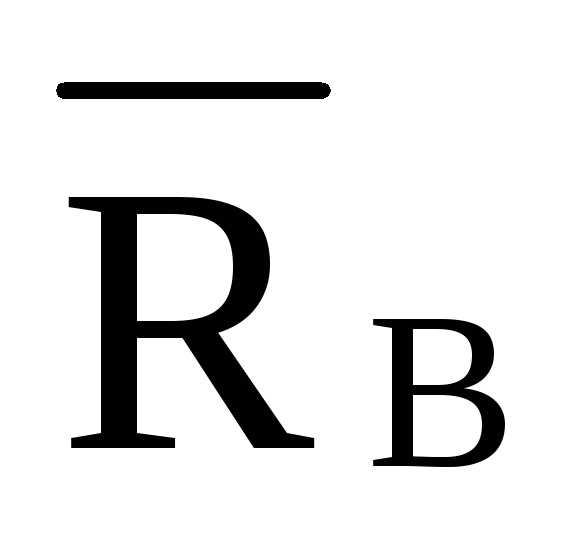 ·8·d
/hD=-
·8·d
/hD=-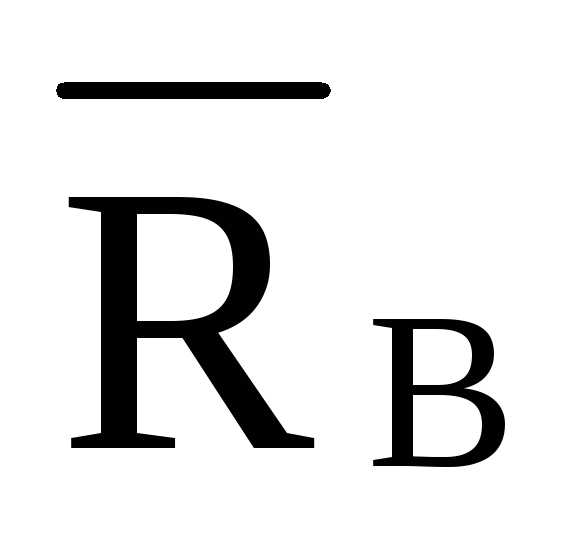 ·8·4
/11,952=
·8·4
/11,952= 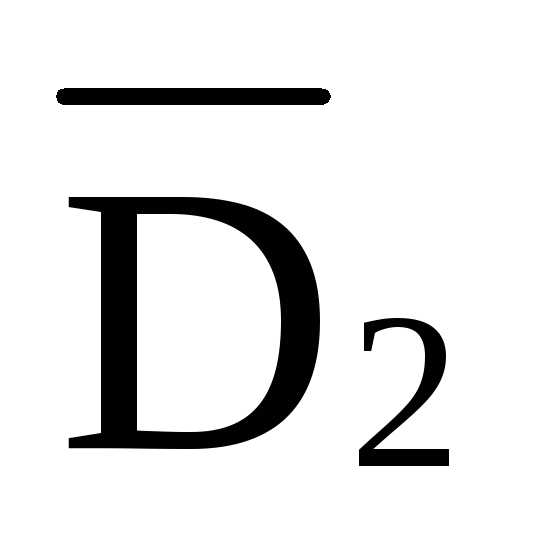 =
=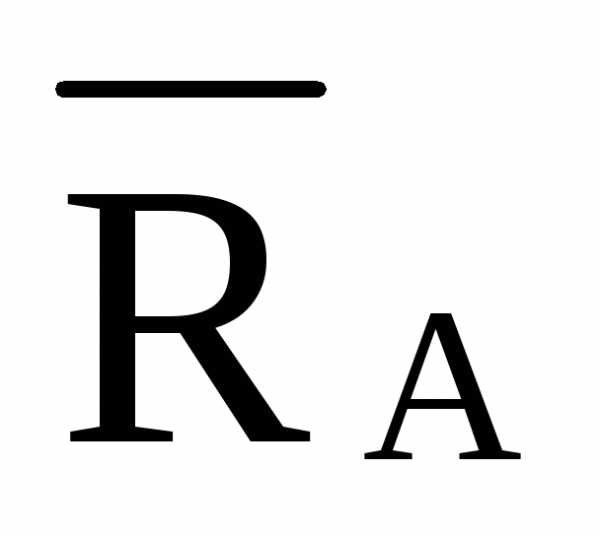 2·d
/hD=
2·d
/hD=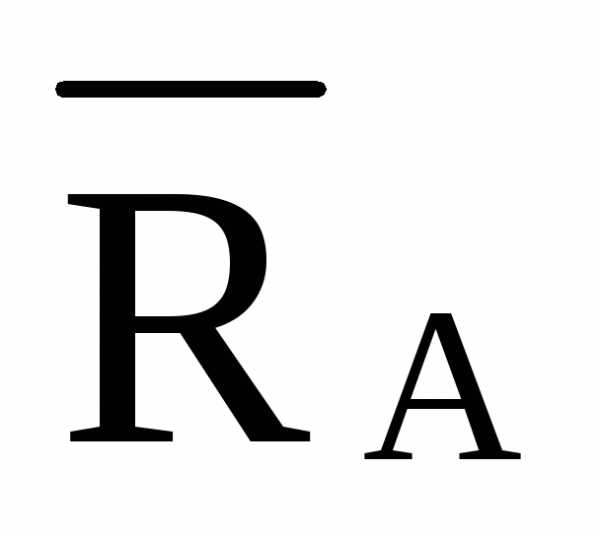 ·2·4
/11,952=
·2·4
/11,952=
=-2,677· =0,669·
=0,669·
л.в. 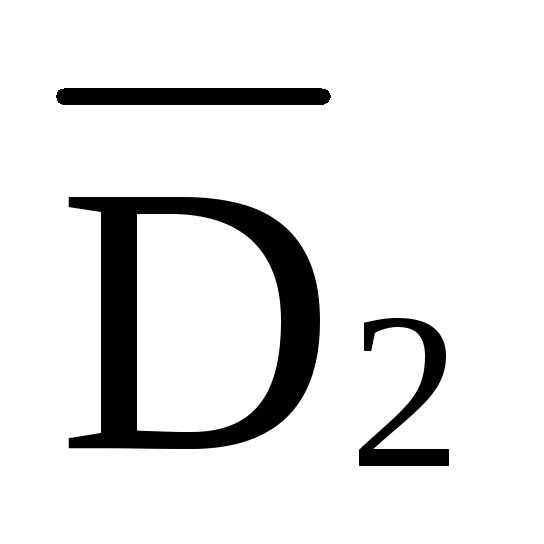 =-2,677·л.в.
=-2,677·л.в.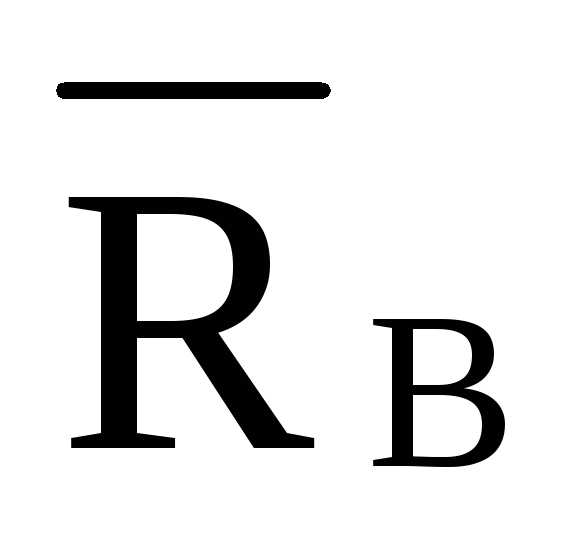 л.в.
л.в. 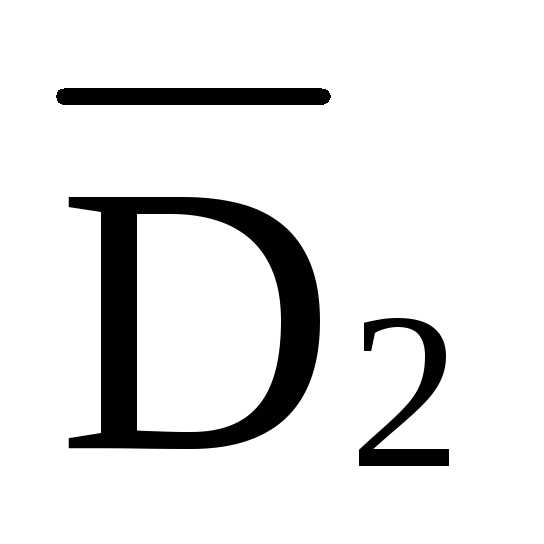 =0,669·л.в.
=0,669·л.в. 
Сечение 2-2
Построение л.в. 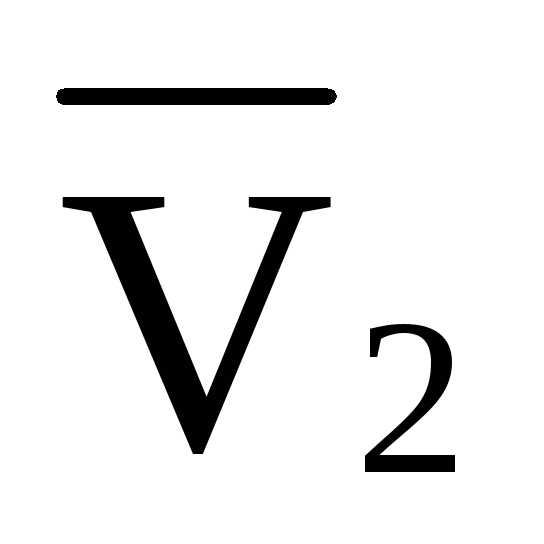
Груз слева Груз справа
Рассматриваем правую часть Рассматриваем левую часть
Σ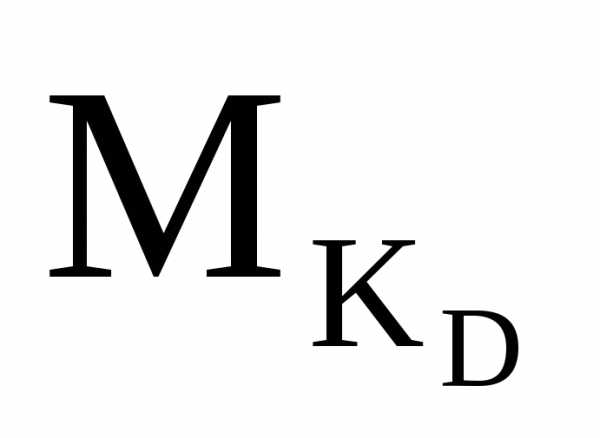 =
0 Σ
=
0 Σ =
0
=
0
— 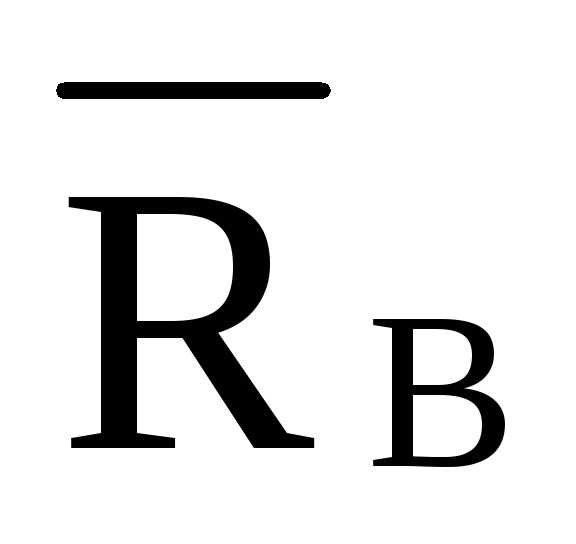 ·8·d
+
·8·d
+ 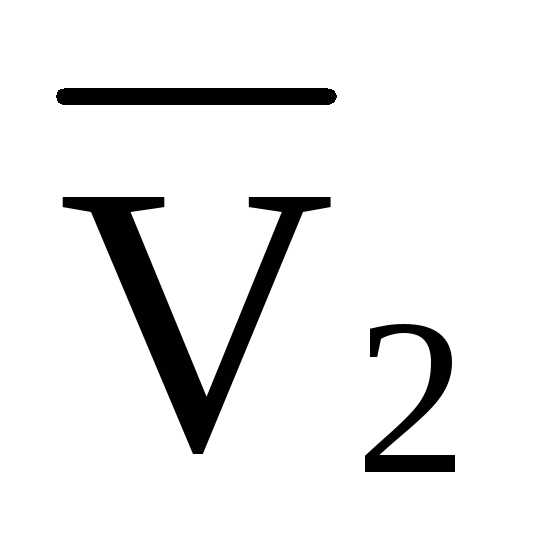 ·4·d =0 —
·4·d =0 —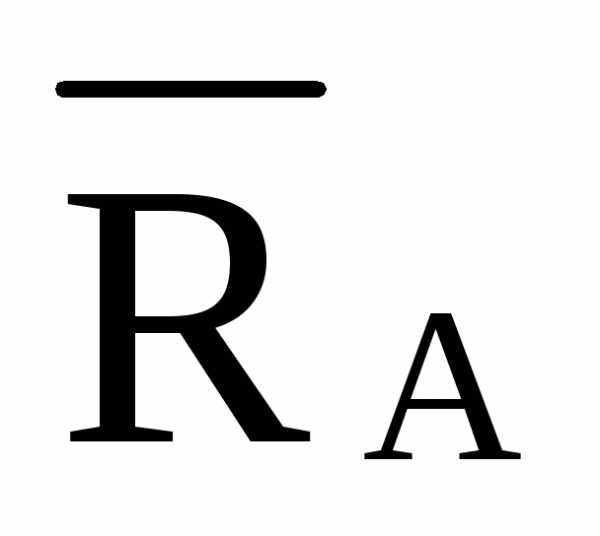 ·2·d
—
·2·d
—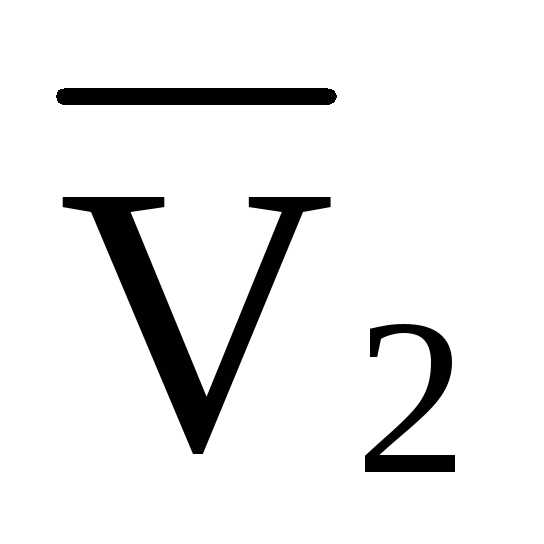 ·4·d
=0
·4·d
=0
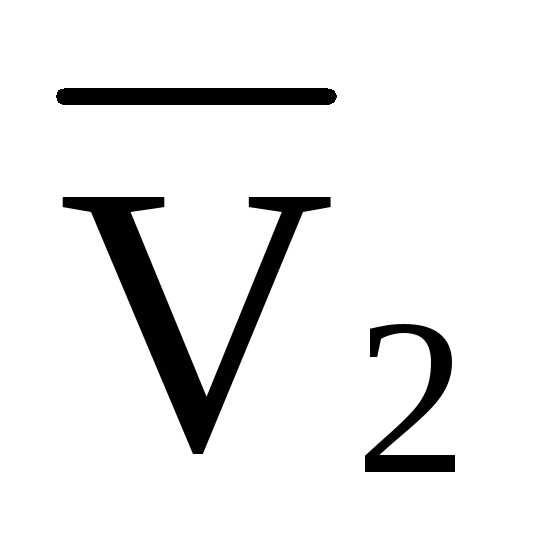 =
=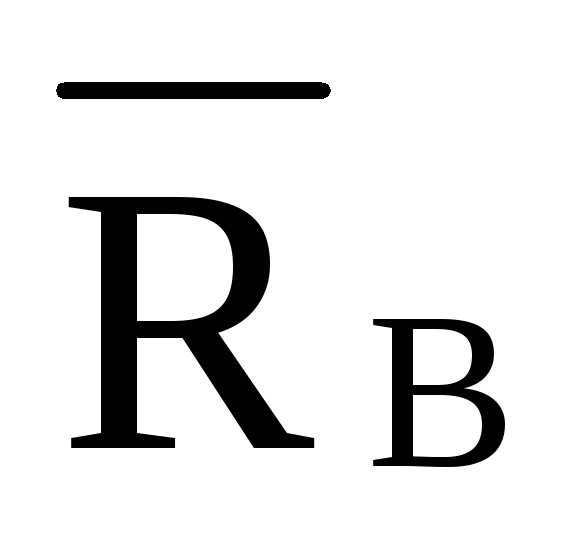 ·8·d
/ 4·d
=
·8·d
/ 4·d
=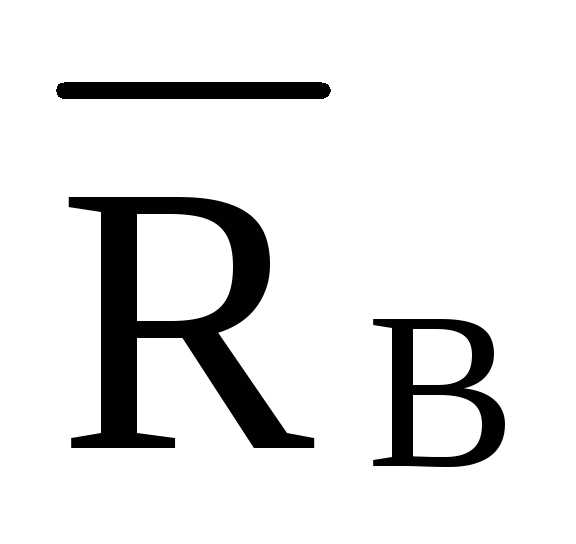 ·2=2·
·2=2·
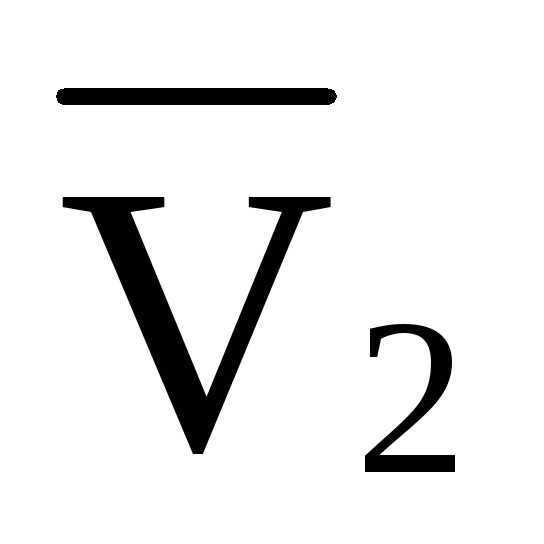 =-
=-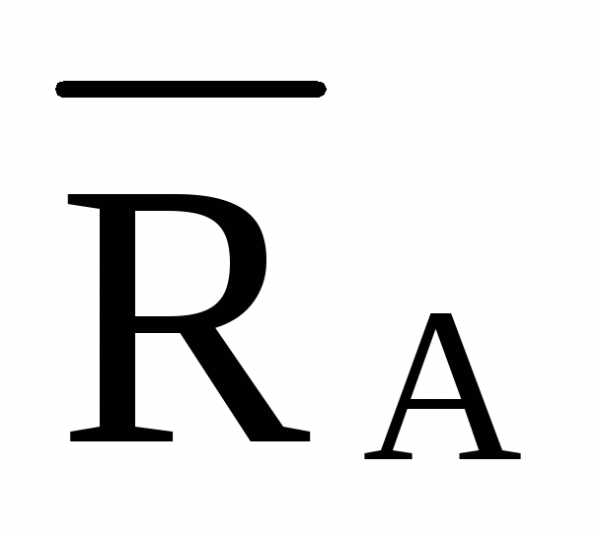 ·2·d
/4·d =-0,5·
·2·d
/4·d =-0,5·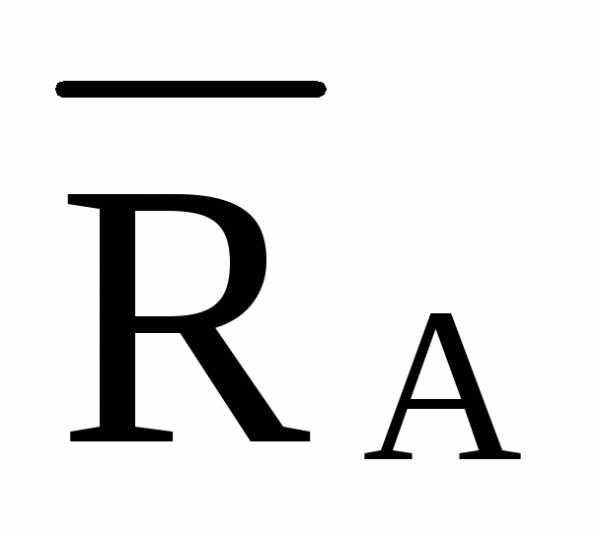
л.в. 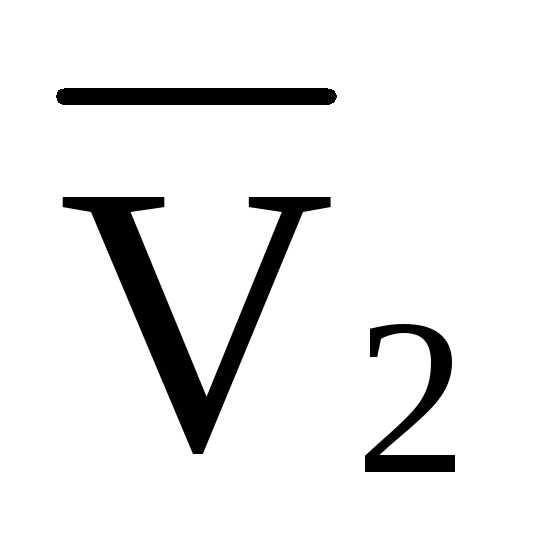 =
2 ·л.в.
=
2 ·л.в.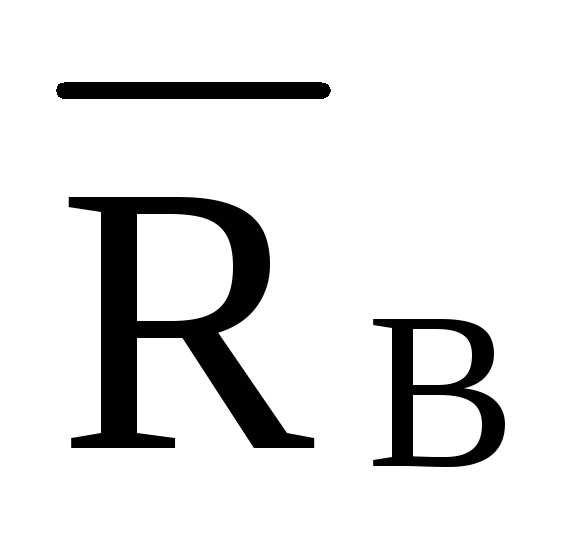 л.в.
л.в. 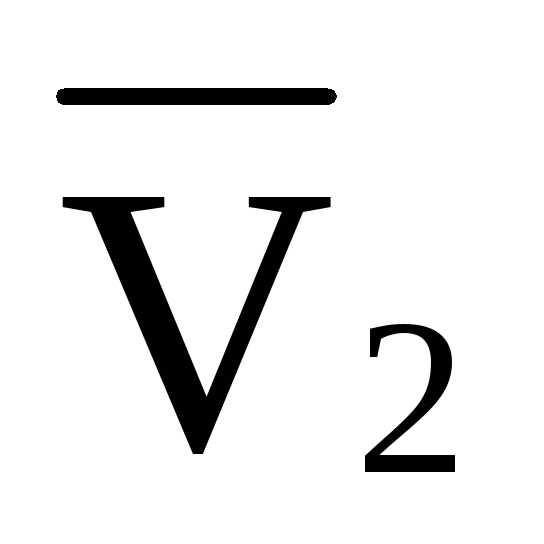 =
-0,5·л.в.
=
-0,5·л.в. 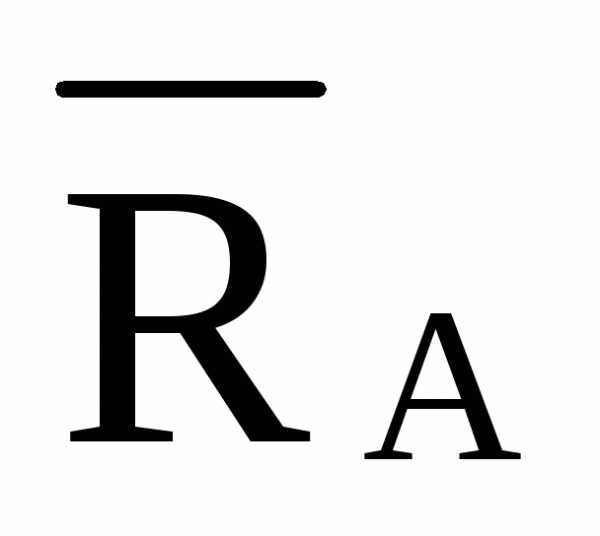
Сечение 3-3
Построение л.в. 
Груз слева Груз справа
Рассматриваем правую часть Рассматриваем левую часть
ΣY= 0 ΣY= 0
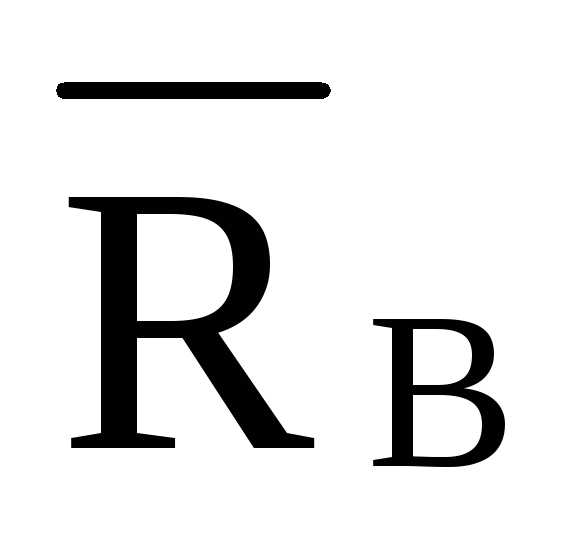 +
+ 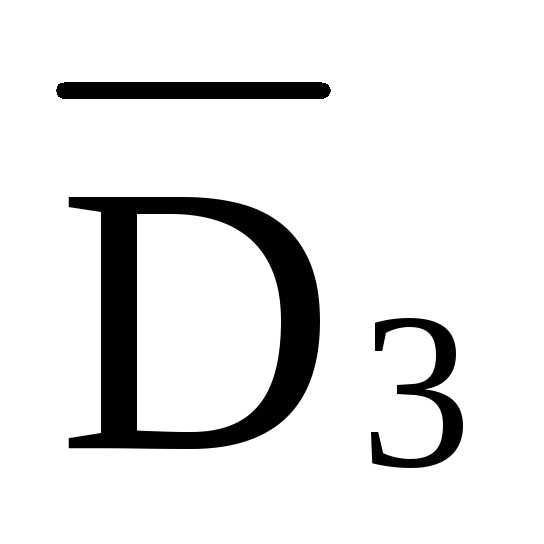 ·
hD =0
·
hD =0 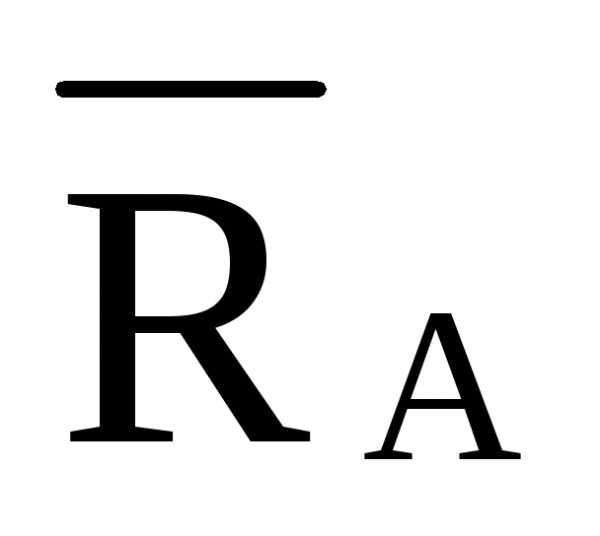 —
—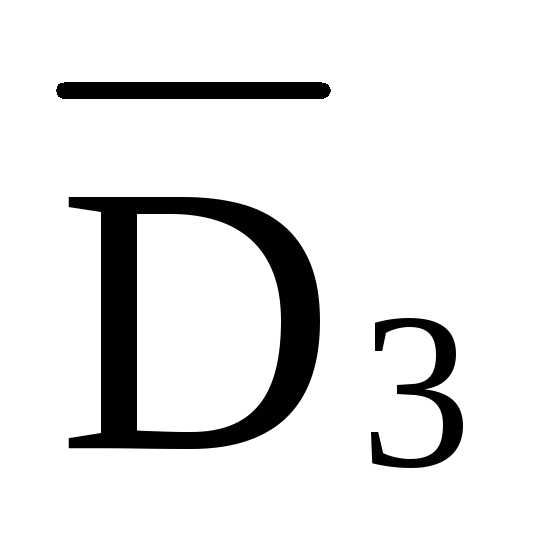 ·Sin γ
=0
·Sin γ
=0
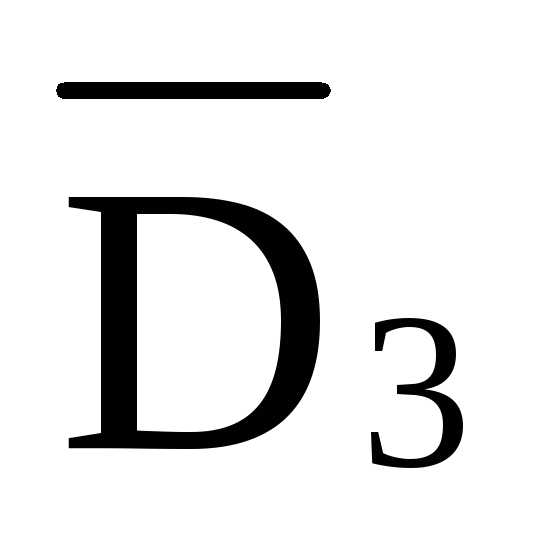 =-
=-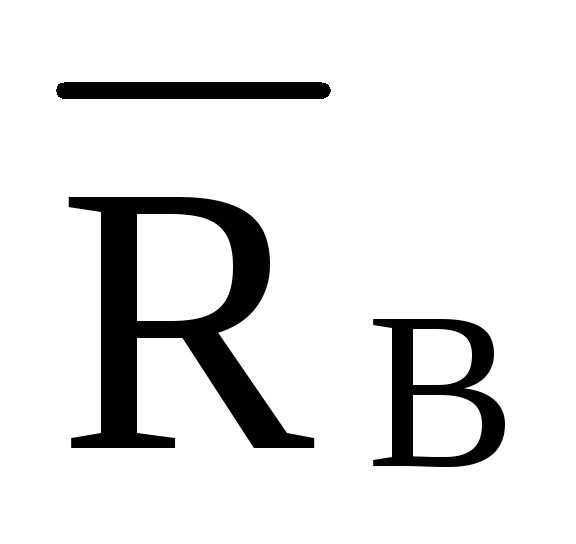 /
Sin γ
=-
/
Sin γ
=-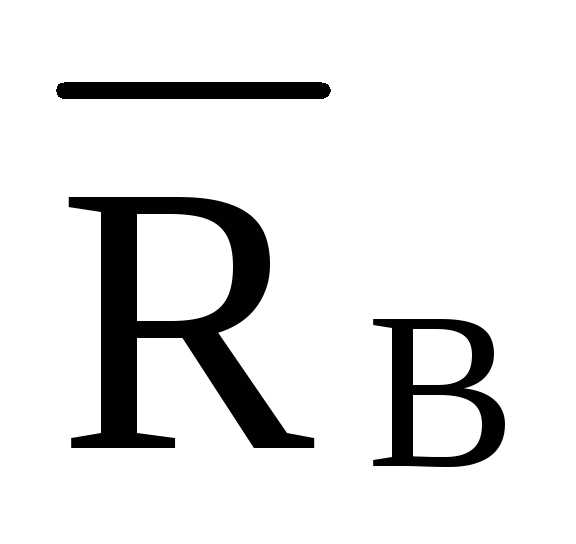 /0,832=
/0,832=  =
=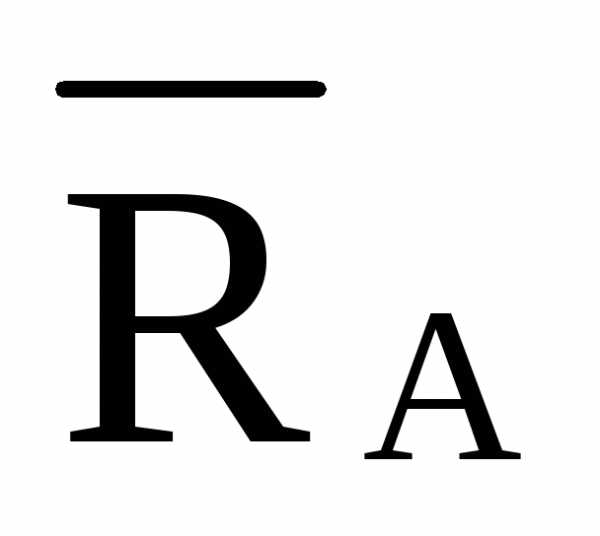 /
Sin γ =
/
Sin γ =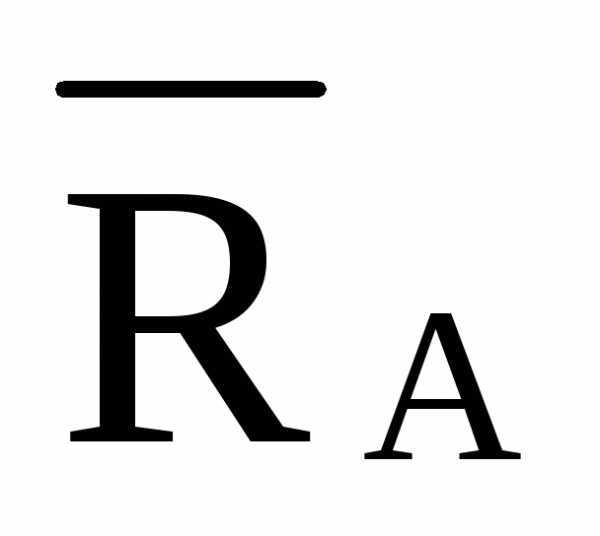 /0,832=
/0,832=
=-1,202· =1,202·
=1,202·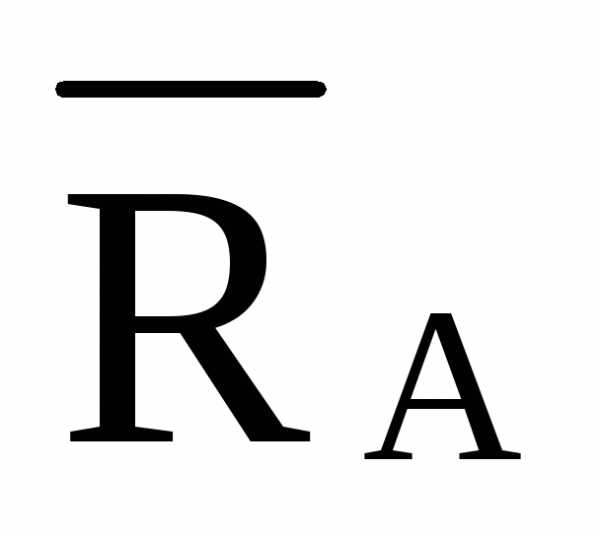
л.в. 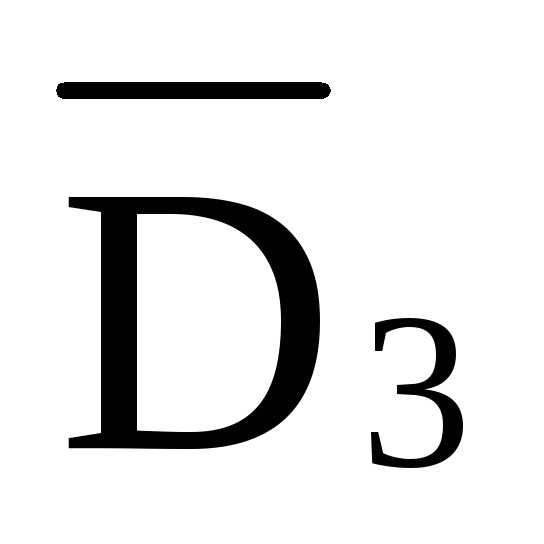 =-1,202·л.в.
=-1,202·л.в.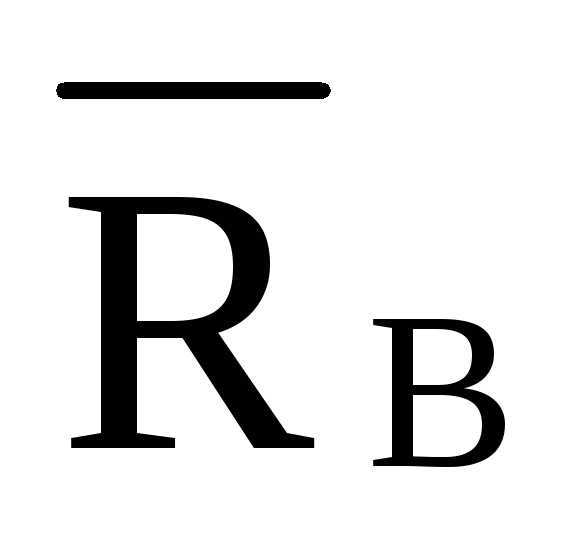 л.в.
л.в.  =
1,202·л.в.
=
1,202·л.в. 
Вырезаем узел. (Сечение 4-4)
Построение л.в. 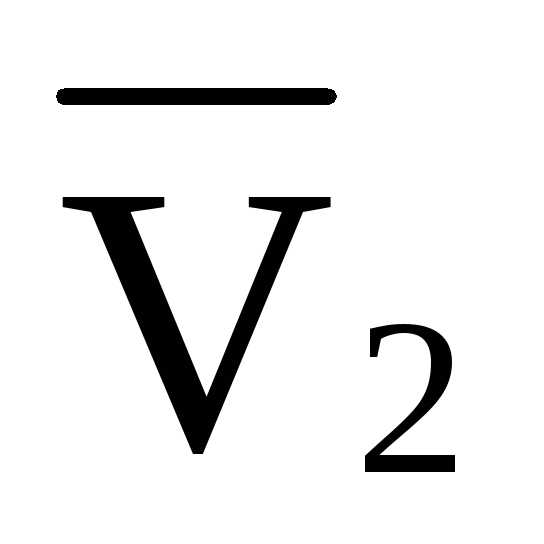
Груз в узле Груза нет в узле
ΣY= 0 ΣY= 0
 =
—
=
—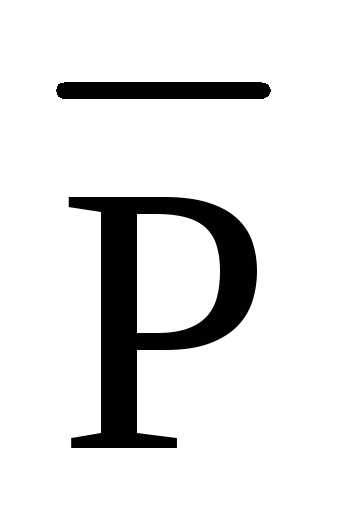 =
-1
=
-1 =
0
=
0
3.3 Определение усилий в стержнях фермы от заданной нагрузки по линиям влияния
Y = ΣPi·
U2 = 0,741·P+0,593·P +0,445·P +0,296·P +0,148·P = (0,741 +0,593 +
+0,445 +0,296 +0,148) ·P = 2,223·P = 2,223·2 = 4,446 кН, что практически равно подсчитанному аналитически U2 = 4,444 кН.
O2 = -0,475·P-0,950·P-0,712·P-0,475·P-0,237·P = -(0,475 + 0,950 +
+ 0,712 + 0,475 + 0,237) ·P= — 2,849· 2 = -5,698 кН, что равно подсчитанному аналитически O2 = -5,698 кН.
D2 = (0,446·P-0,446·P+ 0,335·P+ 0,223·P+ 0,112·P) = (0,446 — 0,446 +
+ 0,335 + 0,223 + 0,112) ·P = 0,670·P = 0,670·2 = 1,34 кН, что практически равно подсчитанному аналитически D2 = 1,339 кН
V2 = (0,333·P- 0,333·P- 0,25·P- 0,167·P- 0,083·P) =(0,333 — 0,333 –
— 0,25 — 0,167 — 0,083) ·P = — 0,5·P = — 0,5·2 = 1,0 кН, что равно подсчитанному аналитически V2 = -1,0 кН.
D3 = (-0,200·P- 0,401·P+ 0,601·P+ 0,401·P+ 0,200·P) = (-0,200 –
— 0,401 + 0,601 + 0,401 + 0,200) ·P = 0,601·P = 0,601·2 = 1,202 кН, что равно подсчитанному аналитически D3 = 1,202 кН
V3 = -1·P= — 2 кН, что равно подсчитанному аналитически V3 = — 2 кН
studfiles.net
Пример расчета треугольной фермы
Пример расчета треугольной фермы.
При расчете промышленных ферм, перекрывающих большие пролеты и работающих под большими нагрузками, может использоваться до 10-15 видов сечений, точнее профилей с различными параметрами сечения. Это связано с тем, что напряжения в стержнях фермы разные и потому максимально точный подбор сечения при промышленных объемах производства ферм дает ощутимую экономию. В частном же строительстве при изготовлении ферм используются 1-2, максимум 3 вида сечений, не только из экономических, но и из эстетических соображений и потому достаточно рассчитать максимально нагруженные стержни и по этим показателям принимать сечение для остальных стержней фермы. В общем виде это может выглядеть примерно так:
Имеется открытая площадка размерами 10х5 м возле дома и эту площадку хочется сделать закрытой, чтобы летом можно было пить чай на улице, не взирая на погодные условия, точнее взирая, но из-под надежного навеса, а еще чтобы можно было поставить машину под навес, сэкономив на гараже, да и вообще чтобы была защита от солнечного зноя в летний день. Вот только 10 метров — пролет большой и балку для такого пролета подобрать трудно, да и слишком массивной будет эта самая балка — скучно и вообще напоминает заводской цех. В таких случаях оптимальный вариант — сделать вместо балок фермы, а потом уже по фермам кидать обрешетку и делать кровлю. Само собой форма фермы может быть любой, но далее будет рассматриваться расчет треугольной фермы, как наиболее простой вариант. Проблемы расчета колонн для подобного навеса рассматриваются отдельно, расчет двух ферм с параллельными поясами или ригелей, на которые будут опирать фермы, здесь также не приводится.
Пока предполагается, что фермы будут располагаться с шагом 1 метр, а нагрузка на ферму от обрешетки будет передаваться только в узлах фермы. Кровельным материалом будет служить профнастил. Высота фермы может быть теоретически любой, вот только если это навес, примыкающий к основному зданию, то главным ограничителем будет форма кровли, если здание одноэтажное, или окна второго этажа, если этажей больше, но в любом случае сделать высоту фермы больше 1 м вряд ли получится, а с учетом того, что надо делать еще и ригеля между колоннами, то и 0.8 м не всегда выйдет (тем не менее примем эту цифру для расчетов). На основании этих предположений уже можно конструировать ферму:
Рисунок 1. Общая предварительная схема навеса по фермам.
На рисунке 1 голубым цветом показаны балки обрешетки, синим цветом — ферма, которую следует рассчитать, фиолетовым цветом — балки или фермы, на которые опираются колонны, изменение цвета от светло-голубого к темно-фиолетовому в данном случае показывает увеличение расчетной нагрузки, а значит для для более темных конструкций потребуются более мощные профили. Фермы на рисунке 1 показаны темно-зеленым цветом из-за совершенно иного характера нагрузки. Таким образом расчет всех элементов конструкции по отдельности, как то:
— стальных листов профнастила
— балок обрешетки (балки обрешетки можно рассматривать как многопролетные балки, если длина балок будет около 5 м, если балки будут делаться длиной около 1 м, т.е. между фермами, тогда это обычные однопролетные балки на шарнирных опорах)
— ферм кровли (достаточно определить нормальные напряжения в поперечных сечениях стержней, о чем речь ниже)
— балок или ферм под фермами кровли (рассчитываются как однопролетные балки или фермы)
— колонн
никаких особых проблем не представляет. Однако целью данной статьи является показать пример расчета именно треугольной фермы, этим мы и займемся. На рисунке 1 можно рассмотреть 6 треугольных ферм, при этом на крайние (переднюю и заднюю) фермы нагрузка будет в 2 раза меньше, чем на остальные фермы. Это означает, что эти две фермы если есть стойкое желание сэкономить на материалах, следует рассчитывать отдельно. Однако из эстетических и технологических соображений лучше все фермы сделать одинаковыми, а это значит, что достаточно рассчитать все лишь одну ферму (показана на рис. 1 синим цветом). В данном случае ферма будет консольной, т.е. опоры фермы будут располагаться не на концах фермы, а в узлах, показанных на рисунке 2. Такая расчетная схема позволяет более равномерно распределить нагрузки, а значит, и использовать для изготовления ферм профили меньшего сечения. Для изготовления ферм планируется использовать квадратные профильные трубы одного типа, а подобрать требуемое сечение профильной трубы поможет дальнейший расчет.
Если балки обрешетки будут опираться сверху на узлы ферм, то нагрузку от навеса из профнастила и снега лежащего на этом профнастиле, можно считать сосредоточенной, приложенной в узлах фермы. Стержни фермы будут свариваться между собой, при этом стержни верхнего пояса скорее всего будут неразрезными длиной примерно 5.06 м. Однако будем считать, что все узлы фермы — шарнирные. Эти уточнения могут показаться незначительной мелочью, однако позволяют максимально ускорить и упростить расчет, по причинам, изложенным в другой статье. Единственное, что нам осталось определить для дальнейших расчетов, сосредоточенную нагрузку, но и это сделать не сложно, если профнастил или балки обрешетки уже рассчитаны. При расчете профнастила мы выяснили, что листы профнастила длиной 5.1-5.3 м представляют собой многопролетную неразрезную балку с консолью. Это означает, что опорные реакции для такой балки и соответственно нагрузки для нашей фермы будут не одинаковыми, однако изменения опорных реакций для 5 пролетной балки будут не такими уж и значительными и для упрощения расчетов можно считать, что нагрузка от снега, профнастила и обрешетки будет передаваться равномерно, как в случае с однопролетными балками. Такое допущение приведет только к небольшому запасу по прочности. В итоге мы получаем следующую расчетную схему для нашей фермы:
Рисунок 2. Расчетная схема для треугольной фермы.
На рисунке 2 а) представлена общая расчетная схема нашей фермы, расчетная нагрузка составляет Q = 190 кг, что вытекает из расчетной снеговой нагрузки 180 кг/м2, веса профнастила и возможного веса балки обрешетки. На рисунке 2 б) показаны сечения, благодаря которым можно рассчитать усилия во всех стержнях фермы с учетом того что ферма и нагрузка на ферму является симметричной и значит достаточно рассчитывать не все стержни фермы, а чуть больше половины. А чтобы не запутаться во многочисленных стержнях при расчете, стержни и узлы ферм принято маркировать. Маркировка, показанная на рис. 2 в) означает, что у фермы есть:
Стержни нижнего пояса: 1-а, 1-в, 1-д, 1-ж, 1-и;
Стержни верхнего пояса: 2-а, 3-б, 4-г, 5-е, 6-з;
Раскосы: а-б, б-в, в-г, г-д, д-е, е-ж, ж-з, з-и.
Если будет рассчитываться каждый стержень фермы, то желательно составить таблицу, в которую следует внести все стержни. Затем в эту таблицу будет удобно вносить полученное значение сжимающих или растягивающих напряжений.
Ну а сам расчет никаких особенных сложностей не представляет, если ферма будет свариваться из 1-2 видов профилей замкнутого сечения. Например, весь расчет фермы можно свести к тому, чтобы рассчитать усилия в стержнях 1-и, 6-з и з-и. Для этого достаточно рассмотреть продольные силы, возникающие при отсечении части фермы по линии IX-IX (рис. 2 г).
Но оставим сладкое на третье, и посмотрим как это делается на более простых примерах, для этого рассмотрим
сечение I-I (рис. 2.1 д)
Если указанным образом отсечь лишнюю часть фермы, то нужно определить усилия только в двух стержнях фермы. Для этого используются уравнения статического равновесия. Так как в узлах фермы шарниры, то и значение изгибающих моментов в узлах фермы равно нулю, а кроме того, исходя из тех же условий статического равновесия сумма всех сил относительно оси х или оси у также равна нулю. Это позволяет составить как минимум три уравнения статического равновесия (два уравнения для сил и одно для моментов), но в принципе уравнений моментов может быть столько же сколько узлов в ферме и даже больше, если использовать точки Риттера. А это такие точки в которых пересекаются две из рассматриваемых сил и при сложной геометрии фермы точки Риттера не всегда совпадают с узлами фермы. Тем не менее в данном случае у нас геометрия достаточно простая (до сложной геометрии мы еще успеем добраться) и потому для определения усилий в стержнях достаточно имеющихся узлов фермы. Но при этом опять же из соображений простоты расчета обычно выбираются такие точки, уравнение моментов относительно которой позволяет сразу определить неизвестное усилие, не доводя дело до решения системы из 3 уравнений.
Выглядит это примерно так. Если составить уравнение моментов относительно точки 3 (рис. 2 д), то в нем будут всего два члена, причем один из них уже известный:
М3 = -Ql/2 + N2-ah = 0;
N2-ah = Ql/2;
где l — расстояние от точки 3 до точки приложения силы Q/2, которое в данном случае и является плечом действия силы, согласно принятой нами расчетной схемы l = 1.5 м; h- плечо действия силы N2-a (плечо показано на рис. 2.2 д) синим цветом).
При этом третий возможный член уравнения равен нулю, так как сила N1-а (на рис. 2.2 д) показана серым цветом) направлена по оси, проходящей через точку 3 и значит плечо действия равно нулю. Единственное, что в этом уравнении нам неизвестно — это плечо действия силы N2-а, впрочем определить его, владея соответствующими знаниями по геометрии, легко.
Наша ферма имеет расчетную высоту 0.8 м и общую расчетную длину 10 м. Тогда тангенс угла α составит tgα = 0.8/5 = 0.16, соответственно значение угла α = arctgα = 9.09о. И тогда
h = lsinα
Теперь нам ничего не мешает определить значение силы N2-a:
N2-a = Ql/(2lsinα) = 190/(2·0.158) = 601.32 кг
Подобным же образом определяется значение N1-а. Для этого составляется уравнение моментов относительно точки 2:
М2 = -Ql/2 + N1-ah = 0;
N1-ah = Ql/2
N1-a = Q/(2tgα) = 190/(2·0.16) = 593.77 кг
Проверить правильность вычислений мы можем, составив уравнения сил:
ΣQy = Q/2 — N2-asinα = 0; Q/2 = 95= 601.32·0.158 = 95 кг
ΣQx = N2-acosα — N1-a = 0; N1-a = 593.77 = 601.32·0.987 = 593.77 кг
Условия статического равновесия выполняются и любое из уравнений сил, использованных для проверки, можно было использовать для определения усилий в стержнях. Вот, собственно и все, дальнейший расчет фермы — чистейшая механика, но на всякий случай рассмотрим еще
сечение II-II (рис.2. e)
На первый взгляд кажется, что более простым будет уравнение моментов относительно точки 1 для определения силы Nа-б, однако в этом случае потребуется для определения плеча силы сначала найти значение угла β. А вот если рассматривать равновесие системы относительно точки 3, то:
М3 = -Ql/2 — Ql/3 + N3-бh = 0;
N3-бh = 5Ql/6;
N3-б = 5Q/(6sinα) = 5·190/(6·0.158) = 1002.2 кг (работает на растяжение)
Ну а теперь все же определим значение угла β. Исходя из того, что известны все стороны некоего прямоугольного треугольника (нижний катет или длина треугольника — 1 м, боковой катет или высота треугольника — 0.16 м, гипотенуза — 1.012 м и даже угол α), то соседний прямоугольный треугольник с высотой 0.16 м и длиной 0.5 м будет иметь tgβ = 0.32 и соответственно угол между длиной и гипотенузой β = 17.744о, полученный из арктангенса. И теперь проще составить уравнение сил относительно оси х:
ΣQx = N3-бcosα + Nа-бcosβ- N1-а = 0;
Na-б = (N1-а — N3-бcosα)/cosβ = (593.77 — 1002.2·0.987)/ 0.952 = — 415.61 кг
В данном случае знак «-» показывает, что сила направлена в сторону, противоположную от той, которую мы приняли при составлении расчетной схемы. И тут пришло время поговорить о направлении сил, точнее, о том значении, которое в это направление вкладывается. Когда мы заменяем внутренние усилия в рассматриваемом поперечном сечении стержней фермы, то под силой направленной от поперечного сечения подразумеваются растягивающие напряжения, если сила направлена к поперечному сечению, то подразумеваются сжимающие напряжения. С точки зрения статического равновесия не важно какое направление силы принимать при расчетах, если сила будет направлена в противоположную сторону, то значит у этой силы будет знак минус. Однако при расчете важно знать, на какое именно усилие рассчитывается данный стержень. Для растягиваемых стержней принцип определения необходимого сечения простейший:
σ = N/F ≤ R
При расчете стержней, работающих на сжатие, следует учитывать множество различных факторов и в общем виде формулу для расчета сжатых стержней можно выразить так:
σ = N/φF ≤ R
Примечание: расчетную схему можно составлять так, чтобы все продольные силы были направлены от поперечных сечений. В этом случае знак «-» перед значением силы, полученный при расчетах, будет показывать, что данный стержень работает на сжатие.
Так результаты предыдущего расчета показывают, что в стержнях 2-а и 3-б возникают растягивающие напряжения, в стержнях 1-а и а-б — сжимающие усилия. Ну а теперь вернемся к цели нашего расчета — определению максимальных нормальных напряжений в стержнях. Как и в обычной симметричной балке, у которой максимальные напряжения при симметричной нагрузке возникают в сечении, наиболее удаленном от опор, в ферме максимальные напряжения возникают в стержнях наиболее удаленных от опор, т.е. в стержнях, отсекаемых сечением IX-IX.
сечение IX-IX (рис. 2. г)
М9 = -4.5Q/2 — 3.5Q — 2.5Q — 1.5Q -0.5Q + 3VA — 4.5N6-зsinα = 0;
N6-з = (15Q — 10.25Q)/(4.5sinα) = 4.75·190/(4.5·0.158) = 1269.34 кг (работает на сжатие)
где VA = 5Q, определяются опорные реакции ферм все по тем же уравнениям равновесия системы, так как ферма и нагрузки симметричные, то
VA = ΣQy/2 = 5Q;
так как горизонтальных нагрузок у нас пока не предусмотрено, то горизонтальная опорная реакция на опоре А будет равна нулю, поэтому HA показано на рисунке 2 б) светло фиолетовым цветом.
плечи у всех сил в данном случае разные, а потому сразу подставлены числовые значения плеч в формулу.
Чтобы определить усилие в стержне з-и, нужно сначала определить значение угла γ (на рисунке не показан). Исходя из того, что известны две стороны некоего прямоугольного треугольника (нижний катет или длина треугольника — 0.5 м, боковой катет или высота треугольника — 0.8 м, то tgγ = 0.8/0.5 = 1.6 и значение угла γ = arctgγ = 57.99о. И тогда для точки 3
h = 3sinγ = 2.544 м. Тогда:
М3 = — 1.5Q/2 — 0.5Q + 0.5Q + 1.5Q + 2.5Q — 1.5N6-зsinα + 2.544Nз-и = 0;
Nз-и = (1.25Q — 4.5Q + 1.5N6-зsinα)/2.544 = (332.5 — 617.5)/2.544 = -112 кг
И теперь проще составить уравнение сил относительно оси х:
ΣQx = — N6-зcosα — Nз-иcosγ + N1-и = 0;
N1-и = N6-зcosα + Nз-иcosγ= 1269.34·0.987 — 112·0.53 = 1193.46 кг (работает на растяжение)
Так как верхний и нижний пояса фермы будут из одного типа профиля, то тратить время и силы на расчет стержней нижнего пояса 1-в, 1-д и 1-ж, равно как и стержней верхнего пояса 4-г и 5-е нет необходимости. Усилия в этих стержнях будут явно меньше уже определенных нами. Если бы ферма была бесконсольной, т.е. опоры располагались на концах фермы, то усилия в раскосах также были бы меньше уже определенных нами, однако у нас ферма с консолями и потому воспользуемся еще несколькими сечениями, чтобы определить усилия в раскосах по приведенному выше алгоритму (подробности расчета не приводятся):
Nб-в = -1527.34 кг — работает на сжатие (сечение III-III, рис. 2 ж), определялось по уравнению моментов относительно точки 1)
Nв-г = 634.43 кг — работает на растяжение (сечение IV-IV, рис. 2 з), определялось по уравнению моментов относительно точки 1)
Nг-д = — 493.84 кг — работает на сжатие (сечение V-V, определялось по уравнению моментов относительно точки 1)
Таким образом самыми загруженными у нас являются два стержня N6-з = 1269.34 кг и Nб-в = — 1527.34 кг. Оба стержня работают на сжатие и если вся ферма будет изготавливаться из одного типа профиля, то достаточно рассчитать один из этих стержней по предельным напряжениям и на основе этих расчетов подобрать необходимое сечение профиля. Однако тут все не так просто, на первый взгляд кажется, что достаточно рассчитать стержень Nб-в, но при расчете сжатых элементов большое значение имеет расчетная длина стержня. Так длина стержня N6-з составляет 101.2 см, в то время как длина стержня Nб-в составляет 59.3 см. Поэтому, чтобы не гадать, лучше рассчитать оба стержня.
стержень Nб-з
Расчет сжатых стержней ничем не отличается от расчета центрально сжатых колонн, поэтому далее приводятся только основные этапы расчета без подробных пояснений.
по таблице 1 (см. ссылку выше) определяем значение μ = 1 (не смотря на то, что верхний пояс фермы будет из цельного профиля, расчетная схема фермы подразумевает шарнирное закрепление стержней в узлах фермы, поэтому более правильным будет принять вышеуказанное значение коэффициента).
Принимаем предварительно значение λ = 90, тогда по таблице 2 коэффициент изгиба φ = 0.625 (для стали С235 прочностью Ry = 2350 кгс/см2, определяется интерполяцией значений 2050 и 2450)
Тогда требуемый радиус инерции составит:
i = μl/λ = 101.2/90 = 1.125 см
По сортаменту для квадратных профильных труб этим условиям удовлетворяет профиль 30х30х2 мм с площадью сечения F = 2.17 см2 (радиус инерции i = √(I/F) = 1.133 см), осталось проверить этот профиль на устойчивость:
1269.34/(0.625·2.17) = 935.92 кгс/см2 < Ry = 2350 кгс/см2;
Примечание: Если расчетное сопротивление профильной трубы, которая будет использоваться для изготовления фермы, известно, то следует принимать известное значение расчетного сопротивления, если расчетное сопротивление не известно, то лучше принимать значение, минимальное из возможных, как в данном случае.
Так как у нас имеется более чем двукратный запас по прочности рассчитывать стержень б-в нет большой необходимости. Ну а дальше количество вариантов конструирования поистине безгранично. Например, можно уменьшить сечение профильной трубы, это приведет к увеличению значения коэффициента гибкости, например, для профильной трубы сечением 25х25х1.5 мм площадью сечения 1.37 см2 i = 0.951 см, λ = 106.4, φ = 0.516 и тогда
1269.34/(0.516·1.37) = 1795.68 кгс/см2 < Ry = 2350 кгс/см2;
Однако чем тоньше стенки трубы, тем труднее их аккуратно сварить. А вот если использовать более крупное сечение, то можно сделать не 6, а 4 или даже 3 фермы, а это экономия по времени работы в 1.5-2 раза. Для изготовления 4 ферм с шагом 1.67 м и даже 3 ферм с шагом 2.5 м вполне можно использовать профильную трубу сечением 30х30х2 мм, при таком шаге только увеличится значение продольной силы:
1269.34·2.5/(0.625·2.17) = 2339.8 кгс/см2 < Ry = 2350 кгс/см2;
Проверим устойчивость стержня б-в для данного сечения. Так как расчетная длина стержня б-в меньше, то соответственно будет меньше и значение λ = 59.3/1.133= 52.3, тогда φ ≈ 0.84
1527.34·2.5/(0.83·2.17) = 2120 кгс/см2 < Ry = 2350 кгс/см2;
Таким образом все необходимые условия по прочности и устойчивости нами соблюдены. Однако если учесть, что в стержнях фермы будут возникать дополнительные напряжения, например, при неравномерном проседании колонн фундамента, что вполне вероятно, то лучше не рисковать, а подбирать сечение с хорошим запасом.
Примечание: При уменьшении количества ферм пролет балок обрешетки значительно увеличивается и значит для балок обрешетки придется использовать профильные трубы большего сечения. Но это и есть тонкости проектирования и поиска оптимального варианта.
А вот если нет возможности расположить опоры фермы так, как показано на рисунке 272.1, а только по концам фермы, то в этом случае ферма будет бесконсольной и нагрузки в стержнях фермы при сохранении геометрии фермы будут совсем другие и тогда усилия во всех стержнях следует просчитывать. Для примера, наибольшее сжимающее усилие будет возникать в стержне N2-а. Из-за перемещения опорной реакции VA из точки 3 в точку 1 и уравнение моментов относительно все той же точки 3 будет иметь следующий вид (сечение I-I):
М3 = -1.5Q/2 + 1.5VA + 1.5N2-asinα = 0;
N2-а = (0.5Q — 5Q)/sinα = — 4.5·190/0.158 = — 5411.88 кг
В данном случае стержень 2-а будет работать на сжатие и усилия в этом стержне будут в 4.2 раза больше, чем при расчетной схеме фермы с консолями и для таких ферм (как минимум четырех) сразу потребуется профильная труба сечением 40х40х2.5 мм. Уменьшение высоты фермы также приведет к увеличению напряжений в стержнях фермы, да и стыки профнастила при уменьшении уклона уже не будут так надежно защищать от атмосферных осадков.
Таковы вкратце основные принципы расчета и проектирования треугольных ферм.
freedocs.xyz
Деревянные фермы. Выбор схемы фермы и её расчет
1. ОБЩИЕ СВЕДЕНИЯ.
В современном промышленном и гражданском строительстве применяют деревянные фермы – однопролетные балочные. В отдельных случаях находят применение также трехшарнирные арки, составленные из балочных ферм или клееных блоков. Деревянные фермы изготовляют из круглого леса или пиломатериалов — брусьев и досок. Фермы имеют следующие элементы: верхний пояс, нижний пояс, решетку (стойки и раскосы).
Взаимное сопряжение указанных элементов в узлах осуществляют при помощи различных соединений (врубки, нагели, хомуты, шпонки).
Верхний пояс балочных ферм при вертикальной нагрузке, направленной сверху вниз, работает на сжатие, а нижний — на растяжение. Усилия в стойках и раскосах зависят как от направления этих стержней, так и от расположения нагрузок.

Самыми ответственными элементами деревянных ферм являются стержни нижнего растянутого пояса, на работе которых в большой мере сказывается вредное влияние неизбежных в строительной древесине пороков (сучков, косослоя, трещин), поэтому при конструировании, отборе лесоматериалов, изготовлении и наблюдении за фермами во время их эксплуатации, стержням нижнего пояса нужно уделять особое внимание.
С целью наиболее рационального использования достоинств конструктивных материалов, растянутые элементы деревянных ферм часто выполняют из стали. Такие фермы называют металлодеревянными.
По очертанию наружного контура фермы подразделяют на: треугольные, прямоугольные (с параллельными поясами), трапецивидные или полигональные с наклонным (двускатным или односкатным) прямолинейным верхним поясом[1], сегментные и многоугольные (рис.1).
При равномерной загрузке всей фермы вертикальной нагрузкой, усилия в стержнях решетки прямоугольных и пологих (уклон ~1/10) полигональных ферм возрастают от середины пролета к опорам, а в треугольных от опор к середине. Характер изменения усилий в поясах и решетке треугольных, прямоугольных и полигональных ферм представлен на рис.2.

Экономичность ферм определяется прежде всего расходом древесины и металла, а также трудоемкостью изготовления и монтажа конструкции.
При оценке типов деревянных ферм в отношении расхода древесины необходимо иметь в виду, что стоимость древесины в большой мере зависит от степени обработки и сортамента применяемых лесоматериалов. Так стоимость окантованных брусьев почти в полтора раза, досок в 2 раза и чистообрезных брусьев примерно в 2,5–3 раза выше стоимости круглых лесоматериалов.
Существенное влияние на расход древесины и металла может оказать очертание наружного контура фермы. Теоретически наивыгоднейшим очертанием контура является такое, при котором контур фермы приближается к очертанию эпюры моментов.
При одних и тех же нагрузках, качестве лесоматериалов, пролетах и высотах ферм наиболее легкими, а следовательно, и требующими наименьшего расхода древесины, будут сегментные фермы и трехшарнирные арки из них. Простота конструкции и экономичность, обусловленные статическими свойствами сегментных ферм, обеспечивают широкое распространение этих ферм в строительстве.
Многоугольные фермы с ломаным очертанием верхнего пояса также имеют относительно небольшой вес и отличаются простотой узловых сопряжений и экономичностью.
Полигональные фермы с наклоном верхнего пояса в 1/10-1/5 получаются более тяжелыми, чем сегментные фермы, но все же значительно более экономичными, чем фермы прямоугольного и треугольного очертания.
Наиболее тяжелыми из всех типов ферм оказываются треугольные фермы. Их применяют, как правило, для кровель из материалов, требующих значительного уклона (черепица, шифер и т.д.).
2. ВЫБОР СХЕМЫ ФЕРМЫ. ОСНОВНЫЕ ПРЕДПОСЫЛКИ К ПРОЕКТИРОВАНИЮ.
В студенческом курсовом
проектировании обычно используются два типа ферм – треугольная ферма и пологая
полигональная ферма (рис.3).
vunivere.ru
Пример расчета треугольной фермы | Файловый клуб FilesClub.net
Пример расчета треугольной фермы.
При расчете промышленных ферм, перекрывающих большие пролеты и работающих под большими нагрузками, может использоваться до 10-15 видов сечений, точнее профилей с различными параметрами сечения. Это связано с тем, что напряжения в стержнях фермы разные и потому максимально точный подбор сечения при промышленных объемах производства ферм дает ощутимую экономию. В частном же строительстве при изготовлении ферм используются 1-2, максимум 3 вида сечений, не только из экономических, но и из эстетических соображений и потому достаточно рассчитать максимально нагруженные стержни и по этим показателям принимать сечение для остальных стержней фермы. В общем виде это может выглядеть примерно так:
Имеется открытая площадка размерами 10х5 м возле дома и эту площадку хочется сделать закрытой, чтобы летом можно было пить чай на улице, не взирая на погодные условия, точнее взирая, но из-под надежного навеса, а еще чтобы можно было поставить машину под навес, сэкономив на гараже, да и вообще чтобы была защита от солнечного зноя в летний день. Вот только 10 метров — пролет большой и балку для такого пролета подобрать трудно, да и слишком массивной будет эта самая балка — скучно и вообще напоминает заводской цех. В таких случаях оптимальный вариант — сделать вместо балок фермы, а потом уже по фермам кидать обрешетку и делать кровлю. Само собой форма фермы может быть любой, но далее будет рассматриваться расчет треугольной фермы, как наиболее простой вариант. Проблемы расчета колонн для подобного навеса рассматриваются отдельно, расчет двух ферм с параллельными поясами или ригелей, на которые будут опирать фермы, здесь также не приводится.
Пока предполагается, что фермы будут располагаться с шагом 1 метр, а нагрузка на ферму от обрешетки будет передаваться только в узлах фермы. Кровельным материалом будет служить профнастил. Высота фермы может быть теоретически любой, вот только если это навес, примыкающий к основному зданию, то главным ограничителем будет форма кровли, если здание одноэтажное, или окна второго этажа, если этажей больше, но в любом случае сделать высоту фермы больше 1 м вряд ли получится, а с учетом того, что надо делать еще и ригеля между колоннами, то и 0.8 м не всегда выйдет (тем не менее примем эту цифру для расчетов). На основании этих предположений уже можно конструировать ферму:
Рисунок 1. Общая предварительная схема навеса по фермам.
На рисунке 1 голубым цветом показаны балки обрешетки, синим цветом — ферма, которую следует рассчитать, фиолетовым цветом — балки или фермы, на которые опираются колонны, изменение цвета от светло-голубого к темно-фиолетовому в данном случае показывает увеличение расчетной нагрузки, а значит для для более темных конструкций потребуются более мощные профили. Фермы на рисунке 1 показаны темно-зеленым цветом из-за совершенно иного характера нагрузки. Таким образом расчет всех элементов конструкции по отдельности, как то:
— стальных листов профнастила- балок обрешетки (балки обрешетки можно рассматривать как многопролетные балки, если длина балок будет около 5 м, если балки будут делаться длиной около 1 м, т.е. между фермами, тогда это обычные однопролетные балки на шарнирных опорах)
— ферм кровли (достаточно определить нормальные напряжения в поперечных сечениях стержней, о чем речь ниже)
— балок или ферм под фермами кровли (рассчитываются как однопролетные балки или фермы)
— колоннникаких особых проблем не представляет. Однако целью данной статьи является показать пример расчета именно треугольной фермы, этим мы и займемся. На рисунке 1 можно рассмотреть 6 треугольных ферм, при этом на к
filesclub.net