Краткий курс сопротивления материалов
Краткий курс сопротивления материалов
ОглавлениеГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ и ОПРЕДЕЛЕНИЯ1.3. КЛАССИФИКАЦИЯ ВНЕШНИХ СИЛ 1.  1.5. ОПОРНЫЕ УСТРОЙСТВА. ОПОРНЫЕ РЕАКЦИИ 1.6. ОСНОВНЫЕ ГИПОТЕЗЫ О СВОЙСТВАХ МАТЕРИАЛА 1.7. ПОНЯТИЕ О РАСЧЕТНОЙ СХЕМЕ 1.8. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ 1.9. НАПРЯЖЕНИЕ. ПОНЯТИЕ О НАПРЯЖЕННОМ СОСТОЯНИИ 1.10. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ 1.11. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ В БРУСЕ 1.12. ВИДЫ ДЕФОРМАЦИЙ БРУСА ГЛАВА 2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОГО БРУСА 2.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ БРУСА 2.3. КОЭФФИЦИЕНТ ПОПЕРЕЧНОЙ ДЕФОРМАЦИИ (КОЭФФИЦИЕНТ ПУАССОНА) 2.4. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ 2.5. НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ 2.6. ЗАКОН ГУКА ПРИ ОДНООСНОМ РАСТЯЖЕНИИ. ПРИНЦИП НЕЗАВИСИМОСТИ ДЕЙСТВИЯ СИЛ 2.7. УДЛИНЕНИЯ И ПЕРЕМЕЩЕНИЯ 2.8. ОПРЕДЕЛЕНИЕ МЕХАНИЧЕСКИХ СВОЙСТВ МАТЕРИАЛА ПРИ РАСТЯЖЕНИИ 2.9. ДИАГРАММЫ УСЛОВНЫХ И ИСТИННЫХ НАПРЯЖЕНИЙ 2.10. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛА 2.11. ЗАКОН РАЗГРУЗКИ И ПОВТОРНОГО НАГРУЖЕНИЯ 2.12. ПЛАСТИЧНЫЕ И ХРУПКИЕ МАТЕРИАЛЫ 2.  13. МЕХАНИЧЕСКИЕ СВОЙСТВА ПРИ СЖАТИИ 13. МЕХАНИЧЕСКИЕ СВОЙСТВА ПРИ СЖАТИИ2.14. ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ 2.15. ПОЛЗУЧЕСТЬ. ПОСЛЕДЕЙСТВИЕ И РЕЛАКСАЦИЯ 2.16. ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ 2.17. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ 2.18. О РАСЧЕТЕ НА ПРОЧНОСТЬ 2.19. ДВА ТИПА РАСЧЕТОВ НА ПРОЧНОСТЬ 2.20. ЭПЮРЫ НОРМАЛЬНЫХ СИЛ, НОРМАЛЬНЫХ НАПРЯЖЕНИЙ И ПЕРЕМЕЩЕНИЙ 2.21. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ РАСТЯЖЕНИИ И СЖАТИИ 2.22. ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ 2.23. МОНТАЖНЫЕ УСИЛИЯ 2.24. НАПРЯЖЕНИЯ ПРИ ДВУХОСНОМ РАСТЯЖЕНИИ И СЖАТИИ 2.25. ЗАКОН ГУКА ПРИ ДВУХОСНОМ И ТРЕХОСНОМ РАСТЯЖЕНИИ 2.26. ИЗМЕНЕНИЕ ОБЪЕМА ПРИ ТРЕХОСНОМ РАСТЯЖЕНИИ 2.27. УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ТРЕХОСНОМ РАСТЯЖЕНИИ И СЖАТИИ 2.28. ЗАКОН ПАРНОСТИ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ ГЛАВА 3. СДВИГ 3.2. ЧИСТЫЙ СДВИГ 3.4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ СДВИГЕ ГЛАВА 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ 4. 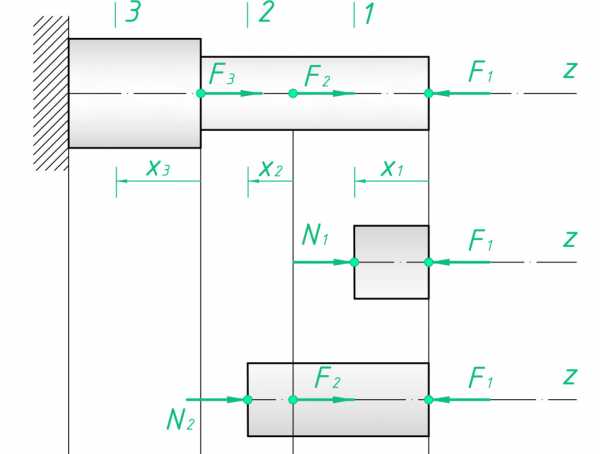 2. ЦЕНТР ТЯЖЕСТИ СЕЧЕНИЯ 2. ЦЕНТР ТЯЖЕСТИ СЕЧЕНИЯ4.3. ЗАВИСИМОСТЬ МЕЖДУ МОМЕНТАМИ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ 4.4. МОМЕНТЫ ИНЕРЦИИ ПРОСТЕЙШИХ ФИГУР 4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЛОЖНЫХ ФИГУР 4.6. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ КООРДИНАТ 4.7. ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ 4.8. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ГЛАВНЫХ ОСЕЙ ГЛАВА 5. КРУЧЕНИЕ 5.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ ЦИЛИНДРИЧЕСКОГО БРУСА КРУГЛОГО СЕЧЕНИЯ 5.3. НАПРЯЖЕНИЯ В РАЗЛИЧНО ОРИЕНТИРОВАННЫХ СЕЧЕНИЯХ И ХАРАКТЕР РАЗРУШЕНИЯ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО СЕЧЕНИЯ 5.4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ 5.5. О НАПРАВЛЕНИИ ВЕКТОРА КАСАТЕЛЬНОГО НАПРЯЖЕНИЯ В КОНТУРНЫХ ТОЧКАХ СЕЧЕНИЯ ЦИЛИНДРИЧЕСКОГО БРУСА 5.6. КРУЧЕНИЕ ТОНКОСТЕННОГО БРУСА ЗАМКНУТОГО ПРОФИЛЯ 5.7. КРУЧЕНИЕ БРУСА ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ 5.8. КРУЧЕНИЕ ТОНКОСТЕННОГО БРУСА ОТКРЫТОГО ПРОФИЛЯ 5.9. ОБОБЩЕНИЕ РАСЧЕТНЫХ УРАВНЕНИЙ ДЛЯ БРУСЬЕВ РАЗЛИЧНЫХ СЕЧЕНИЙ 5.10. ЭПЮРЫ КРУТЯЩИХ МОМЕНТОВ, НАПРЯЖЕНИЙ И УГЛОВ ЗАКРУЧИВАНИЯ 5.  11. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ КРУЧЕНИИ 11. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ КРУЧЕНИИ5.12. ЦИЛИНДРИЧЕСКИЕ ВИНТОВЫЕ ПРУЖИНЫ МАЛОГО ШАГА 5.13. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ ЗАДАЧИ ПРИ КРУЧЕНИИ ГЛАВА 6. ИЗГИБ 6.2. ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ ПРИ ИЗГИБЕ БРУСА 6.3. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ИЗГИБЕ 6.4. ЭПЮРЫ ПЕРЕРЕЗЫВАЮЩИХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ 6.5. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ЧИСТОМ ИЗГИБЕ 6.6. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ. ФОРМУЛА ЖУРАВСКОГО 6.7. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ ТОНКОСТЕННЫХ БАЛОК 6.9. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ 6.10. РАЦИОНАЛЬНЫЕ ФОРМЫ ПОПЕРЕЧНЫХ СЕЧЕНИЙ 6.11. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ ИЗГИБЕ 6.12. ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ УПРУГОЙ ЛИНИИ И ЕГО ИНТЕГРИРОВАНИЕ 6.13. ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ СЕЧЕНИЙ БАЛОК. ИНТЕГРАЛ МОРА 6.14. СПОСОБ ВЕРЕЩАГИНА 6.15. БАЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ ГЛАВА 7. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ 7.2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ПРОСТРАНСТВЕННОМ БРУСЕ МАЛОЙ КРИВИЗНЫ.  ИНТЕГРАЛ МОРА ИНТЕГРАЛ МОРА7.3. ПЛОСКИЕ РАМЫ 7.4. ПРОСТРАНСТВЕННЫЕ РАМЫ 7.5. ПЛОСКОПРОСТРАНСТВЕННЫЕ РАМЫ 7.6. ФЕРМЫ 7.7. СМЕШАННЫЕ СИСТЕМЫ 7.8. ОТНОСИТЕЛЬНЫЕ ПЕРЕМЕЩЕНИЯ СЕЧЕНИЙ СТЕРЖНЕВОЙ СИСТЕМЫ ГЛАВА 8. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ 8.2. ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ КАНОНИЧЕСКИХ УРАВНЕНИЙ 8.3. ПОСЛЕДОВАТЕЛЬНОСТЬ РЕШЕНИЯ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ЗАДАЧ 8.4. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ СЕЧЕНИЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ 8.5. О РАЦИОНАЛЬНОМ ВЫБОРЕ ОСНОВНОЙ СИСТЕМЫ. ИСПОЛЬЗОВАНИЕ ПРЯМОЙ И ОБРАТНОЙ СИММЕТРИИ ГЛАВА 9. КОСОЙ ИЗГИБ. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ 9.2. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ ГЛАВА 10. ОСНОВЫ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ ТЕЛА 10.3. НАПРЯЖЕНИЯ НА ПРОИЗВОЛЬНО НАКЛОНЕННОЙ К ОСЯМ КООРДИНАТ ПЛОЩАДКЕ 10.4. НОРМАЛЬНЫЕ И КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ НА НАКЛОННОЙ ПЛОЩАДКЕ 10.5. ГЛАВНЫЕ ПЛОЩАДКИ И ГЛАВНЫЕ НАПРЯЖЕНИЯ. ИНВАРИАНТЫ НАПРЯЖЕННОГО СОСТОЯНИЯ 10.6. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ГЛАВНЫХ ПЛОЩАДОК 10.  7. ЭЛЛИПСОИД НАПРЯЖЕНИЙ 7. ЭЛЛИПСОИД НАПРЯЖЕНИЙ10.8. ЭКСТРЕМАЛЬНЫЕ ЗНАЧЕНИЯ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ И ПЛОЩАДКИ ИХ ДЕЙСТВИЯ 10.9. КРУГОВАЯ ДИАГРАММА НАПРЯЖЕНИЙ (КРУГИ МОРА) 10.10. НАПРЯЖЕНИЯ НА ПЛОЩАДКАХ, РАВНОНАКЛОННЫХ К ГЛАВНЫМ (ОКТАЭДРИЧЕСКИЕ НАПРЯЖЕНИЯ) 10.12. КЛАССИФИКАЦИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ В ТОЧКЕ ТЕЛА 10.13. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ 10.14. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ГЛАВНЫЕ ПЛОЩАДКИ В БРУСЕ 10.15. ДЕФОРМИРОВАННОЕ СССТОЯНИЕ В ТОЧКЕ ТЕЛА. АНАЛОГИЯ МЕЖДУ ЗАВИСИМОСТЯМИ ТЕОРИИ НАПРЯЖЕНИЙ И ТЕОРИИ ДЕФОРМАЦИЙ 10.16. ОБОБЩЕННЫЙ ЗАКОН ГУКА ДЛЯ ИЗОТРОПНОГО ТЕЛА 10.17. УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ И ЕЕ ДЕЛЕНИЕ НА УДЕЛЬНУЮ ЭНЕРГИЮ ИЗМЕНЕНИЯ ОБЪЕМА И УДЕЛЬНУЮ ЭНЕРГИЮ ИЗМЕНЕНИЯ ФОРМЫ 10.18. ОПРЕДЕЛЕНИЕ ГЛАВНЫХ НАПРЯЖЕНИЙ И ГЛАВНЫХ ДЕФОРМАЦИЙ ПО РЕЗУЛЬТАТАМ ЭКСПЕРИМЕНТА ГЛАВА 11. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ 11.2. НАЗНАЧЕНИЕ ТЕОРИЙ ПРЕДЕЛЬНОГО СОСТОЯНИЯ 11.3. ТЕОРИЯ НАИБОЛЬШИХ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ 11.  4. ТЕОРИЯ НАИБОЛЬШИХ ОТНОСИТЕЛЬНЫХ УДЛИНЕНИЙ 4. ТЕОРИЯ НАИБОЛЬШИХ ОТНОСИТЕЛЬНЫХ УДЛИНЕНИЙ11.5. ТЕОРИЯ НАИБОЛЬШИХ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ 11.6. ТЕОРИЯ УДЕЛЬНОЙ ЭНЕРГИИ ИЗМЕНЕНИЯ ФОРМЫ 11.7. ТЕОРИЯ МОРА 11.8. СООТНОШЕНИЯ МЕЖДУ ПРЕДЕЛАМИ ТЕКУЧЕСТИ ПРИ ПРОСТОМ РАСТЯЖЕНИИ И ЧИСТОМ СДВИГЕ ПО РАЗЛИЧНЫМ ТЕОРИЯМ 11.9. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ВЫБОРЕ ТЕОРИИ ПРЕДЕЛЬНЫХ СОСТОЯНИЙ ПРИ РАСЧЕТАХ 11.10. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ЕЕ ВЛИЯНИЕ НА ПРОЧНОСТЬ ПРИ ПОСТОЯННЫХ ВО ВРЕМЕНИ НАПРЯЖЕНИЯХ 11.11. О МЕХАНИКЕ ХРУПКОГО РАЗРУШЕНИЯ ГЛАВА 12. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ НАПРЯЖЕНИЯХ, ПЕРЕМЕННЫХ ВО ВРЕМЕНИ 12.2. МЕХАНИЗМ УСТАЛОСТНОГО РАЗРУШЕНИЯ 12.3. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 12.4. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ПРЕДЕЛА ВЫНОСЛИВОСТИ. ПРЕДЕЛ ОГРАНИЧЕННОЙ ВЫНОСЛИВОСТИ 12.5. ЗАВИСИМОСТЬ ПРЕДЕЛА ВЫНОСЛИВОСТИ ОТ СТЕПЕНИ АСИММЕТРИИ ЦИКЛА. ДИАГРАММА ПРЕДЕЛЬНЫХ АМПЛИТУД 12.6. ВЕРОЯТНОСТНЫЙ ХАРАКТЕР ЯВЛЕНИЯ УСТАЛОСТИ 12.7. МАЛОЦИКЛОВАЯ УСТАЛОСТЬ 12.8. ФАКТОРЫ, ВЛИЯЮЩИЕ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ 12.9. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ОДНООСНОМ НАПРЯЖЕННОМ СОСТОЯНИИ И ЧИСТОМ СДВИГЕ (ИЗГИБЕ, РАСТЯЖЕНИИ И КРУЧЕНИИ)  10. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОЕ НАПРЯЖЕННОМ СОСТОЯНИИ 10. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОЕ НАПРЯЖЕННОМ СОСТОЯНИИ12.11. СОПРОТИВЛЕНИЕ УСТАЛОСТИ ПРИ НЕСТАЦИОНАРНЫХ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ ГЛАВА 13. РАСЧЕТЫ ЗА ПРЕДЕЛАМИ УПРУГОСТИ 13.2. СХЕМАТИЗАЦИЯ ДИАГРАММ РАСТЯЖЕНИЯ 13.3. РАСЧЕТ ПО НАГРУЗКАМ, ИСЧЕРПЫВАЮЩИМ НЕСУЩУЮ СПОСОБНОСТЬ 13.4. РАСЧЕТ БАЛОК ПО НАГРУЗКАМ, ИСЧЕРПЫВАЮЩИМ НЕСУЩУЮ СПОСОБНОСТЬ 13.5. НЕСУЩАЯ СПОСОБНОСТЬ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК И РАМ 13.6. ЧИСТЫЙ УПРУГОПЛАСТИЧЕСКИЙ ИЗГИБ ПРЯМОГО БРУСА 13.7. РАЗГРУЗКА И ОСТАТОЧНЫЕ НАПРЯЖЕНИЯ ГЛАВА 14. РАСЧЕТ ПРОСТЕЙШИХ ОСЕСИММЕТРИЧНО НАГРУЖЕННЫХ ТОНКОСТЕННЫХ ОБОЛОЧЕК ВРАЩЕНИЯ 14.2. УРАВНЕНИЯ РАВНОВЕСИЯ ЭЛЕМЕНТА СИММЕТРИЧНОЙ БЕЗМОМЕНТНОЙ ОБОЛОЧКИ 14.3. ТЕОРЕМА О ДАВЛЕНИИ НА КРИВОЛИНЕЙНУЮ СТЕНКУ 14.4. РАСЧЕТ СФЕРИЧЕСКИХ И ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК НА НОРМАЛЬНОЕ ДАВЛЕНИЕ ПО БЕЗМОМЕНТНОЙ ТЕОРИИ ГЛАВА 15. РАСЧЕТ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ, ДВИЖУЩИХСЯ С УСКОРЕНИЕМ 15.2. РАСЧЕТ ПОСТУПАТЕЛЬНО ДВИЖУЩИХСЯ СИСТЕМ 15.3. НАПРЯЖЕНИЯ В ТОНКОСТЕННОМ ВРАЩАЮЩЕМСЯ КОЛЬЦЕ 15.  4. РАСЧЕТ РАВНОМЕРНО ВРАЩАЮЩЕГОСЯ ПРЯМОГО БРУСА 4. РАСЧЕТ РАВНОМЕРНО ВРАЩАЮЩЕГОСЯ ПРЯМОГО БРУСА15.5. ВРАЩАЮЩИЕСЯ РАМЫ ГЛАВА 16. УДАР 16.2. УДАР ПАДАЮЩЕГО ГРУЗА ПО УПРУГОЙ СИСТЕМЕ, МАССА КОТОРОЙ МАЛА ПО СРАВНЕНИЮ С МАССОЙ ГРУЗА 16.3. ПРИВЕДЕННАЯ МАССА. КОЭФФИЦИЕНТ ПРИВЕДЕНИЯ 16.4. УДАР ПО СИСТЕМЕ, МАССА КОТОРОЙ СОИЗМЕРИМА С МАССОЙ УДАРЯЮЩЕГО ГРУЗА ГЛАВА 17. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ. ПРОДОЛЬНЫЙ ИЗГИБ 17.2. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СИЛЫ МЕТОДОМ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ УПРУГОЙ ЛИНИИ СТЕРЖНЯ. ФОРМУЛА ЭЙЛЕРА 17.3. ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЭЙЛЕРА 17.5. ПРАКТИЧЕСКИЕ СПОСОБЫ РАСЧЕТА НА ПРОДОЛЬНЫЙ ИЗГИБ 17.6. ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ НАГРУЗКИ 17.7. ДИНАМИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ НАГРУЗКИ ГЛАВА 18. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ 18.3. ПРИБЛИЖЕННАЯ ФОРМУЛА ДЛЯ ОПРЕДЕЛЕНИЯ ПРОГИБА БАЛКИ ПРИ ПРОДОЛЬНО-ПОПЕРЕЧНОМ ИЗГИБЕ 18.4. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДЛЯ ИЗГИБАЮЩИХ МОМЕНТОВ 18.  5. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПРОДОЛЬНО-ПОПЕРЕЧНОМ ИЗГИБЕ 5. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПРОДОЛЬНО-ПОПЕРЕЧНОМ ИЗГИБЕ |
Деформация растяжения — презентация онлайн
1. Деформация растяжения
Деформация, при которой в поперечном сечении бруса возникает одинсиловой фактор—продольная сила N, называется растяжением (сжатием).
Продольной силой N называется равнодействующая внутренних сил,
распределенных по площади поперечного сечения (нормальных напряжений):
N
dA
A
При равномерном распределении нормальных напряжений :
N A
Правило знаков: растягивающая продольная сила считается положительной,
а сжимающая– отрицательной.
Сущность метода сечений заключается в том, что величина продольной
силы в сечении стержня равна сумме всех внешних продольных сил
приложенных по одну из сторон от выбранного сечения.
y
II
I
F =10 кН, F =15 кН, F =55 кН, F =30 кН;
1
F2
F1
A
x
F4
E
F3
C
B
I
D
F5
K
2
3
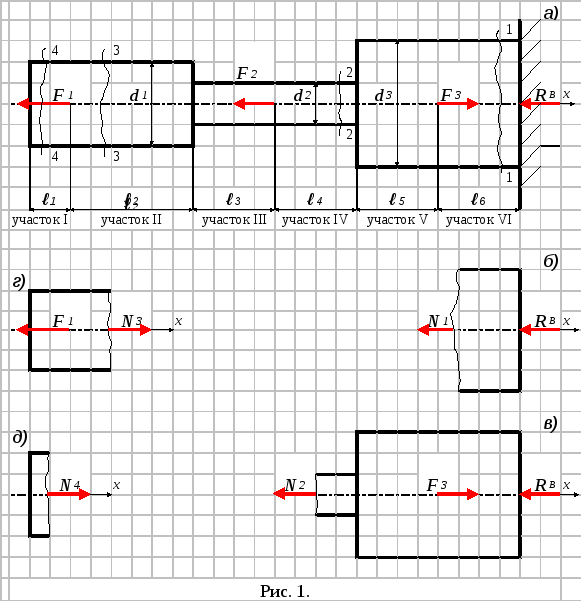
Определим продольные силы в
z сечениях I-I и II-II.
II
N1-1= -F1-F2= -10-15= -25 кН,
4
N11-11= -F1-F2+F3= -10-15+55=30 кН.
2. Построение эпюры продольных сил
Характерными называются сечения стержня где: 1) приложены внешниепродольные силы; 2) происходит ступенчатое, или начинается участок
постепенного изменения площади поперечного сечения бруса.
Эпюрой продольных сил называется график изменения продольной силы
по длине стержня (бруса).
y
Дано: F1=10 кН, F2=15 кН, F3=55 кН,
F4=30 кН.
F2
F1
A
F3
B
C
F5
F4
D
E
K
x
z
Построить эпюру продольных сил
Участок АВ NАВ=-F1=-10 кН.
Участок ВС NВС= -F1-F2= -10-15= -25 кН.
Эпюра N , кН
Участок CD NCD= -F1-F2= -10-15= -25 кН.
Участок DE NDE= -F1-F2+F3=-10-15+55=30 кН
30
15
10
25
Участок ЕК NEK= -F1-F2+F3-F4=
= -10-15+55-15=15 кН.
3. Построение эпюры продольных сил
Правила контроля эпюры продольных силОсновные правила контроля правильности построения эпюры
продольных сил можно сформулировать так:
1.
 В сечении, где приложена сосредоточенная сила F, эпюра
В сечении, где приложена сосредоточенная сила F, эпюрапродольных сил делает скачок на величину этой силы и с ее знаком.
2. Изменение площади поперечного сечения стержня влияния на
эпюру продольных сил не оказывает, независимо от характера этого
изменения (ступенчатое или постепенное).
3. На участке, где приложена равномерно распределенная нагрузка
эпюра продольных сил имеет вид прямой наклонной линии.
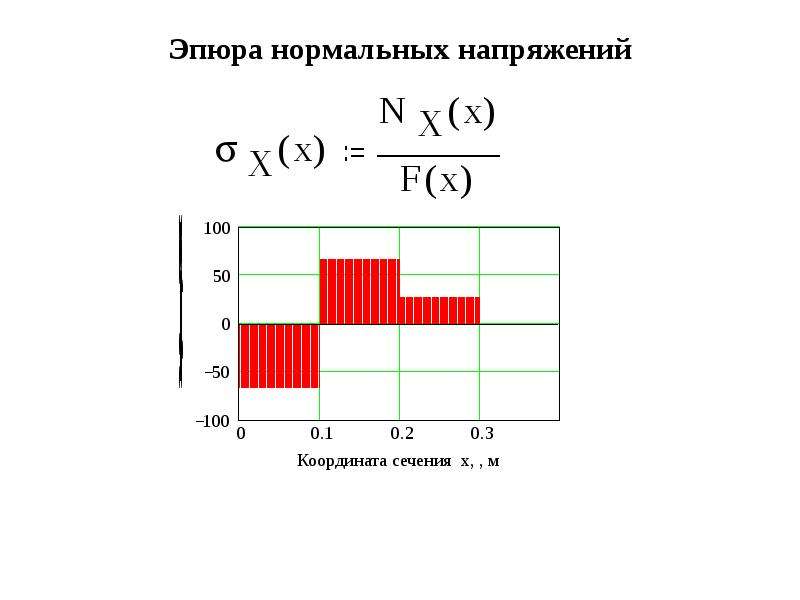
4. Построение эпюры нормальных напряжений
yПостроение эпюры нормальных напряжений
А2
А1
F2
F1
А1
F3
A
B
C
А3
F5
F4
D
E
K
x
Эпюра N , кН
30
15
Дано: А1=200 мм2, А2=250 мм2,
А3=150 мм2,
Построить эпюру нормальных
z напряжений
N
10000
AB AB
50 МПа.
A1
200
N
25000
BC BC
125 МПа .
A1
200
N
25000
CD CD
100 МПа .
A2
250
DE
10
25
N DE 30000
120 МПа .
A2
250
В начале участка ЕК
Эпюра , МПа
120
75
100
1EK
N EK 15000
75МПа ,
A1
200
В конце участка ЕК
2
EK
50
125
100
N EK 15000
100МПа ,
A3
150
5.
 Деформация растяженияПравила контроля эпюры нормальных напряжений
Деформация растяженияПравила контроля эпюры нормальных напряженийОсновные правила контроля правильности построения эпюры
нормальных напряжений можно сформулировать так:
1. На участке или в сечении стержня, где происходит изменение
площади поперечного сечения, нормальные напряжения изменяются
обратно пропорционально изменению площади, если площадь
изменяется ступенчато, то на эпюре наблюдается скачок, если
площадь изменяется постепенно, то эпюра имеет вид прямой
наклонной линии
2. В сечении, где приложена сосредоточенная сила эпюра нормальных
напряжений, делает скачок на величину пропорциональную силе и с
ее знаком.
3. На участке, где приложена равномерно распределенная нагрузка
эпюра нормальных напряжений имеет вид прямой наклонной линии
6. Напряжения в наклонных сечениях
nF
F
Q =Nsin
A A0 cos
0=N/A0
N =Ncos
N=F
F
t
р
N
N cos
N
cos 2 0 cos 2 ,
A
A0 / cos A0
Q
N sin
N
t
cos sin 0,5 0 sin 2
A A0 / cos A0
7.
 Напряжения в наклонных сеченияхЗнак нормального напряжения определяется знаком продольной силы,
Напряжения в наклонных сеченияхЗнак нормального напряжения определяется знаком продольной силы,то есть растягивающее напряжение положительно, сжимающее –
отрицательно.
Касательное напряжение считается положительным, если изображающий
его вектор стремится вращать тело относительно любой точки, лежащей
на внутренней нормали к сечению по часовой стрелке.
N
N cos
N
cos 2 0 cos 2 ,
A
A0 / cos A0
Q
N sin
N
t
cos sin 0,5 0 sin 2
A A0 / cos A0
Наибольшие нормальные напряжения (по абсолютной величине)
действуют в поперечном сечении стержня.
Наибольшие касательные напряжения действуют в сечениях
наклоненных под углом в 45о к оси стержня.
Касательные напряжения в поперечном сечении стержня равны нулю.
8. Закон Гука
Закон Гука имеет два аналитических выражения— через относительные, ичерез абсолютные величины
В относительных величинах
В абсолютных величинах
Nl
l
EA
E
Жесткостью поперечного сечения стержня называют произведение площади
поперечного сечения А на модуль продольной упругости материала Е:
Сп.
 с. АЕ
с. АЕСпособность стержня сопротивляться деформированию оценивают величиной
относительной жесткости стержня, которая равна отношению жесткости
поперечного сечения ЕА к длине стержня l:
С
АЕ
l
Податливость стержня:
l
EA
9. Деформации и перемещения
lкl0
Деформации и перемещения
l lк l0 ,
Относительной продольной деформацией
называется отношение абсолютной продольной
деформации l к первоначальной длине стержня l0:
l
F
l l0
b
b0
Величина, на которую изменится длина бруса
(или одного из его участков) под действием
продольных сил, называется продольной
деформации
b/2
a
a0
a/2
Величина а ( b), на которую изменится размер
поперечного сечения бруса а0 (b0) под действием
продольной силы, называется поперечной
деформацией.
Отношение абсолютной поперечной деформации, а ( b) к первоначальному
размеру сечения бруса а0 (b0), называется относительной поперечной
деформаций:
а/
a
,
a0
b/
b
b0
10.
 Деформации и перемещенияУдлинение стержня постоянного сечения от
Деформации и перемещенияУдлинение стержня постоянного сечения отсобственного веса прямо пропорционально весу Q
и длине стержня l, и обратно пропорционально
удвоенному значению жесткости поперечного
сечения EA
dz
l
l
l
z
0
A zdz
EA
Аl 2
2 EA
Ql
,
2 EA
Q=Az
Изменение длины ступенчатого стержня равно алгебраической сумме
удлинений (укорочений) отдельных его участков:
k
k
N i li
l li
i 1
i 1 Ei Ai
11. Деформации и перемещения
аa/2
0
b
Длина участков а=1,2 м, b=0,8 м, c=1 м;
Модуль упругости Е=2·105 МПа;
Площадь сечения участков стержня:
А1 =20 см2, А2 =40 см2, А3 =15 см2;
Продольная сила F=50 кН.
Удлинения участков бруса
Fa
50 103 1,2
l1
1,5 10 4 м;
11
4
EA1 2 10 20 10
c
c/2
I
II
F
0
I
II
A1
A2
A3
Fb
50 103 0,8
4
l2
0
,
5
10
м;
11
4
EA2 2 10 40 10
Эпюра l
lI-II
l0-II
l
Fc
50 103 1,0
4
l3
1
,
67
10
м
11
4
EA3 2 10 15 10
Полное удлинение стержня:
l l1 l2 l3 1,5 10 4 0,5 10 4 1,67 10 4 3,67 10 4 м
Перемещение сечения 1I-I1 относительно заделки:
lI II l1 2 l2 l3 2 1,5 10 4 2 0,5 10 4 1,67 10 4 2 2,085 10 4 м
Перемещение сечения II относительно сечения I:
l0 II l1 l2 l3 2 1,5 10 4 0,5 10 4 1,67 10 4 2 2,835 10 4 м
12.
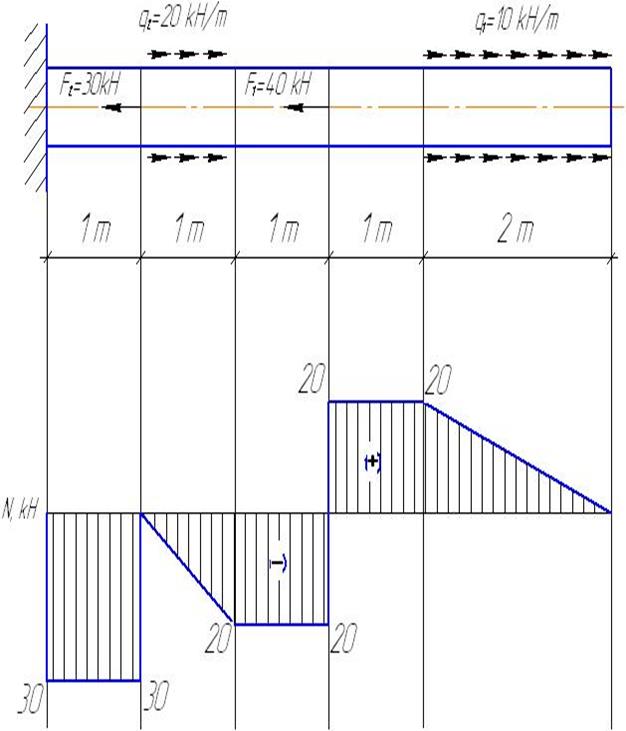 Коэффициент ПуассонаОтношение относительной поперечной деформации º / к относительной
Коэффициент ПуассонаОтношение относительной поперечной деформации º / к относительнойпродольной деформации º взятое по модулю, называется коэффициентом
Пуассона:
/
Коэффициент Пуассона принимает значения в пределах от 0 до 0,5 и
определяется экспериментально. Меньшее значение коэффициента имеют
бетон – 0,16…0,18, стекло – 0,25, большие значения каучук – 0,48, свинец –
0,42, целлулоид – 0,38. У большинства материалов используемых в
машиностроении =0,24…0,36.
Коэффициентом изменения объёма называется безразмерная величина
представляющая собой отношение величины, на которую изменяется объём
бруса при деформации V=Vк-V0 к его первоначальному объёму V0
/
kV 2 1 2 1 2 .
/
a
/
b
/
Коэффициент изменения объема принимает следующие значения: при
сжатии объём бруса уменьшается и kV<0, при растяжении объём
увеличивается и kV>0. Для материалов с коэффициентом Пуассона
0,5 изменение объёма не происходит и kV 0
13.
 Допускаемые напряженияОпасным называется напряжение 0 при котором конструкция становится
Допускаемые напряженияОпасным называется напряжение 0 при котором конструкция становитсяне работоспособной.
Для конструкций из пластичных материалов основной причиной потери
работоспособности являются большие пластические деформации и в этом
случае опасное напряжение равно физическому пределу текучести: 0 = т.
Для пластичных не имеющих физического предела текучести, опасное
напряжение приравнивается к условному пределу текучести: 0 = 0,2.
Для конструкций из хрупких материалов основной причиной потери
работоспособности является разрушение, которое происходит, как правило,
без видимых остаточных деформаций. И в качестве опасного напряжения
принимают предел прочности пч или временное сопротивление разрыву вр.
Под коэффициентом запаса прочности понимают величину,
указывающую во сколько раз необходимо уменьшить опасное напряжение
0 , чтобы прочность конструкции или детали, в заданных условиях
эксплуатации, была гарантирована, а максимальные напряжения, в любом
случае, не превышали предела пропорциональности пц .

Величину коэффициента запаса прочности для пластичных материалов
рекомендуется выбирать из интервала SТ = 1,25-2,5.
Коэффициент запаса прочности для хрупких материалов, изменяется в
пределах Sвр = 2,4 – 5,0.
14. Допускаемые напряжения
Допускаемыми называются наибольшие напряжения, которые можнодопустить в рассчитываемой конструкции из условий ее безопасной,
надежной и долговечной работы.
т
sт
0
0 , 2
S
sт
в р
sв р
для пластичных материалов
для пластичных материалов не
имеющих физического предела
текучести
для хрупких материалов
Пластические свойства материалов оцениваются величиной относительного
остаточного удлинения .
Для оценки приняты следующие условия:
•если <5 % материал считается хрупким;
•если 5 % < < 10 % — хрупко—пластичным;
•если > 10 % — пластичным.
15. Расчеты на прочность при растяжении
Расчётными называются напряжения вычисленные по теоретическим илиэкспериментальным формулам для конкретной конструкции с учетом величины
приложенных к ней внешних нагрузок, размеров и формы ее элементов.

F
A
Условие прочности формулируется так нормальные расчетные напряжения в
любом сечении растянутого (сжатого) стержня не должны превышать
допускаемого значения:
Из условия прочности при растяжении (сжатии) вытекают следующие задачи:
1. Задача проверочного расчета
2. Задача проектного расчета.
F
A
A
F
3. Задача определения максимальной допускаемой грузоподъемности
F A
Понимание диаграмм поперечной силы и изгибающего момента
Статика Последнее обновление: 20 февраля 2023 г.
Диаграммы поперечной силы и изгибающего момента— это мощные графические методы, которые используются для анализа балки под нагрузкой. На этой странице вы узнаете, что такое поперечные силы и изгибающие моменты, почему они полезны, процедуру рисования диаграмм, а также некоторые другие ключевые аспекты.
Если у вас нет настроения читать, просто посмотрите видео!
https://www.youtube.com/watch?v=C-FEVzI8oe8Видео не может быть загружено, поскольку JavaScript отключен: понимание диаграмм поперечной силы и изгибающего момента (https://www. youtube.com/watch?v =C-FEVzI8oe8)
youtube.com/watch?v =C-FEVzI8oe8)
Что такое поперечные силы и изгибающие моменты?
Когда к балке приложены нагрузки, внутри балки возникают внутренние силы в ответ на нагрузки. Мы можем визуализировать эти силы, сделав воображаемый разрез балки и рассмотрев внутренние силы, действующие на поперечное сечение. Эти внутренние силы имеют две составляющие:
- Силы сдвига , ориентированные в вертикальном направлении, параллельно поперечному сечению балки
- Нормальные силы , направленные вдоль оси балки, перпендикулярно поперечному сечению балки
Внутренние силы развиваются таким образом, чтобы поддерживать равновесие. Где бы ни был сделан воображаемый разрез по длине балки, эффект внутренние силы всегда будут уравновешивать действие внешних сил.
Нормальные напряжения будут растягивающими с одной стороны поперечного сечения и сжимающими с другой. Если балка провисает, верхняя часть балки станет короче, и поэтому нормальные силы, действующие в верхней части, будут сжимающими. Нижняя часть балки станет длиннее, поэтому нормальные силы, действующие в нижней части балки, будут растягивающими.
Если балка провисает, верхняя часть балки станет короче, и поэтому нормальные силы, действующие в верхней части, будут сжимающими. Нижняя часть балки станет длиннее, поэтому нормальные силы, действующие в нижней части балки, будут растягивающими.
Эти силы уравновешивают друг друга, поэтому они не создают результирующую силу, перпендикулярную поперечному сечению балки, но создают момент .
Это означает, что внутренние силы, действующие на поперечное сечение балки, могут быть представлены одной результирующей силой, называемой поперечной силой , которая является равнодействующей внутренних сдвигающих сил, и одним результирующим моментом, называемым изгибающий момент , то есть равнодействующая внутренних нормальных сил.
Влияние внутренних сил на поперечное сечение балки можно представить двумя равнодействующими – поперечной силой и изгибающим моментомПочему полезны диаграммы поперечной силы и изгибающего момента?
Диаграммы поперечной силы и изгибающего момента используются для анализа и проектирования балок. Показывая, как поперечная сила и изгибающий момент изменяются по длине балки, они позволяют количественно оценить нагрузку на балку.
Показывая, как поперечная сила и изгибающий момент изменяются по длине балки, они позволяют количественно оценить нагрузку на балку.
Они часто используются в качестве отправной точки для выполнения более подробного анализа, который может включать расчет напряжений в балках или определение того, как балки будут прогибаться.
Сводные листы Efficient Engineer
Сводные листы Efficient Engineer предназначены для представления всей ключевой информации, которую вам необходимо знать по конкретной теме, на одной странице. Это не становится более эффективным, чем это!
Получить итоговые листы!
Балочные нагрузки и опоры
Силы сдвига и изгибающие моменты вдоль балки не зависят от геометрии поперечного сечения балки или материала, из которого изготовлена балка. Они зависят только от двух факторов:
- Как балка нагружена
- Как поддерживается балка
Сначала рассмотрим нагрузки. Наиболее распространенными способами приложения нагрузок к балке являются сосредоточенных сил , распределенных сил и сосредоточенных моментов . Распределенные силы могут быть равномерными или неравномерными.
Наиболее распространенными способами приложения нагрузок к балке являются сосредоточенных сил , распределенных сил и сосредоточенных моментов . Распределенные силы могут быть равномерными или неравномерными.
Закрепленная поддержка
- вертикальное смещение
- горизонтальное смещение
- вращение
Роликовая опора
- вертикальное смещение
- горизонтальное смещение
- вращение
Фиксированная поддержка
- вертикальное смещение
- горизонтальное смещение
- вращение
Когда определенная степень свободы (вращение или поступательное движение) ограничивается опорой, в этом месте возникает соответствующая сила реакции или момент реакции. Например, на шарнирной опоре на балку будут действовать горизонтальные и вертикальные силы реакции, поскольку горизонтальные и вертикальные перемещения сдерживаются, но реактивного момента не будет, поскольку балка может вращаться на шарнирной опоре.
Например, на шарнирной опоре на балку будут действовать горизонтальные и вертикальные силы реакции, поскольку горизонтальные и вертикальные перемещения сдерживаются, но реактивного момента не будет, поскольку балка может вращаться на шарнирной опоре.
Диаграмма свободного тела представляет собой простой эскиз, на котором показаны все внешние нагрузки, действующие на балку, и любые силы реакции от опор. Вычисление диаграммы свободного тела является важным первым шагом в определении диаграмм поперечной силы и изгибающего момента.
Пример конфигурации балки (вверху) и соответствующей схемы свободного тела (внизу) Рассмотрим шарнирную опору в конфигурации балки, показанной выше. Балка может вращаться на этой опоре, поэтому реактивного момента нет, но зато исключены смещения в вертикальном и горизонтальном направлениях, поэтому будут горизонтальные и вертикальные силы реакции. На роликовую опору действует только вертикальная сила реакции. Эти три силы реакции, а также приложенные распределенные и сосредоточенные силы показаны на диаграмме свободного тела.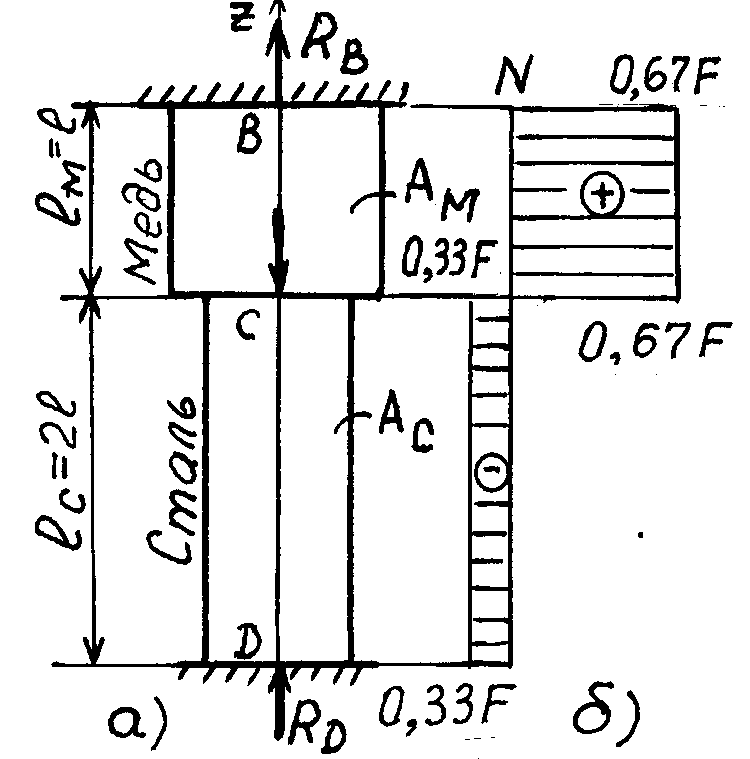
Как нарисовать диаграмму поперечной силы и изгибающего момента
Для построения диаграмм поперечной силы и изгибающего момента необходимо выполнить три основных шага:
Шаг 1
Нарисуйте диаграмму свободного тела балки
Для правильного определения поперечных сил и изгибающих моментов вдоль балки необходимо знать все действующие на нее нагрузки, в том числе внешние нагрузки и реактивные нагрузки на опорах. Нарисовав диаграмму свободного тела, вы определите все эти нагрузки и отобразите их на эскизе.
Шаг 2
Рассчитать силы реакции и моменты реакции на опорах балки
Несмотря на то, что внешние нагрузки известны, силы реакции и моменты на опорах неизвестны – их необходимо рассчитать. Это можно сделать, учитывая тот факт, что все внешние нагрузки, как приложенные, так и нагрузки на опоры, должны уравновешивать друг друга. Если бы они этого не сделали, балка не находилась бы в статическом равновесии.
Это может быть представлено тремя уравнениями равновесия. Эти уравнения утверждают, что сумма сил в горизонтальном направлении, сумма сил в вертикальном направлении и сумма моментов, приложенных к любой точке, должны быть равны нулю.
$$\сумма{F_x} = 0$$
$$\сумма{F_y} = 0$$
$$\сумма{М} = 0$$
Эти уравнения утверждают, что сумма сил в горизонтальном направлении, сумма сил в вертикальном направлении и сумма моментов, приложенных к любой точке, должны быть равны нулю.
$$\сумма{F_x} = 0$$
$$\сумма{F_y} = 0$$
$$\сумма{М} = 0$$
С помощью этих уравнений можно рассчитать силы реакции и моменты на опорах.
Шаг 3
Определите внутренние поперечные силы и изгибающие моменты в каждом месте вдоль балки
Теперь у нас есть вся информация, необходимая для определения поперечных сил и диаграмм изгибающих моментов.
Как уже упоминалось в предыдущей части этой статьи, если мы делаем воображаемый разрез балки в любом месте, внутренние силы и моменты, действующие на поперечное сечение разреза, должны уравновешивать внешние силы и моменты. Это означает, что мы можем еще раз применить уравнения равновесия для расчета поперечных сил и изгибающих моментов вдоль балки.
Начните с одного конца балки и переместите место воображаемого разреза на другой конец, применяя уравнения равновесия и вычисляя поперечные силы и изгибающие моменты при движении вдоль балки.
Выполнив это по всей длине балки, вы получите диаграммы поперечной силы и изгибающего момента.
Условные обозначения
При расчете поперечных сил и изгибающих моментов необходимо использовать постоянное условное обозначение. Наиболее распространенное соглашение о знаках выглядит следующим образом:
- Приложенные силы положительны, если они действуют в направлении вниз.
- Если балка находится слева от воображаемой секущей плоскости, поперечные силы, направленные вниз, положительны. Если балка находится справа от секущей плоскости, поперечные силы, направленные вверх, положительны.
- Если изгибающий момент вызывает провисание, то он положительный, а если вызывает заедание, то отрицательный.
Эти условные обозначения показаны на рисунке ниже.
Общее правило знаков для поперечных сил и изгибающих моментов Давайте рассмотрим пример, чтобы показать процесс определения поперечных сил и диаграмм изгибающих моментов от начала до конца.
Пример — свободно опертая балка
В этом примере мы определим диаграмму поперечной силы и изгибающего момента для свободно опертой балки, несущей две нагрузки.
Конфигурация свободно опертой балки для этого примераПервым шагом является рисование диаграммы свободного тела. На шарнирной опоре действуют горизонтальная и вертикальная силы реакции (точка А), а на роликовой опоре действует одна вертикальная сила реакции (точка В).
Диаграмма свободного тела для примера 1Далее нам нужно применить уравнения равновесия для определения неизвестных сил реакции в точках A и B. Сумма сил в горизонтальном направлении должна быть равна нулю. $H_A$ — единственная сила в горизонтальном направлении, поэтому она должна быть равна нулю:
$$\sum{F_x} = 0$$
$$H_A = 0 \mathrm{kN}$$
сумма сил в вертикальном направлении должна быть равна нулю:
$$\sum{F_y} = 0$$
$$R_B + R_A = 15 + 6$$
И сумма моментов относительно любой точки должна быть равна нулю. Если мы решим взять моменты относительно точки B, мы получим следующее:
Если мы решим взять моменты относительно точки B, мы получим следующее:
$$\sum{M_B} = 0$$
$$(-R_A \cdot 6) + (15 \cdot 5) + (6 \ cdot 2) = 0$$
Мы можем решить это уравнение, чтобы определить, что:
$$R_B = 9 \mathrm{kN}$$
Подстановка $R_B$ в уравнение вертикального равновесия дает:
$$9 + R_A = 15 + 6$$
$$R_A = 12 \mathrm{кН}$$
Все внешние нагрузки, действующие на балку, теперь определены, и можно обновить диаграмму свободного тела.
Обновлена диаграмма свободного тела, показывающая величины всех внешних нагрузок.Теперь мы можем начать рисовать диаграммы поперечной силы и изгибающего момента, начиная с левой стороны балки. Мы можем нарисовать диаграмму свободного тела, показывающую сегмент балки, который был отрезан непосредственно справа от силы реакции 12 кН в точке A.
Диаграмма свободного тела для воображаемого разреза непосредственно справа от шарнирной опорыпоперечная сила V(x) должна уравновешивать силу реакции 12 кН:
$$V(x) = 12 \mathrm{кН}$$
Аналогично, изгибающий момент должен уравновешивать момент, создаваемый реактивной нагрузкой 12 кН:
$$M(x) = 12x$$
Расчет сила сдвига и изгибающий момент из диаграммы свободного тела Сила сдвига будет постоянной, пока мы не достигнем следующей приложенной силы, поэтому мы можем изобразить это на диаграмме силы сдвига.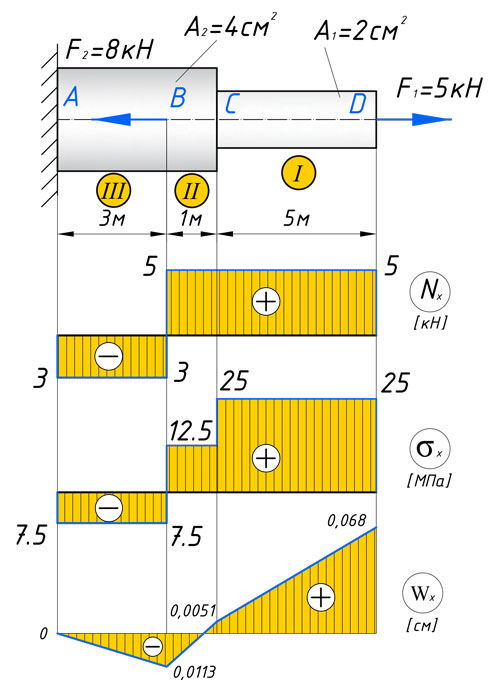 А полученное уравнение для М(х) есть уравнение для прямой линии, которую можно изобразить на диаграмме изгибающих моментов.
А полученное уравнение для М(х) есть уравнение для прямой линии, которую можно изобразить на диаграмме изгибающих моментов.
Затем процесс повторяется, перемещая место воображаемого разреза дальше вправо. На этот раз разрез делается сразу после силы 15 кН, и рисуется диаграмма свободного тела. Силу сдвига и изгибающий момент можно рассчитать, применяя уравнения равновесия.
Диаграммы поперечной силы и изгибающего момента могут быть обновлены.
Этот процесс повторяется до тех пор, пока вся длина балки не будет покрыта. Готовые схемы показаны ниже.
См. также
Фермы — это конструкции (например, мосты или крыши), состоящие из элементов, способных воспринимать только растягивающие или сжимающие осевые нагрузки.
Подробнее
Момент инерции площади описывает, как материал поперечного сечения распределяется относительно определенной оси изгиба.
Узнать больше
Определение, уравнение, диаграмма [Примечания GATE]
Что такое круг Мора?
Комбинация напряжения сдвига и нормального напряжения, действующего в разных плоскостях в напряженном теле. Нормальное напряжение представлено напряжением сдвига, представленным τ. Круг Мора необходим для экзамена GATE. Различные концепции, связанные с этим, помогают получить высокие баллы на экзамене. Посмотрите на диаграмму, показанную ниже:
Нормальное напряжение представлено напряжением сдвига, представленным τ. Круг Мора необходим для экзамена GATE. Различные концепции, связанные с этим, помогают получить высокие баллы на экзамене. Посмотрите на диаграмму, показанную ниже:
По моменту равновесия в напряженном теле τ xy =τ yx
Скачать формулы для GATE Civil Engineering — Fluid Mechanics
Мора Уравнение окружности
И, согласно равновесию сил, напряжения на противоположных сторонах плоскости равны и противоположны по направлению. Следовательно, касательное напряжение будет одинаковым в двух взаимно перпендикулярных плоскостях.
Диаграмма круга Мора
Вариации значения нормального напряжения и напряжения сдвига относительно угла Θ представляют собой форму круга, известного как круг Мора. Круг Мора — это круг, в котором каждая точка представляет собой плоскость в напряженном теле, в которой координата x точки представляет собой нормальное напряжение, а координата y представляет напряжение сдвига, действующее на плоскость.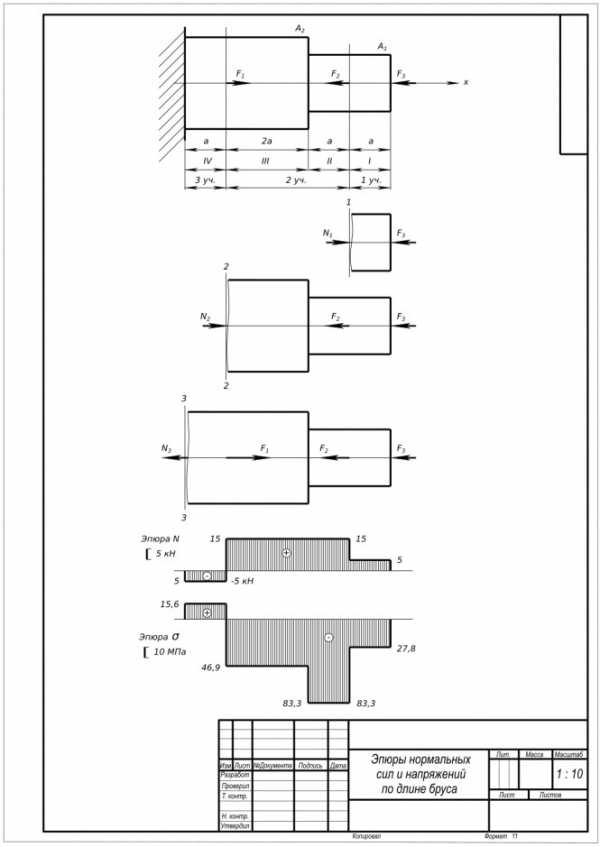 Круговая диаграмма Мора может использоваться для создания различных вопросов в опросном листе GATE, и ее использование наблюдалось на протяжении многих лет.
Круговая диаграмма Мора может использоваться для создания различных вопросов в опросном листе GATE, и ее использование наблюдалось на протяжении многих лет.
Загрузить Формулы для GATE Civil Engineering — Environmental Engineering
Круговая диаграмма Мора для системы плоской деформации
Круг Мора также можно использовать для определения нормальной деформации и деформации сдвига для системы плоской деформации. Для определения напряжения с помощью круга Мора его можно использовать аналогично кругу Мора для стресса. В случае круга Мора ордината максимума деформации на оси деформации сдвига составляет γ max /2, тогда как максимальная ордината круга Мора для напряжения составляет τ макс .
Круговая диаграмма Мора для штамма приведена ниже.
Круг напряжений Мора
Чтобы определить нормальное напряжение и напряжение сдвига на плоскости с помощью метода круга Мора, используется несколько терминов. Эти термины заключаются в следующем.
Главное напряжение: Главное напряжение — это максимальное или минимальное нормальное напряжение, действующее на плоскость, при которой касательное напряжение равно нулю. Максимальное нормальное напряжение известно как главное основное напряжение, а минимальное нормальное напряжение известно как второстепенное главное напряжение, которое представлено как σ 1 и σ 2, соответственно.
Максимальное напряжение сдвига: Максимальное напряжение сдвига — это максимальное напряжение сдвига, действующее на плоскость всего двумерного напряженного тела. Он представлен τ max и равен радиусу круга Мора. В плоскости максимального касательного напряжения нормальное напряжение не равно нулю.
Представление напряжения в круге Мора Для плоского напряжения и деформации
Круг Мора представляет напряжение в двумерной плоскости. Здесь показана взаимосвязь между плоским напряжением и деформацией. Круг Мора представляет собой нормальное напряжение и касательное напряжение в любой плоскости находящегося под напряжением тела. В круге Мора нормальное напряжение представлено по оси x, а касательное напряжение представлено по оси y.
В круге Мора нормальное напряжение представлено по оси x, а касательное напряжение представлено по оси y.
Некоторые важные факты о круге Мора
Круг Мора является очень важным инструментом для определения напряжения или деформации на любой плоскости для находящегося под напряжением тела. Круг Мора — это графический метод определения стресса. Кандидаты могут проверить предыдущие вопросы GATE и понять тенденцию вопросов, заданных кругом Мора на экзамене. Круг Мора помогает визуализировать нормальные напряжения и напряжения сдвига, действующие на плоскости, и помогает определить главные напряжения и максимальные напряжения сдвига вместе с их плоскостями.
- Максимальное напряжение сдвига (τ max )=(σ 1 -σ 2 )/2
- Координата круга Мора обозначается σ x 9 0255 , τ xy
- Центр Круг Мора (C)=((σ 1 +σ 2 )/2, 0)
- σ x +σ y =σ 1 +σ 2 90 255
- Угол между максимальные плоскости сдвига и главного напряжения 45 0 .
