Эпюры нормальных сил — Энциклопедия по машиностроению XXL
Пример 1.2. Построить эпюры нормальных сил, напряжений и перемещений для свободно подвешенного цилиндрического стержня, нагруженного силами собственного веса (рис. 22). Длина стержня I, площадь поперечного сечения / , удельный вес материала у. [c.36]Пример 1.3. Колонна (рис. 23) нагружена силой Р и силами собственного веса. Требуется подобрать такой закон изменения площади поперечного сечения Р — Е (г), чтобы напряжения во всех сечениях были одинаковы и равны Построить эпюры нормальных сил,-напряжений и пе- [c.36]
Строим, далее, эпюру моментов от заданной силы Я и от единичной силы (рис. 232, б и в). Кроме того, на участке АВ, где необходимо учесть растяжение, строим эпюру нормальной силы Вычисляем коэффициенты канонического уравнения + 5Jp = 0, [c.
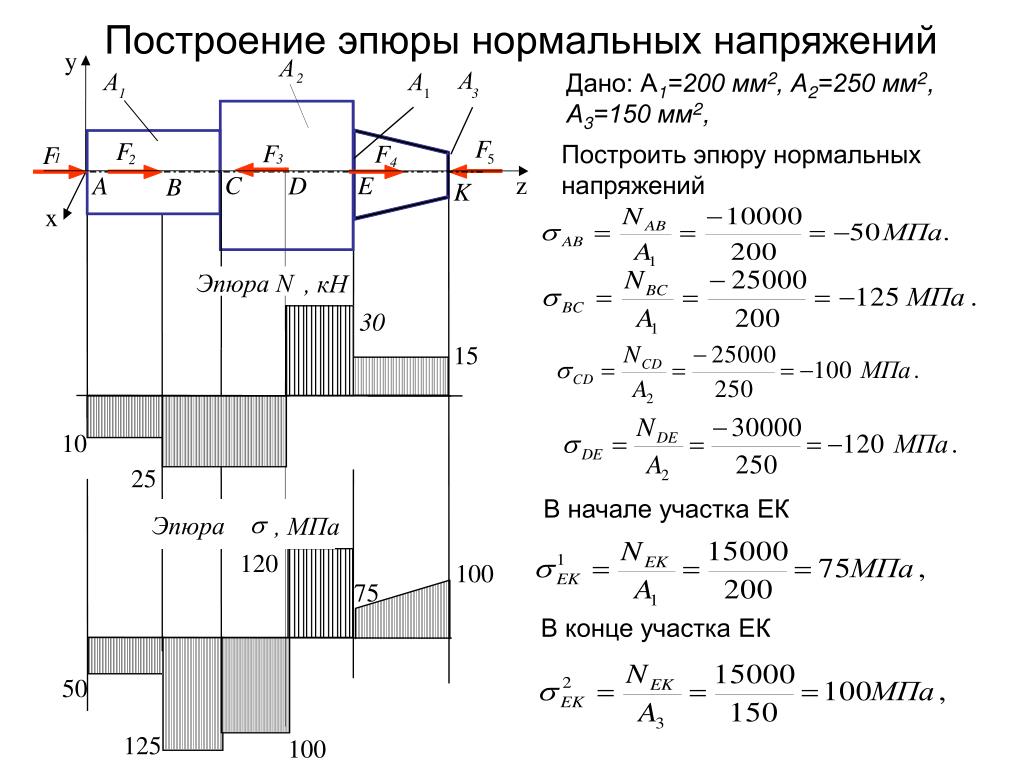
Построение эпюры нормальных сил рассмотрим на конкретном примере. [c.160]
Из условия равновесия любой отсеченной части стержня следует, что продольная сила N в каждом сечении стержня численно равна силе/ . Графиком изменения силы N вдоль стержня (эпюрой нормальной силы в сечении) [c.125]
Пример Э.8. Для жестко заделанного обоими концами бруса, выполненного из одного материала, построить эпюру нормальных сил и напряжений (рис. 2.40, о). [c.218]
Рассмотрим теперь балку-стенку, представленную на рис. 50. Взяв за основу статически определимую раму, построим на контуре балки-стенки эпюру моментов (рис. 51, а) и эпюру нормальных сил (рис. 51,6), которые определяют соответственно [c.111]
Система один раз статически неопределима. Разрезая стержень АВ в верхней точке, получаем основную систему (рнс. 6.19, б). Строям, далее, эпюры моментов от заданной силы и от единичной силы (рнс.
Тонкая стенка с шестью клетками, окаймленными стержнями, растягивается двумя силами Р, приложенными к крайним стержням, и силой 2Р, приложенной к среднему стержню. Выбрать основную систему и неизвестные. Построить эпюры нормальных сил в стержнях и определить погонные касательные усилия в клетках стенки. [c.189]
Положительное значение о соответствует сжатию клеевого слоя. По формулам (6) и (10) можно построить графики изменения касательных и нормальных напряжений в клеевом слое, а по формулам (5) и (9) — построить эпюры нормальных сил и изгибающих моментов в верхней пластине. [c.183]
Требуется подобрать такой закон изменения площади поперечного сечения F=F z), чтобы напряжения во всех сечениях были одинаковы и равны P/Fq. Построить эпюры нормальных сил, напряжений и перемещений.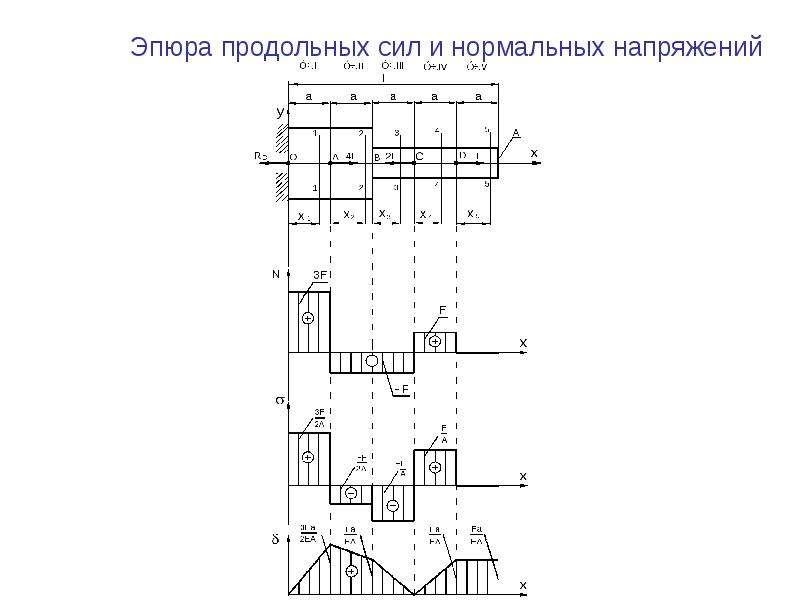
Расчет на прочность. Расчет производят для высоконагруженных винтов по опасному сечению винта, для установления которого строят эпюры нормальных сил и крутящих моментов. Для домкрата расчетная схема и эпюры показаны на рис. 10.5. От чашки домкрата до гайки нормальная сила N равна осевой силе F (грузоподъемность домкрата). В пределах высоты гайки сила F уменьшается до О, а крутящий момент изменяется от О до М . От верхней грани гайки до рукоятки 1 = выше [c.238]
Построение эпюр нормальных сил [c.127]
Построить эпюру нормальных сил для бруса, изображенного на рис. 93, а. [c.127]
Решение. Строим эпюры нормальных сил (рис. 128, б). Определяем напряжения в поперечных сечениях каждого из участников по формуле (17.5) [c.159]
Решение I) строим эпюру нормальных сил от заданной нагрузки 2) сняв внешние силы, прикладываем единичную силу в сечении А в направлении перемещения и строим эпюру нормальных сил от единичной силы 3) составляем интеграл Мора и выполняем интегрирование графоаналитическим способом
[c. 195]
195]
Основная система, нагруженная заданной нагрузкой Р и найденной реакцией X,, показана на рис. 173, ж. Суммарная эпюра нормальных сил приведена на рис. 173,3. [c.202]
| Рис. 2.51. Эпюры нормальных сил в ребрах и в верхних поясах диафрагм при загружении одной волны (сплошная линия) и двух волн (штрих — пунктирная линия) модели с арочными диафрагмами нагрузкой q = = 1200 Н/м2 |
| Рис. 2.53. Эпюры нормальных сил и моментов в среднем ребре модели при односторонней нагрузке =1200 НД( у средней диафрагмы (а) и у крайних диафрагм (б) |
 1.9г)
[c.21]
1.9г)
[c.21]Нормальные силы. Исходными данными для построения эпюры нормальных сил являются тяга двигательной установки F, аэродинамическая осевая сила X и ее распределение qx (х) по длине, масса ракеты т и ее распределение Шх (х) по длине, давление наддува ра в баках (рис. 10.8). Все эти силы и масса меняются при движении ракеты. В дальнейшем при построении эпюр их считают неизменными, — и относят к определенному, фиксированному моменту времени. Погонная масса гпх (х) и аэродинамическая нагрузка qx (л ) связаны с суммарными значениями т и X соотношениями [c.284]
Для определения коэффициента 73 интегрируем, согласно формуле Мора, произведение эпюр нормальных сил в стойках от действия единичных сдвигающих и от единичных поперечных растягивающих сил и на полученное значение делим величину 1/5 [c.21]
Раскрыть статическую неопределимость рам, показанных на рисунке, и построить эпюры нормальной силы, поперечной силы и изгибающего момента при следующих данных р = 4 г, УИо = 4тм,
[c. 249]
249]
Рама замкнутого контура загружена по длине ригеля равномерно распределенной нагрузкой интенсивностью q = 2 т м. Размеры рамы а = 5 м, 2с = 6 м (см. рисунок, схема а). Раскрыть статическую неопределимость рамы, считая жесткость всех участков одинаковой и постоянной, построить эпюры нормальной силы, поперечной силы и изгибающего момента, подобрать двутавровое сечение рамы при [о] = 1600 кг 1см и определить величину прогиба сечения посредине ригеля.
Рамы постоянной жесткости загружены симметрично, как показано на рисунке. Раскрыть статическую неопределимость, построить эпюры нормальной силы, поперечной силы и изгибающего [c.253]
| Рис. 16, Эпюры нормальных сил накатки |
П ример 1.2. Построить эпюры нормальных сил, напряжений и перемещений сечений для ступенчатого стержня, приведенного на рис.
 1.5. Модуль упругости положить постоянным.
[c.13]
1.5. Модуль упругости положить постоянным.
[c.13]Для СО-стержней после построения эпюр нормальных сил и изгибающих моментов система уравнений (7.49), (7.52) становится замкнутой. Вместе с кинематическими граничными условиями типа (1.12) и (5.25) она составляет краевую задачу, которая решается стандартным образом. [c.284]
Тип ста- Конструктивная схема Расчетная схема Эпюры изгибающих моментов Эпюры поперечных сил Эпюры нормальных сил [c.357]
Задачи 8.1—8.10. Построить эпюры нормальной силы М, поперечной силы Q и изгибающего момента М. [c.189]
Аналогично эпюре напряжений а, строится эпюра нормальных сил Ny, = Эта эпюра имеет вид эпюры напряжений но вычерчена в другом масштабе. [c.39]
Эпюра нормальных сил N изображена тремя прямоугольниками (фиг. 400, в). На стойках нормальные силы имеют значение Уд и Ур, а на ригеле Нр.
Перемножение эпюр нормальных сил и эпюр крутящих моментов производится значительно проще, так как эти эпюры чаще всего изображаются прямоугольниками. Принимая в этом случае N = N, = Ы, М = М и М = М по формулам (618) и (619)
[c.407]
Принимая в этом случае N = N, = Ы, М = М и М = М по формулам (618) и (619)
[c.407]
График, показывающий изменение нормальной силы по длине бруса, называют эпюрой нормальных сил. [c.20]
Переходим к построению эпюры N (рис. 2.12, д). Для этого параллельно оси бруса проводим тонкую начальную или базовую линию, перпендикулярно которой в определенном масштабе вправо откладываем отрезки, изображающие положительные значения продольной силы, а влево — отрицательные. Получившаяся ступенчатая фигура, ограниченная основной линией и заштрихованная перпендикулярно базовой линии, и есть искомая эпюра нормальных сил по длине бруса. Читая эпюру на рис. 2.12, д, например, сверху вниз, видим на участке ОС брус растянут, нормальная сила, равная 0,5Р, постоянна до сечения С (эпюра N на участке параллельна базовой линии) при переходе через сечение С эпюра делает скачок , равный абсолютному значению приложенной в этом сечении силы правая (положительная) часть скачка (+0,5/ ) изображает значение нопмалыюй силы чуть выше сечения С, а левая (отрицательная) часть скачка (—р) изображает значение нормальной силы чуть ниже сечения С (т.
Пример 2. Построить эпюры нормальных сил, напряжений п персыеш.е1Н1Й от собственного веса для свободно подвешенного цилиндрического стержня [c.126]
Из условий равновесия любой отсеченной ч сти стержня вытекает, что нормальная сила N в каждом сечении стержня равна внешней силе Р. Построим график изменения силы N вдоль оси стержня. Графики подобного рода называются в сопротивлении материалов эпюрами. Они дают наглядное представление о законах изменения различных исследуемых величин. В данном случае эпюра нормальной силы представлена на рис. 1.7, 6 прямоугольником, поскольку N = Р = onst. На рисунке эпюра N заштрихована линиями, которые проведены параллельно откладываемым на графике значениям N. В данном случае значение силы N откладывают вверх, поэтому штриховка проведена вертикально.
[c.46]
В данном случае эпюра нормальной силы представлена на рис. 1.7, 6 прямоугольником, поскольку N = Р = onst. На рисунке эпюра N заштрихована линиями, которые проведены параллельно откладываемым на графике значениям N. В данном случае значение силы N откладывают вверх, поэтому штриховка проведена вертикально.
[c.46]
Вследствие пространственной работы в расчете также существенно менялось распределение продольных меридиональных сил. Значительно перераспределялись нормальные силы в зоне сопряжения ствола трубы с основанием увеличились значения максимальных растягивающих сил и снизились значения сил сжатия. Нормальные меридиональные силы, полученные в расчетах, представлены на рис. 4.5, s. Кривой 1 на рисунке изображена эпюра дополнительных нормальных меридиональных сил, учитывающих простоанственную работу сооружения, полученных по формуле (4.3). В соответствии с эпюрой максимальные нормальные растягивающие усилия, отнесенные к 1 м сечения, в месте примыкания трубы к основанию увеличиваются, а сжимающие— уменьшаются на 1116,5 кН по высоте трубы пространственная работа сооружения при воздействии усилий Nm влияет в меньшей степени.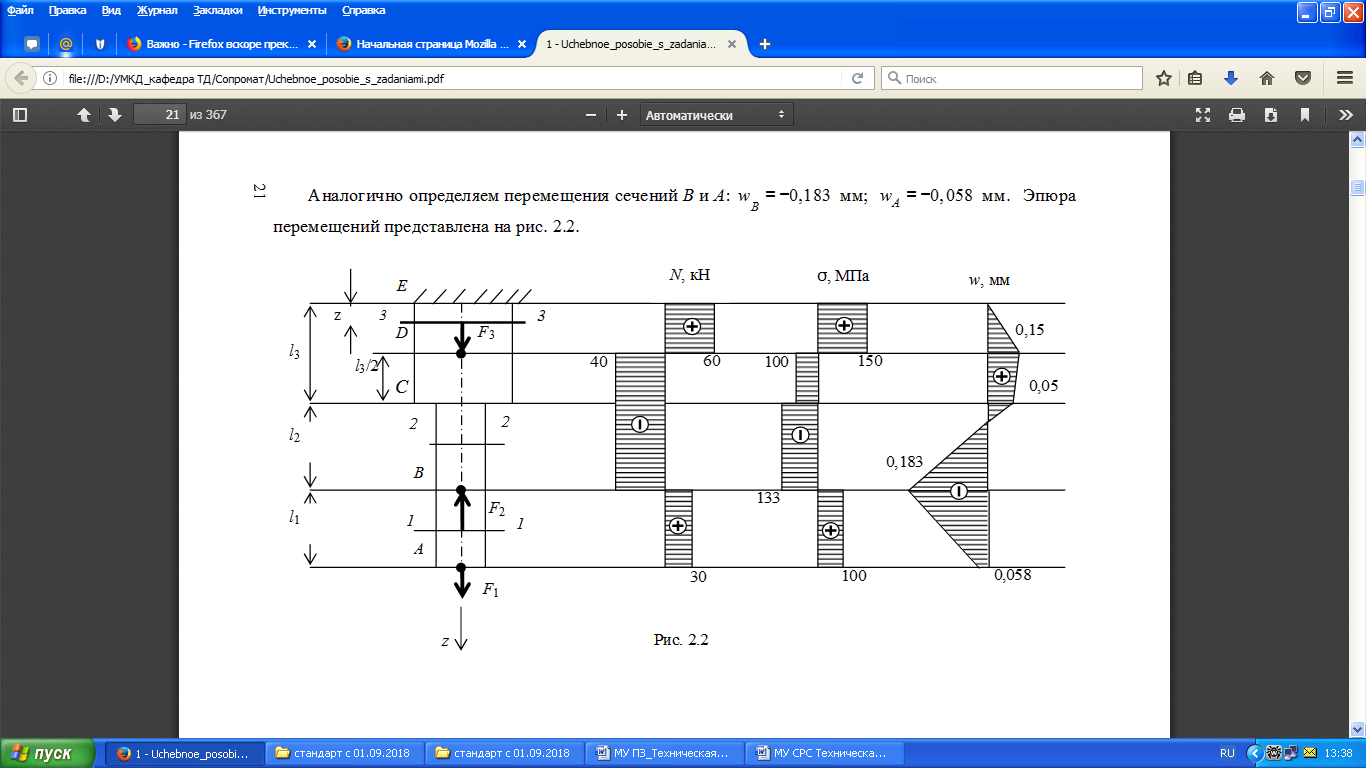 Кривой 2 на рисунке изображена эпюра нормальных сил из консольного расчета трубы с учетом крена основания, геометрической нелинейности в работе сооружения и т. д. При этом погонные нормальные меридиональные силы получены без учета перераспределения усилий при образовании горизонтальных кольцевых трещин, т. е. они соответствуют упругой стадии работы трубы. Эпюра 3 получена суммированием эпюр / и 2 и соответствует распределению нормальных меридиональных сил в трубе от ветра, крена основания и горизонтальных перемещений верхних участков трубы и учитывает влияние пространственной работы сооружения. При этом вследствие пространственной работы трубы максимальные растягивающие нормальные силы в месте сопряжения ствола с фундаментом увеличились на 31%. Эпюры 4, 5 отражают усилия V только от воздействия ветра соответственно в консольном и пространственном расчетах, при этом суммарная горизонтальная составляющая ветровой нагрузки принимается в соответствии с [2]. Эпю-
[c.298]
Кривой 2 на рисунке изображена эпюра нормальных сил из консольного расчета трубы с учетом крена основания, геометрической нелинейности в работе сооружения и т. д. При этом погонные нормальные меридиональные силы получены без учета перераспределения усилий при образовании горизонтальных кольцевых трещин, т. е. они соответствуют упругой стадии работы трубы. Эпюра 3 получена суммированием эпюр / и 2 и соответствует распределению нормальных меридиональных сил в трубе от ветра, крена основания и горизонтальных перемещений верхних участков трубы и учитывает влияние пространственной работы сооружения. При этом вследствие пространственной работы трубы максимальные растягивающие нормальные силы в месте сопряжения ствола с фундаментом увеличились на 31%. Эпюры 4, 5 отражают усилия V только от воздействия ветра соответственно в консольном и пространственном расчетах, при этом суммарная горизонтальная составляющая ветровой нагрузки принимается в соответствии с [2]. Эпю-
[c.298]
Значения изгибающих моментов совпадают с результатами работы [93], полученными методом сил. Непосредственно по значениям граничных параметров рамы могут быть построены эпюры изгибаюшдх моментов М и поперечных сил Q, а эпюру нормальных сил N можно построить, определяя нормальные силы из уравнений равновесия узлов. Соответствующие эпюры представлены на рисунке 2.16.
[c.75]
Непосредственно по значениям граничных параметров рамы могут быть построены эпюры изгибаюшдх моментов М и поперечных сил Q, а эпюру нормальных сил N можно построить, определяя нормальные силы из уравнений равновесия узлов. Соответствующие эпюры представлены на рисунке 2.16.
[c.75]
Раскрыть статическую неопределимость рам, загруженных, как показано на рисунке, построить эпюры нормальной силы, поперечной силы и изгибающего момента при следующих данных Р=Гт, с = 3ж, а = 4л , q 2 т1м, Ж = 6 тм. Жесткость рам постоянТГа и одинакова на всех участках. [c.250]
Реакция Уд sina является нормальной (продольной) силой для подкоса и имеет постоянное значение на протяжении участка АВ. В сечениях ригеля ВС отсутствуют нормальные силы, так как этот участок не подвергается действию продольных нагрузок Что ка-касается стойки D, то она испытывает только.действие сжимающей силы, численно равной реакции Vp.
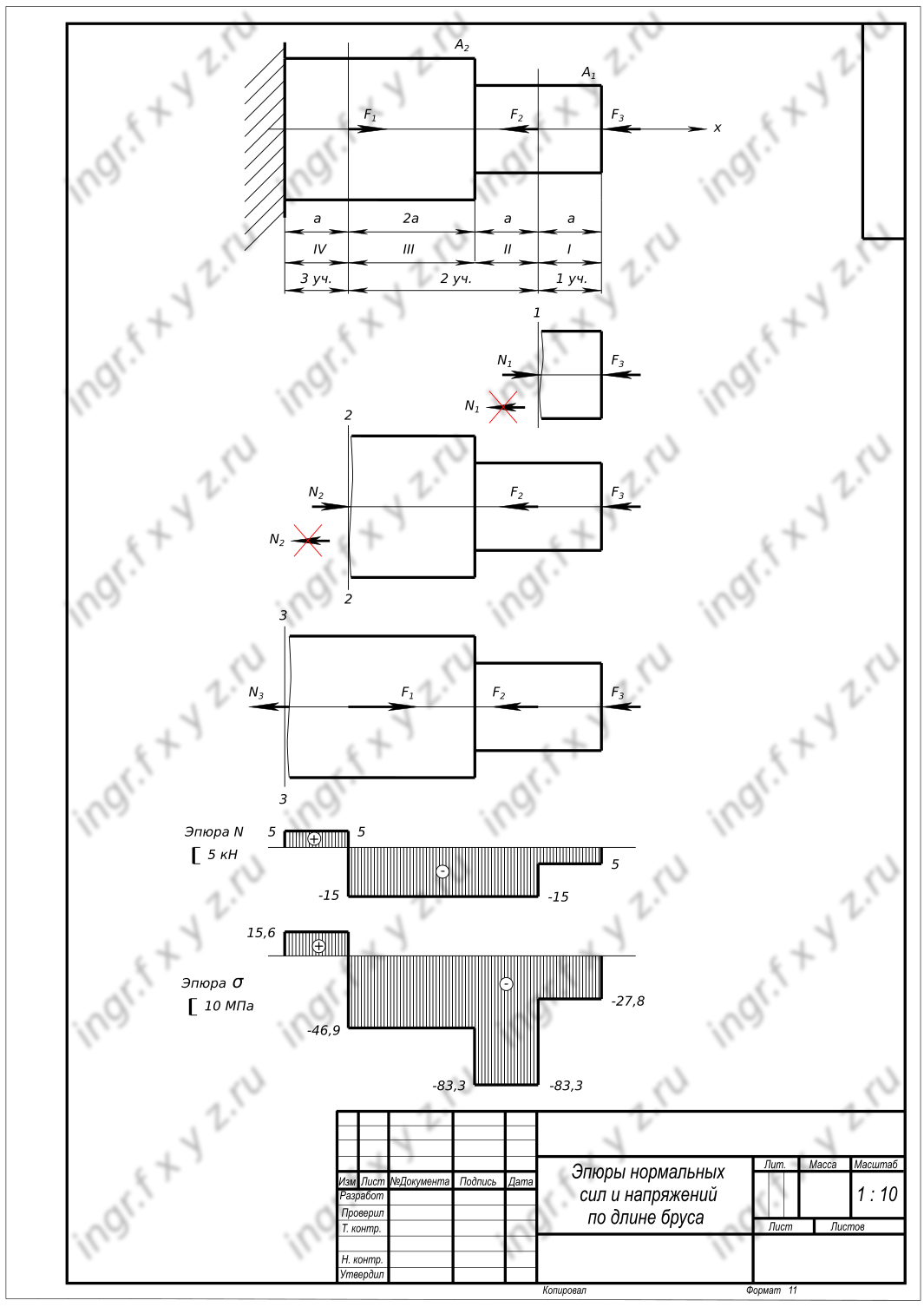 На фиг. 399, в дана эпюра нормальной силы N.
[c.396]
На фиг. 399, в дана эпюра нормальной силы N.
[c.396]Задача 4. Построение эпюры нормальных напряжений от собственного веса грунта. Свойства и состав глинистых и песчаных грунтов
Похожие главы из других работ:
Бетонная водосбросная плотина
5.2 Определение контактных напряжений
Определение нормальных напряжений на контакте бетонная плотина — основание необходимо для расчета прочности сооружения, а также оценки несущей способности основания. Расчет удобно выполнять в табличной форме…
Водосборсная плотина в составе низкого напорного гидроузла
4.2 Расчет контактных напряжений
Для определения нормальных контактных напряжений плотин на нескальном основании используем метод сопротивления материалов…
Геодезическая подготовка перенесения проекта планировки поселения в натуру
2.1.1 Вычисление веса по способу Попова
1. Выбор наиболее слабого места сети, точки максимально удаленной от исходного пункта В. 2. Выбор ходовой линии 3. Расчет невязок в полигонах, как длин ходовой линии в полигоне, со знаком «+/-«…
2. Выбор ходовой линии 3. Расчет невязок в полигонах, как длин ходовой линии в полигоне, со знаком «+/-«…
Геодезическая подготовка перенесения проекта планировки поселения в натуру
2.1.2 Вычисление веса по способу Юршанского
Вычисление обратного веса точки, расположенной в слабом месте сети по способу Юршанского, называемого иначе способом эквивалентной замены производилось на основе замещения частей сети эквивалентным ходом…
Горная электротехника
2. ВЫБОР ВЕЛИЧИН ПИТАЮЩИХ НАПРЯЖЕНИЙ, МЕСТА РАСПОЛОЖЕНИЯ ПУПП И РПП — НН
Проектом предусматривается использование трехфазного переменного тока напряжением 6 кВ, которое от ЦПП с помощью высоковольтного кабеля длиной 1300 м подается на участок…
Моделирование SH-волны
1. Описание волн и создаваемых ими на границе напряжений
Пусть первичная плоская SH-волна падает на границу (z = 0) под углом б и имеет фронт, параллельный оси Oy. Она описывается вектором смещения , также ориентированным вдоль Оу, но не зависящим от у: . Как отмечалось…
Она описывается вектором смещения , также ориентированным вдоль Оу, но не зависящим от у: . Как отмечалось…
Напряжения в призабойной зоне пласта
5. ОСОБЕННОСТИ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ В ПРИЗАБОЙНОЙ ЧАСТИ ВЫРАБОТКИ
Устойчивость горных выработок, особенно проводимых в сложных горно-геологических условиях, в первую очередь зависит от достоверности прогнозирования проявлений горного давления в начальный момент их существования, т.е…
Напряженное состояние пород в условиях залегания
5. ИЗМЕРЕНИЕ ПРИРОДНЫХ НАПРЯЖЕНИЙ В МАССИВЕ ПОРОД
Для определения действующих в массиве горных пород напряжений применяются деформационные, геофизические и геологические методы, а также метод гидроразрыва. Деформационные методы…
Проектирование фундаментов мелкого заложения и свайных фундаментов под них
2.4 Проверка напряжений в основании и уточнение размеров подошвы фундамента
Принятые в первом приближении размеры подошвы фундамента по уточняются исходя из требований СНБ, выражаемых неравенствами: где р — среднее давление под подошвой фундамента.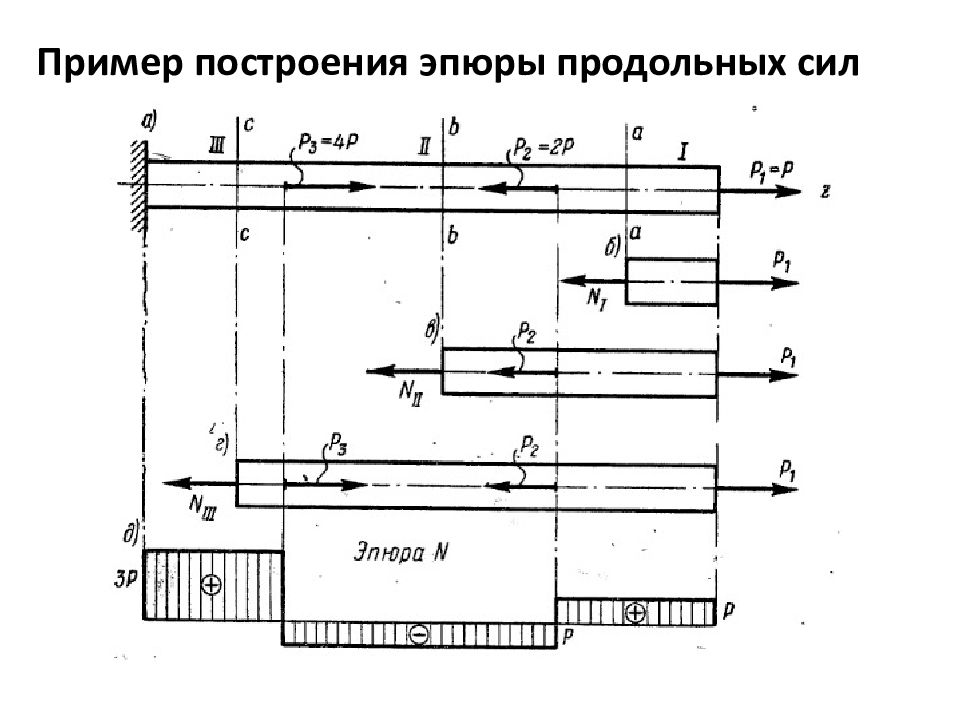 ..
..
Разработка обоснованного проекта устойчивого борта карьера
1.2 Обоснование угла внутреннего трения и удельного веса пород в массиве
Угол внутреннего трения пород — это угол предельного равновесия, при котором одна часть породы относительно другой находится в равновесии при полном отсутствии сцепления между этими частями. Для снижения влияния ошибки в расчете сил трения…
Разработка состава грунтобетона модифицированного французскими углеродными нанотрубками фирмы «Arkema»
3.1.1 Определение плотности грунта(естественной ненарушенной структуры) с и удельного веса грунта ?
Плотностью грунта называется отношение массы грунта к занимаемому им объему(г/см3;т/м3), удельным весом грунта называется вес единицы объема грунта в его естественном состоянии(кН/м3) Таблица 8. № п/п размеры режущего кольца масса…
Свойства и состав глинистых и песчаных грунтов
Задача 2. Определение гранулометрического (зернового) состава сыпучего грунта
глинистый грунт сыпучий песчаный По приведенным в табл. 2 результатам зернового анализа сыпучего грунта постройте кривую зернового состава, определите степень неоднородности и дайте наименование грунта по этим показателям…
2 результатам зернового анализа сыпучего грунта постройте кривую зернового состава, определите степень неоднородности и дайте наименование грунта по этим показателям…
Свойства и состав глинистых и песчаных грунтов
Задача 5. Построение эпюры контактного давления
По приведенным в таблице № 3 данным о нагрузках и размерах фундаментов построить эпюру контактного давления. Таблица № 3 Нагрузки Расстояние а, м Размеры фундамента, м Глубина заложения фундамента, м N1, кН N2, кН M, кНм G…
Сравнительный анализ установившихся потоков газа при различных законах фильтрации
3.2 Задача №2
Тема №2: Плоскорадиальная установившаяся фильтрация однородной несжимаемой жидкости по закону Дарси в однородном пласте (приток к совершенной скважине)…
Сравнительный анализ установившихся потоков газа при различных законах фильтрации
3.3 Задача №4
Тема №4: Плоскорадиальная установившаяся фильтрация однородной несжимаемой жидкости в неоднородных пластах. Дано: Таблица 4 Слоисто — неоднородный Зонально — неоднородный 9,0 6,5 2000 0,20 7 3,5 0,5 0,6 3 4 0,5 0…
Дано: Таблица 4 Слоисто — неоднородный Зонально — неоднородный 9,0 6,5 2000 0,20 7 3,5 0,5 0,6 3 4 0,5 0…
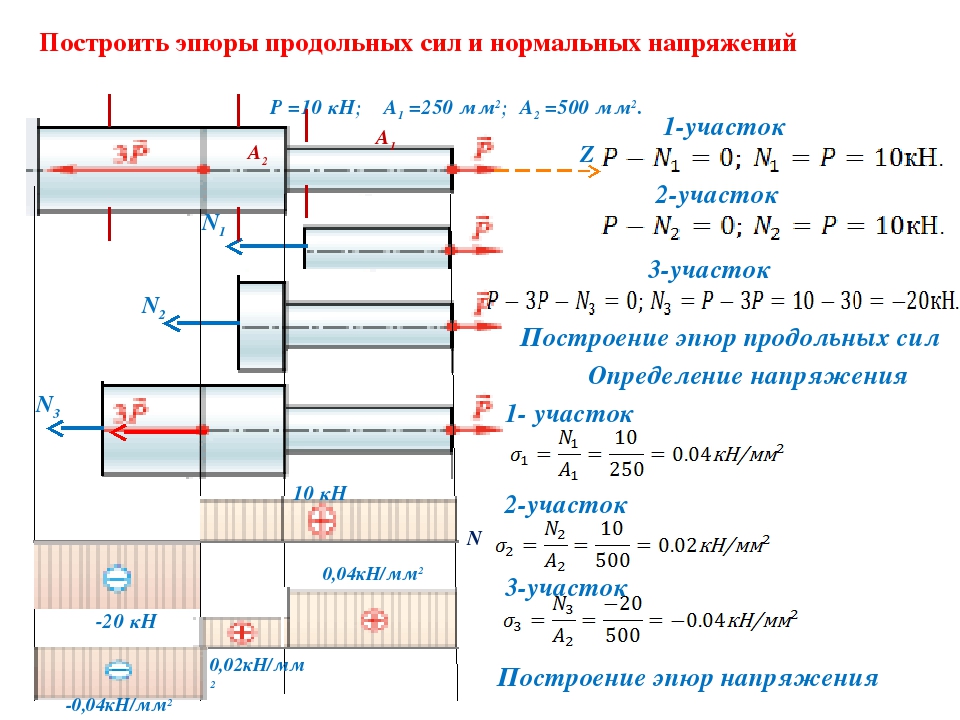
Растяжение и сжатие. Построение эпюр продольных сил и нормальных напряжений
Практическое занятие № 2
Растяжение и сжатие. Построение эпюр продольных сил и нормальных напряжений
Цель работы: овладеть методикой расчета продольных сил и напряжений, а также научиться строить эпюры продольных сил и нормальных напряжений.
1.1 Общие положения
Нагрузка – совокупность активных внешних сил, действующих на рассматриваемое тело.
Напряжение – мера распределения внутренних сил в сечении, их интенсивность.
Поперечное сечение – сечение стержня, перпендикулярное (нормальное) к его центральной оси.
Опасное сечение – поперечное сечение стержня, где возникают наибольшие напряжения.
Эпюра продольной силы – график изменения величины и знака продольной силы по длине бруса.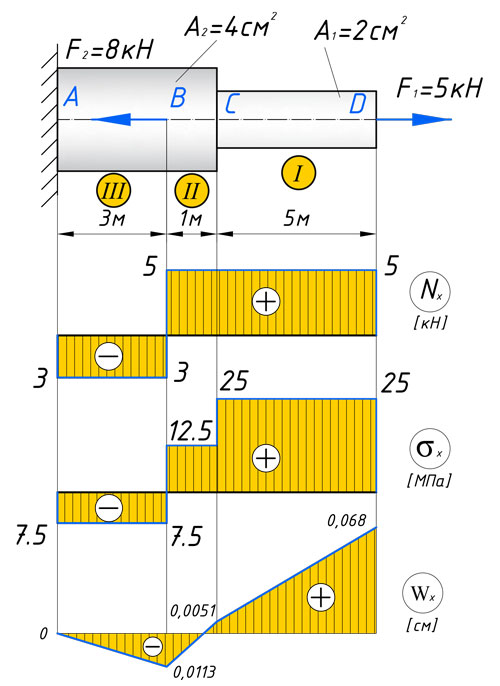
Эпюра нормальных напряжений – график изменения величины и знака нормальных напряжений по длине бруса.
Правило РОЗУ при методе сечений
Р — Разрезаем брус сечениями, перпендикулярными продольной оси бруса.
О – Отделяем одну часть бруса.
З – Заменяем действие внешних сил внутренними силовыми факторами.
У – Уравновешиваем внешние силы внутренними силовыми факторами.
1.2. Пример решения задачи
Дано: Внешние силы: F1 = 45 кH; F2 = 40 кH; F3 = 30 кH.
Площади сечений: A1 = 8 см2; А2 = 6 см2; А3 = 4 см2; А4 = 5 см2.
[pic 1]
Рисунок 1 – Схема нагружения бруса
Задание: рассчитать продольные силы, нормальные напряжения и построить эпюры нормальных сил и напряжений.
Порядок работы
1. Разрезаем брус сечениями, перпендикулярными продольной оси бруса. Традиционно, в таких типах задач продольная ось – это ось z. Линиями сечений будут границы участков бруса, которые продлеваем вниз. Кроме того, границами участков буду точки приложения сил.
Из этих точек также вычерчиваем вертикальные линии (см. рис.). Нумеруем участки римскими цифрами, начиная с участка противоположного линии закрепления бруса в опоре, то есть со свободного конца бруса. В нашем случае справа налево.
2. Определяем продольные силы на каждом участке.
Нормальные силы действуют вдоль оси z и равны сумме проекций на ось всех сил т.е. Nz = ΣFi. При этом положительной считается растягивающая сила, отрицательной сжимающая.
Определяем нормальную силу на первом участке. Справа от проведенного первого участка отсутствуют точки, в которых приложены действующие силы. Точка, где приложена сила F3 будет видна только на втором участке. То есть, на участке I: Nz1 = 0.
На втором участке видна точка приложения и сила F3, которая стремится растянуть брус. Следовательно, NzII = F3 = 30 кH.
На третьем участке нет изменений NzIII = NzII = F3 = 30 кH.
На четвертом участке NzIV = NzIII = 30 кН.
На пятом участке видим две точки приложения сил, т.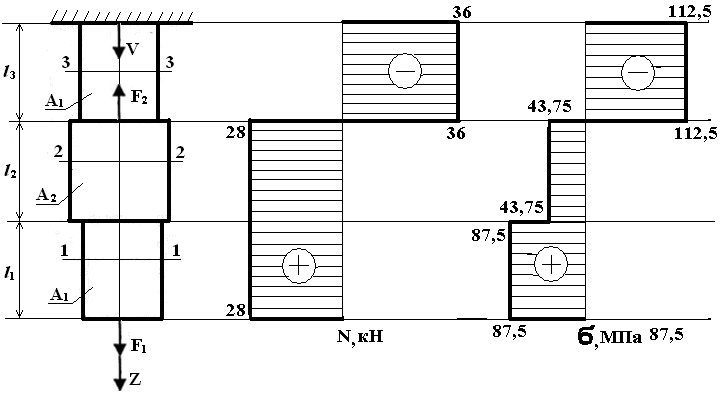 е. NzV = F3 + F2 =30 + 40 = 70 кН.
е. NzV = F3 + F2 =30 + 40 = 70 кН.
На шестом участке три точки приложения, следовательно, NzVI = F3 + F2 – F1 =30 + 40 – 45 = 25 кН.
Определили продольные силы на участках бруса.
[pic 2]
Рисунок 2 — Участки
3. Строим эпюру продольных сил. Эпюра – это график показывающий изменение нормальных сил бруса на участках. Строим по следующим правилам:
Механика материалов: трансформация напряжения » Механика гибких конструкций
Трансформация стресса
Часто, как в случае с сосудами под давлением, которые мы изучали на предыдущем уроке, напряжение в одном направлении действительно мало по сравнению с двумя другими. В этом случае удобно пренебречь малым напряжением, и вместо оценки напряжения, действующего на кубический элемент внутри материала, мы можем исследовать напряжение, действующее на плоскость .
Эти два состояния напряжения, трехмерное напряжение и плоское напряжение, часто обсуждаются в матричной или тензорной форме. Когда мы уменьшаем размерность тензора с 3D до 2D, мы избавляемся от всех членов, содержащих компонент в направлении z , так что
Когда мы уменьшаем размерность тензора с 3D до 2D, мы избавляемся от всех членов, содержащих компонент в направлении z , так что
Теперь, когда мы сократили наше состояние напряжения до двух измерений, мы можем научиться преобразовывать координаты, вдоль которых действуют эти компоненты напряжения, в любую интересующую нас систему координат.Почему мы хотим это сделать? Что ж, взгляните на изображение ниже. >
Два куска дерева, срезанные под углом и склеенные вместе. Дерево разрывается под действием силы растяжения P . Как узнать, сможет ли клеевой шов выдержать результирующее напряжение, создаваемое этой силой? Нам необходимо рассчитать нормальные и касательные напряжения перпендикулярно и параллельно стыку. Следовательно, нам нужно повернуть или преобразовать координаты, связанные с силой P , в направление, связанное с углом клеевого соединения.Затем мы можем оценить напряжения вдоль этих новых направлений, x’ и y’ .
После того, как мы повернули систему координат, нам нужно преобразовать силы, действующие в старой системе координат, в эту новую систему координат. Это означает, что мы должны нарисовать подробную схему свободного тела. Если мы возьмем дифференциальный элемент рядом с началом новой системы координат, мы можем получить силы, действующие на каждую поверхность, из напряжения, умноженного на дифференциальную площадь.
Как вы заметите на диаграмме свободного тела, большая часть сил направлена не в интересующие нас направления, то есть x’ и y’ .Итак, нам нужно разбить эти силы на составляющие, и просуммировать полученные силы по направлениям нашей новой системы координат. Это приводит к длинному, но прямому расчету, приведенному ниже.
Мы можем остановиться здесь, если хотим. Однако, если мы воспользуемся парой тригонометрических тождеств, мы сможем сделать эти уравнения немного более удобными.
Используя эти тождества, мы можем избавиться от всех этих квадратов синусов и косинусов. Окончательный результат для нормальных и касательных напряжений в нашей новой системе координат (обозначаемый тета, который представляет собой вращение против часовой стрелки от оси x до оси x’ ) равен
Окончательный результат для нормальных и касательных напряжений в нашей новой системе координат (обозначаемый тета, который представляет собой вращение против часовой стрелки от оси x до оси x’ ) равен
Мы только что показали, что величина нормального напряжения и напряжения сдвига будет зависеть от выбранной вами системы координат.Если повернуть систему координат на некоторый угол, величина этих напряжений изменится. Как вы можете подозревать, определенные углы будут соответствовать максимальному и минимальному значениям этих напряжений. Один из способов определить экстремумы функции — продифференцировать ее по интересующей нас переменной и приравнять полученное уравнение к нулю.
Мы добавили нижний индекс p к тета, чтобы идентифицировать этот угол как плоскость, соответствующую максимальному и минимальному нормальным напряжениям.Это уравнение имеет два корня, , т.е. , два значения тета удовлетворят его. Эти два значения будут разделены 90 o (или 2*theta будут разделены 180 o ). Один угол будет соответствовать максимальному нормальному напряжению, а другой — минимальному. Мы поговорим об определении того, что есть что, в ближайшее время. Во-первых, отметим, что мы можем повторить ту же процедуру, чтобы определить угол, под которым элемент будет подвергаться максимальному и минимальному сдвигу:
Эти два значения будут разделены 90 o (или 2*theta будут разделены 180 o ). Один угол будет соответствовать максимальному нормальному напряжению, а другой — минимальному. Мы поговорим об определении того, что есть что, в ближайшее время. Во-первых, отметим, что мы можем повторить ту же процедуру, чтобы определить угол, под которым элемент будет подвергаться максимальному и минимальному сдвигу:
Теперь, когда у нас есть плоскости, на которых напряжения будут максимальными и минимальными, нам нужно определить величину этих главных напряжений .Есть разные способы сделать это, но общая идея должна показаться знакомой всем, кто знаком с методами линейной алгебры. Мы стремимся диагонализовать наш тензор плоского напряжения, и полученные собственные значения будут соответствовать экстремумам нашего напряженного состояния.
Наша цель при нахождении главных напряжений в элементе состоит в том, чтобы устранить зависимость уравнений трансформации напряжений от тета.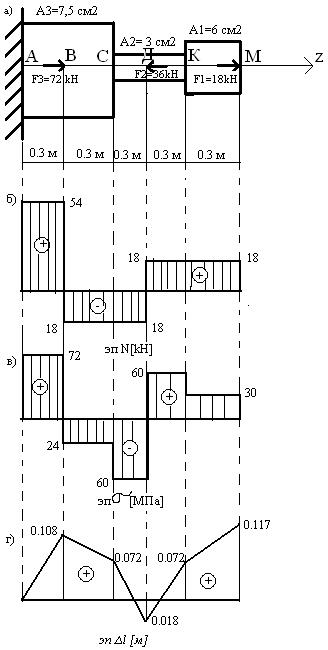 Уравнения, описывающие преобразование напряжений, являются параметрическими уравнениями окружности.Мы можем исключить тета, возведя в квадрат обе части и сложив их (я позволил себе переставить первый член в правой части уравнения, который не зависит от тета и соответствует среднему напряжению).
Уравнения, описывающие преобразование напряжений, являются параметрическими уравнениями окружности.Мы можем исключить тета, возведя в квадрат обе части и сложив их (я позволил себе переставить первый член в правой части уравнения, который не зависит от тета и соответствует среднему напряжению).
Этот расчет выглядит гораздо хуже, чем он есть на самом деле. Опять же, мы просто транспонировали среднее напряжение, возвели в квадрат обе стороны и добавили уравнение для нормального напряжения к уравнению для напряжения сдвига. Вещи просто очень мило. Второй член в правой части каждого уравнения сокращается.То, что у нас осталось, это квадрат синуса плюс квадрат косинуса, и мы помним из наших тригонометрических тождеств, что этот член равен нулю. Полученное уравнение содержит главные нормальные и касательные напряжения. Главное нормальное напряжение возникает, когда касательное напряжение равно нулю, что означает
Главное касательное напряжение — это просто квадратный корень из
Альтернативой использованию этих уравнений для главных напряжений является использование графического метода, известного как круг Мора. Это включает в себя создание графика с сигмой в качестве абсциссы и тау в качестве ординаты, а также построение заданного состояния напряжения. Соглашение о знаках выглядит следующим образом:
Это включает в себя создание графика с сигмой в качестве абсциссы и тау в качестве ординаты, а также построение заданного состояния напряжения. Соглашение о знаках выглядит следующим образом:
Нанесем две точки. Нормальное и касательное напряжение, действующее на правую грань плоскости, составляют одну точку, а нормальное и касательное напряжение на верхнюю грань плоскости составляют вторую точку. Эти две точки лежат на окружности. Центр этого круга — среднее нормальное напряжение. Радиус этой окружности является максимальным напряжением сдвига.Наибольшее значение сигмы соответствует первому главному напряжению, а наименьшее значение сигма соответствует второму главному напряжению.
Сводка
На этом уроке мы узнали, как преобразовать состояние плоского напряжения в новую опорную или координатную систему отсчета. Этот процесс важен, когда необходимо рассмотреть, как внешняя сила вызывает напряжение вдоль заданной плоскости внутри материала. Эта плоскость может быть естественным углом волокон древесины, углом сварного или клеевого соединения или углом надреза внутри конструкции.Этот процесс показал нам, что напряжение в материале будет варьироваться в зависимости от того, какой угол вы рассматриваете, что означает, что будет угол, при котором напряжение будет максимальным или минимальным. Мы рассчитали эти углы и величину главных напряжений в материале. Это важно для определения максимального напряжения, которому подвергается конструкция при сложной нагрузке. Эти главные напряжения будут критериями проектирования, используемыми для предотвращения разрушения материала.
Этот процесс важен, когда необходимо рассмотреть, как внешняя сила вызывает напряжение вдоль заданной плоскости внутри материала. Эта плоскость может быть естественным углом волокон древесины, углом сварного или клеевого соединения или углом надреза внутри конструкции.Этот процесс показал нам, что напряжение в материале будет варьироваться в зависимости от того, какой угол вы рассматриваете, что означает, что будет угол, при котором напряжение будет максимальным или минимальным. Мы рассчитали эти углы и величину главных напряжений в материале. Это важно для определения максимального напряжения, которому подвергается конструкция при сложной нагрузке. Эти главные напряжения будут критериями проектирования, используемыми для предотвращения разрушения материала.
Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта No.1454153. Любые мнения, выводы и заключения или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда.
График зависимости напряжения сдвига от нормального напряжения при испытаниях на прямой сдвиг для…
Контекст 1
… испытание в аппарате прямого сдвига является простым и быстрым методом определения угла трения и сцепления в грунтах . Однако во время этого теста возникла проблема, связанная с размером коробки и его влиянием на достигнутые результаты.В 1938 году Тейлор и Лепс начали работать над этим вопросом. Они исследовали высушенный оттавский песок как в маленьком (76 мм), так и в большом (305 мм) квадратном ящике. Они обнаружили, что угол трения φ′, полученный в результате испытания на большом устройстве, менее чем примерно на 0,5° меньше, чем результат, полученный на маленьком ящике [17]. Бишоп занимался той же проблемой. Он использовал два квадратных ящика, размеры которых составляли 60 мм и 305 мм. Материалом исследования служил сухой песок с пористостью от 0,36 до 0,46. Угол, полученный им при испытании в маленьком ящике, был примерно на 2° выше значений, полученных при использовании большого прибора. Бишоп также исследовал влияние размера частиц гравийных зерен с максимальным размером 32 мм на поведение при сдвиге. Он сказал, что крупные зерна не оказывают существенного влияния на процесс [4]. Палмерия и Миллиган также изучали проблему эффекта масштаба. В своих исследованиях они использовали ящики трех размеров: кубический 1 м, прямоугольный ящик 252 × 152 × 152 мм и квадратный ящик 60 × 60 × 32 мм. Материалом исследования служил сухой кварцевый песок Leighton Buzzard, D 50 которого составлял 0,65 мм. Результаты для всех трех боксов находились в диапазоне от 49° до 50° [12].В 2008 г. Bareither, Benson и Edil опубликовали обширное исследование, касающееся эффекта масштаба в отношении песка с различным содержанием гравия. Они провели испытания 30 образцов в малом (64 х 64 мм) и большом (305 х 305 мм) аппаратах прямого сдвига. В их исследованиях отношение L/D 50 (L–длина коробки сдвига) было равно от 93 до 2033. Они обнаружили, что в случае песка с содержанием гравия менее 30 % результаты, полученные с использованием малый и большой аппарат прямого сдвига настолько похожи, что в обоих случаях исследования дали достоверные значения.
Бишоп также исследовал влияние размера частиц гравийных зерен с максимальным размером 32 мм на поведение при сдвиге. Он сказал, что крупные зерна не оказывают существенного влияния на процесс [4]. Палмерия и Миллиган также изучали проблему эффекта масштаба. В своих исследованиях они использовали ящики трех размеров: кубический 1 м, прямоугольный ящик 252 × 152 × 152 мм и квадратный ящик 60 × 60 × 32 мм. Материалом исследования служил сухой кварцевый песок Leighton Buzzard, D 50 которого составлял 0,65 мм. Результаты для всех трех боксов находились в диапазоне от 49° до 50° [12].В 2008 г. Bareither, Benson и Edil опубликовали обширное исследование, касающееся эффекта масштаба в отношении песка с различным содержанием гравия. Они провели испытания 30 образцов в малом (64 х 64 мм) и большом (305 х 305 мм) аппаратах прямого сдвига. В их исследованиях отношение L/D 50 (L–длина коробки сдвига) было равно от 93 до 2033. Они обнаружили, что в случае песка с содержанием гравия менее 30 % результаты, полученные с использованием малый и большой аппарат прямого сдвига настолько похожи, что в обоих случаях исследования дали достоверные значения. Однако в случае песка с другим содержанием гравия следует учитывать размер ящика [3]. Исследования эффекта масштаба были проведены Cerato и Lutenegger. Они исследовали четыре типа песка и один тип гравия. Анализ проводился на трех аппаратах прямого сдвига с ящиками, размеры которых были следующими: 60×60×26,4 мм, 102×102×40,6 мм и 305×305×177,8 мм. Все образцы были испытаны при трех различных плотностях. Выяснилось, что с увеличением плотности различия в результатах между малым и большим аппаратом уменьшаются.Единственным исключением был песок Оттавы. Результаты, полученные для этого материала, были одинаковыми для всех трех аппаратов при разных плотностях. Авторы объяснили это тем, что песок Оттавы имеет самое большое отношение L/D 50 [5]. Джуэлл и Ворт изучали влияние соотношения L/D 50. Ими доказано, что при L/D 50 ≥ 50 размер зерна не вызывает масштабного эффекта [7]. Моайед и Ализадели исследовали влияние содержания ила на эффект накипи. Они проводили исследования на двух устройствах, маленьком (60 × 60 мм) и среднем (100 × 100 мм).
Однако в случае песка с другим содержанием гравия следует учитывать размер ящика [3]. Исследования эффекта масштаба были проведены Cerato и Lutenegger. Они исследовали четыре типа песка и один тип гравия. Анализ проводился на трех аппаратах прямого сдвига с ящиками, размеры которых были следующими: 60×60×26,4 мм, 102×102×40,6 мм и 305×305×177,8 мм. Все образцы были испытаны при трех различных плотностях. Выяснилось, что с увеличением плотности различия в результатах между малым и большим аппаратом уменьшаются.Единственным исключением был песок Оттавы. Результаты, полученные для этого материала, были одинаковыми для всех трех аппаратов при разных плотностях. Авторы объяснили это тем, что песок Оттавы имеет самое большое отношение L/D 50 [5]. Джуэлл и Ворт изучали влияние соотношения L/D 50. Ими доказано, что при L/D 50 ≥ 50 размер зерна не вызывает масштабного эффекта [7]. Моайед и Ализадели исследовали влияние содержания ила на эффект накипи. Они проводили исследования на двух устройствах, маленьком (60 × 60 мм) и среднем (100 × 100 мм). Испытания включали исследование на Фирузкухском песке, как чистом, так и с добавлением 10, 20 и 30% ила. Тест проводился на уплотненном песке, доведенном до оптимальной влажности. На основании полученных результатов был сделан вывод, что пиковое усилие сдвига уменьшается с увеличением размера ящика и содержания ила [10]. В 2010 г. исследовалась проблема масштабного эффекта в глинистых песках. Всего было проведено 45 испытаний на прямой сдвиг этого грунта плотностью от 1,67 до 1,82 г/см 3 . Резка производилась в трех квадратных ящиках размерами 60, 100 и 300 мм.Исследование ясно показало, что увеличение размера коробки сопровождается увеличением сцепления и уменьшением угла трения [6]. Следующий шаг в изучении эффекта масштаба сделал Чжоу. Он считал, что масштабный эффект зависит не только от размера зерна исследуемого материала. Исследуя изменчивость, форму, вращение, скольжение зерен, средний объем образца, распределение касательных напряжений и развитие зон сдвига, автор показал, что наибольшим фактором, влияющим на объемное трение, является вращение зерен во время испытания [18].
Испытания включали исследование на Фирузкухском песке, как чистом, так и с добавлением 10, 20 и 30% ила. Тест проводился на уплотненном песке, доведенном до оптимальной влажности. На основании полученных результатов был сделан вывод, что пиковое усилие сдвига уменьшается с увеличением размера ящика и содержания ила [10]. В 2010 г. исследовалась проблема масштабного эффекта в глинистых песках. Всего было проведено 45 испытаний на прямой сдвиг этого грунта плотностью от 1,67 до 1,82 г/см 3 . Резка производилась в трех квадратных ящиках размерами 60, 100 и 300 мм.Исследование ясно показало, что увеличение размера коробки сопровождается увеличением сцепления и уменьшением угла трения [6]. Следующий шаг в изучении эффекта масштаба сделал Чжоу. Он считал, что масштабный эффект зависит не только от размера зерна исследуемого материала. Исследуя изменчивость, форму, вращение, скольжение зерен, средний объем образца, распределение касательных напряжений и развитие зон сдвига, автор показал, что наибольшим фактором, влияющим на объемное трение, является вращение зерен во время испытания [18]. .Сложность проблемы масштабного эффекта вдохновила авторов данной статьи на испытание прочностных свойств переработанного заполнителя бетона (RCA). Принятие во внимание предыдущих открытий и инноваций позволит нам получить достоверную информацию о полученных параметрах и серьезно рассмотреть возможность использования RCA в качестве материала для земли под застройку. Испытуемым материалом является бетонный щебень классов от С16/20 до С30/35, поступающий из снесенных зданий. Ситовой анализ показал, что его следует классифицировать как средний песок (MSa) по Еврокоду 7.На рис. 1 показана кривая гранулометрического состава исследуемого материала. Определено оптимальное содержание воды для RCA. Использовалась стандартная энергия уплотнения, равная 0,59 Дж/см 3 , и цилиндр объемом 2,2 дм 3 . Оптимальная влажность равнялась 8,67 %, а максимальная плотность в сухом состоянии равнялась 1,98 г/см 3 . Результаты теста Проктора представлены на рис. 2. Испытание на прямой сдвиг проводили на двух аппаратах с квадратными ящиками: среднем (120×120 мм) и большом (250×250 мм).
.Сложность проблемы масштабного эффекта вдохновила авторов данной статьи на испытание прочностных свойств переработанного заполнителя бетона (RCA). Принятие во внимание предыдущих открытий и инноваций позволит нам получить достоверную информацию о полученных параметрах и серьезно рассмотреть возможность использования RCA в качестве материала для земли под застройку. Испытуемым материалом является бетонный щебень классов от С16/20 до С30/35, поступающий из снесенных зданий. Ситовой анализ показал, что его следует классифицировать как средний песок (MSa) по Еврокоду 7.На рис. 1 показана кривая гранулометрического состава исследуемого материала. Определено оптимальное содержание воды для RCA. Использовалась стандартная энергия уплотнения, равная 0,59 Дж/см 3 , и цилиндр объемом 2,2 дм 3 . Оптимальная влажность равнялась 8,67 %, а максимальная плотность в сухом состоянии равнялась 1,98 г/см 3 . Результаты теста Проктора представлены на рис. 2. Испытание на прямой сдвиг проводили на двух аппаратах с квадратными ящиками: среднем (120×120 мм) и большом (250×250 мм). В каждом из этих устройств было проведено 6 испытаний, 3 из них на воздушно-сухой РХА и 3 после достижения оптимальной влажности. Скорость сдвига была установлена на уровне 0,01 мм/мин. Образец, обозначенный буквой «М», подвергался стрижке в среднем аппарате, тогда как «L» означает, что образец подвергался сдвигу в большом аппарате. В таблице 1 приведены свойства материала, условия испытаний и отношение L/D. Результаты испытаний представлены на рис. 3 и 4. Данные, относящиеся к касательному напряжению и горизонтальной деформации образца, представлены на графиках.В случае обоих рис. 3 и 4 напряжения сдвига выше при испытании в среднем аппарате. Различия в напряжениях невелики и составляют от 1 до 4 кПа. Пики напряжения сдвига в среднем ящике более выражены и их легче локализовать, что может свидетельствовать о заклинивании зерен. На рис. 3 видна характеристика, сильно отличающаяся от касательного напряжения – горизонтальная деформация при разных значениях нормального напряжения. Сдвиг происходит в различных точках, что может быть обусловлено большой угловатостью и шероховатостью зерен.
В каждом из этих устройств было проведено 6 испытаний, 3 из них на воздушно-сухой РХА и 3 после достижения оптимальной влажности. Скорость сдвига была установлена на уровне 0,01 мм/мин. Образец, обозначенный буквой «М», подвергался стрижке в среднем аппарате, тогда как «L» означает, что образец подвергался сдвигу в большом аппарате. В таблице 1 приведены свойства материала, условия испытаний и отношение L/D. Результаты испытаний представлены на рис. 3 и 4. Данные, относящиеся к касательному напряжению и горизонтальной деформации образца, представлены на графиках.В случае обоих рис. 3 и 4 напряжения сдвига выше при испытании в среднем аппарате. Различия в напряжениях невелики и составляют от 1 до 4 кПа. Пики напряжения сдвига в среднем ящике более выражены и их легче локализовать, что может свидетельствовать о заклинивании зерен. На рис. 3 видна характеристика, сильно отличающаяся от касательного напряжения – горизонтальная деформация при разных значениях нормального напряжения. Сдвиг происходит в различных точках, что может быть обусловлено большой угловатостью и шероховатостью зерен. Однако с увеличением влажности явление исчезает, и процесс сдвига одинаков для разных значений нормального напряжения, что видно на рис. 4. На рис. 5 показана зависимость между напряжением сдвига и нормальным напряжением для все тесты. Описание точек пробега на основе линейных уравнений позволило определить угол трения, как показано в таблице 2. Как для сухого, так и для мокрого РКА угол трения, полученный на среднем аппарате, на 1,2° выше значений, полученных на более крупном аппарате.В данной статье представлены результаты исследований, проведенных на переработанном бетонном заполнителе (RCA). Испытания проводились на двух аппаратах прямого сдвига: среднем и большом для изучения эффекта масштаба. В данной работе были сделаны следующие выводы: 1. Уплотнение при оптимальном содержании воды делает образец более однородным и воспроизводимым. 2. Угол трения, полученный при исследованиях в среднем аппарате прямого сдвига, был выше на 1,2° по отношению к значениям, полученным на более крупном аппарате, что явно говорит о наличии масштабного эффекта и для данного материала.
Однако с увеличением влажности явление исчезает, и процесс сдвига одинаков для разных значений нормального напряжения, что видно на рис. 4. На рис. 5 показана зависимость между напряжением сдвига и нормальным напряжением для все тесты. Описание точек пробега на основе линейных уравнений позволило определить угол трения, как показано в таблице 2. Как для сухого, так и для мокрого РКА угол трения, полученный на среднем аппарате, на 1,2° выше значений, полученных на более крупном аппарате.В данной статье представлены результаты исследований, проведенных на переработанном бетонном заполнителе (RCA). Испытания проводились на двух аппаратах прямого сдвига: среднем и большом для изучения эффекта масштаба. В данной работе были сделаны следующие выводы: 1. Уплотнение при оптимальном содержании воды делает образец более однородным и воспроизводимым. 2. Угол трения, полученный при исследованиях в среднем аппарате прямого сдвига, был выше на 1,2° по отношению к значениям, полученным на более крупном аппарате, что явно говорит о наличии масштабного эффекта и для данного материала. 3. Соотношение L/D 50 как в среднем, так и в большом аппарате было намного выше 50, что исключает влияние размера частиц на эффект масштаба. 4. Основной причиной различия углов трения, полученных на разных приборах, авторы считают угловатость и шероховатость частиц материала. Это вызывает заклинивание зерен в среднем ящике, что приводит к более высоким напряжениям сдвига и большим углам трения. 5. Кроме того, следует изучить влияние вращения зерна на результаты, достигаемые при стрижке как крупными, так и средними аппаратами.6. Представляется целесообразным провести прямое испытание РКА на сдвиг при напряжении выше нормального, чего авторы не сделали из-за аппаратуры …
3. Соотношение L/D 50 как в среднем, так и в большом аппарате было намного выше 50, что исключает влияние размера частиц на эффект масштаба. 4. Основной причиной различия углов трения, полученных на разных приборах, авторы считают угловатость и шероховатость частиц материала. Это вызывает заклинивание зерен в среднем ящике, что приводит к более высоким напряжениям сдвига и большим углам трения. 5. Кроме того, следует изучить влияние вращения зерна на результаты, достигаемые при стрижке как крупными, так и средними аппаратами.6. Представляется целесообразным провести прямое испытание РКА на сдвиг при напряжении выше нормального, чего авторы не сделали из-за аппаратуры …
Круг Мора можно использовать для оценки нормальных и касательных напряжений.
действует на плоскость, нормаль которой составляет угол q градусов до максимального главного напряжения, с 1 . | Например, выберите Новый в меню Файл . Затем введите для Sigma1 , 1640 , для Sigma3 , 500 , для Theta , 53 o и для Поровое давление 0 .Далее выберите Graphics , затем Plot Controls. Выберите Круг Мора проверьте коробка с надписью Напряжения . Нормальное и касательное напряжение, действующее на поверхность ориентирован на 27 o до с 1 при разрушении нанесены на круг Мора маленькой жирной точкой (рис. 20). | Рис. 19. Зависимость между главными напряжениями,
нормальное напряжение, напряжение сдвига и тета показаны для блока
диаграмма слева для диаграммы Мора справа. |
Пользовательский график
Очерчивает определенный пользователем компонент напряжения.
Напряжения:
•S1 S2 S3 компоненты главного напряжения σ1 σ2 σ3
•Sxx Syy Szz Sxy Syz Sxz компоненты декартова напряжения σxx σyy σzz τxy τyz τzx
•Tmax максимальное напряжение сдвига ½(σ1 — σ3)
= ¹/3 [(σ1 — σ2)² + (σ2 — σ3)² +(σ3 — σ1)²]½•Smean среднее напряжение σmean = ¹/3 (σ1 + σ2 + σ3)
•Ti Si максимальное касательное и нормальное напряжение в плоскости сетки τip σip
•S1i S3i максимальное и минимальное напряжение, касательное к плоскости сетки σ1i σ3i
•Tu Su максимальное касательное и нормальное напряжение в вездесущей плоскости τub σub.Ориентация вездесущей плоскости сдвига задается с помощью
•S1u S3u максимальное и минимальное напряжение, касательное к вездесущей плоскости σ1u σ3u \]
•Эффективное/Общее эффективное напряжение или компоненты полного напряжения.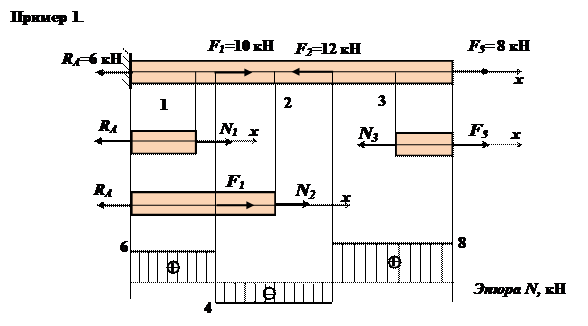 Эти параметры используются только в Map3D Thermal-Fluid Flow, так как этот код позволяет рассчитать стационарное распределение порового давления.
Эти параметры используются только в Map3D Thermal-Fluid Flow, так как этот код позволяет рассчитать стационарное распределение порового давления.
•Индуцированное/абсолютное индуцированное напряжение или компоненты абсолютного напряжения (т. е. напряжение без вклада напряжения перед добычей).
Штаммы:
•e1 e2 e3 главная главная деформация ε1 ε2 ε3
•exx eyy ezz exy eyz exz компоненты декартовой деформации εxx εyy εzz εxy εyz εzx
•emax максимальная деформация сдвига • максимальная деформация сдвига = ¹/3 [(ε1 — ε2)² + (ε2 — ε3)² +(ε3 — ε1)²]½
•evol объемная деформация εvol = (ε1 + ε2 + ε3)
•esi eni максимальный сдвиг и нормальная деформация в плоскости сетки εsi εni
•e1i e3i максимальная и минимальная деформации по касательной к плоскости сетки ε1i ε3i
•esu enu максимальный сдвиг и нормальная деформация в вездесущей плоскости εsu εnu
•e1u e3u максимальная и минимальная деформации касательной к вездесущей плоскости ε1u ε3u
• Упругие/пластические/суммарные компоненты упругой, пластической или полной деформации. Эти параметры используются только в Map3D Non-Linear, так как этот код позволяет рассчитывать нелинейные деформации.
Эти параметры используются только в Map3D Non-Linear, так как этот код позволяет рассчитывать нелинейные деформации.
• Индуцированная/абсолютная индуцированная деформация или компоненты абсолютной деформации (т. е. напряжение без вклада напряжения, предшествующего горным работам).
Смещение:
•ut полное перемещение, его тренд и погружение δt
•ux uy uz декартовы компоненты смещения δx δy δz
•uni перемещение по нормали к плоскости сетки δni
•umi максимальное перемещение по касательной к плоскости сетки δmi
•unu перемещение по нормали к вездесущей плоскости δnu
•umu максимальное перемещение по касательной к вездесущей плоскости δmu
Термический/поток жидкости:
•t температура/напор
•qt общий расход, его тренд и падение.
•qx qy qz Декартовы компоненты потока.
•qni смещение по нормали к плоскости сетки.
•qmi максимальное смещение по касательной к плоскости сетки.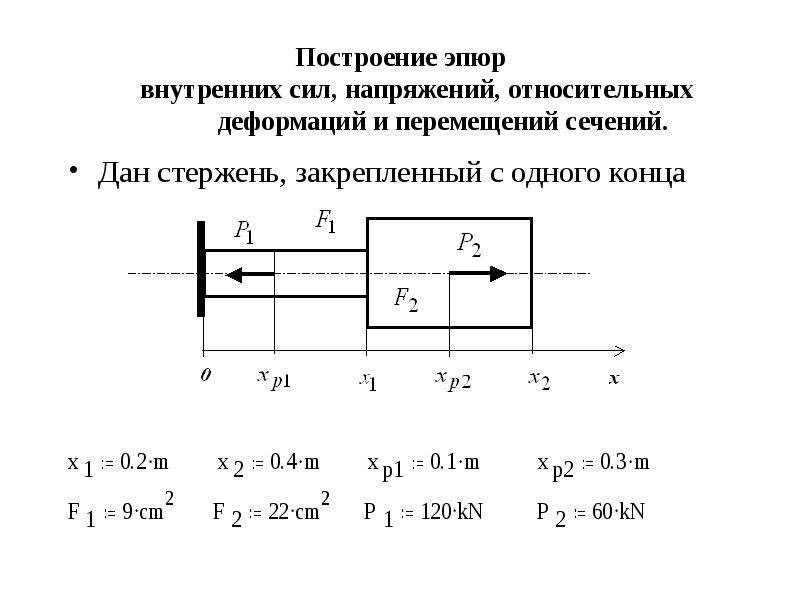
•qnu смещение по нормали к вездесущей плоскости.
•qmu максимальное перемещение по касательной к вездесущей плоскости.
Функции:
•sin() cos() tan() тригонометрические функции синуса, косинуса и тангенса.
•asin() acos() atan() Обратные тригонометрические функции.
• sqrt() функция квадратного корня.
•log() натуральная логарифмическая функция.
•log10() логарифмическая функция по основанию 10.
•exp() экспоненциальная функция (антилогарифмическая).
•abs() абсолютное значение.
•n() an() нормальное и обратное нормальное распределение вероятностей. Аргумент, используемый с нормальным распределением, равен (Δσ1/s), который представляет собой избыточное главное напряжение, деленное на стандартное отклонение (см. ).
•t(,) at(,) t и обратное t распределение вероятностей.Аргумент, используемый с распределением t, равен (Δσ1/(sg),n-2), где Δσ1 представляет собой избыточное главное напряжение, s представляет собой стандартное отклонение, n представляет количество точек данных, а g представляет собой коэффициент [1 + 1/n + (σ3 — σm)²/s3²/(n-1)]½, где σm представляет собой среднее значение σ3, а s3 представляет стандартное отклонение σ3.
•sign() функция знака возвращает +1 для положительных значений, -1 для отрицательных значений и 0 для значений с величиной меньше 10-12.
Прочность:
•ds1 избыточное главное основное напряжение Δσ1 = σ1 – (UCS + q σ3)
•dtmax избыточное максимальное касательное напряжение Δτmax = ½(σ1 – σ3) – [UCS + ½(σ1+σ3) (q-1)]/ (q+1) = [σ1 — (UCS + q σ3) ]/(q+1)
•dtoct избыточное октаэдрическое напряжение сдвига Δτoct = τoct — [UCS + (q–1) σmean ] √(2) /( q+2)
• Вероятность NS1 с использованием нормального распределения N(Δσ1 /std)
•SF-A Прочность/напряжение можно определить как (UCS + q σ3 )/σ1
•SF-B Прочность/напряжение можно определяется как (UCS + q σ3 — σ3)/(σ1 — σ3)
•SF-C Прочность/напряжение может быть определена как [UCS + ½(σ1+σ3) (q-1)]/[ ½(σ1 — σ3)(q+1) ]
•dTip избыточное напряжение сдвига в плоскости Δτip = τip — [Сцепление + σip tan(φ) ]
• Вероятность NTip с использованием нормального распределения N(Δτip /std)
•SFip Прочность/напряжение можно определить как [Сцепление + σip tan(φ) ] / τip
•dSip избыточное напряжение стенки в плоскости Δσip = [ 3 σ1i — σ3i ] — UCS
•RCFip Коэффициент состояния породы для напряжения стенки в плоскости RCFip = [ 3 σ1i — σ3i ]/UCS
• dTub избыточное напряжение сдвига во всех плоскостях Δτub
• Вероятность NTub с использованием нормального распределения N(Δτub /std)
• SFub Прочность/напряжение можно определить как [Сцепление + σub tan(φ)] / τub
• dSub избыточное напряжение стенки в плоскости ub Δσub = [ 3 σ1ub — σ3ub ] — UCS
•RCFub Коэффициент состояния горной породы для напряжения стенки в плоскости ub RCFip = [ 3 σ1ub — σ3ub ]/UCS
•UB# графически отображает набор UB число (1, 2 или 3), имеющее наибольшее значение Δτub
•UCS phi q Параметры прочности Мора-Кулона, определенные с помощью Plot > Коэффициенты прочности > Параметры прочности горной массы. Обратите внимание, что эти параметры определяются только в том случае, если вы указали критерий прочности Мора-Кулона или Друкера-Прагера
Обратите внимание, что эти параметры определяются только в том случае, если вы указали критерий прочности Мора-Кулона или Друкера-Прагера
•sc Параметр прочности Хука-Брауна определяется с помощью параметра График > Коэффициенты прочности > Параметры прочности горной массы. Обратите внимание, что этот параметр определяется только в том случае, если вы указали критерий прочности Хука-Брауна
Местонахождение:
•x y z координата точки сетки.операторы сложения, вычитания, умножения, деления и возведения в степень. Обратите внимание, что сначала вычисляются экспоненциальные числа, затем умножение и деление и, наконец, сложение и вычитание.
•() [] {} стили скобок. Пары скобок должны совпадать.
•> максимальное значение. Например, если уравнение графика указано как s1 > 10, будет построено большее из значений s1 или 10.
•< минимальное значение. Например, если уравнение графика указано как s1 < 10, будет построено меньшее из s1 или 10. 2 ) отображает прочность для критерия Хука-Брауна с sc, равным 60, m, равным 0,1, и s, равным 0,005.
2 ) отображает прочность для критерия Хука-Брауна с sc, равным 60, m, равным 0,1, и s, равным 0,005.
•Диапазон – устанавливает диапазон контура.
•График – регенерирует контурный график.
В раскрывающемся окне можно сохранить до 20 различных уравнений. Они сохраняются между сеансами Map3D в файле map3d.ini.
5.4 Определение нормальных и касательных напряжений в плоскости разлома
5.4 Определение нормальных и касательных напряжений в плоскости разлома Подразделы В этом разделе мы рассмотрим два метода расчета нормальных и касательных напряжений в трещинах и разломах.В первой части рассматривается метод круга Мора, чтобы получить концептуальное представление о проекции напряжения на разломы и максимальное соотношение между напряжением сдвига и эффективным нормальным напряжением.
Во второй части обсуждается тензорный метод, который требует определения трех систем координат и умножения матриц.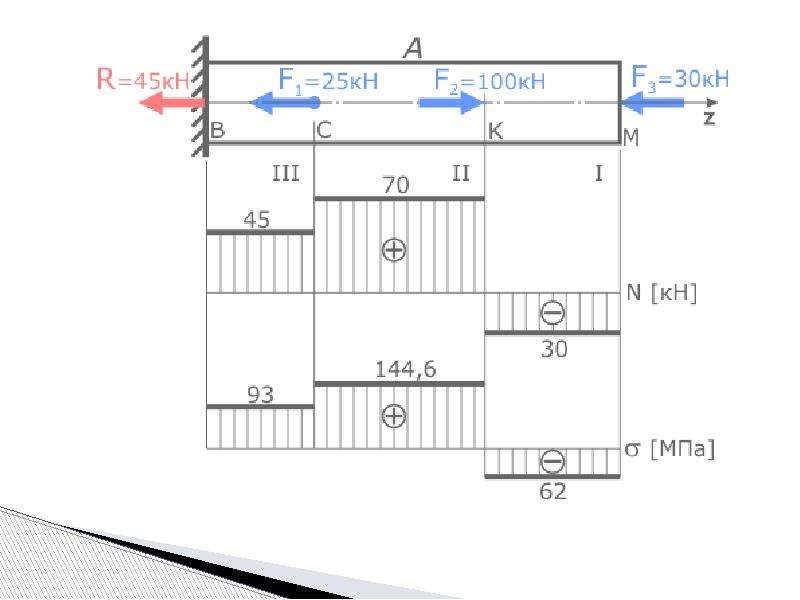 Тензорный метод может быть легко реализован в компьютерном скрипте, но трудоемок при ручной обработке.
Тензорный метод может быть легко реализован в компьютерном скрипте, но трудоемок при ручной обработке.
Трехмерный круг Мора представляет собой графическое представление тензора напряжений и всех его проекций (или возможных значений нормального эффективного напряжения и касательного напряжения) на заданную плоскость.Рассмотрим горизонтальную плоскость на рис. 5.20, нормальным напряжением является вертикальное напряжение, а касательное напряжение отсутствует. Рассмотрим вертикальную плоскость с простиранием восток-запад на рис. 5.20, вы получите минимальное главное напряжение . Рассмотрим вертикальную плоскость простирания север-юг на рис. 5.20, вы получите максимальное главное напряжение.
Точно так же нетривиальные решения проекции напряжения на произвольный угол плоскости включают все точки, ограниченные тремя кругами Мора. Рассмотрим решения вдоль каждой окружности на рис.5.20.
Для этого примера (нормальный разлом, азимут В-З) идеальный разлом возник бы с простиранием В-З и падением 60 (при условии, что
). Это ориентация плоскости с максимальным
.
Это ориентация плоскости с максимальным
.
ЗАДАЧА 5.3: Найти касательные и нормальные действующие напряжения на плоскости разлома при следующих напряженных состояниях и условиях:
РЕШЕНИЕ
ЗАДАЧА 5.4: Найти касательные и нормальные действующие напряжения на плоскости разлома при следующих напряженных состояниях и условиях:
РЕШЕНИЕ
Действующие напряжения: 15 МПа, 30 МПа, 10 МПа. На основе круга Мора с участием и тригонометрия:
В этом подразделе описывается процедура расчета напряжений на произвольной плоскости с учетом ее ориентации относительно географической системы координат и тензор натурных напряжений главных напряжений (с учетом его главных значений и главных направлений).
Первый шаг состоит в определении системы координат главного напряжения и географической системы координат (обе правые системы координат).
Второй шаг включает построение изменения базовой матрицы от главного напряжения до системы географических координат. Эта матрица зависит от проекций элементов новой базы на старую по косинусам направляющих углов , , и (рис.5.22). В таблице 5.3 приведены значения , и для случаев, когда вертикальное напряжение является главным напряжением.
| (5.7) |
Проверьте эту ссылку https://mybinder.org/v2/gh/johntfoster/rotation_widget/master?filepath=rotation_widget-rise.ipynb для анимации , и в произвольных направлениях.
С помощью матрицы мы можем вычислить тензор напряжений как функция ,
(5. 8) 8) |
и поэтому:
| (5.9) |
где верхний индекс означает «транспонировать».
ЗАДАЧА 5.5: Расчет
в случае нормального режима разломного напряжения (МПа, МПа, МПа) с азимутом север-юг.является основным напряжением.
РЕШЕНИЕ
. Тензор главных напряжений равен
Используя Таблицу 5.3 и принимая во внимание, что углы координаты главного напряжения получаются , , и . Результаты изменения матрицы системы координат
Наконец, используя уравнение 5.9
ПРОБЛЕМА 5.6: Рассчитать
в случае сдвигового режима напряжений (МПа, МПа, МПа) с азимутом С-Ю. является основным напряжением.
РЕШЕНИЕ
. Тензор главных напряжений равен
Используя таблицу 5. 3 и учитывая, что
и , углы координаты главного напряжения
,
, и
.
Результаты изменения матрицы системы координат
3 и учитывая, что
и , углы координаты главного напряжения
,
, и
.
Результаты изменения матрицы системы координат
Наконец, используя уравнение 5.9
ЗАДАЧА 5.7: Расчет
в случае взбросового стрессового режима (МПа, МПа, МПа) с азимутом В-З. является основным напряжением.
РЕШЕНИЕ
Тензор главных напряжений равен
Используя таблицу 5.3 и учитывая, что а также , углы координаты главного напряжения получаются , , и . Результаты изменения матрицы системы координат
Наконец, используя уравнение 5.9
ЗАДАЧА 5.8: Расчет
в случае сдвигового режима напряжения (МПа, МПа, МПа) с азимутом 135. является главным напряжением.
РЕШЕНИЕ
Тензор главных напряжений равен
Используя таблицу 5. 3 и учитывая, что
и , углы координаты главного напряжения
,
, и
.Результаты изменения матрицы системы координат
3 и учитывая, что
и , углы координаты главного напряжения
,
, и
.Результаты изменения матрицы системы координат
Наконец, используя уравнение 5.9
Третий шаг состоит в определении системы координат плоскости разлома. Базис системы координат состоит из векторов (падения), (простира) и (нормальа): правый базис d-s-n. Три вектора зависят исключительно от двух переменных: и от неисправности.
Четвертый шаг (последний) состоит в проецировании тензора напряжений, основанного на географической системе координат, на векторы основания разломов. Вектор напряжения, действующий на плоскость разлома (обратите внимание, что он не обязательно совпадает с , или ) и рассчитывается по формуле:
(5. 10) 10) |
Общее нормальное напряжение в плоскости разлома равно (совмещено с ):
| (5.11) |
Эффективное нормальное напряжение в плоскости разлома равно . Касательные напряжения в плоскости разлома совпадают с а также являются:
| (5.12) |
Скалярное произведение используется во всех этих векторных умножениях. Геометрический смысл — проекция одного вектора на другой.
Эффективное нормальное напряжение и абсолютный сдвиг также можно рассчитать с помощью следующих уравнений:
| (5.13) |
| (5.14) |
Угол напряжения сдвига в отношении (горизонтальная линия) и количественно определяет направление ожидаемого движения разлома в плоскости разлома.
| (5.15) |
ЗАДАЧА 5. 9: Рассчитать , , , , и для разлома простиранием 000 и падением 60E в месте с нормальным режимом разломных напряжений (МПа,
МПа,
МПа) с азимутом равным 90.является основным напряжением.
9: Рассчитать , , , , и для разлома простиранием 000 и падением 60E в месте с нормальным режимом разломных напряжений (МПа,
МПа,
МПа) с азимутом равным 90.является основным напряжением.
РЕШЕНИЕ
Тензор главных напряжений равен
Используя Таблицу 5.3 и принимая во внимание, что азимут равен 90, получаем углы координаты главного напряжения , , и . Результаты изменения матрицы системы координат
а общее напряжение в географической системе координат получается
Учитывая ориентацию разлома, вектор нормали к разлому равен
Наконец, напряжения на разломе
МПа.
МПа
МПа
МПа
= 90
ЗАДАЧА 5.10: Рассчитать , , , , и для разлома с простиранием 060 и падением 90 в месте со сдвиговым режимом напряжений (МПа,
МПа,
МПа) по азимуту, равному 120°, является главным напряжением.
РЕШЕНИЕ
. Тензор главных напряжений равен
Используя Таблицу 5.3 и принимая во внимание, что азимут равен 120, углы координаты главного напряжения получаются , , и .Результаты изменения матрицы системы координат
а общее напряжение в географической системе координат получается
Учитывая ориентацию разлома, вектор нормали к разлому равен
Наконец, напряжения на разломе
МПа.
МПа
МПа
МПа
= 0
ПРОБЛЕМА 5.11: Рассчитать , , , , и для сопряженных разломов простирания 045 и 225 оба с падением 60 в месте с нормальным режимом разломных напряжений (
пси,
пси,
psi) с азимутом, равным 90°, является главным напряжением.
РЕШЕНИЕ
. Тензор главных напряжений равен
Используя Таблицу 5. 3 и принимая во внимание, что азимут равен 90, получаем углы координаты главного напряжения
,
, и
.
Результаты изменения матрицы системы координат
3 и принимая во внимание, что азимут равен 90, получаем углы координаты главного напряжения
,
, и
.
Результаты изменения матрицы системы координат
а тензор полных напряжений в географической системе координат дает
Рассмотрим первый разлом с простиранием 045 и падением 60, вектор нормали к разломам есть
Напряжения на этом разломе равны
фунтов на квадратный дюйм
фунтов на квадратный дюйм
фунтов на квадратный дюйм
фунтов на квадратный дюйм
= 56,3
Рассмотрим разлом с простиранием 225 и падением 60, вектор нормали к разломам есть
Напряжения на этом разломе равны
фунтов на квадратный дюйм
фунтов на квадратный дюйм
фунтов на квадратный дюйм
фунтов на квадратный дюйм
= 56,3
ЗАДАЧА 5.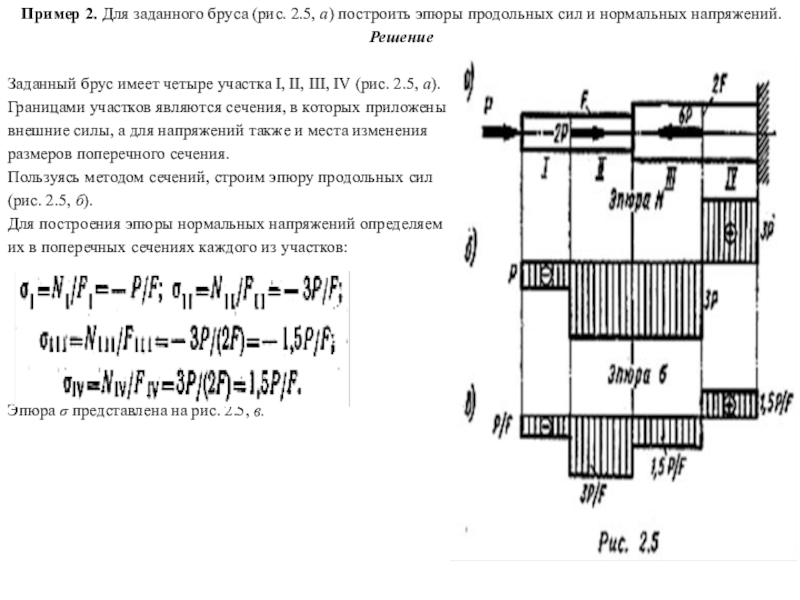 12: вычислить , , , , , и
для разлома простиранием 120 и падением 70 в месте взбросового напряженного режима (
пси,
пси,
psi) с азимутом равным 150 и поровым давлением psi.является основным напряжением.
12: вычислить , , , , , и
для разлома простиранием 120 и падением 70 в месте взбросового напряженного режима (
пси,
пси,
psi) с азимутом равным 150 и поровым давлением psi.является основным напряжением.
РЕШЕНИЕ
. Тензор главных напряжений равен
и поровое давление psi.
Используя Таблицу 5.3 и принимая во внимание, что азимут равен 150, углы координаты главного напряжения получаются , , и . Результаты изменения матрицы системы координат
а общее напряжение в географической системе координат получается
Учитывая ориентацию разлома, вектор нормали к разлому равен
Наконец, напряжения на разломе
фунтов на квадратный дюйм
фунтов на квадратный дюйм,
фунтов на квадратный дюйм,
пси,
фунт/кв.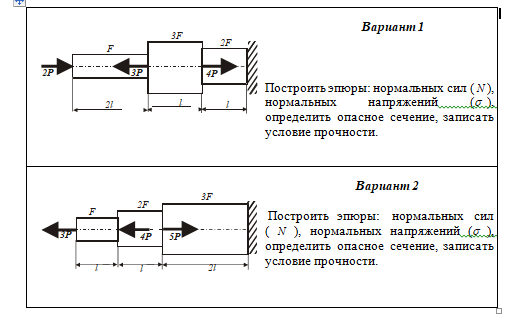 дюйм
дюйм
= 18,21
Отношение сдвига к нормальному эффективному напряжению равно
Пример: сделать трехмерный круг Мора заполненным цветом, соответствующим значение, стереосетка и разломы в 3D.
ДВУХМЕРНОЕ НАПРЯЖЕНИЕ
2 — РАЗМЕРНОЕ НАПРЯЖЕНИЕ
I. ДВУХМЕРНОЕ НАПРЯЖЕНИЕ
А. Определить напряженное состояние для произвольного плоскость — случай 2D пренебрегает направлением z
Б.д = Р между нормалью к плоскости и осью x
C. Разработайте уравнение, которое позволит нам решить для s q и t q для любой плоскости с ориентацией Ðq
D. Не учитывать z, и для описания используются только 4 компонента система
помните: нет вращения вокруг оси Z, поэтому t yx = t xy , поэтому есть только 3 компонента напряжения
Э.Удалить пространственный треугольник ABC
F. Это диаграмма «свободного» тела
G. Хотите определить s и t для самолета AC
H. Чтобы сделать расчеты простыми , выберите удобную длину для переменного тока (гипотеза)
Чтобы сделать расчеты простыми , выберите удобную длину для переменного тока (гипотеза)
1. Где: AC = 1, тогда: AB = cosq , БК = sinq
примечание: есть 4 напряжения (векторные компоненты), которые делают вклады как в нормальную (s ), так и в поперечную (t) напряжение это: s xx , s yy , t xy и t yx
И.Чтобы определить общее напряжение, просто суммируйте все эти компоненты вектора через q
(s xx + t xy )cosq + (s yy + t yx )sinq = s q + t q
2II. РЕШЕНИЯ
A. Этап 1 — вклад s xx к s q и t q
1. Обычный компонент
cos q = с q / с xx cos q ® с q = с xx cos 2 q2.Компонент сдвига
sin q = t q / с xx cos q ® t q = с xx sinq cosq B. Этап 2 — вклад s yy к s q и t q
Этап 2 — вклад s yy к s q и t q
1. Обычный компонент
sin q = s q 2 / s yy sinq® s q 2 = s yy sin 2 0 2. Компонент, работающий на сдвиг cosq = t q 2 / s yy sinq ® t q 2 = — s yy sinq cosq а.s yy отрицательно из-за направления C. Этап 3 — вклад t yx 1. Нормальное напряжение 2. Напряжение сдвига D. Этап 4 — вклад t xy 1. Нормальное напряжение с q 4 = t xy sinq
cosq 2.Компонент сдвига E. t q всего = t 1+2+3+4 q s q = s xx cos 2 q + s yy sin 2 q + 2t xy sinq cosq t q = (s xx — s yy )sinq cosq + t xy (cos 2 q
— грех 2 q) А. Для любого напряженного состояния существует 3 ортогональных
плоскости без напряжения сдвига А. с 1 = макс. главное напряжение B. s 2 = промежуточное главное напряжение C. s 3 = минимальное основное напряжение D. Подстановка в уравнения для s q и т q 1.с хх = с 1 2. с гг = с 3 3. результат: т = (с 1 — с 3 )
sin q cosq A. Эллипс напряжения — 2D, эллипсоид — 3D Б.График круга Мора A. s 1 и s 3 должны быть уравновешены s q Б. с 1 cos q
= с хх К. с 3 sin q
= с гг D. cos 2 q = s xx 2 / s 1 2 и
sin 2 q = s yy 2 / s 3 2 1.грех 2 д
+ cos 2 q = 1 Е. (с хх 2 / с 1 2 ) + ( с уу 2 / с 3 2 Добавить все — s q итого
= с 1+2+3+4 к
Добавить все — s q итого
= с 1+2+3+4 к III.ОСНОВНЫЕ ПЛОСКОСТИ НАПРЯЖЕНИЙ
IV. ОСЬ ГЛАВНОГО НАПРЯЖЕНИЯ
 т ху = 0
т ху = 0 V. НАПРЯЖЕНИЕ (графическое изображение)
VI. ЭЛЛИПС НАПРЯЖЕНИЯ — работает только с обычными компонентами
VII.
 КРУГЛЫЙ УЧАСТОК МОРА
КРУГЛЫЙ УЧАСТОК МОРАA. Помните, что главные напряжения не имеют сдвига. компонент, связанный с ними
1. с хх = с 1
2. с гг = с 3
Б.s q = s 1 cos 2 q + s 3 sin 2 q
C. t q = ( s 1 — s 3 )sin q cosq
D. sin 2 q = 1 — cos2q / 2
E. cos 2 q = 1 + cos2q / 2
F. sinq cosq = sin2q / 2
Г. Заменить на:
| 1. с д = | s 1 (1+cos2 q/2) + s 3 (1- cos2 q/2) |
| = | (с 1 + с 3 ) / 2 + (( с 1 — с 3 ) / 2)cos2 q |
| х = | центр радиус коса |
2. т д = т д = | с 1 — с 3 (sin2 q/2) |
| = | ((с 1 — с 3 ) / 2)sin2 q |
| г = | радиус sina |
H. Угол 2q определяет точка на окружности с координатами (s q , t q ), которые представляют собой компоненты напряжения на наклонной плоскости, определяемой q
И.Координаты в любой точке окружности представляют нормальное и касательное напряжение для этого состояния напряжения
Дж. Среднее напряжение — среднее значение наибольшего/наименьшего главного
напряжения =
(с 1 + с 3 ) / 2
K. Девиаторное напряжение = диапазон напряжений внутри тела d = s 1 — s 3
Трансформация стресса и круг Мора
Введение
Немецкий физик Отто Мор разработал метод графической интерпретации общего напряженного состояния в точке. Этот метод называется кругом Мора и может использоваться для оценки главного напряжения, максимальных касательных напряжений, а также нормальных и касательных напряжений в любой плоскости.
Этот метод называется кругом Мора и может использоваться для оценки главного напряжения, максимальных касательных напряжений, а также нормальных и касательных напряжений в любой плоскости.
Давайте возьмем простой двухмерный элемент напряжения, чтобы понять концепцию преобразования напряжения и то, как можно использовать круг Мора для упрощения процесса.
Элемент напряжения
Элемент напряжения — это полезный способ описания напряжений, действующих в одной точке тела. Рассмотрим простой пример балки с осевой нагрузкой.теперь напряженное состояние в напряженном элементе будет очень простым. Он будет иметь только нормальное напряжение по оси X и нулевое нормальное напряжение по оси Y и нулевое касательное напряжение. Если мы повернем напряженный элемент, чтобы получить напряженное состояние для определенного угла. В зависимости от того, как мы ориентируем элемент напряжения, мы получим разные значения для компонентов нормального напряжения и напряжения сдвига.
Нормальное напряжение и напряжение сдвига для элемента напряжения, ориентированного под определенным углом (или, другими словами, в наклонной плоскости), с использованием уравнений преобразования напряжения .
Уравнение преобразования напряжения
Ниже приведены уравнения преобразования напряжений,
Входными данными для этих уравнений являются нормальные напряжения σ x , σ y и напряжение сдвига τ xy в исходной ориентации элемента, а θ – угол, на который должен быть повернут элемент напряжения, или наклон плоскости, на которую мы нужны нормальные и касательные напряжения.
Когда напряженный элемент вращается, нормальное напряжение и напряжение сдвига будут меняться, и это изменение можно легко понять на примере.
Из этого примера видно, что после поворота элемента на 180 градусов значения нормального напряжения и напряжения сдвига возвращаются в исходное положение. Помните, фактическое состояние напряжения, приложенного к телу, не меняется при вращении элемента.
Помните, фактическое состояние напряжения, приложенного к телу, не меняется при вращении элемента.
Наблюдения из графика
- При определенных углах кривая нормального напряжения достигает максимального и минимального значений, и эти значения разделены углом 90 градусов.
- Это означает, что при определенном угле поворота, когда мы получаем максимальное нормальное напряжение на одной грани (скажем, на грани X), тогда минимальное напряжение будет перпендикулярно этой грани (на грани Y).
- Всякий раз, когда кривая нормального напряжения достигает максимального или минимального значения, напряжение сдвига под этим углом будет равно нулю.
Мы знаем, что плоскость, в которой касательные напряжения равны нулю, называется Главной плоскостью , а соответствующая нормаль — Главные напряжения (σ 1 , σ 2 ). Угол поворота главной плоскости обозначается как θp.
Круг Мора
Это графический метод для простого определения нормальных и касательных напряжений «БЕЗ» с использованием уравнений преобразования напряжения.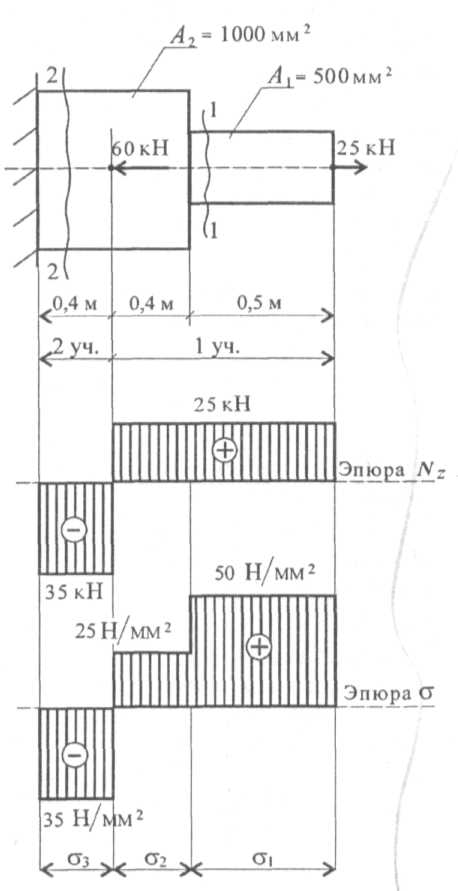
Окружность Мора нарисована на двумерном графике, где нормальное напряжение отложено по горизонтальной оси, а касательное напряжение отложено по вертикальной оси.
Соглашение о знаках
Если касательные напряжения имеют тенденцию вращаться против часовой стрелки, считаются положительными, а касательные напряжения имеют тенденцию вращаться по часовой стрелке, отрицательными. Вот почему касательные напряжения в Y-грани принимаются отрицательными. Таким образом, положительные касательные напряжения откладываются в направлении вниз, а отрицательные касательные напряжения — в направлении вверх.
Нормальные напряжения растяжения по своей природе положительные, а сжимающие по природе отрицательные .
шага, чтобы нарисовать круг Мора
- Установка оси координат (σ – ось X, τ – ось Y)
- Нанесение точек A (σ x ,τ xy ) и B (σ y ,-τ xy ) .
- Используя A и B в качестве диаметра и C в качестве центра, нарисуйте круг.
Обратите внимание, что в точке A θ=0 градусов, а в точке B θ=90 градусов.
i) Метод двойного угла
Трансформация стресса с использованием круга Мора
Предположим, что нам нужны нормальные и касательные напряжения на плоскости, наклоненной под углом θ. В круге Мора σ x и σ y отмечены на одной и той же оси (т. е. 180 градусов), что не является реальным случаем, поскольку σ x и σ y перпендикулярны друг другу (т. е. 90°). градусов).
Таким образом, ориентируясь на CA, найдите точку D на окружности под углом 2θ.Найдите другую точку E, диаметрально противоположную D. Координаты X точек D и E представляют собой нормальные напряжения на гранях x и y соответственно, а координата Y представляет напряжение сдвига на новой наклонной плоскости.
Главные напряжения
Главные напряжения действуют на главную поверхность/плоскость, на которой касательное напряжение равно нулю.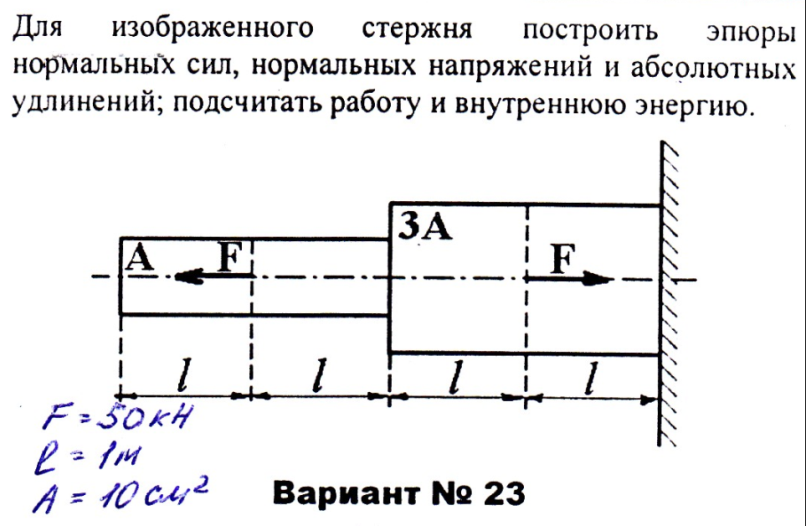 По горизонтальной оси круга Мора значение касательного напряжения всегда будет равно нулю. Следовательно, точки, в которых горизонтальная ось пересекает окружность, дают максимальное и минимальное главные напряжения.Угол между СА и горизонтальной осью составляет 2θp, из которого можно рассчитать наклон главной плоскости (θp).
По горизонтальной оси круга Мора значение касательного напряжения всегда будет равно нулю. Следовательно, точки, в которых горизонтальная ось пересекает окружность, дают максимальное и минимальное главные напряжения.Угол между СА и горизонтальной осью составляет 2θp, из которого можно рассчитать наклон главной плоскости (θp).
Максимальное напряжение сдвига
Визуально можно заметить, что крайние точки окружности по вертикальной оси дают максимальное касательное напряжение. Геометрически максимальное касательное напряжение есть не что иное, как радиус круга Мора.
Угол между CA и вертикалью равен 2θs, а θs — это наклон плоскости, в которой возникает максимальное напряжение сдвига.
ii) Полюсный метод:Что такое шест?
Метод полюса основан на уникальной точке на круге Мора, известной как полюс . Этот полюс уникален, потому что любая линия напряжения, проведенная через полюс, пересекает окружность Мора в точке, представляющей состояние напряжения на плоскости с той же ориентацией, что и линия. Как показано на рисунке, линия, проведенная через полюс и некоторую точку напряжения (σ,τ) на окружности, точно параллельна плоскости с соответствующими σ и τ, что делает этот подход очень интуитивно понятным.
Как показано на рисунке, линия, проведенная через полюс и некоторую точку напряжения (σ,τ) на окружности, точно параллельна плоскости с соответствующими σ и τ, что делает этот подход очень интуитивно понятным.
Как найти поляка?
Давайте найдем полюс в круге Мора на примере. На рисунке показано напряженное состояние элемента и его круг Мора.
Чтобы найти полюс, Из точки A проведите линию, параллельную грани X (зеленая), а из точки B проведите линию, параллельную грани Y (красная). Эти две точки будут пересекаться в точке на окружности, и эта точка называется полюсом.
Трансформация напряжений и главные напряжения: Например, рассчитаем нормальные и касательные напряжения для элемента, повернутого на угол 30 градусов против часовой стрелки.Чтобы определить напряженное состояние наклонной плоскости, проведите две линии от полюса под углом 30 градусов против часовой стрелки от зеленой и красной линий.
 Например, Handin (1966) приводит результаты трехосного стресс-теста.
на песчанике из Верии, штат Огайо.Образец не выдержал ограничения
давление 500 бар и дифференциальное напряжение 1590 бар .
Температуры во время эксперимента поддерживались на уровне 24 o С . Напомним из предыдущих обсуждений, что дифференциальное напряжение равно
до с 1 -с 3 .
Затем мы пишем s 1 -s 3 = 1590 баров . Во время трехосного стресс-теста ограничение
давление поддерживалось равным с 3 .Следовательно, с 1 = 1590 бар + 500
баров = 1640 баров . Когда образец не выдержал, он сломался по изломам.
с 27 о до с 1 .
Этот угол обычно называют углом разлома. Тета ( q ),
угол между нормалью к плоскости трещины и с 1 таким образом, 90 o -27 o = 53 o .
Например, Handin (1966) приводит результаты трехосного стресс-теста.
на песчанике из Верии, штат Огайо.Образец не выдержал ограничения
давление 500 бар и дифференциальное напряжение 1590 бар .
Температуры во время эксперимента поддерживались на уровне 24 o С . Напомним из предыдущих обсуждений, что дифференциальное напряжение равно
до с 1 -с 3 .
Затем мы пишем s 1 -s 3 = 1590 баров . Во время трехосного стресс-теста ограничение
давление поддерживалось равным с 3 .Следовательно, с 1 = 1590 бар + 500
баров = 1640 баров . Когда образец не выдержал, он сломался по изломам.
с 27 о до с 1 .
Этот угол обычно называют углом разлома. Тета ( q ),
угол между нормалью к плоскости трещины и с 1 таким образом, 90 o -27 o = 53 o . Эти отношения
изображены на рисунке 19 и могут быть построены с использованием процедур
описано в предыдущем разделе.
Эти отношения
изображены на рисунке 19 и могут быть построены с использованием процедур
описано в предыдущем разделе.