Построение эпюры нормальных напряжений при изгибе

Пример решения задачи на построение эпюры нормальных напряжений σ при изгибе стальной балки прямоугольного сечения.

Задача

Построить эпюру распределения нормальных напряжений для подобранного ранее прямоугольного сечения двухопорной балки с размерами h=155мм и b=80мм.

Изгибающий момент в опасном сечении балки M_{x max}=47,6кНм.

Другие примеры решений >
Помощь с решением задач >

Пример решения

Предыдущие пункты решения задачи:

1. Определение опорных реакций,
2. Построение эпюр поперечных сил и изгибающих моментов,
3. Подбор размеров прямоугольного сечения балки.

Рассмотрим пример построения эпюры распределения нормальных напряжений в опасном сечении балки.

Прямоугольное сечение имеет три характерных точки:

1 – верхняя,

2 – центр тяжести (середина высоты),

3 – самая нижняя точка.

Для построения эпюры достаточно найти значения в любых двух точках, потому что при изгибе нормальная составляющая полных напряжений по высоте сечения меняется линейно.

где I_x – осевой момент инерции сечения,
y – расстояние от оси х проходящей через центр тяжести сечения до точки в которой рассчитывается напряжение.

Очевидно, что на самой оси x (точка №2) где координата y=0 напряжения отсутствуют.

Наибольшие значения нормальных напряжений будут на максимальном удалении от оси x, то есть при y_max=h/2 (в точках 1 и 3).

Рассчитаем момент инерции прямоугольного сечения

Тогда максимальные напряжения

При изгибе верхний и нижний слой балки испытывают продольную деформацию разных знаков.

Знаки напряжений в точках 1 и 3 определяются по построенной ранее эпюре изгибающих моментов M_x.

В данном случае по ней видно, что в опасном сечении балки эпюра моментов имеет положительное значение (+47,6 кНм), что согласно правила знаков при изгибе говорит о том, что в рассматриваемом месте балки сжимаются верхние слои (нижние соответственно растягиваются).

Другие видео

Поэтому в соответствии с правилом знаков для напряжений, нормальные напряжения в верхней точке 1 будут отрицательны (потому что сжатие), а в точке 3 – положительны (растяжение) или σ_т1=-148,6МПа, σ_т3=148,6МПа.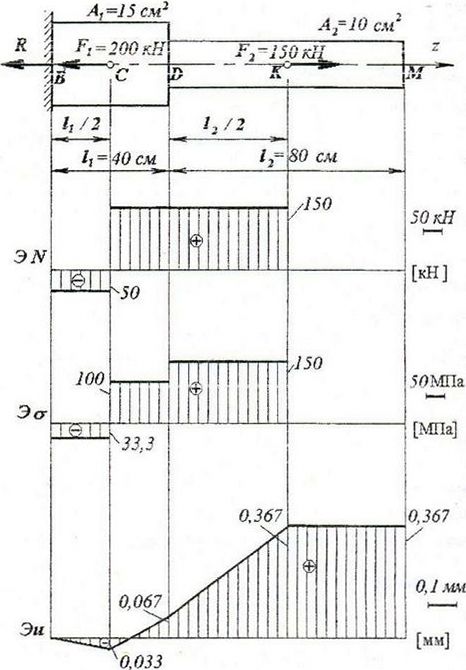

По полученным данным строим эпюру

Как видно по построенной эпюре, нормальные напряжения не превышают заданных допустимых значений, что говорит о том, что размеры прямоугольного сечения были подобраны верно, и прочность балки обеспечена.

Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.

---

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

---

Помощь с решением

---

Поиск формул и решений задач

1.

2.2. Построение эпюры напряжений.

Нормальные напряжения (z) распределяются равномерно по сечению:

где N(z) – продольная сила, A(z) – площадь поперечного сечения.

Для определения положения опасного сечения стержня, в котором возникают максимальные напряжения, определим напряжения в долях 1/А₀.

Участок АВ (0z₁l₂), нормальные напряжения

На участке ВС (l₁z₂2l

2):

Участок СD (0z₃l₃):

По полученным данным строим эпюру ЭА₀ (рис. 1.3 в).

1.2.3. Расчет на прочность. Подбор сечения.

По эпюре напряжений видно, что опасным является сечение В

Условие прочности при растяжении-сжатии имеет вид:

где [] – допускаемое напряжение, которое определено выше для материала Ст30 и равно []=563,8 Мпа.

Тогда условие прочности примет вид

откуда А₀:

Определим напряжения, действующие в сечениях при выбранном значении А₀.

Участок АВ:

Участок ВС:

Участок CD:

По полученным данным строим эпюру действующих в стержне нормальных напряжений Э(рис. 1.3 г).

1.3. Расчет на жесткость стержня постоянного сечения.

Для стержня из стали 30Х, площадью поперечного сечения А=8см

2, представленного на рис. 1.5, необходимо построить эпюры продольных сил и осевых перемещений, выполнить расчет на жесткость.

1.3.1. Построение эпюр продольных сил и перемещений.

Построение эпюры продольных сил. Направим вдоль оси стержня ось z(рис.1.5). Составим уравнение равновесия системы:

Разобьем стержень на 3 участка АВ, ВС и CD, проведем на каждом из них произвольные сечения 1-1, 2-2, 3-3 с заданными координатами этих сеченийz₁,z₂,z₃.

Участок АВ (0z₁l₁):

Участок ВС (0z₂l₂):

На участке DC (0z₃l₃) отбросим левую часть, ее действие заменим продольной силойN₃:

По полученным данным строим эпюру ЭN(рис.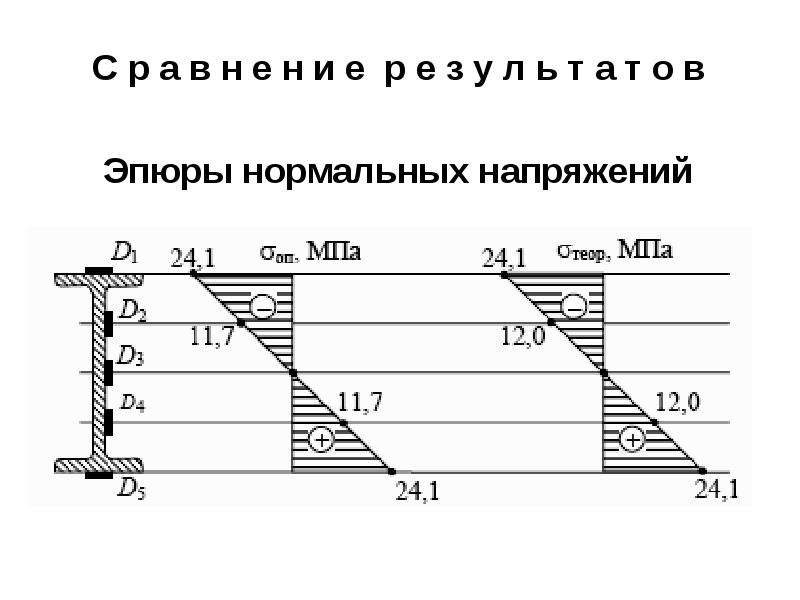

1.5).

Построение эпюры перемещений. Запишем уравнения для перемещений w(z) сечений, считая площади сечений известными:

где w₀– перемещение в начале участка, определяемое начальными условиями;l(z) – удлинение участка (абсолютная деформация участка стержня).

Если продольная сила N(z) зависит от координат сеченияz, то:

Для стали 30Х Е=2*10⁵МПа. В расчетах примем жесткость сечения при растяжении-сжатии ЕА=2*10⁵*8*10²=16*10⁷ Н=16*10⁴ кН.

Рассмотрим участок АВ (0z₁l₁):

Функция w(z₁) – квадратичная парабола. Так как в сечении А – заделка, тоw₀=0 иw₁=0,0026мм. Так как в пределах участка АВ продольная силаN₁не меняет знака, то парабола в пределах участка не имеет экстремума.

Участок ВС (0z₂l₂):

Функция w(z

2) – квадратичная парабола. Так как в пределах участка ВС продольная силаN₂не меняет знака, то парабола в пределах участка не имеет экстремума.

На участке DC (0z₃l₃):

Функция w(z₁) – линейная.

По полученным данным строим эпюру Эw(рис. 1.5).

1.3.2. Расчет на жесткость.

Условие жесткости при растяжении-сжатии

где L– удлинение стержня, [l] – допускаемое удлинение. В данном случае условие жесткости должно выполняться для участкаCD:

Величина [l]=0,001Lпринимается в долях от суммарной длиныL,

Запишем условие жесткости:

Условие жесткости выполняется.

1.4. Расчет на прочность статически неопределимой стержневой системы при растяжении – сжатии.

Стержневая система, состоящая из жесткого стержня АЕ и двух других стержней ВС и ВК, нагружена силой Р=35кН (рис 1.6). Определить коэффициент запаса прочности стержневой системы, если=45

0,l₁=0,6м,l₂=0,3м,l₃=0,6м, А=800мм²,k=1,2, материал – сталь 30Х с пределом текучести_т=845,7МПа.

При известной площади сечения выполняется проверочный расчет на прочность по напряжениям. Величина фактического коэффициента запаса где_пред – предельное значение напряжения для заданного материала._max– максимальное рабочее напряжение, возникающее в заданной стержневой системе от приложенных нагрузок. Сталь 30Х пластичный материал, тогда_пред=_т, следовательно

Механика материалов: трансформация напряжений » Механика гибких конструкций

---

исследования

человек

курсы

блог

---

Трансформация стресса

Часто, как в случае с сосудами под давлением, которые мы изучали на предыдущем уроке, напряжение в одном направлении действительно мало по сравнению с двумя другими. В этом случае удобно пренебречь малым напряжением, и вместо оценки напряжения, действующего на кубический элемент внутри материала, мы можем исследовать напряжение, действующее на

самолет .

Эти два состояния напряжения, трехмерное напряжение и плоское напряжение, часто обсуждаются в матричной или тензорной форме. Когда мы уменьшаем размерность тензора с 3D на 2D, мы избавляемся от всех членов, содержащих компонент в направлении z , так что

Теперь, когда мы сократили наше состояние напряжения до двух измерений, мы можем научиться преобразовывать координаты, вдоль которых действуют эти компоненты напряжения, в любую интересующую нас систему координат. Зачем нам это делать? Что ж, взгляните на изображение ниже. >

Два куска дерева, срезанные под углом и склеенные вместе. Дерево разрывается под действием силы растяжения

P . Как узнать, сможет ли клеевой шов выдержать результирующее напряжение, создаваемое этой силой? Нам необходимо рассчитать нормальные и касательные напряжения перпендикулярно и параллельно стыку. Следовательно, нам нужно повернуть или преобразовать координаты, связанные с силой P , в направление, связанное с углом клеевого соединения. Затем мы можем оценить напряжения вдоль этих новых направлений, х’ и у .

После того, как мы повернули систему координат, нам нужно преобразовать силы, действующие в старой системе координат, в эту новую систему координат. Это означает, что мы должны нарисовать подробную схему свободного тела. Если мы возьмем дифференциальный элемент рядом с началом новой системы координат, мы можем получить силы, действующие на каждую поверхность, из напряжения, умноженного на дифференциальную площадь.

Как вы заметите на диаграмме свободного тела, большая часть сил направлена ​​не в интересующем нас направлении, т. е. х’ и у . Итак, нам нужно разбить эти силы на составляющие, и просуммировать полученные силы по направлениям нашей новой системы координат. Это приводит к длинному, но прямому расчету, приведенному ниже.

Мы можем остановиться здесь, если хотим. Однако, если мы воспользуемся парой тригонометрических тождеств, мы сможем сделать эти уравнения немного более удобными.

Используя эти тождества, мы можем избавиться от всех этих квадратов синусов и косинусов. Окончательный результат для нормальных и касательных напряжений в нашей новой системе координат (обозначенной тета, которая представляет собой вращение против часовой стрелки из x по оси x’ ) задается как

Главное напряжение и круг Мора

Мы только что показали, что величина нормального напряжения и напряжения сдвига будет зависеть от выбранной вами системы координат. Если повернуть систему координат на некоторый угол, величина этих напряжений изменится. Как вы можете подозревать, определенные углы будут соответствовать максимальному и минимальному значениям этих напряжений. Один из способов определить экстремумы функции — продифференцировать ее по интересующей нас переменной и приравнять полученное уравнение к нулю.

Теперь мы можем найти тета, вспомнив соотношение между синусом, косинусом и тангенсом, так что

Мы добавили нижний индекс p к тета, чтобы идентифицировать этот угол как плоскость, соответствующую максимальному и минимальному нормальным напряжениям. Это уравнение имеет два корня, , т. е. , ему удовлетворяют два значения тета. Эти два значения будут разделены 90 ^o (или 2*theta будут разделены 180 ^o ). Один угол будет соответствовать максимальному нормальному напряжению, а другой — минимальному. Мы поговорим об определении того, что есть что, в ближайшее время. Во-первых, отметим, что мы можем повторить эту же процедуру, чтобы определить угол, под которым элемент будет подвергаться максимальному и минимальному сдвигу:

Теперь, когда у нас есть плоскости, на которых напряжения будут максимальными и минимальными, нам нужно определить величину этих главных напряжений . Есть разные способы сделать это, но общая идея должна показаться знакомой всем, кто знаком с методами линейной алгебры. Мы стремимся диагонализовать наш тензор плоского напряжения, и полученные собственные значения будут соответствовать экстремумам нашего напряженного состояния.

Наша цель при нахождении главных напряжений в элементе состоит в том, чтобы устранить зависимость уравнений трансформации напряжений от тета. Уравнения, описывающие преобразование напряжений, являются параметрическими уравнениями окружности. Мы можем устранить тета, возведя в квадрат обе части и сложив их (я позволил себе переставить первый член в правой части уравнения, который не зависит от тета и соответствует среднему напряжению).

Этот расчет выглядит гораздо хуже, чем он есть на самом деле. Опять же, мы просто транспонировали среднее напряжение, возвели в квадрат обе стороны и добавили уравнение для нормального напряжения к уравнению для напряжения сдвига. Вещи просто очень мило. Второй член в правой части каждого уравнения сокращается. То, что у нас осталось, это квадрат синуса плюс квадрат косинуса, и мы помним из наших тригонометрических тождеств, что этот член равен нулю. Полученное уравнение содержит главные нормальные и касательные напряжения. Главное нормальное напряжение возникает, когда касательное напряжение равно нулю, что означает

Главное касательное напряжение — это просто квадратный корень из

Альтернативой использованию этих уравнений для главных напряжений является использование графического метода, известного как круг Мора. Это включает в себя создание графика с сигмой в качестве абсциссы и тау в качестве ординаты, а также построение заданного состояния напряжения. Соглашение о знаках выглядит следующим образом:

Нанесем две точки. Нормальное и касательное напряжения, действующие на правую грань плоскости, составляют одну точку, а нормальное и касательное напряжение на верхнюю грань плоскости составляют вторую точку. Эти две точки лежат на окружности. Центр этого круга — среднее нормальное напряжение. Радиус этой окружности является максимальным напряжением сдвига. Наибольшее значение сигмы соответствует первому главному напряжению, а наименьшее значение сигма соответствует второму главному напряжению.

Сводка

На этом уроке мы узнали, как преобразовать состояние плоского напряжения в новую опорную или координатную систему отсчета. Этот процесс важен, когда необходимо рассмотреть, как внешняя сила вызывает напряжение вдоль заданной плоскости внутри материала. Эта плоскость может быть естественным углом волокон древесины, углом сварного или клеевого соединения или углом надреза внутри конструкции. Этот процесс показал нам, что напряжение в материале будет варьироваться в зависимости от того, какой угол вы рассматриваете, что означает, что будет угол, при котором напряжение будет максимальным или минимальным. Мы рассчитали эти углы и величину главных напряжений в материале. Это важно для определения максимального напряжения, которому подвергается конструкция при сложной нагрузке. Эти главные напряжения будут критериями проектирования, используемыми для предотвращения разрушения материала.

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национальный научный фонд.

Как построить круг Мора

Инженеры чаще всего хотят определить максимальное нормальное напряжение, возникающее в заданной точке для конкретного применения или конструкции.

Круг Мора — это графический инструмент, который обычно используется инженерами для графического анализа основных и максимальных касательных напряжений на любой плоскости, а также для предоставления графических координат этих касательных напряжений.

Однако через точку может проходить бесконечное количество плоскостей, и нормальное напряжение в каждой плоскости будет разным.

ОСНОВНАЯ ПЛОСКОСТЬ или максимальная главная плоскость представляет собой плоскость, на которой значение нормального напряжения имеет МАКСИМАЛЬНОЕ значение, причем это значение обозначается как .0013 МАКСИМАЛЬНОЕ ОСНОВНОЕ НАПРЯЖЕНИЕ .

Аналогично, будет еще одна плоскость, известная как МИНИМАЛЬНАЯ ОСНОВНАЯ ПЛОСКОСТЬ , на которой значение нормального напряжения является минимальным, при этом это значение обозначается как МИНИМАЛЬНОЕ ОСНОВНОЕ НАПРЯЖЕНИЕ .

Типичный двухмерный элемент напряжения показан ниже со всеми указанными компонентами, показанными в положительном смысле:

ТЕМА КРУГ МОРА может быть указана в ТЕМЕ МЕХАНИКА МАТЕРИАЛОВ на странице 81 Поставляемого справочного руководства NCEES , версия 9.4 для компьютерного тестирования.

С помощью графического подхода мы можем определить ГЛАВНЫЕ НАПРЯЖЕНИЯ в каждой плоскости с помощью КРУГА МОРА.

Окружность Мора представляет собой геометрическое представление двухмерного преобразования напряжений, в котором составляющие напряжения  и  находятся как координаты точки, положение которой зависит от угла  для определения формы поперечного сечения.

Окружность Мора используется для определения главных углов (ориентаций) главных напряжений без необходимости включения угла в уравнения преобразования напряжений.

Чтобы нарисовать круг Мора для типичного двумерного элемента, мы можем использовать следующую процедуру для определения главных напряжений.

Определение системы координат напряжения сдвига:

1. Определите систему координат для оси нормали и оси сдвига. Компоненты нормального напряжения растяжения нанесены на горизонтальную ось и считаются положительными. Компоненты нормального напряжения сжатия также нанесены на горизонтальную ось и имеют отрицательные значения.

 

Определите систему координат кручения:

2. Для построения круга Мора касательные напряжения наносятся НАД осью нормальных напряжений, когда пара касательных напряжений, действующих на противоположные и параллельные поверхности элемент, образуют пару ПО ЧАСОВОЙ СТРЕЛКЕ (cw). Напряжения сдвига наносятся НИЖЕ оси нормали, когда напряжения сдвига образуют пару ПРОТИВ ЧАСОВОЙ СТРЕЛКИ (ccw).

 

График Значения напряжения сдвига:

3. Нанесите на график значения напряжения сдвига, указанные в постановке задачи, или нанесите общие точки на оси σ _x и σ _y , как показано ниже.

 

Постройте величину пары:

4. Постройте величину пары, заданную в условии задачи, с парой по часовой стрелке (по часовой стрелке), нанесенной над осью σ _x , и Пара против часовой стрелки (против часовой стрелки) наносится ниже оси σ _x . Если на данный момент не указаны значения, нанесите общие точки выше и ниже оси σ для τ _xy , как показано ниже.

 

Получение центра круга Мора:

точки. Пересечение этой прямой линии и оси — это положение центра окружности.

 

Нарисуйте круг Мора:

6. Нарисуйте круг Мора, приняв соединительную линию за диаметр круга, используя точку пересечения диагональной прямой и оси σ в качестве центра круга.

Анализ напряжений по кругу Мора:

7. Анализ напряжений по кругу Мора – чтобы получить значения нормального напряжения и напряжения сдвига в любой плоскости тета, возьмите угол 2φ в круге Мора, начиная с диагонали круга, и найдите периферийная точка, как показано на рисунке.