Практическая работа № 13 Построение эпюр изгибающих моментов, поперечных и продольных сил для статически определимой рамы.

1.Определяют опорные реакции рамы. Для рам, не имеющих промежуточных шарниров, опорные реакции могут быть определены из трех уравнений равновесия вида:

I) ΣΧ =0; 2) ΣM_А = 0; 3) ΣМ_В = 0.

Для рам, имеющих промежуточный шарнир, необхо­димо иметь четыре уравнения для определения четырех неизвестных реакций (точнее, составляющих реакций), например уравнения:

1) 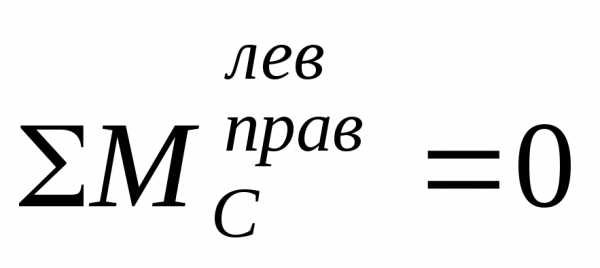; 2) ΣХ = 0; 3) ΣМ_А = 0; 4)ΣМ_В = 0, где С — промежуточный шарнир; А, В — опоры рамы.

При составлении уравнений нужно стремиться к то­му, чтобы каждое из них содержало по одному неизве­стному. Этого можно достичь, выбирая для каждой ра­мы свой порядок составления уравнений. Правильность определения вертикальных реакций можно проверить, используя уравнение 2У=0.

2. Обозначают характерные сечения рамы. Эти сече­ния соответствуют точкам приложения сил, точкам опор, узлов, шарниров. Обозначают стойки и ригель рамы.

3. Определяют значения поперечных сил в характер­ных сечениях. При этом, если раму обходить изнутри, правила определения поперечных сил остаются такими же, как для балок. По найденным значениям стро­им эпюру Q_x. Положительные значения поперечных сил откладываем на чертеже снаружи рамы, а отрицатель­ные — изнутри.

4.Определяют значения изгибающих моментов в ха­рактерных сечениях. Правила определения их остаются такими же, как для балок. По найденным значениям строим эпюру М_х. Ординаты моментов откладываем со стороны растянутого волокна, и знак на эпюре при этом не ставим. Это правило совпадает с правилом, принятым в сопротивлении материалов.

5.Определяют значения продольных сил в элементах рамы: стойках и ригеле. Продольная сила в сечении рав­на сумме проекции всех сил, расположенных по одну сторону от этого сечения (только слева или только справа) на ось элемента. Если сила вызывает сжатие, она принимается со знаком «минус», если растяжение — со знаком «плюс». Значения N

x принято откладывать по обе стороны от оси элемента.

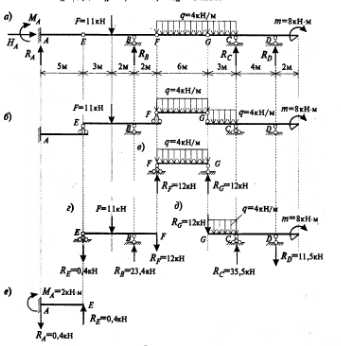
Пример . Построить эпюры М_х, Q_x и N_x для рамы, показанной на рис. 38, а.

Для консольной статически определимой рамы построить эпюры М_х, Q_x, N. Проверить равновесие узла.

Для рам консольного типа эпюры М_х, Q_х, N могут быть построены без определения опорных реакций заделки, если начинать эти построения со стороны свободного конца.

Решение. Построение эпюры Q_х (рис.38,б). За ось абсцисс принимаем ось любого стержня. Перпендикулярно ей мысленно проводим ось ординат и проецирует на нее силы, действующие соответственно слева или справа от рассматриваемого сечения, учитывая правила знаков.

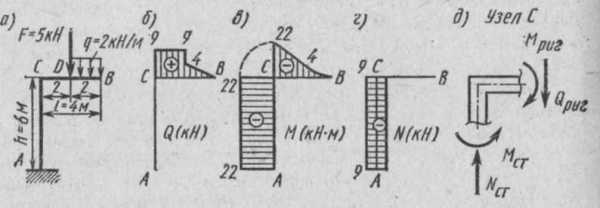
Рис.38

Ригель ВС. Ход справа. Поперечную силу определяем по характерным точкам (аналогично простым балкам).

Стойка АС. Повернемся лицом к стойке, проведем мысленно ось перпендикулярно оси стойки и спроецируем на нее силы ходом справа: Q_С = 0; Q_А = 0. Изобразим полученные результаты графически. Проведем ломаную линию АСВ (рис.38, б) и от нее, как от нулевой, отложим вычисленные ординаты эпюры поперечных сил. Положительные ординаты эпюры для ригеля откладываем вверх от нулевой линии и влево от нулевой линии для стойки. Отрицательные соответственно вниз и вправо от нулевой линии.

Построение эпюры М_х (рис.38,в). Изгибающий момент в сечениях рамы определяем также по характерным точкам ходом справа (со свободного конца).

Ригель ВС.

Стойка АС. Как и при определении поперечной силы, при переходе от ригеля к стойке повернемся на 90 лицом к стойке. Точка С принадлежит одновременно и ригелю и стойке, поэтому М_С^стойки = М_С^риг = − 22 кН·м. Так как в данной задаче непосредственно к стойке не приложены внешние нагрузки, а плечи сил F и Q остаются неизменяемыми, то в любом сечении от С до А изгибающий момент один и тот же.

М_А = М_С= − 22 кН·м. При построении эпюры и изгибающих моментов (как и в балках) положительные ординаты откладываем со стороны растянутых волокон.

Построение эпюры N (рис.38, г). Определяя продольную силу, проецируем заданные силы на ось абсцисс, совмещая ее сначала с ригелем, затем со стойкой. Продольная сила в любом сечении ригеля равна нулю, N_CB = 0, так как справа от сечения действует на­грузка, перпендикулярная его оси. Продольная сила во всех сече­ниях стойки постоянна, так как сама стойка не нагружена и на ось стойки дают проекцию силы F и 2q. N_CA=  F 2q = 5  4 = 9 кН. Ординаты эпюры продольных сил откладываем симметрично по обе стороны оси рассматриваемого элемента. Знак плюс, поставленный на эпюре N, соответствует деформации растяжения, знак минус – сжатия.

Для проверки правильности построения эпюр рассмотрим равновесие узла С. Для этого мысленно вырежем этот узел, проведя два сечения на бесконечно близком расстоянии в ригеле справа от узла, в стойке – слева от него.

Вырезанный таким образом узел дает возможность, рассматривая сечение в ригеле, считать узел отнесенным к левой части ригеля, а при рассмотрении сечения в стойке – к правой части стойки. Прикладываем к узлу С внутренние силовые факторы Q_x, M_x N, беря их значение с эпюр с учетом знака, показывающего направление их действия (рис.38, д).

Из эпюры Q_x видим, что поперечная сила в сечении С ригеля положительна. Поскольку точка С относится к левой части рамы (согласно ранее принятому), Q_риг согласно правилу знаков направляем вниз. На стойке поперечная сила отсутствует.

Из эпюры М_х видим, что изгибающий момент вызывает растяжение верхних волокон. Следовательно, с учетом правила знаков в ригеле изгибающий момент М_С направляем по часовой стрелке, а в стойке (узел С относим к правой части рамы) – против часовой стрелки. Продольная сила N_СА вызывает в сечении сжатие и, следовательно, должна быть направлена в сторону этого сечения.

Для равновесия узла должны соблюдаться следующие условия:

Составим эти уравнения, направив ось х вправо, а ось у вертикально вверх:

Условия равновесия соблюдаются. Следовательно, внутренние силовые факторы определены правильно.

Задание для расчетно-графической работы № 13.

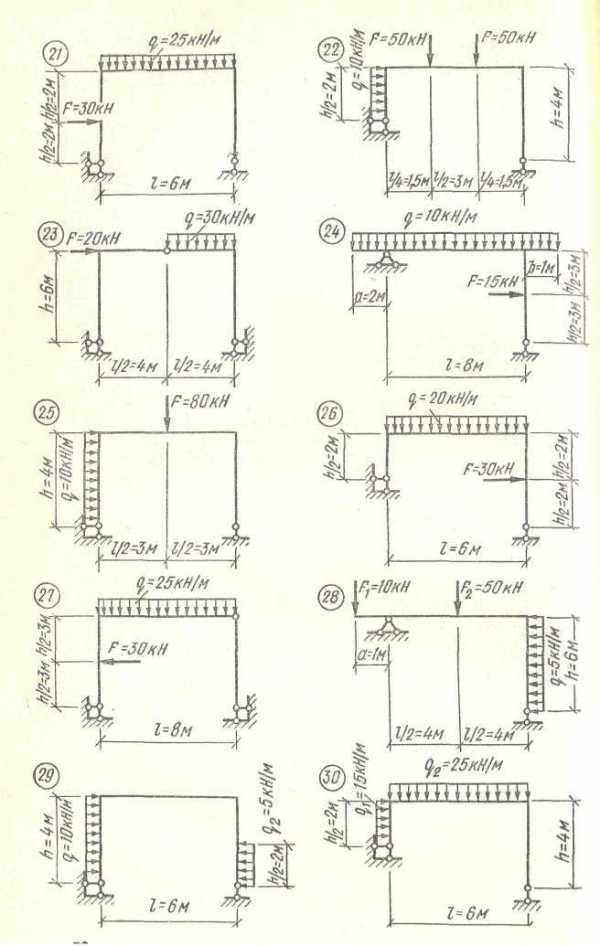
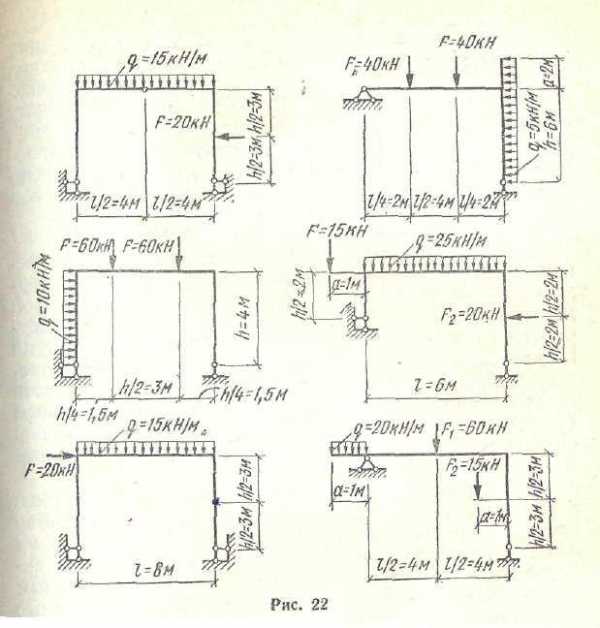
Построить эпюры изгибающих моментов, поперечных и продольных сил для статически определимой рамы

по данным одного из вариантов, показанных на рис. 39..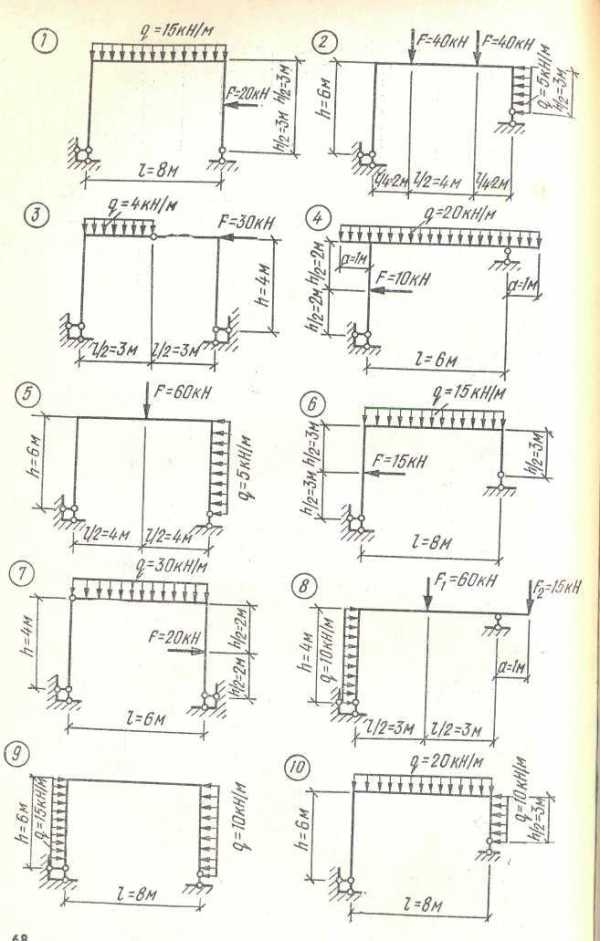

Рис.39

studfiles.net

Проверка эпюр в рамах — Лекции и примеры решения задач по теормеху, сопромату, ТММ и ДМ

Выполним проверку построенных эпюр внутренних силовых факторов для рамы с помощью дифференциальных зависимостей и условий равновесия вырезанных узлов рамы (узловая проверка).

Геометрическая проверка

Начнем с геометрической проверки по дифференциальным зависимостям.

Эпюра N

где

γ – угол наклона касательной к эпюре N относительно оси абсцисс силового участка;
q_z — продольная распределенная нагрузка.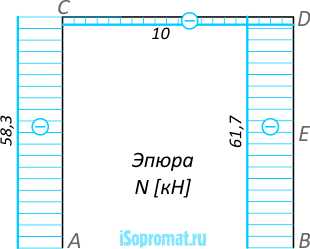

Рис. 1

В рассматриваемом примере на всех участках q_z=0 и, следовательно,
tg γ=0=const,
т.е. эпюра N ограничена прямыми линиями, параллельными базовым линиям.

Эпюра Q

На стойках AC и BD эпюра поперечных сил Q ограничена прямыми линиями, параллельными базовым линиям, т.к. нет распределенных нагрузок и tgα=0=const.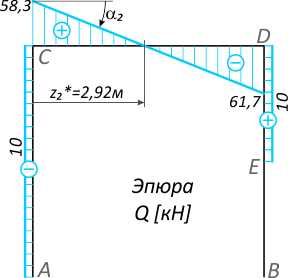

Рис. 2

На ригеле CD
tg α₂ = -(58,3+61,7)/6=-20кН/м=-q=const
— прямая с отрицательным углом наклона к оси абсцисс участка.

Эпюра M

На стойке AC
tg β₁ = -60/6= -10кН=const
— прямая с отрицательным углом наклона к оси абсцисс.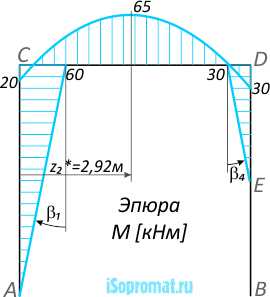

Рис. 3

На ригеле CD эпюра изгибающих моментов M – кривая (парабола) в сечении C при ординате M_C=M₀=20кНм (сжаты нижние слои ригеля), угол наклона касательной к оси абсцисс положителен (против часовой стрелки) и равен
tg β_C=(58,3),
что соответствует ординате Q_C=58,3кН.

С изменением координаты x ордината Q уменьшается до нуля, а следовательно и угол β стремится к нулю в сечении экстремума при ординате M(2,92м)=65кНм.

После экстремума угол наклона касательной становится отрицательным и в сечении D равен:
β_D=arctg(-61,7),
при ординате z=6м:
M_D=M(6м)=30кНм (сжатие нижних слоев).

Кривая получается выпуклостью вверх, т.е. навстречу действию распределенной нагрузки на ригеле CD.

На участке ED стойки BD:
tg β₄=30/3=10кН,
β₄=arctg(10)=const
— прямая с положительным углом наклона к оси абсцисс с началом при ординате M_E=0 и концом при M

D=30кНм (сжатые слои с внутренней стороны рамы).

Проверка равновесия узлов рамы

Рассмотрим равновесие узлов рамы.
Мысленно вырежем из заданной рамы узел C с приложенным к нему внешним моментом m=40кНм.

Рис. 4

В сечениях по стойке AC и ригелю CD прикладываем к узлу векторы внутренних усилий N и Q с учетом знаков и величины.

Действие внутренних изгибающих моментов M направляем в сторону сжатых слоев в окрестности узла C: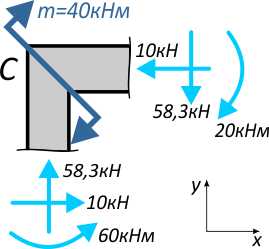

Рис. 5

На эпюре N (рис. 1) видно, что в точке C на вертикальную часть AC действует сжимающая сила 58,3кН, на горизонтальную часть – сжимающая сила величиной 10кН.

На узле C эти силы показаны продольными и сжимающими для фрагментов соответствующих стержней.
С эпюры Q (рис. 2) принимаем значения поперечных сил в точке C:
— на вертикальной части – отрицательная сила величиной 10кН, следовательно, по правилу знаков стремится повернуть узел против хода часовой стрелки;
— на горизонтальный фрагмент узла действует положительная поперечная сила 58,3кН, следовательно, направляем ее «вниз», т.к. она стремится повернуть узел по ходу ЧС.

Эпюра M (рис. 3) была построена на сжатых слоях рамы. По ней видно, что внутренние изгибающие моменты (60кНм и 20кНм) в окрестности точки C стремятся сжать внутренние слои рамы, поэтому направляем так, как показано на рисунке (рис. 5).

Запишем уравнения равновесия:

Во всех трех направлениях, усилия, приложенные к узлу C, уравновешены.

Проверим равновесие узла D.
Внешних сосредоточенных сил и момента в точке D нет, поэтому прикладываем к центрам тяжести сечений рамы только векторы внутренних усилий N и Q и показываем действие внутренних изгибающих моментов M.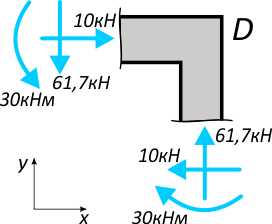

Рис. 6

Записываем и проверяем условия равновесия:

Проверки показали, что эпюры в раме построены правильно.

Другие примеры решения задач >
Лекции по сопромату >

isopromat.ru

Построение эпюр в составных рамах [wiki.eduVdom.com]

Эпюры внутренних усилий в составных рамах можно построить так же, как и в простых, однако часто эту процедуру

удается упростить, если:

1) предварительно найти реакции в соединительных шарнирах;

2) учесть, что при переходе через соединительный шарнир характер эпюр не меняется, если при этом не меняется

характер нагрузки.

Решим задачу определения эпюр внутренних усилий в составной раме:

Делим раму на участки . Для построения эпюр достаточно знать только одну опорную реакцию – Rв,

которую можно найти из условий равновесия части BC:

Rв = q/2.

Находим реакции в соединительном шарнире:

Xс = q Yс = ql.

Теперь построение эпюр на участке 3-2 заданной рамы можно свести к построению эпюр в консоли,

защемленной на правом конце – в точке 2 и загруженной распределенной нагрузкой и найденными реакциями Xс, Yс

Переходя к рассмотрению левой части рамы – AC,

можно отбросить правую часть – BC,

заменив ее действие найденными реакциями отброшенной части: Xс ; Yс .

Отметим, что при переходе через соединительный шарнир C

от участка 2-3 к участку 3-4 меняется характер нагрузки q

а вместе с ней и характер эпюр M и Q ,

но не меняется нагрузка qx, поэтому на всем ригеле N = const.

Правильность построения эпюр (рис. в-д) можно проверить, рассматривая равновесие рамы в целом или ее ригеля.

Нетрудно догадаться, что для рамы, состоящей из двух дисков, рассмотренная выше схема решения будет целесообразной,

если один из дисков присоединен к земле только одной связью.

В тех же случаях, когда диски имеют по две опорные связи, часто удается построить эпюры без определения реакций в

соединительном шарнире.

Построение эпюр внутренних усилий в трех шарнирной раме

Построить эпюры внутренних усилий в трех шарнирной раме .

Решение:

Делим раму на участки и определяем опорные реакции(рис б): $$ \sum M_{B}=0; Y_{A}=ql/4 $$ $$ \sum M_{C}^{\left ( AC \right )}=0;X_{A}=ql/4; $$ $$ \sum X=0; X_{B} =3ql/4; $$$$ \sum X=0; X_{B} =3ql/4; $$ $$ \sum Y=0; Y_{B} =3ql/4; $$ Проверка: $$ \sum M_{C}^{\left ( BC \right )}=X_{B}\cdot l-Y_{B}\cdot l-ql\cdot l/2=3ql^{2}/4-ql^{2}/4-ql^{2/2} =0 $$

Эпюры на участке 1-2 строим как в консоли соответствующей длины, закрепленной в точке 2.

Момент на левом конце ригеля находим из условий равновесия второго узла.

Поскольку ригель не загружен и эпюра M здесь должна быть линейной,

проводим прямую через найденную ординату эпюры M = (q/4)l*2 и шарнир C,

а затем продолжаем ее до 4 узла.

На правой стойке эпюру M можно построить как в консоли,

закреплен-ной в 4 узле и загруженной распределенной нагрузкой и найденными реакциями Xв, Yв.

Однако проще рассмотреть этот участок как простую двух опорную балку,

загруженную концевым моментом в 4 узле (соответствующая эпюра показана пунктиром – рис. в) и распределенной

нагрузкой.

Эпюры Q и N в этом примере нетрудно построить в соответствии с определением (рис. г, д).

Для контроля правильности построения эпюр можно рассмотреть равновесие ригеля (рис. д).

Рекомендуем

subjects/stroymeh/эпюры_в_составных_рамах.txt · Последние изменения: 2013/10/04 01:03 — ¶

www.wiki.eduvdom.com

7.Формула Куравского, постоение эпюры Qпо эпюре м, эпюрыNпо эпюреQ.

Изгибающий момент Mx в произвольном сечении x равен алгебраической сумме моментов всех внешних сил (включая опорные реакции), расположенных по одну сторону от сечения, относительно этого сечения.

Эпюры перерезывающих сил Q проще построить по эпюрам M, используя дифференциальные зависимости между Q и M.

Для определения знака перерезывающей силы Q ось стержня нужно повернуть к эпюре моментов относительно точки их пересечения. Если поворот осуществляется по часовой стрелке, то Q>0, если против часовой стрелки, то Q<0.

Эпюру продольных сил N можно построить по эпюре Q методом вырезания узлов, рассматривая последовательное равновесие узлов системы под действием внешних сил, приложенных в узле, и внутренних сил: известных перерезывающих сил Q и неизвестных продольных сил N, приложенных в разрезанных стержнях. При этом следует помнить, что положительная перерезывающая сила Q вращает узел по часовой стрелке, а положительная продольная сила N направлена от узла(стержень растянут), а так же не забывать прикладывать внешние сосредоточенные силы, если они заданы.

Поскольку для каждого узла можно записать только два уравнения равновесия- уравнения проекций, из которых можно определить неизвестные продольные силы, то

Начинать вырезать узлы нужно с узлов, где имеется не более двух неизвестных продольных сил N, не лежащих на одной прямой.

8.Основные правила построения в статически определимых системах.

Статическая система называется статически определимой, если число опорных реакций соответствует числу степеней свободы , и величины опорных реакций по принципу механического равновесия можно определить из величин внешних нагрузок.

Все другие системы называются статически неопределимыми.

Для расчёта всех статически определимых систем достаточно решать уравнения равновесия:

Для плоских задач есть три условия равновесия. Сумма всех вертикальных сил, всех горизонтальных сил и всех моментов должна быть равна нулю. Σ V=0, Σ H=0, Σ M=0.

9.Принципы расчёта консольных и простых рам, определение опорных реакций, построение эпюр, проверка их правильности.

Построение эпюр

Проверка эпюр

10. Особенности расчёта трёхшарнирных рам с затяжкой и без.

Суть: режем раму по шарниру справа и слева и находим реакции опор.

Трёхшарнирная рама без затяжки

Трёхшарнирная рама с затяжкой

11. Особенности расчёта трёхшарнирных арок с затяжкой и без.

C

q

A

B

Ra

Rb

Hb

Ha

f

l

l

2l

P

Mс^нб

— Балочная эпюра моментов

N(x)

Формула для определения момента в точке

y

Q(x)

M(x)=M^б(x)-H*y



x

Ha

Выражение для поперечной силы

Выражение для продольной силы

С затяжкой

Если сечение ниже затяжки

Если сечение выше затяжки

Если сечение ниже затяжки

выше затяжки

Если сечение ниже затяжки

выше затяжки

12. Особенности расчёта многопролётных балок и рам.

13)Методы определения усилий в фермах

• Способ моментной точки состоит в следующем: сквозным сечением ферму мысленно разрезают на две части так, чтобы в разрез попало не более трех стержней с неизвестными усилиями. Оси перерезанных стержней должны быть не параллельны и не пересекаться в одной точке. Если такое сечение провести удается, то одну из частей фермы отбрасываю , а ее действие оставшуюся часть заменяют неизвестными внутренними продольными силами. Эти силы направляют вдоль осей перерезанных стержней от узлов ( в сторону отброшенной части), предполагая их растягивающими (положительными). Для оставшейся части составляют уравнения равновесия в виде суммы моментов всех сил относительно моментных точек. Моментной точкой (точкой Риттера) называется точка, в которой пересекаются направления всех стержней, попавших в сечение, кроме искомого

• Способ вырезания узлов является частным случаем способа проекций и отличается от последнего проведением только таких разрезов, каждый из которых последовательно отсекает от фермы по одному узлу. После проведения такого разреза остальная чась фермы отбрасывается, а ее влияние заменяется неизвестными продольными силами, направленными вдоль осей разрезанных стержней от узла. Вырезание узлов надо начинать с двухстержневого узла, точнее, с узла, содержащего не более двух неизвестных усилий, которые определяются из условия равенства нулю суммы проекций всех сил, сходящихся в узле, на осиxиyили на оси перпендикулярные к стержням с искомыми усилиями. Переходя от одного узла к другому, вычисляют усилия во всех стержнях фермы.

studfiles.net

4. ПОСТРОЕНИЕ ЭПЮР УСИЛИЙ В РАМЕ

4.1.Постановка задачи и анализ расчетной схемы рамы

Для плоской рамы, изображенной на рис.4.1, требуется построить эпюры усилий М, Q, N от указанной на рисунке постоянной нагрузки. Расчет выполним на ПК с помощью программы SCAD [I], в которой реализуется метод конечных элементов строительной механики.

Перед началом работы на компьютере необходимо выполнить две подготовительных операции:

1) Проверить является заданная рама статически определимой или статически неопределимой системой. Это связано с тем, что для статически определимых систем при нахождении в них только усилий упрощается задание жесткостей стержней при использовании программы SCAD (см. подраздел 1.6 первого раздела учебного пособия).

1		2			10 кН/м

Рис.4.1

2) Вручную разбить раму на конечные элементы типа 2 (стержневой элемент плоской рамы, см. рис.1.3) с учетом особенностей ее конструкции и вида, действующей на нее нагрузки. При этом выбрать начало общей системы осей координат и продумать вопрос о методике построения расчетной схемы МКЭ с помощью программы SCAD.

Первая операция состоит из двух частей:

а) Сначала подсчитываем степень статической неопределимости n рамы.

Для этого используем формулу [3÷5]:
n = (nоп + 3nк ) − (3 + n1ш ) ,	(4.1)

где nоп ─ число неизвестных составляющих опорных реакций во всех опорах рамы;

nк ─ число замкнутых контуров в раме;

3nк ─ число неизвестных усилий, которые необходимо определить во всех замкнутых контурах, чтобы построить в них эпюры указанных усилий;

n1ш─ число уравнений равновесия вида åM1ш = 0 , которые можно

записать для каждого одиночного шарнира дополнительно к имеющимся трем уравнениям равновесия для всей стержневой системы.

В рассматриваемой раме nоп = 4; nк = 0; n1ш = 1. В результате по указанной формуле получаем необходимое условие статической определимости рамы:

studfiles.net

4. ПОСТРОЕНИЕ ЭПЮР УСИЛИЙ В РАМЕ

4.1.Постановка задачи и анализ расчетной схемы рамы

Для плоской рамы, изображенной на рис.4.1, требуется построить эпюры усилий М, Q, N от указанной на рисунке постоянной нагрузки. Расчет выполним на ПК с помощью программы SCAD [I], в которой реализуется метод конечных элементов строительной механики.

Перед началом работы на компьютере необходимо выполнить две подготовительных операции:

1) Проверить является заданная рама статически определимой или статически неопределимой системой. Это связано с тем, что для статически определимых систем при нахождении в них только усилий упрощается задание жесткостей стержней при использовании программы SCAD (см. подраздел 1.6 первого раздела учебного пособия).

1		2			10 кН/м

Рис.4.1

2) Вручную разбить раму на конечные элементы типа 2 (стержневой элемент плоской рамы, см. рис.1.3) с учетом особенностей ее конструкции и вида, действующей на нее нагрузки. При этом выбрать начало общей системы осей координат и продумать вопрос о методике построения расчетной схемы МКЭ с помощью программы SCAD.

Первая операция состоит из двух частей:

а) Сначала подсчитываем степень статической неопределимости n рамы.

Для этого используем формулу [3÷5]:
n = (nоп + 3nк ) − (3 + n1ш ) ,	(4.1)

где nоп ─ число неизвестных составляющих опорных реакций во всех опорах рамы;

nк ─ число замкнутых контуров в раме;

3nк ─ число неизвестных усилий, которые необходимо определить во всех замкнутых контурах, чтобы построить в них эпюры указанных усилий;

n1ш─ число уравнений равновесия вида åM1ш = 0 , которые можно

записать для каждого одиночного шарнира дополнительно к имеющимся трем уравнениям равновесия для всей стержневой системы.

В рассматриваемой раме nоп = 4; nк = 0; n1ш = 1. В результате по указанной формуле получаем необходимое условие статической определимости рамы:

studfiles.net