3)Эпюры продольных сил, поперечных сил, изгибающих моментов, крутящих моментов
Эпю́ра (фр. epure — чертёж) — особый вид графика, показывающий распределение величины нагрузки на объект. Например, для стержня продольнаяось симметрииберётся заобласть определения,и составляются эпюры для сил, напряжений и разных деформаций в зависимости отабсциссы.
Расчёт эпюр напряжения является базовой задачей такой дисциплины, как сопротивление материалов. В частности, только при помощи эпюры возможно определить максимально допустимую нагрузку на материал.
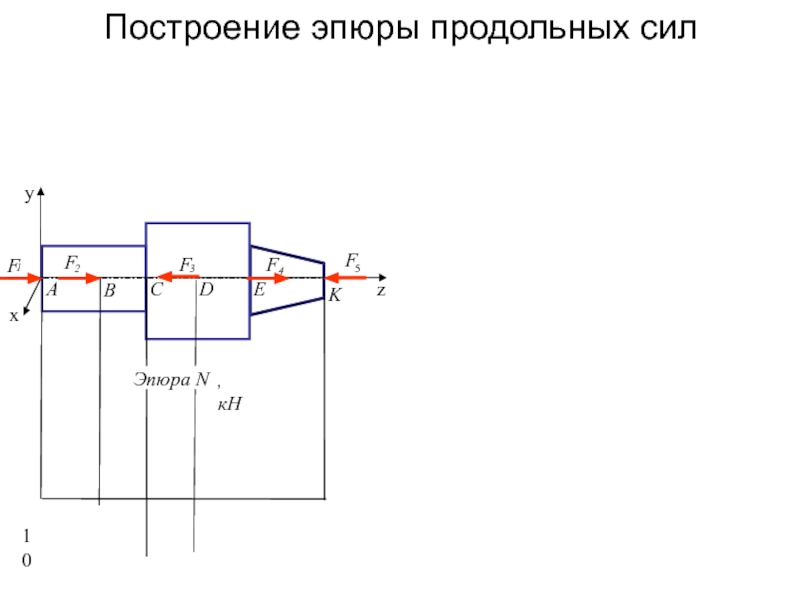
Построение эпюр продольных сил Nz
Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.
Правило знаков
для Nz: условимся считать продольную
силу в сечении положительной, если
внешняя нагрузка, приложенная к
рассматриваемой отсеченной части
стержня, вызывает растяжение и
отрицательной — в противном случае.
Построение эпюр крутящих моментов Мкр.
Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.
Правило знаков для Мкр: условимся считать крутящий момент в сечении положительным, если при взгляде на сечение со стороны рассматриваемой отсеченной части внешний момент виден направленным против движения часовой стрелки и отрицательным — в противном случае.
Определение поперечных сил и изгибающих моментов — сечение 1
Отбросим правую часть балки и заменим ее действие на левую часть поперечной силой и изгибающим моментом . Для удобства вычисления закроем отбрасываемую правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением 1.
Поперечная сила в сечении 1 балки равна алгебраической сумме всех внешних сил, которые видим после закрытия
Видим
только реакцию опоры, направленную
вниз.
кН.
Знак «минус» нами взят потому, что сила вращает видимую нами часть балки относительно первого сечения против хода часовой стрелки (или потому, что одинаково направлена с направлением поперечной силы по правилу знаков)
Изгибающий момент в сечении 1 балки, равен алгебраической сумме моментов всех усилий, которые мы видим после закрытия отброшенной части балки, относительно рассматриваемого сечения 1.
Видим два усилия: реакцию опоры и момент M. Однако у силы плечо практически равно нулю. Поэтому изгибающий момент равен:
кН·м.
Здесь знак «плюс» нами взят потому, что внешний момент M изгибает видимую нами часть балки выпуклостью вниз. (или потому, что противоположно направлен направлению изгибающего момента по правилу знаков)
Определение поперечных сил и изгибающих моментов — сечение 2
В отличие от первого сечения, у силы реакциипоявилось плечо, равное а.
поперечная сила:
кН;
изгибающий момент:
кН·м.
Определение поперечных сил и изгибающих моментов — сечение 3
поперечная сила:
кН;
изгибающий момент:
кН ·м.
Определение поперечных сил и изгибающих моментов — сечение 4
Теперь удобнее закрывать листком левую часть балки.
поперечная сила:
кН;
изгибающий момент:
кН ·м.
Определение поперечных сил и изгибающих моментов — сечение 5
поперечная сила:
кН;
изгибающий момент:
кН ·м.
Определение поперечных сил и изгибающих моментов — сечение 1
поперечная сила и изгибающий момент:
.
По найденным значениям производим построение эпюры поперечных сил (рис. 7.7, б) и изгибающих моментов (рис. 7.7, в).
КОНТРОЛЬ ПРАВИЛЬНОСТИ ПОСТРОЕНИЯ ЭПЮР
Убедимся в правильности построения эпюр по внешним признакам, пользуясьправилами построения эпюр.
Проверка эпюры поперечных сил
Убеждаемся:
под незагруженными участками эпюра
поперечных сил идет
параллельно оси балки, а под распределенной
нагрузкой q – по наклоненной вниз прямой.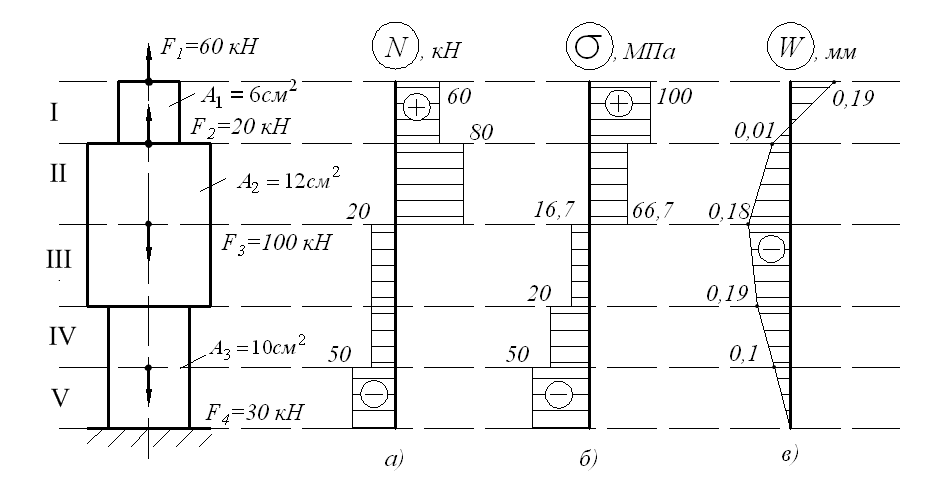 На эпюре продольной силы три
скачка: под реакцией –
вниз на 15 кН, под силой P – вниз на 20 кН
и под реакцией –
вверх на 75 кН.
На эпюре продольной силы три
скачка: под реакцией –
вниз на 15 кН, под силой P – вниз на 20 кН
и под реакцией –
вверх на 75 кН.
Проверка эпюры изгибающих моментов
На эпюре изгибающих моментов видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой q эпюра изгибающих моментов изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре изгибающего момента – экстремум, поскольку эпюра поперечной силы в этом месте проходит через нулевое значение.
4) Стержень, балка, вал, брус, пластина, плита, оболочка
Основными расчетными типовыми элементами на которые делится целая конструкция, являются стержень, брус, оболочка, пластина, массивное тело, балка, ферма.
Стержень — тело, длина которого существенно превышает характерные размеры поперечного сечения.
Брус
— это тот же стержень.
Балка — стержень или брус, работающий на изгиб.
Пластина — тело, у которого толщина существенно меньше двух других размеров.
Оболочка — тело, ограниченное криволинейными поверхностями (искривленная пластина).
Массивное тело — элемент конструкции с размерами одного и того же порядка.Ферма — стержневая конструкция, работающая только на растяжение или сжатие.
Остальное см.конспект.
Построение эпюр продольных сил — Мегаобучалка
Рассмотрим порядок построения эпюр продольных сил в стержне, работающем на растяжение – сжатие (рис. 3.14).
1. В соответствии с общим алгоритмом построения эпюр прежде всего определяем все внешние силовые факторы, действующие на рассматриваемый стержень (рис. 3.14а). Активные силы заданы. Определим реакции связей. В рассматриваемом примере связью является заделка. В заделке при плоской системе сил в общем случае возникают три реакции – две силы и момент.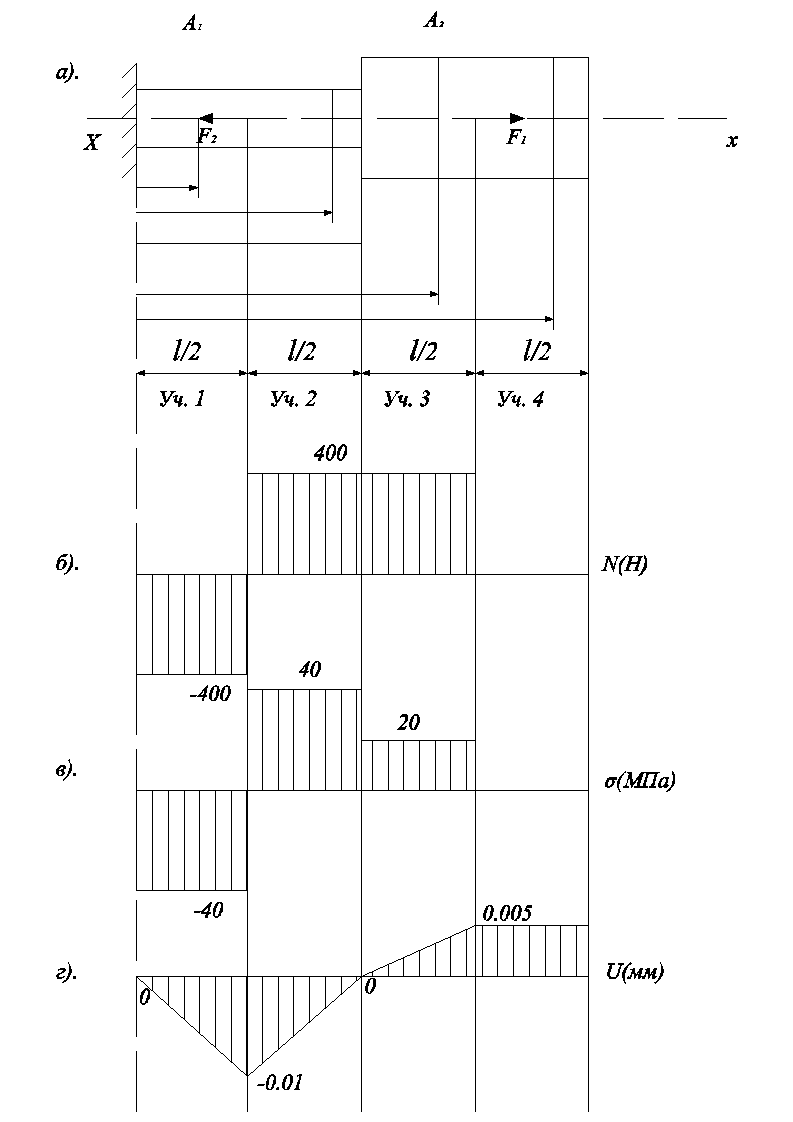 Однако в данном примере активные силы приложены на оси стержня и действуют вдоль оси, представляющей прямую линию. Равнодействующая активных сил направлена вдоль этой прямой и может быть уравновешена силой, действующей также вдоль этой прямой. Таким образом, возникает только одна реакция, направленная вдоль оси стержня. Выбираем систему координат
Однако в данном примере активные силы приложены на оси стержня и действуют вдоль оси, представляющей прямую линию. Равнодействующая активных сил направлена вдоль этой прямой и может быть уравновешена силой, действующей также вдоль этой прямой. Таким образом, возникает только одна реакция, направленная вдоль оси стержня. Выбираем систему координат
ΣFZ = 0; – P3 – P2 + P1 = – 7 – 3 + 5 = 0; = 5 кН.
Если при решении уравнения результат получают со знаком «минус», то направление реакции изменяют на обратное (влево от т. А).
2. Так как в рассматриваемом примере все силы приложены на оси и действуют вдоль нее, то уточнять расчетную схему не следует.
3. Разбиваем стержни на участки, проводя вертикальные линии через точки приложения сосредоточенных сил.
4. На каждом участке методом сечений определяем внутренние силовые факторы.
Рассмотрим участок АВ. Рассечем стержень на две части поперечным сечением на расстоянии z от начала координат (от т. А) и правую часть отбросим (рис. 3.14б). Абсцисса z в пределах участка АВ изменяется от 0 до 1 м, т.е. 0 ≤ z ≤ 1. На рассматриваемую часть стержня действует только внешняя сила , направленная вдоль оси стержня. Эта сила может быть уравновешена силой, также действующей вдоль оси стержня, т.е. продольной силой N. Прикладываем в рассматриваемом сечении продольную силу N. Так как направление силы N неизвестно (от сечения или на сечение), то направляем ее вдоль оси произвольно, например, от сечения. Записываем уравнение статики (составляем условие равновесия) для рассматриваемой части стержня:
ΣFZ = 0; + N = 5 + N = 0; N = — 5
Знак «минус» означает, что сила N должна действовать на сечение. Так как сила N не зависит от абсциссы z, то продольная сила по длине участка АВ не изменяется.
Так как сила N не зависит от абсциссы z, то продольная сила по длине участка АВ не изменяется.
5. Выбираем ось отсчета в виде линии, параллельной оси стержня. При построении эпюры продольных сил принимают следующее правило знаков:
Продольную силу N считают положительной, если имеет место растяжение (N направлена от сечения) и отрицательной, если сжатие (N направлена на сечение).
При горизонтальном расположении оси отсчета положительные значения продольной силы откладывают вверх, отрицательные – вниз. Так как на участке АВ сила N действует на сечение, т.е. имеет место сжатие, то график изменения N на участке АВ представляет собой прямую, параллельную оси отсчета в отрицательной области значений (рис. 1д).
Рассмотрим участок ВС (рис. 3.14в, сеч. II-II). Абсцисса z при начале координат в т. А будет изменяться от 1 м до 1,5 м. Рассуждая так же, как и в предыдущем случае, убеждаемся, что в сечении II-II действует только продольная сила N. Записываем уравнение статики для рассматриваемой части стержня:
Записываем уравнение статики для рассматриваемой части стержня:
ΣFZ = 0; – P3 + N = 5 – 7 + N = 0; N = 7 – 5 = 2 кН.
Эпюра продольной силы на участке ВС представляет собой прямую, параллельную оси отсчета в положительной области значений (рис. 3.14д).
Аналогично можно найти продольную силу и на участке СD.
| P3=7 кН |
| P2=3 кН |
| P1=5 кН |
| =5 кН |
| =5 кН |
| P3=7 кН |
| =5 кН |
| P3=7 кН |
| P2=3 кН |
Рис. 3.14. Построение эпюр нормальных сил
3.14. Построение эпюр нормальных сил
Из эпюры продольных сил следует (рис. 3.14д), что в точках А, В, С и D значения продольной силы изменились скачком на величину сосредоточенных сил в этих точках. Эта закономерность справедлива при действии любой сосредоточенной силы и значительно облегчает построение эпюр продольных сил для стержней, нагруженных сосредоточенными силами.
Так, для рассмотренного примера можно было бы поступить следующим образом.
Рассмотрим стержень, начиная с т. А (слева направо). В т. А в соответствии с отмеченной закономерностью должен быть скачок на величину . Сила в сечении I-I (рис. 3.14а) может быть уравновешена внутренней силой N, равной по модулю и направленной на сечение, т.е. имеет место сжатие и ординату откладываем вниз от оси отсчета (скачок направлен вниз). Если выбрать другое сечение в пределах участка АВ, то результат не изменится. Таким образом, на участке АВ имеем:
NАВ = — = — 5 кН.
График представляет собой прямую, параллельную оси отсчета.
В т. В должен быть скачок на величину силы P3. Так как сила P3 направлена в сторону, противоположную силе , то скачок направлен вверх и продольная сила на участке ВС равна:
NВС = NАВ + 7 = -5 + 7 = 2 кН.
Учитывая скачок в т. С, для участка CD получаем:
NCD = NВС + 3 = 2 + 3 = 5 кН.
Если учесть скачок в точке D от силы P1, то находим:
NCD — P1 = 5 – 5 = 0,
что и должно быть, т.к. ΣFZ = 0.
В заключении отметим основные закономерности:
1. В поперечных сечениях прямого стержня, нагруженного силами, приложенными на оси стержня и направленными вдоль оси, возникает только один внутренний силовой фактор – продольная сила N, т.е. имеет место растяжение или сжатие.
2. В сечениях, где приложены сосредоточенные силы, действующие вдоль оси стержня, на эпюре продольных сил имеет место скачок на величину этих сил.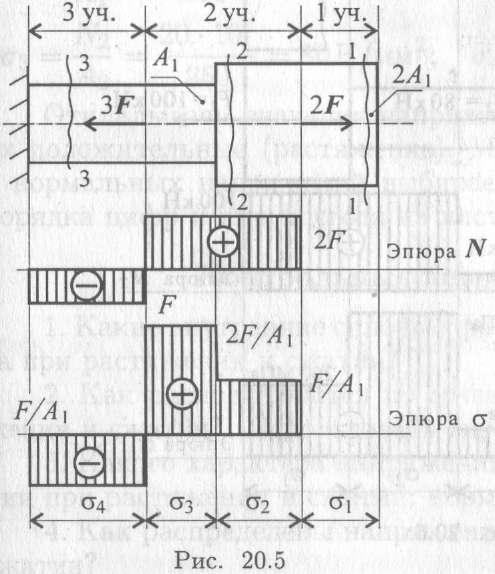
3. Форма и размеры поперечных сечений не влияют на величину продольных сил.
4. Продольная сила в рассматриваемом сечении равна алгебраической сумме проекций на продольную ось всех сил, действующих на рассматриваемую часть стержня. Проекцию любой силы берут со знаком «плюс», если соответствующая ей внутренняя продольная сила направлена от сечения, и «минус» — если на сечение.
Замечание: Это правило справедливо для любой системы внешних сил. В случае криволинейных стержней силы проектируют на ось, перпендикулярную рассматриваемому сечению.
Боковое и продольное ускорение
Основы анализа данных: поперечное и продольное ускорениеСмотреть этот курс
129 долларов США
-ИЛИ-
Или 8 простых платежей всего за $16,13. Мгновенный доступ. Легкая проверка. Нет сборов. — Используйте ту же кассу, что и обычно— Оплата с помощью Visa, Mastercard или PayPal
— Без удостоверения личности, контрактов или документов
— Никаких комиссий, процентов или штрафов
— Мгновенный доступ к курсу
Кроме того, на все сделанные платежи распространяется наша 60-дневная гарантия возврата денег.
Просто выберите предпочитаемую частоту и сумму платежей при оформлении заказа, после чего получите немедленный доступ к своему курсу. » data-html=»true» data-placement=»bottom» data-trigger=»click»>Подробнее
Зарегистрироваться сейчас
8 простых платежей всего по $16,13
Пожизненный доступ к курсу
60-дневная гарантия возврата денег
Боковые и продольные перегрузки
03.10
| 00:00 | — Хотя с датчиками, которые мы уже обсуждали, можно многое сделать, я также считаю, что боковая и продольная перегрузки входят в список основных. |
| 00:11 | Эти датчики сообщают нам, насколько сильно автомобиль поворачивает, тормозит или ускоряется, и дают нам много информации о характеристиках автомобиля и о том, насколько хорошо водитель использует доступное сцепление с дорогой. |
| 00:24 | В частности, мы можем использовать эти датчики для создания графика зависимости поперечной силы G от продольной силы G, который генерирует график, называемый кругом тяги или диаграммой GG. |
| 00:37 | Мы собираемся углубиться в эту тему более подробно немного дальше в курсе, но в двух словах это позволяет нам проанализировать доступное сцепление автомобиля, а также то, насколько хорошо водитель может использовать сцепление при переходе от торможения к прохождению поворота и, наконец, к ускорению. |
| 00:56 | Здесь мы можем увидеть график тягового круга для серии кругов по нашей местной гоночной трассе. |
| 01:02 | Значения ниже горизонтальной нулевой оси указывают на торможение, а выше — на ускорение. |
| 01:08 | Точно так же слева от вертикальной нулевой оси указываются левые углы и наоборот. |
| 01:15 | Этот график показывает нам максимальные боковые и продольные перегрузки, создаваемые автомобилем и водителем. |
| 01:23 | Но что не менее важно, мы можем проанализировать, как водитель переходит от торможения к повороту, а затем от поворота к ускорению. |
| 01:31 | Анализируя, насколько хорошо водитель может ездить по ободу круга сцепления, мы можем узнать, насколько хорошо водитель может использовать доступное сцепление с дорогой. |
| 01:41 | Для максимальной точности лучше всего использовать автономный датчик перегрузки. |
| 01:47 | Он должен быть установлен как можно ближе к центру тяжести автомобиля. |
| 01:51 | Конечно, в большинстве случаев мы не будем точно знать, где находится центр тяжести автомобиля, поэтому нам нужно вернуться к тому, что практично, расположение где-то в трансмиссионном туннеле рядом с центром колесной базы автомобиля, вероятно, является наиболее распространенным компромиссом здесь и довольно хорошей догадкой. |
| 02:09 | Чтобы облегчить нашу жизнь, многие системы регистрации данных включают в себя встроенные трехосевые датчики G. |
| 02:15 | Они также добавляют вертикальную силу G, хотя для наших требований к анализу эта третья ось не очень важна. |
| 02:23 | Если вы используете приборную панель или регистратор, установленный на лобовом стекле, со встроенным датчиком ускорения, то считывание данных будет немного неточным из-за того, что датчик ускорения будет установлен значительно выше центра тяжести автомобиля, и он подвержен ошибкам, возникающим из-за крена кузова при прохождении поворотов.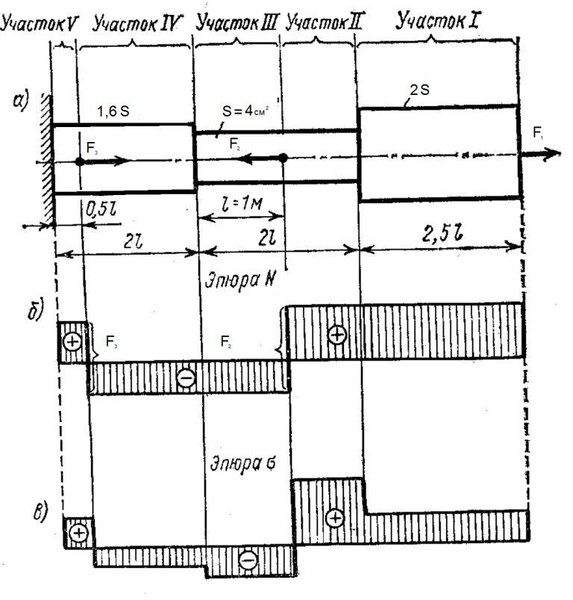 |
| 02:40 | В этом случае, хотя абсолютные числа, генерируемые датчиком G, могут быть не совсем точными, данные по-прежнему полезны в относительном выражении для сравнения различных драйверов и потенциально различных изменений настроек. |
| 02:53 | Независимо от того, где установлен датчик перегрузки, перед использованием важно убедиться, что он обнулен, при этом учитывается угол установки датчика или регистрирующего устройства. |
| 03:04 | Мы обсудим это более подробно далее в курсе. |
Присоединяйтесь к эксклюзивному БЕСПЛАТНОМУ занятию по любимым темам
Выберите свой класс ниже, чтобы получить дополнительную информацию и зарегистрироваться.
Доступен диапазон дат и времени.
Машиностроение EFI Настройка Дино Тюнинг Электропроводка для автоспорта Развал-схождение
Заполните свой гараж автомобилями, грузовиками и мотоциклами, которыми вы управляете, строите или даже мечтаете, чтобы мы могли создавать контент, который вам больше подходит, и делиться им!
ДОБАВЬТЕ ВАШ ПЕРВЫЙ АВТОМОБИЛЬУ меня пока нет машин для добавления
*выберите один из вариантов выше, чтобы закрыть окно
Как я могу визуализировать продольные данные в ggplot2?
Информация о версии: Код для этой страницы был протестирован в R В разработке (нестабильно) (2012-07-05 r59734)
Дата: 2012-07-08
С: вязатьр 0. 6.3
6.3
На этой странице мы демонстрируем, как создавать графики спагетти, изучать общие тенденции, и ищите взаимодействия в продольных данных, используя ggplot2. С данными продольных или повторных измерений, часто есть два аспекта, которые интересны. Во-первых, насколько велика изменчивость между отдельными единицами в данное время или мера? Во-вторых, какова их дисперсия в пределах единиц с течением времени или измерения? Один из удобных способов визуализации оба используют сюжет спагетти. Это рисует график с отдельными линиями для каждой единицы. Пространство между строками представляет межединичную изменчивость, изменение в каждой линии (наклон) представляет внутри изменчивость. Давайте использовать набор данных о переносимости периода человека из Прикладной продольный анализ данных: моделирование изменений и возникновения событий Джудит Д. Сингер и Джон Б. Уиллетт для нашего примера.
Основы
Во-первых, нам нужно прочитать данные, преобразовать числовые индикаторы идентификатора и пола в переменные класса факторов,
и загрузите пакет ggplot2 , который мы будем использовать для построения графиков.
## считывается в наборе данных (данные о допусках из книги ALDA)
допуск <- read.csv("https://stats.idre.ucla.edu/stat/r/examples/alda/data/tolerance1_pp.txt")
## изменить id и male на переменные factor
допуск <- в пределах(допуск, {
идентификатор <- фактор (идентификатор)
мужчина <- фактор(мужчина, уровни = 0:1, метки = c("женщина", "мужчина"))
})
## просмотреть первые несколько строк набора данных
голова (допуск)
## id возрастной допуск мужское время воздействия ## 1 9 11 2,23 самка 1,54 0 ## 2 9 12 1,79 самка 1,54 1 ## 3 9 13 1,90 самка 1,54 2 ## 4 9 14 2,12 самка 1,54 3 ## 5 9 15 2,66 самка 1,54 4 ## 6 45 11 1,12 самец 1,16 0
## загрузить пакет ggplot2 для построения графиков требуется (ggplot2)
## Загрузка необходимого пакета: ggplot2
## Загрузка требуемого пакета: методы
Теперь мы готовы приступить к созданию графиков. Начнем с построения допуска по оси Y.
и время по оси x. Пакет ggplot2 основан на Grammar of Graphics Леланда Уилкинсона.
Теоретическая структура создания графа аналогична тому, как мы можем составить предложение.
Существуют базовые структурные компоненты, которые говорят о том, как одна переменная соотносится с другой.
модификаторы (такие как прилагательные или наречия), которые контролируют такие вещи, как размер, цвет, форма и т. д. Все графики
начните с базового компонента, который определяет используемые данные и указывает, как отображаются переменные.
к графику. В нашем случае набор данных равен ‘ допуск ‘, мы отображаем время на ось х, допуск (переменная внутри
набор данных, а не сам набор данных) к оси Y, и мы сгруппируем вещи по идентификатор . Вся эта информация является
создается и хранится в объекте ‘ p ’ (для сюжета).
Пакет ggplot2 основан на Grammar of Graphics Леланда Уилкинсона.
Теоретическая структура создания графа аналогична тому, как мы можем составить предложение.
Существуют базовые структурные компоненты, которые говорят о том, как одна переменная соотносится с другой.
модификаторы (такие как прилагательные или наречия), которые контролируют такие вещи, как размер, цвет, форма и т. д. Все графики
начните с базового компонента, который определяет используемые данные и указывает, как отображаются переменные.
к графику. В нашем случае набор данных равен ‘ допуск ‘, мы отображаем время на ось х, допуск (переменная внутри
набор данных, а не сам набор данных) к оси Y, и мы сгруппируем вещи по идентификатор . Вся эта информация является
создается и хранится в объекте ‘ p ’ (для сюжета).
## определить базу для графиков и сохранить в объекте 'p' p <- ggplot (данные = допуск, aes (x = время, y = допуск, группа = id))
Обратите внимание, что график еще не создан. Все, что мы сказали, это то, как отображать данные на графике.
Мы не указали что надо рисовать. Нарисованные фигуры называются геомами.
Геометры обычно представляют собой очень простые строительные блоки (хотя есть и более сложные), состоящие из вещей.
как точки, линии и многоугольники. Эти несколько вещей можно комбинировать, чтобы создать практически бесконечный набор визуализаций.
Сейчас мы просто рассмотрим точки и линии. Обратите внимание, что отображение переменных остается неизменным. Все, что нам нужно изменить, это
создаваемая форма.
Все, что мы сказали, это то, как отображать данные на графике.
Мы не указали что надо рисовать. Нарисованные фигуры называются геомами.
Геометры обычно представляют собой очень простые строительные блоки (хотя есть и более сложные), состоящие из вещей.
как точки, линии и многоугольники. Эти несколько вещей можно комбинировать, чтобы создать практически бесконечный набор визуализаций.
Сейчас мы просто рассмотрим точки и линии. Обратите внимание, что отображение переменных остается неизменным. Все, что нам нужно изменить, это
создаваемая форма.
## просто построение точек (также известное как диаграмма рассеяния) p + геометрическая_точка()
## простой сюжет спагетти р + геометрическая_линия ()
Более настраиваемые графики
Эта грамматика графической системы может показаться сложной для простого небольшого точечного графика, и это так.
Его ценность заключается в гибкости для создания гораздо более сложных визуализаций с минимальными изменениями. Мы видим
сюжет спагетти, но, возможно, есть различия в зависимости от пола. Мы могли бы сравнить средний допуск для
самок и самцов, но что, если было взаимодействие между , и мужчина такой, что эффект времени
на толерантность зависит от того, является ли индивидуум женщиной или мужчиной? Визуальный осмотр прост; мы просто
создайте два отдельных сюжета для женщин и мужчин. Чтобы облегчить обнаружение основных половых эффектов, мы наносим
оба подграфика в одинаковых масштабах (по умолчанию).
Мы видим
сюжет спагетти, но, возможно, есть различия в зависимости от пола. Мы могли бы сравнить средний допуск для
самок и самцов, но что, если было взаимодействие между , и мужчина такой, что эффект времени
на толерантность зависит от того, является ли индивидуум женщиной или мужчиной? Визуальный осмотр прост; мы просто
создайте два отдельных сюжета для женщин и мужчин. Чтобы облегчить обнаружение основных половых эффектов, мы наносим
оба подграфика в одинаковых масштабах (по умолчанию).
## фасет (условие) графа, основанного на мужской переменной p + geom_line() + facet_grid(. ~ мужской)
Кроме одного чрезвычайно высокого самца, визуально ничего не «выпрыгивает», но было бы неплохо увидеть средства
слишком. Мы добавляем к графику сводную функцию, которая вычисляет и отображает средние значения. Обратите внимание, что, поскольку мы все еще
огранка на основе мужчина (женщина/мужчина), ggplot2 умеет рассчитывать и строить средние значения отдельно. Мы переопределяем групп = id , которые мы установили в нашем объекте ‘ p ’, иначе мы вычисляли бы среднее значение каждый раз, для каждого id … не очень интересно.
Мы переопределяем групп = id , которые мы установили в нашем объекте ‘ p ’, иначе мы вычисляли бы среднее значение каждый раз, для каждого id … не очень интересно.
p + geom_line() + stat_summary(aes(group = 1), geom = "точка", fun.y = среднее,
форма = 17, размер = 3) + facet_grid(. ~ мужской)
Помимо простоты обработки, есть еще одно преимущество вычисления среднего значения (или любой графической статистики).
расчет в вызове графа. ggplot2 имеет особый порядок работы. Сначала данные считываются и
переменные сопоставляются с осями или любым другим аспектом графика, затем применяются любые преобразования, затем
выполняется огранка или кондиционирование, затем рассчитывается статистика и, наконец, визуализируются графики.
Это означает, что если бы кто-то преобразовал данные (скажем, с помощью логарифмического или квадратного преобразования), средние значения будут
вычислено на преобразованных данных . Пробуя разные способы визуализации данных, очень
удобно, что графики автоматически обновляются до преобразования, огранки и т. д.
д.
## Здесь мы строим логарифмическую базу 10 допуска, теперь вычисляются средние значения
## для зарегистрированных значений, т. е. mean(log(y)) NOT log(mean(y)) --- эти два
## это совсем разные вещи
p + geom_line() + stat_summary(aes(group = 1), geom = "точка", fun.y = среднее значение,
shape = 17, size = 3) + scale_y_log10() + facet_grid(. ~ мужской)
В предыдущих примерах функция, используемая для вычисления суммарного значения y, была средней, но ее можно было любая функция. Например, учитывая высокий балл на мужской в момент времени 3, возможно, мы предпочли бы использовать медианы. Изменение тривиально.
p + geom_line() + stat_summary(aes(group = 1), geom = "точка", fun.y = медиана,
форма = 17, размер = 3) + facet_grid(. ~ мужской)
В качестве альтернативы мы могли бы построить верхний и нижний квартиль (в качестве примечания мы могли бы рассмотреть
соединяя нижний и верхний квартили линией [как планки погрешностей]).
## обратите внимание, что аргумент probs предназначен для квантильной функции, как и для
p + geom_line() + stat_summary(aes(group = 1), geom = "точка", fun.y = квантиль, fun.args=(list(probs = c(0.25, 0.75))), shape = 17, size = 3) + facet_grid(. ~ male)
Дело в том, что фреймворк гибкий — теоретически вы можете использовать любую функцию для Резюме. Теперь нас может заинтересовать оценка общей тенденции в данных. Один из вариантов добавить линию, используя локально взвешенную регрессию (lowess), чтобы «сгладить» всю изменчивость и дать ощущение общего или среднего тренда. Это занимает всего одну короткую строку кода и автоматически рассчитывается отдельно по мужской .
## еще раз обратите внимание, мы используем group = 1, поэтому сглаживание не рассчитывается
## отдельно для каждого id
p + geom_line() + stat_smooth (aes (группа = 1)) + stat_summary (aes (группа = 1),
geom = "точка", fun.y = среднее, форма = 17, размер = 3) + facet_grid(.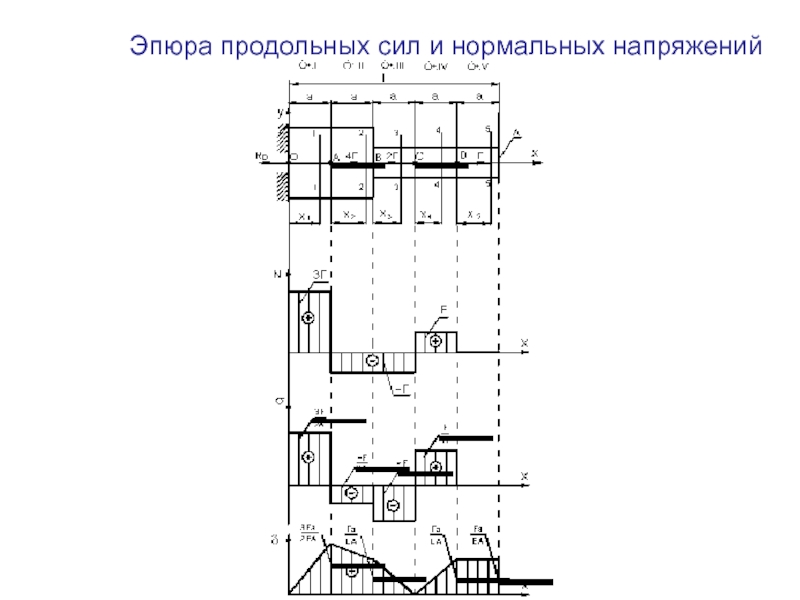 ~ мужской)
~ мужской)
## `geom_smooth()` с использованием метода = 'loess' и формулы 'y ~ x'
Lowess выглядит довольно линейно, поэтому мы можем выбрать линейное сглаживание и отключить затенение стандартной ошибки.
p + geom_line() + stat_smooth(aes(group = 1), method = "lm", se = FALSE) +
stat_summary(aes(группа = 1), геометрия = "точка", fun.y = среднее значение, форма = 17, размер = 3) +
facet_grid(. ~ мужской)
Добавление сглаживания является более гибким, чем мы показывали до сих пор (для получения дополнительной информации см. FAQ
на зубах в ggplot2). Предположим, что между моментами времени 1 и 2
произошло вмешательство, и мы хотим подобрать кусочно-линейную модель, а не общую гладкую. Мы можем
сделать это, создав фиктивную переменную (до/после вмешательства) и ее взаимодействие с время . Единственный
изменение - это немного более сложная формула. По умолчанию y ~ x . « I(x > 1) » создает фиктивный (ИСТИНА/ЛОЖЬ)
переменная, если x ( x в данном случае) больше 1. « * » в формуле запрашивает основные эффекты и
взаимодействие между x и фиктивной переменной от x. Конечно, ggplot2 позаботится о подгонке модели.
отдельно по самцу и рисуем его для нас. Теперь мы можем видеть, что линия тренда «прыгает» после момента 1, и
наклон может изменяться (хотя изменение кажется минимальным, предполагается, что нет взаимодействия
между нашим гипотетическим вмешательством и временем).
« * » в формуле запрашивает основные эффекты и
взаимодействие между x и фиктивной переменной от x. Конечно, ggplot2 позаботится о подгонке модели.
отдельно по самцу и рисуем его для нас. Теперь мы можем видеть, что линия тренда «прыгает» после момента 1, и
наклон может изменяться (хотя изменение кажется минимальным, предполагается, что нет взаимодействия
между нашим гипотетическим вмешательством и временем).
p + geom_line () + stat_smooth (aes (группа = 1), метод = «lm», формула = y ~
x * I (x > 1), se = FALSE) + stat_summary (aes (group = 1), fun.y = среднее значение, geom = «точка»,
форма = 17, размер = 3) + facet_grid(. ~ мужской)
Резюме
Мы создали множество графиков, используя ggplot2 для визуализации
лонгитюдные данные и продемонстрировали, как это возможно
чтобы легко добавлять сводную статистику, искать взаимодействия с категориальными переменными через фасетирование,
попробуйте преобразовать данные и посмотрите на линейные и нелинейные эффекты.