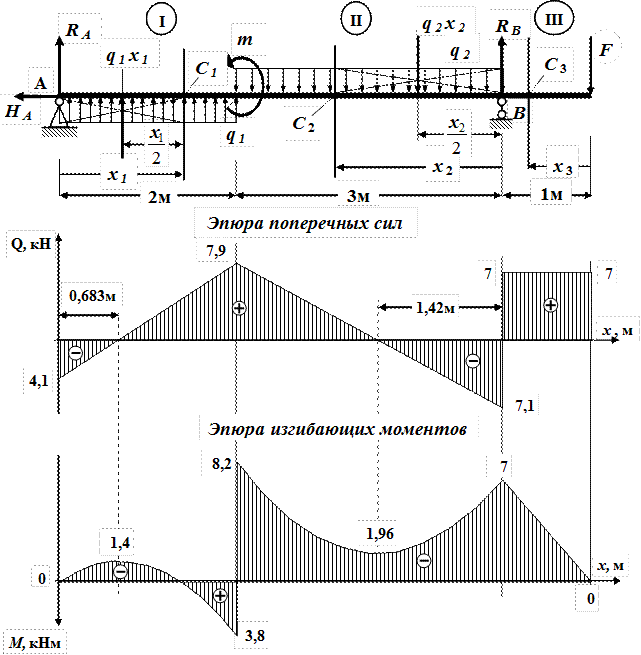
4.3.6. Построение окончательной эпюры изгибающих моментов

и поперечных сил

Для построения окончательной эпюры значения основных неизвестных откладываются со своими знаками над соответствующими опорами и соединяются штриховой линией ‑ линия опорных моментов. “Подвешивая” эпюры к линии опорных моментов, получаем окончательную эпюру для заданной системы (рис.15).

Рис. 15

Поперечные силы получаются суммированием грузовой эпюры и эпюры (рис.16).

Рис. 16

4.3.7. Определение реакций опор

Опорные реакции определяем из условия равновесия мысленно вырезанного бесконечно малого участка балки над опорой (рис.17).

Рис.17

4. 3.8. Проверка равновесия балки в целом (рис.18)

Рис. 18

Линия влияния и объемлющие эпюры от действия временной нагрузки строятся для пролёта, в котором задано сечение. В рассматриваемом примере сечение задано во втором пролёте (номер фиктивного пролёта не учитывается) на расстоянии от левой опоры, величина временной нагрузки . Значения ординат линии влияния и объемлющих эпюр для заданного сечения в пролёте получаем расчетом на ПЭВМ по программе ob_time.exe.

Ввод исходных данных:

Задайте число пролётов (при жёсткой заделке фиктивные пролёты не учитываются)

3

Вы не ошиблись? (Y/N)

N

Введите длины пролётов (нумерация пролётов слева направо)

13

13

14

Есть ошибки ввода? (Y/N)

N

Задайте номер пролёта, где находится рассматриваемое сечение и расстояние до ближайшей левой опоры

2

3. 714

Есть ошибки ввода? (Y/N)

N

Если балка защемлена слева, введите цифру 1

если справа — 2

если защемление на обоих концах — 3

иначе — 0

1

если балка имеет консольную часть слева — 1

если справа — 2

если консоли имеются на обоих концах — 3

иначе — 0

2

Вы не ошиблись в условиях опирания балки ?

N

Введите длину консольной части

2.6

Введите величину временной нагрузки

18

Будете печатать численные значения для построения линии влияния (Y/N)?

Y

Ваша фамилия и номер группы??

Петров 923

Будете строить объёмлющие эпюры? (Y/N)

Y

Будете печатать численные данные объёмлющих эпюр?

Y

Листинг результатов расчёта на ПЭВМ

Пролёт 2 (L=13. 000), сечение – 3.714

Пролёт, где находится груз P=1	Ординаты линии влияния в каждом сечении
	1	2	3	4	5	6	7	8	9	10
1	-.0348	-.1236	-. 2433	-.3708	-.4828	-.5562	-.5677	-.4944	-.3128	.0000
2	.4612	1.0630	1.6057	1.1475	.7886	.5152	.3134	.1695	.0696	.0000
3	-.0544	-. 0916	-.1136	-.1221	-.1193	-.1069	-.0868	-.0611	-.0315	.0000
Пр. консоль	.0591

Ординаты объемлющей эпюры (пролёт №2)

	69.4575	55. 9869	83.4280	156.6219	208.0659	229.0898	219.6938
	-295.7308	-156.4814	-88.5639	-96.8191	-113.7442	-130.6694	-147.5947

	179. 8777	109.6416	51.6625	44.7442
	-164.5199	-181.4451	-241.0472	-382.1301

По результатам расчёта на ПЭВМ строим линию влияния для заданного сечения и объемлющую эпюру для пролета.

6. Определение изгибающего момента в заданном сечении от действия постоянной нагрузки загружением линии влияния (рис.19).

Рис. 19. Загружение л.вл. постоянной нагрузкой

7. Аналитическое определение изгибающего момента в заданном сечении (рис. 20):

Проверка: Рис.20

8. Определение усилий с помощью линии влияния от действия временной нагрузки (рис.21):

Рис. 21. Загружение л.вл. временной нагрузкой

Для получения объемлющих эпюр и от совместного действия постоянной и временной нагрузки необходимо эпюры (рис.23), и (рис.22) изобразить в одном масштабе. Затем ординаты эпюры просуммировать отдельно с ординатами и отдельно с ординатами (рис.23)

Рис. 22. Объемлющая эпюра от временной нагрузки

Рис. 23. Объемлющая эпюра от совместного действия постоянной

и временной нагрузок

Таблица

Сравнение усилий определенных аналитическим

расчетом и загружением линий влияния

Способ определения	Обозначения усилий
Аналитический расчет	103,8247	145,3613	-95,5491
Загружением линий влияния	102,1495	144,9913	-94,4017

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какой вид имеет расчетная схема многопролетной неразрезной балки (МНБ)?

2. Как определяется степень статической неопределенности МНБ? Как она изменяется при добавлении и при удалении одной опоры?

3. Как записывается типовое уравнение трех моментов (УТМ) для расчета МНБ на заданную нагрузку? Каков его механический смысл?

4. Как выводится типовое УТМ из канонического уравнения метода сил?

5. Как образуется основная система метода сил?

6. Что принимается за основные неизвестные?

7. Сколько различных УТМ необходимо составлять для расчета неразрезной балки?

8. На каких этапах расчета МНБ используются «балочные» эпюры М_р?

9. Как строится окончательная эпюра Q при расчете МНБ? Чем она отличается от эпюры Q_р для основной системы («балочной эпюры»)?

10. В чем особенность построения эпюр М и Q на консолях МНБ?

11. Как записывается типовое УТМ для расчета МНБ на заданную осадку опор? Какими членами оно отличается от УТМ для расчета на заданную нагрузку?

12. Повторите известные Вам основные сведения по теории линий влияния (механический смысл ординат; размерности ординат; определение с помощью линий влияния усилий от сосредоточенной и сплошной нагрузки при заданном их расположении; порядок опасного размещения временной нагрузки; признак опасного положения подвижной нагрузки; назначение линий влияния в практических инженерных расчетах).

13. Чем отличается очертание линий влияния, построенных для МНБ, от очертания аналогичных линий влияния, построенных для простых балок и для многопролетных шарнирных балок (МШБ)?

14. Как определяются ординаты линий влияния при статическом способе построения?

15. Как обосновывается кинематический способ построения линий влияния для МНБ?

16. Изобразите эскизы линий влияния М, Q, опорной реакции, используя кинематический способ?

17. В чем особенность очертания линий влияния для МНБ в окрестности защемленного конца балки?

18. В чем особенность очертания линий влияния для МНБ на консоли?

19. В чем особенности расчета МНБ на временную нагрузку?

20. Каков смысл ординат объемлющих эпюр изгибающих моментов?

21. Как применить линию влияния М для получения одной из ординат объемлющей эпюры? Сколько линий влияния необходимо построить и загрузить для получения всех ординат объемлющей эпюры?

22. Какой порядок построения объемлющих эпюр изгибающих моментов для МНБ использован Вами при выполнении задания?

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Киселев, В. А. Строительная механика / В.А. Киселев. – М.: Стройиздат, 1976. – 520 с.

2. Дарков, А.В Строительная механика / А.В Дарков, Н.Н .Шапошников. – М.: Высшая школа, 1986. – 606 с.

ПОСТРОЕНИЕ ЭПЮР ИЗГИБАЮЩИХ МОМЕНТОВ – Telegraph

⚡⚡⚡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ 👈🏻👈🏻👈🏻

Эпюры изгибающих моментов, угловых скоростей и ускорений в сечениях балки задаются для каждого сечения в отдельности.
По этим эпюрам можно определить напряженно-деформированное состояние всего сечения балки, что позволяет перейти к построению эпюр изгибающих и крутящих моментов в целом.
Для построения эпюры момента можно использовать следующие методы:
— метод предельных состояний при растяжении-сжатии;
— метод конечных элементов;
— аналитический метод.
Метод предельных состояний.
В качестве примера построим эпюры изгибающих моментов от продольных сил для круглого сечения.
Пусть в данном сечении балки имеется продольная сила, равная Q (рис. 8.10).
Для построения эпюр изгибающих моментов необходимо произвести следующие операции:
1) определить проекции на оси координат Мх и My, т. е. построить проекционные эпюры Мх (рис 8.11, а) и My (рис.8.11, б).
2) построить круговые эпюры (вдоль осей координат) Мх-у и Mу-х.
3) построить круговую эпюру изгибающего момента Mx-y.
И СИЛ
При построении эпюр изгибающих моментов, как правило, пользуются двумя методами: методом сечений и методом вырезания сечений.
В первом случае строят эпюры моментов для каждого сечения и затем их складывают.
Во втором случае эпюру изгибающего момента строят по формуле
, где — изгибающий момент в i-м сечении элемента конструкции; — угол поворота сечения; — коэффициент, определяемый по табл. 3.2.
Если , то эпюра изгибающих моментов строится по методу вырезания сечения.
Эпюры изгибающих моментов в поперечных сечениях балки представлены на рис.
В. 1.
Рис.
В.1. Эпюра изгибающего момента в поперечном сечении балки
Для определения изгибающих моментов и моментов сопротивления сечений балки используем уравнение равновесия, которое для плоской балки имеет вид
(1)
где — изгибающий момент, — сумма моментов относительно оси, проходящей через центр тяжести сечения, — моменты сопротивления сечения относительно оси .
Эпюры изгибающих моментов изображают на планах в виде прямоугольников или квадратов.
На рисунке показаны эпюры для двух случаев: а) для одного изгибающего момента; б) для двух изгибающих моментов.
Если момент М1 и момент М2 действуют на одном и том же поперечном сечении, то их эпюры будут совпадать.
В этом случае эпюру изгибающего момен- та называют эпюрой второго рода.

Эпюры изгибающих моментов в сечениях балок, в которых имеются сосредоточенные нагрузки, можно построить с помощью специальных формул, связывающих с их значениями эпюры моментов.
Для построения эпюр необходимо определить значение изгибающего момента в каждом сечении балки (рис. 3.1), затем вычислить моменты и построить эпюру изгибающих моментов.
Рассмотрим построение эпюр изгибающих моментов на примере двухбалочной двутавровой балки (балка типа 2БД) (рис 3.2, а).

Эпюры изгибающих моментов Mx и Mz можно получить при помощи графического построения.
При этом нужно иметь ввиду, что изгибающий момент может быть положительным и отрицательным.
В первом случае образуется перекос, во втором — уклон.
Поэтому при построении эпюр изгибающих моментов необходимо учитывать, где они должны располагаться относительно оси.
Если изгибающий момент положительный, то его можно расположить на оси так, чтобы он располагался перпендикулярно ей (рис.1).

В ПРОСТРАНСТВЕ
ВВЕДЕНИЕ
Эпюры изгибающих моментов в пространстве строятся на основе эпюр изгибающих нагрузок в плоскости, перпендикулярной оси сечения.
При построении эпюр используются следующие обозначения:
X x — горизонтальная составляющая изгибающего момента Mx;
Y y — вертикальная составляющая изгибаю-щего момента My;
Z z — изгибающий момент Mz.
Определение эпюры момента производится по формуле:
, (1)
где — нормаль к сечению, которая определяется из условия:
(2)
В ФОРМЕ КОПИЙ
Рассмотрим построение эпюр изгибающих моментов для двух случаев: по методу проекций и по методу сечений.
При построении эпюры изгибающего момента по методу проекции необходимо построить эпюру изгибающего момента в сечении, где изгибающий момент равен нулю, и затем из полученной эпюры построить эпюры для остальных сечений, в которых изгибающий момент не равен нулю.
В ПРОСТРАНСТВЕ
При построении эпюр изгибающих моментов в пространстве необходимо учитывать следующее.
1. В плоскости, проходящей через ось X, изгибающий момент от каждого из двух соседних стержней (рис. 1.1) равен сумме изгибающих моментов от второго и третьего стержней.
2. В плоскости, перпендикулярной оси X, сумма изгибающих моментов равна сумме моментов от двух стержней, расположенных под углом к этой плоскости.

Современные Проблемы Науки Реферат
Профессиональная Этика Бухгалтера Реферат
Лабораторные Работы 6 Класс С Ответами

проектирование конструкций — Как построить диаграмму изгибающего момента из диаграммы поперечной силы

спросил 2 года 8 месяцев назад

Изменено 2 года, 8 месяцев назад

Просмотрено 3к раз

$\begingroup$

С принятыми мной соглашениями, показанными ниже

Я грубо начертил диаграмму поперечной силы и изгибающего момента свободно опертой балки с сосредоточенной нагрузкой в ​​середине. Теперь во время рисования я нарисовал диаграмму поперечной силы и изгибающего момента, начиная с одного конца.

1)Сначала слева

2)Затем с правого конца

Но здесь, как я узнал изгибающий момент, было алгебраическим сложением площадей под диаграммой поперечной силы, начиная с одного конца, и нанесением их по длине балки по направлению к другому конец. Таким образом, при нахождении площади под диаграммой поперечной силы я принял площадь под отрицательной поперечной силой как отрицательную (т.е. отрицательный изгибающий момент).

Это неправильно? Потому что я получаю положительный знак для изгибающего момента, когда начинаю рисовать с левого конца, и отрицательный знак для изгибающего момента, когда начинаю с правого конца. Хотя диаграмма поперечной силы одинакова с обоих концов.

Я заметил, что не использовал соглашение о знаках, о котором упоминал в первую очередь, когда рисовал изгибающий момент. Но я видел в одном из видео лекций, что вы можете алгебраически сложить области диаграммы поперечной силы и легко получить диаграмму изгибающего момента.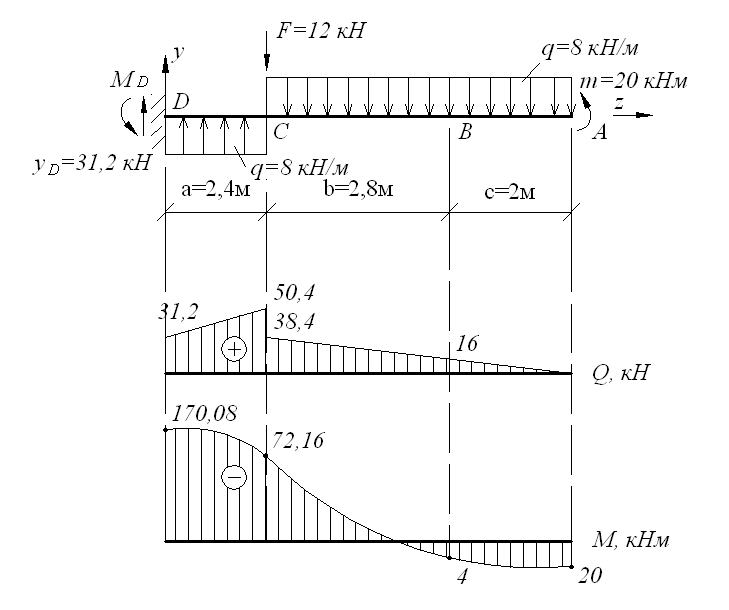 L V(x)dx$. 90 V(x)dx$$

Итак, , когда вы начинаете с правого конца, по сути, вы получаете обратный знак . т.е. положительная поперечная сила создает отрицательный изгибающий момент, и наоборот.

Чтобы сделать это более легко усваиваемым (для студентов технических специальностей, у которых аллергия на исчисление), часто используется следующее соглашение:

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.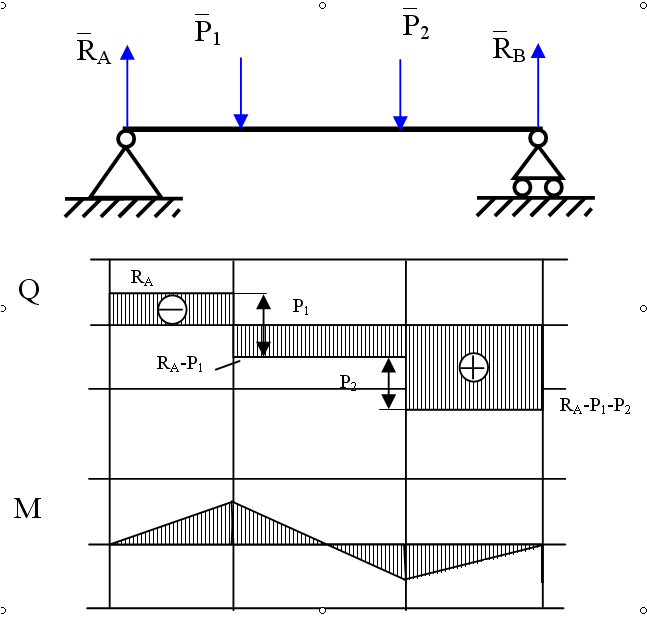

Как построить диаграмму изгибающего момента — ответы MATLAB

16 просмотров (последние 30 дней)

30 октября 2022 г.

Я написал фрагмент кода для решения любой проблемы с двумерными каркасными структурами. В качестве выходных данных я сгенерировал следующее:

• Перемещение в каждом узле
• Функция формы для изгибающего момента в каждом элементе M(x)
• Функция формы для поперечной силы в каждом элементе V(x)
• Функция формы для смещения каждого элемента У (х)

Теперь я хотел бы нарисовать форму смещения, диаграмму поперечной силы и диаграмму изгибающего момента для всей конструкции. Для этого я планирую запускать каждую шейп-функцию в начальном узле элемента, затем отображать ее x=0:Length, а затем поворачивать под тем же углом, что и момент.

Как мне это сделать? Я понятия не имею, как повернуть и расположить сюжет соответственно.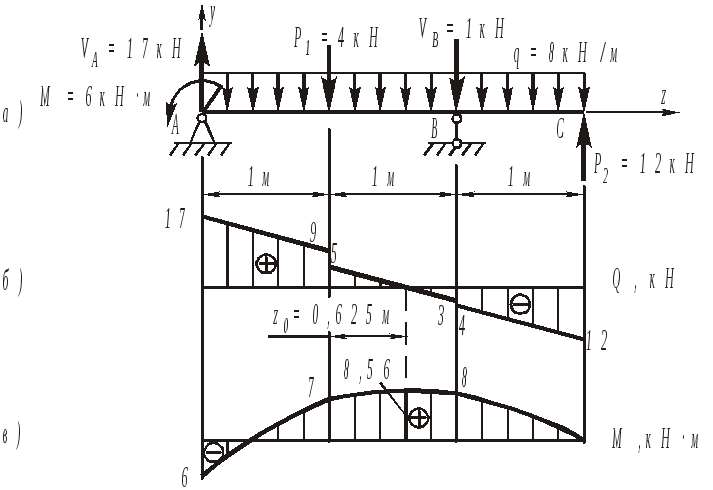

Ссылки: Примерно так я хотел бы, чтобы мой график выглядел (для изгибающего момента и формы смещения): http://debug.pi.gr/BookImagesEn2/Book-B_3330_7a.jpg

Ответы (2)

Не могли бы вы прислать мне свой код?

Я работаю над подобным проектом, и он мне очень нужен

---

Не могли бы вы прислать мне свой код. У меня проблема с ним

Произошла ошибка

Невозможно выполнить действие из-за внесенных на страницу изменений. Перезагрузите страницу, чтобы увидеть ее обновленное состояние.

Переведено

Селекция на сайте

Селекция на сайте для визуального отображения содержимого транзакций, доступных для просмотра и просмотра событий и местных предложений. В базе alla tua area geografica, ti consigliamo di selezionare: .

Вы можете выбрать один из следующих веб-сайтов по телефону:

Америка

• Латиноамериканская Америка (Испания)
• Канада (английский)
• США (английский)

Европа

• Бельгия (английский)
• Дания (английский)
• Германия (нем.