Построение эпюр сопромат: Правила построения эпюр в сопромате.

Содержание

Урок 10 | sopromat

Эпюра изгибающего момента строится вверх положительное направление вниз отрицательное. Правило определения знаков представлено на рисунке (Рис. 4.4).

Рис. 4.4 – Правило знаков для изгибающего момента

Правило знаков для крутящего момента Мz

Крутящий момент считается положительным, если вызывающий его внешний крутящий момент действует относительно рассматриваемого сечения против часовой стрелки (Рис. 4.5).

Рис. 4.5 – Правило знаков при кручении

Пример построения эпюр ВСФ при изгибе

П р и м е р . Для нагруженной консольной балки построить эпюры Qy и Мх.

Построение эпюры Q.

В данном случае будет один участок: 0≤z≤2l.

Для произвольного сечения с координатой z:

Получена линейная зависимость, для построения графика которой нужны значения функции Qy(z) в начале и конце участка:

z=0

z=2l

Построение эпюры M.

Рассмотрим два участка балки.

1-й участок: 0≤z1≤l:

Получена квадратичная зависимость, для построения графика которой нужны значения функции Мх(z1) в начале и конце участка:

В начале участка z=0

В конце участка z=l

2-й участок: l≤z2≤2l:

Получена квадратичная зависимость, для построения графика которой нужны значения функции Мх(z2) в начале и конце участка:

В начале участка z=l

В конце участка z=2l

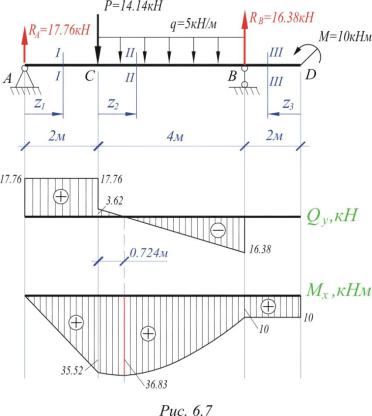
Рис. 4.6 – Пример построения Эпюр

Дифференциальные зависимости между ВСФ при изгибе

Рассмотрим двухопорную балку, нагруженную произвольной нагрузкой qz.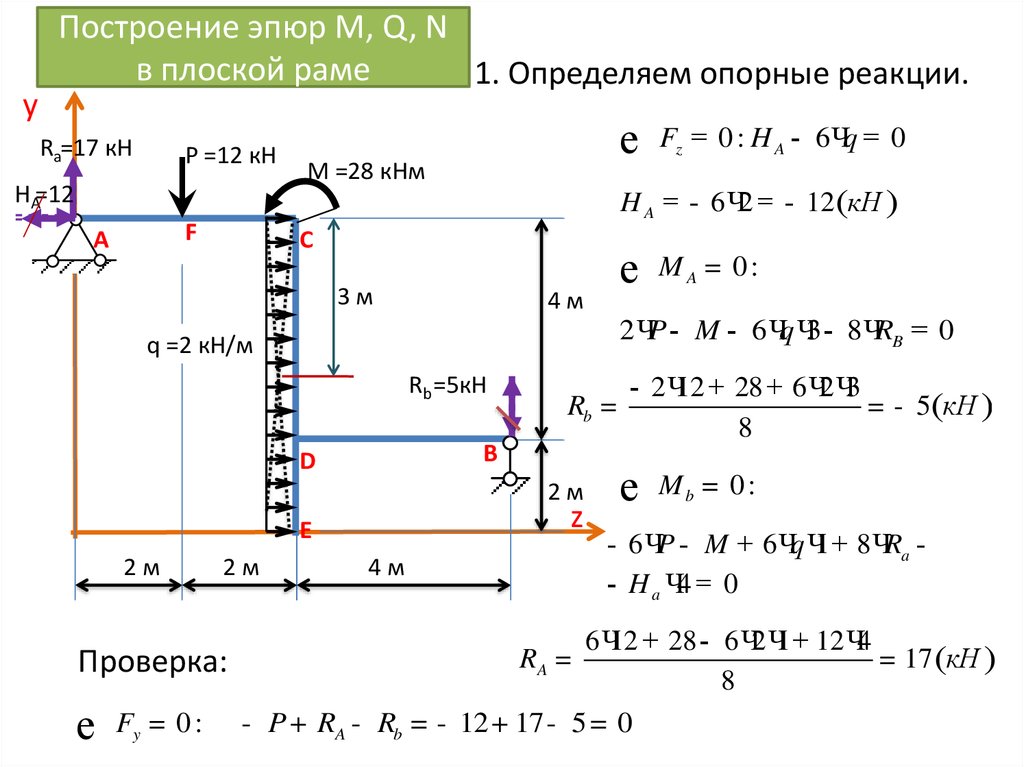

Рис. 4.7 – Двухопорная балка

В окрестностях точки B вырежем бесконечно малый участок балки длиной dz. В силу малости участка можно принять q=const:

Рис. 4.8 –Малый участок

Запишем условия статического равновесия:

(4.1)

(4.2)

Слагаемым можно пренебречь, вследствие малости dz, тогда

(4. 3)

(4.4)

Зависимость (4.3) используется для анализа возрастания или убывания функции Mx слева направо:

если Qy>0, то Mx возрастает;

если Qy<0, то Mx убывает;

если q=0, Qy=const, то Mx=Qy*z+C – наклонная прямая;

если q=const, то Qy=q*z+D – наклонная прямая.

Основные закономерности при построении эпюр Qy и Mx

1)От действия сосредоточенной силы на эпюре Qy – скачок на величину силы в сторону знака ее

воздействия; на эпюре Mx – перелом, острие которого направлено в сторону действия силы.

2)От сосредоточенной пары сил на эпюре Mx – скачок на величину пары в сторону,

противоположную знаку ее воздействия.

3)Если участок пустой (ничем не загружен), на эпюре Qy – прямая, параллельная базе; на эпюре Mx – прямолинейная зависимость.

4)Если участок загружен равномерно распределенной нагрузкой интенсивностью q, то на эпюре Qy – наклонная прямая с угловым коэффициентом, равным q; на эпюре Mx – квадратичная парабола, выпуклость которой направлена в сторону действия распределенной нагрузки.

5)Если на участке действия распределенной нагрузки на эпюре Qy наклонная прямая пересекает базу, то в соответствующем сечении на эпюре Mx – экстремум.

Построение эпюр изгибающих моментов m и поперечных сил q в балке

DTD | Остаточная прочность | Способность к остаточной прочности

В конструкциях с одним путем нагрузки анализ остаточной прочности включал только один критерий отказа для данной структурной геометрии.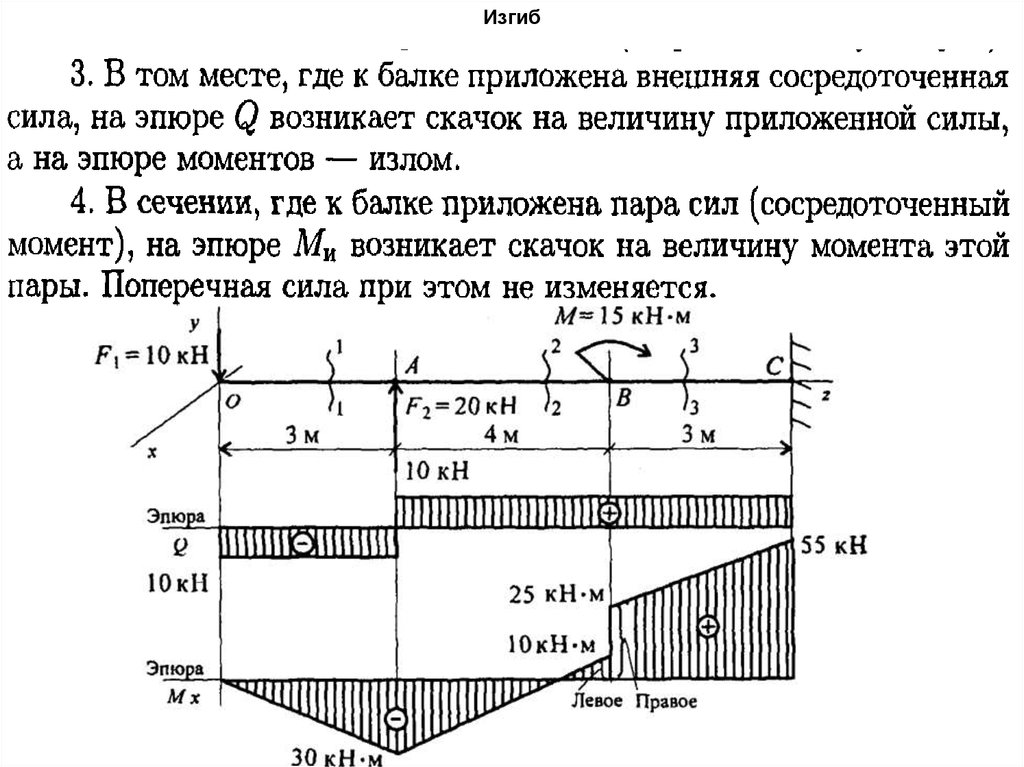 В застроенных сооружениях из-за сложного геометрической конфигурации, может потребоваться один или несколько критериев отказа. учитывать при определении остаточной прочности для всего состав. Следующие пункты изучить эти аспекты анализа остаточной прочности сборных конструкций.

Ранее было объяснено, что безопасность может быть достигнута проектирование конструкции самолета либо как медленного роста трещины, либо как безотказная. Последний случай можно дополнительно классифицировать на два случая: множественный путь загрузки и блокировка трещин. Как правило, конструкции с несколькими путями нагрузки и блокировкой трещин являются сборными конструкциями. В разделе 1.3, определения и требования к этим двум типам сборной конструкции. Обсуждаются. Для полноты структура, показанная на рисунке 4.3.2, анализируется для далее объяснить особенности, присущие множественному пути нагрузки, застроенному состав.

Пока центральный элемент не вышел из строя, все три элемента нести долю от общего груза P .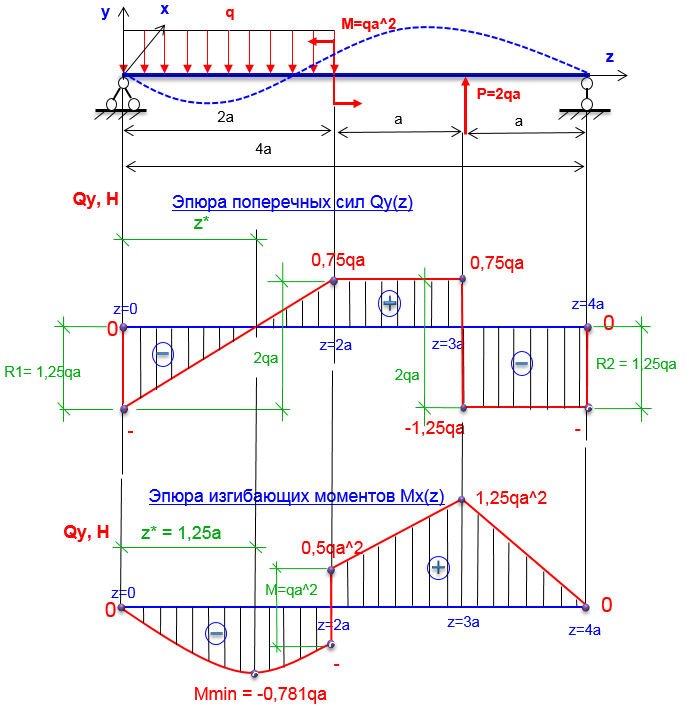

В случае отказа центра член, общая нагрузка P (фактически 1.15 P ) должен быть передан два других члена в момент отказа, если конструкция должна остаться нетронутый.

Остаток Прочностные характеристики конструкции с несколькими путями нагрузки, показанной на рис. 4.3.2, можно объяснить с помощью рис. 4.3.3. Когда один элемент выходит из строя, на рис. 4.3.3 показано чтобы оставшиеся параллельные элементы могли нести требуемую нагрузку без отказ. Остаточная способность показано, что они разрушаются по мере расширения трещины в центральном элементе и по мере того, как трещины в остальных элементах не получается. На рис. 4.3.3 показано прерывистое изменение прочность в результате разрушения элементов. Поскольку уровни нагрузки в других членах резко возрастают, если нагрузка

P необходимо сохранить, оставшиеся члены будут иметь короткую жизнь. Таким образом, второй элемент может выйти из строя через время ( t ₂ ). Показано, что остаточная прочность падает ниже безопасного уровня где-то в время между t ₁ и t ₂ .

Продолжительность временного интервала между отказом первого элемента и разрушением конструкции может быть коротким или длинным в зависимости от «типа отказа» первого члена и требования к нагрузке после этого сбоя. Этот временной интервал доступен для обнаружения сбоя первого члена и ремонт конструкции.

Рисунок 4.3.2. Структура с несколькими путями нагрузки (настроенная) с трещиной в Центральный элемент

Рисунок 4.3.3. Снижение остаточной прочности во время Последовательное разрушение элементов в конструкции, показанной на рисунке 4.3.2

Напряжение разрушения или уровень критического размера дефекта центральный элемент (любой из параллельных элементов) можно оценить, рассматривая проблема аналогична структуре единого пути загрузки. Используя анализ роста усталостной трещины, Кривая распространения трещины получается от минимального обнаруживаемого размера трещины до критическая длина трещины, как показано на рисунке 4. 3.4. В структуре с несколькими путями нагрузки частичная отказ конструкции может произойти в период ее эксплуатации. Но эта неисправность должна быть обнаружена в осмотр до того, как произойдет катастрофический отказ всей конструкции. Подходящий график проверки должен включать анализ структурных характеристик наряду с эксплуатационными требованиями за интервалы между проверками.

Рисунок 4.3.4. Рост трещины в структуре с несколькими путями нагрузки, показанной на рис. 4.3.2

Чтобы проиллюстрировать анализ, связанный с оценкой остаточная прочность сложных конструкций, рассмотрим осевую нагрузку Комбинация обшивка-стрингер с продольным усилением, как показано на рис. 4.3.5. Предполагая, что крепления жесткие, смещения соседних баллы в обшивке и стрингерах будут равны. (Если обшивка и стрингеры изготовлены из одного и того же материала, напряжения в эти два значения также будут равны в случае отсутствия трещины.) Пусть в коже образуется поперечная трещина. Это приведет к большему смещению в кожа, и стрингеры должны следовать за этим большим смещением. В результате они берут на себя нагрузку с кожи, тем самым уменьшая напряжение обшивки за счет более высокого напряжения стрингера. Следовательно, смещения в треснутая кожа будет меньше, чем в неукрепленной пластине с таким же размером трескаться. Это означает, что кожа напряжения ниже, а коэффициент интенсивности напряжений ниже. Чем ближе стрингеры к трещине, тем эффективнее передача нагрузки.

Рисунок 4.3.5. Структура обшивки, застроенная конструкция

Если коэффициент интенсивности напряжений для небольшой трещины в неподкрепленная панель аппроксимируется K = sÖpa , коэффициент интенсивности напряжений для подкрепленной пластины составит K = bsÖpa . Понижающий коэффициент, b = K/ sÖpa , будет уменьшаться, когда вершина трещины приближается к стрингеру. Поскольку стрингеры воспринимают нагрузку от обшивки, напряжение стрингера увеличится с с к л с , где L возрастает с вершиной трещины подходит к стрингеру.

Очевидно, 0 < b < 1 и L > 1. Эти значения зависят от коэффициентов жесткости, жесткость крепления и отношение размера трещины к стрингеру интервал. Как будет показано далее, b и L можно легко рассчитать; в этот достаточно отметить, что б и L различаются в зависимости от длины трещины, как показано на рисунке на рисунке 4.3.6.

Рисунок 4.3.6. Вариант B и L с длиной трещины в усиленной панели с трещиной между ребрами жесткости

Из-за сложности конструкции усиленной обшивки построение диаграммы остаточной прочности значительно сложнее трудный. Рассмотрим сначала условие где происходит резкое повреждение кожи. Когда трещина мала по сравнению с расстоянием между элементами жесткости, остаточная прочность обшивки не зависит от ребер жесткости и начальная часть диаграммы соответствует графику для неподкрепленной панели (см. точка А на рис.

4.3.7). Как только размер трещины становится достаточно большим, чтобы кожа не могла выдержать приложенной нагрузки дальше, стрингер примет на себя часть нагрузки от кожи, тем самым уменьшая кожный стресс. Следовательно, коэффициент интенсивности напряжений в вершине трещины будет ниже из-за уменьшенное напряжение и, таким образом, остаточная прочность структуры кожи будет увеличивается с длиной трещины, как показано на рисунке 4.3.6. По мере дальнейшего увеличения размера трещины в сторону расположение ребра жесткости, нагрузка, передаваемая с обшивки на ребро жесткости также значительно увеличивается, что снижает фактор интенсивности стресса. Остаточная прочность усиленной панели продолжает увеличиваться, как показано на рисунке для более длинных трещин. Из рисунка также можно заметить, что диаграмма остаточной прочности для неподкрепленной панели соответствовала бы пунктирная линия, т. е. сплошной спад остаточной прочности по мере растрескивания размер увеличивается. Это потому что там нет неотъемлемого свойства, присутствующего в структуре одного пути нагрузки, чтобы уменьшить коэффициент интенсивности напряжений в вершине трещины.

Рисунок 4.3.7. Остаточная прочность панели с трещинами как Функция длины трещины для наращенной конструкции с жесткой обшивкой по сравнению с Неукрепленная панель. Внезапный сбой Критерий, используемый для определения остаточной прочности

Диаграмма остаточной прочности конструкции с обшивкой повторяется на рис. 4.3.8, где несколько дополнительных точки интереса определены для аналитика. Для конструкции с трещиной длиной a _A , остаточная прочность определяется как точка A. Поскольку точка A связана с отказом напряжение, превышающее пиковое напряжение ( с _пик ), трещина резко расширяется и полностью выходит из строя панель. Если структура содержит трещину длиной a _C , в диапазоне от до _B и a _D , трещина расширяется резко, но затем останавливается на длине трещины а _Е , где доступная остаточная прочность больше, чем приложенная (отказ) стресс. Это расширение трещины и арест особенность конструкции обшивки-стрингера значительно облегчает контроль встречи Требования к отказоустойчивым конструкциям.

Рисунок 4.3.8. Остаточная прочность панели с трещинами как Функция длины трещины для жесткой структуры нароста. Учитывается только режим повреждения кожи. Критерий внезапного отказа, используемый для определения Остаточная прочность

Перед полным отказом панели уровень напряжения при отказе точка C/E должна быть увеличена до уровня, связанного с точкой F, то есть до с _пик . При повышении напряжения выше уровня точки Е трещина расширяется. от до _E для поддержания равновесие между входным напряжением и остаточной прочностью. Когда напряжение достигает пика с , трещина распространилась на a _F , в этот момент трещина резко расширяется, вызывая разрушение панели. Схема, иллюстрирующая длину трещины под нагрузкой диаграмма, наблюдаемая во время резкого расширения/остановки трещины в обшивочно-стрингерная конструкция представлена на рис. 4.3.9. Таким образом, видно, что остаточная прочность кривую ABCDEF, показанную на рисунке 4.3.8, можно заменить для всех практических целей с кривой, соединяющей точки ABF.

Рисунок 4.3.9. Наблюдается изменение длины трещины под нагрузкой при укреплении корки Конструкция с элементами ареста

При проектировании отказоустойчивой конструкции часто целью является спроектировать структуру для ограничения или остановки нестабильного роста трещины, чтобы катастрофический сбой можно предотвратить. Ряд методов ареста описан у Bluhm [1969], Romauldi. и Сандерс [1959–1960] и Брук [1974]. Фундаментальной концепцией проектирования трещиногасителей является обеспечение в пределах Структура средства для снижения коэффициента интенсивности напряжения вершины трещины. Эта концепция требует использования дополнительных Элементы жесткости, такие как ребра жесткости, усиливающие кольца и т. д., для создания снижение стресса. Это изначально присутствуют в сборных конструкциях, таких как крылья самолетов, фюзеляжи, и т.д..

Как правило, анализ остаточной прочности конструкции с Возможности остановки трещин могут включать более одного критерия разрушения. Например, в жесткой структуре кожи или крыло самолета, анализ должен учитывать повреждение стрингера, отказ и критерии разрушения кожных трещин. Встроенные панели, загруженные до отказоустойчивого уровня, имеют тенденцию демонстрировать существенные локальные деформации ответственных элементов. Таким образом, критерии разрушения зависят также от упругопластического прогиба. допуски как для застежек, так и для элементов обшивки/стрингера. Гюнтер и Возуми [1982] предоставить дополнительные детали анализа остаточной прочности сложных панелей на основе предельная деформация стрингера.

Остаточная прочность диаграмма для структуры, которая демонстрирует поведение медленного роста трещины, будет содержать две кривые, как показано на рисунке 4. 3.10. Нижняя кривая соответствует критической уровень напряжения, при котором начинается медленное распространение трещины. Затем эта нижняя кривая описывает начало медленного слезотечения. Верхняя кривая показывает уровень критического напряжения, при котором неустойчивая происходит быстрое расширение трещины. Когда трещина приближается к элементу жесткости, как объяснялось ранее, уровни остаточной прочности, соответствующие началу медленного растрескивания и быстрое расширение, начало увеличения.

Рисунок 4.3.10. Остаточная прочность панели с трещинами как Функция длины трещины для сборно-струйной конструкции. Критерий разрыва, используемый для определения Остаточное напряжение

Для длины трещины a _i , как показано на рис. 4.3.10, медленное распространение трещины начинается в точке B. Эта конюшня расширение продолжается до точки B¢, где должен произойти быстрый отказ. Однако в связи с непрерывным ростом остаточная прочность усиленной панели, продолжается стабильное распространение трещины произойти за точкой B¢ и до точки C. Поскольку в этот момент остаточная прочность панели начинает снижаться, любое дальнейшее увеличение приложенной нагрузки приведет к быстрому неустойчивому растрескиванию расширение.

Построение диаграммы остаточной прочности следует три шага, представленные в Разделе 4.3.1. Однако из-за сложности конструктивной геометрии оценка требует расчета нагрузок, которые передаются на элементы жесткости или второстепенные элементы от основного несущего элемента конструкции. В зависимости от сложности кривые K против a могут быть получены либо соответствующим численным методом или методом суперпозиции. Методы построения диаграммы остаточной прочности и для анализа остаточной прочности далее обсуждаются в следующих разделах с различными примерами проблем.

Диаграмма предела выносливости по Хею и Смиту

Диаграммы предела выносливости по Хею или Смиту показывают максимальную амплитуду предела текучести как функцию среднего напряжения.

Диаграммы предела усталости

Хотя кривая Вёлера подходит для оценки испытаний на усталость, она неинформативна для инженера. Например, кривая Велера применима только к определенному среднему напряжению. Однако для динамически нагруженных компонентов среднее напряжение на практике часто меняется, что, в свою очередь, влияет на усталостную прочность. Чтобы показать влияние среднего напряжения на усталостную прочность, в диаграмму напряжения-цикла необходимо было бы включить много других кривых для самых разных средних напряжений. Четкость от этого сильно пострадает.

Рисунок: Кривая напряжения-цикла (кривая Вёлера)

По этой причине используются специальные диаграммы, чтобы более наглядно проиллюстрировать влияние среднего напряжения. Наиболее важными диаграммами являются диаграммы, введенные Хэем и Смитом. Если за основу в таких диаграммах брать предел выносливости, то говорят о диаграммах предела выносливости . Если, с другой стороны, в качестве основы используется определенное количество циклов нагрузки, которые необходимо выдержать, говорят о диаграммах усталостной прочности.

Диаграмма Хейя (диаграмма Гудмана)

На диаграмме предела усталости по Хэю амплитуда переносимого напряжения прикладывается непосредственно к среднему напряжению. Такая диаграмма Хея также называется диаграммой Гудмана . Пересечение кривой с вертикальной осью соответствует пределу знакопеременной усталости \(\sigma_{fa}\), так как среднее напряжение здесь равно нулю (коэффициент напряжения \(R=-1\)). Однако пересечение кривой с горизонтальной осью можно интерпретировать как предел прочности при растяжении 9.0214 \(\sigma_u\), так как теоретически образец мог бы разрушиться без существующей амплитуды напряжения, т.е. исключительно из-за приложенного среднего напряжения (коэффициент напряжения \(R=1\)).

Рисунок: Кривая Хея и ее аппроксимация линией Гудмана
Кривая Хея («кривая предела усталости») проходит между вышеупомянутыми точками. Под кривой предела усталости находятся допустимые амплитуды напряжения для данного среднего напряжения. Для упрощения построения диаграммы к кривой Хея приближается прямая линия, так называемая Линия Гудмана . Это приближение приводит к своего рода «естественному запасу прочности», поскольку линия Гудмана проходит ниже кривой Хея. Таким образом, фактически переносимые амплитуды стресса несколько больше, чем предполагает линия Гудмана.
Особенно при высоких средних напряжениях кривая Хея или линия Гудмана имеют только теоретическое значение, поскольку предел текучести уже превышен в этом диапазоне, что приводит к неприемлемым пластическим деформациям. Таким образом, практический предел распространяется не на предел прочности при растяжении \(\sigma_u\), а только на предел текучести \(\sigma_y\) (или на предел текучести при смещении).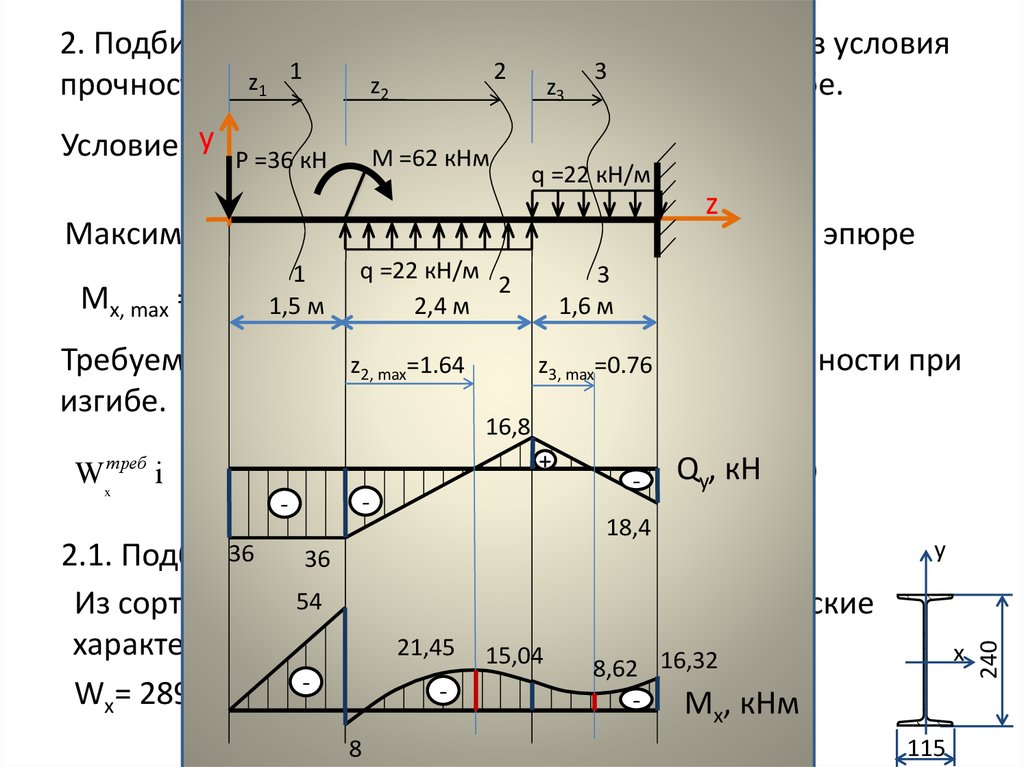
Рисунок: Создание диаграммы усталостной выносливости по Хэю (диаграмма Хейга)
В принципе, сумма среднего напряжения и амплитуды напряжения никогда не должна превышать значение предела текучести. Исходя из значения предела текучести, амплитуда напряжения теоретически может быть увеличена в той же степени, в какой снижается среднее напряжение. По этой причине дополнительным ограничением является прямая линия под углом 45°, которую также называют линией текучести .
Таким образом, на диаграмме получаются две прямые линии (линия Гудмана и линия текучести), которые ограничивают технически допустимое диапазон усталостной выносливости . На практике, поэтому, только знание предела переменной усталости \(\sigma_{fa}\), предела прочности при растяжении \(\sigma_u\) и предела текучести \(\sigma_y\) (или предела текучести при смещении) достаточно для построения упрощенной диаграммы Хея.
Как создать диаграмму Хея
Диаграмма Хея получается путем проведения линии Гудмана от точки знакопеременного предела усталости \(\sigma_{fa}\) по оси Y до точки предела прочности при растяжении \(\ sigma_u\) по оси x. Затем значение предела текучести отмечают по обеим осям и соединяют прямой линией (линии текучести). Гудман и линия текучести теперь отмечают область предела усталостной выносливости.
Чтобы облегчить определение предела выносливости для заданного отношения напряжений \(R\), на диаграмму часто включают выбранные отношения напряжений. Теперь для каждого среднего напряжения на диаграмме Хея можно легко увидеть допустимую амплитуду напряжения для непрерывной работы материала.
Рисунок: Диаграмма Хея с выбранными отношениями напряжений
Расширение диаграммы Хейя для средних сжимающих напряжений
В принципе, диаграмму Хейя можно также расширить до отрицательных средних напряжений, и таким образом можно показать пределы усталости для сжимающих нагрузок. Затем предел текучести при сжатии \(\sigma_{cy}\) используется в качестве предельного значения для среднего напряжения. Это значение вводится по обеим осям так же, как и для напряжения растяжения, а затем соединяются друг с другом прямой линией. Экстраполяция прямой Гудмена ограничивает область. Однако всегда ли допустима эта экстраполяция линии Гудмана, нужно проверять отдельно! Для консервативной оценки этот отрезок также можно считать горизонтальным в первом приближении.
Рисунок: Диаграмма усталостной выносливости по Haigh
Обратите внимание, что из-за эффекта «закрытия трещин» пределы выносливости при сжимающих нагрузках в целом выше, чем при растягивающих нагрузках. Этот эффект особенно заметен при отливке пластинчатого графита, поскольку графитовые пластины допускают лишь относительно низкие растягивающие напряжения из-за их надрезного эффекта. Напротив, чугун с пластинчатым графитом намного лучше поглощает сжимающие напряжения.
Диаграмма Смита
Помимо диаграммы Хея, предел усталости можно также проиллюстрировать на диаграмме, разработанной Смитом. В таком Диаграмма Смита , минимальное напряжение \(\sigma_{min}\) и максимальное напряжение \(\sigma_{mas}\) нанесены в зависимости от среднего напряжения \(\sigma_m\). Исходя из фундаментальных соображений, снова возникают некоторые неподвижные точки.
Рисунок: Создание диаграммы усталостной выносливости по Смиту (диаграмма Смита)
Как построить диаграмму Смита
При среднем напряжении \(\sigma_m=0\) знакопеременный предел усталости \(\sigma_{fa} \) материала, так что значение максимального напряжения равно \(+\sigma_{fa}\), а минимальное напряжение равно \(-\sigma_{fa}\). Другая фиксированная точка возникает, когда среднее напряжение достигает предела прочности при растяжении (\(\sigma_m=\sigma_u\)). В этом случае материал больше не может выдерживать амплитуду напряжения, так как в противном случае предел прочности на растяжение будет превышен. Следовательно, максимальное и минимальное напряжения также соответствуют пределу прочности. Это означает, что кривые для максимального и минимального напряжения должны проходить до этой точки, начиная с точек знакопеременного предела выносливости.
Для упрощения кривые максимального и минимального напряжения могут быть снова аппроксимированы как линии Гудмана .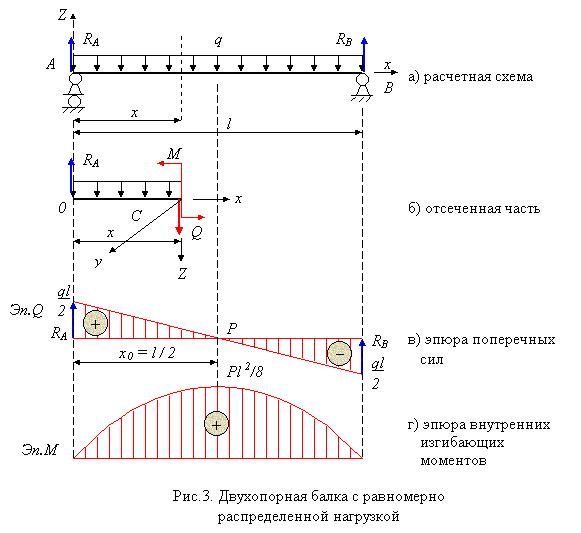 Из практических соображений есть и дополнительное ограничение, так как пока на диаграмме учитывается только критерий разрушения. Однако обычно решающими являются недопустимые деформации, возникающие при напряжениях выше предела текучести . Поэтому линии Гудмана работают только до максимального значения предела текучести. Это относится как к максимальному напряжению (точка A), так и к среднему напряжению (точка B), так как, конечно, среднее напряжение не должно также превышать предел текучести.
Рисунок: Диаграмма Смита
Как только достигается предел текучести в точке А, линия максимального напряжения продолжается как горизонтальная линия. Однако это приводит к соответствующей корректировке минимального напряжения, поскольку амплитуды напряжения до максимального и минимального напряжения должны быть симметричны среднему напряжению. Для этой корректировки расстояние от точки А до линии среднего напряжения симметрично смещается вниз и достигается линия минимального напряжения Гудмана (точка С). Две линии Гудмана и полилиния точек A, B и C теперь ограничивают технически значимый диапазон усталостной выносливости.
На диаграмме Смита допустимое максимальное и минимальное напряжение для долговечной усталостной эксплуатации материала теперь можно считать непосредственно для каждого среднего напряжения. Используя вспомогательную линию под углом 45 градусов, можно относительно легко определить амплитуду напряжения как расстояние до линии Гудмана.
Дополнительную информацию о создании диаграммы Смита также можно найти на сайте construccionenacero.com.
Расширение диаграммы Хея для средних сжимающих напряжений
Расширение диаграммы Смита до отрицательных значений среднего напряжения (сжатие) также легко возможно. Вместо ограничения максимального напряжения пределом текучести при растяжении для ограничения минимального напряжения (точка D) используется предел текучести при сжатии \(\sigma_{cy}\). Среднее напряжение также ограничивается пределом текучести при сжатии (точка E).