Расчет рам. Жемочкин Б.Н. 1965 | Библиотека: книги по архитектуре и строительству

Расчет рам

Жемочкин Б.Н.

Стройиздат. Москва. 1965

406 страниц

Содержание: 

В книге изложены основные методы расчета плоских рам: сил, деформаций, моментных и угловых фокусов. Кратко излагается теория каждого метода и дается полное решение характерных числовых примеров инженерного расчета с построением эпюр внутренних сил. Помимо простых рам рассмотрены сложные многопролетные многоэтажные рамы с ломаными и криволинейными элементами. Кроме того, приводятся основные теоремы о деформациях упругих систем. Описаны некоторые из приближенных методов расчета. Книга предназначена для инженеров-проектировщиков, студентов вузов и аспирантов.

От издательства
Из предисловия автора к 1-му изданию
Введение. Понятие о рамах

Глава I. Общие сведения, основные теоремы о деформациях. Понятие о расчете рам

§ 1. Работа внешних сил
§ 2. Работа внутренних сил
§ 3. Зависимость между работой внешних и внутренних сил. Принцип Лагранжа. Теорема Мора
§ 4. Дополнительная и полная работа
§ 5. Перемещения. Определение перемещений аналитическим путем
§ 6. Теорема о взаимности перемещений
§ 7. Определение перемещений перемножением эпюр
§ 8. Потенциальная энергия
§ 9. Теорема о взаимности работ. Теорема Бетти
§ 10. Зависимость между потенциальной энергией, внешними силами и перемещениями. Теорема Кастилиано
§ 11. Различные способы расчета рам
§ 12. Применение на практике различных способов расчета

Глава II. Способ сил
§ 13. Общий порядок расчета рам способом сил
§ 14. Примеры расчета рам с одной лишней неизвестной
§ 15. Примеры расчета рам с двумя лишними неизвестными
§ 16. Примеры расчета рам с тремя лишними неизвестными
§ 17. Эпюры поперечных и продольных сил
§ 18.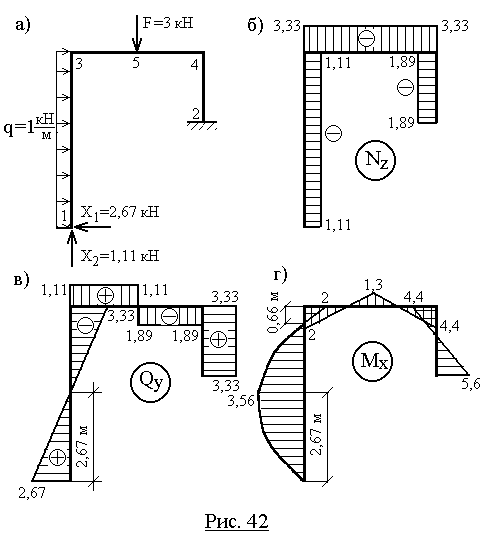

Объемлющие (огибающие) эпюры
§ 19. Упругий центр тяжести
§ 20. Примеры использования упругого центра тяжести
§ 21. Системы со многими неизвестными. Использование симметрии
§ 22. Групповые неизвестные
§ 23. Примеры расчета рам со многими неизвестными
§ 24. Поверка правильности построения эпюр
§ 25. Составление уравнений при помощи теорем Бетти, Мора и Кастилиано
§ 26. Решение уравнений
§ 27. Способ нулевых эпюр
§ 28. Пример расчета рамы способом нулевых эпюр
§ 29. Подбор нулевых вспомогательных эпюр
§ 30. Примеры расчета рам подбором нулевых вспомогательных эпюр
§ 31. Действие температуры
§ 32. Примеры расчета рам на действие температуры
§ 33. Линии влияния
§ 34. Примеры на построение линий влияния

Глава III. Способы трех и четырех моментов
§ 35. Уравнение трех моментов для неразрезной балки

§ 36. Расчет рам способом трех моментов
§ 37. Пример расчета рамы способом трех моментов
§ 38. Уравнение четырех моментов
§ 39. 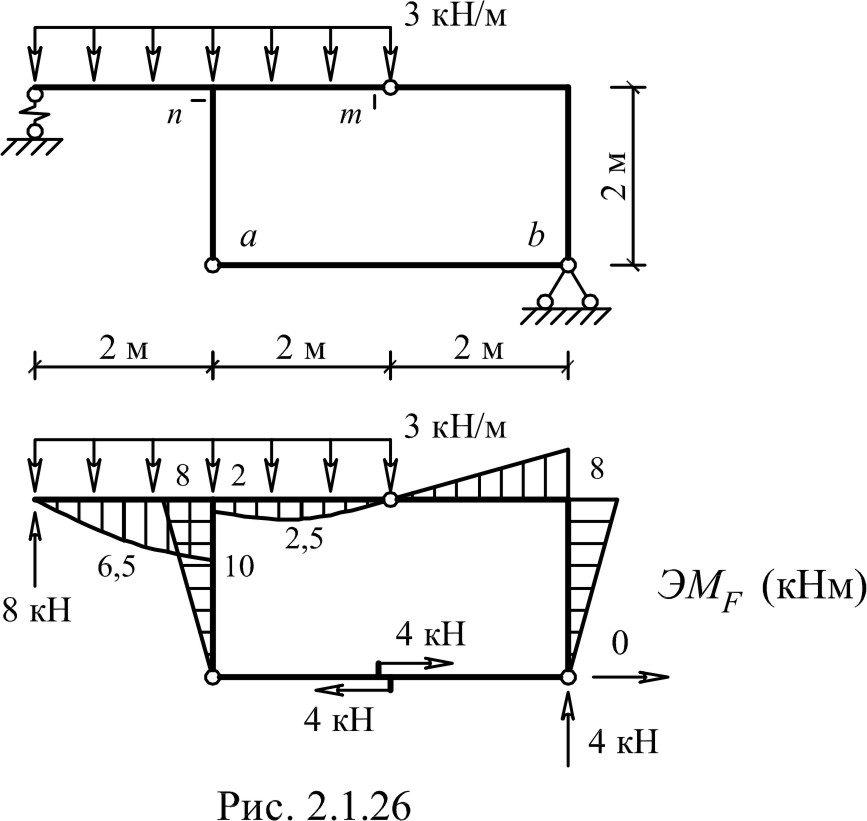Общий порядок расчета рам способом четырех моментов
§ 40. Пример расчета рамы способом четырех моментов

Глава IV. Способ моментных фокусов
§ 41. Общий порядок расчета рам способом моментных фокусов
§ 42. Фокусные отношения. Коэффициенты распределения
§ 43. Моменты по концам загруженного элемента
§ 44. Моменты по концам повернувшегося элемента
§ 45. Примеры расчета рам способом моментных фокусов

Глава V. Способ деформаций
§ 46. Условные обозначения. Правило знаков
§ 47. Общий порядок расчета рам способом деформаций
§ 48. Моменты
§ 49. Поперечные силы
§ 50. Зависимость между линейными смещениями. Диаграммы

§ 51. Основные уравнения угловых деформаций
§ 52. Дополнительные уравнения
§ 53. Примеры расчета рам способом угловых деформаций
§ 54. Решение уравнений способом последовательных приближений
§ 55. Действие температуры
§ 56. Примеры расчета рам на действие температуры
§ 57. Расчет рам с криволинейными и ломаными элементами
§ 58. Пример расчета рамы с криволинейным элементом
§ 59, Линии влияния
§ 60. Примеры на построение линий влияния
§ 61. Применение общего приема для составления уравнений
§ 62. Пример расчета рамы при помощи групповых неизвестных деформаций
§ 63. Смешанные способы
§ 64. Пример расчета рамы смешанным способом

Глава VI. Способ угловых фокусов
§ 65. Общий порядок расчета рам способом угловых фокусов
§ 66. Фокусные отношения
§ 67. Углы поворота по концам загруженного элемента

§ 68. Углы поворота по концам повернувшегося элемента
§ 69. Примеры расчета рам способом угловых фокусов
§ 70. Расчет рам с непараллельными стойками
§ 71. Пример расчета рам с непараллельными стойками

Глава VII. Приближенные способы расчета
§ 72. Постановка вопроса. Случаи применения приближенных способов
§ 73. Простейшие способы расчета рам на вертикальную нагрузку
§ 74.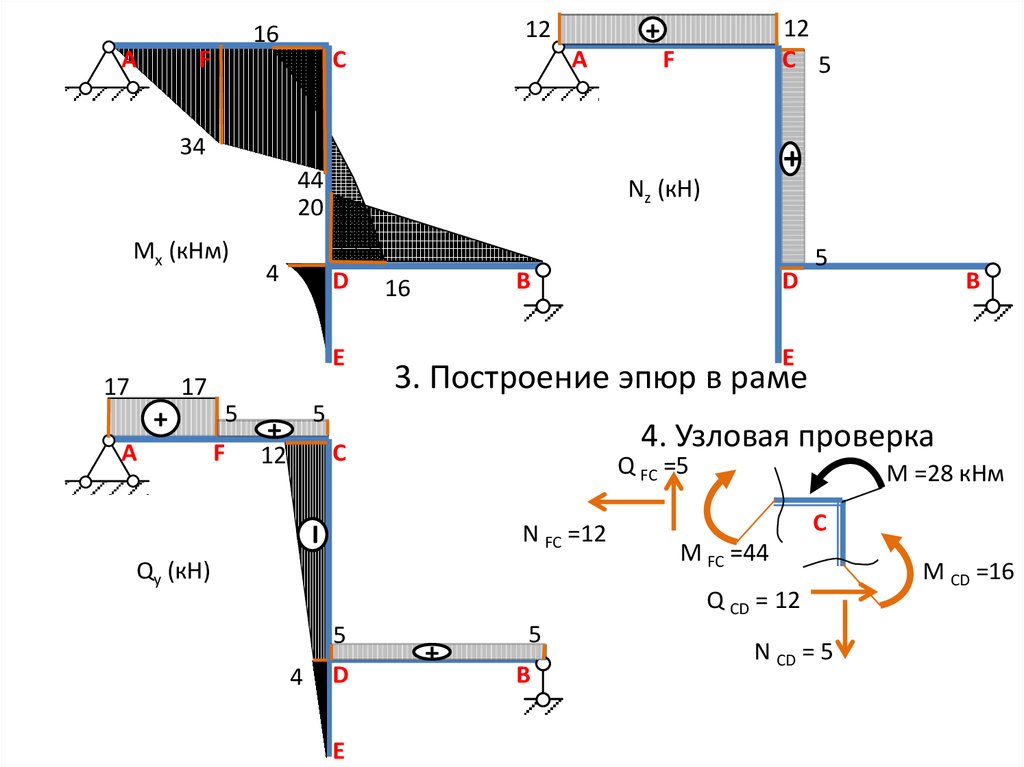 Учет изгиба стоек в многоэтажных рамах при вертикальной нагрузке
§ 75. Примеры расчета рам простейшими способами
§ 76. Более точные способы расчета многоэтажных и многопролетных рам на вертикальную нагрузку
§ 77. Пример расчета рамы более точным способом
§ 78. Расчет рам на горизонтальную нагрузку
§ 79. Пример расчета рамы на горизонтальную нагрузку

От издательства

Предыдущее, первое издание книги профессора Бориса Николаевича Жемочкина (1887—1961 гг.) вышло в свет в 1933 г. в качестве учебного пособия для высших строительных учебных заведений. Эта работа нашла широкое применение не только в учебном процессе; она явилась наиболее полным специализированным пособием для инженеров-проектировщиков в их повседневной деятельности и оказала сильное влияние на дальнейшее развитие методов расчета статически неопределимых систем.

Необходимость нового издания книги «Расчет рам», пользующейся и до настоящего времени большой популярностью, подсказывается прежде всего тем, что здесь компактно изложен учебный курс предмета и дано достаточное число примеров, хорошо разъясняющих вопросы теории. Помимо так называемых классических, основных методов расчета (сил, деформаций, трех и четырех моментов, моментных и угловых фокусов — разработкой последнего мы обязаны Б.Н. Жемочкину), являющихся основой для приближенных методов, здесь изложены некоторые из приближенных методов, разработанных автором. Решение примеров доведено до окончательных результатов; объяснения к ним отличаются ясностью и сжатостью изложения. В состав книги входят и вопросы решения систем линейных уравнений — способом Гаусса и последовательными приближениями.

В новом издании книги почти полностью сохранен текст автора, сделаны лишь незначительные сокращения в нем, исключен параграф, касавшийся применения моментов высоких степеней, изъято четыре примера. В главу о способе угловых фокусов добавлен материал, вошедший в специальное пособие автора «Способ угловых фокусов», выпущенное Стройиздатом в 1932 г.

Из предисловия автора к 1-му изданию

В книге изложены различные применяющиеся на практике способы расчета рам. Знание их необходимо всем проектирующим рамные конструкции для того, чтобы из числа имеющихся способов они могли всегда выбрать тот, который в данных условиях позволяет наиболее просто и легко сделать необходимый расчет.

Книга построена таким образом, что в первой главе даны общие понятия и основные теоремы о деформациях упругих систем; каждому способу расчета в дальнейшем посвящена отдельная глава, наконец в последней главе излагаются приближенные способы расчета рам, которыми можно руководствоваться при проектировании как неответственных сооружений, так и ответственных в тех случаях, когда некоторыми факторами вследствие их малого влияния допустимо пренебречь.

Изложение каждого способа расчета сопровождается достаточным количеством практических примеров.

Пример решения задачи №4 — Мегаобучалка

Рамные системы широко применяют в железобетонных, металлических и деревянных конструкциях. Одно- и многоэтажные рамы используют при возведении фабрично — заводских корпусов, общественных зданий, складов, башен элеваторов, мостов, трибун стадионов, для установки механизмов, при устройстве набережных и т.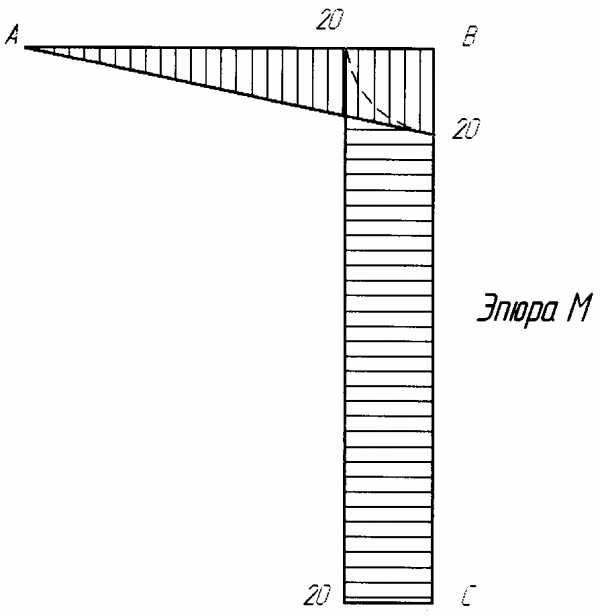 д.

Определение поперечной силы, изгибающего момента, продольной силы, действующих в сечениях рамы, и построение их эпюр является начальной стадией расчета рамных конструкций.

К решению данной задачи можно приступить после изучения темы «Статически определимые плоские рамы». Необходимо иметь в виду, что изучение этой темы невозможно без твёрдых навыков и прочных знаний по теме « Изгиб прямого бруса».

Условие задачи: Для статически определимой рамы построить эпюры Q_Х, М_Х и N. Проверить равновесие узла (рис. 25).

Для рам консольного типа эпюры Q_x, М_х и N могут быть построены без определения опорных реакций заделки, если начинать эти построения со стороны свободного конца.

Условимся при расчете рамы мысленно ставить себя на плоскость чертежа внутрь рамы. Тогда, повернувшись лицом к сечению, в котором определяется внутренний силовой фактор или относительно которого составляется уравнение равновесия, легко представить себе, какую часть рамы следует считать левой, а какую правой. В этом случае при определении внутренних силовых факторов для рам становится возможным пользоваться правилами, применяемыми при построении эпюр для балок.

Рис. 25

Решение: Построение эпюры Q.За ось абсцисс принимаем ось любого стержня. Перпендикулярно ей мысленно проводим ось ординат и проецируем на неё силы, действующие соответственно слева и справа от рассматриваемого сечения, учитывая правила знаков.

Ригель ВС.Ход справа. Поперечную силу определяем по характерным точкам (аналогично простым балкам).

Qв = 0;

Q_D^npaв = q (1 /2) = 4 kH;

Q_D^прав=Q_D^npaв+F =9 kH;

Q_C= Q_D^лев = 9 kH.

Стойка АС.Повернёмся лицом к стойке, проведём мысленно ось перпендикулярно оси стойки и спроецируем на неё силы ходом справа: Q_c = 0; Q_A = 0. Изобразим полученные результаты графически. Проведем ломаную линию ABC (рис.25,6) и от нее, как от нулевой линии, отложим вычисленные ординаты эпюры поперечных сил. Положительные ординаты эпюры для ригеля откладываются вверх от нулевой линии и влево от нулевой линии для стойки. Отрицательные соответственно вниз и вправо от нулевой линии.

Построение эпюры М (рис.25в).Изгибающий момент в сечениях рамы определяем также по характерным точкам ходом справа (со свободного конца).

Ригель ВС. М_В=0;

M_D= -q(l²/8) = -4 kH m;

М_С = — FI / 2 – q*1/2*3/41 = — 22 kH m.

Стойка АС.Как и при определении поперечной силы, при переходе от ригеля к стойке повернёмся на 90°, лицом к стойке. Точка С принадлежит одновременно и ригелю и стойке, поэтому М_С^стойки = М_С^риг = — 22 kH m. Так как в данной задаче непосредственно к стойке не приложены внешние нагрузки, а плечи сил F и Q остаются неизменяемыми, то в любом сечении от С до А изгибающий момент один и тот же. М_А = М_С = -22 kH m. При построении эпюры изгибающих моментов (как и в балках) положительные ординаты откладываем со стороны растянутых волокон.

Построение эпюры N (рис.25г). Определяя продольную силу, проецируем заданные силы на ось абсцисс, совмещая её сначала с ригелем, затем со стойкой. Продольная сила в любом сечении ригеля равна нулю, N_CВ= 0, так как справа от сечения действует нагрузка, перпендикулярная его оси. Продольная сила во всех сечениях стойки постоянна, так как сама стойка не нагружена и на ось стойки дают проекцию силы F и 2q. N_СА = — F — 2q = — 9 kH. Ординаты эпюры продольных сил откладываем симметрично по обе стороны от оси рассматриваемого элемента. Знак плюс, поставленный на эпюре N, соответствует деформации растяжения, знак минус — сжатия.

Для проверки правильности построения эпюр рассмотрим равновесие узла С. Для этого мысленно вырежем этот узел, проведя два сечения на бесконечно близком расстоянии, в ригеле справа от узла, в стойке — слева от него.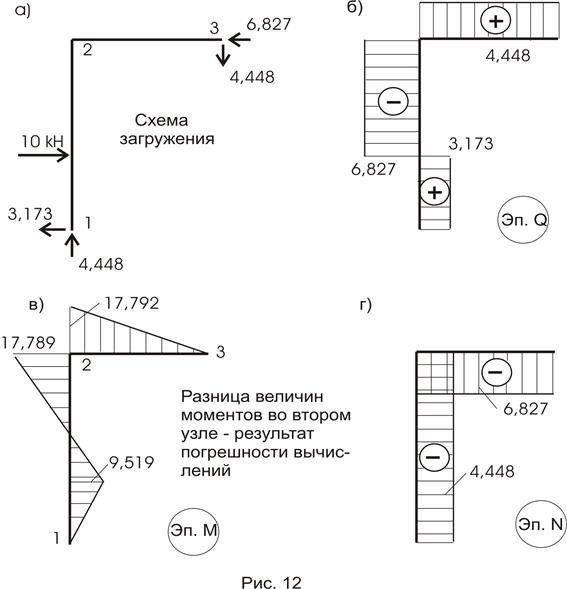

Вырезанный таким образом узел дает возможность, рассматривая сечение в ригеле, считать узел отнесённым к левой части ригеля, а при рассмотрении сечения в стойке — к правой части стойки. Прикладываем к узлу С внутренние силовые факторы Q_x, М_Х и N, беря их значение с эпюр с учетом знака, показывающего направление их действия (рис.25д).

Из эпюры Q_Х видим, что поперечная сила в сечении С ригеля положительна. Поскольку точка С относится к левой части рамы (согласно принятому ранее), Q_риг согласно правилу знаков направляем вниз. На стойке поперечная сила отсутствует.

Из эпюры М_X видим, что изгибающий момент вызывает растяжение верхних волокон. Следовательно, с учетом правила знаков в ригеле изгибающий момент М_C направляем по часовой стрелке, а в стойке (узел С относим к правой части рамы) — против часовой стрелки. Продольная сила N_СА вызывает в сечении сжатие и, следовательно, должна быть направлена в сторону этого сечения.

Для равновесия узла должны соблюдаться следующие условия:

=0; =0; = 0.

Составим эти уравнения, направив ось X вправо, а ось Y вертикально вверх:

= 0 ; = N_ст — Q_pиг = 9-9 =0; = М^стойки — М^риг = 22-22 =0.

Условия равновесия соблюдаются. Следовательно, внутренние силовые факторы определены правильно.

Схемы и методы каркаса дома

Дон Вандерворт, HomeTips © 1997 to 2023

25 октября 2020 г.

Экспертные схемы двух основных типов деревянных каркасных конструкций для стен и крыш домов

В этой статье:

Конструкция платформы
Воздушный каркас
Схема стеновых стоек
Обшивка стен
Обшивка крыши

Для каркаса дома используются два основных метода: конструкция платформы и каркаса баллона. Строительство платформы гораздо более распространено, чем каркас из воздушных шаров, хотя каркас из воздушных шаров использовался во многих двухэтажных домах до 19 века. 30.

Конструкция платформы

В показанной ниже конструкции платформы с рамой стены располагаются поверх чернового пола. Многоэтажные дома строятся по одному уровню за раз, при этом каждый этаж служит платформой для возведения следующей серии стен.

Каркас дома с платформой — стойки проходят от пола до потолка для каждого отдельного этажа.

Каркас из воздушных шаров

В показанной ниже конструкции каркаса из воздушных шаров стойки проходят по всей высоте от глиняного подоконника до верхней плиты, максимум до 20 футов. Этот метод был популярен до 19 века.30-х годов и до сих пор иногда используется для оштукатуренных и других двухэтажных домов с каменными стенами, потому что такие конструкции сжимаются и оседают более равномерно, чем конструкции на платформе.

Но каркас из воздушных шаров более опасен для возведения из-за его веса и высоты, а необходимые длинные прямые стойки для стен становятся все более дорогими, и их трудно найти.

Каркас дома из воздушных шаров — каркасы стен проходят по всей высоте здания

Компоновка каркасов стен и каркасов

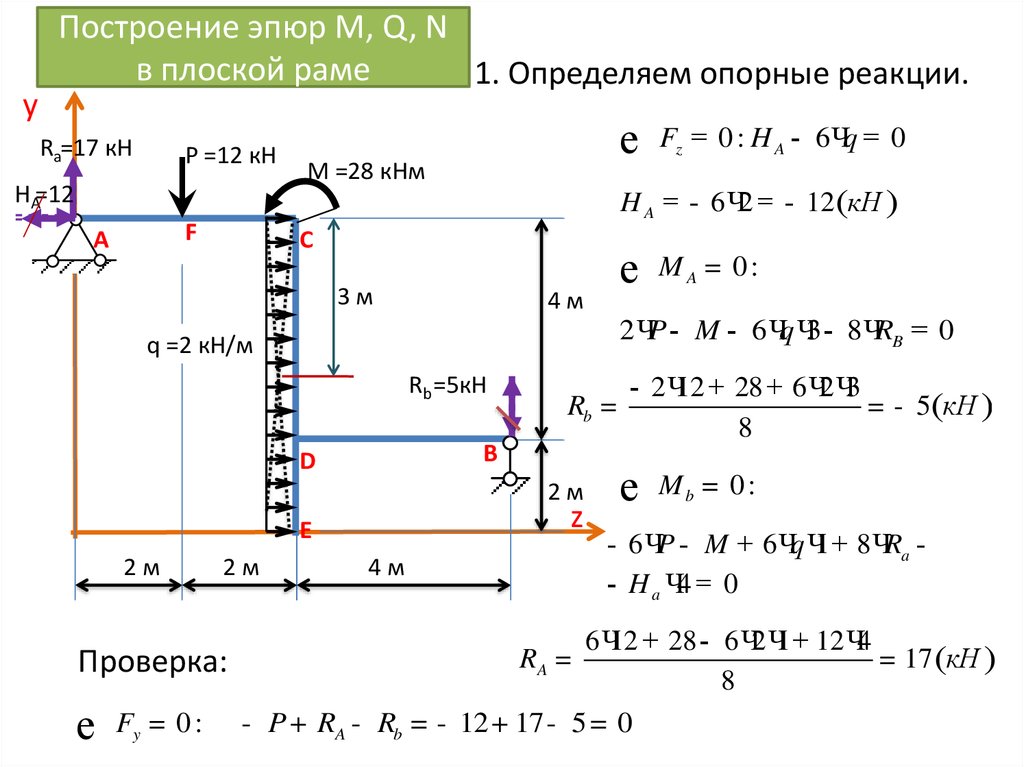При каркасном каркасе как с платформой, так и с шаровидным каркасом стойки стен, а также потолочные и напольные балки располагаются через каждые 16 или 24 дюйма, измеренные от центра к центру. Эти стандартизированные макеты приводят к наименьшему количеству резки и отходов материалов для пола, потолка и стен.

Обычный каркас стеновых стоек — Стеновые стойки расположены на расстоянии 16 или 24 дюймов от центра к центру. многие новые дома имеют стенные стойки размером 2 на 6, размером 16 или 24 дюйма в центре, чтобы укрепить внешние стены и создать большую полость для изоляции стен. Для получения дополнительной информации о каркасе стены см. Как построить внутреннюю стену.

Обшивка стен

Обшивка наружных стен повышает жесткость конструкции и обеспечивает плоскую основу для облицовки сайдингом, штукатурки, кирпича, камня и других видов отделки наружных стен. В старых домах обшивка из диагональных досок — доски толщиной 1/2 дюйма, прибитые по диагонали. Большинство новых домов имеют обшивку из фанеры или аналогичных композитных панелей. Подробнее об этом читайте в разделе Обшивка наружных стен.

Каркас крыши и обшивка

Каркас крыши может быть довольно сложным, в зависимости от сложности конструкции крыши. Ниже представлен каркас двускатной крыши.

Наружная обшивка крыши служит тем же целям для кровельных материалов, что и стеновая обшивка стен. Большинство современных обшивок крыш представляют собой либо фанеру, либо панели из ориентированно-стружечных плит (OSB); Деревянная обшивка с интервалами является обычным явлением для деревянных крыш из гонта. Для получения дополнительной информации об этом см. Основы строительства крыши.

Типовой каркас крыши — это остроконечная вальмовая крыша с одним фронтоном и мансардным окном 9.0002 Получить предварительно проверенного местного подрядчика по возведению каркаса дома

Фасады, планы каркаса, разрезы стен и схемы теней

Помимо планов местности и этажей, существует несколько других типов диаграмм, которые вы, вероятно, увидите в поддержку проекта нового дома. Все это помогает убедиться, что дом построен правильно, а также передать идеи, намерения и детали архитектора или проектировщика.

Среди прочего, эти планы включают фасады, планы каркаса, разрезы стен и схемы теней.

Что такое высоты?

Фасады — это схемы, на которых в масштабе и в деталях показано, как будет выглядеть определенная сторона здания. Например, фасад может быть подробным чертежом фасада дома, показывающим, как он будет выглядеть с улицы, с окнами, облицовкой, дверями, кустами и так далее. Диаграммы высот также могут использовать некоторые цвета и текстуры, чтобы дать более четкое представление о том, как дом должен выглядеть.

Фасады также используются для детального просмотра определенных аспектов интерьера (например, разреза кухни) – в частности, для демонстрации расположения светильников, дверей, шкафов и т.п.

Эти типы диаграмм рисуются путем разметки параллельных и перпендикулярных линий от ключевых точек на заданной стороне плана этажа, которые, вероятно, будут видны со стороны рисуемого здания (например, углы, наружные лестницы, двери). , окна, дымоходы и т. д.), а затем с помощью этих линий изобразить диаграмму на плоском виде сбоку.

Что такое планы?

План каркаса — это план, на котором показаны места, материалы (например, сталь, древесина), размеры, расстояния и количество конструктивных элементов, которые будут использоваться для строительства вашего дома. Обеспечение того, чтобы каркас был построен так, как он задуман, очень важно с инженерной точки зрения, и вполне вероятно, что для полов, крыш и стен будут нарисованы отдельные планы каркаса.

Кроме того, что показано, как устроены такие элементы, как опоры, балки, стропила, связи, балки и подкосы, планы каркаса также будут содержать дополнительные подробные чертежи, где они необходимы, чтобы показать, как различные элементы должны быть закреплены, соединены и закреплены. пристегнут.

Планы каркаса обычно очень конкретны в отношении того, что требуется, по уважительной причине. Например, разные производители окон производят окна разных размеров, поэтому точное указание того, что требуется на этом этапе, помогает убедиться, что соответствующие размеры понятны и что грубые проемы подходят правильно.

Что такое секция стены?

Схемы разрезов (или разрезы стен, или просто «разрезы») являются одним из наиболее важных инструментов, используемых подрядчиком при строительстве вашего дома.

Разрез — это буквально схема поперечного сечения данной части дома, показывающая, что и куда идет.

Схема в разрезе очень подробно покажет, из чего сделаны фундаменты, стены, системы полов и крыши и как они сделаны. Сюда входят такие сведения, как:

• специальные строительные материалы
• обшивка
• требования к изоляции
• высоты
• размеры и глубина рамы
• вентиляционные отверстия
• форма и конструкция карниза
• шаг кровли
• …и многое другое.

Участок стены, скорее всего, будет сопровождаться множеством дополнительных примечаний, подробно объясняющих множество различных вещей, для отображения которых он предназначен, и будет использовать те же штриховки, символы и сокращения, которые вы видите на других планах.

Что такое теневая диаграмма?

Диаграмма теней — это, по сути, план участка и прилегающих территорий, показывающий тени, которые строящийся дом будет отбрасывать в разное время года, в частности, в период зимнего солнцестояния, когда тень от него отбрасывается. вероятно, будет самым длинным.

Схемы теней часто требуются местным советом для целей планирования, чтобы продемонстрировать, что структура, которую вы хотите построить, не будет препятствовать попаданию солнечного света на окружающие объекты. Это особенно важно в районах с небольшими кварталами, где дома строятся вблизи границ или где вы строите многоэтажный дом.

По мере того, как все больше людей устанавливают солнечные панели и важность доступа к солнечному свету как средства экономии энергии становится все более важной, учет теней становится все более важным. Диаграммы теней также являются хорошим способом понять, как будут затенены ваши собственные открытые пространства.

Что такое зеркальный план потолка?

В некоторых случаях, когда на потолке предусмотрены молдинги или определенные элементы, может также предоставляться «отражающий план потолка» (RCP). Это вид того, как потолок будет выглядеть снизу, но «отраженный», чтобы его можно было наложить на план этажа, чтобы указать, куда все пойдет.