Расчет статически неопределимой рамы методом сил

    Для рамы, выбранной согласно варианта, требуется :

    1. Используя индивидуальный шифр, выбрать : расчётную схему рамы, её размеры, жёсткость стержней, действующую нагрузку.

    2. Установить степень статической неопределимости и выбрать основную систему.

    3. Написать каноническое уравнение в общем виде.

    4. Построить в основной системе эпюры Mi от единичных сил и эпюру MF от заданной нагрузки.

    5. Найти коэффициенты и свободные члены канонических уравнений. Сделать проверку правильности нахождения их.

    6. Решить систему канонических уравнений и сделать проверку решения.

    7. Построить окончательную эпюру М. Выполнить статически и кинематическую проверки эпюры М.

    8. По окончательной эпюре М построить эпюру Q.

    9. По Q построить эпюру N.

    10. Выполнить статическую проверку равновесия системы в целом.

    Дано :

№ схемы	a,     м	b,     м	с,     м	d,     м	α	β	γ	F1,    кН	F2,   кН	q1,  кН/м	q2, кН/м
3	3. 8	5.2	4.2	2.1	3	4	2	0	21	0	8

 

                                                                   Решение.

1. Расчётная схема.

    2. Установим степень статической неопределённости и выберем основную систему.

    Степень статической неопределимости (количество лишних связей определим по формуле :

             Л=2Ш+С0-3Д=2×0+5-3×1=2

    где Ш=0 – количество шарниров, соединяющих диски с учётом их кратности ; С0=5 – количество опорных стержней ; Д=1 – число дисков в системе.

    Основную систему (О.С.) примем, как показано на рисунке 1.

    3. Система канонических уравнений имеет вид :

                                                          (1)

    Коэффициенты при неизвестных и свободные члены канонических уравнений (1) определим по формулам :

             δii=  ;  δik=δki=  ;  Δip=          (2)

    4. Строим в основной системе эпюры Mi от единичных сил и эпюру MP от заданной нагрузки.

    На рисунке 2 приведена эпюра изгибающих моментов при нагружении основной системы силой X1=1

    Реакции опор : Mh2=X1(2b+a)=14.2 м ; Yh2=X1=1 м

    Участок AB : M1=0

    Участок BC : M2=0

    Участок BD : M3=X1x3, где 0<x3<a+b ; MB=0 ; MD=(a+b)X1=9 м

    Участок DE : M4=(a+b)X1 ; MD=ME=9 м

    Участок EF : M5=Mh2-Yh2x5, где 0<x5E=Mh2-Yh2b=14.2-5.2=9 м ;

                                                                           MF=Mh2=14.2 м

    Участок FN : M6=0

    Участок FH : M7=Mh2=14.2 м.

    На рисунке 2 приведена эпюра изгибающих моментов при нагружении основной системы силой X2=1.

    Реакции опор : Xh3=X2=1 м

    Участок AB : M1=X2y1, где 0<y1<c+d ; MA=0 ; MB=X2(c+d)=6.3 м.

    Участок BC : M2=0

    Участок BD : M3=X2(c+d)=6.3 м

    Участок DE : M4=Xh3y4, где c<y4<c+d ; MD=Xh3(c+d)=6.3 м ; ME=Xh3c=4.2 м

    Участок EF : M5=Xh3c=4.2 м

    Участок FN : M6=0

    Участок FH : M7=Xh3y7, где 0<y7<c ; MF=Xh3c=4.2 м ; MH=0

 

     На рисунке 3 приведена эпюра изгибающих моментов основной системы от заданной нагрузке.

    Реакции опор :  ΣmH=0 ;

                               MH+0.5q2a2-F2c+0.5q2(c+d)2-F2(2b+2a)=0

                                 MH=

                                кН·м

           ΣYk=0 ; YH-q2a-F2=0 ; YH=q2a+F2=8×3.8+21=51.4 кН

           ΣXk=0 ; XH+F2-q2(c+d)=0 ; XH=q2(c+d)-F2=8×(4.2+2.1)-21=29.4 кН

    Участок AB : M1=-0.5q2y12, где 0<y1<c+d ; MA=0 ;

                              MB=-0.5q2(c+d)2=-0.5×8×(4.2+2.1)2=-158.

76 кН·м

    Участок BC : M2=-F2x2, где 0<x2<a ; MC=0 ; MB=-F2a=-21×3.8=-79.8 кН·м

    Участок BD : M3=-F2x3-0.5q2(c+d)2, где a<x3<2a+b ;

                 MB=-F2a-0.5q2(c+d)2=-21×3.8-0.5×8×(4.2+2.1)2=-238.56 кН·м ;

                 MD=-F2(2a+b)-0.5q2(c+d)2=-21×(2×3.8+5.2)-0.5×8×(4.2+2.1)2=-427.56 кН·м

    Участок DE : M4=-F2(2a+b)-0.5q2(c+d)2

                 MD=-F2(2a+b)-0.5q2(c+d)2=-21×(2×3.8+5.2)-0.5×8×(4.2+2.1)2=-427.56 кН·м

                 ME=-F2(2a+b)-q2(c+d)(0.5(c+d)-d)=-21×12.8-8×6.3×(0.5×6.3-2.1)=-321.72 кН·м

    Участок EF : M5=-q2a(x5+0.5a)+YHx5-XHc-MH, где 0<x5<b

                  ME=-q2a(b+0.5a)+YHb-XHc-MH=

                 =-8×3.8×(5.2+0.5×3.8)+51.4×5.2-29.4×4.2-249.68= -321.72 кН·м

                  MF=-0.5q2a2-XHc-MH=-0.5×8×3.82-29.4×4.2-249.68=-430.92 кН·м

    Участок FN : M6=-0.5q2x62, где 0<x6<a ; MN=0 ;

                   MF=-0.5×8×3.82=-57.76 кН·м

    Участок FH : M7=-XHy7-MH, где 0<y7<c ;

                   MF=-29.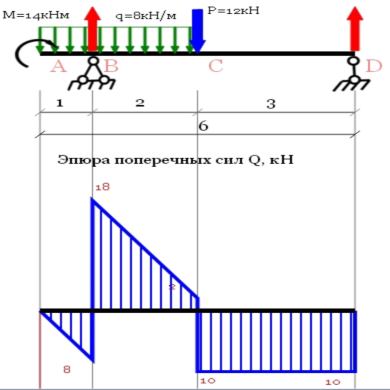 4×4.2-249.68=-373.16 кН·м

                   MH=-249.68 кН·м

    5. Найдём коэффициенты и свободные члены канонических уравнений. Сделаем проверку правильности нахождения их.

    Численные значения коэффициентов при неизвестных и свободных членов уравнений (1) найдём способом перемножения эпюр.

          EJδ11=

               =

              =60.75+85.05+237.143+423.444=806.387

           EJδ22=

     =

         =41.675+89.303+29.327+30.576+12.348=203.229

            EJδ12=EJδ21=

          

 

          EJΔ1p=

         

          EJΔ2p=

          

    Выполним построчные проверки правильности коэффициентов при неизвестных, пользуясь условием :

                              

    где — суммарная единичная эпюра изгибающих моментов, получаемая по зависимости , приведена на рисунке 4.

 

    Перемножение эпюр и выполним пользуясь правилом Верещагина.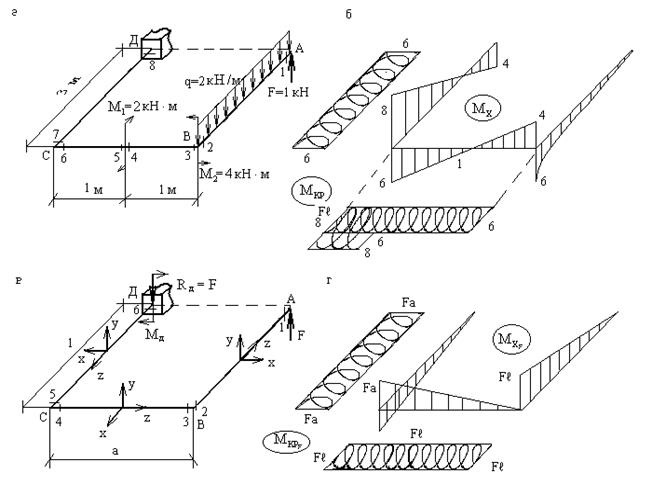

           

           

         

            EJ(δ11+δ12)= 806.387+260.471=1066.858

           

           

             EJ(δ22+δ21)=203.229+260.471=463.7

    Проверим правильность вычисления свободных членов уравнений (1) :

            

            

            

            

            

    =-262.549-1050.197-8412.296-5624.999-10388.172-10750.664=-36488.877

                EJ(Δ1p+Δ2p)=

    Следовательно, коэффициенты δ и Δ определены правильно.

    6. Решим систему канонических уравнений и сделаем проверку решения.

    Подставляя в систему (1) значения, полученных коэффициентов, получим систему :

                 

    Решим, полученную систему.

              Δ= ; Δ1=

              Δ2=

    Тогда : X1= кН ; X2= кН

    Проверку правильности решения системы уравнений произведём путём подстановки полученных значений X1 и X2 в исходные уравнения :

              

    Таким образом, реакции X1 и X2 найдены, верно.

    7. Построим окончательную эпюру М. Выполним статическую и кинематическую проверку эпюры М.

    Окончательная эпюра изгибающих моментов может быть получена по уравнению :

                          M=

    Эпюры изгибающих моментов от фактических значений X1 и X2 приведены на рисунке 5.

    Результирующая эпюра М построена на рисунке 6.

    Проведём проверку правильности окончательной эпюры изгибающих моментов.

    Статическая проверка состоит в том, что проверяем равновесие узла системы под действием изгибающих моментов, приложенных к примыкающим к узлу отсечённым стержням. При этом должно выполнятся условие : ΣMуз=0

     Узел B : ΣMузB=-79.8-0.342+80.142=0

    Узел D :  ΣMузD=29.178-29.178=0

    Узел E :  ΣMузE=2.982-2.982=0

    Узел F :  ΣMузF=57.76-37.732-20.028=0

    Таким образом, равновесие рамы соблюдается.

    Кинематическую проверку выполним по условию :

                  

              

               

    Относительная погрешность вычислений :

                μ=

    Для стержневых систем средней сложности относительная погрешность вычислений должна составлять не более 3%.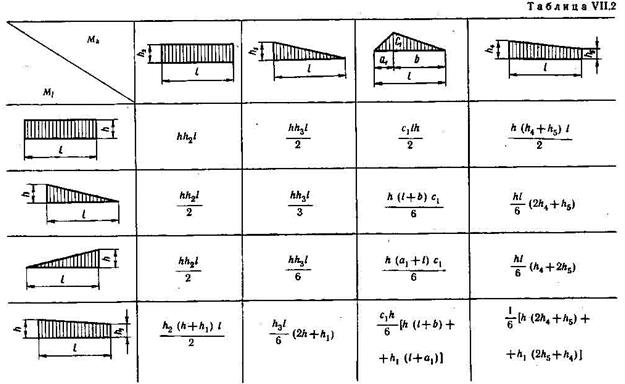

    Статическая и кинематическая проверка выполняются, и, следовательно, окончательная эпюра изгибающих моментов построена – верно.

    8. Построение эпюры Q по эпюре М.

    Для построения эпюры поперечных сил воспользуемся окончательной эпюрой изгибающих моментов М.

    На участках, где эпюра М имеет прямолинейное очертание, поперечная сила численно равна :

                   Q=

    где α – угол наклона эпюры М к оси стержня.

    Если для совмещения с эпюрой изгибающих моментов стержень нужно поворачивать по ходу часовой стрелки, то поперечная сила принимается положительной.

    На участке BC : QBC=tgαBC=  кН

    На участке DB : QBD=tgαBD= кН

    На участке DE : QDE=tgαDE= кН

    На участке EF : QEF=tgαEF= кН

    На участке FH : QFH=tgαFH= кН

    На участках, где эпюра М ограничена параболой, поперечные силы найдём по формуле

                              Qx=                                   (3)

    где — значение поперечной силы в сечениях простой шарнирно опёртой балки.

    Определим поперечную силу Q на участке AB. Для этого определим , рассматривая участок AB как простую шарнирно опёртую балку.

   Реакции балки :

               ΣmB=0  ;  6.3HA-0.5q2·6.32=0  ;  HA=0.5×8×6.3=25.2 кН ; HB=25.2 кН

    На рисунке 7 построена эпюра . 

    Тогда, применяя формулу (3), получим :

                QA= кН

                 QB= кН

    Определим поперечную силу Q на участке FN. Для этого определим , рассматривая участок FN как простую шарнирно опёртую балку.

   Реакции балки :

               ΣmF=0  ;  -3.8VN+0.5q2·3.82=0  ;  VN=0.5×8×3.8=15.2 кН ; VF=15.2 кН

    На рисунке 7 построена эпюра . 

    Тогда, применяя формулу (3), получим :

                QN=

                 QF= кН

 

 

 

 

    Окончательная эпюра поперечных сил приведена на рисунке 8.

    9. По эпюре Q построим эпюру N.

    Эпюру продольных сил N строим по эпюре поперечных сил Q, рассматривая равновесие узлов. Узлы рамы вырезаем в такой последовательности, чтобы каждый рассматриваемый узел содержал не более двух стержней с неизвестными продольными силами. При составлении уравнений равновесия (ΣX=0, ΣY=0) вначале полагаем, что все неизвестные продольные силы являются растягивающими (положительными). Отсечённые узлы рассматриваемой рамы приведены на рисунке 9.

    Узел D : ΣX=0 ; NDB+12.474=0  ;  NDB=-12.474 кН (стержень DB сжат)

                   ΣY=0 ; -NDE-3.28=0  ;  NDE=-3.28 кН (стержень DE сжат)

    Узел Е : ΣX=0 ; -NEF-12.474=0  ;  NEF=-12.474 кН (стержень EF сжат)

    Узел F : ΣX=0  ;  -NFN+NFE-8.521=0  ; NFN=0 (стержень FN не нагружен)

                  ΣY=0 ;   -NFH-30.4-3.278=0  ; NFH=-30.4-3.278=-33.678 кН (стержень FH сжат)

    Узел B : ΣX=0  ;  NBC-NBD-12.479=0 ; NBC=-12.479+12.479=0 (стержень BC не нагружен)

                   ΣY=0 ;  -NBA+3.28-21=0  ;  NBA=-21+3.28=-17.72 кН (стержень BA сжат)

    Окончательная эпюра продольных сил N приведена на рисунке 10.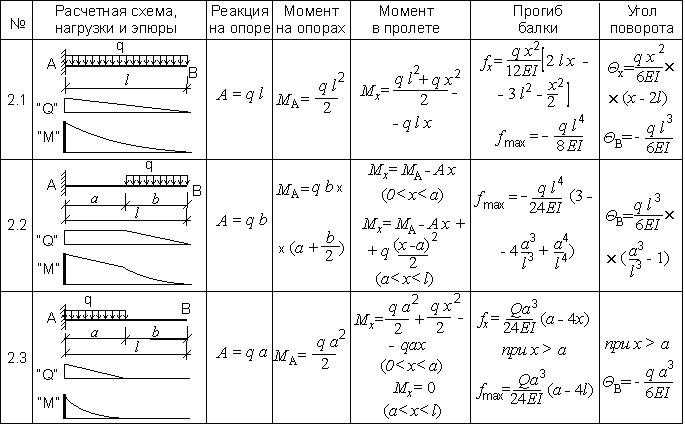

    10. Выполним статическую проверку равновесия системы в целом.

    По эпюрам Q, N и М из условий равновесия опорных узлов получены опорные реакции (рисунок 11) :

                   HH=8.521 кН ; VH=33.678 кН ; MH=1.944 кН·м ;

                   HA=37.921 кН ; VA=17.72 кН

    Для данной системы составляем три уравнения равновесия :

                  ΣX=0  ;  -HH+HA+F2-6.3q2=-8.521+37.921+21-6.3×8=58.921-58.921=0

                  ΣY=0  ;  VH+VA-F2-3.8q2=33.678+17.72-21-3.8×8=51.398-51.4=0

                  ΣmH=0 ;  -MH+0.5q2×3.82-4.2F2-18F2+0.5q2·6.32+14.2VA=0

                 -1.944+0.5×8×3.82-4.2×21-18×21+0.5×8×6.32+14.2×17.72=-468.144+468.144=0

    Таким образом, статические уравнения соблюдаются.

 

 

 

 

 

 

Расчет рам металлоконструкций и решеток катализатора аппаратов нефти и газа читать онлайн бесплатно Константин Владимирович Ефанов

Введение

В практике часто возникает необходимость ручных расчетов на прочность плоских рам, сваренных из стержней металлопроката (прямоугольные пластины, швеллеры, двутавры) от действия нагрузки, приложенной перпендикулярно плоскости рамы. Примерами таких рам являются решетка катализатора в аппаратах нефтепереработки (реакторах и сепараторах), рамах аппаратов в блочном исполнении (аппараты, обвязка и арматура расположены на одной несущей раме, конструкция не относится к объектам капитального строительства), железнодорожных платформах.

В учебной литературе по сопротивлению материалов и строительной механике показан только расчет плоских рам от действия нагрузок, лежащих в плоскости рам и отсутствует методика расчета на нагрузку, приложенную перпендикулярно плоскости рамы. Для того, чтобы применить знания сопротивления материалов для самостоятельной записи выкладок расчета на перпендикулярную нагрузку, необходимо глубокое знание и умение применить расчетные формулы. Это является достаточно трудоемким. Назначение настоящей работы состоит в представлении такой методики для возможности е быстрого применения для расчета рам.

Плоская рама является стержневой системой, т.е. состоящей из тонкостенных стержней конструкцией.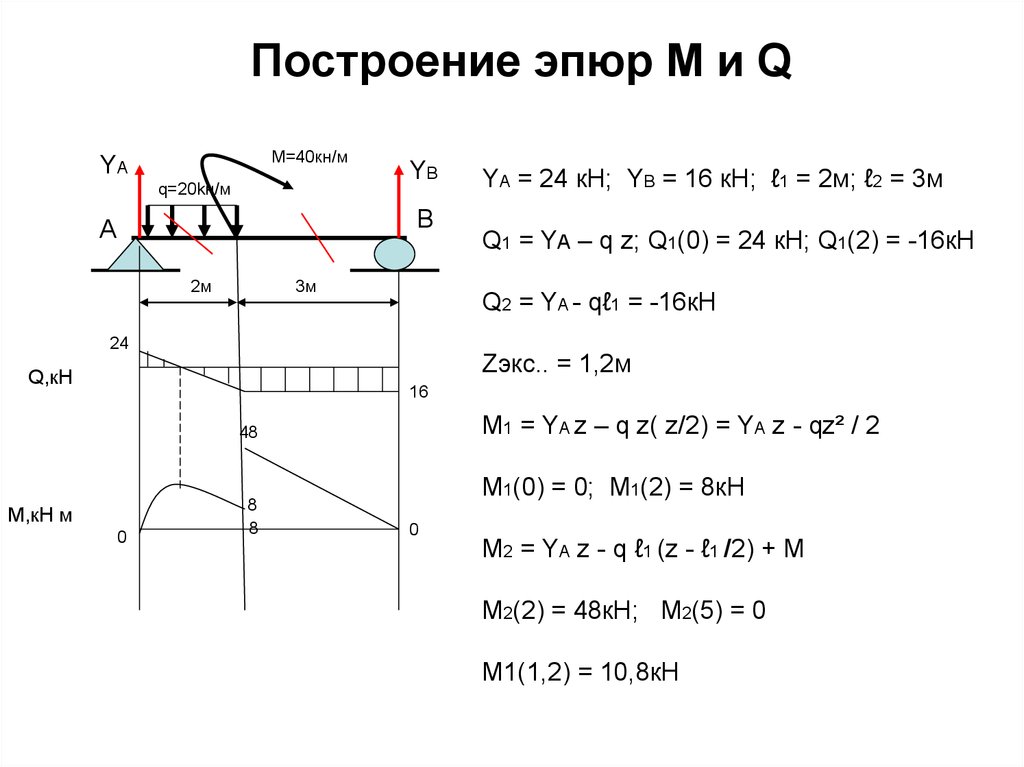 Расчет рамы состоит в расчете тонкостенной стержневой системы. Для строительных металлоконструкций расчет заключается в расчете пространственных стержневых конструкций. Но для строительных конструкций расчет выполняется по предельным нагрузкам, а для машиностроительных изделий по допускаемым напряжениям.

На современной уровне расчеты выполняют методом конечных элементов в специальных компьютерных программах. Строительные конструкции рассчитывают в программах lira, SCAD, Robot и др. В этих же программах можно заложить плоскую раму и выполнит её расчет, но только для рам КМ (конструкций металлических), сваренных из металлопроката. Расчет машиностроительных изделий МКЭ выполняется в программах МКЭ таких как Ansys, SolidWorks Simulation и др. Для расчета таких рам, как рамы платформ, решетки катализатора лучше применять программы МКЭ, предназначенные для расчета машиностроительных изделий. Рама решетки катализатора имеет поперечные балки с прорезями, в которые устанавливаются продольные балки, и такую раму лучше рассчитывать в МКЭ типа Ansys или вручную методом строительной механики (методом сил) или упрощенно методом сопротивления материалов (просто расчет балок на изгиб).

Расчет методом конечных элементов является более теоретически обоснованным по сравнению с методами сопротивления материалов, но последние необходимо знать для понимания поведения конструкции (чувствовать конструкцию) в описании простыми формулами математического аппарата сопротивления материалов. Проектировщик (конструктор) должен иметь представление о распределении напряжений, о виде эпюр усилий и моментов в раме. Для расчетов МКЭ необходимо построение 3D может конструкции, специальные программы, для ручных расчетов достаточно нарисовать схему рамы в тетрадке. Ручной расчет может быть предварительным перед детальным расчетом МКЭ.

В практике автора был случай, когда был доступен только ручной расчет, в том случае это был единственный способ подтвердить прочность конструкции решетки катализатора.

В решетках катализатора нагрузка складывается от действия веса катализатора и действия усилия от давления на поверхность катализатора. Как правило действие давления превышает действие веса катализатора. Например, в случае возможности образования давления в нижней части сепаратора, в верхней части катализатора устанавливают верхнюю решетку для избежание подъёма катализатора так как усилие от давления намного выше усилия веса катализатора на нижнюю решетку (рассматривается подъем всего цилиндрического объема катализатора под действием давления).

Для решеток катализатора расчет заключается в расчете:

– несущих балок на изгиб и кручение с проверкой условия прочности по теории энергетической теории прочности, опирающихся на пояс, приваренный изнутри к обечайке корпуса аппарата;

– решеток катализатора, опирающихся на несущие балки, на которые опирается сетка Джонсона;

– расчете прутьев сетки Джонсона, на которой находится катализатор (или непосредственно или сначала фарфоровые шары для выравнивания потока среды через катализатор).

Для несущих платформ блоков нефтяных аппаратов нагрузка на раму передается при подъеме за строповые устройства от установленного оборудования. Для железнодорожных платформ нагрузка на раму передаётся непосредственно от груза.

Для рам блоков нефтяных аппаратов существует методика расчета рамы по РД 26-18-7-88. Эта методика уступает методике расчета, приведенной в настоящей книге за счет упрощений состоящим в отдельных расчетах на изгиб продольных балок и последующих расчетах поперечных балок.

Расчет несущих балок выполняется методом сопротивления материалов на основании работы [1] (эта работа является лучшим учебником сопромата с изложением расчета балок и рам). Расчет решеток катализатора является наиболее сложной задачей и выполняется с использованием теории [2] и [3] по примерам, приведенным в работах [4] [5] для железнодорожных платформ, где эти расчеты разработаны в отличии от рам в аппаратах нефтепереработки. Но расчет решеток может быть выполнен упрощенно в случае отсутствия знания строительной механики. Расчет прутьев сетки Джонсона выполняется по модели многопролетной балки по теореме трех моментов по работам [1] и [2].

—

ПОСВЯЩАЕТСЯ БОГУ-ТВОРЦУ ТРОИЦЕ!

Благодарность моей маме, работавшей в нефтяном машиностроении.

Расчет несущих балок решетки катализатора

Несущие балки выполняют как правило прямоугольного сечения. Размеры сечения ограничиваются возможностью протаскивания балок через штуцера люков. Балки предпочтительно заводить внутрь аппарата (аппарат колонного типа) через верхний штуцер на днище аппарата, но могут затаскиваться через боковые штуцеры. С учетом этого размеры балок в высоту не более 500мм и с толщиной не менее 80 мм.

Несущие балки подвергаются изгибу и скручиванию. Скручивание возникает из-за несимметричности расположения балок относительно поверхности решетки катализатора. Оценка прочности производится от совместного действия кручения и изгиба, по энергетической теории прочности.

Участок балки, по которому балка опирается на уступ (приварное кольцо) обечайки, рассчитываются на текучесть по площадке контакта (на сжатие) под действием нагрузки от давления на решетку катализатора.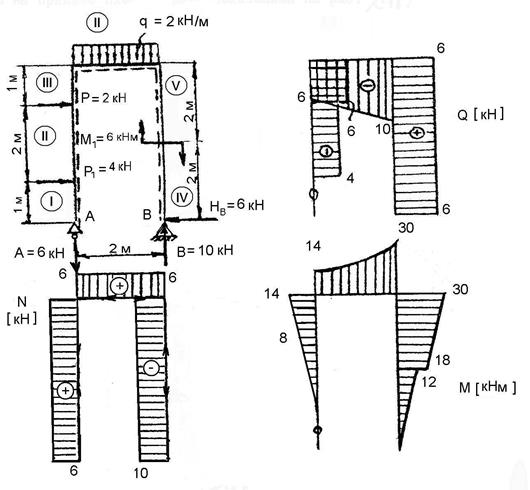 Если по текучести пятно контакта не удовлетворяет условию прочности, на торце балки делают уступ снизу, под который устанавливают вальцованную пластину. На пластину усилие передается от пятна контакта уступа и от сварных швов, которыми сегмент приваривается к боковым поверхностям балки. Давление от балки передается на сегмент, а от сегмента на уступ обечайки. Размеры сегмента подбирают так, чтобы площадь пятна контакта удовлетворяла прочности по текучести (на сжатие).

Введение в анимацию в Python

Питон > Анимации > Введение в анимацию

Предложить редактирование этой страницы

Введение в создание анимации с помощью Plotly в Python.

Новичок в сюжете?

Plotly — бесплатная графическая библиотека с открытым исходным кодом для Python. Мы рекомендуем вам прочитать наше руководство по началу работы, чтобы получить последние инструкции по установке или обновлению, а затем перейти к нашим учебным пособиям по основам Plotly или погрузиться прямо в некоторые учебные пособия по базовым диаграммам.

Анимированные фигуры с помощью Plotly Express¶

Несколько функций Plotly Express поддерживают создание анимированных фигур с помощью animation_frame и animation_group аргументов.

Вот пример создания анимированной точечной диаграммы с помощью Plotly Express. Обратите внимание, что вы всегда должны исправлять x_range и y_range , чтобы ваши данные оставались видимыми на протяжении всей анимации.

В [1]:

 импортировать plotly.express как px
df = px.data.gapminder()
px.scatter(df, x="gdpPercap", y="lifeExp", анимация_frame="год", анимация_группа="страна",
           размер = "поп", цвет = "континент", hover_name = "страна",
           log_x = Истина, size_max = 55, range_x = [100,100000], range_y = [25,90])
 

Анимированные рисунки в Dash¶

Dash — лучший способ создавать аналитические приложения на Python с использованием рисунков Plotly. Чтобы запустить приложение ниже, запустите pip install dash , нажмите «Загрузить», чтобы получить код, и запустите python app.py .

Начните с официальной документации Dash, и узнайте, как без особых усилий создавать и развертывать подобные приложения с помощью Dash Enterprise.

Выход[2]:

Анимированные гистограммы с Plotly Express¶

Обратите внимание, что вы всегда должны исправлять y_range , чтобы ваши данные оставались видимыми на протяжении всей анимации.

В [3]:

 импортировать plotly.express как px
df = px.data.gapminder()
рис = px.bar(df, x="континент", y="поп", цвет="континент",
  animation_frame="год", animation_group="страна", range_y=[0,4000000000])
рис.шоу()
 

Текущие ограничения и предостережения для анимации¶

• Анимации спроектированы так, чтобы работать хорошо, когда каждая строка ввода присутствует во всех кадрах анимации, и когда категориальные значения, сопоставленные с символом, цветом и фасетом, постоянны во всех кадрах. Анимации может вводить в заблуждение или противоречить , если эти ограничения не соблюдаются.
• Хотя Plotly Express поддерживает анимацию для многих типов диаграмм и карт, плавные переходы между кадрами сегодня возможны только для разброса и бара
• Plotly Express будет , а не , автоматически вычислять объединение всех диапазонов x/y/color, поэтому их необходимо указать вручную, чтобы избежать скачков масштаба между кадрами

Анимированные фигуры с графическими объектами¶

В оставшейся части этого раздела описывается низкоуровневый API графических объектов для создания анимированных фигур вручную.

Фреймы¶

Наряду с данными и компоновкой , фреймов могут быть добавлены в качестве ключа в объект фигуры. Ключ кадров указывает на список фигур, каждая из которых будет прокручиваться при запуске анимации.

Добавление кнопок управления к анимации¶

Вы можете добавить кнопки воспроизведения и паузы для управления анимированными диаграммами, добавив updatemenus массива в макет вашего рисунка . Более подробная информация о стиле и размещении кнопок доступна в справочнике Plotly updatemenus .
Кнопки определяются следующим образом:

 "updatemenus": [{"type": "buttons",
                 "buttons": [{"label": "Ваш ярлык",
                              "метод": "анимировать",
                              "args": [см. ниже]}]}] 

Определение аргументов кнопки¶

Кнопка простого воспроизведения¶

В [4]:

 импортировать plotly.graph_objects как есть
рис = идти.Рисунок(
    данные = [go.Scatter (x = [0, 1], y = [0, 1])],
    макет = перейти. Макет (
        xaxis = dict (диапазон = [0, 5], автодиапазон = False),
        yaxis = dict (диапазон = [0, 5], автодиапазон = False),
        title="Начальный заголовок",
        updatemenus=[дикт(
            тип="кнопки",
            кнопки = [дикт (метка = "Воспроизвести",
                          метод = "анимировать",
                          args=[Нет])])]
    ),
    кадры = [go. Frame (данные = [go.Scatter (x = [1, 2], y = [1, 2])]),
            go.Frame(data=[go.Scatter(x=[1, 4], y=[1, 4])]),
            go.Frame(data=[go.Scatter(x=[3, 4], y=[3, 4])],
                     layout=go.Layout(title_text="Конец заголовка"))]
)
рис.шоу()
 

Перемещение точки на кривой¶

В [5]:

 импортировать plotly.graph_objects как есть
импортировать numpy как np
# Генерация данных кривой
т = np.linspace (-1, 1, 100)
х = т + т ** 2
у = т - т** 2
хм = нп.мин(х) - 1,5
хМ = np.max(х) + 1,5
ум = нп.мин(у) - 1,5
yM = np.max(y) + 1,5
N = 50
s = np.linspace(-1, 1, N)
хх = с + с ** 2
уу = с - с ** 2
# Создать фигуру
рис = идти.Рисунок(
    данные = [go.Scatter (х = х, у = у,
                     режим = "линии",
                     строка = dict (ширина = 2, цвет = «синий»)),
          go.Scatter(x=x, y=y,
                     режим = "линии",
                     строка = dict (ширина = 2, цвет = «синий»))],
    макет = перейти. Макет (
        xaxis = dict (диапазон = [xm, xM], autorange = False, zeroline = False),
        yaxis=dict(range=[ym, yM], autorange=False, zeroline=False),
        title_text="Кинематическая генерация плоской кривой", hovermode="ближайший",
        updatemenus=[dict(type="кнопки",
                          кнопки = [дикт (метка = "Воспроизвести",
                                        метод = "анимировать",
                                        args=[Нет])])]),
    кадры = [иди. Кадр (
        данные = [go.Scatter (
            х=[хх[к]],
            у = [уу [к]],
            режим="маркеры",
            маркер = dict (цвет = "красный", размер = 10)))])
        для k в диапазоне (N)]
)
рис.шоу()
 

Перемещение рамки Френе по плоской кривой¶

В [6]:

 импортировать plotly.graph_objects как есть
импортировать numpy как np
# Генерация данных кривой
т = np.linspace (-1, 1, 100)
х = т + т ** 2
у = т - т** 2
хм = нп.мин(х) - 1,5
хМ = np.max(х) + 1,5
ум = нп.мин(у) - 1,5
yM = np.max(y) + 1,5
N = 50
s = np.linspace(-1, 1, N)
хх = с + с ** 2
уу = с - с ** 2
vx = 1 + 2 * с
vy = 1 - 2 * s # v=(vx, vy) - скорость
скорость = np.sqrt (vx ** 2 + vy ** 2)
ux = vx / скорость # (ux, uy) единичный вектор касательной, (-uy, ux) единичный вектор нормали
uy = vy / скорость
xend = xx + ux # конечные координаты единичного касательного вектора в точке (xx, yy)
уенд = уу + уу
xnoe = xx - uy # конечные координаты единичного вектора нормали в точке (xx,yy)
уноэ = уу + их
# Создать фигуру
рис = идти. Рисунок(
    данные = [go.Scatter (х = х, у = у,
                     имя="кадр",
                     режим = "линии",
                     строка = dict (ширина = 2, цвет = «синий»)),
          go.Scatter(x=x, y=y,
                     имя = "кривая",
                     режим = "линии",
                     строка = dict (ширина = 2, цвет = «синий»))
          ],
    layout=go.Layout(ширина=600, высота=600,
                     xaxis = dict (диапазон = [xm, xM], autorange = False, zeroline = False),
                     yaxis=dict(range=[ym, yM], autorange=False, zeroline=False),
                     title="Перемещение рамки Френе по плоской кривой",
                     hovermode="ближайший",
                     updatemenus=[dict(type="кнопки",
                                       кнопки = [дикт (метка = "Воспроизвести",
                                                     метод = "анимировать",
                                                     args=[Нет])])]),
    кадры = [иди. Кадр (
        данные = [go.Scatter (
            x=[xx[k], xend[k], нет, xx[k], xnoe[k]],
            y=[yy[k], yend[k], None, yy[k], ynoe[k]],
            режим = "линии",
            строка = dict (цвет = "красный", ширина = 2))
        ]) для k в диапазоне (N)]
)
рис.шоу()
 

Использование ползунка и кнопок¶

В следующем примере используется хорошо известный набор данных Gapminder для демонстрации возможностей анимации. Эта анимированная пузырьковая диаграмма показывает изменение «ВВП на душу населения» по сравнению с «Ожидаемой продолжительностью жизни» в нескольких странах с 1952 по 2007 год, раскрашенное по соответствующим континентам и рассчитанное по численности населения.

Это также пример создания структуры фигуры как словаря Python, а затем построения фигуры графического объекта из этого словаря.

В [7]:

 импортировать plotly.graph_objects как есть
импортировать панд как pd
url = "https://raw.githubusercontent.com/plotly/datasets/master/gapminderDataFiveYear. csv"
набор данных = pd.read_csv(url)
годы = ["1952", "1962", "1967", "1972", "1977", "1982", "1987", "1992", "1997", "2002",
         "2007"]
# составить список континентов
континенты = []
для континента в наборе данных["континент"]:
    если континент не в континентах:
        континенты.добавление(континент)
# сделать фигуру
fig_dict = {
    "данные": [],
    "макет": {},
    "кадры": []
}
# заполняем большую часть макета
fig_dict["layout"]["xaxis"] = {"range": [30, 85], "title": "Ожидаемая продолжительность жизни"}
fig_dict["layout"]["yaxis"] = {"title": "ВВП на душу населения", "type": "log"}
fig_dict["layout"]["hovermode"] = "ближайший"
fig_dict["layout"]["updatemenus"] = [
    {
        "кнопки": [
            {
                "args": [Нет, {"frame": {"duration": 500, "redraw": False},
                                "fromcurrent": True, "transition": {"duration": 300,
                                                                    "ослабление": "квадратичное вход-выход"}}],
                "этикетка": "Воспроизвести",
                "метод": "анимировать"
            },
            {
                "args": [[Нет], {"frame": {"duration": 0, "redraw": False},
                                  "режим": "немедленный",
                                  "переход": {"длительность": 0}}],
                "метка": "Пауза",
                "метод": "анимация"
            }
        ],
        "направление": "налево",
        "pad": {"r": 10, "t": 87},
        "showactive": Ложь,
        "тип": "кнопки",
        «х»: 0,1,
        "ксанчор": "правильно",
        "у": 0,
        "янчор": "сверху"
    }
]
sliders_dict = {
    "активный": 0,
    "янчор": "сверху",
    "xanchor": "левый",
    "текущая стоимость": {
        "шрифт": {"размер": 20},
        "префикс": "Год:",
        "видимый": Правда,
        "ксанчор": "правильно"
    },
    "transition": {"duration": 300, "easing": "cubic-in-out"},
    «площадка»: {«б»: 10, «т»: 50},
    "длина": 0,9,
    «х»: 0,1,
    "у": 0,
    "шаги": []
}
# сделать данные
год = 1952
для континента на континентах:
    dataset_by_year = набор данных[набор данных["год"] == год]
    dataset_by_year_and_cont = dataset_by_year[
        dataset_by_year["континент"] == континент]
    data_dict = {
        "x": список (набор данных_by_year_and_cont["lifeExp"]),
        "y": список (набор данных_by_year_and_cont["gdpPercap"]),
        "режим": "маркеры",
        "текст": список (набор данных_по_году_и_продолжению["страна"]),
        "маркер": {
            "sizemode": "площадь",
            "ссылка размера": 200000,
            "размер": список (набор данных_по_году_и_конт["поп"])
        },
        "имя": континент
    }
    fig_dict["данные"]. append(data_dict)
# делаем кадры
за год в годах:
    кадр = {"данные": [], "имя": ул (год)}
    для континента на континентах:
        dataset_by_year = набор данных[набор данных["год"] == int(год)]
        dataset_by_year_and_cont = dataset_by_year[
            dataset_by_year["континент"] == континент]
        data_dict = {
            "x": список (набор данных_by_year_and_cont["lifeExp"]),
            "y": список (набор данных_by_year_and_cont["gdpPercap"]),
            "режим": "маркеры",
            "текст": список (набор данных_по_году_и_продолжению["страна"]),
            "маркер": {
                "sizemode": "площадь",
                "ссылка размера": 200000,
                "размер": список (набор данных_по_году_и_конт["поп"])
            },
            "имя": континент
        }
        кадр["данные"].append(data_dict)
    fig_dict["кадры"].append(кадр)
    slider_step = {"аргументы": [
        [год],
        {"frame": {"duration": 300, "redraw": False},
         "режим": "немедленный",
         "переход": {"длительность": 300}}
    ],
        "метка": год,
        "метод": "анимация"}
    sliders_dict["шаги"]. append(slider_step)
fig_dict["макет"]["ползунки"] = [sliders_dict]
рис = идти.Рисунок(fig_dict)
рис.шоу()
 

Важные примечания¶

• Определение перерисовки : Настройка перерисовки : false — это оптимизация точечных диаграмм, чтобы анимация просто вносила изменения, не перерисовывая весь график. Для других типов графиков, таких как контурные графики, каждый кадр должен быть полной перерисовкой графика, т. е. перерисовок: true .

Ссылка¶

Для получения дополнительной информации и атрибутов для создания пузырьковых диаграмм в Plotly см.: https://plotly.com/python/bubble-charts/. Для получения дополнительной документации по созданию анимации с помощью Plotly см. https://plotly.com/python/#animations.

А как насчет Dash?¶

Dash — это платформа с открытым исходным кодом для создания аналитических приложений, не требующая Javascript и тесно интегрированная с графической библиотекой Plotly.

Узнайте, как установить Dash, по адресу https://dash.plot.ly/installation.

Везде на этой странице, где вы видите fig.show() , вы можете отобразить одну и ту же цифру в приложении Dash, передав ее аргументу цифра компонента Graph из встроенного dash_core_components пакет, подобный этому:

 import plotly.graph_objects as go # or plotly.express as px
fig = go.Figure() # или любая функция Plotly Express, например. px.bar(...)
# fig.add_trace( ... )
# fig.update_layout( ... )
импортировать тире
импортировать dash_core_components как DCC
импортировать dash_html_components как html
приложение = тире.Dash()
app.layout = html.Div([
    dcc.Graph(рисунок=рис)
])
app.run_server(debug=True, use_reloader=False) # Отключить перезагрузку, если внутри Jupyter
 

Визуализация данных

Вы должны посмотреть на свои данные. Графики и диаграммы позволяют исследовать и узнать о структуре информации, которую вы собираете. Хорошие данные визуализации также облегчают передачу ваших идей и выводы другим людям. Кроме того, создание эффективных сюжетов из ваши собственные данные — лучший способ развить хороший глазомер для чтения и понимание графиков — хороших и плохих — сделанных другими, независимо от того, представлены в исследовательских статьях, бизнес-презентациях, государственной политике адвокации или сообщений СМИ. Эта книга научит вас, как это сделать.

Моя главная цель — познакомить вас как с идеями , так и с методами визуализации данных разумным, понятным и воспроизводимым способом. Некоторые классические работы по визуализации данных, такие как The Visual Display of Количественная информация (Tufte, 1983), настоящее время многочисленные примеры хорошей и плохой работы вместе с некоторыми общими эмпирические правила, основанные на вкусах, для построения и оценки графиков. В то, что теперь стало большой и процветающей областью исследований, более недавняя работа обеспечивает отличное обсуждение когнитивных основы удачной и неудачной графики, снова обеспечивая много убедительных и ярких примеров (Ware, 2008). В других книгах можно найти хорошие советы о том, как отображать данные в графическом виде. различных обстоятельствах (Каир, 2013 г.; Few, 2009 г.; Munzer, 2014), но решили не знакомить читателя с инструментами используются для создания графики, которую они показывают. Это может быть потому, что используемое программное обеспечение является некоторым (проприетарным, дорогостоящим) методом «укажи и щелкни». приложение, которое требует полностью визуального представления своего собственного, такого как Tableau, Microsoft Excel или SPSS. Или, может быть, необходимое программное обеспечение находится в свободном доступе, но показать, как его использовать, не то, что книга о (Кливленд, 1994). И наоборот, есть отличные поваренные книги, которые предоставляют кодовые «рецепты» для многих видов сюжета (Чанг, 2013). Но по этой причине они не торопятся чтобы познакомить новичка с принципами вывода, который они производить. Наконец, у нас также есть подробные сведения о конкретных программные инструменты и библиотеки, включая ту, которую мы будем использовать в этом книга (Уикхем, 2016). Иногда это может быть трудно для новичков переварить, так как они могут предполагать фон, который читатель не иметь.

Каждая из книг, которые я только что процитировал, стоит вашего времени. Когда обучая людей тому, как делать графику с данными, я неоднократно обнаруживали потребность во введении, мотивирующем и объясняет , почему вы что-то делаете, но это не пропускает необходимые детали как производить изображения, которые вы видите на странице. Итак, у этой книги две основные цели. Во-первых, я хочу, чтобы вы перешли к делу где вы можете воспроизвести для себя почти каждую фигуру в тексте. Во-вторых, я хочу, чтобы вы поняли, почему код написан именно так, а не иначе. такова, что когда вы смотрите на собственные данные, вы можете чувствовать себя уверенно о вашей способности перейти от грубой картины в вашей голове к качественная графика на вашем экране или странице.

Чему вы научитесь

Эта книга представляет собой практическое введение в принципы и практику просмотр и представление данных с помощью R и ggplot. Р — мощный, широко используемый и свободно доступный язык программирования для данных анализ. Возможно, вам будет интересно изучить ggplot после использования R раньше, или вы совершенно не знакомы с R и ggplot и просто хотите графически ваши данные. Я не предполагаю, что у вас есть какие-либо предварительные знания о R.

После установки необходимого нам программного обеспечения мы начнем с обзора некоторые основные принципы визуализации. Мы ориентируемся не только на эстетические аспекты хороших сюжетов, а то, как их эффективность коренится в том, как мы воспринимаем такие свойства, как длина, абсолютная и относительный размер, ориентация, форма и цвет. Затем мы узнаем, как создавать и улучшать графики с помощью ggplot2, мощного, универсального и широко используемая библиотека визуализации для R (Wickham, 2016). ggplot2 библиотека реализует «грамматику графики» (Wilkinson, 2005). Этот подход дает нам согласованный способ создания визуализаций путем выражающие отношения между атрибутами данных и их графическое представление.

С помощью серии рабочих примеров вы научитесь строить графики по частям, начиная с диаграмм рассеяния и резюме отдельных переменные, затем переходим к более сложной графике. Темы охватывали включать построение непрерывных и категориальных переменных, наслоение информация о графике; фасетирование сгруппированных данных для получения эффективных «малократные» участки; преобразование данных для легкого создания визуальных сводки на графике, такие как линии тренда, линейные аппроксимации, диапазоны ошибок, и боксплоты; создание карт, а также некоторые альтернативы картам стоит учитывать при представлении данных на уровне страны или штата. Мы также охватывают случаи, когда мы не работаем напрямую с набором данных, а скорее с оценками из статистической модели. Оттуда мы будем исследовать процесс уточнения сюжетов для выполнения общих задач, таких как как выделение ключевых характеристик данных, маркировка отдельных элементов интерес, аннотирование сюжетов и изменение их общего вида. Наконец, мы рассмотрим некоторые стратегии представления графических результаты в разных форматах и ​​для разных аудиторий.

Если следовать тексту и примерам этой книги, то к концу вы will:

• Понять основные принципы эффективной визуализации данных.
• Имейте практическое понимание того, почему некоторые графики и рисунки работают хорошо, в то время как другие могут не информировать или активно вводить в заблуждение.
• Узнайте, как создавать различные графики в R с помощью ggplot2.
• Уметь улучшать сюжеты для эффективной презентации.

Научиться эффективно визуализировать данные — это больше, чем просто знать как написать код, который производит цифры из данных. Эта книга будет научить вас, как это сделать. Но это также научит вас думать о информации, которую вы хотите показать, и о том, как учитывать аудитории, которой вы его показываете, включая самый распространенный случай, когда аудитория — это вы сами.

Эта книга не является исчерпывающим руководством по R и даже не исчерпывающим Обзор всего, что может сделать ggplot. И это не поваренная книга, содержащая просто примеры конкретных вещей, которые люди обычно хотят делать ggplot. (Оба этих вида книг уже существуют: см. ссылки в Приложении.) Это также не жесткий набор правил или последовательность прекрасно законченные образцы, которыми можно восхищаться, но нельзя воспроизвести. Моя цель — быстро научить вас работать с R и строить графики в хорошо информированный способ, с твердым пониманием основной последовательности шагов — взятие ваших данных, указание взаимосвязи между переменные и видимые элементы, а также наращивание изображений слоями слой — это основа того, что делает ggplot.

Изучение ggplot означает привыкание к тому, как работает R, а также понимание того, как ggplot соединяется с другими инструментами на языке R. Как вы будете работать над книгой, постепенно вы узнаете больше о некоторых очень полезных идиомах, функциях и методах для манипулирование данными в R. В частности, вы узнаете о некоторых инструменты, предоставляемые библиотекой tidyverse , к которой принадлежит ggplot. Точно так же, хотя это и не поваренная книга, как только вы пройдете главу 1 вы сможете увидеть и понять используемый код чтобы произвести почти все цифры в книге. В большинстве случаев вы будете также посмотрите на эти фигуры, построенные по частям, шаг за шагом. Если вы используете книгу так, как она задумана, к концу у вас будет создание версии самой книги, содержащей код, который у вас есть выписали и аннотировали сами. И хотя мы не идем в большой углубление в тему правил или принципов визуализации, обсуждение в главе 1 и его применение во всем книга дает вам больше информации для размышлений, чем просто список графиков типы. К концу книги вы должны уметь смотреть на рисунок и иметь возможность увидеть это с точки зрения грамматики ggplot, понимая, как различные слои, формы и данные собираются вместе, чтобы сделать готовый сюжет.

Правильное настроение

Изучение такого языка программирования, как R, главным образом потому, что в начале кажется, что нужно так много частей. подходят друг к другу, чтобы все работало должным образом. Это может показаться вы должны научиться всему, прежде чем вы сможете что-то сделать. Язык имеет некоторые, возможно, незнакомые концепции, которые определяют, как это работает, например «объект», или «функция», или «класс». Синтаксические правила написания код раздражающе придирчив. Сообщения об ошибках кажутся неясными; страницы справки лаконичный; у других людей, кажется, было не совсем та же проблема, что и ты. Кроме того, вы чувствуете, что выполнение одного дела часто требует узнать немного о какой-то другой части языка. Сделать сюжет вам нужна таблица данных, но, возможно, вам нужно отфильтровать некоторые строки, пересчитайте некоторые столбцы или просто заставьте компьютер увидеть, что он есть в первую очередь. И есть также более широкая среда поддерживающие приложения и инструменты, о которых полезно знать, но включают в себя новые собственные концепции — редакторы, которые подчеркивают то, что вы писать; приложения, помогающие организовать ваш код и его вывод; способы написания кода, позволяющие отслеживать то, что у вас есть сделанный. Все это может показаться немного запутанным.

Не паникуйте. Вы должны с чего-то начать. Начиная с графики более полезным, чем некоторые другие места, где вы могли бы начать, потому что вы сможете увидеть результаты своих усилий очень быстро. Как вы укрепляете свою уверенность и способности в этой области, вы постепенно рассматривайте другие инструменты как вещи, которые помогают вам разобраться в какой-то проблеме, или решить проблему, которая мешает вам сделать изображение, которое вы хотите. Это облегчает их изучение. По мере их приобретения по частям — возможно, первоначально используя их без полного понимание того, что происходит — вы начнете видеть, как они подходят вместе, и быть более уверенным в своей способности делать то, что вы нужно сделать.

Более того, в последнее десятилетие или около того мир анализа данных и программирование в целом открылось таким образом, что помощь стала намного проще подойти. Бесплатные инструменты для кодирования существуют уже давно время, но в последние годы то, что вы могли бы назвать «экологией помощь» стало лучше. Есть больше ресурсов для разучивая различные произведения, и многие из них ориентированы на то, как написание кода на самом деле происходит большую часть времени, то есть, итеративно, подверженным ошибкам и с учетом проблем другие люди столкнулись и решили раньше.

Как пользоваться этой книгой

Эту книгу можно использовать одним из нескольких способов. Как минимум, вы можете сесть и прочитать его для общего обзора передового опыта в визуализация данных, а также множество проработанных примеров графики от их начала до должным образом законченного состояния. Даже если вы не сядьте и поработайте над кодом, вы получите хорошее представление о том, как подумать о визуализации и лучше понять процесс благодаря которому создается хорошая графика.

Более полезно, если вы настроите все, как описано в главе 2, и затем поработайте с примерами⊕Или, если вы принесете свои собственные данные для исследования вместо примеров или вместе с ними, как описано в главе 2, то в итоге вы получите собственную книгу по визуализации данных. Если вы подойдете к книге таким образом, то к концу вам будет удобно пользоваться ggplot в частности, а также вы будете готовы узнать больше о языке R в целом.

Эта книга также может быть использована для преподавания в качестве основной темы курс по визуализации данных или как дополнение к бакалавриату или курсы повышения квалификации по статистике или анализу данных. Моя цель состояла в том, чтобы сделать «скрытые задачи» кодирования и полировки графов более доступными и явное. Я хочу убедиться, что вы не остались с «Как «Нарисуй сову в три шага», характерная для многих руководств. Ты знаешь тот самый. Первые два шага показаны достаточно ясно. Нарисуйте несколько овалы в виде птиц. Сделайте линию для ответвления. Но последний шаг, т. сова, которую мог бы нарисовать Джон Джеймс Одюбон, представлена ​​как простая расширение для читателей, чтобы понять для себя.

Если вы никогда не использовали R или ggplot, вам следует начать с самого начала книги и пройдите свой путь до конца. Если вы знаете о Р уже, но только хочу изучить ядро ​​ggplot, то после установки программного обеспечения, описанного ниже, сосредоточьтесь на главах с 3 по 5. Глава 6 (о моделях) обязательно включает некоторый материал по статистическое моделирование, которое книга не может полностью раскрыть. Это не текст статистики. Так, например, я показываю в целом, как укладывать и работать с различными видами моделей в главе 6, но я не рассматриваю важные детали установки, выбора и полного понимания разные подходы. Даю ссылки в тексте на другие книги для которых этот материал является основным направлением.

Каждая глава заканчивается разделом, предлагающим, куда двигаться дальше (помимо от продолжения чтения книги). Иногда я предлагаю другие книги или веб-сайты для изучения. Я также задаю вопросы или ставлю задачи, которые расширить материал, изложенный в главе, побуждая вас используйте понятия и навыки, которые вы изучили.

Условные обозначения

В этой книге мы чередуем обычный текст (как этот), образцы кода, который вы можете ввести и запустить самостоятельно, и результат этого кода. В основном тексте ссылки на объекты или другие вещи, которые существуют в языке R или в вашем проекте R, такие как таблицы данных, переменные, функции и т. д., также будут отображаться в моноширинный или «пишущий» шрифт . Код, который вы можете ввести прямо в R на консоли, будет в серых полях, а также моноширинным. Вот так:

 my_numbers <- c(1, 1, 4, 1, 1, 4, 1) 

Если вы введете эту строку кода в консоль R, она создаст вещь под названием my_numbers .⊕Дополнительные примечания и информация иногда будет отображаться на полях, как здесь. Однако это не дает никакого результата. Когда мы пишем код, который также производит вывод на консоль, мы сначала видим код (в сером поле), а затем вывод моноширинным шрифтом на белом фоне. Здесь мы складываем два числа и видим результат:

 4 + 1 

 ## [1] 5 

Еще два замечания о том, как это читать. Во-первых, по умолчанию в этой книге все, что возвращается к нам на консоль в результате ввода команды, будет отображаться с двумя символами решетки ( ## ) в начале каждой строки вывода. Это поможет отличить его от команд, которые мы вводим в консоль. Вы не увидите хеш-символов в консоли при использовании R.

Во-вторых, как в книге , так и на консоли, если вывод того, что вы сделали, приводит к ряду элементов (например, числам или наблюдениям из переменной и т. д.), вы часто будете видеть вывод, который включает некоторое число в квадратных скобках в начале строки. . Выглядит это так: [1]. Это не часть самого вывода, а просто счетчик или указатель, отслеживающий, сколько элементов уже распечатано. В случае сложения 4 + 1 мы получили только одну, или [1] , вещь обратно — число пять. Если в результате какой-либо инструкции или команды возвращено больше элементов, счетчик будет отслеживать это в каждой строке. В следующем фрагменте кода мы скажем R показать нам строчные буквы алфавита:

 букв 

 ## [1] "а" "б" "в" "г" "д" "ф" "г" "ч" "и" "к" "к" "л" "м" " н" "о" "р" "к"
## [18] "r" "s" "t" "u" "v" "w" "x" "y" "z" 

Вы можете видеть, как счетчик увеличивается в каждой строке, так как он подсчитывает количество письма напечатаны.

Перед тем, как начать

Книга предназначена для того, чтобы вы активно следили за ней, записывая примеры и экспериментируя с кодом по ходу дела. Вы сможете воспроизвести почти все сюжеты в тексте. Сначала вам нужно будет установить некоторое программное обеспечение. Вот что делать:

1. Получите самую последнюю версию R. R бесплатен и доступен для операционных систем Windows, Mac и Linux. Загрузите⊕ cloud.r-project.org версию R, совместимую с вашей операционной системой. Если вы используете Windows или MacOS, вам следует выбрать один из предварительно скомпилированных двоичных дистрибутивов (т. е. готовых к запуску приложений), ссылки на которые приведены в верхней части веб-страницы R Project.
2. После того, как ⊕ rstudio.com R установлен, загрузите и установите R Studio. R Studio — это «интегрированная среда разработки» или IDE. Это означает, что это интерфейс для R, с которым намного проще работать. R Studio также бесплатна и доступна для платформ Windows, Mac и Linux.

3. Установите⊕ tidyverse.org библиотеку tidyverse и несколько других дополнительных пакетов для R. Эти библиотеки предоставляют полезные функции, которыми мы будем пользоваться на протяжении всей книги. Вы можете узнать больше о семействе пакетов tidyverse на его веб-сайте.

   Чтобы установить tidyverse, убедитесь, что у вас есть подключение к Интернету, а затем запустите R Studio. Тип⊕Я настоятельно рекомендую печатать все примеры кода с самого начала, а не копировать и вставлять. следующие строки кода в командной строке R, расположенной в окне с именем «Консоль», и нажмите «Ввод». В приведенном ниже коде 9Стрелка 0012 <- состоит из двух нажатий клавиш, сначала < , а затем короткого тире или символа минус, - .

 my_packages <- c("tidyverse", "broom", "coefplot", "coefplot",
 "gapminder", "GGally", "ggrepel", "ggridges", "gridExtra",
 "здесь", "межучасток", "поля", "карты", "маппродж",
 "mapdata", "MASS", "quantreg", "rlang", "масштабы",
 "опрос", "срвир", "viridis", "viridisLite", "devtools")
install.