эпюра монжа или комплексный чертеж
Эпюра монжа или комплексный чертеж — это чертеж, составленный из двух или более связанных между собой ортогональных проекций геометрической фигуры.
Пользоваться пространственным макетом для отображения ортогональных проекций геометрических фигур неудобно ввиду его громоздкости, а также из-за того, что при его переносе на лист бумаги, на плоскостях H и W происходит искажение формы и размеров проецируемой фигуры.
Поэтому вместо изображения на чертеже пространственного макета используется эпюра Монжа.
Эпюра Монжа получается преобразованием пространственного макета путем совмещения плоскостей H и W с фронтальной плоскостью проекций V:
— для совмещения плоскости H с V поворачиваем ее на 90 градусов вокруг оси x в направлении движения часовой стрелки. На рисунке, для наглядности, плоскость H повернута на угол чуть меньший 90 градусов, при этом ось y, принадлежащая горизонтальной плоскости проекции, после поворота совпадает с осью z
— после совмещения горизонтальной плоскости, поворачиваем вокруг оси z также на угол 90 градусов профильную плоскость в направлении противоположном движению часовой стрелки. При этом ось y, принадлежащая профильной плоскости проекции, после поворота совпадает с осью x.

После преобразования пространственный макет примет вид, показанный на рисунке. На этом рисунке указана также последовательность взаимного положения пол плоскостей проекций, так запись V[H(W)] указывает, что в этой части эпюра Монжа (ограниченного положительным направлением осей x и z) ближе к нам находится верхняя левая пола фронтальной плоскости проекции V, за ней располагается задняя левая пола горизонтальной плоскости проекции H, далее следует верхняя задняя пола профильной плоскости W.
Так как плоскости не имеют границ, то в совмещенном положении (на эпюре) эти границы не показывают, нет необходимости оставлять надписи, указывающие положение пол плоскостей проекций. Излишне также напоминать, где отрицательное направление координатных осей. Тогда, в окончательном виде эпюра Монжа, заменяющая чертеж пространственного макета примет вид, показанный на рисунке. 
Эпюра Монжа может быть выполнена с помощью:
— обычных чертежных инструментов и приспособлений:
Чертежные инструменты;
Чертежные принадлежности и приборы;
— Программы для построения (рисования) эпюра Монжа: Выполнение чертежа в графическом редакторе.
В качестве примера оформления эпюра Монжа предлагаем решение задачи на построение равнобедренного прямоугольного треугольника ABC: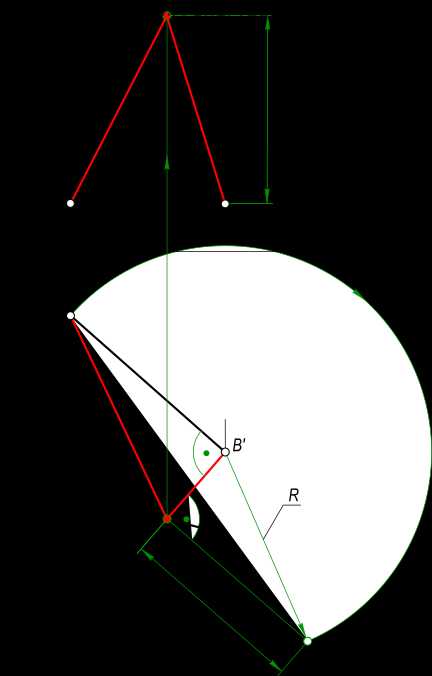
— в черном цвете отображается известное по условию задачи;
— в зеленом цвете отображаются все построения которые ведут к решению задачи;
По условию задачи заданы проекции треугольника ABC(A`B`C`, A»B»…»). Для решения задачи необходимо найти недостающую проекцию C».
chertegik.ru
Лекция 8 Метод проекций. Эпюр Монжа.
1. Метод ортогонального проецирования
2. Точка
3. Прямая линия
4. Вопросы и задания
Метод ортогонального проецирования
Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Гаспаром Монжем — крупным французским геометром конца 18, начала 19 веков, 1789-1818 гг. одним из основателей знаменитой политехнической школы в Париже и участником работ по введению метрической системы мер и весов.
Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остается основным методом составления технических чертежей.
В соответствии с методом предложенным Г. Монжем рассмотрим в пространстве две взаимно перпендикулярные плоскости проекций.
Рис. 89
Одну из плоскостей проекций П1располагают горизонтально, а вторую П2 — вертикально. П1 — горизонтальная плоскость проекций, П2— фронтальная. Плоскости бесконечны и непрозрачны.
Плоскости проекций делят пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций (рис. 89).
Линия пересечения плоскостей проекций называется осью координат и обозначается x21.
Так как эти плоскости непрозрачны, то видимыми для наблюдателя будут только те геометрические объекты, которые располагаются в пределах той же первой четверти.
Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П1 совмещают вращением вокруг оси x12 с плоскостью П2. Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещенные определенным образом одна с другой, называется эпюром Монжа или комплексным чертежом.
Геометрические объекты делятся на: линейные (точка, прямая, плоскость), нелинейные (кривая линия, поверхность) и составные (многогранники, одномерные и двумерные обводы).
Точка
Геометрический объект любой сложности можно рассматривать как геометрическое место точек, по взаимному расположению, которых можно составить представление об объекте, а по расположению их относительно системы координат можно судить о положении его в пространстве.
Точка – одно из основных понятий геометрии. При систематическом изложении геометрии точка обычно принимается за одно из исходных понятий.
Точка в ортогональной системе двух плоскостей проекций
При построении проекции необходимо помнить, что ортогональной проекцией точки на плоскость является основание перпендикуляра, опущенного из данной точки на эту плоскость. Для точки
Проекции точки всегда расположены на прямой, перпендикулярной оси х12 и пересекающей эту ось в точке Ах. Справедливо и обратное, т. е. если на плоскостях проекций даны точки А1 и А2 расположенные на прямой, пересекающей ось х12 в точке Ах под прямым углом, то они являются проекцией некоторой точки А.
Рис. 90
На эпюре Монжа проекции A1 и А2 расположены на одном перпендикуляре к оси х12 При этом расстояние А1АХ — от горизонтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П2, а расстояние А2Ах — от фронтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П1 (рис. 90).
Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи
Точка в ортогональной системе трех плоскостей проекций
В практике изображения различных геометрических объектов, чтобы сделать чертеж более ясным, возникает необходимость использовать третью – профильную плоскость проекций П3, расположенную перпендикулярно к П1 и П2. Плоскости проекций П1, П2 и П3 являются основными плоскостями проекций (рис. 91).
Рис. 91
Третья плоскость, перпендикулярная и П1, и П2, обозначается буквой П3 и называется профильной.
Проекции точек на эту плоскость обозначаются прописными буквами латинского алфавита или цифрами с индексом 3.Плоскости проекций, попарно пересекаясь, определяют три оси Ох, Оу и Oz, которые можно рассматривать как систему декартовых координат в пространстве с началом в точке 0.
Рис. 92
Для получения эпюра точки в системе трех плоскостей проекций плоскости П1 и П3 вращают, до совмещения с плоскостью П2. При обозначении осей на эпюре отрицательные полуоси обычно не указывают. Если существенно только само изображение предмета, а не его положение относительно плоскостей проекций, то оси на эпюре не показывают (рис. 92).
В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат
Сформулируем основные свойства ортогональных проекций на примере точки:
1. Две проекции точки определяют её положение в пространстве.
2. Две проекции точки лежат на одной линии связи.
3. По двум проекциям точки можно построить третью.
Прямая линия
Прямая линия — одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, вдоль которой расстояние между двумя точками является кратчайшим.
Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задаётся на плоскости уравнением 1 — ой степени (линейное уравнение).
Общее уравнение прямой (полное): Ах+Ву+С=0,
где А, В и С — любые постоянные, причем А и В одновременно не равны нулю. Если один из коэффициентов равен нулю, уравнение называется неполным.
Способы графического задания прямой линии
1.Двумя точками (А и В).
2. Двумя плоскостями (а; b).
3. Двумя проекциями.
4. Точкой и углами наклона к плоскостям проекций.
Положение прямой линии относительно плоскостей проекций
Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения.
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями — n.
2.2. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями — m.
2.3. Прямые параллельные профильной плоскости проекций называются профильными — р.
3. Прямые перпендикулярные плоскостям проекций, занимают частное положение в пространстве и называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости оттого, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
3.1. Горизонтально проецирующая прямая – m.
3.2. Фронтально проецирующая прямая – n.
3.3. Профильно проецирующая прямая – р (рис. 93).
Рис. 93
studfiles.net
Связь эпюра Монжа с проекционным чертежом
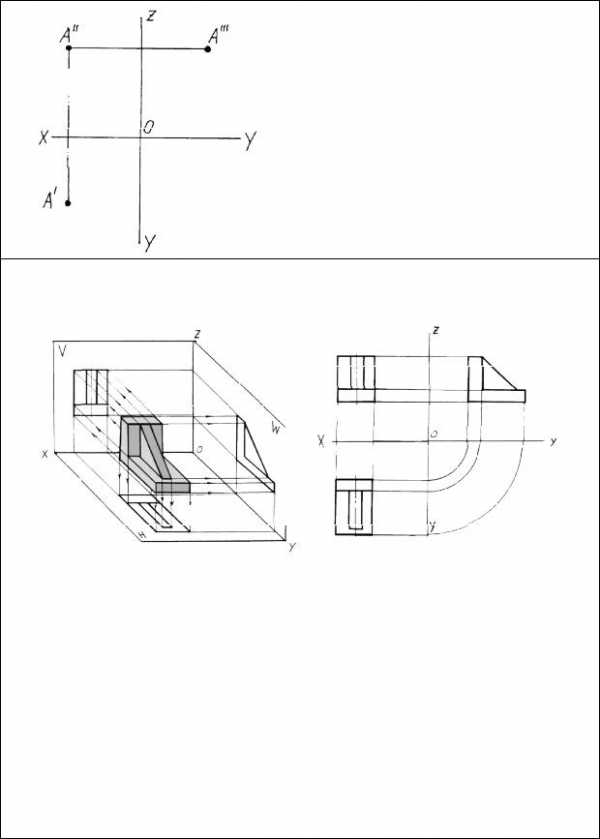
Эпюр Монжа является универсальным способом изображения геометрических объектов на плоскости. Он позволяет не только изобразить объект в проекциях, но и определить его положение в пространстве. Основными проекциями объекта являются:
А/ — горизонтальная проекция; А// — фронтальная проекция; А/// — профильная проекция.
Фронтальная проекция объекта – вид спереди
Профильная проекция объекта – вид слева
Горизонтальная проекция объекта – вид сверху
В проекционном черчении эпюр Монжа является теоретической основой для составления чертежа детали. В отличие от эпюра Монжа
впроекционном черчении проекции называют видами:
-А/ — вид сверху;
-А// — вид спереди;
-А/// — вид слева.
Все свойства эпюра Монжа на чертеже сохраняются.
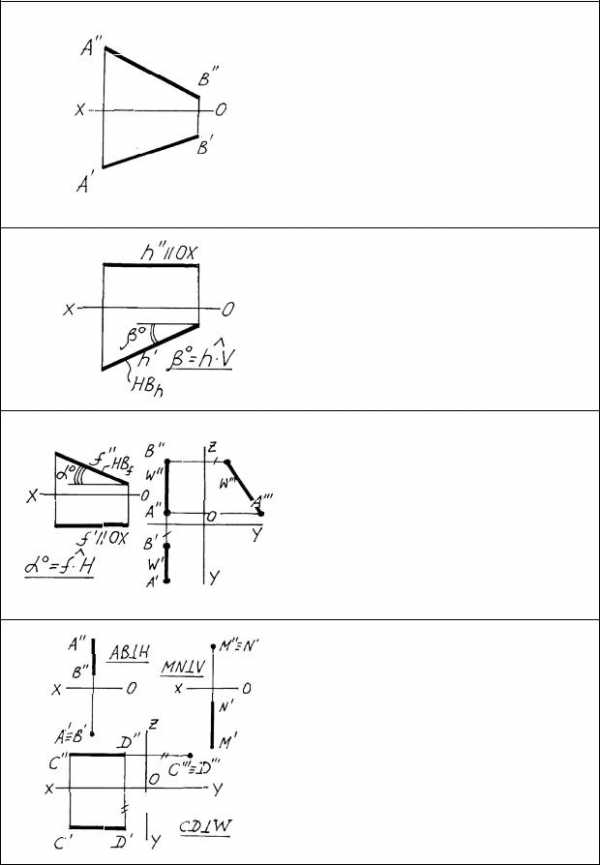
Прямые общего и частного положения
Прямой общего положения называется прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций. Признаком прямой общего положения на эпюре является то, что ни одна проекция прямой не параллельна, не перпендикулярна осям проекций и ни на одной проекции прямая не «выродилась» в точку.
Прямые, параллельные или перпендикулярные плоскостям проекций, называются прямыми частного положения. Горизонталь – это прямая, параллельная горизонтальной плоскости проекций. Главный признак горизонтали на эпюре – h// всегда параллельна оси ОХ.
Фронталь – прямая, параллельная | |||
плоскости V. |
|
| |
Главный | признак | фронтали | на |
эпюре – f / параллельна ОХ. |
| ||
Профильная прямая – прямая, па- | |||
раллельная плоскости W. |
| ||
Горизонтальная и | фронтальная | ||
проекции | этой | прямой | парал- |
лельны осям OZ и OY. |
| ||
Прямые, перпендикулярные плоскостям проекций, называются проецирующими. В зависимости от того, к какой плоскости проекций прямая перпендикулярна, различают горизонтально-, фронтально- и профильно-проецирующие прямые. Главный признак проецирующих прямых на эпюре – на одной из проекций прямая«вырождается» в точку.

Построение следов прямой
Следами прямой называют точки пересечения прямой с плоскостями проекций. На пространственном макете представлены построения следов и их проекций. Различают горизонтальный, фронтальный и профильный следы.
На эпюре представлено построение проекций горизонтального и фронтального следов прямой.
Определение октантов, через которые проходит прямая
В точках следов прямая переходит из одного октанта в другой. Номера октантов можно определить по знакам координат прямой на участках прямой между следами и за их пределами.
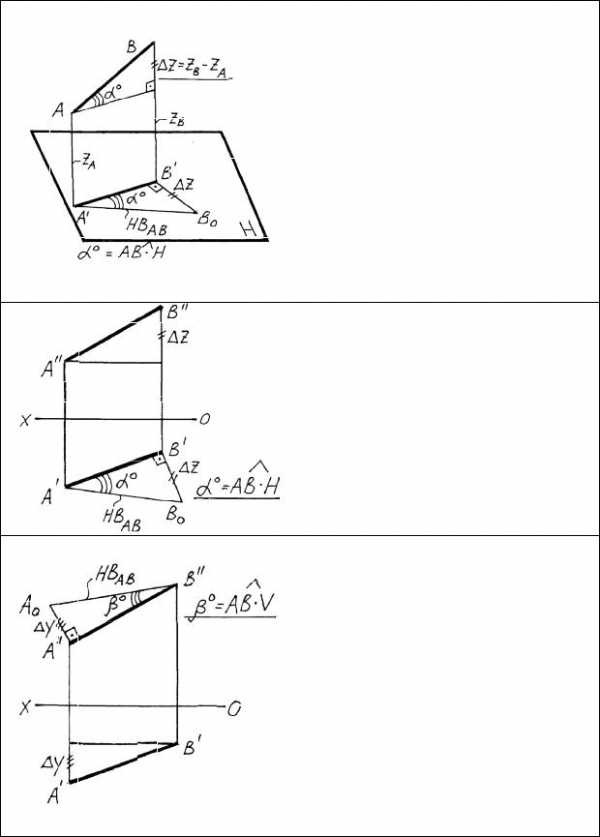
Метод прямоугольного треугольника
Метод | прямоугольного треуголь- | |||
ника | применяется | для | опреде- | |
ления | натуральной | величины | ||
прямой и углов наклона ее к | ||||
плоскостям | проекций. | Если | на | |
проекции | прямой, | например, | ||
горизонтальной, построить | пря- | |||
моугольный | треугольник, одним | |||
катетом | которого является | сама | ||
проекция, а | другим – | разность | ||
аппликат | концов | прямой, то | ||
гипотенуза | будет | натуральной | ||
величиной (НВ) прямой. |
| |||
Если | прямоугольный | треуголь- | |
ник | строится на горизонтальной | ||
проекции прямой, | то | одновре- | |
менно с построением НВ прямой | |||
можно определить | угол | наклона | |
прямой к горизонтальной плос- | |||
кости проекций. |
|
| |
Если прямоугольный треугольник строится на фронтальной проекции, то на катете откладывают разность ординат; если – на профильной, то – разность абсцисс. В первом случае дополнительно определяется угол наклона пря-
мой к фронтальной плоскости проекций, во втором – угол наклона прямой к профильной плоскости проекций.
studfiles.net
1.3. Комплексный чертеж Монжа
Проекция геометрического объекта на одну плоскость, рассмотренная нами ранее, не дает полного и однозначного представления о форме геометрического объекта. Поэтому рассмотрим проецирование хотя бы на две взаимно перпендикулярные плоскости (рис. 1.2), одна из которых расположена горизонтально, а другая вертикально.
Несмотря на наглядность, с чертежом, изображенным на рис 1.2, а работать неудобно, т.к. горизонтальная плоскость на нем показана с искажением. Удобнее выполнять различные построения на чертеже, где плоскости проекций расположены в одной плоскости, а именно, плоскости чертежа. Для этого надо горизонтальную плоскость развернуть вокруг оси ОХ на 90 и совместить с фронтальной так, чтобы передняя пола горизонтальной плоскости ушла вниз, а задняя вверх. Этот метод предложил Г. Монж.
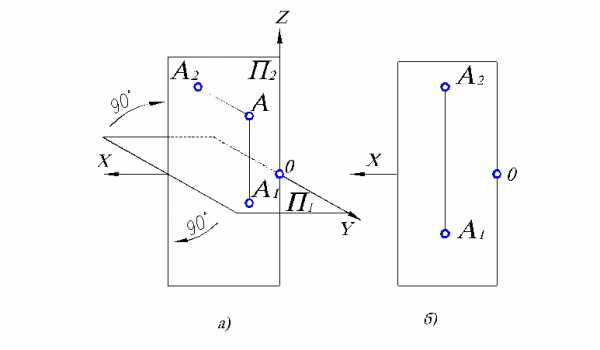
Рис. 1.2. Построение эпюра Монжа:
а) пространственная картина расположения проекций точки А; б) плоскостная картина расположения проекций точки А.
Поэтому чертеж, полученный таким образом (рис. 1.2, б), называется эпюром Монжа или комплексным чертежом.
Обычно двух проекций недостаточно, чтобы составить полное представление о рассматриваемом геометрическом объекте. Поэтому предлагается ввести третью плоскость проекций, ортогональную первым двум (рис.1. 3, а).
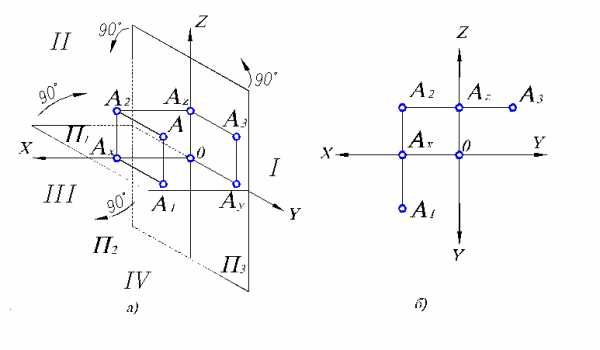
Рис. 1.3. Построение трехкартинного комплексного чертежа (эпюра Монжа):
а) пространственная модель плоскостей проекций; б) трехкартинный комплексный чертеж.
Тогда плоскость П1называется горизонтальной плоскостью проекций, П2 — фронтальной плоскостью проекций (т.к. она расположена перед нами по фронту), П3 — профильной плоскостью проекций (расположена в профиль по отношению к наблюдателю). Соответственно А1— горизонтальная проекция точки А, А2— фронтальная проекция точки А, А3 — профильная проекция точки А.
Оси ОХ, ОY, OZ называются осями проекций. Они аналогичны координатным осям декартовой системы координат с той лишь разницей, что ось ОХ имеет положительное направление не вправо, а влево. Теперь, чтобы получить проекции в одной плоскости (плоскости чертежа) необходимо и профильную плоскость проекций развернуть до совмещения с фронтальной. Для этого ее нужно развернуть на 90 вокруг оси OZ, причем переднюю полу плоскости развернем вправо, а заднюю влево. В результате получим трехкартинный комплексный чертеж (эпюр Монжа), показанный на рис. 1.3, б. Так как ось ОY разворачивается вместе с двумя плоскостями П1и П3 , то на комплексном чертеже ее изображают дважды.
Из этого следует важное правило взаимосвязи проекций. А именно, исходя из рис. 1.3, а, в математической форме его можно записать в виде: А1Аx = ОАy = АzА3. Следовательно, в текстологическом виде оно звучит так: расстояние от горизонтальной проекции точки до оси ОХ равно расстоянию от профильной проекции указанной точки до оси ОZ. Тогда по двум любым проекциям точки можно построить третью. Горизонтальную и фронтальную проекции точки А связывает вертикальная линия связи, а фронтальную и профильную проекции – горизонтальная.
В связи с тем, что комплексный чертеж представляет собой свернутую в плоскости модель пространства, на нем нельзя изобразить проецируемую точку (за исключением случаев, когда ее положение совпадает с одной из проекций). Исходя из этого, следует иметь в виду, что на комплексном чертеже мы оперируем не самими геометрическими объектами, а их проекциями.
studfiles.net
Постоянная прямая эпюра Монжа | Начертательная геометрия
Постоянная прямая эпюра Монжа
Связь между горизонтальной и профильной проекциями точки устанавливается с помощью двух ортогональных отрезков [A`Ay] и [AyA»`] и сопрягающей их дуги окружности, с центром в точке пересечения координатных осей. Положение профильной (горизонтальной) проекции по заданным горизонтальной (профильной) и фронтальной проекциям может быть найдено и без проведения дуги окружности. В этом случае связь между горизонтальной и профильной проекциями устанавливается с помощью ломаной линии A`A0A»` с вершиной A0 на биссектрисе угла, образованного осями y. Биссектриса OA0 — постоянная прямая эпюра Монжа — k0.
В тех случаях, когда нет необходимости в определении положения точки (или любой другой геометрической фигуры) относительно координатной системы плоскостей проекций, можно не указывать на эпюре осей координат.

Постоянная прямая эпюра Монжа
Отсутствие на чертеже осей не мешает определять третью проекцию любой точки по двум заданным, если при этом указаны три проекции какой либо другой точки. Пусть даны три проекции точки A (A`, A», A`»), а также горизонтальная и фронтальная проекции точки B (B`, B»). Требуется найти профильную проекцию B»`. Решение: — Через горизонтальную проекцию точки A` проводим прямую параллельную линии связи (A»A`»), а через профильную проекцию A`» проводим прямую, параллельную линии связи (A`A»), и отмечаем точку их пересечения A0. Точка A0 определяет положение постоянной прямой k0, являющейся биссектрисой угла A`A0A»`. Далее через B` проводим прямую параллельную линии связи (A»A`») (горизонтальную прямую), отмечаем точку B0 ее пересечения с постоянной прямой k0. Через точку B0 проводим вертикальную прямую. Точка ее пересечения с горизонтальной прямой, проведенной через B», определит искомую профильную проекцию B`».
Постоянная прямая эпюра Монжа позволяет решать задачу по определению третьей проекции точки по двум заданным, независимо от того в каком октанте находится точка.
Постоянная прямая эпюра Монжа
Если на безосном чертеже потребуется указать оси, то это всегда можно сделать (с точностью до параллельного переноса). Для этого одну из осей, например x, проводим произвольно следя лишь затем, чтобы она была перпендикулярна линии связи, соединяющей горизонтальную и фронтальную проекции точки. Тогда ось z определится как прямая, перпендикулярная к оси x в точке пересечения оси x с постоянной прямой k0.
+
ngeo.fxyz.ru
Образование и свойства эпюра Монжа
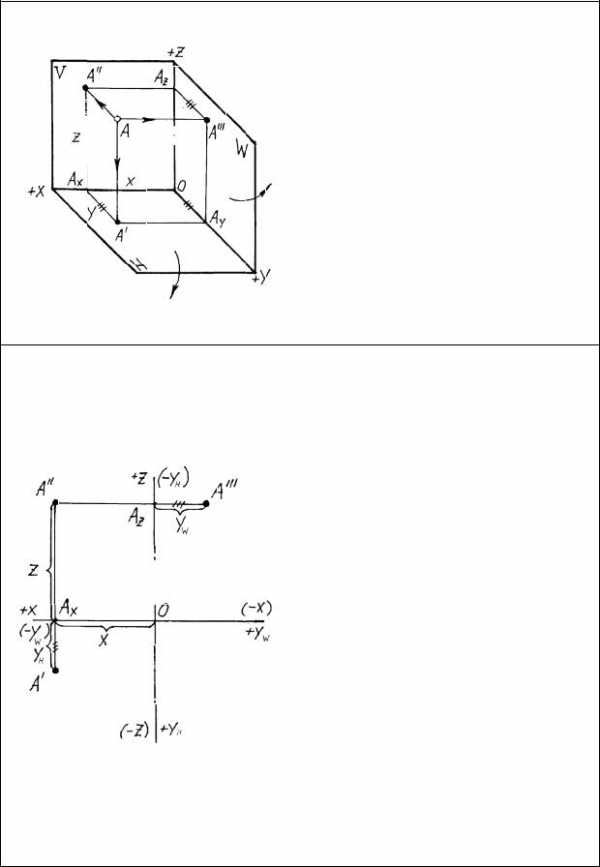
Рассмотрим проецирование точки в одном из октантов, например, в первом. Из пространственного макета видно, что проекции точки находятся в вершинах прямоугольного параллелепипеда. Преобразуем макет так, чтобы плоскости проекций совместились в одну. Для этого мысленно разрежем макет вдоль оси OY и повернем плоскости Н и W (на 90°, как показано на чертеже). При этом саму точку А удалим, оставив только ее проекции и осиOX, OYH ,OYW и OZ.
В результате преобразований получается проекционный чертеж точки, или эпюр Монжа, который имеет следующие свойства:
— горизонтальная проекция точки А/ определяется координатами X и YH;
-фронтальная проекция точкиА// определяется координатами X и Z;
-профильная проекция точки А///
определяется координатами Z и
YW;
-проекции А/ и А// всегда находятся на одной вертикальной линии связи;
-проекции А// и А/// всегда находятся на одной горизонтальной линии связи;
— отрезок АXА/ равен отрезку AZA///, так как они оба являются
координатой Y;
— по двум проекциям точки всегда можно построить третью проекцию.
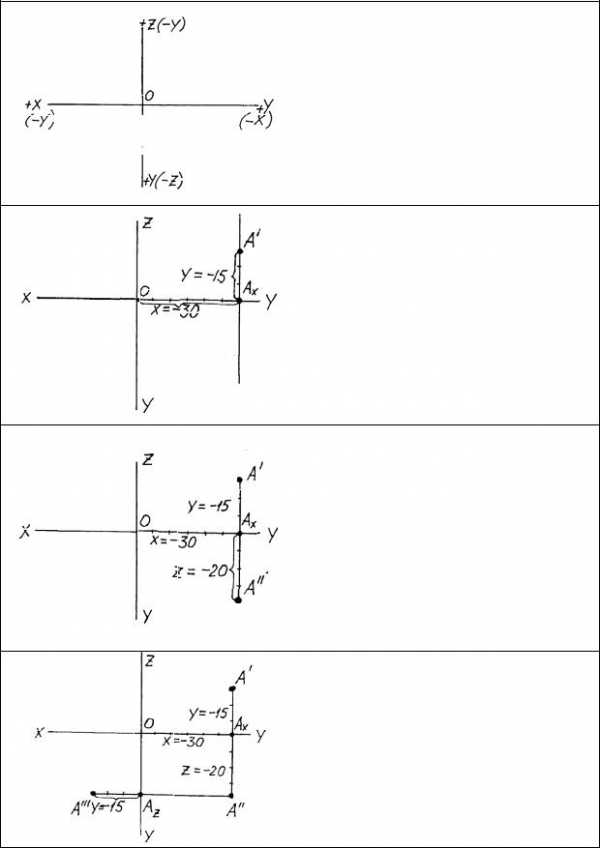
Построение проекций точки по заданным координатам
Необходимо построить проекции точки А с координатами(-30,
-15, -20).
Предварительно по таблице знаков (см. с. 8) определяем номер октанта – седьмой. Вычерчиваем оси координат.
От | начала координат | отклады- | |
ваем координату X (-30) вправо, | |||
так как она со знаком минуси, | |||
получаем | точку АX. Через | точку | |
АX | проводим вертикальную -ли | ||
нию связи. От точки вверх откла- | |||
дываем координату Y (-15) и по- | |||
лучаем | горизонтальную | проек- | |
цию точки А/. |
| ||
От точки Ах вниз откладываем координату Z (-20) и получаем фронтальную проекцию точки А//.
Через точку А// проводим горизонтальную линию связи, и на пересечении с вертикальной осью получаем точку АZ. От нее откладываем влево координату Y (-15) и получаем профильную проекцию точки А///.

Определение октанта по заданному эпюру точки
Предположим, необходимо определить номер октанта, в котором находится точка, если задан эпюр точки в двух или трех проекциях.
Определяем знаки координат точки. Так как точка АX находится влево от начала координат, то координата X имеет знак«плюс». Так как координата Y, использованная для построения горизонтальной проекции точки, отложена вверх, то координата Y имеет знак «минус». Так как координата Z, использованная для построения фронтальной проекции точки, отложена вниз, то координата Z имеет знак «минус». Значит точка А имеет знаки координат (+, -, -).
Определяем номер октанта, в котором находится точка. Это можно сделать двумя способами: по таблице знаков или по модели октантов, которую можно представить зрительным воображением. Второй способ реализуется так: если координата X имеет знак +, то точка А может находиться только вI, II, III или IV октантах; так как координата Y имеет знак «минус», то это может быть только во II и III октантах; если координата Z имеет знак «минус», то точка А может находиться только в III октанте.
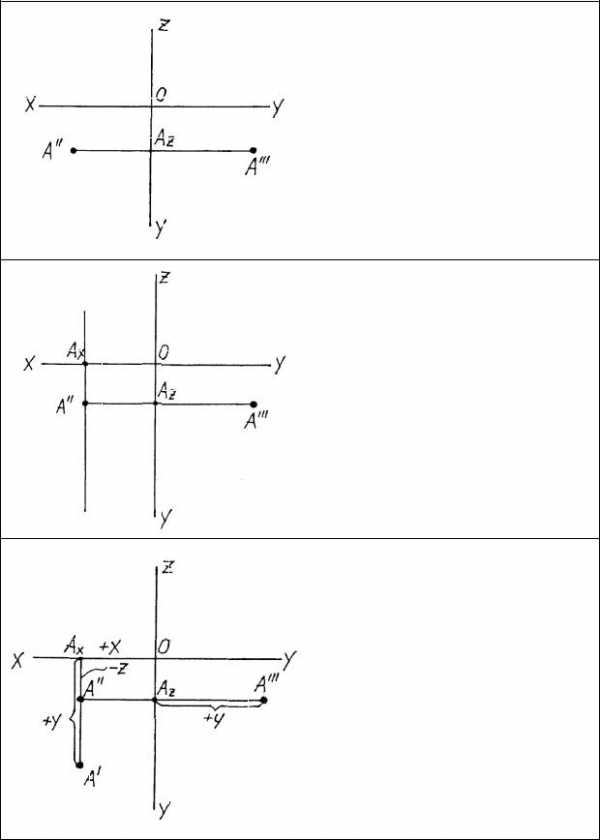
Построение недостающей проекции точки
Предположим, задан эпюр точки А в двух проекцияхА// и А///. Требуется построить недостающую горизонтальную проекцию А/. Построения будем проводить, используя свойства эпюра Монжа.
Так как горизонтальная проекция точки А/ находится на одной вертикальной линии связи с фронтальной проекцией точки А//, то через точку А// проводим эту линию связи. На оси ОХ получаем точку АX.
Недостающая проекция А/ | опре- | ||
деляется | координатами X | и Y. | |
Координата X известна, а коор- | |||
динату Y берем с профильной | |||
проекции (отрезок Аz А///). Так как | |||
отрезок | отложен | вправо, то | |
значит координата Y имеет знак +. | |||
Замеряем | координату Y и от- | ||
кладываем ее от точкиAX вдоль | |||
линии связи вниз. Получаем | |||
искомую | проекцию А/. Точка А | ||
имеет знаки координат (+, +, -) и | |||
находится в IV октанте. |
|
| |
studfiles.net
Ортогональные (прямоугольные) проекции точки. Эпюр Монжа
Изложенный французским ученым Г. Монжем в 1795 г. метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций обеспечил точность и удобную измеримость изображений, т. е. возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путем простых приемов определить размеры отрезков линий и фигур. На практике при изображении различных геометрических объектов, для более полного представления о их формах и размерах, используют третью – профильную – плоскость проекций W,расположенную перпендикулярно к H и V.
Рассмотрим прямоугольное проецирование точки А в системе трех взаимно перпендикулярных плоскостей проекций (рис. 4): горизонтальной Н (П1), фронтальной V (П2)и профильной W (П3). В пространстве эти плоскости образуют восемь трехгранных углов, называемых октантами. Линии пересечения соответствующих плоскостей проекций V, H, W называются осями проекций X, Y, Z. Каждый трехгранный угол (октант) ограничен полами плоскостей проекций, а каждая пола плоскости проекций – соответствующими осями.
Рекомендуется сделать макет октантов из какого-либо материала (плотной бумаги, картона и пр.), применив разную окраску плоскостей проекций. Необходимо внимательно разобраться в пространственной модели плоскостей проекций (рис. 4) и запомнить расположение октантов, какими полами они ограничены.
Например, октант І ограничен верхней левой полой плоскости проекций V, передней левой полой плоскости проекций Н и передней верхней полой плоскости проекций W; октант VІІ ограничен задней правой полой плоскости проекций Н, нижней правой полой плоскости проекций V и задней нижней полой плоскости проекций W.
Например, над горизонтальной плоскостью проекций находятся І, ІІ, V, VІ октанты, справа от профильной плоскости проекций находятся октанты V, VІ, VІІ, VІІІ.
Желательно несколько раз правильно вычертить пространственную модель октантов.
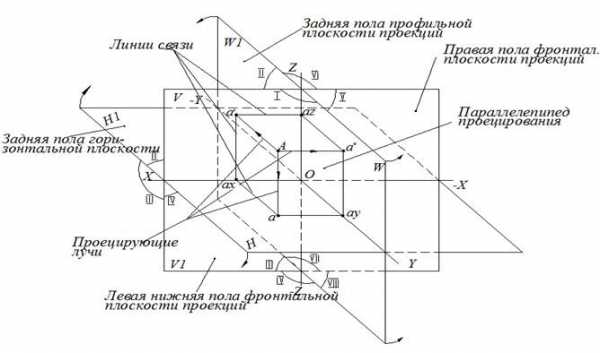
Рис. 4. Пространственная модель октантов:
проецирование точки А
Положение точки А в пространстве определяется расстоянием ее от плоскостей проекций H, V, W. Для определения этих расстояний через точку А следует провести проецирующие лучи, перпендикулярные к плоскостям проекций, определить точки встречи этих лучей с плоскостями проекций. Полученные изображения являются проекциями данной точки: горизонтальной проекцией «а», фронтальной проекцией «а′», профильной «а′′» (рис. 4).
Пользоваться пространственным макетом для отображения ортогональных проекций геометрических фигур неудобно ввиду его громоздкости, а также из-за того, что при его переносе на лист бумаги, на плоскостях H и W происходит искажение формы и размеров проецируемой фигуры. Поэтому вместо изображения на чертеже пространственного макета используется эпюр Монжа(франц. epure – чертеж).
Для получения плоской модели плоскостей проекций необходимо преобразовать пространственную модель октантов так (см. стрелки на рис. 4), что фронтальная плоскость проекций V остается в первоначальном положении, а горизонтальная плоскость проекций Н, передняя ее пола, вращаясь вокруг оси Х, откидывается вниз до совмещения с нижней полой плоскости проекций V. Профильная плоскость проекций W, передняя ее пола, вращаясь вокруг оси Z, уходит вправо до совмещения с правой полой плоскости проекций V.
Плоскости проекций являются жесткими, их деление на полы осями X, Y, Z условно, следовательно, при поворотах задняя пола плоскости проекций Н совмещается с верхней полой плоскости проекций V, а задняя пола плоскости проекций W уходит влево, совмещаясь с левой полой плоскости проекций V (рис. 4). Проекции а, а′, а′′ связаны между собой линиями связи – проекциями проецирующих лучей, исходящих из точки А.
При вращении плоскостей проекций каждая линия связи с соответствующей проекцией точки займет определенное положение относительно осей проекций. Рассматривая параллелепипед проецирования и эпюр Монжа (рис. 4 и 5) делаем выводы, что:
1) фронтальная а′ и горизонтальная а проекции точки А лежат на одной линии связи, перпендикулярной оси Х;
2) фронтальная а′ и профильная а′′ проекции точки А лежат на одной линии связи, перпендикулярной оси Z;
3) удаление профильной проекции а′′ точки А от оси Z равно удалению горизонтальной проекции этой точки от оси Х.
Эти три положения справедливы для точки, лежащей в любом из восьми октантов. Так как плоскости не имеют границ, то в совмещенном положении (на эпюре) эти границы не показывают, нет необходимости оставлять надписи, указывающие положение пол плоскостей проекций. Тогда в окончательном виде эпюр Монжа, заменяющий чертеж пространственного макета, примет вид, показанный на рис. 5.
Рассмотрим несколько задач на построение заданных точек на эпюре Монжа.
Задача. Построить проекции произвольных точек В и С, находящихся во ІІ и V октантах.
Решение. Точка В:
Рассматривая точку В во ІІ октанте (рис. 6а), отмечаем, что при преобразовании его в плоскую модель фронтальная и горизонтальная проекции точки будут находиться выше оси Х, а профильная проекция точки В будет располагаться по линии связи слева от оси Z.
Порядок выполнения графической части задачи (рис. 6б):
1. На оси Х слева от точки О берем произвольную точку bХ.
2. Через точку bХ проводим линию связи перпендикулярно оси Х.
3. На линии связи (выше оси Х) произвольно отмечаем точки b и b′.
4. Строим луч [b′) ⊥ Z и отмечаем точку bZ.
5. От точки bZ влево на линии связи отмечаем точку b′′,причем [b′′bX] = [bbX].
6. Анализ расположения точки В относительно плоскостей проекций: точка В ближе к плоскости проекций Н, т. к. |bX | < |b′X|.
7. Рекомендуется рассмотреть различные комбинации расположения проекций b и b′: проекции b и b′ совпадают, проекция b выше точки b′.
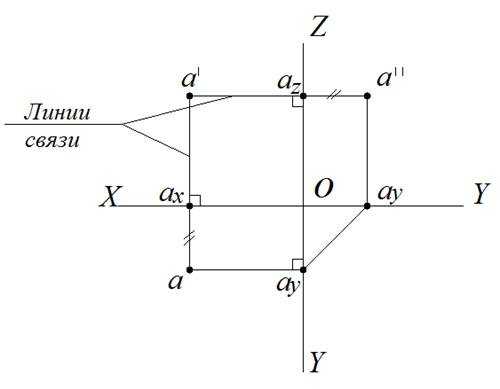
Рис. 5. Эпюр Монжа точки А в І октанте

Рис. 6. Точка В во ІІ октанте:
а – точка В в пространственной модели; б – точка В на эпюре Монжа
Точка С:
Рассматриваем точку С в V октанте (рис. 7а). Линии связи с проекциями точек с′ и с′′ будут располагаться при совмещении плоскостей проекций V и W справа от оси Z. Горизонтальная проекция точки С будет находиться ниже оси Х, т. к. плоскость проекций Н при повороте откидывается вниз.
Рассматриваем точку С в V октанте (рис. 7а). Линии связи с проекциями точек с′ и с′′ будут располагаться при совмещении плоскостей проекций V и W справа от оси Z. Горизонтальная проекция С будет находиться ниже оси Х, т. к. плоскость проекций Н при повороте откидывается вниз.
Построение проекций точки С (рис. 7б):
1. На оси Х вправо от точки О произвольно отмечаем току сX.
2. Через точку сXпроводим линию связи перпендикулярно оси Х.
3. На линии связи произвольно отмечаем точку с′ (выше оси Х) и точку с (ниже оси Х).
4. Строим [с′) ⊥ Z и на луче строим точку с′′ (справа от оси Z), причем |с′′сZ| = |ccX|.
5. Анализ: точка С отстоит дальше от плоскости проекций V, т. к. |с, Х | > |с′, Х|.
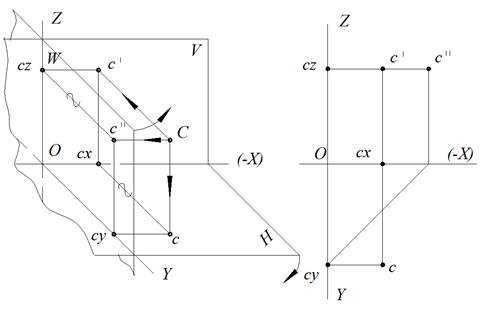
Рис. 7. Точка С в V октанте:
а – точка С в пространственной модели; б – точка С на эпюре Монжа
infopedia.su