1.1.3. Определение грузоподъемности статически определимой конструкции, работающей на растяжение-сжатие (задача № 3) Условие задачи
Рис. 1.5. Схема конструкции в задаче № 3
Конструкция, состоящая из стержней, соединенных шарнирами, загружена силойF(рис. 1.5). Сечения стержней – из стальных прокатных профилей. Площади сечений нужно взять из сортамента (смотри, например, в [1]). Цель расчета:определить значение допускаемой нагрузки;
найти перемещение узла С.
Примечание. Если на схеме, выбранной студентом по [4], один стержень показан более жирным, то его следует считать абсолютно жестким, т. е. деформациями этого стержня следует пренебречь.
Решение
Рис. 1.6. План сил
Для определения усилий используем метод сечений. Для этого нарисуем план сил: рассечем деформируемые стержни конструкции и отброшенные части стержней заменим продольными силамиN1иN2(рис.
и. Откуда
и.
Знак минус показывает, что направление усилия в стержне 2 противоположно показанному на рис. 1.6, т. е. стержень 2 сжат.
Определим напряжения по (1.1) и выберем наиболее напряженный стержень (допустим, что в рассматриваемой задаче это будет стержень 1).
Из условия прочности этого стержня получим значение допускаемой нагрузки:
,.
Найдем перемещение узла С, построив
план перемещений (рис. 1.7). Предварительно
найдем абсолютные деформации стержней l1 иl2по
формуле (1. 3). В рассматриваемой задаче
растянутый стержень 1 будет удлиняться,
а сжатый стержень 2 – укорачиваться.
Для построения плана перемещений
нарисуем схему конструкции в масштабе
и отложим отрезкиl1иl2вдоль
оси каждого стержня, выбрав масштаб для
деформаций так, чтобы картинка плана
перемещений была наглядной. В процессе
деформации стержни поворачиваются
относительно точекА иВ по
дугам. Из-за малости деформаций эти дуги
заменяем касательными, т. е. перпендикулярами
к направлениям стержней (отрезкиина рис. 1.7). На пересечении дуг
(перпендикуляров к направлениям стержней)
находится новое положение узлаCпосле деформации – точкана
рис. 1.7. Вертикальное и горизонтальное
перемещение узлаCдопускается
определять по масштабу, не делая сложных
геометрических выкладок.
3). В рассматриваемой задаче
растянутый стержень 1 будет удлиняться,
а сжатый стержень 2 – укорачиваться.
Для построения плана перемещений
нарисуем схему конструкции в масштабе
и отложим отрезкиl1иl2вдоль
оси каждого стержня, выбрав масштаб для
деформаций так, чтобы картинка плана
перемещений была наглядной. В процессе
деформации стержни поворачиваются
относительно точекА иВ по
дугам. Из-за малости деформаций эти дуги
заменяем касательными, т. е. перпендикулярами
к направлениям стержней (отрезкиина рис. 1.7). На пересечении дуг
(перпендикуляров к направлениям стержней)
находится новое положение узлаCпосле деформации – точкана
рис. 1.7. Вертикальное и горизонтальное
перемещение узлаCдопускается
определять по масштабу, не делая сложных
геометрических выкладок.
Рис. 1.7. План перемещений
Примечание.Если конструкция имеет абсолютно жесткий стержень, то принцип построения плана перемещений тот же.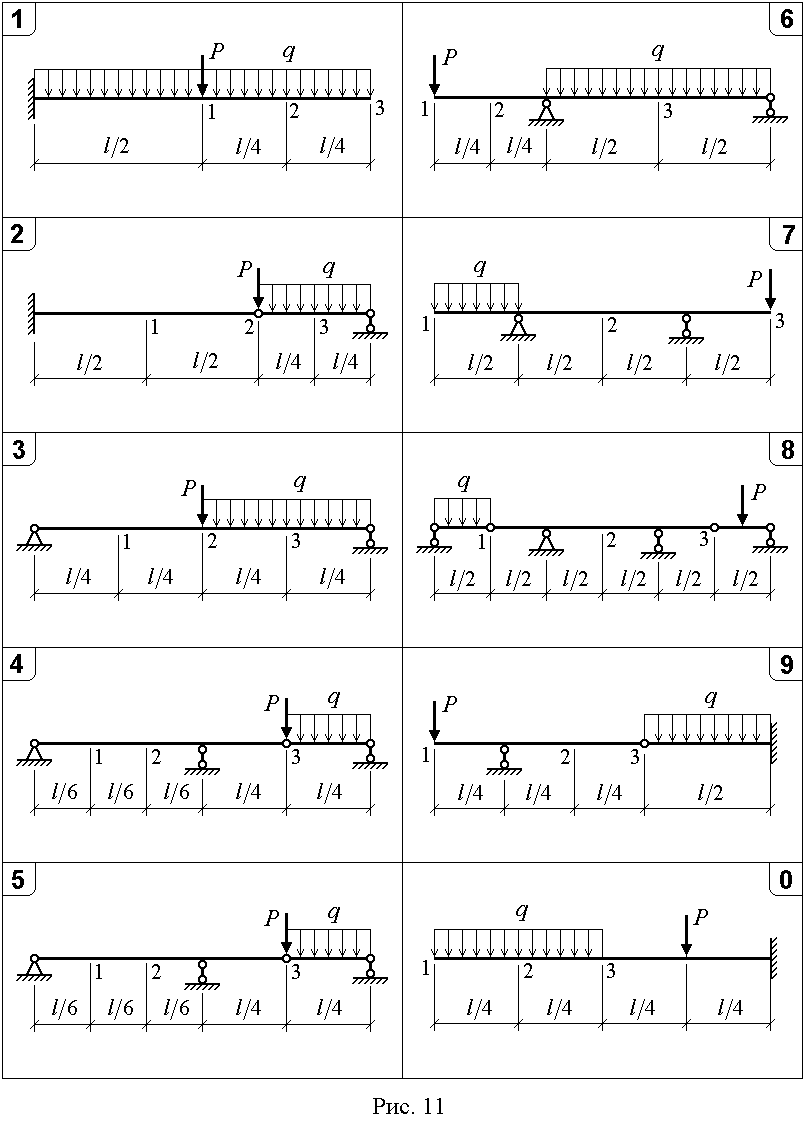 Все точки абсолютно жесткого
стержня могут перемещаться только по
дугам (перпендикулярам к направлению
стержня), поворачиваясь вокруг неподвижного
шарнира. Например, если стерженьАСна рис. 1.7 считать абсолютно жестким,
то точкаС переместится в положениеи горизонтальное перемещение узлаСбудет равно нулю.
Все точки абсолютно жесткого
стержня могут перемещаться только по
дугам (перпендикулярам к направлению
стержня), поворачиваясь вокруг неподвижного
шарнира. Например, если стерженьАСна рис. 1.7 считать абсолютно жестким,
то точкаС переместится в положениеи горизонтальное перемещение узлаСбудет равно нулю.1.2. Расчет статически неопределимых стержневых систем Основные определения
Статически неопределимая система– система, в которой количество неизвестных (опорных реакций, внутренних усилий) больше числа независимых уравнений статики, составляемых для рассматриваемой системы (конструкции). Таким образом, в статически неопределимой системе невозможно найти все неизвестные, пользуясь только уравнениями равновесия. Разность между количеством неизвестных и числом независимых уравнений статики называется степенью статической неопределимости.
Конструкции, состоящие из стержней,
соединенных шарнирами, называются шарнирно-стержневыми. В этих
конструкциях есть стержни, которые
обеспечивают геометрическую неизменяемость
конструкции и при удалении которых
система превращается в механизм. Такие
стержни будем называтьнеобходимыми.
Если же при удалении некоторых стержней
геометрическая неизменяемость конструкции
не нарушается, то такие стержни назовемлишними. В статически определимой
системе есть только необходимые стержни,
в статически неопределимой – число
лишних стержней равно степени статической
неопределимости.
В этих
конструкциях есть стержни, которые
обеспечивают геометрическую неизменяемость
конструкции и при удалении которых
система превращается в механизм. Такие
стержни будем называтьнеобходимыми.
Если же при удалении некоторых стержней
геометрическая неизменяемость конструкции
не нарушается, то такие стержни назовемлишними. В статически определимой
системе есть только необходимые стержни,
в статически неопределимой – число
лишних стержней равно степени статической
неопределимости.
Порядок определения всех неизвестных в статически неопределимых конструкциях (раскрытия статической неопределимости) следующий:
записываем необходимые для определения внутренних усилий и опорных реакций уравнения равновесия;
составляем уравнения совместности деформаций (геометри-ческие уравнения). Количество уравнений совместности деформаций равно степени статической неопределимости;
записываем физические уравнения, связывающие усилия и деформации;
решая полученную систему уравнений, находим все неизвестные.
Если в качестве физических уравнений
используется закон Гука, то такой способ
расчета носит название расчета по
упругой стадии деформаций. После
определения внутренних усилий –
продольных сил в стержнях статически
неопределимой системы – встает задача
обеспечения ее прочности. При расчете
по упругой стадии деформаций считается,
что предельное состояние конструкции
наступает тогда, когда один, наиболее
напряженный, стержень переходит в
предельное состояние (разрушится или
потечет). Поэтому после определения
усилий по этому способу находим напряжения
в стержнях и выбираем стержень, в котором
действует максимальное напряжение. Из
условия прочности этого наиболее
напряженного стержня либо вычисляем
допускаемую нагрузку, либо подбираем
сечения стержней. Следует отметить, что
в большинстве статически неопределимых
конструкций в результате расчета по
этому способу только в одном стержне
напряжения будут равны допускаемым,
остальные же стержни будут недогружены.
Второй способ расчета статически
неопределимых стержневых систем носит
название расчета по предельному
пластическому состоянию.2Благодаря наличию лишних стержней в
статически неопределимой системе,
наступление состояния текучести в одном
(наиболее напряженном) стержне еще не
приводит к нарушению геометрической
неизменяемости всей конструкции.
Остальные стержни, оставаясь упругими,
препятствуют пластическим деформациям
этого стержня. Конструкция продолжает
выполнять свое назначение, перейдя из
упругой стадии работы в упругопластическую.
При увеличении нагрузки в пластическую
стадию работы вовлекаются все новые
стержни. И только тогда, когда в системе
потекутвсе лишние стержни и хотя быодин необходимый,
конструкция превращается в механизм и
не может выполнять свои функции.
определяем, сколько стержней должно потечь, чтобы конструкция превратилась в механизм. Дальнейший расчет возможен по двум вариантам:
если в предельном состоянии текут все стержни системы, то, составляя уравнения равновесия конструкции в предельном состоянии, находим из него значение предельной нагрузки ;
если в предельном состоянии течет только часть стержней, то, не определяя порядка перехода стержней в пластическое состояние, рассматриваем все кинематически возможные варианты предельного состояния конструкции. Находим из уравнений равновесия предельную нагрузку для каждого варианта. Выбираем из всех вариантов минимальное значение предельной нагрузки ;
2) из условия прочности конструкции по
предельному состоянию
либо вычисляем допускаемую нагрузку,
либо подбираем сечения стержней.
Отметим, что расчет по предельному пластическому состоянию является более экономичным, чем расчет по упругой стадии деформаций. Поэтому при сравнении результатов расчета по двум способам должно получиться, что допускаемая нагрузка, найденная расчетом по предельному пластическому состоянию, всегда не меньше нагрузки, полученной расчетом по упругой стадии деформации. Соответственно площади сечений стержней, найденные расчетом по предельному состоянию, должны быть не больше площадей сечений, полученных расчетом по упругой стадии деформаций.
404 Cтраница не найдена
Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.
Размер:
AAAИзображения
Вкл. Выкл.
Выкл.
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
1.
 5: Внутренние силы в плоских фермах
5: Внутренние силы в плоских фермах- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 17611
- Феликс Удойо
- Университет Темпл
Глава 5
Внутренние силы в плоских фермах
5.1 Введение
Ферма представляет собой конструкцию, состоящую из прямых тонких элементов, соединенных на концах штифтами или шарнирами без трения. Ферму можно разделить на простую, составную или сложную. Простая ферма состоит из трех тонких элементов, образующих базовую треугольную ячейку. Дополнительные соединения могут быть сформированы в ферме путем последовательного добавления двух элементов в базовую ячейку, как показано на рисунке 5. 1a. Составная ферма состоит из двух или более простых ферм, соединенных вместе, как показано на рис. 5.1b. Сложная ферма не является ни простой, ни составной, как показано на рис. 5.1c; его анализ является более строгим, чем у ранее заявленных ферм.
1a. Составная ферма состоит из двух или более простых ферм, соединенных вместе, как показано на рис. 5.1b. Сложная ферма не является ни простой, ни составной, как показано на рис. 5.1c; его анализ является более строгим, чем у ранее заявленных ферм.
5.2 Типы ферм
Ниже приведены примеры различных типов ферм для мостов и крыш.
Рис. 5.2. Обычно используемые мостовые фермы. Рис. 5.3. Часто используемые стропильные фермы.5.3 Определенность и устойчивость ферм
Условия определенности, неопределенности и неустойчивости ферм можно сформулировать следующим образом:
где
м = количество элементов.
r = количество реакций поддержки.
j = количество соединений.
5.4 Допущения при анализе ферм
1. Стержни соединены на концах штифтами без трения.
2. Стержни прямые, поэтому на них действуют только осевые силы.
3. Деформации элементов под действием нагрузок пренебрежимо малы и имеют незначительную величину, вызывающую заметные изменения геометрии конструкции.
4. Нагрузки действуют только на соединения из-за расположения элементов.
5.5 Совместная идентификация и обозначения членов
Соединения ферм можно идентифицировать с помощью букв или цифр, в зависимости от предпочтений аналитика. Тем не менее, необходимо поддерживать согласованность выбранного способа идентификации, чтобы избежать путаницы во время анализа. Сила стержня может быть представлена любой буквой ( F или N или S ) с двумя нижними индексами, обозначающими элемент. Например, усилие на элемент F AB в ферме, показанной на рисунке 5.4, представляет собой усилие в соединительных узлах элемента 9.0052 А и В .
Рис. 5.4. Совместная идентификация ( a ) и усилие на стержне ( b ).Пример 5.1
Классифицируйте фермы, показанные на рис. 5.5–рис. 5.9, как устойчивые, детерминированные или недетерминированные, и при необходимости укажите степень неопределенности.
Рис. 5.5. Ферма.
5.5. Ферма.r = 3, м = 9, j = 6. Из уравнения 3.5 9 + 3 = 2(6). Статически определим.
Рис. 5.6. Ферма.г = 3, m = 10, j = 6. Из уравнения 3.5 10 + 3 > 2(6). Статически неопределимы с точностью до 1°.
Рис. 5.7. Ферма.r = 3, м = 9, j = 6. Из уравнения 3.5 9 + 3 = 2(6). Статически определим.
Рис. 5.8. Ферма.r = 3, м = 24, j = 14. Из уравнения 3.5 24 + 3 < 2(14). Статически неустойчив.
Рис. 5.9. Ферма.r = 5, м = 11, j = 7. Из уравнения 3.5 11 + 5 > 2(7).
Сатически неопределенно до 2°.
5.6 Методы анализа ферм
Существует несколько методов анализа ферм, но наиболее распространены два метода: метод соединения и метод сечения (или момента).
5.6.1 Соглашение о знаках
При расчете ферм отрицательная осевая сила на элементе означает, что элемент или соединения на обоих концах элемента находятся в сжатом состоянии, тогда как положительное значение осевой силы на элементе указывает на то, что элемент или соединения на обоих концах элемента находятся в состоянии растяжения.
5.6.2 Анализ ферм методом соединения
Этот метод основан на том принципе, что если структурная система представляет собой тело, находящееся в равновесии, то любое соединение в этой системе также находится в равновесии и, таким образом, может быть выделено из всей системы и проанализировано с использованием условий равновесия. Метод соединения включает в себя последовательную изоляцию каждого соединения в системе ферм и определение осевых усилий в элементах, встречающихся в соединении, с помощью уравнений равновесия. Подробная процедура анализа этим методом изложена ниже.
Процедура анализа
• Проверьте устойчивость и определенность конструкции. Если ферма устойчива и детерминирована, переходите к следующему шагу.
•Определить опорные реакции в ферме.
•Определить элементы нулевой силы в системе. Это неизмеримо сократит вычислительные усилия, связанные с анализом.
•Выберите соединение для анализа. Ни в коем случае в анализируемом соединении не должно быть более двух неизвестных сил стержня.
• Начертите изолированную диаграмму свободного тела выбранного соединения и обозначьте осевые силы во всех элементах, встречающихся в соединении, как растягивающие (т.е. отрывающие от соединения). Если это первоначальное допущение неверно, определенная осевая сила стержня при анализе будет отрицательной, что означает, что стержень находится в состоянии сжатия, а не растяжения.
• Примените два уравнения Σ F x = 0 и Σ F y = 0, чтобы определить осевые силы стержня.
•Продолжить анализ, перейдя к следующему соединению с двумя или меньшим количеством неизвестных сил-членов.
Пример 5.2
Используя метод соединения, определите осевую силу в каждом элементе фермы, показанной на рис. 5.10а.
Рис. 5.10. Ферма.Решение
Реакции поддержки. Применяя уравнения статического равновесия к диаграмме свободного тела, показанной на рис. 5.10б, опорные реакции можно определить следующим образом:
Рис. 5.10в. Две неизвестные силы изначально предполагаются растягивающими (т.е. отрывающими от сустава). Если это исходное предположение неверно, расчетные значения осевых сил будут отрицательными, что означает сжатие.
5.10в. Две неизвестные силы изначально предполагаются растягивающими (т.е. отрывающими от сустава). Если это исходное предположение неверно, расчетные значения осевых сил будут отрицательными, что означает сжатие.Анализ соединения A .
После завершения анализа соединения A, соединения B или D можно проанализировать, так как есть только две неизвестные силы.
Анализ соединения D .
Анализ соединения B .
5.6.3 Члены Zero Force
Анализ сложной фермы можно значительно упростить, если сначала определить «элементы с нулевой силой». Элемент с нулевой силой — это элемент, который не подвергается какой-либо осевой нагрузке. Иногда такие элементы вводят в систему ферм, чтобы предотвратить коробление и вибрацию других элементов. Конструкции ферменных элементов, приводящие к элементам нулевой силы, перечислены ниже:
1. Если существует неколлинеарность между двумя элементами, встречающимися в стыке, на который не действует никакая внешняя сила, то эти два элемента являются элементами с нулевой силой (см.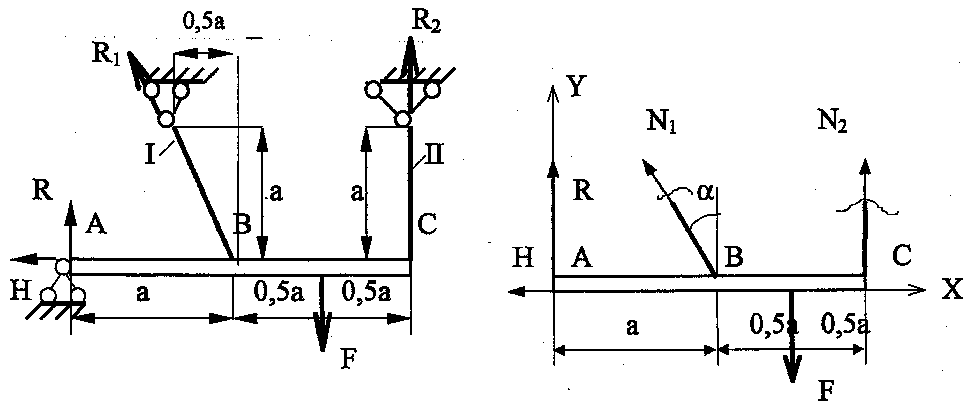 рис. 5.11а).
рис. 5.11а).
2. Если три элемента встречаются в стыке без внешней силы, а два из них лежат на одной прямой, третий элемент является элементом с нулевой силой (см. рис. 5.11b).
3. Если два стержня встречаются в стыке, и сила, приложенная к стыку, параллельна одному стержню и перпендикулярна другому, то стержень, перпендикулярный приложенной силе, является элементом с нулевой силой (см. рис. 5.11c).
Рис. 5.11. Члены нулевой силы.5.6.4 Анализ ферм методом раздела
Иногда определение осевой силы в конкретных элементах ферменной системы методом соединения может быть очень трудоемким и громоздким, особенно когда система состоит из нескольких элементов. В таких случаях использование метода сечения может сэкономить время и поэтому предпочтительнее. Этот метод включает в себя прохождение воображаемого сечения через ферму так, чтобы оно делило систему на две части и прорезало элементы, осевые усилия которых желательны. Осевые силы стержня затем определяются с использованием условий равновесия. Подробная процедура анализа этим методом представлена ниже.
Подробная процедура анализа этим методом представлена ниже.
Процедура анализа ферм методом раздела
•Проверьте устойчивость и определенность конструкции. Если ферма устойчива и детерминирована, переходите к следующему шагу.
•Определить опорные реакции в ферме.
• Сделайте воображаемый разрез в конструкции так, чтобы он включал элементы, осевые усилия которых нужны. Воображаемый разрез делит ферму на две части.
• Прилагайте усилия к каждой части фермы, чтобы удерживать ее в равновесии.
• Выберите любую часть фермы для определения сил стержня.
• Применение условий равновесия для определения осевых усилий стержня.
Пример 5.3
Используя метод сечения, определите осевые усилия в элементах CD , CG и HG фермы, показанной на рисунке 5.12a.
Рис. 5.12. Ферма.Решение
Реакции поддержки. Применяя уравнения статического равновесия к диаграмме свободного тела на рис. 5.12b, опорные реакции можно определить следующим образом:
Рисунок 5. 12d. Все силы, воздействующие на стержень, обозначаются как силы растяжения (т. е. отрыв от соединения). Если это первоначальное предположение неверно, расчетные силы на стержнях будут отрицательными, что указывает на то, что они сжимаются. Любая из двух частей может быть использована для анализа. Левая часть будет использоваться для определения сил стержня в этом примере. Применяя уравнение равновесия к левому сегменту фермы, осевые силы в элементах можно определить следующим образом:
12d. Все силы, воздействующие на стержень, обозначаются как силы растяжения (т. е. отрыв от соединения). Если это первоначальное предположение неверно, расчетные силы на стержнях будут отрицательными, что указывает на то, что они сжимаются. Любая из двух частей может быть использована для анализа. Левая часть будет использоваться для определения сил стержня в этом примере. Применяя уравнение равновесия к левому сегменту фермы, осевые силы в элементах можно определить следующим образом:Осевая сила в элементе CD . Чтобы определить осевую силу в стержне CD, , найдите момент относительно соединения в ферме, где только CD будет иметь момент относительно этого соединения, а все остальные разрезанные элементы не будут иметь момента. Тщательный осмотр покажет, что соединение, отвечающее этому требованию, — это соединение G . Таким образом, принятие момента около G предполагает следующее:
Осевая сила в стержне HG .
Осевая сила в элементе CG . Осевая сила в элементе CG определяется с учетом вертикального равновесия левой части. Таким образом,
Осевая сила в элементе CG определяется с учетом вертикального равновесия левой части. Таким образом,
Резюме главы
Внутренние силы в плоских фермах: Фермы представляют собой конструктивные системы, состоящие из прямых и гибких элементов, соединенных на концах. Допущения при расчете плоских ферм включают следующее:
1.Элементы ферм соединены на концах безфрикционными штифтами.
2. Стержни прямые и подвергаются осевым нагрузкам.
3. Деформации элементов малы и пренебрежимо малы.
4. Нагрузки в фермах действуют только на их соединения.
Элементы фермы могут подвергаться осевому сжатию или осевому растяжению. Осевое сжатие элементов всегда считается отрицательным, а осевое растяжение всегда считается положительным.
Фермы могут быть внешне или внутренне определенными или неопределенными. Внешне детерминированные фермы — это фермы, неизвестные внешние реакции которых можно определить, используя только уравнение статического равновесия. Внешне неопределенными называют фермы, внешняя неизвестная реакция которых не может быть полностью определена с помощью уравнений равновесия. Для определения числа неизвестных реакций, превышающих уравнение равновесия неопределенных ферм, необходимо составить дополнительные уравнения, исходя из совместимости частей системы. Внутренне определенные фермы — это фермы, элементы которых расположены таким образом, что образуется ровно столько треугольных ячеек, чтобы предотвратить геометрическую нестабильность системы.
Внешне неопределенными называют фермы, внешняя неизвестная реакция которых не может быть полностью определена с помощью уравнений равновесия. Для определения числа неизвестных реакций, превышающих уравнение равновесия неопределенных ферм, необходимо составить дополнительные уравнения, исходя из совместимости частей системы. Внутренне определенные фермы — это фермы, элементы которых расположены таким образом, что образуется ровно столько треугольных ячеек, чтобы предотвратить геометрическую нестабильность системы.
Формулировка устойчивости и определенности в фермах следующая:
м + r < 2 j Конструкция неустойчивая
m + r = 2 j Структура определенная
m + r > 2 j Структура не определена
Методы анализа ферм: Двумя распространенными методами расчета ферм являются метод соединения и метод сечения (или момента).
Метод соединения : Этот метод включает изоляцию каждого соединения фермы и учет равновесия соединения при определении осевой силы элемента. Два уравнения, используемые для определения осевых усилий на стержне: ∑ F x = 0 и ∑ F y = 0. Соединения последовательно изолируются для анализа на основе принципа, согласно которому количество неизвестных осевых усилий на стержне должно никогда не должно быть более двух человек в рассматриваемом совместном самолете.
Два уравнения, используемые для определения осевых усилий на стержне: ∑ F x = 0 и ∑ F y = 0. Соединения последовательно изолируются для анализа на основе принципа, согласно которому количество неизвестных осевых усилий на стержне должно никогда не должно быть более двух человек в рассматриваемом совместном самолете.
Метод сечения: Этот метод включает в себя прохождение воображаемого сечения через ферму, чтобы разделить ее на две части. Силы стержня определяются с учетом равновесия части фермы по обе стороны от сечения. Этот метод удобен, когда требуются осевые усилия в определенных элементах в ферме с несколькими элементами.
Практические задачи
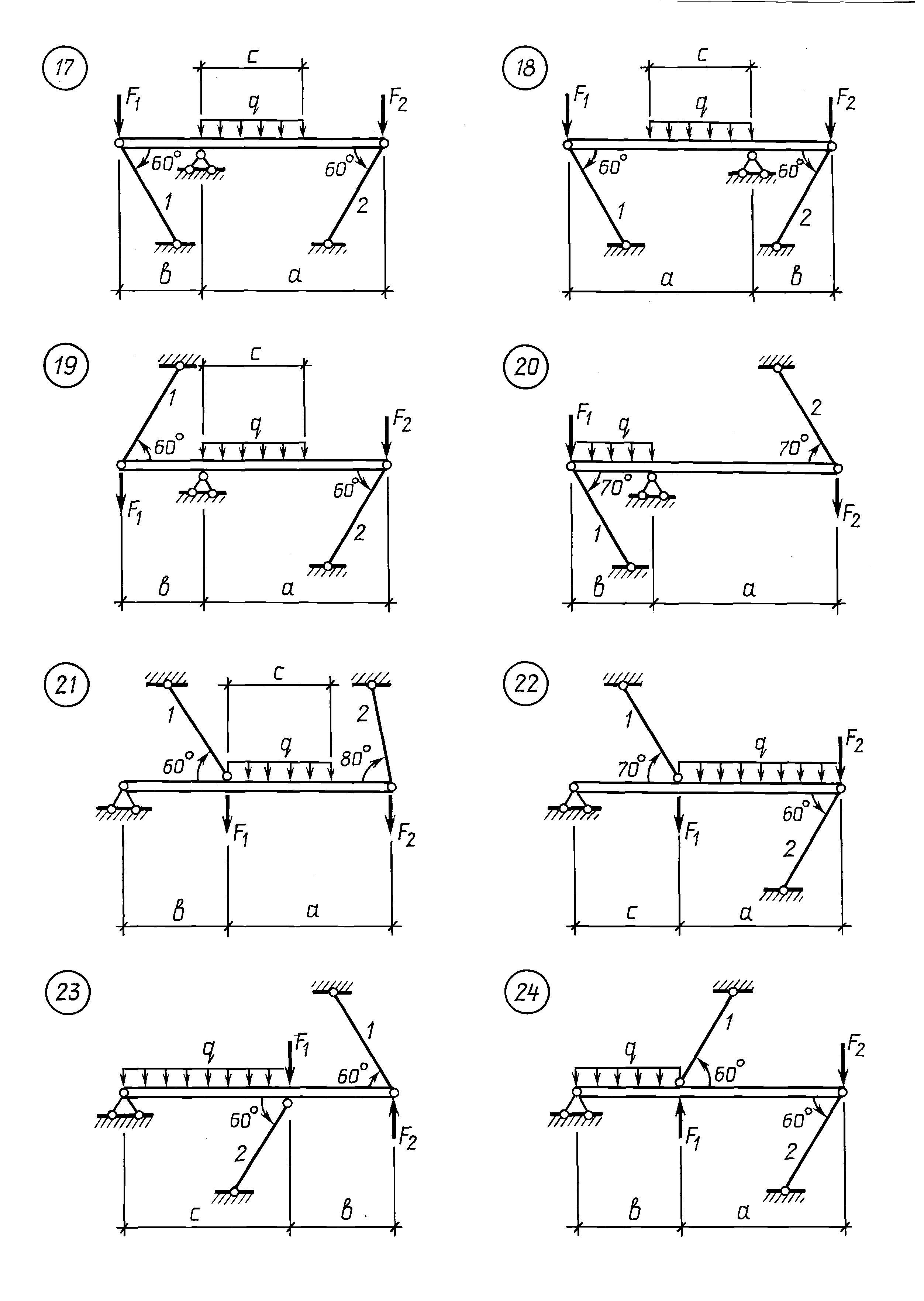
5.1 Классифицируйте фермы, показанные на рис. P5.1a–рис. P5.1r.
P5.1. Классификация ферм.
5.2 Определите усилие в каждом элементе ферм, показанных на рис. P5.2–рис. P5.12, используя метод соединения.
5.3 Используя метод сечения, определите усилия в элементах, обозначенных X, ферм, показанных на рис. P5.13–P5.19..
Рис. П5.13. Ферма.Рис. P5.14. Ферма.Рис. P5.15. Ферма.Рис. P5.16. Ферма.Рис. P5.17. Ферма.Рис. P5.18. Ферма.Рис. P5.19. Ферма.Эта страница под названием 1.5: Внутренние силы в плоских фермах используется в соответствии с лицензией CC BY-NC-ND 4.0 и была создана, изменена и/или курирована Феликсом Удоэйо посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Феликс Удоэйо
- Лицензия
- CC BY-NC-ND
- Версия лицензии
- 4,0
- Теги
- источник@https://temple.
 manifoldapp.org/projects/structural-analysis
manifoldapp.org/projects/structural-analysis
- источник@https://temple.
Расчет армирования статически неопределимой фермы
Скачать книгу PDF
Скачать книгу в формате EPUB
Расчет армирования статически неопределимой фермы
Скачать книгу PDF
Скачать книгу в формате EPUB
- Цзыи Лян 9 ,
- Минджун Вэй 10 и
- Лун Ю 11
- Глава .
- Открытый доступ
- Первый онлайн:
1131 Доступ
Часть серии книг Lecture Notes in Civil Engineering (LNCE, том 286)
Abstract
С замедлением темпов урбанизации и новых зданий в Китае старые дома имеют разную степень проблем с безопасностью. Поэтому все более очевидной становится важность усиления и реконструкции старых домов. Эта статья предназначена для изучения статически неопределимых ферм в зданиях. На основе конечно-элементного анализа сравнивается влияние метода увеличения площади сечения на исходную ферменную конструкцию путем установления схемы реконструкции той же статически неопределимой фермы. Результаты численного моделирования показывают, что предельная несущая способность конструкции увеличивается для достижения цели усиления.
Ключевые слова
- Неопределенная ферма
- Армирование
- Усиление
Цзыи Лян, Минцзюнь Вэй и Лун Юй внесли равный вклад.
Скачать главу в формате PDF
1 Введение
Во время фактического использования конструкции здания на нее будет воздействовать внешняя среда. Следовательно, в определенной степени будут затронуты устойчивость и прочность самого здания, особенно надежность строительной конструкции. Исследование процесса развития зарубежной строительной техники показывает, что, когда инженерное строительство достигнет определенной степени, армирование инженерной конструкции станет одним из основных методов строительства. Из соответствующих исследований видно, что гражданское строительство напрямую влияет на процесс урбанизации. Опираясь на историю развития развитых стран, начальным этапом урбанизации является создание масштабных новостроек. С тех пор город постепенно взрослел в процессе урбанизации, масштабы новых зданий продолжали снижаться, а затем постепенно увеличивалась доля старых домов, которые являются тремя этапами развития города. Если взять в качестве примера гражданское строительство в развитых странах, таких как Соединенное Королевство и Соединенные Штаты, стоимость реконструкции зданий в Соединенном Королевстве в 1978 было более чем в три раза, почти в четыре раза больше, чем в 1965 году. Индустрия ремонта старых домов растет. Согласно отчету об обзоре в Соединенных Штатах, тепло от ремонта старых домов должно было постепенно возрасти в будущем [1]. Развитие гражданского строительства в Китае относительно отсталое и началось относительно поздно. После землетрясения в Таншане национальная группа постепенно стала уделять больше внимания безопасности зданий, особенно старых зданий. Группа сформулировала ряд стандартов, во главе которых стоит стандарт сейсмической оценки промышленных сооружений на предмет сейсмобезопасности. Чтобы соответствовать постепенно улучшающимся строительным стандартам, в Китае также постепенно появляется индустрия укрепления старых зданий [2]. В настоящее время большинство экспертов и ученых провели много исследований по усилению ферменных конструкций на основе реальных случаев.
Если взять в качестве примера гражданское строительство в развитых странах, таких как Соединенное Королевство и Соединенные Штаты, стоимость реконструкции зданий в Соединенном Королевстве в 1978 было более чем в три раза, почти в четыре раза больше, чем в 1965 году. Индустрия ремонта старых домов растет. Согласно отчету об обзоре в Соединенных Штатах, тепло от ремонта старых домов должно было постепенно возрасти в будущем [1]. Развитие гражданского строительства в Китае относительно отсталое и началось относительно поздно. После землетрясения в Таншане национальная группа постепенно стала уделять больше внимания безопасности зданий, особенно старых зданий. Группа сформулировала ряд стандартов, во главе которых стоит стандарт сейсмической оценки промышленных сооружений на предмет сейсмобезопасности. Чтобы соответствовать постепенно улучшающимся строительным стандартам, в Китае также постепенно появляется индустрия укрепления старых зданий [2]. В настоящее время большинство экспертов и ученых провели много исследований по усилению ферменных конструкций на основе реальных случаев. Бай [3] увеличил сечение элемента ферменного перекрытия и достиг цели по усилению связи между верхним и нижним поясами ферменной арки, что играет важную роль в улучшении общих динамических характеристик конструкции после реконструкции. Ян и др. [4] принял метод расширенного сечения для усиления первоначальных элементов нижнего пояса при преобразовании ферменной конструкции коридора ленточного двора, так что из плоскости весь верхний пояс второго пролета исходного коридора может соответствовать требованиям. Ляо и др. [5] применили метод внешнего предварительного напряжения, чтобы существенно улучшить несущую способность компонентов трибуны и сузить или закрыть первоначальный зазор при преобразовании дуговой конструкции трибуны стадиона Wuhan Xinhua Road; он уменьшает прогиб компонентов и удобен в обслуживании, эффективно повышая жесткость здания. Хаяши и др. [6] предложил метод, сочетающий обучение с подкреплением и встраивание графа для оптимизации бинарной топологии ферменных конструкций, достигая цели минимизации общего объема конструкции при ограничениях напряжения и смещения.
Бай [3] увеличил сечение элемента ферменного перекрытия и достиг цели по усилению связи между верхним и нижним поясами ферменной арки, что играет важную роль в улучшении общих динамических характеристик конструкции после реконструкции. Ян и др. [4] принял метод расширенного сечения для усиления первоначальных элементов нижнего пояса при преобразовании ферменной конструкции коридора ленточного двора, так что из плоскости весь верхний пояс второго пролета исходного коридора может соответствовать требованиям. Ляо и др. [5] применили метод внешнего предварительного напряжения, чтобы существенно улучшить несущую способность компонентов трибуны и сузить или закрыть первоначальный зазор при преобразовании дуговой конструкции трибуны стадиона Wuhan Xinhua Road; он уменьшает прогиб компонентов и удобен в обслуживании, эффективно повышая жесткость здания. Хаяши и др. [6] предложил метод, сочетающий обучение с подкреплением и встраивание графа для оптимизации бинарной топологии ферменных конструкций, достигая цели минимизации общего объема конструкции при ограничениях напряжения и смещения.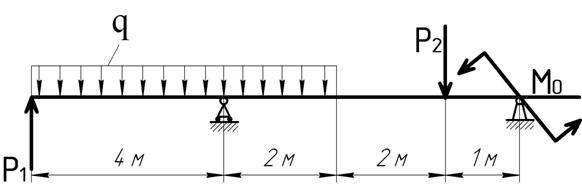 Обсуждая дефекты качества и методы армирования существующего цеха стальных конструкций, Го [7] указал, что, когда прочность стального материала недостаточна, следует применять такие методы армирования, как метод увеличения сечения и метод армирования стальными пластинами. обеспечить соответствие прочности материала требованиям несущей способности и устойчивости стропильной конструкции. Тем не менее, во всем мире относительно мало исследований армированной ферменной конструкции в зданиях. В этой статье обсуждается применение метода армирования, который изменяет площадь поперечного сечения фермы в ферменной конструкции, а программное обеспечение для анализа и расчета конечных элементов Abaqus используется для создания статически неопределимой имитационной модели фермы для имитации эффекта усиления. Основное содержание исследования заключается в следующем: (1) В этом документе излагаются характеристики напряжения статически неопределимой фермы. Затем он устанавливает конечно-элементную модель статически неопределимой фермы с помощью Abaqus.
Обсуждая дефекты качества и методы армирования существующего цеха стальных конструкций, Го [7] указал, что, когда прочность стального материала недостаточна, следует применять такие методы армирования, как метод увеличения сечения и метод армирования стальными пластинами. обеспечить соответствие прочности материала требованиям несущей способности и устойчивости стропильной конструкции. Тем не менее, во всем мире относительно мало исследований армированной ферменной конструкции в зданиях. В этой статье обсуждается применение метода армирования, который изменяет площадь поперечного сечения фермы в ферменной конструкции, а программное обеспечение для анализа и расчета конечных элементов Abaqus используется для создания статически неопределимой имитационной модели фермы для имитации эффекта усиления. Основное содержание исследования заключается в следующем: (1) В этом документе излагаются характеристики напряжения статически неопределимой фермы. Затем он устанавливает конечно-элементную модель статически неопределимой фермы с помощью Abaqus. После этого в работе производится расчет напряженного состояния фермы до армирования, при котором выясняется наиболее неблагоприятное сочетание нагрузок, и выбирается объект расчета армирования; (2) На основе конечно-элементной имитационной модели в статье подробно анализируется напряженное состояние ферм, укрепленных методом увеличения сечения, а также тенденция изменения напряжения и эффект армирования каждой контрольной секции.
После этого в работе производится расчет напряженного состояния фермы до армирования, при котором выясняется наиболее неблагоприятное сочетание нагрузок, и выбирается объект расчета армирования; (2) На основе конечно-элементной имитационной модели в статье подробно анализируется напряженное состояние ферм, укрепленных методом увеличения сечения, а также тенденция изменения напряжения и эффект армирования каждой контрольной секции.
2 Моделирование методом конечных элементов
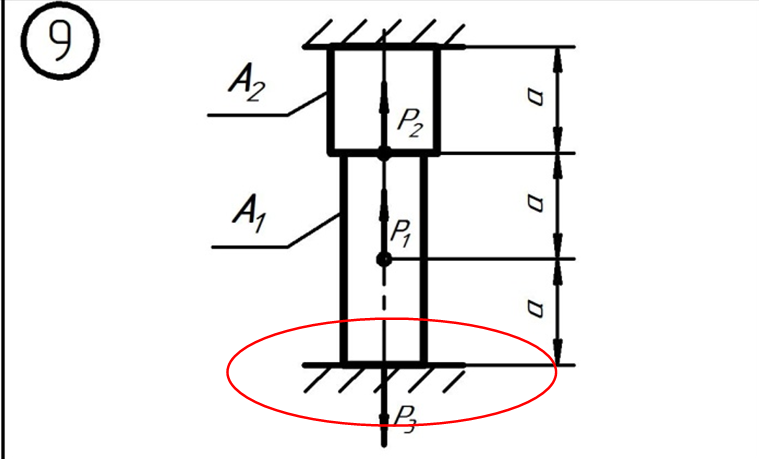
Для более наглядного анализа сходств и различий между двумя методами армирования для этого численного моделирования была выбрана типичная суперстационарная модель фермы. Модель фермы была разработана в соответствии с требованиями стандарта проектирования стальных конструкций GB50017-2017 [8]. Ферма состоит из трех вертикально расположенных квадратных модулей колонн (рис. 1), которые опираются на две неподвижные шарнирные опоры А и В и к которым в левых узлах приложены три горизонтальные заданные силы F. Требуемые конкретные значения указаны в таблице 1.
Требуемые конкретные значения указаны в таблице 1.
Модель фермы [9]
Увеличенное изображение
Таблица 1 Спецификация сверхстатических элементов фермы до армирования [9]Полноразмерная таблица
Ферма была смоделирована с помощью Abaqus программное обеспечение конечных элементов и усилия на каждом стержне фермы были получены из экспериментов по моделированию, как показано в таблице 2. Полученные результаты также сравнивались с двумя наборами точно рассчитанных данных о силе для каждого стержня из аналогичной модели в Rebielak [9].]. Большинство экспериментальных данных отличались от литературных менее чем на 10%. Смоделированные экспериментальные значения попадают в пределы двух точно рассчитанных модельных значений, когда разница между расчетными результатами двух наборов точно рассчитанных моделей в статье превышает 10%. Таким образом, модель смоделирована правильно, а экспериментальные данные, смоделированные программным обеспечением конечных элементов Abaqus, надежны.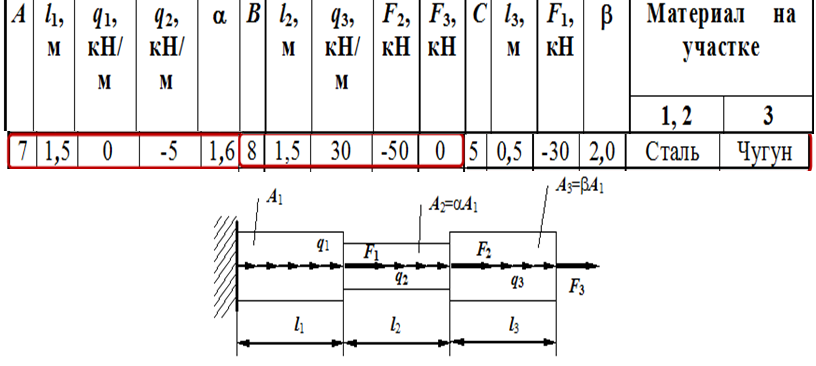
Полноразмерная таблица
3 Анализ и обсуждение модели методом конечных элементов
3.1 Анализ модели методом конечных элементов
Методы применения предварительно напряженной арматуры обычно делятся на две категории, первая из которых представляет собой установку предварительно напряженных элементов в балках, а другая — внешнее применение предварительного напряжения. Принцип заключается в том, что середина ферменного моста подвергается наибольшему изгибающему моменту, а внешнее приложение предварительного напряжения создает направленную вверх опорную силу, которая снижает нагрузку от нагрузки на механизм моста [10].
Фермы, упомянутые в данной статье, не могут быть усилены методами предварительного напряжения, так как они не имеют точек крепления с обеих сторон для фиксации напрягаемых прядей, поэтому для армирования был выбран способ армирования с увеличением площади поперечного сечения [11].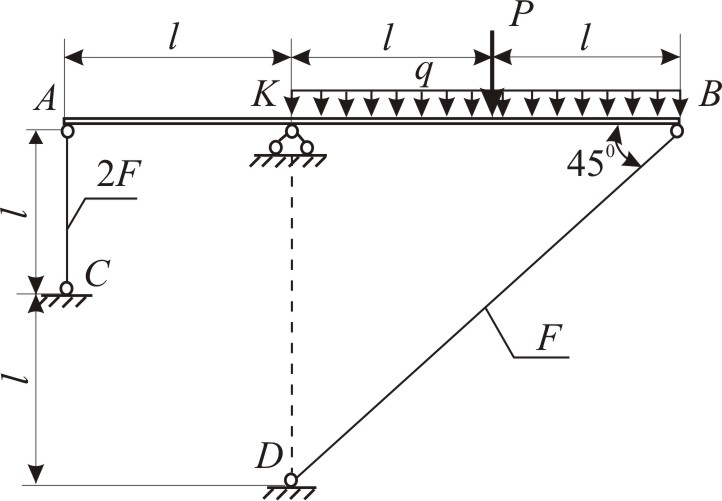
Анализ силового облака балки (рис. 2) показывает, что арматура расположена в наиболее нагруженных местах, то есть в стержне 9 и стержне 10. При слишком высокой нагрузке модифицированный стержень будет поврежден первым по сравнению с к другим стержням, поэтому стержни 9и 10 определяют предельную несущую способность балочной конструкции.
Рис. 2Диаграмма облака сил фермы
Изображение в полный размер
3.2 Метод увеличенного сечения сравнить балку до усиления с балкой после усиления методом увеличенного сечения. С учетом горизонтальной нагрузки и сил стальных балок результаты расчетов были проанализированы, и принятая окончательная схема армирования была определена следующим образом:
На левый конец стержня 9 и на внешний конец стержня 10 были добавлены сварные швеллеры [12]. Площадь поперечного сечения после усиления 1413 мм 2 . Форма поперечного сечения показана на рис. 3, полученная модель № 2.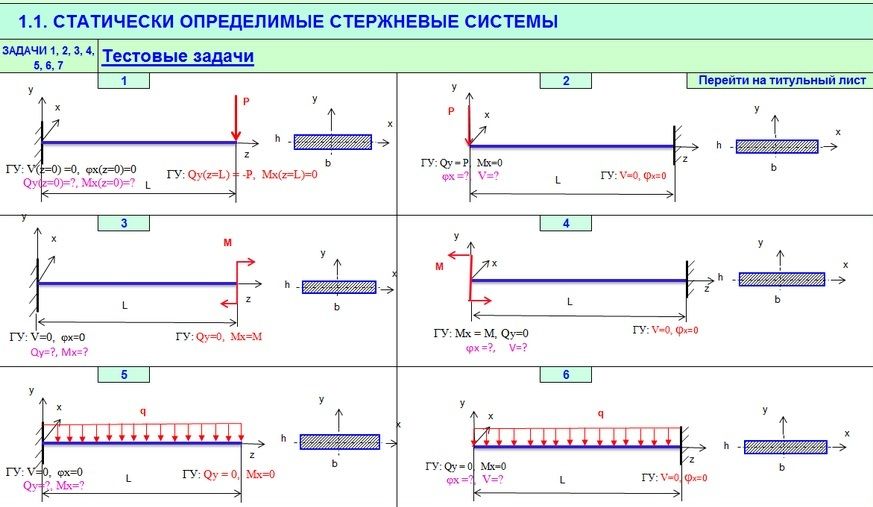
Форма арматуры сечения фермы (в мм) [12]
Изображение в натуральную величину
3.3 Особенности Исследования
С помощью метода увеличения сечения Abaqus была проанализирована производительность балки с последующим армированием. Анализ, основанный на исходной балке, показывает, что сила на балке Стержень 9и стержень 10 является самым большим среди всех балок, как показано на рис. 2, и в случае повреждения балки стержень 9 и стержень 10 будут повреждены раньше других стержней, поэтому создается подмодель для конечной анализ несущей способности этих двух стержней.
Стержень 9, подмодель
- (1)
Оригинальная модель площади поперечного сечения
Для моделирования одностороннего осевого растяжения фермы в лаборатории один конец стержня защемлен, а другой конец подвергается граничному смещению на 100 мм в контрольной точке. Контрольная точка соединена с верхней кольцевой поверхностью стальной трубы «связанной» связью, и для обеспечения синхронизации между контрольной точкой и верхней секцией при движении сетка окончательно разделяется и решается для получения облака напряжений, как показано на рисунке. на рис. 4.
Контрольная точка соединена с верхней кольцевой поверхностью стальной трубы «связанной» связью, и для обеспечения синхронизации между контрольной точкой и верхней секцией при движении сетка окончательно разделяется и решается для получения облака напряжений, как показано на рисунке. на рис. 4.
Нефограмма напряжения стержня 9
Изображение полного размера
Кривая зависимости силы и смещения является результатом для этого напряженного стержня на этапе постобработки (рис. 5). Сила реакции опоры RF2 в уникальной контрольной точке узла выводится в выходной переменной поля ODB. Напротив, его смещение U2 выводится, и кривая зависимости между U2 и RF2 получается с помощью комбинированной команды. Его наивысшая точка является предельным значением прочности на растяжение, как показано на рис. 5. Его наивысшее значение составляет 128,59.1 можно получить, нажав на вертикальную координату KN. После высшей точки кривая падает, потому что поперечное сечение стержня становится тоньше при растяжении, и предел прочности при растяжении снижается.
Кривая зависимости выходной силы от смещения нагруженного стержня 9
Изображение полного размера
- (2)
Модель с двойной площадью поперечного сечения
Тот же метод был использован для измерения предельной несущей способности после увеличения сечения в два раза по сравнению с исходным сечением и получения графика зависимости смещения от силы (рис. 6). Было получено самое высокое значение 256,149 кН.
Рис. 6Кривая зависимости между выходной силой и смещением нагруженного стержня 9, увеличенного на удвоенную площадь сечения
Изображение в полный размер
Между двумя процессами моделирования изменились только размеры поперечного сечения стержня. Материалы, методы анализа и смещения границ были одинаковыми. Можно видеть, что максимальное растягивающее усилие, приложенное к стержню, увеличилось после того, как поперечное сечение модели было увеличено в два раза по сравнению с первоначальным размером, и можно сделать вывод, что метод увеличенного поперечного сечения эффективно повысил предел растяжения.
Моделирование изгиба стержня 10
Шток 10 находится в зоне сжатия, и его повреждение характеризуется неустойчивостью штока. Характерным значением потери устойчивости первого порядка является ее предельная нагрузка при потере устойчивости посредством моделирования потери устойчивости.
- (1)
Оригинальная модель площади поперечного сечения
Стержень смоделирован из того же материала и с той же структурой, что и стержень 9, с линейной заданной динамической потерей устойчивости, установленной на шаге расчета, один конец стержня фиксируется, и к его верхнему концу в контрольной точке прикладывается единичная нагрузка-1, снова контрольная точка связана с верхней поверхностью с помощью «связанная» связь, сетка разделяется и создается рабочий анализ для получения ее облака (рис. 7) с собственным значением 11,812 кН.
Нефограмма напряжения стержня 10
Изображение в натуральную величину
- (2)
Модель с двойной площадью поперечного сечения
Была построена та же модель двойной площади поперечного сечения с теми же свойствами материала, приложенными нагрузками и другими условиями, а поперечное сечение стержня было увеличено в два раза по сравнению с первоначальным размером, а облако напряжений показано на рис. 8. было получено, с увеличением его характеристического значения на 30,398КН.
Рис. 8Нефограмма напряжения стержня 10 увеличена вдвое по площади его сечения
Изображение в натуральную величину
На основании двух прогонов моделирования делается вывод, что увеличение площади поперечного сечения, как и в случае галстука, приводит к значительному увеличению предела усилия. Увеличение сечения, будь то стяжка или стяжной стержень, увеличивает несущую способность.
Увеличение сечения, будь то стяжка или стяжной стержень, увеличивает несущую способность.
3.4 Обсуждение
- (1)
Сравнение общей несущей способности ферм
Испытание на предельную несущую способность фермы проводят методом испытаний, в основе которого лежит принцип непрерывного приложения нагрузок, величина соответствующих осевых усилий близка к предельному значению, измеренному переводником -модель.
- (2)
Пробный расчет грузоподъемности
Моделирование использует 2D-моделирование, направление приложенной нагрузки и точка действия такие же, как и в исходной модели, и поле выводит значение напряжения S11, умножая значение напряжения на стержень с наибольшим и наименьшим напряжением на соответствующее поперечное сечение. площадь сечения 706,86 мм2, чтобы получить его осевую силу, по сравнению с предельной нагрузкой подмодели, можно получить, что его боковая нагрузка может быть увеличена в пределах от 2,65 ~ 2,66 кН, ближайших к его предельной несущей способности при сжатии. При этом предельная несущая способность растянутого стержня намного больше предельной несущей способности сжимаемой зоны, поэтому общий предел сил балки определяется стержнем с наибольшим осевым сжатием. Результаты пробных расчетов приведены в таблице 3.
площадь сечения 706,86 мм2, чтобы получить его осевую силу, по сравнению с предельной нагрузкой подмодели, можно получить, что его боковая нагрузка может быть увеличена в пределах от 2,65 ~ 2,66 кН, ближайших к его предельной несущей способности при сжатии. При этом предельная несущая способность растянутого стержня намного больше предельной несущей способности сжимаемой зоны, поэтому общий предел сил балки определяется стержнем с наибольшим осевым сжатием. Результаты пробных расчетов приведены в таблице 3.
Полноразмерная таблица
- (3)
Пробный расчет модели двухсекционной фермы
Свойства процесса моделирования, этапы анализа и т. д. остаются прежними, измените его площадь поперечного сечения на 1033,77 мм 2 и выполните пробные расчеты для определения предельной нагрузки фермы. Его предельная нагрузка составляет от 6,8 до 6,84 кН. Результаты пробных расчетов представлены в таблице 4.
Его предельная нагрузка составляет от 6,8 до 6,84 кН. Результаты пробных расчетов представлены в таблице 4.
Таблица в натуральную величину
Согласно результатам эксперимента в первую очередь повреждаются сжатые стержни. Тогда предельные значения колеблются от 2,65 до 2,66 кН до усиления поперечной равнодействующей нагрузки в балке. По результатам сжатия их предельные значения колеблются от 6,8 до 6,84 кН после увеличения площади поперечного сечения, и можно сделать вывод, что несущая способность балочной конструкции весьма очевидно улучшается за счет увеличения поперечного сечения.
4 Заключение
В этой статье модель сверхстационарной фермы разработана с использованием численного моделирования. Анализ усиления методом увеличенного сечения с использованием модели Abaqus увеличивает предельную несущую способность фермы и увеличивает предельную несущую способность соответствующего стержня. Работы по укреплению и модификации уменьшают максимальную осевую силу сверхстатической фермы, уменьшают максимальную деформацию и значительно улучшают жесткость конструкции, тем самым достигая цели усиления.
Работы по укреплению и модификации уменьшают максимальную осевую силу сверхстатической фермы, уменьшают максимальную деформацию и значительно улучшают жесткость конструкции, тем самым достигая цели усиления.
Поскольку в этой статье используется численное моделирование и не проводятся эксперименты, в будущем следует провести практическое сравнительное исследование модели, чтобы компенсировать ограничения этого исследования.
Ссылки
Zhang X, Li A, Zhao K (2011) Успехи в оценке и модернизации строительных конструкций. J Eng Mech 28 (01): 1–11 + 25
Google Scholar
Лю Дж. (2020) Технический прогресс в оценке и армировании строительных конструкций. J Jiangxi Build Mater 08: 40–42
Google Scholar
Бай П. (2021 г.) Динамические характеристики конструкции и расчет армирования ферменной арки.
 J Build Technol Dev 48:22
J Build Technol Dev 48:22Google Scholar
Ян Дж., Чжэн К., Хан М. (2013) Проверка и усиление стальной фермы ленточного транспортного коридора. Дж. Инд Констр 43:03
Google Scholar
Ляо М., Гао Дж., Ли Г и др. (2019) Усиление изогнутой конструкции трибуны стадиона Ухань Синьхуа Роуд методом внешнего предварительного напряжения. Инд Констр 49:07
Google Scholar
Хаяси К., Осаки М. (2020) Обучение с подкреплением и встраивание графа для оптимизации топологии бинарной фермы в условиях ограничений напряжения и смещения. J Front Built Environ 6:1–15
Google Scholar
Guo X (2021) Изучение дефектов качества и методов армирования существующего завода металлоконструкций.
 Популярный стенд J 23:14–17+20
Популярный стенд J 23:14–17+20Google Scholar
ГБ 50017-2003 (2003) Нормы проектирования стальных конструкций. China Planning Press, Пекин
Google Scholar
Ребиелак Дж. (2021) Двухэтапный метод, применяемый для приближенных расчетов выбранных типов статически неопределимых ферм. J Методы вычислений 18(03)
Google Scholar
Чжан Г., Чжан Н., Рен Х. (2016) Исследование связанной железобетонной колонны на основе ABAQUS. J Gansu Sci 28(2):5
MathSciNet Google Scholar
Ченг Дж., Ченг Б., Цю Х. и др. (2012) Исследования в области армирования стальных конструкций. J Стальная конструкция 27(11):7
Google Scholar
- «>
Лю З., Чжан Л., Ван Т и др. (2014) Исследование технологии усиления и реконструкции моста со стальными фермами. В: Материалы 15-й научной конференции по строению космоса
Google Scholar
Ссылки для скачивания
Информация об авторе
Авторы и организации
Колледж портового и прибрежного машиностроения, Университет Джимей, Сямэнь, Фуцзянь, Китай
Ziyi Liang
Архитектурно-строительная школа Хэйлунцзянского университета науки и технологий, Харбин, Хэйлунцзян, Китай
Mingjun Wei
CSUST Международный инженерный колледж, Чаншаский университет науки и техники, Чанша, Hunan, China
Long Yu
- Ziyi Liang
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Академия
- Mingjun Wei
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Long Yu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Автор, ответственный за корреспонденцию
Цзыи Лян.
Информация для редакторов
Редакторы и филиалы
Школа гражданского строительства Университета Чунцина, Чунцин, Китай
Ян Ян
Права и разрешения
Открытый доступ Эта глава лицензирована в соответствии с условиями Creative Commons Attribution 4 .0 Международная лицензия (http:/ /creativecommons.org/licenses/by/4.0/), который разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате, при условии, что вы укажете автора(ов) оригинала и источник, а также ссылку на лицензию Creative Commons и указать, были ли внесены изменения.
Изображения или другие сторонние материалы в этой главе включены в лицензию Creative Commons главы, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons главы, а предполагаемое использование вами не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от владельца авторских прав.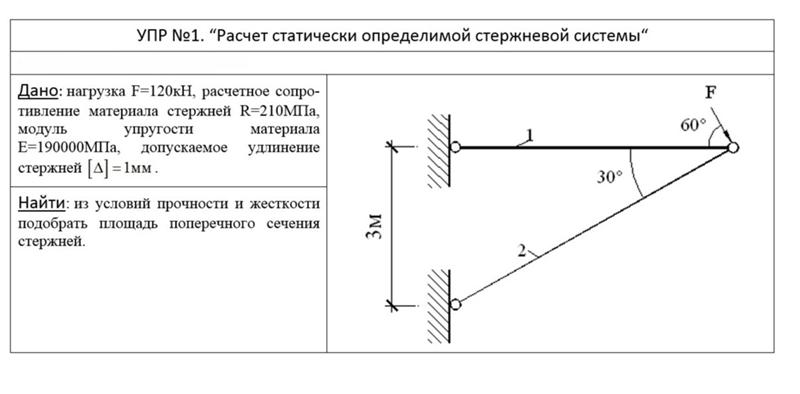
 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав