Плотность смеси — Справочник химика 21
В спектрофотометрии большое значение имеет закон аддитивности оптических плотностей. Если закон поглощения излучения строго выполняется, то оптическая плотность смеси ( >см) [c.465]Плотность смесей подсчитывается следующим образом. Допустим, дана смесь, состоящая по массе из а % первого компонента, в % — второго, с % — третьего и т. д., т. е. в 100 кг этой смеси заключено а кг первого компонента, в кг — второго, с кг — третьего и т. д. Если плотность первого компонента равна рх, второго р2, третьего Рз и т. д., то первый из них в 100 /сг смеси [c.10]
Отсюда плотность смеси определится (по уравнению 1). [c.10]
Сумма объемов всех компонентов 2У, = 2а,/р( дает объем смеси. Тогда плотность смеси [c.27]
Часто при проведении стехиометрических расчетов возникает необходимость вычислений объемов, давлений, плотности или влажности газов, принимающих участие в процессе, а также определения плотности смесей и концентраций компонентов, т.
Сумма массово-объемных концентраций всех компонентов равна массе 1 м смеси, т. е. плотности смеси 1Сг = рсм-Массовая доля -го компонента в смеси [c.28]
Рассмотрим пример расчета плотности смеси масел. [c.297]
Для регулирования плотности смеси паров сырья с катализатором в транспортную линию прежде нагнетали небольшое количество газа (примерно 50 л на т сырья). В настоящее время для этой цели применяют перегретый водяной пар в количестве 0,4—2,0% вес., считая на загружаемое в реактор сырье. [c.149]
Недавно опубликованы [226] следующие данные о плотностях смесей, скоростях циркуляции катализатора и т. д. на установке модели IV мощностью около 2380 м 1 сутки сырья. [c.268]
В интервале давлений 0,05—0,4 МПа наблюдалось возрастание Uh при понижении начального давления горючей смеси. При этом массовая скорость распространения пламени, равная m = u p (где р — начальная плотность смеси), возрастает с повышением давления. [c.119]
[c.119]
Процесс контролируют по изменению плотности смеси. Если необходимо получить хлорбензол, реакцию проводят при температуре около 40 °С и хлор вводят до тех пор, пока плотность смеси не достигнет [c.287]
Рассмотрим элементарный объем реакционной смеси, находящийся между двумя поршнями, поступательно перемещающимися по длине реактора. Если плотность смеси не изменяется в ходе реакции, продолжительность процесса составит (рис. V- ) [c.140]
Обычно под плотностью потока подразумевают плотность смеси на входе в реактор. Для газов плотность определяют при нормальных условиях, т. е. при О °С и 760 мм рт. ст. Плотность газов обычно изменяется в ходе процесса, поэтому время реакции
Плотность смеси нефтепродуктов определяется по формуле [c.26]
Плотность смеси на входе в компрессор Рем =JR + + d ,) пI Т — М) [c.147]
Продолжительность цикла может колебаться от 4 до 14 дней. Ход реакции контролируется по плотности смеси, которая на конечной стадии хлорирования достигает 1,4—1,5 г/см . [c.292]
Ход реакции контролируется по плотности смеси, которая на конечной стадии хлорирования достигает 1,4—1,5 г/см . [c.292]
Существует несколько методов определения плотности нефтепродуктов. Выбор того или другого зависит от имеющегося количества нефтепродукта, его вязкости, требуемой точности определения и отводимого для анализа времени. Простейшим прибором для определения плотности жидких нефтепродуктов является ареометр (плотномер). Градуировка ареометра отнесена к плотности воды при 4 С и его показания соответствуют р. Ареометром можно определить плотность только с точностью до 0,001 для маловязких и 0,005 для вязких нефтепродуктов. Для определения ареометром плотности высоковязкого (более 200 сст при 50° С) нефтепродукта (() ) поступают следующим образом. Нефтепродукт разбавляют равным объемом керосина известной плотности (pj и измеряют плотность смеси (Рсм)- Затем подсчитывают п.лотность нефтепродукта по формуле [c.37]
Средняя плотность смеси компонентов определяется по правилу смешения [c.
 139]
139]Плотность смеси паров избирательного растворителя и воды на верху колонны [c.233]
Рт — плотность смеси газа и твердых частиц [c.617]
Плотность смеси жидких УВ. г/см Плотность газа, г/л Давление, кгс/см Температура, °С [c.126]
Экспериментальные данные, полученные в лабораторных или промышленных условиях, являются основой для проведения дальнейших исследований. Эти данные обычно используются либо для определения констант известных теоретических соотношений, либо как исходный материал для установления аналитических зависимостей. Если в первом случае экспериментальные значения подставляются в соответствующие уравнения (например, коэффициенты диффузии, массопередачи, вязкости, плотности и др.), которые применяются в последующих расчетах, то во втором — совокупность экспериментальных значений используется для установления функциональной зависимости, которой они подчиняются (например, зависимости константы скорости реакции от температуры, зависимости плотности смеси от состава и т. д.). [c.296]
д.). [c.296]Если пренебречь плотностями газа и воздуха, то плотность смесей [c.140]
Решив уравнение состояния относительно мольной плотности смеси (при заданных Т, Р, X), энтальпию и энтропию неидеальных многокомпонентных смесей можно найти из выражений [c.417]
Рассмотрим программу расчета плотности смеси к компонентов в паровой фазе при известном давлении и температуре, если коэффициенты уравнения определяются соотношениями [c.101]
Программа состоит из двух частей. В первой части исходные данные и вспомогательные выражения приводятся к виду, удобному для дальнейшего использования, а во второй — производится собственно расчет плотности смеси. [c.103]
Уравнение состояния (13—18) может быть использовано для расчета плотности смеси при известных значениях Р и Т системы. Отмечается, что для приведенных температур Тг 0,6 и плотностей р > 2 точность составляет величину порядка 1 % как при расчете плотности жидкой, так и паровой фаз [43].
Плотность углеводородных жидкостей. Плотность различных нефтей можно найти в стандартных таблицах. Однако, если нефть содержит значительное количество примесей с высокой упругостью паров (метан, этан, азот), то эти таблицы применять нельзя. Молекулы веществ, имеющих высокую упругость паров, обладают значительной кинетической энергией, которая влияет па плотность смеси. Для определения плотности жидких углеводородов с относительной молекулярной массой ниже 33, молярная доля азота, кислорода и изо-парафинов в которых менее 5%, моишо воспользоваться формулой, которая применима в интервале температур —(140+-184,4)° С, [c.37]
Только когда плотность смеси не изменяется во времени, уравнение (И,2) можно упростить. В этом случае, например, для реагента А получим [c.41]
За счет снижения скоростей потоков в реактореи регенераторе-в них были созданы зоны с псевдокипящей массой частиц катализатора. В связи с этим появилась возможность регулировать глубину крекинга сырья и количество сжигаемого кокса не только пуаем изменения температур и плотностей смесей, но и путем изменения высоты уровня плотной фазы в нижней половине реакционного-аппарата. [c.255]
[c.255]
Плотность смеси паров продуктов каталитического крекинга и крекпнг-газа в низу зоны реакции определяется формуло [c.192]
Здесь уравнения (4.62)—(4.66) описывают средние скорости изменения концентраций инициатора, радикалов, мономеров и суммарной степени превращения в частицах дисперсной фазы. Уравнение (4.67) описывает нестационарный перенос тепла от единичного включения к сплошной фазе. Уравнения теплового баланса (4.68)—(4.69) для реактора и рубашки составлены при допущении полного перемепшвания сплошной фазы в реакторе и теплоносителя в рубашке. Уравнение БСА (4.70) характеризует изменение в течение процесса функции распределения частиц дисперсной фазы по массам р (М, 1). В уравнениях (4.62)—(4.70) введены следующие обозначения / ( г) — эффективность инициирования X — суммарная степень превращения мономеров АЯ — теплота полимеризации — эффективная энергия активации полимеризации 2 — коэффициент теплопроводности гранул р .
Интерполяцией между —160 и —165 С из табл. 2 определяем молярные объемы ь-омпонентои. Отсюда плотность смеси [c.39]
Пло7 ность СЗг при 293 К равна 1,264 г/см , плотность С2Н5ОН — 0,8040 j/ vi . Чему равна плотность смеси, содержащей 80% S, если удельный объем ее является аддитивной функцией состава [c.175]
Задача состоит в том, чтобы по экспериментально полученной зависимости плотности смеси при фиксированной температуре от полного давления ыайти значения констант равновесия реакций полимеризации или их комбинаций, принципиально онреде. тимых но названным данным [3]. При этом необходимо, чтобы способ обработки исходной зависимости в принципе позволял бы определять константы в предположении большого набора возможных молекулярных компонентов смеси. Этим и будет обеспечена принципиальная возможность нахождения констант без априорных предположений о наличии или отсутствии в смеси тех или иных компонентов. Практически возможности способа будут сильно ограничены точностью исходных данных и диапазоном их изменения. Одиако отыскание такого способа авторы считают актуальной задачей, поскольку для ряда систем это позволит получить приемлемые результаты с оценкой их точности, а также установить требования к точности измерений и диапазону изменения экспериментальных условий.
тимых но названным данным [3]. При этом необходимо, чтобы способ обработки исходной зависимости в принципе позволял бы определять константы в предположении большого набора возможных молекулярных компонентов смеси. Этим и будет обеспечена принципиальная возможность нахождения констант без априорных предположений о наличии или отсутствии в смеси тех или иных компонентов. Практически возможности способа будут сильно ограничены точностью исходных данных и диапазоном их изменения. Одиако отыскание такого способа авторы считают актуальной задачей, поскольку для ряда систем это позволит получить приемлемые результаты с оценкой их точности, а также установить требования к точности измерений и диапазону изменения экспериментальных условий.
Секретная шпаргалка по химии. 4.2. Состав смеси газов | Репетитор Богунова В.Г.
Команда «Газы!» была объявлена еще две недели назад. И что?! Легкие задачи порешали и расслабились?! Или вы думаете, что задачи на газы касаются только 28-х заданий ЕГЭ?! Как бы не так! Если газов пока еще не было в 34-х заданиях, это ничего не значит! Задач на электролиз тоже не было в ЕГЭ до 2018 года. А потом как врезали, мама не горюй! Обязательно прочитайте мою статью «Тайны задач по химии? Тяжело в учении — легко в бою!». В этой статье очень подробно рассказывается о новых фишках на электролиз. Статья вызвала шквал самых разных эмоций у преподавателей химии. До сих пор мне и пишут, и звонят, и благодарят, и бьются в конвульсиях. Просто цирк с конями, в котором я — зритель в первом ряду.
А потом как врезали, мама не горюй! Обязательно прочитайте мою статью «Тайны задач по химии? Тяжело в учении — легко в бою!». В этой статье очень подробно рассказывается о новых фишках на электролиз. Статья вызвала шквал самых разных эмоций у преподавателей химии. До сих пор мне и пишут, и звонят, и благодарят, и бьются в конвульсиях. Просто цирк с конями, в котором я — зритель в первом ряду.
Однако, вернемся к нашим баранам, вернее, Газам. Я прошла через огонь и воду вступительных экзаменов и знаю точно — хочешь завалить абитуриента, дай ему задачу на Газы. Почитайте на досуге сборник задач И.Ю. Белавина. Я процитирую одну такую «мозгобойню», чтобы вам жизнь медом не казалась. Попробуйте решить.
И.Ю. Белавин, 2005, задача 229
«Два из трех газов (сероводород, водород и кислород) смешали и получили газовую смесь, плотность которой оказалась равной плотности оставшегося газа. Полученную газовую смесь вместе с равным ей объемом третьего газа под давлением поместили в замкнутый сосуд емкостью 4 л, содержавший азот при н. у. и нагревали при 600 С до окончания химических реакций, затем постепенно охладили. Определите массы веществ, содержавшихся в сосуде после охлаждения, если плотность газовой смеси в сосуде перед нагреванием равнялась 9,25г/л. (Ответ: m(S) = 7,5 г, m(SO2) = 15 г, m(Н2О) = 9 г)»
у. и нагревали при 600 С до окончания химических реакций, затем постепенно охладили. Определите массы веществ, содержавшихся в сосуде после охлаждения, если плотность газовой смеси в сосуде перед нагреванием равнялась 9,25г/л. (Ответ: m(S) = 7,5 г, m(SO2) = 15 г, m(Н2О) = 9 г)»
Ну как, решили? Нет?! А ваши репетиторы?! Извините, это был риторический вопрос. Кстати, мои ученики, абитуриенты 2003-2008 гг. такие задачи щелкали, как семечки, на экзаменах во 2-й медицинский (теперь РНИМУ им. Н.И. Пирогова). Надеюсь, вам понятно, что 34-м задачам ЕГЭ еще есть куда усложняться, perfectio interminatus est (нет предела совершенству), с газами нужно работать, работать и работать. Поэтому команду «Газы!» отменять рано. Итак, поехали!
Сегодня мы поговорим о газовых смесях, затронем понятие плотности газа (абсолютной и относительной), средней молярной массы, решим задачи: определение средней молярной массы и плотности газа по компонентам смеси и наоборот.
• Газовая смесь — смесь отдельных газов НЕ вступающих между собой в химические реакции. К смесям газов относятся: воздух (состоит из азота, кислорода, углекислого газа, водяного пара и др.), природный газ (смесь предельных и непредельных углеводородов, оксида углерода, водорода, сероводорода, азота, кислорода, углекислого газа и др.), дымовые газы (содержат азот, углекислый газ, пары воды, сернистый газ и др.) и др.
• Объемная доля — отношение объема данного газа к общему объему смеси, показывает, какую часть общего объема смеси занимает данный газ, измеряется в долях единицы или в процентах.
• Мольная доля — отношение количества вещества данного газа к общему количеству вещества смеси газов, измеряется в долях единицы или в процентах.
Секретная шпаргалка по химии. 4.2. Состав смеси газов• Плотность газа (абсолютная) — определяется как отношение массы газа к его объему, единица измерения (г/л). Физический смысл абсолютной плотности газа — масса 1 л, поэтому молярный объем газа (22,4 л при н.у. t° = 0°C, P = 1 атм) имеет массу, численно равную молярной массе.
Физический смысл абсолютной плотности газа — масса 1 л, поэтому молярный объем газа (22,4 л при н.у. t° = 0°C, P = 1 атм) имеет массу, численно равную молярной массе.
• Относительная плотность газа (плотность одного газа по другому) — это отношение молярной массы данного газа к молярной массе того газа, по которому она находится
Секретная шпаргалка по химии. 4.2. Состав смеси газов• Средняя молярная масса газа — рассчитывается на основе молярных масс составляющих эту смесь газов и их объемных долей
Секретная шпаргалка по химии. 4.2. Состав смеси газовНастоятельно рекомендую запомнить среднюю молярную массу воздуха Мср(в) = 29 г/моль, в заданиях ЕГЭ часто встречается.
Обязательно посетите страницу моего сайта «Изучаем Х-ОбХ-04. Закон Авогадро. Следствия из закона Авогадро. Нормальные условия. Молярный объем газа. Абсолютная и относительная плотность газа. Закон объемных отношений» и сделайте конспекты по теории. Затем возьмите бумагу и ручку и решайте задачи вместе со мной.
Абсолютная и относительная плотность газа. Закон объемных отношений» и сделайте конспекты по теории. Затем возьмите бумагу и ручку и решайте задачи вместе со мной.
ВАНГУЮ: чует мое сердце, что ЕГЭ по химии 2019 года устроит нам газовую атаку, а противогазы не выдаст!
Задача 1
Определить плотность по азоту газовой смеси, состоящей из 30% кислорода, 20% азота и 50% углекислого газа.Секретная шпаргалка по химии. 4.2. Состав смеси газов
Задача 2
Вычислите плотность по водороду газовой смеси, содержащей 0,4 моль СО2, 0,2 моль азота и 1,4 моль кислорода.Секретная шпаргалка по химии. 4.2. Состав смеси газов
Задача 3
5 л смеси азота и водорода имеют относительную плотность по водороду 12. Определить объем каждого газа в смеси.Секретная шпаргалка по химии.
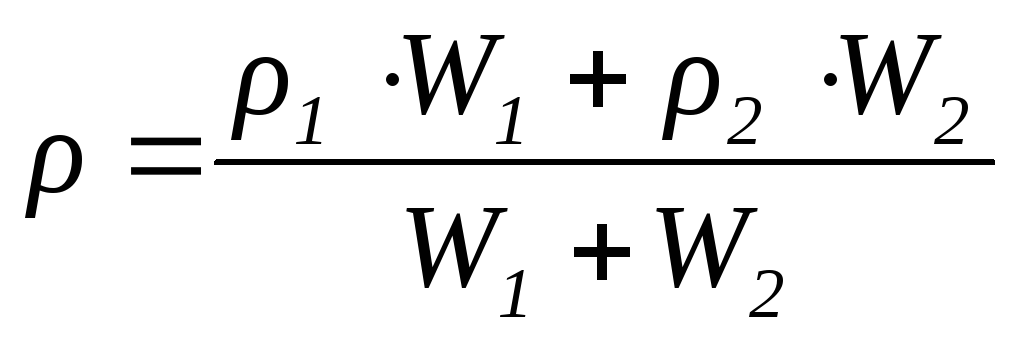 4.2. Состав смеси газов
4.2. Состав смеси газовНесколько задач со страницы моего сайта
Задача 4
Плотность по водороду пропан-бутановой смеси равна 23,5. Определите объемные доли пропана и бутанаСекретная шпаргалка по химии. 4.2. Состав смеси газов
Задача 5
Газообразный алкан объемом 8 л (н.у.) имеет массу 14,28 г. Чему равна его плотность по воздухуСекретная шпаргалка по химии. 4.2. Состав смеси газов
Задача 6
Плотность паров альдегида по метану равна 2,75. Определите альдегидСекретная шпаргалка по химии. 4.2. Состав смеси газов
Ну как? Пошло дело? Если туго, вернитесь к задачам и решайте их самостоятельно до тех пор, пока не щелкнет! А для стимуляции — десерт в виде еще одной задачи И.Ю. Белавина на газы. Наслаждайтесь ее решением самостоятельно!
И. Ю. Белавин, 2005, задача 202
Ю. Белавин, 2005, задача 202
«Сосуд емкостью 5,6 л при н.у. заполнили метаном, затем нагрели до высокой температуры, в результате чего произошло частичное разложение метана. Определите массу образовавшейся сажи, если известно, что после приведения к нормальным условиям объем полученной газовой смеси оказался в 1,6 раза больше объема исходного метана, эта газовая смесь обесцвечивает бромную воду и имеет плотность по воздуху 0,2931. (Ответ: m(C) = 0,6 г)»
Задачи И.Ю. Белавина — это крутой драйв! Попробуйте порешать, и вы откажетесь от просмотра любых ужастиков, поскольку запасетесь адреналином надолго! Но нам нужно спуститься на землю к ЕГЭ, простому и надежному, как первый советский трактор. Кстати, у меня в коллекции припасено немало сюрпризов с газовыми фишками, собранными за все годы работы и бережно хранимыми. Думаю, пришло время сказать им: «И снова здравствуйте!», поскольку ЕГЭ с каждым годом становится «все чудесатее и чудесатее». Но это уже совсем другая история. Читайте мои статьи — и вы подстелите соломку под свою ЕГЭшную попу.
Но это уже совсем другая история. Читайте мои статьи — и вы подстелите соломку под свою ЕГЭшную попу.
Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии http://repetitor-him.ru. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами. Позвоните мне +7(903)186-74-55, приходите ко мне на курс, на бесплатные Мастер-классы «Решение задач по химии». Я с удовольствием вам помогу.
Репетитор по химии и биологии кбн В.Богунова
Плотность смеси жидкостей — Энциклопедия по машиностроению XXL
Задача 1.3. Найти плотность смеси жидкостей р, имеющей следующий массовый состав керосина — 30 %, мазута — 70 %, если плотность керосина р = 790 кг/м , а мазута р = 900 кг/м . [c.12]Более точный метод расчета плотностей смесей жидкостей, применимый в широких интервалах температуры и давления (вплоть до критической точки) основан на использовании уравнений (3. 15.18)—(3.15.21), а также (4.10.2)—(4.10.9), которые описывают модификацию метода применительно к смесям. Для пользования этим методом необходимо знать критические свойства чистых компонентов. В случае использования метода при приведенных температурах, превышающих 0,93, должна быть известна истинная критическая температура смеси. Наконец, для точных расчетов надо располагать значениями параметра бинарною взаимодействия [уравнение (4.10.4)]. В настоящее время этот параметр может быть заранее предсказан только для смесей алифатических углеводородов [7]. Для приближенного определения этого параметра для смесей других жидкостей весьма полезным может оказаться даже ограниченный объем экспериментальной информации.
[c.89]
15.18)—(3.15.21), а также (4.10.2)—(4.10.9), которые описывают модификацию метода применительно к смесям. Для пользования этим методом необходимо знать критические свойства чистых компонентов. В случае использования метода при приведенных температурах, превышающих 0,93, должна быть известна истинная критическая температура смеси. Наконец, для точных расчетов надо располагать значениями параметра бинарною взаимодействия [уравнение (4.10.4)]. В настоящее время этот параметр может быть заранее предсказан только для смесей алифатических углеводородов [7]. Для приближенного определения этого параметра для смесей других жидкостей весьма полезным может оказаться даже ограниченный объем экспериментальной информации.
[c.89]
Пример 2. Произведем расчет простейшего эжектора, состоящего из сопла А и цилиндрической смесительной трубы В, расположенных в пространстве, заполненном неподвижной жидкостью (рис.
 1.9). Из сопла подается струя, которая подсасывает жидкость из окружающего пространства. Пусть на выходе из смесительной трубы скорость и плотность смеси примерно постоянны. Построим контрольную поверхность из сечений J и 2, проходящих нормально к потоку по срезу сопла и срезу смесительной трубы, и боковых поверхностей, направленных параллельно потоку. На всей контрольной поверхности господствует одно и то же давление покоящейся жидкости, т. е. главный вектор сил давления равен нулю.
[c.41]
1.9). Из сопла подается струя, которая подсасывает жидкость из окружающего пространства. Пусть на выходе из смесительной трубы скорость и плотность смеси примерно постоянны. Построим контрольную поверхность из сечений J и 2, проходящих нормально к потоку по срезу сопла и срезу смесительной трубы, и боковых поверхностей, направленных параллельно потоку. На всей контрольной поверхности господствует одно и то же давление покоящейся жидкости, т. е. главный вектор сил давления равен нулю.
[c.41]Какова плотность смеси двух углеводородных жидкостей, если для нее взято 0,4 л нефти (fi = = 850 кг/м ) и 0,6 л керосина (р = 800 кг/м ) 1650 кг/м 3 [c.11]
Если при смешении жидкости не меняют своего суммарного объёма (например, нефтепродукты), то весовая плотность смеси определяется из уравнения [c.381]
Вычисляем параметры на первом участке Xi = 0,004 м. При /ж парциальное давление воздуха Рт. ж = Р Рж при Рг. и = Р — Ри- Плотность воздуха при 1ж и соответственно рг. ж и рг. м — по уравнению состояния идеального газа. Плотность смеси воздуха и водяного пара при tm и tu соответственно рем. ж и рем. U — по уравнению (4-9). В первом приближении среднюю плотность газа и смеси в рассматриваемых слоях находим как рг = = 0,5(рг. ж + рг. м) и Рем = 0,5(рс . ж + Рем. м). Расход смеси 0=0r(l+fi i)-Кинематическая вязкость воды (в пределах /ж = О + 20 °С) v = = (1,789 — 0,0483 ж) 10 . Толщина пленки жидкости на пластине б/ — по уравнению (4-79). Ширина канала для течения газа bf = Ь — 26/.
[c.188]
ж и рг. м — по уравнению состояния идеального газа. Плотность смеси воздуха и водяного пара при tm и tu соответственно рем. ж и рем. U — по уравнению (4-9). В первом приближении среднюю плотность газа и смеси в рассматриваемых слоях находим как рг = = 0,5(рг. ж + рг. м) и Рем = 0,5(рс . ж + Рем. м). Расход смеси 0=0r(l+fi i)-Кинематическая вязкость воды (в пределах /ж = О + 20 °С) v = = (1,789 — 0,0483 ж) 10 . Толщина пленки жидкости на пластине б/ — по уравнению (4-79). Ширина канала для течения газа bf = Ь — 26/.
[c.188]
Для небольших объемных газосодержаний и при состоянии жидкости, далекой от критического, плотность смеси р = р (1 — /3). Тогда после подстановки плотности смеси в выражение (2.18) получим [c.39]
Любой компонент смеси жидкостей диффундирует в смеси со скоростью, зависящей как от градиента концентрации этого компонента, так и от градиентов потенциалов других интенсивных свойств (температуры, давления, концентрации других компонентов и т.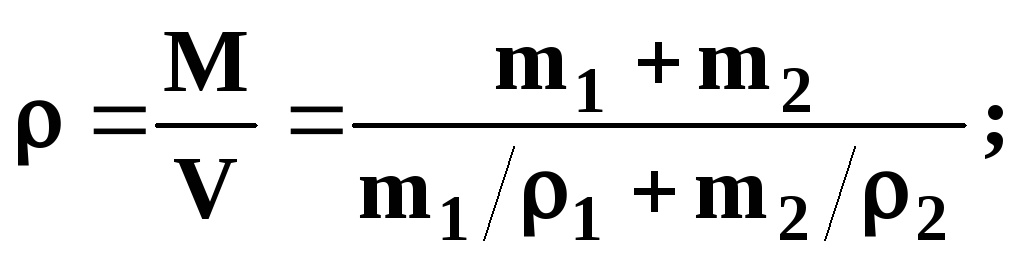 д.). Для простых газов с помощью кинетической теории получено точное уравнение для потока массы компонента в многокомпонентной смеси низкой плотности [Л. 8], однако это уравнение довольно сложно.
[c.29]
д.). Для простых газов с помощью кинетической теории получено точное уравнение для потока массы компонента в многокомпонентной смеси низкой плотности [Л. 8], однако это уравнение довольно сложно.
[c.29]
Символы Т —абсолютная температура, °K(T = 273 + Q и Гв — соответственно температура воздуха и температура адиабатического насыщения (температура мокрого термометра) — температура радиационной поверхности и и — соответственно влагосодержание и критическое влагосодержание пористого тела Ср —удельная изобарная теплоемкость влажного воздуха (парогазовой смеси) р — плотность влажного воздуха v — коэффициент кинематической вязкости а — коэффициент температуропроводности —коэффициент теплопроводности влажного воздуха — коэффициент взаимной диффузии — относительное парциальное давление пара, равное отношению парциального давления пара к общему давлению парогазовой смеси w — скорость движения воздуха р о — относительная концентрация г-ком-понента в смеси, равная отношению объемной концентрации р,- к плотности смеси р(р,о =рУр) Рю—относительная концентрация пара во влажном воздухе влажность воздуха (давление насыщенного пара — химический потенциал г-го компонента М,-— молекулярный вес г-го компонента Л,-—удельная энтальпия г-го компонента R — универсальная газовая постоянная г—удельная теплота испарения жидкости. [c.25]
[c.25]
В данном случае удобнее характеризовать смесь концентрацией газа в смеси средней плотности смеси запишется в таком виде (один штрих отмечает параметры жидкости, а два штриха — газа) [c.203]
Вычислим скорость распространения звука в жидкости с пузырьками газа. Ввиду того, что плотность смеси велика, а упругость обеспечивается упругостью воздушных пузырьков, скорость распространения звука в смеси должна быть низкой. Тогда, если и при распространении звуковой волны в смеси происходит идеальный теплообмен, то можно считать температуру практически постоянной. В этом случае давление и плотность смеси связаны уравнением (8.14). Если же при распространении звуковой волны теплообмен между пузырьками газа и жидкостью не успевает произойти, то для газа в пузырьках справедливо уравнение изо- [c.204]
Первый член представляет изменение количества теплоты, содержащейся в жидкости, а второй — количество выделившейся скрытой теплоты при изменении массовой концентрации пара ф. Изменением количества теплоты, содержащейся в пузырьках пара, можно пренебречь ввиду того, что массовая концентрация пара очень мала. Полагая, что сухой пар подчиняется уравнению состояния для совершенного газа, запишем уравнение для плотности смеси
[c.213]
Изменением количества теплоты, содержащейся в пузырьках пара, можно пренебречь ввиду того, что массовая концентрация пара очень мала. Полагая, что сухой пар подчиняется уравнению состояния для совершенного газа, запишем уравнение для плотности смеси
[c.213]
Эскиз многоплунжерной головки приведен на рис. 12.8. В корпусе 4 головки установлены цилиндры с пружинами 2 и 7. По мере сжатия пружины 1 возрастает давление на формовочную смесь, передаваемое через плунжеры 5 и колодки 6, в связи с чем обеспечивается равномерное распределение плотности смеси по площади опоки. Рабочая жидкость в головку подается от гидростанции по трубам через приемное устройство J. [c.213]
Если жидкость рассматривается как несжимаемая, то V-v = 0. Если, кроме того, раствор является разбавленным, то полную плотность смеси (р) и коэффициент диффузии можно считать практически постоянными. Поэтому после упрощений и деления на р выражение (16-52) принимает вид
[c.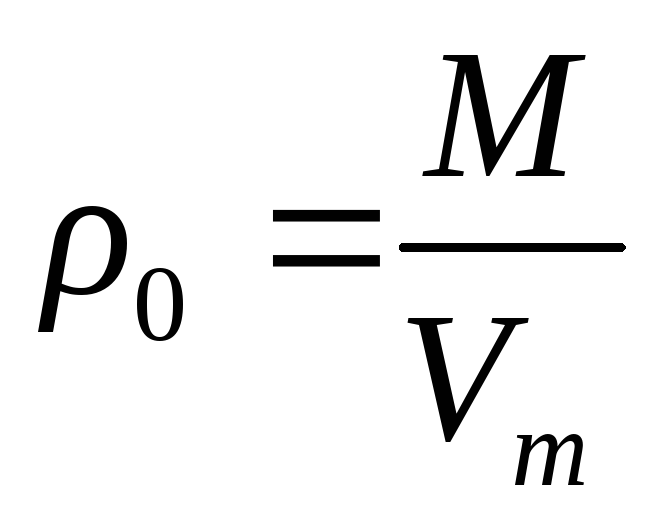 451]
451]
Есть ряд физических процессов, в которых твёрдое тело плавится и затем испаряется. Поэтому любое уравнение состояния, претендующее на описание свойств веществ в широком диапазоне изменения давления и плотности, должно описывать свойства вещества в области смеси жидкости и пара. Здесь будут рассмотрены вопросы построения уравнения состояния в области смеси жидкость — пар в основном так, как они излагаются в [28] — [30]. [c.66]
Кроме только что отмеченных двух основных и достаточно общих свойств сплошной текучей среды 1) непрерывности распределения физических свойств и характеристик движения и 2) текучести, или легкой подвижности, при рассмотрении частных классов задач приходится приписывать модели среды дополнительные макроскопические характеристики, определяющие ее индивидуальные материальные свойства, обусловленные действительными микроскопическими свойствами молекулярной структурой и скрытыми движениями материи. В механике сплошных сред эти характеристики вводятся феноменологически, в форме заданных наперед констант или количественных закономерностей.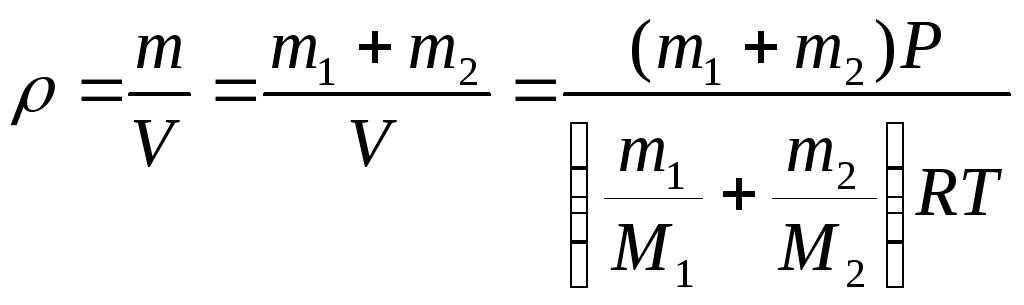 Среди таких характеристик выделим, прежде всего, отражающие вещественные свойства среды при ее равновесном состоянии молекулярный вес и плотность распределения массы (или, короче, просто плотность среды), концентрацию примесей в многокомпонентных и многофазных смесях жидкостей, газов и твердых частиц, затем температуру и теплоемкость среды, электропроводность, магнитную проницаемость и другие физические свойства.
[c.10]
Среди таких характеристик выделим, прежде всего, отражающие вещественные свойства среды при ее равновесном состоянии молекулярный вес и плотность распределения массы (или, короче, просто плотность среды), концентрацию примесей в многокомпонентных и многофазных смесях жидкостей, газов и твердых частиц, затем температуру и теплоемкость среды, электропроводность, магнитную проницаемость и другие физические свойства.
[c.10]
Если лавина из порошкообразного снега падает с вертикального уступа и при этом происходит перемешивание снега с воздухом, то может образоваться такая смесь, плотность которой в несколько раз больше плотности воздуха, но которая, тем не менее, обладает свойствами жидкости . Если, например, плотность смеси в пять раз больше плотности воздуха, то ускорение падения смеси будет составлять 4/5 ускорения свободного падения, следовательно, при падении с высоты 500 м скорость потока будет равна круглым числом 90 м/сек, а соответствующее динамическое давление около 2500 кг/м . В действительности движение потока из смеси снега и воздуха является, конечно, турбулентным. Тем не менее в ядре потока все же может возникнуть чрезвычайно большое динамическое давление, чем и объясняется, что такие пылевые лавины иногда сносят со своего пути целью строения.
[c.487]
В действительности движение потока из смеси снега и воздуха является, конечно, турбулентным. Тем не менее в ядре потока все же может возникнуть чрезвычайно большое динамическое давление, чем и объясняется, что такие пылевые лавины иногда сносят со своего пути целью строения.
[c.487]
Парадокс устойчивости. В чистой среде причиной возникновения конвекции является неустойчивая стратификация по плотности конвекция возникает, если градиент плотности направлен вверх (вверху расположены более плотные слои жидкости) и по величине превосходит определенное критическое значение. Можно было бы думать, что в смеси все усложнения связаны лишь с тем, что теперь имеются две. причины, обуславливающие стратификацию, — неоднородность температуры и неоднородность концентрации. Оказывается, однако, что это не так. Значение градиента плотности само по себе еще не определяет условий возникновения конвективной неустойчивости сме-би.
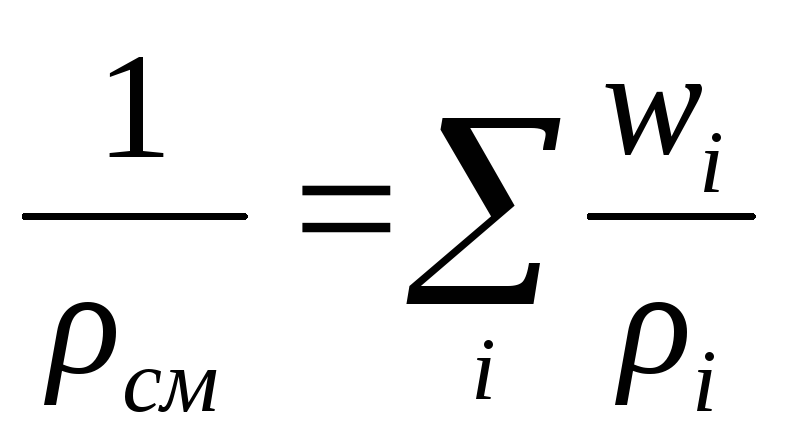 Неустойчивость при определенных условиях может возникнуть, если плотность смеси везде одинакова и даже если градиент плотности направлен вниз.
[c.230]
Неустойчивость при определенных условиях может возникнуть, если плотность смеси везде одинакова и даже если градиент плотности направлен вниз.
[c.230]Во многих экспериментальных работах (см., например, обнаружено, что в стратифицированной смеси при наличии в ней градиентов температуры и концентрации при определенных условиях возникают своеобразные слоистые течения в жидкости образуются чередующиеся вдоль вертикали слои, в которых происходит движение со скоростями, наклоненными на небольшой угол к горизонтали. Из экспериментов следует, что возникновение слоистых течений связано с наступлением некоторых критических условий. Как будет пояснено ниже, это явление связано с неустойчивостью равновесия смеси, при котором градиенты температуры и концентрации наклонены к вертикали (так, однако, что градиент плотности смеси вертикален см. 30). [c.385]
Физическую картину этой неустойчивости можно наглядно представить себе, используя те же рассуждения, что и приведенные в 32 ( парадокс устойчивости ). Для простоты рассмотрим равновесное состояние, при котором градиенты температуры и концентрации легкой компоненты горизонтальны и противоположны по направлению. Пусть, далее, их величины А и В согласованы так, что градиент плотности равен нулю, т. е. РИ + = 0. Речь идет, таким образом, о состоянии равновесия с одинаковой во всех точках плотностью смеси. Пусть для определенности градиент температуры направлен влево, а градиент концентрации — вправо. Будем считать также, что выполнено условие X > О, т. е. неоднородности температуры выравниваются быстрее, чем неоднородности концентрации. Поскольку температура и концентрация не зависят от вертикальной координаты, случайное смещение элемента среды вверх или вниз не приводит к появлению подъемной силы — возмущения такого типа гасятся вязкостью. Иная ситуация возникает при боковом смещении. Если, например, элемент сместится влево, то в новом месте, где температура окружающей среды выше, он будет быстро нагреваться, относительно медленно теряя легкую компоненту.
Для простоты рассмотрим равновесное состояние, при котором градиенты температуры и концентрации легкой компоненты горизонтальны и противоположны по направлению. Пусть, далее, их величины А и В согласованы так, что градиент плотности равен нулю, т. е. РИ + = 0. Речь идет, таким образом, о состоянии равновесия с одинаковой во всех точках плотностью смеси. Пусть для определенности градиент температуры направлен влево, а градиент концентрации — вправо. Будем считать также, что выполнено условие X > О, т. е. неоднородности температуры выравниваются быстрее, чем неоднородности концентрации. Поскольку температура и концентрация не зависят от вертикальной координаты, случайное смещение элемента среды вверх или вниз не приводит к появлению подъемной силы — возмущения такого типа гасятся вязкостью. Иная ситуация возникает при боковом смещении. Если, например, элемент сместится влево, то в новом месте, где температура окружающей среды выше, он будет быстро нагреваться, относительно медленно теряя легкую компоненту.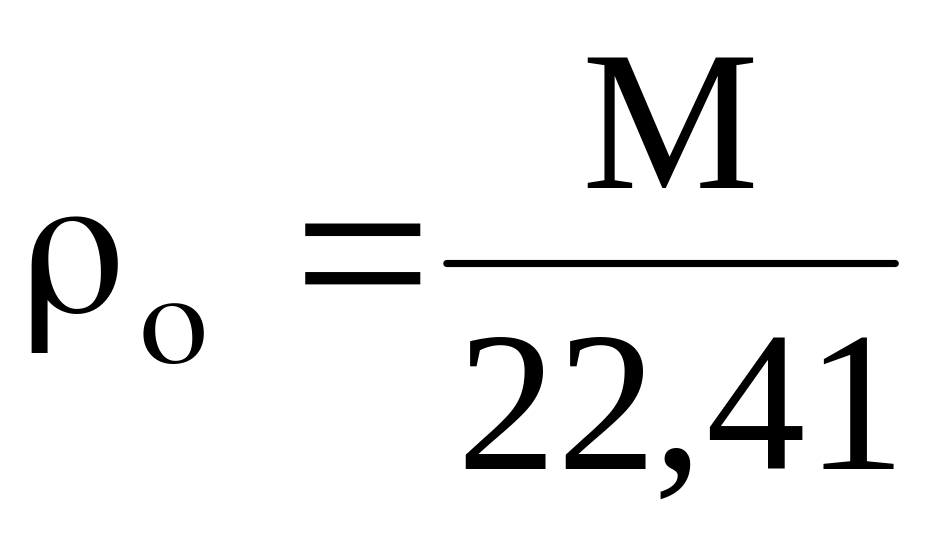 Плотность элемента может оказаться меньше плотности окружающей смеси, и в результате возникнет подъемная сила. Таким образом, при определенном соотношении между градиентами и параметрами жидкости боковое смещение может приве сти к монотонной неустойчивости. Элементы, случайно сместив-щиеся влево, будут всплывать, а элементы, сместившиеся вправо,— тонуть в результате сформируется слоистое течение с траекториями частиц, наклоненными к горизонтали.
[c.385]
Плотность элемента может оказаться меньше плотности окружающей смеси, и в результате возникнет подъемная сила. Таким образом, при определенном соотношении между градиентами и параметрами жидкости боковое смещение может приве сти к монотонной неустойчивости. Элементы, случайно сместив-щиеся влево, будут всплывать, а элементы, сместившиеся вправо,— тонуть в результате сформируется слоистое течение с траекториями частиц, наклоненными к горизонтали.
[c.385]
Рассмотрим теперь задачу о движении взвешенных частиц в турбулентном течении несжимаемой жидкости. Теория этого явления была развита в работах Баренблатта (1953, 1955) (см. также Колмогоров (1954)). Основным предположением указанной теории является допущение о малости размеров взвешенных частиц (по сравнению с характерным масштабом турбулентности), позволяющее считать, что они образуют как бы непрерывно распределенную в основной жидкости примесь. Выражение для полной плотности смеси можно записать в виде
[c. 365]
365]
Исходя из определений для плотности смеси р = Р1 (1 — объемной концентрации пузырьков 2 = и уравнения для линейной сжимаемости жидкости (последнее уравнение (6.2.1)), имеем [c.10]
Напомним, что в практически важной области малых и средних давлений удельные объемы пара в десятки и сотни раз превышают удельный объем насыщенной жидкости. Следовательно, при малых паросодержаннях даже небольшие их изменения резко сказываются на плотности смеси жидкости и пара. Например, при давлении в 20 бар и степени сухости, равной 1%, пар занимает приблизительно 50% общего объема смеси, т. е. ее плотность по сравнению с первоначальной уменьшается вдвое. Столь значительное влияние степени сухости на плотность смеси приводит к тому, что небольшим по абсолютной величине отклонениям паросодержания от его равновесного значения отвечают резкие изменения расхода. [c.180]
Используя корреляцию Маклеода—Сагдена, необходимо знать плотности смесей жидкостей и паров. Погрешности при высоких давлениях редко превышают
[c.523]
Погрешности при высоких давлениях редко превышают
[c.523]
Гл. 7 и 8 в наибольшей степени имеют прикладной характер. В гл. 7 вводятся основные количественные характеристики, обычно используемые при одномерном описании двухфазных потоков в каналах расходные и истинные паросодержания, истинные и приведенные скорости фаз, скорость смеси, коэффициент скольжения, плотность смеси. При рассмотрении методов прогнозирования режимов течения (структуры) двухфазной смеси акцент делается на методы, основанные на определенных физических моделях. Расчет трения и истинного объемного паросодержания дается раздельно для потоков квазигомогенной структуры и кольцевых течений. В гл. 8 описаны двухфазные потоки в трубах в условиях теплообмена. Приводится современная методика расчета теплоотдачи при пузырьковом кипении жидкостей в условиях свободного и вынужденного движения. Сложная проблема кризиса кипения в каналах излагается прежде всего как качественная характеристика закономерностей возникновения пленочного кипения при различных значениях
[c. 8]
8]
Таким образом, описание движения смеси жидкости с пузырьками газа, когда пренебрегается инерцией жидкости в мелкомасштабном движении вокруг пузырьков и тепловыми эффектами, соответствует вязкоупругой среде с замороженной или динамической скоростью звука С/ п объемной вязкостью определяемыми физическими свойствами жидкости ( i, jii) и текущей объемной концентрацией пузырьков аа. Кроме указанных величин, свойства такой среды зависят от исходной плотности жидкости рю, исходной объемной концентрации пузырьков азо и их исходного размера ад. Уравнения, близкие к (1.5.21), для описания трехфазных сред (грунт, жидкость, пузырьки газа) были предложены Г. М. Ляховым (1982). [c.107]
Двукратное превышение расчетного давления над экспериментально полученным объясняется завышенным расходом истекающего из реактора теплоносителя, рассчитанного по гидравлической модели с использованием коэффициента расхода, равного 0,61, и плотности насыщенной жидкости.
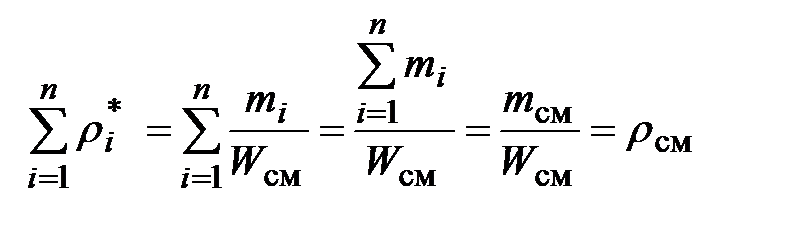 При этом допускалось, что имеет место полное разделение фаз и течет только вода. Давление в реакторе при истечении принималось постоянным. Кроме того, при сопоставлении расчетной модели было принято, что процесс истечения теплоносителя в оболочку (сухой колодец) квазистабилен, что вся масса пароводяной смеси и воздуха проходит через перепускной патрубок в камеру снижения давления и воды в сухом колодце не остается. Смесь при этом принималась однородной и находящейся в термодинамическом равновесии как в сухом колодце, так и в любой точке вдоль пути перепуска.
[c.102]
При этом допускалось, что имеет место полное разделение фаз и течет только вода. Давление в реакторе при истечении принималось постоянным. Кроме того, при сопоставлении расчетной модели было принято, что процесс истечения теплоносителя в оболочку (сухой колодец) квазистабилен, что вся масса пароводяной смеси и воздуха проходит через перепускной патрубок в камеру снижения давления и воды в сухом колодце не остается. Смесь при этом принималась однородной и находящейся в термодинамическом равновесии как в сухом колодце, так и в любой точке вдоль пути перепуска.
[c.102]Построение теоргтических моделей, адекватных физической реальности, и создание инженерных методов расчета оборудования с учетом особенностей двухфазных течений невозможно без изучения волновой динамики газо- и парожидкостных сред. Особенности проявления волновых свойств зависят как от состояния и структуры самой среды, так и от амплитуды и частоты вносимых в нее возмущений. При этом предметом изучения становятся релаксационные и диссипативные процессы, происходящие в двухфазных средах при распространении в них волны возмущения. Времена протекания этих процессов, их взаимное влияние определяют эволюцию генерируемых волн в нестационарных условиях, скорость их распространения и интенсивность. Как показали многочисленные эксперименты, в газодинамике двухфазных потоков паро-(газо-) капельной структуры определяющим является обмен количеством движения между молекулами несущей газовой среды и каплями жидкости. При рассмотрении быстропротекающих процессов в смесях жидкости с пузырьками пара и газа определяющими являются инерционные свойства жидкости при внутренних радиальных ее движениях, возникающих в результате взаимодействия молекул газа в пузырьках с прилегающими к ним объемами жидкости При добавлении пузырьков газа мало меняется средняя плотность среды при достаточно малых концентрациях пузырьков, но характер изменения давления меняется существенно.
[c.32]
Времена протекания этих процессов, их взаимное влияние определяют эволюцию генерируемых волн в нестационарных условиях, скорость их распространения и интенсивность. Как показали многочисленные эксперименты, в газодинамике двухфазных потоков паро-(газо-) капельной структуры определяющим является обмен количеством движения между молекулами несущей газовой среды и каплями жидкости. При рассмотрении быстропротекающих процессов в смесях жидкости с пузырьками пара и газа определяющими являются инерционные свойства жидкости при внутренних радиальных ее движениях, возникающих в результате взаимодействия молекул газа в пузырьках с прилегающими к ним объемами жидкости При добавлении пузырьков газа мало меняется средняя плотность среды при достаточно малых концентрациях пузырьков, но характер изменения давления меняется существенно.
[c.32]
С целью получения жидкостей для гидравлических систем эти масла можно смешивать друг с другом или с другими продуктами, такими как полисилоксановые масла, диэфиры и другие органические жидкости. Масла Халокарбон способствуют повышению стойкости к воспламенению и плотности смесей, уменьшают поглощение ими воды. Они хорошо смачивают
[c.245]
Масла Халокарбон способствуют повышению стойкости к воспламенению и плотности смесей, уменьшают поглощение ими воды. Они хорошо смачивают
[c.245]
Подбором плотности несущей жидкости этот режим движения может быть использован в технологических процессах тонкого разделения смесей частиц с близкими плотностями, которые имеютбольшоезначение при обогащении полезных ископаемых. Кроме того, его можно рекомендовать для применения в металлургии для выплавки металлов с неоднородными свойствами и при получении композиционных материалов. [c.112]
Имеются дискретные хорошо сформировавшиеся пузыри с очень малой плотностью (т. е. содержащие мало частиц). В этих условиях слой состоит из эмульсионной фазы, через которую течет фаза меньшей плотности (называемая иногда фазой пузырей ). При дальнейшем увеличении скорости начинается разрушение пузырей и наблюдаются более мелкие пузыри с повышенной плотностью (содержащие больше частиц). При достаточно высоких скоростях газа в интервале 3—5 фут/с достигаются условия для более однородного псевдоожижения. Наступление этих условий сопровождается быстрым выносом частиц из слоя, так что общая картина движения приближается к характерной для пневмотранспорта, а не для псевдоожиженного слоя..Более высокая устойчивость разбавленной фазы важна при конструировании аппаратуры для проведения реакций в этой фазе, а также для пневматического транспорта свободных частиц. Зенз [108] предложил фазовую диаграмму состояний смеси жидкости с частицами, которая описывает с качественной стороны некоторые из сложных явлений, связанных с распределением частиц и устойчивостью таких систем.
[c.494]
Наступление этих условий сопровождается быстрым выносом частиц из слоя, так что общая картина движения приближается к характерной для пневмотранспорта, а не для псевдоожиженного слоя..Более высокая устойчивость разбавленной фазы важна при конструировании аппаратуры для проведения реакций в этой фазе, а также для пневматического транспорта свободных частиц. Зенз [108] предложил фазовую диаграмму состояний смеси жидкости с частицами, которая описывает с качественной стороны некоторые из сложных явлений, связанных с распределением частиц и устойчивостью таких систем.
[c.494]
Разработан способ определения критической плотности по известным значениям плотности насыщенных жидкости и пара при температурах на 10—15° ниже критической. Методика, проверенная на 28 веществах, имеет точность 2—3%. Предложен метод экспериментального определения энтальпии газообразных смесей путем адиабатного дросселирования исследуемого вещества до идеальногазового состояния.
[c. 120]
120]
Конструкции барботажных газлифт-ных аппаратов. Газлифтные аппараты отличаются от бгфботажных колонн тем, что внутри их корпуса 1 установлены одна или несколько барботажных труб 3, в которые с помощью газораспределителя 2 вводится газ (рис. 6.4.3). При подаче газа в затопленный жидкостью аппарат в барботажных трубах образуется газожидкостная смесь, плотность которой меньше плотности однородной жидкости в циркуляционной зоне (на рис. 6.4.3 — в межтрубном пространстве), вследствие чего в аппарате возникает циркуляция жидкости с восходящим потоком смеси внутри циркуляционной трубы и нисходящим потоком в зазоре между корпусом и циркуляционной трубой. Конструктивное исполнение газлифтных аппаратов может [c.635]
При развитом высокоскоростном турбулентном течении (Re >10 ) пузырьковой жидкости в трубе гидравлическое сопротивление, как и при течении однофазной жидкости, не зависит от вязкости, а определяется только шероховатостью внутренних стенок трубы. В этом случае можно использовать (G. Wallis, 1969) обычные формулы для однофазной жидкости (см. Л. Г. Лойцянский, 1973 V. Streeter, 1961), в которые в качестве плотности следует подставить плотность смеси, а в качестве скорости — средне-массовую (расходную) скорость смеси
[c.176]
В этом случае можно использовать (G. Wallis, 1969) обычные формулы для однофазной жидкости (см. Л. Г. Лойцянский, 1973 V. Streeter, 1961), в которые в качестве плотности следует подставить плотность смеси, а в качестве скорости — средне-массовую (расходную) скорость смеси
[c.176]
Расчет плотности смеси двух углеводородных жидкостей. Измерение наименьшего перепада давления
Таблица 1
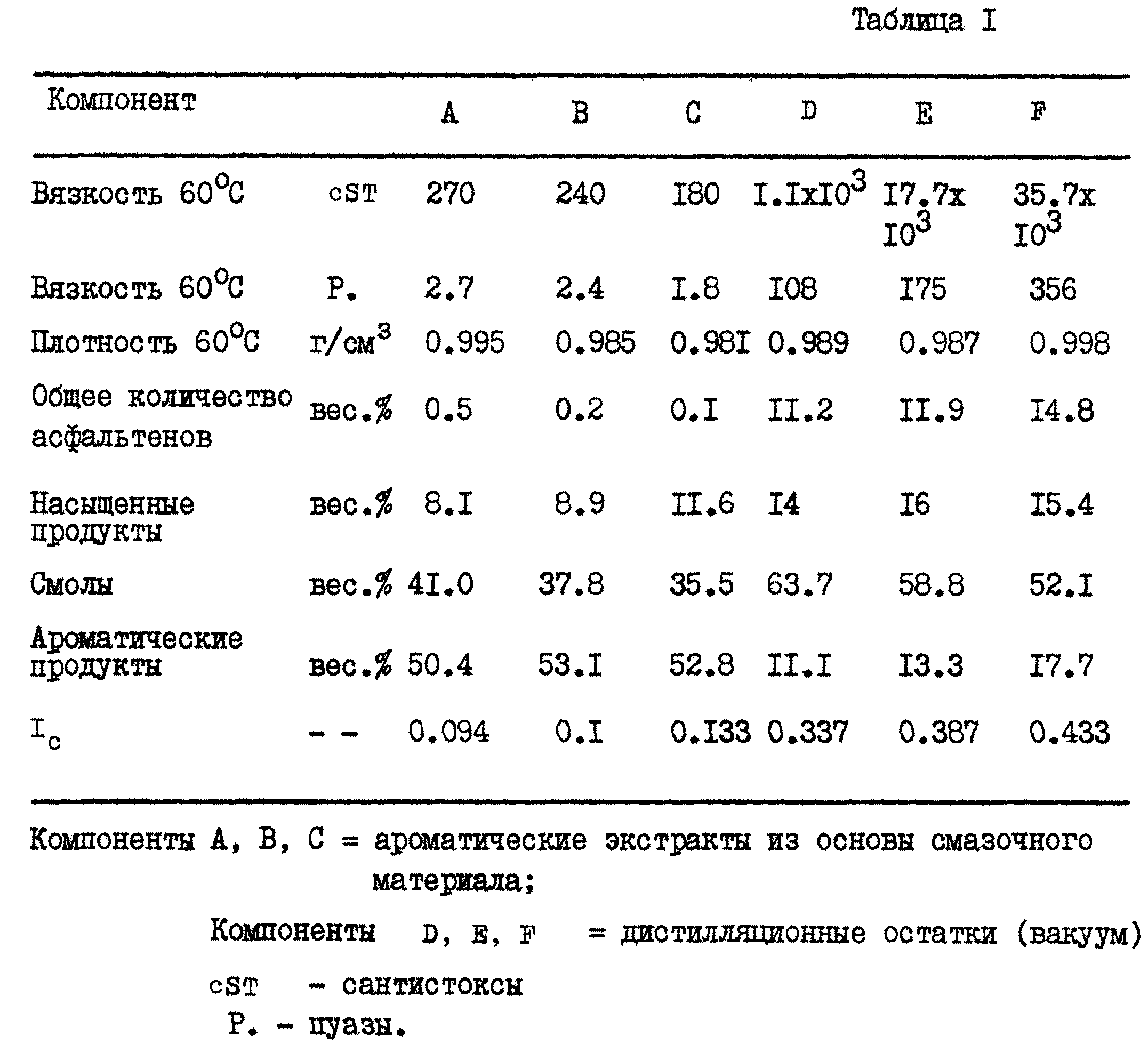
Вопрос. Какова плотность смеси двух углеводородных жидкостей, если для нее взято 0,4л нефти (ρн = 850кг/м3) и 0,6л керосина (ρк = 800кг/м3).
Решение
Определяем плотность смеси по выражению ρсм = Σriρi, где ri – объемные доли жидкостей.
Объем все смеси V = Vн + Vк = 0,4 + 0,6 = 1,0л.
Объемные доли rн = = 0,4; rн = = 0,6.
Плотность смеси ρсм =
0,4∙850 + 0,6∙800 = 820кг/м3.
Ответ: 820кг/м3.
Вопрос. Два одинаковых, считающихся недеформируемыми образца породы при пластовом давлении в лабораторных условиях насыщены один водой, а второй нефтью. Сравните объемы жидкости, вытекающие из образцов при снижении давления до атмосферного.
Решение
Объемы жидкостей вытекающих из пород зависят от плотностей этих жидкостей. Плотность воды 1000кг/м3, плотность нефти 850кг/м3.
Если масса пород М, объемы можно определить
Vв = ; Vн = .
При сравнении этих величин
< , т.е. Vв < Vн.
Ответ: нефти больше
Вопрос. Можно ли при помощи термометра определить величину атмосферного давления?
Решение
Термометр служит только для
измерения температуры, а для измерения атмосферного давления применяют
барометр.
Ответ: для этой цели служит барометр.
Таблица 2
Вопрос. С одной стороны в частично заполненную водой открытую U-образную трубку добавили бензин. Сравните высоты столбов бензина (hб) и воды (hв), отсчитываемые от границы раздела жидкостей.
Решение
Давления в точках раздела жидкостей будет равны Ра + ρв∙g∙hв = Ра + ρб∙g∙hб,
После преобразований получаем ρв∙hв = ρб∙hб, высота столба воды hв = .
Искомая высота уровней h = hб – hб = hб, полученное выражение получается положительным, значит
hб > hв.
Ответ: hб > hв
Вопрос. Прибор для измерения
давления имеет шкалу пределами измерения от 0 до 0,1МПа. Как называется прибор?
Прибор для измерения
давления имеет шкалу пределами измерения от 0 до 0,1МПа. Как называется прибор?
Решение
Для измерения давления ниже атмосферного от 0 до 0,1МПа служат вакуумметры.
Ответ: вакуумметр
Вопрос. По трубопроводу течет вода. Какую из жидкостей (ртуть, четыреххлористый углерод, бензин) нужно залить в двужиткостный дифференциальный манометр, что бы он мог измерить наименьший перепад давления? При этом ρр > ρч.у > ρб.
Решение
Давление зависит от плотности жидкости, поэтому, что бы измерить наименьший перепад давления необходимо залить жидкость с наименьшей плотностью, т. е. бензин.
Ответ: бензин.
Вопрос. На стенке закрытого сосуда с
жидкостью установлены манометр и вакуумметр. Показания каждого из них 2,45кПа,
а расстояние по вертикали между ними 5м. Какая из жидкостей находится в
резервуаре: бензин, вода или ртуть?
Какая из жидкостей находится в
резервуаре: бензин, вода или ртуть?
Решение
Манометр показывает манометрическое давление Рман = 2,45кПа.
Вакуумметр показывает вакуумметрическое давление Рвак = 2,45кПа.
Таблица 3
Вопрос. Под уровнем жидкости находятся две равновеликие поверхности: квадрат и круг. Сравните силы давления жидкости, действующей с одной стороны на каждую из этих фигур.
Решение
Сила давления жидкости на поверхность равна
Р = ρ∙g∙hц∙ω, где hц – центр приложения силы, м, примем равным;
ω – площадь смоченной поверхности, м2, если примем сторону квадрата 1м и диаметр круга 1м, то получим площади смоченных поверхностей:
квадрата ω = 1м2;
круга ω = = 0,785м2.
Площадь квадрата больше, чем
площадь круга, значит сила давления на квадрат, больше чем на круг.
Ответ: на квадрат сила давления больше
Вопрос. Может ли центр давления совпасть с центром тяжести смоченной твердой поверхности.
Решение
Полное гидростатическое давление в точке можно определить по формуле
Р = Ро + ρ∙g∙h,
Где Ро – давление на свободной поверхности жидкости,
h – глубина погружения точки, которая может совпасть с центром тяжести только телом, имеющим прямоугольную форму.
Ответ: Может, если эта поверхность имеет прямоугольную форму.
Вопрос. Что происходит с равнодействующей всех сил давления на плоскую стенку небольшого сосуда, заполненного жидкостью, если его закрыть и над свободной поверхностью в нем создавать постепенно возрастающий вакуум.
Решение
Абсолютное давление на крышку
Рабс
= Ратм – Рвак.
Вакуум – это давление ниже атмосферного, значит, равнодействующая всех сил давления на плоскую стенку сосуда будет уменьшаться.
Ответ: уменьшается.
Таблица 4
Вопрос. Круглое отверстие в боковой вертикальной плоской стенке резервуара с жидкостью может быть закрыто (рис.): плоской (а), сферической (б) или конической (в). Покажите соотношение растягивающих болты усилий для этих крышек.
Энергетическое образование
Примеры решения задач по теме «Смеси идеальных газов»
1. Объемный состав газообразного топлива следующий: $h3 = 10$ %, $Ch5 = 90$ %. Определить среднюю молекулярную массу и газовую постоянную смеси.
2. Объемный состав продуктов сгорания $СО2 = 12.3$ %; $O2 = 7.2$ %; $N2 = 80.5$ %. Определить плотность и удельный объем смеси при $t = 800$ °C и $P_{бар} = 740$ мм.рт.ст.
3. В резервуаре емкостью $V = 155$ м3 находится светильный газ при давлении $Р = 4$ ат и температуре $t = 18$ °C. Объемный состав газа $Н2 = 46$ %; $СН4 = 32$ %; $СО = 15$ %; $N2 = 7$ %. После израсходования некоторого количества газа давление его понизилось до $3.1$ ат, а температура упала до $12$ °С. Определить массу израсходованного газа.
Объемный состав газа $Н2 = 46$ %; $СН4 = 32$ %; $СО = 15$ %; $N2 = 7$ %. После израсходования некоторого количества газа давление его понизилось до $3.1$ ат, а температура упала до $12$ °С. Определить массу израсходованного газа.
4. Массовый состав смеси следующий: $СО2 = 18$ %; $O2 = 10$ %; $N2 = 72$ %. До какого давления нужно сжать эту смесь, находящуюся при нормальных условиях, чтобы при $t = 180$ °C $8$ кг ее занимали объем $40$ л?
5. Анализ продуктов сгорания топлива показал следующий объемный состав: $CO2 = 12.2$ %; $O2 = 7.1$ %; $CO = 10$ %; $N2 = 70.7$ %. Найти массовый состав газов, составляющих продукты сгорания.
6. В резервуаре объемом $10$ м3 находится газовая смесь, состоящая из $1$ кг кислорода и $39$ кг азота. Температура смеси равна $27$ °С. Определить парциальные давления компонентов смеси.
7. Плотность смеси азота и углекислого газа при давлении $1.4$ бар и температуре $45$ °C равна $2$ кг/м3.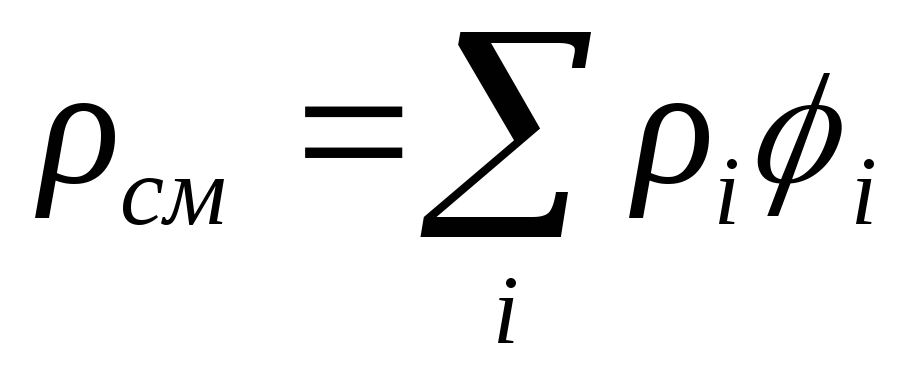 Определить массовый состав смеси.
Определить массовый состав смеси.
8. Определить массовый состав газовой смеси, состоящей из углекислого газа и азота, если известно, что парциальное давление углекислого газа $p_{CO2}=120$ кПа, а давление смеси $p_{см}=300$ кПа.
9. Определить газовую постоянную, удельный объем газовой смеси и парциальные давления ее составяющих, если объемный состав смеси следующий: $CO_2=12$ %, $O_2= 8$ % и $N_2= 80$ %, а общее давление $p=100$ кПа и температура $t=40$ °C.
10. Газовая смесь имеет следующий массовый состав: $CO_2=12$ %, $O_2= 8$ % и $N_2= 80$ %. До какого давления нужно изотермически сжать эту смесь, находящуюся при нормальных условиях, чтобы плотность ее составляла $1.6$ кг/м3?
Основные физико-химические и теплофизические свойства смесей и мороженого
Физико-химические и теплофизические свойства смесей и мороженого существенно влияют на органолептические показатели продукта.
Плотность молочных, сливочных и пломбирных смесей мороженого находится в пределах 1100-1300 кг/м3.
Данные об объемной массе мороженого в зависимости от его взбитости и плотности смеси приведены в таблице.
Объемная масса мороженого, кг/м3
|
Плотность смеси, кг/м3 |
Взбитость, % |
||||||
|
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
|
1050 |
750 |
700 |
656 |
618 |
583 |
553 |
525 |
|
1080 |
771 |
720 |
675 |
635 |
600 |
568 |
540 |
|
1100 |
785 |
733 |
688 |
647 |
611 |
578 |
550 |
|
1110 |
793 |
740 |
694 |
653 |
617 |
584 |
555 |
Взбитость мороженого, а также степень дисперсности воздушных пузырьков в мороженом в значительной мере обусловливают его способность противостоять таянию. Об этом показателе, характеризующем охлаждающий эффект мороженого, судят по продолжительности накопления 10 мл смеси, образующейся при таянии образцов закаленного (-18° С) или мягкого (-6° С) мороженого, помещаемых в термостат (температура воздуха 25° С).
Об этом показателе, характеризующем охлаждающий эффект мороженого, судят по продолжительности накопления 10 мл смеси, образующейся при таянии образцов закаленного (-18° С) или мягкого (-6° С) мороженого, помещаемых в термостат (температура воздуха 25° С).
Коэффициент динамической вязкости смесей в значительной мере определяется свойствами и концентрацией используемого стабилизатора. Этот показатель уменьшается при перемешивании смесей. Вязкость смесей, подвергнутых замораживанию, после размораживания ниже исходной.
Вязкость смесей мороженого зависит и от температуры.
Поверхностное натяжение смесей мороженого со стабилизаторами агароидом, желатином и метилцеллюлозой различное.
Для характеристики реологических свойств смесей и мороженого определяют предельное напряжение сдвига.
Предельное напряжение сдвига мороженого уменьшается с увеличением взбитости продукта. Понижение температуры и связанное с этим увеличение количества вымороженной воды приводит к существенному росту предельного напряжения сдвига, причем чем мельче кристаллы льда, тем меньше предельное напряжение сдвига. После фризерования при температуре -4° С предельное напряжение сдвига не превышает 10 Па. При температуре же -23° C предельное напряжение сдвига молочного мороженого (S = 60%) обычно не более 2350 Па, сливочного (S = 75%) — не более 1960 Па и пломбира (S = 90%) — не более 690 Па.
После фризерования при температуре -4° С предельное напряжение сдвига не превышает 10 Па. При температуре же -23° C предельное напряжение сдвига молочного мороженого (S = 60%) обычно не более 2350 Па, сливочного (S = 75%) — не более 1960 Па и пломбира (S = 90%) — не более 690 Па.
Криоскопическая температура смесей мороженого в зависимости от их состава находится в пределах от -2 до -3,5° С.
В интервале температур от криоскопической до -5° С в лед превращается примерно 45-50% влаги, содержащейся в мороженом.
Полная удельная теплоемкость смесей мороженого увеличивается с повышением содержания в них жира и в интервале температур от 0 до 18° С (в среднем) составляет [в кДж/(кг К)]:
Молочная — 3,39
Сливочная — 3,52
Пломбирная — 3,60
В указанном интервале температур, а также при температурах до 50-55° С на величину полной удельной теплоемкости смесей влияют тепловые эффекты, вызываемые фазовыми превращениями молочного жира.
При температурах выше 55° С такие превращения практически не происходят и удельная теплоемкость смесей мороженого не изменяется. При этих температурах для приближенных расчетов удельную теплоемкость молочной смеси допустимо принимать равной 3,31 кДж/(кг К), сливочной — 3,21 и пломбирной — 3,07 кДж/(кг К).
При этих температурах для приближенных расчетов удельную теплоемкость молочной смеси допустимо принимать равной 3,31 кДж/(кг К), сливочной — 3,21 и пломбирной — 3,07 кДж/(кг К).
Полная удельная теплоемкость мороженого, т. е. удельная теплоемкость с учетом фазовых превращений воды и жира, при температурах, близких к криоскопической, достигает больших величин в связи с интенсивным льдообразованием. Значение же этой теплофизической характеристики при более низких температурах определяется в основном содержанием в мороженом льда, удельная теплоемкость которого вдвое меньше, чем воды. Поэтому с понижением температуры полная удельная теплоемкость мороженого уменьшается.
Полная удельная теплоемкость мороженого при различных температурах, определенная по графику отводимого тепла:
|
Температура мороженого, °С |
Полная удельная теплоемкость мороженого, кДж/(кг К) |
|
|
молочного |
сливочного |
|
|
-8 |
9,9 |
7,1 |
|
-12 |
6,1 |
5,0 |
|
-16 |
4,6 |
4,4 |
|
-20 |
3,8 |
3,6 |
Отводимое тепло при охлаждении и замораживании смесей мороженого может быть определено с помощью графика энтальпий, построенного по экспериментальным данным. В этом графике энтальпий смесей и мороженого за начало отсчета взята температура -20° С, энтальпия мороженого при которой принята равной нулю.
В этом графике энтальпий смесей и мороженого за начало отсчета взята температура -20° С, энтальпия мороженого при которой принята равной нулю.
При этом состав смесей мороженого соответствует данным следующей таблицы.
Состав смесей мороженого:
|
Смесь мороженого |
Содержание, % к массе |
||||
|
жира |
COMO |
сахарозы |
сухих веществ |
воды |
|
|
Молочная |
3,5 |
10,0 |
16,0 |
29,8 |
70,2 |
|
Сливочная |
10,0 |
10,0 |
14,0 |
34,3 |
65,7 |
|
Пломбирная |
15,0 |
10,0 |
16,0 |
41,3 |
58,7 |
|
Плодово-ягодная |
— |
— |
28,0 |
30,95 |
69,05 |
Коэффициенты теплопроводности смесей мороженого возрастают с повышением температуры.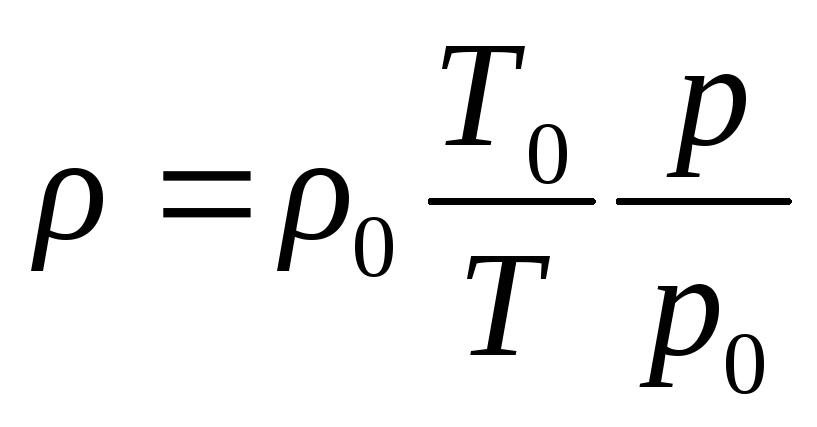
Коэффициенты теплопроводности и температуропроводности мороженого с понижением температуры увеличиваются, поскольку коэффициент теплопроводности льда значительно больше (приблизительно в 4 раза), чем воды.
Фазовые превращения молочного жира значительно меньше влияют на изменение теплофизических свойств мороженого, чем фазовые превращения воды. Это объясняется тем, что в интервале температур от 0 до -20° С отвердевает не более 20% молочного жира от общей его массы в мороженом (до 80% молочного жира отвердевает при положительных температурах). Кроме того, содержание жира в мороженом сравнительно невелико, а удельная теплота его отвердевания (или плавления) значительно меньше, чем воды (соответственно 93,3 и 335 кДж/кг).
Способность мороженого противостоять таянию характеризуют продолжительностью накопления 10 мл смеси, образующейся при таянии образцов определенной формы закаленного (-18° С) или мягкого (-6° С) мороженого. Этот показатель существенно зависит от взбитости мороженого, степени дисперсности воздуха в продукте, содержания в нем влаги и характеризует охлаждающий эффект мороженого.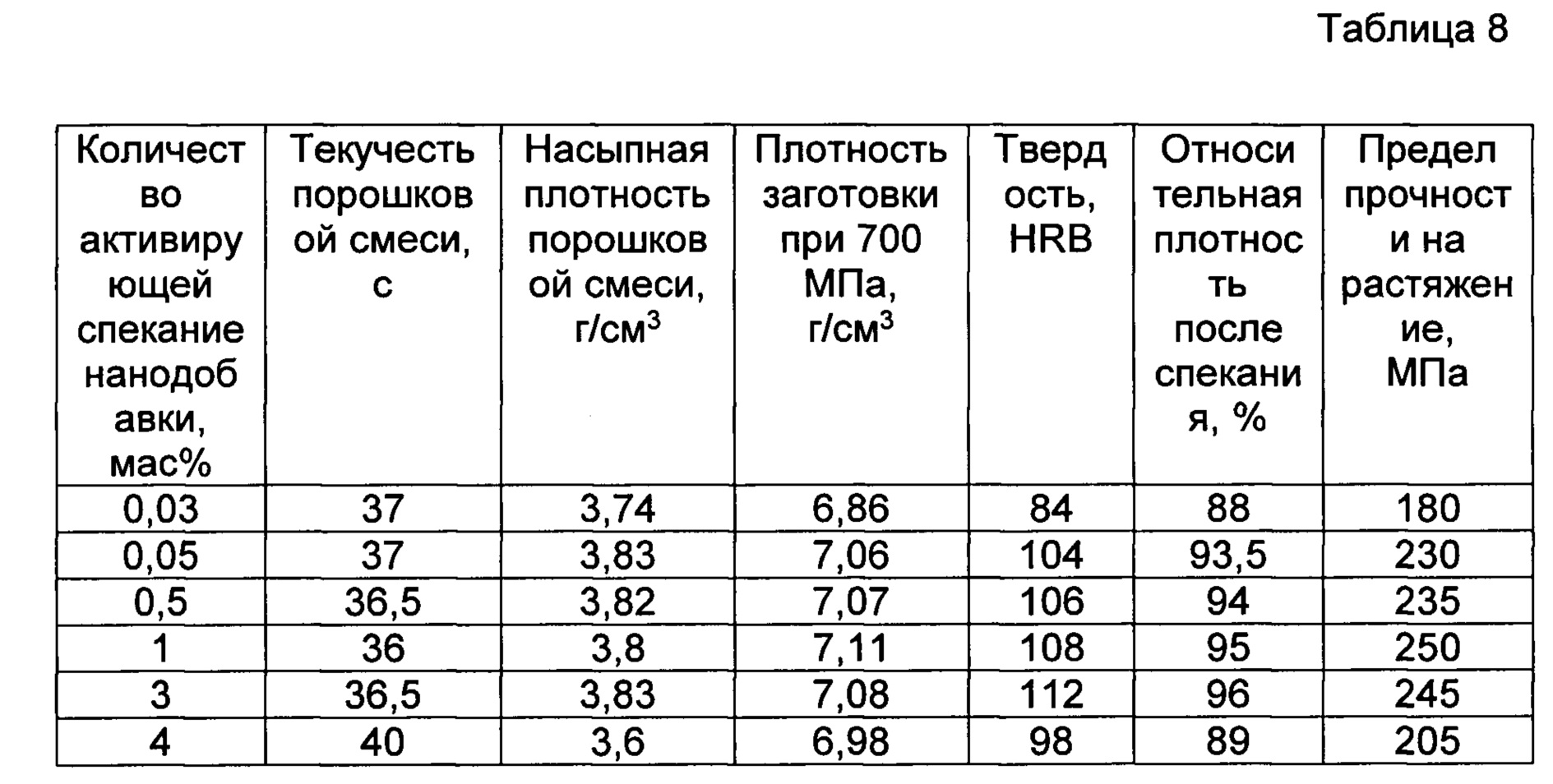
Калькулятор наливного пола. Расчет наливного пола калькулятор.
Калькулятор расхода наливного пола на квадратный метр.
Ремонт всегда связан с выравниванием пола. Если необходимо положить новый паркет или линолеум, то нет смысла укладывать новое напольное покрытие на неровный, в трещинах пол.
Наравне с бетонной стяжкой сегодня активно используются различные наливные полы, которые быстро и эффективно могут выровнять любой пол: заполнить трещины, сравнять выпуклости. Это наиболее простой, быстрый и эффективный способ добиться ровного пола.
Калькулятор наливного пола используется для определения количества материала необходимого для выравнивания пола. То есть, перед началом ремонтных работ, чтобы определить, сколько мешков нужно материала сначала нужно просчитать все на калькуляторе, который работает в онлайн режиме.
Как правило, определить расход наливного пола калькулятор может для всех наливных полов, которые есть в продаже. Сегодня есть такие виды наливных полов, как:
- эпоксидные;
- полиуретановые;
- метилметакрилатные;
- цементо-акриловые.
Для каждого из этих видов наливной пол калькулятор расхода может определить с большой точностью. Сегодня – это наиболее быстрый и эффективный способ произвести все расчеты.
Пользоваться калькулятором намного удобнее, чем мерить на глаз. Если взять дорогой пол и купить недостаточное количество мешков, то потом придется пол доделывать. Пользоваться калькулятором просто. Нужно ввести в поля необходимые данные.
Например, указать вид наливного пола, предполагаемую толщину и размер помещения.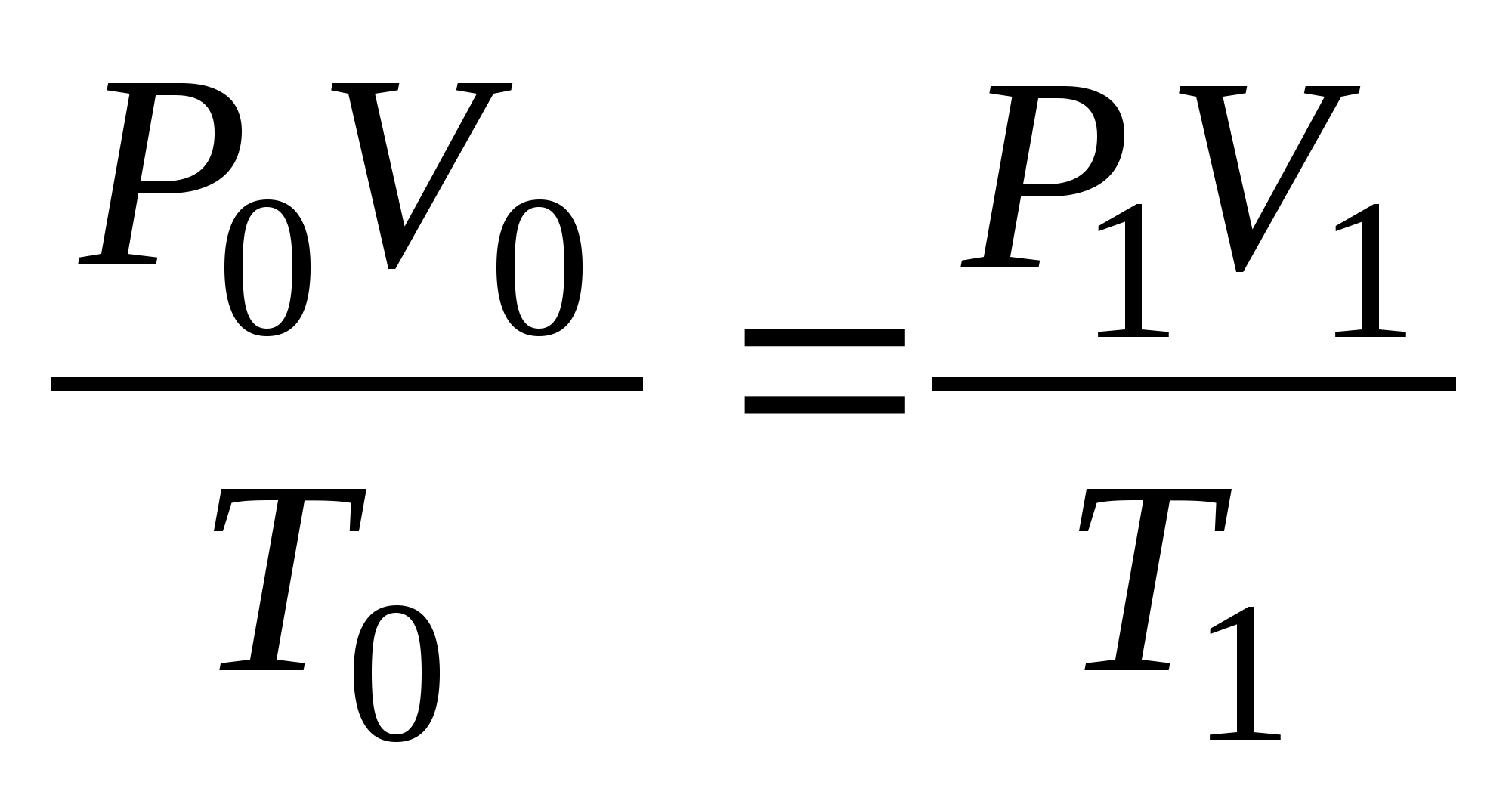 Плотность и вес сухой смеси можно узнать на упаковке. Калькулятор быстро выполнит все подсчеты и сообщит, сколько нужно мешков наливного пола для конкретного помещения. Как правило, на расчеты уходит всего несколько секунд.
Плотность и вес сухой смеси можно узнать на упаковке. Калькулятор быстро выполнит все подсчеты и сообщит, сколько нужно мешков наливного пола для конкретного помещения. Как правило, на расчеты уходит всего несколько секунд.
Можно, например, уменьшить количество дорого наливного пола. Для этой цели можно сначала сделать бетонную стяжку и сверху положить наливной пол. Еще один способ – подстелить обычный песок. Следует также обратить внимание, что количество наливного пола зависит от текучести материала. Если текучесть большая, то такого материала потребуется меньше.
Пользоваться онлайн калькулятором для наливного пола очень удобно. Это сэкономит время и строительные материалы. Пол получится ровным, прочным и красивым. Воспользоваться калькулятором можно в любое время.
Плотности смеси, максимальное правдоподобие и алгоритм Em на JSTOR
Абстрактный Проблема оценки параметров, определяющих плотность смеси, была предметом большого и разнообразного объема литературы, охватывающей почти девяносто лет. В течение последних двух десятилетий метод максимального правдоподобия стал наиболее распространенным подходом к этой проблеме, в первую очередь благодаря появлению высокоскоростных электронно-вычислительных машин. Здесь мы сначала предлагаем краткий обзор литературы, посвященной этой проблеме, и рассмотрим оценку максимального правдоподобия для нее.Затем мы обратимся к предмету, представляющему наибольший интерес, который представляет собой особую итеративную процедуру для численной аппроксимации оценок максимального правдоподобия для задач плотности смеси. Эта процедура, известная как алгоритм EM, представляет собой специализацию контекста плотности смеси общего одноименного алгоритма, используемого для аппроксимации оценок максимального правдоподобия для задач с неполными данными. Мы обсуждаем формулировку, а также теоретические и практические свойства EM-алгоритма для смесей плотностей, уделяя особое внимание смесям плотностей из экспоненциальных семейств.
В течение последних двух десятилетий метод максимального правдоподобия стал наиболее распространенным подходом к этой проблеме, в первую очередь благодаря появлению высокоскоростных электронно-вычислительных машин. Здесь мы сначала предлагаем краткий обзор литературы, посвященной этой проблеме, и рассмотрим оценку максимального правдоподобия для нее.Затем мы обратимся к предмету, представляющему наибольший интерес, который представляет собой особую итеративную процедуру для численной аппроксимации оценок максимального правдоподобия для задач плотности смеси. Эта процедура, известная как алгоритм EM, представляет собой специализацию контекста плотности смеси общего одноименного алгоритма, используемого для аппроксимации оценок максимального правдоподобия для задач с неполными данными. Мы обсуждаем формулировку, а также теоретические и практические свойства EM-алгоритма для смесей плотностей, уделяя особое внимание смесям плотностей из экспоненциальных семейств.
SIAM Review содержит статьи, написанные для широкого
научная аудитория. Статьи включают пояснительные или обзорные статьи.
сосредоточение внимания на важных достижениях в области прикладной или вычислительной математики, или
документы, описывающие математические и вычислительные проблемы в
научные или инженерные приложения. Другие функции включают эссе,
обзоры книг, тематические исследования из отрасли, заметки в классе и проблемы
и решения.
Статьи включают пояснительные или обзорные статьи.
сосредоточение внимания на важных достижениях в области прикладной или вычислительной математики, или
документы, описывающие математические и вычислительные проблемы в
научные или инженерные приложения. Другие функции включают эссе,
обзоры книг, тематические исследования из отрасли, заметки в классе и проблемы
и решения.
«Общество промышленной и прикладной математики является ведущим
международная ассоциация прикладной математики и ее публикации
могли бы стать ядром адекватной коллекции по математике. Один из
цели этой организации состоит в том, чтобы сделать поток информации между
университет и промышленность более гладкими. Прекрасно справляется с этой задачей
и многие из ведущих академических учреждений мира являются членами.»
— Журналы для библиотек, восьмое издание, 1995 г., R. R.
Боукер, Нью-Провиденс, Нью-Джерси
Общество промышленной и прикладной математики (SIAM), штаб-квартира
в Филадельфии, была основана в 1951 году для продвижения применения
математики в науку и промышленность, продвигать математические исследования и
предоставить средства для обмена информацией и идеями между
математиков, инженеров и ученых. SIAM имеет комплексную программу публикаций в области прикладных и вычислительных
математике, включая 11 престижных исследовательских журналов.Для полного
описание наших журналов и недавно анонсированных SIAM Journals Online,
зайдите на http://www.siam.org/.
SIAM имеет комплексную программу публикаций в области прикладных и вычислительных
математике, включая 11 престижных исследовательских журналов.Для полного
описание наших журналов и недавно анонсированных SIAM Journals Online,
зайдите на http://www.siam.org/.
Распределение смеси — Analytica Wiki
Распределение смеси , иногда также называемое плотностью смеси , представляет собой распределение, сформированное из взвешенной комбинации двух или более распределений компонентов. Распределение компонентов может быть одномерным или многомерным.
Двухкомпонентные распределители | Смесь дистрибутивов X1 и X2.X1 взвешено по 0,3, X2 по 0,7 |
Вот пример, в котором распределение смеси формируется из двух нормально распределенных распределений компонентов, учитывая распределение для X1 с весом 0,3 и распределение для X2 с весом 0,7.
Когда использовать
Предположим, у вас есть популяция, в которой каждый индивидуум принадлежит ровно к одной из нескольких групп. Если вы можете оценить распределение некоторой величины для каждой группы, распределение для населения в целом получается как их смесь, при этом каждый компонент взвешивается как доля всего населения, представленного этой группой.
- Пример: На шоссе 67% автомобилей и 33% грузовиков. Вес легковых автомобилей распределяется как
Normal(3200, 300)фунтов, тогда как вес грузовиков распределяется какNormal(12K, 4K). Распределение изменчивости для всех транспортных средств представляет собой смесь из них: распределениеНормальное (3200, 300)имеет вес 0,67, а распределениеНормальное (12K, 4K)имеет вес 0,33.
Распределение веса транспортных средств
Другое использование возникает, когда возможны несколько ситуаций, но вы не знаете, в какой ситуации находитесь. Если у вас есть оценки неопределенности определенной величины для каждой ситуации и у вас есть оценка вероятности оказаться в каждой ситуации, то смесь распределений для каждой ситуации, взвешенных по вероятности, дает вашу чистую неопределенность.
Если у вас есть оценки неопределенности определенной величины для каждой ситуации и у вас есть оценка вероятности оказаться в каждой ситуации, то смесь распределений для каждой ситуации, взвешенных по вероятности, дает вашу чистую неопределенность.
- Пример. Торговец акциями знает, что FDA скоро примет решение о том, будет ли одобрено новое лекарство определенной компании. Он считает, что если это будет одобрено, цена акций компании изменится на
Нормальных (180%, 40%), но если это не будет одобрено, он ожидает, что цена изменится наНормальных (-60%, 30%). ).Поскольку он считает, что вероятность одобрения составляет 50 %, для моделирования прогнозируемого изменения цены акций можно использовать равновзвешенную смесь.
Смешанные оценки также используются при объединении оценок нескольких экспертов. Распределения оценок от каждого эксперта могут быть смешаны с использованием субъективного веса, отражающего доверие к каждому эксперту.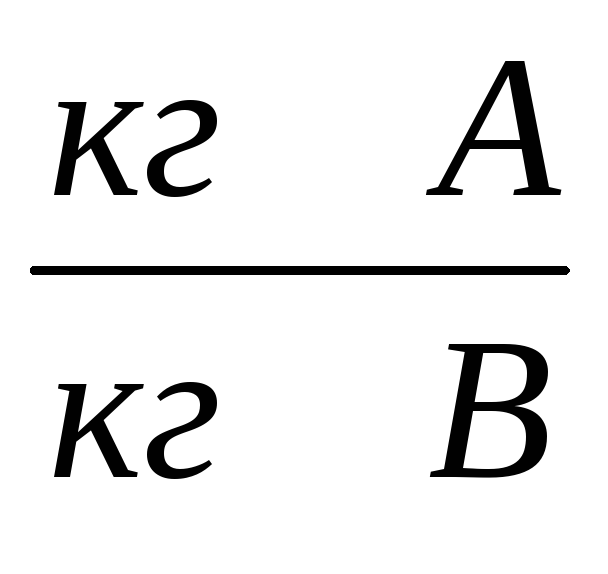
- Относительная достоверность экспертов не является точно определенной величиной, хотя ее все же можно использовать на практике без особых затруднений.Альтернативная интерпретация состоит в том, что вы можете сказать, что один эксперт «прав», а другие ошибаются. Строго говоря, это не имеет смысла, поскольку оценка — это субъективное представление о неопределенности, а не то, что имеет «правильный» или «неправильный» ответ. Однако, используя эту идею, вы можете интерпретировать взвешивание как вероятность того, что каждый эксперт окажется правильным. Математика комбинации такая же, это просто метафора для интерпретации весов.
Когда вы оцениваете неопределенность величины и чувствуете, что неопределенность является бимодальной или мультимодальной, смесь обычно является наиболее прямым и интуитивно понятным способом кодирования мультимодальной неопределенности.Большинство стандартных параметрических распределений являются унимодальными (т. е. имеют только один пик на графике плотности), поэтому их нельзя использовать по отдельности.
Разница между смесью и суммой
Смешанное распределение отличается от распределения взвешенной суммы случайных величин.
- Пример: На дороге 67 автомобилей и 33 грузовика, вес автомобилей распределен как
Normal(3200, 300), а вес грузовиков какNormal(12K, 4K). Распределение общего веса показано здесь (сравните это с распределением веса транспортных средств выше):
Неопределенность в общем весе легковых и грузовых автомобилей
Это вообще не смесь.На самом деле это нормальное распределение, и визуально оно весьма заметно.
Кодирование смесей в Монте-Карло
В наиболее распространенном случае вы закодируете неопределенность в ваших случайных переменных и позволите методу Монте-Карло распространить неопределенность за вас. Смесь НЕ формируется как взвешенная сумма функций распределения. Это будет кодирование распределения взвешенной суммы (например, общего веса легковых и грузовых автомобилей).
Двухкомпонентная смесь обычно кодируется с использованием и IF-THEN-ELSE с Бернулли для предложения If, как в этом примере:
-
Если Бернулли(0.67) Then Normal(3200, 300) Else Normal(12K, 4K)
В более общем случае предположим, что у вас есть массив распределений dists , проиндексированный I , и вектор весов wt , также проиндексированный как I и сумма которых равна 1. Распределение смеси кодируется как
-
ChanceDist(wt, dists, I)
Плотность и суммарная плотность смесей
Аналитические функции плотности и кумулятивные функции плотности формируются из компонентов аналитической плотности и кумулятивных функций плотности с помощью взвешенных сумм.Так, например, аналитическая плотность при x примера смеси легковых и грузовых автомобилей задается выражением
-
0,67*Dens_Normal(x, 3200, 300) + 0,33*Dens_Normal(x, 12K, 4K)
и совокупная плотность
-
0,67*CumNormal(x, 3200, 300) + 0,33*CumNormal(x, 12K, 4K)
См.
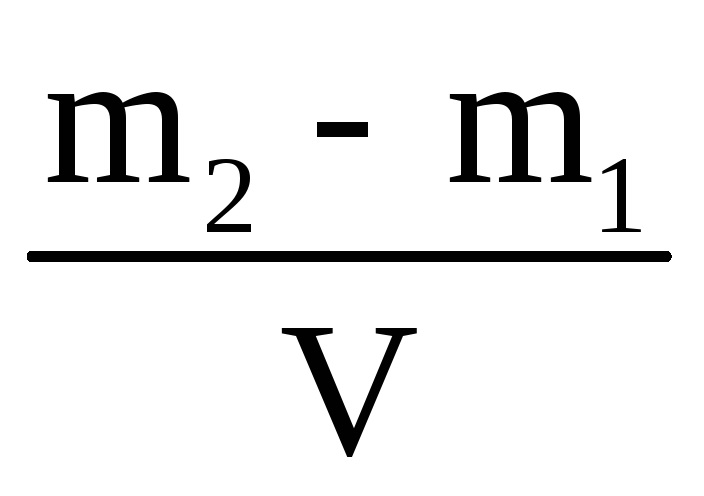 также
такжеПроизошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка браузера на прием файлов cookie
Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
- Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
- Дата на вашем компьютере в прошлом.
 Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере. - Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.
Эдвард — Сети плотности смеси
Сети плотности смеси
Сети плотности смеси (MDN) (Bishop, 1994) представляют собой класс моделей, полученных путем объединения обычной нейронной сети с моделью плотности смеси.
Продемонстрируем на примере Эдварда. Интерактивная версия с блокнотом Jupyter доступна здесь.
Данные
Мы используем те же игрушечные данные из сообщения в блоге Дэвида Ха, где он объясняет MDN. Это обратная задача, в которой для каждого входа \(x_n\) есть несколько выходов \(y_n\).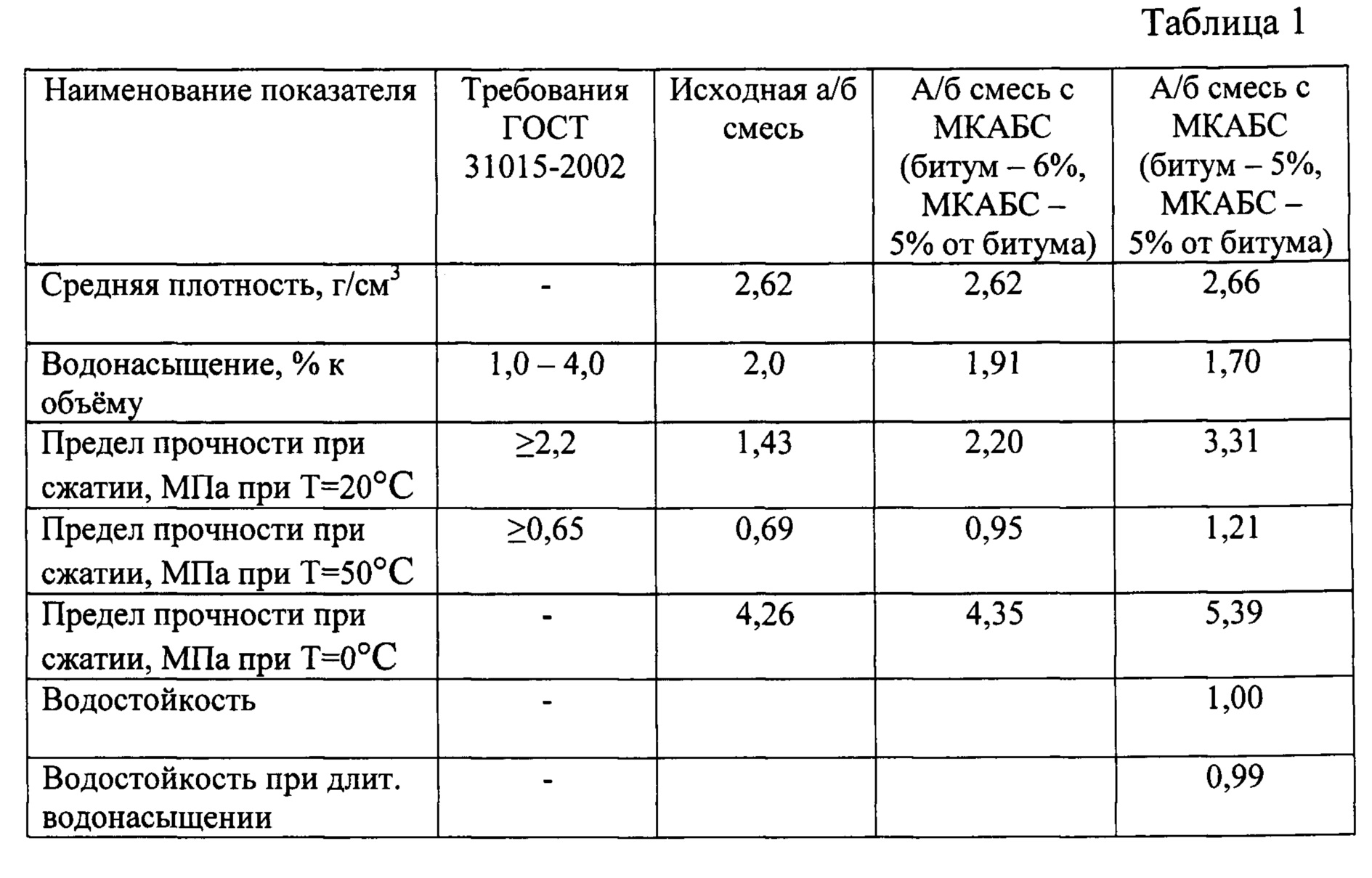
из sklearn.model_selection импорта train_test_split
def build_toy_dataset (N):
y_data = np.random.uniform (-10,5, 10,5, N)
r_data = np.random.normal(size=N) # случайный шум
х_данные = нп.sin(0,75 * y_data) * 7,0 + y_data * 0,5 + r_data * 1,0
x_data = x_data.reshape((N, 1))
вернуть train_test_split (x_data, y_data, random_state = 42)
N = 5000 # количество точек данных
D = 1 # количество функций
X_train, X_test, y_train, y_test = build_toy_dataset(N)
print("Размер признаков в обучающих данных: {}".format(X_train.shape))
print("Размер вывода в обучающих данных: {}".format(y_train.shape))
print("Размер признаков в тестовых данных: {}".format(X_test.shape))
print("Размер вывода в тестовых данных: {}".формат (y_test.shape))
sns.regplot(X_train, y_train, fit_reg=False) ## Размер признаков в обучающих данных: (3750, 1)
## Размер вывода в обучающих данных: (3750,)
## Размер признаков в тестовых данных: (1250, 1)
## Размер вывода в тестовых данных: (1250,) Мы определяем заполнители TensorFlow, которые будут использоваться для ручной загрузки пакетов данных во время логического вывода. Это один из многих способов обучения моделей с данными в Edward.
Это один из многих способов обучения моделей с данными в Edward.
X_ph = tf.заполнитель (tf.float32, [Нет, D])
y_ph = tf.placeholder (tf.float32, [Нет]) Модель
Мы используем смесь из 20 нормальных распределений, параметризованных сетью прямого распространения. То есть вероятности членства, среднее значение и стандартное отклонение для каждого компонента задаются выходными данными сети с прямой связью.
Мы используем tf.layers для построения нейронных сетей. Мы задаем трехслойную сеть с 15 скрытыми элементами для каждого скрытого слоя.
от Эдварда.импорт моделей Категориальная, смешанная, нормальная
определение нейронной_сети (X):
"""loc, масштаб, логиты = NN(x; тета)"""
# 2 скрытых слоя с 15 скрытыми юнитами
сеть = tf.layers.dense(X, 15, активация=tf.nn.relu)
сеть = tf.layers.dense (сеть, 15, активация = tf.nn.relu)
locs = tf.layers.dense (сеть, K, активация = нет)
масштабы = tf.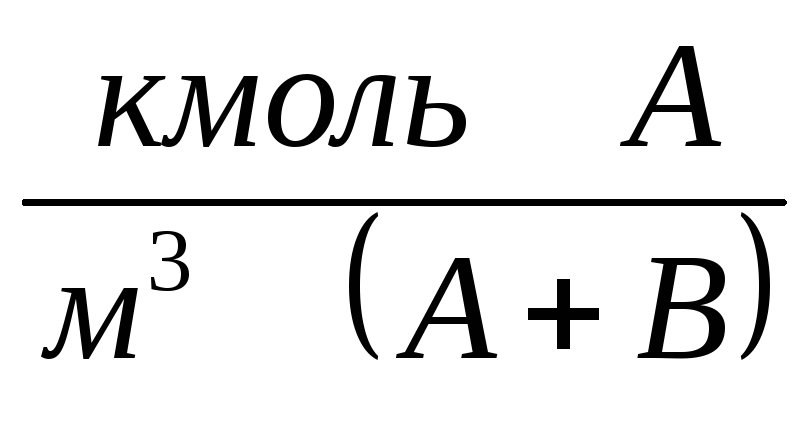 layers.dense (net, K, активация = tf.exp)
logits = tf.layers.dense (сеть, K, активация = нет)
возврат лок, весов, логитов
K = 20 # количество компонентов смеси
лок, весы, логиты = нейронная_сеть (X_ph)
cat = Категориальный (логиты = логиты)
компоненты = [Normal(loc=loc, scale=scale) для loc, scale
в zip (тф.распаковать (tf.transpose (locs)),
tf.unstack (tf.transpose (масштабы)))]
y = Смесь (cat = cat, компоненты = компоненты, значение = tf.zeros_like (y_ph))
layers.dense (net, K, активация = tf.exp)
logits = tf.layers.dense (сеть, K, активация = нет)
возврат лок, весов, логитов
K = 20 # количество компонентов смеси
лок, весы, логиты = нейронная_сеть (X_ph)
cat = Категориальный (логиты = логиты)
компоненты = [Normal(loc=loc, scale=scale) для loc, scale
в zip (тф.распаковать (tf.transpose (locs)),
tf.unstack (tf.transpose (масштабы)))]
y = Смесь (cat = cat, компоненты = компоненты, значение = tf.zeros_like (y_ph)) Обратите внимание, что мы используем случайную переменную Mixture . Он сворачивает назначения членства для каждой точки данных и делает модель дифференцируемой по всем ее параметрам. Он принимает случайную переменную Категорий в качестве входных данных, обозначающую вероятность для каждого назначения кластера, а также компонентов , которые представляют собой список отдельных распределений для смешивания.
Дополнительные сведения о MDN см. в блоге Кристофера Боннета или в Bishop (1994).
в блоге Кристофера Боннета или в Bishop (1994).
Вывод
Мы используем оценку MAP, передавая модель и набор данных. См. это расширенное руководство по оценке MAP в Edward.
вывод = ed.MAP(data={y: y_ph}) Здесь мы будем вручную управлять выводом и тем, как данные передаются в него на каждом шаге. Инициализируйте алгоритм и переменные TensorFlow.
оптимизатор = tf.Train.AdamOptimizer(5e-3)
inference.initialize (оптимизатор = оптимизатор, var_list = tf.trainable_variables ())
сеанс = ed.get_session()
tf.global_variables_initializer().run() Теперь мы обучаем MDN, вызывая inference.update() и передавая данные. Величина inference.loss представляет собой функцию потерь (отрицательное логарифмическое правдоподобие) на этом шаге вывода. Мы также сообщаем о функции потерь для тестовых данных, вызывая inference.loss и отправляя тестовые данные в заполнители TensorFlow вместо обучающих данных.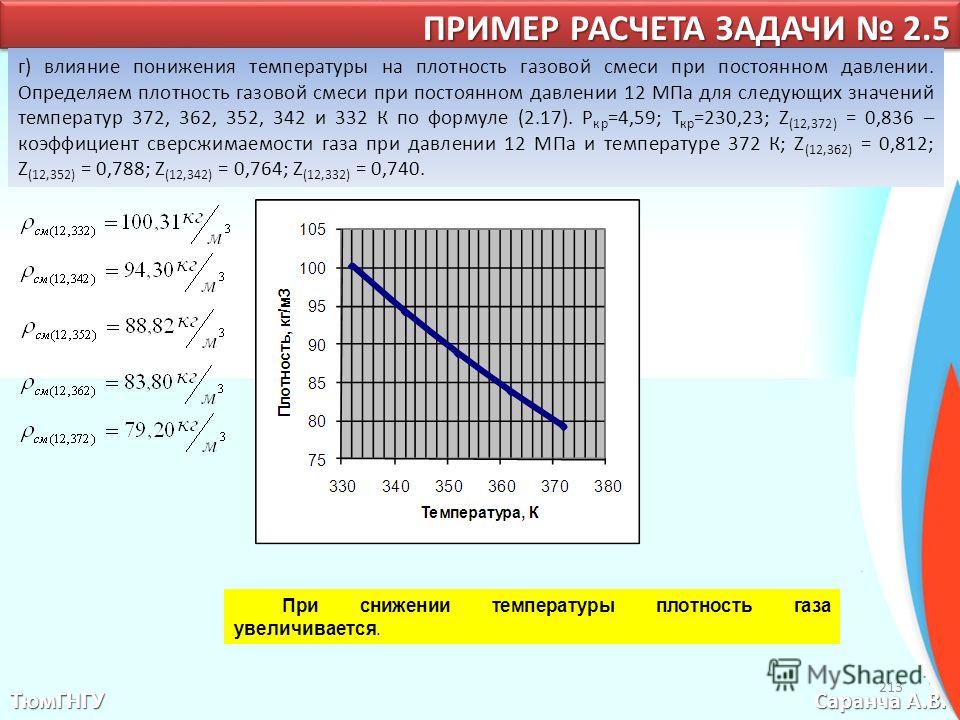 Отслеживаем потери под
Отслеживаем потери под train_loss и test_loss .
n_эпоха = 1000
train_loss = np.zeros (n_epoch)
test_loss = np.zeros (n_epoch)
для i в диапазоне (n_epoch):
info_dict = inference.update(feed_dict={X_ph: X_train, y_ph: y_train})
train_loss[i] = info_dict['потеря']
test_loss[i] = sess.run(inference.loss, feed_dict={X_ph: X_test, y_ph: y_test})
inference.print_progress(info_dict) Обратите внимание, что общий режим отказа при обучении MDN заключается в том, что отдельное распределение смеси схлопывается до точки.Это заставляет стандартное отклонение нормали быть близким к 0 и дает значения NaN. Мы можем предотвратить это, установив порог стандартного отклонения, если это необходимо.
После обучения в течение ряда итераций мы получаем из модели интересующие нас предсказания: предсказанные веса смеси, кластерные средние значения и кластерные стандартные отклонения.
Для этого мы получаем их значения из сеанса, передавая тестовые данные X_test в заполнитель X_ph .
pred_weights, pred_means, pred_std = sess.run(
[tf.nn.softmax(logits), locs, scales], feed_dict={X_ph: X_test}) Давайте построим логарифмическую правдоподобие обучающих и тестовых данных как функции эпохи обучения. Величина inference.loss представляет собой общее логарифмическое правдоподобие, а не потери на точку данных. Ниже мы строим логарифмическую вероятность для каждой точки данных путем деления на размер поезда и тестовых данных соответственно.
рис, оси = пл.подграфики (nrows = 1, ncols = 1, figsize = (16, 3.5))
plt.plot(np.arange(n_epoch), -test_loss/len(X_test), label='Test')
plt.plot(np.arange(n_epoch), -train_loss/len(X_train), метка='Поезд')
plt.legend (размер шрифта = 20)
plt.xlabel('Эпоха', размер шрифта=15)
plt.ylabel('Логарифмическая вероятность', размер шрифта=15)
plt.show() Мы видим, что он сходится примерно после 400 итераций.
Критика
Давайте посмотрим, как работают отдельные примеры. Обратите внимание, что поскольку это обратная задача, мы не можем получить правильный ответ, но мы можем надеяться, что истина лежит в области, где модель имеет высокую вероятность.
На этом графике истина — это вертикальная серая линия, а синяя линия — прогноз сети плотности смеси. Как видите, у нас не плохо получилось.
объект = [0, 4, 6]
рис, оси = plt.subplots (nrows = 3, ncols = 1, figsize = (16, 6))
plot_normal_mix (pred_weights[obj][0], pred_means[obj][0], pred_std[obj][0], оси[0], comp=False)
axes[0].axvline(x=y_test[obj][0], color='black', alpha=0.5)
plot_normal_mix (pred_weights[obj][2], pred_means[obj][2], pred_std[obj][2], оси[1], comp=False)
оси[1].axvline(x=y_test[obj][2], color='black', alpha=0.5)
plot_normal_mix (pred_weights[obj][1], pred_means[obj][1], pred_std[obj][1], оси[2], comp=False)
axes[2].axvline(x=y_test[obj][1], color='black', alpha=0. 5)
5) Мы можем проверить ансамбль, нарисовав образцы прогноза и нанеся их плотность. MDN узнал то, что мы хотели бы, чтобы он узнал.
a = sample_from_mixture(X_test, pred_weights, pred_means, pred_std, amount=len(X_test))
сонс.JointPlot(a[:,0], a[:,1], kind="hex", color="#4CB391", ylim=(-10,10), xlim=(-14,14)) Благодарности
Мы благодарим Кристофера Боннета за написание начальной версии этого руководства. В целом, мы благодарим Криса за то, что он приложил все усилия, чтобы сделать учебные пособия Эдварда доступными и простыми в освоении.
Каталожные номера
Епископ, CM (1994). Сети плотности смеси.
Gamma Mixture Density Networks и их применение для моделирования сумм страховых выплат Лукаша Делонга, Матиаса Линдхольма, Марио В.Вутрих :: SSRN
38 страниц Опубликовано: 23 ноя 2020 Последняя редакция: 14 апреля 2021 г.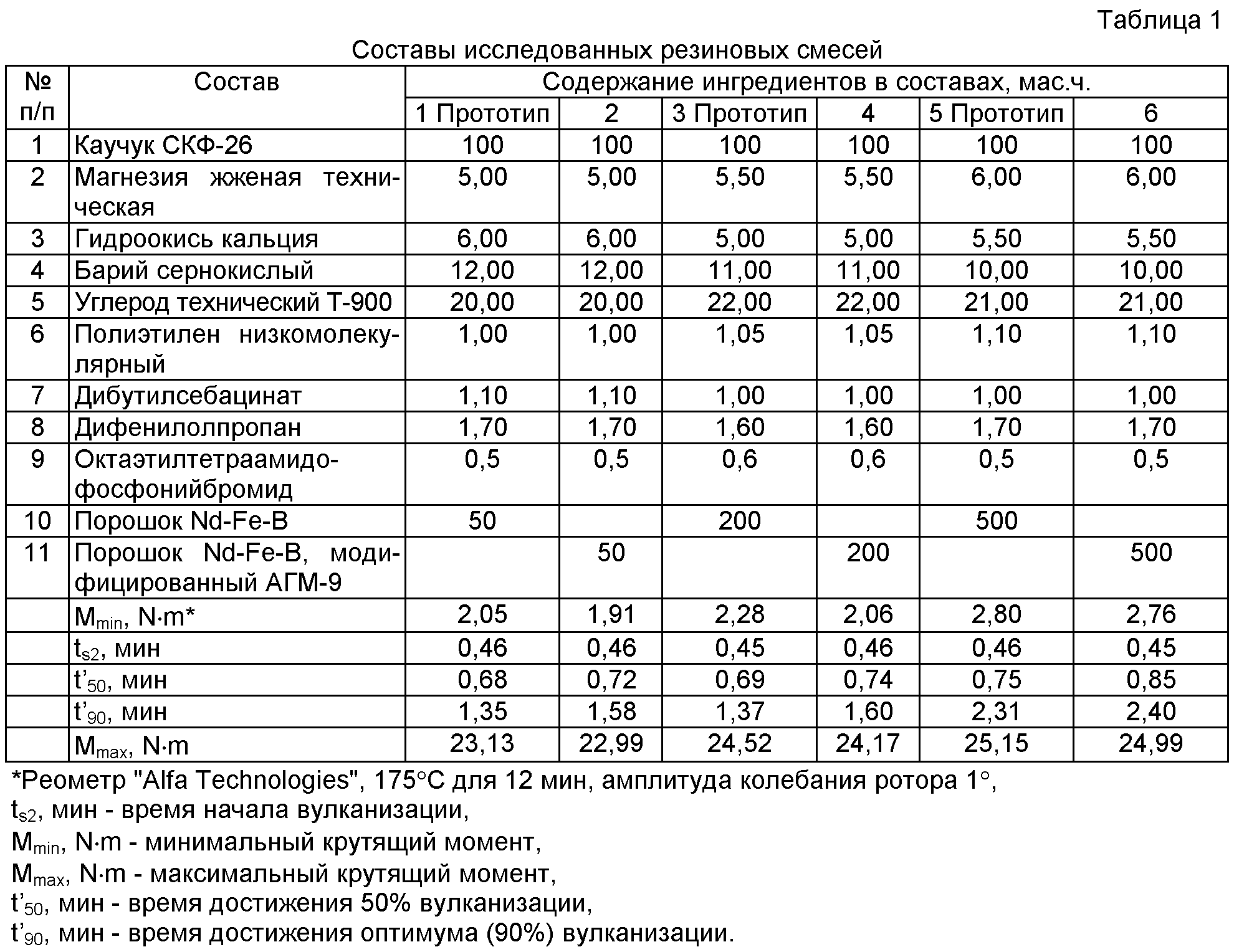
Дата написания: 5 октября 2020 г.
Аннотация
Мы обсудим, как смеси гамма-распределений с вероятностями смешивания, параметрами формы и скорости, зависящими от признаков, могут быть сопоставлены с нейронными сетями.Мы разрабатываем две версии EM-алгоритма для подбора так называемых сетей плотности гамма-смеси, которые мы называем алгоритмом бустинга EM-сетей и алгоритмом прямой сети EM, и тестируем их реализацию вместе с выбором гиперпараметров. Моделирование показывает, что наши алгоритмы очень хорошо работают с синтетическими наборами данных. Далее мы иллюстрируем применение сети плотности гамма-смеси к реальному набору данных о суммах требований по автострахованию и делаем вывод, что сети плотности гамма-смеси могут улучшить соответствие регрессионной модели и прогнозы серьезности претензий, используемые для расчета ставок, по сравнению с Классические актуарные методы.
Ключевые слова: Максимизация ожидания, нейронные сети, бустинг, смеси распределений
JEL Классификация: G22, C45
Рекомендуемое цитирование: Рекомендуемая ссылка
Сети плотности смеси– Георгиос Сарантитис
Введение
Арсенал науки о данных состоит из множества инструментов и методов. Однако, если вы спросите специалиста по обработке и анализу данных/инженера по машинному обучению, какой из них он/она обычно использует, наиболее вероятно, что вы не услышите слов «Гауссовские смешанные модели» (GMM). Но какие они ? Как они работают? Почему они являются важным дополнением к колчану Data Scientist и чем они отличаются от других, более популярных методов?
Однако, если вы спросите специалиста по обработке и анализу данных/инженера по машинному обучению, какой из них он/она обычно использует, наиболее вероятно, что вы не услышите слов «Гауссовские смешанные модели» (GMM). Но какие они ? Как они работают? Почему они являются важным дополнением к колчану Data Scientist и чем они отличаются от других, более популярных методов?
Продолжайте читать эту статью и узнайте, как исследователи применяли их к методам регрессии и классификации, разрабатывая так называемые сети плотности смеси, особый случай нейронных сетей.Кроме того, следите за обновлениями во второй части этого руководства, где мы будем использовать гауссовские смешанные модели для выполнения кластеризации намного лучше, чем известные методы, такие как K-средние.
Формализация GMM
Смешанные модели Гаусса — это модели, которые используются для представления подвыборки всего населения, распределенного нормально. В то время как вся совокупность может не подпадать под случай гауссовского (нормального) распределения, мы могли бы найти две или более подвыборок этой совокупности, которые действительно могут быть описаны с помощью нормального распределения.Таким образом, чтобы описать всю популяцию, мы не будем предполагать гауссово распределение для всей нашей популяции, а скорее синтезируем истинное основное распределение как смесь гауссовских!
В то время как вся совокупность может не подпадать под случай гауссовского (нормального) распределения, мы могли бы найти две или более подвыборок этой совокупности, которые действительно могут быть описаны с помощью нормального распределения.Таким образом, чтобы описать всю популяцию, мы не будем предполагать гауссово распределение для всей нашей популяции, а скорее синтезируем истинное основное распределение как смесь гауссовских!
Теоретически возможно смоделировать любое распределение как смесь гауссианов
Уже на начинает проясняться, что такое GMM и , почему они полезны?
Источник: http://memes.ucoz.com/
Поскольку этот блог посвящен прикладной, деловой стороне науки о данных, я пропущу математическую часть — держу пари, что большинство из вас все равно ее пропустят 🙂 — и попытаюсь объяснить, как сети смешанной плотности используются с теоретический пример и, конечно же, предоставить коды Python для ваших собственных приложений!
A Теоретический пример
Допустим, вы работаете в банке, и ваш менеджер попросил вас спрогнозировать спрос на наличные в банкоматах банка на этот месяц. Сейчас июль, и некоторые из этих банкоматов находятся в довольно туристических районах, а другие нет. Человеческому разуму интуитивно понятно понять и ожидать, что будет две группы банкоматов: ожидается, что группа банкоматов, привлекающая туристов, будет иметь более высокий спрос по сравнению с другой. Если вы разработаете регрессионную модель машинного обучения (скажем, нейронную сеть) для оценки спроса, у вас будет два основных недостатка:
Сейчас июль, и некоторые из этих банкоматов находятся в довольно туристических районах, а другие нет. Человеческому разуму интуитивно понятно понять и ожидать, что будет две группы банкоматов: ожидается, что группа банкоматов, привлекающая туристов, будет иметь более высокий спрос по сравнению с другой. Если вы разработаете регрессионную модель машинного обучения (скажем, нейронную сеть) для оценки спроса, у вас будет два основных недостатка:
- Недостаток 1 : Вы сможете предсказать только условное среднее значение распределения.Это не улучшит ситуацию для руководства, которое хотело бы иметь более широкое представление о спросе при принятии деловых решений.
- Недостаток 2 : Вы не сможете должным образом различить (вероятно) бимодальное распределение, поскольку будете предполагать, что вся популяция характеризуется одним нормальным распределением.
Отказ от ответственности: и пример, и цифры полностью вымышлены
Прежде чем двигаться дальше, я должен уточнить, что этот пример является чисто гипотетическим (но все же правдоподобным). Более того, кто-то может возразить, что в этом примере можно легко получить две подвыборки всего населения только путем разделения на переменную, описывающую туристическое/нетуристическое расположение банкоматов. Хорошая мысль! Но в данном случае я намеренно сказал вам, что есть две разные популяции и что распределение бимодальное, верно? Могут быть случаи — и будут — когда вы не имеете ни малейшего представления о базовом дистрибутиве; и двигаться дальше, предполагая, что нормальность просто неверна….
Более того, кто-то может возразить, что в этом примере можно легко получить две подвыборки всего населения только путем разделения на переменную, описывающую туристическое/нетуристическое расположение банкоматов. Хорошая мысль! Но в данном случае я намеренно сказал вам, что есть две разные популяции и что распределение бимодальное, верно? Могут быть случаи — и будут — когда вы не имеете ни малейшего представления о базовом дистрибутиве; и двигаться дальше, предполагая, что нормальность просто неверна….
Хорошо, давайте посмотрим, как мы можем решить эту проблему и избежать этих двух недостатков. Простая нейронная сеть с прямой связью для целей регрессии, вероятно, выглядит примерно так:
В этой знакомой архитектуре набор входных переменных x «вводится» в нейронную сеть, инициализируются некоторые веса и производится оценка y . Затем начинается фаза обратного распространения, изменение весов в сети, бла-бла, и, наконец, мы получаем наш прогноз…
Теперь проблема в том, что мы получаем только одно значение в качестве прогноза, и давайте предположим, что в нашем гипотетическом примере с банкоматом прогнозируется, что банкомату потребуется 280 000 евро в следующем месяце.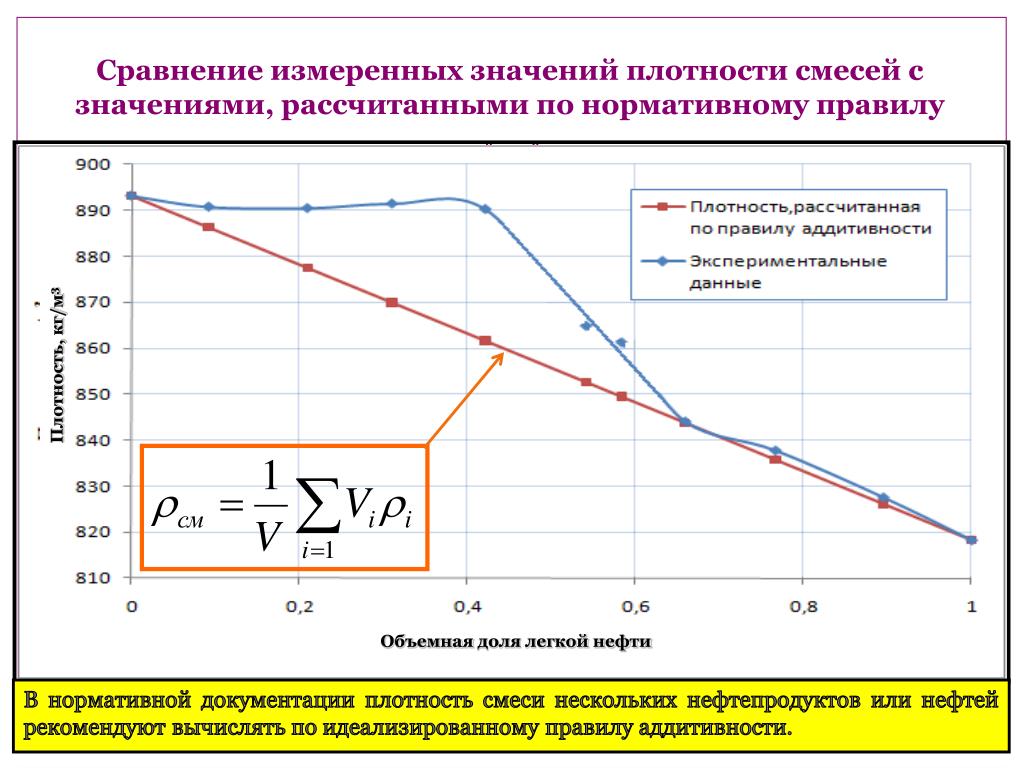 Такая информация хоть и полезна для банка, но не позволяет принимать полностью обоснованные решения. Потому что нам может понадобиться еще несколько банкнот, чтобы удовлетворить спрос, или мы могли бы также положить пару десятых тысяч ниже, чтобы сократить расходы… Другими словами, насколько мы уверены в нашем прогнозе?
Такая информация хоть и полезна для банка, но не позволяет принимать полностью обоснованные решения. Потому что нам может понадобиться еще несколько банкнот, чтобы удовлетворить спрос, или мы могли бы также положить пару десятых тысяч ниже, чтобы сократить расходы… Другими словами, насколько мы уверены в нашем прогнозе?
Этого можно добиться, если вместо одной оценки (условного среднего) вывести вероятность распределений по массиву значений, описываемую средним и дисперсией.Другими словами, условное распределение вероятностей . Для этого нам нужен не один, а два выхода в конце нашей нейронной сети. Вот так:
Теперь больше похоже. Процесс обучения по-прежнему остается прежним, с каждой прямой и обратной фазой, слегка изменяя веса, пока мы не минимизируем нашу ошибку. Разница в том, что мы получаем два значения, одно для среднего значения (μ) и одно для дисперсии (σ), которые, по сути, и нужны для построения нашей функции плотности вероятности. И ты хочешь услышать хорошие новости? Поскольку мы предположили, что это распределение является нормальным, мы можем полностью применить около доверительных интервалов , чтобы убедить нашего босса, что наш прогноз будет между 260 000 и 300 000 евро с, скажем, 95% достоверностью….
И ты хочешь услышать хорошие новости? Поскольку мы предположили, что это распределение является нормальным, мы можем полностью применить около доверительных интервалов , чтобы убедить нашего босса, что наш прогноз будет между 260 000 и 300 000 евро с, скажем, 95% достоверностью….
Ага! О, но подождите! Речь пока идет о одиночном дистрибутиве (и притом нормальном). Мы же говорили, что говорим о смеси гауссов для представления реальной базовой функции, верно? Пока мы построили только один дистрибутив, так где же остальные?
Теперь все становится еще интереснее, когда мы добавим столько пар (μ,σ), сколько распределений, которые, по нашему мнению, описывают наши данные.Конечно, все оценочные распределения не будут иметь одинаковое значение, поэтому нам нужно рассчитать последнее: вес каждого распределения при синтезе нашего окончательного распределения. Такой сети хотелось бы вот так:
Теперь это правильная сеть плотности смеси с двумя распределениями.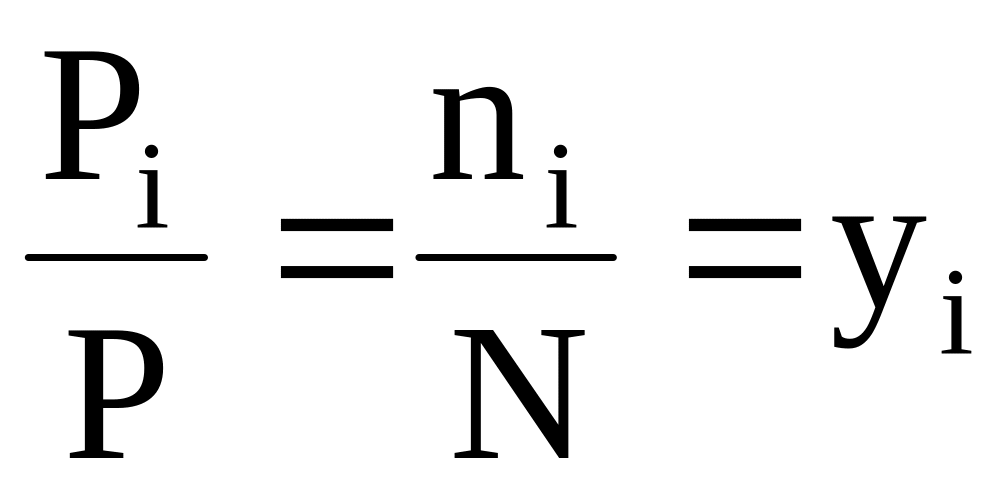 Мы могли бы иметь даже больше, поскольку их количество является еще одним гиперпараметром для настройки нашей нейронной сети…
Мы могли бы иметь даже больше, поскольку их количество является еще одним гиперпараметром для настройки нашей нейронной сети…
Подсказка: Как правило, вы должны использовать в 3-4 раза больше дистрибутивов, чем вы предполагаете; весьма вероятно, что большинство из них будут связаны с низким весом, таким образом незначительно влияя на конечный результат.
Используя нашу гипотетическую сеть Mixture Density Network в нашем опять же гипотетическом примере бимодального распределения спроса на наличные в банкоматах, мы могли бы получить что-то вроде этого:
Мы видим, что реальное базовое распределение данных на самом деле изображено как бимодальное (зеленая линия), как и следовало ожидать. В проиллюстрированном случае нетуристическое распределение ATM имело более высокий вес (α), и поэтому распределение Mixture представляет более высокий пик в этой части графика.
Я надеюсь, что к настоящему моменту вы концептуально поняли, почему и как работает механика сети плотности смеси, а также ее значение для бизнеса на примере выше.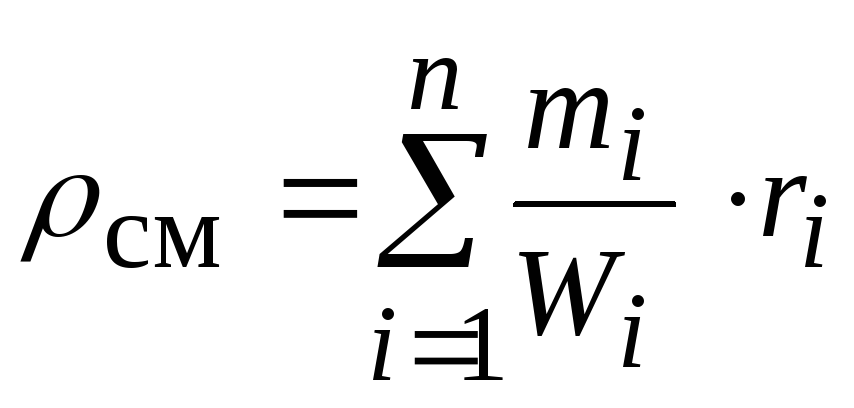 Поскольку это была всего лишь иллюстрация, все числа и графики были жестко запрограммированы и не рассчитывались с использованием фактического MDN. Коды для их воспроизведения можно найти в соответствующем репозитории Github здесь.
Поскольку это была всего лишь иллюстрация, все числа и графики были жестко запрограммированы и не рассчитывались с использованием фактического MDN. Коды для их воспроизведения можно найти в соответствующем репозитории Github здесь.
Теперь давайте закодируем фактический MDN, используя некоторые реальные данные.
Код Python
Прежде чем я вручу вам сам код, пару слов.Во-первых, и самое главное, набор данных очень простой, с ценами на жилье, которые я скачал из репозитория UCI здесь. Он содержит просто набор входных переменных, а выходной переменной является цена дома за единицу площади.
Во-вторых, и вы, возможно, уже подумали об этом, мы должны обсудить а) что именно мы минимизируем в этой архитектуре нейронной сети и б) как веса распределения будут добавляться к 1.
Что касается (а), потеря, которую мы минимизируем в этом типе нейронных сетей, представляет собой среднюю отрицательную логарифмическую потерю правдоподобия y , учитывая набор смешанных параметров.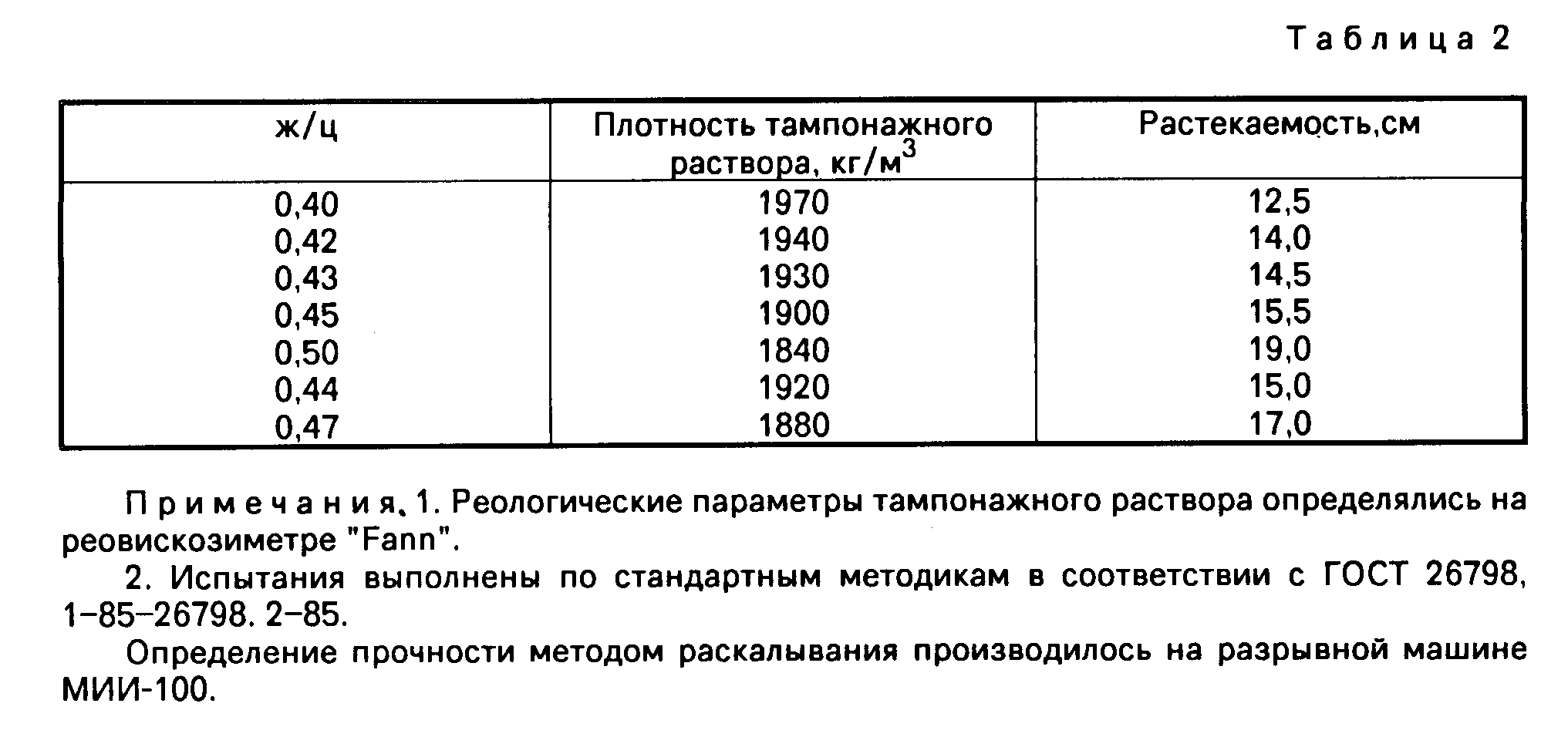
Что касается второго вопроса (b), мы просто применим функцию активации softmax к нейрону alphas , убедившись, что сумма всех альф равна единице .
О, и еще одна важная вещь, о которой следует помнить, это то, что стандартное отклонение больше нуля . Мы можем легко добиться этого, создав измененную версию ELU, просто добавив 1 к ее вычислению.
Объяснив все вышесказанное, вот фактический код.
импортировать numpy как np импортировать панд как pd импортировать тензорный поток как tf из tensorflow_probability импортировать распределения как tf_prob из тензорного потока.keras.models импорт последовательный из tensorflow.keras.layers import Input, Dense, Activation, Concatenate из tensorflow.keras.callbacks импортировать раннюю остановку из tensorflow.keras.optimizers импортирует Адама из sklearn.model_selection импорта train_test_split из sklearn.preprocessing импортировать MinMaxScaler, LabelEncoder импортировать matplotlib.pyplot как plt импортировать Seaborn как sns tf.random.set_seed(42) np.random.seed (42) класс MDN (tf.keras.Model): def __init__(я, no_neurons=100, no_components = 2): супер(MDN, сам).__init__(имя="MDN") self.no_neurons = нет_нейронов self.no_components = нет_компонентов self.hl_1 = Плотный (no_neurons, активация = "relu", name = "hl_1") self.hl_2 = Плотный (no_neurons, активация = "relu", name = "hl_2") self.alpha = Плотный (no_components, активация = "softmax", имя = "альфа") self.mu = плотный (no_components, активация = "nnelu", имя = "mu") self.sigma = Плотный (no_components, активация = "nnelu", name = "sigma") self.conc = Объединить (name="conc") деф вызов(я, входы): х = self.hl_1 (входы) х = я.hl_2(х) alpha_v = self.alpha(x) mu_v = self.mu(x) sigma_v = self.sigma(x) вернуть self.conc([alpha_v, mu_v, sigma_v]) деф ннелу (ввод): #Рассчитать неотрицательный ELU вернуть tf.add (tf.constant (1, dtype = tf.float32), tf.nn.elu (вход)) def vector_unfold (parameter_vector): #Развернуть список заданных параметров вернуть [parameter_vector[:,i*no_components:(i+1)*no_components] для i в диапазоне(no_parameters)] def gnll_loss(y, параметр_вектор): #Рассчитать отрицательное логарифмическое правдоподобие альфа, мю, сигма = vector_unfold (parameter_vector) gm = tf_prob.
MixtureSameFamily(mixture_distribution=tf_prob.Categorical(probs = alpha), component_distribution = tf_prob.Normal (loc = мю, шкала = сигма)) log_likelihood = gm.log_prob (tf.transpose (y)) вернуть -tf.reduce_mean (log_likelihood, ось =-1) #Добавить функцию активации в keras tf.keras.utils.get_custom_objects().update({'nnelu': активация(nnelu)}) #Загрузить данные из https://archive.ics.uci.edu/ml/datasets/Real+estate+valuation+data+set df = pd.read_excel('real_estate.xlsx') #Сплит в поезде/тесте поезд = дф.iloc[:300,] тест = df.iloc[300:,] x_train = train.drop(['Нет','Дата транзакции X1','Цена дома Y за единицу площади'], ось = 1) y_train = train['Цена Y дома за единицу площади'] x_test = test.drop(['Нет','Дата транзакции X1','Цена дома Y за единицу площади'], ось = 1) y_test = test['Цена дома Y за единицу площади'] #Масштабировать значения min_max_scaler = MinMaxScaler() x_train = min_max_scaler.fit_transform(x_train) x_test = min_max_scaler.transform(x_test) # Создайте простую нейронную сеть с прямой связью модель = Последовательный() модель.
добавить(Dense(24, input_dim=x_train.shape[1], kernel_initializer = 'нормальный', активация = "релу")) model.add(Плотный(1, активация = 'линейный')) model.compile(потеря="MeanSquaredError", оптимизатор='адам') history = model.fit (x_train, y_train, validation_split = 0,2, эпохи = 100, batch_size = 32, подробный = 0) #predict на тестовом наборе пред = модель.прогноз(x_test) #Сохранить в фрейм данных и сравнить с реальными значениями results_df = pd.DataFrame({'Real':y_test.values, 'Predicted':[w[0] for w in pred]}) результаты_df.head() результаты_df.илок[18] #Выберите параметры no_parameters = 3 # Всегда должно быть 3: альфа, мю и сигма no_components = 3 #Выберите и настройте в соответствии с приложением no_neurons = 100 #Настраиваемый гиперпараметр #Скомпилируйте и обучите MDN mdn = MDN(no_neurons=no_neurons, no_components=no_components) mdn.compile (потеря = gnll_loss, оптимизатор = 'адам') mdn.fit(x=x_train, y=y_train,epochs=150, validation_data=(x_test, y_test), batch_size=32, подробный=0) #создать функцию построения графика def plot_rate (ax, index, color_index): альфа, мю, сигма = vector_unfold(mdn.
предсказать (x_test [индекс]. изменить форму (1,-1))) gm = tf_prob.MixtureSameFamily( mix_distribution=tf_prob.Categorical(probs=alpha), component_distribution = tf_prob.Normal (loc = mu, scale = sigma)) pyx = gm.prob(x) ax.plot(x,pyx,alpha=1, color=sns.color_palette()[color_index], linewidth=2, label="PDF для прогноза {}".format(index)) # Выберите значения x в соответствии с набором данных х = np.linspace (0,100, int (1e3)) plt.figure(figsize=(10,7)) топор = plt.gca() # Выберите конкретные примеры для построения plot_rate (ах, 18,0) plot_rate (ах, 55,1) топор.set_xlabel("Цена за единицу площади") ax.set_ylabel("p(Цена)") ax.legend (размер шрифта = 16) plt.title('Сеть плотности смеси') plt.tight_layout() plt.savefig('pdf_real_estate.jpg') plt.show() print('Реальное значение наблюдения 18: {}'.format(y_test.iloc[18])) print('Реальное значение наблюдения 55: {}'.format(y_test.iloc[55])) х = np.linspace (0,100, int (1e3)) определение find_pdf (индекс): альфа, мю, сигма = vector_unfold(mdn.
predict(x_test[index].reshape(1,-1))) gm = tf_prob.MixtureSameFamily( mix_distribution=tf_prob.Категориальный (вероятность = альфа), component_distribution=tf_prob.Нормальный( лок = мю, шкала=сигма)) pyx = gm.prob(x) вернуть пикс all_preds = np.array([find_pdf(0)]) для я в диапазоне (1, x_test.shape [0]): temp_pred = np.array([find_pdf(i)]) all_preds = np.concatenate((all_preds, temp_pred), ось=0) df_all_preds = pd.DataFrame(all_preds.T) df_all_preds.index = np.раунд (х, 2) df_all_preds = df_all_preds.sort_index (по возрастанию = ложь) #Построить тепловую карту plt.figure(figsize=(12,6)) sns.heatmap(df_all_preds) plt.savefig('тепловая карта.jpg') plt.show()
Если все работает по плану, вы должны получить следующие цифры. Первый — это распределения двух разных домов из нашего набора данных:
.Второй — это тепловая карта, содержащая все распределения всех точек данных в нашем тестовом наборе. Это даст представление о том, как выглядят наши прогнозы и как они распространяются!
Имейте в виду, что ни нейронная сеть прямого распространения, ни сеть плотности смеси не были точно настроены.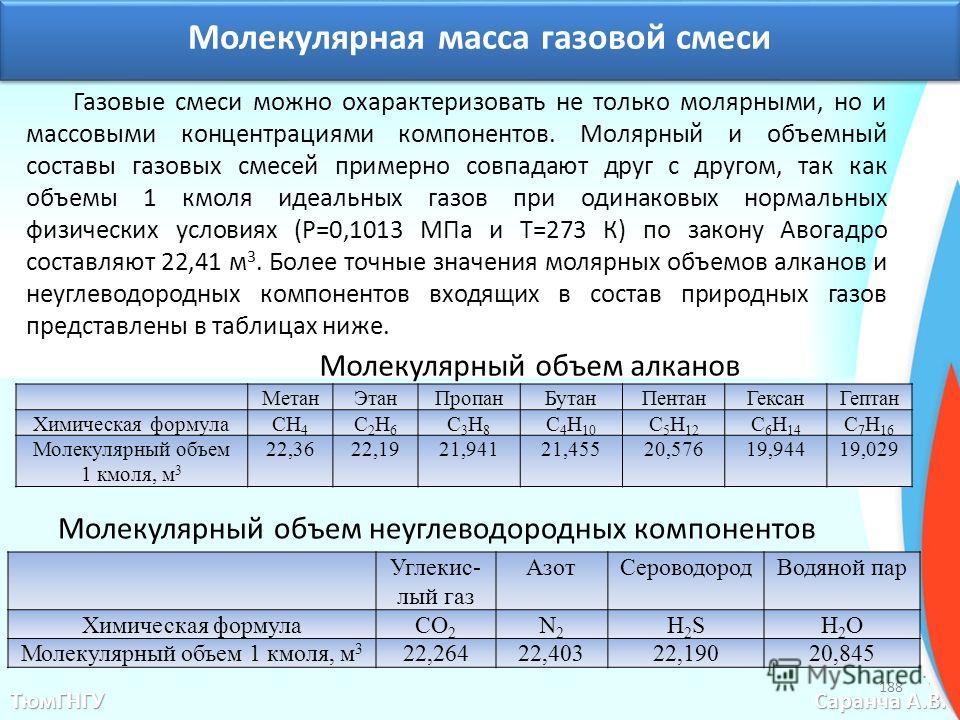 Это всего лишь некоторые гиперпараметры, которые я придумал, для иллюстрации. Не стесняйтесь возиться с ними сами и получить от них максимум удовольствия!
Это всего лишь некоторые гиперпараметры, которые я придумал, для иллюстрации. Не стесняйтесь возиться с ними сами и получить от них максимум удовольствия!
Вы можете найти приведенный выше код в виде блокнота Jupyter, а также код, используемый для поддержки приведенного выше примера банкомата, в соответствующем репозитории Github.
Заключение
И на этом завершается этот пост о сетях плотности смеси, специальной архитектуре нейронной сети, которая использует теорию, лежащую в основе гауссовских моделей смеси, для раскрытия истинного основного распределения данных населения.
Область применения широка и разнообразна, и здесь мы коснулись только самой поверхности. В следующем посте мы увидим, как смешанные модели Гаусса используются в кластеризации, предлагая нам гораздо более надежный способ группировки, чем очень популярный алгоритм K-средних.
Существуют и другие приложения, которые я не буду подробно и аналитически рассматривать, но я призываю вас искать их самостоятельно. Например, смешанные модели Гаусса используются для обнаружения аномалий как прямое следствие лучшего группирования данных, чем традиционные алгоритмы кластеризации.Еще одно использование GMM — в распознавании речи в качестве начальной фильтрации производных функций. Третий — не как классификатор или алгоритм кластеризации как таковой , а как процесс предварительной обработки, исследования данных, чтобы проверить, действительно ли ваше предположение о нормальности действительно для вашего набора данных или нет…
Например, смешанные модели Гаусса используются для обнаружения аномалий как прямое следствие лучшего группирования данных, чем традиционные алгоритмы кластеризации.Еще одно использование GMM — в распознавании речи в качестве начальной фильтрации производных функций. Третий — не как классификатор или алгоритм кластеризации как таковой , а как процесс предварительной обработки, исследования данных, чтобы проверить, действительно ли ваше предположение о нормальности действительно для вашего набора данных или нет…
На сегодня это все. Надеюсь, вам понравились сети Mixture Density Networks, и я надеюсь увидеть вас снова в следующем посте о кластеризации! А пока… продолжайте кодить!
Каталожные номера
[1] http://publications.aston.ac.uk/id/eprint/373/
[2] https://brilliant.org/wiki/gaussian-mixture-model/
[3] https://scikit-learn.org/stable/modules/mixture.html
[4] https://towardsdatascience.com/gaussian-mixture-models-explained-6986aaf5a95
[5] https://github. com/axelbrando/Mixture-Density-Networks-for-distribution-and-uncertainty-estimation
com/axelbrando/Mixture-Density-Networks-for-distribution-and-uncertainty-estimation
[6] https://jakevdp.github.io/PythonDataScienceHandbook/05.12-gaussian-mixtures.html
[7] https://towardsdatascience.com/a-Hitchhikers-guide-to-mixture-density-networks-76b435826cca
Отказ от ответственности
Мнения, выраженные в статье, являются моими собственными и не обязательно выражают мнение моего работодателя. Все используемые числовые примеры либо вымышлены, либо общедоступны в Интернете, а не являются конфиденциальными данными любого рода.
Нравится:
Нравится Загрузка…
РодственныеПлотность смеси
- Плотность смеси
Меланж Densite
En statistiques, on appelle densité mélange ou loi mélange une fonction de densité qui est issue d’une combinaison lineaire de plusieurs fonctions de densité.
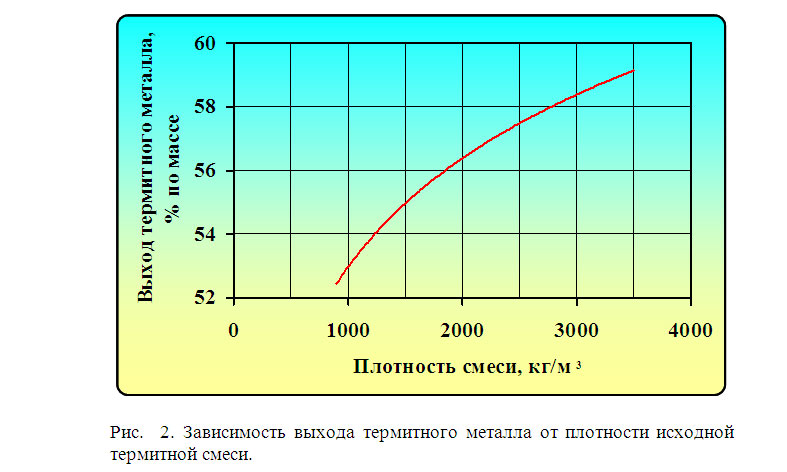
Предварительная функция f ( x ,θ), плотность переменной переменной x параметра θ. Например, si f est une loi normale, alors θ est constitué de la moyenne et de la variance. Si on appelle une famille de paramètres et une famille de scalaires tels que
- ,
цвет, функция г определение по номиналу
является одной из функций плотной смеси г составных частей.
On peut également étendre cette définition au cas où le nombre des composantes est infini. En considérant un ансамбль Ω de paramètres, si on a
цвет, функция
является плотным меланжем.
Par пример, l’image suivante représente la fonction de densité d’un mélange gaussien à deux composantes de Dimension 2
Изделия Autres
Категория : Loi de probabilité
Фонд Викимедиа. 2010.
2010.
Содержание по лицензии CC-BY-SA. Источник: Статья Плотность смеси de Wikipédia en français (авторы)
- Смесь (орг)
- Микстек
Словари Regardez d’autres:
Плотность смеси — В статистике плотность смеси — это функция плотности вероятности, которая представляет собой выпуклую комбинацию других функций плотности вероятности.Рассмотрим функцию плотности вероятности p ( x , a ) для переменной x , параметризованной a . То есть для каждого… … Wikipedia
Смесь (значения) — Смесь может означать: В химии: смесь, комбинация двух или более химических веществ, в которой химические вещества сохраняют свою идентичность. В музыке: смесь (музыка), особый вид органного упора, в котором на каждую ноту приходится несколько труб. Вероятность и… … Википедия
Смешанное распределение — См. также: Смешанная модель.
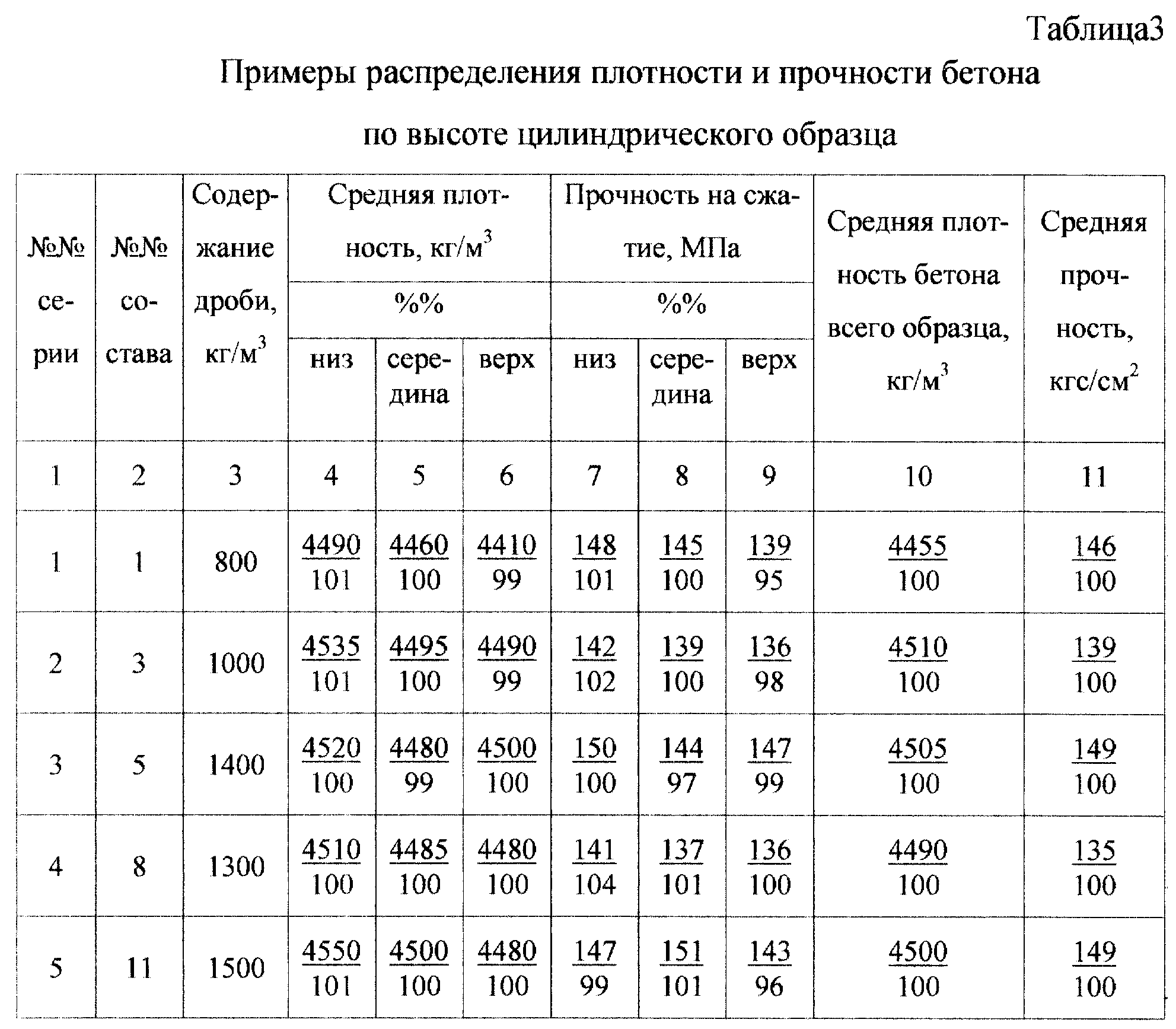 В теории вероятностей и статистике смешанное распределение — это распределение вероятностей случайной величины, значения которой можно интерпретировать как полученные простым способом из базового набора других случайных величин.… … Википедия
В теории вероятностей и статистике смешанное распределение — это распределение вероятностей случайной величины, значения которой можно интерпретировать как полученные простым способом из базового набора других случайных величин.… … ВикипедияСмешанная модель — См. также: Смешанное распределение В статистике смешанная модель — это вероятностная модель для представления присутствия подгрупп в общей совокупности, не требующая, чтобы набор наблюдаемых данных идентифицировал подгруппу… … Википедия
Смесь (вероятность) — Чтобы узнать о других значениях, см. смесь (значения). В теории вероятностей и статистике смесь представляет собой комбинацию двух или более вероятностных распределений.Эта концепция возникает в двух контекстах: смесь, определяющая новое распределение вероятностей из… … Wikipedia
Матрица плотности — Сюда перенаправляется смешанное состояние. Чтобы узнать о психическом состоянии, см.
 Смешанное состояние (психиатрия) . В квантовой механике матрица плотности представляет собой самосопряженную (или эрмитову) положительно-полуопределенную матрицу (возможно, бесконечномерную) следа единицы, которая… … Wikipedia
Смешанное состояние (психиатрия) . В квантовой механике матрица плотности представляет собой самосопряженную (или эрмитову) положительно-полуопределенную матрицу (возможно, бесконечномерную) следа единицы, которая… … WikipediaПлотность — Эта статья о плотности массы.Чтобы узнать о других значениях, см. Плотность (значения). Массовая плотность или плотность материала определяется как его масса в единице объема. Чаще всего для обозначения плотности используется символ ρ (греческая буква rho). В некоторых случаях… … Wikipedia
Плотность воздуха — Плотность воздуха, ρ (греч. rho) (плотность воздуха), представляет собой массу на единицу объема земной атмосферы и является полезной величиной в аэронавтике и других науках. Плотность воздуха уменьшается с увеличением высоты, как и атмосферное давление.Это также меняет… … Wikipedia
Плотность течения — Геол., океаног. См. ток мутности.
