Расчет плотности смеси двух углеводородных жидкостей. Измерение наименьшего перепада давления

Другие предметы \ Гидравлика

Страницы работы

19 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Таблица 1

Вопрос.  Какова плотность смеси двух углеводородных жидкостей, если для нее взято 0,4л нефти (ρ_н = 850кг/м³) и 0,6л керосина (ρ_к = 800кг/м³).

Решение

Определяем плотность смеси по выражению    ρ_см = Σr_iρ_i, где r_i – объемные доли жидкостей.

Объем все смеси     V = V_н + V_к = 0,4 + 0,6 = 1,0л.

Объемные доли       r_н = = 0,4;    r_н = = 0,6.

Плотность смеси      ρ

см = 0,4∙850 + 0,6∙800 = 820кг/м³.

Ответ:  820кг/м³.

Вопрос.  Два одинаковых, считающихся недеформируемыми образца породы при пластовом давлении в лабораторных условиях насыщены один водой, а второй нефтью. Сравните объемы жидкости, вытекающие из образцов при снижении давления до атмосферного.

Решение

Объемы жидкостей вытекающих из пород зависят от плотностей этих жидкостей. Плотность воды 1000кг/м³, плотность нефти 850кг/м³.

Если масса пород М, объемы можно определить

V_в = ;   V_н = .

При сравнении этих величин

 < , т.е. V_в < V_н.

Ответ: нефти больше

Вопрос.  Можно ли при помощи термометра определить величину атмосферного давления?

Решение

Термометр служит только для измерения температуры, а для измерения атмосферного давления применяют  барометр.

Ответ: для этой цели служит барометр.

Таблица 2

Вопрос. С одной стороны в частично заполненную водой открытую U-образную трубку добавили бензин. Сравните высоты столбов бензина (h_б) и воды (h_в), отсчитываемые от границы раздела жидкостей.

Решение

Давления в точках раздела жидкостей будет равны      Р_а + ρ_в∙g∙h_в = Р_а + ρ_б∙g∙h_б,

После преобразований получаем        ρ_в∙h_в = ρ_б∙h_б, высота столба воды         h_в = .

Искомая высота уровней    h = h_б – h_б

 = h_б, полученное выражение получается положительным, значит

h_б > h_в.

Ответ: h_б > h_в

                                                                                                                                                                                            

Вопрос.  Прибор для измерения давления имеет шкалу пределами измерения от 0 до 0,1МПа. Как называется прибор?

Решение

Для измерения давления ниже атмосферного  от 0 до 0,1МПа служат вакуумметры.

Ответ: вакуумметр

Вопрос. По трубопроводу течет вода. Какую из жидкостей (ртуть, четыреххлористый углерод, бензин) нужно залить в двужиткостный дифференциальный манометр, что бы он мог измерить наименьший перепад давления? При этом ρ

р > ρ_ч.у > ρ_б.

Решение

Давление зависит от плотности жидкости, поэтому, что бы измерить наименьший перепад давления необходимо залить жидкость с наименьшей плотностью, т. е. бензин.

Ответ: бензин.

Вопрос. На стенке закрытого сосуда с жидкостью установлены манометр и вакуумметр. Показания каждого из них 2,45кПа, а расстояние по вертикали между ними 5м. Какая из жидкостей находится в резервуаре: бензин, вода или ртуть?

Решение

Манометр показывает манометрическое давление Р_ман = 2,45кПа.

Вакуумметр показывает вакуумметрическое давление Р_вак = 2,45кПа.

Таблица 3

Вопрос. Под уровнем жидкости находятся две равновеликие поверхности: квадрат и круг. Сравните силы давления жидкости, действующей с одной стороны на каждую из этих фигур.

Решение

Сила давления жидкости на поверхность равна

Р = ρ∙g∙h_ц∙ω, где h_ц – центр приложения силы, м, примем равным;

ω – площадь смоченной поверхности, м², если примем сторону квадрата 1м и диаметр  круга 1м, то получим площади смоченных поверхностей:

квадрата  ω = 1м²;

круга ω =  = 0,785м².

Площадь квадрата больше, чем площадь круга, значит сила давления на квадрат, больше чем на круг.

Ответ: на квадрат сила давления больше

Вопрос. Может ли центр давления совпасть с центром тяжести смоченной твердой поверхности.

Решение

Полное гидростатическое давление в точке можно определить по формуле

Р = Р_о + ρ∙g∙h,

Где Р_о – давление на свободной поверхности жидкости,

h – глубина погружения точки, которая может совпасть с центром тяжести только телом, имеющим прямоугольную форму.

Ответ: Может, если эта поверхность имеет прямоугольную форму.

Вопрос. Что происходит с равнодействующей всех сил давления на плоскую стенку небольшого сосуда, заполненного жидкостью, если его закрыть и над свободной поверхностью в нем создавать постепенно возрастающий вакуум.

Решение

Абсолютное давление на крышку

Р_абс = Р_атм – Р_вак.

Вакуум – это давление ниже атмосферного, значит,  равнодействующая всех сил давления на плоскую стенку сосуда будет уменьшаться.

Ответ: уменьшается.

Таблица 4

Вопрос. Круглое отверстие в боковой вертикальной плоской стенке резервуара с жидкостью может быть закрыто (рис.): плоской (а), сферической (б) или конической (в). Покажите соотношение растягивающих болты усилий для этих крышек.

Похожие материалы

Информация о работе

Скачать файл

§ 3. Плотность газожидкостной смеси

Через данное сечение трубы при движении по ней ГЖС про­ходит некоторое количество газа и жидкости. Можно предста­вить, что все газовые пузырьки занимают в сечении трубы сум­марную площадь f_r, а жидкость — остающуюся площадь в том же сечении f_ж, так что

F_г+f_ж=f,

где f — площадь сечения трубы (рис. VI1.8).Плотность ГЖС в таком случае определится как средневзвешенная

(VII.18)

где р_ж и р_г — плотность жидкости и газа при термодинамиче­ских условиях сечения.

Обычно fг/f обозначают через φ. Тогда fж/f=1—φ,

Рс = Рж(1-φ) + Рг φ (VII.19)

Величина φ = fг/f называется истинным газосодержанием по­тока.

Обозначим V — объемный расход газа через данное сечение; q — объемный расход жидкости через то же сечение; с_г — ли­нейная скорость движения газа относительно стенки трубы; с_ж — линейная скорость движения жидкости относительно стенки трубы.

Тогда можно записать следующие соотношения:

f г= V/C_г; f_ж=q/C_ж (VII.20)

и

f= f_Р + f_ж= V/C_г+q/Cж= (VC_ж+qС_р)/С_жС_г (VII. 21)

Подставляя (VII.20) и (VII.21) в (VII.18) и делая некото­рые сокращения, получим

(VII.22)

В восходящем потоке газ движется быстрее жидкости, так как на него действует архимедова сила вытал­кивания.

Обозначим

с_г/с_ж = b>1, (VI 1.23)

(VI 1.24)

Разделив числитель и знаменатель в (VII.22) на q и вводя но­вые обозначения согласно (VII.23) и (VII.24), получим

/ — «3

(VI 1.25)

где r — газовый фактор, приведенный к термодинамическим ус­ловиям рассматриваемого сечения.

При с_г = с_ж b=1 и из (VII.25) следует

(VII.26)

Этот случай соответствует идеальным условиям, при которых образуется идеальная смесь плотностью р_и.

Относительная скорость газа (по отношению к жидкости)

а = с_г-с_ж (VII. 27)

или

с_г = с_ж + α (VII.28)

Подставляя (VII.28) в (VII.23), получим

(VII.29)

Поскольку α >0, то b>1. Увеличение скорости газа при не­изменном объемном расходе V уменьшает f_г и, следовательно, увеличивает f_ж— В результате плотность смеси, как это следует из (VII. 18) и (VII. 19), увеличивается. Таким образом, явление скольжения газа (α >0) при неизменных объемных расходах q и V приводит к утяжелению смеси по сравнению с идеальным случаем. Поэтому чем больше а, тем больше потребуется дав­ление на забое для поднятия данного количества жидкости.

Плотность реальной смеси

Pс=pи+∆p, (VII.30)

г де ∆p — увеличение плотности смеси, обусловленное скольже­нием. Для определения Ар к (VI1.25) прибавим и отнимем р_исогласно (VII.26), получим

Группируя слагаемые и делая некоторые преобразования, имеем

или после приведения к общему знаменателю в квадратных скобках и группировки слагаемых найдем

(VII.31)

Из сопоставления (VII.31), (VII.30) и (VII.26) следует

(VI1.32)

При Ь =1 (отсутствие скольжения газа с_г=с_ж) числитель в (VII. 32) обращается в нуль и ∆р = 0. Утяжеление ГЖС не происходит.’ С увеличением b (b>1) ∆р монотонно увеличива­ется (рис. VII.9). Заштрихованная часть графика показывает увеличение плотности ГЖС за счет скольжения газа.

Из формулы (VII.29) видно, что при одной и той же относительной скорости газа (а = const) b уменьшается при увеличении с_ж, т. е. расхода жидкости. Отсюда следует важный для практики вы­вод — переход на трубы ма­лого диаметра при определен­ных условиях за счет увеличе­ния с_т уменьшит величину b, а это в свою очередь повлечет уменьшение ∆р. Поэтому подъем ГЖС может быть осу­ществлен при меньшем давлении в нижней части трубы (при меньшем забойном давлении). Однако целесообразность пере­хода на трубы меньшего диаметра должна быть проверена рас­четом, так как при этом возрастут потери давления на трение.

В теории движения ГЖС существуют важные понятия, че­рез которые определяется плотность смеси. Это расходное га­зосодержание β и истинное газосодержание φ.

Расходное газосодержание потока ГЖС определяется как отношение объемного расхода газа V к общему расходу смеси V+q:

(VII.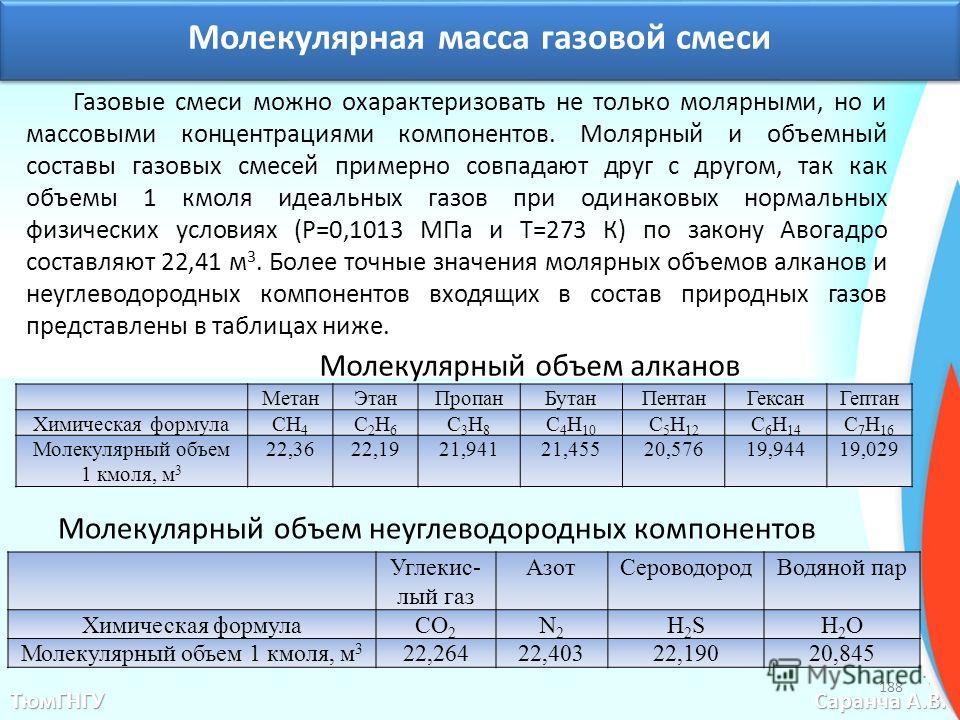 33)

Истинное газосодержание потока ГЖС учитывает скольже­ние газа и поэтому является отношением площади, занятой газом f_г, ко всему сечению трубы f:

(VII.34)

Тогда

Pc=pж(1- φ)+pг φ (VII.35)

Из сопоставления (VII.35) и (VII.25) следует

(VII.36)

(VII.37)

Разделив в (VII.33) числитель и знаменатель на q и исполь­зуя обозначение (VII.24), получим

(VII.38)

Отнимая в (VII.38) по единице и меняя знак, получим

или

Откуда

(VII.39)

Сопоставляя (VII. 39), (VII.38) и (VII.26), видим, что

(VII.40)

Таким образом, плотность иде­альной смеси (VII.40) определяется расходным газосодержанием β, а плотность реальной смеси (VII.35)

—истинным φ.

Найдем формулы связи между φ, β, b и r.

Из (VII.37) и (VII.38) имеем

φ(r+b)=r и β(r+1)=r

откуда

(VII.41)

Решая (VII.38) относительноr, найдем

(VII.42)

Подставляя (VII.42) в (VII.41), получим

Откуда после преобразований

(VII. 43)

Решая (VII.43) относительно Ь, получим

(VII.44)

При движении ГЖС возможны два предельных случая, когда по трубе движется одна жидкость f_г=0, следовательно, φ = f_г/f также равно нулю, и когда по трубе движется один газ f_ж = 0. Аналогично и для расходного газосодержания β. По­этому физически возможными пределами изменениями φ и β будут 0<φ<1, 0<β<1. При отсутствии скольжения газа отно­сительная его скорость равна нулю (а = 0), следовательно, с_г= = с_ж, b=1 и из формулы (VII.43) β = φ

Таким образом, φ(β) для идеального подъемника будет яв­ляться прямой в виде диагонали квадрата линия 1 (рис. VII.10). Во всех других случаях при b>1, т. е. при а>0(с_г>с_ж), полу­чим φ<β

На диаграмме φ(β) линия 2 проходит ниже диагонали. Чем больше скольжение, т. е. чем больше а, а следовательно, и Ь, тем ниже пройдет линия φ(β) .

Относительная скорость газа а зависит от следующих фак­торов: дисперсности газовых пузырьков, а следовательно, структуры движения ГЖС; вязкости жидкой фазы; разности плотностей газа и жидкости, от которой зависит подъемная сила; диаметра трубы и газонасыщенности потока ГЖС.

Попытки теоретического определения величины а не дают надежных результатов. Поэтому оценка относительной скоро­сти газа проводится главным образом экспериментально и со­ставляет основной предмет исследований. По некоторым реко­мендациям предлагается принять φ = 0,833 β во всем диапазоне значений β , представляющем практический интерес. Величина β всегда известна, так как расходами V и q либо задаются, либо вычисляют для заданных термодинамических условий.

Автостопом по сетям плотности смеси | Доктор Оливер Борчерс

Оценка неопределенности прогнозов является элементарной для принятия деловых решений.

Сети плотности смеси помогают лучше понять неопределенность, с которой вы сталкиваетесь в реальном мире.

Фото Ади Гольдштейна на Unsplash

Неопределенность — ключевой элемент каждого решения, которое мы принимаем. Однако в бизнесе менеджеры регулярно сталкиваются с решениями, влекущими за собой разнообразные непредвиденные последствия. Менеджер может иметь дело со следующими вопросами:

• «Как установить цену XYZ на основе атрибутов продукта?»
• «Сколько посещений сайта вызовет реклама?»
• «Какова ожидаемая пожизненная ценность клиента Z-A137?»
• «Сколько мы должны потратить на рекламу, учитывая ситуацию на рынке?»

Каждый из этих вопросов подразумевает решение, которое в идеале является хорошо информированным и учитывает (или, по крайней мере, признает) лежащую в основе неопределенность. Например: неправильное установление цен приводит к снижению доходов, что, в свою очередь, может вызвать необходимость экономии средств.

Фото rawpixel на Unsplash

Этот пост предназначен для аудитории, ориентированной на бизнес-анализ данных . Мы собираемся изучить некоторые технические вопросы о прогнозировании непрерывных значений и о том, как известная линейная модель ограничена в некоторых ситуациях. Затем мы демонстрируем вариант нейронной сети, называемой сетью смешанной плотности (MDN), чтобы обойти эти ограничения. Таким образом, менеджеры могут лучше понять неопределенность, лежащую в основе прогноза.

Вопросы, заданные ранее, требуют предсказания и имеют три общие черты. первое первое, что мы хотим предсказать непрерывное количество (цена, посещения веб-сайта, продажи, вы называете это). Секунда , прогнозы делаются в условиях неопределенности. Таким образом, в идеале мы хотели бы иметь представление о том, насколько мы не уверены в прогнозах. В-третьих, , прогнозы основаны на некоторых входных наблюдениях (атрибуты продукта, клиент, дизайн рекламы). В идеале мы хотели бы не получить один ответ на вопрос, а диапазон ответов для оценки вероятности каждого отдельного ответа. Вкратце: мы ищем вероятностное распределение по диапазону ответов с учетом входных данных. Таким образом, мы улучшаем наше понимание прогноза и можем даже принять более обоснованное решение как менеджер или как клиент.

Время для примера: Предположим, мы собираемся предсказать цену продукта, скажем, наушников. Глядя на гистограмму рыночных цен, мы делаем вывод, что существуют наушники с низкой (~ 30 долларов), средней (~ 60 долларов) и высокой (~ 120 долларов) ценой. Возврат к простому распределению Гаусса для моделирования данных обречен на неудачу, что легко различимо по кривой эмпирического распределения Гаусса. Помните, что нормальное распределение Гаусса (𝒩) параметризовано двумя значениями: средним (μ) и стандартным отклонением (σ). Подгонка 𝒩 к данным на основе выборочного среднего (μ = 47,95) и станд. отклонение (σ = 27,76) присваивает вероятность областям цены, которые мы не наблюдаем на вымышленном рынке (т. Е. Цены от 90 до 110 долларов). Кроме того, отрицательных цен являются «разумными» в соответствии с левой стороной кривой.

Источник: Автор

Базовые данные, генерирующие распределение цен, представляют собой смесь гауссианов. Смесь мультимодальная; таким образом, он демонстрирует несколько «пиков». Чтобы приспособиться к распределению наших вымышленных данных о ценах, мы можем использовать не один, не два, а три адекватно смешанных компонента Гаусса. Нам «просто» нужно выбрать параметры (μ, σ), нормализовать распределения по весу (⍺) и просуммировать их (подробнее об этом позже). Смешивание этих компонентов аккуратно отражает реальные данные, как показано на следующем рисунке.

Источник: Автор

В последующих главах мы будем использовать Tensorflow (www.tensorflow.org) и его расширение Tensorflow-Probability (www.tensorflow.org/probability). Пример был сгенерирован в Tensorflow Probability с использованием значений, показанных ниже во фрагменте кода. В основном мы определяем смесь распределений одного и того же семейства.

Первым решением вопросов, поставленных в начале поста, действительно является выполнение простой линейной регрессии. Мы практически слышим, как вы зеваете: Опять не то .

Но подождите, мы сделаем небольшой технический снимок! Учитывая вектор x входных данных (атрибуты продукта, клиент, …, вы называете это снова) , , мы хотим предсказать y (цена, посещения веб-сайта, …). Точнее: мы стремимся получить вероятность y при условии x : p(y| x ). Если мы предположим гауссово распределение действительных целевых данных (как мы обычно делаем, когда минимизируем квадрат ошибки), то p(y| x ) принимает известную форму:

В практических приложениях мы минимизируем квадрат ошибки выход линейной функции μ с учетом x , ее параметров Θ и целевого значения y для всех пар ( x , y ) в некотором наборе данных 𝔻. Обученная функция фактически «выплевывает» условное среднее гауссовского распределения μ( x , Θ ) с учетом данных и параметров. Он выбрасывает стандарт. девиация и нормировочная постоянная, не зависящие от Θ . Таким образом, модель накладывает несколько важных допущений, которые на практике могут быть очень ограничивающими:

1. Распределение данных является гауссовым. Процитируем [1]:
   «Практические задачи машинного обучения часто могут иметь существенно негауссовские распределения» (стр. 272).
2. Выходное распределение унимодальное. Таким образом, мы не можем объяснить ситуацию, когда x может дать несколько правильных ответов, которые может зафиксировать мультимодальное распределение (как в приведенном выше примере с наушниками).
3. Станд. отклонение σ распределения шума считается постоянным и поэтому не должно зависеть от x (гомоскедастичность, изотропная ковариационная матрица). Опять же, это не всегда так в реальном мире.
4. Функция µ( x , Θ ) является линейной, т.е.0026 + b , , где Θ = { w , b }. Линейные модели считаются более интерпретируемыми. С другой стороны, нейронные сети обеспечивают отличные возможности прогнозирования, потому что они теоретически могут моделировать любую функцию.

Рассмотрим две ситуации, которые графически мотивируют ранее обозначенные технические проблемы:

Источник: Автор

(LHS): Основная функция является линейной. Однако мы наблюдаем два нарушения: Сначала , станд. отклонение распределения (шума) непостоянно. Во-вторых , шум действительно зависит от ввода.

(правая сторона): Мало того, что стандарт. отклонение распределения шума зависит от x , но вывод дополнительно нелинейный . Кроме того, выходное распределение мультимодально . Простое среднее не является разумным решением для некоторых областей данных (около ± 8). Навязывание ранее изложенных предположений может легко ввести в заблуждение, когда мы собираемся предсказать результаты, которые следуют таким сложным шаблонам.

Чтобы учесть указанные ограничения, [2] предложил параметризовать смесь распределений с помощью DNN. Первоначально задуманная в 1994 году [1] [2], MDN недавно нашла ряд различных применений. Например: Siri от Apple в iOS 11 использует MDN для генерации речи [3]. Алекс Грейвс использовал MDN в сочетании с RNN для создания искусственного почерка [4]. Кроме того, есть несколько сообщений в блогах, посвященных теме [5] [6] [7] [8]. Amazon Forecast предлагает своим клиентам MDN в качестве алгоритма [9].], а [10] написал магистерскую диссертацию по этой теме.

Однако мы хотим установить метод для более широкой аудитории . По той простой причине, что многие современные архитектуры нейронных сетей могут быть расширены до MDN (Transformer, LSTM, CovNets, …).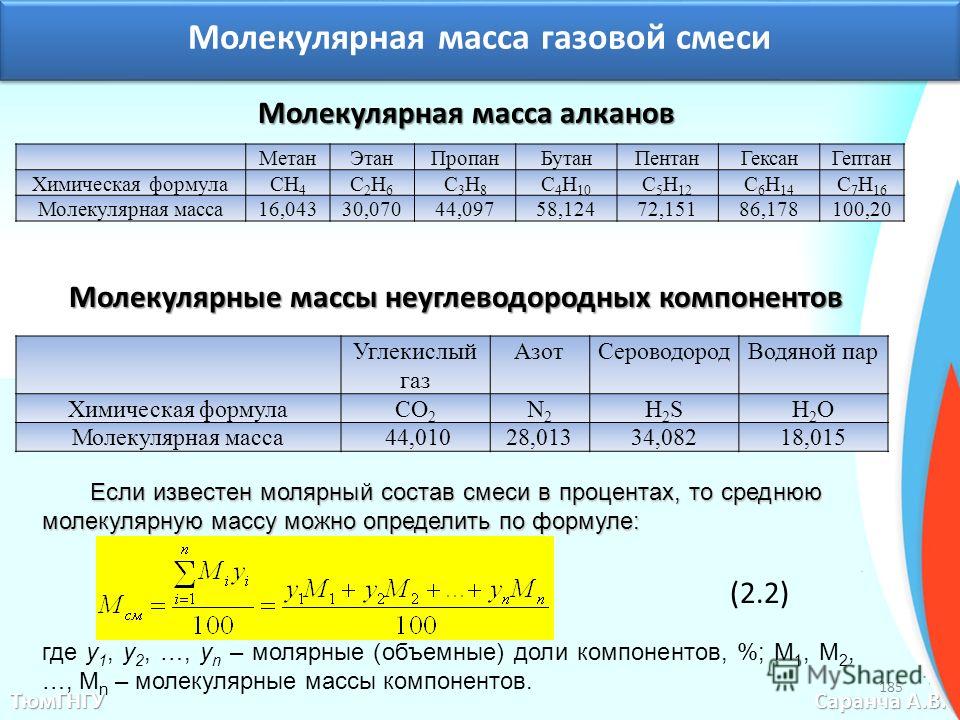 По сути, MDN можно рассматривать как модуль расширения, применимый к широкому спектру бизнес-задач.

Источник: автор

По своей сути концепция MDN проста, понятна и привлекательна: Объедините глубокую нейронную сеть (DNN) и смесь распределений. DNN предоставляет параметры для нескольких распределений, которые затем смешиваются по некоторым весам. Эти веса также предоставляются DNN. Результирующее (мультимодальное) условное распределение вероятностей помогает нам моделировать сложные закономерности, встречающиеся в реальных данных. Таким образом, мы можем лучше оценить, насколько вероятны определенные значения наших прогнозов.

Теоретически гауссовская смесь способна моделировать произвольные плотности вероятности [2], если она адекватно параметризована (например, при наличии достаточного количества компонентов). Формально условная вероятность для смеси определяется как

Подробнее остановимся на каждом параметре в отдельности:

• c обозначает индекс соответствующего компонента смеси. На каждый выход приходится до C компонентов смеси (т. е. распределений), что является определяемым пользователем гиперпараметром.
• ⍺ обозначает параметр микширования. Думайте о параметре микширования как о ползунках, смешивающих вместе C различные аудиосигналы с разной интенсивностью, создавая более насыщенный выходной сигнал. Параметр микширования обусловлен на входе х .
• 𝒟 — соответствующее распределение (аудиосигнал), которое нужно микшировать. Распределение можно выбрать в зависимости от задачи или приложения.
• λ обозначает параметры распределения 𝒟. Если мы обозначим 𝒟 как распределение Гаусса, λ1 соответствует условному среднему μ( x ), а λ2 — условному станд. отклонение σ( x ). Распределения могут иметь несколько параметров (например, у Бернулли и Хи2 по одному, у Гаусса и Бета по два, а усеченная Гауссова имеет до четырех параметров). Это параметры, которые выдает нейронная сеть.

Формулировка условной вероятности как смеси распределений уже решает многочисленные проблемы, связанные с изложенными предположениями. Во-первых, , распределение может быть произвольным, так как теоретически мы можем смоделировать любое распределение как смесь гауссиан [2]. Second Использование нескольких распределений помогает нам моделировать мультимодальные сигналы. Рассмотрим наш пример цены на наушники, который явно мультимодальный. Третий, станд. отклонение теперь зависит от входных данных, что позволяет нам учитывать переменную std. отклонение. Это преимущество сохраняется даже тогда, когда мы используем только одно распределение Гаусса. В-четвертых, проблему линейности функции можно обойти, выбрав нелинейную модель, обуславливающую параметры распределения на входе.

Чтобы получить параметры для смеси, DNN модифицируется для вывода множественных векторов параметров . Мы начинаем с однослойной DNN и активации ReLU. Используя скрытый слой h2( x ), мы вычисляем параметры смеси следующим образом: функция softmax для ограничения вывода. Этот шаг важен, так как смесь вероятностей должна объединиться в одну. Сами ограничения для λ1 и λ2 зависят от распределения, которое мы выбираем для нашей модели. Единственное ограничение, которое мы должны применить для гауссова, заключается в том, что стандартное значение. отклонение
σ( x ) > 0. Этот эффект может быть достигнут несколькими способами. Например, мы могли бы использовать экспоненциальную активацию, предложенную Бишопом [1] [2]. Однако экспонента может привести к численной нестабильности. В качестве альтернативы мы можем использовать простую активацию softplus, аналогичную активации oneplus, использованной в [11]. Либо используем вариант активации ELU со смещением. Из-за недавнего всплеска популярности ELU мы выбираем последнее. Таким образом, мы получаем следующие преобразования:

Выбор ограничений зависит от распределений и данных. Как всегда: разные ограничения могут работать лучше для разных наборов данных. Можно даже утверждать, что с точки зрения бизнеса разумно также ограничивать μ( x ) положительными значениями. Таким образом, мы могли бы сказать, что отрицательные цены не входят в сферу возможностей.

Теперь, когда мы указали параметры и условную вероятность, у нас есть все необходимое для прямой минимизации среднего отрицательного логарифмического правдоподобия (NLL) с использованием некоторой формы градиентного спуска (SGD, Adagrad, Adadelta, Adam, RMSProp и т. д.) .

Код доступен на Github / Colab .

Установив базовую теорию для MDN, мы теперь покажем, как реализовать модель в Tensorflow/Keras. По сути, нам нужны два компонента: пользовательский слой для вычисления параметров и минимизируемая функция потерь. Из соображений численной стабильности и удобства мы будем выполнять большую часть вычислений в функциях Tensorflow. Как мы уже говорили о гибкости фреймворка MDN, мы обсуждаем не все, а важные части, чтобы вы могли создать свою собственную версию. Определить DNN просто:

В зависимости от данных и приложения, возможно, также имеет смысл наложить дополнительную регуляризацию активности на сигмы, чтобы предотвратить std. отклонение от взрыва. Простая регуляризация L2 была бы разумным вариантом.

В примере кода требуется функция активации «неотрицательная экспоненциальная линейная единица», которая гарантирует, что сигмы строго больше нуля. Tensorflow предоставляет очень удобный способ определить требуемую функцию активации. Мы просто делаем nnelu вызываемой функцией и регистрируем ее как пользовательскую функцию активации в Keras.

Оставшийся строительный блок — это реализация функции потерь. Применение Tensorflow-Probability оказывается удобным, потому что мы лишь немного переопределяем пример в начале поста. Для MixtureSameFamily требуется смешанное распределение и распределения компонентов. Первое представляет собой простое категориальное распределение, которое дает веса смеси ⍺( x ). Последнее представляет собой нормальное распределение, параметризованное средним значением и станд. отклонение. Затем мы просто вычисляем логарифмическую вероятность и и его отрицательное среднее. Возвращаясь к вероятности тензорного потока, мы избегаем численного переполнения/недополнения (реализовать это вручную на самом деле может быть довольно сложно).

После определения наиболее важных компонентов MDN остается только составить модель.

Пришло время вернуться к нашим предыдущим примерам. Мы обучаем простой MDN с двумя слоями, 200 нейронами на слой и одним гауссовым компонентом в наборе линейных данных. MDN показывает свою силу: благодаря кондиционированию std. отклонение распределения на входе, MDN может адаптироваться к изменению базового распределения данных. Он четко фиксирует линейный тренд (как и ожидалось), но адаптирует стандартную. отклонение в соответствии с увеличением неопределенности, присутствующей в данных (мне нравится этот график. Он похож на падающую звезду).

Источник: Автор

Чтобы лучше понять результаты, мы дополнительно проводим сравнение среднего отрицательного логарифмического правдоподобия нескольких моделей. А именно, давайте рассмотрим нулевую модель (выборочное среднее и выборочное стандартное отклонение), линейную модель (линейное условное среднее и выборочное стандартное отклонение), DNN (нелинейное условное среднее и выборочное стандартное отклонение) и MDN (нелинейное условное среднее и нелинейное условное стандартное отклонение). DNN и MDN используют одни и те же параметры и программу обучения. К счастью, мы можем отслеживать ход обучения MDN с помощью Tensorboard. Все, что для этого требуется, — это обратный вызов процедуры подгонки. Таким образом, нам не нужно отдельно хранить тренировочные потери. И мы сближаемся!

MDN nll-потеря во время оптимизации. Источник: Автор Источник: Автор

Все модели могут превзойти нулевую модель. Остальные модели работают одинаково с точки зрения MSE, поскольку MSE предполагает, что стандарт. отклонение базового распределения является постоянным. Мы не можем адекватно зафиксировать поведение данных! NLL, который включает в себя std. отклонение, действительно отражает более нюансированную картину. Поскольку базовая функция является линейной, DNN и линейная модель работают одинаково. MDN, однако, составляет лучше подходит для распределения данных , что приводит к наименьшему значению NLL.

Чтобы получить условное среднее значение из плотности вероятности MDN для одной точки данных, вычисляют:

Взгляд на формулу объясняет результат: Среднее значение не включает стандартное значение. отклонение σ( x ). Простой взгляд на среднее значение MDN отбрасывает ценную информацию, которая может понадобиться нам в реальных приложениях. Имея это распределение в наших руках, мы можем вычислить более сложные величины. Например, энтропия Шеннона может служить индикатором нашей уверенности. Или мы могли бы вычислить f-дивергенции, чтобы оценить, насколько похожи прогнозы.

Теперь обратимся ко второму — нелинейному — примеру. Сначала мы используем мин-макс масштабатор, чтобы преобразовать y в разумный диапазон для DNN/MDN, чтобы ускорить обучение.

Источник: Автор

MDN фиксирует не только лежащую в основе нелинейность, но и мультимодальность выходных данных и изменение стандартного значения. отклонение. Распределение, генерирующее данные, фиксируется адекватно. Глядя на условную плотность для x = 8, мы видим, что MDN дает два непересекающихся пика:

Источник: Автор

Возможность моделирования этих сложных распределений отражается в NLL, где MDN достигает наилучшего NLL.

Источник: Автор

Этот пост мы начали с примера прогнозирования цен. После долгих технических доработок вернемся к нашему исходному примеру: прогнозирование цен.

Для простоты анализа мы используем дрозофилу из наборов данных: жилье в Бостоне. Учитывая около 13 независимых переменных, цель состоит в том, чтобы предсказать медианную стоимость домов, занимаемых владельцами, в 1000 долларов США (MDEV). Пример может не обязательно полностью использовать возможности MDN для моделирования мультимодальных распределений. Тем не менее, он показывает, как MDN может моделировать неопределенность цен. Независимые переменные преобразуются с использованием мин-макс масштаба, а цены логарифмически преобразуются.

Источник: Автор

Глядя на NLL, мы наблюдаем такое же поведение, как и в предыдущих примерах. MDN лучше справляется с данными. Таким образом, хотя в примере может и не быть многомодальности, мы, безусловно, выиграем от , моделирующего полную условную вероятность , а не просто точечную оценку.

Источник: Автор

Анализ условных плотностей для разных домов помогает нам лучше принять решение. Мы достаточно уверены в высокой цене дома 18, поэтому, как управляющий, мы можем установить соответствующие цены.

Предсказание для дома 12 очень неубедительно. Может потребоваться, чтобы эксперт-человек непосредственно оценил дело, чтобы установить цену.

Дома 13 и 45 пересекаются по цене. Имеет смысл непосредственно проанализировать их атрибуты, чтобы увидеть, могут ли они служить объектами интереса для покупателей в том же ценовом диапазоне. Хотя мы не используем весь потенциал модели в этом простом наборе данных, мы все же извлекаем выгоду из дополнительных возможностей.

Оценка неопределенности является важным аспектом современного бизнеса. В этом сообщении в блоге освещены теоретические рассуждения, детали реализации, а также некоторые советы и рекомендации по использованию MDN. Мы продемонстрировали возможности MDN в смоделированных и практических приложениях. Благодаря его простоте и модульности мы ожидаем широкий спектр приложений.

По всем вопросам обращайтесь ко мне.

Дополнительная информация

Код доступен на Github / Colab . Руководство было написано для Tensorflow 1.12.0 и Tensorflow-Probability 0.5.0.

Литература

[1] Кристофер М. Бишоп, Распознавание образов и машинное обучение (2006)

[2] Кристофер М. Бишоп, Сети плотности смеси (1994)

[3] Команда Siri, Глубокое обучение для голоса Siri: Сети плотности глубокого смешения на устройстве для синтеза выбора гибридных единиц (2017)

[4] Алекс Грейвс, Генерация последовательностей с помощью рекуррентных нейронных сетей (2014)

[5] ] Кристофер Боннетт, Сети плотности смеси с Эдвардом, Керасом и TensorFlow (2016)

[6] Бинхао Нг, Сети плотности смеси: основы (2017)

[7] Оторо, Сети плотности смеси с TensorFlow (2016)

[ 8] Майк Дузенберри, Сети плотности смеси (2017)

[9] Amazon, Mixture Density Networks (MDN) Recipe (2019)

[10] Axel Brando, Реализация Mixture Density Networks для распределения и оценки неопределенности (2017)

[11] Alex Graves et al. , Гибридные вычисления использование нейронной сети с динамической внешней памятью (2016)

Отказ от ответственности

Высказанные мнения являются исключительно моими собственными и не отражают точку зрения или мнение моего работодателя. Автор не несет никакой ответственности за любые ошибки или упущения в содержании этого сайта. Информация, содержащаяся на этом сайте, предоставляется на условиях «как есть» без каких-либо гарантий полноты, точности, полезности или своевременности.

Моделирование плотности гауссовской смеси, разложение и приложения

. 1996;5(9):1293-302.

дои: 10.1109/83.535841.

Х Чжуан ¹ , Y Huang, K Palaniappan, Y Zhao

принадлежность

• ¹ Отдел электр. и вычисл. инженер, Университет Миссури, Колумбия, Миссури.

• PMID: 18285218
• DOI: 10.1109/83.535841

X Zhuang et al. Процесс преобразования изображений IEEE. 1996.

. 1996;5(9):1293-302.

дои: 10.1109/83.535841.

Авторы

Х Чжуан ¹ , Ю Хуан, К Паланиаппан, Ю Чжао

принадлежность

• ¹ Отдел электр. и вычисл. инженер, Университет Миссури, Колумбия, Миссури.

• PMID: 18285218
• DOI: 10.1109/83.535841

Абстрактный

Мы представляем новый подход к моделированию и разложению гауссовских смесей с использованием надежных статистических методов. Распределение смеси рассматривается как загрязненная гауссова плотность. Используя эту модель и оценщик подбора модели (MF), мы предлагаем рекурсивный алгоритм, называемый алгоритмом гауссовского разложения плотности смеси (GMDD) для последовательной идентификации каждого гауссова компонента в смеси. Предлагаемая схема декомпозиции имеет преимущества, которые желательны, но отсутствуют в большинстве существующих методов. В алгоритме GMDD количество компонентов не нужно задавать априори, доля зашумленных данных в смеси может быть велика, оценка параметров каждого компонента практически независима от начала, а изменчивость формы и размера учитываются плотности компонентов в смеси. Моделирование плотности смеси по Гауссу и его разложение широко применяются в различных дисциплинах, требующих характеризации сигнала или формы волны для классификации и распознавания. Мы применяем предложенный алгоритм GMDD для идентификации и извлечения кластеров, а также для оценки неизвестных плотностей вероятностей. Оценка плотности вероятности путем выявления разложения с помощью алгоритма GMDD, то есть суперпозиции нормальных распределений, успешно применяется для автоматизированной классификации ячеек. Компьютерные эксперименты с использованием как реальных, так и смоделированных данных демонстрируют достоверность и мощность алгоритма GMDD для различных моделей и различных предположений о шуме.

Похожие статьи

• Надежное последовательное моделирование данных с использованием скрытой марковской модели, устойчивой к выбросам.

  Чатзис С. П., Космопулос Д.И., Варваригу Т.А. Чатзис С.П. и др. IEEE Trans Pattern Anal Mach Intell. 2009 сен; 31 (9): 1657-69. doi: 10.1109/ТПАМИ.2008.215. IEEE Trans Pattern Anal Mach Intell. 2009. PMID: 19574625

• Обучение на основе моделей с использованием смеси смесей гауссовского и равномерного распределений.

  Browne RP, McNicholas PD, Sparling MD. Браун Р.П. и др. IEEE Trans Pattern Anal Mach Intell. 2012 апр; 34 (4): 814-7. doi: 10.1109/ТПАМИ.2011.199. IEEE Trans Pattern Anal Mach Intell. 2012. PMID: 22383342

• Последовательная аппроксимация ядерной плотности и ее применение для визуального отслеживания в реальном времени.

  Хань Б., Команичу Д., Чжу Ю., Дэвис Л.С. Хан Б. и др. IEEE Trans Pattern Anal Mach Intell. 2008 г., июль; 30(7):1186-97. doi: 10.1109/ТПАМИ.2007.70771. IEEE Trans Pattern Anal Mach Intell. 2008. PMID: 18550902

• Введение в распределения конечных смесей.

  Эверитт БС. Эверит БС. Статистические методы Med Res. 1996 июнь; 5(2):107-27. дои: 10.1177/096228029600500202. Статистические методы Med Res. 1996. PMID: 8817794 Обзор.

• ExGUtils: пакет Python для статистического анализа с бывшей гауссовой плотностью вероятности.

  Морет-Татай К., Гамерманн Д., Наварро-Пардо Э., Фернандес де Кордова Кастелья П. Море-Татай С. и соавт. Фронт Псих. 2018 1 мая; 9:612. doi: 10.3389/fpsyg.2018.00612. Электронная коллекция 2018. Фронт Псих. 2018. PMID: 29765345 Бесплатная статья ЧВК. Обзор.

Посмотреть все похожие статьи

Цитируется

• Реконструкция изображения TOF-PET с применением нескольких ядер синхронизации на черенковском излучении в BGO.

  Эфтимиу Н., Кратохвиль Н., Гундакер С., Полесел А., Саломони М., Оффрэй Э., Пиццикеми М. Эфтимиу Н. и соавт. IEEE Trans Radiat Plasma Med Sci. 2020 сен;5(5):703-711. doi: 10.1109/trpms.2020.3048642. Epub 2020 31 декабря. IEEE Trans Radiat Plasma Med Sci. 2020. PMID: 34541434 Бесплатная статья ЧВК.

• CATS: инструмент для кластеризации ансамбля внутренне неупорядоченных пептидов на плоском энергетическом ландшафте.

  Эзерски Дж.С., Чунг М.С. Эзерски Дж. К. и соавт. J Phys Chem B. 13 декабря 2018 г. ; 122 (49): 11807-11816. doi: 10.1021/acs.jpcb.8b08852. Epub 2018 7 ноября. J Phys Chem B. 2018. PMID: 30362738 Бесплатная статья ЧВК.

• DEWS (Структура сегментации глубокой гиперинтенсивности белого вещества): полностью автоматизированный конвейер для обнаружения небольших глубоких гиперинтенсивностей белого вещества при мигрени.

  Park BY, Lee MJ, Lee SH, Cha J, Chung CS, Kim ST, Park H. Парк БАЙ и др. Нейроимидж клин. 2018 2 марта; 18: 638-647. doi: 10.1016/j.nicl.2018.02.033. Электронная коллекция 2018. Нейроимидж клин. 2018. PMID: 29845012 Бесплатная статья ЧВК.

• Парцелляция ранней зрительной коры на основе функциональной связности.

  Park BY, Tark KJ, Shim WM, Park H. Парк БАЙ и др. Hum Brain Map.