Пластичность (подвижность) бетона П1-5 на что влияет

Помимо прочности бетона особое значение должно уделяться его пластичности. Именно от этого будет зависеть насколько удобно работать с материалом, скорость уплотнения раствора. Что же за показатель такой – пластичность?

Это способность бетона к заполнению, растеканию и уплотнению его в опалубке. Эта характеристика указывает на удобство работы со смесью. Чем гуще раствор, тем сложнее он растекается, поэтому пластичность его зависит от того, сколько жидкости в составе.

Что еще влияет на пластичность бетонной смеси

• Марка цемента;
• Коэффициент плотности;
• Количество воды и других компонентов;
• Пропорции ингредиентов.

Также на пластичность оказывает положительное влияние гладкий гравий, так как он имеет низкий коэффициент трения с опалубкой. Использование же глинистых и пыльных включений снижает подвижность, поэтому стоит избегать их попадания в раствор.

Всего выделяют 5 категорий пластичности материала: от П1 до П5

К примеру, бетон М100 может иметь следующую подвижность – П2-П5, а вот бетон М400 – П1-П5.

Зависит этот показатель от водоцементного соотношения: чем больше воды добавлено, тем раствор будет подвижнее. Вместе с тем важно понимать, что при производстве материала строго соблюдаются пропорции, а вот добавление воды в уже готовую смесь – огромная ошибка. Таким образом вы автоматически снижаете прочность материала, что негативно скажется на конструкции.

Подбор бетона должен осуществляться с учетом вида работ. Например, малоподвижные смеси П1 и П2 не растекаются. Их чаще перевозят на самосвале. На вид этот материал рассыпчатый. Используется такой раствор для возведения крупных сооружений.

П3 — малоподвижная смесь. Она не подходит она для труднодоступных мест, так как не способна заполнить.

П4 — наиболее востребованный материал, так как он способен заполнить любую форму без пор.

П5 используется преимущественно для изготовления сложных форм. Материал подвижный, что позволяет без труда заполнить труднодоступные места.

Как определить подвижность материала?

Для этого используют специальный конус, формы или вискозиметр. Правда, проводить исследования лучше в лаборатории. На строительной площадке проверить пластичность можно с помощью форм или конуса.

Заключение

Материал с высокой подвижностью рекомендуется использовать для изготовления ж/б конструкций с использованием большого количества арматуры. Пластичная смесь способна заполнить все пустоты, она не нуждается в дополнительной трамбовке бетона. Если же для этих целей используется малоподвижный состав, то он может привести к образованию пор, которые негативно скажутся на надежности и долговечности постройки.

Рекомендуется приобретать готовый бетон от производителя. Так вы, наверняка, получите именно тот материал, который вам нужен. Самостоятельное же изготовление раствора также возможно, но здесь есть риск того, что будут неправильно соблюдены пропорции, а такая ошибка может обойтись очень дорого.
При заказе готового раствора вы получите всю необходимую документацию, что даст дополнительные гарантии, позволит вам быть уверенным в высоком качестве материала.

Автор статьи:
Горбач Максим Викторович.
Начальник производства, стаж больше 10 лет.

как определить пластичность бетона — Бетон Харьков

Статьи

Подвижность бетона: как определить пластичность бетона

Бетон – один из самых используемых строительных материалов, отличающийся высокой прочностью и устойчивостью к климатическим изменениям, влаге и огню. Кроме того, бетон чрезвычайно прочен в застывшем состоянии, а в жидком – пластичен. Именно его пластичность позволяет раствору заполнять любые формы и пустоты, обеспечивая надежность.

Пластичность бетона напрямую влияет на качество работы с ним: если он слишком густой, то мелкие пустоты не заполнятся и бетон не ляжет плотно. Из-за этого рано или поздно состав может начать растрескиваться. Если же бетон слижком жидкий, он может начать вытекать из формы, либо вовсе потеряет крепежные свойства.

Чтобы не ошибиться в густоте состава, следует ориентироваться по его уровням.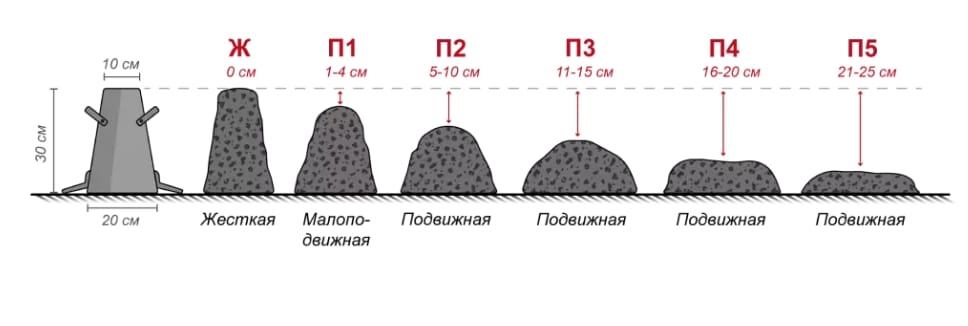

Уровни пластичности бетона

Всего уровней (или марок) подвижности бетона 5:

1.  П1. Смесь настолько плотная, что уложить ее в даже крупные ячайки арматуры невозможно без специального оборудования. Оно оказывает вибрирующее воздействие, которое выгоняет мельчайшие пузырьки воздуха из бетона и формы. Смесь этого уровня используют для укладки фундамента, изготовления крупных бетонных деталей.
2. П2. Все еще слабо подвижный состав,и, хотя все еще требуется дополнительное оборудование, работать с ним уже легче.
3. П3. Средняя степень подвижности. В случае простоты формы (без труднодоступных мест), может использоваться без вибрационного оборудования.
4. П4. Оптимальный вариант пластичности – заполняет простую форму под тяжестью своего веса. Дополнительное оборудование не требуется, достаточно разровнять.
5. П5. Наиболее текучий состав. Используется для заливки сложных форм с трудными местами.

Как подобрать бетон нужной марки подвижности

Уровень подвижности бетона следует выбирать, исходя из:

• цели – для производства бетонных плит или фундамента;
• сложности формы – чем больше труднодоступных мест, тем более жидким должен быть раствор;
• наличия вибрационного оборудования.

Как измерить пластичность бетона

Одним из самых простых способов определения уровня пластичности, является металлический конус. Изделие высотой 30 см, диаметром 30 см и 10 см заполняется послойно бетоном, после чего переворачивается и снимается со смеси. Открытую смесь необходимо оставить на 5 минут, после чего степень оседания получившегося конуса сверить с таблицей:

Степень текучести	На сколько см осел конус
П1	1-1,5 см
П2	5-10 см
П3	10-15 см
П4	15-20 см
П5	Растекся полностью

Изменение уровня: что на него влияет

На уровень подвижности бетона влияет:

• текстура поверхности гравия – чем она ровнее, тем более текучим будет бетон, и наоборот;
• посторонние материалы в составе – глина и пыль снижиют пластичность бетона, а также его надежность;
• использование дополнительных веществ для регулировки пластичности.

На пластичность бетона влияет много факторов: качество составных частей (песка, цемента, гравия) и правила их хранения, соблюдение технологии при замешивании, скорость использования готового раствора. Поэтому важно вначале изучить специфику работы с ним, и только после этого приступать к делу, чтобы не испортить состав.

Предельный анализ и пластичность бетона — 3-е издание

Содержание Описание книги

816 страниц 669 черно-белых иллюстраций

к КПР Пресс

816 страниц

к КПР Пресс

---

Узнайте об электронных книгах VitalSource Открывает всплывающее окно

Также доступна в виде электронной книги по адресу:

• Электронные книги Тейлора и Фрэнсиса
  (покупка для учреждений)Открывается в новой вкладке или окне

Продолжить покупки

Впервые опубликовано в 1984 г., Предельный анализ и пластичность бетона объясняет продвинутым инженерам-проектировщикам принципы теории пластичности и ее применение к проектированию железобетонных и предварительно напряженных железобетонных конструкций, обеспечивая полное понимание предмета, а не чем простое применение текущих расчетных формул.

Полное обновление и пересмотр, Расчет предельных значений и пластичность бетона, добавлено третье издание —

• Формулы расчета армирования для трехмерных полей напряжений, которые позволяют рассчитывать твердые конструкции (также подходят для компьютерной оптимизации нижней границы)
• Улучшенные объяснения теории скольжения трещин и новые решения для балок с произвольными криволинейными трещинами сдвига, неразрезных балок, балок со слабым сдвигом и балок с большим осевым сжатием
• Более точная обработка и решения для балок с круглым поперечным сечением
• Применение теории скольжения трещины к задачам продавливания
• Новые решения, иллюстрирующие влияние начального растрескивания на несущую способность дисков
• Условие текучести для предельного случая диска с изотропной трещиной

Авторы также посвящают совершенно новую главу недавно разработанной теории жестко-пластической динамики для сейсмического проектирования бетонных конструкций. По сравнению с динамическим анализом новая теория проще в использовании и приводит к значительной экономии материалов. В этой главе методы расчета пластичности как для статических, так и для динамических нагрузок теперь рассматриваются в книге 9.0032 .

　

Введение
Теория пластичности
Определяющие уравнения
Принципы экстремума для жесткопластических материалов
Решение задач пластичности
Железобетонные конструкции 90 026 Условия текучести
Бетон
Условия текучести для армированных дисков
Условия текучести для плит
Расчет армирования

Теория обычного бетона
Статические условия
Геометрические условия
Виртуальная работа
Определяющие уравнения
Теория плоской деформации кулоновских материалов
Приложения
Диски
Статические условия
Геометрические условия
Виртуальная работа
Определяющие уравнения
Точные решения для изотропных дисков
Эффективная прочность армированного диска на сжатие ks
Общая теория решений с нижней границей
Модели распорок и связей
Стены сдвига
Решения однородного армирования
Расчет согласно теории упругости
Балки
Балки при изгибе
Балки при сдвиге
Балки при кручении
Комбинированный изгиб, сдвиг и кручение
Плиты
Статические условия
Геометрические условия
Виртуальная работа, граничные условия
Определяющие уравнения
Точные решения для изотропных Плиты
Верхние предельные решения для изотропных плит
Решения для нижней границы

Ортотропные плиты
Аналитические решения для оптимального армирования
Численные методы
Действие мембраны
Пробивной сдвиг плит
Введение
Внутренние нагрузки или колонны
Краевые и угловые нагрузки
Заключительные замечания
Сдвиг в соединениях
Введение
Анализ соединений с помощью теории пластичности
Прочность различных типов соединений
Прочность соединения арматурных стержней
Введение
Местное разрушение Механизм
Механизмы разрушения
Анализ механизмов разрушения
Оценка прочности анкера и соединения
Влияние поперечного давления и опорной реакции
Влияние поперечного армирования
Заключительные замечания

Биография

член парламента Нильсен, Л. К. Хоанг

Добавить в корзину

J&M и Cement Plasticity

Отказ от ответственности: этот пост откровенно технический. Если у вас нет нездорового интереса к нефтепромысловому цементу или моделированию пластичности, или мазохистского влечения к алгебре и исчислению, я бы не рекомендовал вам читать дальше.

Некоторые статьи очень хороши: то, как авторы проводили свои эксперименты и сообщали данные, позволяет нам вернуться к ним и узнать что-то новое. Это случай Джексона и Мерфи.

В 1993 году П.Б. Джексон и К.Э. Мерфи опубликовали документ SPE 25698, в котором они описывают тщательную заливку цемента в кольцевое пространство длиной один метр между концентрическими обсадными трубами. После выдержки в течение 69 часов при температуре 49 градусов по Цельсию (120 градусов по Фаренгейту) они подвергли внутренний корпус пяти циклам повышения давления с 2000 до 10 000 фунтов на квадратный дюйм (от 13,8 до 68,9 МПа).

Авторы отслеживали азимутальную или кольцевую деформацию εθθ внутри и снаружи испытательной установки и тщательно сообщали, когда наблюдали выход газа из кольцевого пространства.

Азимутальная деформация измеряет степень растяжения обсадной трубы и, следовательно, ее расширение под действием внутреннего давления. Тот факт, что кривые деформация-давление (на рисунке выше) не повторяют свои ступени, а окружают область, предполагает, что цемент претерпел постоянную пластическую деформацию.

Во время последних двух циклов, когда давление внутри корпуса случайно упало ниже базового значения 1000 фунтов на квадратный дюйм, возникла утечка газа. После цикла 8000 фунтов на квадратный дюйм поток газа прекратился до того, как давление достигло 1975 фунтов на квадратный дюйм, тогда как в конце последнего цикла (до 10000 фунтов на квадратный дюйм) поток уменьшился до нескольких пузырьков за счет повышения давления до 2080 фунтов на квадратный дюйм и полностью прекратился к тому времени, когда значение было достигнуто 2785.

Интуитивно понятное объяснение: цемент все больше «сжимался», и некоторая пластическая деформация сохранялась после сброса давления. Это привело к отслоению цемента от обсадной колонны и возникновению утечки газа.

Таким образом, это привлекательная и (по-видимому) простая задача смоделировать эксперимент и попытаться воспроизвести деформацию обсадной колонны, а также время и размер микрозазора — так называется крошечный зазор между обсадной колонной и цементом. Но деталей много, и в них скрывается немало чертей. Прежде всего, какие свойства цемента мы должны использовать? В документе говорится, что они использовали что-то близкое к чистому раствору G, смешанному в количестве 1893 кг м-3 и с массовым соотношением вода/цемент 44%. В документе сообщается о трехосном испытании после отверждения суспензии при другой температуре и в течение более длительного времени, чем в эксперименте; однако большой проблемой является то, что образец, использованный в прессе, был сухим.

Оценка свойств цемента

Таким образом, первым шагом является оценка механических свойств и свойств разрушения цемента, а для этого нам нужна его степень гидратации.

Легко смоделировать испытание UCA, и результаты, представленные на графике справа, показывают, что гидратация увеличилась примерно до 35% исходных зерен цемента (фактически 38%, если мы пренебрегаем любой начальной задержкой схватывания). Мы также можем смоделировать настройку в цилиндрической геометрии: температура окружающей среды поддерживается на уровне 49град.С, гарантировал достаточно равномерный температурный профиль и почти постоянную степень гидратации по цементному кольцу.

При степени гидратации 35% можно оценить следующие механические свойства:

• Модуль Юнга, E=9,032 ГПа
• Коэффициент Пуассона, ν=0,318
• Прочность на одноосное сжатие (UCS), fc=16,33 МПа
• Прочность при растяжении, фут=2,25 МПа

Параметры упругости были рассчитаны в недренированных условиях (т. е. поровая вода не может проникать в цемент или выходить из него): это разумно, учитывая незначительную проницаемость затвердевшего цемента — доли микродарси — и короткий временной масштаб эксперимент. Интересно, что для образца, испытанного в лаборатории, та же модель предполагает осушенный модуль Юнга, равный 1,9.6 фунтов на квадратный дюйм в недренированных условиях (значения коэффициента Пуассона составляют соответственно 0,22 и 0,29). В документе сообщается о модуле упругости 2 миллиона фунтов на квадратный дюйм (13,8 ГПа) и коэффициенте Пуассона от 0,25 до 0,30: это говорит о том, что оценки модели достаточно надежны.

Оценка свойств цемента является полезным упражнением: при оценке старых скважин редко бывает что-то лучше, чем UCA, который основан на несовершенной корреляции между скоростью волны сжатия и прочностью на сжатие. Более того, свойства цемента меняются в зависимости от глубины, в зависимости от особенностей перемешивания на поверхности, загрязнения во время закачки и потери жидкости через проницаемые пласты. Даже в современном идеальном мире бывают случаи, когда обширные трехосные испытания невозможны, например. при проектировании скважины. Поэтому обнадеживает то, что можно прибегнуть к надежным оценкам, особенно когда они используются для дополнения измеренных значений в том, что мы могли бы назвать расширенными моделями (я) тестами.

Моделирование эксперимента

Теперь, когда у нас есть представление о механических свойствах, мы можем испытать наш виртуальный цемент. Но подождите: как мы моделируем пластическую деформацию?

На самом деле существует множество моделей пластиковых моделей. Если у вас есть неестественный интерес к моделированию пластической деформации, в Интернете есть красиво и лаконично написанный документ Кристиана Краббенхофта. Нефтепромысловый цемент, технически обычная паста из портландцемента (OPC), часто моделируется с использованием пластичности течения со скрытым параметром повреждения. Помимо выбора базовой формулировки пластичности, нам также необходимо определить форму поверхности текучести и пластический потенциал:

Поверхность текучести изменяется по мере накопления повреждений, процесс, называемый затвердеванием, идет от верхнего предела упругости к прочности материала (мы также можем ввести остаточную прочность, которая сохраняется после разрушения, когда цемент ограничен, но мы теперь он не понадобится). В теории пластичности напряженное состояние всегда будет улавливаться поверхностью текучести: оно не может развиваться, если поверхность не движется из-за накопления повреждений и упрочнения. Эта поверхность должна проходить через прочность на одноосное сжатие, а также на прочность на одноосное и двухосное растяжение; он также должен демонстрировать асимптотическое поведение, согласующееся с (очень немногими) тестами при высоком давлении локализации, доступными в литературе.

Поверхность текучести также должна иметь «шапку», то есть она должна загибаться по оси ξ (вы можете проверить статью Википедии о координатах Хейга-Вестергаарда для краткого ознакомления с этой забавной номенклатурой напряжений). Заглушка гарантирует, что по мере увеличения гидростатического напряжения сжатия ξ цемент переходит от расширяющего к уплотняющему поведению. Безусловно, это не опечатки, а громоздкие термины, говорящие о том, увеличивается ли объем материала при воздействии трехосного напряжения (расширяющего) из-за несовершенного скольжения по микротрещинам, вызывающим пластичность. Или, наоборот, объем материала уменьшается (уплотняется) из-за дробления пор. Поскольку тест говорит нам, что цемент остается сжатым, мы действительно должны установить заглушку.

Существует несколько различных формулировок поверхности текучести: модель под названием Cam-Clay (из Кембриджа и глины) использует непрерывную кривую и была принята, в частности, Тирселином и Буа для своих исследований; мы будем использовать специально построенную поверхность, полученную путем сшивания ветви, откалиброванной на цементных трехосных испытаниях, и эллиптической крышки.

Пластмассовый потенциал — странное животное: оно не фиксируется уровнем повреждения, а следует за состоянием стресса, куда бы оно ни пошло. Вектор нормали к потенциальной поверхности, проходящий через точку, определяет направление пластической деформации. В некоторых случаях две поверхности, текучесть и пластический потенциал, считаются одинаковыми, и в этом случае мы говорим о связанной пластичности. Поскольку цемент излишне сложен, часто предполагается, что пластичность связана с шапкой и не связана с главной ветвью поверхности текучести. На рисунке ниже показан пример проекции обеих поверхностей на плоскость ξ-r ближе к концу теста (хотя должен сказать, что я не уверен, что график действительно способствует ясности).

Теперь, когда у нас есть описание того, как ведет себя цемент, нам нужно подключить конститутивную модель к машине, которая полагается на напряжение и деформацию для заданной конструкции. К счастью, подавляющее большинство задач, связанных с цементированием скважин, являются плоскодеформационными, т.е. двумерными. В случае концентрических луковичных колец, таких как в этом эксперименте, мы можем упростить его до одномерной постановки, разновидности задачи Ламе.

Таким образом, у нас есть два варианта:

• Мы можем использовать чистую и элегантную (и короткую) дифференциальную формулировку в MATLAB, которая опирается на мощные решатели обыкновенных дифференциальных уравнений для интегрирования изменений во времени.
• Или мы можем подключить модель материала к универсальному 3D-решателю конечных элементов, такому как программное обеспечение с открытым исходным кодом CalculiX. Эти программы необходимы для моделирования сложной структуры, но их стратегия решения требует сложной формулировки внутренней процедуры, чтобы заставить напряженное состояние (вычисляемое в каждом узле сетки конечных элементов) оставаться на поверхности текучести.

Совместное использование обоих инструментов в этом простом сценарии позволяет нам сравнить два очень разных численных подхода, применяющих один и тот же материальный закон, и, таким образом, судить о влиянии численных приемов на результат.

MATLAB и CalculiX можно также сравнить с точным аналитическим решением для очень простого случая, а именно изотропного сжатия небольшого образца. На рисунке справа показано, что оба ведут себя очень хорошо, даже несмотря на то, что формулировка пластичности течения имеет особенность на упруго-пластической границе.

Первый сюрприз приходит, когда мы обнаруживаем, что попасть в золотую середину не так-то просто: использование предсказанных свойств цемента отодвигает нас вправо от линии критического состояния и приводит к микропорам размером не более нескольких микрометров. Мы можем попробовать варьировать степень гидратации и прочность на сжатие (которая, в конце концов, обеспечивается эмпирической корреляцией), чтобы увидеть, соответствует ли размер микрокольца наблюдаемому, и если да, то когда. Конечно, размер, а точнее, появление микрокольца на внутренней или внешней границе обсадной колонны, никогда не измерялись. Но у нас есть диапазон давлений, между которыми скорость утечки уменьшалась и исчезала; действительно, не будет магического порогового давления, поскольку шероховатость поверхности требует некоторого сжатия цемента, прежде чем интерфейс снова будет герметизирован. До соприкосновения цемента и стали ширину микрокольца можно рассчитать, изучая деформацию только внутренней обсадной колонны (и MATLAB, и CalculiX предполагают, что внутренняя обсадная колонна всегда разрывается первой).

Хорошее совпадение с границами микрокольца достигается при степени гидратации χ=35% и прочности на сжатие на 10% ниже первоначально рассчитанного значения, т.е. fc=14,7 МПа.

После добавления нового, слегка обновленного набора свойств в обе модели мы получаем хорошую оценку того, когда появится внутреннее микрокольцо и насколько оно станет широким. Интересно, что обе оценки похожи, даже несмотря на то, что MATLAB правильно вычисляет открытие гэпа, используя контактную формулировку; Вместо этого CalculiX полагается на тонкий слой материала, предназначенного только для сжатия, для имитации разрыхления.

Конечно, разные стратегии решения не эквивалентны: MATLAB на самом деле не предполагает, что напряженное состояние прилипает к поверхности текучести (т. е. невязка всегда ≤0), поэтому при определенных обстоятельствах оно может проскользнуть. Небольшие отклонения от фактической поверхности не влияют на результаты, но большие ошибки, такие как наблюдаемые на внутреннем радиусе цемента ближе к концу эксперимента, снижают точность модели MATLAB.