Дисциплина: «Техническая механика» — Студопедия.Нет
Практическая работа № 3.
Тема: Реакции опор двухопорной балки
Цель: Знать три формы уравнений равновесия и уметь ими пользоваться при определении реакций в опорах балочных систем.
Актуализация знаний :
1. Что такое пара сил?
2. Что такое момент пары сил, плечо пары сил?
3. Сформулируйте условие равновесия системы пар сил.
4. Что такое момент силы относительно точки? Как берется знак момента силы относительно точки? Что называется плечом силы?
5. В каком случае момент силы относительно точки равен нулю?
6. Что такое главный вектор и главный момент плоской системы сил?
7. Сформулируйте теорему Вариньона.
Рекомендуемая литература:
1. Аркуша А.И. Техническая механика. Теоретическая механика и сопротивление материалов. – М.: Высшая школа, 2002.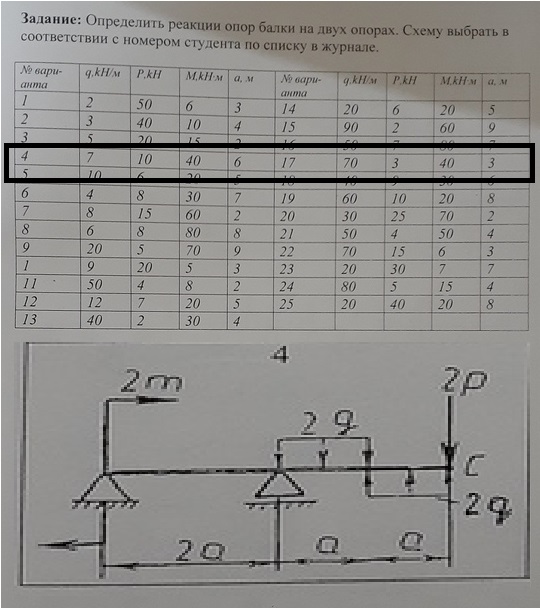
2. Олофинская В.П. Техническая механика: Сборник тестовых заданий. – М.: Форум-Инфра-М, 2002.
Порядок выполнения работы:
Теоретическая часть
Основны формулы и предпосылки расчета
Виды опор балок и их реакции (рис1
Рис.1
Моменты пары сил и силы относительно точки (рис2)
| Главный момент |
Задание 1.Определить величины реакций для балки с шарнирными опорами. Провести проверку правильности решения.
Задание 2. Определить величины реакций в шарнирных опорах балки. Провести проверку правильности решения.
Пример решения задач
ЗадачаДвухопорная балка с шарнирными опорами А и В нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой сил с моментом т (рис. 3а). Определить реакции опор.
3а). Определить реакции опор.
Решение
1. Левая опора (точка А) — подвижный шарнир, здесь реакция направлена перпендикулярно опорной поверхности.
Правая опора (точка В) — неподвижный шарнир, здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем с продольной осью балки.
2. Поскольку на схеме возникнут две неизвестные вертикальные реакции, использовать первую форму уравнений равновесия нецелесообразно.
3. Заменяем распределенную нагрузку сосредоточенной:
Сосредоточенную силу помещаем в середине пролета, далее задача решается с сосредоточенными силами (рис. 6.86).
4. Наносим возможные реакции в опорах (направление произвольное).
5. Для решения выбираем уравнение равновесия в виде
6. Составляем уравнения моментов относительно точек крепления:
Реакция направлена верно.
Реакция отрицательная, следовательно, RAyнужно направить в противоположную сторону.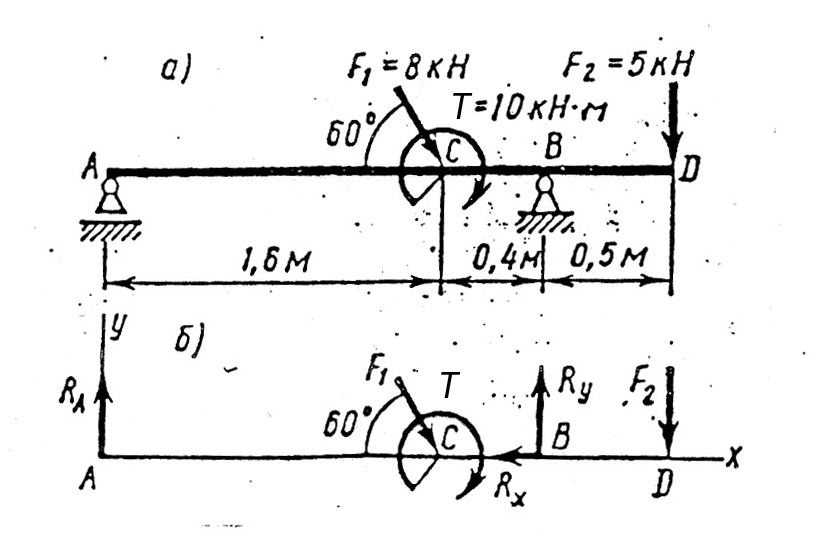
7. Используя уравнение проекций, получим:
Rbx— горизонтальная реакция в опоре В.
Реакция отрицательна, следовательно, на схеме ее направление будет противоположно выбранному.
8. Проверка правильности решения. Для этого используем четвертое уравнение равновесия Σ Fky =0
— RAy — G + RBy — F cos 45° = 0.
Подставим полученные значения реакций.
Если условие выполнено, решение верно:
-5,1 — 12 + 34,6 — 25 · 0,7 = 0.
Контрольные вопросы
1. Сформулируйте аналитическое условие равновесия плоской системы произвольно расположенных сил.
2. Укажите три вида уравнений равновесия плоской системы произвольно расположенных сил.
3. Какие нагрузки называются сосредоточенными и распределенными?
4. Что такое интенсивность равномерно распределенной нагрузки?
5. Как найти числовое значение направления и точку приложения равнодействующей равномерно распределенной нагрузки
Как найти числовое значение направления и точку приложения равнодействующей равномерно распределенной нагрузки
Министерство образования и науки Донецкой Народной Республики
ГПОУ «Донецкий горный техникум им. Е.Т. Абакумова»
Решение задач Определение 📝 величин реакций для балки техническая механи
1. Сколько стоит помощь?
Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.
2. Каковы сроки?
Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат. Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.
Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.
3. Выполняете ли вы срочные заказы?
Да, у нас большой опыт выполнения срочных заказов.
4. Если потребуется доработка или дополнительная консультация, это бесплатно?
Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.
5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?
Да, конечно — оценка стоимости бесплатна и ни к чему вас не обязывает.
6. Каким способом можно произвести оплату?
Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т.д.
7. Предоставляете ли вы гарантии на услуги?
На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.
8. Какой у вас режим работы?
Мы принимаем заявки 7 дней в неделю, 24 часа в сутки.
Практическое занятие №2.
 Плоская система произвольно расположенных сил
Плоская система произвольно расположенных силЗнать теорему Пуансо о приведении силы к точке.
Уметь приводить произвольную плоскую систему сил к точке, определяя величины главного вектора и главного момента системы.
Знать три формы уравнений равновесия и уметь ими пользоваться при определении реакций в опорах балочных систем.
Основные формулы и предпосылки расчета
Виды опор балок и их реакции (рис. П2.1)
Моменты пары сил и силы относительно точки (рис. П2.2)
Главный вектор
Главный момент
Условия равновесия
Проверка:
Проверка:
Упражнения при подготовке к самостоятельной работе
4. Перенести силу F в точку А, используя теорему Пуансо (рис. П2.3).
F = 20кН; АВ = 6м; ВС = 2м.
2. Привести систему сил к точке В, определить главный вектор и главный момент системы сил (рис. П2.4). АВ = 2м; ВС = 1,5м; CD = 1м. F1 = 18кН; F2 = 10кН; F3 = 30кН; т = 36кН-м.
3. Система сил находится в равновесии. Определить величину момента пары т (рис. П2.5).
F1 = F1’ = 10 кН; F2 = F2’ = 20кН.
4. Нанести реакции в опорах балок 1 и 2 (рис. П2.6).
5. Определить величину реакции в опоре А. Приложена распределенная нагрузка интенсивностью q = 5кН/м (рис. П2.7).
6. Записать систему уравнений равновесия для определения реакций в опоре защемленной балки.
7. Записать систему уравнений равновесия для определения реакций в опорах двухопорной балки, закрепленной на двух шарнирах.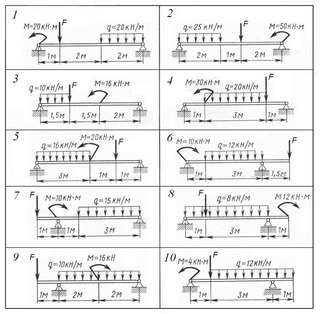
Расчетно-графическая работа №2. Определение реакций в опорах балочных систем под действием сосредоточенных сил и пар сил
Задание 1. Определить величины реакций в опоре защемленной балки. Провести проверку правильности решения.
Расчетно-графическая работа №3. Определение величин реакций в опорах балочных систем под действием сосредоточенных и распределенных нагрузок
Задание 1. Определить величины реакций в заделке. Провести проверку правильности решения.
Задание 2. Определить величины реакций в шарнирных опорах балки.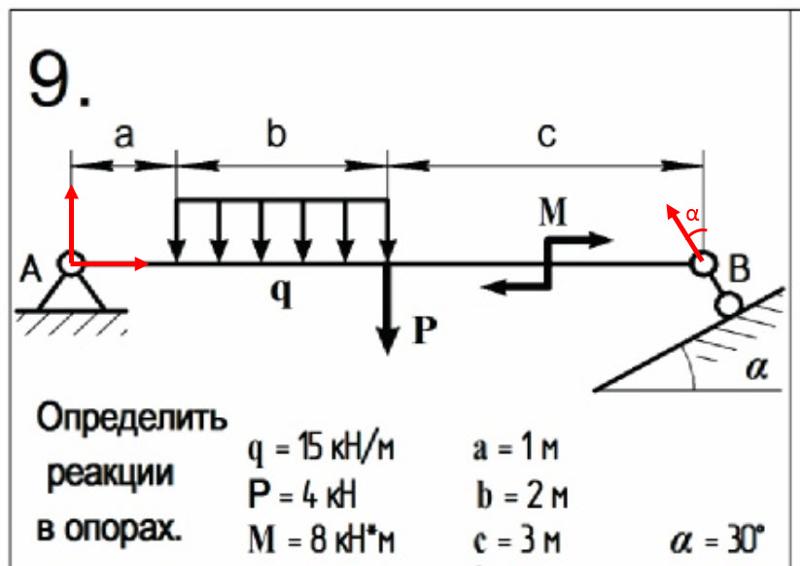 Провести проверку правильности решения.
Провести проверку правильности решения.
При защите работ ответить на вопросы карт с тестовыми заданиями.
Тема 1.4. Статика. Произвольная плоская система сил
Задание для самостоятельной работы 2.
Определить опорные реакции балки на двух опорах по данным одного из вариантов, показанных на схемах. Проверить правильность их определения.
ЛЕКЦИЯ 9
Тема 1.7. Основные понятия кинематики. Кинематика точки
Иметь представление о пространстве, времени, траектории, пути, скорости и ускорении.
Знать способы задания движения точки (естественный и координатный).
Знать обозначения, единицы измерения, взаимосвязь кинематических параметров движения, формулы для определения скоростей и ускорений (без вывода).
Кинематика рассматривает движение как перемещение в пространстве. Причины, вызывающие движение, не рассматриваются. Кинематика устанавливает способы задания движения и определяет методы определения кинематических параметров движения.
Тема 1.4. Плоская система произвольно — FINDOUT.SU
Расположенных сил
Знать теорему Пуансо о приведении силы к точке.
Уметь приводить произвольную плоскую систему сил к точке, определяя величины главного вектора и главного момента системы.
Знать три формы уравнений равновесия и уметь ими пользоваться при определении реакций в опорах балочных систем.
Основные формулы и предпосылки расчета
138 Практическое занятие 2
Главный момент
Упражнения при подготовке к самостоятельной
Работе
1. Перенести силу F в точку А, используя теорему Пуансон (рис. П2.3). F = 20 кН; АВ = 6 м; ВС = 2 м.
Перенести силу F в точку А, используя теорему Пуансон (рис. П2.3). F = 20 кН; АВ = 6 м; ВС = 2 м.
2. Привести систему сил к точке В, определить главный вектор
и главный момент системы сил (рис. П2.4). АВ = 2 м; ВС = 1,5 м;
CD = 1м. F 1 = 18 кН; F 2= 10 кН; F3 = 30 кН; т = 36кН∙м.
Практическое занятие 2 139
3. Система сил находится в равновесии. Определить величину
момента пары т (рис. П2.5). F 1 = F’1 = 10кН; F2 = F’2= 20 кН.
4. Нанести реакции в опорах балок 1 и 2 (рис. П2.6).
5. Определить величину реакции в опоре А. Приложена распределенная нагрузка интенсивностью q = 5кН/м (рис. П2.7).
6. Записать систему уравнений равновесия для определения реакций в опоре защемленной балки.
7. Записать систему уравнений равновесия для определения реакций в опорах двухопорной балки, закрепленной на двух шарнирах.
140 Практическое занятие 2
Расчетно-графическая работа 1
Определение реакций в опорах балочных систем под действием сосредоточенных сил и пар сил
Задание 1. Определить величины реакций в опоре защемленной балки. Провести проверку правильности решения.
Практическое занятие 2 141
Задание 2. Определить величины реакций для балки с шарнирными опорами. Провести проверку правильности решения.
142 Практическое занятие 2
Расчетно-графическая работа 2
Определение величин реакций в опорах балочных систем под действием сосредоточенных и распределенных нагрузок
Задание 1. Определить величины реакций в заделке. Провести проверку правильности решения.
Определить величины реакций в заделке. Провести проверку правильности решения.
Практическое занятие 2 143
Задание 2. Определить величины реакций в шарнирных опорах балки. Провести проверку правильности решения.
При защите работ ответить на вопросы карт с тестовыми заданиями.
144 Практическое занятие 2
Тема 1.4. Статика.
Произвольная плоская система сил
Практическое занятие 2 145
146 Практическое занятие 3
Практическое занятие 3
Тема 1.6. Центр тяжести
Знать методы определения центра тяжести тела и плоских сечений, формулы для определения положения ЦТ плоских сечений.
Уметь определять положение центра тяжести сложных геометрических фигур, определять положение центра тяжести фигур, составленных из стандартных профилей.
Основные формулы и предпосылки расчета
Центры тяжести простейших сечений (рис. П3.1)
Геометрические характеристики стандартных прокатных профилей в Приложении 2.
Методы расчета:
1) метод симметрии;
2) метод разделения на простые части;
3) метод отрицательных площадей.
Координаты центров тяжести сложных и составных сечений:
где Ak — площади частей сечения; xk; y k — координаты ЦТ частей cечения; А —
n
суммарная площадь сечения, А = ∑ Ак .
0
Практическое занятие 3 147
Упражнения при подготовке к самостоятельной
Работе
1. Определить положение центра тяжести каждой из фигур, составляющих сечение (рис. П3.2). Размеры на чертеже указаны в мм.
Определить положение центра тяжести каждой из фигур, составляющих сечение (рис. П3.2). Размеры на чертеже указаны в мм.
2. Определить координату х с изображенного сечения (рис. ПЗ.З).
Замечание. Сечение расчленить на три части.
3. Сколько координат центра тяжести нужно определять расчетным путем для каждого из изображенных сечений (рис. П3.4)?
4. По таблицам ГОСТ определить необходимые параметры сечений (рис. П3.5).
5. Определить координату у с фигуры (рис. П3.5).
6. Какая характеристика сечения определяется по указанной формуле?
148 Практическое занятие 3
Расчетно-графическая работа
Задание 1. Определить координаты центра тяжести заданного сечения.
Практическое занятие 3 149
Задание 2. Определить координаты центра тяжести составного сечения. Сечения состоят из листов с поперечными размерами а х 6 и прокатных профилей по ГОСТ 8239-89, ГОСТ 8240-89 и ГОСТ 8509-86. Уголок выбирается наименьшей толщины.
Определить координаты центра тяжести составного сечения. Сечения состоят из листов с поперечными размерами а х 6 и прокатных профилей по ГОСТ 8239-89, ГОСТ 8240-89 и ГОСТ 8509-86. Уголок выбирается наименьшей толщины.
Размеры стандартных профилей в Приложении 1.
150 Практическое занятие 3
При защите работ ответить на вопросы тестового задания.
Тема 1.6. Статика.
Центр тяжести тела
Практическое занятие 3 151
152 Практическое занятие 4
Практическое занятие 4
Практическая работа. Тема: Определение реакций опор для балочных систем
ПРИМЕРЫ построения эпюр внутренних силовых факторов. Шарнирно закреплённые балки Балка, закреплённая с помощью шарниров, должна иметь не менее двух точек опоры. Поэтому в случае шарнирно закреплённых (шарнирно
Шарнирно закреплённые балки Балка, закреплённая с помощью шарниров, должна иметь не менее двух точек опоры. Поэтому в случае шарнирно закреплённых (шарнирно
ПРИМЕРЫ построения эпюр внутренних силовых факторов 1. Консольные балки Термин консо ль произошёл от французского слова console, которое, в свою очередь, имеет латинское происхождение: в латинском языке
Подробнее4.4. Определение усилий в стержнях, поддерживающих
00 Пространственная система сил Раздел 0. z T α x Q N y F = 0.N, T = 70, T = 7, P = 0, d P = 0, P =, B Q = 0, G =, A α = 0, R =, R = 8, R = 9, T =, =, =, d =. Ответы N X A Z A X B Z B 9.8 9.98. 70.7.7.000
ПодробнееНАХОЖДЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ
Департамент образования города Москвы ГОУ СПО Технический пожарно-спасательный колледж 57 НАХОЖДЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ Методические указания к лабораторной работе по дисциплине «Техническая
ПодробнееЧасть 1 Сопротивление материалов
Часть Сопротивление материалов Рисунок Правило знаков Проверки построения эпюр: Эпюра поперечных сил: Если на балке имеются сосредоточенные силы, то на эпюре, должен быть скачок на величину и по направлению
ПодробнееСБОРНИК ЗАДАЧ ПО ТЕХНИЧЕСКОЙ МЕХАНИКЕ
ÑÐÅÄÍÅÅ ÏÐÎÔÅÑÑÈÎÍÀËÜÍÎÅ ÎÁÐÀÇÎÂÀÍÈÅ В. И. СЕТКОВ СБОРНИК ЗАДАЧ ПО ТЕХНИЧЕСКОЙ МЕХАНИКЕ Рекомендовано Федеральным государственным учреждением «Федеральный институт развития образования» в качестве учебного
И. СЕТКОВ СБОРНИК ЗАДАЧ ПО ТЕХНИЧЕСКОЙ МЕХАНИКЕ Рекомендовано Федеральным государственным учреждением «Федеральный институт развития образования» в качестве учебного
В. К. Манжосов, О. Д. Новикова
Строительный факультет УлГТу В. К. Манжосов, О. Д. Новикова ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ, СТАТИКА Методические указания УЛЬЯНОВСК 2009 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ПодробнееP 1 = = 0 0,1L1 0,3L1 0, 2L2 0,1L
Расчёт статически определимой многопролётной балки на неподвижную и подвижную нагрузки Исходные данные: расстояния между опорами L = 5, м L = 6, м L = 7,6м L4 = 4,5м сосредоточенные силы = 4кН = 6 распределённые
ПодробнееСОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ Кафедра строительной
ПодробнееВВЕДЕНИЕ.
 Кафедра ТПМ ДонНАСА
Кафедра ТПМ ДонНАСАВВЕДЕНИЕ Условие каждого задания контрольной или расчетно-графической работы сопровождается десятью рисунками и одной таблицей числовых значений заданных величин. Вариант выбирается согласно шифру студента.
ПодробнееРешение: Исходные данные: = 2 = 2 = 2
Задача 1 Для данного бруса требуется: — вычертить расчетную схему в определенном масштабе, указать все размеры и величины нагрузок; — построить эпюру продольных сил; — построить эпюру напряжений; — для
ПодробнееТЕОРЕМА О ТРЕХ СИЛАХ
ТЕОРЕМА О ТРЕХ СИЛАХ Если твердое тело находится в равновесии под действием трех непараллельных сил, то линии действия этих сил лежат в одной плоскости и пересекаются в одной точке. ТЕОРЕМА О ТРЕХ СИЛАХ
ПодробнееМЕТОДИЧЕСКИЕ УКАЗАНИЯ
Министерство образования Российской Федерации ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра теории механизмов и машин Л. И. Кудина МЕТОДИЧЕСКИЕ УКАЗАНИЯ и варианты заданий для выполнения контрольной
И. Кудина МЕТОДИЧЕСКИЕ УКАЗАНИЯ и варианты заданий для выполнения контрольной
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика.
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА 1.1. Статика. Статикой называется раздел механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных тел, находящихся под действием сил. Абсолютно
Подробнее+ R A = 0. P(y) = 0; R B
Исходные данные для проведения расчётов: d = 2 м, F 1 = 2 кн, F 2 = 4 кн, F 3 = 5 кн. Найти: усилия в стрежнях 8, 10 и 15. Решение: Выбираем и проводим оси координат. 1. Определяем является ли система
Подробнее), движется равномерно
РАВНОВЕСИЕ ТЕЛ Раздел механики, в котором изучается равновесие тел, называется статикой Равновесным называется состояние тела, неизменное во времени, т е равновесие это такое состояние тела, при котором
ПодробнееЛИНИИ ВЛИЯНИЯ ВНУТРЕННИХ УСИЛИЙ
Глава 7 ЛИНИИ ВЛИЯНИЯ ВНУТРЕННИХ УСИЛИЙ Значения реакций опор конструкции или усилие к каком-либо ее элементе зависят от места приложения нагрузки и ее величины. Исследование этой зависимости необходимо
Исследование этой зависимости необходимо
РАСЧЕТ ТРЕХШАРНИРНЫХ АРОК
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ В. К. Манжосов
ПодробнееТЕОРЕТИЧЕСКАЯ МЕХАНИКА
АСТРАХАНСКИЙ ГОСУДАРСТВЕНННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра теоретической и прикладной механики В.И. Локтев, О.Н. Синельщикова, О.А. Хохлова ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Методическое пособие для подготовки
ПодробнееСТРОИТЕЛЬНАЯ МЕХАНИКА
Томский государственный архитектурно-строительный университет (ТГАСУ) кафедра строительной механики СТРОИТЕЛЬНАЯ МЕХАНИКА Тухфатуллин Борис Ахатович, к.т.н., доцент Томск — 2017 РАСЧЕТНАЯ СХЕМА СООРУЖЕНИЯ
ПодробнееСТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
Глава 8 СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ 8.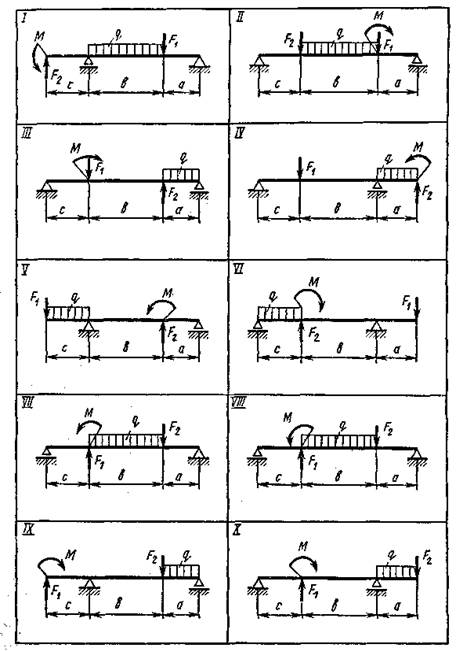 1. Шарнирно закрепленное твердое тело на упругих стержнях Постановка задачи. Определить усилия в стержнях статически неопределимой системы, состоящей из шарнирно
1. Шарнирно закрепленное твердое тело на упругих стержнях Постановка задачи. Определить усилия в стержнях статически неопределимой системы, состоящей из шарнирно
ОПД.Ф СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
ОГЛАВЛЕНИЕ ОПДФ СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ РАСЧЕТ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ПОПЕРЕЧНЫХ СЕЧЕНИЙ ПРОСТЕЙШИХ ФОРМ Методические указания к решению задач и выполнению расчетно-графической работы Предисловие
ПодробнееПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный университет путей сообщения» Кафедра строительной механики Б.П. ДЕРЖАВИН,
ПодробнееСОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Государственный комитет Российской Федерации по высшему образованию Казанский государственный технологический университет СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ Методические указания к самостоятельной работе студентов
ПодробнееТЕОРЕТИЧЕСКАЯ МЕХАНИКА
АСТРАХАНСКИЙ ГОСУДАРСТВЕНННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра теоретической и прикладной механики В.И. Локтев, М.А. Михайлова ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Пособие по решению типовых задач Часть. Статика Астрахань
Подробнее1.2 Для балки на шарнирных опорах требуется:
1 Определить опорные реакции;
2 Построить эпюры Qy, Mx;
3 Подобрать по Mmax размеры двутаврового сечения;
4 Произвести полную проверку прочности (по нормальным, касательным и эквивалентным напряжениям) для двутаврового сечения.
Исходные данные: [σ] = 160 МПа, [τ] = 80 МПа.
Дано: Балка на шарнирных опорах; L = 1 м; M = 30 кН*м; q= 40 кН/м; F = 50 кН (см. приложение Б).
1 Определение опорных реакций
Так как в данной задаче балка закреплена при помощи двух опор – шарнирно-неподвижной и шарнирно-подвижной, то для начала необходимо будет определить величины и направления реакций, возникающих в этих опорах: HB, RB и RC.
Для этого надо составить уравнения равновесия, определив из них значения опорных реакций. При этом из расчетной схемы балки видно, что реакция HB = 0, так как на балку не действует ни одна продольная сила.
ΣMB = 0: — q*2L*5L – M — F*5L + RC*4L = 0
Отсюда RC = (q*2L*5L + M + F*5L) /(4L) = (40*2*5 + 30 + 50*5*1) /(4*1) = + 170 кН
ΣMC = 0: q*L*2L + M + F*L + RB*4L = 0
Отсюда RB = — (q*L*2L + M + F*L) /(4*L) = — (40*1*2 + 30 + 50*1) /(4*1) = — 40 кН
Положительные значения свидетельствуют о том, что первоначальное направление реакций выбрано верно. Отрицательные означают, что необходимо поменять первоначально выбранное направление данной реакции на противоположное.
Итак, проверим, правильно ли найдены непосредственно значения реакций RB и RC:
ΣFY = 0: — q*2L – F — RB + RC = 0
— 40*2 – 50 — 40 + 170 = 0
— 170 + 170 = 0
0 = 0
Отсюда вино, что, раз проверка сходится, то значения и направления реакций RB и RC найдены верно.
2 Построение эпюр Qy, Mx
Теперь можно переходить к рассмотрению каждой из составных частей балки. Необходимо будет сделать разрезы в каждой из них. Затем, отбросив одну из частей, заменить ее действие соответствующим изгибающим моментом Mx и поперечной силой Qy – разумеется, следуя общепринятому правилу знаков.
Итак, рассмотрим каждый из участков – всего их будет 3 (см. приложение Б), и составим уравнения поперечных сил и изгибающих моментов на каждом из них:
I участок: 0 ≤ z1 ≤ 4L
Qy(z1) = — RB = — 40 кН = const
Mx(z1) = + M – RB*z1 (линейное уравнение)
Тогда Mx(z1 = 0) = + 30— 40*0 = 30 кНм
Mx(z1 = 4L = 4) = + 30— 40*4 = — 130 кНм
II участок: 0 ≤ z2 ≤ L
Qy(z2) = RC — RB — q*z2 (линейное уравнение)
Тогда Qy (z2 = 0) = 170 – 40 – 40*0 = 130 кН
Qy (z2 = L = 1) = 170 – 40 – 40*1 = 90 кН
Mx(z2) = RC*z2 — — RB*(z2 + 4) + M (квадратное уравнение)
Тогда Mx(z2 = 0) = 170*0 — — 40*(0 + 4) + 30 = — 130 кНм
Mx(z2 = L = 1) = 170*1 — — 40*(1 + 4) + 30 = — 20 кНм
III участок: 0 ≤ z3 ≤ L
Qy(z3) = RC — RB — F – q*(z3 + 1) (линейное уравнение)
Тогда Qy (z3 = 0) = 170 — 40 — 50 – 40*(0 + 1) = 40 кН
Qy (z3 = L = 1) = 170 — 40 — 50 – 40*(1 + 1) = 0
Mx(z3) = RC*(z3 + 1) — F*z3 – q*–RB*(z3 + 5) +M (квадратное уравнение)
Тогда Mx(z3 = 0) = 170*(0 + 1) — 50*0 – 40*– 40*(0 + 5) +30 = — 20 кНм
Mx(z3 = L = 1) = 170*(1 + 1) — 50*1 – 40*– 40*(1 + 5) +30 = 0
По полученным значениям строятся соответственно эпюры Qy и Mx (см. приложение Б).
Контрольная работа по «Технической механике»
Содержание
Задача № 1. . . . . . . . . . 2
Задача № 2. . . . . . . . . . 4
Задача № 3. . . . . . . . . . 6
Задача № 4. . . . . . . . . . 8
Задача № 5. . . . . . . . . . 11
Литература . . . . . . . . . 13
Задача № 1
Определить величины реакций в опоре защемлённой балки, нагружен-ной силами F1, F2 и парой сил с моментом m. Провести проверку правильности реакций.
Дано: F1 = 10 кН; F2 = 4,4 кН; m = 14 кН⸳м; а = 0,2 м.
[pic 1]
Рисунок 1.1.
Решение. Разобьём балку на 3 участка.
[pic 2]
Рис. 1.2.
Сила в сечении I:
[pic 3]
Сила в сечении II:
[pic 4][pic 5]
Сила в сечении III:
[pic 6]
Сила F1 приложена под углом, поэтому в заделке имеется сила, приложенная по оси Z
[pic 7] откуда
[pic 8]
Изгибающий момент в точке С
[pic 9]
Изгибающий момент в сечении I:
[pic 10]
Изгибающий момент в сечении II:
[pic 11]
при z2 = 0 м [pic 12]
при z2 = 0,4 м [pic 13]
Изгибающий момент в сечении III:
[pic 14]
при z3 = 0 м [pic 15]
при z3 = 0,4 м [pic 16]
Балка неподвижна, поэтому должно соблюдаться условие – момент относительно любой точки равен нулю. Рассчитаем момент относительно точки В
[pic 17][pic 18]
Задача № 2.
Определить величины реакций в шарнирных опорах балки, нагружен-ной силой F, распределённой нагрузкой q, и парой сил с моментом m. Провести проверку правильности решения.
Дано: F = 10 кН; q = 2 кН/м; m = 15 кН⸳м; a = 0,4 м.
[pic 19]
Рисунок 2.1.
Решение.
Заменим равномерно распределённую нагрузку её равнодействующей, приложенной посередине отрезка длинной 2а
[pic 20].
[pic 21]
Рис. 2.2.
Освободим балку от связей, заменив их реакциями связей [pic 22], [pic 23], [pic 24]. При этом учтём наличие в опоре В горизонтальной составляющей, так как сила F приложена под углом. В опоре А нет горизонтальной составляющей, так как сила реакции направлена перпендикулярно плоскости опоры.
Для определения неизвестных реакций составим два уравнения равновесия моментов сил: относительно опоры А и опоры В
[pic 25] и [pic 26].
Уравнение моментов относительно опоры А:
[pic 27],
откуда
[pic 28]
[pic 29]
Уравнение моментов относительно точки В:
[pic 30]
[pic 31][pic 32] [pic 33][pic 34] Для проверки правильности найденных реакций опор составим уравнение проекций сил на вертикальную ось Y
[pic 35]
[pic 36]
Расчет опорных реакций для нависающей балки
Задача 4-2
Просто поддерживаемая балка, показанная на рис. 4-2 (а), имеет выступающую часть на одной боковая сторона. Найдите реакции у опор.
Рисунок 4-2 (а)
Решение:
Данная балка имеет шарнирную опору при A и роликовой опоры в B. Схема свободного тела приведена на Рисунок 4-2 (b), на котором показаны 2 реакции в точке A и одна реакция в точке B.( г. Ось x и ось y показаны на рисунке, а ось z — перпендикулярно плоскости x-y.) Есть три уравнения статическое равновесие ΣF x = 0, ΣF y = 0, ΣM z = 0; доступны для этой 2-х мерной конструкции. Количество неизвестные компоненты реакции равны уравнениям статического равновесие. Следовательно, этот луч статически определен.
Применяя уравнения статики равновесие:
ΣF x = 0; А x = 0; (ур.1)
ΣF y = 0; A y + B y 25 5 4 = 0;
A y + B y = 45 кН; (ур. 2)
Учитывая ось z, проходящую через A, и принимая момент всех сил вокруг оси z (принимая по часовой стрелке ve и против часовой стрелки + ve) ;
ΣM z = 0; Б л 6 25 10 5 4 4 = 0 (ур.3)
Решение уравнения. 3 урожая B y = 55 кН;
Подставляем значение B y в экв. 2 дает A y = 10 кН.
Знак 5 реакции указывает на то, что A y будет в направлении вниз а не вверх, как показано на диаграмме свободного тела.
Вы также можете использовать наш калькулятор выступающей балки для определения значений опорных реакций
Вы можете посетить следующие ссылки на решенные примеры по расчету изгибающего момента и поперечной силы и построению диаграммНепрерывная балка — опорные силы момента и реакции
Непрерывная балка с распределенной нагрузкой
Для неразрезной балки с 3, 4 или 5 опорами и распределенной нагрузкой силы реакции опоры могут быть рассчитаны как
R = c r q L (1)
где
R = сила реакции опоры (Н, фунт f )
c r = коэффициент силы реакции опоры из рисунка выше
q = распределенная нагрузка (Н / м, фунт f / фут)
L = длина пролета (м, фут)
Моменты могут быть рассчитаны как
M = c м q L 2 (2)
где
M = момент балки (Нм, фунт f фут)
c м = моментный коэффициент f из рисунка выше
Пример — Непрерывная балка с распределенной нагрузкой
Силы реакции в концевых опорах для неразрезной балки с 3 опорами и распределенной нагрузкой 1000 Н / м можно рассчитать как
R конец = (0.375) (1000 Н / м)
= 375 Н
= 0,38 кН
Силу реакции в центральной опоре можно рассчитать как
R центр = (1,250) (1000 Н / м)
= 1250 Н
= 1,25 кН
Моменты балки в середине пролета с длиной пролета 1 м можно рассчитать как
M конец = (0.070) (1000 Н / м) (1 м) 2
= 70 Нм
Момент балки в центральной опоре можно рассчитать как
M центр = (0,125) (1000 Н / м) (1 м) 2
= 125 Нм
Сплошная балка с точечными нагрузками
Для неразрезной балки с 3, 4 или 5 опорами и точечными нагрузками силы реакции опоры могут рассчитывается как
R = c r F (3)
где
c r = коэффициент опорной силы реакции из рисунка выше
F = точечная нагрузка (Н, фунт f )
Моменты могут быть рассчитаны как
M = c m FL (4)
где
c m = моментный коэффициент из рисунка выше
Пример — Сплошная балка с точечными нагрузками
Силы реакции в концевых опорах для неразрезной балки с 3 опорами и точечными нагрузками 2 1000 Н можно рассчитать как
R конец = (0.313) (1000 Н)
= 313 Н
= 0,31 кН
Силу реакции в центральной опоре можно рассчитать как
R центр = (1,375) (1000 Н)
= 1375 Н
= 1,4 кН
Моменты балки при точечных нагрузках с длиной пролета 1 м можно рассчитать как
M конец = (0.156) (1000 Н) (1 м)
= 156 Нм
Момент балки в центральной опоре можно рассчитать как
M центр = (0,188) (1000 Н) (1 м )
= 188 Нм
5.5 Метод сопряженного пучка
>> Когда вы закончите читать этот раздел, проверьте свое понимание с помощью интерактивной викторины внизу страницы.
Метод сопряженных балок предоставляет другой способ нахождения наклонов (поворотов) и прогибов определенных балок.Он использует аналогичный набор соотношений, которые существуют между нагрузкой ($ w $) — сдвигом ($ V $) — моментом ($ M $) и кривизной ($ \ phi $) — наклоном ($ \ theta $) — прогибом. ($ \ Delta $). Вспомните отношения между нагрузкой, сдвигом и моментом (уравнения \ eqref {eq: shear-int} и \ eqref {eq: moment-int} из раздела 4.3):
\ begin {align} V (x) & = \ int w (x) \, dx \ label {eq: shear-int} \ tag {1} \\ M (x) & = \ int V (x) \ , dx \ label {eq: moment-int} \ tag {2} \ end {align}
Аналогичным образом вспомните отношения между кривизной, наклоном и прогибом из уравнений \ eqref {eq: curv-slope} и \ eqref {eq: slope-defl}:
\ begin {align} \ theta (x) & = \ int \ phi (x) \, dx \ label {eq: curv-slope} \ tag {3} \\ \ Delta (x) & = \ int \ theta (x) \, dx \ label {eq: slope-defl} \ tag {4} \ end {align}
Здесь есть четкая параллель между двумя наборами отношений.Это показано на Рисунке 5.9. Этот рисунок предполагает, что, если бы мы могли каким-то образом рассматривать диаграмму кривизны, как если бы это была диаграмма нагружения, то мы могли бы определить наклон и прогиб с помощью графического интегрирования, того же метода, который мы в настоящее время можем использовать для определения сдвигов и моментов. Это потенциально может быть простым способом найти уклоны и отклонения.
Рисунок 5.9: Параллельные отношения между нагрузкой / сдвигом / моментом и кривизной / наклоном / прогибом
Итак, давайте создадим сопряженную балку с той же геометрией, что и реальная балка, но с учетом кривизны как нагрузок.В этой новой сопряженной балке «сдвиги» на самом деле будут наклонами реальной балки, а «моменты» — фактически отклонениями реальной балки (с использованием соотношений, показанных на рис. 5.9). Звучит просто, но есть одна проблема: если в этой балке сопряженные срезы представляют реальные уклоны, а сопряженные моменты представляют собой реальные прогибы, то нам также необходимо преобразовать наши граничные условия, чтобы они одинаково влияли на срез и момент в сопряженной балке, как граничные условия на наклон и прогиб в реальной балке.Этот процесс преобразования опор в сопряженные балки показан на рисунке 5.10.
Рисунок 5.10: Преобразование типов опор для анализа методом сопряженных пучков
На рис. 5.10 показаны эквивалентные сопряженные опоры для каждой данной реальной опоры. Например, фиксированный конец реальной балки ограничивает как вращение, так и отклонение ($ \ Delta $ и $ \ theta $ равны нулю на фиксированной опоре). Следовательно, для эквивалентной сопряженной опоры нам нужна опора, которая имеет нулевой сдвиг (эквивалентный нулевому вращению в реальной балке) и нулевой момент (эквивалентный нулевому прогибу в реальной балке).Единственная поддержка, которая соответствует этим требованиям, — это отсутствие поддержки (бесплатная часть). Таким образом, любая неподвижная опора в реальной балке будет заменена свободным концом в сопряженной балке.
Точно так же штифты и ролики на конце реальной балки допускают вращение ($ \ theta \ neq 0 $), но ограничивают отклонение ($ \ Delta = 0 $). Следовательно, для эквивалентной сопряженной опоры нам нужна опора, которая допускает ненулевой сдвиг (обеспечивает вертикальную реакцию), но имеет нулевой момент (не имеет компонента реакции момента).Штифт или ролик также удовлетворяют этим требованиям. Итак, сопряженная опора для штифта или валика в реальной балке — штифт или валик. Обратите внимание, что не имеет значения, выбираете ли вы балку или ролик с точки зрения балки, потому что для проблем с балкой мы обычно не учитываем осевые нагрузки.
Для внутренних опор или опор под балкой штифты (или петли) и ролики также взаимозаменяемы, как и на концах балок; однако условия опоры, которые не находятся на конце балки, немного сложнее, потому что мы должны учитывать, как наклон и сдвиг изменяются в месте опоры, а не только если таковая существует.Для штифта под балкой он допускает вращение, но без отклонения, а наклон балки является непрерывным (в форме балки нет «перегиба»). Это означает, что в сопряженной балке в том же месте должен быть сдвиг в балке, но без момента, и сдвиг должен быть непрерывным (он не должен ступенчато). Напомним, что ступеньки на диаграмме поперечных сил вызваны точечными нагрузками или точечными реакциями, поэтому это означает, что в этом месте сопряженной балки не должно быть опорной реакции. Внутренний шарнир удовлетворяет всем этим требованиям, он передает сдвиг, но не момент, и не имеет связанной с ним внешней опорной реакции, поэтому диаграмма сдвига будет непрерывной в этом месте.
Для внутреннего шарнира в реальной балке верен обратный случай. Он допускает вращение и отклонение (он может двигаться вверх или вниз, так как нет реакции вертикальной опоры). Это также допускает прерывистый уклон в месте расположения петли, то есть балка может иметь изгиб и петлю, что означает, что касательный наклон балки различается с обеих сторон петли. Следовательно, сопряженная опора должна иметь как сдвиг, так и момент и должна иметь прерывистый сдвиг в этом месте на балке.Этим критериям удовлетворяет неразрезная балка с штифтовой опорой. Непрерывность балки позволяет передавать сдвиг и момент, а опорная реакция, обеспечиваемая штифтом, вызывает ступеньку на диаграмме сдвига в этом месте (разрыв в сдвиге).
Некоторые примеры преобразования реальных лучей в сопряженные лучи показаны на рисунке 5.11. Обратите внимание на то, что если реальный луч определен, то сопряженный луч также будет определенным; однако, если реальный луч не определен, то сопряженный луч будет нестабильным, и наоборот.Этот метод наиболее полезен для расчета уклонов и прогибов определенных конструкций.
Рисунок 5.11: Примеры преобразования реального луча в сопряженный луч
Пример
Анализ метода сопряженных пучков будет проиллюстрирован на примере пучка, показанном на рис. 5.12.
Рисунок 5.12: Пример анализа методом сопряженного пучка
Балка, показанная на рис. 5.12, представляет собой простую консольную балку с подпоркой с одноточечной нагрузкой и точечным моментом на конце.Этот луч определен и может быть легко проанализирован с использованием методов из раздела 4.3. Самая трудная часть этого анализа — нахождение реакций на первом этапе. Это можно сделать, сначала проанализировав диаграмму свободного тела элемента CD, чтобы найти реакцию $ C_y $ и сдвиг в шарнире (помня, что момент в C должен быть равен нулю из-за наличия шарнира). Затем диаграмму свободного тела переменного тока можно использовать вместе с перенесенным шарнирным сдвигом, чтобы найти остальные неизвестные реакции.Завершенные диаграммы сдвига и момента для балки показаны на рисунке сразу под балкой. Обратите внимание, что диаграмма моментов равна нулю в месте расположения шарнира, как и ожидалось. Поскольку поперечное сечение и материал для этой балки постоянны ($ EI $ постоянно), диаграмма кривизны ($ \ phi $) — это просто диаграмма моментов, разделенная на $ EI $. Эта диаграмма кривизны показана непосредственно под диаграммой моментов.
Теперь, когда мы построили диаграмму кривизны, мы можем сформировать сопряженную балку (которая показана под диаграммой кривизны).В сопряженной балке изгибы из диаграммы кривизны реальной балки рассматриваются как распределенные нагрузки, а условия опоры преобразуются, как описано в предыдущем разделе и показано на рисунке 5.10. Следовательно, фиксированный конец в точке A становится свободным концом, шарнир в точке C становится опорой для штифта под балкой в этой точке, а концевой ролик в точке D остается роликом.
Первым шагом в анализе сопряженной балки является определение «сил» реакции (которые на самом деле являются кривизной) с использованием глобального равновесия.Результирующие силы реакции показаны на диаграмме свободного тела (FBD) составной балки на рисунке 5.12.
Теперь, рассматривая кривизну как распределенные силы, мы можем построить сопряженную «диаграмму поперечных сил», используя методы из раздела 4.3. Эта диаграмма фактически даст нам наклоны реальной балки. В этом процессе мы должны учитывать площадь под «распределенной нагрузкой», скачки «сдвига» из-за реакций и соответствующий наклон каждой точки на «диаграмме сдвига» (который равен значению нагрузки в таком случае).Полученная диаграмма уклонов ($ \ theta $) показана на рисунке. На этой диаграмме мы должны идентифицировать все уклоны («срезы») в каждой точке балки, а также местоположения любых локальных максимумов или положений нулевого уклона. Все кривые на этой диаграмме являются параболами (поскольку все распределенные нагрузки были линейными). На этой диаграмме показаны реальные уклоны в каждой точке балки (в радианах). Максимальный наклон составляет 103,9 долл. США / EI долл. США, что эквивалентно:
.\ begin {align *} \ frac {103.2} $.
Далее, диаграмма наклона (сопряженная диаграмма «сдвига») может быть графически интегрирована для построения диаграммы прогиба ($ \ Delta $) (или диаграммы сопряженных «моментов»). Этот шаг немного сложнее, потому что теперь мы должны найти области парабол, а не треугольников, используя значения, показанные ранее на рисунке 5.7. В точке A диаграмма наклона имеет нулевое значение, поэтому наклон диаграммы прогиба также равен нулю. Между точкой A и точкой A ‘($ 2.62 \ mathrm {\, m} $ справа от точки A) на диаграмме уклона есть парабола, обозначенная на рисунке буквой «a».3}} {EI} \ end {align *}
Наконец, чтобы добраться до точки максимального отклонения (точка B ‘), нам нужно найти значение частичной параболы’ d ‘. Это сложнее, чем кажется, потому что вспомните, что для областей параболы, показанных на рисунке 5.7, один конец параболической формы должен иметь нулевой наклон. Это не относится к области «d». Следовательно, нам необходимо рассмотреть всю «диаграмму сдвига» между точками B и C, как показано на рисунке 5.13. Площадь «d» может быть вычислена как сумма трех различных площадей.Во-первых, парабола, которая проходит от B до C (с нулевым наклоном в точке C), может быть легко вычислена как $ LM / 3 $. Затем вычтите из нее площадь показанного прямоугольника (высота $ 7,7 / EI $). Это означает, что мы вычли площадь большой параболы над нулевой линией и площадь маленькой параболы над нулевой линией. Таким образом, мы должны снова добавить эту маленькую параболу при использовании $ 2LM / 3 $. Результатом этого является область для ‘d’, равная -72 $ / EI $, что дает общий прогиб в точке B ‘-339 $ / EI $. Поскольку отклонение будет двигаться в противоположном направлении вправо от точки B ‘, мы знаем, что это место максимального отклонения.4})} \\ \ Delta_ {B ‘} & = 13.6 \ mathrm {\, mm} = \ Delta_ {max} \ end {align *}
Рисунок 5.13: Нахождение области сегмента параболы d
Результирующая диаграмма прогиба ($ \ Delta $) на рис. 5.12 полностью состоит из кубических кривых и показывает точную форму смещения балки. Обратите внимание на изгиб формы в точке C (расположение штифта), где наклон резко меняется, как и следовало ожидать.
Примечание. Несмотря на то, что этот пример привел к полным диаграммам сопряженного сдвига и сопряженного момента (реальный наклон и прогиб), также часто используется метод сопряженной балки для определения сдвига и момента в одной точке.Это можно легко сделать, решив непосредственно для внутреннего сопряженного сдвига или сопряженного момента, сделав разрез в сопряженной балке в месте желаемого реального наклона или реального отклонения.
структурное проектирование — Какое значение имеет петля во внутренней структуре балки?
Петля — это точка, вращение которой не ограничено. Для других точек на балке поворот влево от точки должен быть равен повороту вправо от этой же точки; то есть не может быть прерывания во вращениях вдоль балки.
Однако петлине имеют этого ограничения и поэтому допускают прерывистое вращение. А поскольку изгибающий момент создается балкой, которая пытается противостоять изменениям ее кривизны, мы можем сделать вывод, что в шарнире нет внутреннего изгибающего момента.
означает ли это, что изгибающий момент относительно точки B равен нулю
Для ясности: устойчивая конструкция будет иметь нулевой изгибающий момент относительно любой мыслимой точки. Мы склонны выполнять наши вычисления $ \ sum M = 0 $ вокруг опор, потому что это исключает некоторые переменные, но это уравнение равновесия справедливо для любой точки Вселенной.
Но если это так, как мы можем получить ненулевые изгибающие моменты вдоль балки? Ну, это потому, что мы вычисляем внутренний изгибающий момент . А внутренний изгибающий момент рассчитывается как сумма изгибающих моментов по одну сторону от соответствующей точки.
Итак, в середине пролета балки, например, вы вычисляете изгибающий момент, создаваемый всеми нагрузками слева (или справа) от балки, что (обычно) приводит к ненулевому значению, представляющему внутреннюю часть балки. реакция на искривление, ощущаемое в этой точке.
Но шарниры не сопротивляются вращению, поэтому мы знаем, что внутренний изгибающий момент в шарнире равен нулю. Следовательно, изгибающий момент , по обе стороны , шарнира равен нулю. Это то, что отличает петли от других элементов балки. Любая другая точка имеет гарантированный нулевой внешний изгибающий момент (сумма всех нагрузок по всей конструкции), но только петли имеют гарантированный нулевой внутренний изгибающий момент (сумма всех нагрузок слева от петли равна нулю).
Реакции шарнирных опор
Возможность рассчитать силы, действующие на балку, с помощью моментов, помогает нам определить реакции опор, когда балки (или мосты) имеют несколько нагрузок, действующих на них. В этом примере представьте балку длиной 12 м с нагрузкой 60 кг на расстоянии 6 м от одного конца и нагрузкой 40 кг на расстоянии 9 м от того же конца n, т.е. F1 = 60 кг, F2 = 40 кг, d1 = 6 м и d2 = 9 м
Компьютеры ECS предоставили Мы предоставляем как компьютерное оборудование, так и техническую поддержку в течение нескольких лет в отношении нашей большой сети компьютеров, как в офисе, так и подключенных к дому.За это время мы приобрели ряд настольных ПК, изготовленных по индивидуальному заказу, и все они были своевременно поставлены с высококачественным продуктом по …
31 декабря 2020 г. · Gartner — ведущая в мире исследовательская и консультационная компания. . Мы снабжаем бизнес-лидеров незаменимыми идеями, советами и инструментами для достижения их критически важных приоритетов сегодня и построения успешных организаций завтрашнего дня.
реакций и приложенных нагрузок, которые разрешены в вертикальном и горизонтальном направлениях, показанных на рис.47.2b. Из геометрии можно рассчитать, что B y = B x 1. Уравнение (47.2) можно использовать для определения величины опорных реакций. Принимая момент около B, получаем 10A y — 346,4 ¥ 5 = 0, откуда A y = 173,2 кН Приравнивая сумму …
Штифтовая опора — очень распространенный тип опоры, и ее чаще всего сравнивают с шарниром в (посередине) Структурное трехмерное изображение и (справа) реакции, связанные с этим типом поддержки …
При возникновении любых трудностей при использовании этого сайта с программой чтения с экрана или из-за инвалидности, пожалуйста, свяжитесь с нами по телефону 1-800-444-3353 или [адрес электронной почты защищен ] Для потребителей из Калифорнии: дополнительная информация о нашей политике конфиденциальности.Пренебрегая весами опорных элементов, определите составляющую шарнирных сил в точках A и F.
Подставив в mg = 500 Н и T 2 = 4000 Н, мы получим, что T 1 = 9100 Н. Зная значение T 1 позволит вам вычислить значение вертикальной составляющей петли V в уравнении для и значение горизонтальной составляющей петли H в уравнении для.
2- Штифтовая опора и реакции в конструкции Штифтовая опора или шарнирная опора могут противостоять как вертикальным, так и горизонтальным силам, но они не могут сопротивляться моменту.Это означает, что шарнирная опора не может быть переведена. Используя уравнения равновесия, можно найти составляющие горизонтальных и вертикальных сил.
Определение реакций на свободно опертой балке
Для определения реакций свободно опертой балки следующими методами:
- Экспериментальные наблюдения (с использованием пружинных весов)
- Аналитический раствор (с использованием условий равновесия)
Для понимания различных методов расчета реакций
Аппарат:- Балка с простой опорой, модель
- Масса
- Вешалки
- Пружинные противовесы
- Штанга дозатора
Балка — это конструктивный элемент, на который действует сила сдвига и изгибающий момент под действием боковой или поперечной нагрузки.
Реакция:Часть нагрузки, которая передается на опору, называется реакцией
. Типы опор:- Роликовая опора:
Это опора, которая передает сжимающую силу перпендикулярно опорной поверхности.
- Опора петли:
Он способен передавать как горизонтальную, так и вертикальную силу.
- Поддержка исправлений:
Может служить опорой конструкции против любого типа силы (вертикальной, горизонтальной и вращающейся)
Типы балок:Балка с простой опорой : балка, в которой опора обеспечивается на двух концах балки, называется балкой с простой опорой.Минимальным требованием для устойчивости являются три реакции (две вертикальные и одна горизонтальная).
Консольная балка: Балка, конец которой закреплен, а остальные — свободны.
Консольная балка:
Типы нагрузок:- Точечная сосредоточенная нагрузка : Обычно называемая точечной нагрузкой, она прикладывается к сосредоточенной точке или небольшой площади по сравнению с общей площадью.
- Равномерно распределенная нагрузка (UDL): равномерно распределена по площади объекта.Собственный вес члена всегда равен UDL.
- Varying Distributed Load (VDL): это распределенная нагрузка, интенсивность которой постоянно меняется по площади.
1 st Условие: Сумма всех сил, действующих на тело, равна нулю,
Fx = 0, Ʃ Fy = 0, & Ʃ F z = 0
2 nd Условие : сумма всех моментов, действующих на тело, должна быть равна нулю
Ʃ M = 0
Процедура:
- Реакционный аппарат состоит из рамы; два пружинных противовеса прикреплены к концам, которые представляют собой концевые опоры.
- На этих пружинных весах подвешена стальная балка.
- Длина балки 155 см; тогда как расстояние между двумя опорами составляет 117 см (длина пролета). Эта конструкция представляет собой балку с простой опорой. Гири
- подвешиваются с помощью подвесов в различных местах, и записываются показания пружинных весов, которые дают значение реакции.
- Установите прибор, убедитесь, что луч находится точно горизонтально (запишите вес балки).
- Запишите начальные показания пружинных весов и запишите их как нулевую погрешность.
- Подвесьте два одинаковых груза W1 и W2 к балке на одинаковом расстоянии от концов с помощью подвесов. Теперь запишите показания пружинных весов.
- Вычтите начальные показания из отмеченного значения; разница даст вам реакцию на опоры. Повторите эксперимент много раз, меняя вес и расстояние.
| № ОБСН | Пролет | Масса W1 | Масса W2 | А (дюйм) | В (дюйм) | Реакция R1 | Реакция R2 | ||||||
| N | фунт | N | фунт | эксп | анальный | ошибка | эксп | анальный | ошибка | ||||
Примечание : Расстояния A и B указаны от левой опоры
Аналитические расчеты: Учащиеся должны аналитически рассчитать реакции и нарисовать диаграммы для каждой нагрузки, проверить практические результаты и найти ошибку
Наблюдение 1:
Наблюдение 2
Наблюдение 3:
Наблюдение 4:
В чем разница между диаграммами пучка?
Диаграммы балок используются как основной способ научить инженеров основам статической нагрузки.Балки — это элементы конструкции, способные выдерживать нагрузку за счет сопротивления изгибу. Изгибающая сила может быть результатом внешних нагрузок, веса или длины балки. Балки испытывают изгибающий момент и момент сдвига из-за этих нагрузок.
Балки классифицируются на основе их опор. Помимо балок на ферменной опоре, балки подразделяются на следующие группы:
• Простая опора: Балка, опирающаяся на концы, которые могут свободно вращаться и не имеют моментного сопротивления.
• Фиксированный: Балка опирается на оба конца, которые зафиксированы на месте.
• нависает: Простая балка, выходящая за пределы опоры на одном конце.
• Двойной выступ: Простая балка, оба конца которой выходят за пределы ее опор.
• Непрерывный: Балка, проходящая более чем на две опоры.
• Консоль: Выступающая балка закреплена только на одном конце, а другой конец не имеет опоры.
Ниже мы проанализируем некоторые классические примеры нагружения этих категорий балок.
Простая балка
Простая балка выше имеет две опоры и центральную нагрузку.Простая балка имеет две опоры на каждом конце. Эти опоры или реакции ( R ) не являются фиксированными, поэтому они могут свободно перемещаться. Это влияет на то, как нагрузки будут реагировать на опоры с точки зрения сдвига и изгибающего момента. Если бы они были зафиксированы, силы сдвига и момента реагировали бы по-разному (объяснено позже).Первый случай — сосредоточенная нагрузка ( P ), которая действует на балку в ее центре. Значение силы при каждой реакции соответствует нагрузке в центре:
где P — значение силы нагрузки.
Для случая сосредоточенной нагрузки в центре напряжение сдвига ( V ) имеет то же значение, что и сила реакции ( R = V ). Диаграмма сдвига создается путем анализа сил, действующих на балку с одной стороны на другую.Если мы начнем слева, силы реакции будут толкать балку вверх. Это переводится в диаграмму сдвига, как подъем до того же значения и переход без наклона, пока не достигнет центральной нагрузки. Затем величина сдвига направлена вниз на то же значение, что и центральная нагрузка, и продолжается без наклона до тех пор, пока не достигнет второй реактивной нагрузки на другом конце балки.
Момент определяется аналогично. Наклон моментной диаграммы на интервале 0 равен величине сдвига.Изменение момента равно площади под диаграммой сдвига. В этом случае максимальный момент определяется по следующей формуле:
где l — длина балки.
Если нагрузка не была расположена в центре, значение R будет определяться ее местоположением. Предположим, что нагрузка P находится не в центре, а значение расстояния a слева и значение расстояния b справа.Значения реакции будут определяться:
Используя приведенные выше уравнения для реакционных нагрузок, вы можете при необходимости изменить предыдущие формулы.
Эта простая балка испытывает равномерную нагрузку по всему пролету балки.Другой вариант заряжания — это груз в униформе. Нагрузка равномерно распределяется по длине балки. Распределенная нагрузка количественно выражается как нагрузка на расстояние (т. Е. 10 кН-м), а также может быть приравнена к сосредоточенной нагрузке в определенной точке вдоль стержня.Величина силы равна площади под кривой распределенной нагрузки, а место находится в центре масс распределенной нагрузки. В этом случае сила реакции, которая также является максимальной силой сдвига, выражается следующим образом:
, где w равно распределенной нагрузке.
Здесь диаграмма сдвига и диаграмма моментов немного изменяются. В первом случае диаграмма сдвига прямая, пока не встретит нагрузку и не сместится в противоположном направлении.Сдвиг во втором случае имеет непрерывный отрицательный наклон. Чтобы найти поперечную силу в любой точке, используйте уравнение:
Максимальный момент можно определить по:
Фиксированная балка
Балка на изображении выше фиксируется на конце, что влияет на изгибающие моменты, видимые на каждом конце.Для фиксированной балки разница будет видна на диаграмме моментов. Силы реакции такие же, как у простой балки:
где P — значение силы нагрузки.
Диаграмма сдвига будет вести себя так же, как в первом случае простой балки. Однако теперь, когда концы закреплены, момент на опорах будет действовать иначе. Момент в центре и на концах можно выразить с помощью того же уравнения:
Балка навесная
Свисающая балка, в отличие от простой или неподвижной балки, имеет один конец, который не имеет опоры.Свисающая балка имеет первую опору на конце балки, а вторая опора расположена вдоль балки по направлению к центру.В этом конкретном примере часть балки, проходящая через вторую опору, не подвергается сдвигу или изгибу. Визуальное изображение сдвига и изгиба похоже на простую балку. Однако, поскольку в приведенном выше примере отсутствует центральная нагрузка, расчет сдвига будет различным для каждой опоры:
(максимальное значение сдвига при a)
(максимальное значение сдвига при a> b )
Максимальный момент рассчитывается по следующей формуле:
Двойная выступающая балка
Оба конца на изображении выше не поддерживаются.Вместо этого двойная выступающая балка имеет опоры, расположенные ближе к центру балки.Двойная выступающая балка имеет ту же концепцию, что и одинарная, за исключением того, что обе опоры расположены вдоль и в пределах длины балки. В этом случае нагрузка поперек балки является равномерной и влияет на диаграммы сдвига и изгиба более сложным образом. Слева направо первое значение сдвига определяется расстоянием от первой опоры до конца, умноженным на равномерную нагрузку.
Реакционная нагрузка на первую опору определяется по формуле:
, где b и c — расстояния между опорами и оставшееся краевое расстояние соответственно.
Затем значение сдвига изменяется в первом месте опоры и определяется разницей между первым значением сдвига и первой опорной нагрузкой:
Продолжая движение слева направо, реактивная нагрузка на второй опоре составляет:
Теперь третье значение сдвига можно рассчитать как:
, где V4 — сдвиг, вызванный равномерной нагрузкой на правом выступающем крае:
В этом случае профиль импульса сильно отличается.В результате расположения опор имеют место три различных момента. Используя тот же принцип, что и для сдвига, мы можем анализировать значения момента слева направо. Первый изгибающий момент рассчитывается просто по формуле:
Следующий момент, который в приведенном выше примере равен M 3 , рассчитывается по следующему уравнению:
Конечный момент, M 2 , определяется по:
Это три момента, действующие на балку в данном случае.Максимальный момент определяется по:
Сплошная балка
Сплошная опорная балка может выдерживать большие нагрузки, обеспечивая большее сопротивление изгибу по длине балки.Непрерывная балка — это балка, которая нагружена и имеет более двух опор. Эти балки будут испытывать нагрузки, подобные тем, которые обсуждались ранее; однако они будут состоять из одного или нескольких дел. В примере для этой балки точечная нагрузка представляет собой сосредоточенную нагрузку в любом месте между двумя из трех опор.Следующие уравнения представляют собой значения нагрузки для реакций:
Максимальный изгибающий момент в точке нагрузки:
Можно заменить значения a и b на равные значения расстояния, l / 2 . Уравнения упрощаются до:
Консольная балка
Консольная балка будет испытывать больший изгибающий момент, чем дальше будет находиться приложенная нагрузка от закрепленного конца.Консольная балка будет последним случаем, который мы проанализируем. Балка в этом примере закреплена в стене и на нее действует сосредоточенная нагрузка. Изгибающий момент имеет место вокруг неподвижного конца. Значения сдвига и момента просто рассчитываются по формуле:
, когда x> .
Однородная нагрузка на консольную балку создает в балке постепенный сдвиг и изгибающий момент.Балка на изображении выше также является консольной балкой, но на нее действует равномерная нагрузка.