Определение реакций опор и изгибающих моментов
Положительная сторона данного метода заключается в точности определения реакций опор и изгибающих моментов, соответствующих действительной работе рамы. При лю- [c.679]В табл. 47 приведены расчетные формулы для определения реакций опор и изгибающих моментов от сил, передаваемых на валы зубчатыми и червячными передачами. [c.698]
Определение реакций опор и изгибающих моментов [c.23]
В табл. 8 и на рис. 12 приведены формулы для определения реакций опор и изгибающих моментов двухопорных валов с характерными случаями нагружения. [c.23]
| Рис. 12. Определение реакций опор и изгибающих моментов двухопорных валов с приведенными |
 299]
299]| Рис. 12. Определение реакций опор и изгибающих моментов двухопорных валов с приведенными случаями нагружения |
Система два раза статически неопределима. Особенностями ее являются наличие консоли справа и заделки слева. Перенесем силу Р в точку на правой опоре и взамен отброшенной консоли введем момент Р1 (рис. 254, б). Сила Р, приложенная к опоре О, имеет значение только при определении реакций опор изгибающих моментов она не создает. [c.222]
Величина называется жесткостью бруса при изгибе.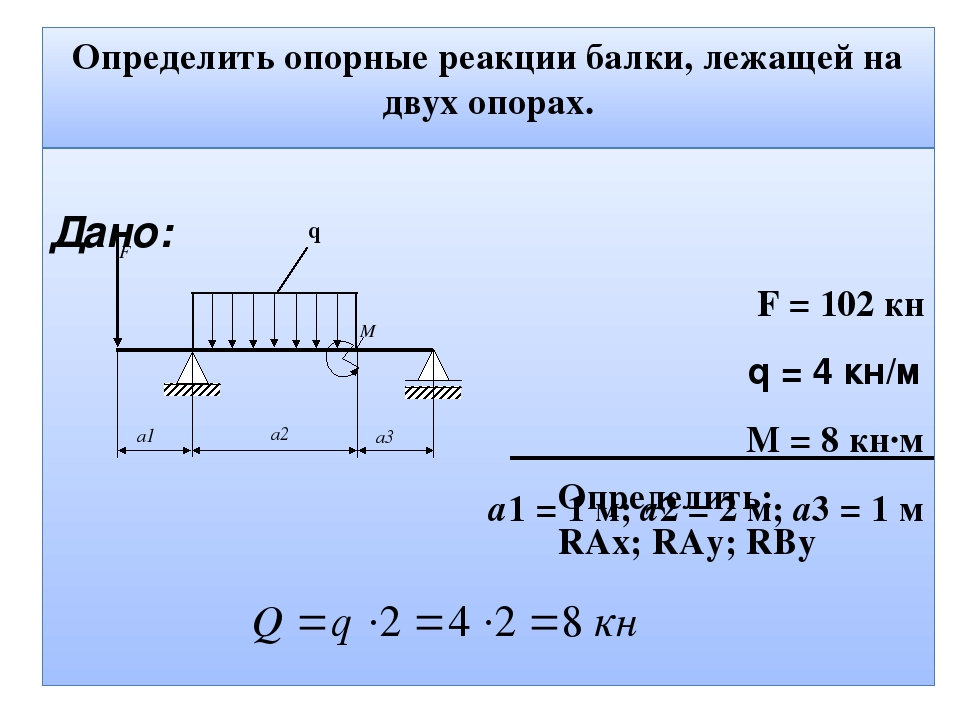 Уравнение упругой линии бруса находят интегрируя уравнение (11.6). Определив реакции опор и построив эпюры изгибающих моментов, брус делят на участки с однородной нагрузкой, и для каждого участка записывают уравнение (11.6), в котором момент 34 зг будет определенной функцией х. Эти уравнения интегри-
[c.141]
Уравнение упругой линии бруса находят интегрируя уравнение (11.6). Определив реакции опор и построив эпюры изгибающих моментов, брус делят на участки с однородной нагрузкой, и для каждого участка записывают уравнение (11.6), в котором момент 34 зг будет определенной функцией х. Эти уравнения интегри-
[c.141]
Построение эпюр. Графики изменения поперечных сил и изгибающих моментов вдоль центральной оси балки называются эпюрами. При построении эпюр поперечных сил и изгибающих моментов в большинстве случаев следует начинать с определения реакций опор. [c.146]
Определение реакций опор, изгибающих и крутящего моментов [c.475]
Определение реакций опор, изгибающих и крутящего моментов опорная реакция
Формулы для определения изгибающих моментов, реакций опор и стрел прогиба оси балок постоянного поперечного сечения приведены в табл. 1-11, [c.19]
Приступим к определению начальных параметров. На левой опоре прогиб у и изгибающий момент М равны нулю, а поперечная сила С — найденной опорной реакции Л=30 кн. Поэтому начальные параметры
[c.303]
На левой опоре прогиб у и изгибающий момент М равны нулю, а поперечная сила С — найденной опорной реакции Л=30 кн. Поэтому начальные параметры
[c.303]
После определения реакций опор оси и 2 можно определить изгибающие моменты в любом ее сечении (рис. 5.3,в). Наибольший изгибающий момент под правой ступицей М2 = = 2 2 момент сопротивления этого сечения оси Подставляя эти значения в формулу (5.9) и используя зависимость (5.10), находят предварительно диаметр оси под ступицей [c.97]
Балка находится в равновесии, если сумма проекций всех сил (включая реакции опор) на осях X и У равна нулю и сумма моментов всех сил относительно любой точки балки равна нулю. Если силы, изгибающие балку, перпендикулярны ее оси, то для определения реакций опор используют только два уравнения равновесия [c.288]
Таким образом порядок определения реакции опор следующий. Определяется изгибающий момент от воздушной нагрузки относительно опоры А (на фюзеляже) в предположении, что опора В отсутствует. Полученное значение момента затем делится на расстояние между опорами, т. е. на длину пролета, и тогда получается значение реакции В. Вычитая полученное значение реакции опоры В из общей нагрузки на крыло р, получим величину реакции опоры А.
[c.137]
Определяется изгибающий момент от воздушной нагрузки относительно опоры А (на фюзеляже) в предположении, что опора В отсутствует. Полученное значение момента затем делится на расстояние между опорами, т. е. на длину пролета, и тогда получается значение реакции В. Вычитая полученное значение реакции опоры В из общей нагрузки на крыло р, получим величину реакции опоры А.
[c.137]
В заделке возникают три реакции (На, Яа, Л а), независимых уравнений статики для плоской системы сил также три. Следовательно, имеем статически определимую систему все реакции определяются из статических уравнений. Однако для консольной балки провести решение можно без определения реакций опор. Для этого нужно, используя метод сечений, начинать построение эпюр со свободного конца балки. Из рис. 5.8, а видно, что балка имеет только один расчетный участок. Выбираем на этом участке произвольное сечение (обозначено волнистой линией) на расстоянии г от свободного конца балки и рассмотрим отдельно часть балки, расположенную справа от сечения.
Для определения требуемого диаметра с1 оси выполняем эскизную компоновку узла сателлита (рис. 11.31, а). Согласно табл. 4.20 составляем расчетные схемы нагружения оси в вертикальной и горизонтальной плоскостях. Затем определяем реакции опор и строим эпюры изгибающих моментов (рис. 11.31, в, г). [c.515]
Определение наибольшего изгибающего момента. Пусть на балку, свободно лежащую на опорах, действуют вертикальные силы I. 2, 3, 4 (рис. 278, а). Отбросив опоры и приложив реакции опор 5 и 6, мы получим уравновешенную систему параллельных сил /, 2, 3, 4. 5, 6, приложенных к балке.
[c.264]
5, 6, приложенных к балке.
[c.264]
Найдя реакции опор, перейдем к определению внутренних усилий, возникающих в поперечных сечениях балки, т. е. изгибающих моментов и поперечных сил. Для этого применим метод сечения.
Рассмотрим прежде всего метод определения опорной реакции. Начертим схему вала в масштабе 1 т (рис. 215). Построим эпюру изгибающих моментов для случая, когда силы Р — Рб отброшены и вместо опоры в точке С приложена искомая сила Яс- Эпюра изгибающих моментов для этого случая, как известно, изображается треугольником Так как сила Яс нам неизвестна, проведем линию 1 1 горизонтально, зададимся произвольной величиной отрезка и построим, таким образом, в произвольном и притом неизвестном нам масштабе треугольник [c.320]
Для определения изгибающего момента от веса груза и тележки рассмотрим произвольное положение последней на мосту (рис. 92, а). Реакция левой опоры балки / д определятся из уравнения моментов действующих сил относительно точки С — ЕМс = 0.
В табл. 24 приведены формулы для определения реакций опор и изгибающих и крутящих моментов в характерных точках колена при расчете коленчатого вала по разрезной схеме. Радиальная и тангенциальная нагрузки считаются приложенными в середине длины шатунной шейки, реакцип в середине коренных. [c.230]
В таблице приведены формулы для определения реакций опор и на фиг. 11 — для определения изгибающих моментов для двухопорных валов с характерными нижеследующей таблицы по заданным из-случаями нагружения. гибающему и крутящему моментам. [c.300]
Под статически определимым понимается состояние тела, находяш егося под нагрузкой, когда для определения неизвестных усилий (реакции в опорах, перере-зываюш,ие силы и изгибающие моменты и т. п.) достаточно уравнений равновесия, а само тело может быть рассмотрено как недеформируемое, абсолютно твердое.
На примерах предыдущего параграфа можно проследить определенную зависимость между очертаниями эпюр поперечных сил и изгибающих моментов и внешней нагрузкой. Для установления этих зависимостей рассмотрим балку (рис. 140, а), нагруженную равномерно распределенной нагрузкой интенсивностью д, соср доточенной силой Р = дан парой сил т = да . Для общности выводов все нагрузки мы задали не в численном виде, а в функции интенсивности д равномерно распределенной нагрузки и некоторого расстояния а. Прежде всего определяем реакции опор Уа и Vв-
[c.223]
Для установления этих зависимостей рассмотрим балку (рис. 140, а), нагруженную равномерно распределенной нагрузкой интенсивностью д, соср доточенной силой Р = дан парой сил т = да . Для общности выводов все нагрузки мы задали не в численном виде, а в функции интенсивности д равномерно распределенной нагрузки и некоторого расстояния а. Прежде всего определяем реакции опор Уа и Vв-
[c.223]
Рассмотрим методику определения изгибающего момента Ai и потеречной силы. Пусть балка, лежащая на опорах А и В (рис. 108), нагружена вертикальными силами Р , Pj. > распределенной нагрузкой интенсивности и моментами Mi, Мо , действующим в вертикальной плоскости симметрии балки. Опорные реакции и Рд в точках А и В можно определить из уравнений равновесия всей балки. [c.157]
Проверочный расчет валов. После предварительного определения диаметра вала обычно вычерчивают эскиз вала с насаженными деталями и устанавливают места расположения опор.
 Затем составляют расчетную схему, в которой вал рассматривается как балка на двух опорах силы от деталей, посалсенных на вал, условно считают сосредоточенными и приложенными посредине шири-НЕл посадочного места детали, а реакции в цапфах — посредине длины цапфы. Далее определяют реакции в опорах вала и строят эпюры сил, изгибающих и крутящих моментов от всех действующих нагрузок.
[c.312]
Затем составляют расчетную схему, в которой вал рассматривается как балка на двух опорах силы от деталей, посалсенных на вал, условно считают сосредоточенными и приложенными посредине шири-НЕл посадочного места детали, а реакции в цапфах — посредине длины цапфы. Далее определяют реакции в опорах вала и строят эпюры сил, изгибающих и крутящих моментов от всех действующих нагрузок.
[c.312]После определения диаметров в намеченных сечениях разрабатывают конструкцию вала, устанавливают места посадки сопряженных G ними деталей (зубчатых или червячных колес, звездочек, шкивов, полумуфт и др.), расположения подшипников—все перечисленные действия воплощают в эскизную компоновку редуктора. Эскизная компоновка редуктора имеет целью установить положение редукторной и открытой передач относительно опор (подшипников), определить расстояние между средними плоскостями подшипников и расстояние от подшипников до открытой передачи, а также расстояние между точками приложения реакций подшипников (методику выполнения эскизной компоновки см.
Приложим эти правила к балке, изображенной на рис. 3.4.3. Распределенная нагрузка направлена вниз в направлении положительной оси у, следовательно, оиа положительна. Каждая из реакций опор равна да и направлепа вверх. По определению, на участке I перерезывающая сила постоянна и равна —qa, на участке III Qy = +да. Так как сосредоточенных сил нет, то согласно правилу (а) эпюра должна быть непрерывна. Поэтому крайние точки эпюр на участках 1 и III нужно соединить прямой. Согласно правилу (з) на левом и правом концах балки изгибающий момент равен нулю, на участках 1 и III по правилу (д) эпюра прямолинейна. Поэтому достаточно вычислить изгибающш момент на границе между первым и вторым, а также вторым и третьим участками. И тут и там этот момент равен — qa(l — а). Отложим соответствующие отрезки по вертикали вверх и соединим концы их прямыми с концами отрезка, изображающего балку. В соответствии с правилом (и) на участке II
[c.86]
Так как сосредоточенных сил нет, то согласно правилу (а) эпюра должна быть непрерывна. Поэтому крайние точки эпюр на участках 1 и III нужно соединить прямой. Согласно правилу (з) на левом и правом концах балки изгибающий момент равен нулю, на участках 1 и III по правилу (д) эпюра прямолинейна. Поэтому достаточно вычислить изгибающш момент на границе между первым и вторым, а также вторым и третьим участками. И тут и там этот момент равен — qa(l — а). Отложим соответствующие отрезки по вертикали вверх и соединим концы их прямыми с концами отрезка, изображающего балку. В соответствии с правилом (и) на участке II
[c.86]
Для определения угла поворота конца консоли рассмотрим еще одно состояние загружЙ1ия (схема в), когда на конце консоли приложен момент At =l. Опорная реакция правой опоры при этом -состоянии загружения и еданичные изгибающие моменты выразятся так [c.198]
Коленчатые валы. Рассматривая одноколенчатый вал (рис. 18) как систему жестко связанных между собой стержней т п р q st, свободно опертых в точках т и t, можно на основании уравнений статики определить изгибающий и крутящий моменты в любом поперечном сечении тогда соответствующие главные напряжения определятся, как было выше указано. Задача становится сложнее для многоколенчатых валов. Главное затруднение заключается в неопределенности опорных условий. Зазоры в подшипниках дают некоторую возможность коленчатому валу поворачиваться на опорах, и от этих отклонений зависит само положение опорных точек. Если предположить, что коленчатый вал оперт посредине подшипников и может свободно поворачиваться на опорах, то задача значительно упрощается, и тогда для определения опорных моментов и реакций опор можно составить уравнения, аналогичные уравнениям для неразрезной балки. Такие исследования
[c.590]
Задача становится сложнее для многоколенчатых валов. Главное затруднение заключается в неопределенности опорных условий. Зазоры в подшипниках дают некоторую возможность коленчатому валу поворачиваться на опорах, и от этих отклонений зависит само положение опорных точек. Если предположить, что коленчатый вал оперт посредине подшипников и может свободно поворачиваться на опорах, то задача значительно упрощается, и тогда для определения опорных моментов и реакций опор можно составить уравнения, аналогичные уравнениям для неразрезной балки. Такие исследования
[c.590]
Расчетные схемы валов. Подшипники качения или скольжения при составлении расчетных схем принимают за шарнирные опоры. Точки приложения реакций берут в серединах подшипников. При двух подшипниках качения, установленных в одной опоре, точку приложения реакции принимают в середине подшипника, ближайшего к пролету. Сдвоенный подшипник качения дает опорное закрепление, промежуточное между шарнирным и жестким замена его в расчетной схе.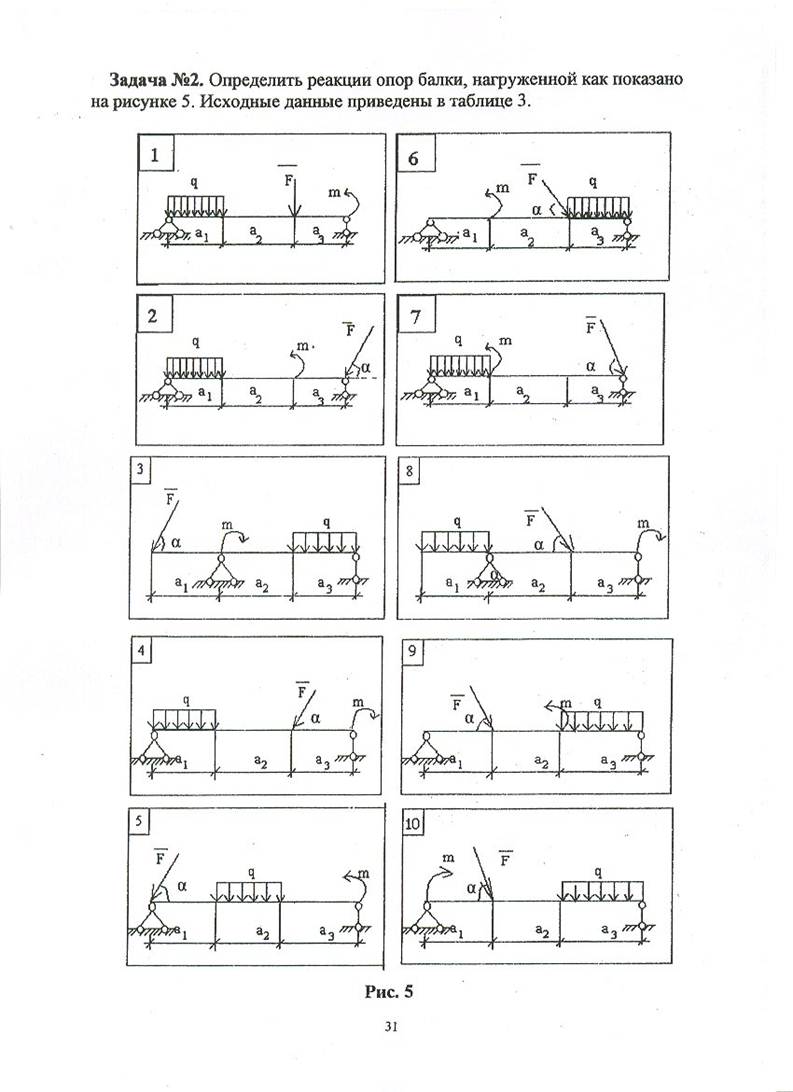 ме шарнирной опорой идет в запас надежности расчета. В отдельных случаях такой подшипник рассматривают как жесткое защемление (заде.пку), при этом расчетной схемой (при определении изгибающих моментов) является статически неопределимая балка. Эта расчетная схема дает погрешность меньшую, чем при с.хематизации сдвоенного подшипника шарнирной опорой, но погрешность идет не в запас надежности.
[c.309]
ме шарнирной опорой идет в запас надежности расчета. В отдельных случаях такой подшипник рассматривают как жесткое защемление (заде.пку), при этом расчетной схемой (при определении изгибающих моментов) является статически неопределимая балка. Эта расчетная схема дает погрешность меньшую, чем при с.хематизации сдвоенного подшипника шарнирной опорой, но погрешность идет не в запас надежности.
[c.309]
После определения (при помощи уравнений трех моментов) величин всех опорных изгибающих моментов можно определять изгибающие моменты и поперечные силы в пролетах нёразрезной балки и ее опорных реакций. При этом каждый пролет можно рассматривать как простую балку на двух опорах, [c.355]
Испытания по этой схеме нагружения (рис. 5.1.1, б) проводятся с целью определения модулей упругости Ei м tl прочности при чистом изгибе П». Нагружение на чистый изгиб осуществляется путем приложения изгибающих моментов по концам стержня. Достоинства схемы чистого изгиба — это однородное напряженное состояние по всей длине образца, отсутствие контактных напряжений в местах приложения сосредоточенных сил (нагрузка и опорные реакции) и исключение влияния концов образца, выступающих за опорами. При этой схеме натружения образец по всей длине доступен для измерений. Из-за отсутствия в образце деформаций сдвига способы измерения прогиба w и относительных деформаций наружных волокон стержня ej при надлежащем конструктивном исполнении нагрузочных приспособлений (т. е. при отсутствии местных искажений упругой линии стержня в сечениях приложения нагрузки) качественно равноценны.
[c.195]
При этой схеме натружения образец по всей длине доступен для измерений. Из-за отсутствия в образце деформаций сдвига способы измерения прогиба w и относительных деформаций наружных волокон стержня ej при надлежащем конструктивном исполнении нагрузочных приспособлений (т. е. при отсутствии местных искажений упругой линии стержня в сечениях приложения нагрузки) качественно равноценны.
[c.195]
Изгиб. Определение опорных реакций. Правила знаков для поперечных сил и изгибающих моментов
12. Изгиб
Очень часто стержни подвергаются действию поперечных сил и внешних пар (рис.31). Под действием таких нагрузок ось стержня искривляется. При этом в поперечных сечениях стержня возникает изгибающие моменты, плоскость действия которых перпендикулярна плоскости поперечного сечения стержня.
Рис.31
Указанный вид нагружения называют изгибом, а стержни,
работающие на изгиб, называют балками. Если изгибающий момент является
единственным внутренним усилием, возникающим в поперечном сечении стержня, то
изгиб называют чистым.
Изгиб называют поперечным, если наряду с изгибающими моментами возникают также и поперечные силы.
Если плоскость действия изгибающего момента проходит через одну из главных центральных осей поперечного сечения стержня, изгиб называют прямым (простым или плоским), в противном случае косым.
12.1. Типы опор балок.
1. Подвижная шарнирная опора.
В данной опоре ограничено перемещение вверх-вниз, поэтому в ней присутствует только одна реакция, перпендикулярная плоскости качения.
2. Неподвижная шарнирная опора.
В данной опоре ограничено перемещение как вверх-вниз, так и вправо-влево, поэтому в ней присутствует реакция, которую обычно представляют в виде двух составляющих: горизонтальной и вертикальной.
3. Жёсткая заделка.
Заделка не допускает ни линейных,
ни угловых перемещений. Реакцию заделки обычно раскладывают на две составляющие
и реактивный момент.
4. Шарнир.
Шарнир допускает угловое перемещение, поэтому реакцию шарнира представляют в виде двух составляющих: вертикальной и горизонтальной
Если опорные реакции конкретной балки могут быть найдены из одних уравнений статики, то балки называют статически определимыми. Если же число опорных реакций больше, чем число уравнений статики, то балки называют статически неопределимыми
12.2. Определение опорных реакций.
Пример 1. Определить реакции опоры консольно закрепленной (глухо заделанной) балки (рис.32). Балка нагружена сосредоточенной силой Р1
и распределенной силой q.Для определения опорных реакций необходимо мысленно отбросить опоры, заменив их соответствующими реакциями.
В данном случае реакцию заделки имеем в виде силы, представленной двумя векторами Ау и Аz, и реактивного момента МА. Составляем уравнения равновесия балки:
Рис.
 32
32сумма сил на ось Xравна нулю, сумма сил на ось Yравна нулю и сумма моментов относительно любой точки балки равна нулю.
; .
; ; , где — равнодействующая распределенной нагрузки q, точка приложения которой находится на середине участка балки а3.
; (сумма моментов относительно точки заделки балки) , откуда , т.е. направление реактивного момента следует поменять на обратное, поскольку результат получился со знаком минус.
Пример 2. Определить реакции опор балки, представленной на рис.33. Балка нагружена сосредоточенной силой Р, распределенной силой q и сосредоточенным моментом Ме.
Рис.33
Поступаем также как и в предыдущем примере, т.е. мысленно отбрасываем опоры, заменяя их реакциями опор, и составляем уравнения равновесия:
; ;;
;
Вместо последнего уравнения можно использовать условие
поскольку значение Аууже найдено. Тогда из выражения определяем Ву.
Тогда из выражения определяем Ву.
Пример 3. Определить реакции опор балки, представленной на рис.34 и нагруженной сосредоточенной силой Р.
Рис.34
Поступаем также как и в предыдущем примере, т.е. мысленно отбрасываем опоры, заменяя их реакциями опор, и составляем уравнения равновесия:
; ; откуда ;
; ; ;
; ; .
Знак минус для реакции Ау говорит о том, что направление данной реакции в противоположную сторону относительно выбранному на чертеже.
Для проверки решения можно воспользоваться условием .
12.3. Определение внутренних усилий в балках.
Внутренние усилия (силовые факторы) в поперечных сечениях балки: изгибающий момент Ми и поперечная сила Q.
Предположим, что мы имеем балку, нагруженную двумя
сосредоточенными силами Р1 и Р2 (рис.35).
Прежде всего, необходимо определить реакции опор, для чего можно применить
рассмотренные выше приемы.
Для определения внутренних силовых факторов применим метод сечений, для чего в интересующем нас месте сделаем мысленный разрез балки на расстоянии z и отбросим одну часть, например правую.
Рис.35
Затем рассмотрим равновесие левой части, заменив левую опору ее реакцией А.
Взаимодействие частей балки заменим внутренними усилиями: изгибающим моментом Ми и поперечной силой Q.
Уравнения равновесия (сумма сил на вертикальную ось y и сумма моментов
Определить реакцию опоры балки — презентация онлайн
2FМ3
q
В
А
а=2 м
2F
q
b=3 м
RA
А
Y
РГЗ №3. Изгиб.
Дано: a = 2 м; b = 3 м; c = 1,5 м; М3 = 45 кН·м;
F=30 кН; q=20 кН/м; [σ] = 100 МПа
Решение:
с=1,5 м
1. Определить реакции опор балки.
M B 0
a
М3
RB
M 3 R A b 2 F ( a b) q a b 0
2
a
M 3 2 F ( a b) q a b
В
2
RA
b
2
45 2 30 (2 3) 20 2 3
2 168 1 168,3 кН
RA
3
3
M A 0
a
M 3 RB b 2 F a q a 0
2
a
M 3 2F a q a
2
RB
b
2
45 2 30 2 20 2
2 68 1 68,3 кН
RB
3
3
Проверка:
Σ Fy =
0 +R –R =
–2F – q·a
A
B
0
–60 – 40 +168,3 – 68,3 = 0
0=0
2F
М3
q
2F
z1
q
I участок 0 ≤ z1
В
А
а=2 м
2.
 Вычислить внутренние силовые
Вычислить внутренние силовыефакторы и построить их эпюры.
b=3 м
QY 2 F q z1
с=1,5 м
RA
RB
z3
М3
z2
2F q
z1
при z1 0 QY 2 30 20 0 60 кН
при z1 2 QY 2 30 20 2 100 кН
z1
2
0
при z1 0 M X 2 30 0 20 0 0 кН м
2
2
при z1 2 M X 2 30 2 20 2 160 кН м
2
M X 2 F z1 (q z1 )
II участок 0 ≤ z2
М3
QY 0 кН
z2
M X М 3 45 кН м
2F
III участок 0 ≤ z3
М3
q
а=2 м
QY RB 68,3 кН
В
А
b=3 м
M X M 3 RB z3
с=1,5 м
М3
RB
z3
68,3
68,3
0
0
– 100
MX = M3 – RB·z3 = 0
z3
Эп. MX (кН·м)
45
0
45
0
z3
– 160
при z3 3 M X 45 68,3 3 160 кН м
Определим, при каком z3 изгибающий
момент МХ будет равен 0,
т.е. решим уравнение вида MX (z3) = 0.
Эп. QY (кН)
– 60
при z3 0 M X 45 68,3 0 45 кН м
M3
45
0,659 м
RB 68,3
3.
 Определить опасное сечение балки.
Определить опасное сечение балки.Опасным является сечение в (·) А,
соответствующее Ммах = –160 кН·м.
4. Определить осевой момент сопротивления и подобрать сечение
соответствующего профиля.
Условие прочности:
МАХ
MХ
WХ
160 103
3
3
0
,
0016
м
1600
см
Осевой момент сопротивления: WХ
100 106
MХ
Подбираем сечение двутавра по сортаменту прокатной стали. Выбираем балку
двутавровую №55 с осевым моментом сопротивления WX = 2035 см3
и выписываем все характеристики выбранного сечения.
Опоры балок: виды, способ установкаа
Постройка дома – серьезное решение и бесценный опыт в жизни любого человека. Перед началом работ стоит продумать все до мелочей: какой материал использовать для возведения стен; какую форму крыши подобрать; чем утеплить.
Случается и так, что после этапа «выгонки» стен работа останавливается на монтаже стропильной системы крыши. Вся причина в том, что не все знают, да и не хотят вникать в тонкости возведения кровли. Когда же застройщик заводит разговор о покупке непонятных «опор балок», а весь материал в наличии, заказчик начинает думать, что его пытаются обмануть.
Когда же застройщик заводит разговор о покупке непонятных «опор балок», а весь материал в наличии, заказчик начинает думать, что его пытаются обмануть.
Недостающий элемент
При монтаже деревянной конструкции специалисты используют опоры для балок из металлического профиля. Этот элемент необходим для надежного закрепления деревянных стропил с учетом усадки материала в будущем.
Опоры балок бывают открытые, закрытые, односторонние и опоры столба для горизонтальной фиксации.
Такие крепежи производятся на заводах, что значительно упрощает их использование, так как по всей поверхности предусмотрены отверстия для шурупов, гвоздей и анкеров разного диаметра. Связано это с тем, что балки могут быть прикреплены к разным поверхностям: дерево, металл, бетон. Соответственно и размер шурупов, гвоздей и т. д. также будет иметь разный диаметр.
Для большей устойчивости к коррозии используется метод горячего оцинкования. В сплав цинка добавляют алюминий и свинец, что значительно улучшает физические данные и срок службы металла.
Внутренние и наружные
Крепления для балок делят на внутренние и наружные. Они отличаются по форме и величине боковых стенок — так называемых «ушей» или «лепестков». Именно по этой части их и различают.
У наружных опор «уши» вывернуты таким образом, что во время монтажа части крепления видны невооруженным глазом, а само крепление обхватывает торец балки. Такие крепления часто можно видеть на строениях с пристройками, где деревянный каркас кровли, как правило, выступает наружу.
Одной из разновидностей наружных опор являются односторонние крепления. Они разделяются на правосторонние и левосторонние. Их используют для вертикального монтажа брусьев к стенам из различного материала.
Внутренние же опоры балок имеют загнутые внутрь «лепестки». По внешнему виду они схожи с наполовину обрезанной металлической коробкой в отверстиях. Такое крепление закрепляют перед монтажом бруса, а диаметр балки должен соответствовать ширине опоры.
Чаще всего их используют для крепления несущих балок, что позволяет увеличить безопасность системы. Они прикрепляются к брусу с внутренней и наружной стороны, повышая устойчивость к большим нагрузкам.
Они прикрепляются к брусу с внутренней и наружной стороны, повышая устойчивость к большим нагрузкам.
Внутренние крепления имеют несколько разновидностей. Одной из них является «невидимая» система, закрепляющаяся с помощью вмонтированного внутрь балки «крючка» и зафиксированного специальными болтами. Столь интересный вариант отлично подходит для помещений с открытыми перекрытиями.
Движимые и недвижимые
Специалисты обязаны учитывать все возможные факторы воздействия на деревянные перекрытия при монтаже кровельной системы. Главными факторами, влияющими на срок службы материалов, являются перепады температур, а также влажность воздуха.
Чтобы избежать различных сюрпризов при установке каркаса, монтажники используют движущиеся опоры балок для крепления бруса к несущей стропиле. Выглядит такой крепеж как металлическая продолговатая пластина с петлёй в виде крючка посередине. Края пластины имеют множество отверстий разного диаметра для гвоздей, шурупов или анкеров.
Движущаяся конструкция позволяет дереву при усадке двигаться, не влияя на всю систему: на крыше при возможных искривлениях не появляются бугры, трещины или ямы.
Как определить реакции опор балки?
Хитрая наука — механика — изучает движение материальных тел и их взаимодействие. В таких расчетах участвуют значения, влияющие на грузоподъёмность, крепость бруса.
С их помощью можно рассчитать, какой вес сможет выдержать несущее перекрытие и какое количество креплений необходимо использовать для фиксации бруса.
В новой архитектуре наиболее оптимальным является использование балок на двух опорах. Такую конструкцию легче всего просчитать, учитывая особенности материала, а также рассчитав небезопасное сечение.
В строительстве используются стальные, бетонные или деревянные балки. Балка на двух опорах чаще всего «появляется» в конструкции мостов и каркасов высотных домов. Это могут быть как двутавровые балки, так и швеллеры, полые трубы и «уголки».
(PDF) Матричный метод расчета реакций упругих опор неразрезной балки, находящейся под действием поезда с нагрузкой Стержень
опирается на семь упругих опор с пропорциональным упругим поведением. Решение
Решение
таких задач аналитически очень сложно. Используя матричные методы и средства
профессионального программного обеспечения MATHCAD, можно решить следующие задачи: бара можно выразить аналитически;
— Функции сил сечения T(x) и M(x) для заданного расстояния y = d1
могут быть выражены аналитически и могут быть построены диаграммы изменения этих усилий
;
— Функции перемещений w (x) и поворотов секций fi (x) могут быть
выражены аналитически для некоторого заданного расстояния: y = d1 и могут быть построены диаграммы
их изменения;
— Можно проводить моделирование влияния относительной жесткости деформаций гиперстатической системы
Ссылки
1.Marin C. — Rezistenţa Materialor Partea I — SolidIni Simple, Editura Biblio-
Theca Târgovişte 2013
2. Marin C. — Rezistenţa Materialor Partea a IIA — Teoria Elaughtţii i Soliccireri
Комплекс, Editura Bibliotheca Târgovişte 2014
3. Marin C. — Проблема Tip de Rezistenţa Материативное резольвата în
Marin C. — Проблема Tip de Rezistenţa Материативное резольвата în
Mathcad, Editura Bibliotheca Târgovişte 2012
4. Марин С. — моделирование нагрузочных нагрузок на непрерывной
луча с семи жесткими опорами, расположенными на одном уровне ( I) Румынский обзор
Precision Mechanics, Optics & Mechatronics, Nr.46/2014, стр. 55-60
5. Марин К. — МОДЕЛИРОВАНИЕ ПОЕЗДА, ДВИЖУЩЕГО НАГРУЗКИ НА НЕПРЕРЫВНОЙ
БАЛКЕ С СЕМЬЮ УПРУГИМИ ОПОРАМИ, РАСПОЛОЖЕННЫМИ НА ОДНОМ УРОВНЕ (II)
The Romanian Review Precision Mechanics, Optics & Mechatronics, 46/2014, pp 61-66
6. Marin C. — МАТРИЧНЫЙ МЕТОД, ИСПОЛЬЗУЕМЫЙ ДЛЯ РАСЧЕТА СИЛ РЕАКЦИИ
В СЛУЧАЕ НЕПРЕРЫВНЫХ БАЛОК, ОПОРНЫХ ЖЕСТКИМИ ПОДШИПНИКАМИ (I, II)
The Romanian Review Precision Mechanics , Оптика и мехатроника, 45/2014, стр. 142-145
7.Марин С. Эне, Gh. — ПРИМЕНЕНИЕ MATHCAD ДЛЯ ПРОЕКТИРОВАНИЯ ДИСКРЕТНЫХ КОНТАКТНЫХ КОЛЕЦ
, ВХОДЯЩИХ В ОПОРНЫЕ СИСТЕМЫ ВРАЩАЮЩИХСЯ БАРАБАНОВ
Научный Вестник Университета ВАЛАХИЯ — МАТЕРИАЛЫ И МЕХАНИКА -SBMM
5(8)/2010, с. .
.
Типы балок, нагрузки и реакции | Инженерыdaily
Конструктивные элементы обычно классифицируют в соответствии с типами нагрузок, которые они поддерживают. Например, стержень с осевой нагрузкой воспринимает силы, векторы которых направлены вдоль оси стержня, а стержень при кручении поддерживает крутящие моменты (или пары), векторы моментов которых направлены вдоль оси.Балки представляют собой элементы конструкции, подверженные боковым нагрузкам, то есть силам или моментам, векторы которых перпендикулярны оси стержня.Балки, показанные на рис. 1, классифицируются как плоские конструкции, поскольку они лежат в одной плоскости. Если все нагрузки действуют в одной и той же плоскости и если все прогибы (показанные пунктирными линиями) происходят в этой плоскости, то мы называем эту плоскость плоскостью изгиба.
| РИС.1 Примеры балок, подвергающихся поперечным нагрузкам |
Балки обычно описываются способом, которым они поддерживаются. Например, балка с шарнирной опорой на одном конце и роликовой опорой на другом (рис. 2а) называется свободно опертой или простой балкой. Существенной особенностью штифтовой опоры является то, что она предотвращает перемещение конца балки, но не препятствует вращению. Таким образом, конец А балки на фиг.2а не может перемещаться ни по горизонтали, ни по вертикали, но ось балки может вращаться в плоскости фигуры.Следовательно, штифтовая опора способна развивать силовую реакцию как с горизонтальной, так и с вертикальной составляющей ( HA и RA ), но не может развивать моментную реакцию.
Например, балка с шарнирной опорой на одном конце и роликовой опорой на другом (рис. 2а) называется свободно опертой или простой балкой. Существенной особенностью штифтовой опоры является то, что она предотвращает перемещение конца балки, но не препятствует вращению. Таким образом, конец А балки на фиг.2а не может перемещаться ни по горизонтали, ни по вертикали, но ось балки может вращаться в плоскости фигуры.Следовательно, штифтовая опора способна развивать силовую реакцию как с горизонтальной, так и с вертикальной составляющей ( HA и RA ), но не может развивать моментную реакцию.
| РИС. 2 Типы балок: (а) простая балка, (б) консольная балка и (в) балка с выступом |
 Конечно, ось луча может свободно вращаться в точке B точно так же, как и в точке A . Вертикальные реакции на роликовых опорах и штифтовых опорах могут действовать либо вверх, либо вниз, а горизонтальные реакции на штифтовых опорах могут действовать либо влево, либо вправо.
Конечно, ось луча может свободно вращаться в точке B точно так же, как и в точке A . Вертикальные реакции на роликовых опорах и штифтовых опорах могут действовать либо вверх, либо вниз, а горизонтальные реакции на штифтовых опорах могут действовать либо влево, либо вправо.| РИС.3 Балка, опирающаяся на стену: (a) реальная конструкция и (b) представление в виде роликовой опоры. Соединение балки с колонной: (c) фактическая конструкция и (d) представление в виде штифтовой опоры. |
Балка, показанная на рис.2б, закрепленная на одном конце и свободная на другом, называется консольной балкой. На неподвижной опоре (или на защемленной опоре) балка не может ни поступать, ни вращаться, а на свободном конце может делать и то, и другое. Следовательно, на неподвижной опоре могут существовать как силовые, так и моментные реакции.
Третий пример на рисунке — балка с выступом (рис.2в). Эта балка просто поддерживается в точках A и B (то есть она имеет штифтовую опору в точках A и роликовую опору в точках B ), но она также выступает за пределы поддержка по телефону B .Выступающий сегмент BC аналогичен консольной балке, за исключением того, что ось балки может вращаться в точке B .
При вычерчивании эскизов балок опоры обозначаем условными обозначениями, подобными тем, которые показаны на рис.2. Эти символы указывают, каким образом удерживается балка, и, следовательно, они также указывают на природу реактивных сил и моментов. Однако символы не представляют реальную физическую конструкцию.Например, рассмотрим примеры, показанные на рис.3. В части (а) рисунка показана широкополочная балка, опирающаяся на бетонную стену и удерживаемая анкерными болтами, которые проходят через прорези в нижней полке балки. Это соединение удерживает балку от вертикального перемещения (вверх или вниз), но не препятствует горизонтальному движению.
Это соединение удерживает балку от вертикального перемещения (вверх или вниз), но не препятствует горизонтальному движению.
Кроме того, любое ограничение поворота продольной оси балки невелико и обычно им можно пренебречь. Следовательно, этот тип опор обычно представлен роликом, как показано в части (b) рисунка.
| Соединение балки с колонной, при этом одна балка крепится к полке колонны, а другая — к стенке колонны (Joe Gough/Shutterstock) |
Второй пример (рис. 3c) представляет собой соединение балки с колонной, в котором балка крепится к полке колонны с помощью болтовых уголков. (См. фото.) Обычно предполагается, что этот тип опоры удерживает балку от горизонтального и вертикального перемещения, но не от вращения (ограничение от вращения незначительно, поскольку и углы, и колонна могут изгибаться).Таким образом, это соединение обычно представляют в виде штифтовой опоры для балки (рис.
 3г).
3г). Последний пример (рис. 3e) представляет собой металлический столб, приваренный к опорной плите, которая прикреплена к бетонной опоре, заглубленной в землю. Поскольку основание стойки полностью зафиксировано как от перемещения, так и от вращения, ее представляют в виде неподвижной опоры (рис. 3f).
Задача представления реальной конструкции идеализированной моделью, как это показано балками на рис. 2, является важным аспектом инженерных работ.Модель должна быть достаточно простой, чтобы облегчить математический анализ, и в то же время достаточно сложной, чтобы с достаточной точностью отображать фактическое поведение конструкции. Конечно, каждая модель является приближением к природе. Например, фактические опоры балки никогда не бывают абсолютно жесткими, поэтому всегда будет небольшое перемещение на штифтовой опоре и небольшое вращение на фиксированной опоре. Кроме того, опоры никогда не бывают полностью свободны от трения, поэтому всегда будет небольшое ограничение перемещения роликовой опоры.
 В большинстве случаев, особенно для статически определимых балок, эти отклонения от идеализированных условий мало влияют на действие балки, и ими можно смело пренебречь.
В большинстве случаев, особенно для статически определимых балок, эти отклонения от идеализированных условий мало влияют на действие балки, и ими можно смело пренебречь.
Несколько типов нагрузок, действующих на балки, показаны на рис.2. Когда нагрузка прикладывается к очень небольшой площади, ее можно идеализировать как сосредоточенную нагрузку, которая представляет собой единую силу. Примерами являются нагрузки P1 , P2 , P3 и P4 на рисунке.Когда нагрузка распределяется вдоль оси балки, она представляется как распределенная нагрузка, такая как нагрузка q в части (а) рисунка. Распределенные нагрузки измеряются их интенсивностью, которая выражается в единицах силы на единицу расстояния (например, ньютоны на метр или фунты на фут). Равномерно распределенная нагрузка, или равномерная нагрузка, имеет постоянную интенсивность q на единицу расстояния (рис.2а). Переменная нагрузка имеет интенсивность, изменяющуюся с расстоянием по оси; например, линейно изменяющаяся нагрузка на рис. 2b имеет интенсивность, линейно изменяющуюся от q1 до q2 . Другим видом нагрузки является пара, иллюстрируемая парой моментов M1 , действующих на выступающую балку (рис.2в).
2b имеет интенсивность, линейно изменяющуюся от q1 до q2 . Другим видом нагрузки является пара, иллюстрируемая парой моментов M1 , действующих на выступающую балку (рис.2в).
В этом обсуждении мы предполагаем, что нагрузки действуют в плоскости рисунка, а это означает, что все силы должны иметь свои векторы в плоскости рисунка, а все пары должны иметь свои векторы моментов, перпендикулярные плоскости рисунка.Кроме того, сама балка должна быть симметрична относительно этой плоскости, что означает, что каждое поперечное сечение балки должно иметь вертикальную ось симметрии. В этих условиях балка будет прогибаться только в плоскости изгиба (плоскость рисунка).
Реакции
Поиск реакций обычно является первым шагом в анализе балки. Зная реакции, можно найти поперечные силы и изгибающие моменты, как описано далее в этой главе.Если балка поддерживается статически определенным образом, все реакции можно найти из диаграмм свободного тела и уравнений равновесия.
| Внутренние расцепители и концевые опоры в модели балки моста (любезно предоставлено Национальной информационной службой по землетрясениям Engineering EERC, Калифорнийский университет, Беркли.) 5 |
| РИС.4 Типы расцепителей внутренних элементов двумерных балок и элементов рамы |

Расчет нагрузок на колонны здания с учетом реакций опор балок
Введение
При ручном проектировании железобетонных конструкций нагрузки на колонны обычно оцениваются с учетом опорных реакций от балок, на которые они опираются, или методом площадей притоков. Последний более популярен из-за своей простоты и скорости, но обычно не может учесть все нагрузки, воздействующие непосредственно на колонны, в то время как первый является более сложным и трудоемким, но очень репрезентативным для всех возможных нагрузок, возлагаемых на колонны. столбец.
Действия по нагружению колонны от реакции опоры балки
(1) Надлежащим образом нагрузите плиту перекрытия и учтите нагрузки в предельном состоянии с учетом соответствующей комбинации нагрузок.
(2) Перенесите нагрузки с плиты на балку, используя соответствующую зависимость. Основываясь на линиях текучести, нагрузки обычно имеют треугольную или трапециевидную форму, но это неудобно для ручного анализа. Эквивалентный UDL (достаточно точный) можно использовать для передачи нагрузки на плиту, используя приведенные ниже формулы;
Эквивалентный UDL (достаточно точный) можно использовать для передачи нагрузки на плиту, используя приведенные ниже формулы;
Односторонние плиты
Длинные пролеты q = nlx/2
Короткий пролет q = nlx/5
Двусторонние плиты
Длинный пролет q = nlx/2(1 – 1/3k 2 )
Короткий пролет q = nlx/3
Где;
q = нагрузка, передаваемая от плиты к балке
n = нагрузка в предельном состоянии по несущей способности
1.4gk + 1,6qk (BS 8110)
1,35gk + 1,5qk (Еврокод 2)
Ly = длина длинного пролета плиты
Lx = длина короткого пролета плиты
k = Ly/Lx
(3) Проанализируйте балки перекрытия полностью, используя любой подходящий метод по вашему выбору, а также принимая во внимание любую дополнительную нагрузку, которая может быть на балку, такую как нагрузка на стену и отделку.
(4) Получите опорные реакции балки, которые представляют собой нагрузку, передаваемую от пола к колонне.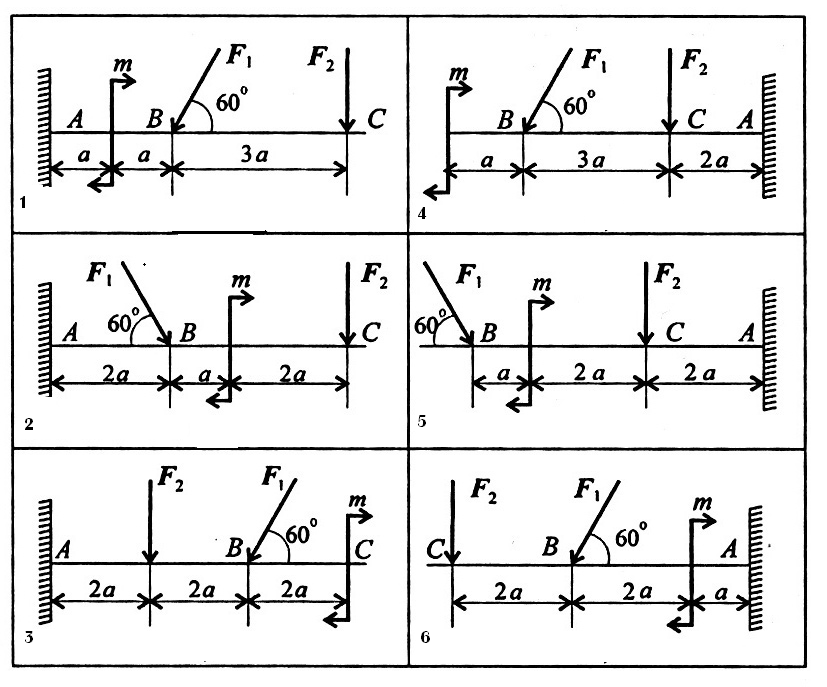
Пример конструкции
В этом посте план этажа, показанный ниже, относится к торговому комплексу, и необходимо получить осевые нагрузки на колонну в крайнем предельном состоянии.
Расчетные данные
Размер всех колонн = 230 x 230 мм
Размер всех балок = 450 x 230 мм
Толщина плиты = 200 мм
Удельный вес бетона = 25 кН/м 3
Удельный вес бетонного блока = 3,47 кН/м 2
fck = 25 Н/мм 2
fyk = 500 Н/мм 2
Комбинация нагрузок = 1,35gk + 1,5qk
Расчетная переменная нагрузка (qk) = 4 кН/м 2
k = Ly/Lx = 6/5 = 1,2 (во всех случаях)
Только внешние балки несут рабочую нагрузку блока.
Анализ нагрузки
Балка крыши
Постоянная нагрузка на балки крыши gk = 6 кН/м
Переменная нагрузка на балку крыши qk = 1,5 кН/м
(Эти значения приняты)
В предельном состоянии, n = 1,35(6) + 1,5 (1,5) = 10,35 кН/м
Анализ нагрузки плиты
Собственный вес бетона = 25 кН/м 3 × 0,2 м = 5,0 кН/м 2
Стяжка и отделка (скажем) = 1,35 кН/м 5 Допуск на часть 1,35 кН/м 25 кН/м 2
Суммарная (gk) = 7,85 кН/м 2
Переменное действие (qk) = 4 кН/м 2
n = 1,35gk + 1,5qk = 1,35(7,85) + 1,5(4) = 16,6 кН/м 2
Нагрузка на стену на балку
Удельный вес песчано-бетонных блоков = 3,47 кН/м 2
Высота стены = 3,5 м
Нагрузка на стену на балку = 3,47 кН/м
Нагрузка на балки
Внешние продольные балки (ось 1:A-D и ось 3:A-D)
Собственный вес балки (с коэффициентом) = 1.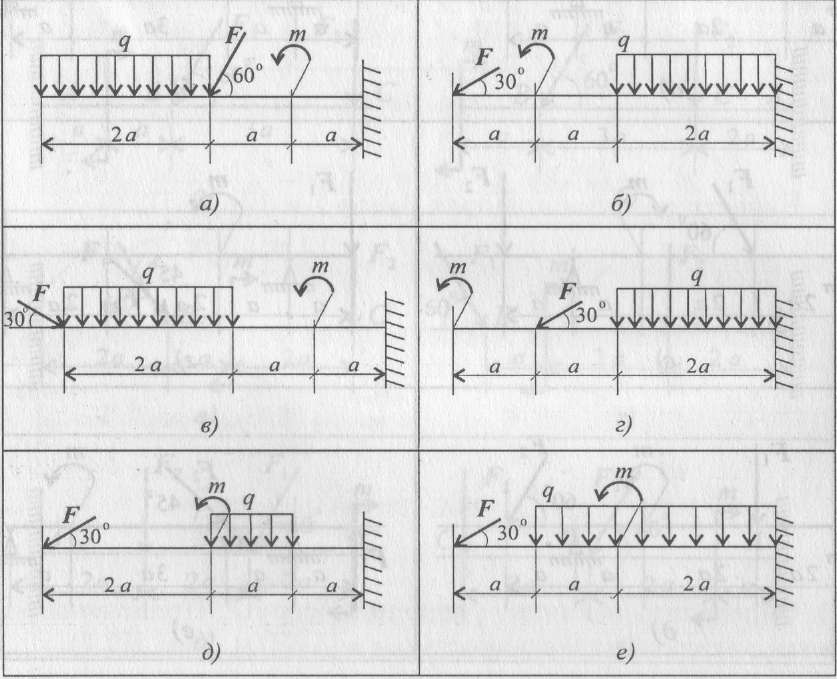 35 × 0,23 м × 0,25 м × 25 = 1,94 кН/м
35 × 0,23 м × 0,25 м × 25 = 1,94 кН/м
Нагрузка от плиты = nlx/2(1 – 1/3k 2 ) = [(16,6 × 5)/2] × (1 – 1/(3 ×1,2 2 )) = 31,893 кН/м
Нагрузка от блочной конструкции = 12,145 кН/м
Общая нагрузка = 45,978 кН/м
Внешние поперечные балки (ось A:1-3 и ось D:1-3)
Собственный вес балки (с коэффициентом) = 1,35 × 0,23 м × 0,25 м × 25 = 1,94 кН/м
Нагрузка от плиты = nlx /3 = (16,6 × 5)/3 = 27,667 кН/м
Нагрузка от блочной конструкции = 12,145 кН/м
Общая нагрузка = 41.752 кН/м
Внутренняя продольная балка (ось 2:AD)
Собственный вес балки (с коэффициентом) = 1,35 × 0,23 м × 0,25 м × 25 = 1,94 кН/м
Нагрузка от плиты = nlx/2(1 – 1/3k 2 ) = [(16,6 × 5)/2] × (1 – 1/(3 × 1,2 2 )) = 2 × 31,893 кН/м = 63,786 кН/м (мы умножили на два, потому что этот луч принимает нагрузка на плиту с двух направлений.)
Нагрузка от блочной конструкции = 0 (внутри здания нет блочной конструкции)
Суммарная нагрузка = 65,726 кН/м
Внутренние поперечные балки (ось B:1-3 и ось C:1-3)
Собственный вес балки (с коэффициентом) = 1. 35 × 0,23 м × 0,25 м × 25 = 1,94 кН/м
35 × 0,23 м × 0,25 м × 25 = 1,94 кН/м
Нагрузка от плиты = nlx/3 = (16,6 × 5)/3 = 2 × 27,667 кН/м = 55,334 кН/м (нагрузка на плиту действует с двух сторон) )
Нагрузка от блочной конструкции = 0
Общая нагрузка = 57,274 кН/м
Собственный вес колонн
Собственный вес колонны (с коэффициентом) = 1,35 × 0,23 м × 0,23 м × 3,75 м × 25 кН/м 3 = 6,695 кН
Расчет конструкций
Небольшое рассмотрение покажет, что опорные реакции для балок перекрытий (равные пролеты) могут быть получены с учетом приведенных ниже коэффициентов поперечной силы;
| Рис. 3: Коэффициент поперечной силы (2 – пролетная балка) |
| Рис. 4: Коэффициент поперечной силы (трехпролетная балка) |
Анализ осевых нагрузок на колонну
Расчет нагрузки на колонну A1
1-й этаж
Нагрузка от продольной балки крыши (1:A-D) = 0. 4 × 10,35 кН/м × 6 м = 24,84 кН
4 × 10,35 кН/м × 6 м = 24,84 кН
Нагрузка от поперечной балки крыши (A:1-3) = 0,375 × 10,35 кН/м × 5 м = 19,41 кН
Собственный вес колонны = 6,695 кН
Итого = 50,945 кН
Первый этаж
Нагрузка сверху = 50,945 кН
Нагрузка от продольной балки перекрытия (1:AD) = 0,4 × 45,978 кН/м × 6 м = 110,347 кН
Нагрузка от поперечной балки перекрытия (A:1-3) = 0,375 × 41,752 кН/м × 5 м = 78,285 кН
Собственный вес колонны = 6,695 кН
Итого = 246,272 кН
Расчет нагрузки на колонну A2
1-й этаж
2 Нагрузка от продольной балки крыши .4 × 10,35 кН/м × 6 м = 24,84 кН
Нагрузка от поперечной балки крыши (A:1-3) = 2(0,625 × 10,35 кН/м × 5 м) = 64,687 кН
Собственный вес колонны = 6,695 кН
Итого = 96,222 кН
Первый этаж
Нагрузка сверху = 96,222 кН
Нагрузка от продольной балки перекрытия (2:AD) = 0,4 × 65,726 кН/м × 6 м = 157,742 кН
Нагрузка от поперечной балки перекрытия (A:1-3) = 2 (0,375 × 41,752 кН/м × 5 м) = 156,57 кН
Собственный вес колонны = 6,695 кН
Итого = 417,229 кН
Расчет нагрузки на колонну B1
1-й этаж
Нагрузка от продольной балки крыши (1:A-D) = (0. 5 × 10,35 кН/м × 6 м) + (0,6 × 10,35 кН/м × 6 м) = 68,31 кН
5 × 10,35 кН/м × 6 м) + (0,6 × 10,35 кН/м × 6 м) = 68,31 кН
Нагрузка от поперечной балки крыши (B:1-3) = 0,375 × 10,35 кН/м × 5 м = 19,41 кН
Собственная вес колонны = 6,695 кН
Всего = 94,415 кН
Первый этаж
Нагрузка сверху = 94,415 кН
Нагрузка от продольной балки перекрытия (1:AD) = (0,5 × 45,978 кН/м × 6 м) + (0,6 × 45,978 кН/м × 6 м) = 303,455 кН
Нагрузка от поперечной балки перекрытия (B:1-3) = 0,375 × 57,274 кН/м × 5 м = 107,388 кН
Собственный вес колонны = 6.695 кН
Итого = 511,953 кН
Расчет нагрузки колонны B2
1-й этаж
Нагрузка от продольной балки крыши (2:A-D) = (0,5 × 10,35 кН/м × 6 м) + (0,6 × 10,35 кН/м × 6 м) = 68,31 кН
Нагрузка от поперечной балки крыши (A:1-3) = 2(0,625 × 10,35 кН/м × 5 м) = 64,687 кН
Собственный вес колонны = 6,695 кН
Всего = 139,692 кН
Первый этаж
Нагрузка сверху = 139,692 кН
Нагрузка от продольной балки перекрытия (2:A-D) = (0. 5 × 65,726 кН/м × 6 м) + (0,6 × 65,726 кН/м × 6 м) = 433,7916 кН
5 × 65,726 кН/м × 6 м) + (0,6 × 65,726 кН/м × 6 м) = 433,7916 кН
Нагрузка от поперечной балки перекрытия (A:1-3) = 2(0,625 × 57,274 кН/м × 5 м) = 357,9625 кН
Собственный вес колонны = 6,695 кН
Всего = 938,141 кН
Как видите, это было очень просто с использованием коэффициентов поперечной силы, учитывая тот факт, что балки были одинакового пролета. Когда балки не равны, вы должны провести анализ и точно передать поперечные силы.Теперь давайте сравним анализ нагрузки колонны B2 методом притока.
Балки, изгиб и граничные условия: граничные условия
Балки, изгиб и граничные условия: граничные условия Общий математический принцип заключается в том, что количество граничных условия, необходимые для определения решения дифференциальной уравнение соответствует порядку дифференциального уравнения. То уравнение статического пучка имеет четвертый порядок (имеет четвертую производную), поэтому каждый механизм поддержки балки должен давать четыре граничные условия.
Консольные балки
Рис. 5: Консольная балка.
Для консольной балки граничные условия следующие:
- w(0)=0 . Это граничное условие говорит о том, что основание балка (у стены) не испытывает никакого прогиба.
- w'(0)=0 . Мы также предполагаем, что луч у стены горизонтально, так что производная функции отклонения равен нулю в этой точке.
- ш»(Д)=0 .Это граничное условие моделирует предположение отсутствие изгибающего момента на свободном конце кантилевера.
- ш»'(Д)=0 . Это граничное условие моделирует предположение, что на свободный конец не действует сила сдвига. луч.
 2 ).
Заметим, что мы могли бы фактически использовать это граничное условие все время, так как если m=0 , сводится к предыдущему случаю.
2 ).
Заметим, что мы могли бы фактически использовать это граничное условие все время, так как если m=0 , сводится к предыдущему случаю.Балки с простой опорой
Рис. 6: Свободно опертая балка.
Просто опертая балка (или простая балка для краткости), имеет следующие граничные условия:
- w(0)=0 . Поскольку балка закреплена на опоре, балка не может испытывать прогиба на левой опоре.
- ш(Д)=0 . Балка также закреплена на правой опоре.
- w»(0)=0 . Что касается консольной балки, то эта граница условие говорит о том, что балка может свободно вращаться и не испытывает никаких крутящий момент. В реальной жизни обычно возникает небольшой крутящий момент из-за трения. между балкой и ее штифтом, но если штифт хорошо смазан, этим крутящим моментом можно пренебречь.
- ш»(Д)=0 . Точно так же луч не испытывает
и изгибающие моменты на его правом креплении.

Вопрос 7
Свободно опертая балка длиной L отклоняется однородной нагрузкой интенсивностью q . Мы предполагаем, что мы знаю E, I, L и q . Давайте использовать это Факт решения для прогиба балки под нагрузкой.- Дважды проинтегрируйте уравнение статической балки . (И пожалуйста, пожалуйста, пожалуйста, помните константы интегрирования!)
- Теперь у вас есть уравнение для w» , которое зависит от двух произвольные константы.Используйте два граничных условия, чтобы найти две константы в терминах свойств балка и нагрузка. (Вычеркните граничные условия, которые вы используете.)
- Константы теперь выражаются через известные величины, поэтому подставьте обратно в уравнение для w» и проинтегрируйте еще два раза, чтобы получить уравнение для w .
- Используйте оставшиеся граничные условия для решения
константы интегрирования через известные величины.

- Постройте график функции отклонения (или -w , если хотите провисание балки) на интервале [0,L] чтобы убедиться, что ваше уравнение имеет смысл.
- В каком положении балка испытывает максимальное отклонение? Где балка испытывает наибольший крутящий момент (самый большой изгибающий момент)? Где балка испытывает наибольшую поперечную силу? Интерпретируйте свои ответы с точки зрения физического смысла этих количества.
Другие балочные опоры
Существует множество других механизмов для поддержки балок. Например, оба конца балки могут быть прикреплены к стене. Или один конец может быть болтами, а другой конец может свободно вращаться. Или луч может быть зажаты с одного конца, но «нависают» над опорой, расположенной в какой-то точке вдоль его длина.Рис. 7: Другие механизмы для поддержки балок.
Вопрос 8
Каждый механизм поддержки имеет связанный с ним набор граничных условий. Чтобы получить некоторое представление о граничных условиях, нарисуйте
идеализированные балки, механизм опоры которых приводит к следующей границе
условия. Лучи должны быть показаны в «отклоненном» положении, как показано
на рисунках на этой странице. Во всех случаях балка поддерживается
только на концах.
Чтобы получить некоторое представление о граничных условиях, нарисуйте
идеализированные балки, механизм опоры которых приводит к следующей границе
условия. Лучи должны быть показаны в «отклоненном» положении, как показано
на рисунках на этой странице. Во всех случаях балка поддерживается
только на концах.- w(0)=0, w(L)=0, w'(0)=0, w'(L)=0 ; (Это называется балка с двойным зажимом . Объяснить, почему.)
- w(0)=0, w(L)=0, w'(0)= 0,2, w'(L)= -0.2 ;
- w(0)=0, w(L)=0, w'(L)= 0, w»(0)= 0 ;
- w(0)=0, w'(0)= 0, w»(L)=0, w»'(L)= -0,5 . (Подсказка: предположим, что кабель соединяется с концом балки в точке x=L .
- Выберите одно из приведенных выше граничных условий и найдите функцию отклонения
для равномерно распределенной нагрузки интенсивностью q .
Проанализируйте функцию отклонения, чтобы определить местоположение максимума.

