Связи и реакции связей

Тело, не связанное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным.

Тело, перемещениям которого в пространстве препятствуют какие-либо другие тела, называется несвободным.

Связями будем называть все тела, которые ограничивают перемещение данного тела.

Сила, с которой данная связь действует на тело, называется реакцией связи.

Направлена реакция связи всегда в сторону, противоположную той, куда связь не дает перемещаться телу.

Типы связей

1. Гладкая поверхность.

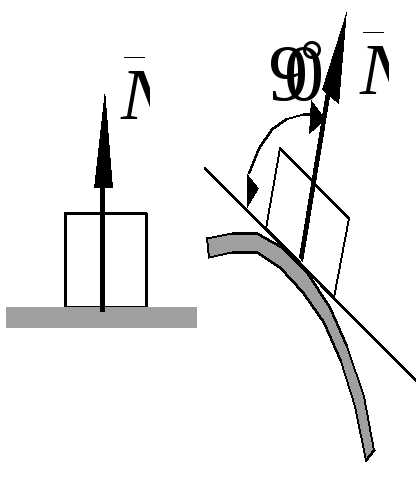
Реакция гладкой поверхности перпендикулярна этой поверхности.

2. Невесомый стержень.

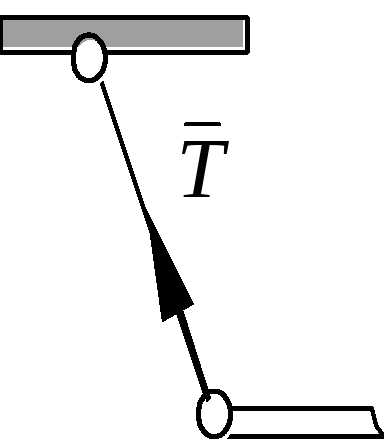
Реакция стержня всегда направлена вдоль его оси. Стержень может работать и на сжатие и на растяжение.

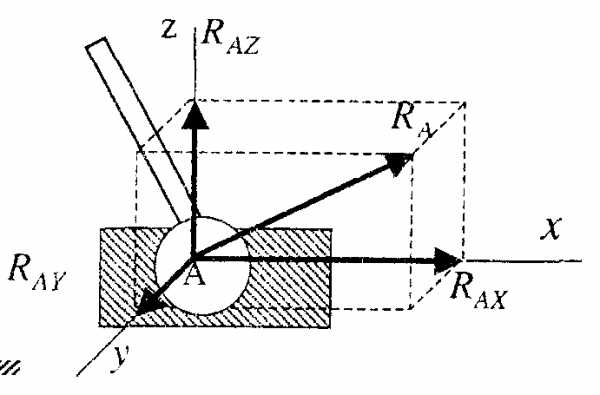
3. Неподвижный цилиндрический шарнир.

К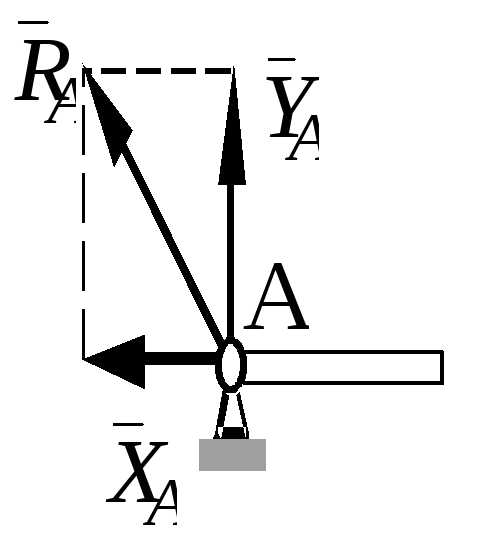ак правило, направление реакцииR_A заранее не известно, поэтому ее раскладывают по двум известным направлениям, например, по направлению координатных осей.

4. Подвижный цилиндрический шарнир.

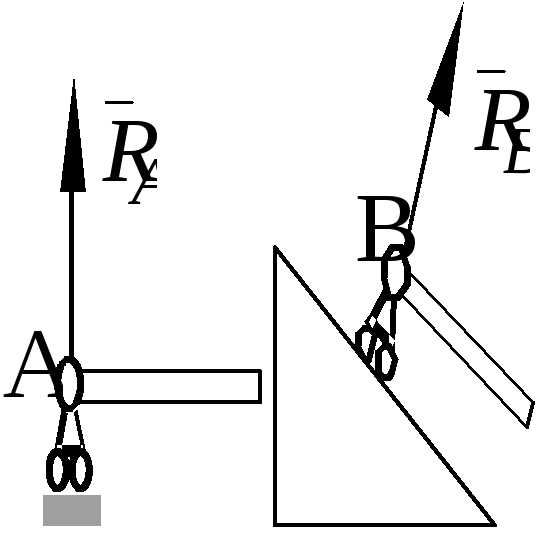
Реакция перпендикулярна плоскости возможного перемещения шарнира.

5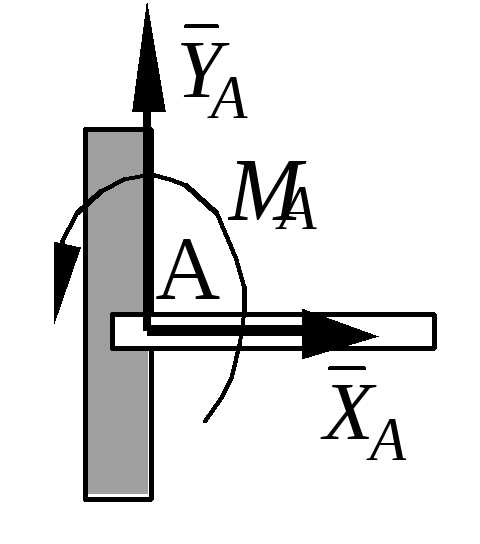.Жесткая заделка.

Реакция в данном случае состоит из трех компонентов: двух составляющих силы X_A, Y_A и реактивного момента M неизвестного направления (понятие момента силы будет рассмотрено позже).

6. Скользящая заделка.

Р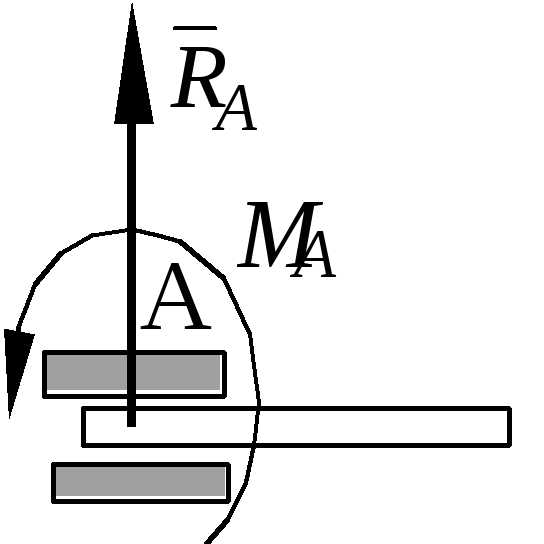еакция включает силу, перпендикулярную оси заделки, и реактивный момент.

Система сходящихся сил

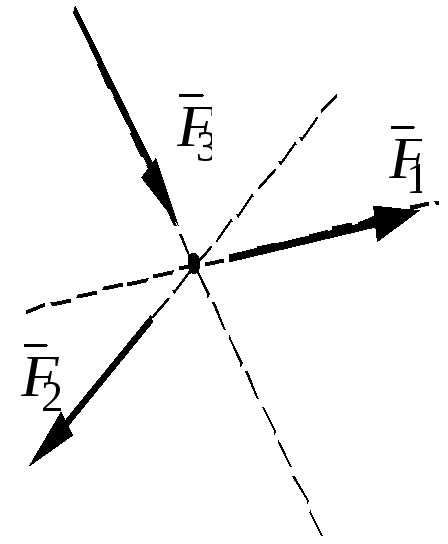
Если линии действия сил пересекаются в одной точке, то такая система называется сходящейся системой сил.

Эту систему можно заменить равнодействующей, построив силовой многоугольник или вычислив ее аналитически по выражениям (1.8)-(1.10).

Условие равновесия сходящейся системы сил

1. В геометрической форме.

Для равновесия сходящейся системы сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым.

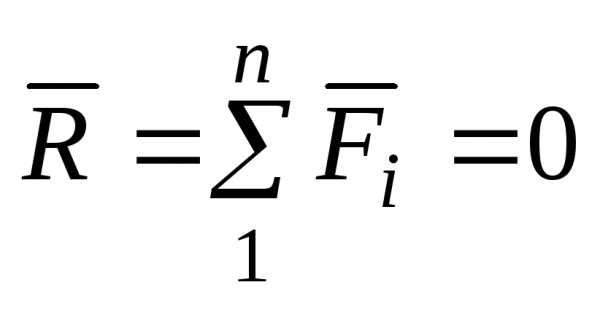. (1.11)

2. В аналитической форме.

Для равновесия сходящейся системы сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из координатных осей были равны нулю

. (1.12)

При решении задач на равновесие сходящейся системы сил иногда удобно пользоваться следующей теоремой о трех силах.

Теорема: Если тело находится в равновесии под действием трех сил, расположенных в одной плоскости, то линии действия этих сил параллельны или пересекаются в одной точке.

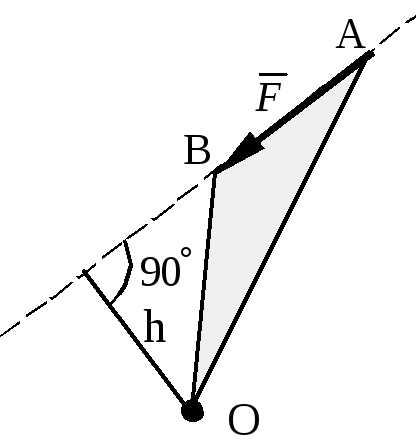
Произвольная плоская система сил Момент силы относительно точки (центра)

Момент силы относительно точки это количественная характеристика вращательного эффекта от действия силы.

Моментом силы относительно точки называется величина, равная взятому с соответствующим знаком произведению модуля силы на плечо, т.е. кратчайшее расстояние от центра до линии действия силы

. (1.13)

Если сила стремится повернуть тело относительно точки против часовой стрелки, то момент положительный, если по часовой стрелке – отрицательный.

Момент силы относительно центра равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через этот центр.

Момент силы численно выражается удвоенной площадью OAB

.

При решении задач для вычисления момента силы в некоторых случаях удобно пользоваться следующей теоремой Вариньона о моменте равнодействующей

.

Теорема: Момент равнодействующей плоской сходящейся системы сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.

, . (1.14)

studfiles.net

Связи и их реакции

Тело, перемещению которого в пространстве препятствует какие-нибудь другие тела, скрепленные или соприкасающиеся с данным, называется несвободным. Все то, что ограничивает перемещение данного тела в пространстве, называется связями.

Пример. Груз висит на веревке, ящик стоит на полу и т.д.

Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется

силой реакции (противодействия) связи или просто реакцией связи.

Силы, приложенные к телу, но не являющиеся реакциями, называются активными.

Направление силы реакции связи противоположно той, куда связь не дает перемещаться телу.

Направления реакций некоторых основных видов связи

1. Гладкая поверхность

Реакция связиN гладкой поверхности или опоры направлена по нормали к поверхностям соприкасающихся тел в точке касания и приложена в этой точке.

а) б) в)

Рис. 1.5

Если одна из соприкасающихся поверхностей является точкой, то реакция направлена по нормали к другой поверхности (рис. 1.5).

2. Нить, стержень.

Реакция Т натянутой нити и нагруженного стержняS направлена вдоль этих связей и приложена в точке контакта (рис. 1.6).

а) б)

Рис. 1.6

3. Цилиндрический шарнир (подшипник, петля).

РеакцияR цилиндрического шарнира лежит в плоскости, перпендикулярной оси шарнира, и может иметь любое направление в этой плоскости. Для определения R ее раскладывают на два взаимноперпендикулярных направления: R_x и R_y (рис. 1.7).

Рис. 1.7

4. Подвижная шарнирная опора.

Реакция связиR направлена перпендикулярно плоскости возможного перемещения шарнира (рис. 1.8).

5

Рис. 1.8

а)

б)

Рис. 1.9

. Шаровый шарнир и подпятник (рис. 1.9, рис. 1.10).

а) б)

Рис. 1.10

Реакция шарового шарнира и подпятника может иметь любое направление в пространстве.

А

Рис. 1.11

а)

б)

ксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей (рис. 1.11).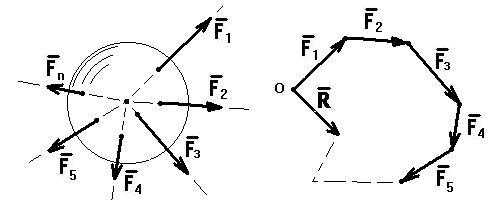

Сложение сил

Геометрический способ сложения сил

В

а)

б)

Рис. 1.12

еличина, равная геометрической сумме сил какой-либо системы называется главным вектором этой системы сил.

Пусть на твердое тело действует плоская система сил (F₁, F₂, F₃, …, F_n) (рис. 1.12).

Из произвольно выбранной точки О откладывается векторF₁, из его конца откладывается вектор F₂ и т.д. Вектор R, замыкающий силовой многоугольник, является результирующим:

Сложение двух сил

Пусть на тело действуют две силы, лежащие в одной плоскости (рис. 1.13).

.

Р

Рис. 1.13

езультирующая сила определяется по правилу параллелограмма, модуль силы определяется по теореме косинусов или синусов: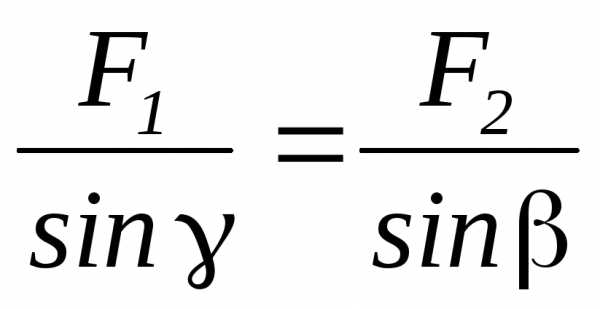

; .

Сложение трех сил не лежащих в одной плоскости

Р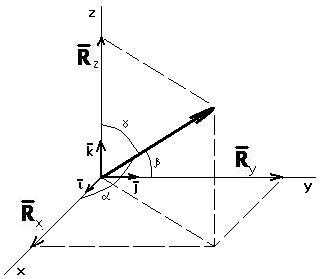ассмотрим три силы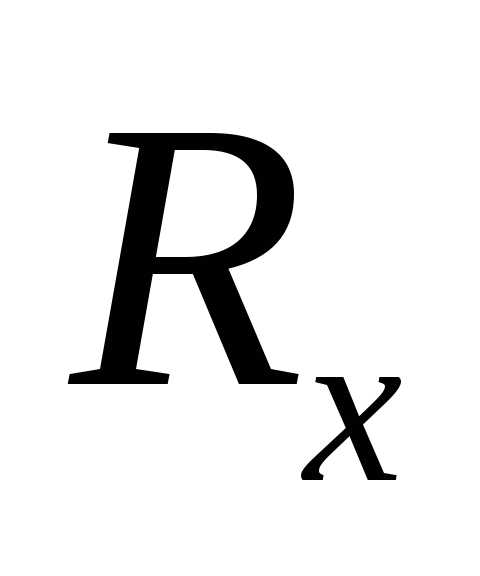,,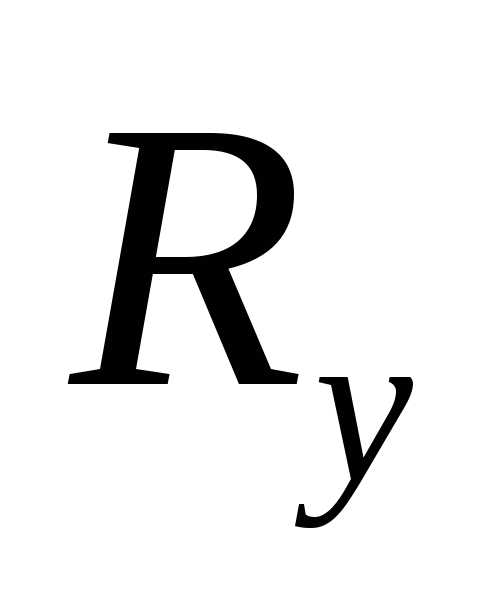не лежащие в одной плоскости (рис. 1.14). Результирующая сила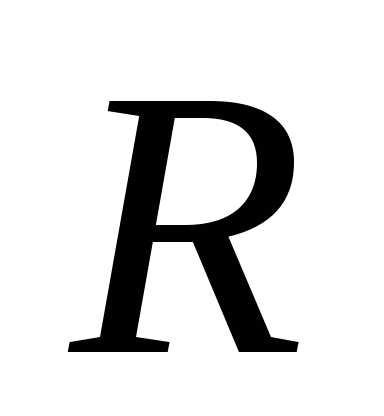равна:

.

Направление силы определим по направляющим косинусам:

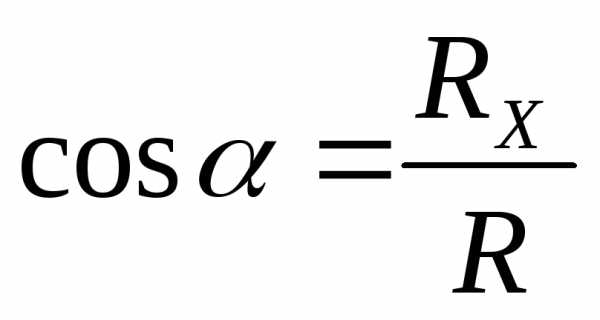
Рис. 1.14

; ; .

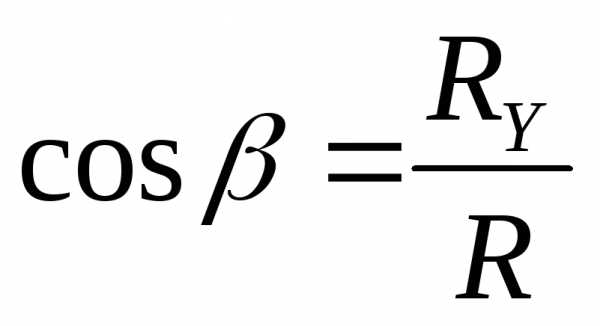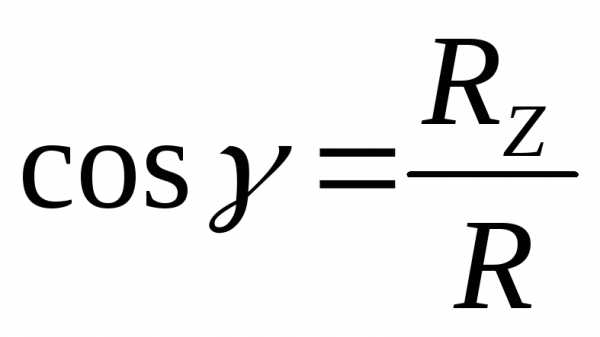Разложение сил

Разложение сил по двум заданным направлениям

Пусть надо силуF разложить по направлениям AB и AD (рис. 1.15).

Рис. 1.15

.

Задача сводится к построению параллелограмма, у которого стороны расположены по направлениям AB и AD и данная сила F является диагональю. Тогда стороны параллелограмма будут искомыми силами.

Разложение сил по трем заданным направлениям.

П

Рис. 1.16

усть направления силы не лежат в одной плоскости. Тогда задача сводится к построению параллелепипеда, у которого диагональю является данная сила, а ребра параллельны заданным направлениям (рис. 1.16).

.

Вопросы для самоконтроля

1. Что изучает статика?

2. Что такое абсолютно твердое тело?

3. Основные виды связей и их реакции?

4. Геометрическое сложение сил?

Задачи, рекомендуемые для самостоятельного решения: 1.1 – 1.6 [2]

Литература: [1], [3], [4].

Лекция 2.

Действия над силами. Система сходящихся сил

Проекция силы на ось и на плоскость

Проекция силы на ось. Пусть сила F образует с осью OX угол  (рис. 2.1), тогда проекция этой силы на ось будет:

F_x = Fcos.

П

Рис. 2.1

роекция силы на ось есть величина скалярная.

Проекция силы на плоскость. Проекцией силы F на плоскость OXY называется вектор F_xy = OB₁, заключенный между проекциями начала и конца силы F на эту плоскость (рис. 2.2.)

П

Рис. 2.2

роекция силы на плоскость есть величина векторная, так как она кроме численного значения характеризуется направлением на плоскости. По модулюF_xy = Fcos, где  — угол между направлением силы F и ее проекцией F_xy.

Аналитический способ задания сил. Для аналитического способа задания силы необходимо выбрать систему координат OXYZ и спроектировать силу на оси координат (рис. 2.3).

Направляющие косинусы определяются по формулам:

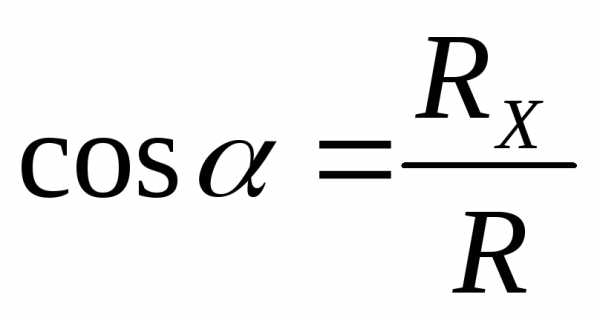
Рис. 2.3

; ; .

.

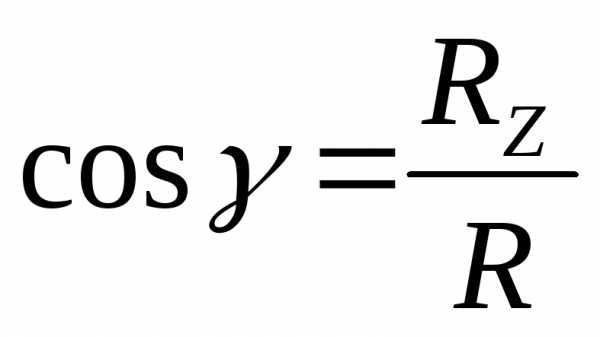Для плоской системы сил:

; ; ; .

studfiles.net

Решение задач на определение реакции связей — Мегаобучалка

 

Задача 1

Два абсолютно жестких стержня АВ и АС соединены шарниром в точке А и прикреплены к полу шарнирами В и С, образуя с полом соответственно углы 45° и 60° (рис. 22 а). К валику шарнира А подвешен на нерастяжимой нити груз D, вес которого Р= 100 кг. Определить усилия, возникающие в стержне АВ и АС. Весом стержней и нити пренебречь.

Решение.

Для определения усилий в стержнях АВ и АС следует рассмотреть равновесие шарнира А. Однако непосредственно приступить к исследованию равновесия узла А невозможно, так как он находится в равновесии под действием трех неизвестных сил: сил реакций стержней АВ и АС и реакции нити AD. Поэтому для определения силы реакции нити предварительно рассмотрим равновесие груза D. Груз D находится в равновесии под действием двух сил: веса Р и силы реакции нити Т. Эти силы направлены в противоположные стороны (рис. 22 б).

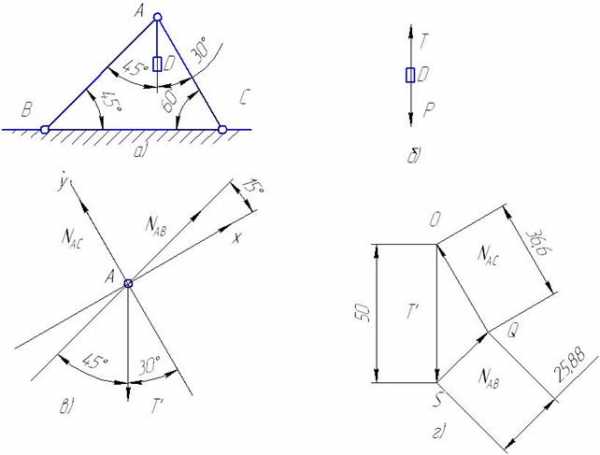
Рис. 22

 

Учитывая условие равновесия груза, получим, что Т = Р = 100 Н.

Теперь, когда одна из трех сил, приложенных к шарниру А, известна, можно изучить равновесие шарнира А. К шарниру А приложена одна известная сила ­ реакция нити Т, направленная по вертикали вниз. Силы реакций N_АВ и N_АС стержней АВ и АС направлены вдоль стержней. На рис. 22 в эти три силы изображены приложенными в шарнире А (направлены ли силы N_АВ и N_АС вдоль стержней вверх или вниз уточнится в последующем решении задачи).

 

Графическое решение задачи.

 

При равновесии шарнира А равнодействующая всех трех сил должна быть равна нулю, следовательно, силы Т, N_АВ и N_АС образуют замкнутый силовой треугольник.

Построение силового треугольника (рис. 22 г) начинаем с силы Т, известной по величине и по направлению. Принимаем масштаб построения М = 2 Н / 1 мм Выбрав точку О, приложим к ней силу Т в выбранном масштабе построений. Длина отрезка графически представляющего вектор Т равняется 50 мм.

Затем, проведя через начало и конец силы Т прямые, соответственно параллельные стержням АС и АВ, получим в пересечении третью вершину Q силового треугольника OSQ. Изобразив на сторонах треугольника SQ и QO стрелки так, чтобы сумма трех сил Т, N_АВ и N_АС равнялась пулю (в каждой из вершин силового треугольника OSQ должен быть расположен конец только одной из трех сил), получим направления сил реакций N_АВ и N_АС и их величину в миллиметрах. Умножив длину в миллиметрах на масштаб получим:

N_АВ = 51,8 Н, N_АС =73,2 Н.

 

Аналитическое решение задачи.

 

Принимаем направление оси y параллельно стержню АС, а направление оси x ей перпендикулярно, тогда угол между силой Т и осью y составит 30°, а угол между силой N_АВ и осью x составит 15° (рис. 22 в).

Составим уравнения равновесия:

S F_x=0

1) N_АВ * cos15°-T*sin30°=0

S F_y=0

2) N_АВ * sin 15°-T*cos 30°+ N_АС =0;

из уравнения 1 N_АВ = T*sin30°/ cos15°= 100* sin30°/ cos15°=51,8 Н;

из уравнения 2 N_АС = T*cos 30°- N_АВ * sin 15° = 100* cos 30°-

— 51,8* sin 15°=73,2Н

Ответ: N_АВ = 51,8 Н, N_АС =73,2 кг.

 

Задача 2

Однородная балка, вес которой равен Р=100 Н, прикреплена к полу шарниром А и опирается другим концом в точке В на выступ вертикальной стены. Определить силы реакций выступа В и шарнира, если балка АВ разует угол 30° с горизонтом (см. рис. 23).

Рис. 23

Решение задачи

Вес балки Р= 100 Н, являющийся единственной задаваемой силой, приложен в середине балки в точке С и направлен по вертикали вниз. На балку наложены две связи: выступ В и шарнир А. Сила опорной реакции выступа В направлена пер­пендикулярно к балке. Направление силы реакции шарнира А заранее неизвестно. Однако в данной задаче можно воспользоваться теоремой о трех непараллельных силах и указать направление линии действия силы реакции шарнира А. Действительно, проведя линии действия сил Р и R_B (рис. 24 а), определим их точку пересечения О. Так как балка находится в равновесии под действием трех сил Р, R_B и R_A, то линии действия этих сил должны пересечься в одной точке, т. е. линия действия силы реакции шарнира R_A должна пройти через эту точку О. Поэтому проводим линию действия силы реакции шарнира R_А через ее точку приложения — шарнир А и точку О.

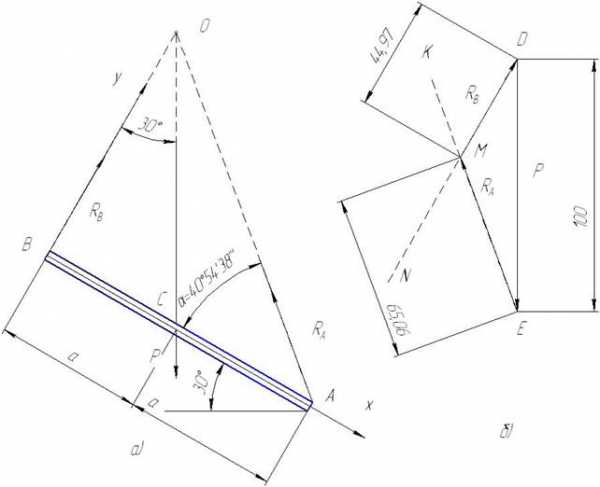
Рис. 24

 

Дальнейшее решение задачи не представляет затруднений.

Графический способ решения задачи

Строим замкнутый силовой треугольник. Из точки D, взятой вне основного рисунка, проводим силу Р, приняв масштаб построения М =1 Н/1 мм. Через начало и конец силы Р ( отрезок DE = 100 мм) проводим прямые DN и ЕК, соответственно параллельные линиям действия сил R_А и R_В (рис.24 б). В точке пересечения прямых DN и ЕК находим третью вершину М силового треугольника DEM. Направляем векторы сил так, чтобы в каждой из вершин силового треугольника был расположен конец одной из сил. Определяем длину отрезков EM и MD, с учетом выбранного масштаба:

R_B = 44,97 Н и R_A = 65,06 Н

Аналитический способ решения задачи

Принимаем направление оси y параллельно реакции R_B, а направление оси x ей перпендикулярно, тогда угол между силой P и осью y составит 30°, а угол между силой R_А и осью x нам неизвестен — обозначим его α (рис. 25 а).

Определим угол α.

Из прямоугольного треугольника ОВС: ОВ = ВС/tg30° = a/0.577

Из прямоугольного треугольника ОВА: tg α = ОВ/АВ = a/(0.577*2a) = 0.866

Отсюда α = 40°54’38»

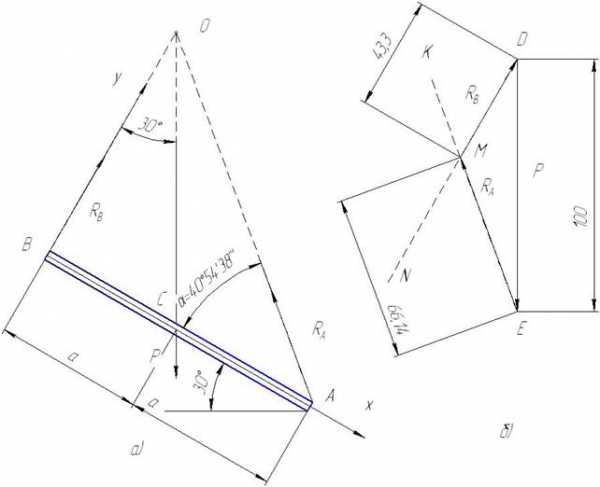
Рис. 25

Составим уравнения равновесия:

S F_x=0

1) — R_А * cos40°54’38»+P*sin30°=0

 

S F_y=0

2) R_А * sin 40°54’38»- P*cos 30°+ R_B =0;

 

из уравнения 1 R_А = P*sin30°/ cos40°54’38»= 100* sin30°/cos40°54’38»= 66,14 Н;

из уравнения 2 R_B = P*cos 30°- R_А * sin 40°54’38» = 100* cos 30°-

— 66,14* sin40°54’38» = 43,3 Н

Ответ: R_А = 66,14 Н, R_B =43,3 кг.

 

megaobuchalka.ru

1.3. Виды связей и их реакции

1. Гладкая (без трения) опорная поверхность. Такая связь препятствует движению тела в одном направлении. Реакция гладкой поверхности направлены всегда по общей нормали к поверхности тела и поверхности связи в их точке касания (рис. 6).

Рис. 6

Рис. 7

2. Гибкая связь. Реакции гибких связей всегда направлены вдоль самих связей к точке их подвеса (рис. 7).

3. Неподвижный цилиндрический шарнир (неподвижная шарнирная опора). Тело может только вращаться вокруг оси шарнира, перпендикулярной плоскости рисунка (рис. 8).

Рис. 8

Реакция R_A проходит через ось шарнира и может иметь любое направление в плоскости. При решении задач целесообразно заменить ее составляющими R_AX и R_AY.

4. Подвижная шарнирная опора. Реакция такой опоры направлена по нормали к опорной поверхности (рис. 9).

Рис. 9

5. Стержень. Стержень – прямолинейный невесомый элемент с двумя шарнирами на концах. При отсутствии нагрузки по его длине реакция стержня направлена вдоль его оси (рис. 10).

Рис.10

Рис.11

6. Шаровой шарнир (рис. 11). Этот вид связи закрепляет какую-нибудь точку тела так, что она не может совершать линейных перемещений в пространстве, при решении задач целесообразно заменить эту силу ее составляющими R_AX, R_AY, R_AZ.

7. Жесткая заделка (неподвижное защемление). Такая связь не допускает не только линейных перемещений, но и поворота тела (рис. 12).

Рис. 12

Со стороны связи на тело действует реакция R_A и момент M_A (момент реакции заделки или реактивный момент). При решении задач рекомендуется силу 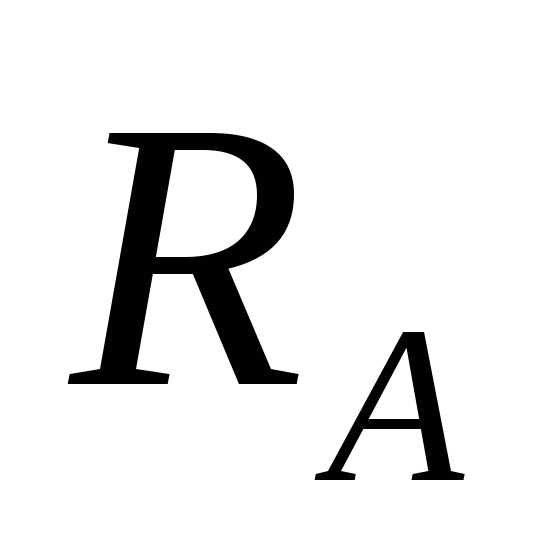заменить ее составляющимиR_AX и M_A.

Равновесие несвободных тел изучается в статике на основании аксиомы связей:

-всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие соответствующими реакциями.

Например, элемент, для которого связями являются шарнирно-неподвижная опора А и стержень ВС (рис. 13,а), можно рассматривать как свободное тело, находящееся в равновесии под действием заданных сил и реакций связей R_AX, R_AY и R_B (рис. 13,б). Значения этих реакций определяются из условий равновесия.

а) б)

Рис. 13

1.4. Плоская система сходящихся сил

Система си, линии действия которых пересекаются в одной точке, называется системой сходящихся сил (рис. 14,а.)

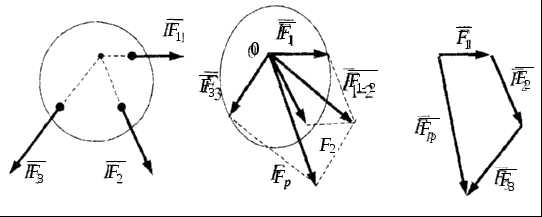
а) б) в)

Рис. 14

Продолжив линии действия заданных сил до пересечения, перенесем точки приложения сил в точку пересечения (рис. 14,б).

Используя последовательно правило параллелограмма, получим:

; .

В общем случае (для n сил): .

Таким образом, система сходящихся сил приводится к равнодействующей, равной их векторной сумме и проходящей через точку их пересечения.

Равнодействующую можно определить графически с помощью векторного (силового многоугольника (рис. 14,в). Для этого последовательно в выбранном масштабе откладываются векторы заданных сил. Равнодействующей системы сил является вектор, соединяющий начало первого вектора с концом последнего.

Равнодействующую можно также определить аналитическим способом. Проекция силы на ось (рис. 15,а) определяется произведением модуля силы на косинус угла между направлением силы и направлением оси.

На рис. 15,б показан многоугольник сил. Из рисунка видно, что

,

где ; , …., .

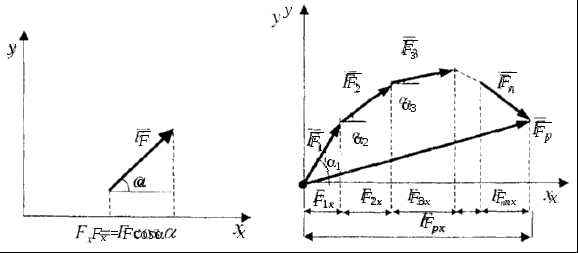
а) б)

Рис. 15

Аналогичные соотношения можно записать и для оси Y.

Т.е. проекция равнодействующей на какую-либо ось равна сумме проекций составляющих сил на ту же ось:

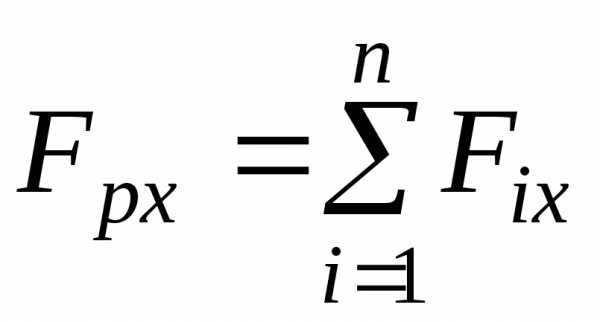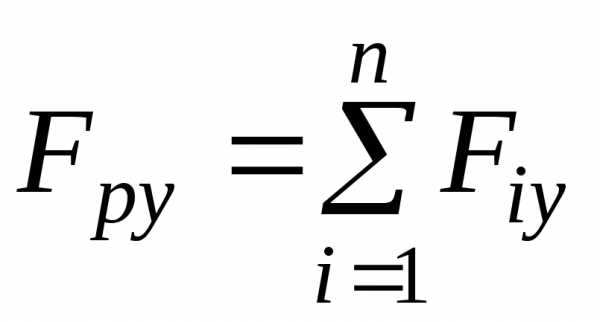, (4)

Равнодействующая определяется так:

(5)

где 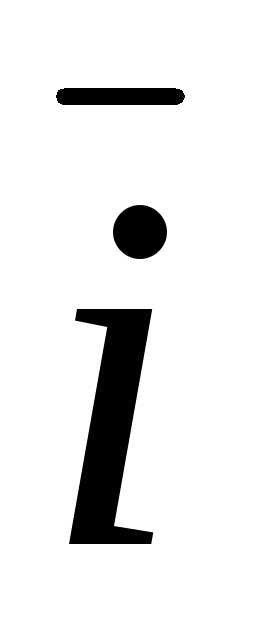,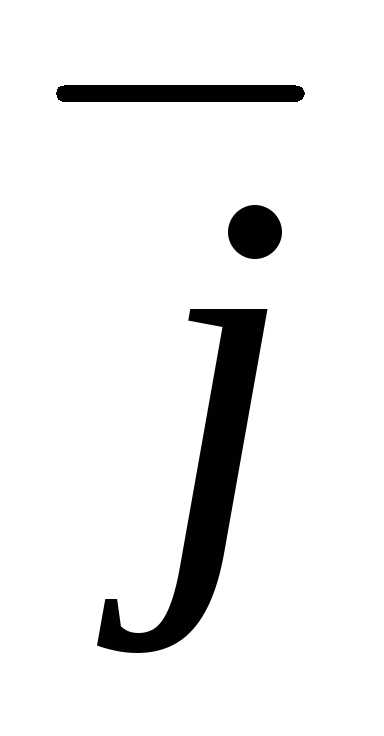– единичные векторы – орты.

Модуль равнодействующей равен

(6)

Направление вектора равнодействующей определяется с помощью направляющих косинусов – косинусов углов между равнодействующей и осями x, y:

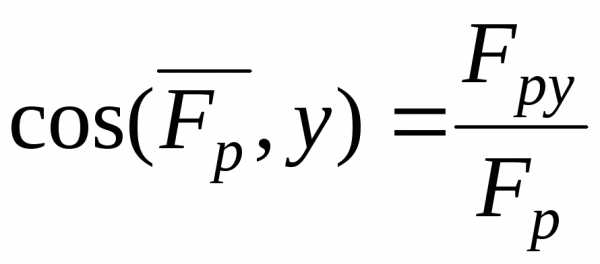, (7)

studfiles.net

Тема 2. Связи и их реакции

Тело, которое может совершать из данного положения любые перемещения в пространстве, называется свободным.

    Тело, перемещениям которого препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещение данного тела, называют связью.

    Сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.

Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного под действием активных(заданных)сил и реакций связей.

    Рассмотрим наиболее часто встречающиеся типы связей на плоскости и направления их реакций.

1. Гладкая плоскость (поверхность) или опора

Реакция N гладкой плоскости (поверхности) или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена к этой точке.

   

2. Гибкая нить (провода, канаты, цепи, ремни)

Реакция Т направлена вдоль нити к точке подвеса.

   

3. Невесомый стержень с шарнирами

Реакция N невесомого стержня направлена вдоль стержня. Обычно реакция Nизображается от тела по стержню, в предположении, что в равновесии стержень растянут.

 

4. Неподвижный цилиндрический шарнир илиподшипник

Реакция R_Aцилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси вращения, т. е. в плоскостиАху. Обычно ее раскладывают на две составляющие Х_Аи Y_Aпо двум взаимноперпендикулярным направлениям.

5. Шарнирно-подвижная опора (опора на катках)

Реакция R проходит через ось шарнира и направлена перпендикулярно к опорной плоскости.

6. Жесткая заделка

Нахождение реакции жесткой заделки сводится к определению составляющих Х_Аи Y_Aпрепятствующих линейному перемещению балки в плоскости действия сил, и алгебраической величине момента m_A, препятствующего вращению балки под действием приложенных к ней сил.

Аксиома связей (принцип освобождения от связей) — одна из аксиом теоретической механики. Может быть сформулирована следующим образом:

Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей.

При этом под связью понимается всё то, что ограничивает движение тела.

Простейший пример применения аксиомы связей: если на горизонтальной поверхности (например, на столе) в поле тяжести Земли (то есть, в «обычных» земных условиях) лежит тело, то мы можем мысленно отбросить горизонтальную поверхность и заменить её действие силой реакции этой поверхности.

5. План решения задач(Рассмотреть на примере)

Приступая к решению задания, необходимо разобраться в условии задачи и рисунке, а затем:

1. Составить расчетную схему, которая включает:

                 — объект равновесия,

                 — активные (заданные) силы,

                 — силы реакции, заменяющие действия отброшенных связей.

2. Определить вид полученной системы сил и выбрать, соответствующие ей, уравнения равновесия;

3. Выяснить, является ли задача статически определимой;

                4. Составить уравнения равновесия и определить из них силы реакции;

                5. Сделать проверку полученных результатов.

При замене связей (опор) силами реакций помнить:

                — если связь препятствует перемещению тела только в одном каком-нибудь направлении, то направление ее реакции противоположно этому направлению;

                — если же связь препятствует перемещению тела по многим направлениям, то силу реакции такой связи изображают ее составляющими, показывая их параллельно выбранным координатным осям  и .

Решение уравнений равновесия будет тем проще, чем меньшее число неизвестных будет входить в каждое из них. Поэтому, при составлении уравнений равновесия следует:

1) координатные оси  и  располагать так, чтобы одна из осей была перпендикулярна к линии действия хотя бы одной из неизвестных сил, в этом случае проекция  неизвестной силы исключается из соответствующего уравнения равновесия;

2) за центр моментов выбирать точку, в которой пересекаются линии действия наибольшего числа неизвестных сил реакций, тогда моменты этих сил не войдут в уравнение моментов.

Если сила  в плоскости  имеет две составляющие ее силы  и , то при вычислении момента силы  вокруг некоторой точки О, полезно применить теорему Вариньона, вычислив сумму моментов составляющих ее сил относительно этой точки (см. рис. 4).

Если к телу в числе других сил приложена пара сил, то ее действие учитывается только в уравнении моментов сил, куда вносится момент этой пары, с соответствующим, знаком.

Пример 1. Шар веса  опирается в точке  на наклонную плоскость, образующую с вертикалью угол , и привязан к стене веревкой, которая образует с вертикалью угол  (рис.13а). Определить реакцию плоскости в точке  и натяжение веревки.

Рис.13

 

Решение: Обозначим искомую реакцию плоскости, направленную по нормали  к этой плоскости, через , а натяжение веревки – через . Линия действия всех трех сил  и  пересекаются в центре шара . Примем вертикаль и горизонталь в точке  за координатные оси и найдем проекции сил  и  на эти оси:

, , ,

, , .

Так как данная система сходящихся сил является плоской, то условия равновесия (4) имеют вид

1) 

2) 

Умножив первое уравнение на , а второе  на  и сложив их, получим

.

Затем из первого уравнения находим

.

В случае, когда веревка, удерживающая шар, параллельна наклонной плоскости , получим , .

Для решения этой же задачи графическим способом, необходимо построить замкнутый силовой многоугольник. Построение силового многоугольника всегда нужно начинать с известных, заданных сил. Из произвольной точки  (рис.13б) проведем вектор , параллельный данной  силе , длина которого в выбранном масштабе изображает модуль этой силы. Затем через точки  и  проводим прямые, параллельные линиям действия искомых сил  и , которые пересекутся в точке . Векторы  и  определяют искомые силы  и .Чтобы найти направление искомых сил на силовом треугольнике , нужно обойти этот треугольник по его периметру, причем направление этого обхода  определяется направлением данной силы . Измерив длину сторон  и  и зная масштаб, в котором построена сила , найдем численные значения сил и .

studfiles.net

3.3 Виды Связей и их реакции

При взаимодействии между телом и его связями возникают силы, противодействующие возможным движениям тела. Тело, стремясь под действием приложенных сил осуществить перемещение, которому препятствует связь, будет действовать на нее с некоторой силой, называемой силой давления на связь. Одновременно по закону о равенстве действия и противодействия связь будет действовать на тело с такой же по модулю, но противоположно направленно силой.

Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции (противодействия) связи или просто реакций связи.

Силовое взаимодействие связи на рассматриваемое тело приводится к силе R и паре сил с моментом М. Сила R называется реакцией связи, а момент М – моментом реакции, опорным или реактивным моментом.

Реакции связи и опорные моменты относятся к пассивным силам, т.к. они не способны сообщить движение телу, т.е. не способны изменить кинематическое состояние тела. Все остальные силы – активные, способные изменить кинематическое состояние тела (не исчезают при устранении связей).

Принцип освобождаемости от связей

Для определения реакций связей используют принцип освобождаемости от связей или аксиому связей:

Всякое несвободное тело можно, мысленно отбросив связи, рассматривать как свободное, если действия связей заменить реакциями связей.

Определение реакций связей является одной из основных задач статического расчета любого сооружения или механизма.

В зависимости от направления реакций связи можно разделить на три группы:

1) направления реакций определяются связями и не зависят от других приложенных сил;

2) направление реакций частично определяются связями и зависят, кроме того, от других приложенных сил;

3) направление реакций заранее неизвестны и зависят от других приложенных сил.

Направление сил реакции (основные правила)

1. Реакция связи всегда противоположна тому направлению, по которому связь препятствует движению тела.

2. Если связь разрешает поступательные движения тела в каком-то направлении, то силы реакции в таком направлении не будет, если связь запрещает движение в каком-то направлении, то реакция будет.

3. Если связь разрешает повороты вокруг нее, то момента реакции не будет, если запрещает повороты, то будет действовать момент реакции.

ОдНосторонние связи (1 группа)

К этой группе относятся следующие, часто встречающиеся в практических задачах связи:

– связь в виде идеально гладкой поверхности;

– свободное опирание тела о связь;

– опора на катках;

– гибкая связь;

– идеальный блок.

3.3.1 Связь в виде гладкой (без трения) поверхности

Любая реальная поверхность является шероховатой и имеет трение. Если при движении по поверхности тело испытывает минимальное трение, например, при скольжении конькобежца по льду, при движении полированного стального или стеклянного бруска по полированной стеклянной или стальной поверхности и т.д. то силой трения можно пренебречь. В этом случае получим идеальную абсолютно гладкую поверхность. Подобное допущение упрощает решение задач.

Гладкая поверхность не дает телу перемещаться только по направлению общего перпендикуляра (нормали) к поверхности соприкасающихся тел в точке их касания. Поэтому реакция N гладкой поверхности или опоры направлена по общей нормали к поверхности соприкасающихся тел в точке их касания и приложена в этой точке.

Пример 1. На гладкой неподвижной горизонтальной плоскости покоится шар (рис. 14 а). Плоскость, ограничивая движение шара, является для него связью. Если мысленно освободить шар от связи (рис. 14 б), то для удержания его в покое к нему в точке касания с плоскостью нужно приложить силу N, равную весу шара G по модулю и противоположную ему по направлению.

Сила N и будет реакцией плоскости. Тогда шар, освобожденный от связи, будет свободным телом, на которое действует задаваемая сила G и реакция плоскости N.

а)	б)
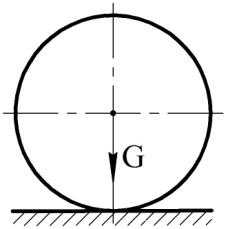
Рис. 14

Пример 2. На рисунке 15 показана связь в виде контакта двух идеально гладких поверхностей: цилиндрической поверхности с неподвижной горизонтальной плоскостью. Реакция связи N направлена также по нормали к опорной поверхности.

а)	б)
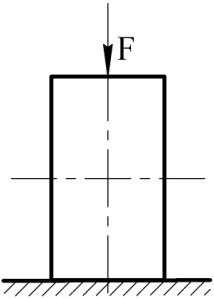
Рис. 15

Сила N и будет реакцией плоскости. Тогда шар, освобожденный от связи, будет свободным телом, на которое действует задаваемая сила G и реакция плоскости N.

studfiles.net

Связи и реакции связей

Связи и реакции связей

Тело называется свободным , если его перемещение в пространстве ничем не ограничено. В противном случае тело называется несвободным , а тела, ограничивающие перемещения данного тела, ¾ связями . Силы, с которыми связи действуют на данное тело, называются реакциями связей .

Основные виды связей и их реакции:

1.

Гладкая поверхность (без трения):

Реакция гладкой поверхности направлена по нормали к этой поверхности (перпендикулярна общей касательной).

2.

Опорная точка (ребро):

Реакция перпендикулярна опирающейся поверхности.

3. Идеальная нить (гибкая, невесомая, нерастяжимая):

Примеры: моделирует трос, канат, цепь, ремень,…

Реакция идеальной нити направлена по нити к точке подвеса.

4. Идеальный стержень (жесткий, невесомый стержень, на концах которого шарниры):

Реакция связи направлена по стержню.

В отличие от нити стержень может работать и на сжатие.

5. Цилиндрический шарнир:

Такая связь позволяет телу перемещаться вдоль оси, поворачиваться вокруг оси шарнира, но не позволяет точке закрепления перемещаться в плоскости, перпендикулярной оси шарнира. Реакция лежит в плоскости, перпендикулярной оси шарнира, и проходит через нее. Положение этой реакции не определено, но она может быть представлена двумя взаимно перпендикулярными составляющими

6. Сферический шарнир:

Такая связь не дает точке закрепления тела перемещаться ни в одном из направлений. Положение реакции не определено, но она может быть представлена тремя взаимно перпендикулярными составляющими.

7. Подпятник:

Реакция данной связи задается аналогично предыдущему случаю.

8. Жесткая заделка:

Такая связь препятствует перемещению и повороту вокруг точки закрепления. Контакт тела со связью осуществляется по поверхности. Имеем распределенную систему сил реакции, которая, как будет показано, может быть заменена одной силой и парой сил.

Аксиома освобождаемости от связей:

Всякое несвободное тело можно считать свободным, если мысленно освободиться от связей, а их действие заменить соответствующими реакциями.

mirznanii.com