Определение опорных реакций балок — Студопедия
Поделись с друзьями:
Цель работы:
1 Научиться определять реакции в опорах балок.
2 Составлять уравнения равновесия плоской системы произвольно-расположенных сил.
3 Научиться определять равнодействующую силу распределенной нагрузки.
Порядок выполнения работы:
1 Заменить распределенную нагрузку ее равнодействующей, которая является сосредоточенной силой. Для равномерно распределенной нагрузки равнодействующая равна произведению интенсивности нагрузки q на длину участка, на котором она действует:
R = q • l, (2)
Перед решением задач рекомендуется уяснить и закрепить порядок нахождения равнодействующей и определения расстояний от нее до опор. При отсутствии навыков решения таких задач необходимо указывать положение равнодействующей относительно опор. В дальнейшем этого можно не делать.
2 Обозначить опоры.
З Освободиться от опор и заменить их действие на балку реакциями. На балку действуют только вертикальные нагрузки и сосредоточенные моменты. Реакции опор при такой нагрузке будут только вертикальными. Обычно их направляют вверх (против действия основной нагрузки) и обозначают реакцию опоры A – RA, а опоры B — RB.
4 Составить уравнения равновесия вида:
∑ Fiх = 0;
∑ Fi у = 0;
∑ МА = 0, (3)
Напомним, что моментом силы относительно точки называется произведение этой силы на плечо – кратчайшее расстояние от этой точки приложения силы (в общем случае до линии действия силы).
Если сила стремится повернуть балку относительно рассматриваемой точки по часовой стрелке, то будем считать ее момент положительным, а если против – отрицательным.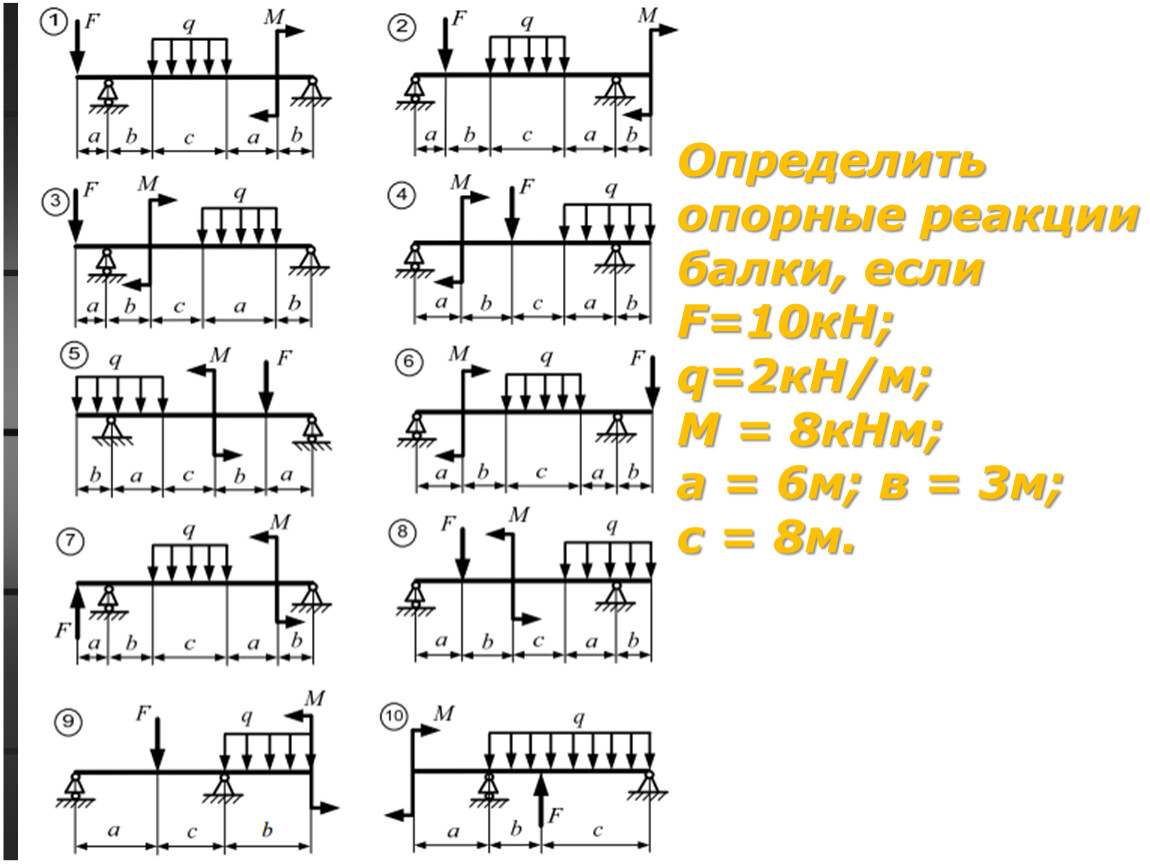
Решить уравнения и найти реакции RA и RB.
5.Выполнить проверку решения. Для этого составляют уравнение равновесия:
∑ МB = 0, (4)
Если оно удовлетворено, то реакции найдены правильно, а если нет, то в решении допущена ошибка.
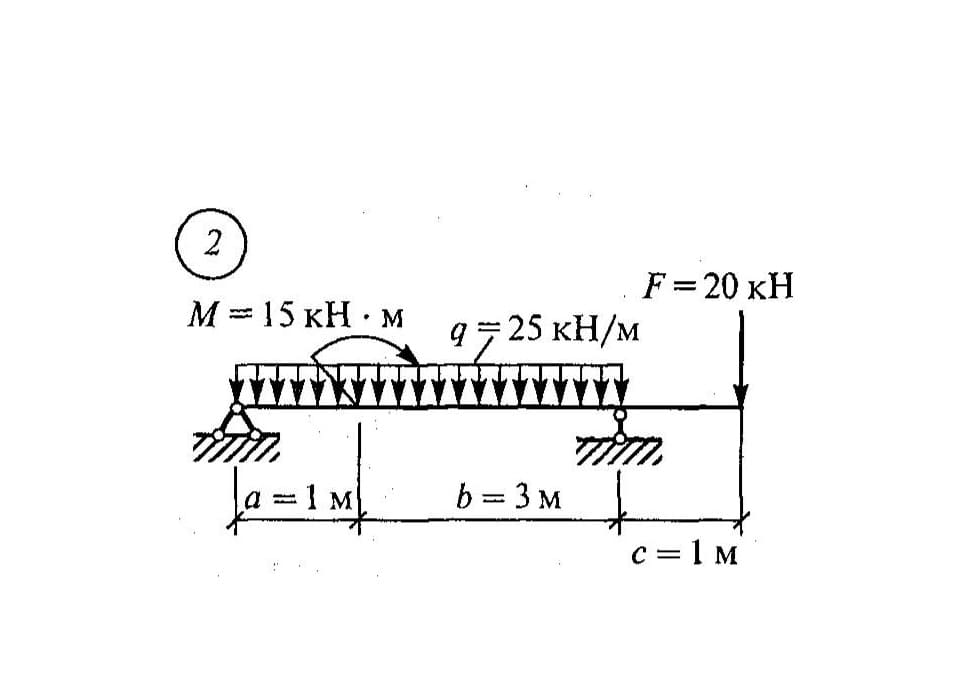
Пример 2 Определить реакции опор балки, если известно
F = 20 кН, М =10 кН× м, q = 1 кН/м (рисунок 5).
Рисунок 5 Схема задачи
Решение:
1 Изображаем балку вместе с нагрузками.
2 Выбираем расположение координатных осей, совместив ось Х с балкой, а ось У
3 Производим необходимые преобразования заданных активных сил: силу, наклонённую к оси балки под углом α, заменяем двумя взаимно перпендикулярными составляющими
Fх = F× сos 30° = 20× 0,866 = 17, 32 кН
Fу = F× сos 60° = 20× 0,5 = 10 кН,
а равномерно распределенную нагрузку — её равнодействующей
Q = q × CD = 1 × 2 = 2 кН,
Равнодействующая Q приложена в середине участка CD, в точке К (рисунок 6).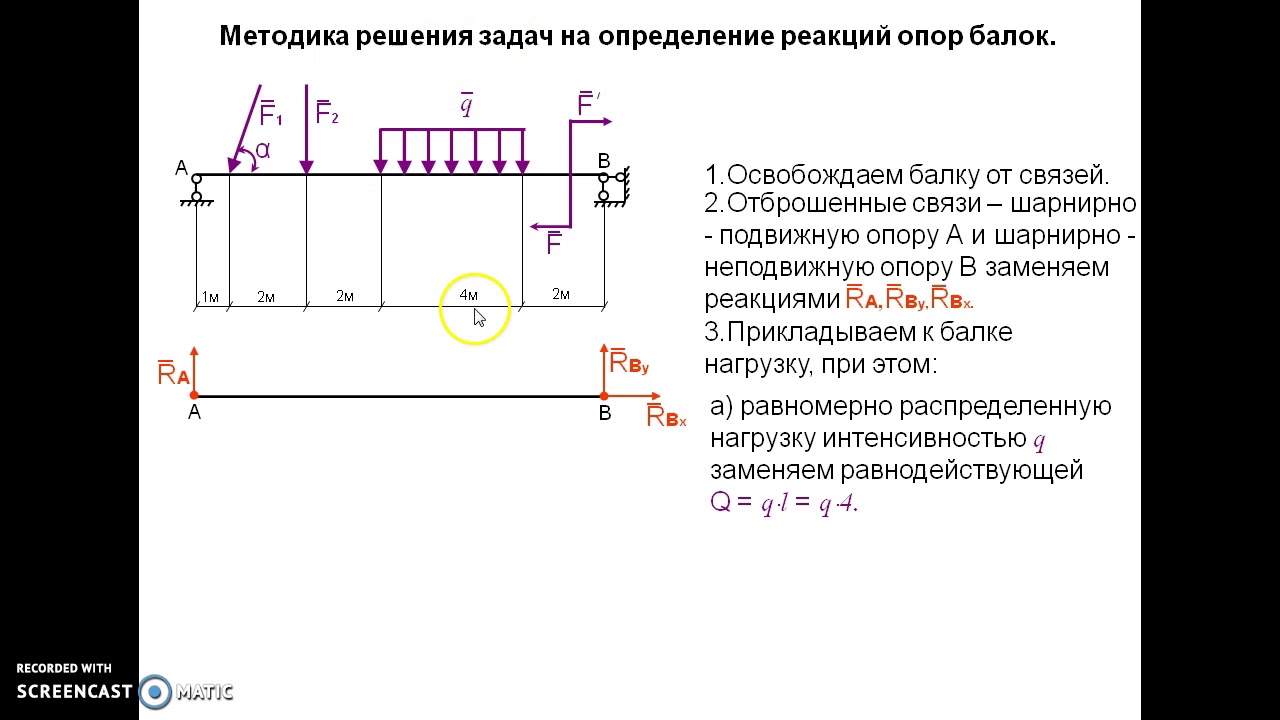
Рисунок 6 Схема преобразования заданных активных сил
4 Освобождаем балку от опор, заменив их опорными реакциями, направленными вдоль выбранных осей координат (рисунок 7).
Рисунок 7 Схема реакций балки
5 Составляем уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор и определяем неизвестные реакции опор.
∑ МА = 0; Fу × АВ + M + Q× AK — RDy ×AD = 0 (1)
∑ МD = 0; RAy ×AD — Fу × ВD + M — Q× KD = 0 (2)
∑ Fiх = 0; RAх — Fх = 0 (3)
6 Определяем реакции опор балок RAy, RDy и RAх решая уравнения.
Из уравнения (1) получаем
RDy = Fу × АВ + M + Q× AK / AD = 10 × 1 + 10 + 2 × 3 / 4 = 6,5 кН
Из уравнения (2) получаем
RAy ×= Fу × ВD — M + Q× KD / AD =10 × 3 — 10 + 2 / 4 = 5,5 кН
Из уравнения (3) получаем
RAх = Fх = F× сos 30° = 20× 0,866 = 17, 32 кН
7 Проверяем правильность найденных результатов:
∑ Fi y = 0; R
Условие равновесия ∑ Fi y = 0 выполняется, следовательно, реакции опор найдены верно.
Таблица 3 Схемы балок (вторая цифра варианта)
Таблица 4 Исходные данные (первая цифра варианта)
| Первая цифра варианта | F, кН | М, кН•м | q, кН/м |
| 0 | 10 | 7 | 5 |
| 1 | 20 | 11 | 6 |
| 2 | 30 | 15 | 7 |
| 3 | 40 | 19 | 8 |
Контрольные вопросы:
1 Что называется моментом силы относительно точки? Как выбирается знак момента?
2 Что такое плечо силы?
3 Изменится ли момент силы относительно данной точки при переносе силы по линии её действия?
4 Сформулировать условия равновесия плоской системы произвольно расположенных сил.
5 В каком случае момент силы относительно точки равен нулю?
6 Как определить равнодействующую равномерно-распределенной нагрузки?
7 Что значит привести силу к данному центру?
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
⇐ Предыдущая12345Следующая ⇒
Тема: Определение опорных реакций балок Цели: 1 Приобретение практических навыков и умений в определении опорных реакций балок. 2 Развитие самостоятельности и нахождение конструктивных решений при выполнении задания.
Последовательность решения задачи: 1 Изобразить балку вместе с нагрузками. 2 Выбрать расположение координатных осей, совместив ось х с балкой, а ось у, направив перпендикулярно оси х; 3 Произвести необходимые преобразования заданных активных сил: силу, наклоненную к оси балки под углом а, заменить двумя взаимно перпендикулярными составляющими, а равномерно распределенную по закону прямоугольника нагрузку – ее равнодействующей, приложенной в середине участка распределения нагрузки; 4 Освободить балку от опор, заменив их действие реакциями опор, направленными вдоль выбранных осей координат; 5 Составить уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор; 6 Проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задачи.
Пример 2. Определить реакции опор балки (рис. 3, а). 1 Изобразим балку с действующими на нее нагрузками (рис. 3, а). 2 Изображаем оси координат х и у. 3 Силу F заменяем ее составляющими и . Равнодействующая qCD равномерно распределенной нагрузки, приложенная в точке пересечения диагоналей прямоугольника (рис. 3, б), переносится по линии своего действия в середину участка CD, в точку К. 4 Освобождаем балку от опор, заменив их опорными реакциями (рис. 2, в). 5 Составляем уравнения равновесия статики и определяем неизвестные реакции опор. а) Из уравнения суммы моментов всех действующих на балку сил, составленного относительно одной из точек опор, сразу определяем одну из неизвестных вертикальных реакций: б) Определяем другую вертикальную реакцию: в) Определяем горизонтальную реакцию: ; 6 Проверяем правильность найденных результатов:
Условие равновесия выполняется, следовательно, реакции опор найдены верно. Варианты к задаче приведены в таблице 2, а графические решения – на рисунке 3.
Контрольные вопросы:
Список литературы: 1 Аркуша А. И. Руководство к решению задач по теоретической механике. М., 1976. 2 Аркуша А. И., Фролов М. И. Техническая механика. М., 1983. 3 Мовнин М. С, Израелит А. Б., Рубашкин А. Г. Руководство к решению задач по технической механике. М., 1977. 4 Никитин Е. М. Теоретическая механика для техникумов. М., 1983. 5 Сборник задач по технической механике. Багреев В. В., Винокуров А. Н., Киселев В. И. и др. Л., 1973. 6 Файн А. М. Сборник задач по теоретической механике. М, 1978.
Рисунок 3 — Графические решения задачи. Таблица 2 – Варианты к задаче
⇐ Предыдущая12345Следующая ⇒
|
Определение реакций на свободно поддерживаемой балке
Содержание
- Цель
- Принцип испытаний:
- Родственная теория
- Балка:
- Типы опор для балки 9000 4
- Роликовая опора:
- Шарнирная или штифтовая опора:
- Фиксированная опора:
- Типы нагрузки
- Сосредоточенная или точечная нагрузка:
- Равномерно распределенная нагрузка (UDL):
- Переменно распределенная нагрузка (VDL):
Цель 900 47
Целью данного эксперимента является сравнение экспериментальных результатов опорных реакций свободно опертой балки с аналитические.
Принцип тестирования:
Тест основан на «Принципе моментов». ‘ Он утверждает, что если система копланарных сил действует на твердое тело, и тело остается в равновесии, несмотря на действующие на него силы, то сумма всех вертикальных сил, действующих на тело, равна нулю, сумма всех горизонтальных сил силы равны нулю, и алгебраическая сумма их моментов в любой точке внутри плоскости также равна нулю. Математически
ΣFx=0; ΣFy=0 и ΣM=0
Связанная теория
Балка:
Балка представляет собой линейный элемент, используемый в качестве несущего элемента конструкции, на который в основном действуют изгибающие моменты. Он обслуживает приложенную нагрузку за счет изгибающего действия, которое в значительной степени зависит от конечных условий балок. Конечные условия и характер приложенной нагрузки, как правило, определяют изгиб балки.
Типы опор для балки
В зависимости от конечных условий балка может поддерживаться следующими способами:
Роликовая опора:
Роликовая опора ограничивает движение балки только в направлении, перпендикулярном поверхности, на которую она опирается. Он не ограничивает поступательное движение параллельно своей поверхности или вращение балки. Поэтому роликовая опора обеспечивает только одну реакцию на конце балки, где она предусмотрена.
Он не ограничивает поступательное движение параллельно своей поверхности или вращение балки. Поэтому роликовая опора обеспечивает только одну реакцию на конце балки, где она предусмотрена.
Как видно из названия, опора петли ведет себя почти так же, как дверная петля. Предотвращает все виды поступательных перемещений элемента. Однако, когда балка подвергается нагрузке, шарнирная опора не может подняться до своего сопротивления, и элемент изгибается, изгибается или поворачивается на конце, где предусмотрен шарнир.
Фиксированная поддержка:
Неподвижная опора обеспечивает фиксацию балки на конце. Это означает, что он сдерживает все виды поступательных и вращательных движений балки в самом конце. Следовательно, при любой внешней нагрузке кривизна балки начинает отклоняться от неподвижной опоры.
Следует иметь в виду, что увеличение числа опор делает балку устойчивой, но статически неопределимой.
Типы нагрузки
Внешняя нагрузка, действующая на балку, может быть любого из следующих типов;
Точечная нагрузка — это нагрузка, прикладываемая к площади, которая очень мала по сравнению с общей площадью элемента. Следовательно, предполагается, что он действует в точке. На следующем рисунке показана точечная нагрузка, действующая на балку на расстоянии от левой опоры.
Этот тип нагрузки равномерно распределяется по определенной площади элемента. Слово «распределенная» означает, что внешняя сила является нагрузкой на площадь. Кроме того, UDL не меняет своей интенсивности и направления в течение всего времени действия. На рисунке ниже показана равномерно распределенная нагрузка интенсивностью « q ”, действующая на весь пролет балки L.
Чтобы применить уравнения равновесия, UDL преобразуется в эквивалентную точечную нагрузку. Эквивалентная нагрузка фактически представляет собой площадь диаграммы нагрузки и действует в центре тяжести диаграммы нагрузки.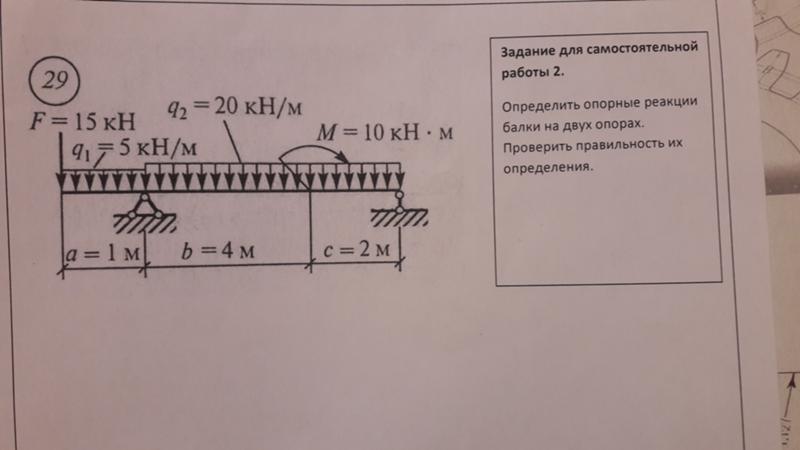
Как видно из названия, этот тип нагрузки различается по величине и неравномерно распределяется по пролету, на который она действует. На следующем рисунке показана переменно распределенная нагрузка величиной «w», действующая на конкретную секцию пролета балки L.
Опять же, эквивалентная точечная нагрузка вычисляется путем вычисления площади диаграммы нагрузки, которая в данном случае является треугольником, и результирующая эквивалентная нагрузка действует в центре треугольника.
Устройство
- Устройство с просто поддерживаемой балкой: оно состоит из двух пружинных противовесов, которые действуют как концевые опоры балки и обеспечивают экспериментальные значения сил реакции, когда балка подвергается внешней нагрузке. Применяемые грузы размещены в подвижных подвесках, которые легко скользят по длине балки и могут быть установлены в любой точке.
- Пружинные весы для измерения силы реакции балки
- Грузы для приложения нагрузки к балке в сборе
- Вешалки для гирь
- Рулетка для измерения длины балки или ее сечения.

Рис.: Одноопорный балочный аппарат
Процедура испытаний
- Расположите пружинные противовесы в местах, где должны быть смоделированы граничные условия опоры. Это точки, в которых будут развиваться силы реакции, и их значение будет определяться пружинными противовесами.
- Запишите начальное показание на пружинных балансах перед нагрузкой на балку.
- Измерьте пролет балки с помощью рулетки и запишите значение как «L». Следует иметь в виду, что размах балки в этом случае будет равен межцентровому расстоянию между двумя пружинными противовесами.
- Нагрузите балку, поместив грузы в подвески, которые висят на балке. На балку можно воздействовать любым количеством нагрузок. Однако при нагружении следует учитывать прочность материала балки на изгиб.
- Измерьте и запишите расстояние каждого груза от любой опоры.
- После того, как балка нагружена, убедитесь, что сборка свободна от какой-либо другой нагрузки, на которую не обращают внимания.

- Запишите окончательные показания на пружинных балансах. Разница между начальным и конечным показаниями пружинных весов дает силу реакции, развиваемую на конкретном конце балки.
- Аналитически определите реакции носителя и сравните с экспериментальными результатами.
- Повторите процесс, изменив величину и положение приложенной нагрузки.
Равновесие подразумевает следующее;
ΣFy=0;
R A +R B =W 1 +W 2
ΣM=0;
R B (L)=W 1 (L 1 ) +W 2 (L 2 )
Наблюдения и расчеты
Длина луча, L (см)
Начальное показание на первом пружинном балансе без нагрузки = (фунты)
Начальное показание на втором пружинном балансе без нагрузки = (фунты)
Экспериментально задается опорная реакция на конкретном конце балки по,
| Старший № | Вес, Ш 1 | Вес, Ш 2 | Расстояние л 1 | Расстояние л 2 | Реакция, R А | Реакция, R B | ||||
| ( фунтов ) | ( фунтов ) | (см) | (см) | ( фунтов. ) ) | ( фунтов ) | |||||
| Расшир. | Ана. | Дифференц. | Расшир. | Ана. | Дифференц. | |||||
| 1. | ||||||||||
| 2. | ||||||||||
| 3. | ||||||||||
| 4. | ||||||||||
Результаты
Результаты испытаний приведены ниже;
Экспериментальное значение R A =
Аналитическое значение R A =
Разница в процентах
Экспериментальное значение R b =
Аналитическое значение Значение R b =
Разница в процентах
Обсуждение
отклонение результатов эксперимента от результатов анализа указывает на некоторые случайные, человеческие или систематические ошибки при выполнении теста. К ним относятся ошибочные измерения длины, неточное считывание показаний пружинных весов, позиционирование груза с отклонением от центральной оси балки или любой другой незамеченный источник нагрузки, такой как вибрация испытательной установки и т. д.
К ним относятся ошибочные измерения длины, неточное считывание показаний пружинных весов, позиционирование груза с отклонением от центральной оси балки или любой другой незамеченный источник нагрузки, такой как вибрация испытательной установки и т. д.
Фиксированная концевая опора (2D и 3D) Реакции в расчете конструкций
Anre A 28 июня 2021 г.
Реакции — это силы, возникающие в опорах конструкции, когда эти опоры сдерживают перемещение в данной точке. Если опора не сдерживает движение в этой точке, реакции нет. Исходя из этого, выделяют несколько видов опор, предусмотренных для конструкции.
| Фиксированная концевая опора (2D и 3D) Реакции в расчете конструкций |
Все компоненты конструкции соединяются и соединяются с помощью опор и соединений, как показано на рис.1 ниже. На рисунке показана балка, поддерживаемая двумя колоннами на концах балки.
| Рис.1. Опоры в каркасной конструкции здания Изображение предоставлено: Библиотека ASCE |
Подробнее о различных типах опор можно прочитать в статье: Типы опор в расчете конструкций — граничные условия
Нет времени читать??? Смотреть видео
Рекламные объявления
Реакции опоры фиксированного конца в 2D
В дальнейшем мы собираемся представить количество реакций на каждой опоре как r e
Рассмотрим балку AB с одним концом, закрепленным в точке «A». а конец «В» свободен и подвергается нагрузке под углом θ. Нагрузка приводит к отклонению точки B.
Мы обсудим реакции в точках «B» и «Á», чтобы понять, как возникают реакции в опорах.
Реакции в конце B
- Под действием нагрузки «P»,
конец А остается таким, а конец В отклоняется.

- Результаты прогиба в точке B при смещении Δy ненулевое значение и соответствующее Θb (наклон в точке B).
- Реакции в B отсутствуют, т.к. конец не сдержан. Конец свободен двигаться.
Поддержка Реакции @ B = r e =0;
Реакции в конце A
- Фиксированный end ‘A’ ограничивает перемещение конечной БАЛКИ в направлении x, в результате перемещение которого по оси x равно нулю. Следовательно, изменение в расстояние Δx = 0; Объявления
- Аналогично, Конец ‘A’ ограничивает перемещение по оси y, поэтому Δy = 0;
- Отличие, конец B, конец A не допускает никакого отклонения, т.е. (Δy = 0), и, следовательно, наклон в точке A θА = 0;
Следовательно, при
Конец A, (фиксированный конец) горизонтальный,
вертикальные и вращательные движения ограничены; Δх= 0; Δу =
0; θA = 0, что приводит к реакциям Rx, Ry и M. Где Rx — реакция, вызванная в направлении x, Ry — реакция в направлении Y, а сопротивление вращению создает реакцию в виде момента M.
Поддержка Реакции на фиксированном конце A = r e = ( Rx , Ry и M) = 3 nos
Здесь созданный момент ‘M’ равен Mz относительно оси Z.
Реакции фиксированной концевой опоры в 3D
Описанную выше консольную балку можно представить в 3D, как показано ниже. Здесь реакции формируются по всем трем направлениям. Отсюда число опорных реакций = 6;
Объявления
Это Rx, Ry, Rz, Mx, My и Mz.
| Реакции фиксированной концевой опоры в 3D |
Как показано на 3D-рисунке фиксированной опоры, продольная ось элемента проходит вдоль оси X а оси Y и Z являются боковой осью.
Момент, создаваемый вокруг продольной оси конструкции (в данном случае вокруг оси X — Mx), приведет к скручиванию конструкции. Этот момент называется крутящим моментом.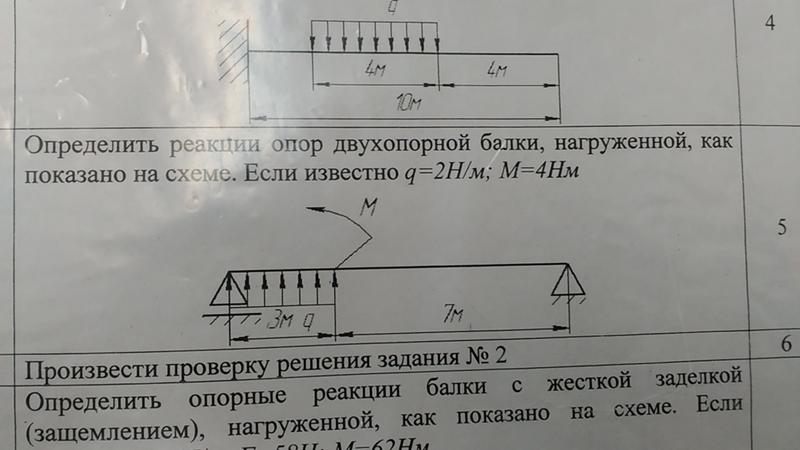

 Нарушение авторских прав; Мы поможем в написании вашей работы!
Нарушение авторских прав; Мы поможем в написании вашей работы! В Казахстане, находившемся далеко от политических центров Российской империи…
В Казахстане, находившемся далеко от политических центров Российской империи…
 ..
..