Опір матеріалів – Лекція №1 Тема. Вступ. Наука про опір матеріалів. Об’єкти вивчення.

Содержание

Лекція №1 Тема. Вступ. Наука про опір матеріалів. Об’єкти вивчення.

Опір матеріалів — це наука про інженерні методи розрахунків на міцність, жорсткість і стійкість елементів машин та споруд. Під міцністю розуміють здатність конструкції, її частин та деталей витримувати певне навантаження не руйнуючись.

Жорсткість — це здатність конструкції та її елементів протистояти деформуванню (змінювання форми та розмірів) під дією зовнішніх сил.

Стійкістю називають здатність конструкції або її елементів зберігати певну початкову форму пружної рівноваги.

Об’єкти вивчення опору матеріалів

Стержнем називається тіло в якого один розмір (довжина) перевищує два інших (поперечних) розміру. Стержні в залежності від виду поперечного перерізу бувають:

1. Круглого перерізу;

2. Квадратного, прямокутного;

3. Прокатного профілю;

Оболонка — це тіло, обмежене криволінійними поверхнями, які розташовані на близькій відстані одна від одної.

Поверхня рівновіддалена від зовнішніх поверхонь оболонки називається серединою. За формою серединною поверхні оболонки розрізняються на циліндричні, конічні, сферичні. Якщо серединна поверхня — є площиною, то розрахунковий об’єкт називають пластинкою. Тіла, в яких всі три розміри одного порядку називають масивними.

Види деформації стержня. Поняття про деформований стан матеріалу.

Реальні тіла можуть деформуватися, тобто змінювати свою форму і розмір. Деформації тіл відбуваються внаслідок навантажування їх зовнішніми силами або зміни температури. Деформації бувають пружні, тобто такі, що зникають після припинення дії сил, які спричинили їх, та пластичні, або залишкові, — ті, що не зникають. В опорі матеріалів вивчають такі основні види деформації стержня.

а) Розтягання (стиск):

3.Кручення

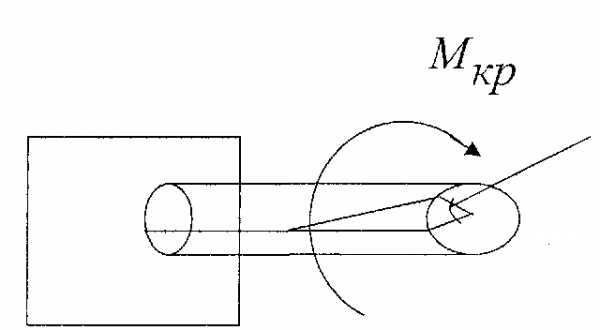
-відносний кут закручування

4. Згин

Основні гіпотези науки про опір матеріалів

  1. Гіпотеза про суцільність матеріалу. Припускається, що матеріал суцільно заповнює форму тіла.

  2. Гіпотеза про однорідність та ізотропність. Матеріал вважається однорідним та ізотропним, тобто в будь-якому об’ємі та в будь-якому напрямі властивості матеріалу вважаються однаковими.

  3. Гіпотеза про малість деформації. Припускається, що деформації малі порівняно з розмірами тіла.

  4. Гіпотеза про ідеальну пружність матеріалу. Припускається, що всі тіла абсолютно пружні.

Зовнішні і внутрішні сили. Метод перерізів.

Зовнішніми силами називають сили взаємодії між розглядаємим елементом конструкції та пов’язаними з ним тілом.

Зосереджена сила

2.

Рівномірно розподілене навантаження

Рівнодійна розподіленого навантаження чисельно рівна площі його епюри і прикладена в центрі її ваги.

3. Зосереджений момент

4 .Крутний момент

[Мкр] = кН •т

Бувають навантаження, які не є наслідком контакту двох тіл наприклад сила інерції, власна вага. Ці сили прикладені в кожній точці об’єму, які займає тіло і тому називаються об’ємними або масовими.

Внутрішні сили

Між сусідніми частинами тіла завжди є певні сили взаємодії, тобто внутрішні сили, які в усіх випадках намагаються зберегти тіло як єдине ціле, протидіють зовнішнім силам, що прикладені до тіла. Внутрішні сили часто називають зусиллям. Для виявлення внутрішніх сил в опорі матеріалів широко застосовують метод перерізів.

Розглянемо довільне тіло

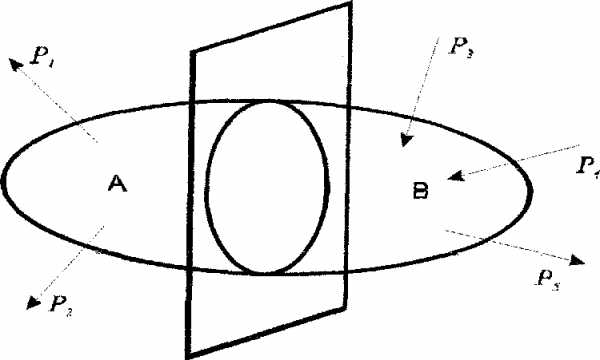
Проведемо переріз

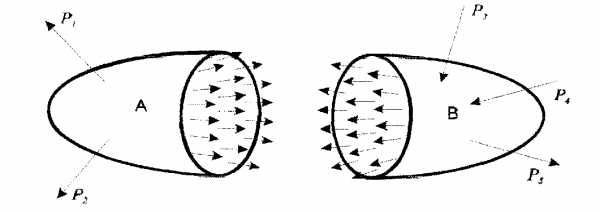
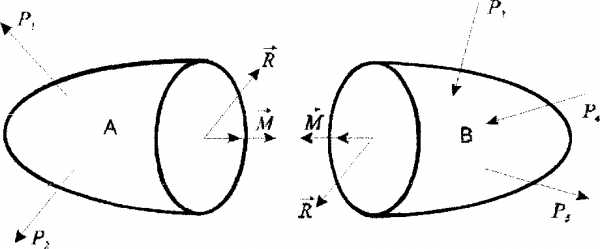
Внутрішні сили можна звести до однієї точки (як правило це центр ваги перерізу), внаслідок чого маємо головний вектор та головний момент внутрішніх сил

Якщо головний векторта головний момент М спроекціювати на осіто на кожному боці маємо шість внутрішніх силових факторів:

три силита три моменти. Ці

величини називають внутрішніми зусиллями стержня в перерізі стержня.

Зусилля N спричиняє поздовжню деформацію стержня

(розтягання або стискання) і зветься поздовжня сила.

та спричиняє зсув боків перерізу відповідно в напрямку

осейта у, вони звуться поперечні сили або перерізуючи сили.

спричинює кручення перерізу зветься крутний момент

спричинюють згин, звуться згинальні моменти

Напруження в перерізі

Р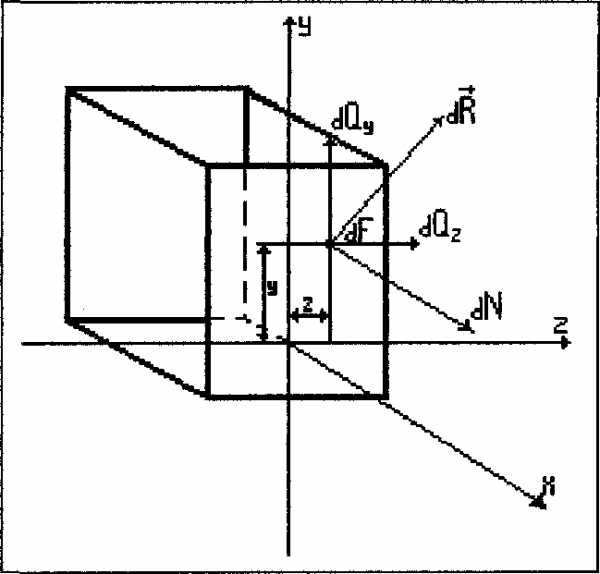озглянемо нескінченно малий елемент площіУнаслідок малості елемента можна вважати, що внутрішні зусилля, які діють в його різних точках, однакові за модулем та напрямом. Тоді їхня рівнодійнабуде проходити через центр ваги елемента’, координати якого та.

Отже, зводячи все до центра ваги елемента

, матимемо головний векторта

головний момент , що дорівнює 0

, т.к. центр ваги тоді:

— нормальне напруження

— дотичні напруження Напруження виміряють у Па

Отже, напруженням називається внутрішня сила віднесена до одиниці площі в даній точці

Повне напруження:

, тобто значення повного зусилля, яке припадає на одиницю площі.

Очевидно:

С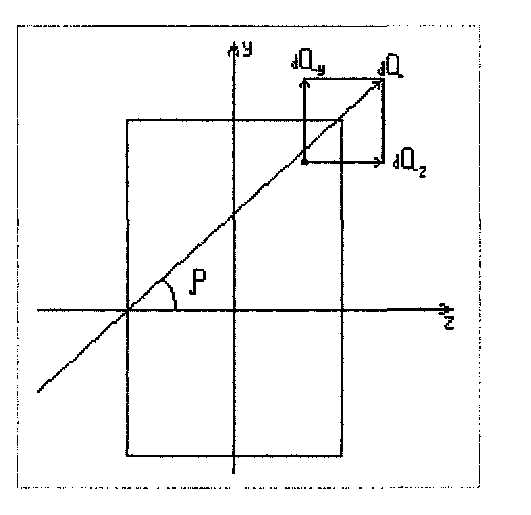татичні рівняння та інтегральні рівняння рівноваги

-відстань від центра ваги перерізу до лінії дій

studfiles.net

Опір матеріалів — Howling Pixel

О́пір матеріа́лів — наука про інженерні методи розрахунку на міцність, жорсткість і стійкість елементів конструкцій, машин і споруд. Опір матеріалів відноситься до фундаментальних дисциплін загальноінженерної підготовки фахівців з вищою технічною освітою.

Це перша дисципліна, що встановлює зв’язок між фундаментальними науковими дисциплінами (фізика, вища математика і теоретична механіка) і прикладними задачами та методами їхнього розв’язку, котрі виникають при проектуванні машин і механізмів, цивільних і промислових споруд, мостів, ліній електропередач, літальних апаратів і реактивної техніки. Практично всі спеціальні дисципліни підготовки інженерів за різними спеціальностями містять розділи курсу опору матеріалів, оскільки створення працездатної нової техніки неможливе без аналізу і оцінки її міцності, жорсткості і стійкості.

Завдання дисципліни та об’єкт вивчення

Завданням опору матеріалів, як одного з предметів прикладної механіки, що ґрунтується на положеннях механіки деформівного твердого тіла є розрахунок на міцність

через визначення деформацій і напружень в твердому пружному тілі, яке піддається силовій або тепловій дії.

Типовими задачами розрахунків на міцність є:

  • задача аналізу (перевірка міцності та жорсткості): при заданих навантаженнях визначити напруження і деформації та перевірити, чи не перевищують вони допустимих значень;
  • задача синтезу (проектувальні розрахунки): підбір матеріалів та визначення розмірів елементів конструкцій при заданих навантаженнях;
  • розрахунок вантажопідйомності: при заданих параметрах конструкції визначення граничних або руйнівних навантажень.

Це ж завдання серед інших розглядається в курсі теорії пружності. Проте методи розв’язку цієї загальної задачі в цих курсах істотно відрізняються один від одного. Опір матеріалів вирішує її головним чином для бруса (стрижня, балки чи вала), базуючись на низці гіпотез геометричного та фізичного характеру. Такий метод дозволяє отримати, хоч і не у всіх випадках достатньо прості але цілком точні формули для обчислення напружень чи деформацій. В опорі матеріалів до брусів можуть бути віднесені і такі будівельні конструкції, як багатометрові колони будівель, балки перекриття, пояси, стійки і розкоси ферм, та (для порівняння) голка побутової швейної машини.

Тому, об’єктом вивчення в опорі матеріалів є напружено-деформований стан і роботоздатність конструкцій та її елементів, форма яких може бути приведена до форми бруса (стрижня, балки вала).

Як правило, саме через оцінний характер результатів, що одержуються за допомогою математичних моделей цієї дисципліни, при проектуванні реальних виробів всі міцнісні характеристики матеріалів чи розміри конструкцій вибираються з суттєвим запасом (у декілька разів відносно результату, отриманого при розрахунках, але зазвичай не більше, ніж в 9 разів).

Реальний об’єкт і розрахункова схема

Повне врахування усіх властивостей реального об’єкта при його розрахунку принципово неможливо через нескінченну їхню складність. Тому першим кроком при аналізі роботи конструкції є спрощення задачі. Реальний об’єкт замінюють

розрахунковою схемою.

Щоб вибрати розрахункову схему, треба з множини зовнішніх впливів, геометричних особливостей об’єкта і фізичних властивостей матеріалу виділити найсуттєвіші у цьому завданні і відкинути ті, що мало впливають на результат аналізу. Ступінь спрощень залежить від необхідної точності, математичних можливостей, а також від того, яка сторона явища розглядається в задачі.

При виборі розрахункової схеми доводиться ідеалізувати геометричні параметри об’єкта, фізичні властивості матеріалу, зовнішній вплив, опори і в’язі.

Методи науки

Методи опору матеріалів характеризуються:

  • експериментально-теоретичним підходом до вирішення задач;
  • застосуванням законів фізики, механіки та математичного апарату;
  • широким використанням передумов, що спрощують вирішення задачі, котрі базуються на визначеному переліку гіпотез.

Основні гіпотези та принципи опору матеріалів

Важливим кроком при виборі розрахункової схеми є опис механічних властивостей матеріалу. Відмова від поняття жорсткого тіла вимагала введення гіпотез, що описують ці властивості. Немає такої фізичної моделі, яка б повністю відображала поведінку усіх матеріалів. Для одних придатні одні допущення, для інших — інші. Проте є деякі загальні гіпотези і принципи, що використовуються в більшості задач опору матеріалів.

Гіпотези

Для побудови теорії опору матеріалів вводять деякі гіпотези щодо структури і властивостей матеріалів, а також про характер деформацій.

  1. Гіпотеза про однорідність та ізотропність. Матеріал вважається однорідним та ізотропним, тобто в будь-якому об’ємі та в будь-якому напрямі властивості матеріалу вважаються однаковими. Хоч кристали, з яких складаються метали, анізотропні, проте їхнє хаотичне розташування дає змогу макрооб’єми металів вважати ізотропними. Інколи припущення про ізотропію є неприйнятним, наприклад для деревини, властивості якої вздовж і поперек волокон відрізняються.
  2. Гіпотеза про суцільність матеріалу. Припускається, що матеріал суцільно заповнює форму тіла. Атомістична теорія дискретної будови речовини до уваги не береться.
  3. Гіпотеза про малість деформацій. Припускається, що деформації малі, порівняно з розмірами тіла. Це дає змогу здебільшого нехтувати змінами в розташуванні зовнішніх сил відносно окремих частин тіла й складати рівняння статики для недеформованого стану тіла. Малі відносні деформації розглядаються як нескінченно малі величини.
  4. Гіпотеза про ідеальну пружність матеріалу. Припускається, що всі тіла абсолютно пружні. Відхилення від ідеальної пружності, які завжди спостерігаються для реальних тіл, неістотні і ними нехтують до певних меж деформування. Більшість задач опору матеріалів вирішують у припущенні лінійно деформованого тіла, при якому справедливий закон Гука, що відображає пряму пропорційність між деформаціями та навантаженням.
  5. Гіпотеза плоских перерізів (гіпотеза Бернуллі). Поперечні перерізи, що були плоскими і нормальними до осі стержня до прикладання навантаження, залишаються плоскими і нормальними до його осі після деформації.

Принципи

  1. Принцип незалежності й додавання дії сил (принцип суперпозиції). Зусилля в будь-якому елементі конструкції, спричинені різними факторами, дорівнюють сумі зусиль, спричинених кожним із цих факторів, і не залежать від порядку їхнього прикладання. Це справедливо і стосовно деформацій.
  2. Принцип Сен-Венана. В перерізах, достатньо віддалених від місць прикладання навантаження, деформація тіла не залежить від конкретного способу навантаження і визначається лише статичним еквівалентом навантаження.

Види деформацій

Внаслідок дії навантаження або зміни температури реальні тіла деформуються, тобто змінюють свої форму і розміри. При деформуванні тіла його точки переміщаються в просторі відносно свого вихідного положення.

При навантажуванні твердого тіла у ньому виникають внутрішні сили взаємодії між частками, що протидіють зовнішнім силам. Деформації бувають пружні, тобто такі, що зникають після припинення дії сил, які спричинили їх, та пластичні (залишкові), — ті, що не зникають.

При збільшенні навантаження внутрішні сили також зростають, але до певної межі, яка залежить від властивостей матеріалу. Настає момент, колі вже тіло не здатне чинити опір зростанню навантаження. Тоді воно руйнується.

В опорі матеріалів вивчають такі основні види деформацій стрижня: розтягання-стискання, зсув (зріз), кручення та згинання. Розглядаються і складніші види деформацій, що отримуються поєднанням перелічених.

Деформація розтягання-стискання

Розтягання або стискання виникає тоді, коли до стержня вздовж осі прикладені протилежно спрямовані сили. При цьому відбувається переміщення перерізів вздовж осі стержня, що при розтяганні подовжується а при стисканні вкорочується. Зміну Δl початкової довжини l називають абсолютним подовженням при розтяганні (абсолютним укороченням при стисканні). Відношення абсолютного подовження (укорочення) Δl до початкової довжини l стержня називають середнім відносним подовженням і, як правило позначають ε

ϵ=Δll{\displaystyle \epsilon ={\frac {\Delta l}{l}}}

На розтягання або стискання працюють багато елементів конструкцій: стержні ферм, колони, штоки поршневих машин, стяжні гвинти тощо.

Деформація зсуву (зрізу)

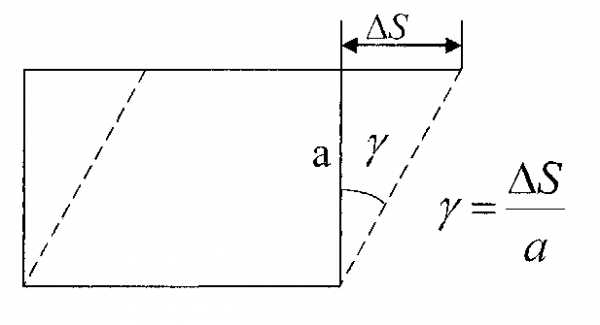
Зсув або зріз виникає тоді коли зовнішні сили зміщують два паралельних плоских перерізи один відносно одного при незмінній відстані між ними. Зміщення а (див. рис.) називають абсолютним зсувом. Відношення абсолютного зсуву до відстані h між площинами, що зміщуються (тангенс кута γ) називають відносним зсувом. Унаслідок малості кута γ при пружних деформаціях його тангенс вважають рівним куту перекосу розглядуваного елемента

γ=ah{\displaystyle \gamma ={\frac {a}{h}}}

Відносний зсув є кутовою деформацією, яка характеризує перекіс елемента. На зсув та зріз працюють заклепки й болти, що скріплюють елементи, які зовнішні сили намагаються зсунути один відносно одного.

Деформація кручення

Кручення виникає при дії на стержень зовнішніх сил, які утворюють момент відносно осі стержня (див.рис.). Деформація кручення супроводжується поворотом перерізів стержня один відносно одного навколо його осі. Кут повороту одного перерізу стержня відносно іншого, що перебуває на відстані l, називають кутом закручування на довжині l. Відношення кута закручування α до довжини l називають відносним кутом закручування:

θ=αl{\displaystyle \theta ={\frac {\alpha }{l}}}

На кручення працюють вали, шпинделі верстатів та ін.

Деформація згинання

Деформація згинання (див.рис.) полягає у викривленні осі прямого стрижня або в зміні кривизни кривого стрижня. У прямих стержнях переміщення точок δ, які спрямовані перпендикулярно до початкового положення осі, називають прогинами. На згинання працюють осі залізничних вагонів, ресори, зуби шестерень, балки міжповерхових перекриттів, важелі та ін.

Складний опір

Складний опір — напружений стан, що виникає у стрижні, брусі або іншому пружному тілі під впливом двох або більше найпростіших деформацій: розтягу-стиску і згину, кручення і згину, косого згину тощо[1].

Випадки складного опору умовно поділяють на два види. До першого виду належать випадки складного опору, при яких у небезпечних точках бруса напружений стан є одноосьовим. У цю групу об’єднують: згин з розтяганням, косий згин, позацентрове розтягнення-стиснення тощо.

До другої групи належать такі випадки складного опору, коли напружений стан є плоским. Наприклад, згин з крученням, розтягнення (стиснення) кручення і т. д. Для цього випадку при оцінюванні напружено-деформованого стану вдаються до застосування теорій міцності.

Див. також

Примітки

  1. ↑ Складний опір // Українська радянська енциклопедія : у 12 т. / гол. ред. М. П. Бажан ; редкол.: О. К. Антонов та ін. — 2-ге вид. — К. : Головна редакція УРЕ, 1974–1985.

Література

  • Короткий курс опору матеріалів: Навч. посіб. / І. М. Ольховий, Б. М. Стасюк, В. З. Станкевич; Нац. ун-т «Львів. політехніка». Ін-т дистанц. навчання. — Л. : Вид-во Нац. ун-ту «Львів. політехніка», 2004. — 194 c. — (Сер. Дистанц. навчання; № 18).
  • Опір матеріалів / Посацький С. Л. − Львів: Видавництво Львівського університету, 1973. − 403 с.
  • Опір матеріалів. Конспект лекцій / Олександр Володимирович Мильніков. − Тернопіль: Видавництво ТНТУ, 2010. − 257 с.
  • Опір матеріалів: Навч. посіб. для студентів ВНЗ. Рекомендовано МОН / Шваб’юк В. І. — К., 2009. — 380 с.
  • Опір матеріалів. Підручник / Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993 .- 655 с. ISBN 5-11-004083-4
  • Основи опору матеріалів: навч. посіб. [для студентів ден. та заоч. форм навчання мех., машинобуд., транспорт. і енергет. спец. ВНЗ] / В. С. Кравчук, О. Ф. Дащенко, Л. В. Коломієць, О. М. Лимаренко. — Одеса: Стандартъ, 2014. — 322 с. : іл. — Бібліогр.: с. 298 (13 назв). — ISBN 978-966-413-482-5
  • Сопротивление материалов / Писаренко Г. С. − 5-е изд., перераб. и доп. − К.:Вища школа, Головне видавництво, 1986. − 775 с.
Балка (конструкція)

Ба́лка — це конструктивний елемент у вигляді стрижня (бруса), який сприймає зовнішні навантаження й передає їх на опори. Найпоширенішим видом деформації балок є згин.

Згин може виникати під дією зовнішніх поперечних сил (зосереджених або розподілених по довжині балки) та моментів пар сил. Опорами балки можуть бути колони, підвіси, стіни.

Балки використовують у конструкціях будинків, мостів, естакад, машин, верстатів тощо.

Брус

Брус — конструктивний елемент, товщина і ширина якого набагато менші за довжину. Може використовуватися як підпора або балка.

При розрахунках брус замінюють його подовжньою віссю. Брус, що працює на розтягування-стиснення зазвичай називають стрижнем, на кручення — валом, а на вигин — балкою.

За геометричною формою бруси можна розділити на прямолінійні і криволінійні, за виглядом поперечного перетину — на бруси постійного і змінного перетину, а також ступінчасті, за виглядом навантаження — плоскі і просторові.

Границя міцності

Грани́ця мі́цності або тимчасовий опір руйнуванню — умовне механічне напруження, що відповідає найбільшому зусиллю, що досягається в процесі деформування зразка матеріалу, досягнутому до поділу зразка на частини, котре відповідає максимуму на діаграмі деформування і зазвичай позначається σB{\displaystyle \sigma _{B}}.

Границя текучості

Грани́ця пли́нності (англ. yield strength, yield point) — в прикладній механіці визначається як напруження σт в матеріалі, при якому він починає деформуватися пластично. Спочатку, при менших навантаженнях матеріал деформується пружно, тобто він може відновлювати свою форму після зняття навантаження. При збільшенні навантаження і перевищенні границі плинності у матеріалі з’являються незворотні деформації.

Деформація

Деформа́ція (від лат. deformatio — «спотворення») — зміна розмірів і форми твердого тіла під дією зовнішніх сил (навантажень) або якихось інших впливів (наприклад, температури, електричних чи магнітних полів).

При деформації точки твердого тіла змінюють своє положення. Точка із радіус-вектором r{\displaystyle \mathbf {r} } при деформації має нове положення r′{\displaystyle \mathbf {r} ^{\prime }}, тобто здійснить переміщення u=r′−r{\displaystyle \mathbf {u} =\mathbf {r} ^{\prime }-\mathbf {r} }. Поле переміщень є однією з характеристик деформації, але воно незручне для математичного опису, оскільки, наприклад, при видовженні стрижня точки біля його початку зміщуються зовсім мало, а в кінці — доволі значно. Набагато важливіше те, наскільки точка тіла змістилася щодо сусідньої. Тому деформацію математично найзручніше описувати похідними від переміщення, які утворюють тензор, що отримав назву тензора деформації.

Деформація згину

Деформа́ція зги́ну або згин — тип деформації бруса (балки), що полягає у викривленні осі прямого бруса чи зміні кривини осі кривого бруса в результаті виникнення згинальних моментів у його перерізах від прикладених навантажень (поперечних сил і/або згинальних моментів у площині, що проходить через вісь бруса).

Локальна деформація різних частин тіла при згинанні різна. Наприклад, у випадку, зображеному на рисунку, верхня частина балки стискається, а нижня — розтягується.

Деформація зсуву

Деформа́ція зсу́ву — вид деформації, при якому величина зміщення кожної точки тіла зростає в напрямку, перпендикулярному до напрямку зміщення.

Деформація зсуву схематично показана на діаграмі праворуч. Вона виникає, якщо закріпити тіло в основі й прикласти силу (F) до бічної грані.

Закон Гука

Закон Гука встановлює лінійну залежність між деформаціями та механічними напруженнями.

Закон Гука справедливий для малих пружних деформацій.

Механіка

Механіка (від грец. Μηχανική, mechane — знаряддя, споруда, мистецтво побудови машин) — в загальному розумінні наука про механічний рух та рівновагу тіл і взаємодію, що виникає при цьому між тілами. Належить до природничих наук. Також це розділ фізики який вивчає закон механічного руху і механічної взаємодії. Термін «механіка» ввів у науку Арістотель. Вольтер уважав, що «історія механічних мистецтв є, імовірно, найкориснішою з усіх».

Механіку поділяють на загальну механіку, механіку суцільних середовищ і прикладну механіку. В кожному з цих розділів розрізняють статику, кінематику й динаміку. До загальної механіки відносять аналітичну механіку, небесну механіку, балістику, теорію гіроскопів, теорію стійкості руху, а також теорію коливань, біомеханіку, теоретичну механіку тощо. Основу механіки суцільних середовищ становить гідроаеромеханіка, газова динаміка, механіка деформованого твердого тіла. До прикладної механіки відносять механіку ґрунтів і сипких тіл, будівельну механіку, опір матеріалів та ін.

Механічна жорсткість

Механі́чна жо́рсткість (англ. Stiffness) — здатність пружного тіла, конструкції чи її елементів чинити опір деформуванню (змінюванню форми і/або розмірів) від прикладеного зусилля уздовж обраного напрямку у заданій системі координат. Характеристика обернена до механічної податливості.

Модуль Юнга

Мо́дуль Ю́нга (модуль пружності першого роду або модуль пружності під час розтягу) — фізична величина, що характеризує пружні властивості ізотропних речовин, один із модулів пружності.

За ДСТУ 2825-94: Модуль пружності під час розтягу — відношення нормального напруження до відповідної лінійної деформації за лінійного напруженого стану до границі пропорційності.

Позначається латинською літерою E (від англ. Elasticity), вимірюється в Н/м² (ньютонах на метр в квадраті) або Па (паскалях), переважно в гігапаскалях. Названо на честь англійського фізика XIX століття Томаса Юнга. Часто ще цю фізичну величину називають модулем пружності першого роду.

Модуль Юнга для випадку розтягу-стискання стрижня осьовою силою розраховується наступним чином:

E=F/SΔl/l=FlSΔl,{\displaystyle E={\frac {F/S}{\Delta l/l}}={\frac {Fl}{S\Delta l}},}

де: F — осьова сила;

S — площа поверхні (перерізу), по якій розподілена дія сили;
l — довжина стрижня, що деформується;
Δl{\displaystyle \Delta l} — модуль зміни довжини стрижня в результаті пружної деформації.

Модуль Юнга встановлює зв’язок між деформацією розтягу й механічним напруженням направленим на розтяг.

σ=FS=EΔll=Eϵ{\displaystyle \sigma ={\frac {F}{S}}=E{\frac {\Delta l}{l}}=E\epsilon },

де: σ — механічне напруження, визначається, як сила, що припадає на одиницю площі поперечного перерізу тіла,

ϵ=Δll{\displaystyle \epsilon ={\frac {\Delta l}{l}}} — величина відносної деформації (відносне видовження).

Наведена формула справедлива при малих пружних деформаціях.

Міцність

Мі́цність — здатність матеріалу чинити опір незворотній (пластичній, в’язкій) деформації і руйнуванню (розділенню на частини) під дією навантажень або інших факторів (усадка, нерівномірне температурне поле і т. д.). Втрата міцності або перевищення її граничного значення призводить до руйнування матеріалу і деталі чи конструкції з нього виготовленої. Міцність є однією з основних механічних характеристик матеріалу.

Розрізняють міцність власне матеріалу і конструкційну міцність, а за способом прикладання навантаження: статичну (короткочасну та тривалу) і динамічну міцність (в умовах ударних та циклічних навантажень).

Показники міцності: тимчасовий опір або границя міцності, границя пружності, границя текучості, границя тривалої міцності, границя витривалості.

Напруження

Напрýження (механі́чне напру́ження) — міра інтенсивності внутрішніх сил, розподілених по перетинах, тобто зусилля, що припадають на одиницю площі перетину тіла. В Міжнародній системі одиниць напруження обчислюють у паскалях, Па.

При вирішенні питання про міцність конструкції недостатньо знати тільки систему сил, що діють на цю конструкцію. Необхідно знати ще її розміри та матеріал, з якого вона зроблена. На початку XIX століття Оґюстен-Луї Коші, відомий французький математик і механік, увів поняття напруження, яке одночасно характеризувало й силові фактори, що діяли в перерізі, й геометричні розміри цього перерізу. Напруження в загальному — це відношення сили, що діє по площадці до величини (площі) цієї площадки.

Причинами виникнення напружень є дія зовнішніх сил, температурних полів (термічні напруження) чи проходження у матеріалі тіла фізико-хімічних процесів.

У гірництві — міра внутрішніх сил, які виникають у масиві гірських порід, в окремих елементах машин і споруд під впливом зовнішніх сил (навантажень, змін температури тощо).

Опір матеріалів (альбом)

«Опір матеріалів» — альбом українського гурту «Тартак». У кінці 2009 року гурт виставив його для вільного скачування на своїй офіційній сторінці. Диск презентовано у квітні 2010 року.

Пластичність матеріалу

Пласти́чність (рос. пластичность, англ. plasticity, нім. Plastizität f) — здатність матеріалу незворотно змінювати свою форму й розміри при деформації. Крім того — здатність при замішуванні з водою утворювати тісто, яке під впливом зовнішньої дії може набирати будь-якої необхідної форми без проявів тріщин та зберігати надану форму після припинення цієї дії, при сушінні та випалюванні.

Стрижень (механіка)

Стри́жень, також стержень — об’єкт (тіло), довжина якого значно перевищує його інші розміри. Під терміном «значно» мається на увазі у 10 і більше разів.

В опорі матеріалів застосування того чи іншого розрахункового методу залежить від моделі тіла, котра визначається співвідношенням характерних розмірів. Виходячи з класифікації тіл за геометричною ознакою стрижень є найпростішою формою тіла і найчастіше розглядається опором матеріалів як об’єкт дослідження. В основу даної геометричної класифікації покладено співвідношення розмірів а не абсолютне їх значення, тому до стрижнів відносять і багатометрові колони будівель, окремі елементи фермових конструкцій і швейну голку.

Основними геометричними характеристиками стрижня, необхідними для розрахунків є його вісь і поперечний переріз. У переважній більшості вважається що стрижень як конструкційний елемент працює лише на розтягування-стиснення. При появі поперечних сил, згинальних або (та) крутильних моментів такий елемент називають балкою або валом.

Стійкість (опір матеріалів)

Стійкість — здатність конструкції або її елементів зберігати певну початкову форму пружної рівноваги, відповідаючи на малі збільшення статичного навантаження малими приростами деформацій. Стійкість конструкції відноситься до одного з видів конструкційної міцності.

Традиційні розрахунки на міцність та жорсткість в опорі матеріалів передбачають, що між зовнішніми силами та спричиненими ними внутрішніми силами пружності рівновага є стійкою. Але це трапляється не завжди.

Пружна рівновага буде стійкою, якщо деформоване тіло при будь-якому відхиленні від стану рівноваги намагається повернутися до стану рівноваги і повертається до нього після припинення зовнішнього впливу. Пружна рівновага буде нестійкою, якщо деформоване тіло, виведене з неї продовжує деформуватися в напрямі наданого йому відхилення і після припинення зовнішньої дії у вихідний стан не повертається. Між цими двома станами рівноваги існує перехідний стан, що зветься критичним, при якому деформоване тіло перебуває у байдужій рівновазі.

Стан тіла, яке перебуває на границі стійкої і нестійкої рівноваги, називається критичним, а величина сили, яка спричиняє такий стан — критичною силою і позначається Pкр. Можна стверджувати, що досягнення навантаженням критичних значень рівнозначно руйнуванню конструкції, оскільки нестійка форма рівноваги буде втрачена, що приведе до необмеженого зростання напружень і деформацій. Особлива небезпека руйнування в результаті втрати стійкості полягає у тому, що, як правило, вона відбувається раптово і при значеннях напружень далеких від допустимих.

Отже при розрахунку на стійкість критичне навантаження подібне до руйнувального. Для забезпечення запасу стійкості необхідно, щоб задовольнялась умова:

P⩽[P],{\displaystyle P\leqslant [P],} де
[P]=PKPkCT.{\displaystyle [P]={\frac {P_{KP}}{k_{CT}}}.}

Тут P — діюче навантаження, kCT — коефіцієнт запасу стійкості.

Розрізняють декілька форм втрати стійкості тонкостінних конструкцій.

Тартак (гурт)

Тартак — український репкор-гурт, заснований у Луцьку 1996 року. Станом на 2019 рік гурт випустив 10 альбомів.

Ферма (конструкція)

Фе́рма (фр. ferme, від лат. firmus — «міцний», «сильний») — тримальна геометрично незмінна конструкція, що складається з прямолінійних стрижнів, вузлові з’єднання яких в розрахунках вважаються шарнірними.

Стрижні у вузлових ферм з’єднуються жорстко: зварюванням, болтами, заклепками, фасонками чи взагалі роблячи всю ферму монолітною конструкцією. Попри це, експерименти показують, що згинальні моменти в прямолінійних стрижнях значно менші порівняно з поздовжніми зусиллями. Тому у практичних розрахунках величинами згинальних моментів нехтують і при побудові розрахункової схеми ферми припускають, що у вузлах встановлені ідеальні циліндричні шарніри.

Іншими мовами

This page is based on a Wikipedia article written by authors (here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

howlingpixel.com

Опір матеріалів

TR | RU | KK | BE | EN |
опір матеріалів

Закони класичної механіки
Закон збереження маси •Закон збереження імпульсу •Закон збереження енергії •Нерівність Клаузіуса
Механіка деформівного
твердого тіла
Тверде тіло:

Напруження •Деформація •Теорія малих деформацій •Теорія великих деформацій •Теорія пружності •Механіка контактної взаємодії •Опір матеріалів •Теорія пластичності •Механіка руйнування

Механіка рідин та газів
Флюїд: Тиск •Гідростатика (закон Архімеда; закон Паскаля) •Гідродинаміка (закон Бернуллі) •В’язкість (ньютонівська рідина; неньютонівська рідина)

Рідина: Поверхневий натяг •Капілярний ефект
Газ: Рівняння стану ідеального газу (Закон Гей-Люссака; Закон Бойля — Маріотта; закон Шарля) •Реальний газ
Плазма

Реологія
В’язкоеластичність •Розумні рідини (Магнетореологічна рідина, Електрореологічна рідина, Феромагнітна рідина) • Реометрія
Основні рівняння
Рівняння неперервності •Рівняння Ейлера •Рівняння Нав’є — Стокса •Рівняння дифузії •Закон Гука
Вчені
Ньютон •Стокс •Нав’є •Коші •Гук, Бернуллі

О́пір матеріа́лів — наука про інженерні методи розрахунку на міцність, жорсткість і стійкість елементів конструкцій, машин і споруд. Опір матеріалів відноситься до фундаментальних дисциплін загальноінженерної підготовки фахівців з вищою технічною освітою.

Це перша дисципліна, що встановлює зв’язок між фундаментальними науковими дисциплінами (фізика, вища математика і теоретична механіка) і прикладними задачами та методами їхнього розв’язку, котрі виникають при проектуванні машин і механізмів, цивільних і промислових споруд, мостів, ліній електропередач, літальних апаратів і реактивної техніки. Практично всі спеціальні дисципліни підготовки інженерів за різними спеціальностями містять розділи курсу опору матеріалів, оскільки створення працездатної нової техніки неможливе без аналізу і оцінки її міцності, жорсткості і стійкості.

Зміст

  • 1 Завдання дисципліни та об’єкт вивчення
  • 2 Реальний об’єкт і розрахункова схема
  • 3 Методи науки
  • 4 Основні гіпотези та принципи опору матеріалів
    • 4.1 Гіпотези
    • 4.2 Принципи
  • 5 Види деформацій
  • 6 Посилання
  • 7 Див. також

Завдання дисципліни та об’єкт вивчення

Модель поведінки стрижня (балки) під дією навантаження

Завданням опору матеріалів, як одного з предметів прикладної механіки, що ґрунтується на положеннях механіки деформівного твердого тіла є розрахунок на міцність через визначення деформацій і напружень в твердому пружному тілі, яке піддається силовій або тепловій дії.

Типовими задачами розрахунків на міцність є:

  • задача аналізу (перевірка міцності та жорсткості): при заданих навантаженнях визначити напруження і деформації та перевірити, чи не перевищують вони допустимих значень;
  • задача синтезу (проектувальні розрахунки): підбір матеріалів та визначення розмірів елементів конструкцій при заданих навантаженнях;
  • розрахунок вантажопідйомності: при заданих параметрах конструкції визначення граничних або руйнівних навантажень.

Це ж завдання серед інших розглядається в курсі теорії пружності. Проте методи розв’язку цієї загальної задачі в цих курсах істотно відрізняються один від одного. Опір матеріалів вирішує її головним чином для бруса (стрижня, балки чи вала), базуючись на низці гіпотез геометричного та фізичного характеру. Такий метод дозволяє отримати, хоч і не у всіх випадках достатньо прості але цілком точні формули для обчислення напружень чи деформацій. В опорі матеріалів до брусів можуть бути віднесені і такі будівельні конструкції, як багатометрові колони будівель, балки перекриття, пояси, стійки і розкоси ферм, та (для порівняння) голка побутової швейної машини.

Тому, об’єктом вивчення в опорі матеріалів є напружено-деформований стан і роботоздатність конструкцій та її елементів, форма яких може бути приведена до форми бруса (стрижня, балки вала).

Як правило, саме через оціночний характер результатів, що одержуються за допомогою математичних моделей цієї дисципліни, при проектуванні реальних виробів всі міцнісні характеристики матеріалів чи розміри конструкцій вибираються з суттєвим запасом (у декілька разів відносно результату, отриманого при розрахунках, але зазвичай не більше, ніж в 9 разів).

Реальний об’єкт і розрахункова схема

Повне врахування усіх властивостей реального об’єкта при його розрахунку принципово неможливо через нескінченну їхню складність. Тому першим кроком при аналізі роботи конструкції є спрощення задачі. Реальний об’єкт замінюють розрахунковою схемою.

Щоб вибрати розрахункову схему, треба з множини зовнішніх впливів, геометричних особливостей об’єкта і фізичних властивостей матеріалу виділити найсуттєвіші у цьому завданні і відкинути ті, що мало впливають на результат аналізу. Ступінь спрощень залежить від необхідної точності, математичних можливостей, а також від того, яка сторона явища розглядається в задачі.

При виборі розрахункової схеми доводиться ідеалізувати геометричні параметри об’єкта, фізичні властивості матеріалу, зовнішній вплив, опори і в’язі.

Методи науки

Методи опору матеріалів характеризуються:

  • експериментально-теоретичним підходом до вирішення задач;
  • застосуванням законів фізики, механіки та математичного апарату;
  • широким використанням передумов, що спрощують вирішення задачі, котрі базуються на визначеному переліку гіпотез.

Основні гіпотези та принципи опору матеріалів

Важливим кроком при виборі розрахункової схеми є опис механічних властивостей матеріалу. Відмова від поняття жорсткого тіла вимагала введення гіпотез, що описують ці властивості. Немає такої фізичної моделі, яка б повністю відображала поведінку усіх матеріалів. Для одних придатні одні допущення, для інших — інші. Проте є деякі загальні гіпотези і принципи, що використовуються в більшості задач опору матеріалів.

Гіпотези

Для побудови теорії опору матеріалів вводять деякі гіпотези щодо структури і властивостей матеріалів, а також про характер деформацій.

  1. Гіпотеза про однорідність та ізотропність. Матеріал вважається однорідним та ізотропним, тобто в будь-якому об’ємі та в будь-якому напрямі властивості матеріалу вважаються однаковими. Хоч кристали, з яких складаються метали, анізотропні, проте їхнє хаотичне розташування дає змогу макрооб’єми металів вважати ізотропними. Інколи припущення про ізотропію є неприйнятним, наприклад для деревини, властивості якої вздовж і поперек волокон відрізняються.
  2. Гіпотеза про суцільність матеріалу. Припускається, що матеріал суцільно заповнює форму тіла. Атомістична теорія дискретної будови речовини до уваги не береться.
  3. Гіпотеза про малість деформацій. Припускається, що деформації малі, порівняно з розмірами тіла. Це дає змогу здебільшого нехтувати змінами в розташуванні зовнішніх сил відносно окремих частин тіла й складати рівняння статики для недеформованого стану тіла. Малі відносні деформації розглядаються як нескінченно малі величини.
  4. Гіпотеза про ідеальну пружність матеріалу. Припускається, що всі тіла абсолютно пружні. Відхилення від ідеальної пружності, які завжди спостерігаються для реальних тіл, неістотні і ними нехтують до певних меж деформування. Більшість задач опору матеріалів вирішують у припущенні лінійно деформованого тіла, при якому справедливий закон Гука, що вдображає пряму пропорційність між деформаціями та навантаженням.
  5. Гіпотеза плоских перерізів (гіпотеза Бернуллі). Поперечні перерізи, що були плоскими і нормальними до осі стержня до прикладання навантаження, залишаються плоскими і нормальними до його осі після деформації.

Принципи

  1. Принцип незалежності й додавання дії сил (принцип суперпозиції). Зусилля в будь-якому елементі кострукції, спричинені різними факторами, дорівнюють сумі зусиль, спричинені кожним із цих факторів, і не залежать від порядку їхнього прикладання. Це справедливо і стосовно деформацій.
  2. Принцип Сен-Венана. В перерізах, достатньо віддалених від місць прикладання навантаження, деформація тіла не залежить від конкретного способу навантаження і визначається лише статичним еквівалентом навантаження.

Види деформацій

Внаслідок дії навантаження або зміни температури реальні тіла деформуються, тобто змінюють свої форму і розміри. При деформуванні тіла його точки переміщаються в просторі відносно свого вихідного положення.

При навантажуванні твердого тіла у ньому виникають внутрішні сили взаємодії між частками, що протидіють зовнішнім силам. Деформації бувають пружні, тобто такі, що зникають після припинення дії сил, які спричинили їх, та пластичні (залишкові), — ті, що не зникають.

При збільшенні навантаження внутрішні сили також зростають, але до певної межі, яка залежить від властивостей матеріалу. Настає момент, колі вже тіло не здатне чинити опір зростанню навантаження. Тоді воно руйнується.

Приклад деформації розтягання стержня

В опорі матеріалів вивчають такі основні види деформацій стрижня: розтягання-стискання, зсув (зріз), кручення та згинання. Розглядаються і складніші види деформацій, що отримуються поєднанням перелічених.

Деформація розтягання-стискання

Розтягання або стискання виникає тоді, коли до стержня вздовж осі прикладені протилежно спрямовані сили. При цьому відбувається переміщення перерізів вздовж осі стержня, що при розтяганні подовжується а при стисканні вкорочується. Зміну Δl початкової довжини l називають абсолютним подовженням при розтяганні (абсолютним укороченням при стисканні). Відношення абсолютного подовження (укорочення) Δl до початкової довжини l стержня називають середнім відносним подовженням і, як правило позначають ε

На розтягання або стискання працюють багато елементів конструкцій: стержні ферм, колони, штоки поршневих машин, стяжні гвинти тощо.

Деформація зсуву (зрізу)

Деформація зсуву

Зсув або зріз виникає тоді коли зовнішні сили зміщують два паралельних плоских перерізи один відносно одного при незмінній відстані між ними. Зміщення а (див. рис.) називають абсолютним зсувом. Відношення абсолютного зсуву до відстані h між площинами, що зміщуються (тангенс кута γ) називають відносним зсувом. Унаслідок малості кута γ при пружних деформаціях його тангенс вважають рівним куту перекосу розглядуваного елемента

Відносний зсув є кутовою деформацією, яка характеризує перекіс елемента. На зсув та зріз працюють заклепки й болти, що скріплюють елементи, які зовнішні сили намагаються зсунути один відносно одного.

Деформація кручення

Деформація кручення

Кручення виникає при дії на стержень зовнішніх сил, які утворюють момент відносно осі стержня (див.рис.). Деформація кручення супроводжується поворотом перерізів стержня один відносно одного навколо його осі. Кут повороту одного перерізу стержня відносно іншого, що перебуває на відстані l, називають кутом закручування на довжині l. Відношення кута закручування α до довжини l називають відносним кутом закручування:

На кручення працюють вали, шпинделі верстатів та ін.

Деформація згинання

Деформація згинання балки

Деформація згинання (див.рис.) полягає у викривленні осі прямого стрижня або в зміні кривизни кривого стрижня. У прямих стержнях переміщення точок δ, які спрямовані перпендикулярно до початкового положення осі, називають прогинами. На згинання працюють осі залізничних вагонів, ресори, зуби шестерень, балки міжповерхових перекриттів, важелі та ін.

Посилання

  • Опір матеріалів. Підручник /Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993 .- 655 с. ISBN 5-11-004083-5
  • Опір матеріалів: Навч. посіб. для студентів ВНЗ. Рекомендовано МОН / Шваб’юк В. І. — К., 2009. — 380 с.
  • Мильніков О.В. Опір матеріалів. Конспект лекцій / Олександр Володимирович Мильніков. − Тернопіль: Видавництво ТНТУ, 2010. − 257 с.

Див. також

  • Границя пружності
  • Границя міцності
  • Балка
  • Пружна деформація
  • Закон Гука
  • Модуль Юнга
  • Теорії міцності

опір матеріалів

Опір матеріалів Інформацію Про


Опір матеріалів Коментарі

Опір матеріалів
Опір матеріалів
Опір матеріалів Ви переглядаєте суб єкт.

Опір матеріалів що, Опір матеріалів хто, Опір матеріалів опис

There are excerpts from wikipedia on this article and video

www.turkaramamotoru.com

Опір матеріалів — Gpedia, Your Encyclopedia

О́пір матеріа́лів — наука про інженерні методи розрахунку на міцність, жорсткість і стійкість елементів конструкцій, машин і споруд. Опір матеріалів відноситься до фундаментальних дисциплін загальноінженерної підготовки фахівців з вищою технічною освітою.

Це перша дисципліна, що встановлює зв’язок між фундаментальними науковими дисциплінами (фізика, вища математика і теоретична механіка) і прикладними задачами та методами їхнього розв’язку, котрі виникають при проектуванні машин і механізмів, цивільних і промислових споруд, мостів, ліній електропередач, літальних апаратів і реактивної техніки. Практично всі спеціальні дисципліни підготовки інженерів за різними спеціальностями містять розділи курсу опору матеріалів, оскільки створення працездатної нової техніки неможливе без аналізу і оцінки її міцності, жорсткості і стійкості.

Завдання дисципліни та об’єкт вивчення

Модель поведінки стрижня (балки) під дією навантаження

Завданням опору матеріалів, як одного з предметів прикладної механіки, що ґрунтується на положеннях механіки деформівного твердого тіла є розрахунок на міцність через визначення деформацій і напружень в твердому пружному тілі, яке піддається силовій або тепловій дії.

Типовими задачами розрахунків на міцність є:

  • задача аналізу (перевірка міцності та жорсткості): при заданих навантаженнях визначити напруження і деформації та перевірити, чи не перевищують вони допустимих значень;
  • задача синтезу (проектувальні розрахунки): підбір матеріалів та визначення розмірів елементів конструкцій при заданих навантаженнях;
  • розрахунок вантажопідйомності: при заданих параметрах конструкції визначення граничних або руйнівних навантажень.

Це ж завдання серед інших розглядається в курсі теорії пружності. Проте методи розв’язку цієї загальної задачі в цих курсах істотно відрізняються один від одного. Опір матеріалів вирішує її головним чином для бруса (стрижня, балки чи вала), базуючись на низці гіпотез геометричного та фізичного характеру. Такий метод дозволяє отримати, хоч і не у всіх випадках достатньо прості але цілком точні формули для обчислення напружень чи деформацій. В опорі матеріалів до брусів можуть бути віднесені і такі будівельні конструкції, як багатометрові колони будівель, балки перекриття, пояси, стійки і розкоси ферм, та (для порівняння) голка побутової швейної машини.

Тому, об’єктом вивчення в опорі матеріалів є напружено-деформований стан і роботоздатність конструкцій та її елементів, форма яких може бути приведена до форми бруса (стрижня, балки вала).

Як правило, саме через оцінний характер результатів, що одержуються за допомогою математичних моделей цієї дисципліни, при проектуванні реальних виробів всі міцнісні характеристики матеріалів чи розміри конструкцій вибираються з суттєвим запасом (у декілька разів відносно результату, отриманого при розрахунках, але зазвичай не більше, ніж в 9 разів).

Реальний об’єкт і розрахункова схема

Повне врахування усіх властивостей реального об’єкта при його розрахунку принципово неможливо через нескінченну їхню складність. Тому першим кроком при аналізі роботи конструкції є спрощення задачі. Реальний об’єкт замінюють розрахунковою схемою.

Щоб вибрати розрахункову схему, треба з множини зовнішніх впливів, геометричних особливостей об’єкта і фізичних властивостей матеріалу виділити найсуттєвіші у цьому завданні і відкинути ті, що мало впливають на результат аналізу. Ступінь спрощень залежить від необхідної точності, математичних можливостей, а також від того, яка сторона явища розглядається в задачі.

При виборі розрахункової схеми доводиться ідеалізувати геометричні параметри об’єкта, фізичні властивості матеріалу, зовнішній вплив, опори і в’язі.

Методи науки

Методи опору матеріалів характеризуються:

  • експериментально-теоретичним підходом до вирішення задач;
  • застосуванням законів фізики, механіки та математичного апарату;
  • широким використанням передумов, що спрощують вирішення задачі, котрі базуються на визначеному переліку гіпотез.

Основні гіпотези та принципи опору матеріалів

Важливим кроком при виборі розрахункової схеми є опис механічних властивостей матеріалу. Відмова від поняття жорсткого тіла вимагала введення гіпотез, що описують ці властивості. Немає такої фізичної моделі, яка б повністю відображала поведінку усіх матеріалів. Для одних придатні одні допущення, для інших — інші. Проте є деякі загальні гіпотези і принципи, що використовуються в більшості задач опору матеріалів.

Гіпотези

Для побудови теорії опору матеріалів вводять деякі гіпотези щодо структури і властивостей матеріалів, а також про характер деформацій.

  1. Гіпотеза про однорідність та ізотропність. Матеріал вважається однорідним та ізотропним, тобто в будь-якому об’ємі та в будь-якому напрямі властивості матеріалу вважаються однаковими. Хоч кристали, з яких складаються метали, анізотропні, проте їхнє хаотичне розташування дає змогу макрооб’єми металів вважати ізотропними. Інколи припущення про ізотропію є неприйнятним, наприклад для деревини, властивості якої вздовж і поперек волокон відрізняються.
  2. Гіпотеза про суцільність матеріалу. Припускається, що матеріал суцільно заповнює форму тіла. Атомістична теорія дискретної будови речовини до уваги не береться.
  3. Гіпотеза про малість деформацій. Припускається, що деформації малі, порівняно з розмірами тіла. Це дає змогу здебільшого нехтувати змінами в розташуванні зовнішніх сил відносно окремих частин тіла й складати рівняння статики для недеформованого стану тіла. Малі відносні деформації розглядаються як нескінченно малі величини.
  4. Гіпотеза про ідеальну пружність матеріалу. Припускається, що всі тіла абсолютно пружні. Відхилення від ідеальної пружності, які завжди спостерігаються для реальних тіл, неістотні і ними нехтують до певних меж деформування. Більшість задач опору матеріалів вирішують у припущенні лінійно деформованого тіла, при якому справедливий закон Гука, що відображає пряму пропорційність між деформаціями та навантаженням.
  5. Гіпотеза плоских перерізів (гіпотеза Бернуллі). Поперечні перерізи, що були плоскими і нормальними до осі стержня до прикладання навантаження, залишаються плоскими і нормальними до його осі після деформації.

Принципи

  1. Принцип незалежності й додавання дії сил (принцип суперпозиції). Зусилля в будь-якому елементі конструкції, спричинені різними факторами, дорівнюють сумі зусиль, спричинених кожним із цих факторів, і не залежать від порядку їхнього прикладання. Це справедливо і стосовно деформацій.
  2. Принцип Сен-Венана. В перерізах, достатньо віддалених від місць прикладання навантаження, деформація тіла не залежить від конкретного способу навантаження і визначається лише статичним еквівалентом навантаження.

Види деформацій

Приклад деформації розтягання стержня

Внаслідок дії навантаження або зміни температури реальні тіла деформуються, тобто змінюють свої форму і розміри. При деформуванні тіла його точки переміщаються в просторі відносно свого вихідного положення.

При навантажуванні твердого тіла у ньому виникають внутрішні сили взаємодії між частками, що протидіють зовнішнім силам. Деформації бувають пружні, тобто такі, що зникають після припинення дії сил, які спричинили їх, та пластичні (залишкові), — ті, що не зникають.

При збільшенні навантаження внутрішні сили також зростають, але до певної межі, яка залежить від властивостей матеріалу. Настає момент, колі вже тіло не здатне чинити опір зростанню навантаження. Тоді воно руйнується.

В опорі матеріалів вивчають такі основні види деформацій стрижня: розтягання-стискання, зсув (зріз), кручення та згинання. Розглядаються і складніші види деформацій, що отримуються поєднанням перелічених.

Деформація розтягання-стискання

Розтягання або стискання виникає тоді, коли до стержня вздовж осі прикладені протилежно спрямовані сили. При цьому відбувається переміщення перерізів вздовж осі стержня, що при розтяганні подовжується а при стисканні вкорочується. Зміну Δl початкової довжини l називають абсолютним подовженням при розтяганні (абсолютним укороченням при стисканні). Відношення абсолютного подовження (укорочення) Δl до початкової довжини l стержня називають середнім відносним подовженням і, як правило позначають ε

ϵ=Δll{\displaystyle \epsilon ={\frac {\Delta l}{l}}}

На розтягання або стискання працюють багато елементів конструкцій: стержні ферм, колони, штоки поршневих машин, стяжні гвинти тощо.

Деформація зсуву (зрізу)

Деформація зсуву

Зсув або зріз виникає тоді коли зовнішні сили зміщують два паралельних плоских перерізи один відносно одного при незмінній відстані між ними. Зміщення а (див. рис.) називають абсолютним зсувом. Відношення абсолютного зсуву до відстані h між площинами, що зміщуються (тангенс кута γ) називають відносним зсувом. Унаслідок малості кута γ при пружних деформаціях його тангенс вважають рівним куту перекосу розглядуваного елемента

γ=ah{\displaystyle \gamma ={\frac {a}{h}}}

Відносний зсув є кутовою деформацією, яка характеризує перекіс елемента. На зсув та зріз працюють заклепки й болти, що скріплюють елементи, які зовнішні сили намагаються зсунути один відносно одного.

Деформація кручення

Деформація кручення

Кручення виникає при дії на стержень зовнішніх сил, які утворюють момент відносно осі стержня (див.рис.). Деформація кручення супроводжується поворотом перерізів стержня один відносно одного навколо його осі. Кут повороту одного перерізу стержня відносно іншого, що перебуває на відстані l, називають кутом закручування на довжині l. Відношення кута закручування α до довжини l називають відносним кутом закручування:

θ=αl{\displaystyle \theta ={\frac {\alpha }{l}}}

На кручення працюють вали, шпинделі верстатів та ін.

Деформація згинання

Деформація згинання балки

Деформація згинання (див.рис.) полягає у викривленні осі прямого стрижня або в зміні кривизни кривого стрижня. У прямих стержнях переміщення точок δ, які спрямовані перпендикулярно до початкового положення осі, називають прогинами. На згинання працюють осі залізничних вагонів, ресори, зуби шестерень, балки міжповерхових перекриттів, важелі та ін.

Складний опір

Складний опір — напружений стан, що виникає у стрижні, брусі або іншому пружному тілі під впливом двох або більше найпростіших деформацій: розтягу-стиску і згину, кручення і згину, косого згину тощо[1].

Випадки складного опору умовно поділяють на два види. До першого виду належать випадки складного опору, при яких у небезпечних точках бруса напружений стан є одноосьовим. У цю групу об’єднують: згин з розтяганням, косий згин, позацентрове розтягнення-стиснення тощо.

До другої групи належать такі випадки складного опору, коли напружений стан є плоским. Наприклад, згин з крученням, розтягнення (стиснення) кручення і т. д. Для цього випадку при оцінюванні напружено-деформованого стану вдаються до застосування теорій міцності.

Див. також

Примітки

Література

  • Короткий курс опору матеріалів: Навч. посіб. / І. М. Ольховий, Б. М. Стасюк, В. З. Станкевич; Нац. ун-т «Львів. політехніка». Ін-т дистанц. навчання. — Л. : Вид-во Нац. ун-ту «Львів. політехніка», 2004. — 194 c. — (Сер. Дистанц. навчання; № 18).
  • Опір матеріалів / Посацький С. Л. − Львів: Видавництво Львівського університету, 1973. − 403 с.
  • Опір матеріалів. Конспект лекцій / Олександр Володимирович Мильніков. − Тернопіль: Видавництво ТНТУ, 2010. − 257 с.
  • Опір матеріалів: Навч. посіб. для студентів ВНЗ. Рекомендовано МОН / Шваб’юк В. І. — К., 2009. — 380 с.
  • Опір матеріалів. Підручник / Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993 .- 655 с. ISBN 5-11-004083-4
  • Основи опору матеріалів: навч. посіб. [для студентів ден. та заоч. форм навчання мех., машинобуд., транспорт. і енергет. спец. ВНЗ] / В. С. Кравчук, О. Ф. Дащенко, Л. В. Коломієць, О. М. Лимаренко. — Одеса: Стандартъ, 2014. — 322 с. : іл. — Бібліогр.: с. 298 (13 назв). — ISBN 978-966-413-482-5
  • Сопротивление материалов / Писаренко Г. С. − 5-е изд., перераб. и доп. − К.:Вища школа, Головне видавництво, 1986. − 775 с.

www.gpedia.com

Опір матеріалів для напряму підготовки “Будівництво”. Частина І

ЗМІСТ

 

1. Загальна інформація

1.1. Анотація курсу

1.2. Методичні поради щодо вивчення навчальної дисципліни (рекомендації про послідовність вивчення 

1.3. Рекомендації щодо вивчення теоретичної частини курсу

1.4. Методичні вказівки

1.5. Форми поточного та підсумкового контролю. 

 

2. Навчальний посібник  (Заліковий кредит 1 ).

 

2.1.  Розділ 1.  Вступ. Основні поняття і положення

2.1.1. Лекційний матеріал.

Тема І. Задачі курсу та зміст предмету

1.1 Предмет опору матерiалiв. Основні поняття та терміни

1.2 Короткий iсторичний нарис розвитку науки про опір матеріалів

1.3 Основнi гiпотези опору матеріалів (модель реального здатного деформуватися тiла)

1.4 Основнi констуктивнi форми

1.5 Класифiкацiя сил

1.6 Види простих деформацiй

1.7 Поняття про напругу та деформацiю в точцi навантаженого тіла

Тема ІІ. Геометричні характеристики плоских перерізів

2.1 Статичний момент плоского перерiзу вiдносно осi. Визначення центра ваги складеного перерiзу

2.2 Моменти iнерцiї плоских перерiзiв

2.3 Моменти iнерцiї простих перерiзiв

2.4 Залежнiсть мiж моментами iнерцiї при параллельному перенесеннi осей координат

2.5 Змiна моментiв iнерцiї при поворотi системи координат вiдносно iї початку

2.6 Головнi осi та головнi моменти iнерцiї

2.7 Поняття радiуса iнерцiї. Головнi радiуси iнерцiї. Еліпс інерції

2.1.2. Питання до самоконтролю знань.

2.1.3. Практичні вправи та завдання

2.1.4. Тестове завдання з відповідями для самоконтролю знань

2.1.6. Перелік літератури

 

2.2.  Розділ 2.  Прості деформації бруса

2.2.1. Лекційний матеріал.

Тема І. Центральний розтяг (стиск) бруса

1.1. Поздовжнi сили

1.1.1 Поздовжнi сили i їх епюри

1.1.2 Напруга, деформацiя, закон Гука при розтязi (стиску)

1.2. Механічні характеристики будівельних матеріалів

1.3. Методи розрахунків в опорі матеріалів

1.3.1 Метод руйнівних навантажень

1.3.2 Метод допустимих напруг

1.3.3 Метод граничних станiв

1.3.4 Основнi види задач опору матерiалiв

1.4. Врахування власної ваги бруса при розтязі (стиску)

1.4.1 Напруга та деформацiя при розтязi (стиску) із врахуванням власної ваги

1.4.2 Поняття критичної i допустимої довжини стержня

1.4.3 Брус рiвного опору при розтязi (стиску)

1.5. Статично невизначні задачі при розтязі (стиску)

1.5.1 Загальнi поняття про статично невизначнi системи

1.5.2 Загальний метод розкривання статичної невизначностi

1.5.3 Приклади розв’язання статично невизначних задач при розтязi (стиску)

1.5.4 Монтажні (початкові) зусилля

1.5.5 Температурна напруга

Тема ІІ. Зсув

2.1 Напруга, деформацiя, закон Гука при зсувi

2.2 Потенцiальна енергiя пружних деформацiй при зсувi

2.3 Контактна деформацiя зминання

2.4 Приклади розрахункiв на зсув та зминання

Тема ІІІ. Кручення валів

3.1 Епюра крутних моментів

3.2 Напруга в поперечних перерізах круглого вала при крученні

3.3 Розрахунки на міцність та жорсткість при крученні

2.2.2. Питання до самоконтролю знань.

2.2.3. Практичні вправи та завдання

2.2.4. Підготовка до виконання лабораторних робіт.

2.2.5. Тестове завдання з відповідями для самоконтролю знань

studcon.org

Опір матеріалів — значення слова, визначення слова, слово означає

Опір матеріалів, наука про міцність і деформованість елементів (деталей) споруд і машин. Основні об’єкти вивчення С. м. — стрижні і пластини, для яких встановлюються відповідні методи розрахунку на міцність, жорсткість і стійкість при дії статичних і динамічних навантажень. С. м. базується на законах і виводах теоретичною механіки, але, окрім цього враховує здатність матеріалів деформуватися під дією зовнішніх сил. Фізіко-механічні характеристики (межа текучості, межа міцності, модуль пружності і т.п.), необхідні для оцінки міцності і деформатівності матеріалів, визначаються за допомогою випробувальних машин і спеціальних вимірювальних приладів — тензометрів . При випробуваннях забезпечуються необхідні умови завантаження і висока точність виміри деформацій випробовуваних зразків матеріалів. Найбільш характерне випробування на розтягування зразків, що є стрижнями круглого перетину або смуги з перетином у вигляді вузького прямокутника. За результатами цих випробувань будується т.з. діаграма розтягування-стискування . Маючи в своєму розпорядженні діаграму випробування і користуючись розробленими в С. м. методами розрахунку, можна передбачити, як поводитиметься реальна конструкція, виготовлена з того ж матеріалу.

  Основний вміст і методи С. м. При деформації твердого тіла під навантаженням змінюється взаємне розташування його мікрочасток, унаслідок чого в телі виникає внутрішня напруга. У С. м. визначаються найбільша напруга в елементах споруд або деталях машин. Вони порівнюються з нормативними величинами, тобто з напругою, яка можна допустити, не опасаючись пошкодження або руйнування цих елементів (деталей). Перевірці підлягають також деформації тіла і переміщення його окремих крапок. Окрім необхідної міцності, конструкція має бути також стійкою, тобто володіти здатністю при малих випадкових короткочасних діях, що порушують її рівновагу, лише трохи відхилятися від вихідного стану. Виконання цієї вимоги залежить від зовнішніх сил, геометрія елементу (деталі) і від фізичних констант матеріалу.

  Для розрахунку елементів конструкцій в С. м. розробляються наближені інженерні методи, що використовують кінематичні і статичні гіпотези, які в більшості випадків виявляються досить близькими до дійсності. При виведенні розрахункових формул для визначення напруги і переміщень виробляється схематизація елементу споруди, що розраховується, його опорних закріплень і навантаження, що діє, інакше кажучи, створюється розрахункова схема (модель) об’єкту.

  При побудові загальної теорії розрахунку в С. м. розглядаються т.з. тіла, що ідеалізуються, з властивостями, що лише приблизно відображають поведінку реальних об’єктів. Тіла вважаються однорідними (з властивостями, однаковими в усіх точках), суцільними (без порожнеч), такими, що володіють пружністю (здатністю відновлювати свої розміри після зняття навантаження) ізотропними (з однаковими пружними властивостями по всіх напрямах). На основі вивчення простих деформацій — розтягування-стискування, кручення, вигину в С. м. виводяться формули, що дозволяють для кожного з цих видів деформацій визначати напруги, переміщення і деформації в окремих крапках тіла. За наявності одночасно два або декілька простих деформацій, що протікають в пружній стадії (для якої справедлива лінійна залежність між напругою і деформаціями), напруга і деформації, знайдені окремо для кожного виду, підсумовуються.

  Багато матеріалів (наприклад, бетон) володіють властивістю повзучості (див. Повзучість матеріалів), унаслідок якої деформації можуть зростати з часом при незмінному навантаженні. У С. м. встановлюються закони розвитку повзучості і час, протягом якого вона помітно виявляється, а також розглядається дія на стрижень ударного навантаження, при якому виникає динамічна напруга; останні визначаються по наближених формулах, виведених на основі ряду допущень. При розрахунку елементів складної форми, для яких аналітичні формули вивести не удається, застосовують експериментальні методи (наприклад, оптичний, лакових покриттів, муарових смуг і ін.), розподіли деформацій, що дозволяють отримувати наочну картину, по поверхні досліджуваного елементу (деталі) і обчислювати напругу в його окремих крапках. Найбільшу трудність представляє визначення т.з. залишкової напруги, яка може виникати в елементах конструкцій, що не несуть навантаження (наприклад, при зварці або в процесі плющення сталевих профілів).

  Одне з важливих завдань С. м. полягає в створенні т.з. теорій міцності на основі яких можна перевірити міцність елементів в складному напруженому стані, виходячи з прочностних характеристик, отриманих дослідним дорогою для простого розтягування-стискування. Існує ряд теорій міцності; у кожному окремому випадку користуються тією з них, яка найбільшою мірою відповідає характеру вантаження і руйнування матеріалу.

  Історична довідка. Історія С. м., як і багатьох ін. наук нерозривно пов’язана з історією розвитку техніка . Зародження науки о С. м. відноситься до 17 в.; її основоположником вважається Галілей, який вперше обгрунтував необхідність вживання аналітичних методів розрахунку замість емпіричних правил. Важливим кроком в розвитку С. м. з’явилися експериментальні дослідження Р. Гуку (60—70-і рр. 17 ст), що встановив лінійну залежність між силою, прикладеною до розтягнутого стрижня, і його подовженням (закон Гуку). У 18 ст великий внесок у розвиток аналітичних методів в С. м. був зроблений Д. Бернуллі, Л. Ейлером і Ш. Кулоном, що сформулювали найважливіші гіпотези і що створили основи теорії розрахунку стрижня на вигин і кручення. Дослідження Ейлера в області подовжнього вигину послужили основою для створення теорії стійкості стрижнів і стрижньових систем. Т. Юнг ввів (1807) поняття про модуль пружності при розтягуванні і запропонував метод його визначення.

  Важливий етап в розвитку С. м. пов’язаний з публікацією (у 1826) Л. Навьє першого курсу С. м., що містив систематизований виклад теорії розрахунку елементів конструкцій і споруд. Принципове значення мали праці А. Сен-Венана (2-я половина 19 ст). Ним вперше були виведені точні формули для розрахунку на вигин кривого бруса і сформульований принцип, згідно з яким розподіл напруги в перетинах, віддалених на деякій відстані від місця додатка навантаження, не пов’язано із способом її застосування, а залежить лише від рівнодійної цього навантаження.

  Великі заслуги в розвитку С. м. належать російському вченим М. Ст Остроградському, дослідження якого в області С. м. будівельної механіки, математики і теорії пружності придбали світову популярність, і Д. І. Журавському, що вперше встановив (1855) наявність дотичної напруги в подовжніх перетинах бруса і отримав формулу для їх визначення (ця формула застосовується і в сучасній практиці інженерних розрахунків). Загальне визнання отримали дослідження Ф. С. Ясинського, подовжнього вигину, що розробив (1893) теорію, в пружній стадії і за її межами (рекомендації Ясинського послужили основою для розробки сучасних нормативних документів в СРСР і за кордоном).

  На початку 20 ст розширення масштабів вживання залізобетонних і сталевих конструкцій, поява складних машин і механізмів зумовили швидкий розвиток науки о С. м. Були опубліковані класичні підручники С. П. Тимошенко по С. м. і будівельній механіці, праці А. Н. Дінника по подовжньому вигину, стійкості стислих стрижнів і ін.

  Подальшому вдосконаленню методів С. м. сприяло створення в СРСР ряду науково-дослідних установ для проведення досліджень в області розрахунку конструкцій. З’явилися нові розділи С. м. Великий вплив на розвиток С. м. надали праці Н. М. Беляєва в області пластичних деформацій, А. А. Ільюшина по теорії пластичності, Ю. Н. Работнова і А. Р. Ржаніцина по теорії повзучості. Значним вкладом в науку о С. м. з’явилася створена Ст З. Власовим теорія розрахунку тонкостінних стрижнів і оболонок. Важливі фундаментальні дослідження виконані радянськими ученими Н. І. Безуховим, Ст Ст Болотіним, А. Ф. Смирновим, В. І. Феодосьевим і ін.

  Сучасні тенденції розвитку науки о С. м. Одне з найважливіших завдань С. м. — встановлення причин і характеру руйнування матеріалів, що вимагає всестороннього теоретичного і експериментального вивчення процесів, що відбуваються в мікрооб’ємах тіла, зокрема характеру виникнення і розвитку тріщин. Встановлено існування такої (граничних) напруги, перевищення якої спричиняє за собою прогресуюче зростання тріщин, що вже з’явилися, що приводить кінець кінцем до руйнування тіла. Якщо напруга менше вказаної межі, то тіло, що має тріщини, знаходиться в змозі трещиноустойчивості. В деяких випадках під дією навантаження руйнування в мікроелементах поширюються на весь об’єм тіла (особливо при високих температурах). Дослідження цих питань вимагає створення нового важливого розділу механіки тіла, що деформується, — механіки руйнування. Ще недостатньо вивчена низка запитань т.з. втомній міцності матеріалів, зокрема міцність елементів (деталей) машин при їх тривалому циклічному вантаженні.

  У зв’язку з появою нових конструкційних матеріалів (наприклад, пластмас, легких сплавів) виникла необхідність створення теорій міцності, що відображають специфічні властивості цих матеріалів. Сучасні технологічні процеси (наприклад, із застосуванням високого тиску) дозволяють отримувати матеріали вельми високою міцністю, поведінка яких під навантаженням недостатньо вивчено і вимагає цілеспрямованих досліджень.

  Літ.: Тимошенко С. П., Історія науки про опір матеріалів з короткими відомостями з історії теорії пружності і теорії споруд, М., 1957; Работнов Ю. Н., Опір матеріалів, М.. 1962; Феодосьев Ст І., Опір матеріалів, М., 1974; Опір матеріалів, М., 1975.

  Під редакцією А. Ф. Смирнова.

vseslova.com.ua

ОПІР МАТЕРІАЛІВ. Елементарна теорія опору матеріалів

— наукова дисципліна, що вивчає деформації та умови міцності тіл, що дає загальні основи для правильного призначення розмірів елементів конструкцій. Знання опору матеріалів необхідно для забезпечення надійності конструкцій будь-якого призначення. У стр-ве опір матеріалів набуває особливого значення у зв’язку з великими розмірами споруд та величинами діючих на них сил.

Основи опору матеріалів відносяться до області прикладної фізики, а за характером вирішуваних завдань опір матеріалів входить до складу техннч. механіки. За методом опір матеріалів є експериментально-теоретич. дисципліною, що поєднує досвід з теоретич. висновками. Експериментальні дослідження з опору матеріалів, на відміну від аналогічних досліджень в області физич. металознавства і подібних материаловедч. дисциплін, носять характер механічний випробувань, при яких не вивчаються відбуваються в матеріалі структурні зміни.

Застосування експериментальних методів у спротиві матеріалів переслідує двояку мету: 1) вивчення властивостей матеріалів, проводиться при однорідному напруженому стані на зразках найпростішої форми; 2) дослідження неоднорідного напруженого стану в деталях при моделюванні реальних умов їх роботи. За допомогою дослідів першого виду вивчаються як індивідуальні характеристики механічних властивостей матеріалів, так і загальні закономірності, що описують розвиток деформацій і руйнувань в залежно від виду напруженого стану, а також від швидкості деформування і темп-ри. Дослідження 2-го напряму служать для перевірки правильності припущень, покладених в основу розрахунку, або використовуються як спосіб прямого експериментального розв’язання задачі.

Для проведення експериментальних досліджень застосовуються машини, що забезпечують необхідні умови нагруженпя зразків, і прилади, дозволяють з достатньою точністю вимірювати їх деформації. Найбільше поширення в лабораторіях С. м. отримали машини для випробувань на розтяг-стиск, зазвичай пристосовані і для випробувань на вигин. З тієї ж схемою конструюється більшість пульсаторів, службовців для випробувань матеріалів на втому. До обладнання лабораторій опір матеріалів відносяться також преси, машини для випробувань на кручення і копри для випробувань на удар. Лабораторії дослідницького типу мають, крім того, машинами для випробувань матеріалів при складному напруженому стані (створюваному в тонкостінних трубчастих зразках шляхом накладення дії поздовжньої сили, крутного моменту і внутр. тиску) і стендами для вивчення несучої здатності елементів конструкцій при різних видах нагруженпя. В будує, справі велику роль грають також натурні випробування, що проводяться шляхом вимірювання деформацій як у процесі зведення споруд і їх пробному навантаженні, так і в подальшому при їх експлуатації. Значення натурних випробувань полягає не тільки в можливості отримання цілком реальної оцінки цієї споруди, але і в тих загальних висновках про роль масштабного фактора, к-рие вдається отримати на основі порівняння з результатами лабораторних випробувань.

Для вимірювання деформацій служать різноманітні механічний, оптико-механічний, електричних ма. і пневматич. тензометри (див. Деформацій вимірювання). Прилади такого роду дозволяють проводити вимірювання тільки на поверхні конструкції. Однак у більшості випадків саме у поверхні і розташовуються ділянки, які знаходяться в найгірших умовах і тому представляють найбільший інтерес. Оскільки у поверхні 3 складових напруги (одне нормальне і два дотичних) дорівнюють нулю, для оцінки напруженого стану в околі к.-л. точки поверхні досить виміряти поблизу цієї точки деформації тільки за 3 напрямами (напр., з допомогою тензометрів, встановлених по сторонах рівностороннього трикутника). При означає, неоднорідності напруженого стану, особливо при вивченні концентрації місцевих напружень, потрібне застосування досить великих моделей і малобазных тензометрів, одночасно забезпечують велику збільшення вимірюваної деформації. Чутливість нек-рих сучасних тензометрів оцінюється величинами порядку 0,01 мікрона і вище, але вони вимагають забезпечення особливо ретельної температурної компенсації і виключення впливу інших можливих побічних факторів. З розвитком пластич. деформацій, зважаючи їх означає, розмірів, застосовувана апаратура може бути значно спрощена.

На відміну від теорії пружності, користується строгими математич. прийомами розв’язання задач, в С. м. розвиваються наближені теоретнч. методи, що використовують кинематич. або статич. гіпотези, найпростішим прикладом к-рих є допущення про збереження плоскої форми поперечних перерізів в вигнутих стрижнях. До такого роду гіпотез відносяться припущення про збереження лінійності нормалей в теорії пластин і оболонок, про однаковій формі деплаиации перерізів в умовах чистого і изгибного кручення, про рівномірності розподілу згинальних касат. напружень по товщині стінки стрижня і т. д. більшості випадків такі гіпотези виявляються досить близькими до насправді не тільки при пружному, але і при пружно-пластичному деформуванні.

Елементарна теорія опору матеріалів зазвичай розглядає лише різні види деформації стержнів (див. Розтяг-стиск, Крутіння, Вигин, Складний опір), причому обмежується стадією, для до-рій справедливий принцип накладання, або,інакше, про допущення незалежності дії сил, що передбачає лінійність співвідношень між переміщеннями і силами.

Більш складними і разом з тим досить важливими для практики є нелінійні задачі опору матеріалів, к-рие не можна вирішувати на основі зазначеного припущення. Порушення лінійності зв’язку між переміщеннями і силами можуть бути обумовлені двома причинами: відхиленнями поведінки матеріалу від закону Гука (тобто від лінійної залежності між деформаціями і напругами) і розвитком значить, переміщень, к-рие, вносячи геометрич. зміни в стан системи, помітно змінюють умови рівноваги між внутр. зусиллями і навантаженням, так і характер впливу деформацій різних елементів тіла на розвиток переміщень. Прикладом першого випадку може бути пружно-пластичний поперечний вигин короткого товстого бруса. Прогини такого бруса, залишаючись малими порівняно з його розмірами і не вносячи помітних змін у його конфігурацію, тим не менш наростають швидше, ніж навантаження. Прикладом другого випадку може служити поперечний вигин тонкого довгого стрижня, к-рий в межах пружного стану матеріалу здатний давати переміщення, порівнянні з його довжиною.

Складність отримання рішень, що дозволяють досить повно описувати явища нелінійного деформування конструкцій, змушує шукати більш простих шляхів отримання оцінки їх несучої здатності. Одним з способів є оцінка несучої здатності по граничному пружному станом. На цій основі будуються розрахунки але типовим напруженням. Однак вказаний спосіб, особливо при врахуванні місцевих напружень, зазвичай веде до вельми значить, заниження реаль — йой несучої здатності конструкцій, т. к. піки напруги, визначені при допущенні повної відсутності у матеріалу пружних недосконалостей, що виявляються в дійсності згладженими навіть при крихкому матеріалі (див. Крихкість), а при виникненні пластичних деформацій (див. Пластичність) характер розподілу напруг стає зовсім іншим. В останньому випадку значно більш близькою до дійсності виявляється оцінка несучої здатності конструкції по граничному стану, до-рої визначається можливістю наростання переміщень без збільшення навантаження при практично рівномірний розподіл інтенсивності напружень у місцях розвитку великих пластичних деформацій.

Особливий коло завдань виникає при оцінці опору конструкцій динамічних навантажень і тривалої міцності їх в умовах повільно протікаючих процесів в матеріалі: повзучості, усадочних деформацій (в в’яжучих речовинах, а також і зниження міцності при дії змінних навантажень. У цій галузі велику роль відіграють досвідчені дані. Результати експериментальних досліджень і наближені розрахунки елементів конструкцій в зазначених умовах див. в статтях Динаміка споруд, Динамічна стійкість, Удар.

 

Літ.: Беляєв Н. М., Опір матеріалів, 14 изд., М., 1965; Смирнов А.Ф [та ін], Опір матеріалів, М., 1961; Работнов Ю. Н., Опір матеріалів, М., 1962.

 

 

Опір матеріалів. Відомості з опору матеріалів

Опір матеріалів — наука про міцність і деформованості елементів (деталей) споруд, машин і механізмів. … деформацію. Твердість — спосіб. ність матеріалів чинити опір проник.

 

ВИГИН в опорі матеріалів

Опір матеріалів — наука про міцність і деформованості елементів (деталей) … Згин бруса під дією сил і моментів, що лежать в одній площині

 

МІЦНІСТЬ -… межа міцності при зсуві, справжнє опір…

Це дозволить багаторазово збільшити міцність матеріалів. … Літ.: Філоненко-Бородич М. М. [та ін], Курс опору матеріалів, 4 изд., М., 1955-56; Ільюшин А. А., Ленський Ст. З…

 

МЕХАНІЧНІ ВЛАСТИВОСТІ. Будівельні матеріали

Р. Механічні властивості. 1. міцність. Властивість матеріалу чинити опір руйнуванню під … Опором удару називається здатність матеріалу чинити опір ударним впливам.

 

БУДІВЕЛЬНІ МАТЕРІАЛИ. Основні властивості будівельних…

Твердість — здатність матеріалу опиратися проникнення в нього іншого брлее твердого тіла. … Опір матеріалу стирання визначають на колах стирання або піскоструминним…

Довідник майстра будівельника

 

… Закон Гука. міцністю, твердістю, стираністю, опором…

Опір матеріалів механічного руйнування характеризується їх міцнісними властивостями … Міцність — здатність матеріалу пручатися руйнуванню, а також необоротного зміни…

 

Механічні властивості твердих тіл — тверді і м’які тіла, в’язкі і…

Якщо матеріал може чинити опір проникненню в нього інших тіл, то він твердіше, ніж інші. Під твердістю розуміють опір матеріалу, яке він створює при вдавлюванні або…

 

… механічні властивості, що характеризують міцність матеріалу…

Опір втоми при підвищенні темп-ри знижується, однак у меншою мірою, ніж тривала … Механічні властивості відображають здатність матеріалу чинити опір силових, теплових…

 

БУДМАТЕРІАЛИ: Механічні властивості будматеріалів

Механічні властивості відбивають здатність матеріалу чинити опір силовим, тепловим, усадкових або … Механічні властивості матеріалів детально вивчаються в курсі опору матеріалів.

 

Шкала твердості Мооса

Міцність — властивість матеріалу чинити опір руйнуванню під дією напруг, що виникають від навантаження. … Опір стирання визначають для матеріалів, призначених для підлог…

bibliograph.com.ua