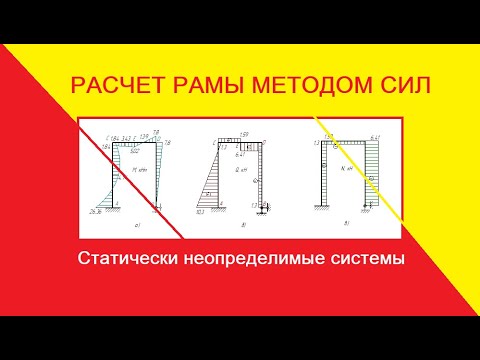
Метод сил в сопромате

 

 

Заказать решение           Способ оплаты

 

При решении задач сопромата, статически неопределимой называется такая система, которая не может быть рассчитана при помощи одних только уравнений статики, так как имеет лишние связи. Для расчета таких систем составляются дополнительные уравнения, учитывающие деформации системы.

Оговоримся, что здесь и далее понятие “расчет” подразумевает только построение эпюр внутренних силовых факторов, возникающих в элементах системы, а не расчет на прочность, жесткость и т.д.

Статически неопределимые системы обладают рядом характерных особенностей:

1. Статически неопределимые конструкции являются более жесткими, чем соответствующие статически определимые, так как имеют дополнительные связи.
2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках.
3. Нарушение лишних связей в статически неопределимой системе не всегда приводит к разрушению, в то время как потеря связи в статически определимой системе делает ее геометрически изменяемой.
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.

Основными методами расчетастатически неопределимых систем являются:

 

1. Метод сил. Здесь в качестве неизвестных рассматриваются усилия – силы и моменты.
2.Метод перемещений. Неизвестными являются деформационные факторы – углы поворотов и линейные смещения.
3.Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть – перемещения.
4. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую – методом сил.
Помимо указанных аналитичеких методов при расчете особо сложных систем используются различные численные методы.

 

Канонические уравнения метода сил

 

Для получения дополнительных уравнений, о которых говорилось в предыдущем параграфе, нужно прежде всего превратить заданную, n раз статически неопределимую систему, в статически определимую, удалив из нее лишние связи. Полученная статически определимая система называется основной. Отметим, что преобразование заданной системы в статически определимую не является обязательным. Иногда используется модификация метода сил, в которой основная система может быть статически неопределимой, однако изложение этого вопроса выходит за рамки этого пособия. Устранение каких-либо связей не изменяет внутренние усилия и деформации системы, если к ней приложить дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Значит, если к основной системе приложить заданную нагрузку и реакции удаленных связей, то основная и заданная системы станут эквивалентными.

В заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе, перемещений быть не может, поэтому и в основной системе перемещения по направлениям отброшенных связей должны равняться нулю. А для этого реакции отброшенных связей должны иметь строго определенные значения.

Условие равенства нулю перемещения по направлению любой i-ой связи из n отброшенных на основании принципа независимости действия сил имеет вид:

 

 

где первый индекс означает направление перемещения и номер отброшенной связи, а второй указывает на причину, вызвавшую перемещение, т.е. — это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи; — перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки.

В методе сил реакцию k-ой связи принято обозначать через Xk. С учетом этого обозначения и в силу справедливости закона Гука перемещения можно представить в виде:

 

 

где — единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией т.е. реакцией, совпадающей по направлению с Xk, но равной единице.

Подставляя (2) в (1), получим:

 

 

Физический смысл уравнения (3): перемещение в основной системе по направлению i-ой отброшенной связи равно нулю.

Записывая выражения, аналогичные (3), для всей совокупности отброшенных связей, получим систему канонических уравнений метода сил:

 

 

Вид уравнения (4), т.е. количество слагаемых в каждом из них и их общее число, определяется только степенью статической неопределимости системы и не зависит от ее конкретных особенностей.

 

Коэффициенты системы канонических уравнений (4) определяются методом Мора-Верещагина путем перемножения соответствующих эпюр. Все эти коэффициенты, как указывалось выше, представляют собой перемещения; коэффициенты, стоящие при неизвестных – единичные перемещения, а свободные члены – грузовые. Единичные перемещения делятся на главные, расположенные по главной диагонали и имеющие одинаковые индексы и побочные (). Главные перемещения всегда положительные, в отличие от побочных.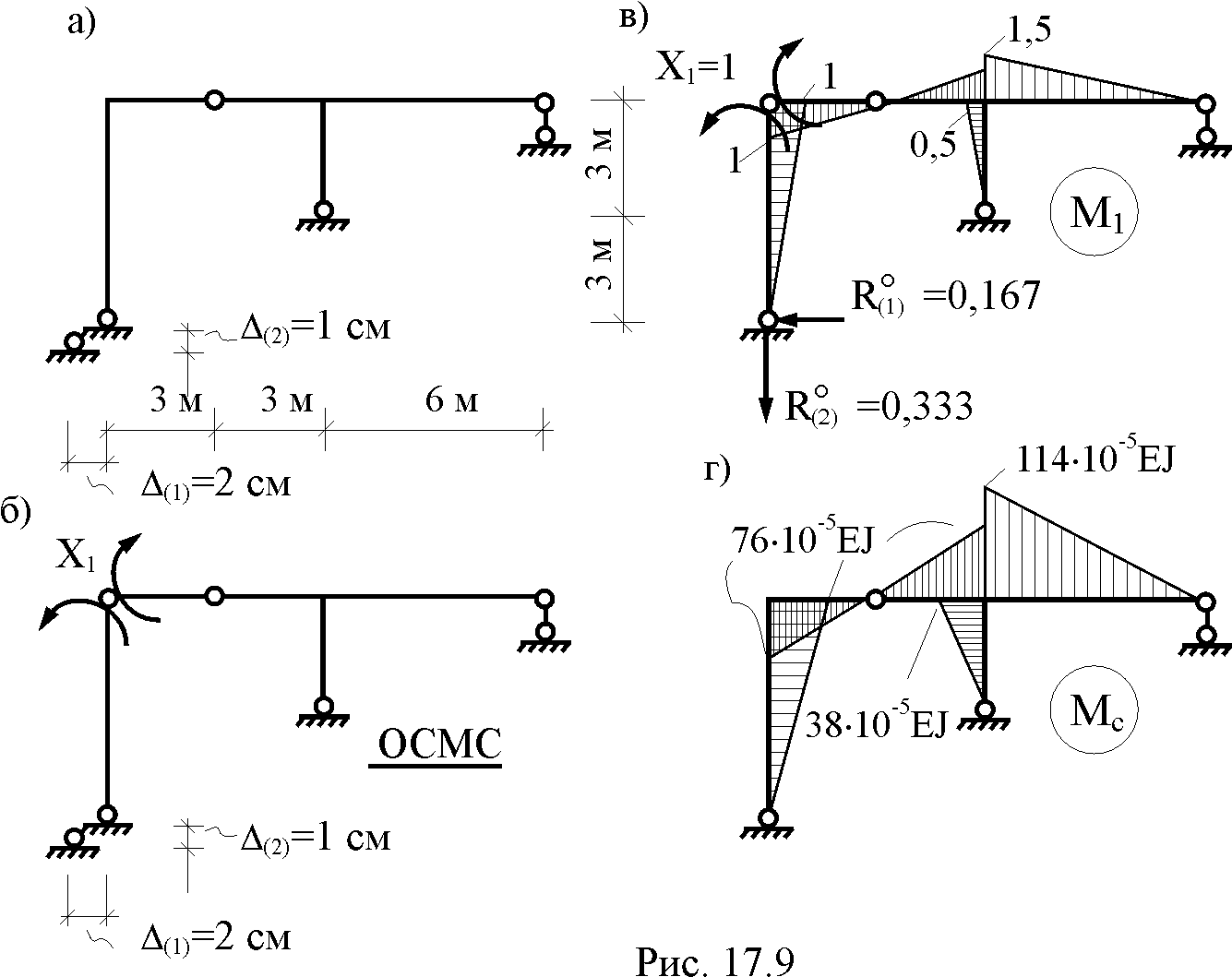 Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е. .

 

Алгоритм расчета методом сил

 

Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил:

1. Определить степень статической неопределимости.
2. Выбрать основную систему.
3. Сформировать эквивалентную систему.
4. Записать систему канонических уравнений.
5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции.
6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений.
7. Построить суммарную единичную эпюру.
8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов.
9. Решить систему (4), т.е. определить реакции лишних связей.
10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры).
11. Выполнить статическую и кинематическую проверки.
Отметим, что пункты 7, 8, 11 приведенного алгоритма не являются безусловно необходимыми, хотя и позволяют контролировать правильность выполнения расчета. А для систем с одной лишней связью пункты 7 и 8 просто лишены смысла, так как в этом случае суммарная единичная эпюра совпадает с единичной.
Остановимся подробнее на некоторых из вышеперечисленных этапов расчета.

 

Выбор основной системы

 

Это важнейший этап расчета, так как рациональный выбор основной системы существенно упрощает вычислительную работу. Рассмотрим возможные способы удаления лишних связей, что и определяет вид основной системы.

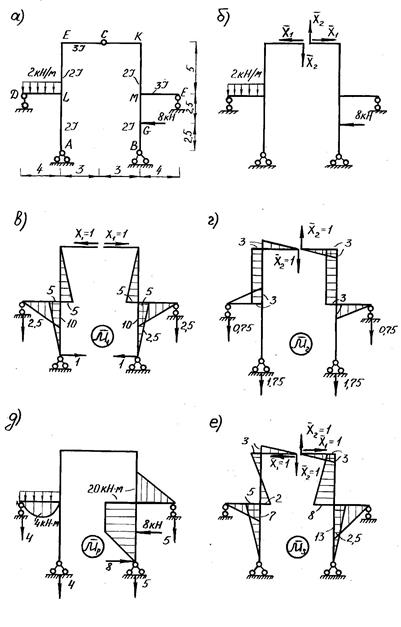
1. Отбрасывание лишних связей осуществляется полным удалением некоторых опор или их заменой опорами с меньшим числом связей. Реакции, действующие в направлениях отброшенных связей, являются лишними неизвестными. На рис.1,б, в, г показаны различные варианты эквивалентной системы, полученные этим способом для рамы (рис.1,а).

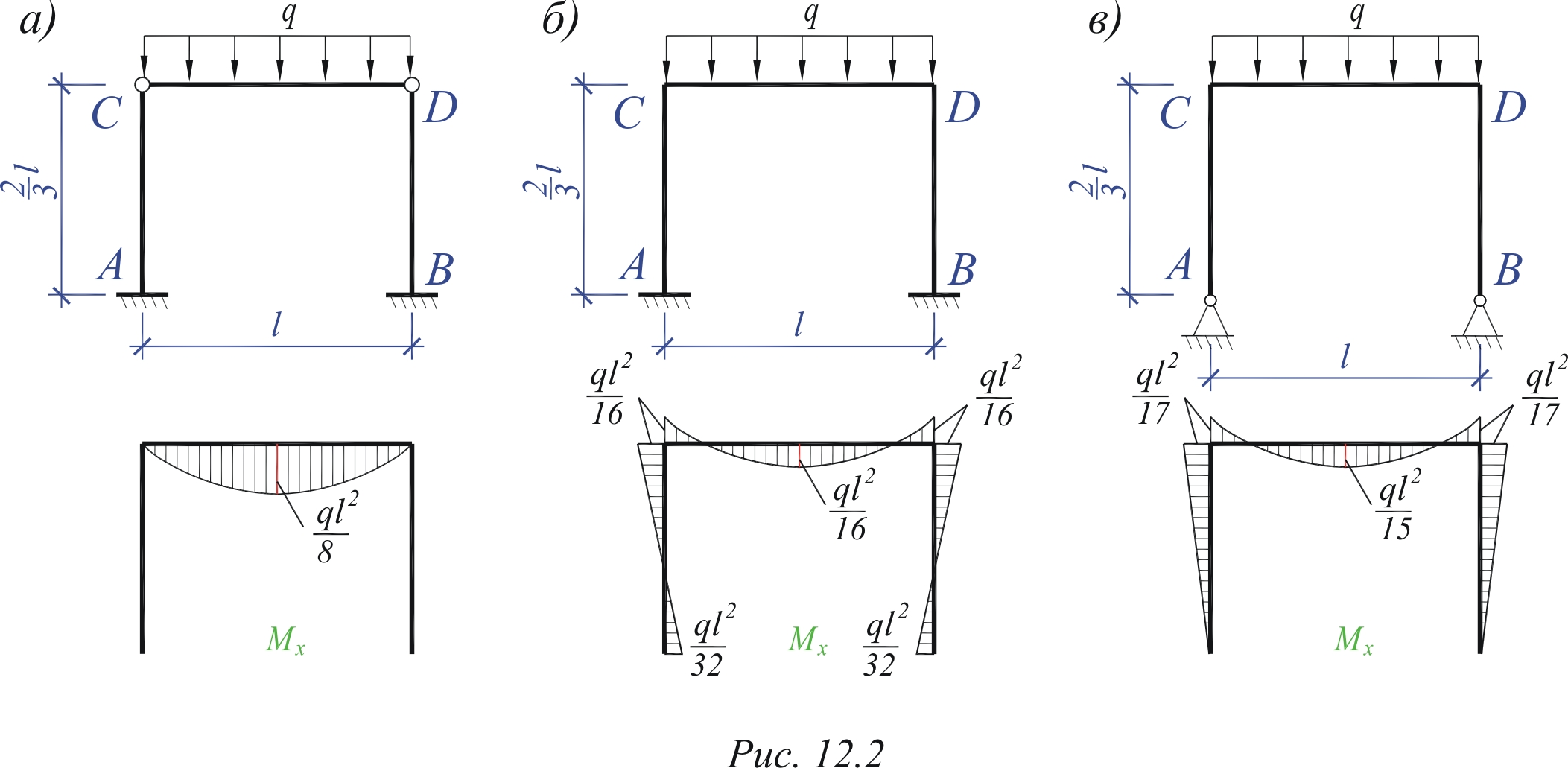
2.Постановка шарниров в промежуточных сечениях стержней позволяет в каждом таком сечении установить связь, соответствующую изгибающему моменту. Эти моменты являются лишними неизвестными. Для рамы, имеющей степень статической неопределимости n=3 (рис.2,а), при выборе основной системы необходимо поставить три шарнира. Положение этих шарниров может быть произвольным, но удовлетворяющим требованию геометрической неизменяемости системы (рис.2,б).

3. Рассечение стержня устраняет три связи, соответствующие внутренним усилиям M, Q, N (рис.2,в). В частных случаях (рис.2,г) рассечение стержня по шарниру освобождает две связи (рис.2,д), а рассечение прямолинейного стержня с шарнирами по концам – одну связь (рис.2,е).

 

рис. 1

 

Среди связей статически неопределимой системы различают абсолютно необходимые и условно необходимые. К абсолютно необходимым относятся связи, при удалении которых система становится геометрически изменяемой. Для абсолютно необходимой связи характерна статическая определимость усилия в ней, т.е. реакция такой связи может быть вычислена из условия равновесия. При выборе основной системы абсолютно необходимые связи отбрасывать нельзя.

 

 

рис. 2

 

Связи, при удалении которых система продолжает оставаться геометрически неизменяемой, называются условно необходимыми. Система, у которой удалили такую связь, может являться основной системой метода сил.

 

Вычисление коэффициентов и свободных членов канонических уравнений

 

Этому этапу расчета предшествует построение единичных и грузовых эпюр внутренних силовых факторов (для балок и рам – эпюр изгибающих моментов). Единичные эпюры строятся от действия безразмерной единичной силы или безразмерного единичного момента, совпадающих по направлению с направлением соответствующей лишней неизвестной в эквивалентной системе, и обозначаются через , а единичная эпюра – через .

 

Грузовая эпюра строится от внешней нагрузки, приложенной к основной системе. При этом можно строить одну эпюру от одновременного действия всех внешних нагрузок или несколько эпюр, отдельно от каждой из приложенных нагрузок. Такое разбиение одной грузовой эпюры на несколько  более простых, как правило, целесообразно только тогда, когда среди действующих нагрузок есть равномерно распределенная, и эпюра моментов на соответствующем участке под ней является знакопеременной. При этом в каждом каноническом уравнении число свободных членов будет равно числу построенных грузовых эпюр.

Единичные и грузовые перемещения (коэффициенты и свободные члены канонических уравнений) в общем случае можно вычислить методом Мора. Для балок и рам это можно сделать при помощи правила Верещагина.

 

Универсальная проверка коэффициентов и свободных членов канонических уравнений

 

Для выполнения универсальной проверки необходимо построить суммарную единичную эпюру — эпюру моментов от одновременного действия всех единичных сил, приложенных к основной системе:

 

Перемножим суммарную единичную эпюру с эпюрой :

 

 

Таким образом результат перемножения суммарной и i-ой единичной эпюр — это перемещение по направлению i-ой связи от совместного действия единичных лишних неизвестных. Это перемещение равно сумме коэффициентов i-го канонического уравнения:

 

 

Такая проверка называется построчной и выполняется для каждого канонического уравнения.
Вместо n построчных проверок чаще всего выполняется одна – универсальная поверка, которая состоит в перемножении суммарной единичной эпюры самой на себя и проверке условия:

 

 

Если универсальная проверка выполняется, значит единичные перемещения вычислены правильно; если нет – необходимо выполнить построчные проверки, что позволит уточнить перемещение, при вычислении которого допущена ошибка.

Для выполнения проверки грузовых перемещений необходимо перемножить суммарную единичную и грузовую эпюры изгибающих моментов:

 

 

Таким образом, проверка свободных членов системы канонических уравнений (4) состоит в выполнении условия:

 

 

Построение окончательных эпюр внутренних силовых факторов

 

Окончательные эпюры можно построить двумя способами.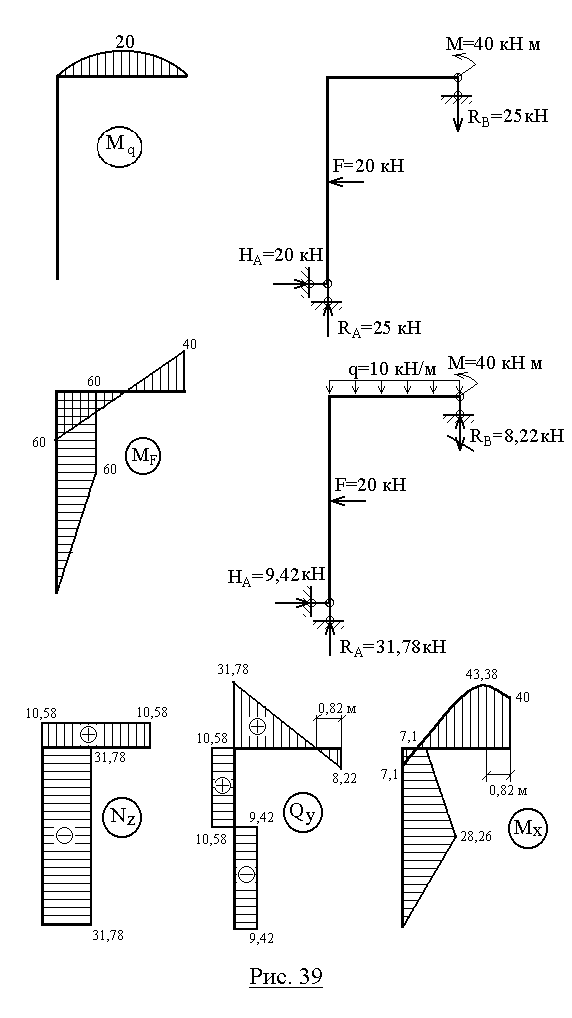

Так как при найденных значениях лишних неизвестных Xi выполняются условия совместности деформаций, то из расчета основной системы можно получить все искомые внутренние усилия заданной системы. На основании принципа независимости действия сил для изгибающих моментов получим:

 

или, учитывая, что

 

 

приходим к выражению:

 

 

Аналогично определяется продольные и поперечные силы:

 

Второй способ основан на том, что в результате вычисления реакций лишних связей Xi исходная статически неопределимая система приведена к статически определимой системе, загруженной внешними нагрузками и реакциями лишних связей. Поэтому окончательные эпюры внутренних силовых факторов можно построить для эквивалентной системы, вычислив предварительно (и то не всегда) из условий равновесия опорные реакции последней.

Недостатком первого способа является то обстоятельство, что для его реализации необходимо дополнительно построить эпюры Qi, Ni (i=1, 2, …,n), Qf, Nf, которые не используются в расчете методом сил и поэтому не были построены ранее.

В связи с этим для построения окончательных эпюр более рациональным представляется второй способ, а условие (8) можно использовать в качестве дополнительной проверки.

 

Проверка окончательной эпюры изгибающих моментов

 

Эта проверка выполняется в двух вариантах: статическая и кинематическая.

При статической проверке, выполняемой обычно для рам, вырезаются узлы и записываются условия их равновесия под действием узловых сосредоточенных моментов и изгибающих моментов на концах стержней. Эта проверка является вспомогательной и выполняется автоматически при правильных эпюрах изгибающих моментов в основной системе и при выполнении кинематической проверки.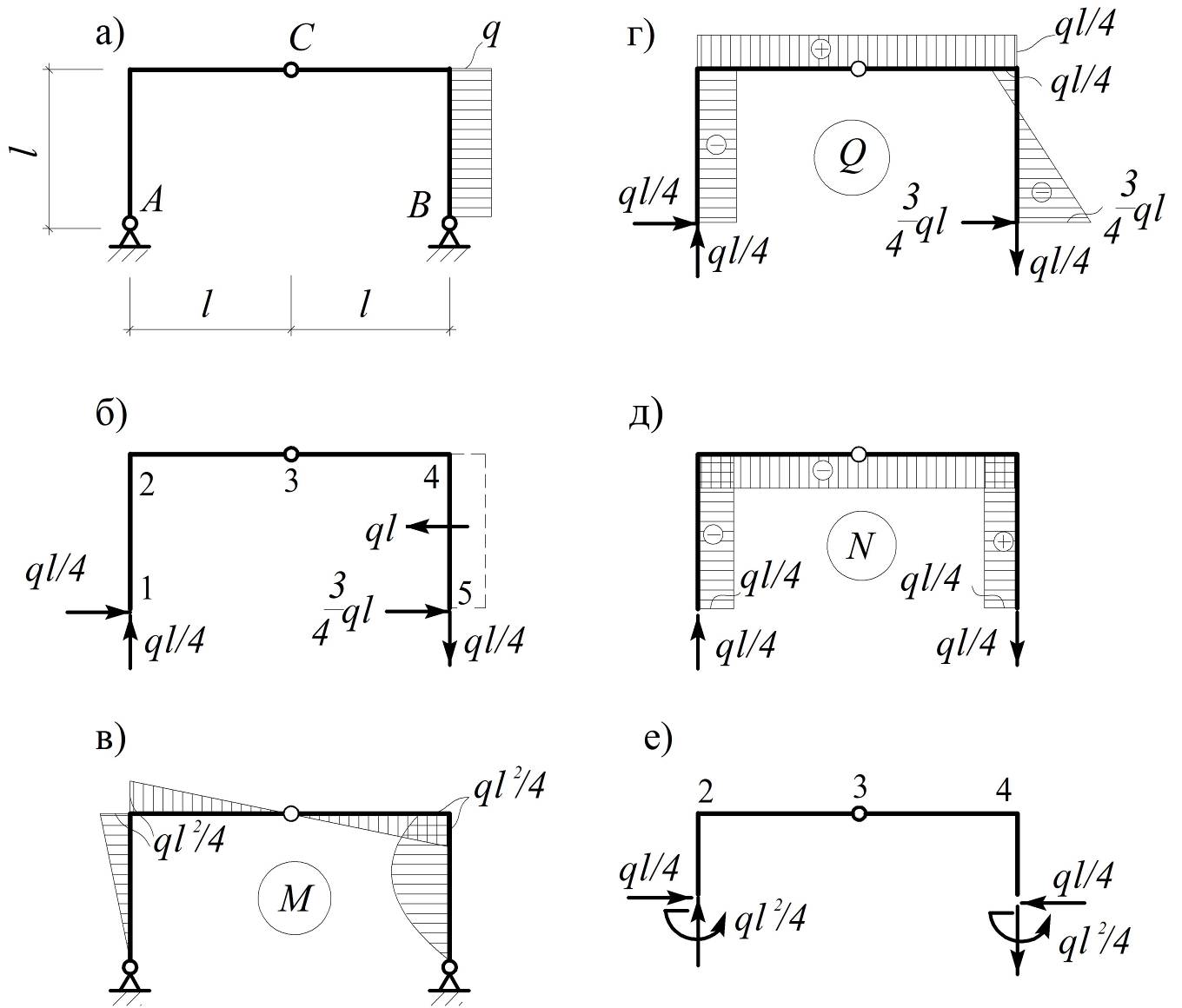

Статическая проверка эпюр Q и N состоит в том, что для любой отсеченной части рамы сумма проекций на две оси всех действующих сил – внешних нагрузок и  внутренних усилий – должна быть равна нулю.

Основной проверкой окончательной эпюры моментов в методе сил является кинематическая проверка, которая может быть построчной или универсальной.<br /> При построчной проверке каждая единичная эпюра моментов перемножается с окончательной эпюрой моментов М:

 

 

Таким образом, в результате перемножения каждой единичной эпюры с окончательной эпюрой моментов получим ноль:

 

Вариантом построчной проверки является проверка по замкнутомуконтуру, состоящая в том, что сумма приведенных (т.е. деленных на жесткость соответствующего стержня или его участка) площадь эпюры М, находящихся внутри каждого замкнутого бесшарнирного контура, должна быть равна сумме приведенных площадей, находящихся снаружи этого контура.

Суммируя выражения типа (11) для всех n, получим выражение, служащее для универсальной кинематической проверки окончательной эпюры изгибающих моментов:

 

 

Формулу (12) можно интерпретировать следующим образом: условное перемещение эквивалентной, или, что то же самое, заданной системы по направлению всех неизвестных от действия всех неизвестных и внешних нагрузок, равно нулю.

 

Определение перемещений в статически неопределимых системах

 

Для определения перемещения в статически неопределимой системе используется тождественность заданной и эквивалентной систем в том смысле, что если условия совместности деформаций выполняются, т.е. справедливы уравнения (4), то перемещения в эквивалентной системе соответствуют перемещениям заданной системы. Тогда, построив для основной системы эпюру изгибающих моментов от единичной силы (или единичного момента) приложенной в направлении искомого перемещения, величину перемещения находим по формуле:

 

 

 

где М – эпюра изгибающих моментов от внешней нагрузки, построенная для статически неопределимой системы.

Отметим, что при вычислении перемещения можно поступить и наоборот: единичную эпюру моментов построить в статически неопределимой заданной системе, а эпюру моментов от внешних нагрузок М – в основной (статически определимой) системе.

 

Пример расчета

 

Построить эпюры продольных, поперечных сил и изгибающих моментов для плоской рамы (рис.3,а).

Степень статической неопределимости рамы:

n = r — s = 4 — 3 = 1

 

Выбираем основную систему, отбрасывая на правой опоре горизонтальный стержень (рис.3,б),  т.е. заменяем шарнирно-неподвижною опору на шарнирно-подвижную. На базе основной системы формируем эквивалентную систему (рис.3,в).

Заменяя реакцию лишней связи соответствующей единичной силой, (рис. 3,г) строим эпюру моментов M1 (рис.3,д).

Грузовая эпюра моментов (рис.3,ж), построенная от одновременного действия всех внешних нагрузок (рис. 3,е), является знакопеременной на участке, где действует нагрузка q. Это создает определенные трудности (хотя и не непреодолимые!) при ее перемножении с единичной эпюрой M1. В связи с этим целесообразно построить две грузовых эпюры – отдельно от нагрузки q (эпюра Mq) и от совместного действия F и M (эпюра MF). Эти варианты нагружения и эпюры представлены на рис.3,з и рис.3,а,б,в.

При таком разбиении внешней нагрузки каноническое уравнение метода сил содержит два грузовых перемещения и имеет вид:

 

 

Вычислим коэффициенты канонического уравнения:

 

 

Реакция лишних связи:

 

Эпюры Nz, Qy, Mx для заданной системы, загруженной нагрузками F, M, q и X1 (рис.3,г) представлены на рис.3,д,е,ж.

Как уже говорилось, при построении эпюр Nz и Q в рамах ординаты можно откладывать в любую сторону, но обязательно указывать знаки; а при построении эпюр Mx знаки можно не указывать, но обязательно откладывать ординаты со стороны сжатых волокон соответствующих элементов.

В рассмотренном примере универсальная проверка правильности вычисления коэффициентов канонического уравнения и свободных членов не выполнялась, так как рама имеет степень статической неопределимости n = 1, а, значит, суммарная единичная эпюра (если ее построить) совпадет с единичной эпюрой M1. В этом случае можно (и желательно!) проверить правильность выполнения расчета при помощи универсальной кинематической проверки окончательной эпюры моментов Mx.

Выполним эту проверку для рамы, рассмотренной в последнем примере (рис.3,а). Должно выполняться условие:

 

Покажем отдельно фрагменты перемножаемых эпюр (рис.3,д и рис.4,ж) для ригеля (рис.5,а,б) и стойки (рис.5,в,г) с указанением всех характерных размеров и соответствующих им ординат. Причем стойка (на рис.5,в,г) показана в горизонтальном положении.

Точка пересечения кривой на ригеле эпюры  Mx с осью (рис. 5,б) определяется следующим образом. Обозначим координату произвольного сечения, отсчитываемую от правого конца ригеля, через z, тогда момент Mx определяется в виде:

 

 

откуда z = 3,77 м (второй корень этого уравнения лишен физического смысла).

 

рис. 3

 

 

рис. 4

 

 

следовательно, расчет выполнен правильно.

 

 

 

Заказать решение

Антипин М.И. Расчет плоских статически определимых ферм

• формат doc
• размер 340.5 КБ
• добавлен 04 марта 2010 г.

Методическое пособие по расчету плоских ферм. Уделяется внимание конструкции ферм, расчету ферм – определению внутренних усилий в стержнях различными способами. Приводятся примеры расчета плоской фермы.

Читать онлайн

Похожие разделы

1. Академическая и специальная литература
2. Металлургия
3. Металловедение
4. Механические и физические свойства металлов
5. Дефекты металлов
6. Усталость металлов

Смотрите также

• формат doc
• размер 3.63 МБ
• добавлен 05 декабря 2009 г.

Содержание: общие указания по выполнению расчетно-проектировочных работ. Используемые обозначения. Растяжение-сжатие. Расчет статически определимых стержневых систем. Примеры решения задач. Подбор сечения стержня, подверженного растяжению-сжатию (задача № 1). Определение напряжений и перемещений в стержне при растяжении-сжатии с учетом собственного веса (задача № 2). Определение грузоподъемности статически определимой конструкции, работающей на р…

• формат doc
• размер 3.61 МБ
• добавлен 05 декабря 2009 г.

Содержание: Общие указания по выполнению расчетно-проектировочных работ. Используемые обозначения. Изгиб. Расчет статически определимых балок. Примеры решения задач. Определение внутренних усилий в балках (задачи № 12–15). Пример 1. Пример 2. Проверка прочности балок при плоском поперечном изгибе (задачи № 16–19).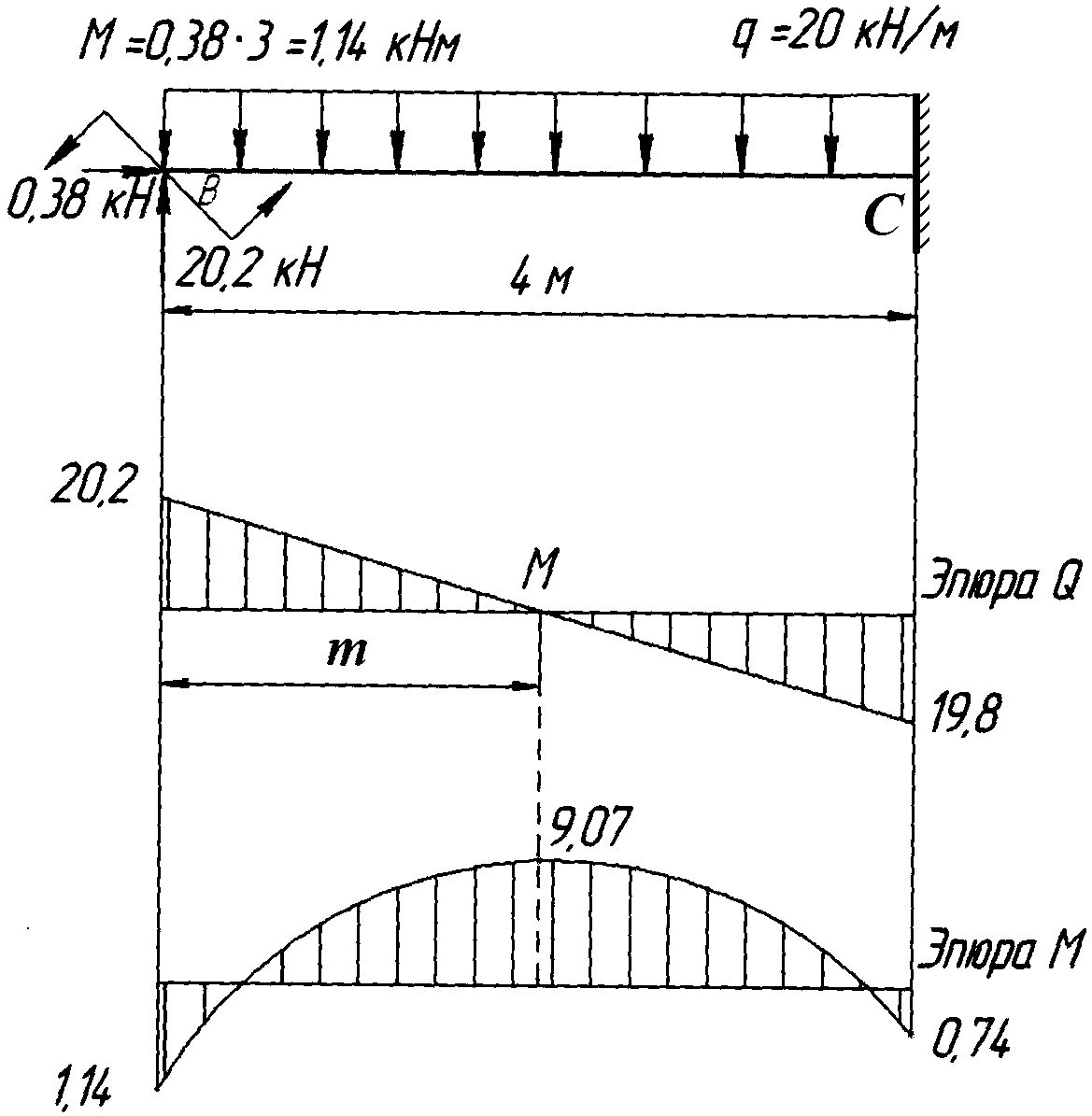 Пример 1. Пример Пример 3. Определение перемещений и проверка жесткости балок (задачи № 19, 20). Примеры решения задач Определение пер…

• формат doc
• размер 1.65 МБ
• добавлен 04 апреля 2009 г.

Северодонецк, ТИ СНУ им. В. Даля. Расчет статически неопределимых стержней при растяжении. Расчет круглого вала на прочность и жесткость при кручении. Полный расчет балок на прочность. Расчет плоских рам. Статически неопределимые рамы. Сложный изгиб. Расчет на устойчивость сжатого стержня. Расчет на прочность при ударных нагрузках. Заархивированная папка с файлами .DOC.

Практикум

• формат pdf
• размер 730.86 КБ
• добавлен 25 ноября 2011 г.

Методические указания.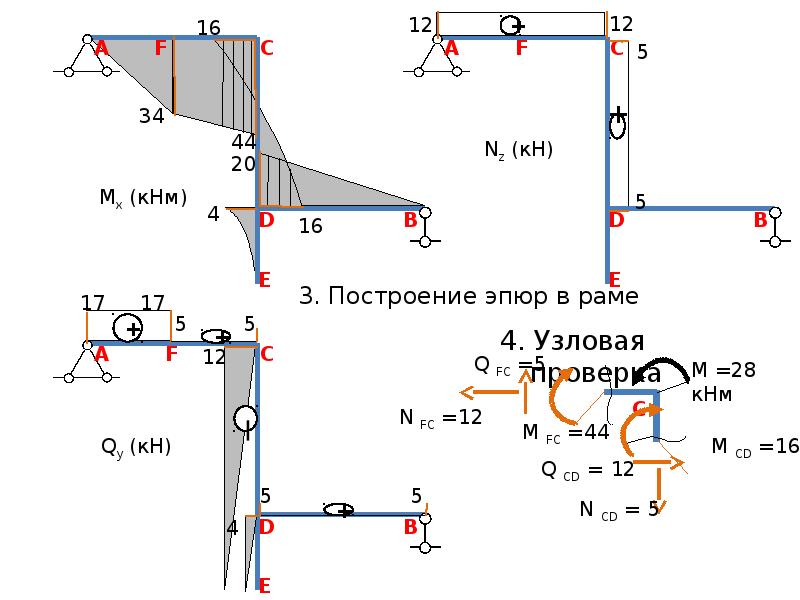 Краснодар: Изд. КубГТУ, 2008. — 43 с. Содержание: Задача Геометрические характеристики плоских сечений Задача Расчет ступенчатого стержня на осевое растяжение Задача Расчет статически неопределимой стержневой системы Задача Кручение вала круглого поперечного сечения Задача Плоское напряженное состояние в точке тела Задача Расчеты на прочность при плоском изгибе Задача Расчет статически неопределимой балки Задача Косой изг…

• формат doc
• размер 1004.73 КБ
• добавлен 15 апреля 2010 г.

Расчет стержневых статически неопределимых систем при растяжении (сжатии). Расчет валов и пружин на жесткость и прочность при кручении. Построение эпюр внутренних силовых факторов для балок и рам. Задачи на прочность и жесткость при изгибе статически определимых систем. Расчет статически неопределимых систем по методу сил. Расчеты на прочность при сложном напряженном состоянии.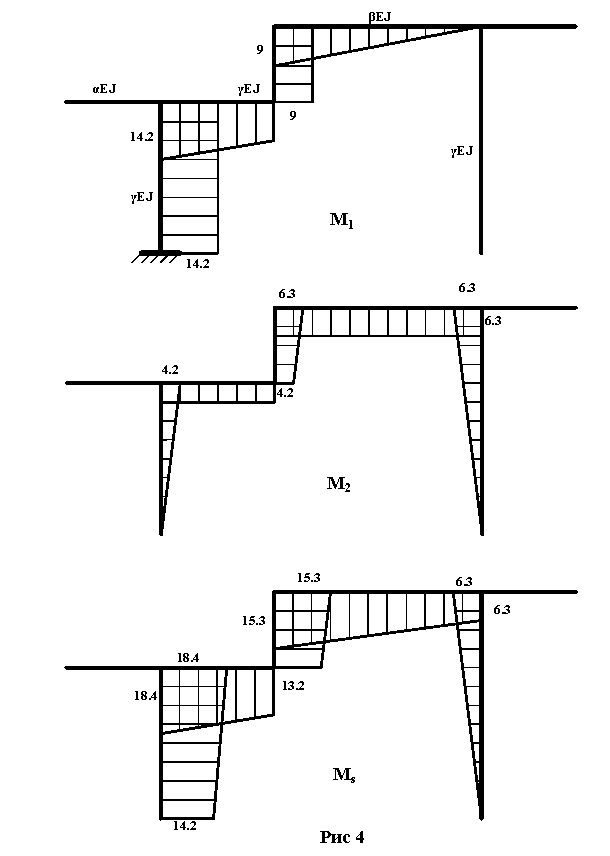

Задачи на прочность при циклических напряжениях. Расчеты элементов ко…

program

• формат exe
• размер 336.35 КБ
• добавлен 12 февраля 2008 г.

Программа для решения задач по сопромату. Расчет плоских балок и рам методом конечных элементов. Расчет статически неопределимых балок и рам. Построение эпюр изгибающих моментов, перерезываюших и продольных сил. Расчет перемещений и реакций опор.rn

program

• формат exe
• размер 372.59 КБ
• добавлен 12 января 2009 г.

Полюс — программа для расчета стержневых конструкций. Полюс умеет выполнять расчет статически определимых и неопределимых конструкций на статическое силовое, кинематическое и температурное воздействие. Расчет ведется с помощью одного из вариантов метода перемещений, который разработал профессор Петрозаводского Государственного Университета Ю.Б.Гольдштейн. Изюминка программы — простой, интуитивно-понятный интерфейс, позволяющий задать и получить р…

software

• формат txt, doc, exe, gif, htm
• размер 319.93 КБ
• добавлен 03 октября 2010 г.

В архиве программа, методическое указание к применению и два примера. Программа может быть полезна при расчете плоских ферм при выполнении курсовых проектов и расчетно-графических работ студентами очной и заочной форм обучения.

software

• формат exe, txt
• размер 4.06 МБ
• добавлен 03 января 2012 г.

Программа с графическим интерфейсом для расчета статически определимых балок, которая сама сделает за вас сложные расчеты, построит за вас эпюры поперечних сил и изгибательных моментов, и даже подготовит отчет о этих расчетах, который вы сможете распечатать.rn

• формат pdf
• размер 815.93 КБ
• добавлен 06 февраля 2009 г.

В сборнике представлены примеры решения задач для студентов большинства Российских вузов по темам: — Растяжение и сжатие: статически определимые системы статически неопределимые системы; — Кручение круглого бруса; — Изгиб плоских балок; — Геометрические характеристики плоских сечений; — Устойчивость сжатых стержней.

Статически определяемые: определение, балки, фермы, примеры статически определимая структура и статически неопределимая структура.

Почти все конструкции, спроектированные на площадке, являются неопределенными, поскольку они обеспечивают большую жесткость и устойчивость, повышая общий коэффициент безопасности. И статистически детерминированная структура также используется во многих местах в строительстве. Все функции напряжения легко вычисляются в детерминированных структурах, поэтому анализ становится довольно простым.

Статически определимые конструкции — это конструкции, на которые не действуют избыточные силы. Из-за нулевой избыточности мы можем анализировать его с помощью только уравнения равновесия. Шесть уравнений равновесия доступны для пространственной конструкции, а три — для планировочной конструкции, включая горизонтальное равновесие, вертикальное равновесие и равновесие моментов. При этом наличие этих уравнений равновесия будет зависеть от типа нагружения и опор и т. д. Остановимся подробнее на статически определимых конструкциях.

Статически определяемые конструкции PDF

Загрузить формулы для GATE Civil Engineering — Structural Analysis

Содержание

• 1. Что такое статически определяемые конструкции?
• 2. Статически определяемые балки
• 3. Разница между статически определенными и неопределенными конструкциями
• 4. Статически определяемые фермы
• 5. Примеры статически определяемых балок

Читать полностью Статья

Статически определимыми конструкциями называются конструкции, для анализа которых требуются только уравнения равновесия с целью нахождения неизвестных параметров, а неопределенной конструкции требуются условия совместности наряду с уравнениями равновесия. Эти типы структур легко анализировать в природе, и они являются просто стабильными структурами. Удалив любую из опорных реакций, она станет неустойчивой структурой или механизмом.

Опорные реакции равны имеющимся уравнениям равновесия в статически определимой конструкции. Это можно сделать, вычислив степень статической определенности конструкции, независимо от того, является ли структура статически определенной или неопределимой. Степень статической детерминированности такой конструкции всегда равна нулю.

Балки представляют собой тип конструкций, которые используются в основном для восприятия поперечных нагрузок. Балки могут сопротивляться воздействию поперечной силы и изгибающих моментов, вызванных внешней нагрузкой. По степени статической определенности ее можно разделить на статически определимую и статически неопределимую балку. Оба типа балок используются в процессе строительства в зависимости от типа конструкции и критериев нагрузки.

Статически определимые балки легко анализировать на опорные реакции, поскольку в таких балках не требуются условия совместимости. Недостаток его в том, что если какая-либо реакция поддержки станет равной нулю, она сразу выйдет из строя.

Как известно, как статически определимые, так и статически неопределимые конструкции являются устойчивыми структурами, и оба типа структур имеют свои преимущества и недостатки друг перед другом. Вот некоторые различия между детерминированными и неопределенными структурами, которые помогут лучше понять:

• Статически детерминированная структура может быть просто проанализирована с помощью уравнений равновесия, в то время как неопределенная структура требует условий совместимости вместе с уравнениями равновесия.
• Степень статической неопределенности детерминированной конструкции всегда равна нулю, а для неопределенной конструкции она будет больше нуля.
• В детерминированных структурах нет избыточных реакций, в то время как в случае неопределенных структур они доступны.

Загрузить формулы для GATE Civil Engineering — Geotechnical Engineering

Ферма — это тип конструкции, которая может воспринимать только осевую нагрузку; либо он будет на сжатие, либо на растяжение. В ферменной конструкции все элементы соединены через штифты, и нагрузки действуют только на них. В зависимости от условий поддержки фермы она будет классифицироваться как статически неопределяемая ферма или статически неопределимая ферма. В детерминированной ферме все опорные реакции можно найти только с помощью уравнений равновесия. Тем не менее, условия совместимости требуются в ферме неопределенного типа, наряду с уравнениями равновесия для анализа опорных реакций.

Ферменные конструкции используются там, где не требуется устойчивость к изгибающему моменту, поскольку ферма не может оказывать сопротивление изгибу, поскольку она соединена штифтами. В случае ферменной конструкции предусмотрено несколько элементов, несущих нулевые нагрузки, эти элементы также называются элементами с нулевой силой, и такие элементы обеспечивают большую жесткость конструкции.

В строительных работах используются многие балки, статически определимые по своей природе. Но во многих случаях предпочтение отдается статически неопределимым балкам из-за их преимуществ, таких как большая устойчивость, большая жесткость и т. д. Здесь приведены некоторые примеры статически неопределимых балок с их характеристиками, которые помогают понять, что такое статические балки:

Свободно поддерживаемая балка: это статически определимая балка, поддерживаемая шарнирной опорой на одном конце и роликовой опорой на другом конце балки. Этот луч в основном используется в качестве детерминированного луча.

Консольная балка: это определенная балка, опирающаяся на фиксированную опору на одном конце и свободно поддерживаемая на другом.

Загрузить формулы для GATE Civil Engineering — Transport Engineering

Часто задаваемые вопросы о статически определяемой конструкции

• Что такое статически определимая конструкция?

  Статически определяемая конструкция — это конструкция, которой нужны только уравнения равновесия для расчета опорных реакций и других неизвестных параметров конструкции.

• Что такое статически неопределимая конструкция?

  Статически неопределимая конструкция — это конструкция, для которой требуются условия совместимости конструкции вместе с уравнениями равновесия для расчета опорных реакций и других неизвестных параметров конструкции.

• Какова степень статической неопределенности статически определимой конструкции?

  В статически определимой конструкции не будет никаких избыточных реакций, поэтому степень статической неопределенности будет только нулевой.

• Как можно говорить, что балка статически определима?

  Луч будет находиться в статически определенных или неопределенных условиях, и это будет зависеть от степени статической неопределенности лучей. Если степень статической неопределенности луча равна нулю, это будет детерминированный луч.

• В чем преимущество статически определимой конструкции?

  В статически определенной конструкции не будет никаких избыточных реакций, поэтому такие конструкции допускают их движение при изменении температуры. В то время как в случае неопределенных конструкций индуцируются температурные напряжения.

ESE & GATE CE

Civil Engg.GATEGATE CEESE CEESEBARC CEAFCAT CE

Избранные статьи

Следите за нашими обновлениями

Наши приложения

• BYJU’S Exam Prep: приложение для подготовки к экзамену

GradeStack Learning Pvt. Ltd.Windsor IT Park, Tower — A, 2nd Floor,

Sector 125, Noida,

Uttar Pradesh 201303

[email protected]

калькулятор неопределенного луча — Googlesuche

Все eBilderVideosShoppingMapsNewsBucher

suchoptionen

Free Калькулятор балок для статически неопределимых балок

optimbeam.com › балка-калькулятор

Простой в использовании онлайн-калькулятор статически неопределимой балки. Обеспечивает опорные реакции, изгибающий момент, поперечную силу, прогиб и диаграммы напряжения.

Ähnliche Fragen

Что такое вычислитель луча?

Как узнать, какой размер балки мне нужен?

По какой формуле рассчитывается балка?

Калькулятор луча | Оптимальный луч | Бесплатная пробная версия

optimbeam. com

Простой в использовании онлайн-калькулятор статически неопределимой балки. Обеспечивает опорные реакции, изгибающий момент, поперечную силу, прогиб и диаграммы напряжений.

BEAMGURU.COM — Калькулятор балки и балки рамы/фермы …

beamguru.com

Этот калькулятор балки предназначен для расчета и построения изгибающего момента … Расчет статически неопределимых балок, рамы и фермы.

Перейти к расчету балки · Калькулятор рамы/фермы · Перейти к конструктору сечений · Поддержка

Бесплатный калькулятор балки — Civils.ai

диаграммы моментов, диаграммы поперечной силы, расчет сил реакции и измерение прогиба балки …

Бесплатный онлайн калькулятор луча | Реакции, сила сдвига и т. д. — SkyCiv

skyciv.com › free-beam-calculator

11.05.2023 · Бесплатный онлайн-калькулятор луча. Рассчитайте реакции, поперечную силу, изгибающий момент, прогиб и напряжение для консольных или свободно опертых балок.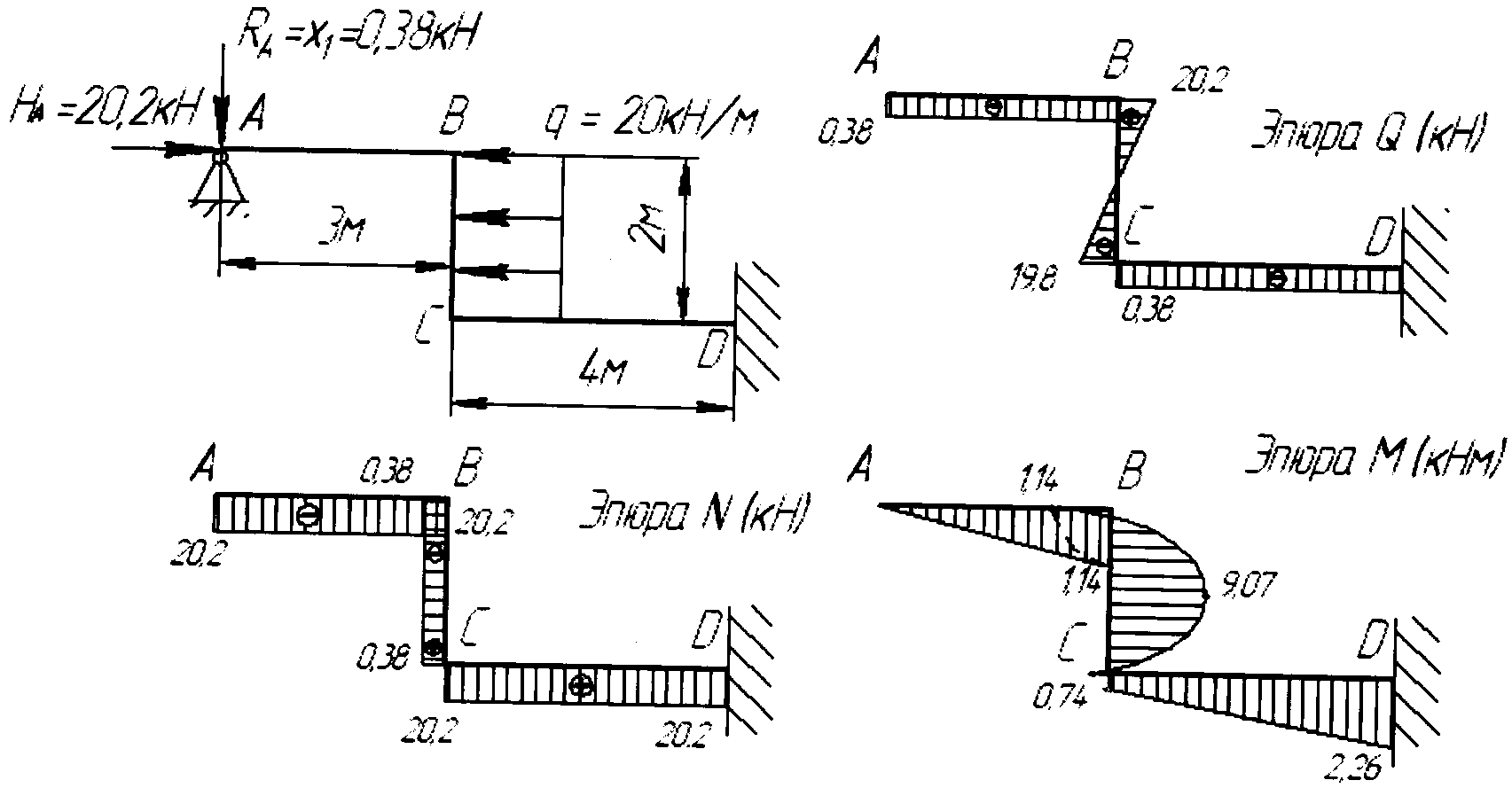

Бесплатный калькулятор луча — ClearCalcs

clearcalcs.com › freetools › Анализ луча

Самый мощный бесплатный онлайн-калькулятор луча. Простое моделирование сдвига, момента и прогиба с неограниченным количеством опор, интерактивными диаграммами …

Отклонение — калькулятор несущих балок

deflection.app

Отклонение — самое интерактивное, быстрое и точное приложение для расчета несущих балок. Визуальное проектирование и получение инженерных результатов, графиков, …

Калькулятор балки — PolyBeam прост и удобен в использовании!

www.polystruc.com › составная балка

Определение сил сечения и расчет статически неопределимых балок с помощью калькулятора балок PolyBeam! Загрузите БЕСПЛАТНУЮ версию PolyBeam уже сегодня!

Калькулятор для балок: опорные реакции, изгибающий момент и напряжения

www.johannes-strommer.com › калькуляторы › расчет балок

Расчет сил, моментов, напряжений, углов и прогиба статически определенных или неопределимых лучи.