расчет многопролетной балки

Расчет статически определимой многопролетной балки

Для балки, требуется:

1. Произвести проверку геометрической неизменяемости.
2. Построить эпюры изгибающих моментов и перерезывающих сил.
3. Построить линии влияния M и Q для заданного сечения, а также линию влияния одной опорной реакции (по выбору студента).
4. Определить по линиям влияния M, Q и R от заданной нагрузки и сравнить результаты пунктов 2 и 4.
5. Для заданного сечения определить наибольшее (по абсолютной величине) положительные и отрицательные значения М при действии заданной системы подвижных нагрузок.
6. Для заданного сечения определить наибольший и наименьший изгибаемый момент от сочетания неподвижных и подвижных нагрузок.

Данные:

Схема нагружения балки:

Система подвижных нагрузок:

1. Проверка геометрической неизменяемости системы.

Количество подвижный звеньев механизма:

Число кинематических пар пятого класса:

Число кинематических пар четвертого класса:

Степень подвижности механизма вычисляется по формуле Чебышевского:

2. Построение эпюры изгибающих моментов

и перерезывающих сил

Составляем «этажную» схему, заменяя шарнир двухсвязной опорой

Расчет балки начинаем с определения опорных реакций. В первую очередь следует определить реакции подвесных элементов, так как для расчета основного элемента необходимо знать числовые значения давлений от подвесных элементов в шарнирах.

Элемент Ш₁Ш₂:

Проверка:

Элемент AB:

Проверка:

Элемент CD:

Проверка:

Элемент AP:

Элемент AP:

Элемент ВШ₁:

Элемент Ш₁Ш₂:

Элемент Ш₂C:

Элемент CD:

Элемент DP:

Далее представлены эпюры изгибающих моментов и перерезывающих сил (все промежуточные значения указаны ранее):

3. Построить линии влияния M и Q для заданного сечения, а также линию влияния одной опорной реакции.

Линии влияния изображены ниже:

4. Определить по линиям влияния M, Q, R от заданной нагрузки.

Полученные значения согласуются с ранее рассчитанными.

5. Определить наибольшее значение М при действии заданной системы подвижных нагрузок.

Расположение крайней левой нагрузки (G₁) меняем по всей длине вала:

6. Определить для заданного сечения наибольший и наименьший изгибаемый момент от сочетания неподвижных и подвижных нагрузок.

Наибольшие (наименьшие) изгибаемые момент:

почта для связи: [email protected]

Copyright 2007-2010 Левашов Максим Васильевич

При использовании контента сайта активная ссылка на сайт  обязательна.

косой изгиб 1

косой изгиб 2

косой изгиб 3

расчет реакции опор

определение геометрических характеристик бруса

расчеты стержня при растяжении

изгиб балки

анализ НДС

осесимметричный изгиб

расчет стержневых систем  в САПР

Автоматизация строительных расчетов в среде Маткад и САПР

Автоматизация строительных расчетов в среде Маткад и САПР

расчет многопролетной балки

расчет трехшарнирной системы

расчет колонны

Beamcalc

Beamcalc bootstrap html templates

Подобрать сечение балки?

Как подобрать сечение балки за 3 минуты? Правильно ли будет подобрано сечение, каким будет запас прочности? Какой сортамент использовать, какую марку стали? Где самое опасное сечение, а где можно сэкономить? Эти вопросы сводят с ума тысячи проектировщиков. ..

Многопролетная балка?

Балка имеет более двух опор, да еще и шарнир в пролёте? Боже, я забыла все формулы из сопромата, да и формул таких нет, нужно делать полноценный расчёт! Как справиться с этим, если начальник кричит «Давай-давай, вчера нужно закончить!»

Как задать нагрузки на балку

Правильно собрать нагрузки на балку, ничего не пропустив? Как показать их наглядно и просто? О черт, нагрузки меняют положение, знак и  значение — толщина отчёта растет как на дрожжах, я в них тону!

ВЫХОД ЕСТЬ!

Программа Beam решит все ваши проблемы с подбором сечения балки для любых нагрузок — сосредоточенные силы, моменты, распределенные нагрузки, плюс собственный вес!

Неограниченная длина балки 

Вы можете задать длину балки в один километр! Шаг задания длины — 1мм! Такого еще не было в истории расчёта балок!

Неограниченое количество нагрузок

У вас много нагрузок, они не лезут в окна ввода расчётных программ? В Beam все нагрузки наглядны, расположены на балке и в таблице нагрузок, каждая имеет свой значок и величину, да еще их можно двигать прямо по балке!

О ПРОГРАММЕ

Что, зачем и почему

Назначение

Расчёт на прочность и жесткость многопролетных статически неопределимых балок, построения эпюр прогибов, углов поворота, изгибающих моментов, напряжений и поперечных сил, возникающих в балке от приложенных внешних нагрузок.

Легко и просто использовать

Программа производит проверку и подбор сечения стальных балок, описанных в сортаменте металлопроката, абсолютно бесплатно поставляемом с программой!

Экспорт в распростаненные форматы

Результаты расчёта можно экспортировать в формат HTML, который откроет любой браузер, а также в MS Word, для передачи отчета коллеге или сразу в пояснительную записку проекта!

Расчёт «на лету»

Любое иземнение исходных данный мгновенно отображается в расчётной схеме и результатах расчёта. Прекрасная, быстрая и глубокая обратная связь, вы можете воистину  проектировать, а не пытаться разгадывать ребусы!

Что такое изогнутая ось балки?

От слова «Сопромат» болит голова, знания из института на дне черепной коробки, и ты сомневаешься — были ли они там когда-либо? 

Тошнит от эпюр?

Эпюры строить вручную — такое мучение! Правила знаков для эпюр не выучить никогда, для строителей и механиков они различны — и кто это только всё придумал?

Разрушился мост?

Вы посчитали балку моста, но забыли учесть нагрузку НК-80, и вот результат? Что же делать?

Развалилось здание?

Заложили главные балки из двутавра 70Б1, но не учли марку стали — за это прокуратура завела на вас дело?

Опять обрушение?

Неверно рассчитали реакцию промежуточной опоры в многопролетной балке — не знаете, что теперь будет?

.

..а мы знаем:

ПОПРОБУЙ ПРОГРАММУ BEAM!

СКАЧАТЬ!

ВОЗМОЖНОСТИ ПРОГРАММЫ

Всё, о чем вы мечтали, но боялись спросить

Статический расчёт многопролётных статически неопределимых балок на нагрузки, действующие в вертикальной плоскости. Нагрузками могут являться: сосредоточенная сила F, изгибающий момент M, равномерно и неравномерно распределённая нагрузка Q, а также собственный вес балки.

Подбор сечения балки из сортаментов проката или проверка пользовательского сечения. Расширение количества сортаментов.

Построение эпюр прогибов, углов поворота сечений, изгибающих моментов и перерезывающих сил с нахождением максимальных и минимальных значений и их привязок.

Экспорт результатов расчета в формат HTML (htm) и MS Word (doc).

Поддержка множества единиц измерения для нагрузок и расстояний.

Поддержка двух языков (En/Ru).

Проектирование и прототипирование

Любое изменение в расчетной схеме мгновенно вызывает корректировку результата — и вот вы не занимаетесь рутиной, а именно проектируете, с большой буквы этого слова!

Быстро и просто

Теперь подобрать сечение любой балки можно менее, чем за одну минуту! Не нужно иметь семь пядей во лбу, чтобы делать это, с расчётом справится даже стажер!

Легко проверить

Назначили сечение балок, но забыли, какие нагрузки и напряжения действуют в них? Создание отчёта одной кнопкой, и вы никогда не забудите, где и какая сила стояла на принятой вами балке!

Опыт и инновации

Вы быстро поднимитесь в собственных глазах, едва начнете пользоваться программой BEAM. Ничто так не мотивирует, как быстро и качественно выполненная работа!

1. Метод расчёта — составление и решение дифференциального уравнения изогнутой оси балки.
2. Программа откомпилирована с опциями Range check и Overflow check. Переполнений и выходов за границы массивов не наблюдалось, а если такое и случиться — вы увидите окно об ошибке.
3. Внутренний формат вычисления силовых факторов (прогибов, углов поворота, моментов и перерезывающих сил) — Extended (20 знаков после запятой)! 
4. Программа
   НЕ имеет сертификатов Госстроя, ВНИИЖБ, ЦНИПСК им.»Мельникова» и прочих регалий. Всё же, учитывая тот факт, что применение данной программы весьма и весьма серьёзно и ответственно — расчёт несущих конструкций на прочность довольно сильно влияет на безопасную жизнедеятельность человека под или над этими конструкциями, программа была проверена на нескольких десятках расчётах балок, выполненных вручную — результаты построения эпюр моментов M и перерезывающих сил Q — 100%.
5. Эпюры прогибов строятся в зависимости от текущего сечения (пользовательского или из сортамента), так как в уравнении изогнутой оси общий множитель — EJx. Поэтому при выборе другого элемента сортамента меняются эпюры прогибов и углов поворота (при этом эпюры M и Q — неизменны, как им и положено быть).
6. Расчётный параметр — относительный прогиб, равный отношению прогиба к длине наибольшего пролета балки, по которому также производится подбор и проверка сечения.

ПРИМЕРЫ ОТЧЁТОВ В ПРОГРАММЕ

BEAM

Легко и просто создать отчет по выполненному расчёту и вставить его в свой проект.

Попробуй и убедись!

В формате PDF

В формате WORD

Остались еще вопросы?

СПРАВКА К ПРОГРАММЕ BEAM!

ПОСМОТРЕТЬ

ЧТО ГОВОРЯТ СЧАСТЛИВЫЕ ПОЛЬЗОВАТЕЛИ О ПРОГРАММЕ 

BEAM

Комментарии и отзывы зарегистрированных пользователей программы

Лучше инструмента для подбора сечения балок для своих коллег я не нашел. Быстро, точно, профессионально, результат наглядный, ничего лишнего. Сразу видно — делал профессионал.

Нужно было рассчитать балку в гараже для подвески тельфера, также считали балку над воротами. Все получилось, спасибо. Стоит до сих пор, не рухнуло. Как вы нас выручили, просто нет слов.

Я проектирую стальные каркасы. Что бы я делал без этой программы, просто не представляю. Спасибо огромное, вы просто душка.

До окончания распродажи программы

BEAM осталось совсем немного!
Cпешите зарегистрировать вашу копию программы BEAM!

Купить одну копию на один компьютер. Для личного пользования, периодическое использование программы. 

Купить

До трёх отличных копий — на рабочий и домашний компьютер, а также на ноутбук.

Купить

Для профессиональных проектировщиков, для проектных отделов и институтов.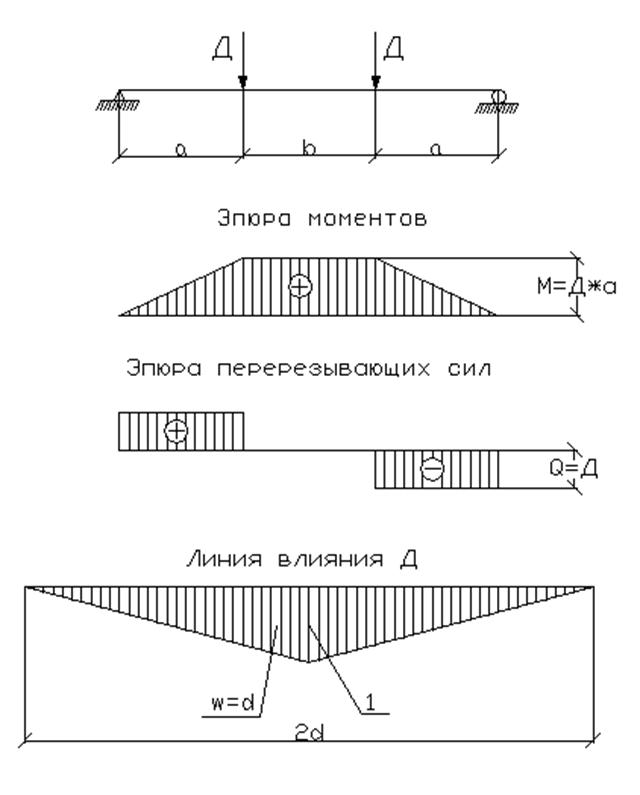 Почувствуй всю мощь и не испытывай ограничений!

Купить

ОСТАЛИСЬ ВОПРОСЫ — СВЯЖИТЕСЬ СО МНОЙ!

Напишите, что вы думаете о моей программе, свои пожелания или вопросы, я обязательно отвечу.

Ваше Имя

Сообщение

Ограничение ответственности!

Программа написана ЧАСТНЫМ лицом, её применение производится вами НА СВОЙ СТРАХ И РИСК, автор НИКАКОЙ ответственности за возможные последствия применения своей программы НЕ НЕСЁТ.

Несущие нагрузки многопролетной балки • кирки Инженерия

Начало » Упражнения » Инженерная механика II » Несущие нагрузки многопролетной балки

В этом упражнении рассчитываются опорные реакции симметричной многопролетной балки, опертой на три колонны . Вот онлайн-калькулятор здесь для расчета несимметричных многопролетных балок.

Задача

Неразрезная балка на неподвижной опоре и двух плавающих опорах (многопролетная балка) с симметричной шириной колонны l нагружена линейной нагрузкой q ₀ . Насколько велики нагрузки на подшипники?

Многопролетная балка под линейной нагрузкой

Решение

На первом этапе определяются уравнения для реакций опоры. Для последующего определения внутренних усилий балка разбивается на две области. Горизонтальные силы далее в следующих уравнениях не рассматриваются, так как они, очевидно, равны нулю. Моменты поворота влево положительные.

Определение несущих нагрузок

Несущие реакции и сечения балки 92 \]

Это приводит к системе уравнений с 2 ​​уравнениями и 3 неизвестными. Следующим шагом является определение внутренних сил в двух сечениях I и II. Чтобы иметь возможность интегрировать функцию линейной нагрузки от 0 до x, она сформулирована как функция вспомогательной координаты ξ. Нормальные силы обозначаются через N, поперечные силы через Q и изгибающие моменты через M _b .

Определение внутренних сил

Секция I

Внутренние силы и моменты в секции I 9{4}}\, {q_0}}{48 E I} \]

\[ \tag{32} {F_{\mathit{Az}}}=\frac{11 л\, {q_o}-5 л\ , {q_0}}{16} \]

\[ \tag{33} {F_{\mathit{Bz}}}=-\frac{11 л\, {q_o}-21 л\, {q_0}} {8} \]

\[ \tag{34} {F_{\mathit{Cz}}}=\frac{11 л\, {q_o}-5 л\, {q_0}}{16} \]

И для полноты

\[ \tag{35} F_{Ax} = 0 \]

Формула отклонения вала

— Googlesuche

AlleBilderShoppingVideosMapsNewsBücher

suchoptionen

Простая основа этого метода заключается в том, что изменение наклона между двумя точками Δθ = Δx. (M/EI) …. Δx — расстояние между точками. Результирующее изменение отклонения явно равно Δθ.

Отклонения вала — Roy Mech

roymech.org › Полезные_таблицы › Привод › Отклонения вала

Hervorgehobene Snippets

Bilder

Alle anzeigen

300Ägen

Alle anzeigen hnliche Fragen

Что такое прогиб вала?

Как рассчитать прогиб?

Каков допустимый прогиб вала?

Что такое отклонение неподвижного вала?

Расчет прогиба стального вала — SFERAX

sferax. ch › faq › расчет прогиба стального вала

f 1 = прогиб под действием центральной нагрузки в мм. P = нагрузка в кп. L = расстояние между опорами в мм. D = диаметр вала в мм. f 2 …

Прогиб вала, часть 1 — YouTube

www.youtube.com › смотреть

12.07.2018 · Введение в анализ прогиба вала, часть 1. UIUC SE 410, Проектирование компонентов.
Dauer: 10:25
Прислан: 12.07.2018

Расчет прогиба вала — Mc Nally Institute

mcnallyinstitute.biz › 10-html

18.02.2018 · Прогиб вала и точка максимальной эффективности насоса 10-8 · Y = степень изгиба вала в дюймах. · F = Общая сила на валу. · L = The …

Справочные данные — уравнения для расчета величины отклонения вала

www.mysamick.com › техника › техника_12_04

Справочные данные — уравнения для расчета величины отклонения вала.

Простой расчет прогиба в ступенчатых валах

www.machinedesign.com › архив › статья › расчет.