Расчет двутавровой балки на устойчивость
Двутавровую балку при расчете на изгиб необходимо рассчитывать не только по несущей способности и деформациям, но и на устойчивость. Ведь бывают случаи, когда балка удовлетворяет первым двум условиям и не удовлетворяет третьему. Это в свою очередь приводит к тому, что двутавр несет все вышележащие конструкции (обрушения нет), но в то же время потерял свое проектное положение — завалился на бок.
На данной странице представлен калькулятор, который позволяет определить будет ли заваливаться двутавр или нет. Расчет реализован согласно п. 8.4.1 СП 16.13330.2017 «Стальные конструкции».
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Обращаю ваше внимание, что в нецелых числах необходимо ставить точку, а не запятую, то есть, например, 5.7 м, а не 5,7. Также, если что-то не понятно, задавайте свои вопросы через форму комментариев, расположенную в самом низу.Исходные данные
Длина пролета (L) — расстояние между крайними опорами.
Расчетная нагрузка — сумма всех нагрузок (например, от конструкций перекрытия, покрытия пола, перегородок, снега и т.д.), приложенных на балку, помноженных на коэффициенты надежности по нагрузке.
Расчетное сопротивление Ry — сопротивление проката на растяжение, сжатие и изгиб по пределу текучести. Подбирается из нижеследующей таблицы:
Подбирается из нижеследующей таблицы:
Расчетная длина Lef — расстояние между опорами, которые расположены сбоку. Если опор (закреплений) нет, то данная величина равна длине пролета, т.е. Lef = L. Для балок типов 2 и 6 в случае, если нет других закреплений Lef = 2L.
Количество закреплений — количество точек закрепления сжатого (верхнего) пояса двутавра от поперечных смещений. То есть сколько опор препятствует наклону балки. Такими опорами можно считать балки сопоставимой жесткости (деревянные балки не считаются), приходящиеся в стык к рассчитываемой балке или лежащие сверху ее, которые соединены с последней посредством сварки или болтов и которые ограничены от горизонтального смещения. Также такой опорой считается место присоединения горизонтальной связи.
Коэффициент условий работы — подбирается по таблице 1 п. 4.3.3 СП 16.13330.2017 «Стальные конструкции», находится в пределах от 0,75 до 1,2.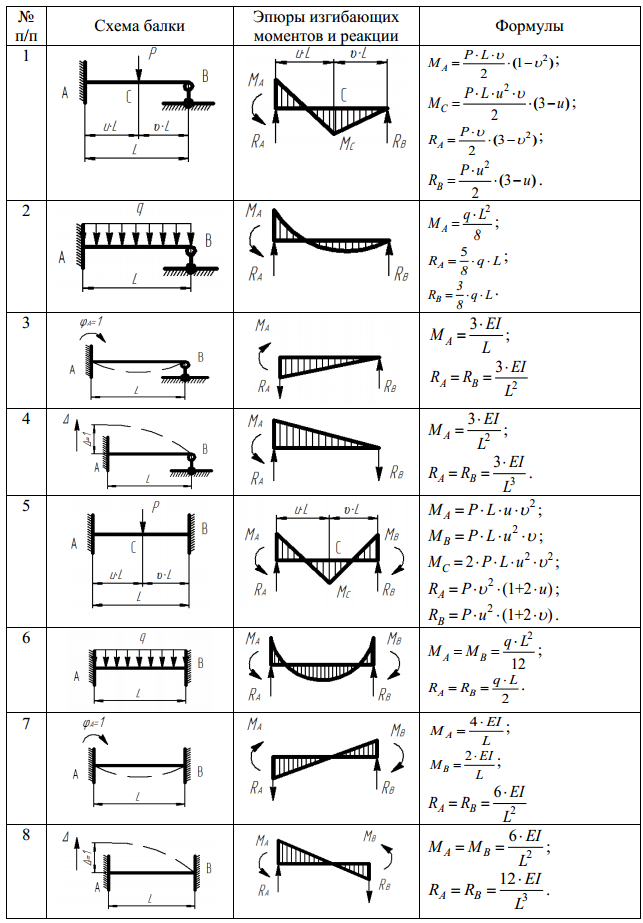
Размер (h x b) — высота и ширина двутавра.
Вес балки — вес двутавра на один погонный метр. Чтобы получить общую массу балки, необходимо эту величину умножить на длину балки.
Wx— момент сопротивления сечения относительно оси Х.
Ix и Iy— моменты инерции сечения относительно оси Х и Y, соответственно.
It— момент инерции при свободном кручении.
Коэф. A, P, G1, Gb — коэффициенты необходимые для расчета.
Коэф. использования (К) — если он меньше 1, то балка по устойчивости не проходит и требуется либо увеличить сечение балки, либо добавить опор, препятствующие опрокидыванию.
Добавить комментарий
Балки. Расчет балок — презентация онлайн
1. Лекция 4. Балки. Часть 2
ПреподавательЮдина Евгения Васильевна
Лекция 4. Балки. Часть 2
Расчет балок
2.
 Металлические балкиПрокатной двутавр – длина пролета 6-9 м
Металлические балкиПрокатной двутавр – длина пролета 6-9 мСварной двутавр – длина пролета более
9 м и значительные нагрузки
3. Металлические балки
4. Металлические балки
Балочная клетка — система несущихбалок в составе конструкции покрытия
(перекрытия)
5. Металлические балки
Особенности работы и расчета• Возникновение нормальных и
касательных напряжений
• Возможна потеря общей устойчивости
(выпучиваться и закручиваться в
вертикальной плоскости)
• Возможна потеря местной устойчивости
при тонком и высоком сечении
• Прогиб балки
6. Металлические балки
Особенности работы и расчета7. Металлические балки
8. Металлические балки
9. Металлические балки
1-ое предельное состояние1. Расчет на прочность
2. Расчет на общую устойчивость
3. Расчет на местную устойчивость
2-ое предельное состояние
Расчет по деформациям
10. Металлические балки
1-ое предельное состояниеРасчет прочности
(проверка нормальных
напряжений)
11.
 Металлические балки1-ое предельное состояние
Металлические балки1-ое предельное состояниеРасчет на прочность
(проверка касательных
напряжений)
12. Металлические балки
1-ое предельное состояниеРасчет на прочность
(проверка касательных напряжений)
13. Металлические балки
1-ое предельное состояниеПроверка общей
устойчивости
Проверка общей устойчивости не требуется, если
верхний пояс балок развязан из плоскости
сплошным жестким настилом (железобетонные
плиты, металлический настил и т.п.)
14. Металлические балки
1-ое предельное состояниеПроверка местной устойчивости
15. Металлические балки
16. Металлические балки
1-ое предельное состояниеПроверка местной
устойчивости верхнего
пояса
17. Металлические балки
1-ое предельное состояниеПроверка местной устойчивости для стенки
18. Металлические балки
2-ое предельное состояниеРасчет по деформациям
19. Деревянные балки
• Малоэтажное строительство• Скатные кровли многоэтажных зданий
• Промышленные здания с химически
агрессивной средой
• Временные сооружения
20.
 Деревянные балкиКонструкция сечения:
Деревянные балкиКонструкция сечения:•Цельная древесина (в перекрытиях — шаг
не более 1,5 м)
•Клееное сечение
21. Деревянные балки
22. Деревянные балки
23. Деревянные балки
24. Деревянные балки
25. Деревянные балки
3 стадии от начала работы доразрушения:
•1) При небольших изгибающих моментах
– древесина работает упруго (напряжения
изменяются линейно)
26. Деревянные балки
3 стадии от начала работы доразрушения:
•2) При увеличении момента –
добавление пластических деформаций,
смятие крайних волокон (складки
древесины), нейтральная ось опускается
ниже центра тяжести сечения
27. Деревянные балки
3 стадии от начала работы доразрушения:
•3) При дальнейшем увеличении момента
– пластические деформации растут,
происходит разрыв крайних растянутых
волокон
28. Деревянные балки
29. Деревянные балки
30. Деревянные балки
31.
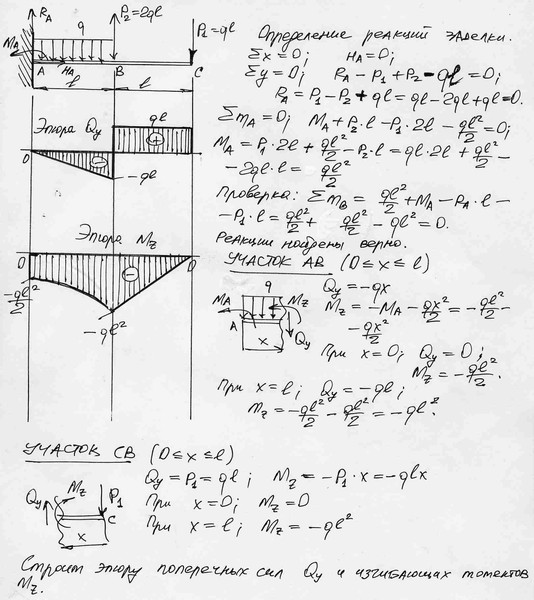 Деревянные балкиРасчет прочности на изгиб
Деревянные балкиРасчет прочности на изгибведется по 1-ой стадии работы
материала (расчетное
сопротивление при изгибе
принимается равным расчетному
сопротивлению сжатия)
32. Деревянные балки
1-ое предельное состояние1. Расчет на прочность
2. Расчет на общую устойчивость
2-ое предельное состояние
Расчет по деформациям (прогиб)
33. Деревянные балки
1-ое предельное состояние34. Деревянные балки
1-ое предельное состояние35. Деревянные балки
1-ое предельное состояние36. Деревянные балки
37. Деревянные балки
2-ое предельное состояниеПрогиб:
38. Железобетонные балки
39. Железобетонные балки
40. Железобетонные балки
41. Железобетонные балки
42. Железобетонные балки
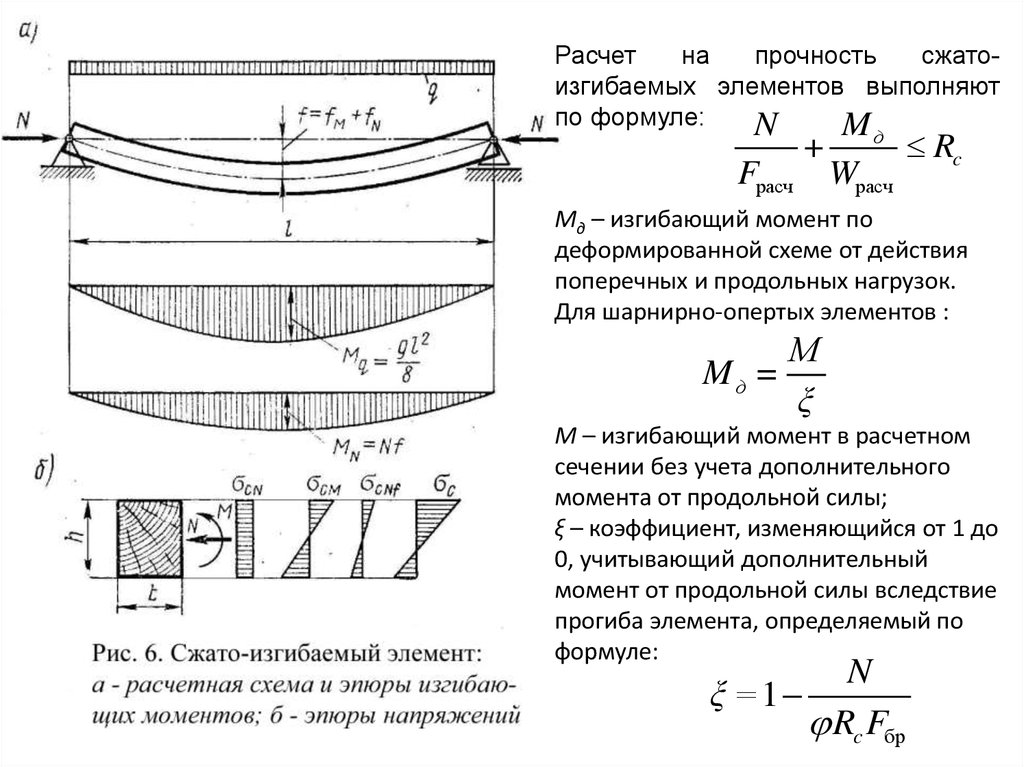
Расчет на прочность:•Обеспечение прочности нормального
сечения (определение количества
стержней и диаметр продольной
арматуры )
•Обеспечение прочности наклонного
сечения ( определение диаметра и шага
постановки поперечных стержней)
43.
 Железобетонные балки
Железобетонные балки44. Железобетонные балки
45. Железобетонные балки
46. Железобетонные балки
47. Железобетонные балки
48. Железобетонные балки
49. Железобетонные балки
50. Железобетонные балки
51. Железобетонные балки
52. Железобетонные балки
53. Железобетонные балки
54. Железобетонные балки
55. Железобетонные балки
56. Железобетонные балки
57. Железобетонные балки
58. Железобетонные балки
59. Железобетонные плиты
60. Железобетонные плиты
61. Железобетонные плиты
62. Железобетонные плиты
63. Железобетонные плиты
64. Железобетонные плиты
65. Железобетонные плиты
66. Железобетонные плиты
67. Железобетонные плиты
68. Железобетонные плиты
69. Железобетонные плиты
70. Железобетонные плиты
71. Железобетонные балки и плиты
2-ое предельное состояние72. Железобетонные балки и плиты
2-ое предельное состояние73.
 Железобетонные балки и плиты
Железобетонные балки и плиты74. Железобетонные балки и плиты
75. Железобетонные плиты
76. Железобетонные балки и плиты
77. Железобетонные балки и плиты
78. Железобетонные балки и плиты
79. Железобетонные балки и плиты
80. Железобетонные балки и плиты
81. Железобетонные плиты
Пример расчета — Расчет местоположения поддержки.
- Дом
- Образование
- Подготовка к профессиональным экзаменам
- Примеры расчета
- Пример расчета — Расчет местоположения поддержки.
Серия лекций Keller’s Keller Seismic Knowledge: Тестирование таблицы колебаний начинается в 20 апреля 2023
Подробнее
Содержание [скрыть]
- Описание
- Выбранные темы
Выбранные темы
Пример расчета: собственные периоды вибрации для систем Пример расчета: осевая сила на колонне Пример расчета: сдвигающая сила на колонне Пример расчета: момент опрокидывания панели Изменение длины стержня, нагруженного в удлинении. Пример расчета — расчет осевых усилий на элементах фермы. Пример расчета — расчет диаграмм стержней. Пример расчета — расчет диаграмм стержней для балки. Пример расчета — балка с внутренним шарниром (часть A). Найдите пример расчета реакций — балка с внутренним шарниром (часть B). Расчет диаграмм стержней. Пример расчета — анализ рамы. Пример расчета — анализ рамы — равномерная нагрузка. Пример расчета — поиск центра тяжести (поверхности). Пример расчета — расчетное болтовое соединение натяжных пластин (EC3). , Изменение температуры. Пример расчета — незатухающая свободная вибрация (часть A). Пример расчета — незатухающая свободная вибрация (часть B). Пример расчета — оценка матриц структурных свойств. Пример расчета — угловое ускорение, угловая скорость. Пример расчета — соединение срезным болтом EC3. Пример расчета — потеря устойчивости колонны (EC3). Пример расчета — расчет диаграмм стержней. Пример расчета — расчет диаграмм стержней. Пример расчета — расчет уравнения упругой кривой.
Пример расчета — расчет осевых усилий на элементах фермы. Пример расчета — расчет диаграмм стержней. Пример расчета — расчет диаграмм стержней для балки. Пример расчета — балка с внутренним шарниром (часть A). Найдите пример расчета реакций — балка с внутренним шарниром (часть B). Расчет диаграмм стержней. Пример расчета — анализ рамы. Пример расчета — анализ рамы — равномерная нагрузка. Пример расчета — поиск центра тяжести (поверхности). Пример расчета — расчетное болтовое соединение натяжных пластин (EC3). , Изменение температуры. Пример расчета — незатухающая свободная вибрация (часть A). Пример расчета — незатухающая свободная вибрация (часть B). Пример расчета — оценка матриц структурных свойств. Пример расчета — угловое ускорение, угловая скорость. Пример расчета — соединение срезным болтом EC3. Пример расчета — потеря устойчивости колонны (EC3). Пример расчета — расчет диаграмм стержней. Пример расчета — расчет диаграмм стержней. Пример расчета — расчет уравнения упругой кривой. Пример расчета — плоское напряжение. Пример расчета — кольцевое сечение, Напряжение. Пример расчета — Допустимая сила сдвига для балки. Пример расчета — Расчет прогиба. Теорема Кастильяно. Пример расчета — определение поперечной силы и момента. Пример расчета — определение величин F1, F2. Пример расчета — внутренние силы. Пример расчета — расчет осевых сил элементов фермы. Пример расчета — расчет моментов инерции Ix и Iy. Пример расчета — расчет напряжения сдвига для температурной нагрузки. Пример расчета — расчет силы растяжения с использованием виртуальной работы. Пример расчета — крутящий момент — напряжение. Пример расчета — железобетонная колонна при напряжении. Пример расчета — консольная балка с равномерной нагрузкой. Пример расчета — консольная балка с точечными нагрузками. Пример расчета — нагрузка на стержень Пример расчета — максимальный прогиб Пример расчета — схема стержня. Пример расчета — минимально допустимый диаметр. Пример расчета — критическая нагрузка. Пример — Пример расчета трения — Модуль упругости сечения S Пример расчета — Пластмассовая нейтральная ось.
Пример расчета — плоское напряжение. Пример расчета — кольцевое сечение, Напряжение. Пример расчета — Допустимая сила сдвига для балки. Пример расчета — Расчет прогиба. Теорема Кастильяно. Пример расчета — определение поперечной силы и момента. Пример расчета — определение величин F1, F2. Пример расчета — внутренние силы. Пример расчета — расчет осевых сил элементов фермы. Пример расчета — расчет моментов инерции Ix и Iy. Пример расчета — расчет напряжения сдвига для температурной нагрузки. Пример расчета — расчет силы растяжения с использованием виртуальной работы. Пример расчета — крутящий момент — напряжение. Пример расчета — железобетонная колонна при напряжении. Пример расчета — консольная балка с равномерной нагрузкой. Пример расчета — консольная балка с точечными нагрузками. Пример расчета — нагрузка на стержень Пример расчета — максимальный прогиб Пример расчета — схема стержня. Пример расчета — минимально допустимый диаметр. Пример расчета — критическая нагрузка. Пример — Пример расчета трения — Модуль упругости сечения S Пример расчета — Пластмассовая нейтральная ось. Пример расчета — Потеря устойчивости колонны (EC3). Пример расчета — Соединение срезным болтом EC3. Пример расчета — Диаграмма стержня. Треугольная нагрузка. Пример расчета — крутящий момент-напряжение. Пример расчета — угловое ускорение, угловая скорость. угловое ускорениеИзменение температурыСреднее напряжение сдвига в сосуде под давлениемДопустимая сила сдвига балкиПримеры расчетаРасчет изменения длины стержняПружинные сборки в серии/параллельно: Две пружины в серииФерма против тросаРасчет вертикального отклонения балкиИзгибная трещина в бетонной балкеМаксимальный коэффициент вертикального сдвигаКолонна в изгибеБалки: максимум момент
Пример расчета — Потеря устойчивости колонны (EC3). Пример расчета — Соединение срезным болтом EC3. Пример расчета — Диаграмма стержня. Треугольная нагрузка. Пример расчета — крутящий момент-напряжение. Пример расчета — угловое ускорение, угловая скорость. угловое ускорениеИзменение температурыСреднее напряжение сдвига в сосуде под давлениемДопустимая сила сдвига балкиПримеры расчетаРасчет изменения длины стержняПружинные сборки в серии/параллельно: Две пружины в серииФерма против тросаРасчет вертикального отклонения балкиИзгибная трещина в бетонной балкеМаксимальный коэффициент вертикального сдвигаКолонна в изгибеБалки: максимум момент
См. также
ПРОЧИТАТЬ АРТИКУЛМембраны
16 сентября 2022 г. 0045 Усталость
16 сентября 2022 г.
Усталость является инициированием и распространением трещин…
Новости по теме
События отрасли
Инженер-конструктор (thestructuralengineer. info) использует сторонние файлы cookie для улучшения нашего веб-сайта и вашего удобства при его использовании.
info) использует сторонние файлы cookie для улучшения нашего веб-сайта и вашего удобства при его использовании.
Чтобы узнать больше о файлах cookie, которые мы используем, и о том, как их удалить, посетите нашу страницу о файлах cookie. Разрешить файлы cookie
Боковая нестабильность балки – Расчет значения критического напряжения |
Боковая устойчивость обычно обеспечивается для балки, колонны или стены с боковой распоркой. Боковая распорка — это конструктивный компонент, который предотвращает скручивание или коробление балки или колонны. Боковая нестабильность является результатом недостаточной боковой устойчивости , то есть свойство объекта развивать силы или подвергаться воздействию сил, которые восстанавливают или поддерживают его исходное состояние (положение). Нестабильная в боковом направлении конструкция или конструктивный элемент может перевернуться, прогнуться вбок или упасть. На приведенной ниже схеме показана типичная сборка каркаса фюзеляжа (состоящего из внутреннего фланца, внешнего фланца и стенки) самолета, прикрепленного к панели между двумя стабилизаторами (клипсами).
- Эквивалентная эластичность
Мы предполагаем, что внутренняя полка рамы ведет себя как двухшарнирная балка на уровне стабилизаторов (клипс). Шипы считаются ограничениями с определенной жесткостью.
Жесткость на изгиб (вокруг оси X) можно рассчитать по следующей формуле:
Где:
– α : упругая постоянная эквивалентных дискретных опор (см. рис. 2)
– I X_WEB : инерция паутины (см. рис. 1) вокруг оси X.
– t a : толщина стенки (см. рис. 1)
– h a : высота стенки шпангоута
– (см.
Поступательная жесткость на уровне внутренней полки составляет:
- Напряжение нестабильности (линейно-упругое)
Энергетический метод позволяет определить критическую нагрузку потери устойчивости (см. «Теория упругой устойчивости» Тимошенко/Гере, п. 2.10), рассматривая деформацию упругой линии как синусоидальный ряд с волновым узлом на каждом конце (концы находятся на уровне стабилизаторов/зажимов).
«Теория упругой устойчивости» Тимошенко/Гере, п. 2.10), рассматривая деформацию упругой линии как синусоидальный ряд с волновым узлом на каждом конце (концы находятся на уровне стабилизаторов/зажимов).
За счет минимизации этой энергии деформации достигается наименьшее критическое напряжение потери устойчивости (линейная упругость), которое составляет:
с:
• Ec: модуль упругости (сжатие) элемента жесткости
• I Zt : минимальная инерция секции внутренней полки
• S t : площадь секции внутренней полки
• L: расстояние между стабилизаторами/накладками
• м: количество полуволн
• β: поступательная жесткость на уровне внутренней полки
Параметр «m» (количество полуволн) является целым числом, большим или равным 1, и зависит от того, что стабилизаторы расположены на волновые узлы по предположению. Это количество полуволн «m», на которые делится стержень при потере устойчивости, можно вычислить, наложив условие минимума вышеприведенного выражения (сделав производную по параметру «m»). Параметр I Zt — минимальная инерция внутренней полки по отношению к оси Z, проходящей через ЦТ (центр тяжести) секции внутренней полки, и ее можно рассчитать следующим образом:
Параметр I Zt — минимальная инерция внутренней полки по отношению к оси Z, проходящей через ЦТ (центр тяжести) секции внутренней полки, и ее можно рассчитать следующим образом:
- Определение m 0 путем минимизации σ Боковая нестабильность ”
Чтобы минимизировать σ Боковая нестабильность необходимо определить «m» следующим образом: значения σ Боковая нестабильность :
С:
• Ec: модуль упругости при сжатии элемента жесткости;
• I Zt : Инерция внутреннего фланца относительно оси Z;
• L: длина моделирующей балки между стабилизаторами;
• m 0 : количество полуволн. Это число всегда больше 1;
• β: поступательная жесткость на уровне внутренней полки
Значение «м» 0 ”, определяемый приведенным выше уравнением, может быть не целым числом. Но для того, чтобы иметь волновой узел на уровне стабилизаторов, необходимо иметь целочисленное значение «m».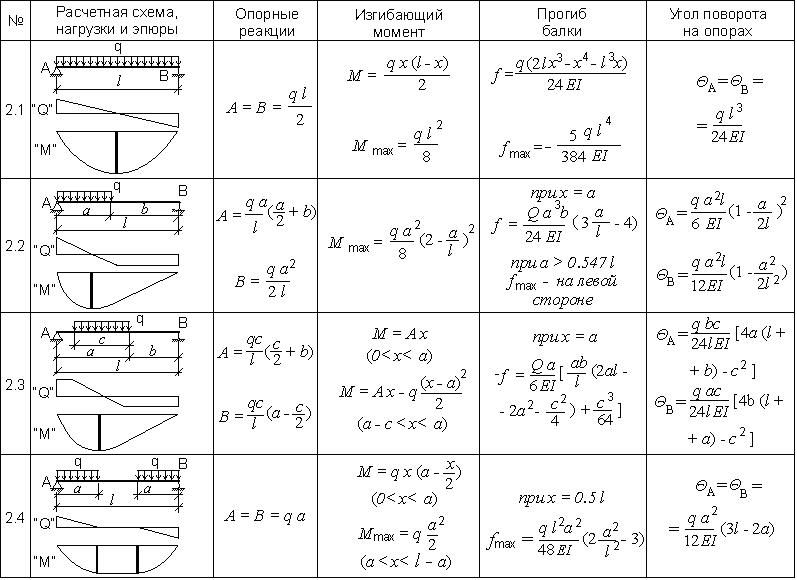 Таким образом, расчет σ Боковая нестабильность выполняется с учетом двух ближайших целочисленных значений, образующих вычисленное «m», и будет учитываться значение «m», которое дает минимальное значение σ Боковая Неустойчивость .
Таким образом, расчет σ Боковая нестабильность выполняется с учетом двух ближайших целочисленных значений, образующих вычисленное «m», и будет учитываться значение «m», которое дает минимальное значение σ Боковая Неустойчивость .
Допустимая σ Боковая нестабильность , рассчитанное с m 0 ≥1, представляет собой напряжение потери устойчивости, когда стабилизаторы бесконечно далеко друг от друга.
Если σ Боковая неустойчивость (Целое число (m 0 )) > σ Боковая нестабильность (Целое число (m 0
)) 43 м = целое число ( m 0 + 1) , иначе m = Целое число (m 0 ) , где Целое число (m 0 ) = целая часть m 0 . Если 1>m 0 , то мы будем использовать предыдущее уравнение, взяв m=1:Следовательно, окончательные уравнения для расчета σ Боковая нестабильность :
с:
Затем мы рассчитаем критическое напряжение следующим образом:
- Поправка на пластичность
необходимо учитывать эффект пластичности материала на коэффициент 9 = η 5 * σ Боковая нестабильность 044 5 = ж (Е Т ,в ) = g(σ Боковая нестабильность ).
Сходимость достигается, когда:
Коэффициент пластичности рассчитывается как отношение между E T и E C :
С:
- E T — модуль тангенса, рассчитанный следующим образом:
- E C — модуль сжатия Юнга
чтобы использовать Fcy.
- Численный пример
Учитывая следующую сборку (состоящую из рамы и панели), рассчитайте максимально допустимую поперечную нестабильность.
| Материал : 7175 T7351 | |
| Допустимое натяжение: 903 9016 Ftu = 425 МПа | |
| Допустимое сжатие: | Fcy = 415 МПа |
| Модуль Юнга (сжатие) | E c = 72000 МПа |
| Коэффициент Рамберга | n = 11 |
Межрамное расстояние: L=525 мм S t и I Zt
Шаг 2: Расчет β
90 18 Расчет м o
Шаг 4: Расчет критического напряжения
6 Шаг 5: 4 9 9017 Шаг 5: Коррекция пластичности
If σ Боковая нестабильность ≤ Fcy / 2 тогда E T = E C , иначе:
В этом случае σ Боковая нестабильность = 623 МПа > Fcy / 2 = 208 МПа.
 условий работы
условий работы А
А использования (K)
использования (K)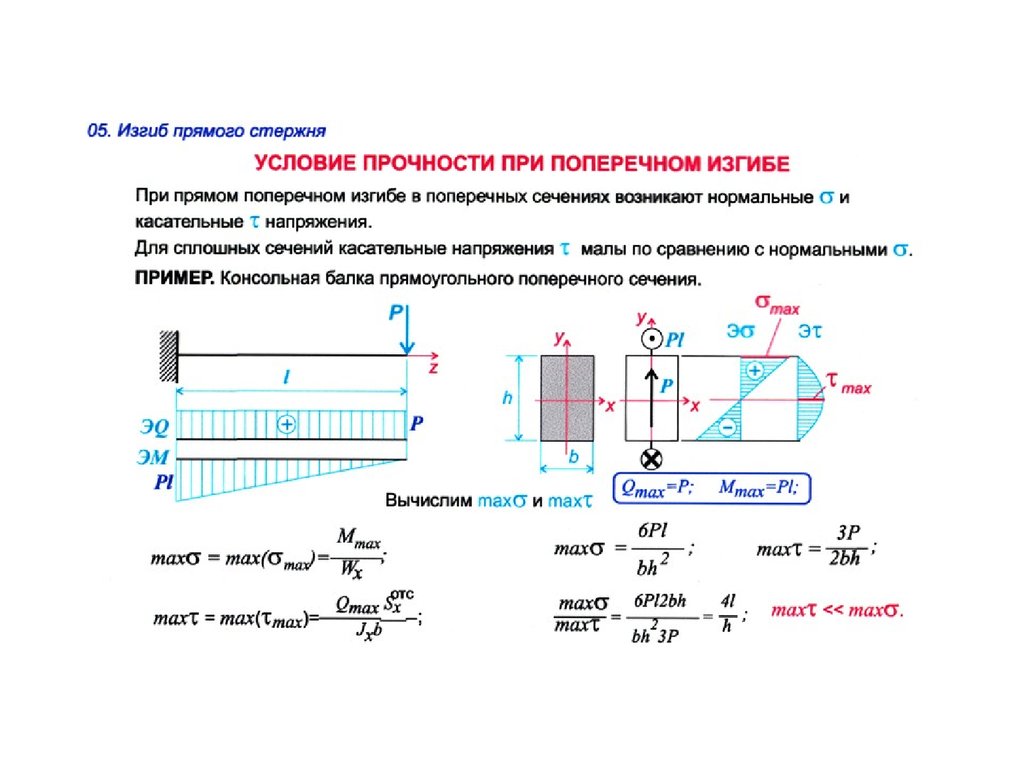 А
А использования (K)
использования (K)