5.3.1.2. Расчет балок на изгиб и кручение

Алгоритм расчета изгибающего момента и алгоритм расчета крутящего момента аналогичны для валов и балок, однако эпюры максимальных напряжений для балок не строят, так как балки, как правило, имеют одинаковое сечение по всей длине и эпюра напряжений повторяет эпюру изгибающих моментов. Поэтому опасное сечение определяется по эпюре моментов, так как в этом сечении, где действует наибольший (по абсолютной величине) момент, возникают и наибольшие напряжения.

На основе условия прочности max проводят либо проверочный расчет на прочность – определяют коэффициент запаса n и сравнивают его с рекомендуемым значением [n]:

n оп/ max n ,

либо проектный расчёт на прочность – подбирают поперечное сечение балки по осевому моменту сопротивления сечения:

W Mmax / .

При заданной форме сечения по W определяют все размеры сечения. Для двутавра, швеллера из таблиц стандарта выбирают номер балки требуемого профиля с ближайшим к найденному значением W. При этом допускаемая перегрузка не должна превышать 5%, а недогрузка – 15%.

Пример

Для стальной балки определить размеры квадратного поперечного сечения, если допускаемое напряжение 160МПа. Эпюра изгибающих моментов для этой балки приведена на рис. 4.

Решение.

Из эпюры определяем опасное сечение. Это будет сечение в опоре В, где действует максимальный изгибающий момент

Mmax 4кН·м.

Из условия прочности определим требуемый момент сопротивления сечения:

W Mmax /[ ].

Для квадратного сечения (h=b) осевой момент сопротивления

W b3 /6,

где b – сторона квадратного сечения.

31

Рис. 4. Результаты расчета балки

Отсюда получаем

b 36 Mmax ;

[ ]

b 36 4 103 0,05313м.

160 106

По ГОСТ 6639–69 на нормальные линейные размеры из Ra40

выбираем bн=53 мм, тогда Wн=0,0533/6=2,48·10-5м3.

Максимальное напряжение в балке с выбранным размером

max Мmax /Wн;

max 4 103 /(2,48 10 5) 161,21МПа.

32

Перегрузка составит

max [ ] 100%; [ ]

161,21 160 100% 0,76%, 160

что не превышает допускаемого значения.

5.3.2.Расчет крепежных соединений

5.3.2.1.Расчет резьбовых соединений

Резьбовыми соединениями называются разъемные соединения, собранные с помощью специальных крепежных деталей или резьбы, выполненнойнасоединяемыхдеталях.

Резьбовые соединения являются наиболее распространенными из разъемных соединений, применяемых в машиностроении, что обусловлено их достоинствами: высокой несущей способностью и надежностью, простотой сборки, разборки, малой стоимостью, возможностью применения стандартных деталей, малыми габаритами и т.д.

К основным деталям резьбовых соединений относятся болты, винты, шпильки, гайки, резьбовые вставки.

Винты, снабжённые гайками, называются болтами (рис. 5, а). Их применяют для соединения деталей сравнительно небольшой толщины и имеющих место для размещения гайки и головки винта. Болты целесообразно использовать в соединениях, часто подвергающихся сборке и разборке.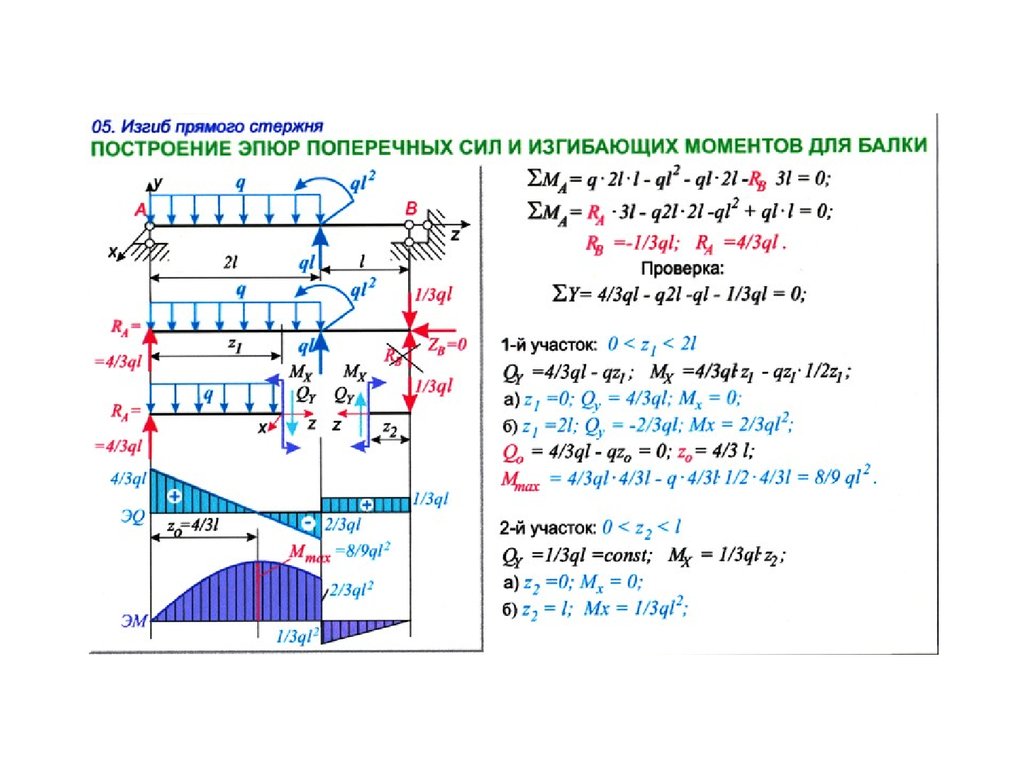 Если болтовое соединение неприменимо, а в детали можно сделать резьбовое отверстие, то используют винты (рис. 5, б). Недостатком винтового соединения является изнашивание резьбового отверстия детали при частой сборке. В других случаях для соединения используют шпильки с гайками (рис. 5, в) или в резьбовое отверстие одной из соединяемых деталей завинчивают деталь из более твёрдого износостойкого металла, имеющую вид втулки с наружной и внутренней резьбой (рис. 5, г).

33

а

б

в

г

Рис. 5. Резьбовое соединение

Все геометрические параметры большинства резьб и допуски на них стандартизированы. Болты и гайки, используемые в соединениях, имеют различный диаметр, шаг резьбы, классы прочности и вид покрытия. Они изготовлены в соответствии со стандартами на крепежные детали.

Примеры условных обозначений болтов приведены в ГОСТ 7798–70, гаек – в ГОСТ 5915–70, шайб – в ГОСТ 11371–78.

Алгоритм расчета болтовых соединений при различных случаяхнагружения

В настоящее время для расчета болтовых соединений существует несколько видов расчетов. В том случае, когда требуется выяснить основные параметры болтового соединения, проводят проектный расчет. Если необходимо оценить прочность болтового соединения, осуществляют проверочный расчет. Бывают случаи, когда надо знать допустимую внешнюю нагрузку, при этом проводят расчет на нагрузочную способность.

При действии на болтовое соединение переменных нагрузок в качестве проверочного расчета проводят расчет болтовых соединений на выносливость.

Искомые неизвестные величины можно определить исходя из условий прочности болтовых соединений в зависимости от условий нагружения.

Расчет болтов,нагруженныхосевойсилой

На стержень болта действует только внешняя осевая нагрузка.

34

Примерами такого соединения могут служить грузовая скоба, рым-болт, нарезанный участок крюка для подъема груза (рис.

6).

Алгоритм расчета болта, нагруженного внешнейосевойнагрузкой:

1. Условие прочности по напряжению растяжения стержня имеет вид

	р		F		4 F		p	,
			A d2
		1

где F – растягивающая сила; А – площадь поперечного сечения болта по резьбе; d1 – внутренний диаметр резьбы.

2. Допускаемое напряжение растяжения можно определить по зависимости

p Т ,

[s]

где Т – предел текучести материала болта,

МПа; [s] – коэффициент запаса прочности. Рис. 6. Крюковая

подвеска

3. Значения Т можно принять в зависимости от класса прочности болта по ГОСТ 7798–70, коэффициент запаса прочности [s] по табл. 3, 4 [1].

Таблица 3

Значения коэффициентов запаса прочности и допускаемых напряжений при расчете болтовых соединений

Вид нагрузки		Допускаемое	Рекомендуемые напряжения
		напряжение	Затяжка		Статическая	Переменная
					нагрузка	нагрузка
Растягивающая			Контроли-		[s]=1,2–1,5	[sТ]=1,2–1,5
внешняя нагрузка:		[ р]=0,6 Т	руемая
без затяжки болтов			Неконтро-		[s]= 2,5–4	[sТ]=2,5–4
с затяжкой болтов		[ р]= Т/[s]	лируемая
Поперечная внешняя нагрузка	Болты постав-	[ р]= Т/[s]	Контролируемая [s]=1,2–1,5
	лены с зазором		Неконтролируемая [s] = 2,5–4
	Болты постав-	[τср]=0,4 Т – статическая нагрузка
	лены без зазора	[τср]=(0,2-0,3) Т		– переменная нагрузка
			[ см]=0,8 Т – сталь
			[ см]= (0,4-0,5) в – чугун

35

				Таблица 4
Значения коэффициентов запаса прочности при расчете болтов
	с неконтролируемой затяжкой
Материал болта	Постоянная нагрузка		Переменная нагрузка
	М6–М16	М16–М30	М6–М16	М16–М30
Углеродистая сталь	5–4	4–2,5	12–8,5	8,5
Легированная сталь	6,5–5	5–3,3	10–6,5	6,5

Расчет болтовых соединений, собираемых с предварительной затяжкой

При сборке машин болтовые соединения предварительно затягиваются силой затяжки Fзат, а в процессе работы они нагружаются внешней осевой растягивающей силой F (рис. 7).

Этот вид нагружения болтов широко распространен, так как предварительная затяжка обеспечивает герметичность соединения и отсутствие взаимных смещений деталей, нарушающих работу машины. К болтовым соединениям такой категории относятся фланцевые, фундаментные, шатунные, резьбовые детали крепления крышек двигателей внутреннего сгорания, сосудов, находящихся под внутренним давлением, и т.д.

Рис. 7. Схема работы болтового соединения

36

Алгоритм расчета болтовых соединений, собираемых с предварительнойзатяжкой:

1. После приложения внешней силы F суммарное усилие (см. рис. 7), растягивающее болт, равно

FБ Fзат FБ Fзат F,

а суммарное (остаточное) усилие, сжимающее детали,

FД Fзат FД Fзат (1 ) F,

где – коэффициент внешней нагрузки, он показывает, какая часть (т. е. FБ F ) внешней нагрузки F дополнительно растягивает болт,

	Д	,
	Д Б

здесь λБ – податливость болта; λД – податливость деталей.

Условие нераскрытия (герметичности) стыка деталей состоит в наличии FД, сжимающей стык и после приложения внешней силы,

т. е. FД < 0.

2. Внешняя сила Fкр в момент раскрытия стыка (FД = 0) называется критической силой и определяется как

Fкр Fзат .

1

При этом усилие в болте становится равным внешней силе:

FБ = Fкр.

Податливость болта

	Б				lБ	,
			Е
				Б	А
					Б

где lБ, ЕБ, АБ – соответственно длина, модуль нормальной упругости материала и площадь поперечного сечения болта.

Суммарная податливость деталей

	Д	Д1 Д 2		l	Д1		lД 2	,
				ЕД1 АД			ЕД 2 АД

где lД1, lД2 – соответственно толщина соединяемых деталей; ЕД1, ЕД2 – модули нормальной упругости материала деталей и прокладки; АД – расчетная площадь поперечного сечения деталей и прокладки.

3. Определение необходимой величины предварительной затяжки болта и расчет его на прочность при статических нагрузках.

37

Усилие затяжки Fзат болта определяется из условия нераскрытия стыка:

Fзат K (1 ) F ,

гдеК–коэффициентзапасазатяжкипристатическойнагрузке(табл. 5). Дополнительно отметим, что на практике нераскрытие стыка

деталей зависит не только от значения силы затяжки Fзат, но и от её сохранения в процессе эксплуатации. Последнее зависит от многих факторов: качества обработки поверхностей стыка, числа стыков, точности резьбы, надёжности стопорения резьбы, качества прокладки. Эти факторы сложно поддаются учёту, особенно при переменных во времени нагрузках. Поэтому в ряде случаев логично принимать

Fзат ≈ K·F.

Таблица 5

Значения различных коэффициентов, применяемых при расчете болтовых соединений

Нагрузка	Коэф-	Рекомендуе-	Примечания
	фициент	мые значения
Предвари-	К	1,25–2	Статистическая нагрузка
тельно затя-		2–4	Переменная нагрузка
нутое болто-		1,3–2,5	Мягкая прокладка
вое соедине-		2–3,5	Металлическая фасонная прокладка
ние		3 5	Металлическая плоская прокладка
		0,2–0,3	Жесткие фланцы
		0,5–0,7	Податливые фланцы
Поперечная	fc	0,15–0,2	Для сухих стальных и чугунных
внешняя			поверхностей
нагрузка	К	1,3–1,5	Статистическая нагрузка
		1,8–2	Переменная нагрузка

4. Эквивалентные напряжения в болте

		экв		4 FБ,Р		p	,
				d2
			1

где d1 – внутренний диаметр резьбы болта; [σр]– допускаемые напряжения растяжения материала болта; FБ,Р – расчётное усилие в болте.

Расчет FБ,Р может быть выполнен по двум вариантам:

вариант 1 – болт можно подтягивать после приложения внешней силы F (т.е. непосредственно в процессе работы). В этом случае усилие в болте

38

FБ,Р 1,3 F [K (1 ) ];

вариант 2 затяжка болта производится при отсутствии внешней силы F:

FБ,Р F [1,3 K (1 ) ].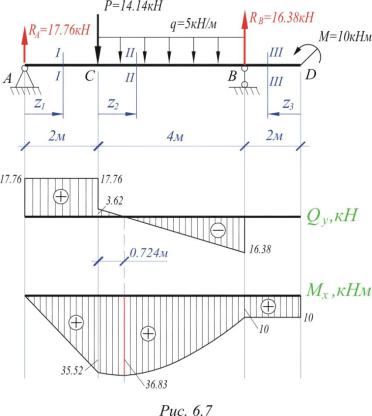

Расчетболтов,нагруженныхпоперечнойсилой

Примером могут служить крепления различных кронштейнов. Условием работоспособности болтового соединения, нагруженного силами, действующими в плоскости стыка, является отсутствие сдвига деталей. Болтовые соединения, нагруженные поперечной сдвигающей силой, могут быть выполнены в двух вариантах постановки болтов: с зазором (рис. 8, а) и без зазора (рис. 8, б).

Рис. 8. Болтовые соединения, нагруженные поперечной сдвигающей силой с зазором (а) и без зазора (б)

при постановке болтов

Установка болта с зазором

Основными критериями работоспособности болтовых соединений, нагруженных поперечной силой при установке болтов с зазором (см. рис. 8, а), являются отсутствие сдвига между деталями, прочность стержня болта на растяжение с кручением и соединяемых деталей на смятие (на плоскости стыка).

Для обеспечения относительной неподвижности соединяемых деталей необходимо затянуть болт такой силой затяжки Fзат, чтобы

39

возникающая при этом между деталями сила трения была больше внешней сдвигающей силы F, т.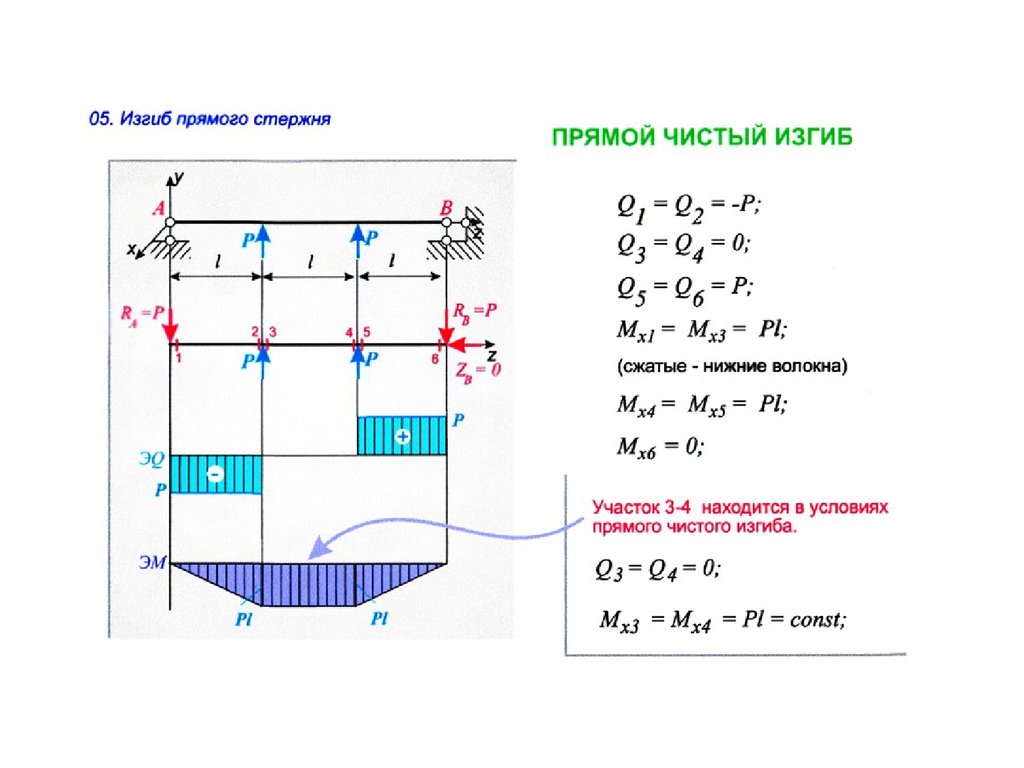 е.

Ff >F,

или с учетом коэффициента запаса затяжки K

Ff =K·F,

здесь создаваемая затяжкой сила трения определяется зависимостью

Ff =Fзат·fc·i;

F		K F	,
зат		fc i

где fc – коэффициент трения в стыке; i – число стыков деталей в соединении (в соединении, показанном на рис. 8, а, i = 2).

При расчете такого соединения принимают K по табл. 5.

В момент начала относительного сдвига деталей предельная внешняясдвигающаясилаFпр будетравнасилетрениямеждудеталями,т.е.

Fпр = Ff = Fзат·fс·i.

Таким образом, величина предельной сдвигающей силы зависит от материала соединяемых деталей (от коэффициента трения в стыке между ними), числа стыков и наибольшей для данного соединения силы затяжки.

Условие прочности стержня болта на растяжение с кручением:

σэкв ≤ [σр],

или для метрической резьбы

экв 1,3 4 F2зат p .

d1

По условию прочности соединяемых деталей на смятие,

σсм ≤ [σсм],

или

см Fзат см .

АД

Для предельного случая силу затяжки определяем

[Fзат] = АД[σсм],

где AД – деформируемая площадь деталей; [σсм] – допускаемое напряжение смятия материала деталей.

Предельная допускаемая сдвигающая сила, определяющая нагрузочную способность болтового соединения, при максимально допустимой силе затяжки [Fзат] равна

40

[Fпр ] [Fзат ] fc i .

K

Установка болта без зазора

При постановке болта без конструктивного зазора (см. рис. 8, б) отверстие под него калибруют разверткой. Поэтому диаметр стержня болта d принимается равным диаметру отверстия dотв . При расчете элементов соединения на прочность не учитывают силы трения в стыке, так как затяжка болта может практически отсутствовать (в общем случае болт можно заменить штифтом, пальцем или осью).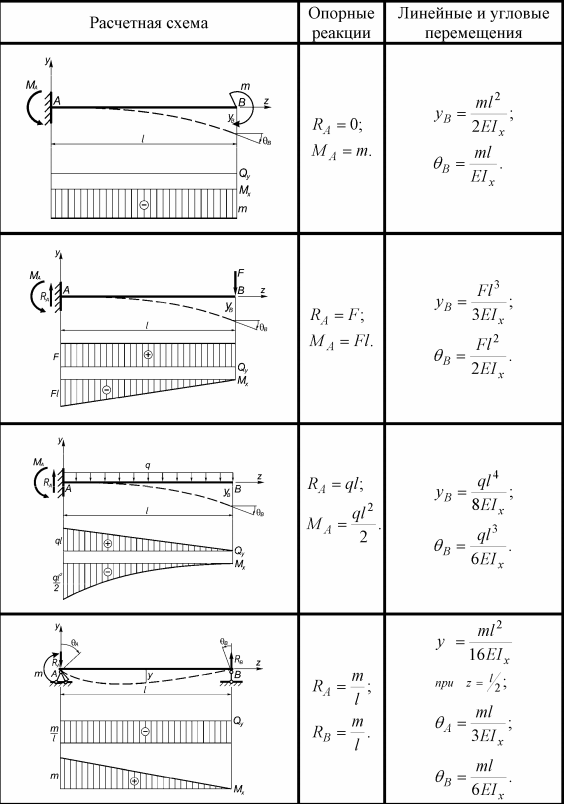 Стержень болта рассчитывают по напряжениям среза и смятия.

Условие прочности на срез

ср	4 F			ср ,
	d2
		i

здесь i – число плоскостей среза (в соединении на рис. 8, б, i = 2). Условие прочности болта на смятие (см. рис. 8, б) для средней

детали

F

см1 d 1 см ,

для крайних деталей

F

см2 2 d 2 см ,

где δ1, δ2 – соответственно толщина средней и крайней деталей. Данные формулы справедливы как для болта, так и для деталей. Расчет производится по наибольшему напряжению смятия σсм, а

допускаемое напряжение [σсм] определяют по менее прочному материалу болта или соединяемых деталей.

Пример

Рассчитать резьбовой участок крюка для подъема груза (см. рис. 6), воспринимающий максимальную нагрузку F = 11,5 кН. Материал крюка сталь 20 (ГОСТ 1050–88).

Решение:

1. Определение допускаемого напряжения.

Гайка навёрнута на резьбовой участок крюка без затяжки, поэтому он воспринимает только внешнюю растягивающую нагрузку от веса груза.

41

Для заданного материала σТ = 240 МПа. Тогда допускаемое на-

пряжение [σр] = 0,6σТ = 0,6 ·240 =144 МПа.

2. Определение внутреннего диаметра резьбы. Из условия прочности на растяжение

	р			4 F				p ,
			d12
внутренний диаметр резьбы
		d1				4 F			;
					[ p ]
d1			4 11500					10,08мм.
			3.14 144
Подбираем резьбу	М12				с			шагом 1,5 мм, для которой

d1 = 10,376 мм > 10,08 мм.

Ответ: резьба М12 ГОСТ 24705–81.

Расчет фундаментного болта. Крепление различного технологического оборудования может осуществляться за счет применения фундаментных болтов.

Алгоритм расчетафундаментногоболта

Расчётная нагрузка на фундаментные болты, Н:

РН P0 n G M yy21 ,

i

где Р0 – расчётная вертикальная сила, действующая на фундамент от технологического оборудования, Н; G – вес технологического оборудования, Н; М – расчётный опрокидывающий момент, Н∙м; п – число фундаментных болтов; y1 – расстояние от оси опрокидывания до наиболее удалённого болта, м; yi – расстояние от оси опрокидывания до i-го болта, м.

Усилие предварительной затяжки от действия вертикальной нагрузки, Н:

Рзв Kст (1 ) Pн,

где Кст – коэффициент стабильности затяжки для болтов с отгибом при динамической нагрузке; χ – коэффициент внешней нагрузки; Рн – расчётная вертикальная нагрузка, Н.

Усилие предварительной затяжки от сдвигающей силы, Н:

42

Рзг	Kст		Q G f	,
			n f

где f – коэффициент трения при установке на подкладки; Q – расчётная сдвигающая нагрузка, Н.

Суммарное усилие предварительной затяжки, Н:

Рз Рзв Pзг.

Необходимая площадь сечения болтов, см2:

F Pз Рн , 100 p

где [σр] – допустимое напряжение растяжения, МПа. Определяем допустимое напряжение болта на разрыв, МПа:

p l 0,287 p ,

где α – коэффициент, зависящий от числа циклов нагрузок.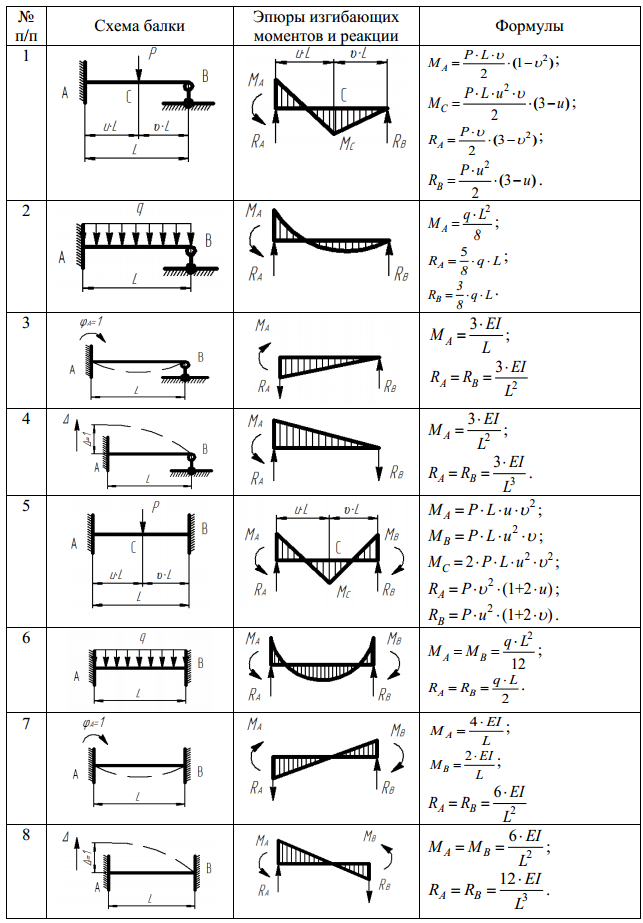 Площадь сечения болта из условия выносливости, см2:

F		Рн			,
	200
в
			p д

где [σр]д – допустимое напряжение материала болта.

Пример

Рассмотрим крепление технологического оборудования к полу за счет применения фундаментных болтов (рис. 9).

Расчётная нагрузка на фундаментные болты, Н:

				РН			P0 G		M y1	;
							n		yi2
РН		25 31					200 0. 2				248,5кН.
				0,2		2 0,22
	4							0,22 0,22

Усилие предварительной затяжки от действия вертикальной нагрузки, Н:

Рзв Kст (1 ) Pн;

Рзв 1,3 (1 0,5) 248,5 161,5 кН.

Усилие предварительной затяжки от сдвигающей силы, Н:

Рзг	Kст		Q G f	;
			n f

43

Рзг 1,3 30 31 0,2 10,1 кН. 4 0,2

Суммарное усилие предварительной затяжки, Н:

Рз Рзв Pзг;

Рз 161,5 10,1 171,6 кН.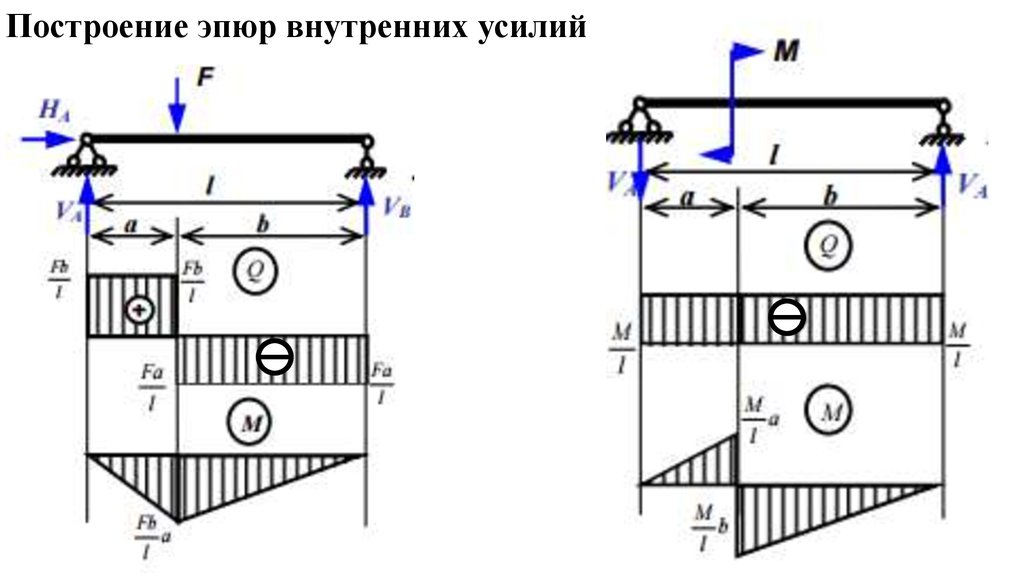

Рис. 9. Расчет фундаментного болта:

а – общий вид фундаментного болта;

б– расположение фундаментных болтов

Необходимая площадь сечения болтов, см2:

F Pз Рн , 100 p

где [σр] = 140 МПа – допустимое напряжение растяжения.

F 171,6 103 0,5 248,5 103 0,2см2. 100 140 106

Выбираем фундаментный болт М10, F = 0,571 см2 (табл. 6).

Определяем допустимое напряжение болта на разрыв, МПа:

p l 0,287 p ;

44

решение задач. Лекции. Кручение. Построение эпюр крутящих моментов.

Меню сайта Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления. Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. + Полное расписанное решение! Теперь и для статически неопределимых балок! Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты

Базовый курс лекций по сопромату, теория, практика, задачи.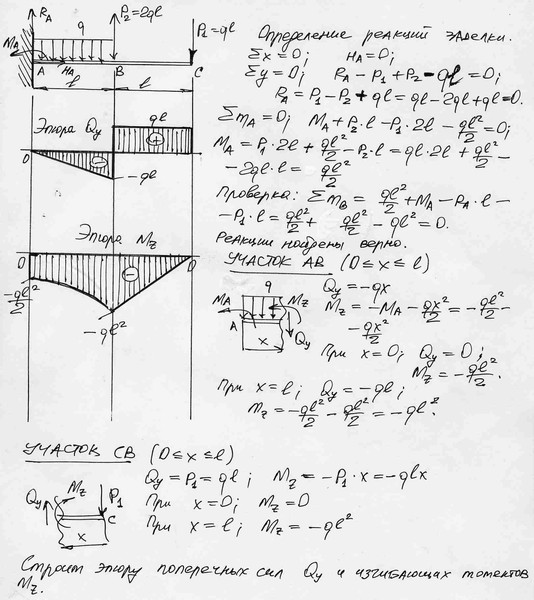 ::Оглавление:: 2. Кручение. 2.1. Построение эпюр крутящих моментов. Стержень испытывает кручение, если в его поперечных сечениях возникают крутящие моменты, т.е. моменты, лежащие в плоскости сечения. Обычно эти крутящие моменты Тк возникают под действием внешних моментов Т (рис. 2.1). Внешние моменты передаются на вал, как правило, в местах посадки на него шкивов, зубчатых колес и т.п. Однако и поперечная нагрузка, смещенная относительно оси стержня, вызывает крутящие моменты (рис. 2.2), но в указанном слечае в поперечных сечениях наряду с крутящими моментами возникают и другие внутренние усилия — поперечные силы и изгибающие моменты. Вращающиеся и работающие на кручение стержни называют валами. Вместо аксонометрического изображения будем применять главным образом плоское, как более простое. Внешние скручивающие моменты и внутренние крутящие моменты будем изображать в виде линии с двумя кружочками. В одном из них будем ставить точку, обозначающую начало стрелки (на нас), в другом — крестик, обозначающий конец стрелки, направленный от нас (рис. 2.3). Для определения крутящих моментов Тк возникающих в сечениях вала под действием внешних скручивающих моментов или поперечной нагрузки, будем применять метод сечений. Сделаем мысленный разрез стержня (рис. 2.3), например по а — а, отбросим одну часть стержня, в данном случае левую, и рассмотрим равновесие оставшейся правой части. Взаимодействие частей стержня заменим крутящим моментом Тк, уравновешивающим внешний момент Т. Для равновесия отсеченной части необходимо, чтобы алгебраическая сумма всех моментов, действующих на нее, была равна нулю. Отсюда в рассматриваемом случае получим, что Тк = Т. Если на отсеченную часть будет действовать несколько внешних моментов, то, проведя аналогичное рассуждения, можно убедиться, что крутящий момент в сечении численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения. Для наглядного представления о характере распределения и величине крутящих моментов по длине стержня строят эпюры (графики) этих моментов. Построение их вполне аналогично построению эпюр продольных сил при растяжении или сжатии. Для построения эпюр необходимо условиться о правиле знаков. Общепринятого правила знаков для крутящих моментов не существует. Может быть принято любое правило знаков. Важно лишь принятое правило выдержать на всем протяжении эпюры. Примем следующее правило знаков (рис. 2.4). Крутящий момент в сечении а — а считается положительным, когда внешний момент вращает отсеченную часть против часовой стрелки, если смотреть на отсеченную часть со стороны сечения. Если же внешний момент вращает отсеченную часть по часовой стрелке (при взгляде со стороны сечения), то крутящий момент в сечении будем считать отрицательным. Построение эпюры крутящих моментов поясним на следующем примере (рис. 2.5): рассмотрим вал CD, опирающийся на подшипники B и A и находящийся в равновесии под действием приложенных к нему в сечениях E, K и L моментов. Сделав сечение а — а где-либо на участке DL и рассмотрев равновесие правой отсеченной части, убедимся, что Тк = 0. Если мы сделаем затем сечение b — b в любом месте участка LK, то из условия равновесия правой от сечения части получим Тк = 20 кН * м. Момент считаем положительным в соответствии с принятым правилом знаков. Сделав сечение с — с на участке KE из условия равновесия правой части, получаем 20 — 30 — Тк = 0. Откуда Тк = -10 кН * м. Получившаяся эпюра имеет форму двух прямоугольников. Важно заметить, что в местах приложения внешних моментов ординаты эпюры скачкообразно изменяюися на величину приложенного здесь внешнего момента. Если заданы поперечные нагрузки, вызывающие кручение стержня (рис. 2.2), то предварительно вычисляют внешние скручивающие моменты, создаваемые этими силами. В случае, представленном на рис. 2.2, внешний скручивающий момент от силы F равен T = Fr. После определения внешних моментов определяют внутренние крутящие моменты и строят эпюры, как указано выше. ::Оглавление:: Полезные ресурсы по теме «Построение эпюр» 1. Он-лайн программа (версия 2004 года), которая выдаст расписанное решение любой балки. Пример результата. Кроме построения эпюр эта программа так же подбирает профиль сечения по условию прочности на изгиб, считает прогибы и углы поворота в балке. 2. Он-лайн программа (версия 2008 года), которая строит 4 вида эпюр и рассчитывает реакции для любых балок (даже для статически неопределимых).

Сообщество Поиск людей Вход Решение задач Заказать задачу Профессиональное решение задач в короткие сроки. Расчет редукторов Расчет редуктора он-лайн Расчет любого редуктора он-лайн. Записка + чертежи Для Android (рекомендую) NEWMobile Beam 2. 0 Программа для расчета балок на прочность на Вашем Android устройстве… Java 2 ME

Калькулятор постоянной кручения и формулы

Создано Луисом Хойосом

Рассмотрено Стивеном Вудингом

Основано на исследовании

Budynas RG, Sadegh AM «Формулы Рорка для напряжения и деформации (таблица 10.1) “ McGraw-Hill Education ( 2020)

Последнее обновление: 18 января 2023 г.

Содержание:

• Что такое постоянная кручения?
• Важные моменты, которые следует учитывать при использовании этого калькулятора
• Формулы для констант кручения
• Пример: Как рассчитать коэффициент кручения балки прямоугольного сечения
• Часто задаваемые вопросы

Если вы искали, как рассчитать коэффициент кручения двутавровых балок и многих других конструкционных профилей, больше не ищите!

При изучении поведения балок, подвергающихся кручению, мы обычно ориентируемся на круглые стержни.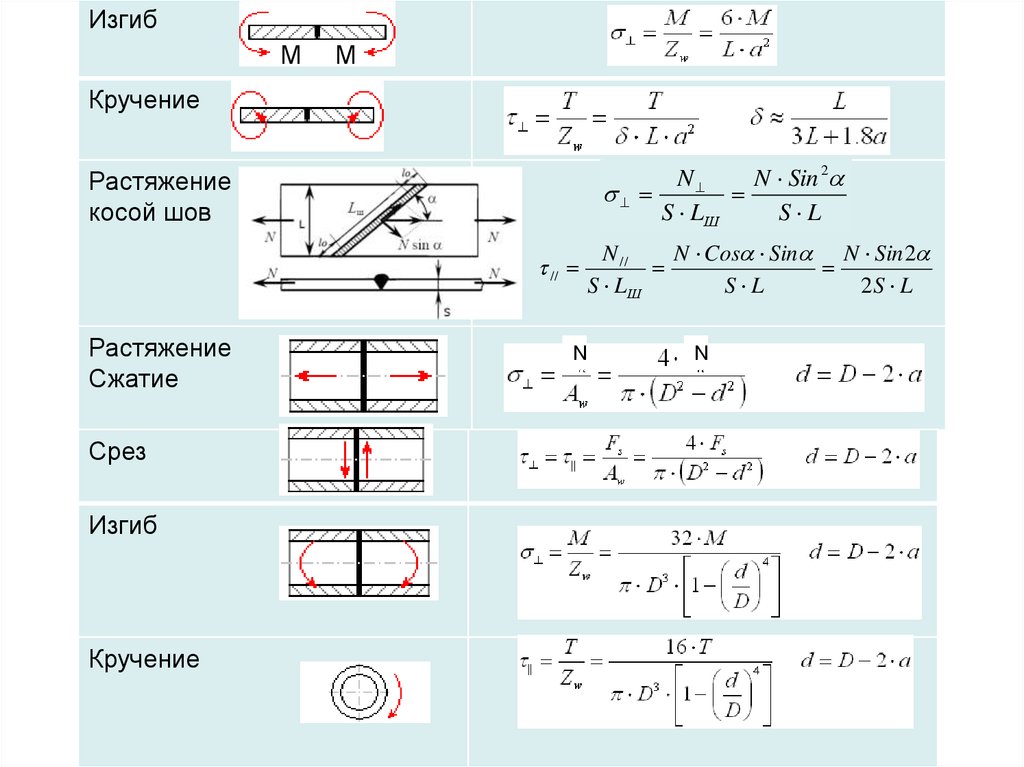 Тем не менее, иногда необходимо выйти за рамки, так как некоторые некруглые элементы могут испытывать скручивающие нагрузки (примером этого является размах крыла самолета). По этой причине мы создали этот инструмент!

Продолжайте читать, чтобы узнать больше о постоянной кручения, что следует учитывать при расчете постоянной кручения и формулах этого калькулятора.

🙋 Как только вы получите постоянную кручения, вы можете использовать ее в нашем калькуляторе угла закручивания.

Что такое постоянная кручения?

Помимо модуля сдвига и длины балки, постоянная кручения (также известная как постоянная кручения ) равна одно из свойств, описывающих крутильную жесткость некруглых балок (аналогично полярному моменту инерции). В отличие от модуля сдвига, это геометрическое свойство, так как оно зависит только от формы и размеров поперечного сечения.

Как мы видели в нашем калькуляторе полярного момента инерции, для расчета угла закручивания балки при кручении с использованием полярного момента инерции поперечное сечение стержня должно оставаться плоским и неискаженным, что происходит только в круглых сечениях. .

Сравнение деформаций, полученных в круглых и прямоугольных стержнях при кручении.

К счастью, мы можем получить аналоговые выражения полярного момента инерции для различных геометрий, используя передовые процедуры механики твердого тела. Постоянная кручения — это свойство, которое позволяет нам рассчитать угол закручивания некруглых стержней:

ϕ=TLKG\phi = \frac{TL}{KG}ϕ=KGTL​

В этом уравнении:

• ϕ\phiϕ — угол закручивания;
• ТТТ — Крутящий момент, приложенный к балке;
• LLL — длина вала;
• GGG — Модуль сдвига материала вала; и
• KKK — Постоянная кручения балки, которую мы получаем с помощью этого калькулятора.

Постоянная кручения в этой формуле имеет ту же функцию, что и полярный момент в круглом стержне, но мы назвали его здесь символом ККК, чтобы различать оба.

Прежде чем рассматривать формулы, давайте рассмотрим некоторые аспекты, которые стоит учитывать при использовании этого инструмента и уравнений.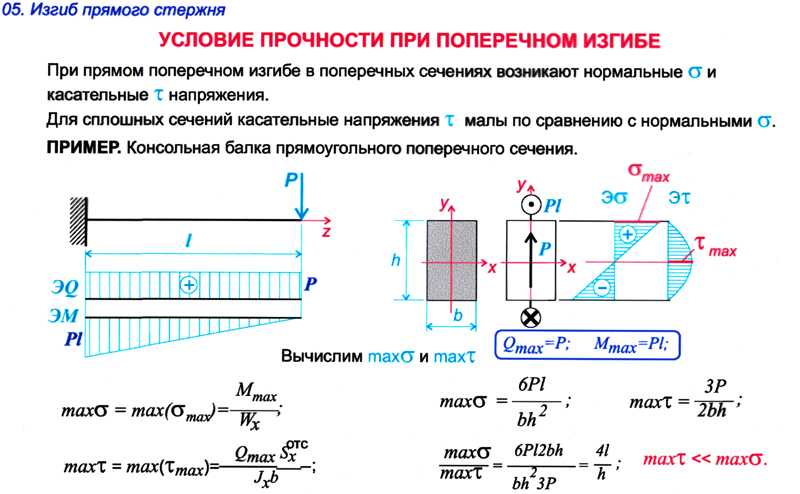

Что важно учитывать при использовании этого калькулятора

Формулы, используемые в этом калькуляторе, основаны на следующих предположениях:

1. Балка прямая и равномерная .
2. Стержень нагружен только равными и противоположными парами кручения , приложенными к его концам в плоскостях, перпендикулярных его оси.
3. Напряжение в стержне не превышает предела упругости .

🙋 Второе условие означает, что концевые секции могут свободно деформироваться (нет сил, удерживающих их в соответствующих плоскостях). Если это второе условие не выполняется (имеются фиксированные концы или пары, применяемые в секциях, отличных от концов), фактический угол закручивания будет другим. Чем отличается? Эффект не так велик в компактных поперечных сечениях, но разница может быть значительной для открытых тонкостенных элементов.

Если вас интересуют случаи, когда второе условие неприменимо, вы можете посмотреть раздел 10.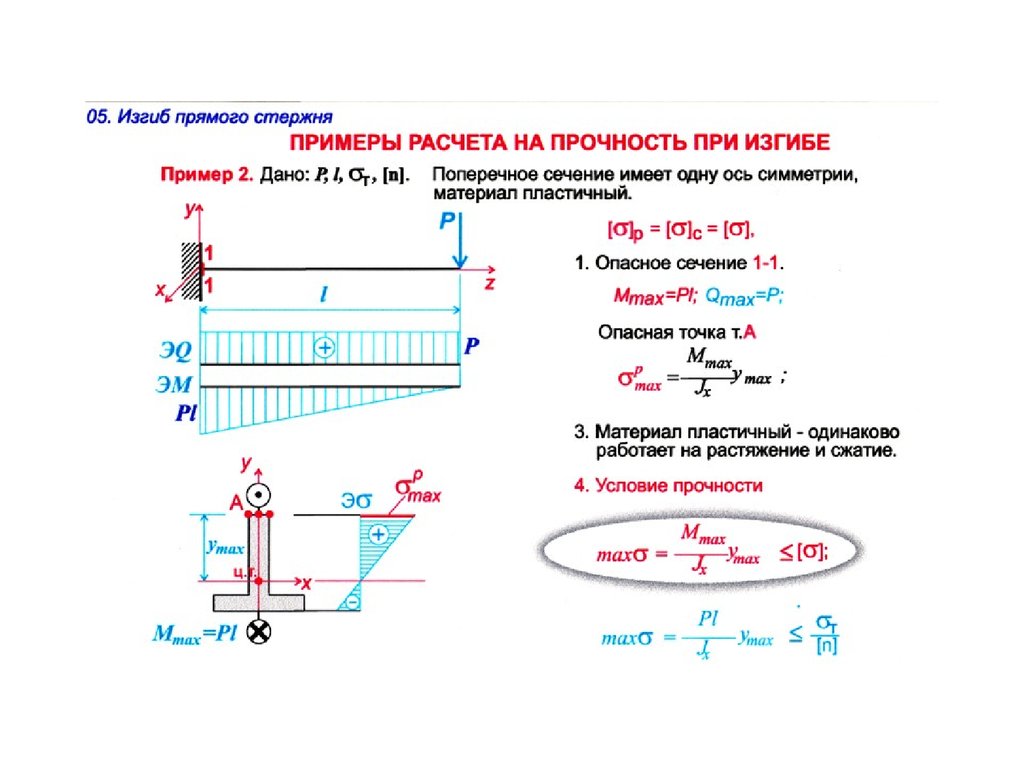 3 работы Budynas & Sadegh.

Формулы для констант кручения

Ниже приведены формулы для констант кручения, лежащие в основе этого калькулятора. Как вы можете заметить, полярный момент инерции и постоянная кручения равны для круглых профилей. Вот несколько замечаний о точности этих формул:

• Хотя формулы тонкостенный эллипс и тонкостенный прямоугольник основаны на математическом анализе, они содержат ошибку, которая зависит от того, насколько точно геометрия соответствует следствию второго предположения предыдущего раздела (не открытый тонкостенный элемент).
• Формула сплошной прямоугольник является упрощенным вариантом с погрешностью не более 4%.
• Формула для двутавровой балки основана на экспериментальных методах с погрешностью (редко) до 10%. 93/3K2​=cd3/3

  D=tt1(0,15+0,1rb)D = \frac{t}{t_1}(0,15+0,1\frac{r}{b})D=t1​ t​(0.15+0.1br​)

  α=tt1(0. 4 \end{align*}K=3ab3−0,21b4−0,0175a4b8=310 мм (5 мм)3 −0,21 (5 мм)4- 0,0175 (10 мм)4(5 мм)8​=284,73 мм4 94284,73 мм4

Часто задаваемые вопросы

В чем разница между полярным моментом инерции и постоянной кручения?

Оба являются мерой жесткости балки при кручении, но есть некоторые различия:

• С помощью полярного момента инерции мы можем рассчитать только угол кручения в круглых элементах.
• С помощью постоянной кручения мы можем рассчитать угол кручения в балках с поперечными сечениями, выходящими за круговую геометрию.

Что такое единицы постоянной кручения?

Обычно используемыми единицами постоянной кручения являются мм ⁴ в Международной системе единиц и в ⁴ в обычной системе США. Установки м ⁴ и футов ⁴ также используются, хотя и реже.

Как рассчитать постоянную кручения квадратного сечения?

Для расчета жесткости квадратного сечения:

1. Возведите длину стороны квадрата в четвертую степень . Например, для квадрата 5 см: (5 см)⁴ = 625 см⁴ .
2. Умножить предыдущий результат на 9/64 . В текущем примере результатом будет (9/64) × 625 см⁴ = 87,89 см⁴ .
3. Вот оно! Вы также можете воспользоваться нашим калькулятором и рассчитать коэффициент кручения двутавровых балок и многих других форм.

Как рассчитать постоянную кручения двутавровой балки?

Для двутаврового сечения формула для постоянной кручения ( K ) выглядит следующим образом:

K = 2 K ₁ + K ₂ + 2 αD ⁴ ,

где:

• К ₁ = аб ³/3 — 0,21 б ⁴ — 0,0175 б ⁸/ а ⁴ ;

• К ₂ = кд ³/3 ;

• D = [( b + r )² + rd + d ²/4]/[2 r + b ] ; и

• α = ( t / t ₁)(0,15 + 0,1 r / b )

  • Если b < d , то t / t ₁ = b / d 900 10 ; и
  • Если d < b , затем т / т ₁ = д / б .

  a ширина полки, b толщина полки, c высота стенки, d — ширина полотна, r — ширина полотна. радиус скругления балки.

  Эти формулы действительны, пока d < 2( b + r ) .

Луис Ойос

Входные данные

Секция

Формула, используемая в этом расчете, основана на экспериментальных методах, погрешность редко достигает 10%.

Этот расчет действителен, пока d < 2(b + r).

Ответ

Постоянная кручения (K)

Посмотреть 34 похожих калькулятора материалов и механики сплошной среды am Дизайн для кручения | Рабочий пример

В этой статье рассматривается метод расчета балки на кручение на рабочем примере. Существуют основные шаги, которые необходимо выполнить так же, как и при проектировании продольной арматуры балки.

При расчете балки на кручение рассчитываются требования к звену кручения и дополнительная площадь армирования, которая должна быть добавлена ​​к продольной арматуре.

Что еще более важно, звенья жесткости на кручение отличаются от обычных поперечных звеньев , предусмотренных для балок. Торсионные звенья заканчиваются на двух концах, в отличие от диалогового звена.

• Пролет балки = 5 м
• Пролет консоли = 2 м
• Высота балки = 600 мм
• Ширина балки = 300 мм
• Диаметр поперечного звена = 10 мм
• Крышка к усилению = 25 мм
• Расчетная нагрузка на балку, включая все коэффициенты нагрузки = 4 кН/м ²
• Марка бетона C30
• Характеристический предел текучести = 460 кН/м ²

Расчет изгибающего момента при кручении

Изгибающий момент = 4 x 2 x 5 = 40 кНм

Изгибающий момент на опору = 40 / 2 = 20 кНм

Расчет напряжения сдвига при кручении, v

_т

v _т  = 2T / [ ч _мин ² (ч _макс – ч _мин /3)]

T = 20 кНм, ч _мин = 300, ч _макс = 600

v _t = 2 х 20 х 10 ⁶ / [ 300 ² (600 – 300/3)] = 1,24 Н/мм ²

Из таблицы 2. 3 BS 8110, часть 2,

v _{t min} = 0,36 Н/мм ²   и v _tu = 4,38 Н/мм ²

v _{t мин} < v _tu и v _t >  v _{t min} , Следовательно, необходимо предусмотреть усиление на кручение .

В этом рабочем примере мы не собираемся проектировать балку на сдвиг и изгиб. Однако для этой конструкции нам необходимо знать напряжение сдвига и способность балки к сдвигу. Таким образом, давайте примем некоторые значения напряжения сдвига.

Скажем, v = 0,25 Н/мм ² и v < v _c 

Балка состоит из двух сегментов в соответствии с требованием жесткости на сдвиг и кручение.

• v _t ≤ v _{t min} Номинальная арматура, работающая на сдвиг, достаточна, и расчет балки на кручение не требуется.
• v _t > v _{t min}  Исполнение для звеньев, работающих на срез.

Мы можем легко рассчитать сегмент, в котором нам нужны только номинальные сдвиговые звенья.

Сначала рассчитаем крутящий момент, определяющий минимальное требование для крутильных звеньев.

T = v _{t min} h _min ² [(h _max – h _min /3)]/2

T = 0,37x 300 90 354 2 [(600 – 300/3 )]/2 = 8,33 кНм

Теперь рассчитаем расстояние до этого момента

Скажем, х,

х = (8,33/20) х 2,5 = 1,0 м На расстоянии 1,5 м от каждой опоры.

Расчет звеньев на номинальный сдвиг

A _sv / S _v ≥ 0,4b / 0,95f _yv

Учитывать стержни T10 = 78 x 2 = 157 мм ²  * две ножки, следовательно, площадь арматуры умножить на 2; (78 х 2).

S _v ≤ 157 x 0,95 x 460 / (0,4 x 300) = 575 мм

Обеспечьте номинальные срезные звенья T10 на расстоянии 250 мм. Это также удовлетворяет требованию минимального поперечного сечения звеньев.

Расчет расчетного торсионного усиления

A _sv / S _v = T / [0,8x ₁ y ₁ (0,95f _yv )]

9000 3

x ₁ = наименьшее межцентровое расстояние сдвига звенья

x ₁ = 300 – 25 – 10/5 = 230 мм

x ₁ = наибольшее расстояние между центрами звеньев

x ₁ = 600 – 25 – 10/5 = 530 мм

S _v ≤ 157 x 0,8 x 230 x 530 x 0,95 x 460 = 334 мм

Обеспечить торсионную арматуру, торсионные звенья T10 на расстоянии 200 мм

Расчет дополнительной продольной арматуры

Можно использовать следующее уравнение, приведенное в BS 8110, часть 2.