Построение эпюр внутренних силовых факторов
Графики, показывающие, как изменяются внутренние усилия при переходе от сечения к сечению, называют эпюрами.
1. Построение эпюр продольных сил при растяжении (сжатии).
Растяжение или сжатие стержня вызывается силами, действующими вдоль его оси. В этом случае в поперечных сечениях возникает один внутренний силовой фактор — продольная сила . Для определения внутренней продольной силы используют метод сечений.
| Определим
продольную силу  .
Запишем уравнение равновесия для
оставшейся части: .
Запишем уравнение равновесия для
оставшейся части: |
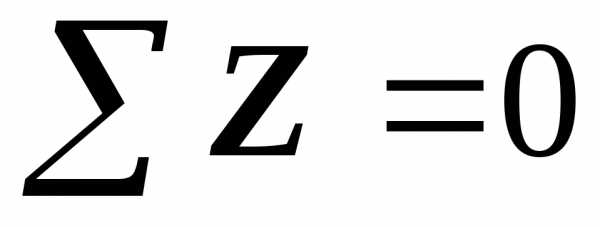
Рис. 19.
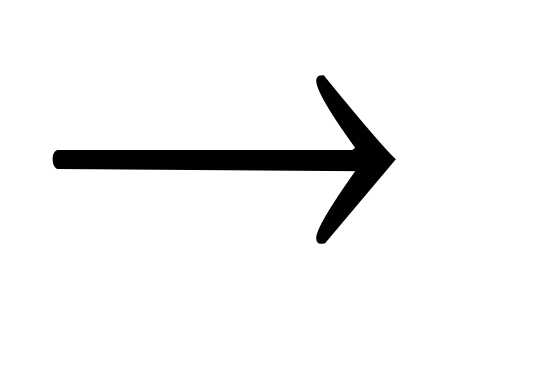
;
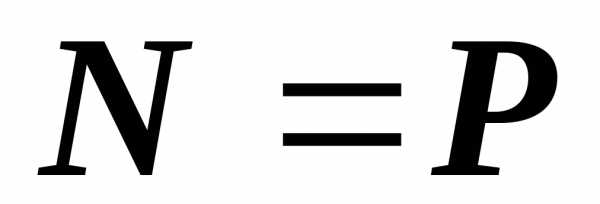 .
.  В случае растяжения
продольная сила считается положительной
и направлена от сечения.
В случае растяжения
продольная сила считается положительной
и направлена от сечения.
Пример: Для стержня
показанного на рис. 20 построить эпюру
продольных сил 
1. Определяем опорную реакцию в заделке:
 ;
;
2. Разбиваем стержень на участки. Границами участков являются точки приложения внешних сил.
3. Используя метод сечений, определяем продольную силу на каждом участке. Продольную силу на каждом участке будем направлять от сечения, предполагая, что она вызывает растяжение.
1 Уч-к: ;
;(раст.)
2 Уч-к: ;
; (раст.)
3
уч-к: 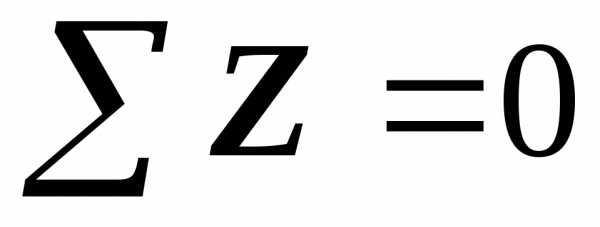 ;;
(сж.)
;;
(сж.)
Рассмотрим проверку определения продольной силы, например, на
3 -м участке, рассматривая стержень слева от сечения.
3
уч-к (слева):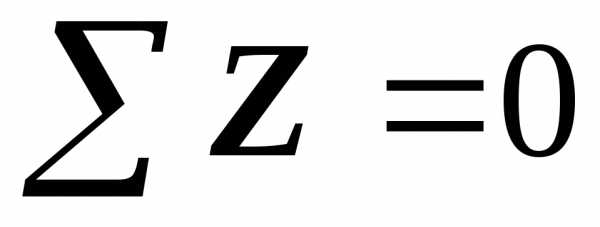 ;;(сж.)
;;(сж.)
Таким образом, можно рассматривать стержень с любой стороны от сечения.
4.
Строим эпюру продольных сил  .
.
5. Проверяем эпюру по скачкам и характеру линий (из практики).
На
основе метода сечений можно
сформулировать правило построения
эпюры  по характерным точкам:
по характерным точкам:
Продольная
сила 
 .
.2. Построение эпюр крутящих моментов.
Если внешняя нагрузка на стержень состоит только из моментов, плоскости которых перпендикулярны к его оси, то имеет место деформация кручения (рис. 21).
| Брус,
работающий на кручение, называется валом.
В этом случае в поперечных сечениях
возникает внутренний силовой фактор
— крутящий момент |
Рис. 21
На практике часто бывают заданы не моменты ,
приложенные к дискам, шкивам или
зубчатым колесам, а передаваемые на
них или снимаемые с них мощности
,
приложенные к дискам, шкивам или
зубчатым колесам, а передаваемые на
них или снимаемые с них мощности
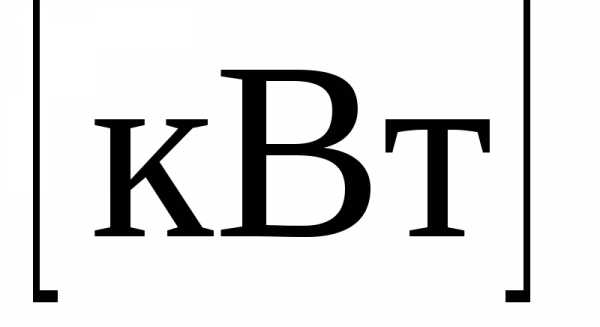 и частота вращения вала
и частота вращения вала
 .
Между этими величинами существует
зависимость:
.
Между этими величинами существует
зависимость:
 .
Если задана угловая скорость вращения
вала
.
Если задана угловая скорость вращения
вала
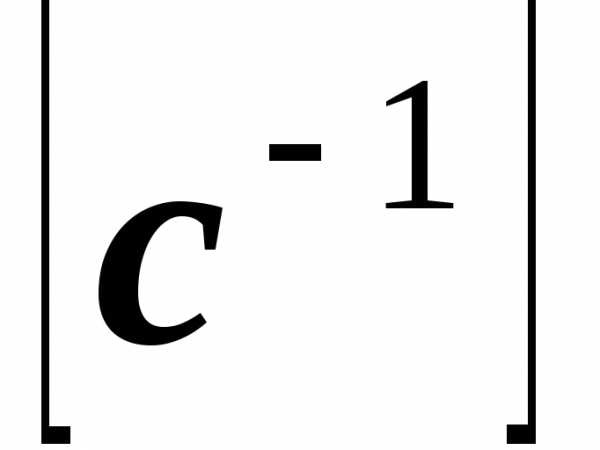 ,
то
,
то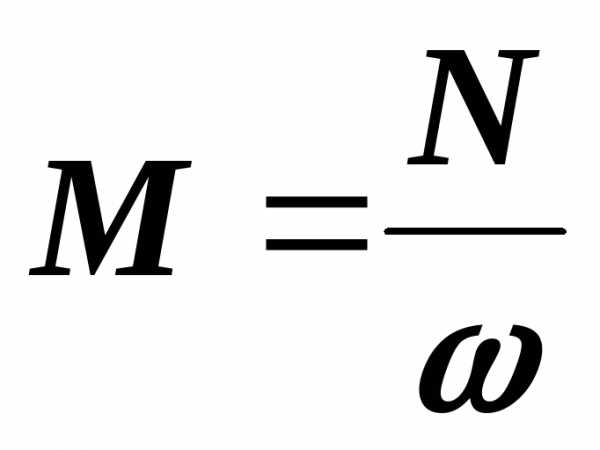
 .
. На
основе метода сечений можно
сформулировать правило построения
эпюр внутренних крутящих моментов 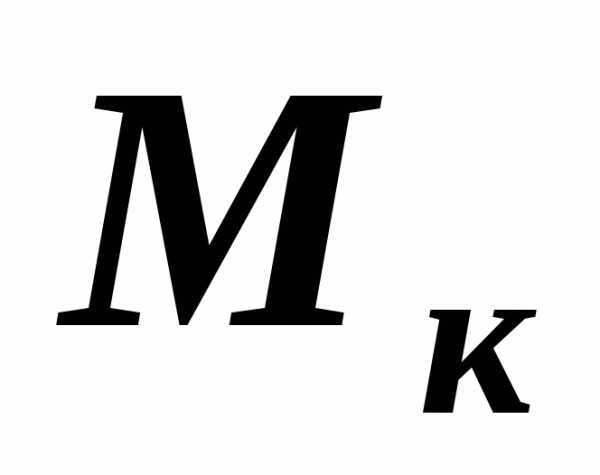 .
.
Крутящий
момент 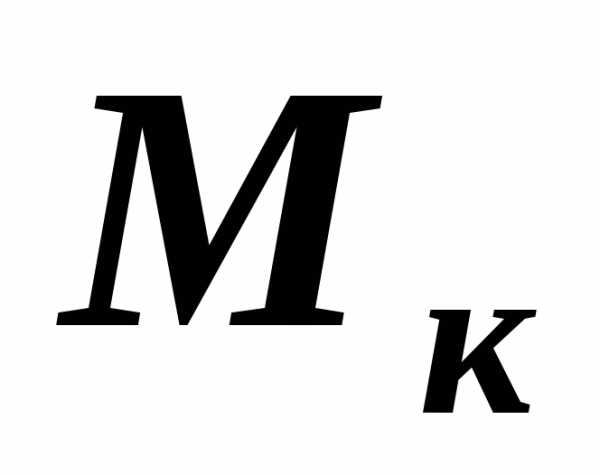 в сечении равен алгебраической сумме
внешних скручивающих моментов
в сечении равен алгебраической сумме
внешних скручивающих моментов
 .
. Эпюры
крутящих моментов строятся аналогично
эпюрам продольных сил. Правила
проверки построения эпюр  аналогичны правилам проверки эпюр
аналогичны правилам проверки эпюр .
.
studfiles.net
СТУДЕНТУ построение эпюр ВСФ — Стр 2
Сабанаев И.А., Алмакаева Ф.М. МАХП и ПСМ НХТИ КГТУ
2. В сечении, в котором приложен внешний сосредоточенный момент, на эпюре внутреннего момента Mx должен быть скачок(ступенька) на величину и направление этого момента.
3.На концах балки внутренний момент должен быть равен нулю, если нет внешнего момента.
4.В промежуточном шарнире изгибающий момент равен нулю, поэтому эпюра Мх
вшарнире должна пройти через ноль, т.е. пересечь ось.
5.На участке, на котором приложена равномерно распределенная нагрузка, эпюра Qy – наклонная прямая линия, а эпюра Мх – парабола.
6.На участке, на котором эпюраQy – положительна, эпюра Мх возрастает, Qy отрицательна – Мх убывает, Qy равна нулю – Мх постоянная прямая.
7.В сечении, в котором эпюра Qy пересекает ось, эпюра Мх обязательно имеет экстремум.
Шестое и седьмое правила являются следствием теоремы Журавского, согласно
которой поперечная сила есть первая производная от изгибающего момента по координате:
dMdzx =( M x )’ = Qy .
Примеры построения эпюр ВСФ при плоском изгибе
Пример 8. Построим эпюры ВСФ для балки, изображенной на рис. 7. Опорные реакции для нее мы вычислили в примере 1.
l, q – заданы, RA = RB = 0,5 ql
Для вычисления ВСФ применяем метод сечений. Балка содержит всего один участок. В произвольном месте на этом участке проведем сечение. Начало координат расположим, например, в точке А.
Чтобы показать, что сечение проведено действительно в произвольном месте участка, покажем, что расстояние до сечения есть величина переменная«Z» (рис. 28), которая может принимать любое значение в диапазоне 0 £ Z £ l.
|
| Y |
|
|
R | B |
| q | RA |
|
| |||
|
|
|
| |
HB | В |
| А | |
|
|
| l | Z |
|
|
|
| |
|
|
| Z |
|
Рис. 28. Схема для расчета ВСФ к примеру 8
Теперь отбросим правую часть балки и вычислим ВСФ в сечении, применяя метод сечений.
Поперечная сила в сечении равна сумме двух внешних сил, оставшихся в левой части бруса – это сосредоточенная силаRA и сила, возникающая от действия распределенной нагрузки q.
Опорная реакция в уравнение будет подставлена со знаком«+» в соответствии с правилом знаком для Qy (рис. 25), а распределенная нагрузка – со знаком минус.
Полная сила от действия нагрузки рассчитывается как площадь прямоугольника: высота фигуры q, а ширина – расстояние от т.В до сечения, т.е. Z (рис. 29).
studfiles.net
Построение эпюр внутренних силовых факторов
Графики, показывающие, как изменяются внутренние усилия при переходе от сечения к сечению, называют эпюрами.
1. Построение эпюр продольных сил при растяжении (сжатии).
Растяжение
или сжатие стержня вызывается силами,
действующими вдоль его оси. В этом
случае в поперечных сечениях возникает
один внутренний силовой фактор —
продольная сила  .
Для определения внутренней продольной
силы используют метод сечений.
.
Для определения внутренней продольной
силы используют метод сечений.
| Определим
продольную силу |
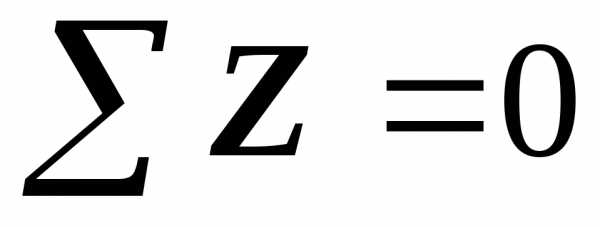
Рис. 19.
;
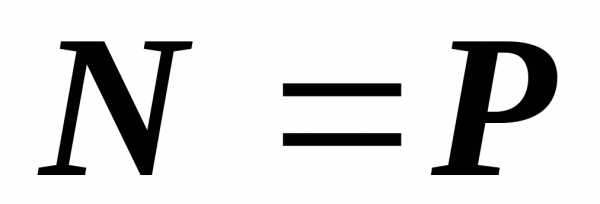 .
.  В случае растяжения
продольная сила считается положительной
и направлена от сечения.
В случае растяжения
продольная сила считается положительной
и направлена от сечения.
Пример: Для стержня
показанного на рис. 20 построить эпюру
продольных сил  .
.
1. Определяем опорную реакцию в заделке:
 ;
;
2. Разбиваем стержень на участки. Границами участков являются точки приложения внешних сил.
3. Используя метод сечений, определяем продольную силу на каждом участке. Продольную силу на каждом участке будем направлять от сечения, предполагая, что она вызывает растяжение.
1 Уч-к: ;
;(раст.)
2 Уч-к: ;
; (раст.)
3
уч-к:  ;;
(сж.)
;;
(сж.)
Рассмотрим проверку определения продольной силы, например, на
3 -м участке, рассматривая стержень слева от сечения.
3
уч-к (слева):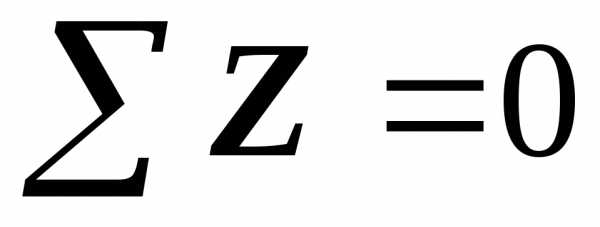 ;;(сж.)
;;(сж.)
Таким образом, можно рассматривать стержень с любой стороны от сечения.
4.
Строим эпюру продольных сил  .
.
5. Проверяем эпюру по скачкам и характеру линий (из практики).
На
основе метода сечений можно
сформулировать правило построения
эпюры  по характерным точкам:
по характерным точкам:
Продольная
сила  в сечении равна алгебраической сумме
внешних сил, действующих по одну
сторону от сечения. Если внешняя
сила направлена от сечения, то она
вызывает растяжение и дает положительное
слагаемое в выражении для внутренней
продольной силы
в сечении равна алгебраической сумме
внешних сил, действующих по одну
сторону от сечения. Если внешняя
сила направлена от сечения, то она
вызывает растяжение и дает положительное
слагаемое в выражении для внутренней
продольной силы .
.
2. Построение эпюр крутящих моментов.
Если внешняя нагрузка на стержень состоит только из моментов, плоскости которых перпендикулярны к его оси, то имеет место деформация кручения (рис. 21).
| Брус,
работающий на кручение, называется валом.
В этом случае в поперечных сечениях
возникает внутренний силовой фактор
— крутящий момент |
Рис. 21
На практике часто бывают заданы не моменты ,
приложенные к дискам, шкивам или
зубчатым колесам, а передаваемые на
них или снимаемые с них мощности
,
приложенные к дискам, шкивам или
зубчатым колесам, а передаваемые на
них или снимаемые с них мощности
 и частота вращения вала
и частота вращения вала
 .
Между этими величинами существует
зависимость:
.
Между этими величинами существует
зависимость: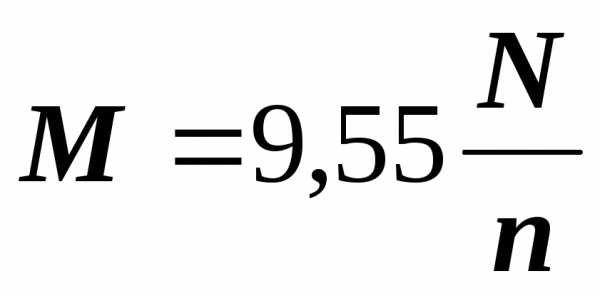
 .
Если задана угловая скорость вращения
вала
.
Если задана угловая скорость вращения
вала
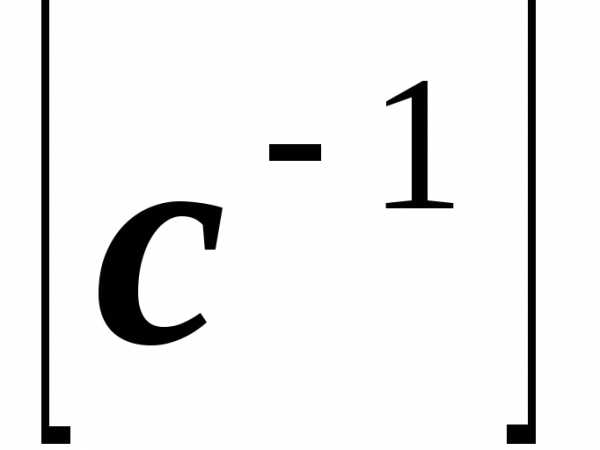 ,
то
,
то
 .
. На
основе метода сечений можно
сформулировать правило построения
эпюр внутренних крутящих моментов 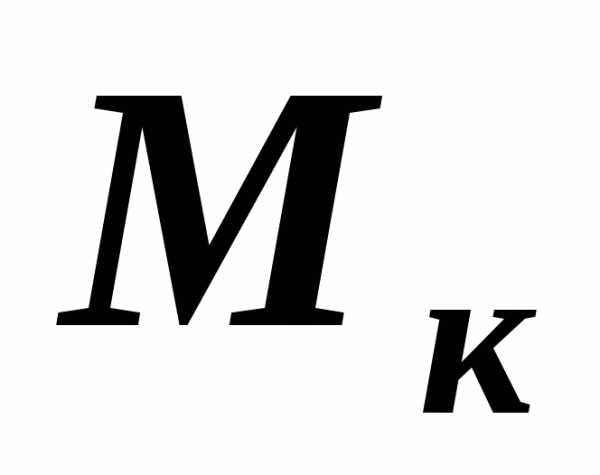 .
.
Крутящий
момент  в сечении равен алгебраической сумме
внешних скручивающих моментов
в сечении равен алгебраической сумме
внешних скручивающих моментов ,
действующих по одну сторону от
сечения. Если при взгляде на вал со
свободного торца внешний момент
стремится повернуть сечение против
часовой стрелки, то он дает
положительное слагаемое в выражении
для внутреннего крутящего момента
,
действующих по одну сторону от
сечения. Если при взгляде на вал со
свободного торца внешний момент
стремится повернуть сечение против
часовой стрелки, то он дает
положительное слагаемое в выражении
для внутреннего крутящего момента .
.
Эпюры
крутящих моментов строятся аналогично
эпюрам продольных сил. Правила
проверки построения эпюр  аналогичны правилам проверки эпюр
аналогичны правилам проверки эпюр .
.
studfiles.net
Задача 1.7 Построение эпюр внутренних силовых факторов при плоском изгибе
Для двух схем, указанных на рис. 1.7.1, требуется построить эпюры поперечных сил и изгибающих моментов. Числовые данные приведены в табл. 1.7.1.
Таблица 1.7.1
Числовые данные для задачи 1.7
№ варианта | А, м | q, кН/м | F, кН | M, кНм |
1 | 0,5 | 20 | 15 | 5 |
2 | 0,7 | 15 | 20 | 10 |
3 | 0,9 | 10 | 25 | 15 |
4 | 1,0 | 5 | 30 | 20 |
5 | 0,1 | 25 | 10 | 25 |
6 | 0,3 | 30 | 5 | 30 |
7 | 0,5 | 5 | 5 | 35 |
8 | 0,7 | 10 | 15 | 40 |
9 | 0,9 | 15 | 10 | 45 |
10 | 1,0 | 20 | 30 | 50 |
I | |
II | |
III F | |
IV | |
V | |
VI | |
VII Рис. 1.7.1. | |
VIII | q |
IX q | F |
X | M F q |
Продолжение рис.1.7.1.
Пример решения и методические указания к задаче 1.7
Для однопролетной балки с двумя консолями, схема которой показана на рис. 1.7.2 построить эпюры поперечных сил и изгибающих моментов.
Дано:  .
.
Рис. 1.7.2
Решение
1. Определяем реакции опор. Для этого вычерчиваем расчетную схему (рис. 1.7.3, а). Направление реакций опор выбираем произвольно.
Выбираем направление координатных осей (рис. 1.7.3, а). Составляем уравнения равновесия для плоской системы:
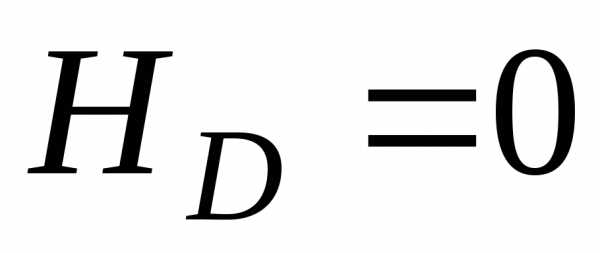
а
б
в
Рис. 1.7.3
Знак «–» говорит о том, что реакция RD на самом деле направлена вниз. Поэтому изменяем направление данной реакции на рис. 7.3, а.
Выполняем проверку:

Значит расчет выполнен верно.
2. Определяем количество участков.
Начало новому участку дает:
а) каждое изменение закона распределения нагрузки
б) каждое изменение закона распределения площади поперечного сечения.
в) излом.
Балка имеет четыре участка.
3. Методом сечений определяем в пределах каждого участка законы распределения поперечных сил Qy и изгибающих моментов Mz и строим эпюры поперечных сил (рис. 1.7.3, б) и изгибающих моментов (рис. 1.7.3, в).
Первый участок .
Произвольно проводим сечение 1-1 (рис. 1.7.3, а).
Отбрасываем правую часть балки. При расчетах целесообразно оставлять ту часть балки, относительно которой удобнее вести расчет.
Заменяем действие правой части балки внутренними усилиями Qy1 и Mz1, возникающими в поперечном сечении 1-1. Положительные направления для поперечной силы и изгибающего момента указаны на рис. 1.7.4. Следует помнить, что студенты-механики должны всегда строить эпюры изгибающих моментов на сжатых волокнах.
Рис. 1.7.4
Из условия равновесия левой части балки (рис. 1.7.5) запишем выражения для Qy1 и Мz1:
Рис. 1.7.5
Второй участок
Рассмотрим равновесие левой части балки относительно сечения 2-2 (рис. 1.7.6) чтобы определить выражения для Qy2 и Мz2
Рис. 1.7.6
Данное выражение – это уравнение наклонной прямой. Для построения данной линии необходимо определить значение Qy2 в двух точках. Возьмем точки соответствующие началу и концу участка.
При  ,
,
при 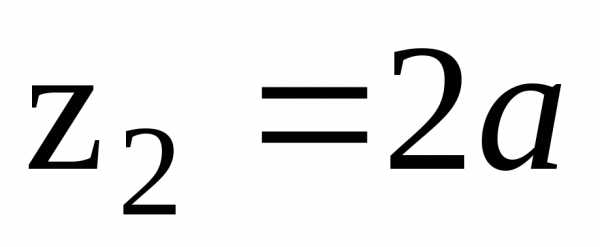
Разные знаки Qy2 в сечениях при  и
и говорят о том, что эпюраQz на данном
участке пересекает ось z,
а в том сечении, где эпюра поперечных
сил меняет знак, как известно, эпюра М принимает
экстремальное значение. Поэтому
необходимо определить данное сечение.
С этой целью выражение для Qy приравняем
нулю.
говорят о том, что эпюраQz на данном
участке пересекает ось z,
а в том сечении, где эпюра поперечных
сил меняет знак, как известно, эпюра М принимает
экстремальное значение. Поэтому
необходимо определить данное сечение.
С этой целью выражение для Qy приравняем
нулю.
,
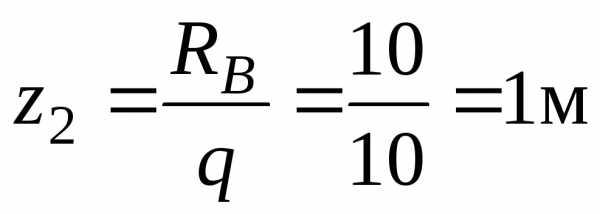 ,
,
.
Полученное выражение – уравнение параболы. Для построения данной линии необходимо определить значение Mz2, как минимум, в 3-х точках:
при  ;
;
при  ;
;
при 
Третий участок
Рассмотрим равновесие правой части балки относительно сечения 3-3 (рис. 1.7.7).
Рис. 1.7.7
Составим выражения
для  и
и :
:
при 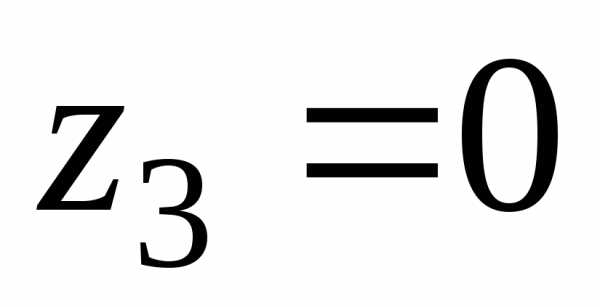 ;
;
при  .
.
Четвертый участок .
Составим выражения
для  и
и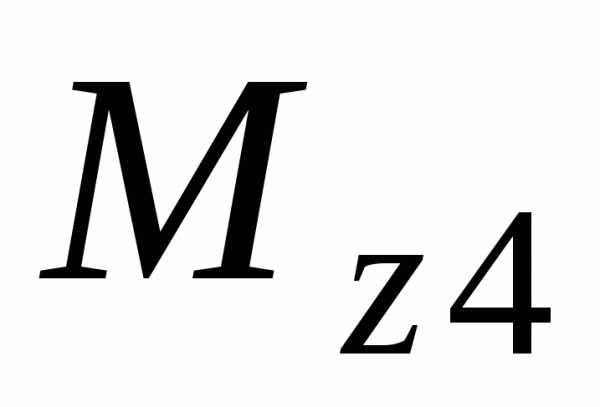 ,
рассмотрев равновесие правой части
балки относительно сечения 4-4 (рис.
1.7.8)
,
рассмотрев равновесие правой части
балки относительно сечения 4-4 (рис.
1.7.8)
Рис. 1.7.8
,
при 
 ,
,
при  .
.
Отличительной особенностью построения эпюр поперечных сил и изгибающих моментов для балки защемленной одним концом от однопролетной балки с двумя консолями является определение реакций опор. Рассмотрим это на примере. Определим реакции для балки, представленной на рис. 1.7.9.
Рис. 1.7.9
Выбираем направление координатных осей и заменяем жесткую заделку реакциями RA, HA и МА (рис. 1.7.10). Направление реакций выбираем произвольно.
Рис. 1.7.10
Составляем уравнения равновесия для плоской системы:
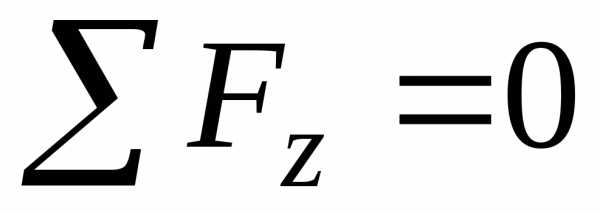
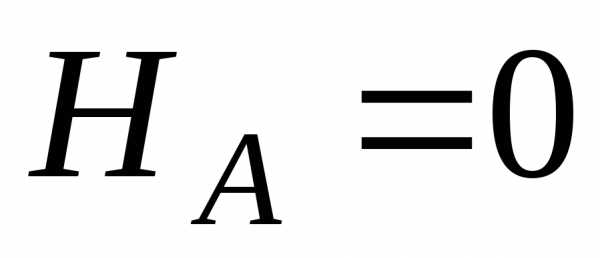
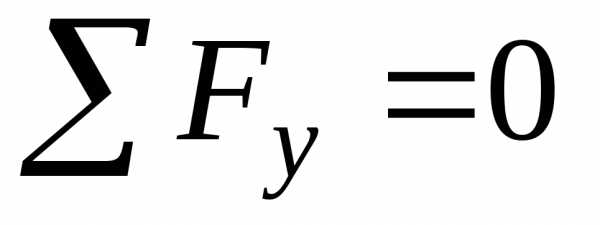
.
Выполняем проверку:
Значит расчет выполнен верно.
Остальные пункты расчета для балки, защемленной одним концом, совпадают с пунктами расчета для однопролетной балки с двумя консолями, изложенными выше.
Следует отметить, что реакции опор в балках с жестким защемлением на первом этапе можно не определять, а начать расчет со свободного конца путем построения эпюр можно прийти к значениям силовых факторов (RA, HA, MA).
studfiles.net
1.2. Построение эпюр внутренних силовых факторов
Видно, что вал работает на совместное действие растяжения (сжатия), кручения и изгиба в вертикальной (ух) и горизонтальной (zx) плоскостях. Рассмотрим каждую деформацию отдельно, используя принцип независимости действия сил.
Определим опасную точку вала. Для этого установим, как меняются по длине вала внутренние силовые факторы, т.е. построим их эпюры.
Растяжение (сжатие). Вал нагружен двумя сосредоточенными продольными силами N1 и реакцией RCx=N1 в опоре С, которые вызывают на участке Cd сжатие. Построим эпюру нормальных сил ЭN.
Кручение. Два скручивающих момента Т1 и Т2 вызывают кручение на участке AD. Эпюру крутящих моментов ЭТ строим так же, как и при чистом кручении.
Изгиб в вертикальной плоскости ух. Эпюра ЭМz изгибающих моментов относительно оси z строится от сил Р2y, R1, RCy и RBy и изгибающего момента МN1, действующих в вертикальной плоскости. Из уравнений статического равновесия определим RCy и RBy:
MC(Fi)= –P2yl1+RBy l1 +l2+ l3)–MN1-R1 l1 +l2)=0;
MB(Fi)= P2yl2+ l3)–RCy l1 +l2+ l3)-MN1+R1l3 =0.
откуда
H;
H.
Проверим правильность определений реакций. Для этого запишем уравнения статического равновесия в виде суммы проекций всех сил Fi на ось у:
Y(Fi)=–P2y+RCy+RBy–R1=-6755+5103.6+2597.8-946.4=0
Следовательно, реакции RCy и RВу найдены верно.
Так как балка нагружена только сосредоточенными силовыми факторами, то изгибающий момент Мz на всех участках будет постоянен или меняться по линейному закону. Вычислим изгибающие моменты Mz в сечениях А, С, D и В:
MzC= 0 Нм;
MzD= RCy l1 =5103.6*0.25=1275.9 Нм;
MzA= RCyl1 + l2 )- P2y*l2 =5103.6*(0.25+0.4)-6755*0.4=615.34 Нм;
MzB= 0 Нм.
По полученным значениям строим эпюру ЭМz.
Изгиб в горизонтальной плоскости zx. Эпюра ЭМу изгибающих моментов относительно оси у строится от сил Р1 и P2z. Из уравнений статического равновесия определим реакции в опорах С и B (RCz и RBz):
MC(Fi)= -P1l1 + l2)+RBz l1 +l2 + l3 )+P2zl1=0;
MB(Fi)= –P2zl2 + l3 ) –RCz l1 +l2 + l3 )+P1l3 =0.
откуда
H;
H.
Для проверки правильности определения реакций запишем уравнения статического равновесия в виде суммы проекций всех сил Fi на ось z:
Z(Fi)=P2z+RCz+RBz–P1=3900-2052.63+752.63-2600=0
Следовательно, реакции RCz и RВz найдены верно.
Изгибающий момент Му на всех участках будет постоянен или меняться по линейному закону, так как балка нагружена только сосредоточенными силовыми факторами. Вычислим изгибающие моменты Mу в сечениях А, С, D и В:
MyC=0;
MyD= RCzl1=-2052.63*0.25=-513.16 Нм;
MyA= RCz (l1+l2)+P2zl2=-2052.63(0.25+0.4)+3900*0.4=225.79 Нм;
MzB= 0.
По полученным значениям строим эпюру ЭМz.
Построение эпюры суммарных изгибающих моментов. Поскольку вал имеет круглое поперечное сечение, определим в сечениях величину суммарного изгибающего момента . В сечениях А, С,D и В их значения будут соответственно равны
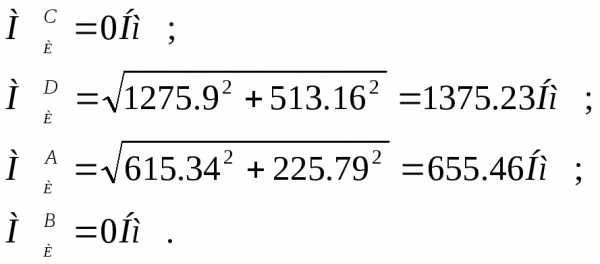
По полученным данным построим эпюру суммарных изгибающих моментов ЭМИ.
1.3. Расчет диаметра вала
Для определения опасного сечения находим величины эквивалентных моментов по третьей теории прочности . Тогда в сечениях А,C, D и В вала:

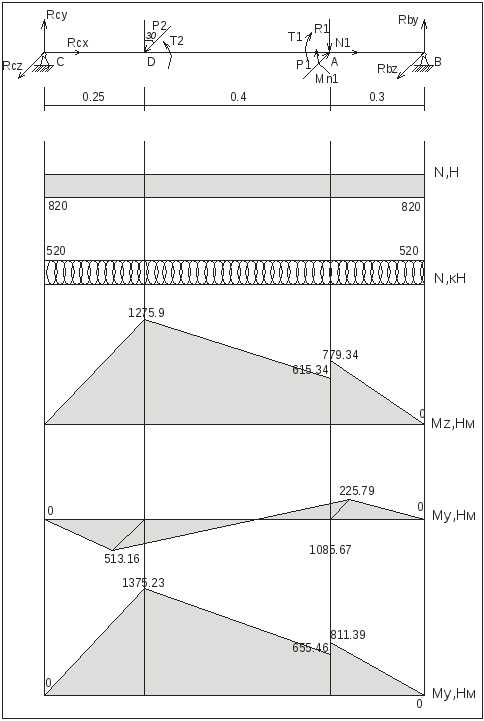
Анализ результатов показывает, что опасным является сечение С, в котором эквивалентный момент достигает максимального значения и равен Мэкв max=1470.26 Нм.
Найдем
допускаемое напряжение  Так как сталь 12Xh4A
пластична, то за пред принимаем Т.
Согласно [3, с.648] Т=800
МПа, коэффициент запаса для пластичных
материалов n=1.52.
Примем n=2,
тогда
Так как сталь 12Xh4A
пластична, то за пред принимаем Т.
Согласно [3, с.648] Т=800
МПа, коэффициент запаса для пластичных
материалов n=1.52.
Примем n=2,
тогда  МПа.
МПа.
Из условия прочности
,
где
Wос=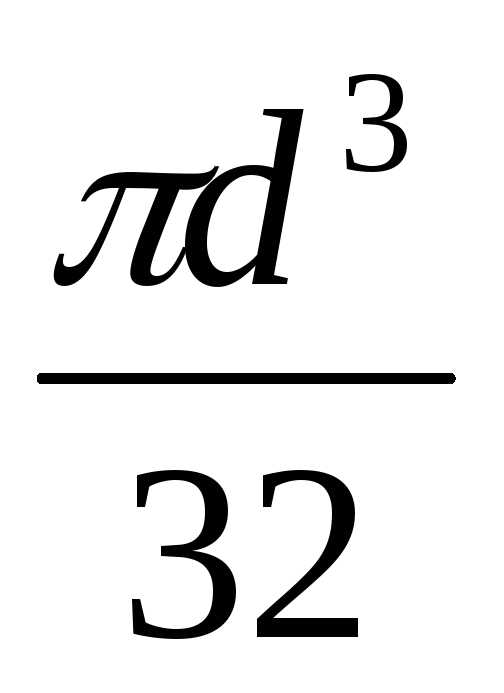 – осевой момент сопротивления для
круглого поперечного сечения диаметромd,
определим расчетный диаметр вала
– осевой момент сопротивления для
круглого поперечного сечения диаметромd,
определим расчетный диаметр вала
В соответствии с ГОСТ 6636-69 (ряд Ra40) округляем dрасч до ближайшего большего значения и принимаем d=34 мм.
Вычислим геометрические характеристики этого сечения:
— площадь поперечного сечения ;
— осевой момент инерции ;
— осевой момент сопротивления ;
— полярный момент инерции ;
— полярный момент сопротивления .
Рассмотрим опасное сечение вала, в котором действует суммарный изгибающий момент МИ=1375.23 Нм, крутящий момент Т=520 Нм и продольная сила N=820 Н.
Нормальные
напряжения от изгиба И определяются по формуле 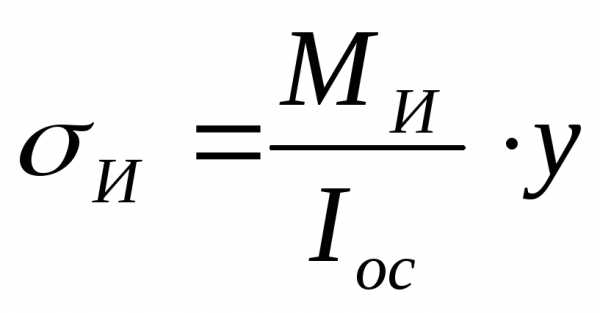 .
На внешних волокнах в точках А и В они
наибольшие и равныМПа.
.
На внешних волокнах в точках А и В они
наибольшие и равныМПа.
Нормальные напряжения от растяжения [1] определим как МПа. Касательные напряжения по сечению меняются по линейному закону [1] (r – расстояние от центра сечения до точки, в которой определяем напряжение). Максимальные напряжения возникают на контуре сечения
МПа.
Построим эпюры этих напряжений ЭИ, Эр, Э.
В опасной точке А имеет место плоское напряженное состояние. В этой точке действуют максимальные эквивалентные напряжения экв max. Определим их по III теории прочности:
МПа
Видно, что условие прочности экв max[] выполняется,
так как 378.42 МПа<400 МПа.
Определим недогрузку вала , учитывая, что диаметр вала выбран больше расчетного:
.
Недогрузка меньше 15%. Таким образом, диаметр вала d=34 мм из условия статической прочности подобран правильно.
studfiles.net
Построение эпюр внутренних силовых факторов — КиберПедия
Растяжение (сжатие). Вал нагружен двумя сосредоточенными продольными силами: N1 и реакцией RCz = N1 в опоре С (рис. 5.2, б), которые вызывают на участке CD растяжение. Построим эпюру нормальных сил ЭN (рис. 5.2, в).
Кручение. Два скручивающих момента T1 и T2(рис. 5.2, г) вызывают кручение на участке АD. Эпюру крутящих моментов ЭT строим так же, как и при чистом кручении (рис. 5.2, д).
Изгибв вертикальной плоскостиyz (рис. 5.2, е). Эпюра ЭMx изгибающих моментов строится от сил Р2, R1, RCy и RBy и изгибающего момента , действующих в вертикальной плоскости. Из уравнений статического равновесия определим RCy и RDy:
откуда
Проверим правильность определения реакций. Для этого запишем уравнения статического равновесия в виде суммы проекций всех сил на ось Ax:
.
Следовательно, реакции и определены верно.
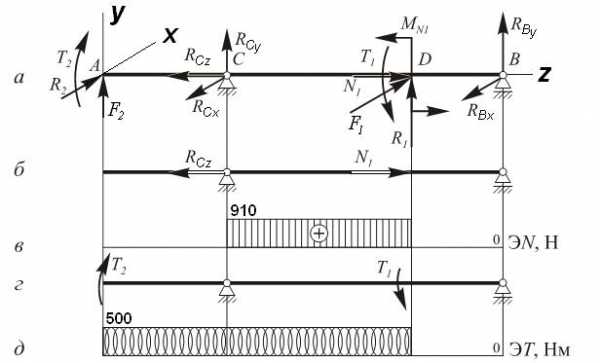
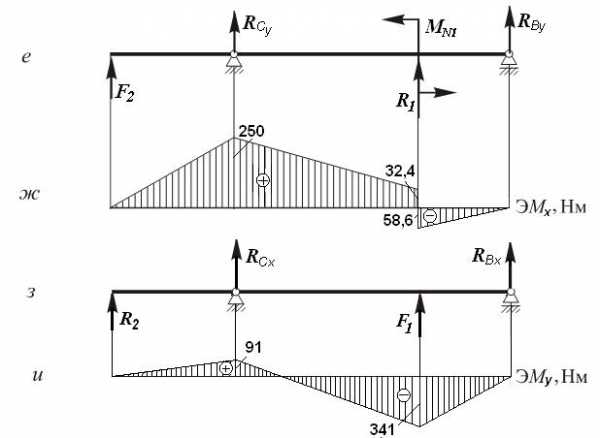
Рис. 5.2
Так как балка нагружена только сосредоточенными силовыми факторами, то изгибающий момент Mxна всех участках будет постоянен или меняться по линейному закону. Вычислим изгибающие моменты Mx в сечениях A, C, D и B:
По полученным значениям строим эпюру ЭMx (рис. 5.2, ж).
Изгибв горизонтальной плоскостиzx (рис. 5.2, з). Эпюра ЭMy изгибающих моментов относительно оси y строится от сил F1и R2. Из уравнений статического равновесия определим реакции в опорах C и D (RCx и RDx ):
;
,
откуда
Н;
Н.
Для проверки правильности определения реакций запишем уравнения статического равновесия в виде суммы проекций всех сил Fiна ось y:
.
Следовательно, реакции и найдены верно.
Изгибающий момент Myна всех участках будет постоянен или меняться по линейному закону, так как балка нагружена только сосредоточенными силовыми факторами. Вычислим изгибающие моменты My в сечениях A, C, D и B:
;
Нм;
Нм;
.
По полученным значениям изгибающих моментов строим эпюру ЭMy (рис. 5.2, и).
Построение эпюры суммарных изгибающих моментов.Поскольку вал имеет круглое поперечное сечение, определим в сечениях величину суммарного изгибающего момента . В сечениях A, C, D и B их значения будут соответственно равны
;
;
.
По полученным данным построим эпюру суммарных изгибающих моментов ЭMи (рис. 5.2, к).
Расчет диаметра вала
Для определения опасного сечения находим величины эквивалентных моментов по третьей теории прочности . Тогда сечениях A, C, D и В вала:
;
;
.
Анализ результатов показывает, что опасным является сечение С, в котором эквивалентный момент достигает максимального значения и равен .
Найдем допускаемое напряжение . Так как сталь 40ХН пластична, то за sпред принимаем предел текучести sТ.. Согласно табл. П3 sТ = 750 МПа, коэффициент запаса для пластичных материалов n = 1,5¸2,5. Примем n = 2, тогда .
Из условия прочности
,
где – осевой момент сопротивления для круглого поперечного сечения диаметром d, определим расчетный диаметр вала
мм.
В соответствии с ГОСТ 6636-69 (табл. П4, Ra40) округляем dрасч до ближайшего большего значения и принимаем d = 26 мм. Вычислим геометрические характеристики этого сечения:
— площадь поперечного сечения м2;
— осевой момент инерции м4;
— осевой момент сопротивления м3;
— полярный момент инерции = м4;
— полярный момент сопротивления
м3.
Рассмотрим опасное сечение вала D, в котором действуютсуммарный изгибающий момент Ми = 342 Нм, крутящий момент Т = 500 Нм и продольная сила N = 910 Н (рис. 5.3).
Нормальные напряжения от изгиба определяются по формуле . ( – осевой момент инерции, у – координата точки сечения по оси y). На внешних волокнах (в точке K, рис. 5.3) они равны .
Нормальные напряжения от растяжения определим как МПа. Касательные напряжения .
Построим эпюры этих напряжений Э , Э , Э (рис. 5.3).
В опасной точке А имеет место плоское напряженное состояние (рис. 5.3, в). В этой точке действуют максимальные эквивалентные напряжения sэкв max. Определим их по III теории прочности:
МПа.
Видно, что условие прочности выполняется, так как 352 МПа < 375 МПа.
Определим недогрузку вала, учитывая, что диаметр вала выбран больше расчетного:
.
Недогрузка Ds меньше допустимого значения 15%. Таким образом, диаметр вала подобран правильно.
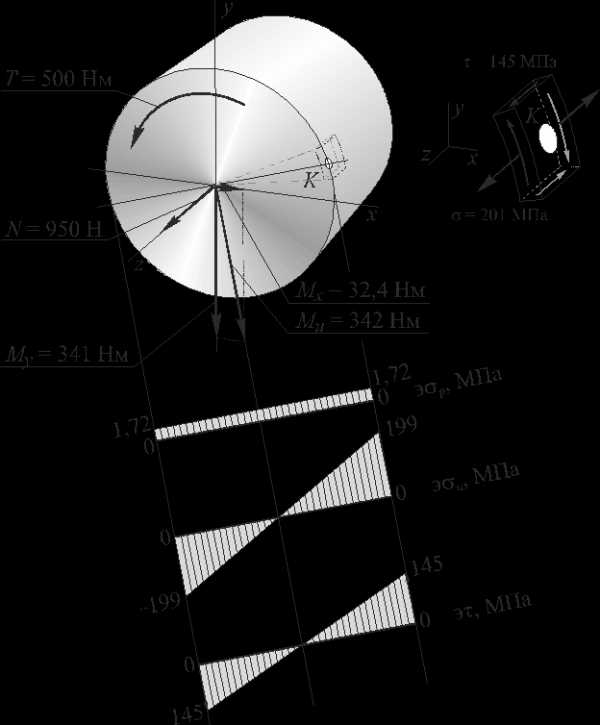
Рис. 5.3
Расчет вала на жесткость
В расчетах примем модуль упругости (стали) E = 210 ГПа, жесткость сечения EJoc = 210·109·2,24·10-8= 4704 Нм2. Для определения перемещений используем способ Верещагина [2].
cyberpedia.su
Общие правила построения эпюр внутренних силовых факторов
В общем случае при действии внешних нагрузок в поперечных сечениях элементов конструкции возникают три внутренних силовых фактора: поперечная сила Q, продольная сила N и изгибающий момент M.
Продольная сила N в произвольном поперечном сечении балки численно равна алгебраической сумме проекций на ось балки всех сил, действующих по одну сторону от рассматриваемого сечения.
Поперечная сила Q в произвольном поперечном сечении балки численно равна алгебраической сумме проекций на нормаль к оси балки всех сил, действующих по одну сторону от рассматриваемого сечения.
Изгибающий момент М в произвольном поперечном сечении балки численно равен алгебраической сумме моментов всех сил, действующих по одну сторону от рассматриваемого сечения.
Для определения внутренних силовых факторов используется метод сечений. При построении эпюр необходимо руководствоваться правилами знаков поперечных, продольных сил и изгибающих моментов (рисунок 2.1):
– продольная сила N считается положительной, если внешние силы относительно рассматриваемого сечения вызывают растяжение;
– поперечная сила Q считается положительной, если внешние силы относительно рассматриваемого сечения вращают отсеченную часть балки по ходу часовой стрелки;
– изгибающий момент M считается положительным, если внешние нагрузки относительно рассматриваемого сечения растягивают нижние волокна.
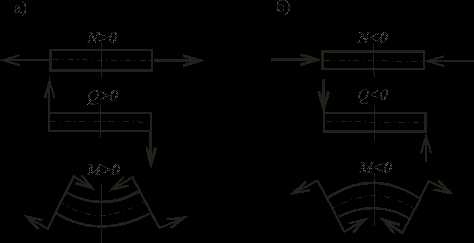
Рисунок 2.1 – Правило знаков внутренних силовых факторов
Для определения величины опорных реакций применяют три известных уравнения статики:
, , ,
где А, В – моментные точки, которыми чаще всего выступают опоры.
Причем последнее уравнение служит для проверки правильности определения неизвестных реакций. Следует также отметить, что если в результате расчета реакция получается отрицательной, то ее направление на расчетной схеме изменяют на противоположное, а само значение реакции при этом будет положительным.При составлении уравнений статики для определения опорных реакций рекомендуется придерживаться правил, принятых в теоретической механике, или же следующих правил знаков:
— сила принимается положительной, если ее направление совпадает с выбранным положительным направлением координатной оси;
— моменты сил, вращающие в одну сторону относительно моментной точки, имеют одинаковый знак.
Построение эпюр внутренних силовых факторов в системах с жестким защемлением производится без определения реакций, действующих в заделке, путем рассмотрения характерных участков конструкции со свободного (незащищенного) конца.
Границами характерных участков балки являются опорные сечения, точки приложения сосредоточенных сил или моментов, начало и окончание действия распределенной нагрузки. В рамах к характерным сечениям относятся также узлы. На каждом участке проводится произвольное сечение на расстоянии z от начала соответствующего участка, составляются в общем виде выражения для действующих ВСФ с учетом правила знаков, и в полученные выражения подставляются границы характерного сечения. Полученные значения ВСФ откладываются на соответствующих эпюрах под характерными участками перпендикулярно нулевой линии.
После построения эпюр производится контроль правильности их построения:
а)Если участок балки нагружен сосредоточенной силой, то эпюра поперечных сил на данном участке будет очерчена прямой линией, параллельной нулевой линии эпюры. Изгибающий момент на участке будет изменяться по линейному закону.
б) На участках с распределенной нагрузкой эпюра очерчивается прямой наклонной линией, а эпюра – квадратной параболой с выпуклостью, направленной навстречу действию распределенной нагрузки. Если на участке с эпюра пересекает нулевую линию эпюры, то под этой точкой пересечения изгибающий момент будет иметь экстремальной значение.
в) В сечении, где приложена внешняя сосредоточенная сила, на эпюре Q будет скачок на величину и в направлении действия этой внешней силы.
г) В сечении, где приложен внешний сосредоточенный момент, на эпюре М будет наблюдаться скачок на величину и в направлении действия этого внешнего момента.
В отличие от балок, ось рамы представляет собой ломаную линию. Нулевые линии эпюр также представляют в виде ломаных линий, а каждый характерный участок можно рассматривать как отдельную балку. При определении величин продольных и поперечных сил применяется правило знаков, представленное на рисунке 2.1. При построении эпюр Q и N положительные ординаты откладывают с внешней стороны контура рамы, а отрицательные – внутри контура. При составлении выражения изгибающего момента руководствуются произвольным правилом знаков. Например, все нагрузки, которые будут сжимать наружные волокна рамы, принимают со знаком «плюс». В любом случае, эпюра М строится со стороны сжатого волокна, причем знак на ней не указывается. Также следует помнить, что узлы рамы должны находиться в равновесии, то есть сумма изгибающих моментов в примыкающих к узлу сечениях должна равняться нулю или, если в этом узле приложен внешний сосредоточенный изгибающий момент, значению этого момента.
Пример построения эпюр внутренних силовых факторов для балки
Исходные данные: расчетная схема балки с указанием численных величин нагрузок и линейных размеров.
Требуется: построить эпюры внутренних силовых факторов.
В поперечных сечениях балки возникают два ВСФ: поперечная сила (Q) и изгибающий момент (M). Вычерчиваем заданную балку с указанием всех нагрузок и линейных размеров. Определяем реакции опор.
;
;
;
;
Проверка правильности определения реакций:
.
Разбиваем балку на участки, на каждом из которых проводим произвольное поперечное сечение на расстоянии z от начала соответствующего участка (см. рисунок 2.2, а). Изображаем нулевые линии для построения эпюр поперечных сил (эпюра Q) и эпюры изгибающего момента (эпюра М). Записываем в общем виде выражения для определения ВСФ для каждого участка балки и при помощи полученных уравнений рассчитываем их численные значения в характерных сечениях.
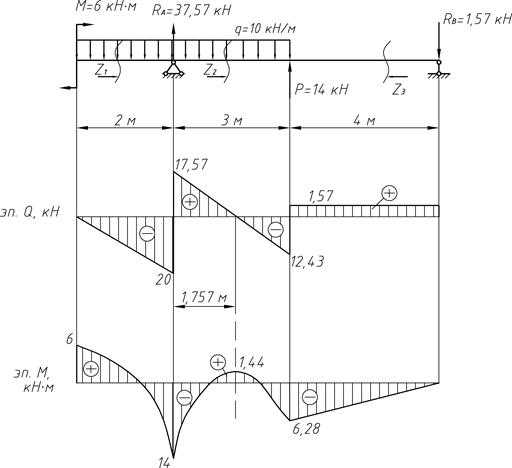
Рисунок 2.2 – Расчетная схема балки и эпюры внутренних силовых факторов
1 участок: .
;
.
2 участок: .
;
Так как на этом участке эпюра Q пересекает нейтральную линию, то в этой точке пересечения изгибающий момент будет иметь экстремальное значение:
;
откуда ;
.
3 участок: .
;
Полученные точки соединяем линиями, замыкающими поле эпюры. В поле эпюры в кружке ставим знак рассматриваемого внутреннего силового фактора и наносим штриховку. Линии штриховки перпендикулярны нулевой линии эпюры (рисунок 2.2, б, в).
Пример построения эпюр внутренних силовых факторов в раме
Исходные данные: расчетная схема рамы с указанием численных величин нагрузок и линейных размеров.
Требуется: построить эпюры внутренних силовых факторов.
Вычерчиваем заданную раму (рисунок 2.3, а) с указанием всех нагрузок и линейных размеров в численном виде. Определяем реакции опор:
;
;
;
;
;
.
Проверка правильности определения реакций:
.
Разбиваем раму на участки, на каждом из которых проводим произвольное поперечное сечение на расстоянии z от начала соответствующего участка (см. рисунок 2.3, а). Изображаем нулевые линии для построения эпюр нормальных (эпюра N) и поперечных (эпюра Q) сил, эпюры изгибающего момента (эпюра М).
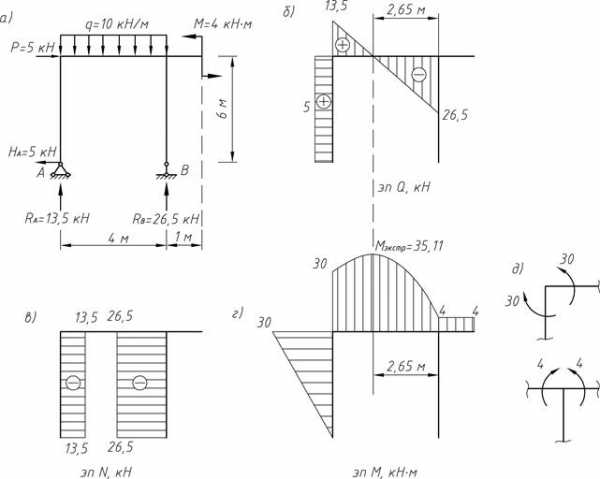
Рисунок 2.3 – Расчетная схема рамы и эпюры внутренних силовых факторов
Записываем в общем виде выражения для определения ВСФ для каждого участка рамы и при помощи полученных уравнений рассчитываем их численные значения в характерных сечениях рамы.
1 участок: .
;
;
.
2 участок: .
;
;
.
3 участок: .
;
;
.
4 участок: .
;
;
Так как на четвертом участке эпюра Q пересекает нулевую линию, требуется провести исследование на экстремум:
;
откуда ;
.
Строим эпюры поперечных и продольных сил, изгибающих моментов (рисунок 2.3, б−г). Проверяем равновесие узлов рамы (рисунок 2.3, д) – узлы уравновешены.
3 Расчетно-проектировочное задание №3. Расчет статически определимой балки при изгибе
infopedia.su
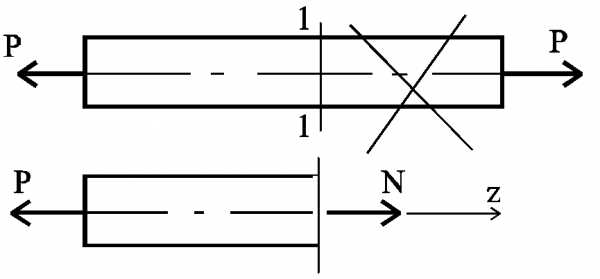
 в сечении
в сечении

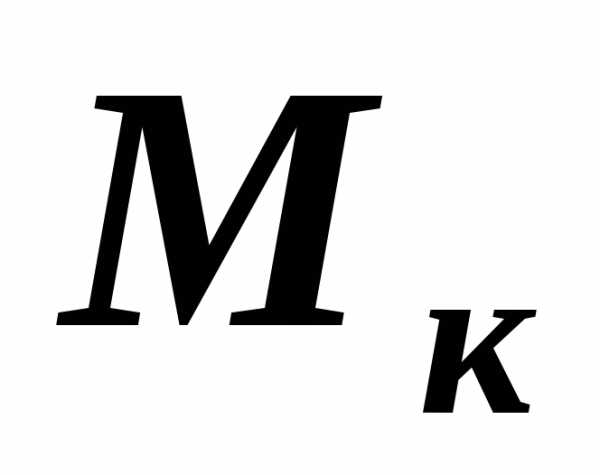

 в сечении
в сечении .
Рассечем стержень этим сечением
и отбросим одну из частей. Действие
отброшенной части заменим внутренней
продольной силой
.
Рассечем стержень этим сечением
и отбросим одну из частей. Действие
отброшенной части заменим внутренней
продольной силой .
Запишем уравнение равновесия для
оставшейся части:
.
Запишем уравнение равновесия для
оставшейся части:
 .
.