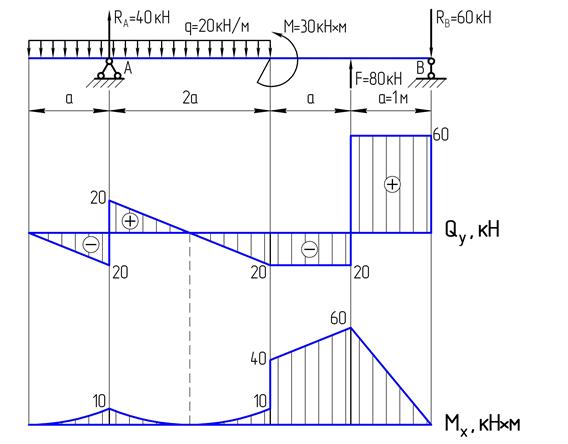
Онлайн построение эпюр изгибающих моментов: СОПРОМАТ ГУРУ. Расчет балки онлайн. Построение эпюр

Содержание

Расчет силовых нагрузок на вал и построение эпюр изгибающих моментов и крутящего момента

1. Домашнее задание по курсу «Детали машин» №4

«Проверочный расчет
тихоходного вала редуктора»

2. 1. Расчет силовых нагрузок на вал и построение эпюр изгибающих моментов и крутящего момента:

1.1. Расчет силовых нагрузок:
1.1.1. Расчетная схема вала редуктора:
Fr
RA
Fa
Ft
A
Х
C
l1
d2
RB
FM
B
D
T2
l2
l3

3. 1.1.2. Тангенциальная сила, н:

Ft
2 T 2 2 1000 T 2
d2
d2
1.1.3. Радиальная сила, н:
Fr
Ft tg
cos
20 o — угол зацепления; tg 0 , 364
угол наклона зубьев.
соs = соs0 = 1 для прямозубой передачи.

4. 1.1.4. Осевая сила, н:

Fa Ft tg
tgβ = tg0 = 0, поэтому при прямозубом зацеплении осевая сила отсутствует.
1.1.5. Сила реакции в муфте, н:
F м 0 , 3 Ft

5. 1.2. Построение эпюр изгибающих моментов и крутящего момента:

2.1. Построение эпюр изгибающих моментов в вертикальной плоскости:
Fr
RA
Fa
Х
A
C
l1
d2
RB
B
l2
D
l3

6. Определение опорных реакций от радиальной Fr и осевой Fa сил:

MB 0;
d2
0;
Ray ( l 1 l 2 ) F r l 2 Fa
2
d
F r l 2 Fa 2
2 ,н;
Ray
( l1 l2 )
MA 0;
d2
0;
Rby ( l 1 l 2 ) F r l 1 Fa
2
d
F r l 1 Fa 2
2 , н.
Rby
( l1 l2 )
Проверяем правильность определения реакций:
R y 0 ; Ray Fr Rby 0

7. Если реакции найдены правильно, строим эпюру изгибающих моментов от сил радиальной и осевой:

М иy Ray l 1 , н м
Fr
RA
Fa
Х
A
C
l1
Миy
d2
RB
B
l2
D
l3

8. 1.2.2. Построение эпюр изгибающих моментов в горизонтальной плоскости:

Ft
RA
RB
Х
A
C
l1
d2
B
l2
D
l3

9. Определение опорных реакций от тангенциальной силы Ft:

MB 0;
Rax l 1 l 2 Ft l 2 0 ;
F l
Rax t 2 , н ;
l 1 l 2
MA 0;
Rbx l 1 l 2 Ft l 1 0 ;
Ft l 1
,н;
Rbx
l 1 l 2
Rax Rbx
Проверяем правильность определения реакций:
R x 0 ; Rax Ft Rbx 0

10.

Если реакции найдены правильно, строим эпюру изгибающих моментов от тангенциальной силы:М их Raх l 1 , н м
Ft
RA
RB
Х
A
C
l1
Мих
d2
B
l2
D
l3

11. 1.2.3. Построение суммарной эпюры изгибающего момента от действия тангенциальной, радиальной и осевой сил:

2
2
M И M их
M иу
,н м
Fr
Fa
Ft
A
C
l1
МИ
Х
d2
B
l2
D
l3

12. 1.2.4. Построение эпюры изгибающих моментов от действия силы FМ:

На консольном участке вала находится полумуфта, которая нагружает
вал дополнительно поперечной силой .
RA
FМ
RB
Х
A
B
C
l1
l2
D
l3

13. Определение опорных реакций от действия силы FМ :

MA 0;
RbM l 1 l 2 F M ( l 1 l 2 l 3 ) 0 ;
F ( l 1 l 2 l 3 )
RbМ M
,н;
l 1 l 2
Меняем направление реакции в точке В
MB 0;
RaM l 1 l 2 F M l 3 0 ;
RaМ
FM l 3
,н;
l 1 l 2
Проверяем правильность определения реакций:
R М 0 , RaM RbM F M 0

14.

Если реакции найдены правильно, строим эпюру изгибающих моментов от действия силы реакции в муфте:M ИM RaM ( l 1 l 2 ), н м
RA
RB
Х
A
B
C
l1
МИМ
FМ
l2
D
l3

15. 1.2.5. Построение суммарной эпюры изгибающих моментов от действия всех сил:

M И M И М ИМ , н м
Fr
RA
Fa
Ft
A
C
l1
МИ
Х
d2
RB
FM
B
l2
D
l3

16. 1.2.6. Построение эпюры крутящего момента:

Х
A
B
C
l1
T2
l2
Т2
D
l3
Сводная эпюра изгибающих и крутящих моментов

18. 2. Уточненный расчет тихоходного вала редуктора

Уточненный расчет выполняют, как проверочный для определения
расчетного коэффициента запаса прочности:
SП
S S
S 2 S 2
Коэффициент запаса прочности по нормальным напряжениям:
S
1
k a
ср .
Коэффициент запаса прочности по касательным напряжениям:
S
1
k a
ср .
Пределы выносливости материала вала при симметричных циклах изгиба
и кручения, если нет табличных данных, тогда для углеродистых сталей:
1 0 ,43 B , МПа
1 0 ,58 1 , МПa
Расчетный коэффициент запаса прочности определяют в опасном
сечении.

Опасным считается сечение вала, для которого коэффициент
запаса прочности имеет наименьшее значение, оно может не совпадать с
сечением, где возникают наибольший изгибающий и крутящий моменты,
поэтому следует проверять все опасные сечения.
S П 1 ,5 4

20. Опасные сечения в точках С и Е

21. 2.1. Проверка прочности сечения в точке С:

Дано:
dз.к.= …
МиС= …
Т2 = …
b=…
t1 = …
В=520МПа,
т =280МПа,
τТ =170МПа,
-1 =250МПа,
τ-1 =150МПа

22. Напряжения изгиба изменяются по симметричному циклу, напряжения кручения – по отнулевому (пульсирующему) циклу:

а И
ср . 0
а ср .
MИ
W И .НЕТТО
, МПа ;
К
Т2
, МПа.
2
2 W K .НЕТТО

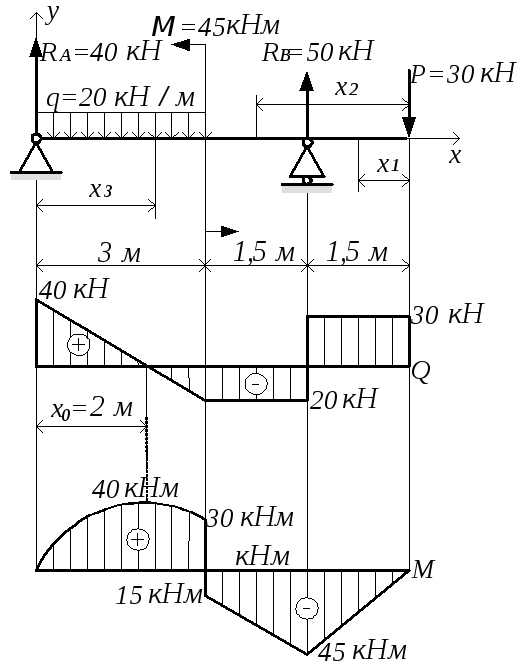
23. 2.1.1. Моменты сопротивления валов при изгибе Wи.нетто и кручении Wк.нетто в сечении ослабленном шпоночным пазом определяются:

W и .нетто
d з3.к b t 1 d з .к t 1 2
, мм 3
32
2 d з .к
W к .нетто
d з3.к b t 1 d з .к t 1 2
, мм 3
16
2 d з .

24. 2.1.2. Коэффициенты концентрации напряжений при изгибе К и кручении К вала, ослабленного шпоночным пазом определяются:

2.1.2. Коэффициенты концентрации напряжений при изгибе К и
кручении К вала, ослабленного шпоночным пазом определяются:

25. 2.1.3. Масштабные факторы при изгибе  и кручении  для углеродистых сталей определяются из таблицы, в соответствии с

2.1.3. Масштабные факторы при изгибе и кручении для
углеродистых сталей определяются из таблицы, в соответствии с
пределом прочности и диаметром вала в данном сечении.

26. 2.1.4. Коэффициент β, зависящий от степени шероховатости поверхности (способ обработки) определяется по таблице, для

качественных поверхностей способ обработки шлифование:

27. 2.1.5. Коэффициенты, зависящие от соотношения пределов выносливости при симметричном и пульсирующем циклах напряжений ψ и ψ ,

2.1.5. Коэффициенты, зависящие от соотношения пределов
выносливости при симметричном и пульсирующем циклах напряжений
ψ и ψ , выбирают в соответствии с маркой материала:
0 ,15 — углеродистая сталь σв = 350…550 МПа,
0 , 2 — углеродистая сталь σв = 650…750 МПа,
0 , 25.

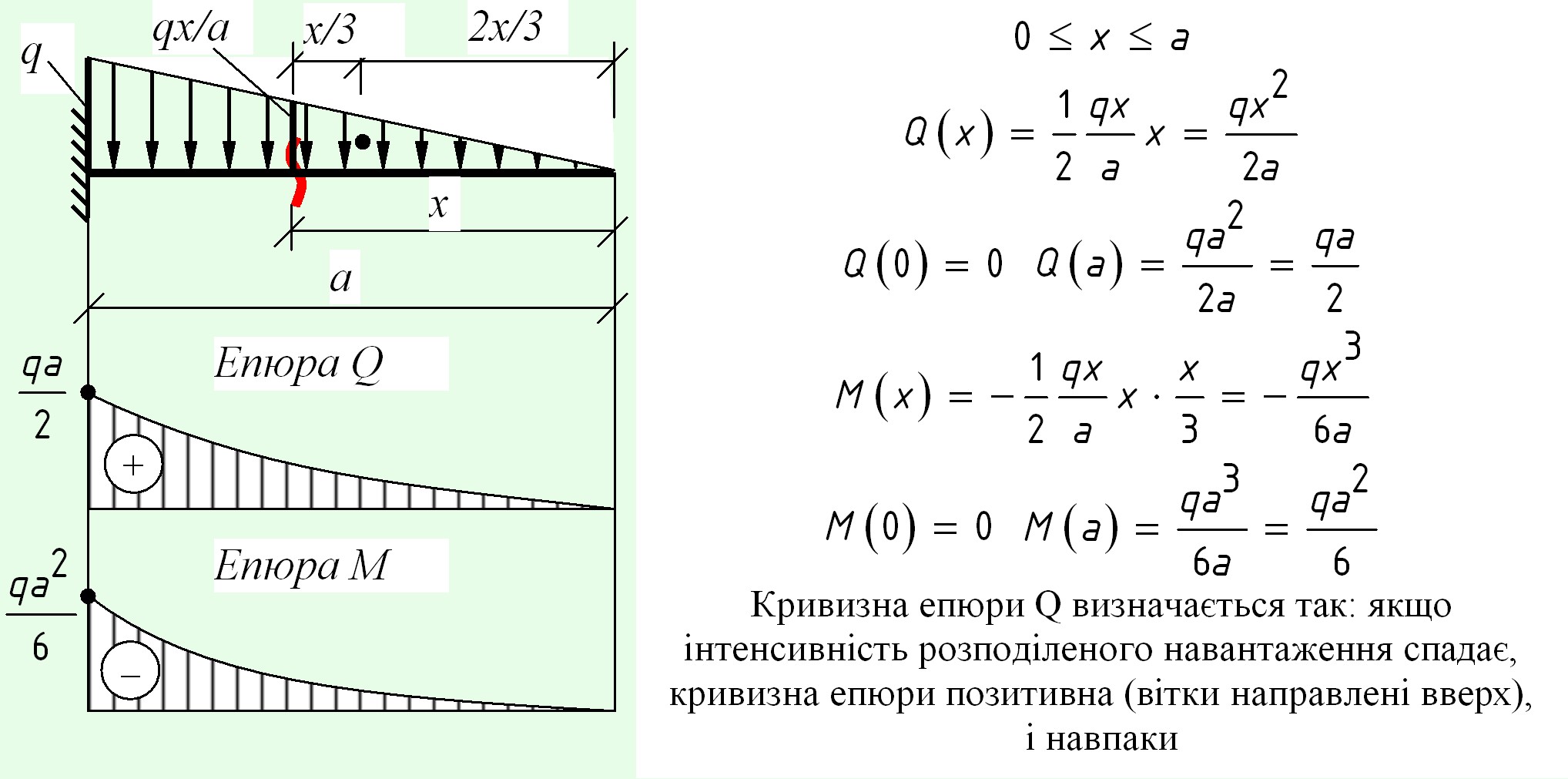..0 , 3 — легированная сталь,
0 ,05 — углеродистая сталь,
0 ,1 — легированная сталь,
Подставляем значения в формулы, расчетное значение коэффициента
запаса прочности сравниваем с допускаемым , если условие выполняется,
тогда прочность вала в данном сечении обеспечена.

28. 2.2. Проверка прочности сечения в точке Е:

Дано:
dп= …
r=
МиЕ= …
Т2 = …
В=520МПа,
т =280МПа,
τТ =170МПа,
-1 =250МПа,
τ-1 =150МПа
r 0 ,4 d з .к . d п
A
МИ
Х
C
B
lст.
МиЕ
l2
D

29. Напряжения изгиба изменяются по симметричному циклу, напряжения кручения – по отнулевому (пульсирующему) циклу:

а И
ср . 0
а ср .
MИ
W И .НЕТТО
, МПа ;
К
Т2
, МПа.
2
2 W K .НЕТТО

30. 2.2.1. Моменты сопротивления валов при изгибе Wи.нетто и кручении Wк.нетто для сплошного круглого сечения определяются :

W и .нетто
d з3.к
, мм 3
32
W к .нетто
d з3.к
, мм 3
16

31.

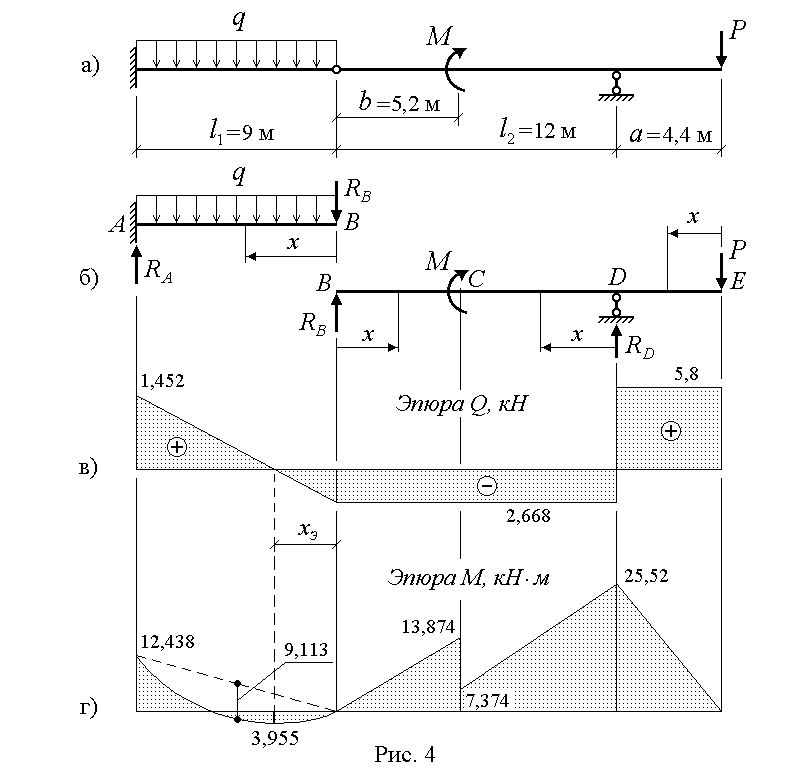2.2.2. Коэффициенты концентрации напряжений при изгибе К и кручении К вала, с галтелью определяются:2.2.2. Коэффициенты концентрации напряжений при изгибе К и
кручении К вала, с галтелью определяются:

32. 2.2.3. Масштабные факторы при изгибе  и кручении  для углеродистых сталей определяются из таблицы, в соответствии с

2.2.3. Масштабные факторы при изгибе и кручении для
углеродистых сталей определяются из таблицы, в соответствии с
пределом прочности и диаметром вала в данном сечении.

33. 2.2.4. Коэффициент β, зависящий от степени шероховатости поверхности (способ обработки) определяется по таблице, для

качественных поверхностей способ обработки шлифование:

34. 2.2.5. Коэффициенты, зависящие от соотношения пределов выносливости при симметричном и пульсирующем циклах напряжений ψ и ψ ,

2.2.5. Коэффициенты, зависящие от соотношения пределов
выносливости при симметричном и пульсирующем циклах напряжений
ψ и ψ , выбирают в соответствии с маркой материала:
0 ,15 — углеродистая сталь σв = 350…550 МПа,
0 , 2 — углеродистая сталь σв = 650…750 МПа,
0 , 25.

35. Предельные отклонения размеров отверстий и валов (по ГОСТ 2546-82) и колец подшипников качения класса точности О (по СТ СЭВ

773-77).

11. Расчет реакций в опорах валов и построение эпюр изгибающих и крутящих моментов

Величины реакций в опорах валов необходимы для проверочного расчета выбранных подшипников по динамической грузоподъёмности, а суммарные изгибающие моменты – для проверочного расчета валов на устойчивость.

Для некоторого упрощения расчета можно принять окружную силу от перекоса соединения полумуфт вала электродвигателя 1-го вала и 3-го вала и исполнительного устройства равной

F_M =0,1· F_ti =0,1∙527,5=52,75Н

приложенной к оси (на его конце) и по направлению с окружающей силой на шестерне Z₁ или колеса Z₄. Вылет конца вала относительно оси подшипника

l_в =3,5·d_1-1=3,5∙17=59,5=0,0595м

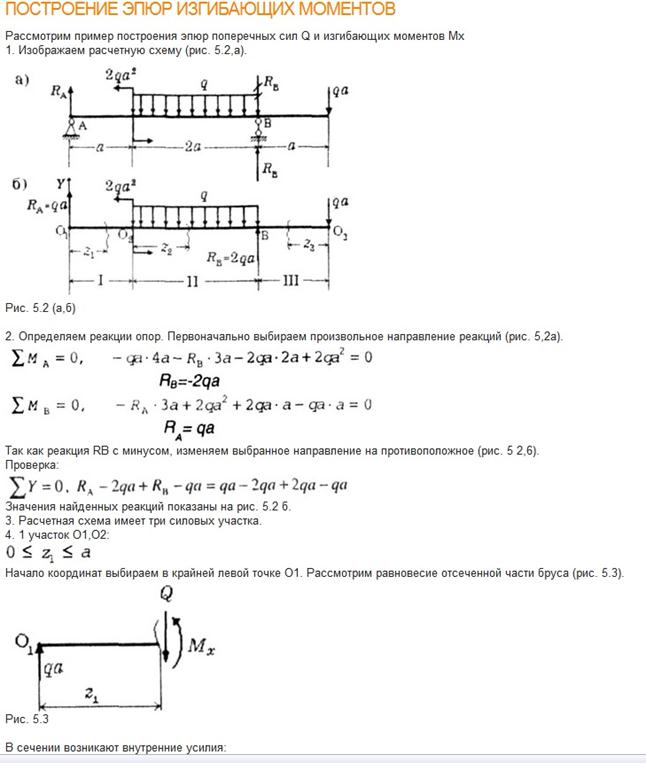
Рисунок 11.1.Расчетная схема первого вала редуктора(а),приведение сил к оси вала и эпюры изгибающих моментов в вертикальной(б) и горизонтальной(в) , крутящий момент(г).

1. Входной вал:

Силы, действующие в зацеплении:

окружная: F_t₁=527,53 Н;

радиальная: F_r₁=194,7 Н;

осевая: F_o₁=144,5 Н;

Расчет реакций в опорах и изгибающих моментов в вертикальной плоскости:

— момент от осевой силы F_о1

M_o₁= F_o₁∙ d_д1/2= 144,5∙0,04868/2=3,52Н·м (1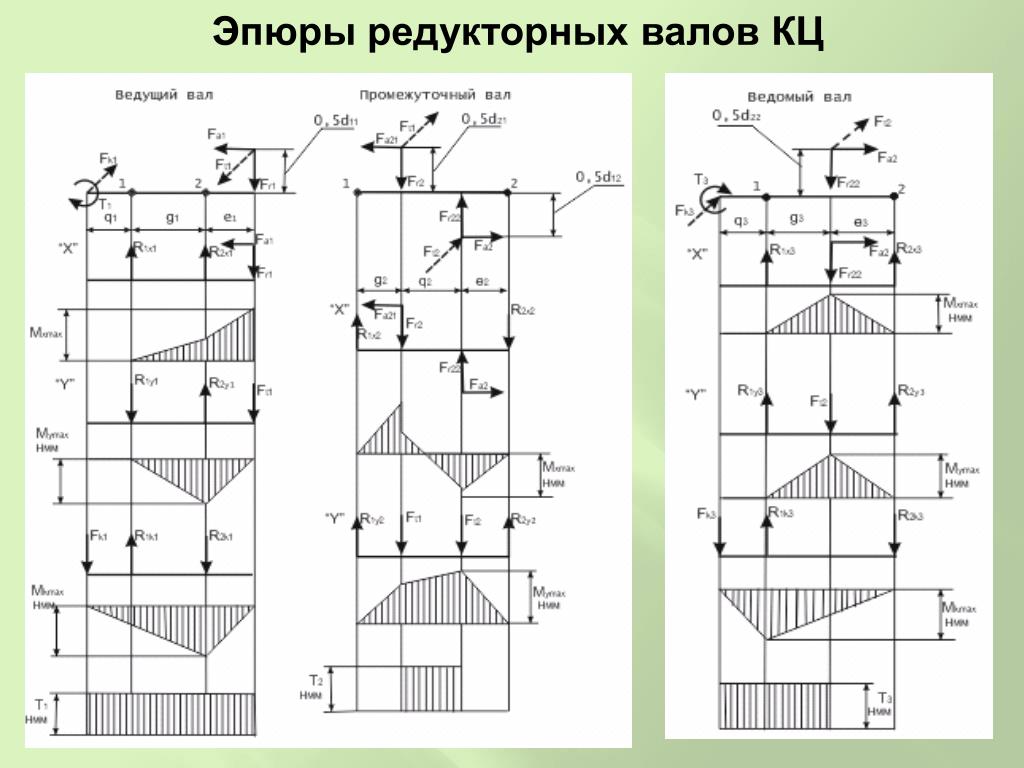1. 1)

-осевая реакция

А₁=- F_o₁ = -144,5Н

-сумма моментов действующих сил относительно левой опоры Л:

∑ = M_o₁— F_r₁∙ а + ∙2а =0 (11.2)

откуда =( F_r₁∙а- M_o₁)/2а=(194,7∙0,038-3,52)/0,076=51Н (11.3)

-сумма моментов действующих сил относительно правой опоры П:

∑ = M_o₁+F_r₁∙ а — ∙2а =0 (11.4)

Откуда =( F_r₁∙а+ M_o₁)/2а=(194,7∙0,038+3,52)/0,076=143,7Н

Проверка: F_r₁ — — =194,7-143,7-51=0

-изгибающий момент в сечении 2(слева)

=∙а=143,7∙0,038=5,46Н·м (11.

-изгибающий момент в сечении 2(справа)

=∙а=51∙0,038=1,94Н·м (11.6)

Расчет реакций в опорах и изгибающих моментов в горизонтальной плоскости:

-сумма моментов действующих сил относительно левой опоры Л:

∑ = F_м1∙д –F_t₁∙ а + ∙2а =0 (11.7)

Откуда =( F_t₁∙ а — F_м1∙д)/2а=(527,53∙0,038-52,75∙0,0595)/0,076=222,47 Н

-сумма моментов действующих сил относительно правой опоры П:

∑ = F_t₁∙ а — ∙2а +F_м1∙(д+2а) =0 (11.8)

Откуда =( F_t₁∙ а + F_м1∙(д+2а))/2а=(527,53∙0,038+52,75∙0,1355)/0,076=357,81

Проверка :- —+F_t₁ + F_м1=-222,47-357,81+52,75+527,53=0

-изгибающий момент в сечении 2 вала:

=∙а- F_м1 ∙(д+а)=∙а=222,47∙0,038=8,45 Н·м (11. 9)

-изгибающий момент в сечении 1 вала:

=- F_м1∙д=-52,75∙0,0595=-3,13 Н·м (11.10)

Равнодействующая реакция:

— в левой опоре

∑ R_л===385,56Н (11.11)

— в правой опоре

∑ R_п===228,24Н (11.12)

-осевая в левой опоре

A= F

o₁=144,5 Н.

Равнодействующий изгибающий момент:

-в сечении 1

M_и1= =- F_м1∙д=-52,75∙0,0595=-3,13 Н·м

-в сечении 2

∑ M_и2===10,06 Н·м

2. Промежуточный вал вал:

Силы, действующие в зацеплении:

окружная: F_t₂=527,53 Н;

радиальная: F_r₂=194,7 Н;

осевая: F_o₂=144,5 Н;

окружная: F_t₃=2533,8Н;

радиальная: F_r₃=938,95Н;

осевая: F_o₃=483,96Н;

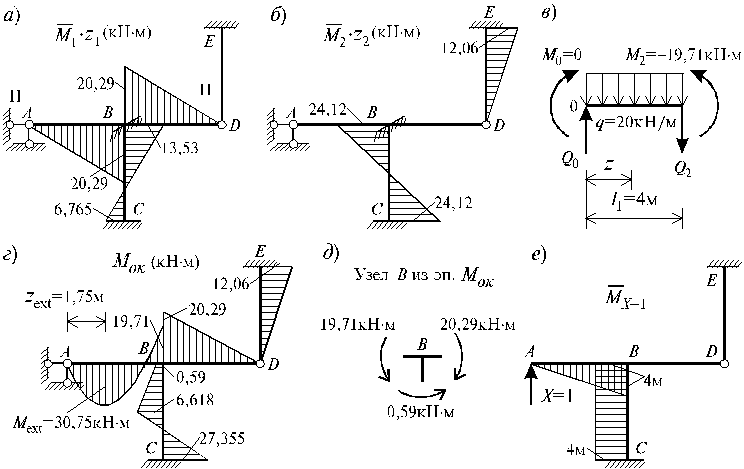
Рисунок 11.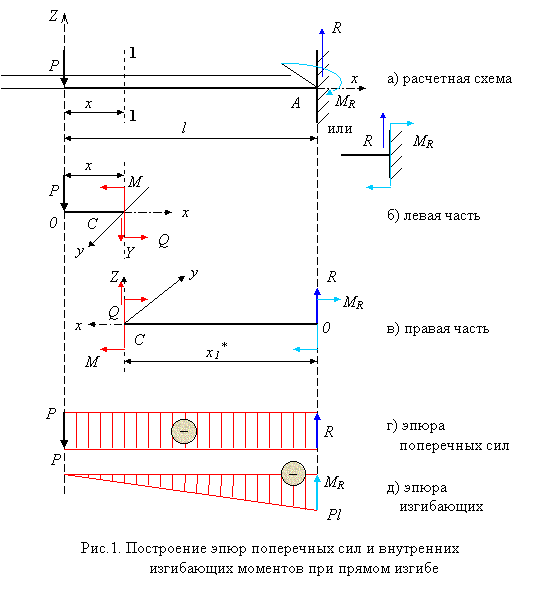 2

Расчет реакций в опорах и изгибающих моментов в вертикальной плоскости:

— момент от осевой силы

==144,54·0,23124/2=16,7Н·м

-момент от осевой силы :

==483,96·0,04837/2=11,7Н·м

-осевая реакция

=—=144,54-483,96=-339,42Н

-сумма моментов действующих сил относительно левой опоры Л:

∑=·a+( + +b)=0

откуда

=(·a+ ( + +b)=

(-16,7+11,7+194,7∙0,038+938,95∙0,1435)/0,1885=727,52Н

-сумма моментов действующих сил относительно правой опоры П:

∑=——(а+ +с)=0

= (-

·+ ( + +b) =

=(-11,7+16,7+194,7∙0,1505+938,95∙0,045)/0,1885=406,13Н

Проверка:+——=727,52+406,13-938,95-194,7=0

-изгибающий момент в сечении 2 (слева):

=∙ = 406,13∙0,038=15,43 Н∙м

-изгибающий момент в сечении 2 (справа):

=∙= 727,52∙0,1505=109,5 Н∙м

-изгибающий момент в сечении 3 (слева):

=∙ = 406,13∙0,1435=58,28 Н∙м

-изгибающий момент в сечении 2 (справа):

=∙ = 727,52∙0,045=32,74 Н∙м

Расчет реакций в опорах и изгибающих моментов в горизонтальной плоскости.

-сумма моментов действующих сил относительно левой опоры Л:

∑=∙—∙(+—(

+ +b)=0

откуда ∙—∙(+))/ ( + +b)=(527,53∙0,038-2533,8∙0,1435)/0,1885=-1822,55Н

-сумма моментов действующих сил относительно правой опоры П:

∑=∙∙(++( + +b)=0

откуда =∙∙(+/( + +b)=(-2533,8∙0,045+527,53∙0,1505)/0,1885=-183,72Н

Проверка:—++=2533,8-527,53-1822,55-183,72=0

-изгибающий момент в сечении 2 вала:

=∙=-183,72∙0,038=-6,98 Н∙м

-изгибающий момент в сечении 3 вала:

=∙=-26,36+55,65=29,29

Равнодействующая реакция:

-в левой опоре

∑ =Н

-в правой опоре

∑ =Н

-осевая в левой опоре

A=—=483,96-144,54=339,42Н

Равнодействующий изгибающий момент:

-в сечении 2

∑ =Н

-в сечении 3

∑ =Н

3. Выходной вал:

Рисунок 11.3

Силы, действующие в зацеплении:

окружная: F_t₄=2533,8Н;

радиальная: F_r₄=938,95 Н;

осевая: F_o₄=483,96 Н;

F_M₂ =0,1· F_t₄ =0,1∙2533,8=253,38Н

l_в2 =3,5·d_3-3=3,5∙50=175=0,175м

Расчет реакций в опорах и изгибающих моментов в вертикальной плоскости:

— момент от осевой силы F_о1

M_o₄= F_o₄∙ d_д4/2= 483,96 ∙0,231/2=55,9Н·м

-осевая реакция

А₃=- F_o₄ = -483,96 Н

-сумма моментов действующих сил относительно левой опоры Л:

∑ = -M_o₄— F_r₄∙ а + ∙2а =0

откуда =( F_r₄∙б+M_o₄)/2б=(938,95∙0,045+55,9)/0,09=1090,6Н

-сумма моментов действующих сил относительно правой опоры П:

∑ = -M_o₁+F_r₄∙ б — ∙2б =0

Откуда

=( F_r₄∙б- M_o₄)/2б=(938,95∙0,045-55,9)/0,09=-151,64Н

Проверка: F_r₄ — — =938,95-1090,6-(-151,64)=0

-изгибающий момент в сечении 3(слева)

=∙б=-151,64∙0,045=-6,82Н·м

-изгибающий момент в сечении 3(справа)

=∙б=1090,6∙0,045=49,08Н·м

Расчет реакций в опорах и изгибающих моментов в горизонтальной плоскости:

-сумма моментов действующих сил относительно левой опоры Л:

∑ = F_м2∙( д₂+2б) +F_t₄∙ б — ∙2б =0

Откуда =( F_t₄∙ б + F_м2∙(д+2б))/2б=(67,15+114,02)/0,09=2013 Н

-сумма моментов действующих сил относительно правой опоры П:

∑ = -F_t₄∙ б + ∙2б +F_м2∙ д₂ =0

Откуда =( F_t₄∙ б — F_м2∙ д₂)/2б=(114,02-44,34)/0,09=774,18

Проверка : +— F_t₄ — F_м2=2013+774,18 -2533,8-253,38=0

-изгибающий момент в сечении 3 вала:

=-∙б=∙а=-774,18∙0,045=-34,83Н·м

-изгибающий момент в сечении 1 вала:

=∙2б + F_t₄∙ б=-69,68+114,02=44,3 Н·м

Равнодействующая реакция:

— в левой опоре

∑ R_л===788,9Н

— в правой опоре

∑ R_п===2289,45Н

-осевая в левой опоре

A= F_o₄=483,96 Н.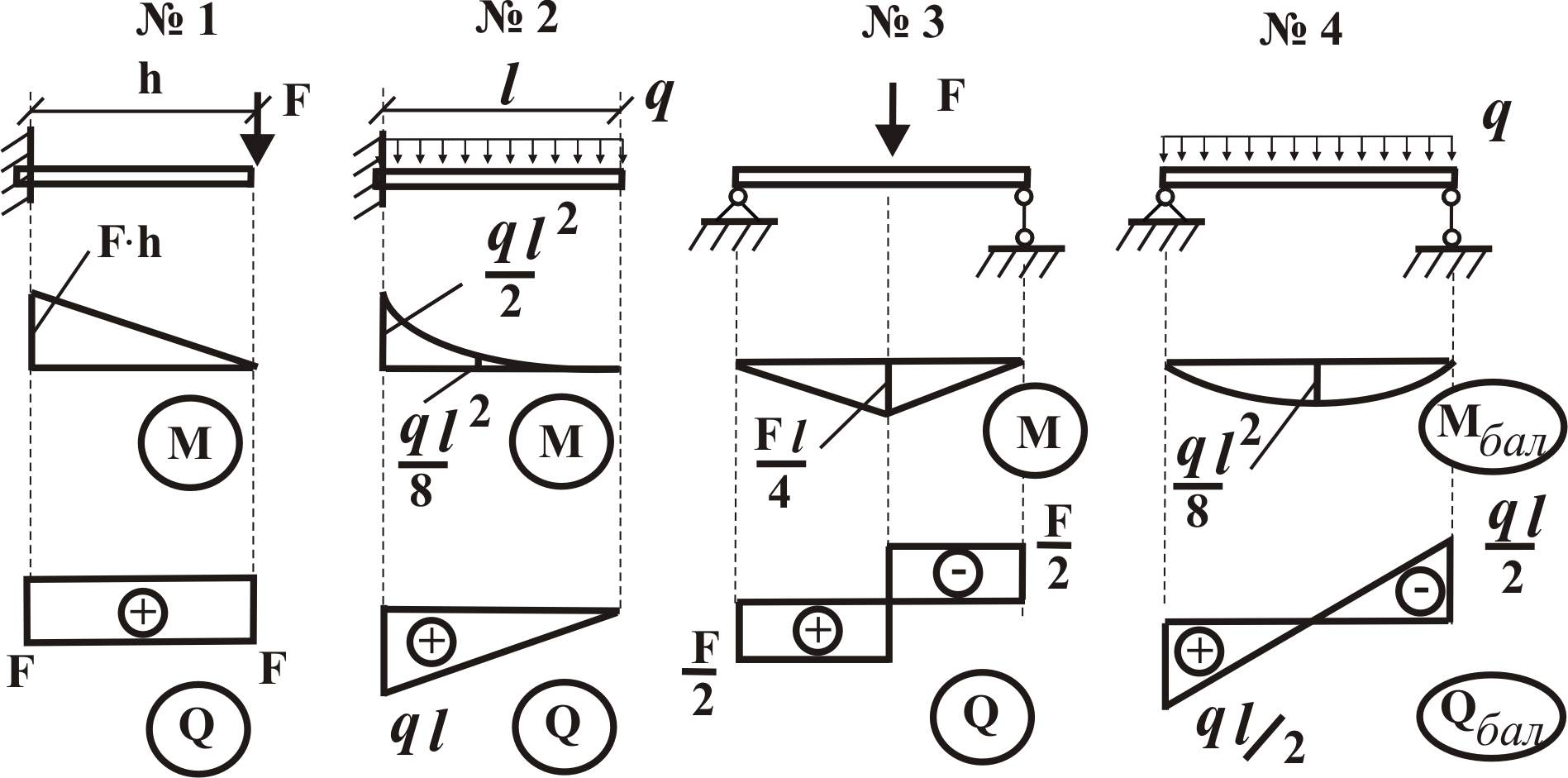

Равнодействующий изгибающий момент:

-в сечении 1

M_и1= = F_м2∙ д₂=253,38∙0,175=44,34 Н·м

-в сечении 3

∑ M_и3===35,2 Н·м

Построение графиков — Документация по anaStruct 1.0

Объект SystemElements реализует несколько методов построения графиков для получения стандартных результатов построения графиков. Каждый график метод имеет те же параметры. Плоттер основан на бэкенде Matplotlib, и можно получить рисунок и сделать свои модификации. Координаты x и y модели должны быть положительными для плоттера. работать должным образом.

Обратите внимание, что возможности построения графиков требуют, чтобы anaStruct был установлен с подмодулем «график» (например, pip установить анаструктуру [участок] )

Структура

SystemElements.show_structure( verbosity=0 , scale=1.0 , offset=(0, 0) , figsize=None , show=True , supports=True 9 0013, values_only=False , аннотации = Ложь ) [источник]

Постройте структуру.

Параметры

фактор – влияет на масштаб изображения.
многословность ( int ) – 0: вся информация, 1: скрыть информацию.
масштаб ( float ) – Масштаб графика.
offset ( Tuple [ float , float ]) — Смещение расположения графиков на рисунке.
figsize ( Необязательный [ Tuple [ float , float ]]) — изменение размера фигуры.
show ( bool ) — построить результат или вернуть цифру.
values_only ( bool ) — возвращает значения, которые будут отображаться в виде кортежа, содержащего два массива: (х, у)
аннотации ( bool ) — если True, аннотации структуры отображаются. Он включает название раздела. Примечание: работает, только если уровень детализации равен 0.

Изгибающие моменты

SystemElements.show_bending_moment( factor = None , verbosity = 0 , scale = 1 , offset = (0, 0) , figsize = None , show = True , values_only=False ) [источник]

Постройте изгибающий момент.

Параметры

коэффициент ( Дополнительный [ с плавающей запятой ]) – влияет на масштаб изображения.
многословие ( int ) – 0: вся информация, 1: скрыть информацию.
масштаб ( float ) – Масштаб графика.
offset ( Tuple [ float , float ]) — Смещение расположения графиков на рисунке.
figsize ( Необязательный [ Tuple [ float , float ]]) — изменение размера фигуры.
show ( bool ) — построить результат или вернуть цифру.
values_only ( bool ) — возвращает значения, которые будут отображаться в виде кортежа, содержащего два массива: (х, у)

Осевые силы

SystemElements.show_axial_force( factor = None , verbosity = 0 , scale = 1 , offset = (0, 0) , figsize = None , show=True , values_only=False ) [источник]

График осевой силы.

Параметры

коэффициент ( Дополнительный [ с плавающей запятой ]) – влияет на масштаб изображения.
многословность ( int ) – 0: вся информация, 1: скрыть информацию.
масштаб ( float ) – Масштаб графика.
offset ( Tuple [ float , float ]) — Смещение расположения графиков на рисунке.
figsize ( Необязательный [ Tuple [ float , float ]]) — изменение размера фигуры.
show ( bool ) — построить результат или вернуть цифру.
values_only ( bool ) — возвращает значения, которые будут отображаться в виде кортежа, содержащего два массива: (x, y)

Силы сдвига

SystemElements.show_shear_force( factor = None , verbosity = 0 , scale = 1 , offset = (0, 0) , figsize = None , show = True 9 0013, values_only=False ) [источник]

Постройте поперечную силу.

Параметры

коэффициент ( Дополнительный [ с плавающей запятой ]) – влияет на масштаб изображения.
многословность ( int ) – 0: вся информация, 1: скрыть информацию.
масштаб ( float ) – Масштаб графика.
offset ( Tuple [ float , float ]) — Смещение расположения графиков на рисунке.
figsize ( Необязательный [ Tuple [ float , float ]]) — изменение размера фигуры.
show ( bool ) — построить результат или вернуть цифру.
values_only ( bool ) — возвращает значения, которые будут отображаться в виде кортежа, содержащего два массива: (х, у)

Силы реагирования

SystemElements. show_reaction_force( verbosity=0 , scale=1 , offset=(0, 0) , figsize=None , show=True )[источник]

Постройте график силы реакции.

Параметры

многословность ( int ) – 0: вся информация, 1: скрыть информацию.
масштаб ( float ) – Масштаб графика.
offset ( Tuple [ float , float ]) — Смещение расположения графиков на рисунке.
размер ( Необязательный [ Кортеж [ float , float ]]) — Изменить размер фигуры.
show ( bool ) — построить результат или вернуть цифру.

Смещение

SystemElements.show_displacement( factor = None , verbosity = 0 , scale = 1 , offset = (0, 0) , figsize = None , show = True , linear=False , values_only=False ) [источник]

Постройте смещение.

Параметры

коэффициент ( Дополнительный [ с плавающей запятой ]) – влияет на масштаб изображения.
многословность ( int ) – 0: вся информация, 1: скрыть информацию.
масштаб ( float ) – Масштаб графика.
offset ( Tuple [ float , float ]) — Смещение расположения графиков на рисунке.
figsize ( Необязательный [ Tuple [ float , float ]]) — изменение размера фигуры.
show ( bool ) — построить результат или вернуть цифру.
linear ( bool ) — Не оценивать значения смещения между элементами
values_only ( bool ) — возвращает значения, которые будут отображаться в виде кортежа, содержащего два массива: (х, у)

Сохранить цифру

Когда для параметра show установлено значение False , возвращается фигура Matplotlib, и фигура может быть сохранена с правильным титулы.

 из анаструктурного импорта SystemElements
импортировать numpy как np
импортировать matplotlib.pyplot как plt
х = np.arange (0, 10)
у = np.sin (х)
СС = СистемныеЭлементы ()
ss.add_element_grid(х, у)
ss.add_support_hinged (node_id = [1, -1])
рис = ss.show_structure(show=False)
plt.title('Синусоида')
plt.savefig('my-figure.png')

Вопросы с несколькими вариантами ответов (MCQ) с ответами на диаграмму поперечной силы и изгибающего момента

Вопросы с несколькими вариантами ответов (MCQ) с ответами на диаграмму поперечной силы и изгибающего момента

1-A балка является элементом конструкции

Осевое растяжение или сжатие
Поперечные нагрузки и пары
Крутящий момент
Нет нагрузки, но его ось должна быть горизонтальной, а поперечное сечение — прямоугольным или круглым

(Ответ: б)

2-Какие из следующих балок являются статически определимыми?

Только свободно опертые балки
Консольный, выступающий и просто поддерживаемый
Неподвижные балки
Неразрезные балки

(Ответ: b)

3-A Консольная балка, у которой

Оба конца поддерживаются роликами или шарнирами
Один конец закреплен, а другой свободен
Оба конца фиксированы
У которого оба или один конец имеет выступ

(Ответ: b)

4-В кантилевере, несущем равномерно изменяющуюся нагрузку, начиная с нуля на свободном конце, диаграмма поперечной силы

Горизонтальная линия, параллельная оси x
Линия, наклоненная к оси x
следует параболическому закону
следует кубическому закону

(Ответ: в)

5-В кантилевере, несущем равномерно изменяющуюся нагрузку, начиная с нуля на свободном конце, диаграмма изгибающего момента

Горизонтальная линия, параллельная оси x
Линия, наклоненная к оси x
следует параболическому закону
следует кубическому закону

(Ответ: d)

6-В свободно опертой балке изгибающий момент на конце

Всегда равен нулю, если он не несет пары на конце
Равен нулю, если балка имеет только равномерно распределенную нагрузку
равен нулю, если балка имеет только сосредоточенные нагрузки
Может быть или не быть нулем

(Ответ: а)

7-Для любой части балки между двумя сосредоточенными нагрузками диаграмма поперечной силы представляет собой

Горизонтальную прямую линию
Вертикальная прямая
Линия, наклоненная к оси x
Парабола

(Ответ: а)

8-Для любой части балки между двумя сосредоточенными нагрузками диаграмма изгибающего момента представляет собой

Горизонтальную прямую линию
Вертикальная прямая
Линия, наклоненная к оси x
Парабола

(Ответ: c)

9-Для любой части балки, подвергаемой равномерно распределенной нагрузке, диаграмма поперечной силы представляет собой

Горизонтальная прямая линия
Вертикальная прямая
Линия, наклоненная к оси x
Парабола

(Ответ: c)

10-Для любой части балки, подвергаемой равномерно распределенной нагрузке, диаграмма изгибающего момента

Горизонтальная прямая линия
Вертикальная прямая
Линия, наклоненная к оси x
Парабола

(Ответ: d)

11-Внезапный скачок в любом месте на диаграмме изгибающего момента балки вызван

Пара, действующая в этой точке
Пара, действующая в другой точке
Сосредоточенная нагрузка в точке
Равномерно распределенная нагрузка или Равномерно изменяющаяся нагрузка на балку

(Ответ: а)

12-В балке с простой опорой, имеющей длину = l и подверженной сосредоточенной нагрузке (W) в средней точке.

Расчет силовых нагрузок на вал и построение эпюр изгибающих моментов и крутящего момента

1. Домашнее задание по курсу «Детали машин» №4

2. 1. Расчет силовых нагрузок на вал и построение эпюр изгибающих моментов и крутящего момента:

3. 1.1.2. Тангенциальная сила, н:

4. 1.1.4. Осевая сила, н:

5. 1.2. Построение эпюр изгибающих моментов и крутящего момента:

6. Определение опорных реакций от радиальной Fr и осевой Fa сил:

7. Если реакции найдены правильно, строим эпюру изгибающих моментов от сил радиальной и осевой:

8. 1.2.2. Построение эпюр изгибающих моментов в горизонтальной плоскости:

9. Определение опорных реакций от тангенциальной силы Ft:

10.

11. 1.2.3. Построение суммарной эпюры изгибающего момента от действия тангенциальной, радиальной и осевой сил:

12. 1.2.4. Построение эпюры изгибающих моментов от действия силы FМ:

13. Определение опорных реакций от действия силы FМ :

14.

15. 1.2.5. Построение суммарной эпюры изгибающих моментов от действия всех сил:

16. 1.2.6. Построение эпюры крутящего момента:

18. 2. Уточненный расчет тихоходного вала редуктора

20. Опасные сечения в точках С и Е

21. 2.1. Проверка прочности сечения в точке С:

22. Напряжения изгиба изменяются по симметричному циклу, напряжения кручения – по отнулевому (пульсирующему) циклу:

23. 2.1.1. Моменты сопротивления валов при изгибе Wи.нетто и кручении Wк.нетто в сечении ослабленном шпоночным пазом определяются:

24. 2.1.2. Коэффициенты концентрации напряжений при изгибе К и кручении К вала, ослабленного шпоночным пазом определяются:

25. 2.1.3. Масштабные факторы при изгибе  и кручении  для углеродистых сталей определяются из таблицы, в соответствии с

26. 2.1.4. Коэффициент β, зависящий от степени шероховатости поверхности (способ обработки) определяется по таблице, для

27. 2.1.5. Коэффициенты, зависящие от соотношения пределов выносливости при симметричном и пульсирующем циклах напряжений ψ и ψ ,

28. 2.2. Проверка прочности сечения в точке Е:

29. Напряжения изгиба изменяются по симметричному циклу, напряжения кручения – по отнулевому (пульсирующему) циклу:

30. 2.2.1. Моменты сопротивления валов при изгибе Wи.нетто и кручении Wк.нетто для сплошного круглого сечения определяются :

31.

32. 2.2.3. Масштабные факторы при изгибе  и кручении  для углеродистых сталей определяются из таблицы, в соответствии с

33. 2.2.4. Коэффициент β, зависящий от степени шероховатости поверхности (способ обработки) определяется по таблице, для

34. 2.2.5. Коэффициенты, зависящие от соотношения пределов выносливости при симметричном и пульсирующем циклах напряжений ψ и ψ ,

35. Предельные отклонения размеров отверстий и валов (по ГОСТ 2546-82) и колец подшипников качения класса точности О (по СТ СЭВ

11. Расчет реакций в опорах валов и построение эпюр изгибающих и крутящих моментов

Построение графиков — Документация по anaStruct 1.0

Структура

Изгибающие моменты

Осевые силы

Силы сдвига

Силы реагирования

Смещение

Сохранить цифру

Вопросы с несколькими вариантами ответов (MCQ) с ответами на диаграмму поперечной силы и изгибающего момента

Добавить комментарий Отменить ответ