Онлайн калькулятор расхода огнезащитной краски

Онлайн калькулятор расхода огнезащитной краски

Таблица расхода ОГНЕТИТАН RМ

Двутавр СТО АСЧМ 20-93 ГОСТ 26020-83 ГОСТ 8239-89 ГОСТ 19425-74 СВАРНОЙ
по размерам Швеллер ГОСТ 8240-97 Уголок ГОСТ 8509-93, 8510-86 Профиль ГОСТ 30245-2003 Труба по размерам

Двутавры СТО АСЧМ 20-93

Нормальные двутавры	Широкополочные двутавры	Колонные двутавры
10Б1 12Б1 12Б2 14Б1 14Б2 16Б1 16Б2 18Б1 18Б2 20Б1 25Б1 25Б2 30Б1 30Б2 35Б1 35Б2 40Б1 40Б2 45Б1 45Б2 50Б1 50Б2 50Б3 55Б1 55Б2 60Б1 60Б2 70Б0 70Б1 70Б2	20Ш1 25Ш1 30Ш1 30Ш2 35Ш1 35Ш2 40Ш1 40Ш2 45Ш1 50Ш1 50Ш2 50Ш3 50Ш4 60Ш1 60Ш2 60Ш3 60Ш4 70Ш1 70Ш2 70Ш3 70Ш4 70Ш5 80Ш1 80Ш2 90Ш1 90Ш2 100Ш1 100Ш2 100Ш3 100Ш4	20К1 20К2 25К1 25К2 25К3 30К1 30К2 30К3 30К4 35К1 35К2 40К1 40К2 40К3 40К4 40К5

Результаты расчета

 

Профиль не выбран

Приведенная толщина металла:мм
Обогреваемый периметр:мм
Площадь поверхности / 1м:м²
Площадь поверхности / 1 т:м²

Предел огнестойкости конструкции (Огнезащитная эффективность)	Толщина покрытия, мм	Расход, кг на 1м²	Расход, кг на 1т	Расход, кг на 1м
R45 (45 минут)	—	—	—	—
R60 (60 минут)	—	—	—	—
R90 (90 минут)	—	—	—	—
R120 (120 минут)	—	—	—	—

 

Расчёт прогиба и прочности деревянной балки онлайн

Скачать, сохранить результат

• Вы можете сохранить результат расчёта в формате PDF на ваше устройство, выбрав «Сохранить как PDF» в окне печати. Либо просто распечатайте результаты на бумагу.

Балка с любым поперечным сечением – это основополагающий элемент объемных конструкций, а деревянная балка – важный компонент зданий и сооружений. Постоянные и временные перекрытия и консоли повсеместно выполняются из брёвен, бруса или собранных в пакет досок.

Балки способны успешно воспринимать статические и динамические нагрузки: работающий человек, оборудование и имущество, интерьер и мебель уверенно размещаются на перекрытии. Предварительный расчёт прочности как оценка несущей способности призван обезопасить возводимое сооружение от поломки и придать ему необходимую жесткость – основу долговечности.

Стандартная оценка заключается в применении специализированных методик расчёта. Для этого потребуется комплексное знание механики, сопротивления материалов и других инженерных тонкостей. Гораздо проще и быстрее – провести расчет деревянной балки онлайн, с помощью отдельного инструмента в виде простого калькулятора.

Проверка балки на прогиб теперь выполняется за считанные секунды – что кардинально ускоряет работу специалиста и снижает затраты времени.

Возможности инструмента

Калькулятор прогиба деревянной балки позволяет оценить основные параметры планируемого пролётного элемента:

• размеры поперечного сечения;
• длину самой балки;
• её прогиб под планируемой нагрузкой.

Параллельно учитывается сорт древесины, что немаловажно из-за прямой зависимости между качеством пиломатериалов и механическими свойствами изделия.

Точность величины прогиба как отклонения от прямолинейности зависит от типа закрепления расчётного элемента. Жёсткая заделка обоих концов, наличие шарнирных соединений или вовсе свободный конец означают разное поведение материала балки.

Мастеру достаточно понять, как будет закрепляться каждый элемент перекрытия, измерить геометрию участка и оценить нагрузку – этого хватит для укрупнённого расчёта. Если нет точного значения приходящейся на пол массы, можно применить среднестатистические значения:

• перекрытие между этажами – до 400 кг/кв. метр;
• чердачное перекрытие – до 200 кг/кв. метр.

Порядок расчёта

 Сорт пиломатериала.

Оценивается по внешнему виду и наличию дефектов, прописывается в документации по качеству на партию товара.

Для справки: сопротивление сортов древесины  Приняты на основании СП 64.13330.2017 «Деревянные конструкции»

• 1-ого сорта — 9 МПа,
• 2-ого сорта — 8.34 МПа
• 3-его сорта — 5.56 МПа.
• Тип заделки концов.

Нужно определить, как будет закрепляться расчётная балка:

Тип нагрузки.

Расчет деревянной балки на прочность онлайн-калькулятор проводит комплексно – для чего важен характер давления.

Линейные размеры сечения.

Необходимо задать размеры поперечного сечения — и определить таким образом мощность балки. Калькулятор работает с наиболее распространёнными типами сечения – прямоугольным и квадратным (при задании одинаковых ширины и высоты).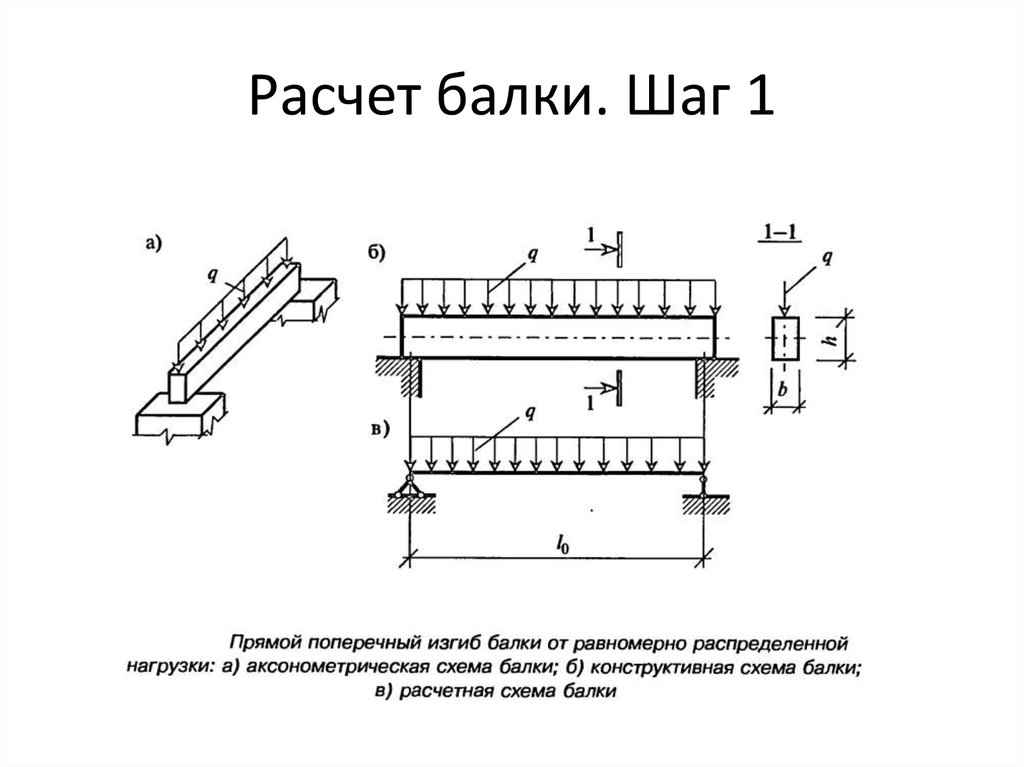

Длина балки.

На этом этапе важно ввести не полную длину – а расстояние между крайними точками, находящимися в подвешенном состоянии. Проблема заключается в распространённой ошибке: прогибу подвергается только не опирающаяся часть.

Для информации:
— принято считать, что сопротивление дерева на изгиб: для 1-ого сорта — 9 МПа, для 2-ого сорта — 8.34 МПа и для 3-его сорта — 5.56 МПа. Это следует из СП 64.13330.2017 «Деревянные конструкции» при коэффициентах Mв=0.9 (нормальная эксплуатация), Mт=0.8 (температура до 50 градусов), Мсс=0.9 (срок службы 75 лет), Мдл=0.66 (совместное действие постоянной и кратковременной нагрузок).

Смотрите также:

Калькулятор расходимости и диаметра лазерного луча и формула

Я хочу рассчитать

Тип

Дивергенция Диаметр луча

Параметры

Первый диаметр

Первый диаметр

Второй диаметр

Второй блок диаметра

Расстояние между диаметрами

Расстояние между диаметрами ед.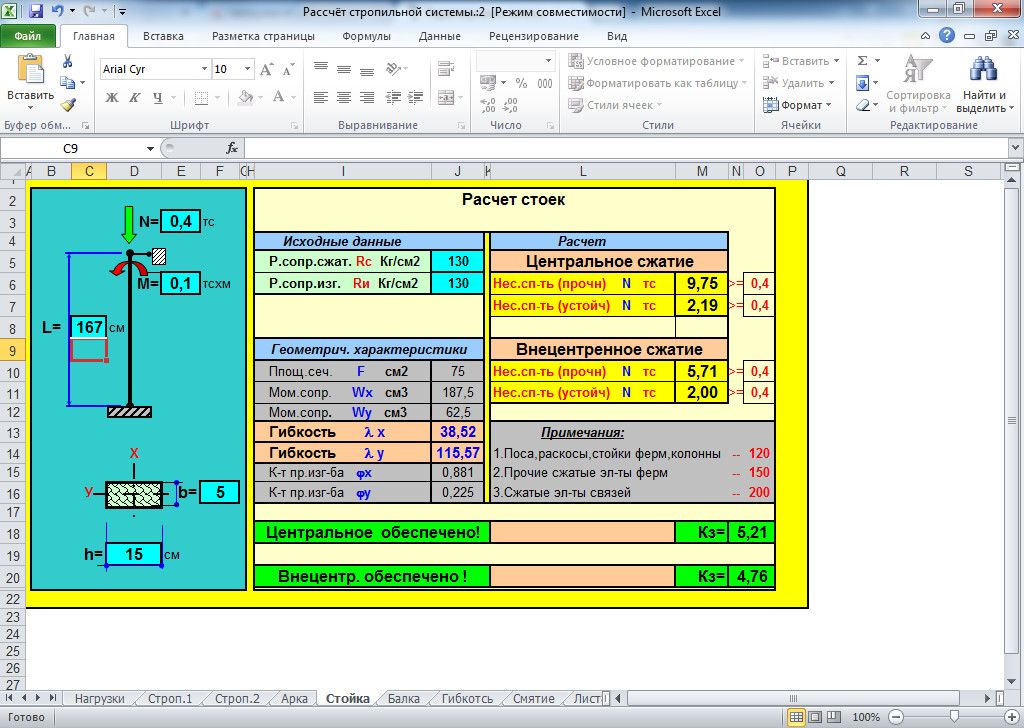 µmmmcmmmkminchesfeet

Начальный диаметр

Единица измерения исходного диаметра

Дивергенция (полуугла)

Единица дивергенции (полуугла) мрад°

Расстояние

Единица измерения расстояния µmmmcmmmkminchesfeet

Как работает калькулятор расходимости и диаметра лазерного луча?

В оптике расходимость лазерного луча означает, насколько луч распространяется на расстояние. Представьте себе конус, вершина которого является теоретическим источником лазерного луча (где диаметр луча будет точным). Если вы измерите угол между двумя векторами, один из которых идет от вершины конуса к центру основания, а второй — от вершины конуса к стороне основания, то полученный угол — это то, что вы бы назвали расхождением полуугол.

Очевидно, что полный угол будет вдвое больше. Затем, зная три из четырех параметров, среди которых начальный диаметр, конечный диаметр, расстояние между диаметрами и угол расхождения, вы получите всю необходимую информацию для расчета четвертого параметра. Кроме того, если человек ясно понимает картину, он поймет, что начальный диаметр может быть, по сути, любым диаметром по оси Z и не обязательно должен быть на выходе из лазера.

Нажмите, чтобы увеличить

Формулы для диаметра и расходимости лазерного луча

Как и для всех наших лазерных вычислителей, мы предполагаем, что луч имеет форму идеального луча TEM₀₀ Гаусса и что расходимость постоянна. Это означает, что мы также предполагаем, что оба диаметра находятся внутри одной и той же однородной, непрерывной и изотропной среды. В противном случае дивергенция была бы функцией пространства, а значит, не постоянной. Эти уравнения можно использовать для расчета диаметров лазерного луча и расходимости (половинного угла).

Ссылка: Салех, Б.Е.А., и Тейч, М.К. (2007). Основы фотоники (2-е изд.). Wiley-Interscience.

$$ \text{Расхождение (полуугол)} = Arctan\left(\frac{\text{Второй диаметр}(м) — \text{Первый диаметр}(м)}{2 \times \text{Расстояние между диаметрами }(м)}\справа) $$

Щелкните правой кнопкой мыши, чтобы скопировать

$$ \text{Диаметр луча}(м) = 2 \times \text{Расстояние}(м) \times Tan(\text{Расхождение(полуугол)}) + \text{Начальный диаметр}(м) $$

Щелкните правой кнопкой мыши, чтобы скопировать

Связанные калькуляторы

• Преобразователь длины волны и частоты

• Калькулятор пиковой плотности мощности лазера и формула

• Калькулятор размера лазерного пятна и ширины луча и формулы

Посмотреть все калькуляторы

Диаграммы внутренних усилий для двухопорной балки

Этот онлайн-калькулятор показывает диаграммы внутренних усилий для простой (двухопорной) балки, с одной стороны шарнирно закрепленной, а с другой опирающейся на ролики, под действием системы нагружения. Калькулятор графически изображает изгибающий момент M и поперечную силу Q, действующие вдоль стержня. Построение необходимо для определения положения наиболее нагруженного (опасного) участка балки.
Теория и расчетные формулы находятся под калькулятором.

Просто введите данные системы нагрузки в приведенную ниже таблицу и получите диаграммы свободного тела, поперечной силы и изгибающего момента.

Shear force and bending moment in the two-support beam

Distance between supports, m

Load

	  Distance to the support A	  Load	  Значение	  Direction	  Moment direction	  Range	  Difference

Кол-во на странице:

51020501001000

Нагрузка

Расстояние до опоры A

Может быть отрицательным, если нагрузка действует слева от опоры A

Сила нагрузки, кН Равномерно распределенная нагрузка, кН/м Линейно распределенная нагрузка, кН/м Момент, кН*м

НаправлениеВнизВверх

Направление момента По часовой стрелкеПротив часовой стрелки

РазностьУменьшениеУвеличение

Import dataImport error

«Один из следующих символов используется для разделения полей данных: табуляция, точка с запятой (;) или запятая (,)» Пример: -50,5;L;50,5;вверх;против часовой стрелки;50,5;увеличение

Загрузка данные из файла .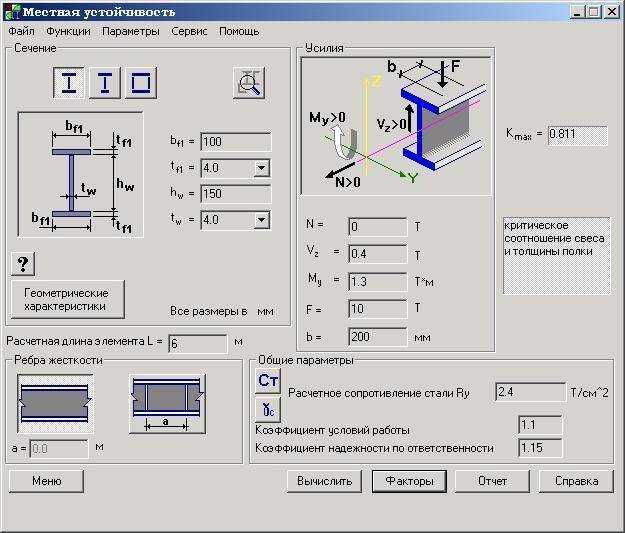 csv.

• Перетащите файлы сюда

Показать подробности

Точность расчета

Знаки после запятой: 2

Диаграммы поперечной силы и изгибающего момента

Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.

Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.

Внутренние силы

На следующем рисунке показаны внутренние силы в балке под нагрузкой.

Балка под нагрузкой. Внутренние силы в сечении.

Для определения внутренних сил в точке В проведем воображаемый разрез перпендикулярно оси x по осям y и z.

Схема свободного тела сегментов балки

Схема свободного тела сечения балки выставляет внутренние силы, действующие в точке B, как внешние. Составляющая силы N _B , действующая вдоль оси x, называется нормальной силой . Мы пропускаем вычисление нормальной составляющей силы в калькуляторе, так как он допускает только нагрузки, действующие перпендикулярно балке.
Составляющая внутренней силы Q _B , действующая параллельно поперечному сечению, называется поперечной силой . Калькулятор получает только компонент y силы шептала, потому что компонент z равен нулю для перпендикулярных нагрузок.
Парный момент M _B называется изгибающим моментом .
Изгибающий момент равен сумме всех силовых моментов, приложенных к сегменту балки относительно центра тяжести сечения.
Компоненты силы препятствуют относительному переносу между двумя сегментами, а парный момент предотвращает относительное вращение. ¹

Диаграммы внутренних сил путем интегрирования.

Найдем формулы для расчета значений поперечной силы Q(x) и изгибающего момента M(x) отдельно для разных отрезков балки.
Границы сегментов имеют выступающие точки: концы балок, места опор, точки приложения сосредоточенных сил и сосредоточенных моментов, границы распределенных нагрузок.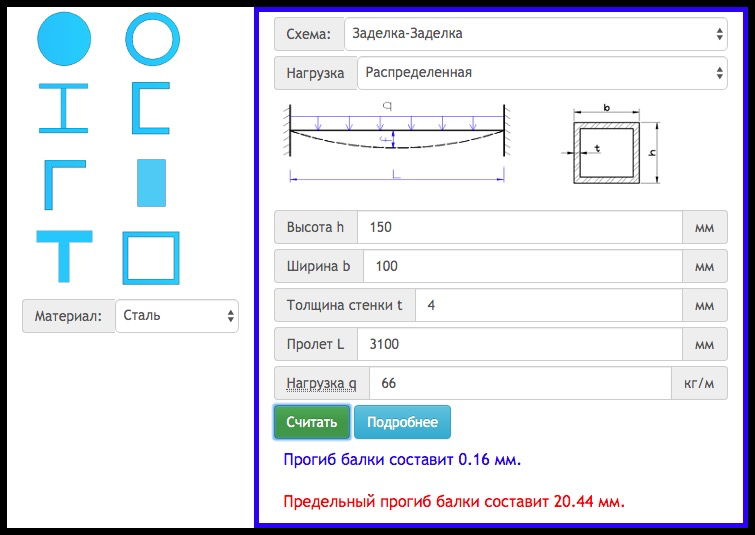
Для каждого сегмента вычисляется интеграл функции распределенной нагрузки q (x) для определения поперечной силы Q (x). Следующим шагом является вычисление интеграла Q(x) для определения функции изгибающего момента M(x) в соответствии с формулами:

²

Распределенная нагрузка q (x) в нашем калькуляторе может быть линейной, линейно убывающей или возрастающей. В первом случае q(x) — постоянная, во втором — линейная функция: q(x) = kx + b. При отсутствии распределенных нагрузок в сечении поперечная сила будет постоянной.
Таким образом, чтобы найти функции Q (x), а также M (x), необходимо будет получить неопределенный интеграл от многочлена и вычислить константу интегрирования. Константу интегрирования легко найти, если известна некоторая точка, через которую проходит искомая функция. См.: Полиномиальный интеграл.

В качестве такой точки возьмем значения Q(x) и M(x) по левой границе каждого отрезка.
Q (x _l ) будет равно значению функции поперечной силы для предыдущего сегмента в крайней правой точке сегмента плюс величина сосредоточенной силы (или опорной реакции) в этой точке, если таковая имеется. Если сила действует вверх, то изменение Q(x) положительно, в противном случае отрицательно.
M (x _l ) будет равно значению функции изгибающего момента M (x) для предыдущего отрезка в его крайней правой точке, сдвинутой на величину приложенного к этой точке сосредоточенного момента, если он есть. Если сосредоточенный момент направлен по часовой стрелке, то сдвиг положительный, в противном случае — отрицательный.

Значение Q(x) на левой кромке балки будет соответствовать сумме сосредоточенных сил и реакции опоры в этой точке или равно нулю, если таковых нет. Величина М(х) на концах балки равна сумме значений сосредоточенных моментов, приложенных к концам балки. Если в этих точках нет сосредоточенных моментов, то М(х) будет равно нулю.

Знаки М(х) и Q(х) могут быть связаны с характером деформации балки под действием внешних сил. Если изгибающий момент в сечении положительный, то балка в этом сечении изгибается выпуклостью вниз, если он отрицательный, то балка изгибается выпуклостью вверх.

Пример

Рассмотрим расчет Q(x) и M(x) на примере:

Схема свободного тела двухопорной балки

Откройте этот пример в калькуляторе.

1. Во-первых, найти реакцию поддержки. Вы можете увидеть, как это сделать на этой странице.
   Расчетные опорные реакции:
   
   
2. Разделение балки на сегменты по ключевым точкам: 0, 2, 4, 5, 6.
   Участок А — граничные точки: 0,2
   Участок В — граничные точки: 2,4
   Участок С — граничные точки: 4,5
   Сегмент D — граничные точки: 5,6
3. Для каждого сегмента:
   • найти формулу распределенной нагрузки q(x)
   • интегрируйте его, чтобы получить формулу силы сдвига Q(x).
   • снова проинтегрируйте, чтобы получить формулу изгибающего момента M(x).
     Константы интегрирования вычисляются по координате левой границы отрезка по формулам для предыдущего отрезка
     Участок А, граничные значения

     Сегмент А

     Распределенная нагрузка равна: q(x) = 5. Интегрируем q(x), чтобы найти поперечную силу:
     
     Найти постоянную интегрирования C = Q(x)+5x в точке x=0. В норме поперечная сила на концах балки равна нулю, а на левом конце она изменяется опорной реакцией V _A =11,56кН, направленной вверх. Итак, поперечная сила в точке 0 равна: Q(0) = 0 + 11,56 = 11,56.
     Отсюда C = 11,56 — 5 ⋅ 0 = 11,56
     Поперечная сила для сегмента А:
     
     Интегрируя функцию поперечной силы Q(x), получаем формулу изгибающего момента:
     
     У нас нет сосредоточенных моментов в точке 0, поэтому M( 0) = 0,
     Подставив x = 0 и M(0) = 0 в выражение для C = M(x) + 2,5x ² — 11,56x = 0 + 2,5 · 0 ² — 11,56 0, получим значение C = 0
     Изгибающий момент для сегмента A:
     

Участок B, граничные значения

Участок B

Чтобы найти функцию распределенной нагрузки q(x), мы используем линейное уравнение из двух точек.
По точкам (2;0) и (4;8) находим это уравнение: q(x) = 4x-8.
Интегрируйте эту функцию, чтобы найти формулу поперечной силы.

По формуле предыдущего отрезка Q(x) вычислить Q на левой границе: Q(2)=-5∙2+11,56 = 1,56. Аналогично предыдущему отрезку найти интеграл и постоянную интегрирования по точке (2;1.56).
Формула поперечной силы сегмента B:
^{см. расчет}
Найти значение момента в точке x=2 по формуле предыдущего сегмента M(x): M(2) = -2,5 ∙ 2 ² + 11,56 ∙ 2 + 0 = 13,12 .
Интегрирование Q(x) и вычисление константы интегрирования по левому граничному значению получить формулу изгибающего момента для отрезка B:
^{см. расчет}

отрезок C, граничные значения

отрезок C

Рассчитать поперечную силу в точке 4 по отрезку B поперечную силу Q(x) по формуле: Q(4 ) = -2 ∙ 4 ² + 8 ∙ 4 – 6,44 = -6,44.
Сосредоточенная сила F _1=4кН резко меняет значение Q(x) в точке x=4. Она направлена ​​вниз, поэтому сложение отрицательное: Q(4) = -6,44 — 4 = -10,44
На этом отрезке нет распределенной нагрузки, поэтому поперечная сила постоянна.
Формула поперечной силы на участке С:

Значение изгибающего момента в точке x=4 рассчитывается по формуле M (x) для предыдущего участка: M(4) = -0,67 ∙ 4 ³ + 4 ∙ 4 ² – 6,44 ∙ 4 + 15,33 = 10,91
Интегрируем Q(x) и вычисляем C по граничному значению получаем формулу изгибающего момента отрезка С:
^{см. расчет}

Участок D, граничные значения

Участок D 903 Поскольку распределенной нагрузки нет, поперечная сила вдоль этого отрезка постоянна.

Сила сдвига на участке D:

Рассчитать граничное значение M(5) по предыдущей формуле M(x): M(5) = -10,44 ∙ 5 + 52,67 = 0,47
Сосредоточенный момент M ₁ изменений M _х на данный момент. Сосредоточенный момент направлен по часовой стрелке, поэтому сложение положительное: M(5) = 0,47 + 10 = 10,47
Интегрируем Q(x) и получаем C получаем формулу изгибающего момента для сегмента D:
см.