2. Построения эпюры материалопотока

Эпюра представляет собой графическое изображение материалопотока на данном участке трассы.

При помощи эпюры создается наглядная схема перемещения грузов между пунктами отправления и назначения, определяется транспортная работа, устанавливается наиболее выгодное распо­ложение стоянок транспорта.

Особое значение эпюра материалопотока имеет для разработки маршрутов работы транспорта, обеспечивая наибольшую произ­водительность транспортных средств и снижение стоимости доставки продукции.

Показатели, которые рассчитываются при построении эпюры материалопотока:

P = Q×l_ср;

l_гр = P/Q;

K_н = Q_max/Q_min,

где Q – объем перевозки в разных направлениях, т;

l_ср

– среднее расстояние перевозки, км;

l_гр– груженый пробег, км;

Р – транспортная работа (грузооборот), ткм.

Данные объема перевозок между пунктом отправления и назначения приведены в табл. 1.2.

Расстояние между пунктами, км: А – Б (Б – А) — 15 км; Б – В (В – Б) — 20 км; В – Г (Г – В) — 30 км.

Таблица 1.2

Исходные данные для построения эпюры материалопотока

Пункты отправления	Объем перевозок, Т				Отправлено (вывоз), Т
	Пункты назначения
	А	Б	В	Г
А	=	200	300	400	900
Б	100	=	200	300	600
В	200	300	=	100	600
Г	300	100	200	=	600
Получено (ввоз), Т	600	600	700	800	2700

Решение.

При построении эпюры мы имеем два направления продвиже­ния материалопотока (АГ и ГА). Условимся, что вверх от нулевой отметки мы будем откладывать то направление, которое имеет наибольший объем перевозок по сравнению с другим.

1. Определяем объем перевозок в направлениях:

Направление АГ Q_АГ = Q_АБ + Q_АВ + Q_АГ +Q_БВ + Q_БГ + Q_ВГ =200 + 300 + 400 + 200 + 300 + 10 = 1500 т.

Направление ГА: Q_ГА = Q_ГА + Q_ГБ + Q_ГВ +Q_ВА + Q_ВБ + Q_БА = 300 + 100 + 200 + 200 + 300 + 100 = 1200 т.

Так как АГ > ГА, т. е. 1500 > 1200, то направление АГ откладывается вверху.

Общий объем перевозок: Q_об = Q_АГ + Q_ГА = 1500 + 1200 = 2700 т.

2. Определяем транспортную работу в направлениях:

Направление АГ: Р_АГ = 200 × 15 + 300 × 35 + 400 × 65 + 200 × 20 + 300 × 50 + 100 × × 30 = 61 500 ткм.

Направление ГА: Р_ГА = 300 × 65 + 100 × 50 + 200 × 30 + 200 × 35 + 300 × 20 + 100 × ×15 = 44 000 ткм.

Общая транспортная работа: Р_об = Р_АГ + Р_ГА = 61 500 + 44 000 = = 105 500 ткм.

Среднее расстояние перевозки: l_ср = Р_об / Q_об = 105500 / 2700 = 39,0 км.

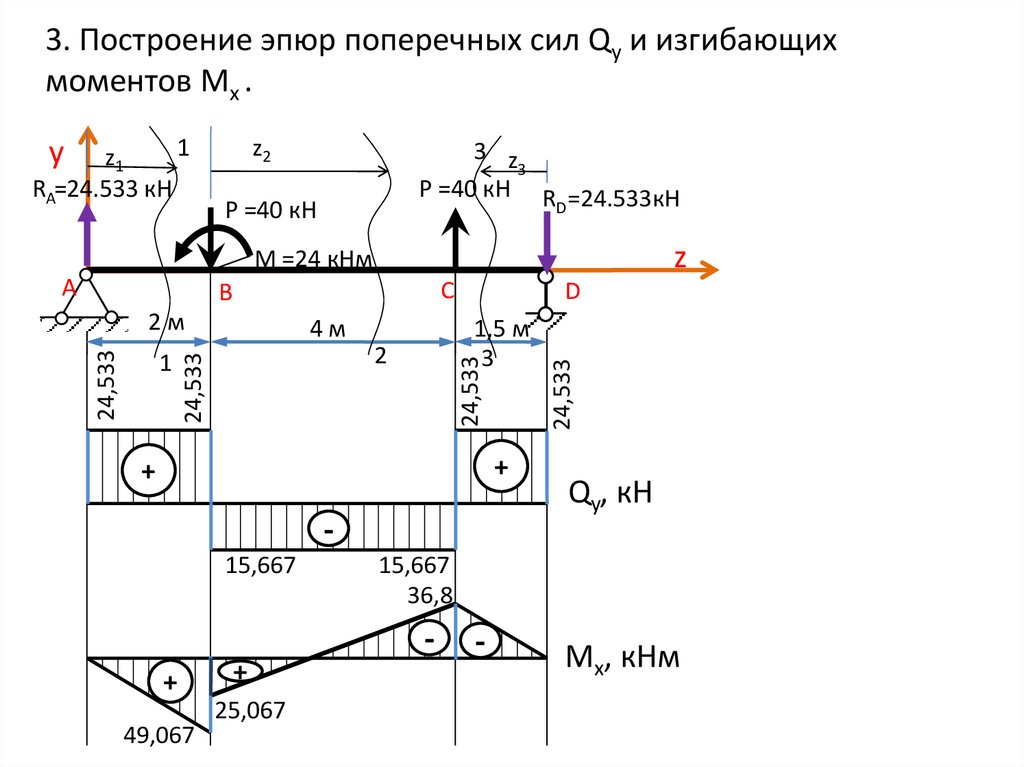
3. Построение эпюры материалопотока (рис. 1.1).

Рис. 1.1. Эпюра материалопотока

Эпюра строится в координатах «объем перевозки — расстояние».

«Объем перевозки» Q, т, откладывается по оси ординат, а «расстояние перевозки» l, км, — по оси абсцисс. Эпюра строится в соответствии с выбранным масштабом.

Для удобства построения начинают с объема перевозок, идущего от пункта А к пункту Г, т. е. с самого дальнего. Полученное пространство между осевой и проведенной линией заштриховывается. Затем откладывается объем перевозок из А в пункт В, т. е. 300 т. Откладываем не от 0, а от объема, который имеется на данном участке. Полученное пространство также заштриховывается. Аналогично откладываются и следующие объемы перевозок. Нижняя часть эпюры строится таким же способом, что и верхняя.

Грузопотоки могут быть также изображены в виде схемы. Схемы грузопотоков строятся с использованием карты района перевозок, на которой нанесены пункты или микрорайоны отправления и назначения груза, т. е. грузообразующие и грузопоглощающие точки. Карту района перевозок делят на квадраты последовательным нанесением на равном расстоянии взаимно перпендикулярных линий.

Полученные таким образом квадраты кодируют по буквенно-цифровой системе (по типу шахматной доски): по горизонтали — буквы, по вертикали — цифры. Затем сетку квадратов с нанесенными на них грузопунктами переносят на чистый лист чертежной бумаги с соблюдением масштабов, причем сетка может быть пропорционально увеличена или уменьшена. Зная количество тонн груза, подлежащее перевозке из пунктов отправления в пункты назначения, выбираем масштаб и наносим грузопотоки линиями определенной ширины в соответствии с принятым масштабом. Масштаб для всех грузопотоков, изображенных на данной схеме, может быть только один, т. е. нельзя изображать грузопотоки в различных масштабах. На рис. 1.2 показана схема грузопотоков.

Грузопотоки могут также иметь вид картограммы. Картограмма — это графическое изображение грузопотоков на карте по действительным путям перемещения грузов.

При помощи схем и эпюр создается наглядная схема перемещения грузов, определяется транспортная работа в тонно-километрах (которая равна площади грузопотоков в масштабе), устанавливается наиболее выгодное расположение стоянки автотранспорта или автохозяйства, чтобы непроизводительные пробеги из гаража к месту работы или обратно были минимальными.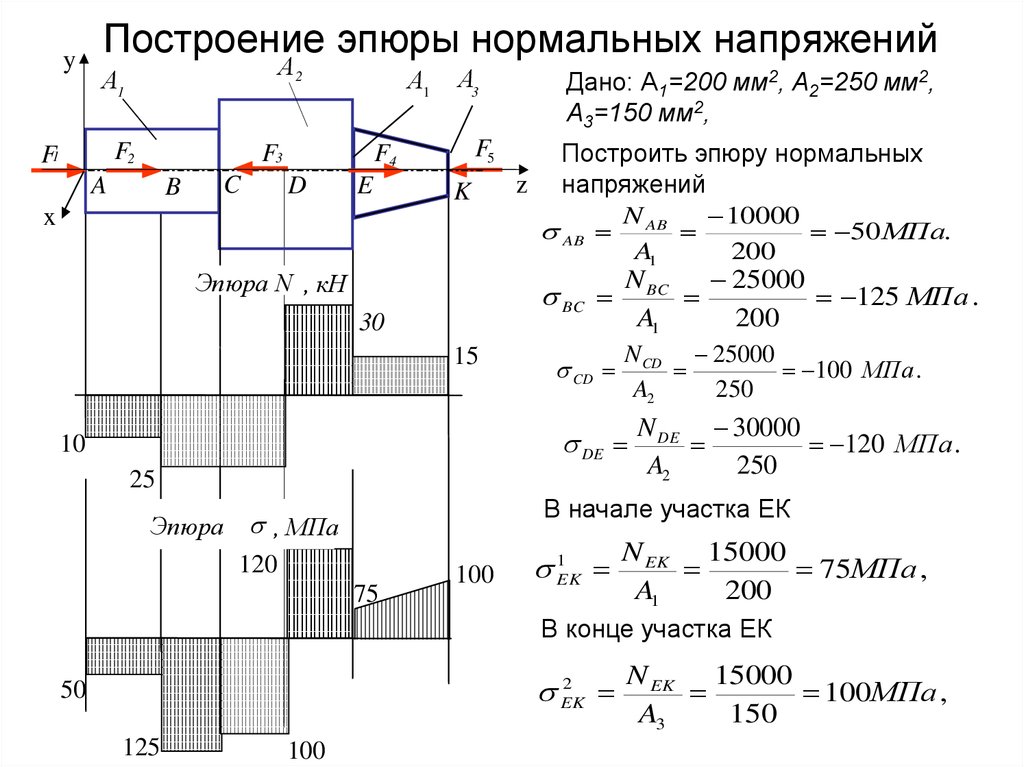

Особое значение имеют схемы, эпюры, картограммы грузопотоков для разработки маршрутов работы транспорта, обеспечивающих наибольшую производительность транспортных средств и снижение стоимости доставки.

Задачи

Задача 1.1.

Используя данные табл. 1.3 построить эпюру материалопотока

Таблица 1.3

Синус, косинус, тангенс и котангенс в тригонометрии: определения, формулы, примеры

Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии без таблиц и графиков.

Синус, косинус, тангенс и котангенс. Определения

Зачем разделять понятия синуса, косинуса, тангенса и котангенса?

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Что такое синус?

Синус угла (sin α) — это отношение противолежащего этому углу катета к гипотенузе.

Что такое косинус?

Косинус угла (cosα) — это отношение прилежащего катета к гипотенузе.

Что такое тангенс?

Тангенс угла (tg α) — это отношение противолежащего катета к прилежащему.

Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

Синус и косинус можно представить через экспоненту (экспоненциальная функция).

Приведем иллюстрацию. 

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.

Что и почему важно и принято помнить в ходе такого нахождения?

Важно помнить!

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг — вся числовая прямая, то есть эти функции могут принимать любые значения.

Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором — теорему косинусов.

Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы. 

Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).

Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞. 

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.

                                                                 

Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y). 

Синус (sin или син) угла поворота

Синус угла поворота α — это ордината точки A1(x , y).  sin α=y

Косинус (cos) угла поворота

Косинус угла поворота α — это абсцисса точки A1(x , y). cos α=икс

Тангенс (tg) угла поворота

Тангенс угла поворота α — это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx

Котангенс (ctg) угла поворота

Котанг угла поворота α — это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Важно помнить!

Простое правило: синус и косинус определены для любых углов α.

Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)

Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)

При решении практических примеров не говорят «синус угла поворота α». Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь. 

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10π равен синусу угла поворота величиной 10π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности — точка A c координатами (1, 0).

Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.

Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус (sin) числа t

Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t=y

Косинус (cos) числа t

Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t=x

Тангенс (tg) числа t

Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k ,   k ∈ Z   ( α = π 2 + π · k ,   k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k ,   k ∈ Z   ( α = π · k ,   k ∈ Z ). 

Можно сказать, что sin α, cos α, tg α, ctg α — это функции угла альфа, или функции углового аргумента. 

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k ,   k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k ,   k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс — основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело. 

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью  соотношений сторон прямоугольного треугольника. Покажем это.

                                                                     

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.  

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе. 

sin α=A1HOA1=y1=y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Синус, косинус, тангенс и котангенс: основные формулы

​​​​​​​

Создать график онлайн и найти кратчайший путь или использовать другой алгоритм

Создать график и найти кратчайший путь. На странице помощи вы найдете обучающее видео.

График

Алгоритм создания

Вставьте свой алгоритм ниже и нажмите «Выполнить».

Введите название

Установить матрицу смежности. Используйте запятую «,» в качестве разделителя

Матрица мультиграфа содержит вес минимальных ребер между вершинами.

Матрица неверна. Используйте запятую «,» в качестве разделителя. Матрица должна быть квадратной

Настройте матрицу заболеваемости. Используйте запятую «,» в качестве разделителя.

Матрица неверна. Используйте запятую «,» в качестве разделителя.

Ваш алгоритм отправлен на проверку и в случае успеха он будет добавлен на сайт.

Невозможно создать график. Матрица смежности имеет неправильный формат. Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «Справка», чтобы открыть справку о формате матрицы смежности

.

Невозможно создать график. Матрица заболеваемости имеет неправильный формат. Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «Справка», чтобы открыть справку о формате матрицы заболеваемости

.

Невозможно создать график. Список краев имеет неправильный формат. Нажмите кнопку «исправить», чтобы исправить список краев, или кнопку «Справка», чтобы открыть справку о формате

.

Какие функции мы должны добавить в первую очередь?

Напишите, пожалуйста, какой алгоритм вы бы хотели видеть на этом сайте?

Наш сервис уже поддерживает следующие функции: Поиск кратчайшего пути с помощью алгоритма Дейкстры, Матрица смежности, Матрица инцидентности.

Непрозрачность

Выбор и перемещение объектов мышью или перемещение рабочей области.

Перетащите курсор для перемещения объектов

Выбор и перемещение объектов мышью или перемещение рабочей области.

Перетащите курсор для перемещения объектов

Щелкните в рабочей области, чтобы добавить новую вершину. Перечисление вершин

Выберите первую вершину ребра

Выберите вторую вершину ребра

Выберите начальную вершину кратчайшего пути

Выберите конечную вершину кратчайшего пути

Длина кратчайшего пути составляет %d

Путь не существует

Нажмите на объект, чтобы удалить

Добавить ребро

Режиссер

Ненаправленный

Матрица смежности

Сохранить

Отменить

наименьшее расстояние

Матрица заболеваемости

Сохранение графика

закрыть

Количество подключаемых компонентов

Количество слабо связанных компонентов

Что вы думаете о сайте?

Имя (электронная почта для обратной связи)

Обратная связь

Отправить

Чтобы задать нам вопрос или отправить нам комментарий, напишите нам по телефону

исправить матрицу

помощь

Матрица имеет неправильный формат

Сохранить изображение графика

Полный отчет

Краткий отчет

Граф не имеет эйлерова цикла

Граф имеет эйлеров цикл

Обработка. ..

Добавить вершину

Переименовать вершину

Переименовать

и

Редактировать вес

не имеет веса

Переименование группы

Проголосовать

Рекомендовать алгоритмы

Граф не имеет эйлерова пути

Граф имеет эйлеров путь

График минимальных расстояний

Проверить, чтобы сохранить

Показать матрицу расстояний

Матрица расстояний

Выберите источник максимального расхода

Выберите сток максимального расхода

Максимальный поток от %2 до %3 равен %1

Поток из %1 в %2 не существует

Источник

Раковина

Граф не имеет гамильтонова цикла

Граф имеет гамильтонов цикл

Граф не имеет гамильтоновой траектории

Граф имеет гамильтонов путь

Выбрать начальную вершину обхода

Порядок обхода:

Изгиб кромки

Отменить

Сохранить график

По умолчанию

Вершинный стиль

Стиль кромки

Цвет фона

Мультиграф поддерживает не все алгоритмы

не имеет веса

Используйте Cmd⌘ для выбора нескольких объектов.

Используйте Ctrl для выбора нескольких объектов.

Группа перетаскивания.

Группа копирования

Удалить группу

Поиск в ширину

Раскраска графа

Найти подключенные компоненты

Поиск в глубину

Найти цикл Эйлера

Найти эйлеров путь

Алгоритм Флойда-Уоршалла

Упорядочить график

Найти цикл Гамильтона

Найти гамильтонов путь

Найти максимальный расход

Поиск минимального остовного дерева

Визуализация на основе веса

Радиус и диаметр графа поиска

Найти кратчайший путь с помощью алгоритма Дейкстры

Вычислить степень вершин

Вес минимального остовного дерева

При расчете мы не учитывали направление ребер.

График отключен

Выберите первый график для проверки изоморфности. Нажмите на любой узел графа

Выберите второй график для проверки изоморфности. Нажмите на любой узел графа

Выберите шаблон графика, щелкнув любой узел графика

Выбираем граф, в котором будем искать изоморфные подграфы. Нажмите на любой узел этого графа

Графы изоморфны

Графики не изоморфны

Количество изоморфных подграфов

Граф не содержит изоморфных подграфов

Поиск изоморфных подграфов

Изоморфный подграф #

Для использования алгоритма необходимо создать 2 отдельных графика

Проверка изоморфизма графов

График отключен

Граф содержит только одну вершину

Радиус графика

Диаметр графика

Центральный

Периферийный

Максимальная степень графа

Номер цвета

Готово

Действия

Общий стиль кромки

Выбранный стиль кромки

Общий стиль вершин

Выбранный стиль вершин

Найти все пути

Количество путей от

от

до

это

Путь #

Выберите финишную вершину

Выберите начальную вершину

Найти все кратчайшие пути из вершины

Расстояние от

Путь к

Найдите самый длинный путь

Длина самого длинного пути из

Специальные действия

Перевернуть все кромки

Сделать все ребра неориентированными

Сделать все ребра направленными

Неверный формат списка ребер

исправить

Повторное использование сохраненного фронта

Prism — GraphPad

Лучшее решение для анализа и построения графиков, специально разработанное для научных исследований.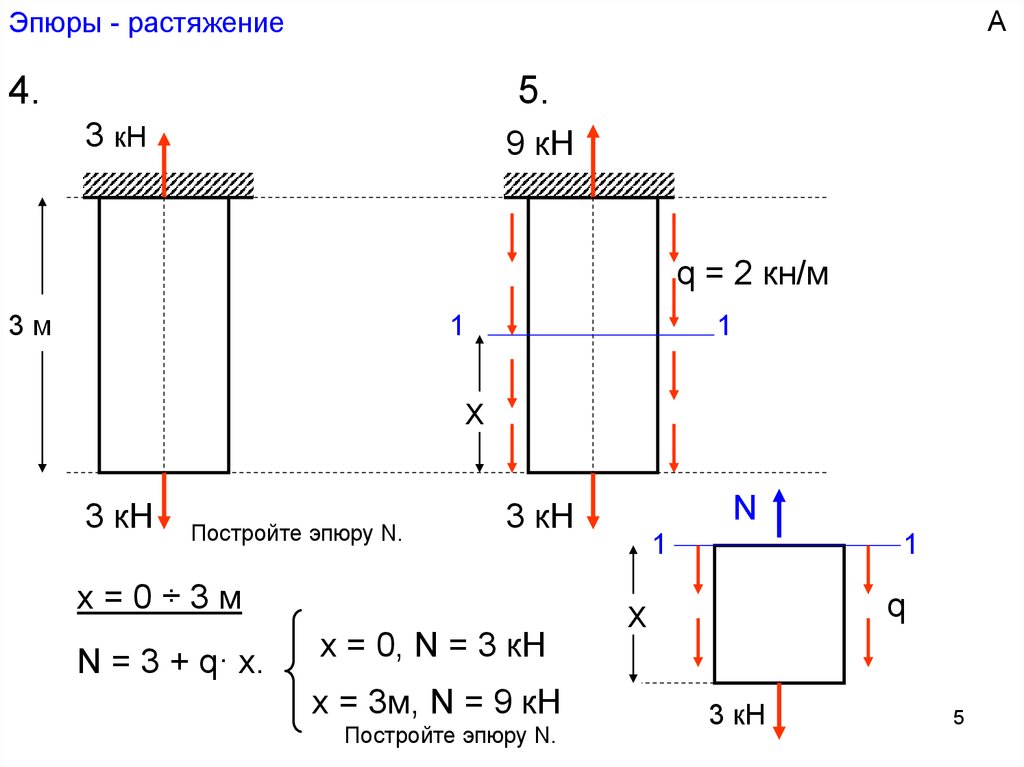 Присоединяйтесь к ведущим мировым ученым и узнайте, как использовать Prism для экономии времени, выбора более подходящего анализа, а также для создания элегантных графиков и представления результатов научных исследований.

Начать бесплатную пробную версию

Цены

Узнайте, что нового

Упрощенный комплексный анализ и мощная статистика

Эффективная организация данных

Prism специально отформатирован для анализа, который вы хотите выполнить, включая анализ количественных и категорийных данных. Это упрощает правильный ввод данных, выбор подходящего анализа и создание потрясающих графиков.

Начать бесплатную пробную версию

Выполнить правильный анализ

Избегайте статистического жаргона. На понятном языке Prism представляет обширную библиотеку анализов от общих до высокоспецифичных: t-тесты, одно-, двух- и трехфакторный дисперсионный анализ, линейная и нелинейная регрессия, кривые доза-реакция, бинарная логистическая регрессия, анализ выживаемости, главный компонент.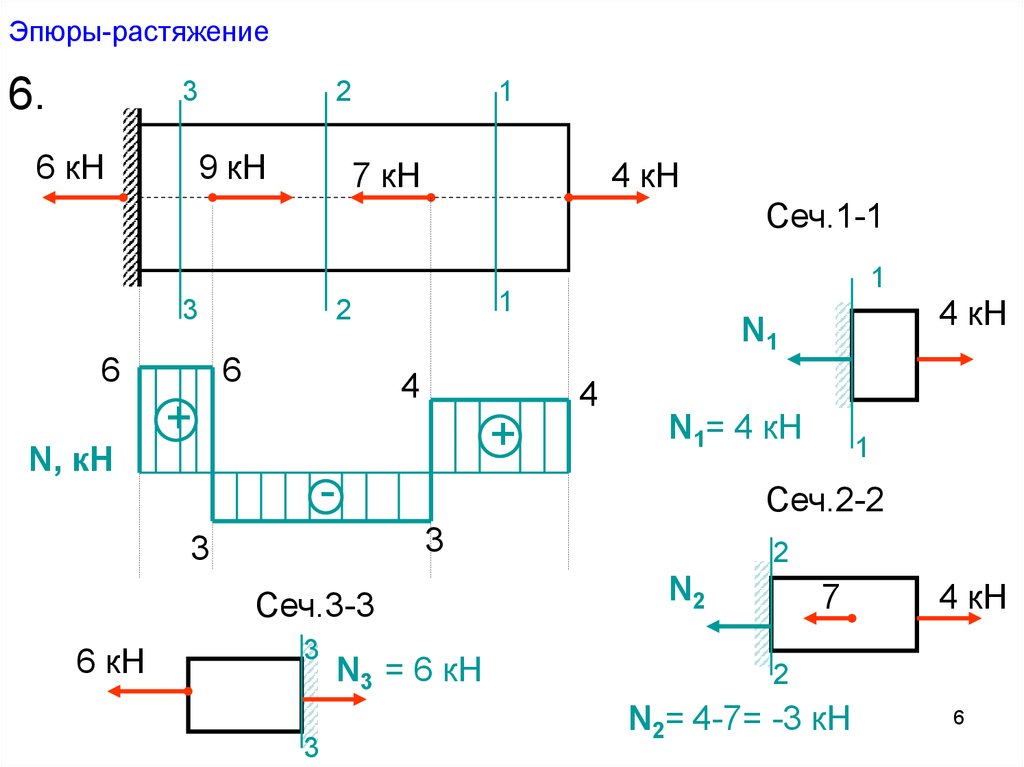 анализ и многое другое. Для каждого анализа есть контрольный список, который поможет вам понять необходимые статистические допущения и подтвердить, что вы выбрали подходящий тест.

Начать бесплатную пробную версию

Получать полезную помощь в процессе работы

Уменьшить сложность статистики. Онлайн-помощь Prism превосходит ваши ожидания. Практически на каждом этапе вы получаете доступ к тысячам страниц руководств пользователя Prism. Учитесь с помощью видеоуроков, руководств и учебных материалов Prism Academy. Просмотрите портфолио графиков и узнайте, как создавать различные типы графиков. Учебные наборы данных также помогут вам понять, почему вы должны выполнять определенные анализы и как интерпретировать ваши результаты.

Начать бесплатную пробную версию

Работайте умнее, а не усерднее

Регрессионный анализ одним щелчком мыши

Ни одна другая программа не упрощает подбор кривых так, как Prism. Выберите уравнение, и Prism сделает все остальное — подгонит кривую, отобразит таблицу результатов и параметров функции, нарисует кривую на графике и интерполирует неизвестные значения.

Начните бесплатную пробную версию

Сосредоточьтесь на своих исследованиях, а не на программном обеспечении

Prism выполнит программирование за вас. Графики и результаты автоматически обновляются в режиме реального времени. Любые изменения в данных и анализах — прямой ввод данных, пропуск ошибочных данных, исправление опечаток или изменение выбора анализа — мгновенно отражаются в результатах, графиках и макетах.

Начать бесплатную пробную версию

Автоматизируйте свою работу без программирования

Автоматически добавляйте несколько парных сравнений в свой анализ одним щелчком мыши. Для настройки параметров этих линий и звездочек просто нажмите кнопку на панели инструментов еще раз. Внесите коррективы в данные или анализ, и результаты, отображаемые на графике, будут обновляться автоматически.

Начать бесплатную пробную версию

Самый быстрый способ создать элегантную графику и поделиться своей работой

Бесчисленные способы настройки графиков

Сосредоточьтесь на истории ваших данных, а не на манипулировании вашим программным обеспечением. Prism позволяет легко создавать нужные вам графики. Выберите тип графика и настройте любую часть — порядок расположения данных, стиль точек данных, метки, шрифты, цвета и многое другое. Варианты настройки безграничны.

Начать бесплатную пробную версию

Исследуйте свои данные

Сосредоточьте свои усилия на анализе наиболее важных данных. Настройте способ представления взаимосвязей в данных, чтобы эффективно исследовать большие наборы данных.

Начать бесплатную пробную версию

Экспорт графиков качества публикации одним щелчком мыши

Сокращение времени публикации. Prism позволяет настраивать экспорт (тип файла, разрешение, прозрачность, размеры, цветовое пространство RGB/CMYK) в соответствии с требованиями журналов. Установите настройки по умолчанию, чтобы сэкономить время.

Начать бесплатную пробную версию

Улучшить совместную работу

Делитесь не только своими графиками. Полная запись ваших данных Prism позволяет эффективно сотрудничать с другими учеными. Все части вашего проекта Prism (необработанные данные, анализы, результаты, графики и макеты) содержатся в одном файле, которым вы можете поделиться одним щелчком мыши. Теперь другие могут легко следить за вашей работой на каждом этапе, повышая четкость ваших выводов и оптимизируя ваши совместные усилия.

Начать бесплатную пробную версию

Узнайте, что нового в Prism!

Представляем еще более мощный Prism с улучшенной визуализацией данных и настройкой графиков, более интуитивно понятной навигацией и более сложным статистическим анализом.

Расширенная визуализация данных и настройка графиков

Пузырьковые диаграммы

Создание пузырьковых диаграмм непосредственно из необработанных данных, кодирование переменных для положения (координаты X и Y), цвета и размера

Скрипичные диаграммы

Визуализация распределений больших наборов данных с помощью расширенных или усеченных графиков скрипки

Оценочные графики

Автоматическое отображение результатов анализа

Сглаживание сплайна

количество узлов или точек перегиба

Подробнее

Улучшенные возможности построения графиков и настройки

Звезды на графике

Автоматически добавлять несколько результатов сравнения к графикам

Автоматически маркировать гистограммы

Аннотировать гистограммы значениями средних, медиан или размеров выборки, чтобы подчеркнуть, что важно в вашей работе

Улучшенные сгруппированные графики

Легко создавать графики показывать как отдельные точки (разброс), так и столбцы для среднего (или медианы) и столбцы погрешностей

Подробнее

Подробнее Интуитивная навигация

Удобный поиск связанных листов

Новая семейная панель показывает семейство листов, связанных с текущим листом, и цепочки анализов автоматически имеют отступ ; выбор вкладок для отображения или скрытия

Улучшенный поиск

Поиск по листам с выделением или примечаниями определенного цвета

Подробнее

Теперь с восемью видами таблиц данных

Таблица данных с несколькими переменными

Каждая строка представляет отдельный предмет, а каждый столбец — отдельную переменную, что позволяет выполнять множественную линейную регрессию (включая регрессию Пуассона), извлекать подмножества данных в другие типы таблиц или выбирать и преобразовывать подмножества данных. данные. Таблицы с несколькими переменными Prism поддерживают текстовые переменные и позволяют определять типы переменных

Вложенная таблица данных

Анализ и визуализация данных, содержащих подмножества в связанных группах; Выполнение вложенных t-тестов и вложенного однофакторного дисперсионного анализа с использованием данных в этих таблицах

Подробнее

Более сложный статистический анализ

Выполнение повторных измерений ANOVA даже при отсутствии данных

Теперь Prism автоматически подгонит модель смешанных эффектов для завершения этого анализа

Выполнение простой и множественной логистической регрессии

Подгонка модели к бинарный результат (да/нет, выигрыш/проигрыш, успешно/неудачно), основанный на одной предикторной переменной (простая логистическая регрессия) или многих предикторных переменных (множественная логистическая регрессия)

Анализ основных компонентов (PCA)

Рассчитайте и выберите основные компоненты, которые описывают наибольшую степень дисперсии ваших данных. Выберите один из методов отбора, включая параллельный анализ с помощью моделирования Монте-Карло, порог собственного значения, порог пропорции дисперсии и т. д.

Множественный t-критерий (и непараметрический) анализ

Одновременное выполнение нескольких независимых тестов сравнения двух выборок. Выберите из параметрических/непараметрических тестов и укажите, являются ли данные непарными/парными

Анализ категориальных переменных с текстом в методах множественной линейной и множественной логистической регрессии

Кодирование не требуется! Prism автоматически кодирует категориальные переменные и выполняет анализ. Укажите ссылку и организуйте все уровни категориальных переменных в модели для получения четких, удобочитаемых результатов

Интерполяция из множественной линейной и множественной логистической регрессии

Используйте указанную модель для прогнозирования значений зависимой переменной на основе данных в таблице данных или с использованием теоретические значения, указанные в анализе

Подробнее

Начните бесплатную 30-дневную пробную версию

Кредитная карта не требуется.

Откройте для себя множество статистических функций, доступных в Prism

Статистические сравнения

• Парные и непарные t-тесты. Сообщает значения P и доверительные интервалы.
• Автоматически генерировать график вулкана (разность со значением P) на основе множественного анализа t-критерия.
• Непараметрический критерий Манна-Уитни, включая доверительный интервал разности медиан.
• Тест Колмогорова-Смирнова для сравнения двух групп.
• Критерий Уилкоксона с доверительным интервалом медианы.
• Выполните сразу несколько t-тестов, используя False Discovery Rate (или множественные сравнения Бонферрони), чтобы выбрать, какие сравнения являются открытиями для дальнейшего изучения.
• Обычные или повторные измерения Дисперсионный анализ с последующими тестами Тьюки, Ньюмана-Кеулса, Даннета, Бонферрони или Холм-Сидака для множественных сравнений, пост-тестом на тренд или критерием наименьшего значения Фишера.
• Однофакторный дисперсионный анализ без допущения популяций с равными стандартными отклонениями с использованием дисперсионного анализа Брауна-Форсайта и Уэлча с последующими соответствующими тестами сравнения (Games-Howell, Tamhane T2, Dunnett T3)
• Многие тесты множественных сравнений сопровождаются доверительными интервалами и множественностью скорректированные значения P.
• Коррекция по Гринхаусу-Гейссеру, поэтому повторные измерения одно-, двух- и трехфакторного дисперсионного анализа не должны предполагать сферичность. Когда это выбрано, множественные сравнительные тесты также не предполагают сферичность.
• Непараметрический однофакторный дисперсионный анализ Крускала-Уоллиса или Фридмана с посттестом Данна.
• Точный критерий Фишера или критерий хи-квадрат. Рассчитайте относительный риск и отношение шансов с доверительными интервалами.
• Двухфакторный дисперсионный анализ, даже с отсутствующими значениями в некоторых посттестах.
• Двухфакторный дисперсионный анализ с повторными измерениями одного или обоих факторов. Множественные сравнения Tukey, Newman-Keuls, Dunnett, Bonferroni, Holm-Sidak или Fisher’s LSD, проверяющие основные и простые эффекты.
• Трехфакторный дисперсионный анализ (ограничен двумя уровнями по двум факторам и любым количеством уровней по третьему).
• Анализ данных повторных измерений (одно-, двух- и трехфакторный) с использованием модели смешанных эффектов (аналогичен дисперсионному анализу повторных измерений, но с возможностью обработки отсутствующих данных).
• Сравнение данных из вложенных таблиц данных с использованием вложенного t-критерия или вложенного однофакторного дисперсионного анализа (с использованием модели смешанных эффектов).

Нелинейная регрессия

• Подберите одно из 105 встроенных уравнений или введите свое собственное. Теперь включает семейство уравнений роста: экспоненциальный рост, экспоненциальное плато, Гомперца, логистическое и бета (рост, а затем спад).
• Введите дифференциальные или неявные уравнения.
• Введите разные уравнения для разных наборов данных.
• Глобальная нелинейная регрессия — общие параметры для наборов данных.
• Надежная нелинейная регрессия.
• Автоматическая идентификация или устранение выбросов.
• Сравните модели, используя F-критерий дополнительной суммы квадратов или AICc
• Сравните параметры между наборами данных.
• Применение ограничений.
• Различно взвешивайте баллы несколькими способами и оцените, насколько хорошо работает ваш метод взвешивания.
• Примите автоматические начальные оценочные значения или введите свои собственные.
• Автоматически отображать кривую в указанном диапазоне значений X.
• Количественная оценка точности подбора параметров с помощью SE или CI. Доверительные интервалы могут быть симметричными (традиционно) или асимметричными (что более точно).
• Количественная оценка симметрии неточности с асимметрией Хоугарда.
• График доверительных интервалов или диапазонов предсказания.
• Проверка нормальности остатков.
• Запускает или повторяет проверку адекватности модели.
• Сообщите ковариационную матрицу или набор зависимостей.
• Простая интерполяция точек из кривой наилучшего соответствия.
• Сопоставьте прямые линии с двумя наборами данных и определите точку пересечения и оба наклона.

Анализ выживаемости

• Анализ выживаемости Каплана-Мейера. Выполните непараметрический анализ выживаемости для разных групп и сравните расчетные кривые выживаемости для каждой группы с тестом логарифмического ранга (включая тест на тенденцию).
• Регрессия пропорциональных рисков Кокса. Выполните полупараметрический анализ выживаемости, который позволяет включать дополнительные непрерывные или категориальные переменные-предикторы (ковариаты). Автоматически создавайте графики оценочных кривых выживаемости для любого набора значений переменных-предикторов.

Анализ основных компонентов

• Выбор компонентов с помощью параллельного анализа (моделирование Монте-Карло), критерия Кайзера (порог собственного значения), порог пропорции дисперсии и т. д.
• Автоматически генерируемые графики осыпи, графики загрузки, двойные графики и многое другое.
• Используйте результаты в последующих приложениях, таких как регрессия главных компонентов.

График с несколькими переменными

• Укажите переменные, определяющие координаты осей, цвет и размер.
• Создание пузырьковых графиков.

Статистика по столбцам

• Расчет описательной статистики: минимум, максимум, квартили, среднее, SD, SEM, CI, CV, асимметрия, эксцесс.
• Среднее или среднее геометрическое с доверительными интервалами.
• Частотные распределения (бин к гистограмме), включая кумулятивные гистограммы
• Проверка нормальности четырьмя методами (новый: Андерсон-Дарлинг).
• Критерий логарифмической нормальности и вероятность выборки из нормального (гауссова) и логнормального распределения
• Создайте график QQ как часть проверки нормальности.
• Один образец t-критерия или критерия Уилкоксона для сравнения среднего (или медианы) столбца с теоретическим значением.
• Выявление выбросов с помощью метода Граббса или ROUT.
• Проанализируйте набор значений P, используя множественные сравнения Бонферрони или подход FDR для выявления «значительных» результатов или открытий.

Простая линейная регрессия и корреляция

• Расчет наклона и точка пересечения с доверительными интервалами.
• Проведите линию регрессии через указанную точку.
• Подгонка для воспроизведения значений Y или среднего значения Y.
• Тест на отклонение от линейности с помощью теста циклов.
• Расчет и построение графика остатков четырьмя различными способами (включая график QQ).
• Сравните наклоны и точки пересечения двух или более линий регрессии.
• Интерполировать новые точки вдоль стандартной кривой.
• Корреляция Пирсона или Спирмена (непараметрическая).

Обобщенные линейные модели (GLM)

• Создавайте модели, связывающие несколько независимых переменных с одной зависимой переменной, используя новую таблицу данных с несколькими переменными.
• Множественная линейная регрессия (когда Y является непрерывным).
• Регрессия Пуассона (когда Y считается; 0, 1, 2, …).
• Логистическая регрессия (когда Y является бинарным; да/нет, годен/не годен и т. д.).

Клиническая (диагностическая) лабораторная статистика

• Графики Бланда-Альтмана.
• Кривые характеристик оператора приемника (ROC).
• Регрессия Деминга (линейная регрессия II типа).