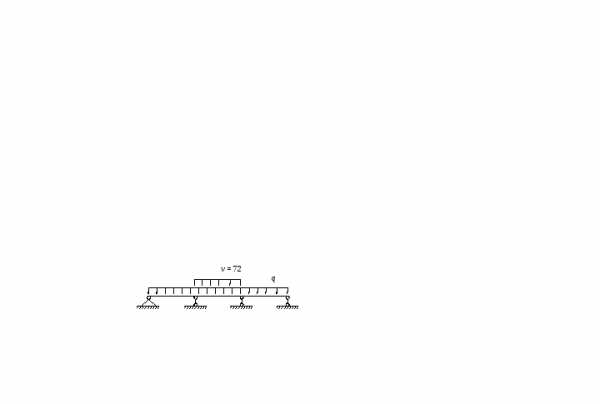
Определение усилий (m, q) и построение огибающей эпюры моментов Краткие методические рекомендации:
расчет усилий в равнопролетных ригелях (к ним относятся и ригели с пролетами, отличающимися друг от друга менее 20 % !) производится с использованием таблиц [8, 10]; при этом значения усилий в расчетных сечениях ригеля вычисляются по формулам
; ,
где , , , – табличные коэффициенты, дифференцируемые в зависимости от числа пролетов, положения сечения и рассматриваемой схемы загружения ригеля;
i, j – соответственно, порядковый номер варианта загружения и индекс расчетного сечения;
для неравнопролетных ригелей расчет усилий для каждого загружения производится обычными методами строительной механики;
в зданиях с полным каркасом расчет ригеля ведется как элемента многопролетных рам, усилия в сечениях которого определяются по аналогичным схемам [8, 10];
при количестве пролетов ригеля более пяти, расчет ригеля может выполняться как для пятипролетного в предположении, что усилия во всех упущенных средних пролетах одинаковы и равны усилиям в среднем пролете 5и пролетного ригеля;
расчетными сечениями ригеля являются все опорные и пролетные, причем, в крайних пролетах они расположены на расстоянии 0,425 l0 от крайних опор, а в промежуточных – посередине пролета;
построение огибающей эпюры моментов на данном этапе производится по упрощенной схеме, т.е. путем сложения (алгебраического!) ординат эпюр от загружения постоянной нагрузкой (схема № 1) и рассматриваемого варианта загружения временной нагрузкой.
Изгибающие моменты и поперечные силы в расчетных сечениях ригеля
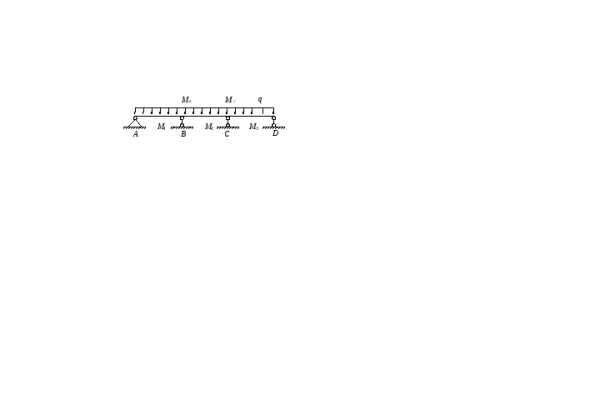
Все расчеты усилий представлены для 2х пролетов ригеля (в виду одинаковости возможных максимальных значений усилий в симметрично расположенных по длине ригеля сечениях) и с обозначениями, соответствующими схеме в табл. 5.2
Из нее следует, что расчет рабочей арматуры необходимо выполнять для следующих значений моментов:
в крайних пролетах кНм
в среднем пролете кНм
кНм
на промежуточных опорах кНм
Расчетные значения перерезывающих сил равны:
на опоре А кН
на опоре В (слева) кН
на опоре В (справа) кН
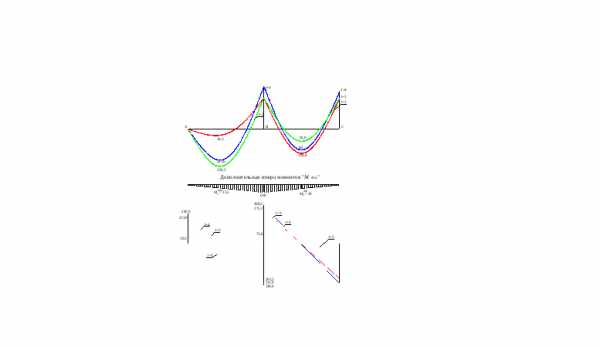
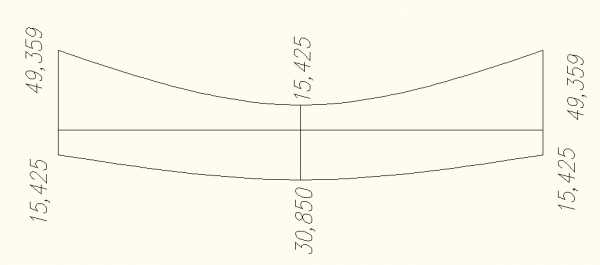
Рисунок 5.2
и перерезывающих сил.
К определению усилий в сечениях ригеля
Таблица 5.2
Номер схемы | Схема загружения | Изгибающие моменты, кНм | Перерезывающие силы, кН | ||||
М1 | М2 | МВ | QA | QВл | QВпр | ||
1 |
| 0,08 · 26,57 · 5,62= 66,7 | 0,025 · 26,57 · 5,52= 20,1 | – 0,1 · 26,57 · 5,52= –81,1 | 0,4 · 26,57 · 5,6 = 59,5 | – 0,6 · 26,57 · 5,6 = –89,2 | 0,5 · 26,57 · 5,5 = 73,1 |
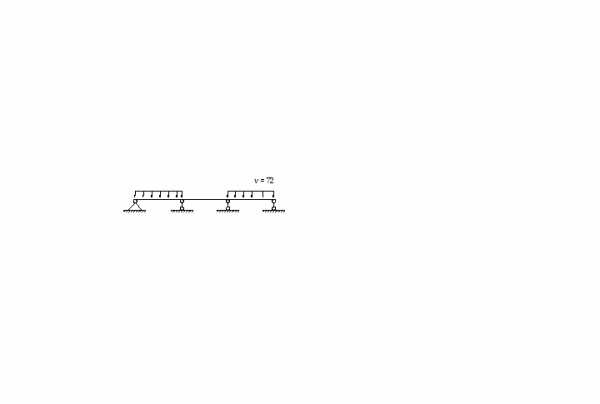
2 |
| 0,1 · 72 · 5,62= 225,8 | –0,05 · 72 · 5,52= –112,9 | – 0,05 · 72 · 5,52= –110,9 | 0,45 · 72 · 5,6 = 59,5 | – 0,55 · 72 · 5,6 = –110,9 | 0,00 |
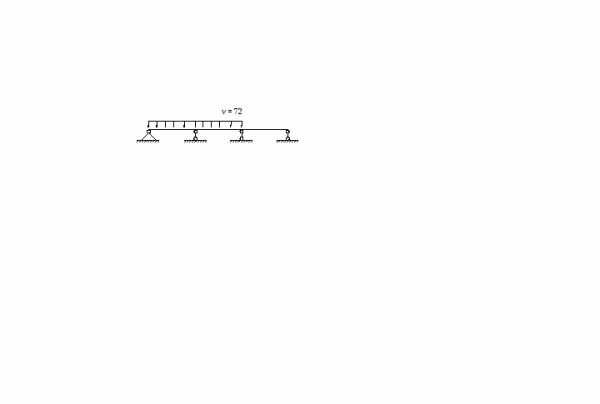
3 |
| –0,025 · 72 · 5,62= –56,4 | –0,075 · 72 · 5,52= –169,3 | – 0,05 · 72 · 5,52= –110,9 | – 0,05 · 72 · 5,6 = –20,2 | – 0,5 · 72 · 5,6 = –202 | – 0,5 · 72 · 5,6 = –202 |
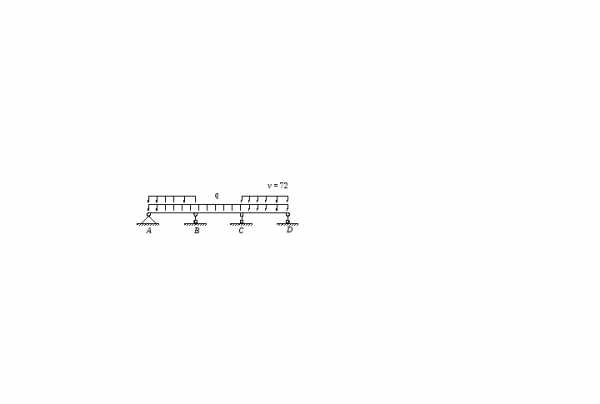
4 |
| – *) | – *) | – 0,117 · 72 · 5,5 2= –259,5 | 0,383 · 72 · 5,6 = 154,4 | – 0,617 · 72 · 5,6 = –248,8 | – 0,583 · 72 · 5,6 = 235,1 |
1+2 |
| 292,5 | – 92,8 | – 192,7 | 240,9 | – 311,0 | 73,6 |
1+3 |
| 10,3 | 189,4 | –192,7 | 39,3 | 275,1 | |
1+4 |
| – *) | – *) | – 341,3 | 213,9 | – 338,0 | 308,2 |
Примечание: 1) *) графы не заполнены ввиду отсутствия в таблицах [6, 7] значений коэффициентов для данного вида загружения (они не показательны!)
2) выделены экстремальные значения усилий
studfiles.net
На основании полученных данных мы можем построить так называемую «огибающую» эпюру моментов, т.е. такую эпюру, на которой будут учтены значения моментов в пролетах при временной нагрузке по схемам г) и д). Другими словами мы на основную эпюру «М б+в» наложим эпюры «Мб+г» и «Мб+д«. Огибающая эпюра нужна нам для того, чтобы определить пределы, в которых изгибающий момент будет вызывать растяжение верхней зоны сечения плиты.
Дополнительных данных будет не так уж и много
Мб+д1(l/2) = 74.73 — 12.032 = 62.7 кгс·м
Мб+г2 = 34.326 — 21.06 = 13.266 кгс·м
Мб+д3 = 47.47 — 18.049 = 29.52 кгс·м
Мб+гВ = Мб+дВ = — 108.7 — 24.064 = — 132.76 кгс·м
Мб+гС = Мб+дС = — 81.53 — 18.049 = — 99.58 кгс·м
Огибающая эпюра для выбранных расчетных схем будет выглядеть так:
Рисунок 316.2
Теперь, когда максимальные значения моментов на опорах и в пролетах определены, подобрать требуемую арматуру для всех пролетов не сложно.
Например, для первого пролета на приопорном участке потребуется армирование при h0 = 6 см и при Rb = 117·0.9 = 105.3 кг/см2:
am = 156.9/(1·0.062·1053000) = 0.0414
As = 105.3·100·6(1 — √‾(1 — 2·0.0414)) / 3600 = 0.742 см2.
Получается, что даже для самого нагруженного участка плиты шириной 1 м достаточно 4 стерженей d = 5 мм с площадью 0.79 см2. При этом коэффициент армирования получается:
μ% = 100·0.79/100·6 = 0.13 %
что в 2-4 раза меньше рекомендуемого. С учетом того, что в остальных пролетах и на остальных опорах момент меньше, мы можем уменьшить высоту плиты. Согласно СНиП 2.01.03-84 п.5.3 толщина плит междуэтажных перекрытий в жилых зданиях должна быть не менее 5 см. Согласно п.5.5 высота защитного слоя при высоте конструкции до 100 мм — не менее 10 мм и не менее диаметра арматуры. Исходя из этих требований мы можем принять высоту плиты 6 см, а расстояние а = 1.5 см, что обеспечит высоту защитного слоя 10 мм даже при диаметре арматуры 10 мм. Тогда при h o = 4.5 см
am = 156.9/(1·0.0452·1053000) = 0.0736
As = 105.3·100·4.5(1 — √‾(1 — 2·0.0736)) / 3600 = 1.007 см2.
Тогда для армирования приопорных участка (опоры В и Е) достаточно 4 стерженей d = 6 мм с площадью 1.13 см2, для надежности можно принять 5 стержней диаметром 6 мм и высоту ho = 4.7 см.
Такое уменьшение высоты плиты приведет к ощутимому изменению значения постоянной нагрузки, но также и к изменению параметров тавровой балки. Поэтому и плита и балки при таком изменении параметров нуждаются в перерасчете.
Уточненное расчетное значение постоянной нагрузки составит:
qп = (0.06·1 + 0.11·0.24/1.62)2500·1.1 + 200 = 210+200 = 410 кг/м
Значение временной нагрузки оставляем без изменения. Тогда при соотношении нагрузок 410/451.7 = 0.91 значение расчетных моментов при максимальной нагрузке составит:
Мб+вВ = Мб+вЕ = — 156.85·0.91 = — 142.34 кгс·м
Мб+вС = Мб+вD = — 117.65·0.91 = — 106.8 кгс·м
Мб+в1 = Мб+в5 = 116.1·0.91 = 105.4 кгс·м
Мб+в1(l/2) = Мб+в5(l/2) = 107.83·0.91 = 97.9 кгс·м
Мб+в2 = Мб+в4 = 45.54·0.91 = 41.3 кгс·м
Мб+в3 = 68.64·0.91 = 62.3 кгс·м
Уточненная огибающая эпюра моментов будет выглядеть так:
Рисунок 316.3
Примечание: Следует учитывать, что в чистом виде эти данные можно применить только для первого и последнего метров плиты. Так как железобетонные балки, на которые опирается плита, в отличие от стен — опор А и F, будут прогибаться и чем ближе к середине, тем больше прогиб будет стремиться к максимальному. Такой прогиб будет приводить к перераспределению моментов. Для приближенных расчетов можно уменьшить значение моментов на опорах В и Е на 10% и на столько же увеличить значение моментов в 1 и 5 пролете. Более точный учет влияния проседающих опор — отдельная история.
Согласно Пособия по проектированию «Армирование элементов монолитных железобетонных зданий» 2007 года издания толщину балочных плит в перекрытиях жилых и общественных зданий с отношением сторон l2/l1 >2 следует принимать не менее 70 мм, а защитный слой бетона — не менее 20 мм. В целом это очень правильное требование, однако оно не предусматривает возможную разницу в длине пролетов, а шаг ребер — балок 1.6 м является довольно частным. Тем не менее при использовании для бетонной смеси щебня с крупностью зерен более 30 мм это требование следует выполнять.
pouznaval.ru
Справочный материал для построения огибающей эпюры моментов в сборном неразрезном ригеле балочного перекрытия
Поиск Лекций| Значения коэффициентов для трехпролетных балок | 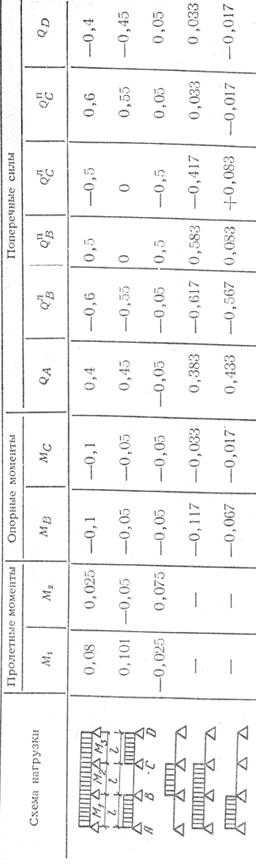 | Значения коэффициентов для двухпролетных балок |
ПРИЛОЖЕНИЕ 6.3.
Пример №1. Построение огибающих эпюр моментов и поперечных сил во второстепенной балке монолитного перекрытия
Исходные данные:
— расчетная постоянная нагрузка на второстепенную балкуперекрытия составляет:
g = 7,77 кН/м;
— расчетная временная (полезная) нагрузка на второстепенную балкуперекрытия составляет:
р =19,24 кН/м;
— расчетная полная нагрузка на второстепенную балку составляет:
q = g + р = 7.77 + 19.83 = 27.01 кН/м;
— расчетные пролеты второстепенной балки составляют:
lo1 =5,725м, lo2 =5,7м.
— соотношение временной и постоянной нагрузок составляет:
р / g = 19.83 / 7.77 = 2,48.
Для определения цифровых коэффициентов из таблиц Приложения 1 указанное выше соотношение принято равным 2.5 ввиду незначительной разницы между этими двумя величинами.
Примечание. В курсовом проекте следует применять интерполирование между значениями коэффициентов двух смежных строк, соответствующих ближайшим значениям вычисленного соотношения.
 |
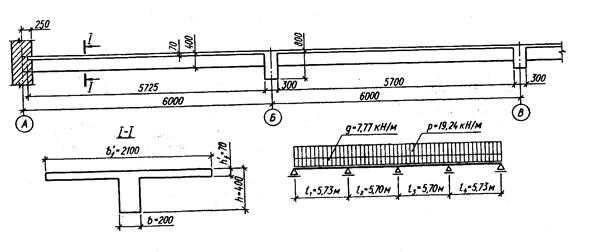| Рис. 6.3.1. Конструкция, расчетная схема и сечение второстепенной балки (к примеру №1). |
Расчет значений огибающей эпюрымоментов выполним с использованием Приложения 1 в табличной форме (см. табл. 6.3.1).
Расчет значений огибающей эпюрыпоперечных сил выполним по формулам:
QA = 0.4× q×lo1 = 0,4 × 27,01 × 5,725 = 61,9 кН;
QBлев = 0.6×q×lo2 = 0,6 × 27,01 × 5,725 = 92,9 кН;
QBправ= QС = 0,5 × q × lo2 = 0,5× 27,01 × 5,725 = 77 кН.
Таблица 6.3.1.
Расчет значений ординат огибающей эпюры моментов в сечениях второстепенной балки:
| Номер | Расстояние от левой опоры до сечения | Значения коэффициентов | Расчетные моменты, кН×м | |||||
| пролета | сечения | +b | -b | Мmax | Mmin | |||
| 2¢ 5 | 0.2l01 0.4l01 0.425l01 0.6l01 0.8l01 1.0l01 | 0.065 0.090 0.091 0.075 0.020 - | - - - - - 0.0715 | 57.6 79.8 80.7 66.5 17.7 - | - - - - - — 63.4 | |||
| 7 ¢ | 0.2l02 0.4l02 0.5l02 0.6l02 0.8l02 1.0l02 | 0.018 0.058 0.0625 0.058 0.018 - | 0.033 0.012 0.008 0.009 0.027 0.0625 | 15.8 50.9 54.9 50.9 15.8 - | — 29.0 — 10.5 — 7.0 — 7.9 -23.7 — 54.9 | |||
| Примечание. Для пролета №1 значение q×l012 = 27.01×5.7252 =886.8 кН×м; для пролета №2 — q×l022 = 27.01×5.732 = 877.6 кН×м. Именно на эти значения следует умножать коэффициенты +b и -b, соответственно, согласно формуле (1) методуказаний, при вычислении моментов Мmax и Mmin. | ||||||||
По результатам расчета построены огибающие эпюры усилий для заданной второстепенной балки (см. рис. 6.3.2).
А
Б
| Рис. 6.3.2. Огибающая (объемлющая) эпюра моментов (А) и поперечных сил (Б) во второстепенной балке (для примера №1). |
ПРИЛОЖЕНИЕ 6.4.
Пример №2. Построение эпюры материалов во второстепенной балке монолитного перекрытия
Исходные данные:
Для второстепенной балки примера №1 произвести конструирование сечений продольной арматурой с использованием эпюры материалов.
Из расчета нормальных сечений по условию прочности подобрана продольная рабочая арматура в местах действия максимальных расчетных моментов (в данном примере этот расчет не приводится). Результаты расчета продольной арматуры и принятая в сечениях продольная рабочая арматура приведены в табл. 6.4.1.
Таблица 6.4.1.
Армирование сечений второстепенной балки:
| Номер расчетного сечения | Площадь As по расчету см2 | Принятая продольная арматура | |
| Количество и диаметр стержней | Asфакт (см2) | ||
| 2′ 7′ | 6.45 6.33 4.12 5.23 | 2Æ16 A-III + 2Æ14 A-III 2Æ16 A-III + 2Æ14 A-III 3Æ14 A-III 2Æ16 A-III + 1Æ14 A-III | 7.1 7.1 4.02 5.56 |
Вначале следует произвести расчеты Мсеч,і по ф.(5), рекомендованные в разделе 4 методуказаний. Результаты указанных расчетов сведены в табл. 6.4.2.
Таблица 6.4.2.
Результаты определения мест теоретического обрыва и отгиба стержней для заданной второстепенной балки:
| Колич. и диаметр стержней | As, (см2) | x= , где хпо ф.(6) | h = 1- 0.5x | Мсеч,і по ф.(5) | Количество обрываемых (отгибаемых) стержней | Расст. от точек теоретич. обрыва (отгиба) стержня до опоры (вычислено аналитически) (м) | ||||||
| слева | справа | |||||||||||
| Пролет 1 (при b=2.1м) | ||||||||||||
| 2Æ16 A-III + 2Æ14 A-III | 7.1 | 0.043 | 0.979 | 91.3 | - | - | - | |||||
| 2Æ16 A-III | 4.02 | 0.024 | 0.988 | 52.2 | 2Æ14 A-III | 1.04(отгиб) | 1.96(обрыв) | |||||
| Пролет 2 (при b=2.1м) | ||||||||||||
| 3Æ14 A-III | 4.62 | 0.028 | 0.986 | 59.9 | - | - | - | |||||
| 2Æ14 A-III | 3.08 | 0.019 | 0.991 | 40.1 | 1Æ14 A-III | 1.93(обрыв) | 1.93(отгиб) | |||||
| Над опорой В(при b=0.2м) | ||||||||||||
| 2Æ16 A-III + 2Æ14 A-III | 7.1 | 0.45 | 0.775 | 72.3 | - | - | - | |||||
| 2Æ16 A-III | 4.02 | 0.255 | 0.873 | 46.1 | 2Æ14 A-III | 0.57(обрыв) | 0.43(отгиб) | |||||
| 2Æ12 A-III | 2.26 | 0.143 | 0.928 | 27.6 | 2Æ16 A-III | 1.21(обрыв) | 0.88(обрыв) | |||||
| Над опорой С(при b=0.2м) | ||||||||||||
| 2Æ16 A-III + 1Æ14 A-III | 5.56 | 0.352 | 0.824 | 60.2 | - | - | - | |||||
| 2Æ16 A-III | 4.02 | 0.255 | 0.873 | 46.1 | 1Æ14 A-III | 0.32(отгиб) | 0.32(отгиб) | |||||
| 2Æ12 A-III | 2.26 | 0.143 | 0.928 | 27.6 | 2Æ16 A-III | 1.0(обрыв) | 1.0(обрыв) | |||||
После выполнения расчетов выполняются графические построения эпюры материалов в соответствии с рекомендациями разд. 4 методуказаний. Результаты выполнения указанных действий приведены на рис. 6.4.1.
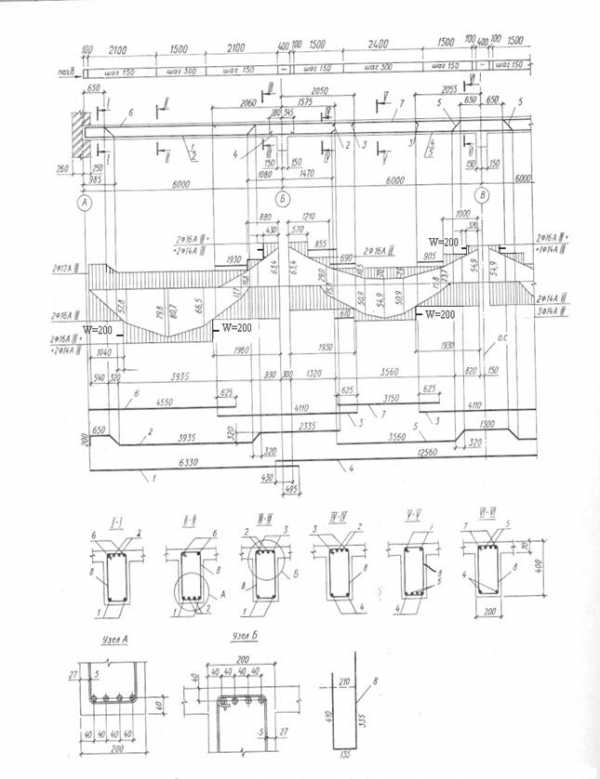
Рис. 6.4.1. Эпюра материалов для второстепенной балки, армированной отдельными стержнями (к примеру №2)
ЛИТЕРАТУРА
1. СНиП 2.03.01-84. Бетонные и железобетонные конструкции.- Введ. 01.01.1985.
2. Железобетонные конструкции. Общий курс / Под ред. В.Н. Байкова.- М.: 1991.
3. Проектирование железобетонных конструкций: Справочное пособие / Под ред. А.Б. Голышева. – 2-е изд., Киев, Будівельник, 1990.
4. Железобетонные конструкции (расчет и конструирование) / Под ред. А.С. Ривкина. — Киев, 1972.
5. Методические указания к выполнению курсового проекта №1 по дисциплине «Железобетонные и каменные конструкции» (для студентов специальности 7.094101 – ПГС).- Макеевка, 2006.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
|
ТОП 10: |
Таблица №3
-Нормативная:
-Расчётная:
-При расчёте на выносливость:
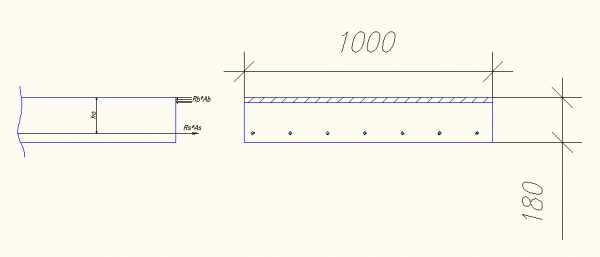
Рис.8 Огибающие эпюры М 2.2Подбор рабочей арматуры плиты
Рис.9 Схема к подбору сечения плиты откуда следует: где х – высота сжатой зоны; Аb— площадь сжатой зоны; Rb – расчётное сопротивление бетона; Rs –расчётное сопротивление арматуры плиты; hо – рабочая высота сечения; А площадь арматуры; m –коэффициент условий работы; и — толщины соответственно нижнего и верхнего защитных слоев. Условие прочности: >Мр, где Мр— наибольший расчетный момент. Для плиты принят бетон класса В27,5, Rb=14,3МПа и арматура класса A400 диаметром 12мм, Rs=340 МПа . ,
n – количество стержней арматуры. Задаваясь различным количеством стержней арматуры добьёмся выполнения условия прочности.
Определение количества нижней арматуры в среднем сечении
Определение количества верхней арматуры в среднем сечении
Определение количества нижней арматуры в опорном сечении
Определение количества верхней арматуры в опорном сечении
Проверка высоты сжатой зоны. Проверку высоты сжатой зоны проводим согласно п.7.61 [1]. где х – высота сжатой зоны; h0– рабочая высота; xпр– предельное значение высоты сжатой зоны. Значение xпр определяется по формуле: , где w = 0,85-0,008 Rb, при этом расчетное сопротивление бетона Rb следует принимать в МПа. Напряжения в арматуре s1, МПа, следует принимать равными Rs — для ненапрягаемой арматуры. Напряжение s2 является предельным напряжением в арматуре сжатой зоны и должно приниматься равным 500 МПа. ; ; Данные представлены в таблицах для подбора арматуры, все условия выполняются.
|
infopedia.su
Построение эпюр изгибающих моментов и поперечных сил — Мегаобучалка
С точки зрения статики второстепенная балка представляет собой многопролетную неразрезную балку, загруженную равномерно распределенной нагрузкой интенсивности Fsb = Gsb + Qsb =9,32 + 16,88 = 26,2 кН/м, промежуточными опорами которой служат главные балки, а крайними — стены.
Рисунок 6 — Расчетная схема второстепенной балки
Статический расчет второстепенной балки выполняется с учетом перераспределения усилий в стадии предельного равновесия конструкции.
В зависимости от схемы расположения временной нагрузки в одном и том же сечении второстепенной балки могут возникать как положительные, так и отрицательные изгибающие моменты. Для определения этих моментов строят огибающую эпюру изгибающих моментов, используя табличные коэффициенты.
Эпюру изгибающих моментов строят для 2,5 пролета, так как все промежуточные пролеты армируют так, как третий (если число пролетов больше трех).
Величина ординат огибающей эпюры моментов определяется по формуле:
(1.41)
где β — коэффициент, зависящий от соотношения временной и постоянной нагрузки
Таблица 7 — Значения коэффициента b
| 2,0 | Номера точек | |||||||||
| -0,0715 | -0,03 | -0,009 | -0,006 | -0,024 | -0,0625 | -0,023 | -0,003 | -0,003 | -0,023 | -0,0625 |
Вычисляем значения поперечных сил на опорах:
— на опоре А и K:
(1.42)
— на опоре В (слева) и опоре E (справа):
(1.43)
— на опоре В (справа) и на всех промежуточных опорах слева и справа:
(1.44)
В приложении 8 приведены значения коэффициента b при значениях через 0,5.
Результаты расчета сведены в таблицу 8 и отображены в графической части.
Таблица 8 – Определение расчетных значений и изгибающих моментов
| № пролета | № точки | Расстояние от левой опоры (в долях от lsb,расч) | Значения b | кН×м | Значения Мsd, кН×м | ||
| +b | -b | + Мsd | — Мsd | ||||
| max | 0,2 0,4 0,425 0,6 0,8 1,0 | 0,065 0,090 0,091 0,075 0,020 - | - - - - - 0,0715 | 826,03 | 53.69 | 0.00 | |
| 74.34 | 0.00 | ||||||
| 75.17 | 0.00 | ||||||
| 61.95 | 0.00 | ||||||
| 16.52 | 0.00 | ||||||
| 0.00 | 59.06 | ||||||
| max | 0,2 0,4 0,5 0,6 0,8 1,0 | 0,018 0,058 0,0625 0,058 0,018 - | 0,03 0,009 - 0,006 0,024 0,0625 | 836,37 | 15.05 | 25.09 | |
| 48.51 | 7.53 | ||||||
| 51.77 | 6.27 | ||||||
| 48.51 | 5.02 | ||||||
| 15.05 | 20.07 | ||||||
| 0.00 | 51.77 | ||||||
| max | 0,2 0,4 0,5 0,6 0,8 1,0 | 0,018 0,058 0,0625 0,058 0,018 - | 0,023 0,003 - 0,003 0,023 0,0625 | 836,37 | 15.05 | 19.24 | |
| 48.51 | 2.51 | ||||||
| 51.77 | 2.51 | ||||||
| 48.51 | 2.51 | ||||||
| 15.05 | 19.24 | ||||||
| 0.00 | 51.77 |
1.3.4 Расчет нормальных сечений и подбор арматуры в расчетных сечениях второстепенной балки
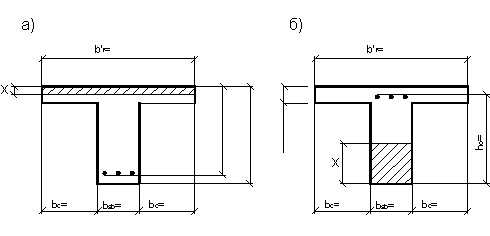
Рисунок 7 – Расчетные нормальные сечения второстепенной балки;
в пролете (а) и на опоре (б)
Определение площади сечения арматуры при действии положительного момента ведем как для таврового сечения с полкой в сжатой зоне. При действии отрицательного момента полка находится в растянутой зоне, следовательно расчетное сечение будет прямоугольным.
Размеры сечения, принятые по расчету:
мм, мм; мм; =80 мм.
Задаемся величиной с1 = 30 мм в пролёте и с2 = 50 мм на опоре.
Тогда рабочая высота сечения:
; .
Предполагая, что нейтральная ось проходит по нижней грани полки, определяем область деформирования для прямоугольного сечения шириной beff = 2250 мм и положение нейтральной оси при расчете тавровых сечений:
(1.31)
, следовательно, сечение находится в области деформирования 1в (таблица 6.8).
С помощью таблицы 6.6 находим величину am, а затем изгибающий момент по формуле:
(1.48) где — коэффициент, учитывающий длительность действия нагрузки, неблагоприятного способа её приложения;
Так как в 1-ом пролете , то нейтральная линия проходит в полке и расчет производится как для элементов прямоугольного сечения с шириной b = beff = 2000 мм.
Для бетона класса С12/15: εcu = 3,5‰; ωc = 0,810; k2 = 0,416; C0 =1,947.
Для арматуры S500: Es = 2·105 МПа; fyd = 417 МПа.
(1.33)
(1.34)
(1.35)
В пролете 1 (нижняя арматура) Msd = 75,17 кНм; d1 = 0,37 м; b = beff = 2250 мм.
Вычисляем значение коэффициента по формуле:
(1.32)
где — коэффициент, учитывающий длительность действия нагрузки, неблагоприятного способа её приложения;
, следовательно, растянутая арматура достигла предельных деформаций.
Находим относительное плечо пары сил:
(1.36)
Требуемая площадь сечения растянутой арматуры:
(1.37)
Принимаем 2 стержня Ø16 мм с Ast= 4,02 см2 и 1 стержень Ø12 мм с Ast= 1,131 см2.
В пролете 2 (нижняя арматура) Msd = 51,77 кНм; d1 = 0,37 мм; b = beff = 2250 мм.
Вычисляем значение коэффициента :
, следовательно, растянутая арматура достигла предельных деформаций.
Находим относительное плечо пары сил:
Требуемая площадь сечения растянутой арматуры:
Принимаем 2 стержня Ø12 мм с Ast= 2,26 см2 и 1 стержень Ø12 мм с Ast= 1,131 см2.
Минимальная площадь продольной арматуры:
As,min = ρmin·bsb·d1 = 0,0013·200·417 = 0,813 см2. (1.49)
В опорных сечениях действуют отрицательные моменты, плита расположена в растянутой зоне, поэтому сечение балки рассматривают как прямоугольное с шириной b = 200 мм = 0,20 м.
Результаты расчета сводим в таблицу 9.
Таблица 9 — Определение площади сечения рабочей арматуры второстепенной балки
megaobuchalka.ru
3.6. Построение эпюры материалов
Прочность балки должна быть обеспечена по всей ее длине, однако не следует забывать и экономическую сторону проектирования. Площади сечения арматуры найдены по усилиям в наиболее загруженных сечениях балки и, естественно, по мере уменьшения нагибающих моментов по длине балки часть стержней обрывают или переводят в другую зону. При помощи построения эпюры материалов определяются места обрывов и уточняются места отгибов стержней.
Эпюра материалов представляет собой графическое изображение значений моментов, которые могут быть восприняты балкой в любом сечении. Сопоставляя эпюру материалов с огибающей эпюрой моментов, можно проверить прочность сечения балки в любой точки по ее длине.
В любом сечении балки момент внешних сил не должен быть больше того момента, который может быть воспринят бетоном и арматурой в этом сечении, т.е. эпюра материалов должна везде перекрывать эпюру моментов. Чем ближе на всем протяжении балки эпюра материалов подходит к огибающей эпюре моментов, тем экономичнее запроектирована балка.
К
началу построения эпюры материалов
балка должна быть заармирована. Для
построения эпюры материалов по фактической
площади арматуры 
в середине пролета и на опоре согласно
структуре 6 (рис. 3.11) определяют момент МRd, воспринимаемый
арматурой 
.
Затем в масштабе, принятом для построения
эпюры изгибающих моментов (см. рис. 3.10),
проводят горизонтальную линию,
соответствующую МRd.
Эта
горизонтальная линия должна быть
расположена несколько дальше эпюры
изгибающих моментов от нулевой линии,
что показывает, на сколько фактическая
площадь арматуры 
близка к расчетной 
.
Если горизонтальная линия пересекает
эпюру изгибающих моментов, то это говорит
о недостаточном количестве арматуры 
поставлено недостаточно, или об ошибке
в вычислениях.
Затем подсчитывают момент МRd для доводимых до опоры стержней и снова проводят горизонтальную линию на эпюре изгибающих моментов. Точка пересечения этой линии с эпюрой моментов и будет точкой теоретического обрыва (отгиба стержней арматуры). Таким же образом поступают и при определении мест обрыва (отгиба) других стержней.
Рис. 3.10. Схема расположения отгибов
Из точек теоретического обрыва (т.т.о.) проводят перпендикулярные линии до пересечения их с горизонтальными линиями МRd и окончательно строят эпюру материалов, которая имеет ступенчатый вид в местах теоретического обрыва стержней, и наклонный вид в местах отгиба стержней.
С целью восприятия изгибающего момента от возможного частичного защемления балки на опоре в стене, в первом пролете арматуру не обрывают, а отгибают на крайнюю опору. Начало отгиба располагают на расстоянии 50-60 мм от внутренней грани стены.
| Рис. 3.11. Структура 6. Расчет ординат эпюры материалов |
Не
следует забывать, что сечения балки при
расчете прочности на действие отрицательных
изгибающих моментов рассматриваются
как прямоугольные с шириной, равной
ширине ребра, а при расчете на действие
положительных моментов – как тавровые
с шириной полки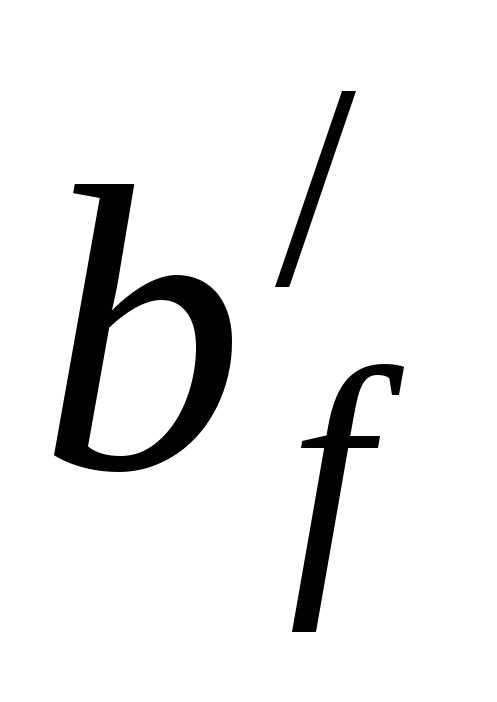 
(для монолитных ребристых перекрытий
тавровые сечения имеют развитую полку,
нейтральная ось, как правило, проходит
в полке, т.е.
,
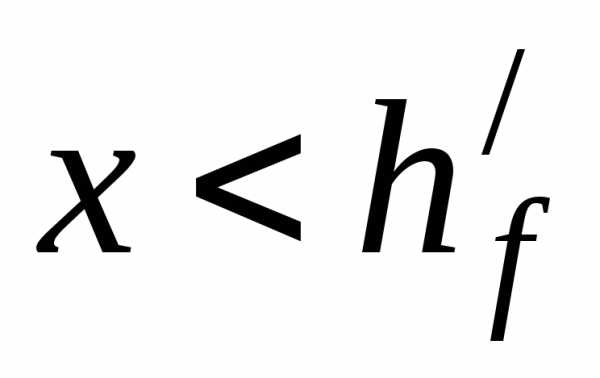и тавровое сечение рассчитывается, как
прямоугольное с шириной, равной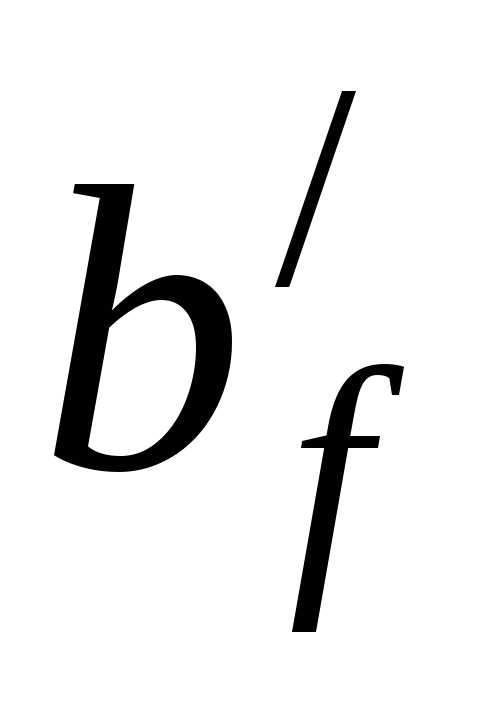
).
Нижние (не крайние) растянутые стержни вязаных каркасов в пролетах, как правило, не обрывают, а отгибают и заводят на опоры. На эпюре материалов уменьшение несущей способности сечений балки показывают в виде наклонных участков. Отгибаемые нижние стержни считаются вступившими в работу в точке нижнего отгиба, а отгибаемые верхние стержни – в точке верхнего отгиба.
Соответственно с переводом стержней в верхнюю зону балки возрастают ординаты эпюры материалов для отрицательных моментов и уменьшается эпюра материалов для положительных моментов.
Место расположения отгибов должно быть уточнено и увязано с эпюрой изгибающих моментов: начало отгиба в растянутой зоне должно отстоять от нормального к продольной оси элемента сечения, в котором отгибаемый стержень полностью используется по моменту не менее чем на d/2, а конец отгиба должен быть расположен не ближе того сечения, в котором отгиб не требуется по эпюре моментов (рис. 3.10).
Для обрываемых стержней места их теоретического обрыва определяют по точке пересечения прямых эпюры материалов с ветвями огибающей эпюры моментов.
В местах обрыва стержней эпюра материалов состоит из горизонтальных прямых с вертикальными уступами. Высота этих уступов пропорциональна сечению включающихся и выключающихся из работы стержней.
Расстояния от граней опор до точек теоретического обрыва определяются аналитически из подобия треугольников, образованных ординатами огибающей эпюры моментов и эпюры материалов. При построении эпюры материалов на чертеже в достаточно крупном масштабе (например, 1:20) можно допустить определение вышеуказанных расстояний путем их измерения.
Для обеспечения прочности наклонных сечений на действие изгибающего момента в элементах постоянной высоты продольные растянутые стержни, обрываемые в пролете, должны заводиться за точку теоретического обрыва (т.е., за сечение, нормальное к продольной оси балки, в котором эти стержни перестают требоваться по расчету) на длину lbd, тем самым определяется место фактического обрыва стержней.
studfiles.net
Расчет главной балки
Главную балку рассчитывают по схеме неразрезной многопролетной балки таврового сечения, загруженной сосредоточенными силами в местах расположения второстепенных балок. За расчетный пролет главной балки принимают пролет в осях.
Изгибающие моменты и поперечные силы для расчетных сечений определяют по огибающим эпюрам, построенным с учетом различных схем приложения нагрузок и перераспределения моментов из-за возникновения пластических шарниров.
Огибающая эпюра моментоввключает в себя максимальные ординаты эпюр от всех возможных комбинаций полезных нагрузок. Величины усилий, возникающих в балках при различных комбинациях нагрузок, могут быть рассчитаны по справочным данным.
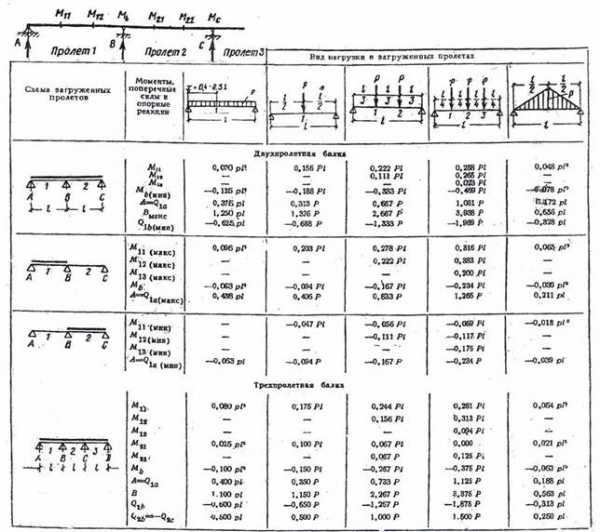
Рис. 56. Определение усилий в многопролетных неразрезных балках
Учитывая влияние пластических шарниров, необходимо уменьшить ординаты эпюр изгибающих моментов в опасных сечениях (на опорах) путем суммирования с дополнительно построенными эпюрами противоположного знака.
Рис. 57. Схемы построения огибающих эпюр
Величина максимальной ординаты добавочных эпюр не должна превышать 30% от уменьшаемой ординаты эпюры моментов на опоре.
По огибающей эпюре моментов, построенной с учетом работы пластических шарниров в главной балке, строят эпюру поперечных сил, используя методы строительной механики.
Расчет армирования главной балки.Армирование главной балки проектируют вязаным каркасом с отогнутыми стержнями. При этом площади сечения растянутой арматуры на опоре и в пролете с учетом перераспределения моментов, должны быть примерно одинаковыми.
При подборе сечения арматуры необходимо учитывать, что ширина сжатой зоны на опоре и в пролете главной балки bf/ при тавровом сечении будет различной, что может потребовать корректировки огибающей эпюры моментов.
Подбор сечения растянутой арматуры на опоре производят на момент по грани колонны, который меньше момента по оси на величину Mгр = М – Q hк /2.
Рис. 58. Схема расположения расчетного момента на грани колонны
При расчете главных балок должна быть обеспечена прочность по наклонному сечению в пределах участка между хомутами, между опорой и отгибом и между отгибами. Усилия Qsw и Qs.inc определяют как сумму проекций на нормаль к продольной оси элемента предельных усилий в хомутах и отгибах, пересекающих опасную наклонную трещину.
Длину проекции опасной наклонной трещины определяют из минимума выражения: Qb + Qs.inc + Qsw, где в значение Qb вместо с подставляют со, принимаемое не более 2 hо и не более значения с, а также не менее hо, если с > hо.
Расчет главной балки на действие изгибающего момента по опасному наклонному сечению производят из условия
М £ Мs + Мsw + Мs.inc.
Момент М определяют от внешней нагрузки, расположенной по одну сторону от расчетного наклонного сечения, относительно оси, перпендикулярной плоскости действия момента и проходящей через точку приложения равнодействующей усилия Nb в сжатой зоне.
Моменты Мs + Мsw + Мs,inc определяют как сумму моментов относительно той же оси от усилий соответственно в продольной арматуре, хомутах и отгибах, пересекающих растянутую зону наклонного сечения.
Рис. 59. Схема действия усилий в наклонном сечении
Расчет наклонных сечений на действие момента производят в местах обрыва или отгиба продольной арматуры, а также в приопорной зоне главных балок.
Конструирование арматурыначинают с составления эскиза армирования в соответствии с конструктивными требованиями нормативных документов. Сечения главной балки принимают одинаковыми во всех пролетах.
Пользуясь эскизом арматуры строят эпюру материалов, которая показывает действительную несущую способность в растянутой зоне различных сечений главной балки.
С этой целью на огибающую эпюру моментов в масштабе действующих усилий строят полосы, соответствующие моментам в арматурных стержнях, равных Mi = Asi Rs z ho.
Сумма высот всех полос соответствует несущей способности балки в опасном сечении. Линия, ограничивающая сумму полос, представляет собой контур эпюры материалов. Эпюра материалов не должна врезаться в огибающую эпюру моментов, поскольку несущая способность балки ни в одном сечении не должна быть меньше действующего усилия.
По эпюре материалов можно графически определить места теоретического обрыва арматурных стержней. За место теоретического обрыва арматурный стержень должен быть заведен на длину зоны анкеровки стержня, определяемой по формуле W = (Q – Rs As.inc Sin a) / 2 qsw + 5d ³ 20d,
где Q – поперечная сила в опорном сечении;
a – угол наклона отгибов к продольной оси балки.
Вид эпюры материалов для главной балки, армированной сварными каркасами, показан на рис. 60.
Рис. 60. Огибающая эпюра балки, армированной сварными каркасами
в
Рис. 61. Вид арматурных стержней вязаного каркаса главной балки
Похожие статьи:
poznayka.org