Кольца жби 1,5 метра без замка и комплектующие — СептикКонструкт
+79101486878 в Нижнем Новгороде
- Home
- Каталог
- Бетонные кольца для канализации
- Кольца жби 1,5 метра без замка и комплектующие
Категория: Кольца жби 1,5 метра без замка и комплектующие.
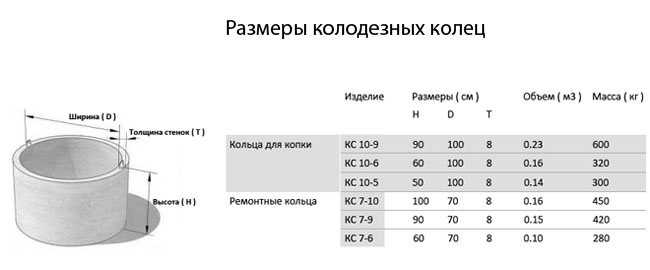
- Высота: 150 мм
- ⌀ Dвнеш.: 1700 мм
- Марка бетона: М300
- Класс бетона: B22.5
- F, циклов : 200
- Водопоглощение: W4
- Вес: 950 кг
- Рекомендуемая сезонность использования: Круглогодичный
Артикул pn15
103 в наличии
Категория: Кольца жби 1,5 метра без замка и комплектующие.
- ⌀ Dвнутр. : 1500 мм
- Высота: 890 мм
- Стенка: 90 мм
- ⌀ Dвнеш.: 1700 мм
- Марка бетона: М250
- Класс бетона: B20
- F, циклов : 100
- Водопоглощение: W4
- Вес: 1700 кг
- Объём внутр.
- Рекомендуемая сезонность использования: Круглогодичный
Артикул kcd_15_9
2 в наличии
Подробнее…
Категория: Кольца жби 1,5 метра без замка и комплектующие.
- ⌀ Dвнутр. : 1500 мм
- Высота: 290 мм
- Стенка: 90 мм
- ⌀ Dвнеш.: 1700 мм
- Марка бетона: М250
- Класс бетона: B20
- F, циклов : 100
- Водопоглощение: W4
- Вес: 325 кг
- Объём внутр.: 512 л
- Рекомендуемая сезонность использования: Круглогодичный
Артикул kc_15_3
103 в наличии
Категория: Кольца жби 1,5 метра без замка и комплектующие.
- ⌀ Dвнутр. : 700 мм
- Высота: 150 мм
- ⌀ Dвнеш.: 1700 мм
- Марка бетона: М300
- Класс бетона: B22.5
- F, циклов : 200
- Водопоглощение: W4
- Вес: 632
- Рекомендуемая сезонность использования: Круглогодичный
Артикул pp152
101 в наличии
Категория: Кольца жби 1,5 метра без замка и комплектующие.
- ⌀ Dвнутр. : 1500 мм
- Высота: 890 мм
- Стенка: 90 мм
- ⌀ Dвнеш.: 1700 мм
- Марка бетона: М250
- Класс бетона: B20
- F, циклов : 100
- Водопоглощение: W4
- Вес: 1000 кг
- Объём внутр.: 1573 л
- Рекомендуемая сезонность использования: Круглогодичный
Артикул kc_15_9
25 в наличии
Подробнее…
Категория: Кольца жби 1,5 метра без замка и комплектующие.
- ⌀ Dвнутр. : 700 мм
- Высота: 150 мм
- ⌀ Dвнеш.: 1700 мм
- Марка бетона: М300
- Класс бетона: B22.5
- F, циклов : 200
- Водопоглощение: W4
- Вес: 628 кг
- Рекомендуемая сезонность использования: Круглогодичный
Артикул pp151
103 в наличии
Категория: Кольца жби 1,5 метра без замка и комплектующие.
- ⌀ Dвнутр. : 1500 мм
- Высота: 590 мм
- Стенка: 90 мм
- ⌀ Dвнеш.: 1700 мм
- Марка бетона: М250
- Класс бетона: B20
- F, циклов : 100
- Водопоглощение: W4
- Вес: 650 кг
- Объём внутр.: 1043 л
- Рекомендуемая сезонность использования: Круглогодичный
106 в наличии
Оставайтесь с нами!
Добавьте закладку на эту страницу СептикКонструкт — бетонные кольца
КС-15-5 V-0.22 P-0.55 1680/1500х490х90, объем 0.22, наименование для деления на таблицы Кольца стеновые, цена с ндс 1,711
Прокладка коммуникаций – неотъемлемая часть, как частного, так и капитального строительства. Для того чтобы продлить ресурс трубопроводов, линий и прочих сетей широко используются универсальные железобетонные колодцы, в числе которых популярные изделия марки КС 15-5.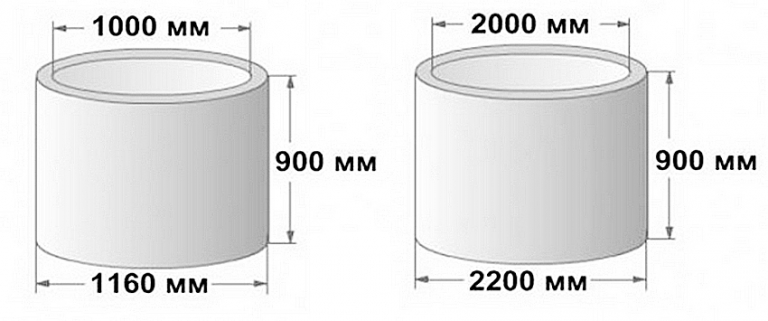
Описание и назначение
Железобетонные кольца раздельного типа КС 15-5 широко задействуются в сфере строительства и представляют собой изделия круглой цилиндрической формы, предназначенные для возведения и ремонта систем коммуникаций в виде газопроводных, канализационных, дренажных, водопроводных, а также сетевых колодцев. Устанавливают при возведении септиков — специальных сооружений, предназначенных для очистки стоков. Помимо этого изделия находят применение для возведения скважин и колодцев в частном секторе. Стеновые кольца задействуются для сооружения туннелей ориентированных на прокладку коммуникаций в виде тепло- и электросетей, телефонных линий, магистралей связи. Высокая степень универсальности позволяет использовать КС 15-5 для частных нужд, в загородном домостроении, в сельском хозяйстве и животноводстве, прочих сферах деятельности человека.
Технические параметры
Характеристики бетонных и железобетонных конструкций газопроводных, водопроводных и канализационных колодцев КС 15-5, а также требования к ним изложены в межгосударственном стандарте ГОСТ 8020-2016.
его действие распространяется на колодцы круглой формы, включая коллекторы и самотечные канализационные системы.
Изделия КС 15-5 производят со следующим набором характеристик:
- диаметр внешний/внутренний – 1680/1500 мм;
- толщина стенок – 490 мм
- расчетная масса – 550 кг;
- объем – 550 куб. м.
Технология производства
Кольца железобетонные КС 15-5 производят на основе тяжелого бетона с применением усиливающих конструкцию армирующих элементов. Изготовление железобетонных колец осуществляется в соответствии с регламентом требований отраслевого стандарта ГОСТ 8020-2016. При изготовлении кольцевых изделий находит применение арматура с толщиной в пределах от 6 мм до 10 мм. Габаритные размеры изделий находят отражение в его материалоемкости и стоимости. В качестве материала для производства чаще всего применяется бетон марок М200 – М500 с классом прочности:
- В30 для конструкций из бетона;
- В25 для железобетонных изделий, а также колец стенового типа;
- В20 для всех прочих конструкционных изделий.
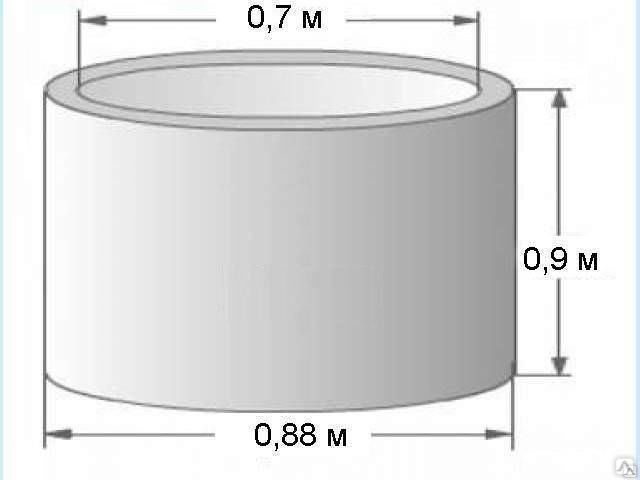
Показатели морозостойкости и водонепроницаемости используемого для производства колец бетона должна быть не ниже, чем F50 и W4. При использовании изделий в условиях агрессивных сред, поверхность должна иметь антикоррозийную защиту, которая выполняется в виде полимерного или битумного защитного покрытия. В случае, если колодцы предназначены для транзита и транспортировки сильноагрессивных жидкостей, а также активных газовых сред, защитное покрытие должно обладать высокой химической стойкостью, не уступающей полиэтилену. При закладке колец ниже уровня грунтовых вод их показатель водонепроницаемости должен быть в 1,2 выше максимального давления внешней среды. В данном случае рекомендуемая толщина полимерного защитного покрытия составляет не менее 4 мм.
При производстве рабочих камер колодцев КС 15-5 находит применение технология вибропрессования или способ радиального прессования, которые минимизируют объем воздушных прослоек, способствуя повышению прочности и надежности изделий.
Для подъема при перемещении в ходе проведения погрузочно-разгрузочных, а также монтажных работ, железобетонные изделия КС 15-5 оснащаются стальными петлями. С их помощью осуществляется строповка грузов кранами и другими грузоподъемными механизмами.
Разновидности и особенности монтажа
В зависимости от назначения кольца КС 15-5 могут использоваться для сооружения канализационных, водопроводных и газопроводных сетей.
В свою очередь канализационные кольца конструктивно могут изготавливаться как с замком, так и без него. Фальцы, расположенные в торцевой части железобетонных изделий предназначены для плотного их соединения друг с другом. Замки способны обеспечить не только герметизацию колодца в целом, но и обеспечить его высокую механическую прочность. В случае конструктивного отсутствия замков на торцах колец их соединение реализуется за счет использования скоб и бетонного раствора.
Для монтажа колодцев КС 15-5 заранее производится выемка грунта на необходимую глубину, после чего кольца поочередно опускаются в шахту и закрепляются в рабочем положении. Места соединения подлежат обработке посредством бетонного раствора. Сверху колодца устанавливается плита с круглым отверстием под крышку.
Кольца стеновые КС 15-5 – изделия из железобетона, предназначенные для возведения части колодца, расположенной под землей, представляя собой неотъемлемый элемент при возведении любых видов подземных колодцев, без которых недопустимо сооружений конструкции. Изделие может выполнять различные функции как защитный элемент и основа инженерной коммуникации.
Совместно с элементами КС находят применение плиты перекрытий и днищ колодцев соответствующего габаритного размера.
Для установки изделий КС 15-5 в рабочее положение находит применение техника и механизмы с соответствующей грузоподъемностью.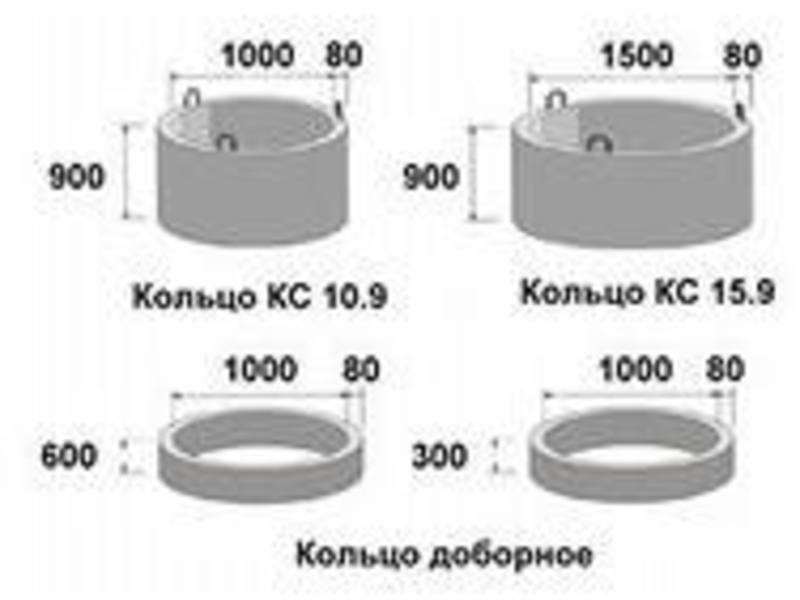
Унифицированная конструкция колец позволяет использовать при сооружении инженерных коммуникаций типовые проекты, реализуя монтажные и строительные работы в сжатые сроки. Особенности монтажа и установки ЖБИ не предъявляют высоких требований к погодным условиям, в связи с чем строительные работы могут производиться как в летнее, так и в зимнее время года. Простота монтажа и укладки стеновых колец позитивно отражается на сметной стоимости объектов, позволяя сократить расходы на возведение коммуникаций.
Маркировка
При обозначении железобетонных колец, конструкций для колодцев, и разделении их на марки, находит применение цифробуквенный код согласно нормам стандарта ГОСТ 23009, в котором приводится следующая информация:
- вид изделия и его тип по классификации ГОСТ 8020-2016;
- габаритный размер внутреннего диаметра кольца;
- значение высоты элемента.
Все размеры для доступности и простоты восприятия указываются в дециметрах.
Во второй группе индекса приводятся данные о классе прочности изделий в виде колец или принадлежности к группе по несущей способности для плит перекрытий. В третьей части маркировки могут содержаться сведения о степени проницаемости материала:
- О – обозначаются изделия, выполненные из материала с особо низкой проницаемостью;
- П — из бетона с повышенной проницаемостью.
Последний параметр играет важную роль при выборе элементов, которые будут функционировать в условиях постоянного воздействии агрессивных сред.
В соответствии со стандартом ГОСТ 8020-2016 колодцы марки КС 15-5 относятся к категории стеновых цилиндрических изделий
Бетонные изделия обозначаются дополнительно литерой «Б», фибробетонные – «ФБ». При обозначении колец с наличием конструктивных фальцевых стыков в конце аббревиатуры указывается литера «Ф».
Рабочие камеры, а также изделия в виде стеновых колец, которые имеют внутренний полиэтиленовый чехол, дополнительно маркируются буквой «Ч» в конце обозначения.
Железобетонное изделие с маркировкой КС 15-5 представляет собой стеновое кольцо с внешним диаметром 1160 мм и высотой 190 мм.
Гарантия и контроль качества
Конструкционные элементы КС 15-5 – рабочие секции колодцев, которые должны удовлетворять требованиям отраслевого стандарта ГОСТ 13015 по следующим характеристикам:
- водонепроницаемость и морозостойкость бетона;
- наличие коррозионной защиты, в том случае, когда это предусмотрено проектной документацией;
- заданный уровень трещиностойкости и прочности, позволяющие выдерживать длительно нормативные нагрузки;
- соответствие марок сталей, применяемых при производстве используемых в конструкции закладных и арматурных изделий, монтажных петель;
- параметр фактической прочности бетона, его соответствие проектным показателям;
- качество изделий в области необходимой толщины защитного слоя бетона, предотвращающего коррозию арматуры в соответствии с ГОСТ 31384.
Готовые изделия КС 15-5 не должны иметь трещин толщиной более 0,1 мм, выступающих частей арматурных конструкций. Предельная величина допустимых отклонений от линейных размеров изделий, в зависимости от габаритов, составляет от ±5% до ±20%. Перед реализацией кольца, днища и крышки проходят испытания на предмет прочности и трещиностойкости, морозоустойчивости и влагостойкости в соответствии с регламентом отраслевого стандарта ГОСТ 8829. Проверка изделий на предмет полного соответствия стандартам и заявленным характеристикам позволяет исключить из продажи бракованные ЖБИ, являясь гарантией качества, надежности и долговечности элементов и инженерных конструкций построенных на их основе.
Транспортировка и хранение изделий производится в рабочем положении. Высота штабеля при этом зависит от габаритов изделий и может составлять от 2 до 6 изделий, но не более 1,8 метра.
Оценка железобетонных цилиндрических резервуаров с однослойными стенками
%PDF-1.
7
%
1 0 объект
>
эндообъект
6 0 объект
>
эндообъект
2 0 объект
>
транслировать
application/pdf10.1016/j.proeng.2016.07.192
com
HWivg6)m{Ͼ gr»@d
) ВИсследование модели восстанавливающей силы на стыке железобетонной колонны с круглыми трубами
На этой странице
РезюмеВведениеРезультатыВыводыДоступность данныхРаскрытиеКонфликты интересовБлагодарностиСсылкиАвторское правоСтатьи по теме Гистерезисная кривая нагрузки-перемещения и кривая скелета этого нового типа соединения получены с помощью псевдостатического испытания при малоцикловой циклической нагрузке на верх колонны. Результаты показывают, что этот новый тип соединения обладает хорошими характеристиками рассеивания сейсмической энергии. На основе теста предложена трехчастная модель скелетной кривой, учитывающая три характерные точки предела текучести, предела и отказа, и дано выражение модели скелетной кривой. Исследован закон деградации жесткости образцов под действием возвратно-поступательной нагрузки и приведено выражение закона деградации жесткости. Подробно описан закон гистерезиса образцов нового типа.
Справедливость модели проверяется путем сравнения экспериментальной кривой с модельной кривой. Модель может быть использована в упруго-пластическом сейсмическом анализе во времени на стыке круглой трубчатой стальной железобетонной (CTSRC) колонны.
1. Введение
Модель восстанавливающей силы используется для объяснения взаимосвязи между нагрузкой и смещением конструкции под повторяющейся нагрузкой, которая может отражать способность конструкции восстанавливать первоначальную деформацию после разгрузки. При изучении сейсмических характеристик конструкции модель восстанавливающей силы является основой анализа сейсмического напряжения, который в основном отражает характеристики конструкции, такие как потребление энергии, пластичность, прочность и жесткость. С 19В 40-х годах сейсмическая инженерия провела обширные исследования по моделированию кривой структурной восстанавливающей силы. Исследователи предложили следующие модели: модель Рамберга–Осгуда [1, 2], предложенная Дженнингсом, показана на рис.
1(а). Модель в основном используется для описания характеристик восстанавливающей силы металлических материалов, а также используется в грунтовых и железобетонных изгибаемых конструкциях; как показано на рисунке 1 (b), Клаф [3] предложил относительно раннюю модель, учитывающую ухудшение жесткости при нагрузке и разгрузке, которая в основном предлагается в качестве модели характеристики восстанавливающей силы железобетонных изгибаемых элементов. Такеда и др. [4] предложили тройную модель деградации жесткости линии, как показано на рисунке 1(c). Модель получена в результате испытания малоциклового возвратно-поступательного нагружения железобетонных колонн и основана на результатах испытаний. Поскольку она имеет на одну точку трещины больше, чем модель с двумя линиями, она может более точно отражать механические характеристики железобетонных конструкций из стали.
В последние годы была проведена серия исследований моделей соотношения нагрузки и смещения различных новых конструкций при повторяющихся нагрузках.
Ян и др. установил гистерезисную модель соединения сталежелезобетонных сверхвысокопрочных бетонных колонн и сталежелезобетонных балок и предложил количественный метод сейсмического повреждения и коэффициента затухания [5]. Чжан и Хан предложили модель прогнозирования реакции деформации на циклическую боковую нагрузку железобетонных колонн, подвергающихся осевому сжатию и циклическому сдвигу; сравнение между предсказанным циклическим ответом и экспериментальными результатами показывает, что предложенная модель может предсказать наблюдаемый гистерезисный ответ изгиба-сдвига критических RC колонн хорошо [6]. Юка и Хидеки предложили гистерезисную модель двутавровой балки с учетом коэффициента гибкости, а также предложили гистерезисную модель, подходящую для однородного момента и антисимметричного момента [7]. Чжан и др. изучали гистерезисное поведение шести колонн бетонного каркаса с изоляцией из стеклянных шариков (колонны GIC) и одной колонны обычного бетонного каркаса; результаты могут служить теоретической основой для упруго-пластического анализа колонны СИЦ при сейсмическом воздействии [8].
Хао и др. предложил эффективный метод расчета монотонной кривой и гистерезисной кривой двутавровой балки под действием изгибающего момента. Точность предсказания гистерезисного поведения двутавровой балки проверяется сравнением с численными результатами [9].]. Ван и др. провели нелинейный анализ динамики во времени для нового типа соединения рассеивания энергии гибридной рамы из бамбуковой стали и предложили модель восстанавливающей силы соединения с лучшими характеристиками [10]. Ли и др. предложил инновационный метод для учета влияния динамических воздействий и деградации на анализ сейсмических характеристик железобетонных каркасных конструкций [11]. Се и др. провели квазистатические испытания на трех образцах свай в масштабе 1/10 и установили гистерезисную модель сборной сваи, которая хорошо согласовывалась с результатами испытаний [12]. Ву и др. изучали модель восстанавливающей силы композитных соединений h-сталежелезобетонных колонн (далее – соединения MPSC), которая обладает высокой точностью и может быть использована для расчета соединений MPSC [13].
Сонг и др. спроектировали десять внутренних соединений железобетонных колонн и кольцевых балок из ПВХ-углепластика (PCCC-RBIJ) и одно внутреннее соединение бетонных колонн и кольцевых балок из ПВХ (контрольное внутреннее соединение) и изучили их модели восстанавливающей силы [14]. Ни и др. провел углубленное экспериментальное исследование сейсмических характеристик стен жесткости из высокопрочного железобетона и предложил модель восстанавливающей силы стен жесткости из высокопрочного железобетона, состоящую из скелетных кривых и группы эмпирических гистерезисных законов [15].
Колонна CTSRC представляет собой композитную конструкцию нового типа. Относительные исследования [16–18] показывают, что он обладает высокой способностью к сжатию и сдвигу и превосходными сейсмическими характеристиками и может в полной мере использовать характеристики высокопрочных материалов. На этом основании авторами предложен новый тип соединения колонны CTSRC [19–21]. Применяя низкоцикловую возвратно-поступательную нагрузку к верхней части колонны, изучается зависимость смещения нагрузки при возвратно-поступательной нагрузке.
В основном существует два метода анализа и изучения модели восстанавливающей силы: один основан на фундаментальных исследованиях стального стержня, стальной трубы и бетона и связи между стальным стержнем и бетоном, стальной трубой и бетоном, чтобы получить идеализированную материальную конститутивную модель и структурную деформационную модель и получить гистерезисную кривую отношения восстанавливающей силы итерационным методом; второй – прямое моделирование результатов испытаний [22, 23]. В данной работе второй метод используется для исследования характеристик восстанавливающей силы соединения нового типа на основе квазистатического испытания и измеренных гистерезисных кривых. Создана модель восстанавливающей силы, подходящая для соединения нового типа, которая обеспечивает основу для будущего упруго-пластического динамического анализа конструкций.
2. Подготовка к испытаниям и результаты
2.1. Схема проектирования и нагружения образца
В этой статье были спроектированы два полномасштабных соединения в конструкции рамы.
Номера экземпляров Ш-1 и Ш-2. Основные различия между двумя образцами заключаются в коэффициенте усиления кольцевой балки и форме кольцевой балки. Номера и параметры образцов показаны в таблице 1.
Высота и ширина двух образцов составляют 4375,0 мм и 3370,0 мм соответственно. Наружный диаметр круглой стальной трубы составляет 400,0 мм. Чтобы гарантировать, что круглая стальная труба не несет продольной нагрузки, круглая стальная труба была отсоединена в области стыка, и от верхнего и нижнего краев бетонной кольцевой балки оставлено кольцевое отверстие диаметром 15,0 мм. Другие конструкции и размеры показаны на рис. 2 (на примере образца Ш-1).
Квазистатическое испытание обычно делится на нагрузку на торец колонны и на нагрузку на торец балки. Поскольку при нагрузке на конец колонны можно учитывать влияние силы тяжести второго порядка [24], в этой статье был принят режим нагрузки на конец колонны: во-первых, вертикальная нагрузка постепенно прикладывается к 1500 кН домкратом в верхней части колонны в три этапа и нагрузка длится несколько минут; во-вторых, сервопривод MTS используется для приложения малоцикловой возвратно-поступательной нагрузки к верхней части колонны, а управление нагрузкой используется до текучести.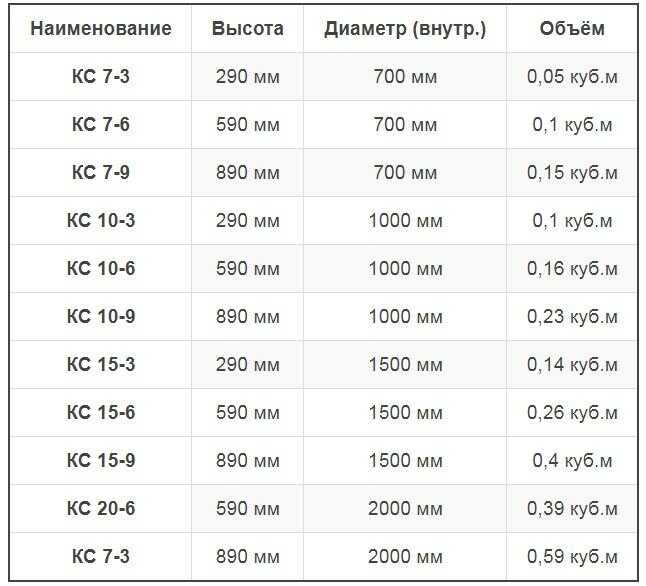
После текучести нагрузка осуществляется в соответствии с кратным пределу текучести смещения верха колонны, и каждый цикл выполняется три раза, пока образец не будет поврежден или горизонтальная нагрузка верха колонны не упадет ниже 85%. его пиковой нагрузки. Схема испытательного устройства и схема нагрузки показаны на рис. 3.9.0035
2.2. Результат испытаний
Гистерезисные кривые нагрузки-перемещения двух образцов показаны на рис. 4. Из рисунка видно, что гистерезисные кривые двух образцов полные, что свидетельствует об очень хороших характеристиках рассеивания сейсмической энергии.
3. Создание модели восстанавливающей силы
Модель восстанавливающей силы для нелинейного анализа состоит из трех частей: скелетной кривой, закона деградации жесткости и гистерезисных характеристик. Результаты показывают, что разумная модель восстанавливающей силы может отражать характеристики гистерезисного напряжения фактической конструкции или компонента и быть простой и практичной в допустимых пределах, чтобы облегчить анализ эффективного упруго-пластического отклика.
3.1. Модель скелетной кривой
Каркасная кривая определяет характерные точки модели восстанавливающей силы, которая является соединительной линией характерных точек на гистерезисной кривой 1/4. В этом испытании характерные точечные нагрузки и смещения двух образцов соединения различны. Для облегчения сравнения скелетные кривые двух образцов сначала рассматриваются как безразмерные. Формула следующая: где — максимальная положительная и обратная нагрузка на вершину колонны, а — смещение, соответствующее максимальной положительной и обратной нагрузке. Результаты представлены в таблице 2, а безразмерные скелетные кривые образцов получены, как показано на рисунке 5.
Из приведенного выше рисунка видно, что скелетные кривые двух образцов после безразмерной обработки все еще демонстрируют свои собственные регулярные характеристики. Анализируя гистерезисные кривые и безразмерные скелетные кривые образцов, можно видеть, что скелетные кривые двух образцов можно приблизительно аппроксимировать ломаной линией.
Таким образом, скелетная кривая в этой статье принимает форму трех ломаных линий, учитывающих предел текучести, предельную нагрузку и ухудшение жесткости, и моделируется соединительной линией трех характерных точек. Тремя характерными точками являются предел текучести, предельная точка нагрузки и точка разрушения (когда несущая способность уменьшается в 0,85 раза от точки предельной нагрузки).
По безразмерным значениям характерных точек образцов в табл. 2 координаты характерных точек, соответствующих образцам Ш-1 и Ш-2, даны следующим образом: (−Δ u / | −Δ max | , − P u /| − P max), (Δ− | у /| −Δ макс. | , − P y /| − P макс. | ), (0, 0), ( +Δ y /+Δ макс. 0079 макс ), (1, 1), и ( +Δ u /+Δ макс.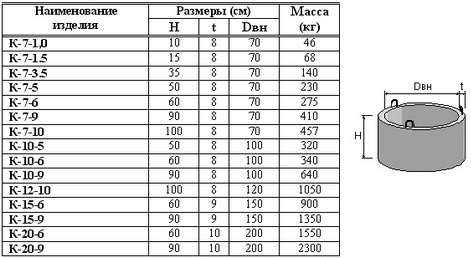
2 ).
Приняв эти координатные точки в качестве контрольных точек регрессионного анализа и соединив характерные точки, можно построить трехкратную линейную модель скелетной кривой двух образцов, как показано на рисунке 6.9.0035
На рис. 6 контрольные точки A и A’ — это точки положительной и обратной текучести, B и B’ — точки положительной и обратной предельной нагрузки, а C и C’ — точки положительной и обратной прочности. В соответствии с контрольными точками на кривой скелета можно получить трехкратное выражение скелетной кривой двух образцов, как показано в таблице 3.
3.2. Закон о снижении жесткости
В соответствии с гистерезисной кривой и скелетной кривой жесткость образца при нагрузке и разгрузке имеет определенную степень деградации. Ниже приводится закон деградации нагрузочной и разгрузочной жесткости образца при повторном нагружении [25]. Как показано на рисунке 7, K1 — положительная жесткость при разгрузке, K2 — жесткость при обратной нагрузке, K3 — жесткость при обратной разгрузке, K4 — жесткость при положительной нагрузке, a — положительная точка разгрузки, b — обратная точка нагружения, c — обратная точка разгрузки, d — положительная точка нагружения, Δ 1 — смещение, соответствующее положительной точке разгрузки a , Δ 2 — остаточная деформация при положительной разгрузке до нуля, Δ 3 — перемещение, соответствующее точке обратной разгрузки c , Δ 4 — остаточная деформация при обратной разгрузке до нуля, и значения других символов такие же, как указано выше.
3.2.1. Закон деградации жесткости образца при положительной разгрузке (K
1 ) Как показано на рисунке 7, наклон линии ab представляет собой положительную жесткость при разгрузке K 1 . Отсортировав данные кривой гистерезиса двух образцов, можно получить значение наклона линии ab при различных амплитудах смещения каждого образца, и оно может быть безразмерным. Абсцисса Δ 1 / Δ max+ , ордината K 1 /К 0+ . Можно получить диаграмму рассеяния закона деградации положительной жесткости при разгрузке (K 1 ) каждого образца, где Δ max + представляет собой смещение, соответствующее точке пика, когда образец соединения находится под положительной нагрузкой. K 0+ представляет начальную упругую жесткость сустава при положительной нагрузке. После удаления очевидных особых точек методом нелинейной аппроксимации данных была получена кривая закона деградации и ее формулы регрессии положительной жесткости при разгрузке K 1 каждого образца можно получить, как показано на рисунке 8 и уравнениях (2) и (3).
Формулы регрессии К 1 следующие:
3.2.2. Закон деградации жесткости образца при обратном нагружении (K
2 )Как показано на рисунке 7, наклон линии bc представляет собой жесткость при обратном нагружении K 2 . Используя тот же метод, что и в разделе 3.2.1, кривую закона деградации и ее формулы регрессии жесткости при обратной нагрузке K 2 каждого образца можно получить, как показано на рисунке 9 и уравнениях (4) и (5).
Формулы регрессии К 2 следующие:
3.2.3. Закон деградации жесткости образца при обратной разгрузке (K
3 ) Как показано на рисунке 7, наклон линии cd соответствует жесткости при обратной разгрузке K 3 . Используя тот же метод, что и в разделе 3.2.1, кривую закона деградации и ее формулы регрессии обратной жесткости разгрузки K 3 каждого образца можно получить, как показано на рисунке 10 и уравнениях (6) и (7).
Формулы регрессии К 3 следующие:
3.2.4. Закон деградации жесткости образца при положительной нагрузке (K
4 )Как показано на рисунке 7, наклон линии da представляет собой положительную жесткость при нагрузке K 4 . Используя тот же метод, что и в разделе 3.2.1, кривую закона деградации и ее формулы регрессии положительной жесткости при нагрузке K 4 каждого образца можно получить, как показано на рисунке 11 и уравнениях (8) и (9).
Формулы регрессии К 4 следующие:
3.3. Описание правила гистерезиса
Кривую фактической восстанавливающей силы на стыке колонны CTSRC трудно описать, поэтому необходимо создать упрощенную модель, которая может отражать фактические характеристики восстанавливающей силы. В соответствии с моделью скелетной кривой и законом деградации жесткости в сочетании с гистерезисной кривой была установлена модель восстанавливающей силы образцов, как показано на рисунке 12.
9.0035
Правило гистерезиса описывается следующим образом: (1) Когда образец находится под положительной нагрузкой, соотношение между нагрузкой и смещением развивается по скелетной кривой OABC. Если образец разгружается в сечении OA (положительная нагрузка не поддается), жесткость при положительной нагрузке не вырождается, и связь между нагрузкой и перемещением возвращается вдоль сечения AO (линия разгрузки AO ). Если образец разгружается в AB (уступает положительное нагружение), положительная жесткость нагружения начинает вырождаться, и связь между нагрузкой и перемещением возвращается по линии ab (линия разгрузки ab ). Если образец разгружается в сечении BC (нагрузка прошла пиковую точку), соотношение между нагрузкой и смещением возвращается в сечении eb (линия разгрузки eb ). (2) Когда образец разгрузка до b точка и затем нагрузка обратная, связь между нагрузкой и перемещением развивается вдоль blA’B’C’.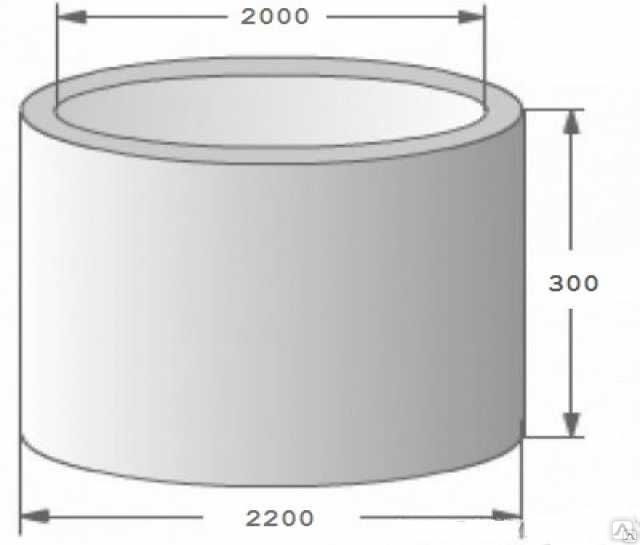
Если образец разгружается в сечении 1 A’ (обратное нагружение не поддается), то жесткость при обратном нагружении не вырождается, и связь между нагрузкой и перемещением возвращается вдоль сечения линии A’O (линия разгрузки А’О ). Если образец разгружается в сечении A’B’ (обратное нагружение уступает), жесткость при обратном нагружении вырождается, и связь между нагрузкой и перемещением возвращается вдоль сечения кд (линия выгрузки кд ). Если образец разгружается в сечении B’C’ (обратная нагрузка прошла пиковую точку), соотношение между нагрузкой и смещением возвращается в сечение fd (линия разгрузки равна fd ). (3) Когда образец разгружается до точки d , а затем снова нагружается, соотношение между нагрузкой и перемещением развивается по d 2 ABC , последующее нагружение и разгрузка такое же, как и при первом нагружении.
4. Проверка модели устойчивости
4.1. Проверка скелетной кривой
Модель скелетной кривой можно получить, соединив характерные точки спереди, и модель скелетной кривой сравнивается с измеренной скелетной кривой, как показано на рисунке 13.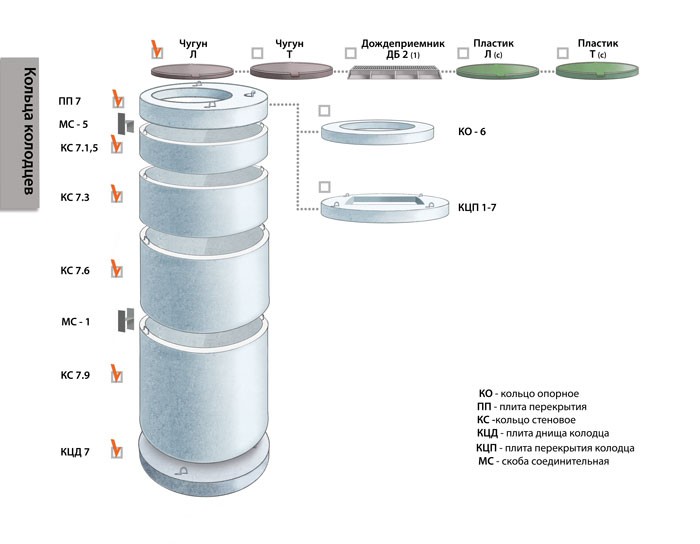
Можно видеть, что модель скелетной кривой может лучше отражать закон изменения смещения нагрузки двух совместных образцов.
4.2. Проверка кривой гистерезиса
Кривая гистерезиса, построенная по приведенному выше правилу гистерезиса, сравнивается с экспериментальной кривой гистерезиса, как показано на рис. 14, и результаты показывают, что они совпадают.
5. Выводы
На основе гистерезисной кривой нагрузки-перемещения и скелетной кривой, полученных в результате испытаний, мы создали модель восстанавливающей силы, подходящую для соединений нового типа. Эта модель в основном состоит из трех частей: трехкратной линейной скелетной модели, полученной из данных испытаний, конкретной формулы расчета снижения жесткости и математического описания гистерезисных правил.
Из приведенных выше результатов видно, что модель восстанавливающей силы на стыке колонны CTSRC имеет следующие характеристики: (1) При малоцикловой циклической нагрузке положительная и обратная нагрузка и жесткость разгрузки соединения нового типа составляет равна исходной жесткости соединения на стадии упругости (2).
Когда образец переходит на стадию текучести, начальная жесткость положительной и обратной нагрузки и разгрузки постепенно дегенерирует, и деградация на ранней стадии более очевидна, чем на ранней стадии. более поздняя стадия (3) По сравнению с положительной жесткостью при разгрузке и жесткостью при обратной разгрузке образца ухудшение жесткости при положительной жесткости при нагрузке и жесткости при обратной нагрузке более очевидно
Модель восстанавливающей силы может отражать гистерезисное поведение соединения нового типа и может использоваться для упругопластического сейсмического анализа во времени на стыке колонны CTSRC.
Доступность данных
Данные, использованные для поддержки результатов этого исследования, можно получить у соответствующего автора по запросу.
Раскрытие информации
Эта статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons Attribution, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Конфликт интересов
Авторы заявляют об отсутствии потенциального конфликта интересов в отношении исследования, авторства и/или публикации этой статьи.
Благодарности
Это исследование было поддержано Национальным фондом естественных наук Китая (№ 51408052), Молодежным научно-техническим проектом провинции Шэньси (№ 2016KJXX-51), Ключевым планом исследований и разработок провинции Шэньси (№ 2018SF-354), и специального фонда фундаментальных научных исследований в центральных университетах Чанъаньского университета (№ 300102289).205).
Ссылки
Рамберг В. и Осгуд В., «Описание кривой окраски стали по трем параметрам», Тех. Представитель Национального консультативного комитета по аэронавтике, Моффет-Филд, Калифорния, США, 1943 г., Технические примечания №: 902.
Посмотреть по адресу:
Google Scholar
П. Дженнингс, «Периодический отклик общей податливой конструкции, Журнал инженерно-механического отдела , вып.
90, нет. 20, стр. 131–165, 1964.Посмотреть по адресу:
Сайт издателя | Google Scholar
Р. Клаф и С. Джонстон, «Влияние снижения жесткости на требования к пластичности при землетрясениях», в Proceedings of the 2nd Japan National Conference on Earthquake Engineering , стр. 227–232, Токио, Япония, сентябрь. 1966.
Посмотреть по адресу:
Google Scholar
Т. Такеда, М. А. Созен и Н. Н. Нильсен, «Реакция железобетона на смоделированные землетрясения», Журнал структурного отдела , том. 96, нет. 12, стр. 2557–2572, 1970.
Посмотреть по адресу:
Сайт издателя | Google Scholar
C. Yan, D. Yang, Z. Ma, and J. Jia, «Гистерезисная модель соединения колонны SRUHSC и балки SRC с учетом повреждений», Materials and Structures , vol.
50, нет. 1, 2017.Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Чжан и С. Хан, «Гистерезисная модель железобетонных колонн, критических к изгибу и сдвигу», Journal of Earthquake Engineering , vol. 22, нет. 9, стр. 1639–1661, 2018.
Посмотреть по адресу:
Сайт издателя | Google Scholar
О. Юка и И. Хидеки, «Гладкая гистерезисная модель Н-образных стальных балок», Ce/Papers , vol. 3, нет. 3–4, стр. 145–150, 2019.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Чжан, Г. Ма, С. Ду, Ю. Лю, З. Ли и Ю. Ф. Чен, «Гистерезисное поведение и модель восстанавливающей силы бетонных колонн с изоляцией из армированного стеклопакета с полыми стенками (GIC)», KSCE Journal of Civil Engineering , vol.
23, нет. 7, стр. 3049–3065, 2019.Посмотреть по адресу:
Сайт издателя | Google Scholar
Q. Hao, T. Motohide, T. Naoki, and S. Yu, «Монотонная и гистерезисная модель для H-образных балок, включающая характеристики износа из-за локальной потери устойчивости», Thin-Walled Structures , об. 157, ID статьи 107016, 2020.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Y. Wang, Y. Feng, D. Huang, Z. Huang, and Z. Chen, «Модель восстанавливающей силы соединения, рассеивающего энергию, и нелинейный динамический анализ гибридной рамы», Journal of Building Engineering , vol. 32, ID статьи 101762, 2020.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Ли, Р. Ли, К. Ли и Д. Ван, «Разработка гистерезисной модели с динамическим эффектом и износом для анализа сейсмических характеристик железобетонных конструкций», Journal of Structural Engineering , том.
146, нет. 10, 2020.Посмотреть по адресу:
Сайт издателя | Академия Google
К. Се, К. Чжао, К. Яо, В. Хао и Ф. Ху, «Сейсмические характеристики сборных сборных мостовых колонн, соединенных с предварительно напряженным стальным стержнем с резьбой: экспериментальные испытания и гистерезисная модель», Достижения в области проектирования конструкций , том. 23, нет. 9, стр. 1975–1988, 2020.
Посмотреть по адресу:
Сайт издателя | Google Scholar
C. Wu, X. Liu, W. Pan и B. Mou, «Модель восстановления силы для модульной сборной железобетонной колонны из сборных сталей и композитных соединений H-образной стальной балки», Journal of Building Engineering , vol. 42, 2021.
Посмотреть по адресу:
Сайт издателя | Google Scholar
З.
Сонг, Ф. Ю, Н. Чжан и Ю. Фанг, «Модель для прогнозирования гистерезисного поведения нагрузки и смещения внутренних соединений замкнутых бетонных колонн и кольцевых балок из ПВХ и углепластика при низкой циклической нагрузке, Композитные конструкции , вып. 265, 2021.Посмотреть по адресу:
Сайт издателя | Google Scholar
X. Ni, S. Cao, and Y. Hou, «Гистерезисная модель стен жесткости, построенных с использованием высокопрочной арматуры», Конструкционный бетон , том. 22, нет. 3, стр. 1378–1395, 2021.
Посмотреть по адресу:
Сайт издателя | Google Scholar
X. Чжоу, Дж. Лю и С. Чжан, «Экспериментальное исследование сейсмического поведения квадратных стальных труб, ограниченных стальными железобетонными короткими колоннами», Journal of Building Structures , vol. 31, нет. 7, pp.
49–55, 2010.Просмотр по адресу:
Google Scholar
Дж. Лю, X. Чжан и С. Чжан, «Поведение при осевом сжатии круглой стальной трубы, заключенной в стальной армированный высокопрочный бетон короткие столбцы» Журнал строительных конструкций , вып. 30, нет. 2, pp. 242–248, 2009.
Посмотреть по адресу:
Google Scholar
X. Zhou и J. Liu, «Сейсмические характеристики и прочность трубчатых стальных железобетонных (SRC) коротких колонн», Журнал исследований конструкционной стали , том. 66, нет. 1, стр. 28–36, 2010 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Дай, С. Ни и Т. Чжоу, «Конечно-элементный анализ гистерезисного поведения квадратной стальной трубы, ограниченной стальной железобетонной колонной, стальной рамой, кольцевой балкой», Журнал Цзилиньского университета (Техническое и технологическое издание) , том.
48, нет. 5, стр. 1426–1435, 2018.Просмотр по адресу:
Google Scholar
Ю. Дай, С. Ни и Т. Чжоу, «Сейсмическое поведение круглой стальной трубы, заключенной в стальную железобетонную колонну из стали H» соединение кольцевой балки рамы», Journal of South China University of Technology , vol. 47, нет. 5, стр. 110–122, 2019.
Посмотреть по адресу:
Google Scholar
Ю. Дай, С. Ней и Т. Чжоу, «Несущая способность круглой стальной трубы, ограниченной соединением стальной балки бетонной колонны H-SRC с кольцевой балкой», Journal of Jilin University (Engineering and Technology Edition) , vol. 51, нет. 3, стр. 977–988, 2021.
Просмотр по адресу:
Google Scholar
Z. Guo и X. Lv, «Экспериментальное исследование гистерезисной модели железобетонных колонн с высоким коэффициентом осевого сжатия», China Журнал гражданского строительства , том.
37, нет. 5, стр. 32–38, 2004.Просмотр по адресу:
Google Scholar
Г. Чжан, X. Лв и Б. Лю, «Исследование моделей упругости высокопрочных железобетонных каркасных колонн», Engineering Mechanics , vol. 24, нет. 3, pp. 83–90, 2004.
Посмотреть по адресу:
Google Scholar
China Construction Industry Press, Code for Seismic Test Methods of Buildings , China Construction Industry Press, Пекин, Китай, 2015.
Л. Цзэн, Исследования по сейсмическим характеристикам и методам расчета соединений рамы из армированного сталью высокопрочного бетона с высокими эксплуатационными характеристиками , Сианьский университет архитектуры и технологий, Сиань, Китай, 2008 г.
90, нет. 20, стр. 131–165, 1964.
50, нет. 1, 2017.
23, нет. 7, стр. 3049–3065, 2019.
146, нет. 10, 2020.
Сонг, Ф. Ю, Н. Чжан и Ю. Фанг, «Модель для прогнозирования гистерезисного поведения нагрузки и смещения внутренних соединений замкнутых бетонных колонн и кольцевых балок из ПВХ и углепластика при низкой циклической нагрузке, Композитные конструкции , вып. 265, 2021.
49–55, 2010.
48, нет. 5, стр. 1426–1435, 2018.
37, нет. 5, стр. 32–38, 2004.Copyright
Copyright © 2021 Yan Dai и другие. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.