КО 6 по стандарту: ГОСТ 8020-90
| Наименование | Длина | Ширина | Высота |
1. Описание и сфера применения
Кольцо опорное – мультифункциональное изделие из армированного железобетона, применяемое в качестве компонента дренажных, водоотводных и инженерных систем (инфраструктурные сети: водопровод, канализация, газопровод, линии телефонной связи). Дополнительная область применения: частное (гражданское) строительство. В этом случае кольца используются при строительстве индивидуальных канализационных систем (септиков).
Основная задача изделия – не допускать осыпания грунта в смотровую зону колодца, попадания инородных тел и проникновения посторонних лиц.
Особенность изделия состоит в широком диапазоне эксплуатационных температур, низкой подверженности нагрузкам и способности функционировать практически в любых климатических условиях.
Покупать опорно центрирующие кольца рекомендуется у производителей с безупречной репутацией. За долгие годы работы на территории Пермского края, компания «Ассортимент ЖБИ Пермь» заслуженно приобрела статус доверенного поставщика многих строительно-инженерных организаций. Чтобы оставить заявку на приобретение опорных колец или иной продукции из армированного бетона, свяжитесь со специалистами компании по многоканальному телефону в Перми: (342) 201-95-15, или отправьте заявку на э/п: perm@tdajbi.
ru.
2. Специфика производства
а) Производственные методы
Высокое качество продукции производственного объединения «Ассортимент ЖБИ Пермь» обеспечено строгим соблюдением технических нормативов к изготовлению железобетонных изделий. Технология состоит из следующих этапов:
— замешивание бетонной смеси;
— грунтовка арматурной сетки;
— монтаж арматурного каркаса в формы;
— заливка смеси в металлические формы, покрытые гидрофобным веществом для упрощения извлечения готовых изделий;
— вибропрессование, обеспечивающее равномерность и однородности бетонной смеси, отсутствие воздушных пузырьков в готовом изделии;
— просушка изделий;
— извлечение колец;
— дополнительная сушка или термическая обработка для придания требуемой по заказу прочности на сжатие.
Детальное соблюдение производственного алгоритма обеспечивает неизменное качество продукции и соответствие её требованиям ГОСТ.
б) Материалы для изготовления
При подборе конкретных материалов для производства опорных колец, учитываются эксплуатационные требования к изделиям (обусловленные особенностями климатических условий и степенью агрессивности среды, в которых будет функционировать колодец).
При изготовлении колец используется качественный цемент с маркировкой прочности на сжатие не менее В15, с морозостойкостью не менее F50, а также влагостойкостью класса W2. Высокие эксплуатационные характеристики изделий также обеспечены добавлением в смесь специальных пластифицирующих и укрепляющих компонентов. Для армирующей металлической сетки используется сталь с маркировкой прочности А (I-III).
в) Производственные нормы
Стандарты изготовления на опорно направляющие кольца задекларированы в Государственном Стандарте 8020-90, а также отражают требования, изложенные в Серии 3.
900-3. Производственный контроль (ОТК) объединения «Ассортимент ЖБИ Пермь» обеспечивает соответствие каждого изделия требованиям федеральных и международных стандартов и технических регламентов, а также обязательное достижение каждым изделием отпускной прочности на сжатии, влаго-, и морозостойкости.
3. Стандарты упаковки, транспортировки и хранения
После извлечения и просушки готовых изделий, они маркируются и снабжаются техническими паспортами. Затем кольца перемещаются в складскую зону, где укладываются в штабеля в соответствии с требованиями к хранению (установка деревянных перемычек между кольцами, исключающих избыточное давление и деформацию изделий). При перевозке продукции (как классическим грузовым автотранспортом, как и с помощью железнодорожного и речного сообщения), штабеля изделий фиксируются к подвижным бортам с помощью пластиковой ленты и системы подпорок.
На кольца опорные цена устанавливается исходя из условий заказа (объёмов поставки, специфики материалов при изготовлении), но всегда остаётся доступной как для крупных застройщиков, так и небольших строительных компаний Перми и области.
Для приобретения опорных колец или консультации по продуктовым особенностям других железобетонных изделий, производимых компанией «Ассортимент ЖБИ Пермь», позвоните нам по телефону в Перми: (342) 201-95-15 (многоканальный), или напишите на официальную электронную почту: [email protected]. Выбор профессиональных застройщиков – это наше кольцо опорное!
Объем колодезного кольца в Нижнекамске: 542-товара: бесплатная доставка [перейти]
Партнерская программаПомощь
Нижнекамск
Каталог
Каталог Товаров
Одежда и обувьОдежда и обувь
СтройматериалыСтройматериалы
Текстиль и кожаТекстиль и кожа
Здоровье и красотаЗдоровье и красота
Детские товарыДетские товары
ЭлектротехникаЭлектротехника
Продукты и напиткиПродукты и напитки
ПромышленностьПромышленность
Вода, газ и теплоВода, газ и тепло
Дом и садДом и сад
Сельское хозяйствоСельское хозяйство
Все категории
ВходИзбранное
ООО «Энки» КЦД 12-9 Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное с дном КЦД-10-10 Тип: кольцо колодца, Высота: 1000 мм
ПОДРОБНЕЕКирпичный завод авангард Кольцо ЖБИ колодезное КС 10-9чс Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное К-8-3 Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное КС 10-9 Тип: кольцо колодца, Высота: 890мм, Внешний диаметр: 1000мм
ПОДРОБНЕЕКольцо колодезное железобетонное с дном КСД 10-9 Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное К-15-9ч Тип: кольцо колодца, Высота: 900 мм
ПОДРОБНЕЕКольцо колодезное К-15-9 Тип: кольцо колодца, Высота: 900 мм
ПОДРОБНЕЕКольцо колодезное К-15-9 Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное К-7-9 Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное с днищем КЦД-10-9 Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное с днищем ЖБИ ( 1000-900мм ) КСД 10-9ч Тип: кольцо колодца, Высота: 900 мм,
ПОДРОБНЕЕКольцо колодезное КС-7-9 Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное с днищем с четвертью КЦД-10-9ч Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное К-10-10 Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное КС 12-9 ТУ Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное КС-10-9 Тип: кольцо колодца, Назначение: промышленность
ПОДРОБНЕЕКольцо колодезное К-10-10ч Тип: кольцо колодца, Высота: 1000 мм
ПОДРОБНЕЕКольца колодезные КС-10-3 Тип: кольцо колодца, Высота: 300 мм
ПОДРОБНЕЕКольца доборные КС-7-10 Тип: кольцо колодца, Высота: 1000 мм
ПОДРОБНЕЕлитрахКольцо стеновое КС 7-0,10 Тип: кольцо колодца
ПОДРОБНЕЕКольцо КС 7-10 Сафоново Тип: кольцо колодца, Внешний диаметр: 840 мм
ПОДРОБНЕЕКольцо колодезное К-7-10 Тип: кольцо колодца, Высота: 1000 мм
ПОДРОБНЕЕ10 300
Кольцо колодезное с днищем КЦД-20-10 Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное ЖБИ ( 800-900 мм ) КС 8-9 с четвертью Тип: кольцо колодца, Высота: 900мм, Внешний
ПОДРОБНЕЕКольцо колодезное с четвертью КС 15-9ч Тип: кольцо колодца, Назначение: промышленность
ПОДРОБНЕЕКольцо КЦД 10-9ч (замок) Сафоново Тип: кольцо колодца
ПОДРОБНЕЕКольцо колодезное железобетонное замковое КСЗ 10-9 Тип: кольцо колодца, Высота: 900 мм
ПОДРОБНЕЕ2 страница из 18
Объем колодезного кольца
Задача о кольце для салфеток
Задача о кольце для салфеток
Недавно я был с группой деловых людей, когда один из них поднял проблему вычисления объема, который остается, когда круглый цилиндр удаляется из центра сферы. Поскольку оставшаяся фигура напоминает кольцо для салфеток, это иногда называют проблемой кольца для салфеток. Удивительный факт состоит в том, что объем не зависит от радиуса, 93. См. диаграмму поперечного сечения ниже.Объем кольца = объем сферы — объем цилиндра — 2 x объем торцевой крышки.Весь расчет приведен здесь. 93, стандартная формула объема сферы.
Меня как единственного присутствующего математика попросили объяснить, как получается этот ответ. Мы были, однако, в ресторане на обеде, и, поскольку основное блюдо вот-вот должно было быть подано, мне не хотелось начинать строчить на салфетках (кольца для которых, как это бывает, не были предусмотрены).
Плач Локхарта
Наконец, в колонке за прошлый месяц я полностью воспроизвел эссе о математическом образовании K-12, написанное учителем математики из Нью-Йорка (имеющим докторскую степень) по имени Пол Локхарт. Публикация эссе Локхарта породила для меня большое количество писем по электронной почте и, по-видимому, гораздо больший поток для самого Пола.
Угол Девлина обновлен в начале каждого месяца.
Математик Кит Девлин (email: [электронная почта защищена]) Исполнительный директор Центра Изучение языка и информации в Стэнфордский университет и Математик в выпуске выходного дня NPR.
Последняя книга Девлина, Раскрытие преступлений с помощью математики:
ЦИФРЫ ЗА NUMB3RS,
книга-компаньон к хиту
телевизионный криминальный сериал NUMB3RS,
и написан в соавторстве с профессором Гэри Лорденом
Калифорнийского технологического института, ведущий математик
советник по сериалу. Он был опубликован
в сентябре от Plume.Исчисление I — Объемы тел вращения / Метод колец
Онлайн-заметки Пола
Дом
/
Исчисление I
/
Приложения интегралов
/ Объемы тел вращения / Метод колец
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.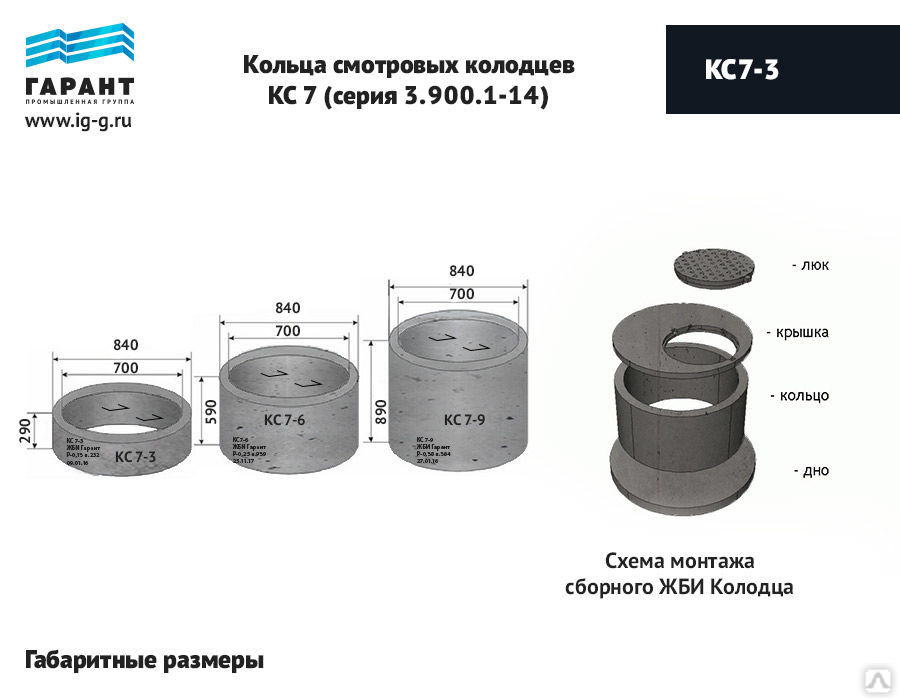
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 6.3: Объем с кольцами
В этом разделе мы начнем рассматривать объем тела вращения. Сначала мы должны определить, что такое тело вращения. Чтобы получить тело вращения, мы начинаем с функции \(y = f\left( x \right)\) на интервале \(\left[ {a,b} \right]\).
Затем мы вращаем эту кривую вокруг заданной оси, чтобы получить поверхность тела вращения. Для целей этого обсуждения давайте повернем кривую вокруг оси \(x\), хотя это может быть любая вертикальная или горизонтальная ось. Выполнение этого для приведенной выше кривой дает следующую трехмерную область. 9{{\,d}}{{A\влево(y\вправо)\,dy}}\]
где \(A\left( x \right)\) и \(A\left( y \right)\) — функции площади поперечного сечения твердого тела.
Есть много способов получить площадь поперечного сечения, и мы увидим два (или три, в зависимости от того, как вы на это смотрите) в следующих двух разделах. Будем ли мы использовать \(A\left( x \right)\) или \(A\left( y \right)\) будет зависеть от метода и оси вращения, используемой для каждой задачи.
Одним из самых простых способов получения площади поперечного сечения является разрезание объекта перпендикулярно оси вращения. При этом поперечное сечение будет либо твердым диском, если объект является твердым (как в нашем примере выше), либо кольцом, если мы выдолбили часть твердого тела (в конце концов мы это увидим). 92}} \справа)\]
, где снова оба радиуса будут зависеть от заданных функций и оси вращения. Также обратите внимание, что в случае твердого диска мы можем думать о внутреннем радиусе как о нуле, и мы придем к правильной формуле для твердого диска, и поэтому это гораздо более общая формула для использования.
Кроме того, в обоих случаях, является ли площадь функцией \(x\) или функцией \(y\), будет зависеть от оси вращения, как мы увидим.
Этот метод часто называют 92} — 4x + 5\), \(x = 1\), \(x = 4\) и ось \(x\) вокруг оси \(x\).
Показать решениеПервое, что нужно сделать, это получить эскиз ограничивающей области и твердого тела, полученного вращением области вокруг оси \(x\). Нам не нужен идеальный набросок кривых, нам просто нужно что-то, что позволит нам почувствовать, как выглядит ограниченная область, чтобы мы могли получить быстрый набросок твердого тела. Имея это в виду, мы можем заметить, что первое уравнение представляет собой просто параболу с вершиной \(\left( {2,1} \right)\) (вы помните, как получить вершину параболы правильно?) и открывается вверх и поэтому нам не нужно тратить много времени на наброски.
Вот оба этих эскиза.
Итак, чтобы получить поперечное сечение, мы разрезаем тело в любой точке \(x\). Ниже приведены несколько эскизов, показывающих типичное поперечное сечение. На рисунке справа показан разрез объекта с типичным поперечным сечением без крышек.
Эскиз слева показывает только кривую, которую мы вращаем, а также ее зеркальное отображение в нижней части твердого тела.
В этом случае радиус — это просто расстояние от оси \(x\) до кривой, и это не что иное, как значение функции в этом конкретном \(x\), как показано выше. Тогда площадь поперечного сечения 94\\ & = \frac{{78\pi }}{5}\end{align*}\]
В приведенном выше примере объект был твердым, но более интересными объектами являются те, которые не являются твердыми, поэтому давайте взглянем на один из них.
Пример 2. Определите объем твердого тела, полученного путем вращения части области, ограниченной \(y = \sqrt[3]{x}\) и \(\displaystyle y = \frac{x}{4}\), которая лежит в первом квадранте относительно оси у. Показать решение Сначала получим график ограничивающей области и график объекта. Помните, что нам нужна только часть ограничивающей области, которая находится в первом квадранте. Есть часть ограничивающей области, которая также находится в третьем квадранте, но нам это не нужно для этой задачи.
3}\\ y & = \frac{x }{4}\hspace{0,65 дюйма} \Rightarrow \hspace{0,5 дюйма}x = 4y\end{align*}\]
Вот пара эскизов границ стен этого объекта, а также типичное кольцо. Эскиз слева включает заднюю часть объекта, чтобы дать небольшой контекст фигуре справа.
Внутренний радиус в данном случае — это расстояние от оси \(y\) до внутренней кривой, а внешний радиус — это расстояние от оси \(y\) до внешней кривой. Оба они тогда являются расстояниями \(x\) и, таким образом, задаются уравнениями кривых, как показано выше. 92\\ & = \frac{{512\pi }}{{21}}\end{align*}\]
После этих двух примеров мы можем теперь сделать обобщение об этом методе. Если мы вращаемся вокруг горизонтальной оси (например, оси \(x\)), то площадь поперечного сечения будет функцией \(x\). Точно так же, если мы вращаемся вокруг вертикальной оси (например, оси \(y\)), то площадь поперечного сечения будет функцией \(y\).
Оставшиеся два примера в этом разделе помогут нам не слишком привыкнуть к идее всегда вращаться вокруг оси \(x\) или \(y\).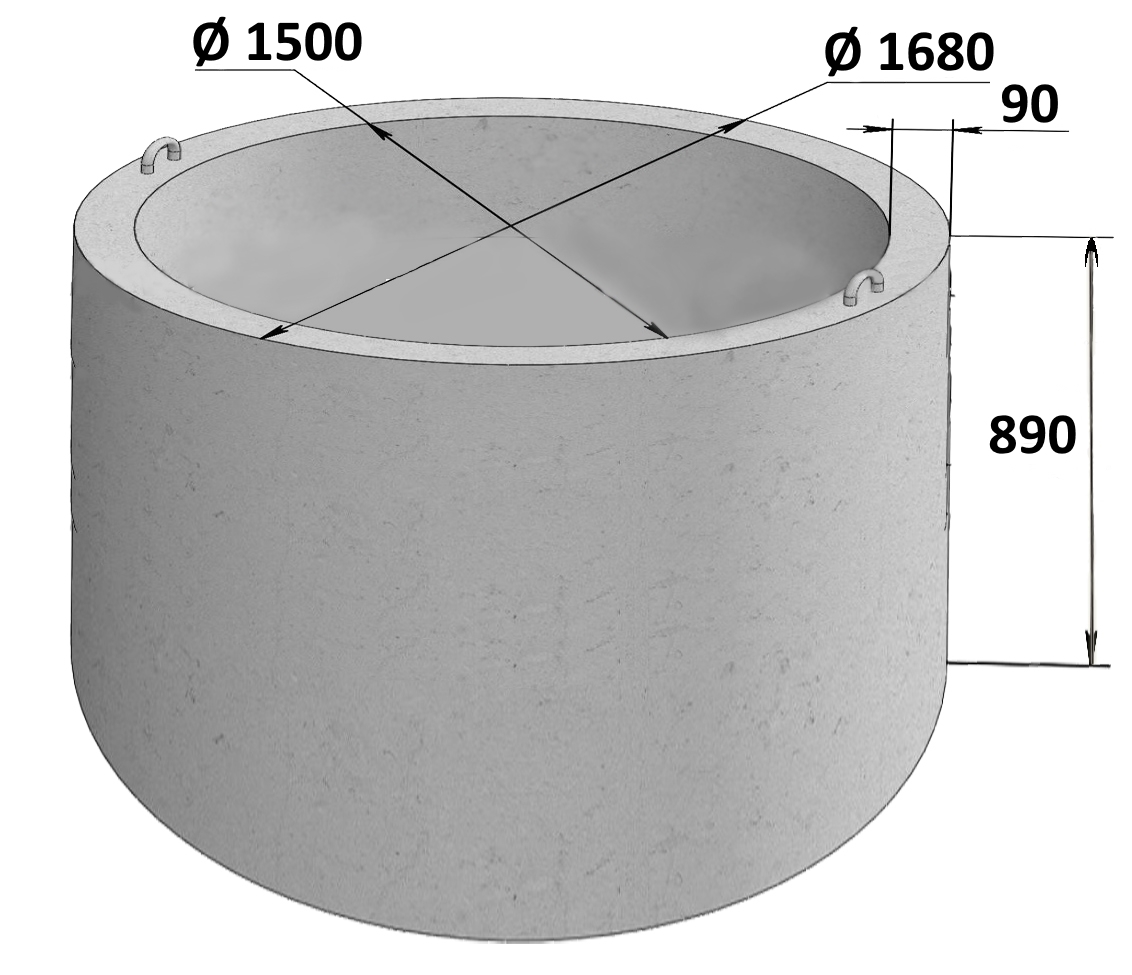
92} — 2x\) и \(y = x\) относительно прямой \(y = 4\).
Сначала нарисуем ограничивающую область и сплошное тело.
Опять же, мы будем искать объем стен этого объекта. Кроме того, поскольку мы вращаемся вокруг горизонтальной оси, мы знаем, что площадь поперечного сечения будет функцией \(x\).
Вот пара эскизов границ стен этого объекта, а также типичное кольцо. Эскиз слева включает заднюю часть объекта, чтобы дать небольшой контекст фигуре справа.
Теперь нам нужно быть осторожными при определении внутреннего и внешнего радиуса, так как они не будут такими простыми, как в предыдущих двух примерах.
Давайте начнем с внутреннего радиуса, так как он немного понятнее. Во-первых, внутренний радиус НЕ равен \(x\). Расстояние от оси \(x\) до внутреннего края кольца равно \(x\), но нам нужен радиус, а это расстояние от оси вращения до внутреннего края кольца. Итак, мы знаем, что расстояние от оси вращения до оси \(х\) равно 4, а расстояние от оси \(х\) до внутреннего кольца равно \(х\).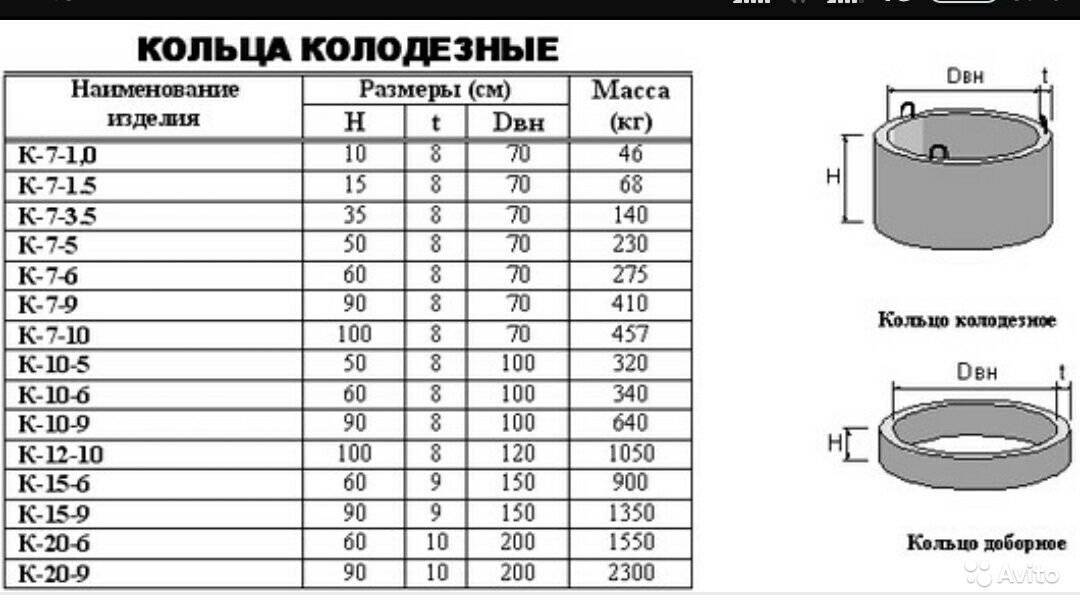
Тогда внутренний радиус должен быть разницей между этими двумя. Или, 92} + 2х + 4\]
Обратите внимание, что, учитывая расположение типичного кольца на приведенном выше эскизе, формула для внешнего радиуса может выглядеть не совсем правильно, но на самом деле она верна. Как показано на рисунке, внешний край кольца находится ниже оси \(x\), и в этой точке значение функции будет отрицательным, и поэтому, когда мы делаем вычитание в формуле для внешнего радиуса, мы фактически будем вычитать от отрицательного числа, которое имеет чистый эффект добавления этого расстояния к 4 и дает правильный внешний радиус. Точно так же, если внешнее ребро находится над осью \(x\), значение функции будет положительным, поэтому здесь мы будем делать честное вычитание, и в этом случае мы снова получим правильный радиус. 93\\ & = \frac{{153\pi }}{5}\end{align*}\]
Пример 4. Определить объем твердого тела, полученного вращением области, ограниченной \(y = 2\sqrt {x — 1} \) и \(y = x — 1\) вокруг прямой \(x = — 1\) .
Показать решениеКак и в предыдущих примерах, сначала нарисуем ограниченную область и твердое тело.
Теперь заметим, что, поскольку мы вращаемся вокруг вертикальной оси, площадь поперечного сечения будет функцией \(y\). Это также означает, что нам придется переписать функции, чтобы получить их с точки зрения \(y\). 92}}}{4} + 1\\ y & = x — 1\hspace{0.75in} \Rightarrow \hspace{0.5in}x = y + 1\end{align*}\]
Вот пара эскизов границ стен этого объекта, а также типичное кольцо. Эскиз слева включает заднюю часть объекта, чтобы дать небольшой контекст фигуре справа.
Внутренний и внешний радиусы для этого случая аналогичны и отличаются от предыдущего примера. Этот пример похож в том смысле, что радиусы — это не просто функции. В этом примере функциями являются расстояния от оси \(y\) до краев колец. Однако центр кольца находится на расстоянии 1 от оси \(y\). Это означает, что расстояние от центра до краев равно расстоянию от оси вращения до оси \(y\) (расстояние, равное 1), а затем от оси \(y\) до края кольца.