Нормальные напряжения при изгибе | ПроСопромат.ру
При выводе формулы для вычисления нормальных напряжений рассмотрим такой случай изгиба, когда внутренние силы в сечениях балки приводятся только к изгибающему моменту, а поперечная сила оказывается равной нулю. Этот случай изгиба носит название чистого изгиба. Рассмотрим средний участок балки, подвергающийся чистому изгибу.
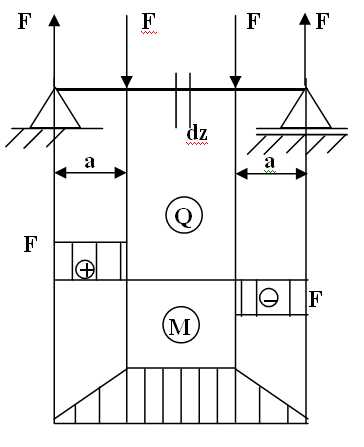 В нагруженном состоянии балка прогибается так,что ее нижние волокна удлиняются,а верхние укорачиваются.
В нагруженном состоянии балка прогибается так,что ее нижние волокна удлиняются,а верхние укорачиваются.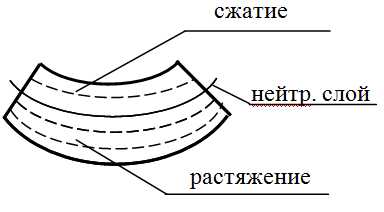
Поскольку часть волокон балки растягивается, а часть сжимается, причем переход от растяжения к сжатию происходит плавно, без скачков, в средней части балки находится слой, волокна которого только искривляются, но не испытывают ни растяжения, ни сжатия. Такой слой называют
Линии, проведенные на боковой поверхности балки перпендикулярно оси, остаются плоскими при изгибе. Эти опытные данные позволяют положить в основу выводов формул гипотезу плоских сечений (гипотеза Бернулли). Согласно этой гипотезе сечения балки плоские и перпендикулярные к ее оси до изгиба, остаются плоскими и оказываются перпендикулярными изогнутой оси балки при ее изгибе.
Допущения для вывода формул нормального напряжения: 1) Выполняется гипотеза плоских сечений. 2) Продольные волокна друг на друга не давят (гипотеза о ненадавливании) и, следовательно, каждое из волокон находится в состоянии одноосного растяжения или сжатия. 3) Деформации волокон не зависят от их положения по ширине сечения. Следовательно, и нормальные напряжения, изменяясь по высоте сечения, остаются по ширине одинаковыми. 4) Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости. 5) Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков. 6) Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания.
Рассмотрим балку произвольного сечения, но имеющую ось симметрии.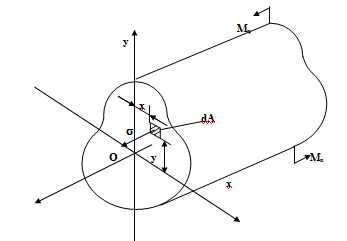 Изгибающий момент представляет собой результирующий момент внутренних нормальных сил, возникающих на бесконечно малых площадках и может быть выражен в интегральном виде: (1), где y — плечо элементарной силы относительно оси х
Изгибающий момент представляет собой результирующий момент внутренних нормальных сил, возникающих на бесконечно малых площадках и может быть выражен в интегральном виде: (1), где y — плечо элементарной силы относительно оси х
Выделим на среднем участке балки и рассмотрим участок длиной dz, подвергающийся изгибу. Изобразим его в укрупненном масштабе.
К выводу формул при изгибе: а) участок балки до деформации; б) участок балки после деформации
Сечения, ограничивающие участок dz, параллельны друг другу до деформации, а после приложения нагрузки повернутся вокруг своих нейтральных линий на угол . Длина отрезка волокон нейтрального слоя при этом не изменится и будет равна:, где -это радиус кривизны изогнутой оси балки. А вот любое другое волокно, лежащее ниже или выше нейтрального слоя, изменит свою длину. Вычислим относительное удлинение волокон, находящихся от нейтрального слоя на расстоянии у. Относительное удлинение — это отношение абсолютной деформации к первоначальной длине ,тогда:
Сократим на и приведем подобные члены, тогда получим:(2) Эта формула выражает геометрическую сторону задачи о чистом изгибе: деформации волокон прямо пропорциональны их расстояниям до нейтрального слоя.
Теперь перейдем к напряжениям, т.е. будем рассматривать физическую сторону задачи. в соответствии с допущением о ненадавливании волокон используем закон Гука при осевом растяжении-сжатии:, тогда с учетом формулы (2) имеем (3),т.е. нормальные напряжения при изгибе по высоте сечения распределяются по линейному закону. На крайних волокнах нормальные напряжения достигают максимального значения, а в центре тяжести сечения равны нулю. Подставим
Тогда ,откуда (4) ,где — это кривизна изогнутой оси балки, а — жесткость сечения балки при изгибе.
Подставим полученное выражение кривизны (4) в выражение (3) и получим формулу для вычисления нормальных напряжений в любой точке поперечного сечения: (5)
Т.о. максимальные напряжения возникают в точках, наиболее удаленных от нейтральной линии. Отношение (6) называют осевым моментом сопротивления сечения. Его размерность см3, м3. Момент сопротивления характеризует влияние формы и размеров поперечного сечения на величину напряжений.
Тогда максимальные напряжения: (7)
Условие прочности при изгибе: (8)
При поперечном изгибе действуют не только нормальные, но и касательные напряжения,т.к. имеется поперечная сила. Касательные напряжения усложняют картину деформирования, они приводят к искривлению поперечных сечений балки, в результате чего нарушается гипотеза плоских сечений. Однако исследования показывают, что искажения, которые привносят касательные напряжения, незначительно влияют на нормальные напряжения,подсчитанные по формуле (5). Таким образом ,при определении нормальных напряжений в случае поперечного изгиба теория чистого изгиба вполне применима.
Нейтральная линия. Вопрос о положении нейтральной линии.
При изгибе отсутствует продольная сила, поэтому можно записать Подставим сюда формулу нормальных напряжений
Условие (отсутствие момента внутренних сил относительно силовой линии) даст или с учетом (3) . По тем же соображениям (см. выше) . В подынтегральном выражении — центробежный момент инерции сечения относительно осей х и у равен нулю, значит, эти оси являются главными и центральными и составляют прямой угол. Следовательно, силовая и нейтральная линии пр прямом изгибе взаимно перпендикулярны.
Установив положение нейтральной линии, несложно построить эпюру нормальных напряжений по высоте сечения. Ее линейный характер определяется уравнением первой степени.
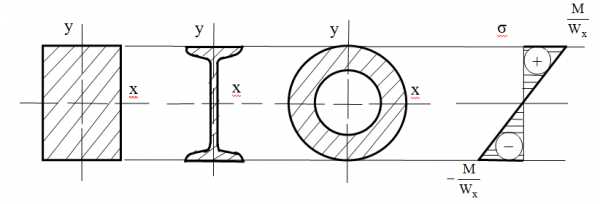
Характер эпюры σ для симметричных сечений относительно нейтральной линии, М<0
prosopromat.ru
Напряжение (сопромат)
Напряженное состояние в точке тела является ключевым понятием в сопромате. Необходимость введения понятия напряжения в точке для суждения об интенсивности внутренних сил в некоторой точке сечения стержня вызвана неравномерным распределением внутренних сил по длине и поперечному сечению в общем случае нагружения.
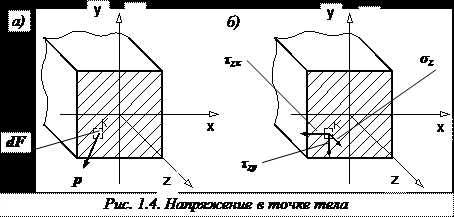
Напряжение в точке тела K (обозначено буквой p) – это интенсивность внутренней силы , возникающей на бесконечно малой площадке в окрестности данной точки (рис. 1.4, а).
В количественном выражении .
|
Понятие о напряжении в точке твердого тела в некотором смысле напоминает понятие о давлении, действующем, например, внутри жидкости. Однако давление в точке жидкости одинаково во всех направлениях. Если проведем через точку K тела другое сечение, иной будет внутренняя сила. Следовательно, иным будет и напряжение, хотя оно возникает в той же самой точке K.
Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении).
Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши.
Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальное напряжение ( – сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения ( – тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают.
Между полным (), нормальным () и касательными напряжениями ( и ) существует зависимость:
.
Касательные напряжения служат мерой тенденции одной части сечения смещаться (или скользить) относительно другой его части.
Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону (то есть равная, приблизительно, весу одного яблока). Как мы увидим в дальнейшем, эта единица напряжения мизерно мала. В сопромате чаще используются другие единицы:
1 МПа = 106 Па; 1 кН/см2 = 107 Па.
В технической системе единиц напряжения измеряются в килограммах силы на миллиметр (сантиметр) в квадрате (кгс/мм2 или кгс/см2) . Следует запомнить, что 1 кН/см2 » 1 кгс/мм2.
sopromato.ru
Сопромат.in.ua: Напряжения
Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади:Па=Н/м2 (МПа = 106 Н/м2, кгс/см2=98 066 Па ≈ 105Па, тс/м2 и т. д.).
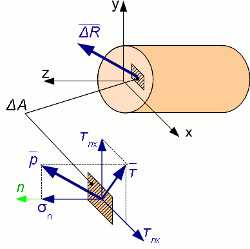 Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим [math]∆\vec{R}[/math]. Полное среднее напряжение на этой площадке [math]\vec{р} = ∆\vec{R}/∆A [/math]. Найдем предел этого отношения при [math]∆A \to 0[/math] . Это и будет полным напряжение на данной площадке (точке) тела.
Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим [math]∆\vec{R}[/math]. Полное среднее напряжение на этой площадке [math]\vec{р} = ∆\vec{R}/∆A [/math]. Найдем предел этого отношения при [math]∆A \to 0[/math] . Это и будет полным напряжение на данной площадке (точке) тела.\textstyle \vec{p} = \lim_{\Delta A \to 0} {\Delta\vec{R}\over \Delta A}
Полное напряжение [math]\vec p[/math], как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к площадке – касательное напряжение [math]\tau_n[/math]. Здесь n – нормаль к выделенной площадке.
Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – [math]\tau_{nx}, \tau_{ny}[/math]. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.
$$\vec{p} = \left[\matrix{\sigma _n \\ \tau _{nx} \\ \tau _{nx}} \right]$$
Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением [math]\vec p [/math], а с его составляющими [math]σ_x,\tau _{xy}, \tau _{xz} [/math] . В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ.
Тензор напряжений
При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – [math]σ_x,\tau _{xy}, \tau _{xz} [/math]Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений
$$ T _\sigma = \left[\matrix{
\sigma _x & \tau _{yx} & \tau _{zx} \\
\tau _{xy} & \sigma _y & \tau _{zy} \\
\tau _{xz} & \tau _{yz} & \sigma _z
}\right]$$
Здесь первый столбец представляет компоненты напряжений на площадках,
нормальных к оси x, второй и третий – к оси y и z соответственно.
При повороте осей координат, совпадающих с нормалями к граням выделенного
элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю.
Площадка, на которой касательные напряжения равны нулю, называется главной площадкой.
Нормальное напряжение на главной площадке называется главным напряжением
Нормаль к главной площадке называется главной осью напряжений .
В каждой точке можно провести три взаимно-перпендикулярных главных площадки.
При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС).
Связь внутренних усилий и напряжений
Внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам. Напряжения – мера, характеризующая распределение внутренних сил по сечению.
Предположим, что нам известно напряжение в каждой элементарной площадке. Тогда можно записать:Продольное усилие на площадке dA: dN = σzdA
Поперечная сила вдоль оси х: dQ x = [math]\tau {zx}[/math] dA
Поперечная сила вдоль оси y: dQ y = [math]\tau {zy}[/math] dA
Элементарные моменты вокруг осей x,y,z: $$\begin{array}{lcr}
dM _x = σ _z dA \cdot y \\
dM _y = σ _z dA \cdot x \\
dM _z = dM _k = \tau _{zy} dA \cdot x — \tau _{zx} dA \cdot y
\end{array}$$
Выполнив интегрирование по площади поперечного сечения получим:

То есть, каждое внутренне усилие есть суммарный результат действия напряжений по всему поперечному сечению тела.
Связанные статьи
метки: напряжения
sopromat.in.ua
Нормальные касательные напряжения — поперечный изгиб (сопромат)
При поперечном изгибе в сечении балки помимо изгибающего момента () возникает поперечная сила (). Поэтому в поперечном сечении при поперечном изгибе наряду с нормальными напряжениями () возникают и касательные напряжения ().
На основании закона парности касательные напряжения возникают и в продольных сечениях балки. Вследствие этого при поперечном изгибе отмечаются сдвиги продольных слоев балки относительно друг друга.
При поперечном изгибе гипотеза плоских сечений нарушается, поскольку поперечные сечения балки искривляются (рис. 7.9).
Исследования показали: если балка является достаточно длинной, влияние искривления поперечного сечения на значения нормальных напряжений невелико, поэтому влиянием сдвигов на закон распределения нормальных напряжений при изгибе пренебрегают, формула нормальных напряжений при поперечном изгибе: .
Проанализируем формулу Журавского:
Поперечная сила () для конкретного сечения и момент инерции поперечного сечения относительно нейтральной оси являются постоянными величинами, поэтому касательные напряжения изменяются по высоте поперечного сечения по тому же закону, что и отношение статического момента отсеченной части поперечного сечения () к ширине поперечного сечения (), в котором они вычисляются.
Во всех точках поперечного сечения, расположенных на расстоянии y от нейтральной линии (по всей ширине сечения ), касательные напряжения при поперечном изгибе одинаковы.
В самых удаленных от нейтральной оси точках поперечного сечения касательные напряжения при поперечном изгибе равны 0, поскольку в этом случае .
Наибольшие касательные напряжения возникают в точках поперечного сечения, расположенных на нейтральной оси. Напомним, что в этих точках нормальные напряжения равны нулю
sopromato.ru
5. Нормальные напряжения при чистом изгибе. Основные гипотезы. Формула нормальных напряжений. Эпюра распределения нормальных напряжений по высоте поперечного сечения.
Гипотезы:
1) гипотеза плоских сечений (гипотеза Бернулли), согласно которой поперечные сечения балки, плоские и перпендикулярные к геометрической оси балки до деформации, остаются плоскими после деформации;
2) гипотеза об отсутствии боковых давлений, согласно которой отдельные продольные волокна балки испытывают только одноосное растяжение или сжатие;
3) гипотеза постоянства напряжений по ширине поперечного сечения, согласно которой напряжения для точек, равноудаленных от нейтрального слоя равны между собой.
σ=Му/Ix.
σmax=M/WxH;
σmin=M/WxB , WxH=Ix/hHWxB=Ix/hB(WxHWxB– моменты
сопротивления относительно оси Ох для
нижних и верхних волокон.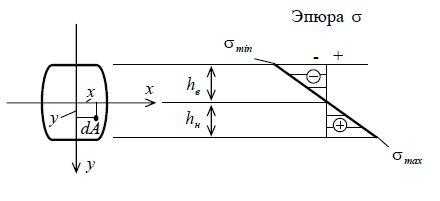
6. Касательные напряжения при изгибе (формула Журавского). Эпюра распределения касательных напряжений по высоте поперечного сечения.
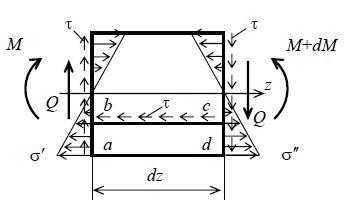
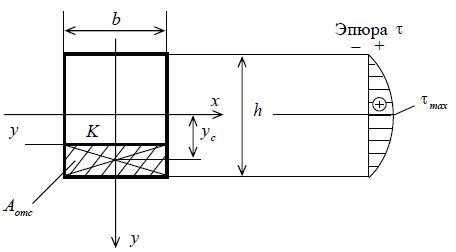
Sx — статический момент отсеченной части относительно оси ОХ
7. Анализ напряжённого состояния при изгибе. Главные напряжения при изгибе. Траектория главных напряжений.
Согласно формулам, в поперечных сечениях, работающих на изгиб, возникают нормальные и касательные напряжения:
;
Следовательно, в произвольной точке балки при изгибе имеет место плоское напряженное состояние. Определим главные напряжения, действующие по главным площадкам.
Величиной нормальных напряжений, действующих по горизонтальны площадкам, пренебрегаем, поэтому формулы главных напряжений примут следующий вид:
; ; ;
Наглядное представление о направлении внутренних усилий в нагруженном теле дают траектории главных напряжений. Траектория главных напряжений – линия, в каждой точке которой касательная совпадает с направлением главного напряжения в этой точке. На рисунке сплошными линиями показаны траектории главных растягивающих напряжений σ1 , а пунктирными – главных сжимающих напряжений σ3. По траекториям σ1 можно судить о том, где и в каком направлении могут появиться трещины, если материал балки плохо работает на растяжение. При армировании железобетонных балок арматуру целесообразно располагать по направлению растягивающих напряжений. Эту задачу помогает решать определение траекторий главных напряжений.
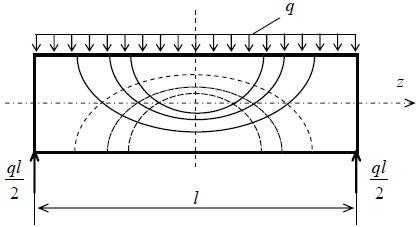
8. Расчет на прочность при изгибе. Подбор сечения. Рациональное сечение балок.
Метод предельных состояний:
σmax≤γcR (для пластичных материалов)
σрmax≤γcRр; σсmax≤γcRс (для хрупких)
γc — коэффициент условий работы.
Метод допускаемых напряжений:
σmax≤[σ],( для пластич. мат-лов)
σрmax≤[σp]; σcmax≤[σc](для хрупких)
[σ] — допуск. напряжение;
Подбор сечения:
β — коэффициент [сечение: круглое — 8, прямоугольное — 6, двутар — 3]
9. Определение перемещений при изгибе, универсальные уравнения углов поворота сечения и прогибов.
Прогиб v — это перемещение центра тяжести поперечного сечения перпендикулярно к исходному положению геометрической оси балки. Угол поворота сечения γ-это угол между плоскостью поперечного сечения до деформации и плоскостью поп. сечения после деформации. γ=dv/dz.
Универсальные уравнения
;
;
studfiles.net
1. Общие понятия и основные положения
1.Основные гипотезы в сопротивлении материалов.
В сопротивлении материалов принимаются гипотезы о сплошном, однородном, изотропном и линейно упругом теле.
Материал конструкции принимается однородным и сплошным, при этом не учитывается анатомическая структура или молекулярное строение тела. Свойства материала не зависят от формы и размеров тела и одинаковы во всех его точках.
Материал конструкции изотропен, т. е. его свойства по всем направлениям одинаковы.
Материал конструкции является идеально упругим и способен полностью восстанавливать первоначальные форму и размеры, после устранения причин, вызвавших деформацию.
2.Внешние силы и их классификация.
Все силы могут быть разделены на объемные и поверхностные. К объемным относятся силы тяжести, силы инерции и т. п.
Если внешние силы являются результатом контактного взаимодействия, то они относятся к поверхностным силам.
Поверхностные силы могут быть разделены на сосредоточенные и распределенные силы.
Сосредоточенные силы передаются на конструкцию через небольшую площадку, поэтому условно считают, что они приложены в точке.
Распределенная сила (нагрузка) передается на конструкцию через определенную площадь.
По времени действия на конструкцию различают постоянные и временные нагрузки.
Постоянной называют нагрузку, действующую непрерывно в течении всего срока службы сооружения (собственный вес конструкции).
Временная нагрузка имеет ограниченную продолжительность действия (ветровая нагрузка, вес снега).
3.Основные объекты, изучаемые в сопромате.
1) Брус – элемент конструкции, одно из измерений которого существенно больше двух других.
2) Стержень – брус с прямолинейной геометрической осью
3) Балка – горизонтальный или наклонный стержень, работающий на изгиб
4) Пластина – плоский элемент конструкции, отличающийся тем, что толщина ее мала по сравнению с двумя другими размерами
5) Оболочка – в отличие от пластины ее внешние контуры образованы не плоскостями, а криволинейными поверхностями.
6) Массивное Тело – элемент конструкции, основные размеры которого достаточно велики и одного и того же порядка
4.Понятие о расчетной схеме.
Расчетная схема конструкции — это его упрощенная схема, освобожденная от несущественных в данном случае особенностей. Удачно выбранная расчетная схема даст результаты расчета, близкие к реальным. При неудачном выборе – результаты расчетов окажутся далеки от истины, что может привести к плачевным последствиям. Выбор расчетной схемы конструкции в сопротивлении материалов производят в соответствии с гипотезами (допущениями).
5.Внутренние силы. Метод мысленных сечений. Напряжение полное, нормальное и касательное. Размерность напряжения.
Внутренние силы – силы взаимодействия между отдельными элементами сооружения или отдельными частями элемента, возникающие под действием внешних сил.
Для определения внутренних усилий применяется метод сечений. В общем случае на рассчитываемый элемент конструкции, находящийся в равновесии действует произвольная система сил. Мысленно проводим плоскость (для бруса обычно проводится перпендикулярно его продольной оси) и рассекаем на две части рассматриваемый элемент. Левую часть мысленно отбрасываем, а правую оставляем в рассмотрении. Действие отброшенной левой части учитываем внутренними усилиями.
Если все внутренние усилия приводятся к:
N (продольная сила) – простое растяжение или сжатие
Qx,Qy (поперечные силы) – сдвиг
Mz (крутящий момент) – кручение
Mx, My (изгибающие моменты) – изгиб
Интенсивность нормальных сил называется нормальным напряжением σ
Касательных сил— касательным напряжением τ.
Нормальное и касательное напряжение являются составляющими полного напряжения p в рассматриваемой точке. Полное напряжение может быть определено также по формуле:
studfiles.net
5.4. Нормальные напряжения при чистом изгибе
Чистый изгиб – это самый простой случай нагружения балки (рис.5.10). Он имеет место и при другой схеме нагружения (рис.5.13.). Силовая плоскость совпадает с одной из главных осей поперечного сечения – осью y (рис.5.13). В сечении действует только нормальное напряжение σ, касательное τ равно нулю ввиду равенства нулю поперечной силы Q.
Формулу для σ можно вывести только из рассмотрения картины деформации балки (рис.5.14,б). Опыты, поставленные на эластичных (например, резиновых) моделях, позволяющих легко получить значительные деформации, показывают, что нанесённая на поверхность прямоугольная сетка линий (рис.5.14,а) деформируется (рис.5.14,б) следующим образом:
а) продольные линии искривляются по дуге окружности;
б) контуры поперечных сечений остаются прямыми;
в) линии контуров сечений пересекаются с продольными волокнами под прямым углом.
Далее,
замеряя расстояния между аналогичными
точками контура каких-либо двух сечений,
можно обнаружить, что при деформации
верхние продольные волокна укорачиваются
(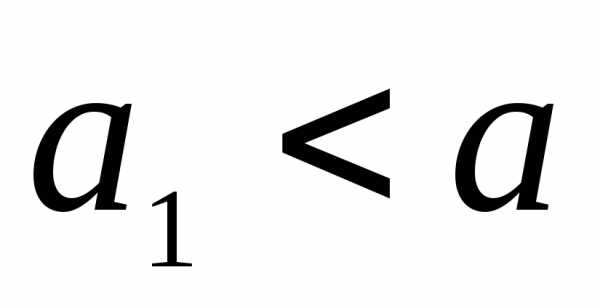 ),
а нижние – удлиняются (
),
а нижние – удлиняются (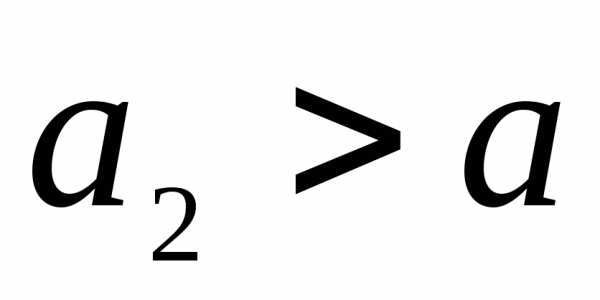 ).
Ясно, что есть такие волокна, длина
которых остается неизменной (
).
Ясно, что есть такие волокна, длина
которых остается неизменной (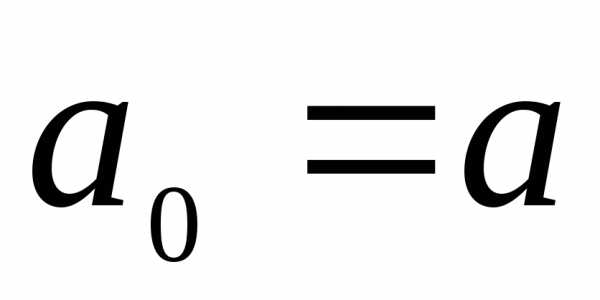 ),
они лишь искривляются. Совокупность
волокон, не меняющих своей длины при
изгибе балки, называется
нейтральным слоем (НС). Поперечное сечение пересекается с
нейтральным слоем по прямой, которая
называется нейтральной
линией (НЛ).
),
они лишь искривляются. Совокупность
волокон, не меняющих своей длины при
изгибе балки, называется
нейтральным слоем (НС). Поперечное сечение пересекается с
нейтральным слоем по прямой, которая
называется нейтральной
линией (НЛ).
Таким образом, при чистом изгибе балка деформируется следующим образом.
1. Плоские поперечные сечения остаются плоскими и поворачиваются так, что остаются нормальными к изогнутой оси – справедлива гипотеза плоских сечений.
2. Продольные волокна удлиняются и укорачиваются, но друг на друга не давят – имеет место линейное напряжённое состояние.
3. В поперечном направлении (вдоль оси z) деформация постоянна.
а б
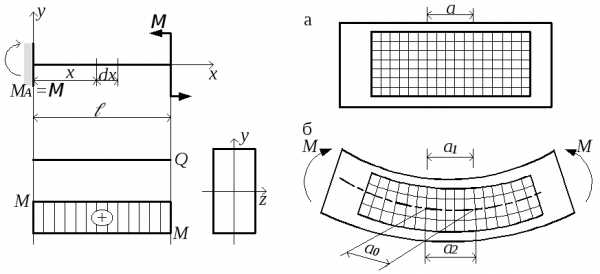
Рис.5.13 Рис.5.14
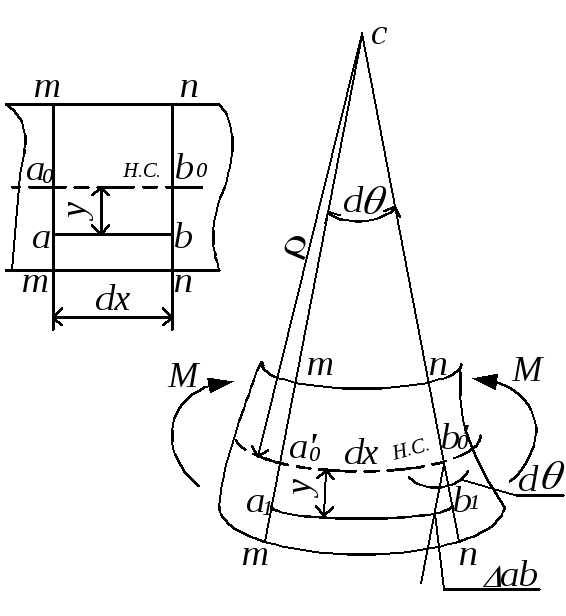
Выделим
элемент двумя смежными поперечными
сечениями m-m
и n-n,
отстоящими друг от друга на расстоянии
dx
(рис.5.15,а), и, приняв во внимание гипотезу
плоских сечений, покажем его деформированное
состояние (рис.5.15,б). Сечения m-m
и n-n
остаются плоскими и поворачиваются на
угол dθ,
элемент a0b0 нейтрального слоя превращается в дугу 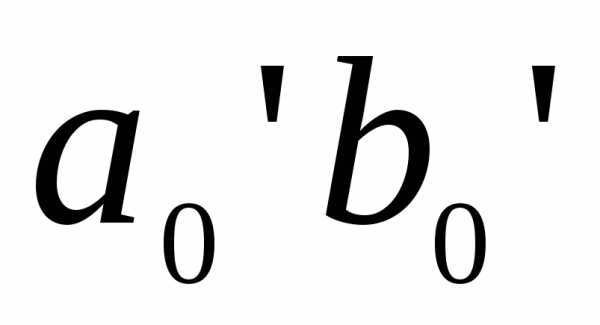 с радиусом ρ.
Волокна нейтрального слоя не изменяют
своей длины при деформации, поэтому
с радиусом ρ.
Волокна нейтрального слоя не изменяют
своей длины при деформации, поэтому
,
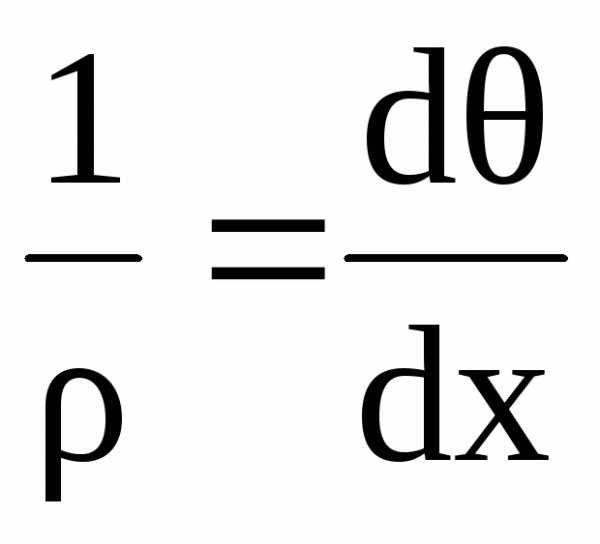 . (5.8)
. (5.8)
Произвольное
волокно 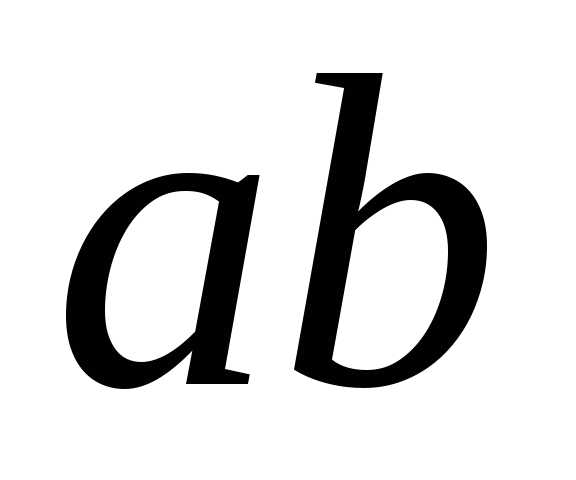 ,
находящееся на расстоянии y
от нейтрального слоя, превращается в
криволинейное волокно
,
находящееся на расстоянии y
от нейтрального слоя, превращается в
криволинейное волокно 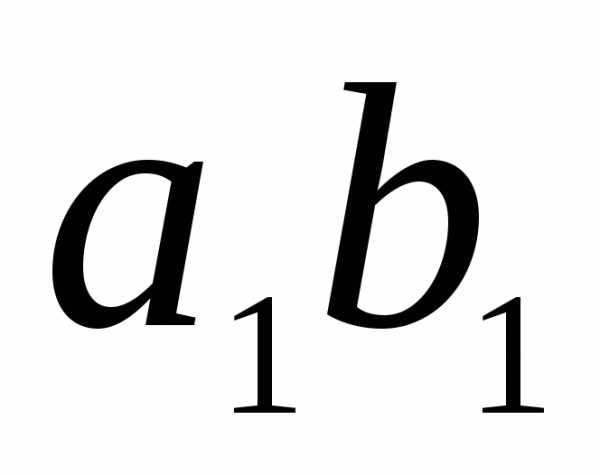 .
Абсолютное удлинение его ∆ab
может быть показано на рис.5.15,б, если из
точки b′0 провести прямую, параллельную Cm
.
Абсолютное удлинение его ∆ab
может быть показано на рис.5.15,б, если из
точки b′0 провести прямую, параллельную Cm
, (5.9)
Относительное удлинение этого волокна
. (5.10)
Подставив выражение (5.8) в выражение (5.10), получим
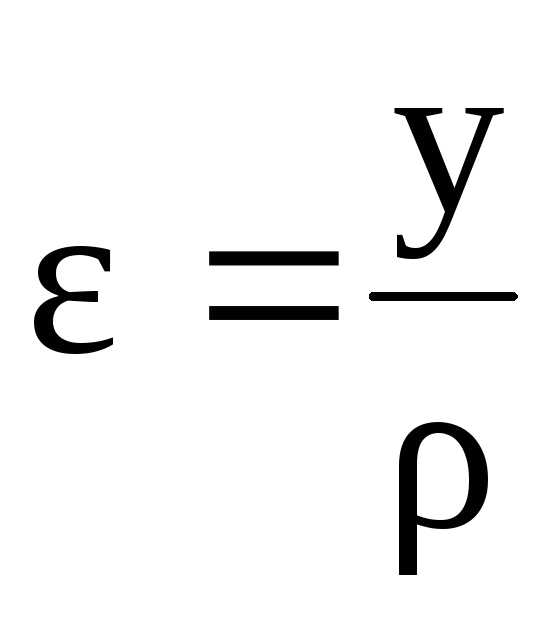 . (5.11)
. (5.11)
Таким образом, рассмотрение геометрической стороны задачи показало, что относительная продольная деформация пропорциональна расстоянию волокна от нейтральной оси.
а б Рис.5.15 | Физическая сторона задачи выражается законом Гука. Для волокон, находящихся в линейном напряжённом состоянии, его следует записать в виде Исключив ε из формул (5.11) и (5.12), получим |
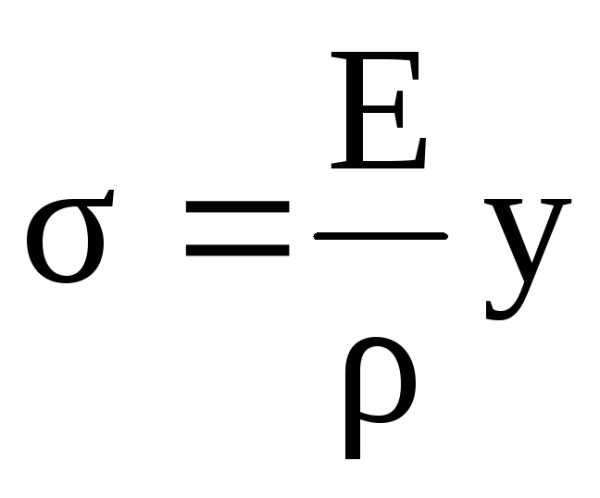 . (5.13)
. (5.13)
Формулой (5.13) пока пользоваться невозможно, т.к. неизвестны радиус кривизны нейтрального слоя ρ и положение нейтральной оси в сечении. Для определения этих величин рассмотрим статическую сторону задачи (рис.5.16).
Запишем уравнения статики для отрезка балки длиной x, находящегося под действием постоянного изгибающего момента M и нормальных напряжений σ.
Нужно записать шесть уравнений статики
∑х = 0, ∑у = 0, ∑z = 0,
∑Mx = 0, ∑My = 0, ∑Mz = 0.
Из них три дают тождество 0 = 0. Остаются три уравнения
∑х = 0, ∑My = 0, ∑Mz = 0.
Запишем их по порядку, подставляя σ по формуле (5.13).
. (5.14)
Поскольку 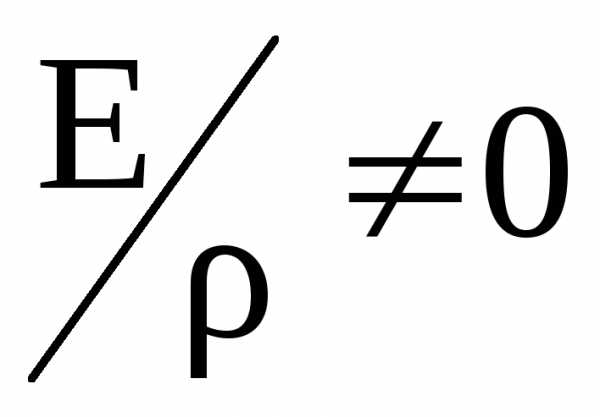 ,
, 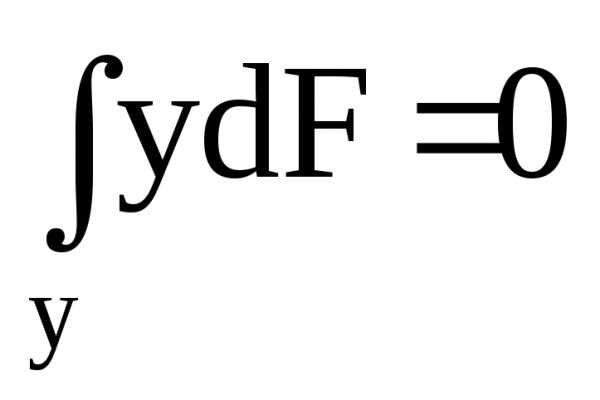 ,
а это статический момент сечения
относительно нейтральной линии.
,
а это статический момент сечения
относительно нейтральной линии.
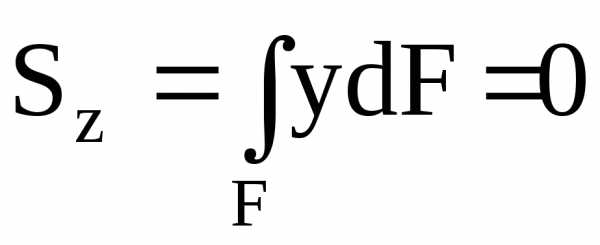 . (5.15)
. (5.15)
.
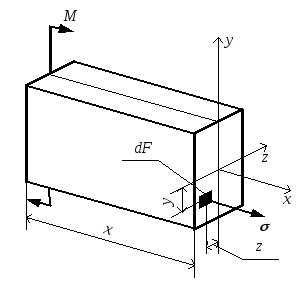
Рис.5.16
По
той же причине, что и в предыдущем
уравнении, 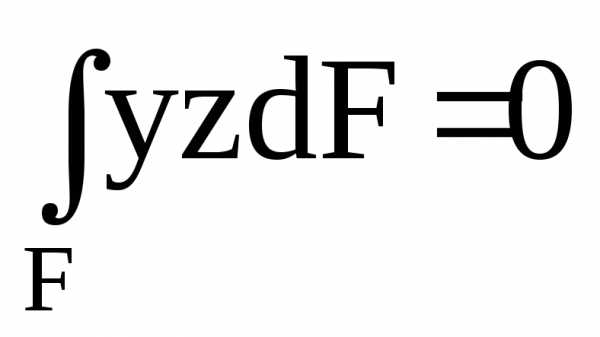 .
Это другая геометрическая характеристика
сечения – центробежный момент инерции
.
Это другая геометрическая характеристика
сечения – центробежный момент инерции
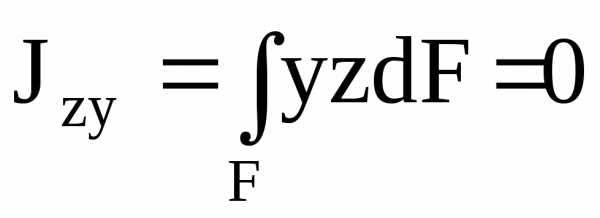 . (5.16)
. (5.16)
На основании равенства (5.15) заключаем, что ось z – нейтральная линия сечения – проходит через центр тяжести поперечного сечения. Равенство (5.16) показывает, что оси y и z – главные центральные оси сечения. Этим определяется положение нейтральной линии сечения.
Таким образом, если силовая линия совпадает с одной из главных центральных осей сечения, то изгиб будет плоским и нейтральная линия сечения совпадает с другой главной центральной осью.
Из третьего уравнения (5.13) определим радиус кривизны нейтрального слоя.
.
Вспомнив,
что 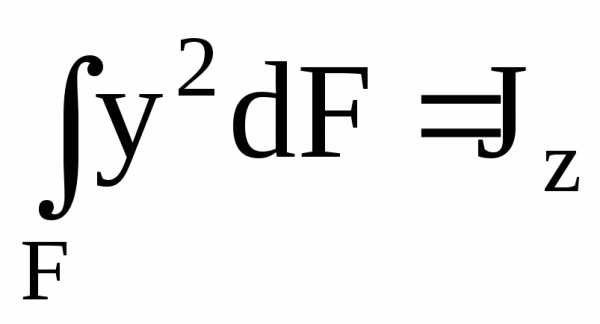 ,
представляет собой момент инерции
сечения относительно оси z,
можем последнюю формулу записать в
виде
,
представляет собой момент инерции
сечения относительно оси z,
можем последнюю формулу записать в
виде
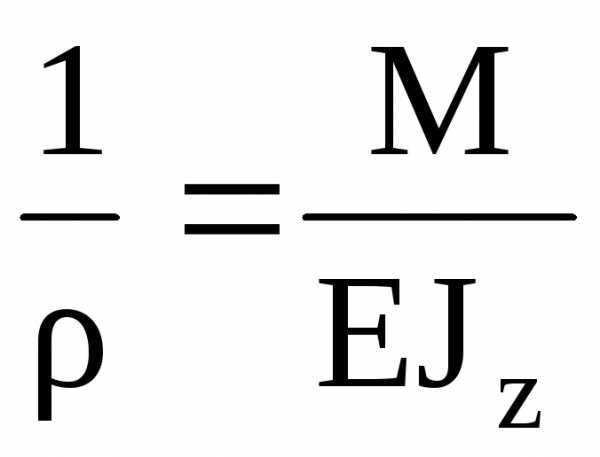 . (5.17)
. (5.17)
Наконец, подставив формулу (5.17) в выражение (5.13), получим формулу для нормального напряжения при чистом изгибе
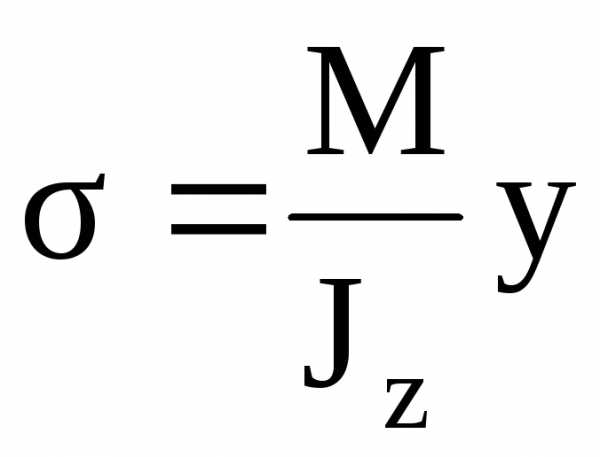 . (5.18)
. (5.18)
Формула (5.17) в приведённом выводе была вспомогательной, однако она имеет и большое самостоятельное значение. Её можно трактовать как закон Гука при изгибе, поскольку она связывает деформацию (кривизну нейтрального слоя 1/ρ) с действующим изгибающим моментом.
Произведение EJ носит название жёсткости сечения при изгибе и имеет размерность кНсм2.
Рис.5.17
Формула (5.18) показывает, что величина σ линейно возрастает по мере удаления от нейтральной линии (рис.5.17). При этом напряжения постоянны по ширине сечения. При изменении знака изгибающего момента поменяется и знак напряжений (верхние волокна окажутся растянутыми, нижние – сжатыми).
studfiles.net
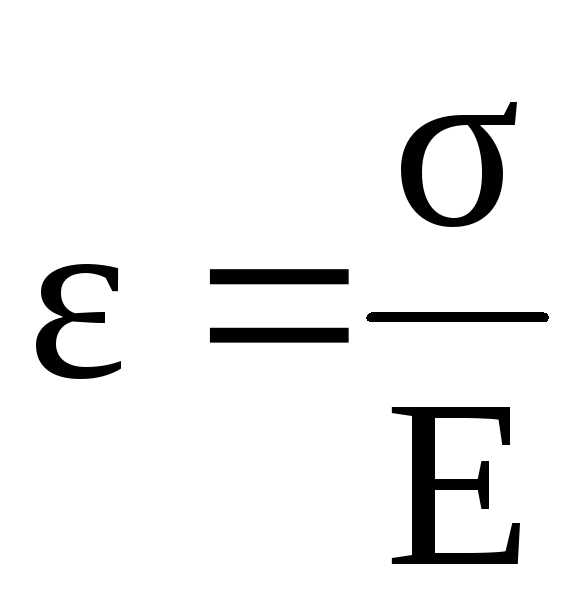 .
(5.12)
.
(5.12)