Нормальные напряжения при изгибе | ПроСопромат.ру
При выводе формулы для вычисления нормальных напряжений рассмотрим такой случай изгиба, когда внутренние силы в сечениях балки приводятся только к изгибающему моменту, а поперечная сила оказывается равной нулю. Этот случай изгиба носит название чистого изгиба. Рассмотрим средний участок балки, подвергающийся чистому изгибу.
В нагруженном состоянии балка прогибается так,что ее нижние волокна удлиняются,а верхние укорачиваются.
Поскольку часть волокон балки растягивается, а часть сжимается, причем переход от растяжения к сжатию происходит плавно, без скачков, в средней части балки находится слой, волокна которого только искривляются, но не испытывают ни растяжения, ни сжатия. Такой слой называют нейтральным слоем. Линия, по которой нейтральный слой пересекается с поперечным сечением балки, называется нейтральной линией или нейтральной осью сечения. Нейтральные линии нанизаны на ось балки. Нейтральная линия — это линия, в которой нормальные напряжения равны нулю.
Нейтральные линии нанизаны на ось балки. Нейтральная линия — это линия, в которой нормальные напряжения равны нулю.
Линии, проведенные на боковой поверхности балки перпендикулярно оси, остаются плоскими при изгибе. Эти опытные данные позволяют положить в основу выводов формул гипотезу плоских сечений (гипотеза Бернулли). Согласно этой гипотезе сечения балки плоские и перпендикулярные к ее оси до изгиба, остаются плоскими и оказываются перпендикулярными изогнутой оси балки при ее изгибе.
Допущения для вывода формул нормального напряжения: 1) Выполняется гипотеза плоских сечений. 2) Продольные волокна друг на друга не давят (гипотеза о ненадавливании) и, следовательно, каждое из волокон находится в состоянии одноосного растяжения или сжатия. 3) Деформации волокон не зависят от их положения по ширине сечения. Следовательно, и нормальные напряжения, изменяясь по высоте сечения, остаются по ширине одинаковыми.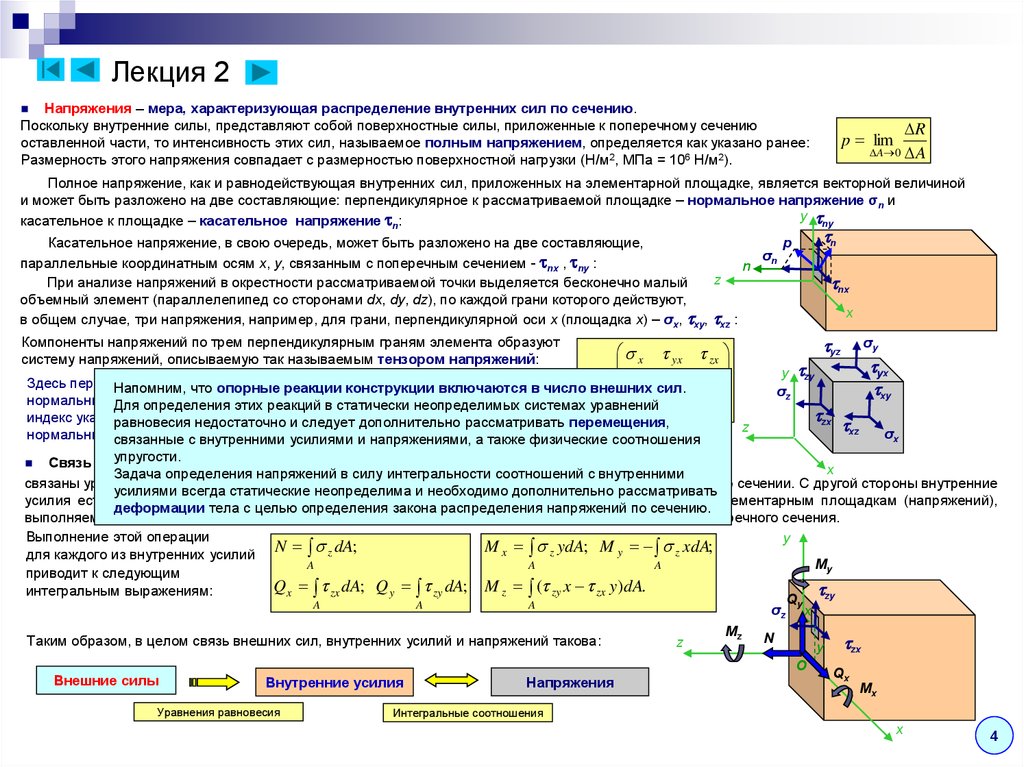 4) Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости. 5) Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков. 6) Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания.
4) Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости. 5) Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков. 6) Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания.
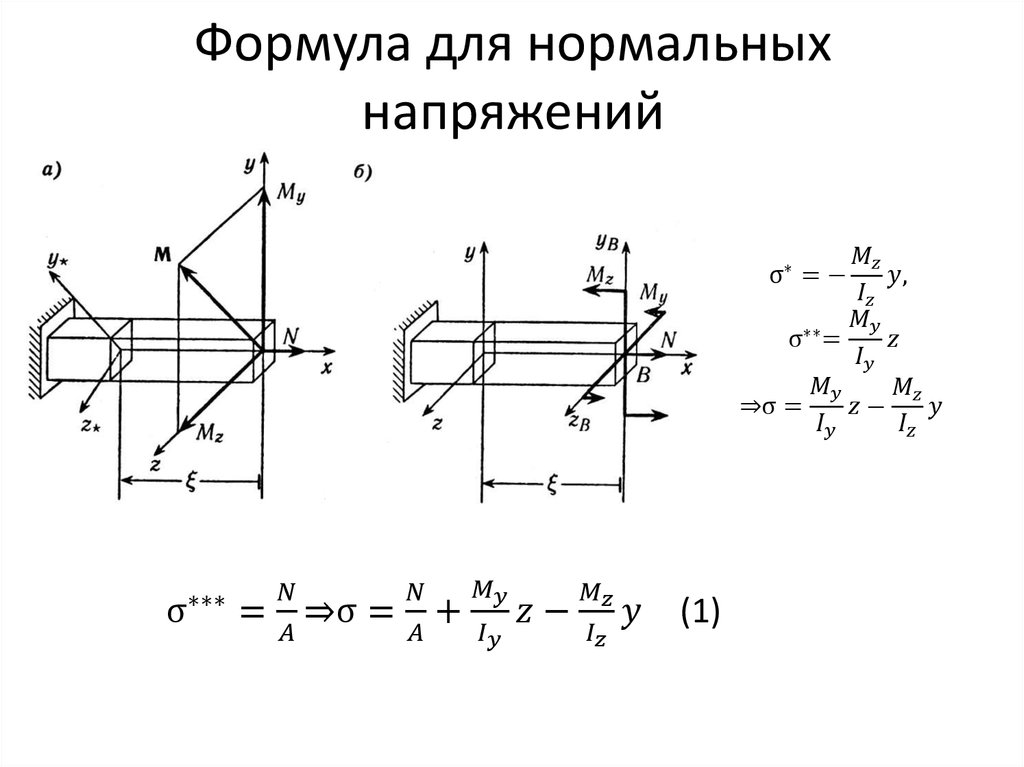
Рассмотрим балку произвольного сечения, но имеющую ось симметрии.Изгибающий момент представляет собой результирующий момент внутренних нормальных сил, возникающих на бесконечно малых площадках и может быть выражен в интегральном виде: (1), где y — плечо элементарной силы относительно оси х
Формула (1) выражает статическую сторону задачи об изгибе прямого бруса, но по ней по известному изгибающему моменту нельзя определить нормальные напряжения, пока не установлен закон их распределения.
Выделим на среднем участке балки и рассмотрим участок длиной dz, подвергающийся изгибу.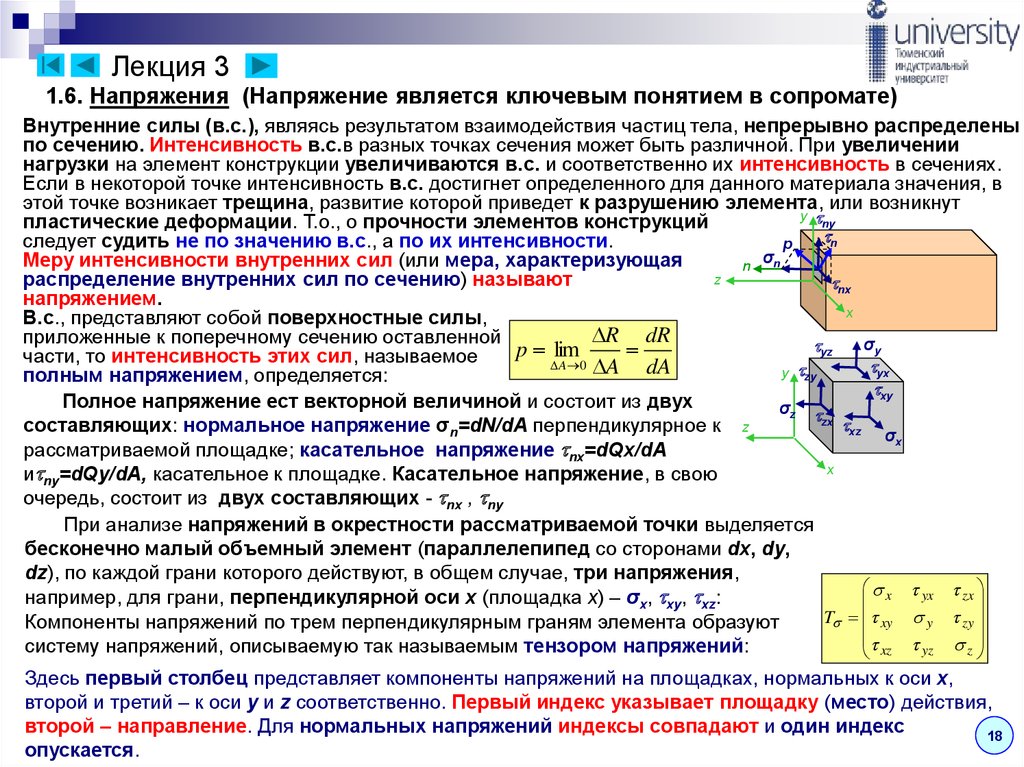 Изобразим его в укрупненном масштабе.
Изобразим его в укрупненном масштабе.
К выводу формул при изгибе: а) участок балки до деформации; б) участок балки после деформации
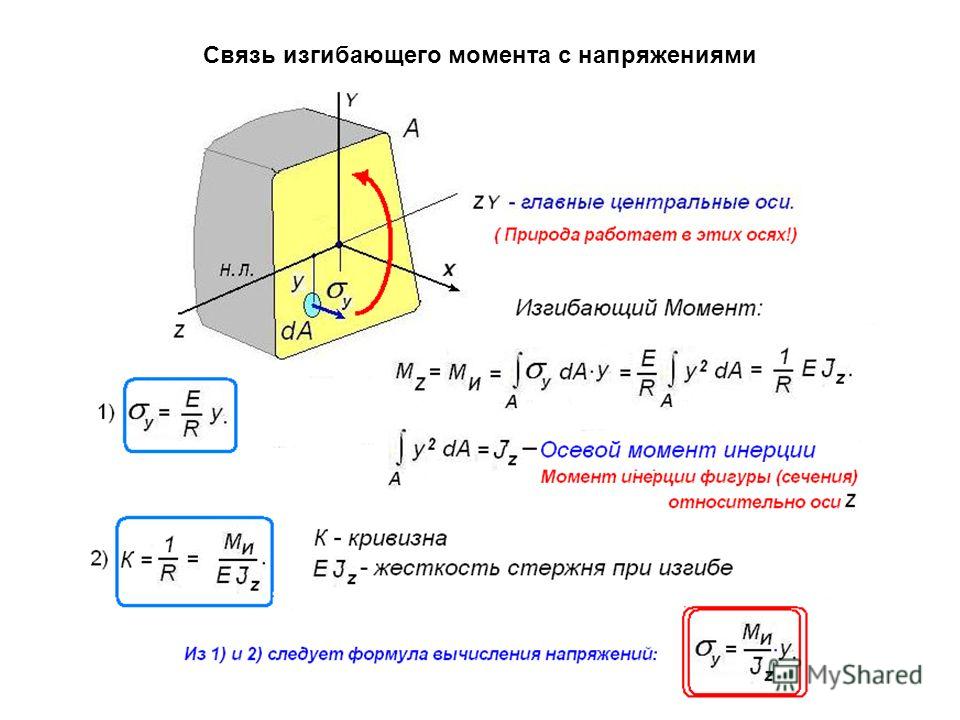
Сечения, ограничивающие участок dz, параллельны друг другу до деформации, а после приложения нагрузки повернутся вокруг своих нейтральных линий на угол . Длина отрезка волокон нейтрального слоя при этом не изменится и будет равна:, где -это радиус кривизны изогнутой оси балки. А вот любое другое волокно, лежащее ниже или выше нейтрального слоя, изменит свою длину. Вычислим относительное удлинение волокон, находящихся от нейтрального слоя на расстоянии у. Относительное удлинение — это отношение абсолютной деформации к первоначальной длине ,тогда:
Сократим на и приведем подобные члены, тогда получим:(2) Эта формула выражает геометрическую сторону задачи о чистом изгибе: деформации волокон прямо пропорциональны их расстояниям до нейтрального слоя.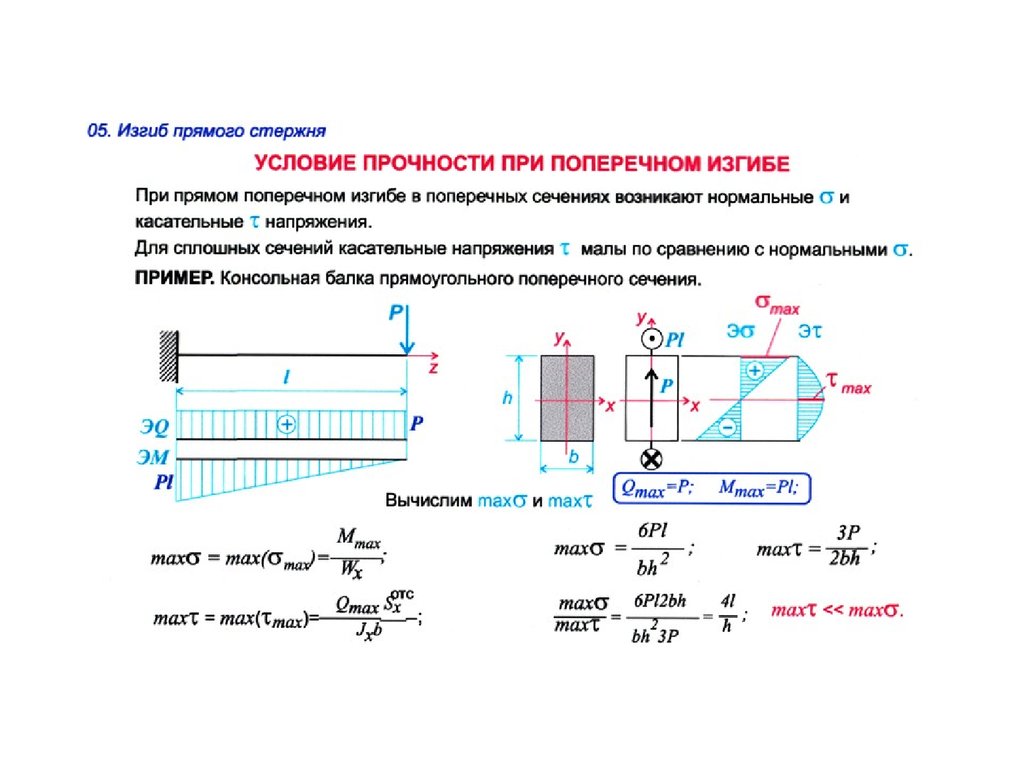
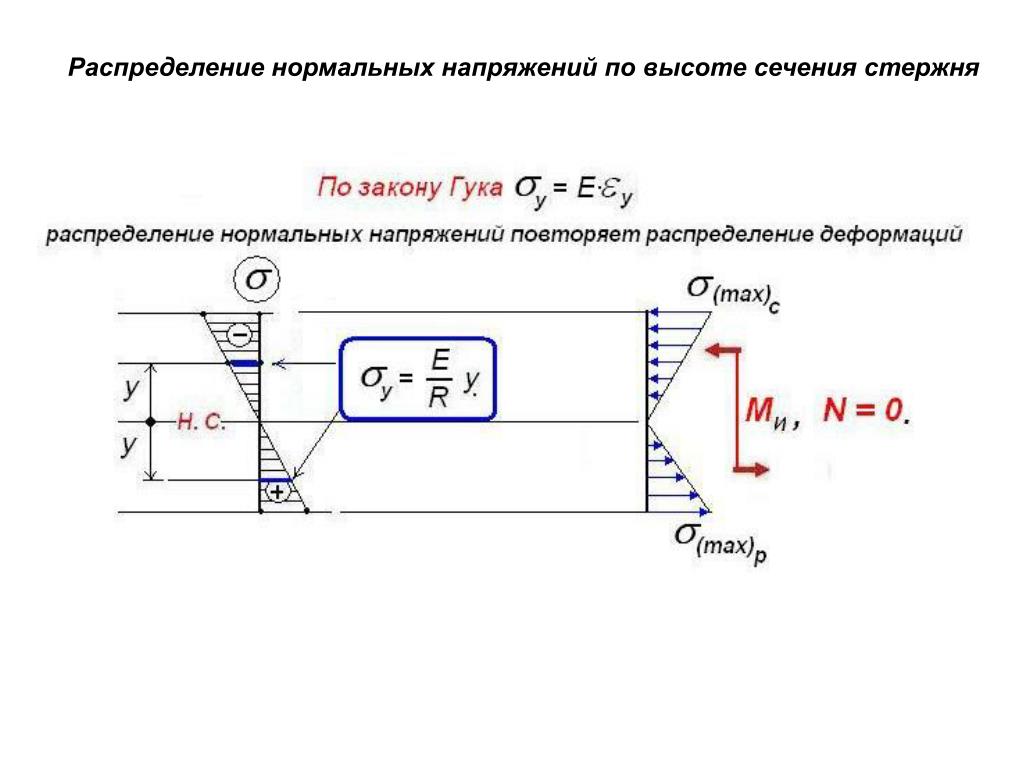
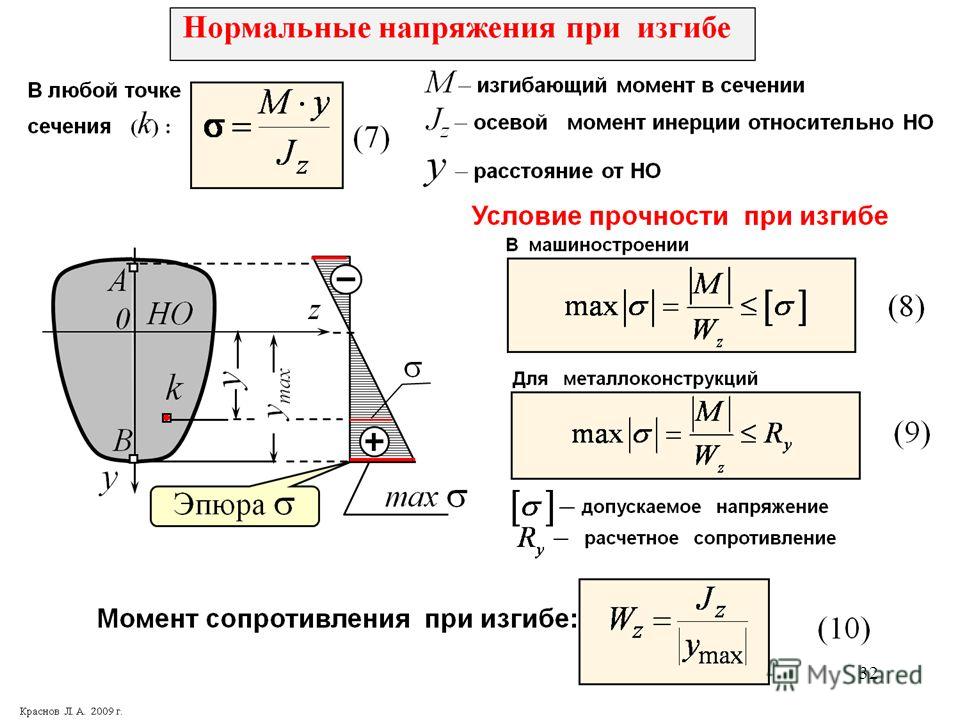
Теперь перейдем к напряжениям, т.е. будем рассматривать физическую сторону задачи. в соответствии с допущением о ненадавливании волокон используем закон Гука при осевом растяжении-сжатии:, тогда с учетом формулы (2) имеем (3),т.е. нормальные напряжения при изгибе по высоте сечения распределяются по линейному закону. На крайних волокнах нормальные напряжения достигают максимального значения, а в центре тяжести сечения равны нулю. Подставим (3) в уравнение (1) и вынесем за знак интеграла дробь как постоянную величину, тогда имеем. Но выражение — это осевой момент инерции сечения относительно оси х — Iх. Его размерность см4, м4
Тогда ,откуда (4) ,где — это кривизна изогнутой оси балки, а — жесткость сечения балки при изгибе.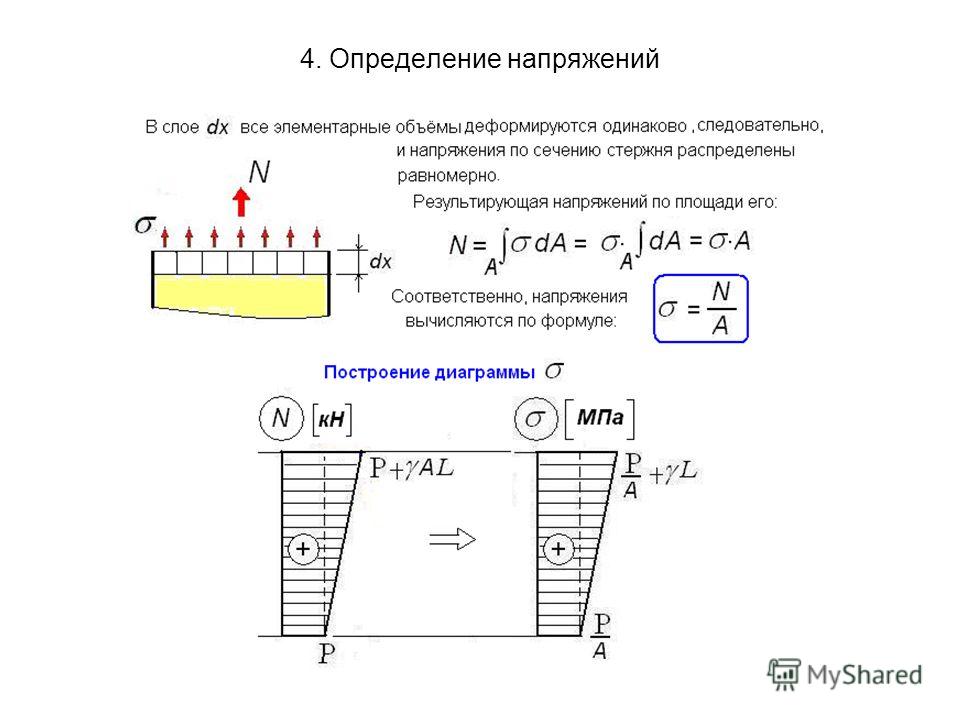
Подставим полученное выражение кривизны (4) в выражение (3) и получим формулу для вычисления нормальных напряжений в любой точке поперечного сечения: (5)
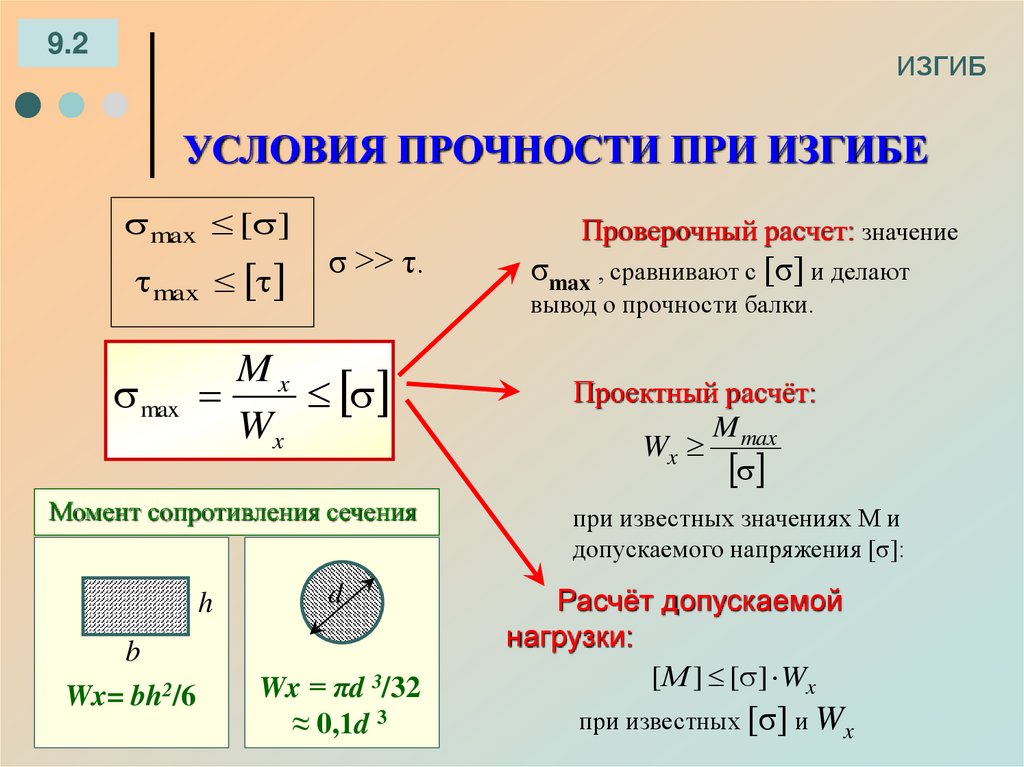
Т.о. максимальные напряжения возникают в точках, наиболее удаленных от нейтральной линии. Отношение (6) называют осевым моментом сопротивления сечения. Его размерность см3, м3. Момент сопротивления характеризует влияние формы и размеров поперечного сечения на величину напряжений.
Тогда максимальные напряжения: (7)
Условие прочности при изгибе: (8)
При поперечном изгибе действуют не только нормальные, но и касательные напряжения,т.к. имеется поперечная сила. Касательные напряжения усложняют картину деформирования, они приводят к искривлению поперечных сечений балки, в результате чего нарушается гипотеза плоских сечений.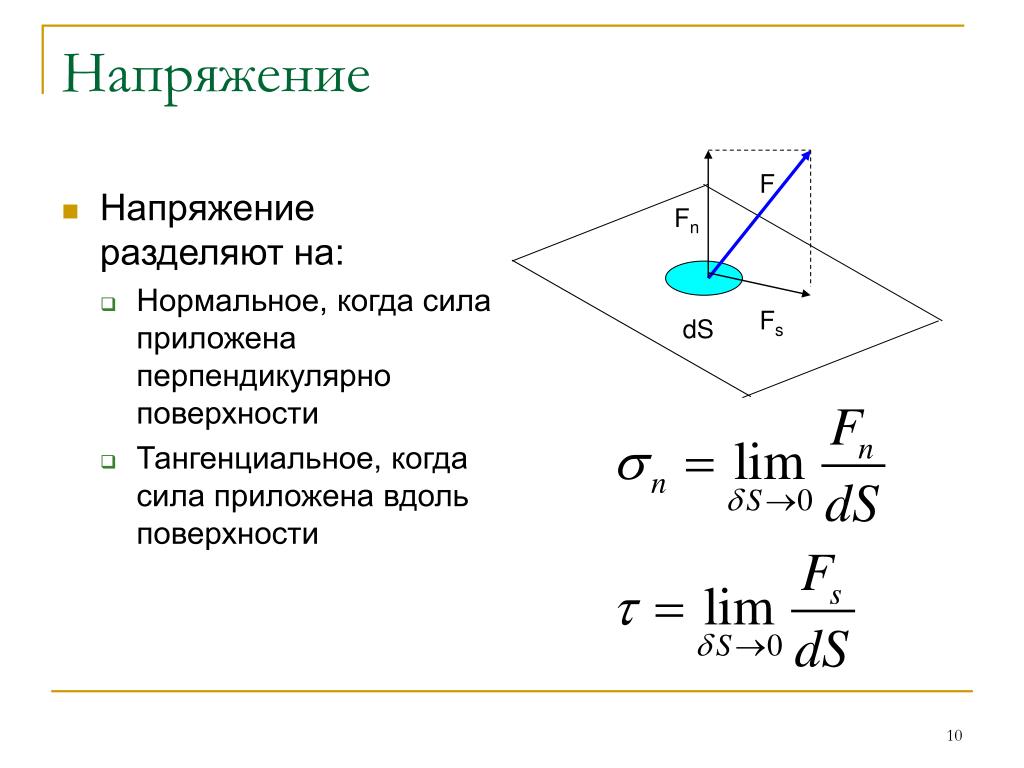 Однако исследования показывают, что искажения, которые привносят касательные напряжения, незначительно влияют на нормальные напряжения,подсчитанные по формуле (5). Таким образом ,при определении нормальных напряжений в случае поперечного изгиба теория чистого изгиба вполне применима.
Однако исследования показывают, что искажения, которые привносят касательные напряжения, незначительно влияют на нормальные напряжения,подсчитанные по формуле (5). Таким образом ,при определении нормальных напряжений в случае поперечного изгиба теория чистого изгиба вполне применима.
Нейтральная линия. Вопрос о положении нейтральной линии.
При изгибе отсутствует продольная сила, поэтому можно записать Подставим сюда формулу нормальных напряжений (3) и получим Так как модуль продольной упругости материала балки не равняется нулю и изогнутая ось балки имеет конечный радиус кривизны, остается положить, что этот интеграл представляет собой статический момент площади поперечного сечения балки относительно нейтральной линии-оси х , и, поскольку он равен нулю, то нейтральная линия проходит через центр тяжести сечения.
Условие (отсутствие момента внутренних сил относительно силовой линии) даст или с учетом (3) .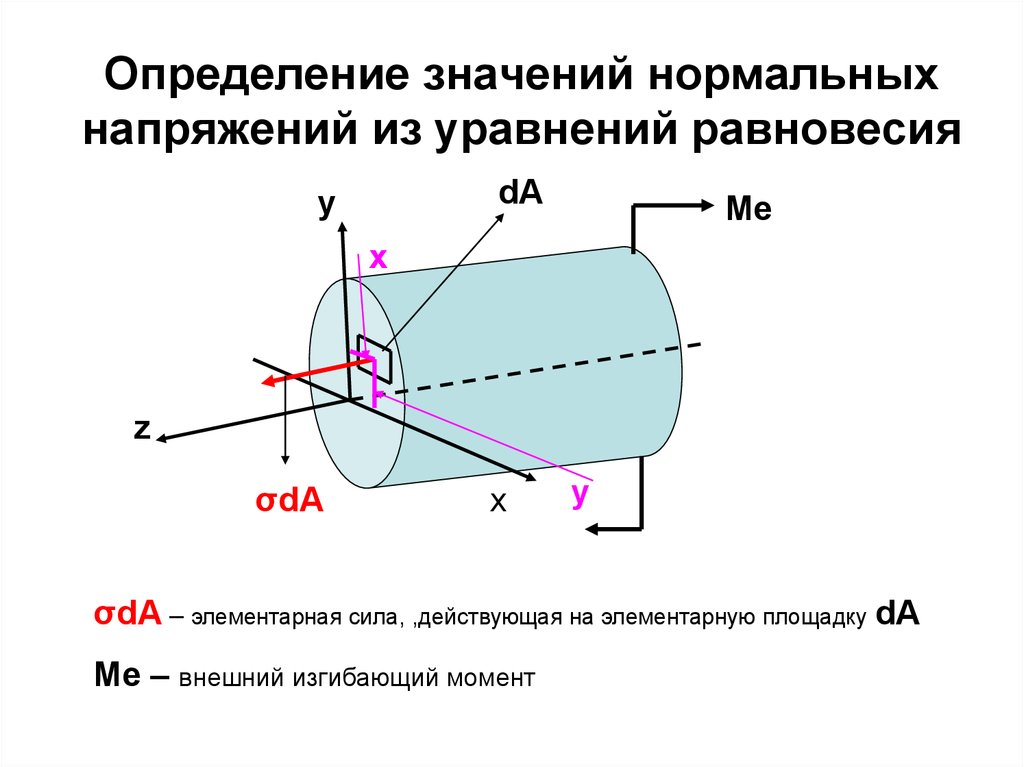 По тем же соображениям (см. выше) . В подынтегральном выражении — центробежный момент инерции сечения относительно осей х и у равен нулю, значит, эти оси являются главными и центральными и составляют прямой угол. Следовательно, силовая и нейтральная линии пр прямом изгибе взаимно перпендикулярны.
По тем же соображениям (см. выше) . В подынтегральном выражении — центробежный момент инерции сечения относительно осей х и у равен нулю, значит, эти оси являются главными и центральными и составляют прямой угол. Следовательно, силовая и нейтральная линии пр прямом изгибе взаимно перпендикулярны.
Установив положение нейтральной линии, несложно построить эпюру нормальных напряжений по высоте сечения. Ее линейный характер определяется уравнением первой степени.
Характер эпюры σ для симметричных сечений относительно нейтральной линии, М<0
Напряжения. Связь внутренних усилий и напряжений
1. Лекция 2
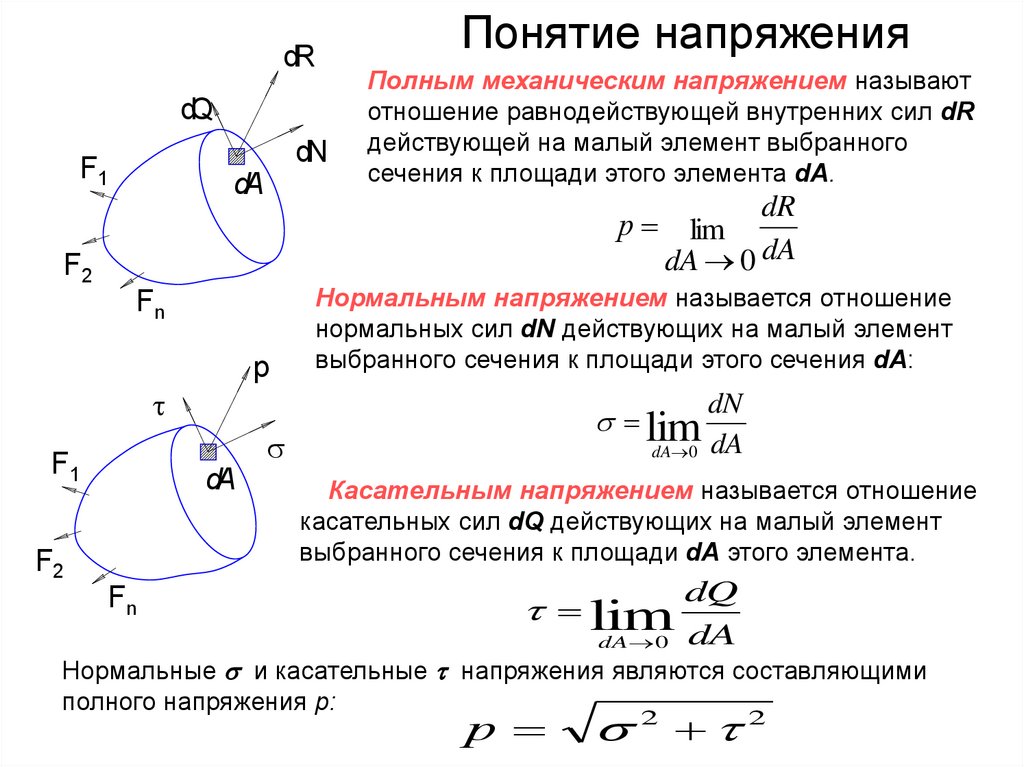
Напряжения – мера, характеризующая распределение внутренних сил по сечению.Поскольку внутренние силы, представляют собой поверхностные силы, приложенные к поперечному сечению
оставленной части, то интенсивность этих сил, называемое полным напряжением, определяется как указано ранее:
Размерность этого напряжения совпадает с размерностью поверхностной нагрузки (Н/м2, МПа = 106 Н/м2).

R
A 0 A
p lim
Полное напряжение, как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной
и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и
y ny
касательное к площадке – касательное напряжение n:
Касательное напряжение, в свою очередь, может быть разложено на две составляющие,
параллельные координатным осям x, y, связанным с поперечным сечением — nx , ny :
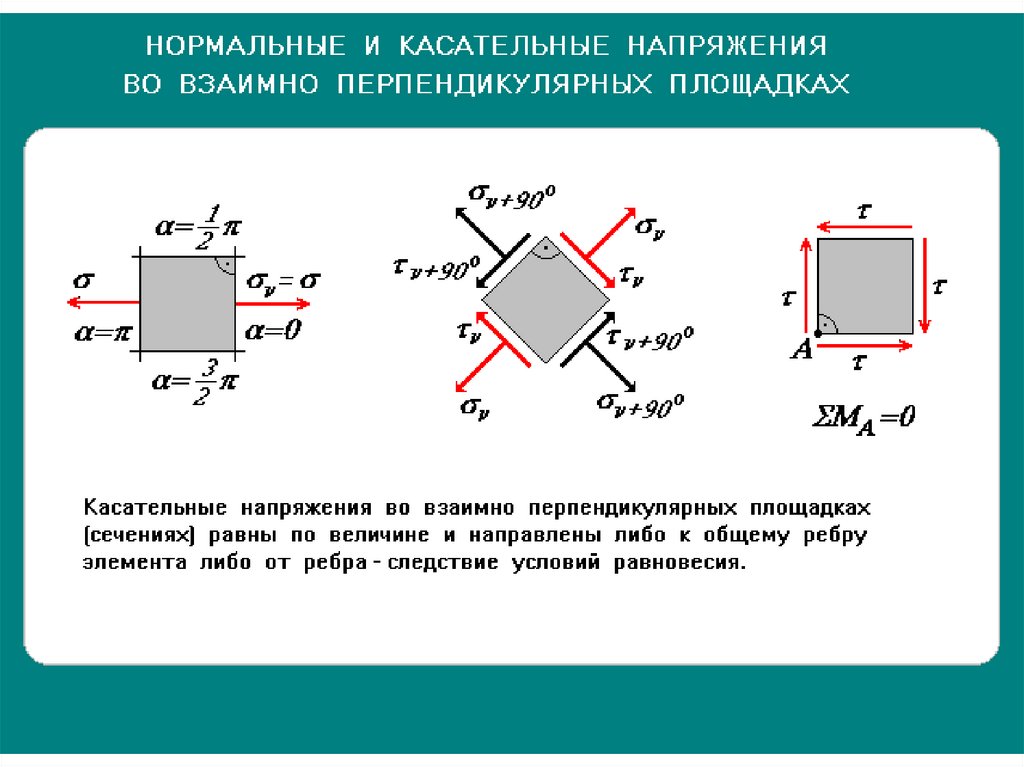
При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый
объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют,
в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – σx, xy, xz :
Компоненты напряжений по трем перпендикулярным граням элемента образуют
систему напряжений, описываемую так называемым тензором напряжений:
Здесь первый столбец представляет компоненты напряжений на площадках,
нормальных к оси x, второй и третий – к оси y и z соответственно.
 Первый
Первыйиндекс указывает площадку (“место”) действия, второй – направление. Для
нормальных напряжений индексы совпадают и один индекс опускается.
z
x yx zx
T xy y zy
xz yz z
n
σn
n
p
nx
x
yz
y
σz
z
σy
yx
xy
zy
zx
xz
σx
Связь внутренних усилий и напряжений – Внутренние усилия в сечении, как было показано выше,
x
связаны уравнениями равновесия с внешними силами, приложенными к оставленной части бруса при его сечении. С другой стороны внутренние усилия есть
результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам (напряжений), выполняемое сложением,
которое для элементарных сил сводится к интегрированию по площади поперечного сечения.
Выполнение этой операции
y
M x z ydA; M y z xdA;
N z dA;
для каждого из внутренних усилий
My
A
A
A
приводит к следующим
Q x zx dA; Q y zy dA; M z ( zy x zx y )dA.
интегральным выражениям:
zy
Qy
A
A
A
σz x
Mz
N
Таким образом, в целом связь внешних сил, внутренних усилий и напряжений такова:
z
y zx
O
Qx
Внешние силы
Напряжения
Внутренние усилия
M
x
Уравнения равновесия
Интегральные соотношения
x
4
2. Лекция 2
Напряжения – мера, характеризующая распределение внутренних сил по сечению.Поскольку внутренние силы, представляют собой поверхностные силы, приложенные к
поперечному сечению оставленной части, то интенсивность этих сил, называемое полным
напряжением, определяется как указано ранее:
Размерность этого напряжения совпадает с размерностью поверхностной нагрузки (Н/м2, МПа =
106 Н/м2).
R
A 0 A
p lim
Полное напряжение, как и равнодействующая внутренних сил, приложенных на элементарной
площадке, является векторной величиной и может быть разложено на две составляющие:
перпендикулярное к рассматриваемой площадке – нормальное напряжение σn и касательное к
площадке – касательное напряжение n:
Касательное напряжение, в свою очередь, может быть разложено на две составляющие,
параллельные координатным осям x, y, связанным с поперечным сечением — nx , ny :
При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый
объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в
общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – σx,
xy, xz :
Компоненты напряжений по трем перпендикулярным граням элемента образуют
систему напряжений, описываемую так называемым тензором напряжений:
x yx zx
T xy y zy
yz
z
xz
yz
σy
yx
zy
σz
zx
y
p
xz
σx
Здесь первый столбец представляет
компоненты напряжений на площадках,
нормальных к оси x, второй и третий – к оси y
и z соответственно.
 Первый
Первыйиндекс указывает площадку (“место”)
действия, второй – направление. Для
нормальных напряжений индексы
совпадают и один индекс опускается.
ny
n
σn
nx
x
Напомним, что опорные реакции конструкции включаются в число внешних сил.
Для определения этих реакций в статически неопределимых системах уравнений
равновесия недостаточно и следует дополнительно рассматривать перемещения,
связанные с внутренними усилиями и напряжениями, а также физические соотношения упругости.
Задача определения напряжений в силу интегральности соотношений с внутренними
усилиями всегда статические неопределима и необходимо дополнительно рассматривать
деформации тела с целью определения закона распределения напряжений по сечению.
Связь внутренних усилий и напряжений
–
Внутренние усилия в сечении, как было показано выше,
связаны уравнениями равновесия с внешними силами, приложенными к
оставленной части бруса при его сечении. С другой стороны внутренние усилия есть
результат приведения к центру поперечного сечения внутренних сил, приложенных
к элементарным площадкам (напряжений), выполняемое сложением, которое для
элементарных сил сводится к интегрированию по площади поперечного сечения.

Выполнение этой операции
для каждого из внутренних усилий
приводит к следующим
интегральным выражениям:
N z dA;
A
Q x zx dA; Q y zy dA;
A
A
M x z ydA; M y z xdA;
A
A
M z ( zy x zx y )dA.
A
Таким образом, в целом связь внешних сил, внутренних усилий и напряжений такова:
Внешние силы
Напряжения
Внутренние усилия
Уравнения равновесия
Интегральные соотношения
7. Лекция 2 (продолжение – 2.2)
Перемещения – переход точек тела в новое положение вследствие изменения формы и размеров тела под действием нагрузки.Полное перемещение точки в пространстве раскладывается на компоненты u, v и w, параллельные осям x, y и z, соответственно.
Перемещения рассматриваемой точки зависит от деформации всех нагруженных областей тела и включают в себя перемещения как жесткого
целого ненагруженных областей. Таким образом, перемещения не могут характеризовать степень деформирования в окрестности
рассматриваемой точки.

■
Деформация в точке – мера деформирования материала в ее окрестности. Выделим в рассматриваемой точке тела элементарный
объем (параллелепипед со сторонами dx, dy, dz) и рассмотрим его возможные изменения размеров и формы.
Пусть за счет деформации длины его ребер получат абсолютные удлинения dx, dy и dz:
dy
y
Относительные линейные деформации в точке:
dx
dy
dz
x
; y
; z
.
dy
dx
dy
dz
z
Кроме линейных деформаций, связанных с изменением размеров линейных
элементов возникают угловые деформации или
углы сдвига, связанные с изменением формы.
x
Например, в плоскости xy могут возникать малые
tg xy
изменения первоначально прямых углов параллелепипеда:
dy
x
y
xy .
dy
xy
dx
Такие угловые деформации в общем случае могут иметь место во всех трех
x
плоскостях. Все относительные деформации весьма малы и имеют для реальных
материалов порядок ≈10-4-10-3.

Таким образом, совокупность относительных линейных и угловых деформаций определяют деформированное
состояние в точке и образуют тензор деформаций, подобный тензору напряжений:
Примечание: Половинные углы сдвига используются в целях получения аналогичных формул преобразования с тензором напряжений.
x
dx
dx
dz
dz
x
1
T xy
2
1
xz
2
1
yx
2
y
1
yz
2
В зависимости от того, какие из компонент относительных деформаций имеют нулевое значение
в рассматриваемой области или для всего тела различают следующие простые виды деформаций:
1.
Линейная деформация – εz ≠ 0, углы сдвига равны нулю, остальными линейными относительными деформациями пренебрегается
(характеризуется абсолютным и относительным удлинением).
2.
Плоская деформация – εz ≠ 0, εx ≠ 0 или εy ≠ 0, остальные относительные деформации равны нулю (характеризуется абсолютным и
относительным сужением площади поперечного сечения).
 Эти виды деформаций обычно реализуются при растяжении-сжатии.
Эти виды деформаций обычно реализуются при растяжении-сжатии.3.
Объемная деформация – εz ≠ 0, εx ≠ 0, εy ≠ 0, углы сдвига равны нулю(характеризуется абсолютным и относительным изменением объема).
4.
Чистый сдвиг – линейные относительные деформации равны нулю, углы сдвига не равны нулю (характеризуется изменением формы,
изменение объема не происходит). Это вид деформации также возникает при кручении.
В соответствии с видом деформации вначале последовательно изучают такие простейшие напряженно-деформированные состояния как
растяжение-сжатие, чистый сдвиг и кручение, чистый изгиб. Далее изучаются более сложные – поперечный изгиб, сложное сопротивление,
продольный изгиб.
1
zx
2
1
zy
2
z
5
10. Лекция 2 (продолжение – 2.3)
■Определение внутренних усилий – Внутренние усилия определяются методом сечений в совокупности точек по длине бруса с целью
обнаружения их максимальных значений. График изменения внутреннего усилия по оси бруса называется эпюрой.

Общий порядок построения эпюр внутренних усилий:
1.
Если необходимо, то определяются опорные реакции так, как это делается в курсе теоретической механики (выбрать объект, отбросить
связи, заменить отброшенные связи реакциями, составить уравнения равновесия). Реакции можно не находить, если они не входят в число
внешних сил, приложенных по одну сторону от рассматриваемых сечений.
уравнения
равновесия
получаем
выражение
на участке
1 :является любой
N I I F1 F2 .
2.
Определяется число участков по длинеИз
бруса,
на которых
нагрузка
или геометрия
брусадля
не продольной
изменяется. силы
Границей
участка
шаги
3 и 4 для следующих
участков:
фактор, влияющий на резкое (скачкообразное)Повторяем
изменение
рассматриваемого
внутреннего
усилия (начало или конец бруса, перелом оси бруса,
место расположения опоры, точка приложения
силы или
другого
фактора, например,
сосредоточенного
3.
 внешней
внешнейПроведемсосредоточенной
сечение II-II на втором
участке
и определим
текущую координату
сечениямомента,
и пределы ее
начало или конец распределенной нагрузки). изменения: 0 z2 b.
3.
На каждом из участков проводится сечение,
отстоящее
отчасть,
началазаменим
участка ее
на действие
некотором
произвольном
(переменном)
расстоянии. Для
4. Отбросим
левую
продольной
силой
NII-II
Z i 0; N II II F2 0.
координаты.
каждого сечения указывается текущая координата
(z) от начала
участка
или от начала
бруса на
и записываются
пределы изменения
и составим
уравнение
равновесия
в проекции
ось z :
При выборе начала локальных координат в начале участка нижний предел всегда равен нулю.
Из уравнения равновесия получаем выражение для продольной силы на участке 2 :
N II II F2 .
4.
Для рассматриваемого сечения определяется выражение внутреннего усилия в функции от координаты z рассмотрением равновесия
III III
получаем
для участка
3 (0 z3 c):
оставленной части или используя установленныеАналогично
определения
для вычисления
внутреннего
усилия по внешним
расположенным
по одну
0; N
0.

N III III 0.
Z i силам,
сторону от сечения.
Полученные выражения показывают, что продольная сила в сечении равна алгебраической сумме
5.
По полученным выражениям строится эпюра изменения усилия подстановкой верхнего и нижнего пределов, и если необходимо,
проекций на ось бруса сил, взятых по одну сторону от сечения!
N Fxiправ Fxiлев .
других значений координат в разрешенном интервале, обычно в середине интервала.
Знак
слагаемых
положителен,
если рассматриваемая
сила направлена
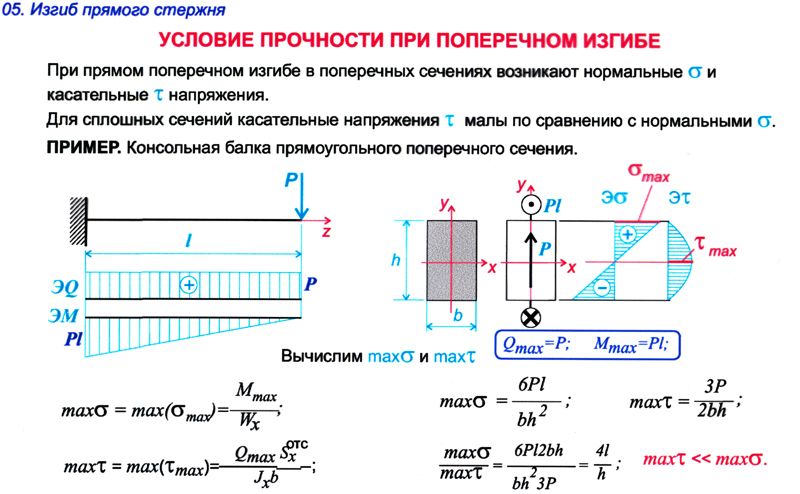
Внутренние усилия при растяжении- сжатии
– При
растяжении-сжатии
в поперечном
сечении стержня
возникает лишь один силовой
от сечения, т.е. будучи приложена к сечению вызывает растяжение части бруса по другую сторону
фактор – продольная сила N. В соответствии с методом сечений величина и направление продольной силы может быть найдены из
от сечения.
уравнения равновесия в проекции на ось, совпадающую с осью стержня, составленного для оставленной части:
оставл.
 части
частиN Zi
0;
Продольная сила считается положительной, если она вызывает растяжение, т.е. направлена от сечения (в сторону внешней нормали), и
отрицательной, если она вызывает сжатие, т.е. направлено к сечению.
z1
z2
z3 III
I
II
Пусть прямолинейный
брус нагружен
силами
F , F : эпюру продольных сил:
Используя
полученные выражения
дляпродольными
продольной силы
построим
1
F1 F2
a
NI-I
I
b
II
c
F1 F2
NII-II F2
NIII-III
III
2
При построении эпюры N, положительные значения обычно откладываются вверх от базисной линии
1. вправо,
Реакции
левой
опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением
или
если
она вертикальна.
лишь
сил,
приложенных
к правым
оставленным
частям
(справазначения
от сечений).
Пусть F1=250 кН, F2=100 кН.
Откладывая
не каждом
из участков
продольной силы в некотором
2.
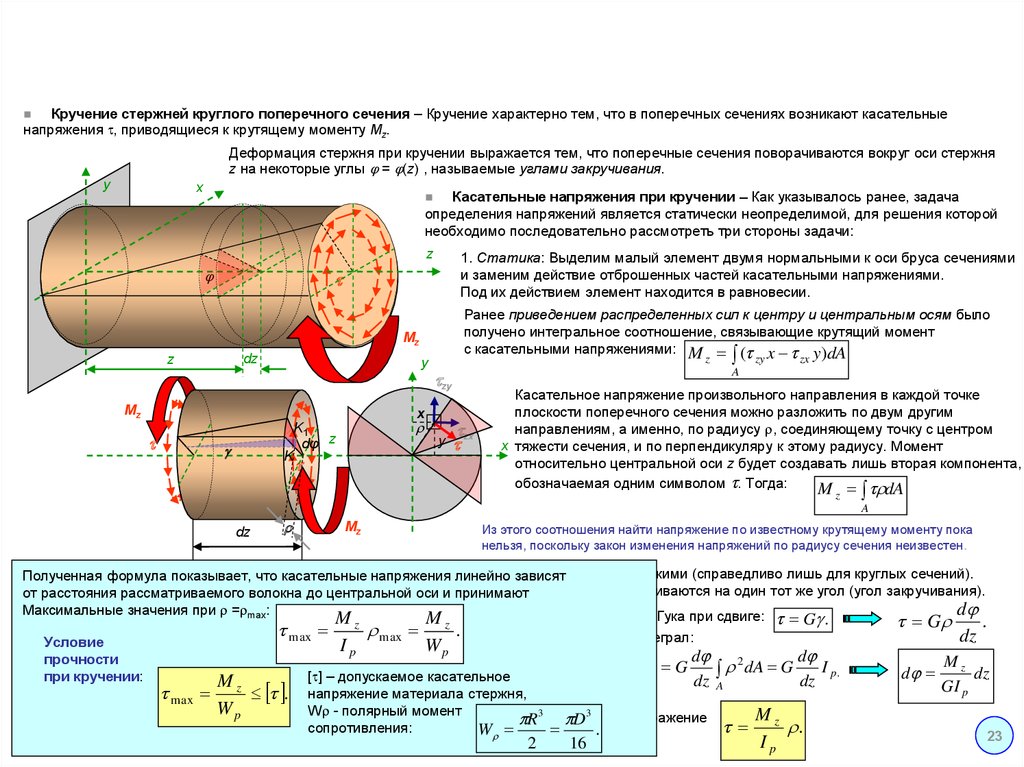
Число
участков
3
выбранном масштабе получаем эпюру N:
3. Проведем сечение I-I на первом участке и определим текущую координату сечения и пределы ее
Обратите
что скачки на эпюре N располагаются в точках приложения внешних
изменения:
0 z1внимание,
a.
сосредоточенных сил и равны величинам этих сил. Соответственно
скачок на левом конце
4. Отбросим левую часть, заменим ее действие продольной силой NI-I
эпюры дает величину опорной реакции.
и составим уравнение равновесия в проекции на ось z :
I I
Z i 0; N
F1 F2 0.
6
11. Лекция 2 (продолжение – 2.4)
■Внутренние усилия при кручении – При кручении в поперечном сечении стержня возникает лишь один силовой фактор – крутящий момент Mz. В
соответствии с методом сечений величина и направление крутящего может быть найдены из уравнения равновесия в моментах относительно оси,
совпадающей с осью стержня, составленного для оставленной части:
Крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали он поворачивает сечение
по ходу часовой стрелки.

Внимание! Это правило знаков условное и не совпадает с принятыми правилами знаков моментов, углов поворота в теоретической механике и
математике, поскольку связано не с системой координат, а с видом деформации оставленной части, точно также, как правило знаков для продольного
усилия связано не с направлением оси z, а с видом деформации рассматриваемой части бруса.
Построение эпюры крутящих моментов принципиально ничем не отличается от построения эпюры продольных сил. Положительные значения
откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз.
z1
z2
z3 III
I
II
Пусть прямолинейный брус нагружен внешними сосредоточенными крутящими моментами M1, M2:
M1
a
MI-I
I
b
II
M2
III
c
M2
M1
MII-II
M2
MIII-III
1. Используя
Реакции
левой опоры
можно недля
определять,
в этом построим
примере можно
ограничиться
рассмотрением
полученные
выражения
крутящегот.
 к.
к.момента
эпюру крутящих
моментов:
лишь
сил,
приложенных
к
правым
оставленным
частям
(справа
от
сечений).
Пусть M1=250 Нм, M2=100 Нм. Откладывая не каждом из участков значения крутящего момента
2.вЧисло
участков
-3
некотором
выбранном
масштабе получаем эпюру Mz:
3.Обратите
Проведем
сечение I-I
первом
текущую
координату
сечения
и пределы ее
внимание,
чтонаскачки
научастке
эпюре иMопределим
в точках
приложения
внешних
z располагаются
изменения:
0 z1 моментам
a.
сосредоточенных
и равны величинам этих моментов. Соответственно скачок
левом конце
эпюры
величину
опорногокрутящим
момента.моментом MzI-I и составим уравнение равновесия
4.на
Отбросим
левую
часть,дает
заменим
ее действие
в моментах относительно оси z :
I I
M zi 0; M z M1 M 2 0.
M zI I M 1 M 2 .
Из уравнения равновесия получаем выражение для крутящего момента на участке 1 :
Повторяем шаги 3 и 4 для следующих участков:
3.
 Проведем сечение II-II на втором участке и определим текущую координату сечения и пределы ее
Проведем сечение II-II на втором участке и определим текущую координату сечения и пределы ееизменения: 0 z2 b.
4. Отбросим левую часть, заменим ее действие крутящим моментом MzII-II
II II
и составим уравнение равновесия в моментах относительно оси z :
M i 0; M z
Из уравнения равновесия получаем выражение для крутящего момента на участке 2 :
Аналогично получаем для участка 3 (0 z3 c):
III III
M zi 0; M z
Полученные выражения показывают, что крутящий момент в сечении
равен алгебраической сумме моментов внешних сил относительно
оси бруса, взятых по одну сторону от сечения!
II II
M 2.
III III
0.
Mz
0.
M 2 0.
Mz
M z M ziправ M ziлев .
Знак слагаемых положителен, если рассматриваемый внешний крутящий момент
вращает сечение по часовой стрелке при взгляде на сечение со стороны внешней нормали.
7
Рабочее напряжение, электрическая прочность и интервалы
Что такое «рабочее напряжение» в целях безопасности и какое значение оно имеет для безопасности оборудования?
НЕКОТОРЫЕ ОПРЕДЕЛЕНИЯ
Вот некоторые определения «рабочего напряжения»:
МЭК 950, первое издание, подпункт 1.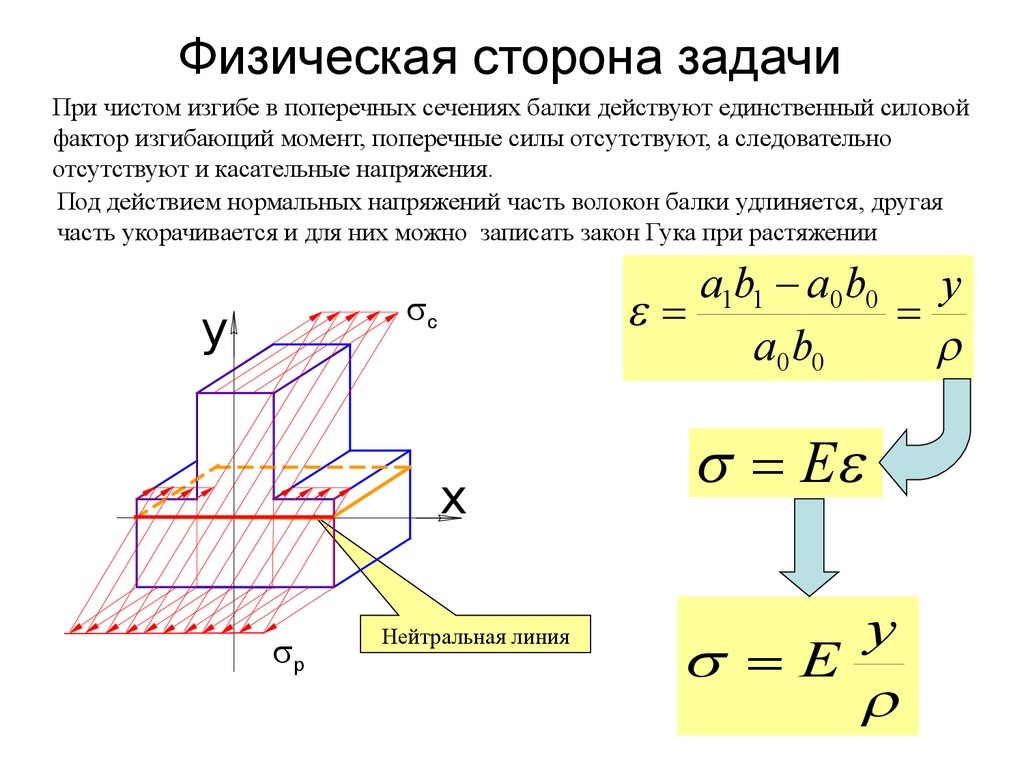 2.9.6:
2.9.6:
EN 60950, первое издание, подпункт 1.2.9.6:
МЭК 950, второе издание, подпункт 1.2.9.6: 11 UL 1950, первое издание, пункт 1.2.9.6:
CSA 950, первое издание, пункт 1.2.9.6:
«Рабочее напряжение: максимальное напряжение, которому подвергается или может подвергаться рассматриваемая изоляция, когда оборудование работает при номинальном напряжении в условиях нормальной эксплуатации».
28A (Центральный офис) 29, пункт 3.5:
(пересмотр IEC 664, включая IEC 664A)
«Наивысшее среднеквадратичное значение напряжения переменного или постоянного тока, которое может возникнуть (локально) через изоляцию оборудования, питаемого при номинальном напряжении, без учета переходных процессов, в условиях разомкнутой цепи или в нормальных условиях эксплуатации».
МЭК 742, первая редакция:
«Рабочее напряжение обозначает самое высокое среднеквадратичное значение.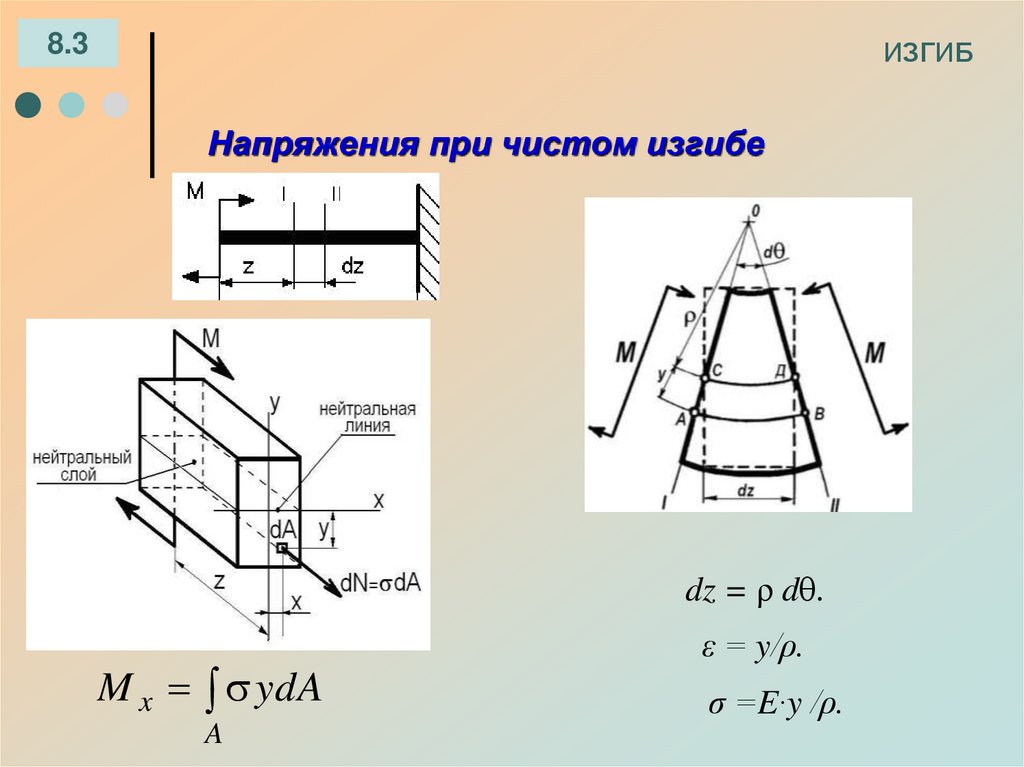 напряжение, которое может возникнуть в любой системе изоляции при номинальном входном напряжении, фазовом угле и переходных процессах, если пренебречь, в условиях холостого хода или во время нормальной работы.
напряжение, которое может возникнуть в любой системе изоляции при номинальном входном напряжении, фазовом угле и переходных процессах, если пренебречь, в условиях холостого хода или во время нормальной работы.
«При рассмотрении системы изоляции между обмотками, не предназначенными для соединения вместе, рабочим напряжением считается максимальное напряжение, возникающее на любой из этих обмоток.
«Обратите внимание на то, что рабочее напряжение относительно земли ввода может отличаться от кажущегося значения в однофазных системах без нейтрали и в трехфазных системах без заземленной нейтрали при соединении по схеме «звезда» или «треугольник». соединение используется. Выходное напряжение трансформатора может быть искусственно повышено по отношению к земле из-за условий, возникающих в приборе или оборудовании».
МЭК 335, второе издание, пункт 2.2:
«Рабочее напряжение означает максимальное напряжение, которому может подвергаться рассматриваемая деталь, когда прибор работает при номинальном напряжении и в нормальных условиях использования.
«Нормальные условия использования включают изменения напряжения внутри прибора, вызванные вероятными событиями, такими как срабатывание автоматического выключателя или выход из строя лампы.
«При определении рабочего напряжения не учитывается влияние возможных переходных напряжений на питающую сеть».
МЭК 65,
МЭК 348,
МЭК 601-1,
МЭК 1010.
«Рабочее напряжение» не определено в этих стандартах.
РАБОЧЕЕ НАПРЯЖЕНИЕ
За исключением IEC 335, мы можем заключить, что рабочее напряжение – это напряжение, за исключением переходных перенапряжений, на изоляции при нормальных условиях эксплуатации.
С точки зрения безопасности нас интересует только основная, дополнительная и усиленная изоляция. Следовательно, рабочее напряжение (за исключением переходных перенапряжений) — это напряжение на основной, дополнительной или усиленной изоляции при нормальных условиях эксплуатации.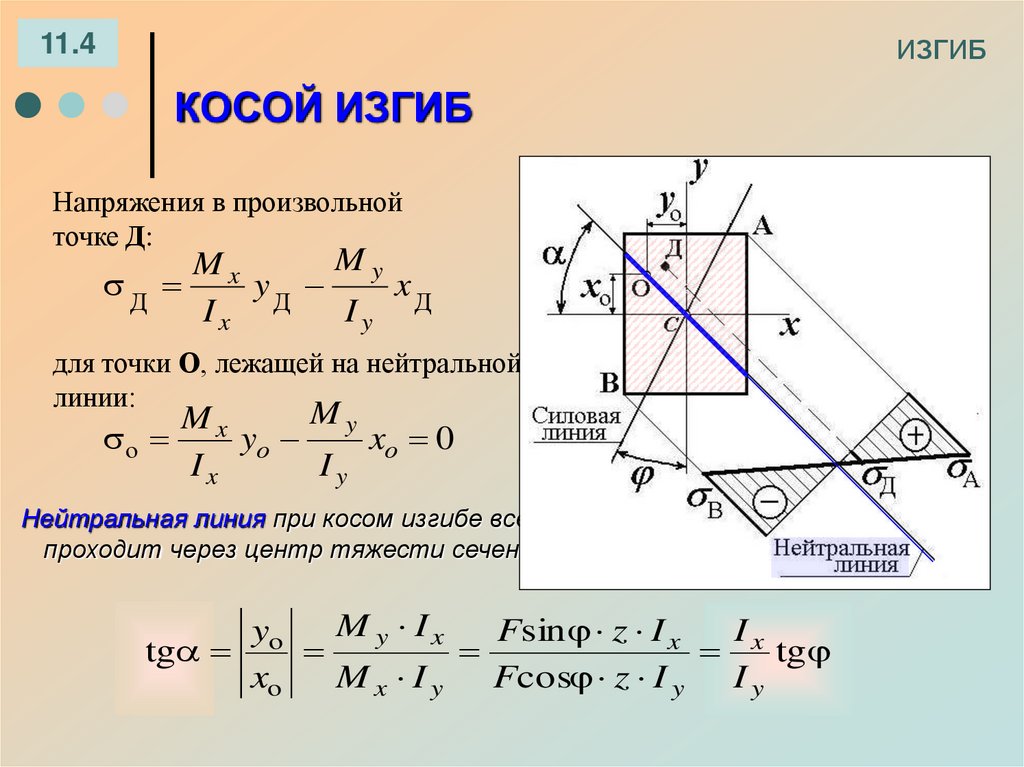
Неисправность защитной изоляции может привести к травме. Наша цель – предотвратить выход из строя основной, дополнительной или усиленной изоляции при нормальных условиях эксплуатации. Изоляция считается поврежденной, если приложенное к ней напряжение превышает ее электрическую прочность.
В этом обсуждении рассматривается, как рабочее напряжение используется для прогнозирования значения напряжения, приложенного к изоляции, и как определить, что электрическая прочность изоляции выше, чем приложенное напряжение.
Таким образом, мы можем быть уверены, что защитная изоляция не выйдет из строя в результате приложенного к ней напряжения.
ЭЛЕКТРИЧЕСКАЯ ПРОЧНОСТЬ
Давайте сначала рассмотрим взаимосвязь между рабочим напряжением и напряжением электрической прочности (hi-pot).
Мне нравится думать о мире как о двух видах цепей.
Цепи первого типа широко распространены и имеют множество различных нагрузок, многие из которых являются индуктивными или естественным образом генерируют и вводят в цепь переходные перенапряжения.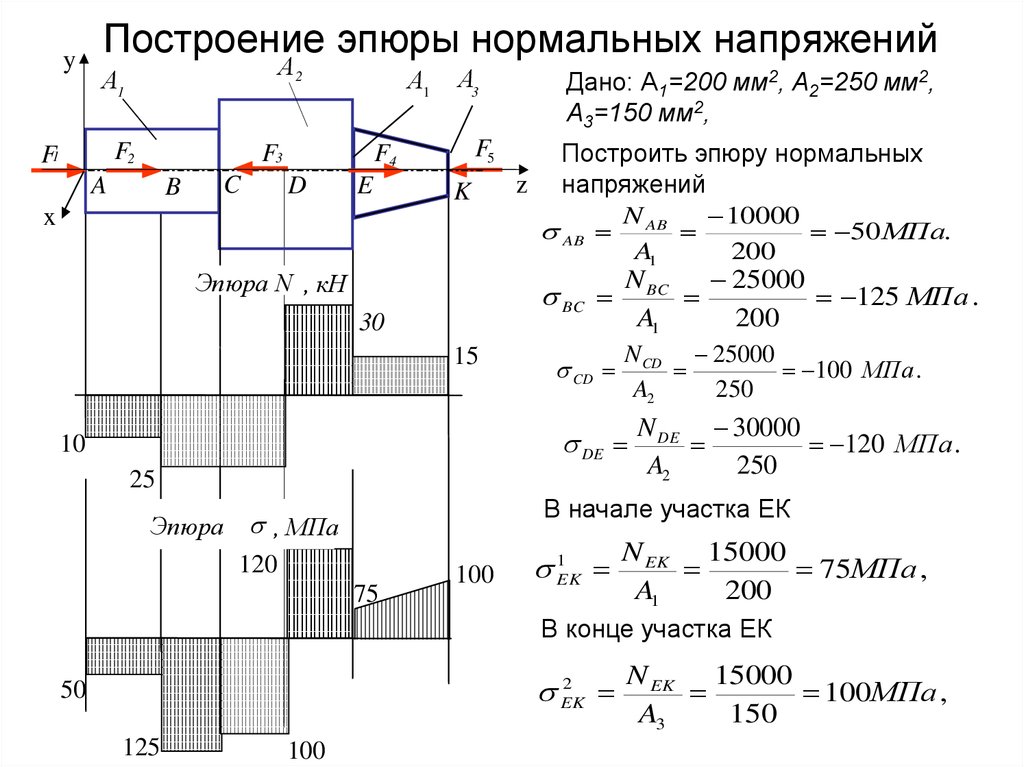
Поскольку переходные перенапряжения являются нормальными в цепях такого типа, изоляция, используемая в цепи, должна иметь электрическую прочность, равную или превышающую максимальное ожидаемое переходное перенапряжение для цепи. Одним из эмпирических правил, связывающих электрическую прочность с напряжением сети (т. е. рабочим напряжением), является традиционное соотношение 2 В + 1000, где V — номинальное (рабочее) напряжение сети.
В течение многих лет 2В + 1000 была стандартной формулой для определения напряжения электрической прочности изоляции. Последние стандарты безопасности, основанные на IEC 664, используют таблицы для определения напряжения электрической прочности для любого значения рабочего напряжения.
Обратите внимание, что хотя переходные перенапряжения являются нормальным состоянием сетевых цепей, значение рабочего напряжения не включает такие перенапряжения.
Используя как формулу, так и IEC 664, мы находим, что требуемая электрическая прочность для рабочего напряжения сети до 250 вольт составляет около 1500 вольт.
Второй тип цепей имеет ограниченное распространение, имеет ограниченное количество строго контролируемых нагрузок и надлежащим образом изолирован от сетевых цепей, так что в нем практически отсутствуют переходные перенапряжения. Вторичные цепи постоянного тока оборудования являются примерами цепей такого типа. Наличие кратковременных перенапряжений во вторичных цепях постоянного тока является ненормальным.
Изоляция, используемая во втором типе цепей, должна иметь электрическую прочность, равную или превышающую максимальное рабочее напряжение для этой цепи.
Следовательно, изоляция с электрической прочностью более 1500 вольт будет пригодна для использования
в сети с номинальным (рабочим) напряжением до 250 вольт.
Такая же изоляция пригодна и для использования во вторичной цепи постоянного тока с номинальным (рабочим) напряжением до 1500 вольт.
Рабочее напряжение является основой для определения напряжения электрической прочности (hi-pot), необходимого для основной, дополнительной или усиленной изоляции.
РАССТОЯНИЯ
Теперь рассмотрим зависимость между рабочим напряжением и расстояниями между проводниками рабочего напряжения.
Электрическая прочность прямо пропорциональна расстоянию через изолирующую среду: чем больше расстояние, тем больше электрическая прочность. Электрическая прочность большинства изоляционных сред измеряется в вольтах на расстояние. Следовательно, зазоры (расстояние через изолирующие среды) являются косвенной мерой электрической прочности изолирующих сред.
(Параметр вольт/расстояние также зависит от формы электрического поля в изолирующей среде. Максимальное значение вольт/расстояние имеет место при «однородном» поле, а минимальное значение вольт/расстояние возникает при наихудшем случае «неоднородного» поля . )
)
Стандарты безопасности обычно публикуют таблицы рабочего напряжения и расстояния в воздухе (зазоры). Таким образом, рабочее напряжение используется для определения зазора.
Однако значения безопасного расстояния во многих из этих таблиц намного превышают значения вольт на расстояние для воздуха для рабочего напряжения. Точно так же значения безопасного расстояния также больше, чем значение вольт на расстояние для переходного перенапряжения или высокого напряжения.
Таким образом, хотя рабочее напряжение действительно используется для определения безопасного расстояния из таблицы в стандарте, часто нет физической или математической связи между значением безопасного расстояния и либо рабочим напряжением, либо переходным перенапряжением, либо высоким напряжением. .
Многие стандарты безопасности не содержат требований к расстоянию до твердой изоляции. Тест Hi-Pot является единственным механизмом, с помощью которого твердая изоляция оценивается и определяется как маловероятная.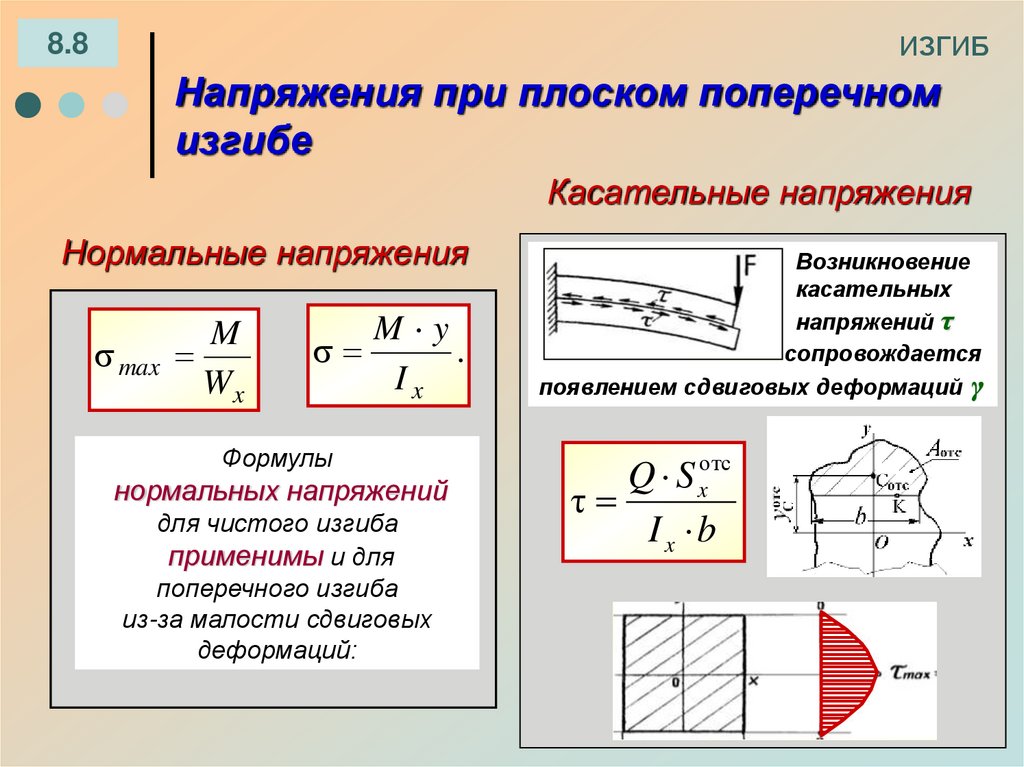 Это нормально, так как почти любая твердая изоляция любой используемой толщины будет иметь электрическую прочность более 3000 вольт. По словам одного остряка, даже сжимающе-мягкий Charmin мистера Уиппла имеет электрическую прочность более 3000 вольт.
Это нормально, так как почти любая твердая изоляция любой используемой толщины будет иметь электрическую прочность более 3000 вольт. По словам одного остряка, даже сжимающе-мягкий Charmin мистера Уиппла имеет электрическую прочность более 3000 вольт.
Некоторые стандарты безопасности публикуют минимальные значения расстояния для твердой изоляции, независимо от характеристик изоляции в вольтах на расстояние. Как и в случае с зазорами, такие значения не зависят от приложенного напряжения. Граница между твердой изолирующей средой и изолирующей средой атмосферного воздуха представляет собой особый случай. В сфере безопасности это обычно называют расстоянием утечки. Примером такого интерфейса является выход выводов из корпуса оптопары в воздух.
Этот интерфейс вызывает особую озабоченность, поскольку он часто подвергается отложению третьего, неконтролируемого материала (т. е. загрязнению поверхности твердой изоляции). Поэтому авторы норм безопасности опубликовали различные схемы, по которым интерфейс должен иметь больший размер, чем требуется для чисто воздушной изоляции.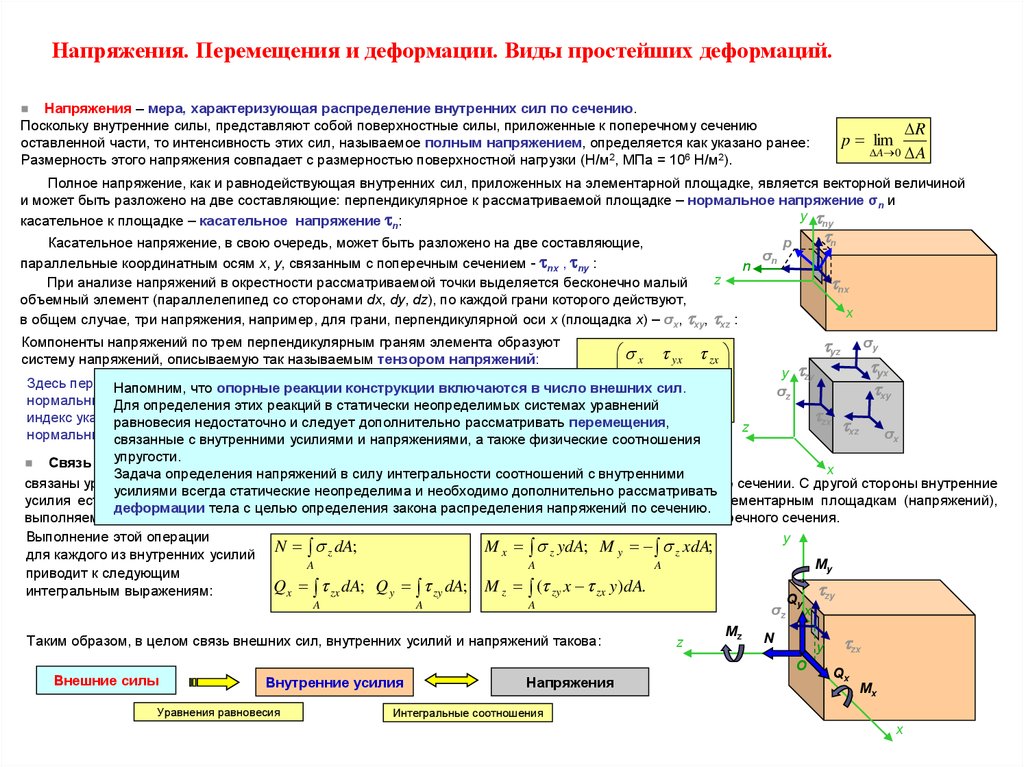
Однако выход из строя интерфейса (утечка) из-за скопления загрязнений является долговременным механизмом отказа. Следовательно, электрическая прочность интерфейса (утечка) основана на рабочем напряжении, а не на переходном перенапряжении. Следовательно, когда рабочее напряжение намного меньше, чем переходное перенапряжение (как в случае применения в сети), требования к путям утечки намного меньше, чем требования к зазорам. Точно так же, когда рабочее напряжение и переходные перенапряжения равны, требования к путям утечки намного превышают требования к зазорам.
Очевидно, что большее из двух расстояний, пути утечки или зазора, имеет приоритет в качестве требования к границе раздела (утечке).
Конструкция из двух проводников в воздухе также подвержена загрязнению. В этом случае загрязнение скапливается непосредственно на проводниках, что эффективно уменьшает расстояние в воздухе (зазор) между двумя проводниками.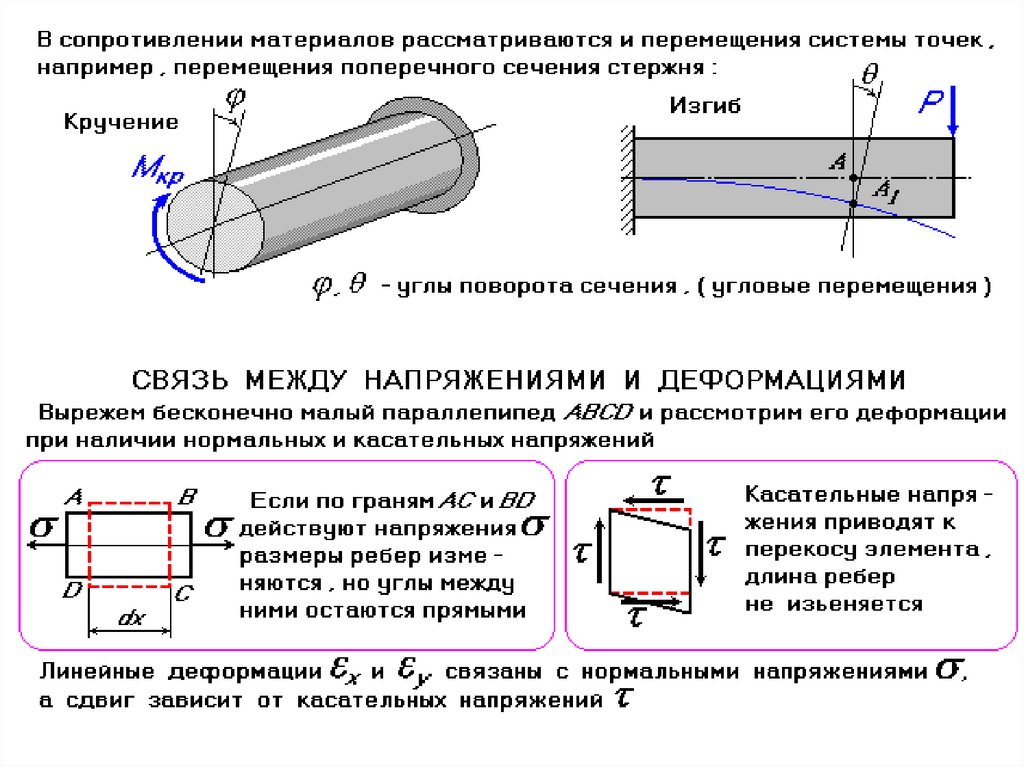 Эта проблема в основном направлена на очень малые значения зазора (т. е. значения электрической прочности менее 1500 вольт, среднеквадратичное значение), когда загрязнение может полностью перекрыть воздушный зазор.
Эта проблема в основном направлена на очень малые значения зазора (т. е. значения электрической прочности менее 1500 вольт, среднеквадратичное значение), когда загрязнение может полностью перекрыть воздушный зазор.
Рабочее напряжение является основой для определения пути утечки основной, дополнительной или усиленной изоляции.
Переходное перенапряжение является основой для определения расстояния по воздуху (зазор) и расстояния по твердой изоляции для основной, дополнительной или усиленной изоляции. Рабочее напряжение является основой для определения электрической прочности, достаточной для того, чтобы выдерживать обычно возникающие переходные перенапряжения.
Напомним, что расстояние через изоляцию является косвенной мерой электрической прочности этой изоляции. Обратите внимание, что общие стандарты безопасности независимо определяют высокое напряжение (электрическая прочность) и расстояния (которые определяют электрическую прочность). Любое соответствие между напряжением высокого напряжения и расстояниями чисто случайно. Как правило, стандарты безопасности требуют таких расстояний, чтобы электрическая прочность намного превышала максимальное напряжение.
Как правило, стандарты безопасности требуют таких расстояний, чтобы электрическая прочность намного превышала максимальное напряжение.
Однако публикация IEC 664 представляет собой попытку установить соответствие между высоким напряжением и расстоянием через изоляцию.
ЗАКЛЮЧЕНИЕ
По рабочему напряжению мы определяем значение испытательного напряжения высокого напряжения, прямого показателя электрической прочности. По рабочему напряжению мы определяем минимальные значения зазора, косвенного показателя электрической прочности. Поэтому рабочее напряжение является основой для определения минимальной электрической прочности изоляции.
Авторские права Ричарда Нута, 1993 г. Первоначально опубликовано в Информационном бюллетене по безопасности продукции, том. 6, № 4, июль-август-сентябрь 1993 г.
Ричард Нут — консультант по безопасности продукции, занимающийся безопасным проектированием, безопасным производством, сертификацией безопасности, стандартами безопасности и судебными расследованиями.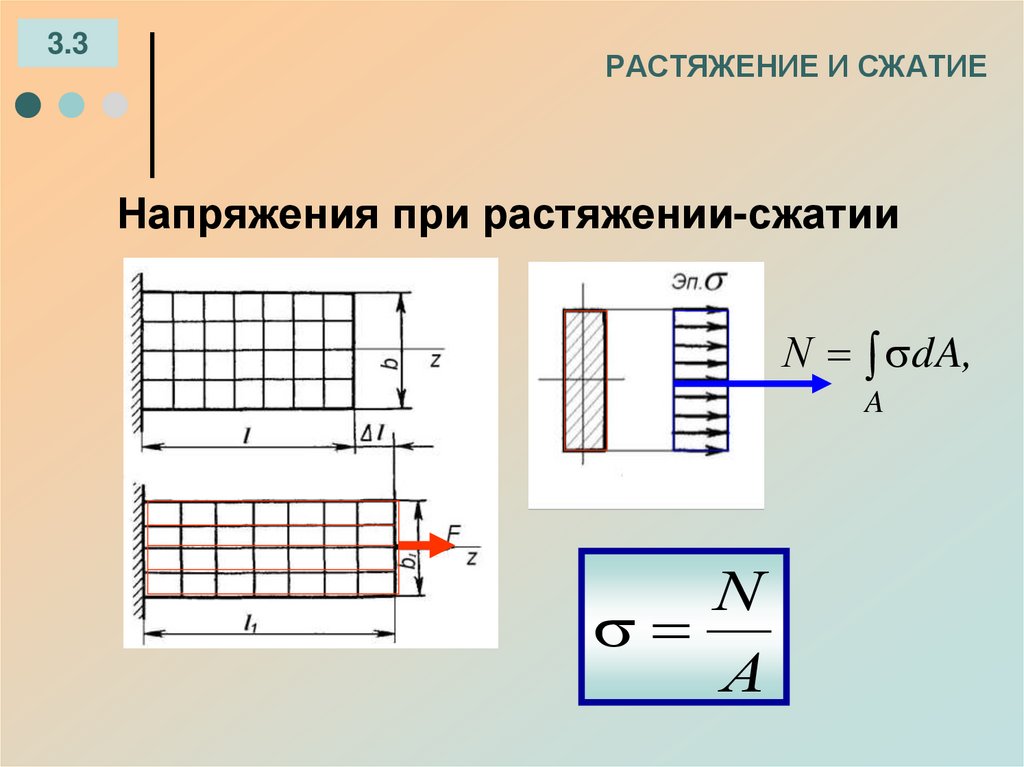
Что такое напряжение автомобильного аккумулятора?
Опубликовано в рубрике Автомобильный аккумулятор
Аккумулятор дает вашему автомобилю зарядку и многое другое. Без него вы не сможете поднять и опустить окна, запереть двери или включить музыку. Поэтому, когда что-то играет такую большую роль в вашей жизни за рулем, вполне естественно задаться вопросом, как это работает.
СКОЛЬКО ВОЛЬТ В АККУМУЛЯТОРНОЙ БАТАРЕЕ АВТОМОБИЛЯ?
Говоря о напряжении автомобильного аккумулятора, мы обычно говорим о 12-вольтовой батарее. Если мы присмотримся повнимательнее, то увидим, что напряжение автомобильного аккумулятора может варьироваться от 12,6 до 14,4.
- При выключенном двигателе напряжение полностью заряженного автомобильного аккумулятора составляет 12,6 вольт. Это известно как «напряжение покоя».
- При работающем двигателе напряжение аккумуляторной батареи обычно повышается до 13,5–14,5 вольт. Аккумулятор повышается до этих более высоких уровней генератором переменного тока.
Чтобы лучше объяснить, давайте сделаем шаг назад и рассмотрим неотъемлемую роль типичной 12-вольтовой батареи в системе запуска и зарядки вашего автомобиля.
- Аккумулятор накапливает электроэнергию.
- Стартер преобразует электрическую энергию в механическую для запуска двигателя.
- После запуска двигателя генератор вырабатывает электрический ток, который заменяет энергию, потребляемую стартером от аккумуляторной батареи.
Эти три шага повторяются снова и снова, приводя двигатель в действие, поскольку электрическая энергия снова преобразуется в механическую энергию, а генератор переменного тока заряжает аккумулятор для подачи дополнительного тока.
Теперь, когда мы рассмотрели, сколько вольт в автомобильном аккумуляторе и как работает аккумулятор, мы готовы перейти к силе тока.
Сила тока или амперы — это способ описать ток автомобильного аккумулятора. Номинальная сила тока будет отличаться в зависимости от количества опций вашего автомобиля. Проще говоря: автомобиль с большим количеством опций будет иметь аккумулятор с большей силой тока. Типичная сила тока батареи колеблется от 450 до 750 CCA.
Проще говоря: автомобиль с большим количеством опций будет иметь аккумулятор с большей силой тока. Типичная сила тока батареи колеблется от 450 до 750 CCA.
Эй, минуточку! Что такое КЦА? CCA означает «Ампер холодного пуска» и указывает на количество ампер, которое 12-вольтовая батарея может обеспечить при температуре 0ºF в течение 30 секунд при поддержании напряжения 7,2 В или более. Чем выше CCA, тем больше стартовая мощность.
Надлежащее техническое обслуживание может помочь вашей батарее продолжать работать так, как задумано . Как правило, рекомендуется проверять аккумулятор не реже одного раза в 6 месяцев/6000 миль. График для вашего конкретного автомобиля указан в руководстве пользователя. Нет инструкции? Без проблем! Джиффи Любе 9Технические специалисты 0210 ® могут получить доступ к графику технического обслуживания вашего автомобиля и рекомендуемым процедурам.
Если у вас возникли проблемы с аккумулятором, но вы находитесь между плановыми проверками технического обслуживания, не стесняйтесь проверить свой автомобиль.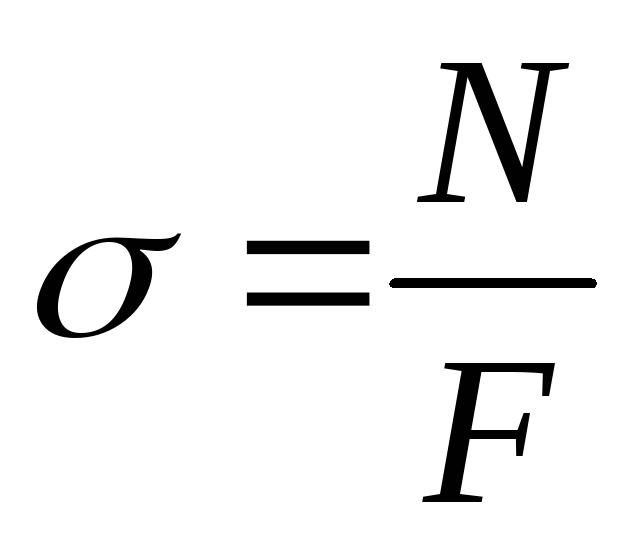 Симптомы неисправности аккумуляторной батареи включают:
Симптомы неисправности аккумуляторной батареи включают:
- Тусклый свет (фары и/или внутреннее освещение)
- Горят индикаторы «Check Engine» или «Charging»
- Аксессуары, такие как сиденья с электроприводом и окна, не работают
ОБРАЩАЙТЕСЬ В JIFFY LUBE ДЛЯ ОБСЛУЖИВАНИЯ И ОБСЛУЖИВАНИЯ АККУМУЛЯТОРНОЙ БАТАРЕИ
Ваша аккумуляторная батарея является сложной и ключевой для работы вашего двигателя. Вот почему вы должны доставить свой автомобиль в Jiffy Lube для обслуживания аккумулятора. Когда вы привозите свой автомобиль в один из 2000 пунктов по всей стране для проверки аккумуляторной батареи, ожидайте, что обученный специалист Jiffy Lube:
- Задаст вопросы о вашем стиле вождения, чтобы определить, какое влияние он может оказать на систему запуска и зарядки вашего автомобиля.
- Визуально осмотрите аккумулятор, включая прижим и соединения
- Выполните тщательную очистку терминала (при необходимости с вашего разрешения)
- Замена кабелей (при необходимости с вашего разрешения)
- Осмотрите соединения и при необходимости подтяните их
- Используйте мультиметр для проверки уровня заряда аккумулятора
- Проверьте и отрегулируйте уровень жидкости в аккумуляторе (если возможно)
Помните, что последовательное и тщательное техническое обслуживание аккумуляторной батареи может помочь продлить срок ее службы и обеспечить эффективную работу системы запуска/зарядки.