Статика 2 — Стр 2

Составим проверочное уравнение:

n

k 1

MС (Fk ) 0, (4)

M Q CE RBCB sin60 YACA 0.

Подставим в (4) значения всех величин

6 6 1,5 ( 5,77) 3 0,866 4 3 0, 0 0.

Задача решена правильно.

Определим полную реакцию RA шарнираА:

RA X A YA , RA X A2 YA2 42 2,32 4,6 кН.

Ответ: RA = 4,6 кН, RB = – 5,77кН.

Знак “минус” у реакции стержня В означает, что

направление вектора RB противоположно направлению, принятому первоначально. Стержень сжат.

Задача 2. Определить реакции связей ломаного стержня АСВ, изображенного на рисунке 7. В точке D закреплён канат, переброшенный через блок K и несущий на конце тело G.

Дано: G = 4 кН, М = 6кН·м, q = 3 кН/м, АС = BD = 2 м,

СD = 1 м, = 30 , = 60 .

Определить: RA и RB .

РЕШЕНИЕ

Изображаем ломаный стержень без связей (рисунок 8). Стержень нагружен сосредоточенной силой T G , парой сил с моментом М, равномерно распределённой нагрузкой

интенсивностью q, которую заменяем сосредоточенной силой Q (равнодействующей), приложенной в середине пролёта АС

Q= q AC = 3·2=6кН.

Вточке А стержень закреплён неподвижным цилиндрическим шарниром. Реакцию шарнира представляем

составляющими RAx , RAy , направленными параллельно

выбранным координатным осям. Направление составляющих произвольное.

В точке В стержень опирается на опору на катках. Реакция RB перпендикулярна поверхности, по которой

может перемещаться каток, и направлена от поверхности.

На тело действует плоская произвольная система сил, для которой достаточно трёх условий равновесия. Искомых

величин тоже три: RAx , RAy , RB , т.е. задача статически

определима.

Записываем условия и составляем уравнения равновесия:

n

Fkx 0, RAx + T·sin + RB sin = 0, (5)

k 1

n

Fky 0, Q + RAy + T·cos − RB·cos = 0, (6)

k 1

n

M A (Fk ) 0, − Q·AE − M + mA(T ) + mA( RB ) = 0. (7)

k 1

Для определения моментов сил T и RB

воспользуемся теоремой Вариньона о моменте равнодействующей.

mA (T ) mA (Tх ) mA (Tу ) T sin CD T cos AC,

mA (RB ) mA (RBx ) mA (RBy ) RB sin (BD DC) RB cos AC.

		q
	А	C
		M
		D
		β
	K
		B
	G
	Рисунок 7 – Схема
		задачи

		Q
х	RAx	А			C
		E				M
		RAy
		Т х			D
		Т		β	Т	у
		RB			RBy
			RBx B
					у
	Рисунок 8 – Схема сил

Подставляя эти зависимости в уравнение (7), выразим значение реакции RB:

R Q 0,5 AC P sin CD P cos AC M 88,36 кН.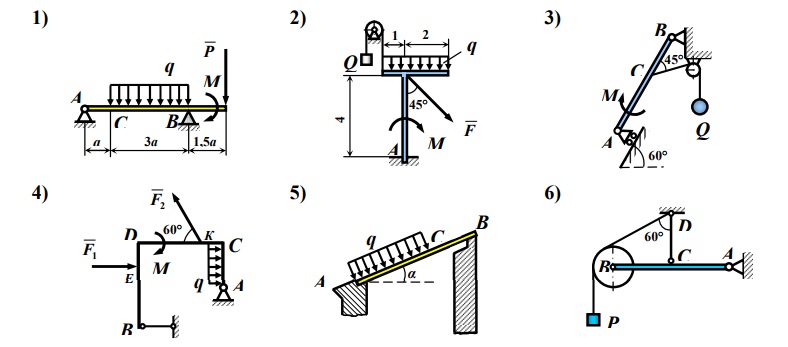

B AC cos BD DC sin

Из уравнения (5) определяется RАx

RАx = − Tsin − RBsin = − 47,60кН.

Из уравнения (6) определяется RАy:

RАy = RB cos − Q − T cos = 67,98кН.

Составляем проверочное уравнение моментов относительно точки D. В это уравнение войдут все

n

определяемые величины: mD (Fk ) 0 ,

k 1

RAx·DC+ Q·0,5·AC − M − RB·sin ·BD + RAy·AC = 0,

47,62 1 6 2 0,5 6 88,36 0,5 2 67,98 2 0 ,

0 ≡ 0.

Задача решена правильно.

RA RAx2 RAy2 47,62 67,982 83 кН.

Ответ: RB= 88,36 кН, RA = 83кН. Знак минус у составляющей RAx означает, что направление этой

составляющей реакции шарнира А противоположно показанному на рисунке 8.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Данная тема содержит 25 вариантов заданий по 6 за-дач в каждом. Рисунки к задачам по вариантам помещены на страницах 76 – 88.

Искомыми величинами в большинстве задач являются реакции связей, наложенных на абсолютно твёрдое тело.

Примечание − Во всех вариантах трением в шарнирных связях и блоках пренебречь.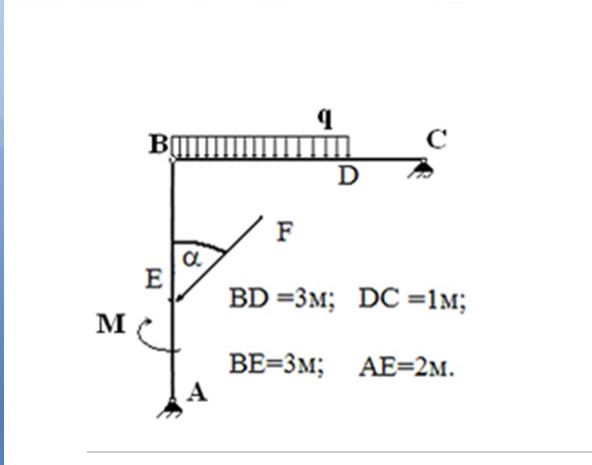

ВАРИАНТЫ ЗАДАНИЙ

Задание 2.01

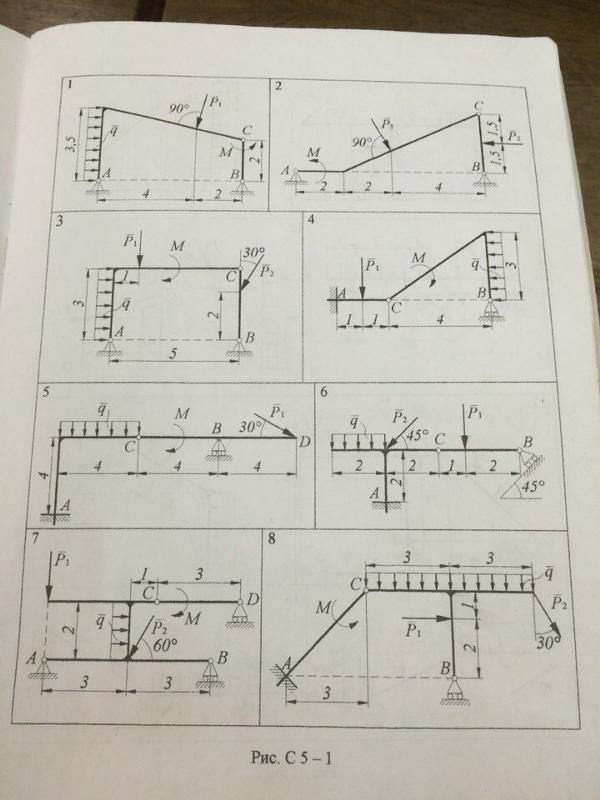
2.01.1. Определить реакции заделки консольной балки АВ, находящейся под действиемпары сил с моментомМ = 2,5 кН м, равномерно распределённой нагрузки

интен-сивностьюq = 1,5 кН/м,	сосредоточенной	силы
P = 3 кН, если а = 0,8 м.

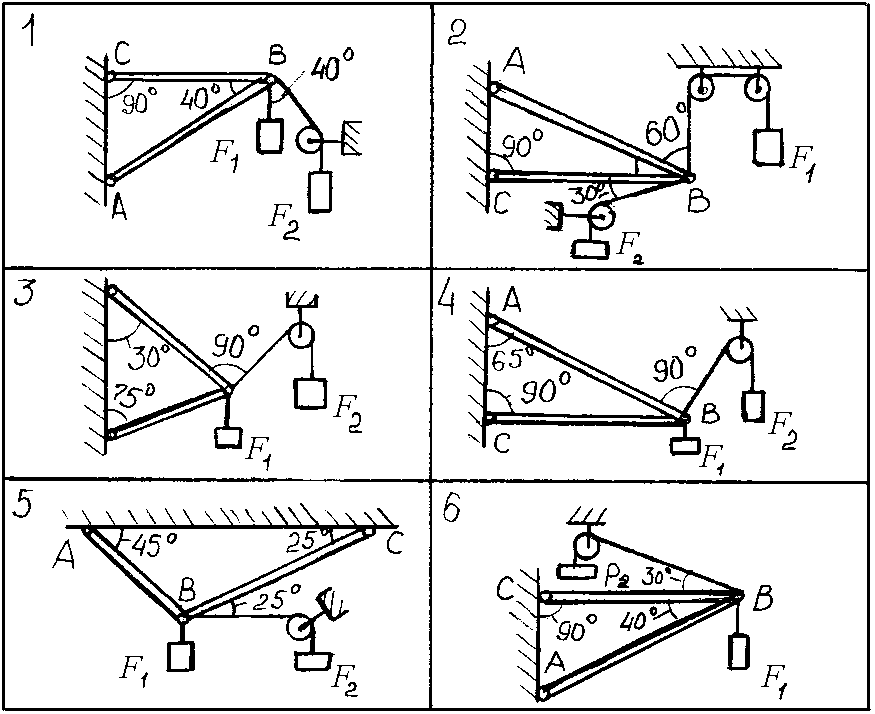
2.01.2.Однородная балка ВС весом 400 Н удерживается

вравновесии при помощи невесомых стержней АВ, СD и ЕK. Определить их реакции, если F = 150 Н.

2.01.3.Балка АВ длиной 8 м и весом 60 Н концом А закреплена шарнирно, в точке Dопирается на выступ стены. К точке В балки прикреплена верёвка с грузом весом Q = 10 Н на конце, перекинутая через блок Е. На балку действует пара

сил с моментом М = 10 Н м. Определить реакции опор А и D, если DВ = ¼АВ.

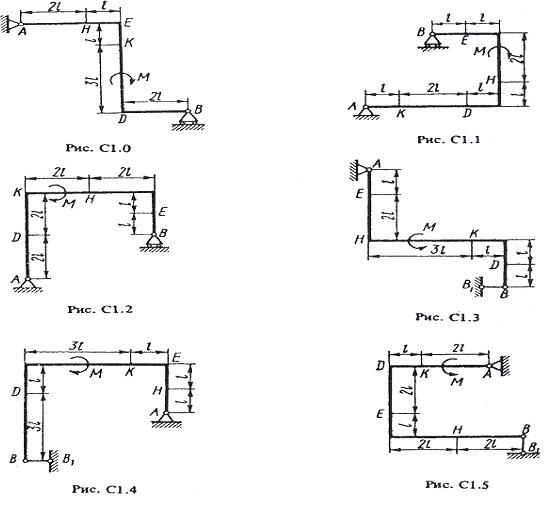
2.01.4.Жёсткая рама закреплена в точке А шарнирно, а

вточке В прикреплена к шарнирной опоре на катках.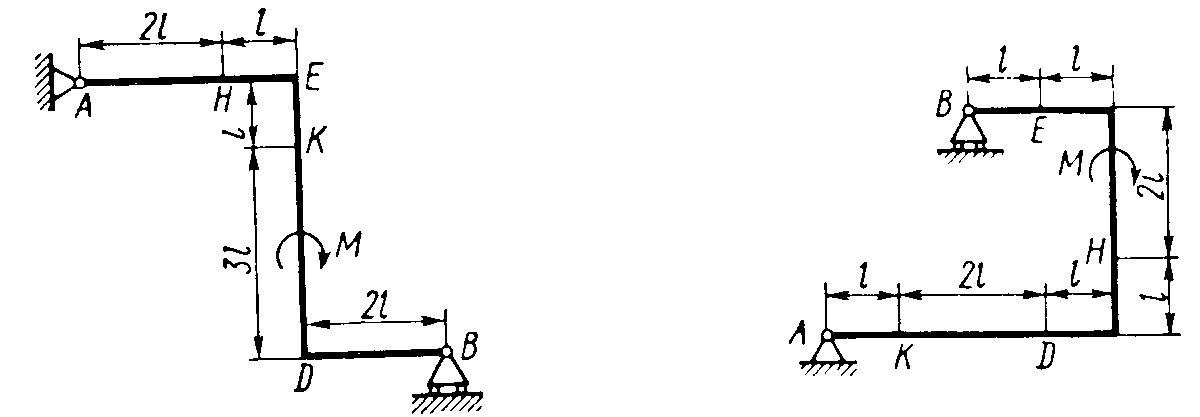 На раму

действует пара сил с моментом М = 10 кН м, равномерно распределённая нагрузка интенсивностьюq = 2 кН/м и две сосредоточенные силы F1 = 3 кН и F2 = 5 кН. Определить реакции связей, если АЕ = СK = а,АС = 3а,

KD = 2а,ВD = 4аиа = 0,8 м.

2.01.5. Однородная плита АВ весом 100 Н свободно опирается в точке А на гладкую плоскость и удерживается под углом 45° к горизонту двумя стержнями ВСиВD, ∆ВСD равносторонний. Точки С и D лежат на горизонтальной прямой. Пренебрегая весом стержней и считая крепления в точках В, Си D шарнирными, определить реакцию опоры А и усилия в стержнях.

2.01.6. Определить реакции жёсткой заделки однород-

ной балки АВ	весом 100 Н, если вес груза
Р = 50 Н,q = 200 Н/м,	АС = СD = 0,4 м,ВD = 0,6 м. Весом и

размерами блока В пренебречь.

Задание 2.02

2.02.1. Определить реакции заделки консольной балки АВ, находящейся под действием равномерно распределённой нагрузки интенсивностью q = 2,3 кН/м и пары сил с моментом М = 3,5 кН м, если, а = 2 м.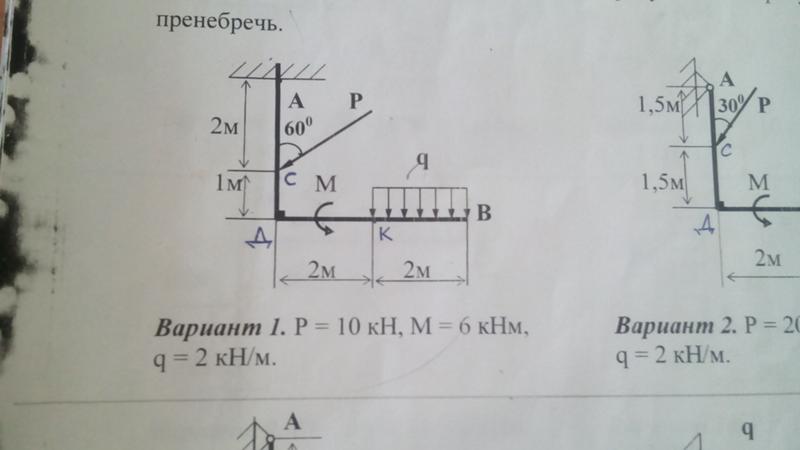

2.02.2. Определить реакции опор А и В рамы, находящейся под действием равномерно распределённой нагрузки интенсивностью q =1,5 кН/м, сосредоточенной силы F = 30 кН и пары сил с моментом М = 10 кН м. Размеры на рисунке даны в метрах.

2.02.3.Однородная балка АВ весом 24 кН, закреплённая

вточке А шарнирно, опирается в точке Е на выступ стены. В точке В прикреплена веревка с грузом Q = 28 кН на конце, перекинутая через блок D. На балку действует пара сил с

моментом М = 10 кН м и сила	F = 24 кН,	приложенная в
точке С. Определить опорные	реакции,	если АС = ⅛АВ,
АЕ = ⅝АВ, АВ = 8 м.
2.02.4. Ломаный стержень	закреплён	в точке Ашар-

нирно, а в точке В невесомым стержнем. На стержень действует пара сил с моментом М = 6 кН м,равномерно распределённая нагрузка интенсивностью q = 1,5 кН/м и две

сосредоточенные силы F1 = 7 кН и F2 = 10 кН.		Определить
реакции	связей,	если

ВЕ = ЕD = 1,5а,DK = KС = СА = 2а,а = 0,4 м.

2.02.5. Однородная плита АВ весом 100 Н свободно опирается в точке А на гладкую плоскость и удерживается

под углом 45° к горизонту двумя стержнями ВСиВD, ∆ВСD равносторонний. Пренебрегая весом стержней и считая крепления в точках В, СиD шарнирными, определить реакцию опоры А и усилия в стержнях.

2.02.6. Определить реакции связей однородной балки АВ весом 0,6 кН, если вес груза Р = 3,4 кН, АВ = 1 м,АС = 0,3 м,r = 0,15 м. Весом блока В пренебречь.

Задание 2.03

2.03.1. Определить реакции опор балки АВ, находящейся под действием равномерно распределённой нагрузки

интенсивностью	q = 1,2 кН/м,	сосредоточенной
силыP = 1,7 кН и	пары сил с	моментом М = 2 кН м,
еслиа = 3 м.

2.03.2. Определить реакции заделки консольной балки АВ, находящейся под действием равномерно распределённой нагрузки интенсивностью q = 10 кН/м, сосредоточенной силы F = 40 кН и пары сил с моментом М = 25 кН м, если а = 1 м.

2.03.3. Однородная балка АВ весом 20 кН, закреплённая концом А шарнирно, опирается в точке Е на выступ стены. В

точке В	к	балке прикреплена		верёвка	с	грузом	весом
Q = 10 кН	на конце. В		точке D к балке приложена				сила
F = 12 кН.		На балку	действует	пара	сил	с моментом
М = 8 кН м.		Определить опорные		реакции,		учитывая, что
АD = DЕ = ВЕ = 1 м.

2.03.4. Ломаный стержень закреплён в точке А шарнирно, а в точке В невесомым стержнем. На стержень действует пара сил с моментом М = 4 кН м, равномерно распределённая нагрузка интенсивностью q = 0,3 кН/м и две сосредоточенные силы F1 = 4 кН и F2 = 7 кН. Определить

реакции

связей,

если

ЕС = СK = KD = DВ = 2а,

АЕ = аиа =0,4 м.

2.03.5.Однородный стержень АВ весом 600 Н концом А опирается на гладкий горизонтальный пол и гладкую стену, а другим концом на гладкую плоскость. К концу В стержня прикреплена верёвка, перекинутая через блок С и несущая на конце груз весом Р = 50 Н.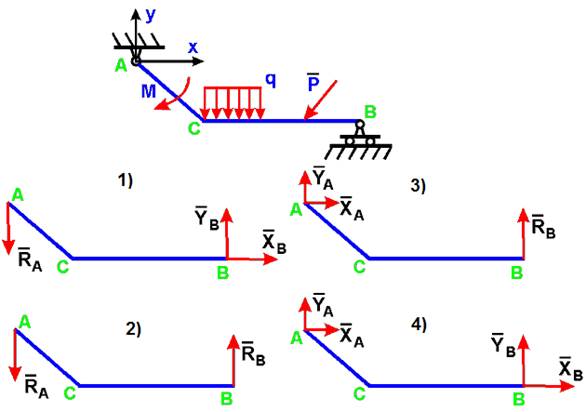 Определить силы давления стержня АВ на опорные плоскости.

2.03.6.Определить реакции жёсткой заделки однород-

нойбалки АВ весом 400 Н, если	вес	груза
Р = 300 Н,q = 150 Н/м,АС = СD = DВ = 2 м.	Весом	и
размерами блока В пренебречь.

Задание 2.04

2.04.1. Определить реакции заделки консольной балки АВ, находящейся под действием сосредоточенной силы P = 0,6 кН, равномерно распределённой нагрузки интенсивностьюq1 = 1,2 кН/м и q2 = 0,8 кН/м и пары сил с моментом М = 1,5 кН м, если а1 = 3 м,а2 = 2 м.

2.04.2. Определить реакции опор А и В ломаного стержня, находящегося под действием равномерно распре-

делённой	нагрузки интенсивностью q = 8 кН/м,	сосредо-
точенной	силы F = 10,2 кН и пары сил с	моментом

М= 12 кН м.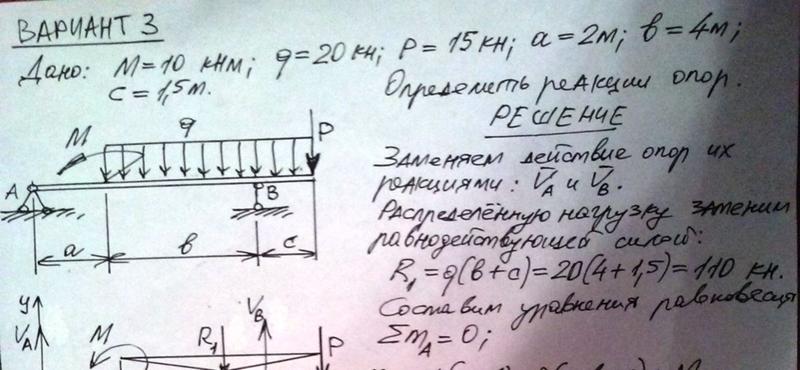 Размеры на рисунке даны в метрах.

2.04.3.Однородный стержень АВвесом 100 кН концом А закреплён шарнирно, а концом В опирается на гладкую поверхность. В точке С к стержню прикреплена верёвка, перекинутая через блок D и имеющая на своём конце груз Ввесом Q = 60 кН. На стержень действует пара сил с

моментом М = 20 кН м. Определить реакцию шарнира А и давление стержня на плоскость, еслиАВ = 2 м иАС = ¼АВ.

2.04.4.Жёсткая рама закреплена в точке А шарнирно, а

вточке В прикреплена к невесомому стержню. На раму

действует пара сил с моментом М = 10 кН м, равномерно распределённая нагрузка интенсивностью q = 0,3 кН/м и две сосредоточенные силы F1 = 3 кН и F2 = 5 кН. Определить реакции связей, если ЕС = KD = а, СK = 2а, АЕ = DВ = 3а

иа = 0,5 м.

2.04.5.Однородная балка весом 600 Н и длиной 4 м опирается одним концом на гладкий пол, а промежуточной точкой В на столб высотой 3 м, образуя угол 30°. Конец С балки удерживается верёвкой АС, протянутой параллельно полу.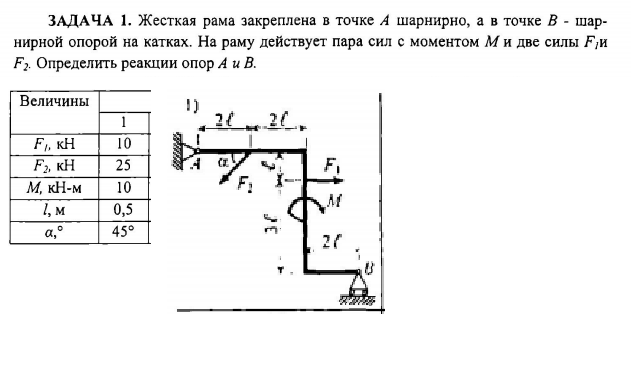 Пренебрегая трением, определить реакции связей.

2.04.6.Определить реакции связей однородной балки АВ весом 10 кН, если вес груза Р = 5 кН,АС = СО = ОВ. Весом и размерами блока пренебречь.

Задание 2.05

2.05.1. Определить реакции заделки консольной балки АВ, находящейся под действием равномерно распределённой нагрузки интенсивностью q = 0,6 кН/м, сосредоточенных сил P1 = 2 кН и P2 = 1,3 кН и пары сил с моментом М = 0,5 кН м, если а = 1,5 м.

2.05.2. Определить реакции опор балки АВ, находящейся под действием равномерно распределённой нагрузки интенсивностью q = 2 кН/м,пары сил с моментом М = 2 кН м и сосредоточенных сил F1 = 10 кН,F2 = 5 кН, если а = 1,5 м.

2.05.3. Однородный брус АВ длиной 80 см и весом 100 Н, в точке А закреплён шарнирно, а в точке С опирается на выступ стены. Брус удерживается в равновесии при помощи верёвки с грузом Р = 400 Н на конце и перекинутой

через блок D. На брус действует пара сил с моментом

М= 100 Н м. Определить реакции опор, еслиАС = ¼АВ.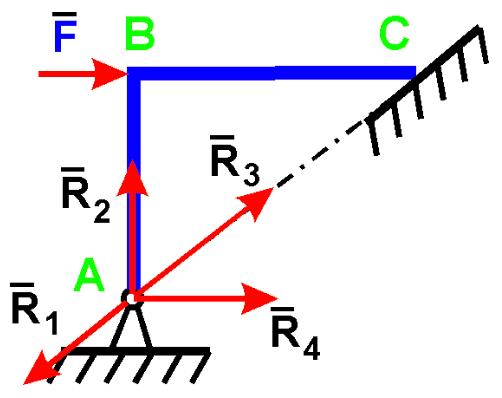

2.05.4.Жёсткая рама закреплена в точке А шарнирно, а в точке В прикреплена к шарнирной опоре на катках. На раму

действует момент пары сил М = 4 кН м, равномерно распределённая нагрузка интенсивностью q = 0,5 кН/м и две сосредоточенные силы F1 = 4 кН и F2 = 6 кН. Определить реакции связей, если СK = KD = DВ = 2а, АЕ = а, ЕС = 3а

иа = 0,4 м.

2.05.5. Верхний конец В бруса АВ, длиной 6 м, стропил односкатной крыши свободно лежит на гладкой опоре, а нижний конец А упирается в выступ стены. Угол ската крыши = 30°. На брус АВ действует равномерно распределённая нагрузка интенсивностью q = 1,5 кН/м. Определить реакции опор в точках А и В.

2.05.6. Определить опорные реакции однородной балки АВ весом 250 кН, если вес груза Р = 100 кН,АО = ОВ. Весом и размерами блока Опренебречь.

Задание 2.06

2.06.1. Определить реакции связей балки АВ, находя-

щейся под	действием	пары	сил с	моментом
М = 2,4 кН м,сосредоточенной силы			P = 3 кН,	равномерно
распределённой	нагрузки	интенсивностью		q1 = 0,6 кН/м,
q2 = 0,8 кН/м, если а = 1,5 м.

2.06.2. Определить реакции заделки консольной балки, находящейся под действием равномерно распределённой нагрузки интенсивностью q = 3 кН/м, сосредоточенной силы F = 4,2 кН и двух пар сил с моментами М1 = 2,5 кН м,М2 = 3 кН м, соответственно, если а = 1 м.

Аксиома связей (принцип освобождаемости от связей)

Аксиома связей

Аксиома связей (принцип освобождаемости от связей)
Всякое несвободное тело можно рассматривать как свободное, если действие связей заменить силами, называемыми силами реакций связей.

Аксиома связей, или, как ее еще называют принцип освобождаемости от связей, заключается в том, что мы отбрасываем связи, и вместо них вводим силы и (или) моменты сил. То есть, заменяем связи на силы, которые называются пассивными силами или силами реакций.
Более подробно связи рассматриваются на странице
Понятие механических связей и их классификация.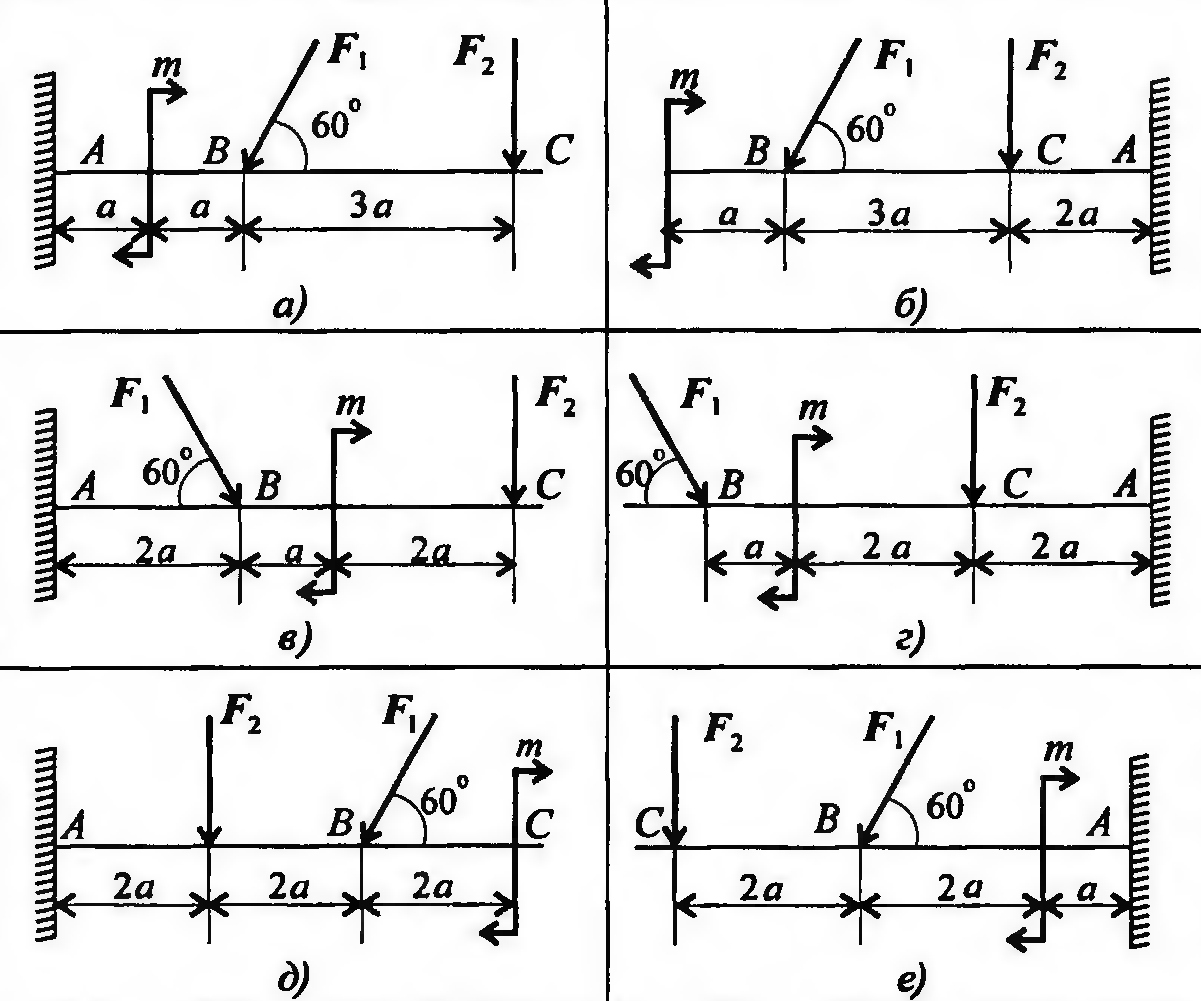
Виды связей и соответствующие им силы реакций приводятся на странице
Связи и их реакции в технической механике.
Ниже мы рассматриваем несколько примеров применения аксиомы связей.

Сама аксиома связей не является аксиомой как таковой, а является следствием дифференциальных уравнений движения точек механической системы. Выделение принципа освобождаемости от связей в отдельную аксиому имеет историческую причину.

Связи можно рассматривать как ограничения на возможные перемещения тела или материальной точки, вызванные взаимодействием с другими телами или точками. С математической точки зрения связи являются уравнениями или неравенствами, связывающие координаты и скорости точек системы.

Согласно фундаментальным законам механики, причиной возникновения ускорений точек являются действующие на них силы. Обычно сначала мы вводим силы, а по ним вычисляем траектории движения точек системы. Наличие связей несколько меняет ситуацию. При наложении связей мы заранее задаем либо законы движения некоторых точек, либо налагаем на координаты и скорости системы определенные условия.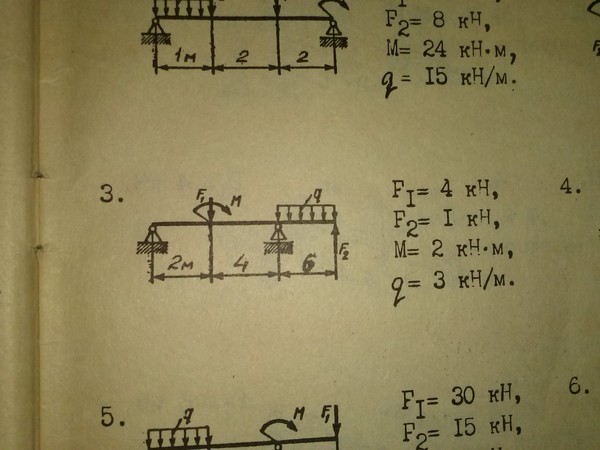

Но основными фундаментальными законами механики являются дифференциальные уравнения движения точек системы, в которых ускорения точек определяются действующими на них силами (второй закон Ньютона). Тогда, чтобы выполнялись предварительно введенные ограничения в виде связей, мы должны ввести дополнительные силы, обеспечивающие выполнение уравнений связей. Такие силы выделяются в отдельную группу; они называются реакциями связей. Реакции связей не заданы изначально, а их значения определяются из уравнений связей. По этой причине их называют пассивными силами.

Определения

Приведем определения некоторых терминов, используемых в формулировке аксиомы связей.

Связи

– это ограничения на возможные перемещения тела или материальной точки, вызванные взаимодействиями с другими телами или точками. С математической точки зрения, связи являются уравнениями или неравенствами, связывающие координаты и скорости точек механической системы, а также время.

Свободное тело

Тело называется свободным, если на его перемещение не наложены связи, то есть если его перемещение ничем не ограничено.

Несвободное тело

Тело называется несвободным, если на его перемещение наложена одна или несколько связей, то есть если его перемещение ограничено другими телами.

Силы реакций связей

– это силы, добавляемые в систему для того, чтобы выполнялись условия связей. Говорят, что они являются силами, с которыми связи действуют на данное тело. Их также называют пассивными силами.

Активные силы

– это силы, действующие на тело, которые не являются силами реакций связей, то есть не являются пассивными силами.

Разделение сил на активные и пассивные является следствием причины их возникновения. Активные силы, как правило, известны и не зависят от наложенных на систему связей. Пассивные силы мы вводим для того, чтобы их действие приводило к соблюдению условий связей. Пассивные силы заранее неизвестны, они полностью определяются уравнениями связей. Хотя их направления часто определяются видом связи, но абсолютные величины зависят от действия других сил.

Кроме этого, пассивные силы никогда не являются причиной движения механической системы. Система начинает движение именно благодаря действию активных сил.

Аксиома связей в статике

Одной из самых востребованных задач в механике является задача на равновесие конструкции, находящейся под действием внешних сил. Элементы такой конструкции представляют собой систему соединенных между собой тел, закрепленных на опорах к неподвижному основанию. Виды опор подбираются таким образом, чтобы система и ее элементы находились в покое. Требуется найти силы, действующие в опорах и отдельных элементах конструкции.

С математической точки зрения, опоры и узлы, соединяющие отдельные элементы конструкции между собой, являются связями, поскольку они препятствуют свободному перемещению элементов конструкции.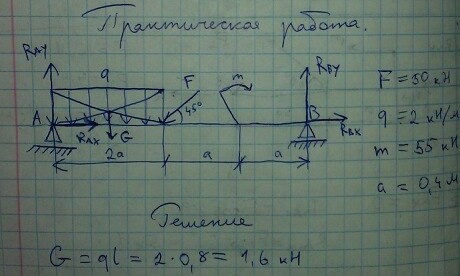 Таким образом, в статике мы имеем дело с системой тел со связями, все элементы которой находятся в покое. Для определения сил, действующих в опорах и узлах, мы применяем аксиому о связях. То есть, освобождаем все элементы системы от связей, и прикладываем вместо них силы реакций. Тем самым получаем систему, состоящую из свободных, не связанных между собой тел. На эту систему кроме заданных активных сил, также действуют и пассивные силы реакций, которыми заменены связи. Далее мы определяем величины пассивных сил так, чтобы система находилась в состоянии покоя.

Пассивные силы могут включать в свой состав также и пары сил (моменты). Направления пассивных сил и моментов зависят от вида применяемой связи. См. Связи и их реакции в технической механике. Заменив связи реакциями, каждый элемент конструкции становится свободным телом или свободной материальной точкой. Абсолютные значения реакций и их компонент находятся из условий равновесия. То есть мы подбираем величины реакций таким образом, чтобы каждый элемент системы, рассматриваемый как свободное тело, покоился.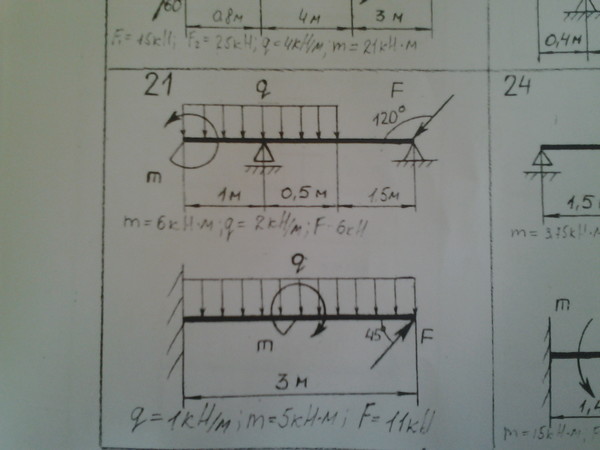

Зависимость между отдельными телами системы осуществляется за счет применения закона действия и противодействия (3-й закон Ньютона). Согласно этому закону, реакция, с которой первое тело действует на второе, равна по абсолютной величине и противоположна по направлению реакции, с которой второе тело действует на первое. Таким образом, реакции, возникающие в точке соединения двух элементов конструкции связаны между собой: они равны по абсолютной величине и противоположны по направлению.

Далее мы рассмотрим несколько примеров применения принципа освобождаемости от связей.

Примеры применения аксиомы связей

Ломаный брус

Ломаный брус со связями.

Рассмотрим плоскую конструкцию, в которой на ломаный брус AB действуют сила P, равномерно распределенная нагрузка q и момент силы M. Опора A – бискользящая заделка; опора B – неподвижный шарнир.

Освобождение от связей в ломаном брусе.

Освобождаемся от связей, вводя вместо них реакции. Опора A является бискользящей заделкой. В ней точка A, принадлежащая брусу может свободно перемещаться как по вертикали, так и по горизонтали. Поскольку препятствия перемещения точки A нет, то сила реакции в ней отсутствует. Но в заделке фиксировано направление конца бруса. То есть он не может поворачиваться относительно центра поворота в точке A. При попытке поворота, возникает препятствие вращению в виде момента сил, который мы обозначим как . Поскольку задача плоская, то пара сил с моментом лежит в плоскости рисунка, а вектор момента – перпендикулярен этой плоскости. Здесь – единичный вектор, направленный вдоль оси системы координат. Эта ось перпендикулярна плоскости рисунка и направлена на нас.

Опора B является неподвижным шарниром. В ней точка B, принадлежащая брусу не может свободно перемещаться как по вертикали, так и по горизонтали. При попытке перемещения, возникает сила, препятствующая этому перемещению. Поэтому в точке B имеется сила реакции , которая может иметь произвольное направление. Ее удобно разложить на составляющие , направленные вдоль осей координат. Здесь – единичные векторы, направленные вдоль осей системы координат. Величины являются проекциями на оси координат. Они могут принимать положительные, отрицательные или нулевые значения. Если какая-либо из этих величин отрицательна, то соответствующей ей вектор или направлен противоположно оси координат. Абсолютная величина силы реакции:
.

Поскольку в шарнире B не происходит препятствия вращению закрепленного конца, то в реакцию связи в точке B момент сил не входит.

Таким образом, конструкция со связями, изображенная на верхнем рисунке, эквивалентна конструкции, в которой связи заменены реакциями. Всего имеется три величины реакции: . Поскольку задача плоская, то имеется три линейно независимых уравнения равновесия, из которых можно определить значения этих реакций.

Составная конструкция

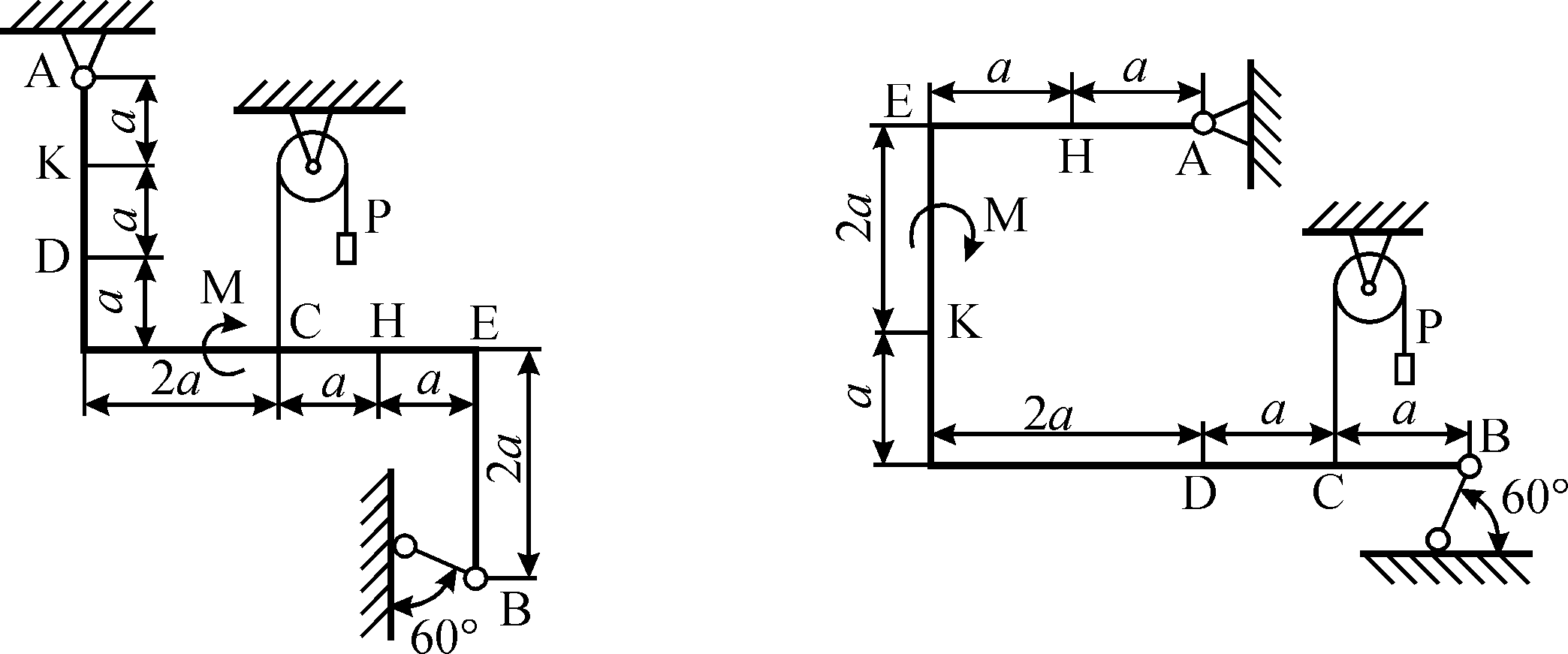
Составная конструкция со связями.

Рассмотрим составную конструкцию, состоящую из рамы AC и стержня CB. На конструкцию действуют силы , равномерно распределенная нагрузка q и пара с моментом M. Опора A – жесткая заделка; в точке B – опора на катках. Рама и стержень соединены скользящей заделкой в точке C.

Освобождение от связей в раме.

Освобождаемся от связей. Рассмотрим раму AC. Опора A является жесткой заделкой. В ней точка A, принадлежащая раме, не может перемещаться ни по вертикали, ни по горизонтали. Поэтому в состав реакций входит сила , имеющая произвольное направление, действие которой направлено на препятствие перемещению. Ее удобно разложить на составляющие , направленные вдоль осей координат:
.
Здесь – единичные векторы, направленные вдоль осей координат; – проекции вектора на оси координат. Проекции могут иметь как положительные, так и отрицательные значения. В случае отрицательного значения, соответствующая составляющая направлена противоположно оси координат.

Поскольку в жесткой заделке, рама не может поворачиваться относительно центра вращения A, то в реакцию также входит момент , препятствующий повороту вокруг A. Вектор момента направлен перпендикулярно плоскости фигуры:
.
Здесь – единичный вектор вдоль оси z, которая перпендикулярна плоскости фигуры и направлена на нас; – проекция момента на ось z. Если , то вектор направлен вдоль оси z. На рисунке это соответствует закручиванию против часовой стрелки. Если , то направлен противоположно оси z – закручивание по часовой стрелке.

Таким образом, реакция в жесткой заделке A представлена силой и моментом . Она задается тремя числами , которые могут иметь положительные, отрицательные или нулевые значения.

Узел C является скользящей заделкой. В нем точка C, принадлежащая раме, может свободно перемещаться вдоль направляющей, которая направлена вдоль оси x, но не может перемещаться в перпендикулярном направлении – вдоль оси y. Кроме этого, рама не может поворачиваться относительно центра C. Поэтому реакция в точке C представлена силой и моментом .

Таким образом, реакция в скользящей заделке C задается двумя числами , которые могут иметь положительные, отрицательные или нулевые значения.

Освобождение от связей в стержне.

Рассмотрим стержень CB. Согласно закону действия и противодействия, силы, действующие на стержень в узле C со стороны рамы, равны по величине и противоположны по направлению силам, действующим в этом узле на раму со стороны стержня. Поэтому реакция в узле C состоит из силы и момента .

Опора в точке B является опорой на катках. В ней точка B может свободно перемещаться вдоль поверхности, но не может перемещаться в перпендикулярном направлении. Поэтому возникает сила реакции , направленная перпендикулярно поверхности:
,
где – единичный вектор нормали к поверхности.

Поскольку стержень может свободно поворачиваться относительно центра B, то момент сил, препятствующий повороту, отсутствует. Поэтому реакция в точке B состоит из одной силы .

Таким образом, составная конструкция со связями, изображенная на верхнем рисунке эквивалентна двум свободным телам – раме и стержню, в которых связи заменены реакциями. Мы нашли, что всего имеется шесть величин, определяющих реакции в точках соединений: .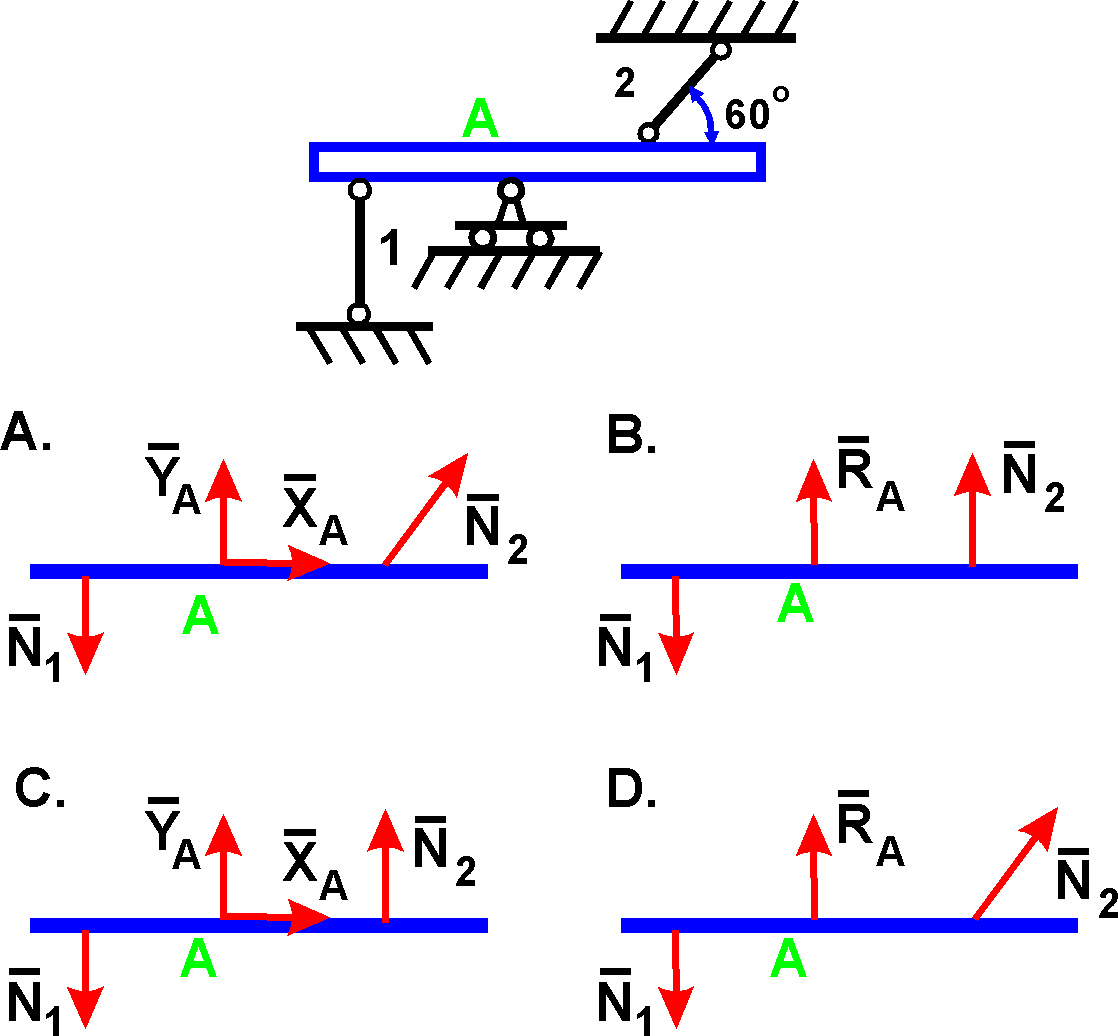 Поскольку задача плоская, то для каждого тела можно составить по три линейно независимых уравнения равновесия – всего шесть уравнений, из которых можно определить шесть неизвестных: .

Плита, поддерживаемая стержнями

Плита со связями.

Рассмотрим прямоугольную однородную плиту ABDE, на которую действуют сила тяжести G и заданная сила P. Плита поддерживается невесомыми жесткими стержнями 1, 2, 3, 4, 5, 6, концы которых закреплены шарнирами.

Освобождение от связей в плите.

Освобождаемся от связей. Реакцией жесткого невесомого стержня с номером i является сила , направленная вдоль стержня, от одного конца к другому. Отбрасываем все стержни, а в точке крепления i-го стержня к плите, вводим силу реакции
.
Здесь – единичный вектор, направленный вдоль стержня. На рисунке мы выбрали направления этих векторов таким образом, что если , то i-й стержень сжат; если , то растянут. Правда, в сопротивлении материалов, такой выбор знаков в величинах не является общепринятым.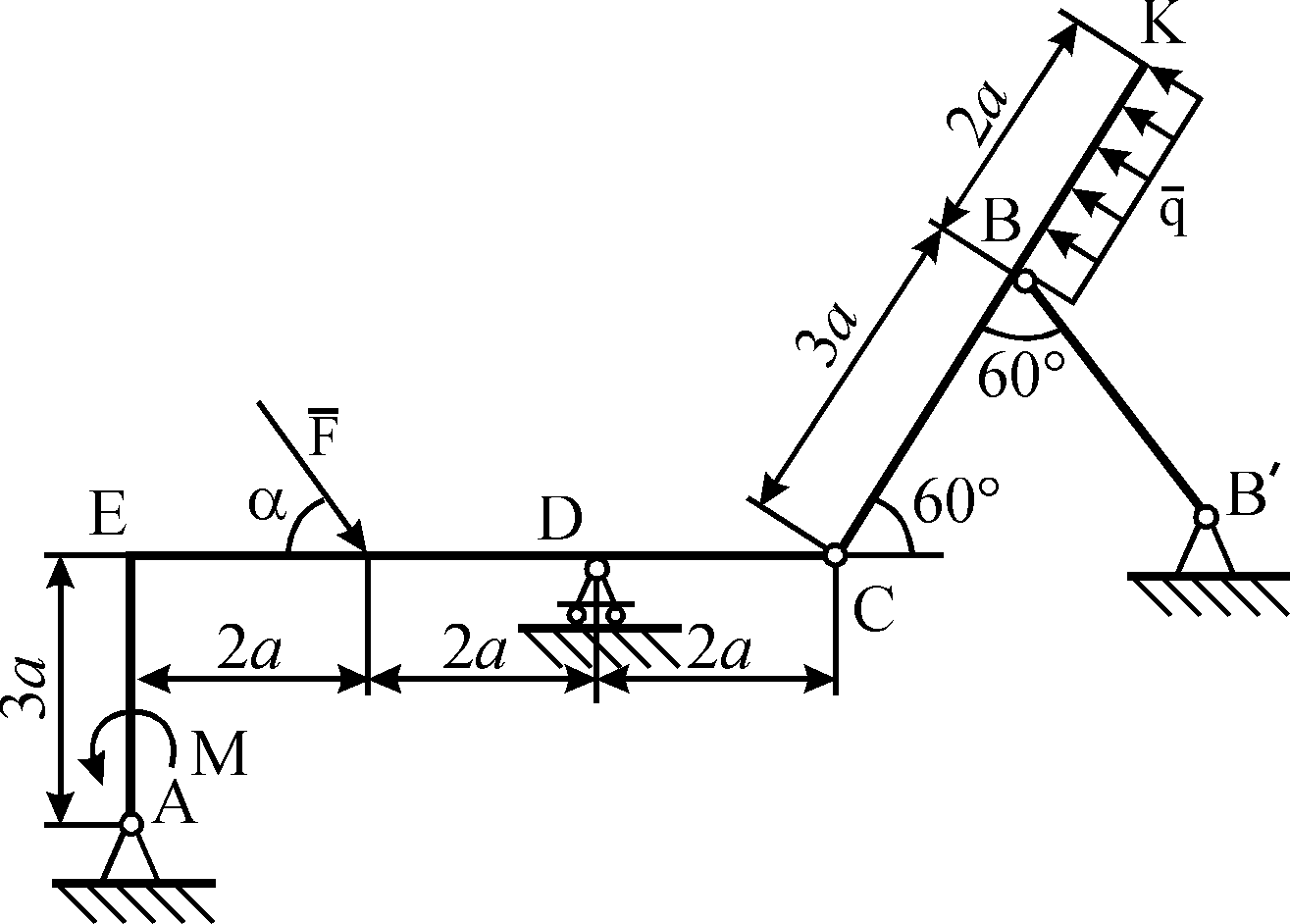 Там принято, что если усилие в стержне положительно, то он растянут, а если отрицательно, то сжат. Но для нас это не имеет значения.

Таким образом, плита со связями в виде стержней, изображенная на верхнем рисунке, эквивалентна плите, в которой связи заменены реакциями. Всего имеется шесть величин реакций: . Поскольку конструкция трехмерная, то имеется шесть линейно независимых уравнений равновесия, из которых можно определить шесть значений усилий в стержнях.

Использованная литература:
Н. Н. Бухгольц. Основной курс теоретической механики, часть 1. Москва, «Наука», 1965.

Ответил: 2) Определить реакции на изогнутые…

1 Введение в статику2 Основные операции с системами сил3 Результативные системы сил4 Компланарный анализ равновесия5 Трехмерное равновесие6 Балки и канаты7 Сухое трение8 Центроиды и распределенные нагрузки9 Моменты и произведения инерции площадей10 Виртуальная работа и потенциальная энергия expand_more

Вопросы главы expand_more

Задача 10.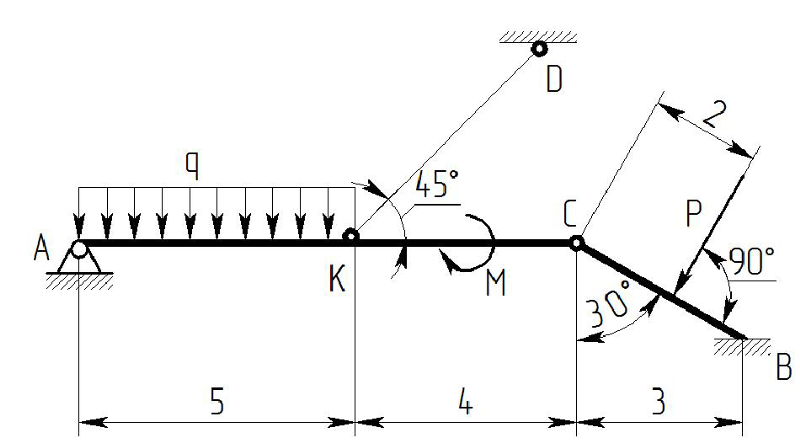 1P: Определить количество степеней свободы для каждого из показанных механизмов. Задача 10.2P: Однородный брусок веса W удерживается в равновесии парой С0. Найдите C0 через W, L и . Задача 10.3P: Стержни AB и AC механизма однородны с весом W каждый. Определить требуемую величину P… Задача 10.4P: Вес каждого однородного стержня механизма рычажный механизм равен W. Определите горизонтальную силу F, необходимую для… Задача 10.5P: Лодка массой 1800 кг подвешена на двух параллельных тросах одинаковой длины. Расположение центра… Задача 10.6P: Лампа массой 2,4 кг с центром тяжести в точке G поддерживается параллелограммным соединением… Задача 10.7P: Механизм состоит из двух однородных стержней с грузом. показано на рисунке. Определить горизонталь… Задача 10.8P: Для показанной рамы найти горизонтальную составляющую опорной реакции в точке B. Весами пренебречь… Задача 10.9P: Четырехзвенный механизм поддерживает однородный ящик веса W. Пренебрегая весом механизма,… Задача 10.10P Задача 10. 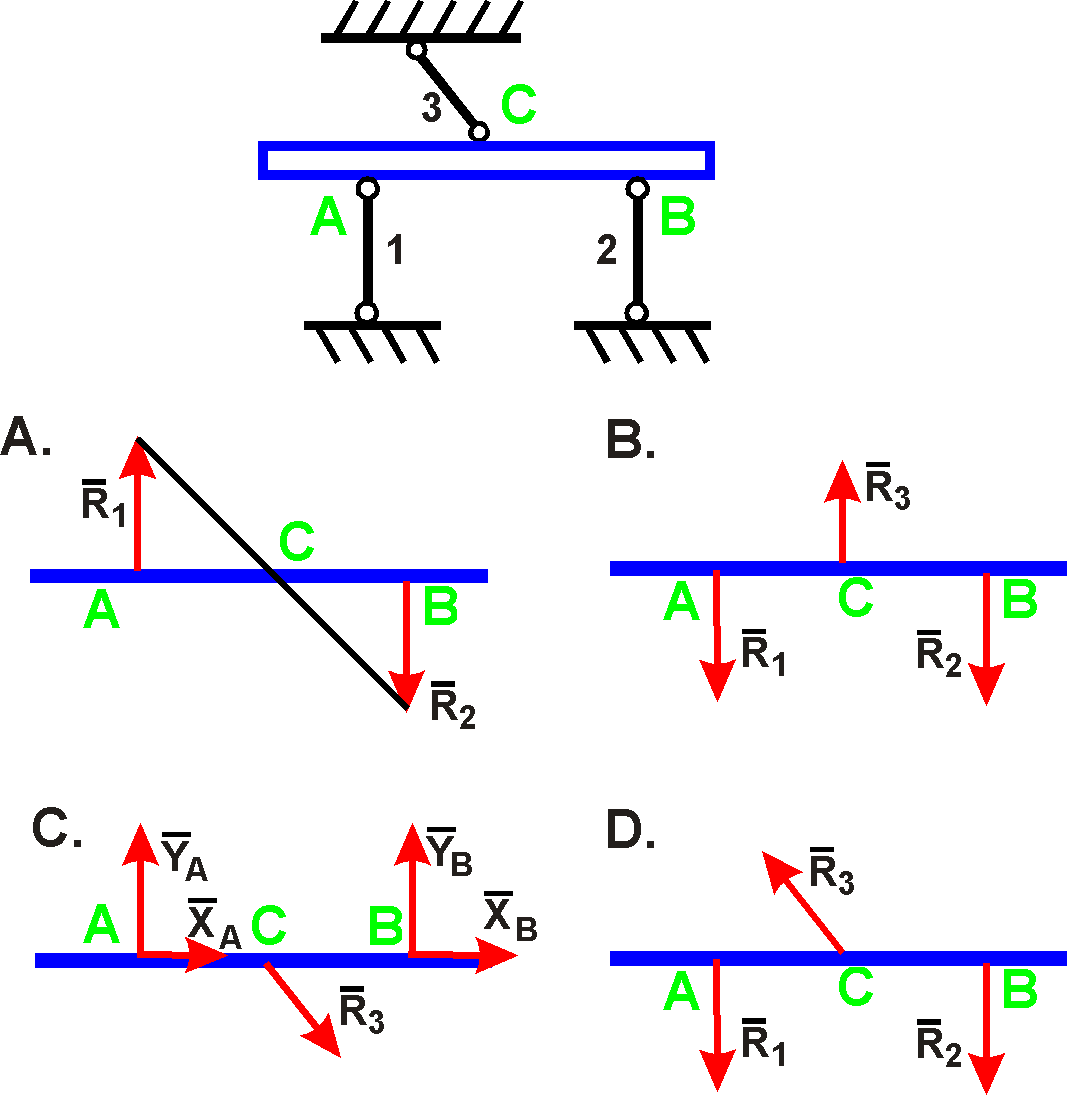11P: Определить отношение P/Q сил, необходимых для поддержания равновесия механизма для …Задача 10.12P: Найти вертикальную силу P, которая будет удерживать рычаг в положении =40. Пружина жесткости… Задача 10.13P: Рычажный механизм тормозной системы состоит из рычага педали DAB, шатуна BC и… Задача 10.14P: Автоматический буровой робот должен выдерживать тягу 32 фунта при кончик сверла. Определить… Задача 10.15P: Определить пару C, для которой механизм находился бы в равновесии в положении =25. Пренебрежение… Задача 10.16P: Домкрат-ножницы используются для подъема веса W. Определите пару C, необходимую для поддержки… Задача 10.17P Задача 10.18P: Рассчитайте крутящий момент C0, который должен быть приложен к рукоятке винта. домкрат, чтобы поднять… Задача 10.19P: Определите силу F и угол a, необходимые для удержания рычажного механизма в положении 1=60,=15. Каждая… Задача 10.20P: Найдите мгновенный центр вращения стержня AB для каждого показанного случая. Задача 10.21P Задача 10. 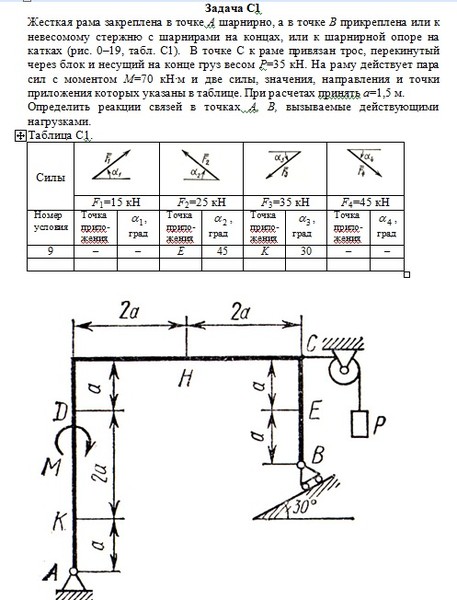22P: Определите силу P, которая будет удерживать механизм в равновесии в показанном положении. Задача 10.23P Задача 10.24P Задача 10.25 Задача 10.26P: Определите отношение P/Q, при котором рычажный механизм будет находиться в равновесии в показанном положении. Пренебрежение… Задача 10.27PПроблема 10.28PПроблема 10.29P: Если сила, подводимая к составному рычагу, равна P = 30 фунтов, рассчитайте выходную силу Q. Задача 10.30P: Определите реакцию ролика в точке F из-за приложенной силы P = 60 фунтов. PЗадача 10.35PЗадача 10.36P: Для показанных плоскогубцев определите соотношение между величиной приложенных сил P и… Задача 10.37P: При активации силой P захват см руки робота может захватывать объекты за применение… Задача 10.38P Задача 10.39P: Петля того типа, что используется в некоторых автомобилях, в которых дверь DE кажется вращающейся… Задача 10.40P: Пружина, прикрепленная к скользящему кольцу, способна выдерживать растяжение и сжатие. Пружина… Задача 10.41P: Груз W подвешен к концу B невесомого стержня, который опирается на стены в точках A и C. 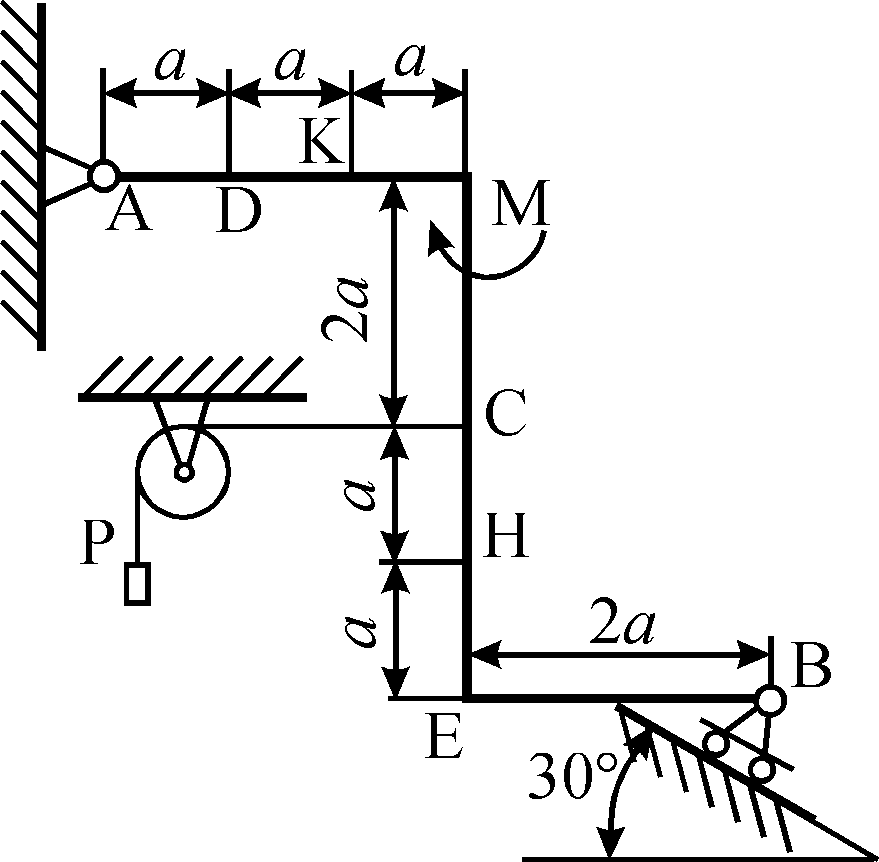… Задача 10.42P: Однородный стержень веса W и длины L = 1,8R лежит в полусферической полости радиуса R…. Задача 10.43П: Тонкий однородный стержень согнут под прямым углом и помещен на цилиндрическую поверхность. Определить… Задача 10.44P: Изображенное тело состоит из полусферы и цилиндра, причем оба имеют одинаковую плотность веса …. Задача 10.45P Задача 10.46P: Однородный стержень AB веса W и длины L прикреплен к скользящее кольцо в точке A и к скользящему… Задача 10.47P: Однородные стержни грузов W1 и W2 приварены к двум шкивам, соединенным ремнем…. Задача 10.48P Задача 10.49P: Полуцилиндр радиуса r расположен на цилиндрической поверхности радиуса R. При отсутствии проскальзывания… Задача 10.50P Задача 10.51P: Пружина, прикрепленная к однородному стержню веса W, не деформируется при =0. Определить наименьший… Задача 10.52P: Пружина соединена с веревкой, которая проходит по цилиндрической поверхности и прикреплена к углу… Задача 10.53P: Найти положения равновесия 30-фунтового однородного стержня и исследовать их устойчивость . Задача 10.54P: Механизм незначительного веса поддерживает вес W. Найдите значение для равновесия. Является ли… Задача 10.55P: Решите Prob. 10.54, предполагая, что A и B соединены пружиной жесткости k = 0,3 Вт/b и свободны… Задача 10.56P: Жесткость идеальной пружины, сжатой ползунком C, равна k = 250 Н/м. Пружина… Задача 10.57P: Найдите устойчивое положение равновесия системы, описанной в Prob. 10,56, если m = 2,06 кг. Задача 10.58P: Однородный брусок AB весом W = kL находится в равновесии, когда =65. Найдите значение, для которого… Задача 10.59P: Вес однородного стержня AB равен W. Жесткость идеальной пружины, прикрепленной к B, равна k, и… Задача 10.60P: Невесомые стержни AB и CE вместе с грузом BE весом 5 фунтов образуют связь параллелограмма. Задача 10.61PЗадача 10.62P: Стержень ABC поддерживается тремя одинаковыми идеальными пружинами. Обратите внимание, что пружины всегда… format_list_bulleted

равновесие — Существуют ли силы реакции, действующие на невесомые соединительные стержни?

спросил 1 год, 8 месяцев назад

Изменено 1 год, 8 месяцев назад

Просмотрено 89 раз

$\begingroup$

На уроке прикладной математики наш учитель сказал нам, что на невесомые соединенные стержни не действуют силы реакции. Но ,

, как на этом рисунке, у меня есть невесомый стержень (AB), прикрепленный к стене с помощью A, и (BC) стержень, который имеет вес W, удерживается в равновесии с горизонтальной силой T. Мой вопрос заключается в том, что если нет сил реакции с невесомым стержнем (я показал эти силы как x и y), при рассмотрении системы BC, как стержень BC останется в равновесии.

Извините, если это глупый вопрос… Я знаю, что невесомые стержни идеальны, но мне нужно пояснение по этому поводу…

• силы
• равновесие

$\endgroup$

$\begingroup$

Дело не в том, что на стержень не действуют никакие силы, а в том, что результирующая сила должна быть равна нулю, иначе стержень (будучи предположительно невесомым и невесомым) мгновенно разогнался бы до бесконечной скорости.

Так как этого не происходит (стержень прикреплен к стене на шарнире), мы знаем, что сила, действующая на стержень со стороны шарнира, должна точно уравновешивать силу, действующую на стержень со стороны второго, утяжеленного, стержня.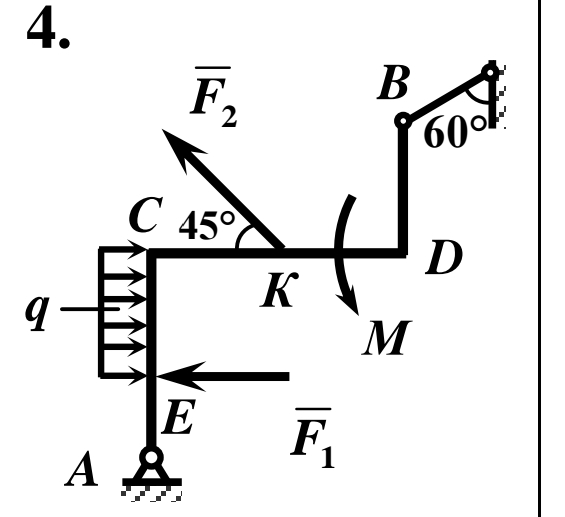

Зная это, нет смысла делать какие-либо расчеты для определения сил, действующих на невесомый (и невесомый) стержень.

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.