Как определить реакции опор?
Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:
На балку давит нагрузка – сила, в свою очередь, балка давит на опоры.
И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.
Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка
Жёсткая заделка — это один из вариантов закрепления элементов конструкций.
Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).
Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.
В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.
Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо.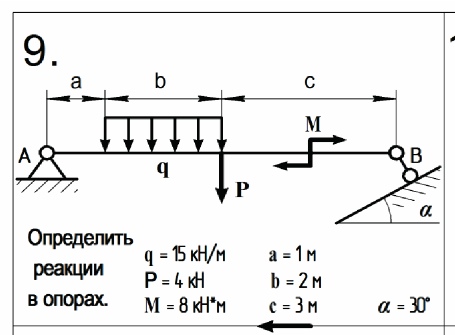
Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:
На изображении показано, как определить момент силы F, относительно точки O.Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.
Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:
Введём систему координат: направим ось x вдоль балки, а ось y вертикально.
Обозначим реакции в опорах как HA, RA и RB:
Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:
Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:
Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.
Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо.
И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:
Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:
Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:
Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы.
Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:
Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:
Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).
Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:
Покажем реакции в заделке и выполним расчёт:
Для этой задачи выгоднее использовать другую форму условий равновесия:
А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением.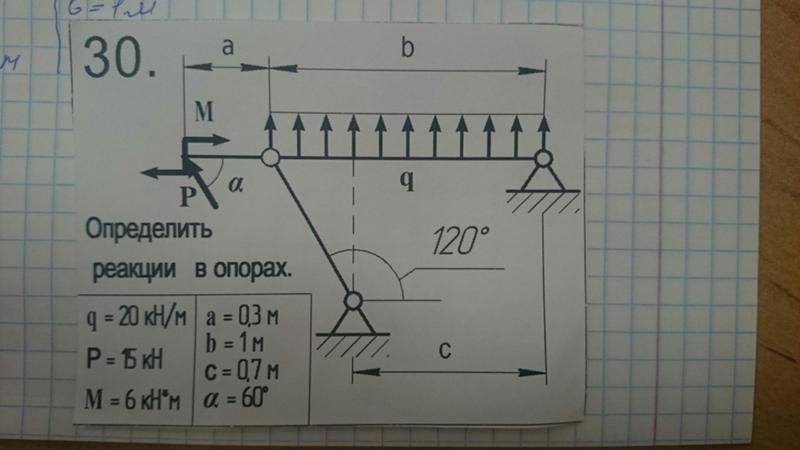
Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:
С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.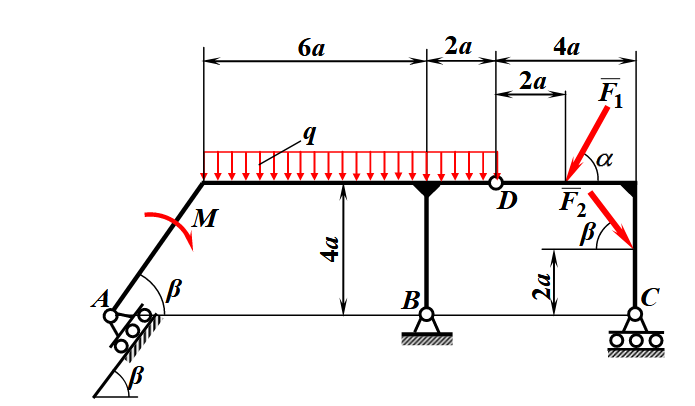
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:
Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.
Выполняем расчёт реакций опор:
Меняем направление реакции RA:
Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:
Как видим, расчет реакций выполнен правильно!
Задание С.3. Определение реакций опор составной конструкции (система двух тел)
Страница 1 из 29
Конструкция состоит из двух частей. Установить, при каком способе соединения частей конструкции модуль реакции, указанной в таблице, наименьший, и для этого варианта соединения определить реакции опор, а также соединения С.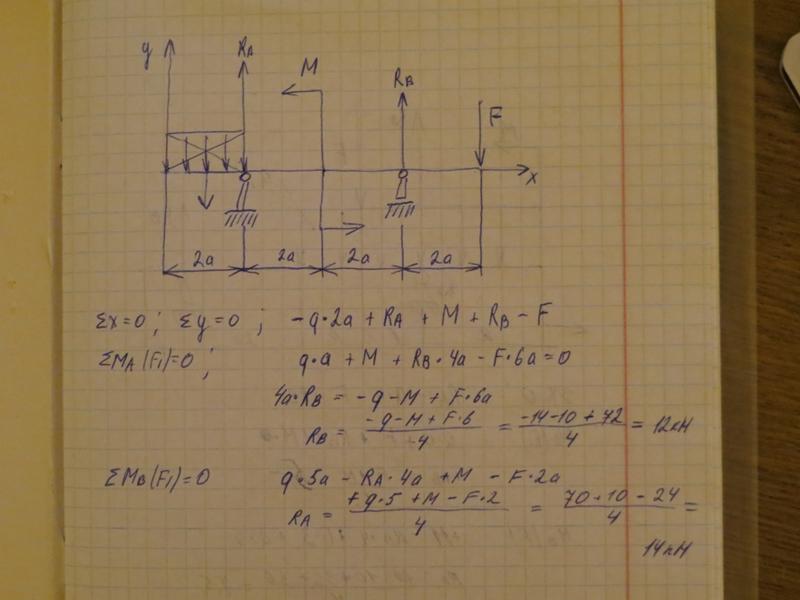
На рисуке показан первый способ соединения — с помощью шарнира С. Второй способ соединения — с помощью скользящей заделки, схемы которой показаны в таблице.
Номер варианта | P1 | P2 | M, кН • м | q, кН/м | Исследуемая реакция | Номер варианта | P1 | P2 | M, кН • м | q, кН/м | Исследуемая реакция |
кН | кН | ||||||||||
1 | 5,0 | — | 24,0 | 0,8 | ХА | 16 | 7,0 | 10,0 | 14,0 | 3,8 | Rb |
2 | 6,0 | 10,0 | 22,0 | 1,0 | Ra | 17 | 9,0 | 12,0 | 26,0 | 4,0 | Ra |
3 | 7,0 | 9,0 | 20,0 | 1,2 | Rb | 18 | 11,0 | 10,0 | 18,0 | 3,5 | Мв |
4 | 8,0 | — | 18,0 | 1,4 | МА | 19 | 13,0 | 9,0 | 30,0 | 3,0 | Мв |
5 | 9,0 | — | 16,0 | 1,6 | Ra | 20 | 15,0 | 8,0 | 25,0 | 2,5 | Rb |
6 | 10,0 | 8,0 | 25,0 | 1,8 | Ма | 21 | 10,0 | 7,0 | 20,0 | 2,0 | Ra |
7 | 11,0 | 7,0 | 20,0 | 2,0 | Rb | 22 | 5,0 | 6,0 | 15,0 | 1,5 | Ra |
8 | 12,0 | 6,0 | 15,0 | 2,2 | МА | 23 | 8,0 | 5,0 | 10,0 | 1,4 | Ra |
9 | 13,0 | — | 10,0 | 2,4 | Ха | 24 | 11,0 | 4,0 | 5,0 | 1,3 | Ma |
10 | 14,0 | — | 12,0 | 2,6 | Ra | 25 | 14,0 | 6,0 | 7,0 | 1,2 | Rb |
11 | 15,0 | 5,0 | 14,0 | 2,8 | Rd | 26 | 12,0 | 8,0 | 9,0 | 1,1 | Rb |
12 | 12,0 | 4,0 | 16,0 | 3,0 | Rb | 27 | 10,0 | 7,0 | 11,0 | 1,0 | Xa |
13 | 9,0 | 6,0 | 18,0 | 3,2 | Ra | 28 | 8,0 | 9,0 | 13,0 | 1,2 | Ra |
14 | 6,0 | — | 20,0 | 3,4 | MA | 29 | 6,0 | 10,0 | 15,0 | 1,4 | Ma |
15 | 5,0 | 8,0 | 22,0 | 3,6 | Mb | 30 | 10,0 | 12,0 | 17,0 | 1,6 | Mb |
Вариант 1
Ошибка в тексте? Выдели её мышкой и нажми CTRL + Enter
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
Помог сайт? Ставь лайк!
Опоры: разные типы и расчет их реакции
Последнее обновление: 8 ноября 2022 г.
Мост Золотые Ворота, Эйфелева башня и скучная бетонная плита над головой имеют несколько общих черт.
Одна из этих вещей заключается в том, что все они имеют достаточную структурную поддержку — совершенно по-разному и в разных размерах, но все структуры рухнули бы, если бы их не было.
Хорошо, это крайние примеры, НО: все структурные опоры — большие и малые конструкции — следуют одним и тем же принципам.
Итак, в этой статье мы узнаем, что такое несущие конструкции, какие типы опор используются и как рассчитать силы реакции опор.
Начнем.
🙋♂️ Что такое (структурные) опоры?
Опоры в конструкциях обеспечивают передачу нагрузок, действующих на поддерживаемую конструкцию, на следующий элемент, например, фундамент, колонну и т. д.
Давайте рассмотрим пример.
Скамья: деревянные балки, поддерживаемые стальной пластиной.О деревянных «балках» скамейки и ее опорах можно сказать следующее
- Статическая система деревянных балок представляет собой просто опертую балку
- Нагрузки на балку представляют собой собственный вес балок и люди (постоянная нагрузка) и снеговая нагрузка
- Эти нагрузки проходят через балку и к опорам
- Опоры представляют собой роликовую и штифтовую опору (подробнее об этом далее в статье)
- Опорные усилия равны внешним нагрузкам (подробнее об этом позже)
- Опорные силы передаются следующей конструкции (стальной пластине/кронштейну)
Теперь опоры должны выдерживать опорную силу.
Если стальные пластины (опоры) не выдерживают опорной силы, конструкция (скамейка) разрушается.
Если стальные пластины (опоры) не выдерживают опорной силы, конструкция (скамейка) разрушается.Далее в этой статье вы узнаете, как рассчитать опорные силы и какие различные типы используются при проектировании конструкций.
Ежедневный Пример
Большинство элементов на этой земле не двигаются, потому что они каким-то образом поддерживаются структурой.
Давайте рассмотрим пример.
Пример яблока для демонстрации отказа поддержки.Это яблоко, например, достаточно поддерживается столом и поэтому никуда не движется.
Слово достаточно играет здесь роль.
Поскольку, как только внешние нагрузки, действующие на элемент, превышают силы реакции, которые может принять опора, опоры разрушатся, или элемент будет вращаться или «соскальзывать».
В примере с нашим яблоком нам нужно лишь приложить небольшой груз сбоку к яблоку, и оно соскользнет.
В этом сценарии нагрузка больше, чем могут выдержать силы горизонтальной реакции.
🙆 Различные типы опор
Для каждой конструкции требуются разные опоры, так как выбор опоры оказывает большое влияние на поведение конструкции.
Благодаря опорам конструкция может быть жесткой, гибкой, жесткой – не только опора, но и ее влияние.
Например, жесткая рама, как уже следует из названия, довольно жесткая по сравнению с рамой с двумя шарнирами, что допускает гораздо большую деформацию и прогиб.
1. Штифтовая опора
Штифтовая опора
Штифтовые опоры допускают 2 силы реакции, горизонтальную и вертикальную, и допускают вращение. Это означает, что Момент на опоре булавки равен 0. Но будьте осторожны.
Это только в том случае, если также используется шарнир, а НЕ в случае сплошной балки.
Static Systems
Simply supported beam, Columns, Continuous beams
Reactions
Horizontal $R_x$, Vertical $R_z$
Examples
Bridge bearings, Wood beam supports и т. д.
Давайте углубимся и посмотрим на примеры Static System, где используются штифтовые опоры.
Примеры
Просто поддерживаемая балка (1 штифтовая опора)
Пример: Штифтовая опора используется в свободно опертой балке. Горизонтальная и вертикальная сила реакции.
Деревянная стропильная крыша (2 штифтовых опоры)
Пример: Штифтовая опора, используемая в статической системе стропильной крыши. Горизонтальные и вертикальные силы реакции на обеих опорах.Деревянная стропильная крыша (1 штифтовая опора)
Пример: Штифтовая опора, используемая в статической системе стропильной крыши. Горизонтальные и вертикальные силы реакции на штифтовые опоры.2. Роликовая опора
Роликовая опора
Роликовые опоры допускают только 1 силу реакции, горизонтальную ИЛИ вертикальную, а также допускают вращение. Момент на роликовой опоре равен 0. В свободно опертой балке на роликовую опору действует вертикальная сила реакции, а в колонне реакция представляет собой горизонтальную силу. Мы покажем примеры этого позже.
Статические системы
Простые поддерживаемые луча, колонны, непрерывные балки
Реакции
Horizontal $ R_X $ OR (❗).
Опоры деревянных балок и т. д.
Давайте углубимся и посмотрим на примеры Static System, в которых используются роликовые опоры.
Примеры
Просто поддерживаемая балка (1 роликовая опора)
Пример: Роликовая опора используется в свободно опертой балке. Сила вертикальной реакции.Колонна (1 роликовая опора)
Пример: роликовая опора, используемая в статической системе колонны. Горизонтальная сила реакции на ролике.Неразрезная балка (2+ роликовые опоры)
Пример: Роликовая опора, используемая в статической системе неразрезной балки. Вертикальные силы реакции на обоих роликах.❗Обратите внимание, что балка на средней опоре воспринимает изгибающие моменты.
В информационном блоке мы узнали, что роликовая опора не воспринимает изгибающие моменты, и это правда.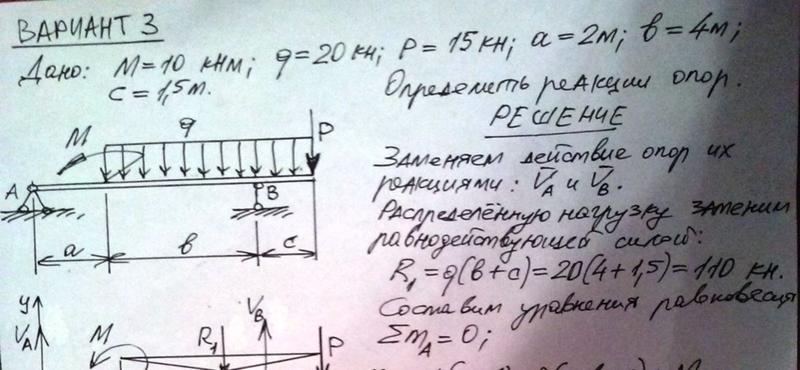
НО балка не разделена на 2 части и не соединена между собой шарниром роликовой опоры. Это одна сплошная деталь, и поэтому она может воспринимать изгибающие моменты.
Деревянная ферменная крыша (1 роликовая опора)
Пример: Штифтовая опора, используемая в статической системе ферменной крыши. Горизонтальные и вертикальные силы реакции на штифтовые опоры.3. Фиксированная опора
Фиксированная опора
Фиксированные опоры допускают 3 силы реакции, горизонтальную и вертикальную силу реакции и момент. Таким образом, фиксированная опора не позволяет свободно вращаться. Неподвижная опора часто используется для повышения прочности, получения неподдерживаемых пролетов, таких как свесы крыши, или для ограничения деформаций конструкции.
Static Systems
Cantilever beam, Rigid frame
Reactions
Horizontal $R_x$, Vertical $R_z$ and Moment $M_R$
Examples
Cantilever balconies , Стальные каркасные конструкции, монолитные бетонные опоры и т.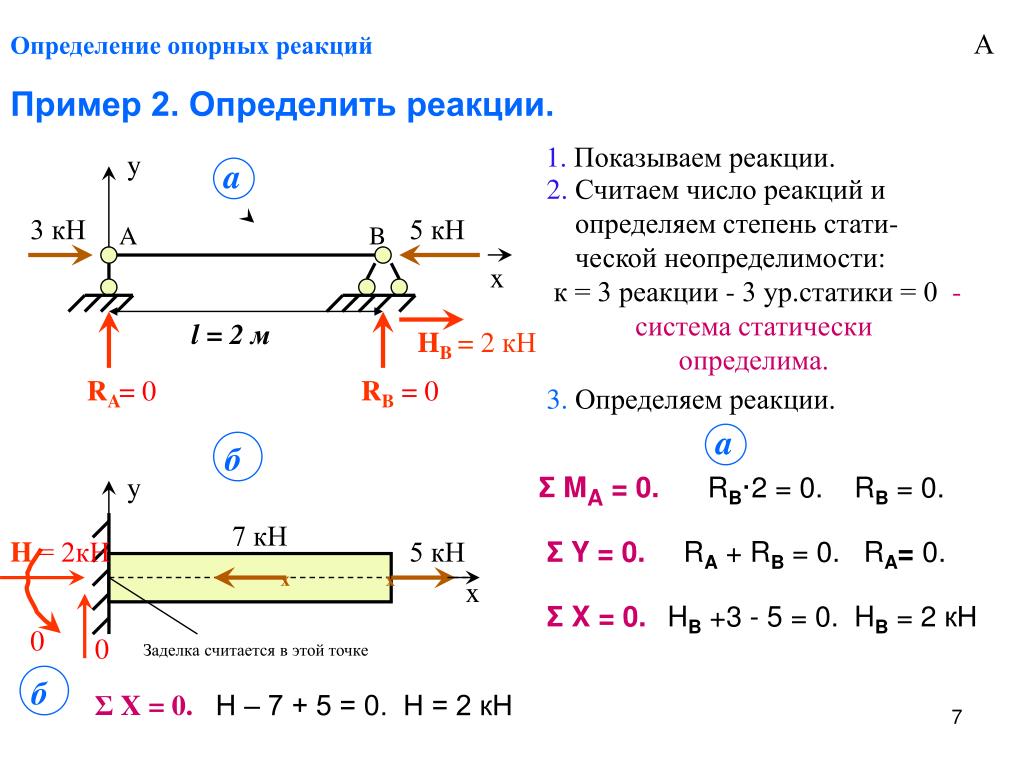
д.
Давайте углубимся и рассмотрим примеры статической системы, в которых используются фиксированные опоры.
Примеры
Консольная балка (1 фиксированная опора)
Пример: Неподвижная опора, используемая в консольной балке. Вертикальная и горизонтальная реактивная сила и момент.Жесткая рама (2 фиксированные опоры)
Пример: роликовая опора, используемая в статической системе колонн. Горизонтальная сила реакции на ролике.Бетонное ядро высотного здания (1 фиксированная опора) – вертикальная консоль
Пример: роликовая опора, используемая в статической системе неразрезной балки. Вертикальные силы реакции на обоих роликах.4. Пружинная опора
Пружинная опора
Пружинные опоры допускают 1 Силу Реакции, однако опора может быть также дополнительно ограничена в другом направлении или вращении.
Кроме того, можно добавить еще одну пружину, если этого требует конструкция. В примере с вантовым мостом (внизу) пружинная опора ведет себя аналогично роликовой опоре. Основное отличие состоит в том, что пружинная опора позволяет деке (прогибаться), а каток — нет. Следовательно, вертикальная сила реакции пружинной опоры меньше, чем у роликовой опоры.
Static Systems
Beam supported by cables, beam/column supported by foundation/earth
Reactions
Horizontal $R_x$, Vertical $R_z$ and Moment $M_R$
Примеры
Вантовый мост (кабели), высотный монолитный бетонный сердечник, опирающийся на (свайный) фундамент
Давайте углубимся и посмотрим на примеры статической системы, где Пружинные опоры используются.
Примеры
Вантовый мост
Для расчета изгибающего момента в настиле вантового моста тросы, поддерживающие настил, можно смоделировать как пружинную опору с пружинной жесткостью соответствующего троса.
2D-эскиз вантового моста
Эскиз вантового моста.Статическая система настила моста (приблизительно)
Пример: Статическая система вантового настила моста. Кабели аппроксимируются пружинными опорами.В самом первом приближении тросы можно смоделировать как пружинные опоры.
Теперь, когда мы показали все различные типы опор и объяснили их на множестве различных примеров, следующим шагом является расчет сил реакции.
📖 Как рассчитать силы реакции опор
Чтобы рассчитать силы реакции, нам сначала нужно знать, является ли конструкция статически определимой или неопределимой.
Для статически определимых конструкций силы реакции можно рассчитать с помощью 3 уравнений равновесия.
- $\sum H = 0$: Сумма всех горизонтальных внешних нагрузок и сил реакции равна 0.
- $\sum V = 0$: Сумма всех вертикальных внешних нагрузок и сил реакции равна 0.
- $ \sum M = 0$: сумма всех моментов равна 0.
Для статически неопределимых конструкций необходимо использовать более совершенные методы для расчета сил реакции, такие как метод силы.
В этом уроке мы рассмотрим только статически определяемые конструкции.
Пример – стропильная крыша
Выбранная статическая система имеет 2 шарнирные опоры A и B. Каждая из них имеет горизонтальную и вертикальную реактивную силу.
2 внешние силы Q – вертикальная точечная нагрузка – и P – горизонтальная точечная нагрузка – действуют на статическую систему.
Q = 2 кН
P = 3 кН
Начнем с определения трех уравнений равновесия.
$\sum H = 0: A_x – B_x – P = 0$
$\sum V = 0: A_z + B_z – Q = 0$
Момент в определенной точке статической системы от внешней нагрузки рассчитывается как
Нагрузка $\cdot$ Расстояние до точки.
Мы выбираем момент равновесия в точке A.
$\sum M = 0: B_z \cdot 8m + P \cdot 3m – Q \cdot 4m = 0$
Единственное уравнение, в котором мы имеем только 1 Неизвестен момент равновесия. Поэтому сначала решим это уравнение.
$B_z = \frac{Q \cdot 4м – P \cdot 3м}{8м} = \frac{2 кН \cdot 4м – 3 кН \cdot 3м}{8м} = -0,125кН$
Отсюда мы можем вычислить $A_z$
$\sum V = A_z + B_z – Q = 0$
$A_z = 0,125 кН + 2 кН = 2,125 кН$
Чтобы получить две горизонтальные силы реакции $A_h $ и $A_v$ мы определяем еще один момент равновесия в верхнем шарнире, но только с учетом левой балки.
Момент равновесия в верхней петле. Расчет горизонтальной силы реакции.$\sum M = 0: A_x \cdot 3m – A_z \cdot 4m = 0$
$A_x = 2,125кН \cdot \frac{4m}{3m} = 2,83 кН$
$A_x$ вставляется в уравнение горизонтального равновесия, чтобы получить $B_x$.
Уравнение горизонтального равновесия
$\sum H = 0: A_x – B_x – P = 0$
$A_x – B_x – P = 0$
$B_x = 2,83 кН – P = -0,17 кН$
Теперь мы успешно рассчитали все 4 силы реакции поддержки.
$A_z = 2,125 кН$
$A_x = 2,83 кН$
$B_z = -0,125 кН$
$B_x = -0,17 кН$
Теперь, когда все силы реакции вычислены и рассчитаны, мы можем двигаться дальше. рассчитайте внутренние силы элементов, как мы это делали в этих статьях
- Свободно опертая балка
- Консольная балка
- Арочная конструкция
После определения внутренних сил можно рассчитать элементы так, как мы делали это в следующих статьях.
- Расчет деревянных балок крыши
- Расчет устойчивости деревянных колонн
- Расчет устойчивости ригеля
А теперь я хотел бы узнать от вас, поняли ли вы концепцию 3 уравнений равновесия?
Потому что я помню, что мне понадобился почти весь 1-й семестр, чтобы по-настоящему понять, как рассчитывать моменты и делить силы на горизонтальную и вертикальную составляющие.
Так что дайте нам знать в комментариях✍️
3.4: Расчет опорных реакций для плоских конструкций
Опорные реакции для статически определимых и устойчивых конструкций на плоскости определяются с помощью уравнений равновесия. Процедура расчета описана ниже.
Процедура расчета опорных реакций
- Нарисуйте диаграмму конструкции в свободном теле, указав все неизвестные реакции с помощью стрелочной диаграммы.
- Проверьте устойчивость и определенность конструкции, используя уравнение 3.3 или 3.4. Если структура классифицируется как детерминированная, приступайте к анализу.
- Определите неизвестные реакции, применяя три уравнения равновесия. Если расчетная реакция приводит к отрицательному ответу, первоначально предполагаемое направление неизвестной реакции, как показано стрелкой на диаграмме свободного тела, неверно и должно быть исправлено, чтобы показать противоположное направление. После внесения поправки величина силы должна быть указана в виде положительного числа в скорректированном наконечнике стрелки на диаграмме свободного тела 9. 0028
0028Пример 3.3
На консольную балку действует равномерно распределенная нагрузка и наклонная сосредоточенная нагрузка, как показано на рис. 3.9а. Определить реакции на опоре A .
\(рис. 3.9\). Балка
Решение
Диаграмма свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.9b. Опорные реакции, как показано на диаграмме свободного тела, равны \(A_{y \prime}\) \(A_{y \prime}\) и \(M\).
Расчет реакций. Перед расчетом опорных реакций распределенную нагрузку следует заменить единой равнодействующей силой, а наклонную нагрузку разложить на вертикальную и горизонтальную составляющие. Величина равнодействующей силы равна площади под прямоугольной нагрузкой и действует через центр тяжести прямоугольника. Как видно на рис. 3.9c, \(P=[(4 \mathrm{kN} / \mathrm{m})(2 \mathrm{m})]\), и его расположение находится в центре тяжести прямоугольной нагрузки \ (=\left[\left(\frac{1}{2}\right)(2 \mathrm{m})\right]\).
Пример 3.4
Простая балка длиной 12 футов несет равномерно распределенную нагрузку в 2 тысячи фунтов на фут по всему пролету и сосредоточенную нагрузку в 8 тысяч фунтов в середине пролета, как показано на рис. 3.10a. Определить реакции в опорах \(A\) и \(B\) балки.
\(рис. 3.10\). Простой луч.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.10b.
Расчет реакций. Распределенная нагрузка сначала заменяется единой равнодействующей силой, как показано на рис. 3.10c. Величина равнодействующей силы равна площади прямоугольного нагружения (распределенная сила). Таким образом, \(P=[(2 \mathrm{k} / \mathrm{ft})(12 \mathrm{ft})]\), и его расположение находится в центре тяжести прямоугольной нагрузки \(=\left[ \left(\frac{1}{2}\right)(12 \mathrm{ft})\right]\) Поскольку в этом примере нагрузка симметрична, реакции на обоих концах балки равны, и их можно определить с помощью уравнений статического равновесия и принципа суперпозиции следующим образом:
\(\begin{array}{l} +\стрелка вверх \sum F_{y}=0 \\ A_{y}=B_{y}=\left(\frac{2 \times 12}{2}\ справа)+\frac{2}{2}=13 \mathrm{kips} \\
Пример 3.
5
Балка с выступом подвергается переменной нагрузке, как показано на рис. 3.11а. Определить реакции на опорах \(A\) и \(B\).
\(рис. 3.11\). Балка с навесом.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.11b.
Расчет реакций. Обратите внимание, что распределенная нагрузка в балке треугольная. Распределенная нагрузка сначала заменяется единой равнодействующей силой, как показано на рис. 3.11c. Величина единой равнодействующей силы равна площади под треугольным нагружением. Таким образом, \(\rho=\left(\frac{1}{2}\right)(6 \mathrm{m})(10 \mathrm{kN} / \mathrm{m})\), а его центроид равен в центре загрузки (6м). Применение уравнений равновесия дает следующее:
\(\begin{array}{l} \curvearrowleft+\sum M_{A}=0 \\ -\left(\frac{1}{2}\right)(10)(6)(3)+3 B=0 \\ B_{y}=30 \mathrm{kN} \quad \quad B_{y}=30 \mathrm{kN} \\ \uparrow+\sum F_{y}=0 \\ 30+A_{y }-\left(\frac{1}{2}\right)(6)(10)=0 \quad \mathrm{A}_{\mathrm{y}}=0\\ \rightarrow+\sum \mathrm{ F} _ {\ mathrm {x}} = 0 \\ \ mathrm {A} _ {\ mathrm {x}} = 0 \ quad \ quad \ mathrm {A} _ {\ mathrm {x}} = 0 \ end {массив}\)
Пример 3.
6
Балка с выступающими концами выдерживает три сосредоточенные нагрузки в 12 тысяч фунтов, 14 тысяч фунтов и 16 тысяч фунтов и момент 100 тысяч фунтов на фут, как показано на рисунке 3.12a. Определить реакции на опорах
\(рис. 3.12\). Брус с выступающими концами.
Решение
Схема свободного тела. Диаграмма свободного тела балки показана на рисунке 3.12b.
Расчет реакций. Применение уравнений равновесия дает следующее:
\(\begin{array}{l} +\curvearrowleft M_{A}=0 \\ -100+12(2)-14(2)-16(8)+ 4 B_{y}=0 \\ B_{y}=58 \text { тыс.фунтов } \quad \quad B_{y}=58 \text { тыс.фунтов } \uparrow \\ +\uparrow \sum F_{y}=0 \\ 58+A_{y}-12-14-16=0 \quad A_{y} = 26 \text { тысяч фунтов } \uparrow\\ +\rightarrow \sum F_{x}=0 \\ A_{x} =0 \quad \quad A_{x} \end{массив}\)
Пример 3.7
Составная балка подвергается нагрузкам, показанным на рис. 3.13а. Найти опорные реакции в точках \(A\) и \(B\) балки.
\(рис.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.13b.
Идентификация основных и дополнительных структур. Для правильного анализа составной структуры необходимо идентифицировать основные и дополнительные части структуры для правильного понимания их взаимодействия. Взаимодействие этих частей показано на рис. 3.13c. Первичная конструкция — это часть составной конструкции, которая может выдерживать приложенную внешнюю нагрузку без помощи дополнительной конструкции. С другой стороны, дополнительная конструкция является частью составной конструкции, которая зависит от основной конструкции для поддержки приложенной внешней нагрузки. Для данной структуры часть \(AC\) является первичной структурой, а часть \(CB\) является дополнительной структурой.
Расчет реакций. Анализ сложной структуры всегда должен начинаться с анализа дополнительной структуры, поскольку дополнительная структура поддерживается первичной структурой.
Расчет комплементарной конструкции \(CB\) .
Расчет опорной реакции. Диаграмма изолированного свободного тела комплементарной структуры показана на рис. 3.13c. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), которая равна площади прямоугольной нагрузки, как показано на рис. 3.13d и рис. 3.13e. Применяя уравнения равновесия и учитывая, что из-за симметрии нагрузки опорные реакции в точке C и B равны по величине, дает следующее:
\(\begin{array}{l} +\стрелка вверх \sum F_{y}=0 \\ B_{y}=C_{y} =\frac{10(7)}{2}=35 \mathrm{кН} \quad B_{y}=\mathrm{C}_{y}=\frac{10(7)}{2}=35 \ mathrm{k} \end{array}\)
Анализ первичной структуры \(AC\) .
Расчет опорной реакции. Заметим, что до расчета реакций реакция в точке \(С\) дополнительной структуры прикладывается к основной структуре в качестве нагрузки.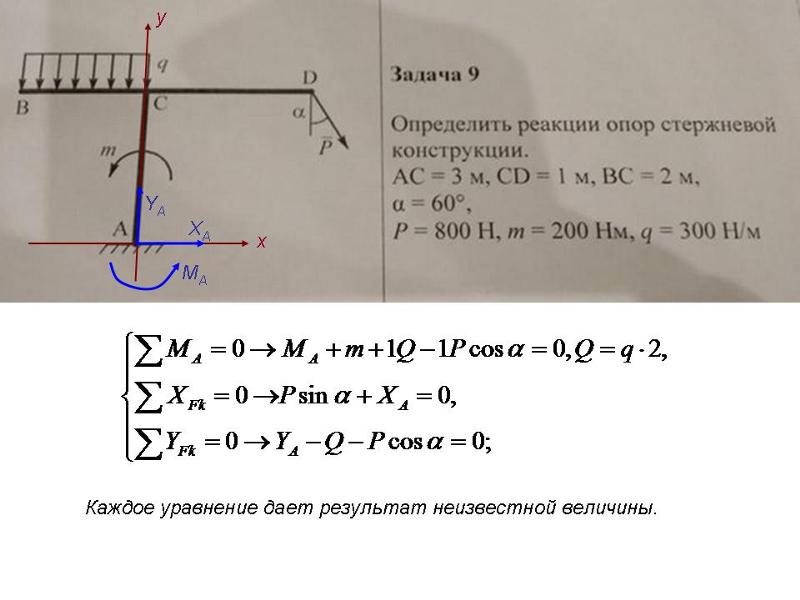
Величина приложенной нагрузки такая же, как и у комплементарной конструкции, но противоположна по направлению. Применение уравнений равновесия предполагает следующее: \(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ -25(2)-35(4)+M_{A}=0 \ \
M_{A}=190 \mathrm{kN} \cdot \mathrm{m} \quad M_{A}=190 \mathrm{kN} \cdot \mathrm{m} \curvearrowleft \\ +\uparrow \sum F_{ y}=0 \\ \mathrm{A}_{\mathrm{y}}-25-35=0 \\ \mathrm{A}_{\mathrm{y}}=60 \mathrm{kN} \quad \ mathrm{A}_{\mathrm{y}}=60\mathrm{kN} \uparrow\\ +\rightarrow\sum\mathrm{F}_{\mathrm{x}}=0 \\ \mathrm{A} _ {\ mathrm {x}} = 0 \ quad \ mathrm {A} _ {\ mathrm {x}} = 0 \ конец {массив} \)
Пример 3.8
Найдите реакции опор \(A\), \(C\) и \(E\) составной балки, несущей равномерно распределенную нагрузку 10 тысяч фунтов/фут по всей длине, как показано на рис. 3.14a.
Рис. 3.14. Составной луч.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.14b.
Идентификация основных и дополнительных структур. Диаграмма взаимодействия для данной структуры показана на рис. 3.14в. AB является основной структурой, а BD и DE являются дополнительными структурами.
Расчет реакций.
Анализ дополнительной структуры \(DE\) .
Расчет опорной реакции. Диаграмма изолированного свободного тела показана на рис. 3.14c. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)) равной площади прямоугольной нагрузки, как показано на рис. 3.14d. Применяя уравнения равновесия и отмечая, что из-за симметрии нагрузки опорные реакции в точках \(D\) и \(E\) равны по величине, можно сделать следующее:
\(\begin{array}{ l} +\стрелка вверх \sum F_{y}=0 \\ D_{y}=E_{y}=\frac{10(8)}{2}=40 \mathrm{kips} \quad E_{y}= 40 \mathrm{kips} \uparrow \end{массив}\)
Анализ дополнительной структуры \(BD\) .
Расчет опорной реакции. Диаграмма изолированного свободного тела показана на рисунке 3.
14e. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), равной площади прямоугольной нагрузки, как показано на рис. 3.14f. Нагрузка от комплементарной конструкции приложена в точке \(D\). Применение уравнений равновесия предполагает следующее:
\(\begin{array}{l} +\curvearrowleft \sum M_{B}=0 \\ -10(8)\left(\frac{8}{2} \right)-40(8)+4 C_{y}=0 \\ C_{y}=160 \text { тысяч фунтов } \quad C_{y}=160 \text { тысяч фунтов } \uparrow \\ +\uparrow \ сумма F_{y}=0 \\ 160-B_{y}-10(8)-40=0 \\ B_{y}=40 \text { тыс.фунтов } \end{array}\)
Анализ первичной структуры \(AB\) .
Расчет опорной реакции. Заметим, что до расчета реакций равномерная нагрузка заменяется единой равнодействующей силой, а реакция в точке \(B\) дополнительной конструкции прикладывается к основной конструкции как нагрузка. Применение требования равновесия дает следующее:
\(\begin{array}{l} \quad+\curvearrowleft \sum M_{A}=0 \\ \mathrm{M}-10(10)\left(\frac{ 10}{2}\right)+40(10)=0 \\ M_{A}=100 \mathrm{kips} .
\mathrm{ft} \quad \quad M_{A}=100 \mathrm{kips} . \mathrm{ft} \curvearrowleft \\ +\uparrow \sum F_{y}=0 \\ A_{y}-10(10)+40=0 \\ A_{\mathrm{y}}=60 \mathrm{ тысяч фунтов} \quad \quad A _{\mathrm{y}}=60 \mathrm{kips} \uparrow\\ +\rightarrow \sum \mathrm{F}_{\mathrm{x}}=0 \\ A_{x }=0 \quad \quad A_{x}=0 \end{массив}\)
Пример 3.9
Найдите реакции опор \(A\), \(B\), \(E\) и \(F\) нагруженной составной балки, как показано на рис. 3.15а.
\(рис. 3.15\). Составной луч.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.15b.
Идентификация основной и дополнительной структуры. Диаграмма взаимодействия для данной структуры показана на рис. 3.15в. \(CD\) является дополнительной структурой, а \(AC\) и \(DF\) являются первичными структурами.
Расчет реакций.
Анализ дополнительной структуры \(CD\) .
Расчет опорной реакции. Диаграмма изолированного свободного тела показана на рис.
3.15c. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), равной площади прямоугольной нагрузки, как показано на рис. 3.15d. Применяя уравнения равновесия и отмечая, что из-за симметрии в нагружении опорные реакции в точках \(C\) и \(D\) равны по величине, можно сделать следующее:0003
\(\begin{array}{l} +\стрелка вверх \sum F_{y}=0 \\ C_{y}=D_{y}=\frac{10(4)}{2}=20 \mathrm {kN} \end{array}\)
Анализ первичной структуры \(AC\) .
Расчет опорной реакции. Обратите внимание, что реакция в \(AC\) комплементарной структуры применяется как направленная вниз сила той же величины в той же точке первичной структуры. Применение уравнения равновесия предполагает следующее:
\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ -24(2)-20(5.5)+4 B_{y} =0\В_{у}=39.5 \mathrm{kN} \quad \quad B_{y}=39,5 \mathrm{kN} \uparrow\\ +\uparrow \sum F_{y}=0 \\ \mathrm{A}_{y}+39,5 -24-20=0 \\ A_{y}=4,5 \mathrm{kN} \quad \quad A_{y}=4,5 \mathrm{kN} \стрелка вверх\\ +\стрелка вправо \sum \mathrm{F}_{ \mathrm{x}}=0 \\ A_{x}=0 \quad \quad A_{x} = 0 \end{array}\)
Анализ первичной структуры \(DF\) .
Расчет опорной реакции. Диаграмма изолированного свободного тела показана на рис. 3.15f. Во-первых, распределенная нагрузка заменяется единой равнодействующей силой (\(P\)), равной площади треугольной нагрузки, как показано на рис. 3.15g. Применяя уравнения равновесия и отмечая, что опорная реакция в точке \(D\) дополнительной конструкции действует как нагрузка на основную конструкцию, можно сделать следующее:0003
\(\begin{array}{l} +\curvearrowleft \sum M_{F} =0 \\ -20+\left(\frac{1}{2} \times 8 \times 10\right)\left (\frac{2}{3} \times 8\right)+20(8)-4 E_{y}=0 \\ E_{y}=88,33 \mathrm{kN} \quad E_{y}=88,33 \ mathrm{kN} \uparrow \\ +\uparrow \sum F_{y}=0 \\ F_{y}+88,33-\left(\frac{1}{2} \times 8 \times 10\right)-20 =0 \\ F_{y}=28,33 \mathrm{kN} \quad F_{y}=28,33 \mathrm{kN}стрелка вверх \end{массив}\)
Пример 3.10
Определение реакции на опорах A и D кадра, показанного на рис. 3.16а.
\(рис.
3.16\). Рамка.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.16b.
Расчет реакций. Распределенные нагрузки в колонне \(AB\) и балке \(BC\) сначала заменяются одиночными результирующими силами, определяемыми как площадь их соответствующего оттенка нагрузки, как показано на рисунке 3.16c. Применение условий равновесия предполагает следующее:
\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ D_{y}(6)-\left(\frac{1}{2}\right)(6) (3)(3)-(2)(8)(4)=0 \\ D_{y}=15,7 \text { тыс.фунтов } \quad D_{y}=15,7 \mathrm{kips} \uparrow \\ +\ стрелка вверх \sum F_{y}=0 \\ \mathrm{A}_{y}+15,17-3(6)=0 \\ A_{y}=2,830 \mathrm{kips} \quad A_{y}=2,830 \mathrm{kips} \uparrow \\ +\rightarrow \sum \mathrm{F}_{\mathrm{x}}=0 \\ -\mathrm{A}_{x}+(2 \times 8)=0 \\ A_{x}=16 \mathrm{kips} \quad A_{x}=16 \mathrm{kips} \leftarrow \end{массив}\)
Пример 3.11
Жесткая рама нагружена, как показано на рис. 3.17а. Определить реакции на опоре \(D\).
\(рис. 3.17\). Жесткая рама.
Решение
Схема свободного тела. Диаграмма свободного тела всей балки показана на рисунке 3.17b.
Расчет реакций. Распределенная нагрузка в части AB рамы сначала заменяется единой равнодействующей силой, как показано на рис. 3.17c. Применение уравнений равновесия позволяет сделать следующее:
\(\begin{aligned} &+\curvearrowleft \sum M_{D}=0\\ &-M_{D}-16(8)+(4 \times 14)\left(\frac{14}{ 2}\right)-10(10)=0\\ &M_{D}=164 \text { тысяч фунтов } \mathrm{ft} \quad M_{D}=164 \text { тысяч фунтов } \mathrm{ft} \curvearrowright \mathrm{A}\\ &+\uparrow \sum F_{y}=0\\ &D_{y}-4(14)-10=0\\ &D_{y}=66 \text { тысяч фунтов } \ quad D_{y}=66 \text {kips} \uparrow\\ &+\rightarrow \sum\mathrm{F}_{\mathrm{x}}=0\\ &-D_{x}+16=0\ \ &D_{x}=16 \text { тысяч фунтов } \quad D_{x}=16 \text { тысяч фунтов } \leftarrow \end{aligned}\)
Пример 3.12
Найдите реакции на опорах E и F рамы, показанной на рис.
3.18а.
\(рис. 3.18\). Рамка.
Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.18b.
Расчет реакций. Распределенные нагрузки сначала заменяются единичными равнодействующими силами, как показано на рис. 3.18c. Применение уравнений статического равновесия позволяет сделать следующее:
\(\begin{array}{l} +\curvearrowleft \sum M_{E}=0 \\ \left(\frac{1}{2} \times 4 \times 8\right)\left(\frac {1}{3} \times 4\right)-(4\times 7)\left(\frac{7}{2}\right)-\left(\frac{1}{2} \times 4 \times 8\right)\left(\frac{7}{2}+\frac{1}{3} \times 4\right)+7 F_{y}=0 \\ F_{y}=22 \mathrm{kN } \quad F_{y}=22 \mathrm{kN} \uparrow \\ +\uparrow \sum F_{y}=0 \\ E_{y}+22-2\left(\frac{1}{2} \times 4 \times 8\right)-4(7)=0 \\ E_{y}=38 \mathrm{kN} \quad E_{y}=38 \mathrm{kN} \uparrow \\ +\rightarrow \ сумма \mathrm{F}_{\mathrm{x}}=0 \\ E_{x}=0 \quad E_{x}=0 \end{массив}\)
Пример 3.13
Определите реакции опоры A жесткой рамы, показанной на рис.
3.19а.
\(рис. 3.19\). Жесткая рама.
Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.19b.
Расчет реакций. Распределенная нагрузка в столбце \(AB\) сначала заменяется одной равнодействующей силой, как показано на рис. 3.19c. Применение уравнений статического равновесия позволяет сделать следующее:
\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ -M_{A}-20(3)-\left(\frac{1}{2} \times 10 \times 10\right)\left(\frac{1}{3} \times 10\right)=0 \\ M_{A}=-226,67 \mathrm{kN} \cdot \mathrm{m} \quad \quad M_{A}=226,67 \mathrm{kN} \cdot \mathrm{m} \curvearrowleft \\ +\uparrow \sum F_{y}=0 \\ A_{y}-20=0 \\ A_{y}= 20 \mathrm{kN} \quad \quad A_{y}=20 \mathrm{kN} \uparrow\\ +\rightarrow \sum F_{x}=0 \\ -A_{x}+\left(\frac{ 1}{2} \times 10 \times 10\right)=0 \\ A_{x}=50 \mathrm{kN} \quad \quad A_{x}=50 \mathrm{kN} \leftarrow \end{array }\)
Пример 3.14
Определите реакции опор \(A\) и \(E\) рамы, шарнирно закрепленной в \(C\), как показано на рис.
3.20a.
\(рис. 3.20\). Рамка.
Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.20b.
Расчет реакций. Реакции в составной раме рассчитываются с учетом диаграмм свободного тела как всей рамы, так и ее части. Перед расчетом реакций распределенную нагрузку в колонне заменяют единой равнодействующей силой. Вертикальные реакции в \(Е\) и \(А\) и горизонтальные реакции в \(А\) находятся путем применения уравнений статического равновесия и рассмотрения диаграммы свободного тела всей рамы. Горизонтальная реакция в \(E\) находится при рассмотрении части \(CDE\) диаграммы свободного тела.
\(\begin{array}{l} +\curvearrowleft \sum M_{A}=0 \\ 8 E_{y}-(2 \times 10)\left(\frac{10}{2}\right )-10(4)=0 \\ E_{y}=17.5 \text { тыс.фунтов } \quad \quad E_{y}=17.5 \mathrm{kips} \uparrow \\ +\uparrow \sum F_{y}= 0 \\ A_{y}+17,5-10=0 \\ A_{y}=-7,5 \text { тысяч фунтов } \quad \quad A_{y}=7,5 \text { тысяч фунтов } \downarrow \end{array}\ )
Знак минус означает, что первоначально предполагаемое направление \(A_{y}\) было неправильным.
Следовательно, \(A_{y}\) действует вниз, а не вверх, как первоначально предполагалось. Это должно быть исправлено при последующем анализе.
Чтобы определить \(E_{x}\), рассмотрим момент сил в элементе \(CDE\) относительно шарнира.
\(\begin{array}{l} \curvearrowleft +\sum M_{C}=0 \\ 17,5(4)-10 E_{x}=0 \\ E_{x}=7 \text { тысяч фунтов } \quad \quad E_{x}=7 \text { тыс.фунтов } \leftarrow \\ +\rightarrow \sum F_{x}=0 \\ -A_{x}-7+2 \times 10=0 \\ A_{ x}=13 \text { тысяч фунтов } \quad \quad A_{x}=13 \text { тысяч фунтов } \leftarrow \end{массив}\)
Пример 3.15
Найдите реакции в опорах \(A\) и \(B\) нагруженной рамы на рис. 3.21а. Рама шарнирно закреплена в точке \(D\).
\(рис. 3.21\). Загруженный кадр.
Решение
Схема свободного тела. Схема свободного тела рамы показана на рисунке 3.21b.
Расчет реакций. Распределенная нагрузка в столбце \(AC\) сначала заменяется единой результирующей силой путем нахождения области нагрузки, как показано на рис.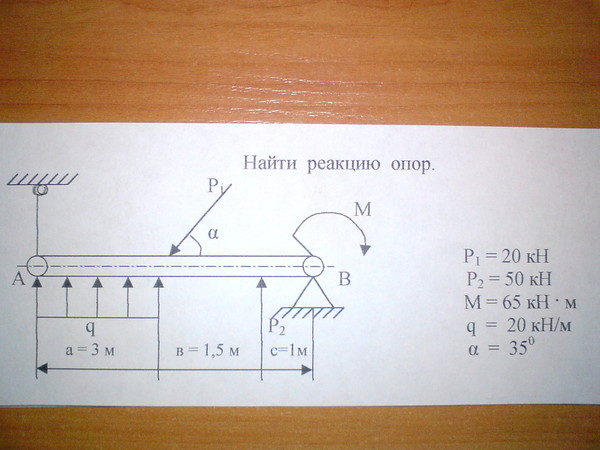
3.21. Реакция в точке \(B\) вычисляется путем принятия момента сил в части \(DB\) рамы относительно штифта в точке \(D\), а остальные реакции определяются путем применения других условий равновесия.
\(\begin{align} &+\curvearrowleft \sum M_{D}=0\\ &B_{y}(0)-15(4)=0\\ &B_{y}=0\\ &+n \sum M_{A}=0\\ &M_{A}+6 \times 0-\left(\frac{1}{2} \times 8 \times 20\right)\left(\frac{1}{3) } \times 8\right)-12(3)+15(4)=0\\ &M_{A}=189,33 \mathrm{kN} \cdot \mathrm{m} \quad M_{A}=189,33 \mathrm{ кН} \cdot \mathrm{m} \curvearrowright\\ &+\стрелка вверх \sum F_{y}=0\\ &A_{y}+0-12=0\\ &A_{y}=-12 \mathrm{kN } \quad A_{y}=12 \downarrow \end{aligned}\)
Знак минус означает, что первоначально предполагаемое направление A y неверно. Следовательно, A y действует вниз, а не вверх, как первоначально предполагалось. Это должно быть исправлено при последующем анализе.
\(\begin{array}{l} +\стрелка вправо \сумма F_{x}=0 \\ -A_{x}-15+\left(\frac{1}{2} \times 8 \times 20 \right)=0 \\ A_{x}=65 \mathrm{kN} \quad \quad A_{x}=65 \mathrm{kN} \rightarrow \end{array}\)
Краткое изложение главы
Условия статического равновесия: Конструкция находится в состоянии статического равновесия, если равнодействующая всех действующих на нее сил и моментов равна нулю.
Математически это выражается следующим образом:
\(\Сигма F=0\) \(\Сигма M=0\)
Для тела на плоскости существуют следующие три уравнения равновесия:
\(\Sigma F_{X}=0\) \(\Sigma F_{Y}=0\)∑ \(\Sigma M_{0}=0\)
Типы опор: Различные символические представления используются для моделирования различных типов опор для конструкций. Ролик используется для моделирования опоры, которая препятствует вертикальному движению конструкции, но допускает горизонтальное перемещение и вращение. Штифт используется для моделирования опоры, которая предотвращает горизонтальные и вертикальные перемещения, но допускает вращение. Неподвижная опора моделирует опору, предотвращающую горизонтальные и вертикальные перемещения и повороты.
Детерминированность, неопределенность и устойчивость структур: Структура является детерминированной, если число неизвестных реакций равно числу статических равновесий. Таким образом, для определения опор такой конструкции достаточно уравнений статического равновесия.
С другой стороны, статически неопределимая структура — это структура, в которой количество неизвестных реакций превышает уравнения равновесия. Для анализа неопределенной конструкции нужны дополнительные уравнения, и эти уравнения можно получить, рассматривая совместность конструкции. Неопределенные конструкции иногда необходимы, когда необходимо уменьшить размеры элементов или увеличить жесткость элементов. Стабильная структура — это структура, в которой опорные реакции не параллельны и не параллельны друг другу. Формулировки устойчивости и определенности балок и шпангоутов следующие:
Балки и рамы: | \(3 m+r<3 j+C\) Структура неустойчива |
|
|
| \(3 m+r=3 j+C\) Структура детерминированная |
|
|
| \(3 m+r>3 j+C\)Структура не определена |
Практические задачи
3.
1 Классифицируйте конструкции, показанные на рисунках P3.1a–P3.1p, как статически определимые или неопределимые, а также статически устойчивые или неустойчивые. Если неопределенно, укажите степень неопределенности.
\(Рис. П3.1\). Структурная классификация.
3.2. Определите опорные реакции для балок, показанных на рис. P3.2–рис. P3.12.
\(Рис. П3.2\). Луч.
\(Рис. П3.3\). Луч.
\(Рис. П3.4\). Луч.
\(Рис. П3.5\). Луч.
\(Рис. П3.6\). Луч.
\(Рис. П3.7\). Луч.
\(Рис. П3.8\). Луч.
\(Рис. П3.9\). Луч.
\(Рис. П3.10\). Луч.
\(Рис. П3.11\). Луч.
\(Рис. П3.12\). Луч.
3.3. Определите опорные реакции для рам, показанных на рис. P3.13–рис. P3.20.
\(Рис. П3.13\). Рамка.
\(Рис. П3.14\). Рамка.
\(Рис. П3.15\). Рамка.
\(Рис. П3.16\). Рамка.
\(рис. 3.17\). Рамка.
\(рис. 3.18\). Рамка.
\(рис. 3.19\). Рамка.
\(Рис. 3.20\). Рамка.
3.4 Определите опорные реакции для ферм, показанных на рис. P3.21–рис. P3.27.
\(рис. П3.21\). Ферма.
\(Рис. P3.22\). Ферма.
\(Рис. П3.23\). Ферма.
\(рис. П3.24\). Ферма.
\(Рис. P3.25\). Ферма.
\(рис. П3.26\). Ферма.
\(Рис. P3.27\). Ферма.
Эта страница под названием 3.4: Расчет опорных реакций для плоских конструкций распространяется под лицензией CC BY-NC-SA 4.0, ее автор, ремикширование и/или куратор Рене Альдерлистен (TU Delft Open) через исходный контент, который был отредактирован к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.