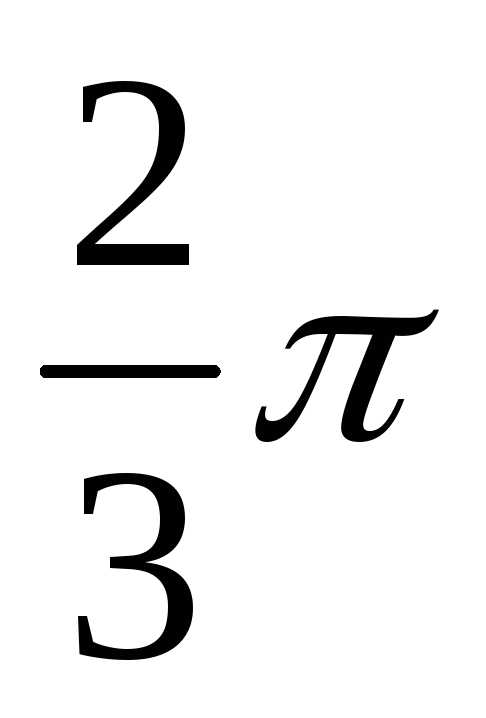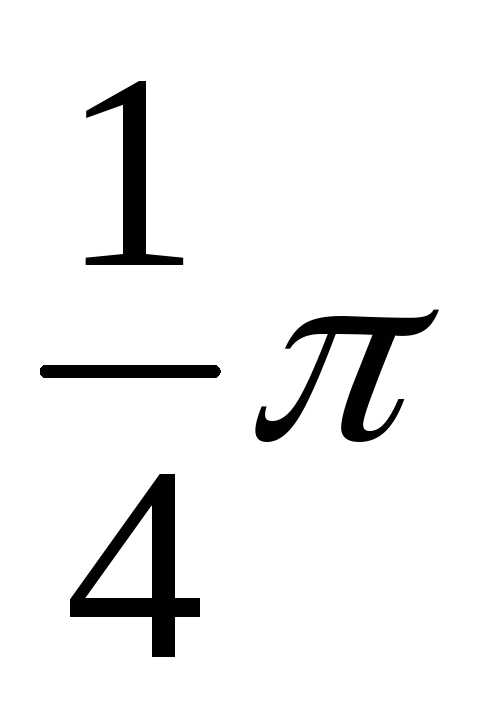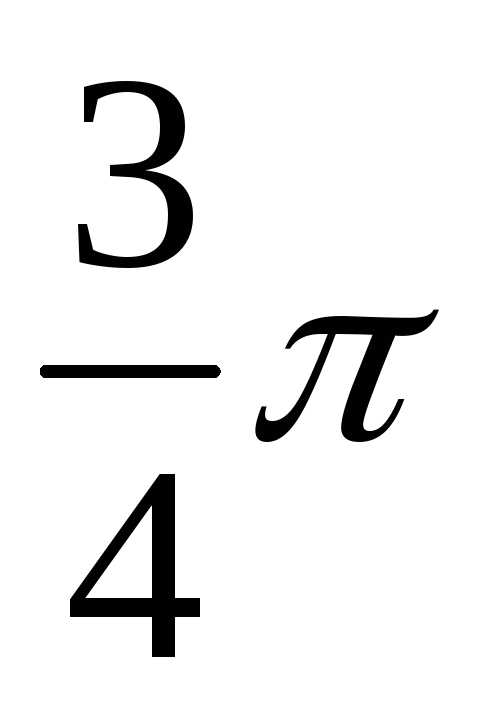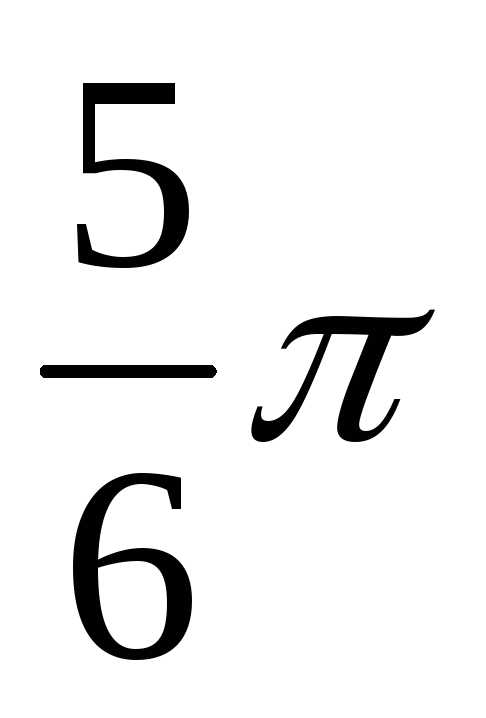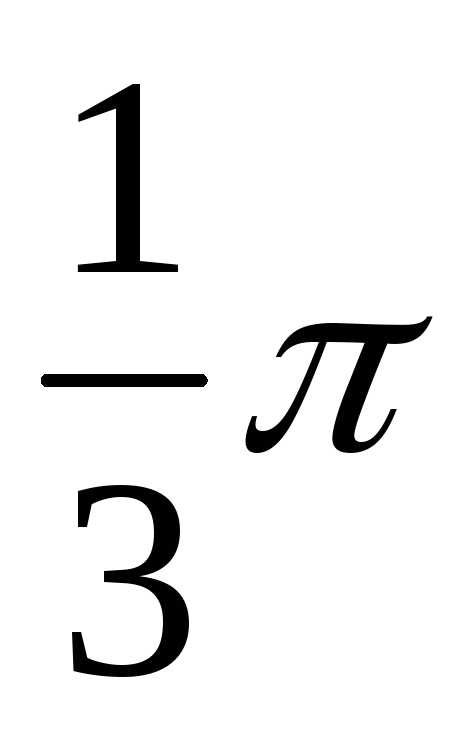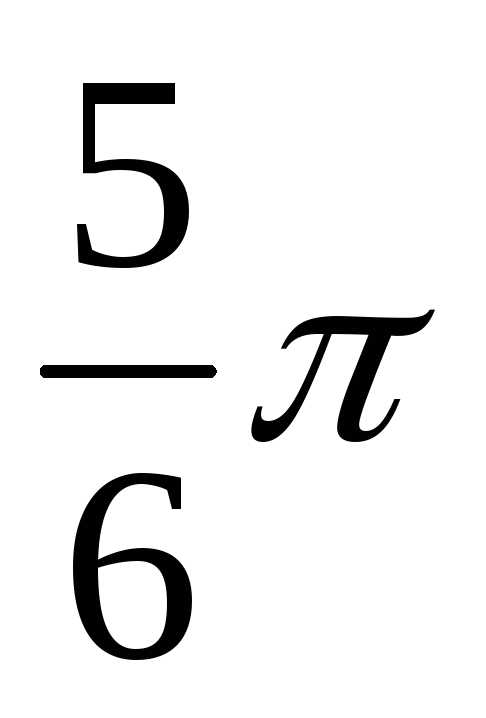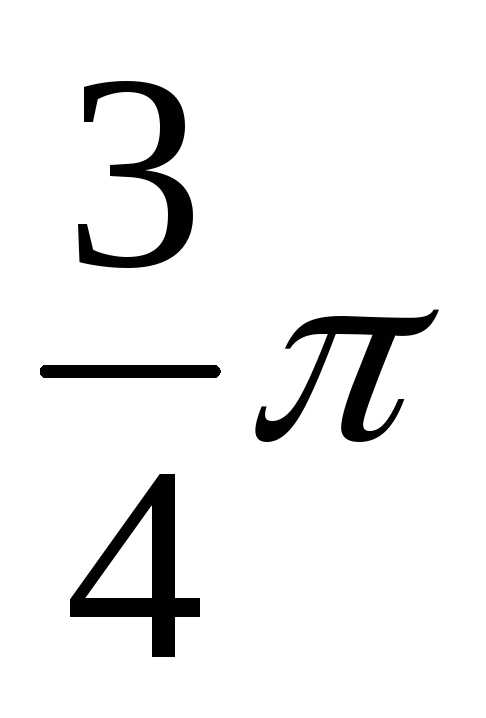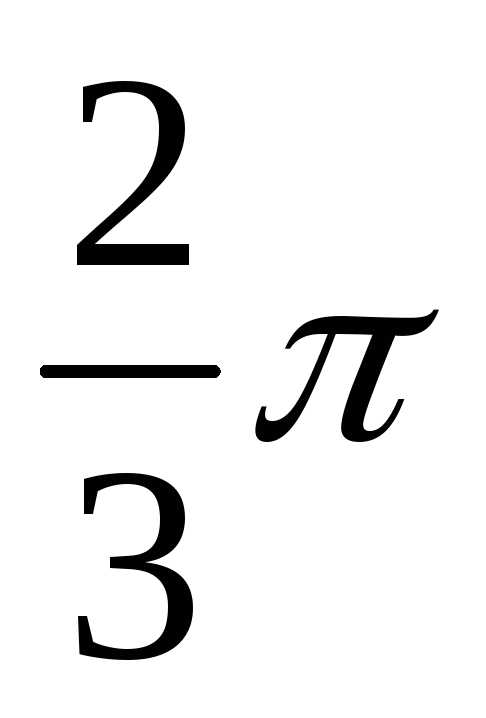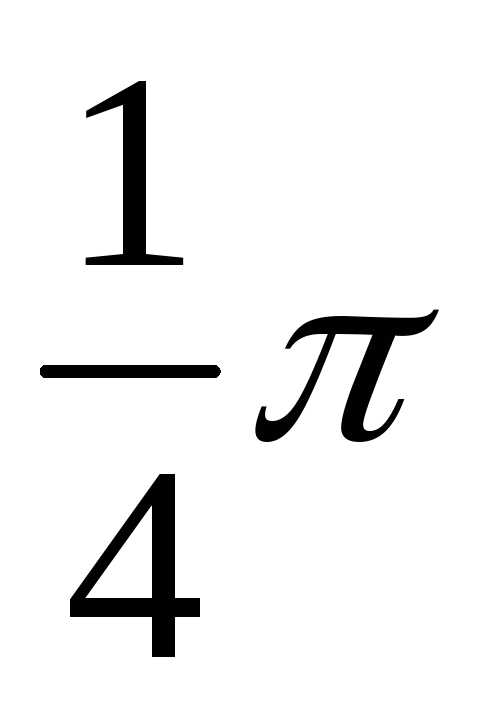Определение реакций опор составной конструкции
Для определения реакций опор составной конструкции, мы мысленно разбираем конструкцию на отдельные элементы, каждый из которых является твердым телом. Вместо связей в опорах и точках соединений составных элементов прикладываем силы реакций. Вид сил реакций зависит от крепления опоры или точки соединения тел. Для каждого тела, входящего в конструкцию, мы составляем уравнения равновесия. В результате получаем систему уравнений. Если задача является статически определимой, то эта система имеет единственное решение. Если задача не является статически определимой, то система уравнений имеет бесконечно много решений. Выбрать единственное решение, методами статики, нельзя. Это можно сделать методами сопротивления материалов.
При составлении уравнений равновесия стоит заметить, что иногда целесообразно составлять уравнения для всей конструкции в целом, или к группе ее элементов, рассматривая их как единое целое.
Силы, возникающие в точках соприкосновения частей конструкции, связаны между собой законом равенства действия и противодействия:
Сила, с которой первое тело действует на второе, равна по абсолютной величине и противоположна по направлению силе, с которой второе тело действует на первое.
Методы определения реакций опор твердых тел рассмотрены на странице
«Определение реакций опор твердого тела».
Далее рассмотрен пример решения задачи на определение реакций опор составной конструкции.
Пример решения задачи на определение реакций опор составной конструкции
Условие задачи
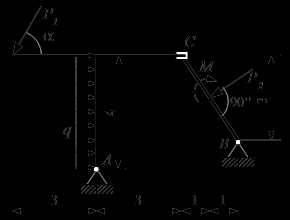
Составная конструкция.
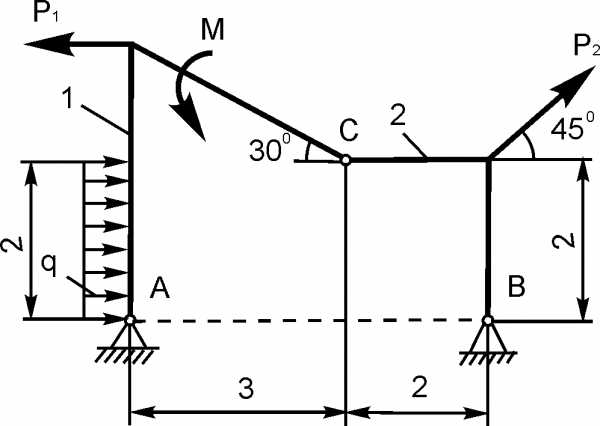
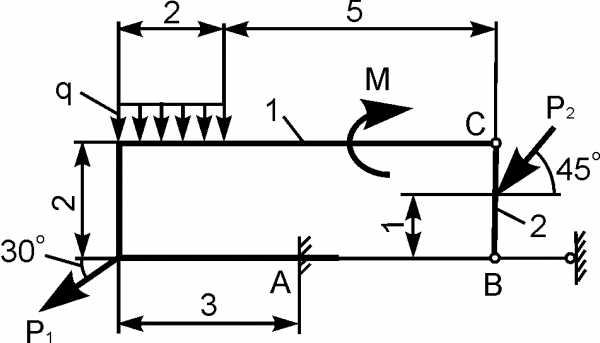
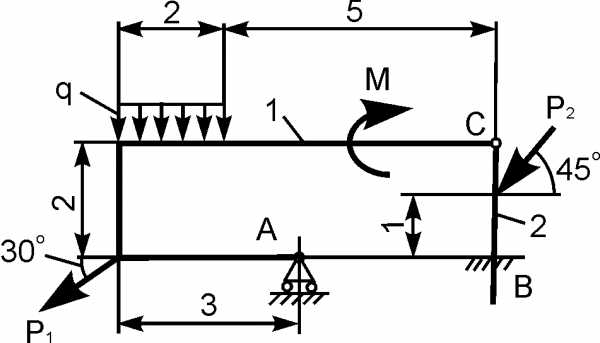
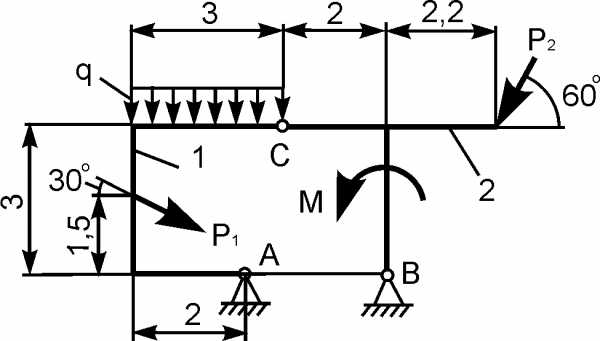
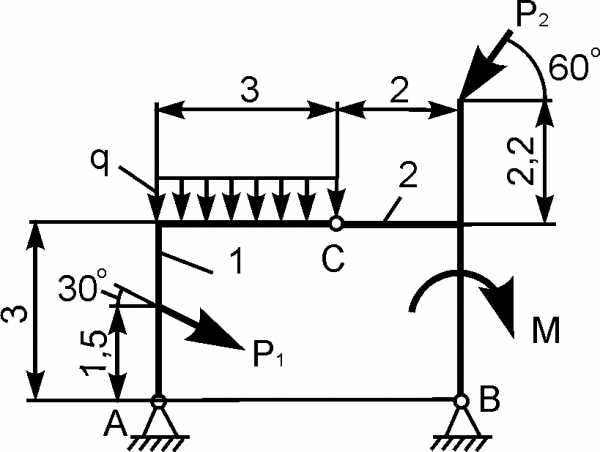
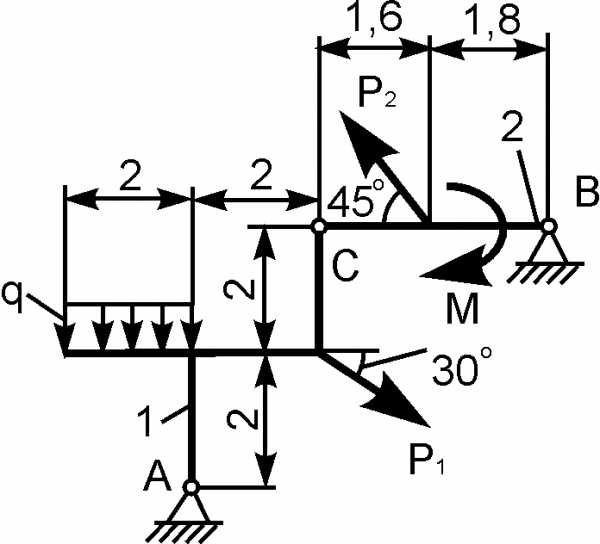
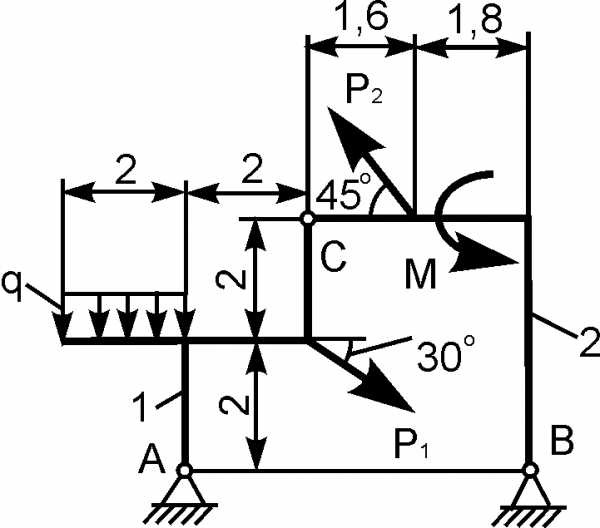
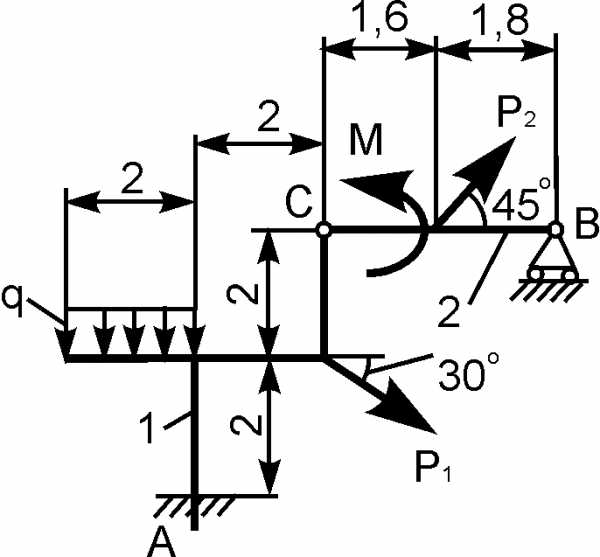
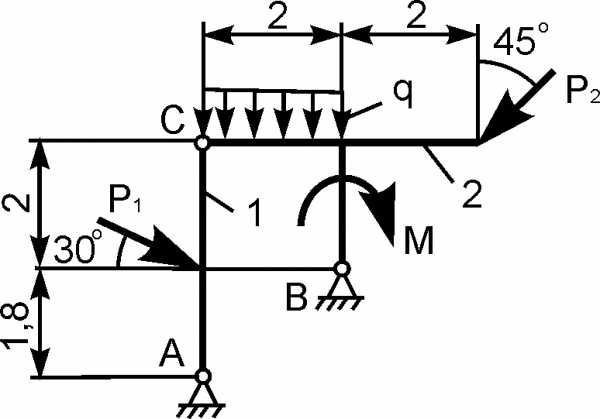
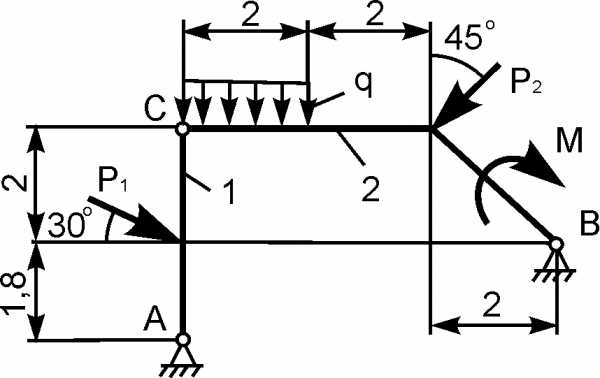
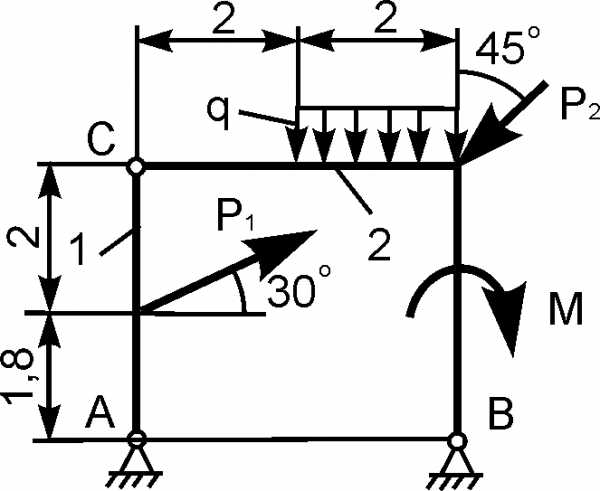
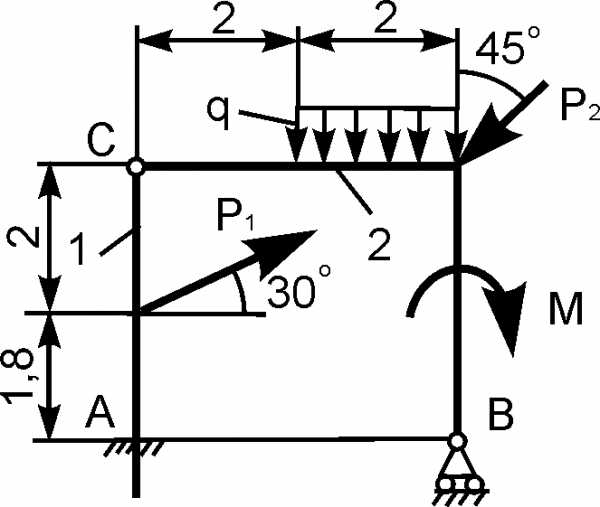
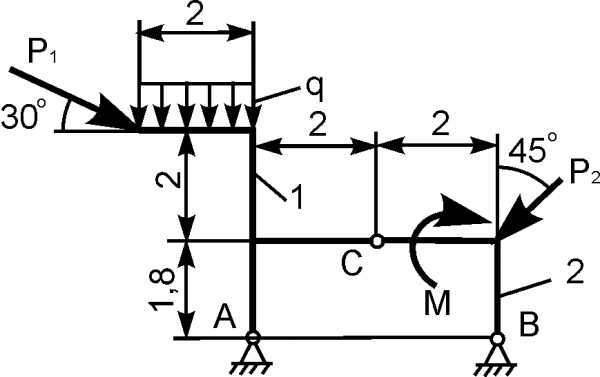
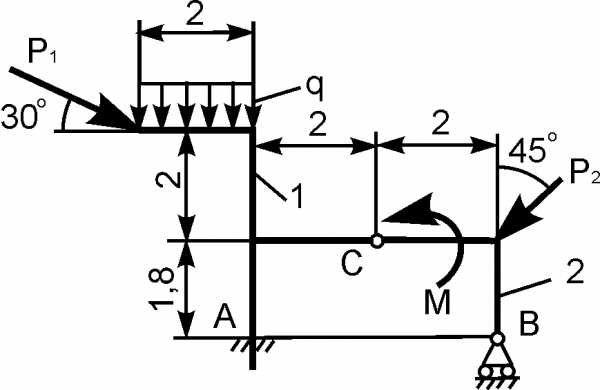
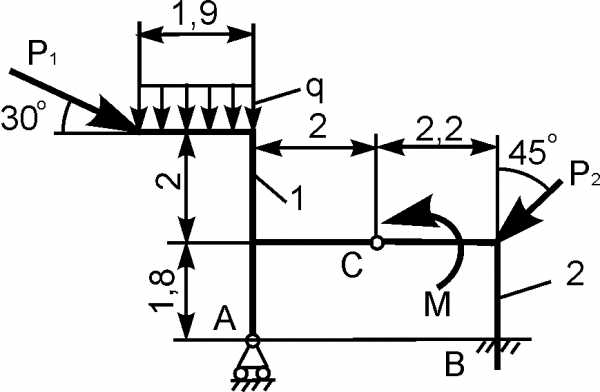
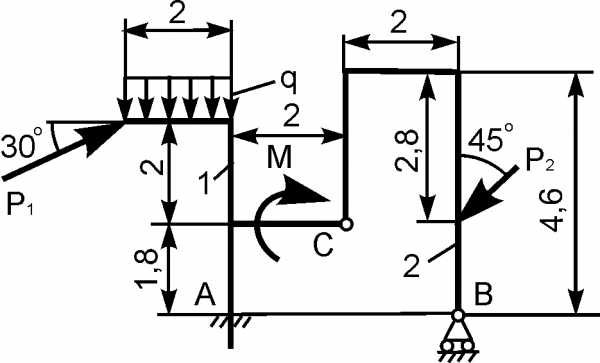
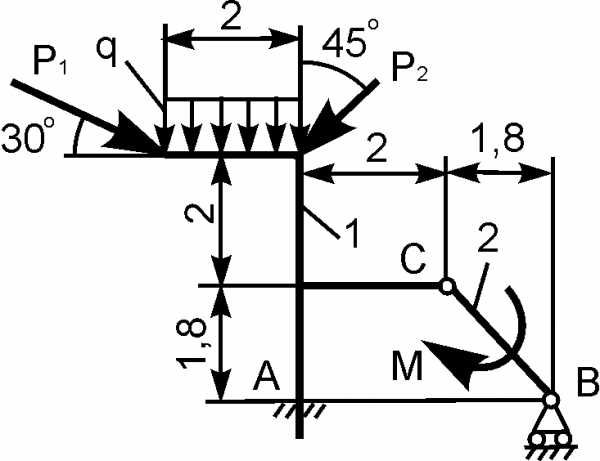
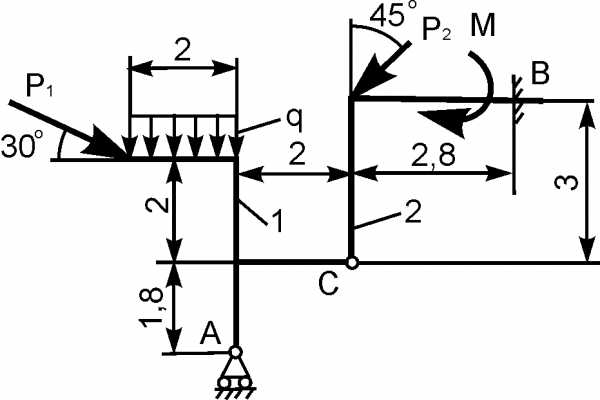
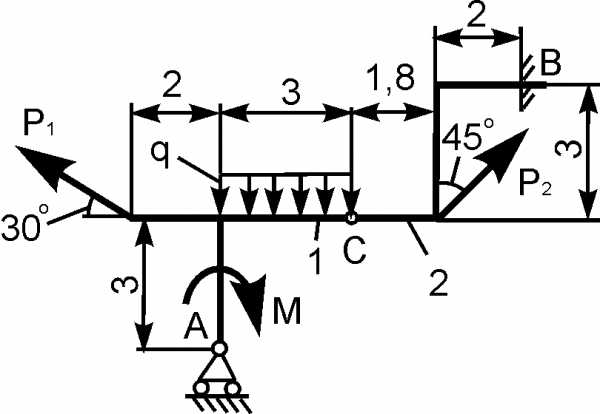
Для составной конструкции, изображенной на рисунке, определить реакции опор в шарнирах A и B, а также реакции в скользящей заделке C. Расстояния указаны в метрах.
Дано:
P1 = 5 kН; P2 = 7 kН; M = 22 kН·м; q = 2 kН/м; α = 60°.
Решение задачи
Равновесие стержня CB
Мысленно разъединим конструкцию. Рассмотрим равновесие стержня CB. Проводим систему координат Axyz с началом в точке A. Ось Az перпендикулярна плоскости рисунка и направлена на нас.
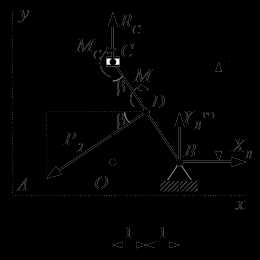
Реакции опор, поддерживающие равновесие правой части конструкции.
Соединение в точке C является скользящей заделкой. Заменим это соединение силами реакций. Разложим их на две составляющие: на силу , параллельную оси y; и на момент (пару сил) MC. Их направления выбираем произвольно. Если мы не угадаем с направлением, то значение соответствующей реакции будет иметь отрицательное значение.
Шарнирную опору в точке B заменим силами реакций и , параллельными осям координат.
Рассмотрим геометрию системы. Из прямоугольного треугольника OBC имеем:
м;
м;
;
.
Здесь β – угол между стержнем CB и вертикалью CO. Поскольку , то угол между направлением силы и горизонталью также равен β.
Составляем уравнения равновесия. Сумма проекций сил на ось x равна нулю.
;
;
;
(П1) .
Сумма проекций сил на ось y равна нулю.
;
;
;
(П2) .
Составляем уравнение для моментов. Возьмем ось Bz′, проходящую через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой оси равна нулю:
;
(П3.1) .
Вычисляем моменты сил. Ось Bz′ направлена на нас. По правилу правого винта, положительным направлением моментов сил является направление против часовой стрелки.
Силы реакций пересекают ось Bz′. Поэтому их моменты равны нулю.
Плечом силы является отрезок OB. Тогда
.
Поскольку , то отрезок DB является плечом силы . Момент этой силы:
.
Подставим в (П3.1):
;
(П3) .
Равновесие конструкции в целом
Рассмотрим равновесие всей конструкции в целом. Шарнирную опору в точке A заменим силами реакций и , параллельными осям координат.
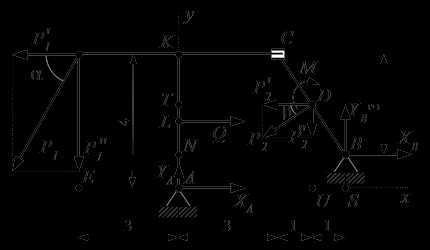
Реакции опор, поддерживающие равновесие всей конструкции.
Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
kН.
Точка приложения равнодействующей находится в центре тяжести эпюры – в точке L, посередине отрезка KA:
|KL| = |LA| = 2 м.
Силы и разложим на составляющие вдоль осей координат:
; ;
; ;
; .
Составляем уравнения равновесия. Сумма проекций сил, действующих на всю конструкцию, на ось x равна нулю.
;
;
;
(П4) .
Сумма проекций сил на ось y равна нулю.
;
;
;
(П5) .
Сумма моментов сил относительно оси z, проходящей через точку A перпендикулярно плоскости рисунка, равна нулю:
;
(П6.1)
.
Вычисляем моменты сил. Силы реакций и пересекают ось Az. Поэтому их моменты равны нулю.
Момент от некоторой силы относительно оси Az равен произведению плеча силы на абсолютное значение этой силы, взятое с соответствующим знаком. Если сила направлена в положительном направлении (против часовой стрелки), то знак момента положительный. В противном случае – отрицательный. Чтобы найти плечо, через вектор силы проводим прямую. Длина перпендикуляра, опущенного из точки A на эту прямую равна плечу силы относительно оси Az.
В результате уравнение (П6.1) принимает вид:
;
(П6)
.
Решение уравнений равновесия
Итак, мы получили следующую систему линейных уравнений:
(П1) ;
(П2) ;
(П3) ;
(П4) ;
(П5) ;
(П6)
.
В ней шесть уравнений и шесть неизвестных. Решаем систему.
Из уравнения (П1): kН.
Из уравнения (П4) имеем:
kН.
Из уравнения (П6) находим:
kН.
Далее из уравнений (П2), (П3) и (П5) последовательно находим:
kН.
kН.
kН.
Решение системы уравнений оказалось простым во многом благодаря тому, что мы подходящим образом выбрали оси, относительно которых вычисляли моменты. А также за счет того, что мы удачно выбрали части конструкции, для которых составляли уравнения (правую часть и всю конструкцию в целом). Можно составить уравнения равновесия и другими способами. Например, можно составить уравнения равновесия для левой и правой частей конструкции и выбрать другие оси для вычисления моментов. Если бы мы сделали это неудачно, то нам пришлось бы решать систему из шести линейных уравнений с шестью неизвестными другим способом, например, методом Крамера. Количество вычислений было бы больше, но в результате мы все равно получили бы одни и те же значения сил реакций.
Проверка правильности решения
Сделаем проверку правильности решения задачи. Для этого рассмотрим равновесие левой части конструкции.
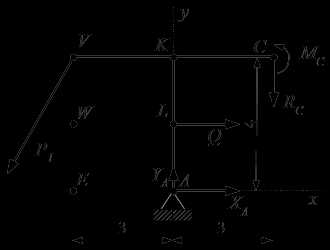
Реакции опор, поддерживающие равновесие левой части конструкции.
По закону равенства действия и противодействия, в скользящей заделке C, на раму действуют сила и момент MC. Их направления противоположны силе и моменту, действующих в точке C на правую часть конструкции, а абсолютные значения равны.
Через точку V проведем ось Vz′′, перпендикулярно плоскости рисунка. Если мы определили значения реакций правильно, то сумма моментов сил относительно этой оси должна равняться нулю:
.
Все правильно.
Ответ
kН; kН; kН; kН; kН; kН·м.
Отрицательные значения реакций и указывают на то, что они направлены в сторону, противоположную той, которая изображена на рисунке.
Использованная литература:
Сборник заданий для курсовых работ по теоретической механике, под редакцией проф. А.А. Яблонского, Москва «Интеграл-пресс», 2006.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Типы реакций связи
Нить, трос | Невесомый стержень | Гладкая поверхность | Шарнир на катках | ||
Плоская система сил y x | Пространственная z система сил y x | ||||
Направляющая | Цилиндрический шарнир | ||||
Две направ-ляющие | Петля | ||||
Плоский шарнир | Сферический шарнир, подпятник | ||||
Жесткая заделка | Жесткая заделка | ||||
Примечание.
Для пространственной системы сил в случае цилиндрического шарнира или петли реакции связей изображены при наличии в реальной задаче второй опоры. При отсутствии второй опоры должны быть добавлены два реактивных момента относительно осей x и z.
В
задачах на опрокидывание вместо уравнения
моментов используется неравенство 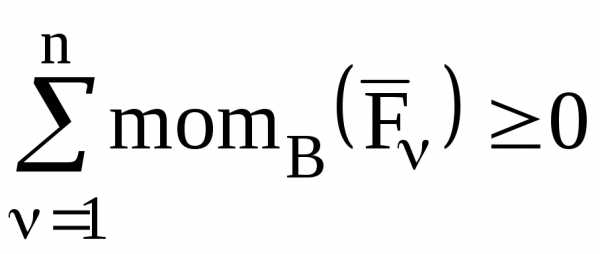 ,
где В – точка, относительно которой
происходит опрокидывание.
,
где В – точка, относительно которой
происходит опрокидывание.
Пример 1
2Балка BD, закрепленная, как указано на рис. 34, находится в равновесии, и на нее действуют следующие силы: F1=6Н, p=2Н/м, F=F=25Н (а=1м, h=2м, ,DE==3м).
Определить реакции опор BиDв двух случаях: без учета и с учетом веса стержняDE.
Случай 1а(невесомый стерженьDE).
Рис. 34
5 Равномерно распределенная на отрезке
3а нагрузка (рис. 34) заменена сосредоточенной
силой P
= p3a
(рис. 35). Точка приложения силы  находится в середине отрезка. Пара сил
находится в середине отрезка. Пара сил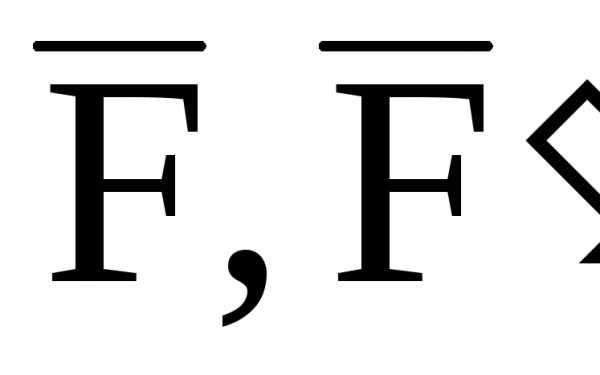 заменена моментом парыкН.
заменена моментом парыкН.
Опоры B и D (рис. 34) заменены реакциями опор: (рис. 35).
Рис. 35
6 РПЛ
7
8 Из
1-го уравнения Н –10,39
Н,
–10,39
Н,
из
2-го уравнения 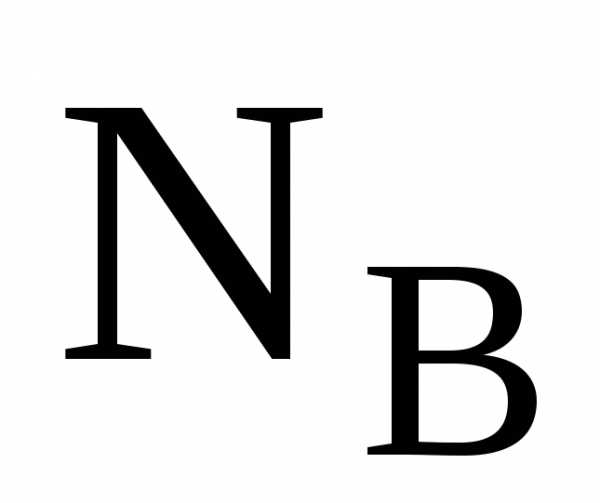
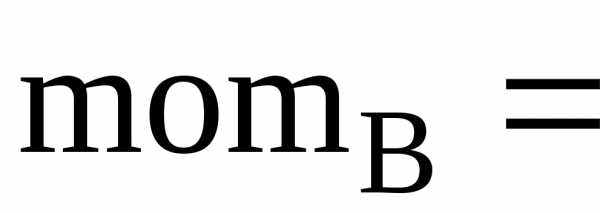 106,00 Нм.
106,00 Нм. 9 Ответ: 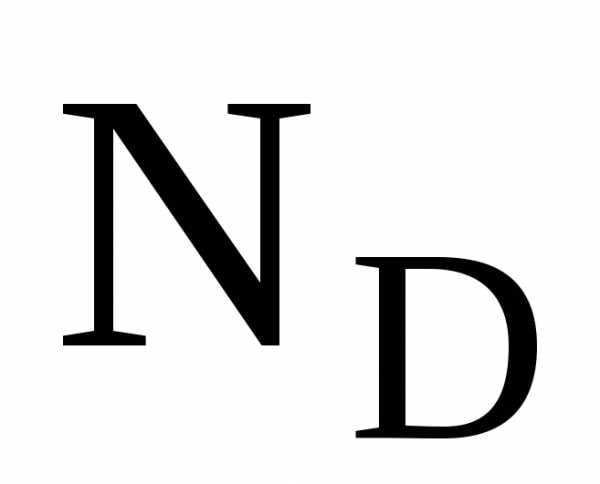 =
–10,39 Н,
=
–10,39 Н,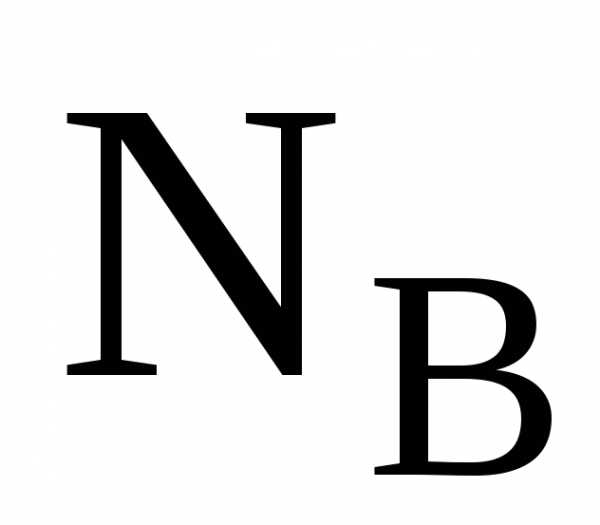 =18,00
Н,
=18,00
Н, =106,00
Нм.
=106,00
Нм.
Случай 1б (учитывается вес стержня DE – P1=4Н)
Составная конструкция.
n=2
= 1 (равновесие всей конструкции BDE)
Опоры в точках B и E заменены реакциями опор (рис. 36).
6 РПЛ
7
Рис. 36
=2 (равновесие стержня DE)
5 Опоры D и E заменены реакциями опор: (рис. 37).
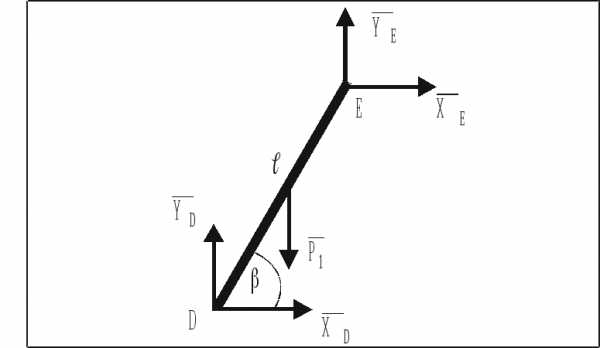
Рис. 37
РПЛ
7
8 Из 1-го уравнения ,
из 4-го уравнения ,
из 6-го уравнения ,
из 5-го уравнения ,
из 2-го уравнения ,
из 3-го уравнения .
9 Ответ: ,,,
,,.
Пример 2
2 Два стержня
BD
и DE
соединенные шарнирно и закрепленные,
как указано на рис. 38, находятся в
равновесии и на них действуют следующие
силы и моменты: 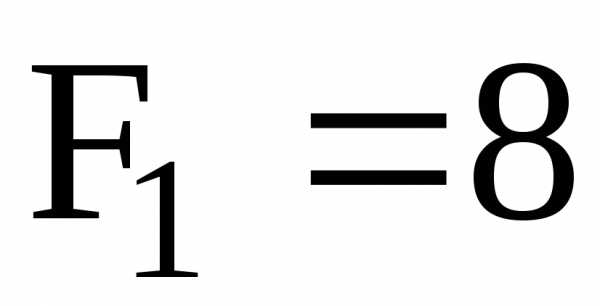 Н,
Н,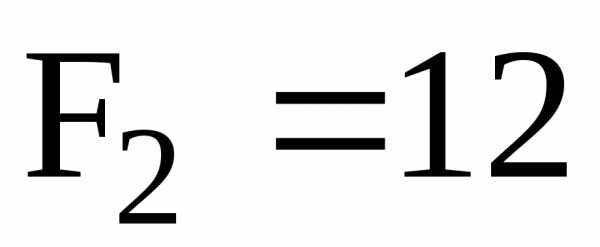 Н,
Н,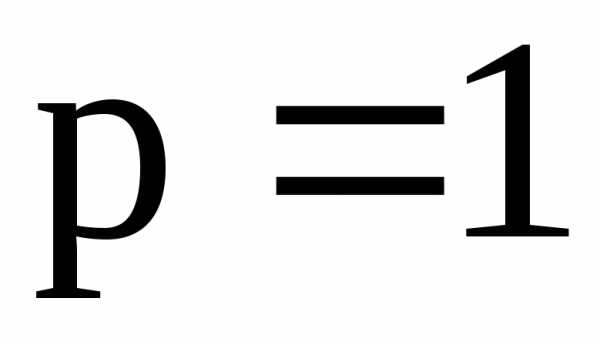 Н/м,
Н/м,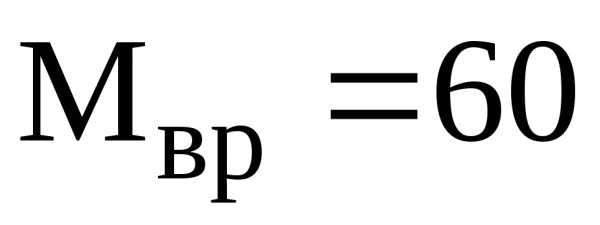 Н/м
(а=2м,).
Н/м
(а=2м,).
Найти: реакции опор B, E и шарнира D.
Рис. 38
3 Составная конструкция
4 n=2
Неизвестных реакций связи, действующих на систему двух стержней BD и
В точке D добавятся 2 неизвестные силы реакции связи, а уравнений равновесия дополнительно получится 3.
Итого: 6 (3+3) уравнений равновесия — 6 (4+2) неизвестных реакций связи.
=1 (равновесие всей конструкции BDE)
5
Рис. 39
Здесь P=pa=2Н.
6 РПЛ
7
5 =2 (равновесие стержня DE)
Рис. 40
6 РПЛ
7
8 Система шести уравнений 1-6 для шести неизвестных:
из
6-го уравнения Н 24,22 Н,
24,22 Н,
из
5-го уравнения YD= –9,00 Н,
из
4-го уравнения Н 12,11
Н,
12,11
Н,
из
3-го уравнения 4
Н,
из 2-го уравненияН –13,92
Н,
–13,92
Н,
из 1-го уравнения XB= 16,11 Н.
9 Ответ: XB=16,11 Н, YB
XD=12,11 Н, YD= – 9,00 Н, NE=24,22 Н.
Примечание.
Можно составить по три уравнения равновесия для стержней BD и DE с учетом что:
,
т.е. внутренние силы соответственно попарно равны и противоположны по направлению (рис. 41).
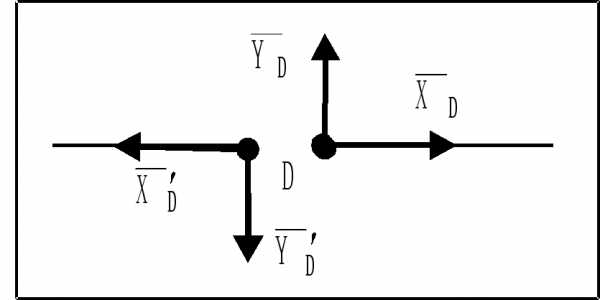
Рис. 41
Пример 3
2 Дверь весом Р=100Н удерживается в равновесии силой F и пружиной (рис. 42).
Найти
реакции подпятника в точке O,
петли в точке В и реактивный момент
пружины, если F=60Н, ОВ=3м, ОD=ОО1=1м,
ЕН=НD, 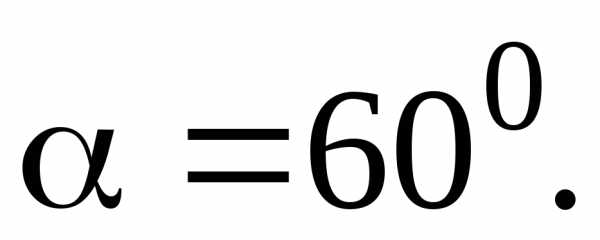
Рис. 42
3 Один объект равновесия.
5
Рис. 43
Для
определения
момента силы  относительно координатных осей удобно
разложить ее на составляющие вдоль этих
осей:
относительно координатных осей удобно
разложить ее на составляющие вдоль этих
осей:
6 РПР.
7
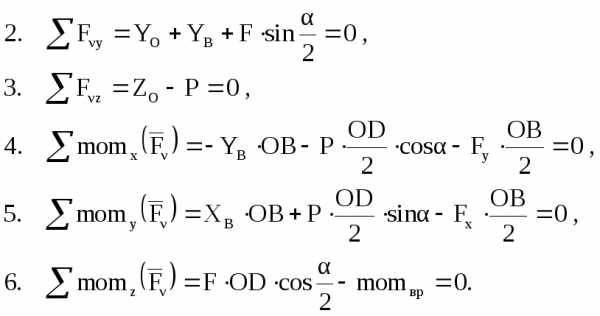
8 Из 6-го уравнения momвр = 25,98 Н,
из 5-го уравнения XB11,55 Н,
из 4-го уравнения YB –23,33 Н,
из 3-го уравнения ZО =100,00 Н,
из 2-го уравнения YО –28,63 Н,
из 1-го уравнения XО 18,45 Н.
9 Ответ: XО =18,45 Н, YО = – 28,63 Н, ZО =100,00 Н,
XB =11,55 Н, YB = –23,33 Н, momвр = 25,98 Нм.
Пример 4
2 Вал с дисками, каждый весом Р и радиуса , удерживается в равновесии грузами весом Р1 и Р2 и силой F (рис. 44).
Определить
реакции подшипников в точках О и В и
величину силы F,
если P=0,5Н,
Р1=15Н,
Р2=10Н,
=0,5м,
=2м,
a=0,5м,
b=d=1м,
c=3м, 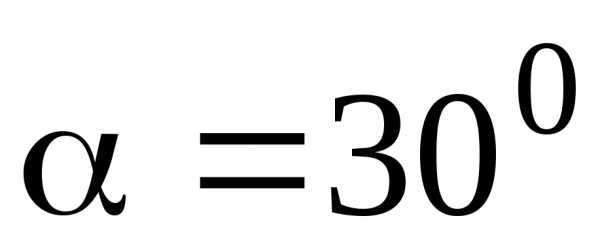 .
.
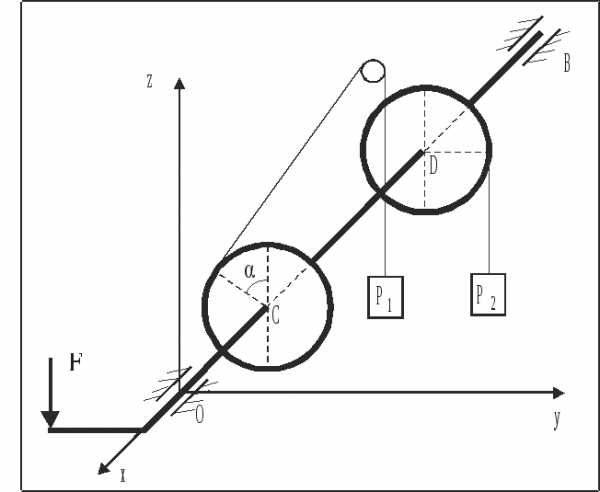
Рис. 44
3 Один объект равновесия (АТТ).
5
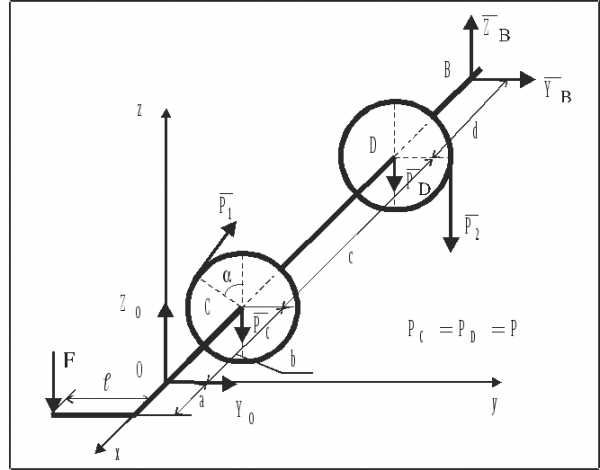
Рис. 45.
6 РПР.
5.
8 Из 5-го уравнения ,
из
3-го уравнения 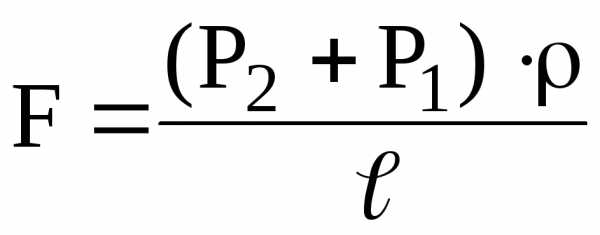 ,
,
из 4-го уравнения
,
из 2-го уравнения
,
из 1-го уравнения .
9 Ответ: YО = –10,39Н, YB= –2,60Н, ZО = –9,87Н,
ZB= –0,13Н, F=6,25Н.
* Внешними реакциями связи называются реакции связи с которыми действуют на рассматриваемые объекты другие объекты.
** Внутренними реакциями связи называются реакции связи с которыми действуют друг на друга части рассматриваемого объекта.
219
studfiles.net
Связи и их реакции
Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными. Тела, ограничивающие свободу перемещения других тел, называются по отношению к ним связями.
Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.
Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными. Ниже приведены примеры замены связей их реакциями. На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.
а – тело весом G на гладкой поверхности;
б – действие поверхности заменено реакцией – силой R;
в – в точке А связь «опорная точка» или ребро;
г – реакции направлены перпендикулярно
опираемой или опирающейся плоскостям
Рисунок 1.1
Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1). Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль троса (нити, цепи, стержня) (рисунок 1.2).
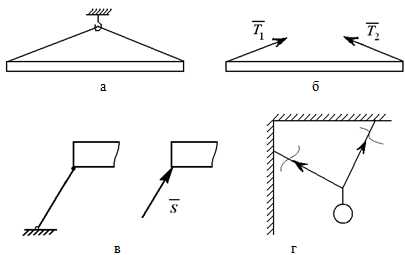
б – действие тросов заменено силами Т1 и Т2;
в – связь «идеальный стержень»;
г – связь «идеальная нить»
Рисунок 1.2
Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3, а или 1.3, б). Она может быть заменена либо силой R с углом α (рисунок 1.3, в), либо двумя силами, например, XA и YA (рисунок 1.3, г).
Рисунок 1.3
Всегда можно перейти от R и α к XA и YA (и наоборот):
XA = Rcosα; YA = Rsinα;
Шарнирно-подвижная опора (рисунок 1.4, а) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное. Реакция направлена по нормали к опорной поверхности (рисунок 1.4, б).
Рисунок 1.4
Связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), их действие заменено силами XA, YA и RB.
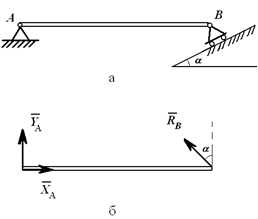
Рисунок 1.5
Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросим втулку – получим действие на стержень силы RD и момента MD.
Рисунок 1.6
На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет момент MC (рисунок 1.7, б).
Рисунок 1.7
Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила RA с углом α (или XA и YA) и момент ΜA (рисунок 1.8).
Рисунок 1.8
На рисунках 1.9 – 1.15 показаны примеры замены сил, расположенных в пространстве, их реакциями.
Шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменена системой сил (рисунок 1.9, б) XA, YA и ZA, т.е. силой, неизвестной по величине и направлению.
Рисунок 1.9
На рисунке 1.10, а показан вал, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами XA, YA, ZA и XB, ZB (рисунок 1.10, б).
Рисунок 1.10
На рисунках 1.11 и 1.12 приведены примеры замены различных связей их реакциями.
Рисунок 1.11
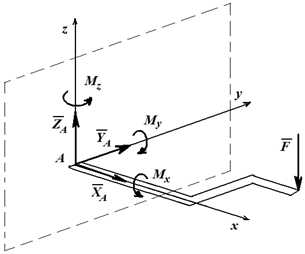
Рисунок 1.12
>> Проекция силы на ось
isopromat.ru
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ СОСТАВНОЙ ПЛОСКОЙ КОНСТРУКЦИИ
•Определить реакции связей в точках А и В составной плоской конструкции, состоящей из двух твердых тел. Схемы конструкций приведены на рис. исходные данные указаны в табл
Составная конструкция — это система тел, каким-либо образом связанных между собой.
•Отбрасываем опоры А и
В и заменяем их действие на конструкцию реакциями. Заменяем равномерно распределенную
нагрузку интенсивностью q равнодействующей силой Q.
•Разделим конструкцию на две части по шарниру С. В сечении С, где имеется шарнир, две части конструкции взаимодействуют между собой. Силы взаимодействия в шарнире С раскладываем на две составляющие XC и YC вдоль координатных осей х, у. Рассмотрим равновесие выделенной части конструкции CB, показанной на рис.7. Запишем уравнение моментов относительно точки С .
mС (Fk ) 0; | M RB sin 300 (a b) RB cos300 a P a cos P asin 0 | |||
| RB |
| M P a cos P asin | |
|
|
| ||
| sin 300(a b) cos300a | |||
|
|
| ||
• Составим уравнения равновесия для всей конструкции АСВ, применив аксиому отвердевания.
Fkx 0; | X A RB cos300 Psin 0 ; |
Fky 0; | Y A P cos RB sin 300 Q 0 ; |
| m A ( F k ) 0 ; | M | A M Q | l 2 P sin 2 a P cos | l |
| R B sin 30 | 0 (b l ) | R B cos 30 | 0 ( 2 a ) 0 . |
|
•Решая совместно уравнения равновесия конструкции находим искомые реакции связей в точке А .
X A RB cos300 Psin
Y A P cos RB sin 300 Q
M A M Q l 2 Psin 2a Pcos l RB sin 300 (b l) RB cos300 (2a)
Подставим числовые значения величин из табл. в полученные выражения, находим неизвестные силы реакции:
studfiles.net
1.22. Определение реакций опор составных конструкций
Статически определимые задачи – задачи, в которых реакции внешних связей находятся из уравнений равновесия.
В
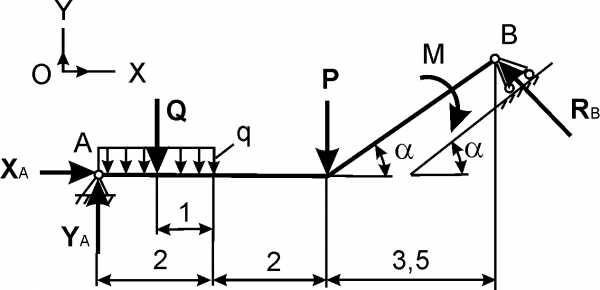
Рис. 1.60
таких задачах число неизвестных реакций равно числу уравнений равновесия, которые могут быть составлены для механической системы (рис. 1.60).Дано: Р, М, q. Определить реакции внешних связей в точках А и В.
Порядок решения таких задач рассмотрен ранее, поэтому сразу же записывают уравнения равновесия для плоской произвольной системы сил:
∑ Fix = 0 = XА – RBsinα = 0; (1)
∑ FiY = 0 = YA – Q – P + RBcosα = 0; (2)
∑ MiA = 0 = – Q·1 – P·4 – M + RBsinα·3,5tgα + RBcosα·7,5 = 0. (3)
Очевидно, что из трех уравнений равновесия легко находятся реакции внешних связей XA, YA, RB.
Статически неопределимые задачи – задачи, в которых реакции внешних связей не могут быть найдены из уравнений статического равновесия, составленных для данной механической системы.
Для балки (рис. 1.61) можно составить только три уравнения равновесия, в которые входят четыре неизвестные реакции XA, YA, XB, YB.
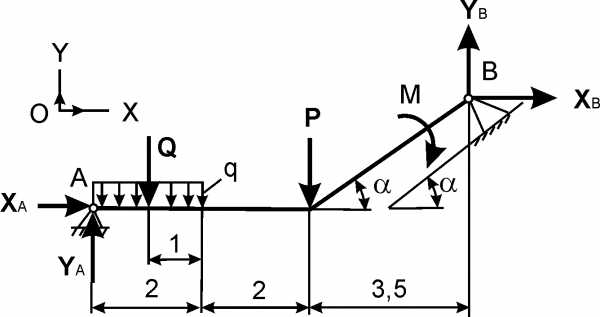
Рис. 1.61
Дано: Р, М, q. Определить реакции внешних связей в точках А и В.
Подробное решение такой задачи (статически неопределимой) рассматривается в курсе сопротивления материалов.
1.23. Алгоритм решения задач на определение реакций внешних связей для составных конструкций
Существует целый класс задач на равновесие составной конструкции, которые могут быть решены методами статики твердого тела. Решение таких задач проводится по следующему алгоритму.
Выбирается система отсчета.
Выделяется механическая система (составная конструкция), равновесие которой рассматривается.
К механической системе прикладываются активные нагрузки. Если задана распределенная нагрузка, то она приводится к сосредоточенной силе.
Согласно аксиоме связей внешние связи, наложенные на механическую систему, отбрасывают, и действие их заменяют соответствующими реакциями.
Записываются уравнения равновесия, соответствующие системе сил, действующей на составную конструкцию (система активных сил и реакций внешних связей).
Установив, что число неизвестных реакций внешних связей превышает число уравнений равновесия, составную конструкцию расчленяют по внутренним связям.
Рассматривают равновесие каждого из тел составной конструкции, которое находится в покое под действием активных сил, реакций внешних связей и реакций внутренних связей.
Для каждого из тел конструкции записывают соответствующие уравнения равновесия.
Полученную систему уравнений решают в наиболее удобной последовательности и находят неизвестные реакции внешних и внутренних связей.
Обычно при расчете используются не все уравнения равновесия, составленные для механической системы и для каждого из тел в отдельности. Поэтому оставшиеся уравнения используют для проверки полученных результатов.
1.24. Варианты курсового задания с 3 «Определение реакций опор составной конструкции (система двух тел)»
Методологию расчета реакций внешних связей, наложенных на составную конструкцию, рассмотрим на примере выполнения курсового задания С 3, которое входит в контрольную работу обучающегося.
Конструкция состоит из двух тел. Определить реакции внешних связей, наложенных на составную конструкцию. Варианты расчетных схем конструкций и приложенные к ним нагрузки приведены в табл. 1.3.
Таблица 1.3
Номер варианта | Расчетная схема | Исходные данные | Определяемые величины |
1 | 2 | 3 | 4 |
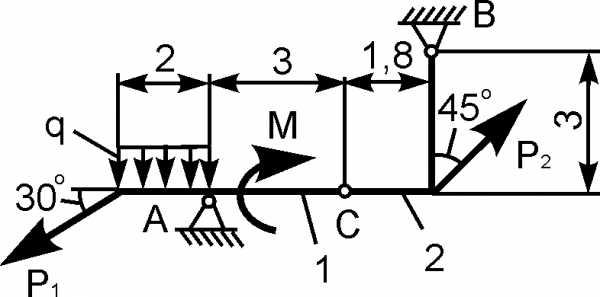
1 | | Р1 = 10 кН; Р2 = 10 кН; М = 6 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
Продолжение табл
. 1.3
1 | 2 | 3 | 4 |
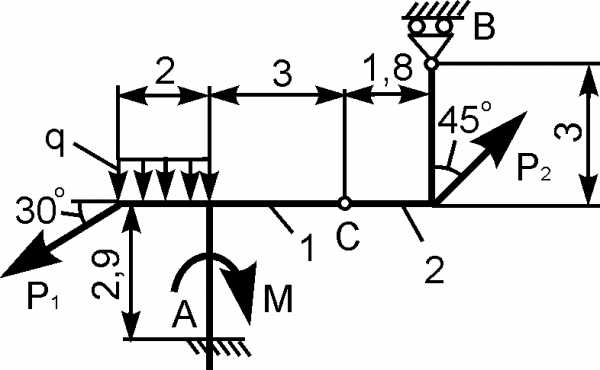
2 | | Р1 = 6 кН; Р2 = 10 кН; М = 12 кН·м; q = 1 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
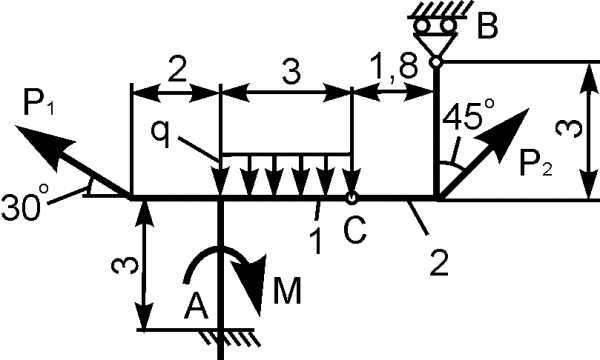
3 | | Р1 = 8 кН; Р2 = 10 кН; М = 3 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
4 | | Р1 = 5 кН; Р2 = 12 кН; М = 4 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
5 | | Р1 = 6 кН; Р2 = 8 кН; М = 3 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
6 | | Р1 = 4 кН; Р2 = 6 кН; М = 10 кН·м; q = 2 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
7 | | Р1 = 7 кН; Р2 = 8 кН; М = 15 кН·м; q = 2 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
8 | | Р1 = 8 кН; Р2 = 8 кН; М = 16 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
9 | | Р1 = 10 кН; Р2 = 10 кН; М = 6 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
10 | | Р1 = 10 кН; Р2 = 3 кН; М = 9 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
11 | | Р1 = 12 кН; Р2 = 5 кН; М = 6 кН·м; q = 1 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
12 | | Р1 = 11 кН; Р2 = 3 кН; М = 8 кН·м; q = 4 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
13 | | Р1 = 10 кН; Р2 = 12 кН; М = 8 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
14 | | Р1 = 10 кН; Р2 = 2 кН; М = 12 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
15 | | Р1 = 15 кН; Р2 = 10 кН; М = 5 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
16 | | Р1 = 16 кН; Р2 = 10 кН; М = 4 кН·м; q = 1 кН/м | XA = ? YA = ? MA = ? RВ = ? |
17 | | Р1 = 17 кН; Р2 = 3 кН; М = 6 кН·м; q = 6 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
18 | | Р1 = 18 кН; Р2 = 9 кН; М = 4 кН·м; q = 8 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
19 | | Р1 = 19 кН; Р2 = 7 кН; М = 12 кН·м; q = 2 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
20 | | Р1 = 20 кН; Р2 = 12 кН; М = 8 кН·м; q = 4 кН/м | XA = ? YA = ? MA = ? RВ = ? |
21 | | Р1 = 21 кН; Р2 = 10 кН; М = 12 кН·м; q = 6 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
22 | | Р1 = 22 кН; Р2 = 12 кН; М = 10 кН·м; q = 5 кН/м | XA = ? YA = ? MA = ? RВ = ? |
23 | | Р1 = 23 кН; Р2 = 9 кН; М = 5 кН·м; q = 8 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
24 | | Р1 = 24 кН; Р2 = 10 кН; М = 12 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
25 | | Р1 = 25 кН; Р2 = 10 кН; М = 8 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
Продолжение табл. 1.3
1 | 2 | 3 | 4 |
26 | | Р1 = 26 кН; Р2 = 16 кН; М = 6 кН·м; q = 6 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
27 | | Р1 = 27 кН; Р2 = 10 кН; М = 4 кН·м; q = 3 кН/м | XA = ? YA = ? XВ = ? YВ = ? |
28 | | Р1 = 28 кН; Р2 = 18 кН; М = 8 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
29 | | Р1 = 28 кН; Р2 = 20 кН; М = 6 кН·м; q = 2 кН/м | XA = ? YA = ? MA = ? RВ = ? |
Окончание табл. 1.3
1 | 2 | 3 | 4 |
30 | | Р1 = 30 кН; Р2 = 20 кН; М = 6 кН·м; q = 1 кН/м | RA = ? XB = ? YВ = ? MВ = ? |
studfiles.net
6.3. Задание с5. Определение реакций опор составной конструкции (система двух тел).
Найти реакции опор и давление одного тела на другое. Схемы конструкций представлены на рис. С5а, на котором все размеры указаны в метрах. Необходимые для решения задач данные приведены в табл. С5-1.
Указание: номер схемы конструкции на рис. С5.1 соответствует последней цифре шифра “б”.
Примечание: 1. На всех схемах тела соединены промежуточным шарниром С.
2. Направление угла α отсчитывается согласно показанным на схемах стрелкам.
Таблица С5-1
Цифра шифра “а” | Р1 | Р2 | q1 | q2 | М1 | М2 | α |
кН | кН/м | кН·м | радиан | ||||
0 | 2 | 4 | 0 | 2 | 5 | 5 |
|
1 | 3 | 4 | 3 | 0 | 4 | 8 |
|
2 | 3 | 2 | 0 | 6 | 2 | 3 |
|
3 | 6 | 3 | 4 | 0 | 6 | 1 |
|
4 | 7 | 10 | 0 | 4 | 3 | 4 |
|
5 | 4 | 7 | 2 | 0 | 7 | 2 |
|
6 | 4 | 8 | 0 | 3 | 1 | 3 |
|
7 | 5 | 6 | 6 | 0 | 6 | 2 |
|
8 | 10 | 3 | 0 | 5 | 10 | 8 |
|
9 | 1 | 2 | 1 | 0 | 4 | 1 |
|
Рис. С5а
При решении задачи С5 рассматриваем равновесие двух твердых тел. В этом случае приходится рассматривать равновесие каждого тела в отдельности, учитывая при этом силы, с которыми действуют друг на друга тела, входящие в систему. Эти силы согласно аксиоме равенства действия и противодействия всегда равны между собой по модулю и противоположны по направлению. Если система находится в покое, то силы, приложенные к каждому из твердых тел, входящих в данную систему, уравновешиваются и, следовательно, для каждого из этих тел можно составить уравнения равновесия так же, как в предыдущих задачах статики.
Решение задач на равновесие системы двух тел возможны двумя способами.
Первый способ. Вначале рассматриваем равновесие всей системы в целом. Прикладываем к системе все внешние силы, распределенные нагрузки и моменты. При этом учитываем, что силы, с которыми тела, входящие в систему, действуют друг на друга, являются внутренними. Следовательно, при равновесии данной системы можно составлять для нее уравнения равновесия, так же как это делали для одного твердого тела, причем в эти уравнения равновесия войдут только внешние силы.
Затем рассматриваем равновесие какого-либо одного тела системы. При этом силы, с которыми на это тело действует другое тело, рассматриваются как силы внешние, которые, наряду с силами заданными, приложенными к точкам данного тела, будут входить в уравнения равновесия.
Второй способ отличается от первого тем, что мы последовательно рассматриваем равновесие каждого тела, входящего в систему.
При решении задач и первым и вторым способами система координат выбирается один раз и в дальнейшем не меняется.
Пример выполнения задания С5.
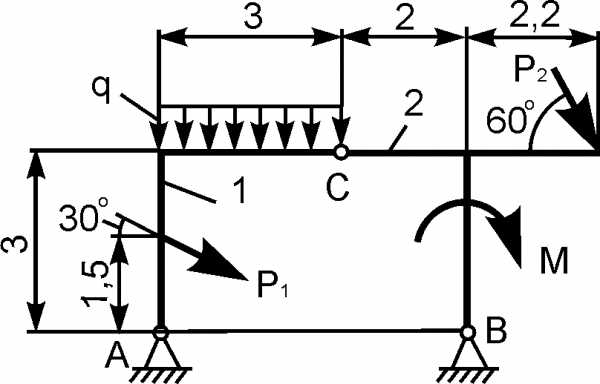
Определить реакции опор и давление в промежуточном шарнире конструкции, изображенной на рис. С5б.
Дано: Р1 = 20 кН; Р2 = 10 кН; qmax = 2 кН/м; М = 12 кН·м; углы и размеры (в метрах) указаны на рис. С5б.
Определить реакции опор А и В и давление в шарнире С.
Решение.
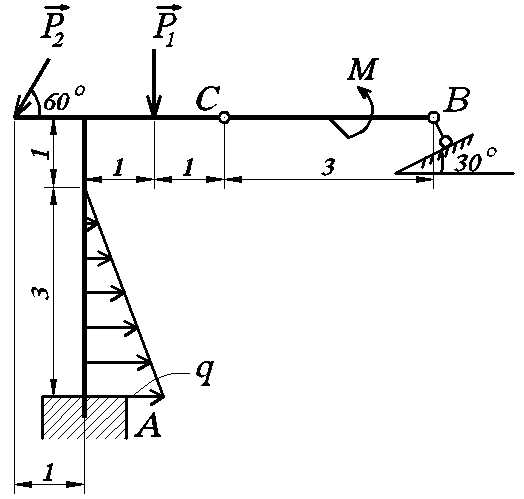
Рис. С5б
Решение задачи ведем в соответствии с краткой методикой решения задач статики (стр. 7) и рекомендациями, приведенными на стр. 17.
1. Рассмотрим вначале равновесие звена ВС (это звено выбираем постольку, поскольку на это звено, как покажем ниже, действуют три неизвестные реакции и задача таким образом является статически определимой. Если вначале рассмотреть левую часть конструкции – звено АС, то эта часть задачи окажется статически неопределимой, т.к. на АС действуют 5 неизвестных реакций). На отдельном рисунке (рис. С5в) изображаем расчетную схему. Выбираем систему координат ХУ.
2. Связями для звена ВС являются шарнир С и стержень, соединяющий точку В с наклонной поверхностью.
3. Отбрасываем
связи, заменяя их действие реакциями:
реакцию шарнира С представляем
составляющими 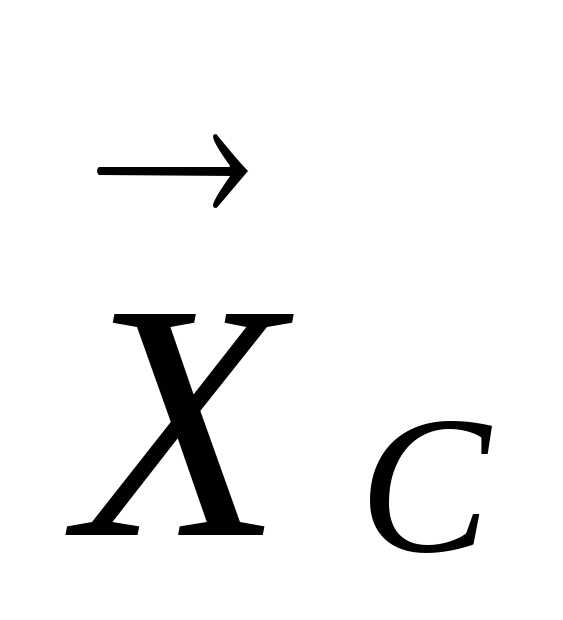 и
и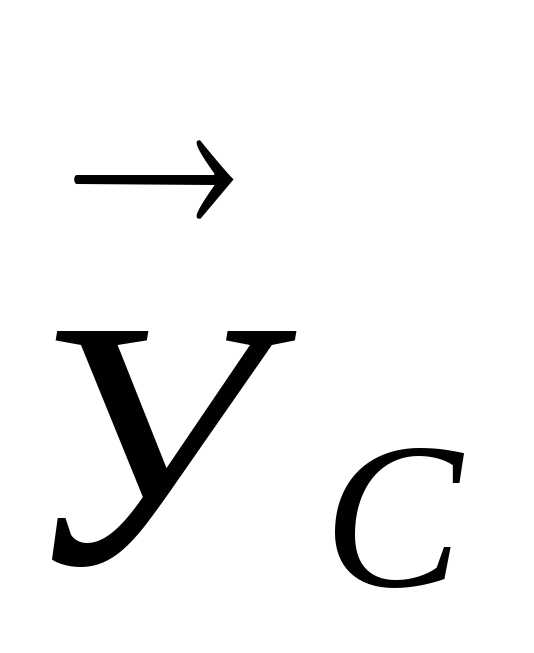 ,
направление которых выбираем произвольно;
реакцию стержня
,
направление которых выбираем произвольно;
реакцию стержня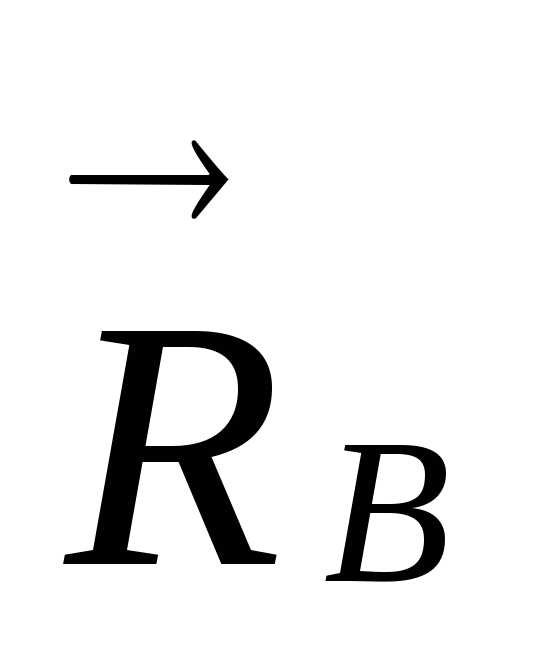 направляем вдоль стержня так, как
показано на рисунке.
направляем вдоль стержня так, как
показано на рисунке.
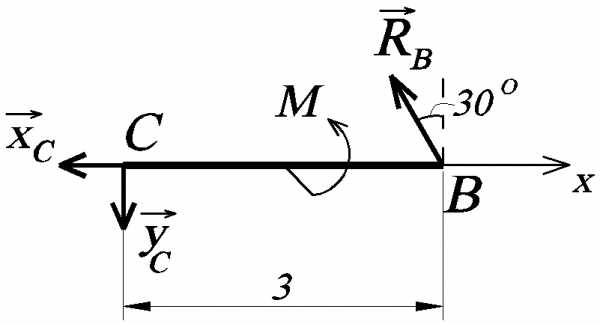
Рис. С5в
Таким образом,
звено ВС находится в равновесии под
действием сил 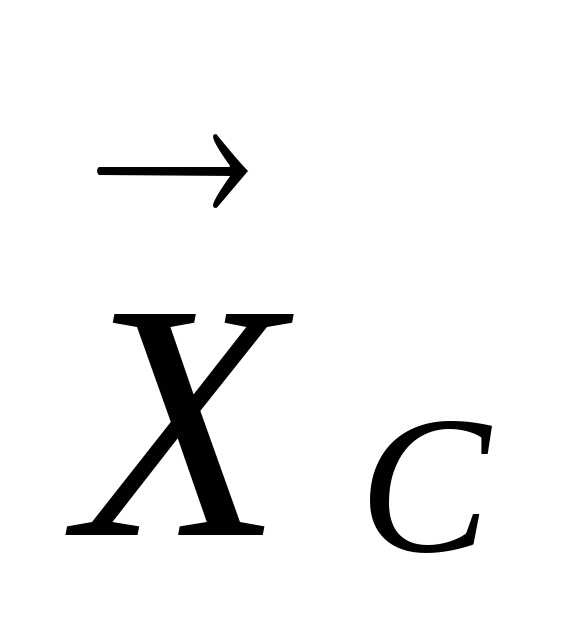 ,
,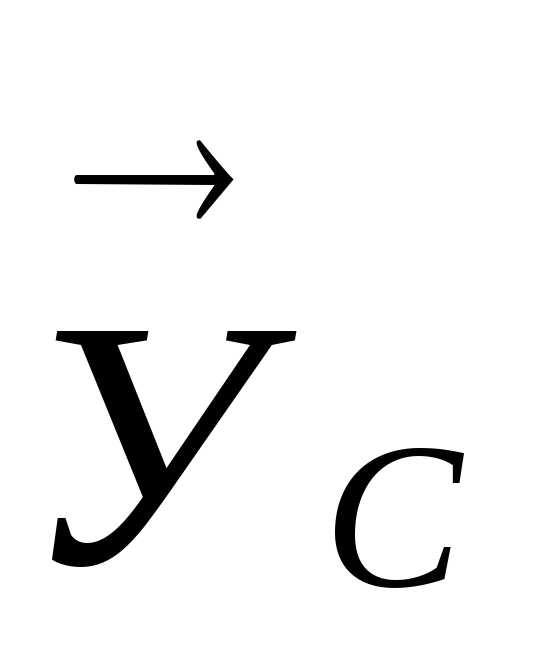 и
и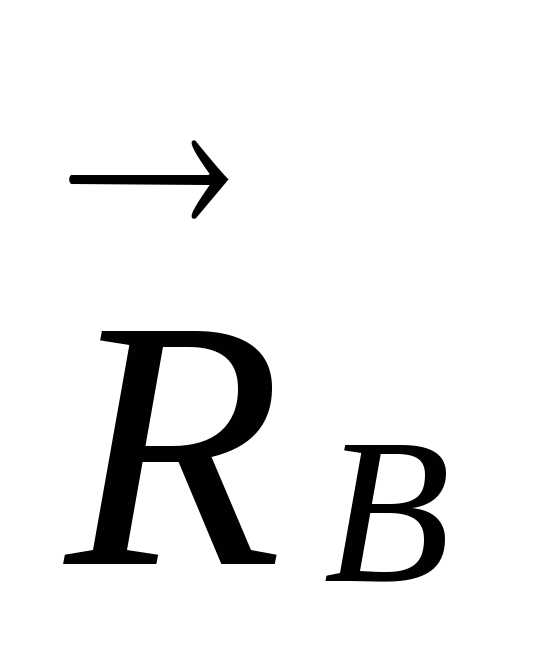 и момента М, расположенных в плоскости
чертежа.
и момента М, расположенных в плоскости
чертежа.
4. Составляем три уравнения равновесия для плоской произвольной системы сил:
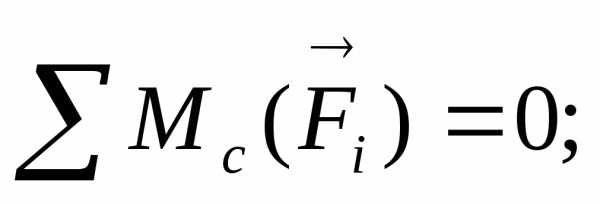 ,
(1)
,
(1)
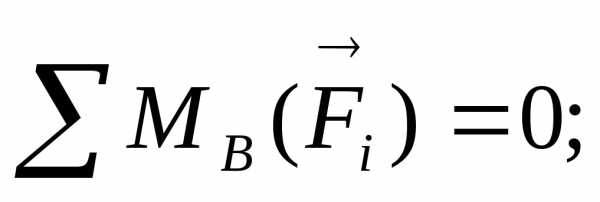 ,
(2)
,
(2)
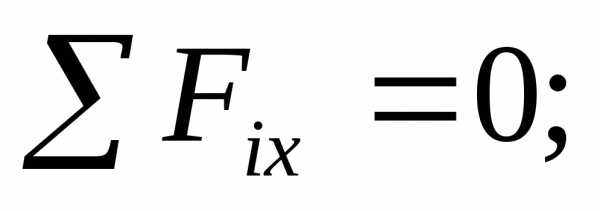 .
(3)
.
(3)
Учитывая условие задачи, из уравнения (1) находим
.
Из уравнения (2)
находим 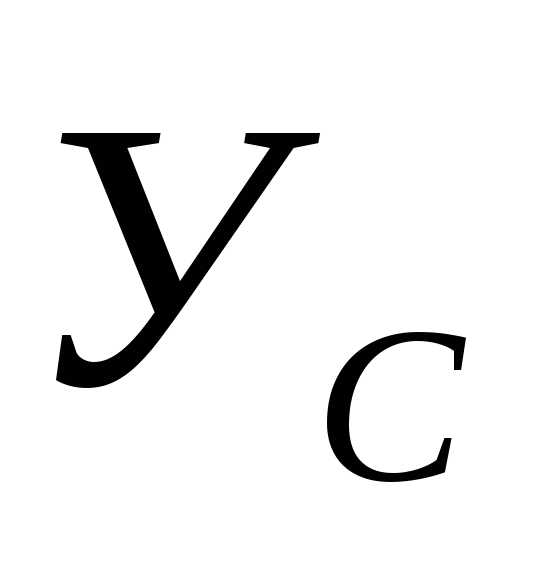 :
:
.
Из уравнения (3)
определяем 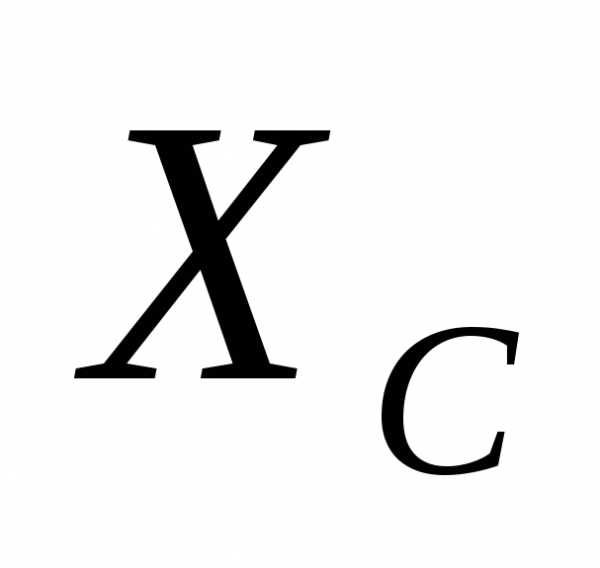 :
:
.
Рассмотрим теперь
равновесие звена АС (расчетная схема
приведена на рис. С5г). Система координат
остается прежней. Неравномерно
распределенную нагрузку с максимальной
интенсивностью qmax заменим сосредоточенной силой 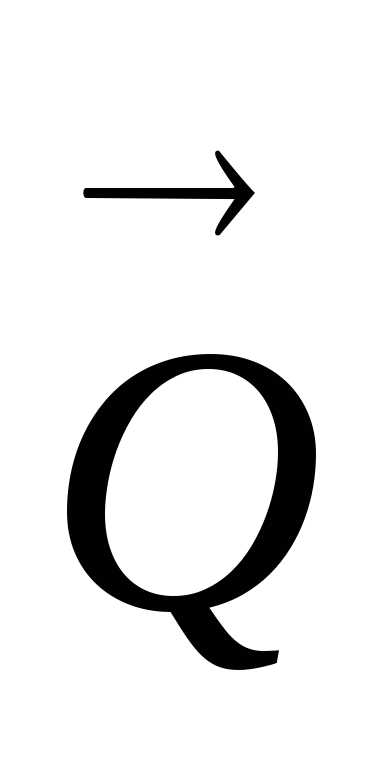 ,
которая направлена в ту же сторону, что
и нагрузка. Модуль этой силы равен:
,
которая направлена в ту же сторону, что
и нагрузка. Модуль этой силы равен:
Линия действия этой силы, приложенной к звену АС, проходит через центр тяжести фигуры распределения (треугольника).
С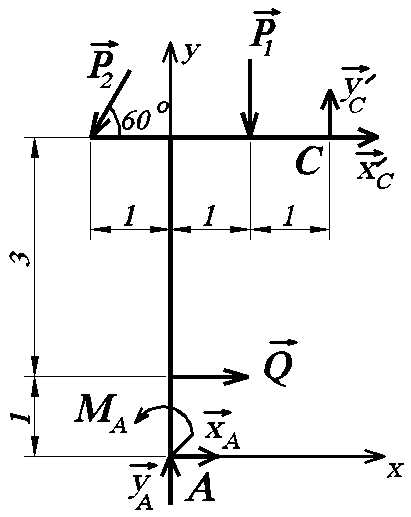 вязями
для АС являются жесткая заделка
(защемление) в опоре А и шарнир С.
вязями
для АС являются жесткая заделка
(защемление) в опоре А и шарнир С.
Показываем
составляющие реакции заделки 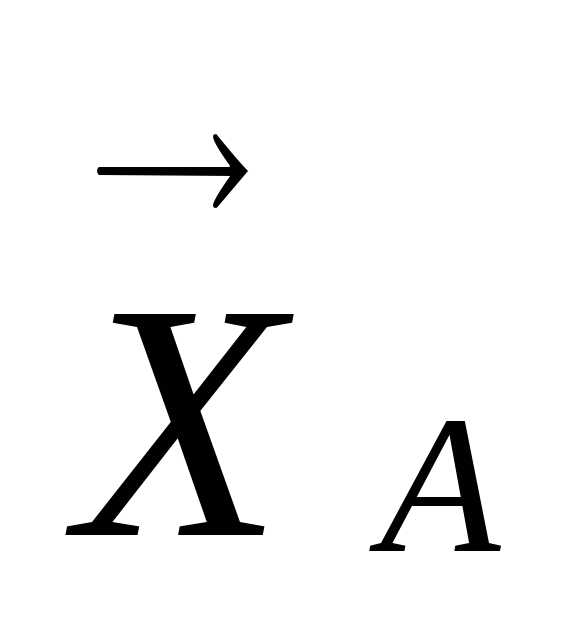 и
и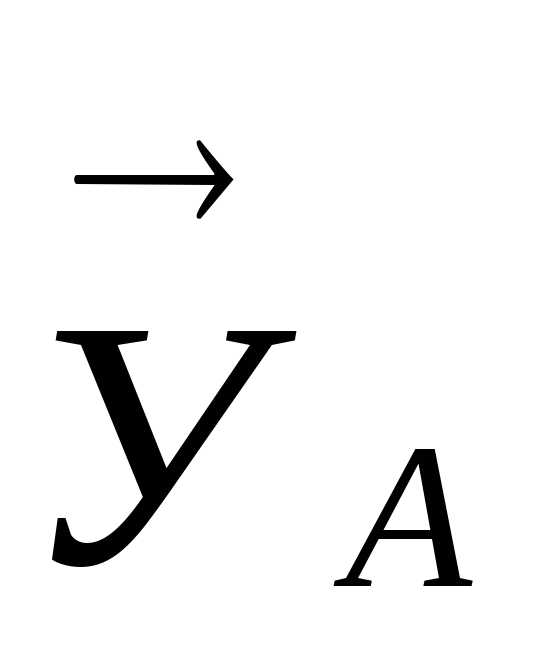 и реактивный момент
и реактивный момент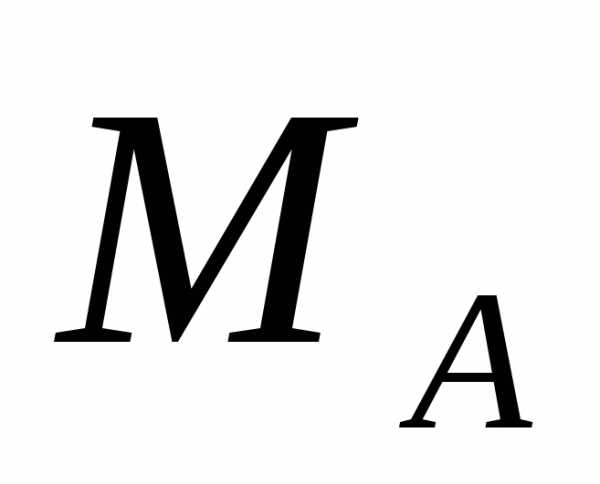 .
Учитываем, что сила действия равна силам
противодействия и направлена в
противоположные стороны, поэтому
реакции
.
Учитываем, что сила действия равна силам
противодействия и направлена в
противоположные стороны, поэтому
реакции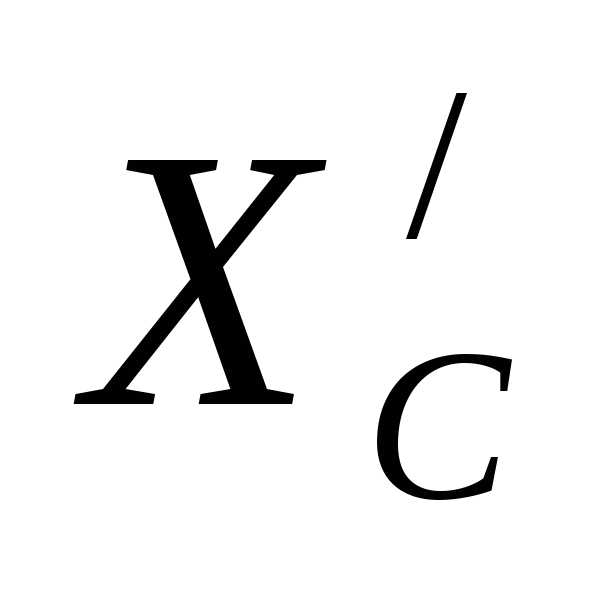 и
и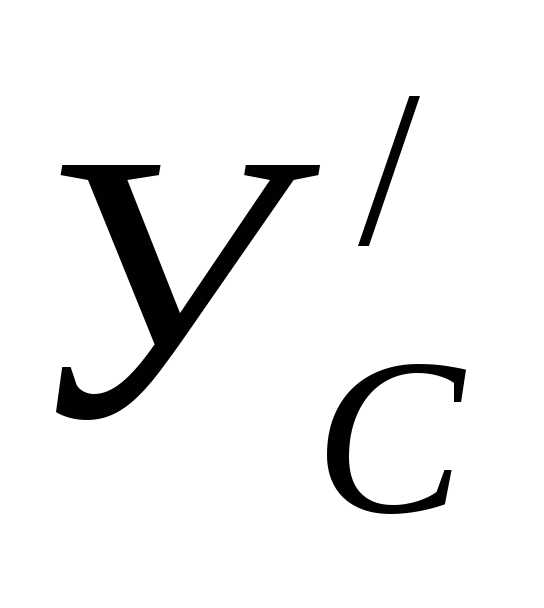 соответственно равны:
соответственно равны:
Рис. С5г
. (4) Звено АС находится
в равновесии под действием сил 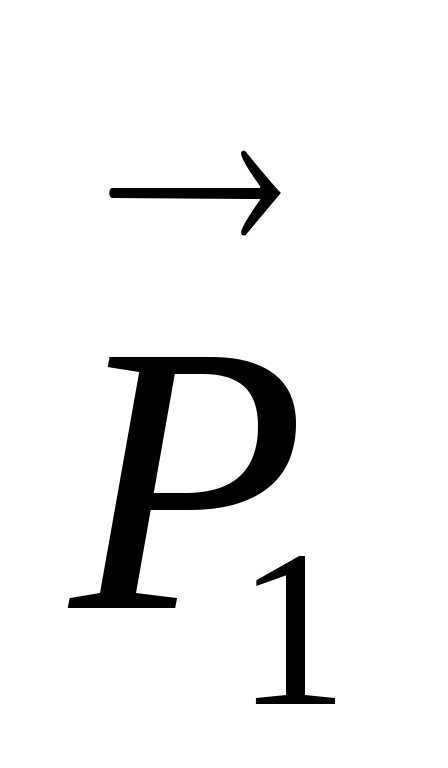 ,
,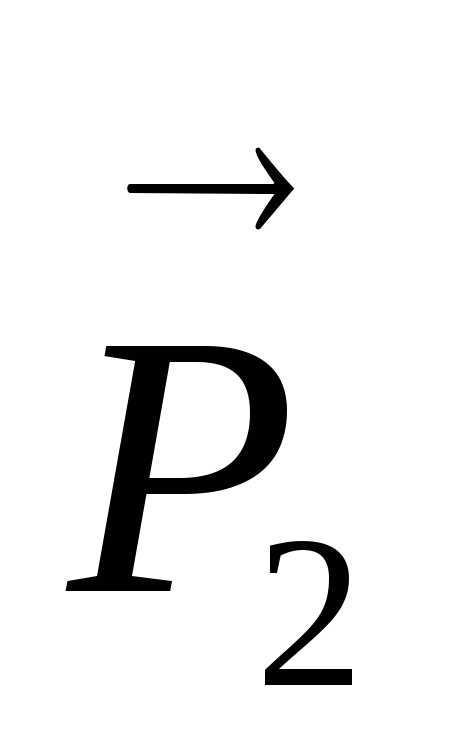 ,
,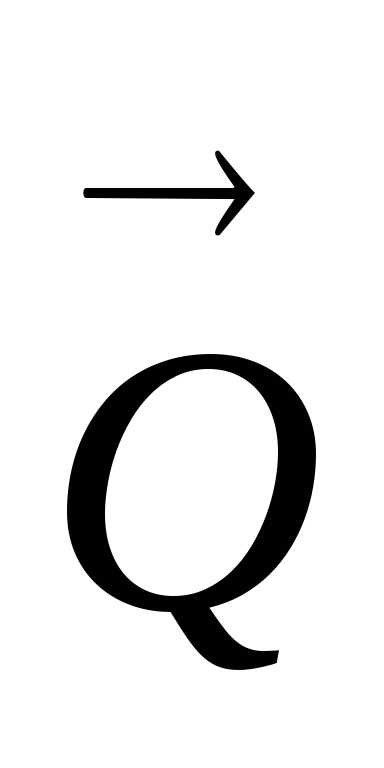 ,
,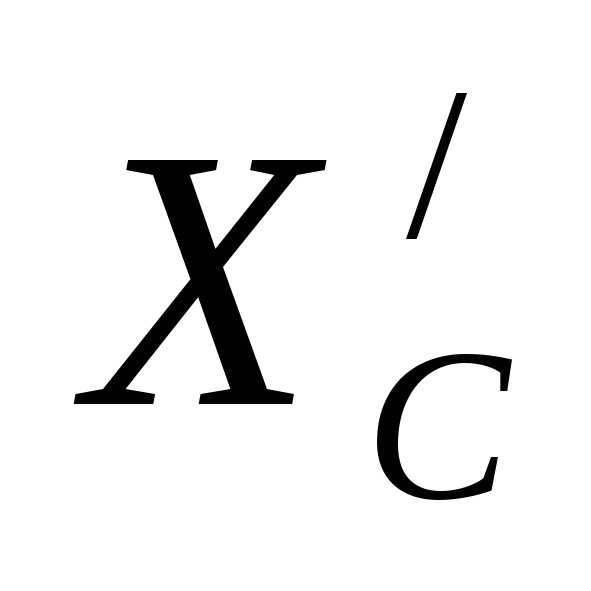 ,
,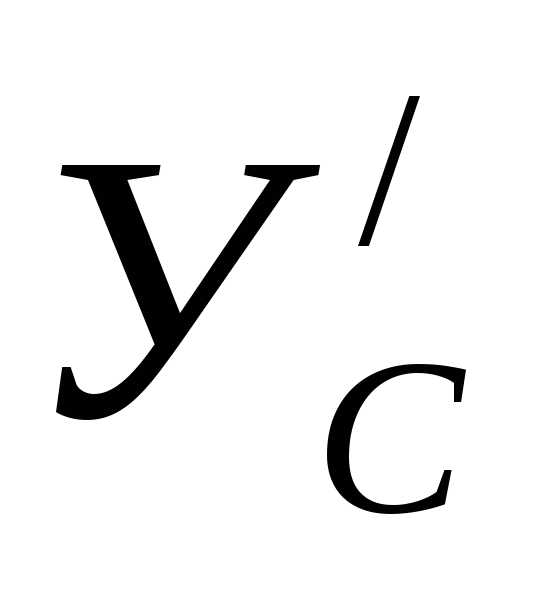 ,
,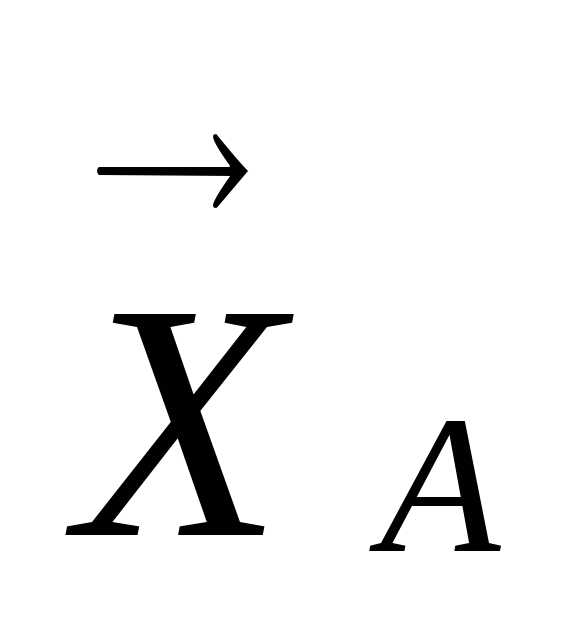 ,
,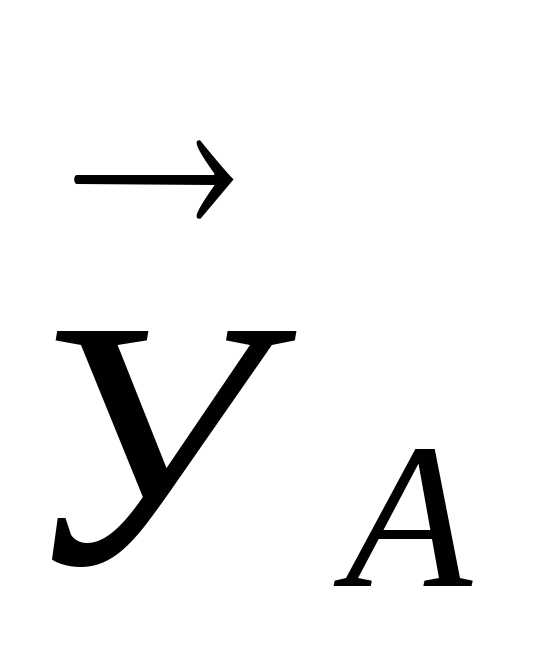 и реактивного момента
и реактивного момента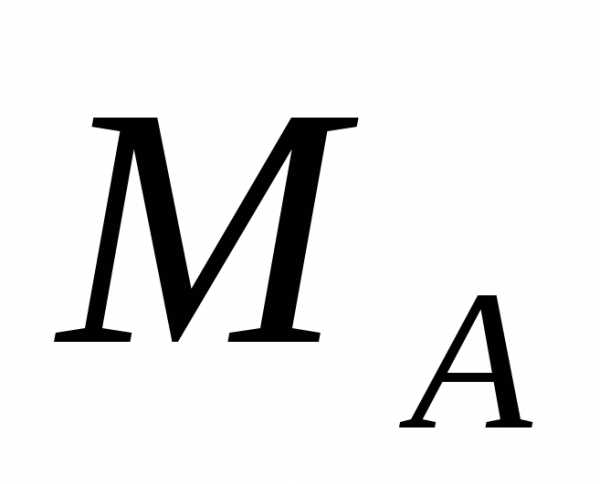 .
Все силы и момент находятся в одной
плоскости.
.
Все силы и момент находятся в одной
плоскости.
Составляем три уравнения равновесия:
, (5)
, (6)
. (7)
Из уравнения (5) с учетом (4) находим
.
Из уравнения (6) находим
.
Из уравнения (7) определяем реактивный момент:
.
Ответ: ,,,,,
.
Обращаем внимание
на то, что при решении систем уравнений
значение каждой из величин должно
подставляться в последующее уравнение
с тем знаком, с которым эта величина
получилась при решении предыдущего
уравнения. Так, при решении задачи С5,
при нахождении реакции 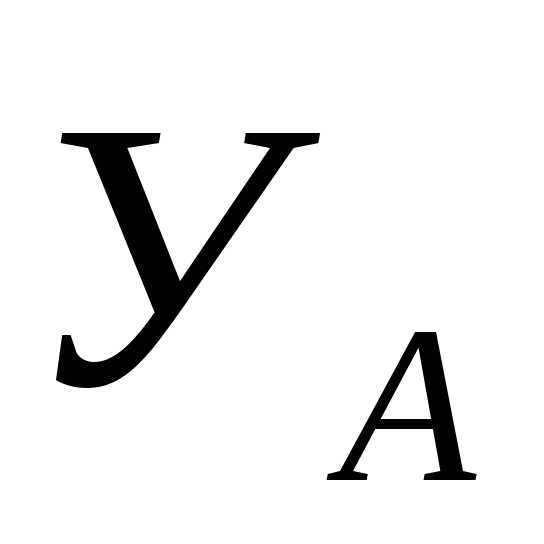 мы подставляем значение
мы подставляем значение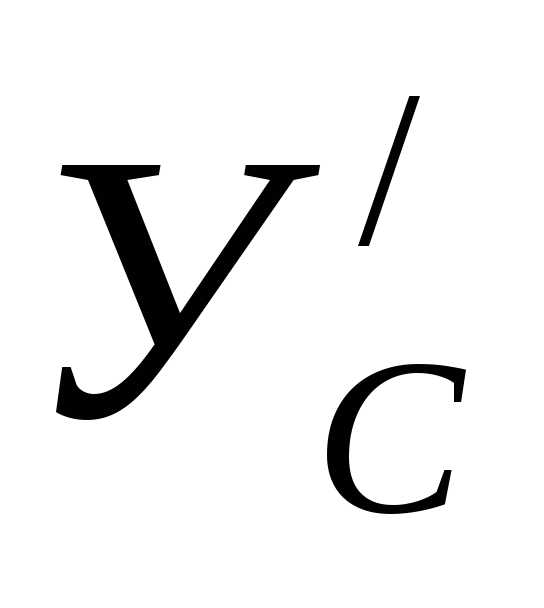 с тем же знаком, какой был получен из
уравнения (2).
с тем же знаком, какой был получен из
уравнения (2).
По этой причине не следует, как это иногда делают, найдя, что, например, , изменять направление этой силы на чертеже, т.к. это может привести к ошибкам при решении последующих уравнений равновесия.
Покажем теперь, как решить эту задачу другим способом.
Н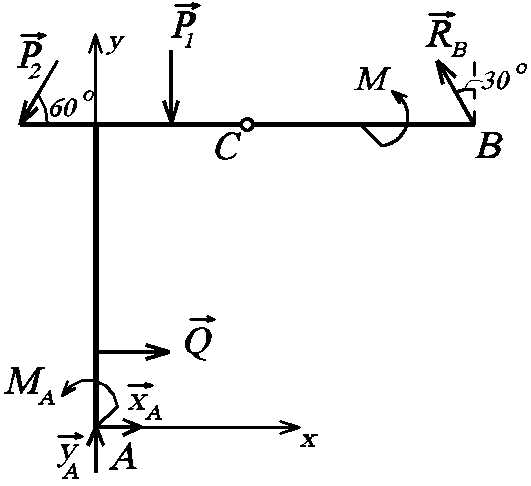 а
первом этапе решения задачи рассмотрим
равновесие всей конструкции АСВ. На
рис. С5д изобразим расчетную схему.
Покажем конструкцию АСВ (без опор А и
В) и внешние силы
а
первом этапе решения задачи рассмотрим
равновесие всей конструкции АСВ. На
рис. С5д изобразим расчетную схему.
Покажем конструкцию АСВ (без опор А и
В) и внешние силы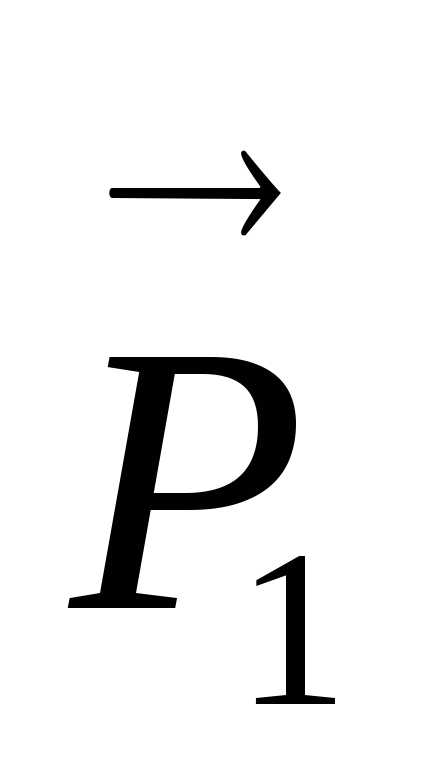 ,
,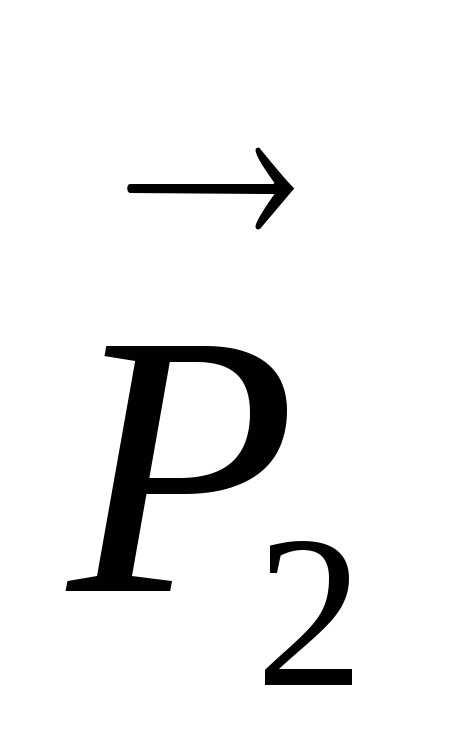 ,
,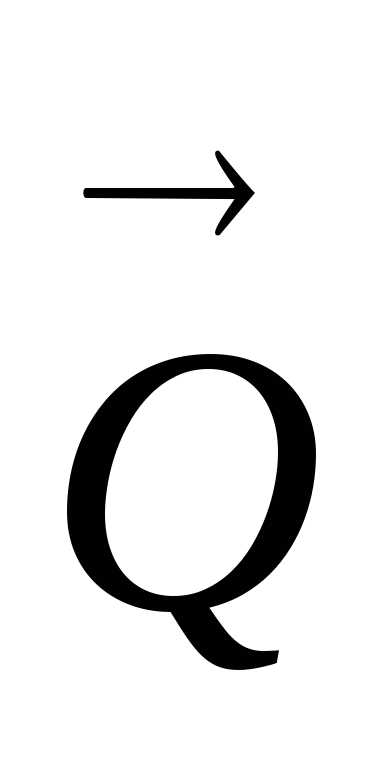 и моментМ.
Связями для конструкции АСВ являются:
и моментМ.
Связями для конструкции АСВ являются:
— опора А – жесткая заделка;
— опора В – стержень.
О
Рис. С5д
тбрасывая связи, покажем на расчетной схеме реакции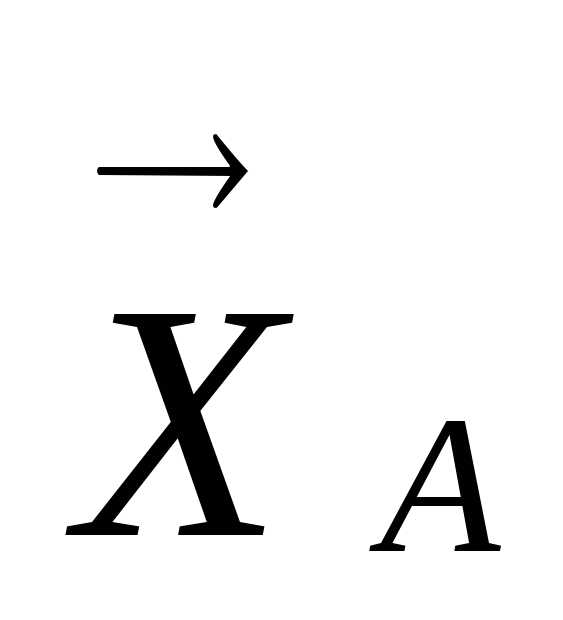 ,
,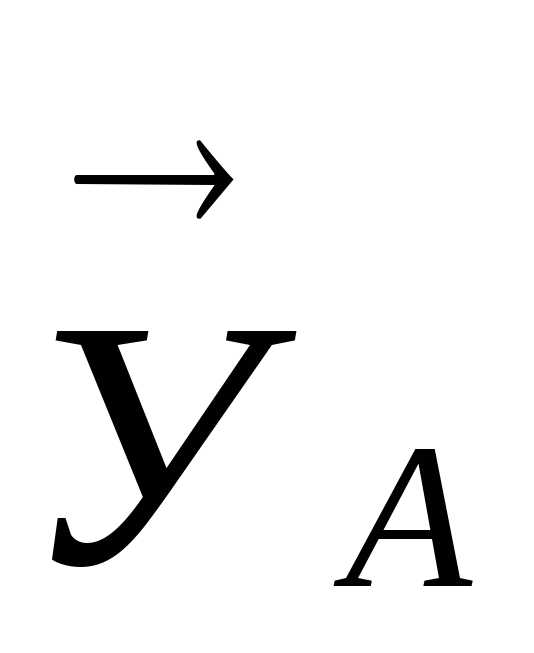 и реактивный момент
и реактивный момент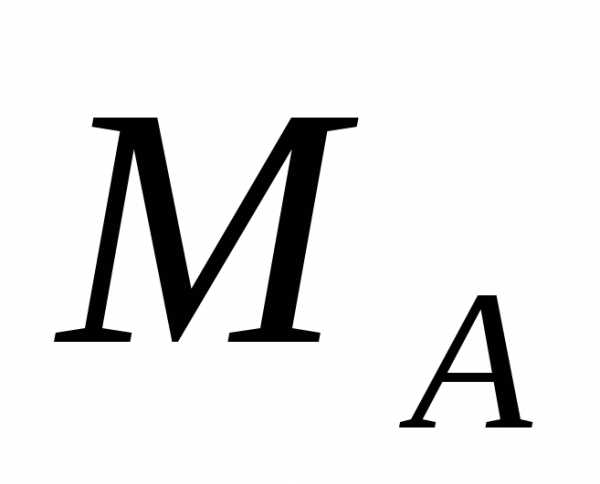 и реакции стержня
и реакции стержня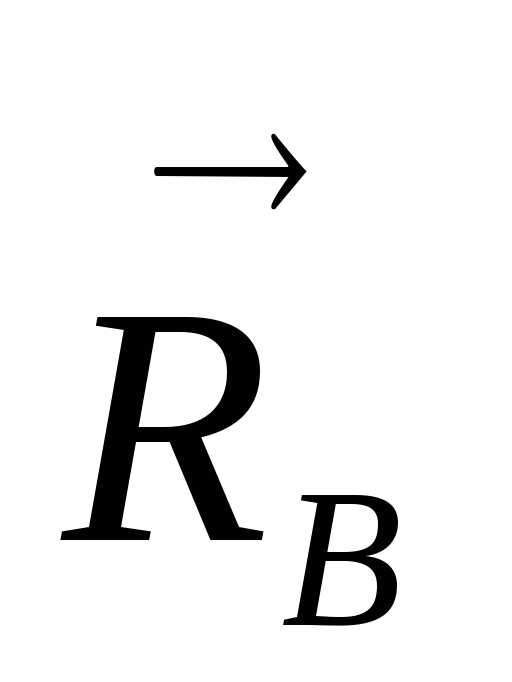 в выбранной системе координат ХАУ.
в выбранной системе координат ХАУ.Таким образом, конструкция АСВ находится в равновесии под действием плоской произвольной системы сил. Составляем три уравнения равновесия:
;
;
.
Полученная система
уравнений не решается относительно
неизвестных, т.к. их количество (четыре: 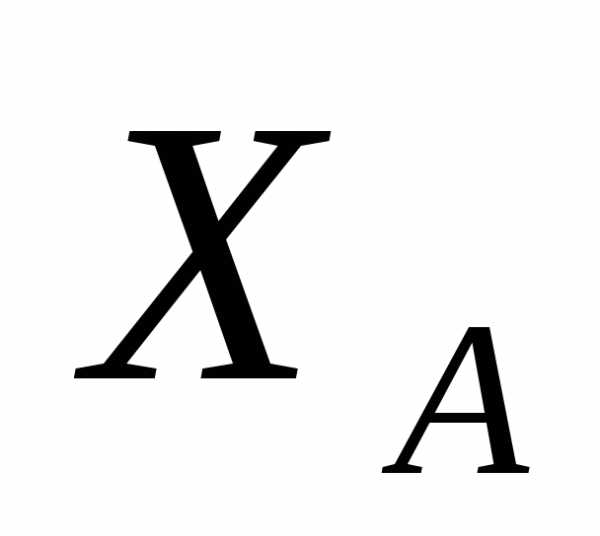 ,
,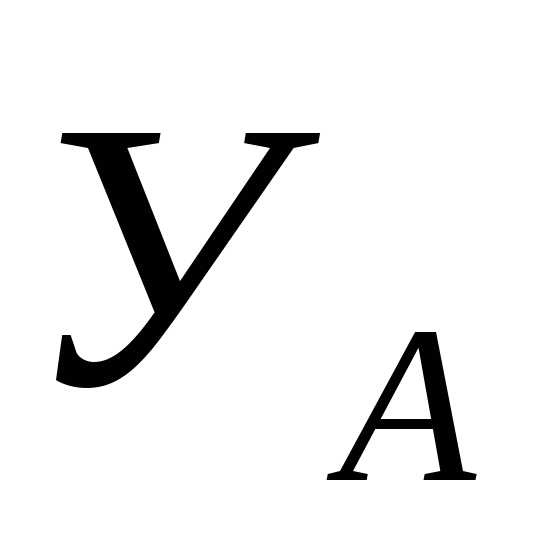 ,
,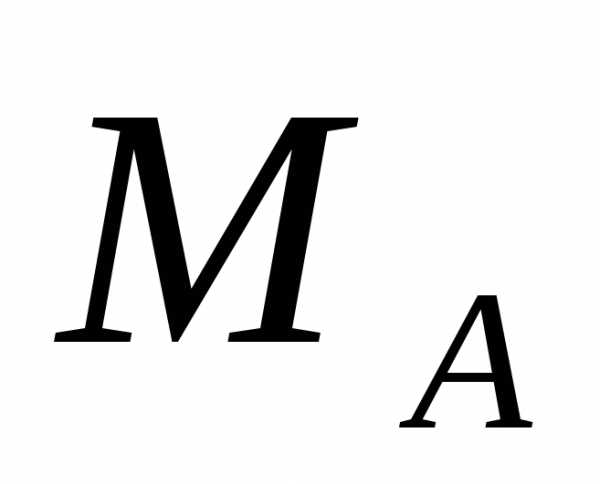 и
и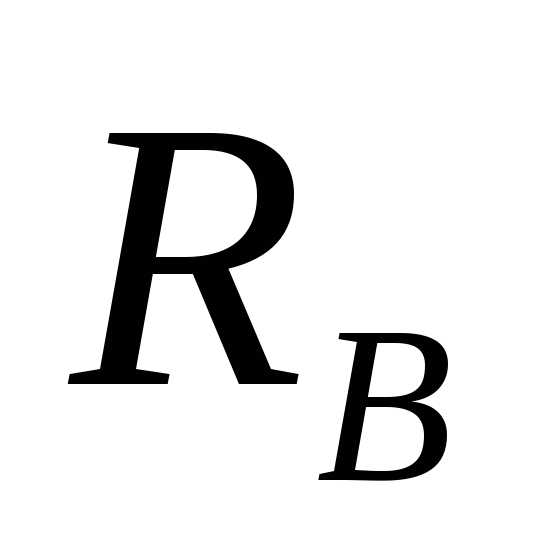 )
превышает количество уравнений. Поэтому
переходим к рассмотрению равновесия
звена ВС. Повторять ход решения задачи
на равновесие звена ВС нет необходимости:
решение этой части задачи, приведенное
выше, дало следующие результаты:;;.
С учетом этих значений находим:
)
превышает количество уравнений. Поэтому
переходим к рассмотрению равновесия
звена ВС. Повторять ход решения задачи
на равновесие звена ВС нет необходимости:
решение этой части задачи, приведенное
выше, дало следующие результаты:;;.
С учетом этих значений находим:
— из уравнения (1):
;
— из уравнения (2):
;
— из уравнения (3):
.
Ответ: ;;;;
; .
Краткий анализ приведенных выше двух способов решения задачи на равновесие системы двух тел показывает, что решать такие задачи целесообразнее, рассматривая последовательно равновесие каждого тела. При этом система из трех уравнений равновесия проще, потому, что содержит, как правило, не более трех неизвестных реакций.
studfiles.net
1.9. Опоры, связи и их классификация
Обычно заданные внешние нагрузки, приложенные к брусу не бывают взаимноуравновешенными; неподвижность конструкции под действием этих нагрузок обеспечивается благодаря наличию опор, соединяющих ее с основанием. Другими словами, для того, чтобы балка могла воспринимать нагрузку и передавать ее на основание, она должна быть соединена с ним опорными устройствами, которые на расчетной схеме моделируются опорными связями. В опорах возникают реакции (реакции связей), которые вместе с заданными нагрузками представляют уравновешенную систему внешних сил, действующих на конструкцию. На практике применяют несколько типов опорных связей, или, как говорят, несколько типов опор. Опорные реакции зависят от устройства опоры. Различают три основных типа опор.
1. Шарнирно-неподвижная опора A (рис. 1.7,а). Эта опора допускает свободный поворот сечения балки над опорой в одной плоскости относительно оси цилиндрического шарнира, но не дает возможности смещаться ни по вертикали, ни по горизонтали. Подразумевается, что шарнир не оказывает сопротивления вращению примыкающего к нему сечения балки. В такой опоре направление действия опорной реакции неизвестно, поэтому для ее определения ее представляют разложением на две составляющие, действующие в направлении осей принятой общей системы координат.
2. Шарнирно-подвижная опора A (рис. 1.7,б). Эта опора допускает перемещение в одном направлении, например по горизонтали, и поворот сечения над опорой вокруг цилиндрического шарнира. В такой опоре возникает одна реакция, которая направлена перпендикулярно плоскости опирания катков (вдоль опорной связи).
3. Заделка A (рис. 1.7,в). Такая опора не допускает поворота и перемещения по двум направлениям сечения балки, примыкающего к заделке. Реакции в заделке состоят из вертикальной силы, горизонтальной силы и момента.
а) б) в)
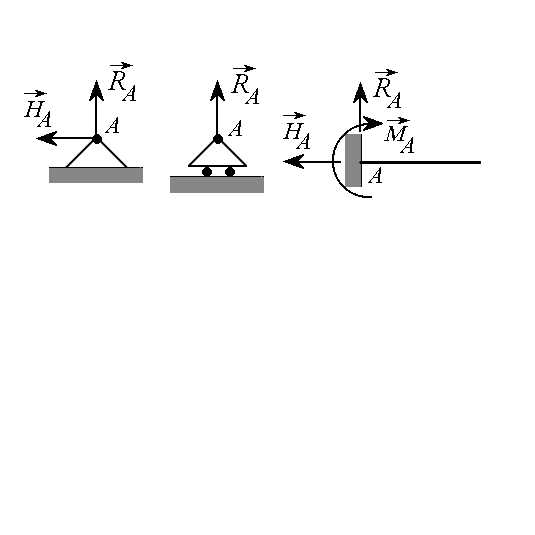
Рис. 1.7
1.10. Статически определимые и статически неопределимые балки
При определении опорных реакций балки будем пользоваться уравнениями статики, выражающими условия равновесия всех внешних сил, приложенных к ней (в том числе и реакций). Таких уравнений для сил, лежащих в плоскости, можно записать три. Следовательно, в случае наличия трех неизвестных реакций их можно определить при помощи уравнений статики. Поэтому балки, в которых число уравнений равновесия достаточно для определения всех опорных реакций, называют статически определимыми. Балки, для определения опорных реакций которых уравнений статики недостаточно, называют статически неопределимыми.
1.11. Определение реакций в опорных связях
Поскольку внешняя нагрузка обычно бывает задана, то для вычисления всех действующих на балку сил приходится определять неизвестные опорные реакции. Эта задача подробно изучалась в курсе теоретической механики. Напомним вкратце методы определения реакций. Уравнения равновесия тела, загруженного плоской системой сил, в связанной с балкой системе координат xyzмогут быть записаны в трех вариантах:
1) ; здесь сумма моментов берется относительно любой точкио, лежащей в плоскости действия сил;
2) ; в этом варианте осьoxне должна быть перпендикулярной прямойAB;
3); применяя этот вариант, необходимо помнить, что точкиA, B иCне должны лежать на одной прямой. При определении опорных реакций необходимо стремиться так составить уравнения, чтобы в каждое из них входило только одно неизвестное. Этого можно добиться, составляя два уравнения моментов относительно опорных точек (вариант 2). Тогда, определив опорные реакции, обычно проводят проверку по уравнению проекций всех сил на вертикальную ось, т. е..
Иначе говоря, сумма вертикальных реакций должна равняться сумме всех вертикальных внешних сил.
studfiles.net