3.2. Пример определения нагрузки на главную балку в балочной клетке нормального типа

Исходные данные принимаем по примеру п. 2.1.5.

Шаг главных балок В = 5 м; пролет главной балки А = 12 м; нормативная нагрузка на балку настила — q^н_бн = 0,208 кН/см; расчетная нагрузка на балки настила — q^р_бн 0,2483 кН/см; вес балки настила =1,575 кН; шаг балок настила –а = 1 м; пролет балок настила — =В = 5 м.

Нормативное значение сосредоточенной силы на главную балку по (3.2):

0,208·500+1,575 = 105,575 кН.

Рис. 3.2. Расчетная схема главной балки к примеру 3.2

Эквивалентная нормативная погонная нагрузка на главную балку по (3.1):

105,575/100 = 1,05575 кН/см.

Расчетное значение сосредоточенной силы на главную балку по (3. 4):

0,2483·500+1,575·1,05=125,8 кН.

Эквивалентная погонная расчетная нагрузка на главную балку по (3.3):

125,8/100 = 1,258 кН/см.

3.3. Пример определения нагрузки на главную балку в балочной клетке усложненного типа

Схему балочной клетки см. на рис. 3.1.

Исходные данные принимаем по примеру 2.2.4. Шаг главных балок

В = 5 м; пролет главной балки А = 12 м; нормативная погонная нагрузка на вспомогательную балку — q^н_вб = 0,63 кН/см; расчетная погонная нагрузка на вспомогательную балку — q^р_вб = 0,74 кН/см; вес вспомогательной балки

= 2,85 кН, шаг вспомогательных балок – а = 3 м; пролет вспомогательной балки- =В = 5 м.

Нормативное значение сосредоточенной силы на главную балку по (3.2):

0,63·500+2,85 = 317,85 кН.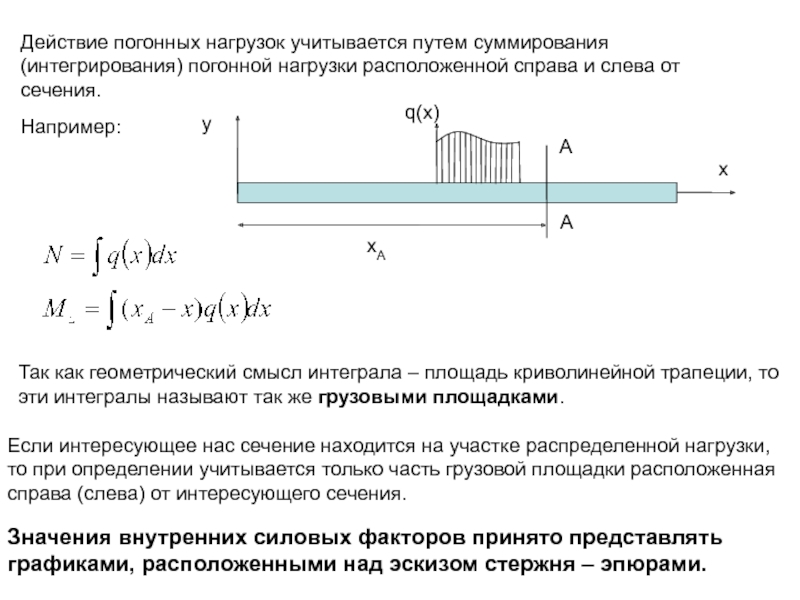

Эквивалентная нормативная погонная нагрузка на главную балку по (3.1):

317,85/300=1,06 кН/см.

Расчетное значение сосредоточенной силы на главную балку по (3.4):

0,74·500+2,85·1,05=372,99 кН.

Эквивалентная погонная расчетная нагрузка на главную балку по (3.3):

372,99/300 = 1,243 кН/см.

3.4. Определение внутренних усилий в главной балке

Статический расчет главной балки производится как для разрезной однопролетной шарнирно опертой балки. За расчетные усилия принимаются максимальные значения изгибающего момента и перерезывающей силы, вычисленные по расчетным значениям нагрузок.

, (3.7)

, (3.8)

где — коэффициент, учитывающий собственную массу главной балки, принимаемый по табл. 3.1.

_{Значения коэффициента}

Таблица 3. 1

Длина балки, м	6	9	12	15	18
	1,03	1,04	1,05	1,06	1,08

3.4.1. Пример определения усилий в главной балке

Расчетная погонная нагрузка на главную балку 1,243 кН/см.

Пролет главной балки =А = 12 м.

Коэффициент, учитывающий собственную массу главной балки =1,05. Расчетную схему см. на рис. 3.1, б.

Расчетный изгибающий момент главной балки по (3.2.1):

1,243·1200²·1,05/8 = 234927 кН·см.

Расчетная перерезывающая сила главной балки по (3.2.2):

1,243·1200·1,05/2 = 783,09 кН.

3.5. Подбор сечения главной балки

В соответствии с требованиями СНиП [4] расчет разрезных балок из стали с пределом текучести до 530 МПа (53 кН/см²), несущих статическую нагрузку следует выполнять с учетом развития пластических деформаций в наиболее нагруженном сечении (в середине пролета главной балки).

Сечение главной балки назначается в зависимости от величины требуемого момента сопротивления сечения

, (3.9)

где — коэффициент, учитывающий работу балки в упругопластической стадии работы материала, значение которого на стадии подбора сечения можно принять равным 1.12;

R_y — расчетное сопротивление стали, табл. 51* [4];

= 1 — коэффициент условий работы [4].

а) Определение высоты сечения главной балки.

Высота главной балки определяется из трех условий:

Рис. 3.2 Сечение главной балки

1 — конструктивно, в зависимости от пролета балки: h_констр=;

2 — из условия наименьшего расхода стали на балку

, (3.10)

где k — конструктивный коэффициент, значение которого для сварной балки принимается равным 1,15; t_w — толщина стенки, предварительно назначаемая 1 см;

3 — из условия обеспечения необходимой жесткости балки при полном использовании несущей способности материала, т.е. из условия обеспечения предельного прогиба f_и = l/350 (табл. 19 [2] поз.2,д).

. (3.11)

Высоту главной балки целесообразно назначать близкой к оптимальной и кратной 10 см при соблюдении условия h_min< h< h_опт.

б) Расчет и конструирование стенки главной балки.

Толщина стенки t_w определяется по трем формулам:

1) По эмпирической формуле

(мм) (3.12)

2) Из условия прочности стенки на срез

, (3.13)

где R_s = 0,58

R_y — расчетное сопротивление стали срезу.

3) Из условия обеспечения местной устойчивости стенки, без укрепления ее продольным ребром жесткости

. (3.14)

Окончательная толщина стенки (t_w) назначается не меньше второго и третьего значений. Кроме того, толщину стенки согласовывают с сортаментом на листовую сталь по ГОСТ 19903-74^*; t_w = 0,8; 1.0; 1.2; 1.4; 1.6; 1.8 см.

Стенки высоких балок (2 м и более) укрепляются продольными ребрами жесткости, так как в противном случае они получаются очень толстыми и делают балку тяжелой и неэкономичной. Для таких балок третье условие не учитывается.

Высоту стенки h_w определяют предварительно задавшись приблизительной толщиной поясов

t_f из соотношения t_f = 2t_w

h_w= h — 2t_f. (3.15)

в) Расчет и конструирование поясов главной балки.

В сварных балках пояса обычно принимаются из универсальной стали по ГОСТ 82-70* толщиной не более 32 мм. Есть рекомендации назначать толщину полки не менее 12 мм и не более 3t_w.

12 мм< t_f < 3t_w.

Ширину горизонтальных листов b_f обычно принимают равной 1/3 -1/5 высоты балки из условия обеспечения ее общей устойчивости:

b_f = (1/3-1/5)h.

Кроме того, ширину пояса рекомендуется назначать не менее 18 см по конструктивным соображениям и не более 30 толщин пояса из условия обеспечения местной устойчивости пояса.

18 см < b_f < 30t_f

Учитывая вышеизложенные рекомендации, определяются размеры поясных листов в зависимости от требуемого момента инерции поясов

(3.16)

Требуемая площадь сечения поясных листов

, (3.17)

где h₀ = h — t_f.

Ширина поясных листов

(3.18)

Из условия обеспечения местной устойчивости сжатого пояса балки в соответствии [4], ширину свеса b_ef, определяемую как b_ef = b_f / 2 — t_w / 2, проверяют по формуле

b_ef / t_f < 0,11h

ef / t_w, (3. 19)

где h_ef = h₀.

Если условие (3.19) не выполняется, необходимо изменить параметры сечения и сделать проверку заново.

г) Определение геометрических характеристик сечения

главной балки.

Окончательно назначив все размеры сечения в соответствии с сортаментом на листовую сталь по ГОСТ определяют геометрические характеристики сечения: момент инерции J_х и момент сопротивления W_х

, (3.20)

. (3.21)

д) Проверка прочности принятого сечения по нормальным

напряжениям.

Выполняется в соответствии с [4] по формуле:

, (3.22)

где — по таблице 66[4], в зависимости от отношения площади полки А_fк площади стенки А_w.

е) Проверка жесткости главной балки.

Если принятая высота сечения больше минимальной: h > h_min, то жесткость балки обеспечена.

Вес погонного метра и допустимая нагрузка

• Главная
• Вычислить
• Оплетка металлическая (ОМ)
• Вес погонного метра и допустимая нагрузка

Распечатать

Расчет допустимой нагрузки на оплетку, а также погонного веса оплетки при известных параметрах:

Название	Ед.	Диапазон	Значение
Параметры оплетки:
Количество прядей, Ns	шт		2436486496
Количество нитей в пряди, Nw	шт	от 3 шт до 18 шт
Диаметр нити, Dw	мм	от 0,2 мм до 0,65 мм
Угол плетения, α	град	от от 30° до 70°
Параметры стали для изготовления нити:
Плотность стали, ρ (Плотность стали SUS304 равна 7900 кг/м3, стали SUS 321 — 7950 кг/м3)	кг/м3
Напряжение предела прочности, ςвр (Для мягкой стали SUS304 равно ~880 Н/мм2)	Н/мм2
Параметры рукава, планируемого для оплетения:
Диаметр условно-проходной рукава, DN	мм		6810121620253240506580100125150200250300
Допустимое осевое усилие на однослойную оплетку, Fax1: Расчет допустимого усилия производится с коэффициентом запаса 3	H:
Допустимое осевое усилие на двухслойную оплетку, Fax2 Двухслойная оплетка имеет на 87% большую допустимую нагрузку, чем однослойная	H
Допустимое давление в рукаве на однослойную оплетку, Pb Рассчитанное давление является пределом прочности оплетки, но не рукава. При расчете важно не путать эти величины. Предел прочности рукава в целом в значительной степени зависит от его конструкции и способа присоединения оплетки к арматуре.	Bar
Масса погонного метра (ориентировочно), m Использовать только для ориентировочных расчетов. Точное значение может значительно разниться в зависимости от используемого оборудования при производстве, его настроек, а также качества материалов.	кг

ФИО *

Телефон *

Основы текущего

Главная > Поддержка > Основы тока

Основы тока

Ток подразделяется на два типа: Постоянный ток (DC): постоянный ток однонаправленный поток электрического заряда, что означает, что его направление остается постоянный. Примерами источника питания постоянного тока являются батарея и солнечная батарея, и т. д. Постоянный ток или постоянный ток подходит для использования с устройствами постоянного тока не менять полярность. Переменный ток (AC): AC – это электрический ток, который направление циклически меняется. Обычная форма волны переменного тока питание синусоидальное с частотой 50 или 60 Гц. Примерами источников питания переменного тока являются источники питания общего пользования. к жилым домам и предприятиям, аудио- и радиосигналы, и т. д. Потребляемая электрическая мощность Электрическая мощность, потребляемая электроприборами постоянного тока, может быть определяется напряжением, на котором они работают, и током, на который они потребляется. Потребляемая мощность постоянного тока = Напряжение (В) X Ток нагрузки (Ампер) = Вт Электрическая мощность, потребляемая электроприборами переменного тока, больше сложнее, чем электрические приборы постоянного тока, потому что направление тока периодически изменяется, то значение напряжения и ток следует измерять в терминах RMS (среднеквадратичный) исключить изменение направления тока. Электроприборы переменного тока или нагрузки переменного тока классифицируются на два типа следующим образом; Линейная нагрузка — электрическая нагрузка, потребляющая мощность переменного тока как реальная мощность, так и кажущаяся мощность с коэффициентом мощности 1. Примером линейной нагрузки является лампа накаливания. Нелинейная нагрузка генерирует гармоники токи в дополнение к исходному переменному току и его коэффициент мощности меньше 1. Примеры нелинейной нагрузки люминесцентные лампы, электронный балласт люминесцентных лампа, ПК и телевизор и т. д. Каждый тип нагрузки переменного тока имеет разные характеристики потребляемого тока а на рисунках ниже показана токовая характеристика линейного нагрузка и нелинейная нагрузка с одинаковым входным напряжением при одинаковой мощности рейтинг нагрузки. Токовая характеристика лампы накаливания , с коэффициентом мощности = 1 Токовая характеристика комплекта ПК, у которого коэффициент мощности = 0,52

Что такое Вт и ВА? Ватт единица мощности. Он измеряет уровень энергии использования или производства и его символом является W . ВА или вольт-ампер – единица потребляемой электроэнергии. при нелинейной нагрузке. Он измеряет кажущуюся мощность. Пример Компьютер потребляет энергию как нелинейную нагрузку, затем ВА должна быть единицей измерения, указывающей потребляемую мощность на ПК. ИБП используется для питания ПК после пропало питание, тогда мощность ИБП должна быть указана в ВА также. Измерение мощности переменного тока (Ватт) Для измерения фактической мощности переменного тока электроприборов, измерение требуется оборудование под названием «Измеритель мощности». Этот оборудование будет измерять напряжение и ток одновременно и сделайте расчет, чтобы получить мощность в «Ваттах». На следующих рисунках показаны размеры ПК с 17-дюймовым экраном. контролировать энергопотребление с помощью измерителя мощности. Расчет полной мощности переменного тока (ВА) Мы можем измерить мощность того же набора ПК с 17-дюймовым экраном. контролировать, измеряя напряжение (RMS) и ток (RMS) после расчет мощности путем умножения рабочего напряжения на потребляемое текущий. Полная мощность переменного тока = Напряжение (СКЗ) X Ток нагрузки (СКЗ) = ВА = 229,3 X 1,10 = 252,23 ВА Отношение мощности переменного тока и Полная мощность переменного тока Мощность переменного тока (Ватт) = Полная мощность переменного тока X Коэффициент мощности = (ВА) X Коэффициент мощности Коэффициент мощности (пф) системы электроснабжения переменного тока определяется как отношение реальной мощности к полной мощности и составляет число от 0 до 1. Коэффициент мощности линейной нагрузки равен единице (=1) и коэффициент мощности нелинейной нагрузки меньше единицы (<1). Из образца ПК с 17-дюймовым монитором мы можем рассчитать коэффициент мощности по Вт 132 пф = ВА X pf = 252,23 X pf = 132 / 252,23 = 0,523

Что такое линейные и нелинейные нагрузки и как улучшить коэффициент мощности

Что такое линейные и нелинейные нагрузки?

Сегодня мы хотели бы продолжить наш разговор о коррекции коэффициента мощности и наших советах по его улучшению. Обязательно прочитайте первую часть, если вы еще этого не сделали!

Ранее мы писали о линейных и нелинейных нагрузках , но толком не объяснили, что они из себя представляют.
Основное различие между ними заключается в том, как они потребляют ток от формы волны сетевого питания.
В случае линейных нагрузок соотношение между кривыми напряжения и тока синусоидальное и ток пропорционален напряжению в любой момент времени.

К линейным нагрузкам относятся, например, двигатели, трансформаторы, реакторы или конденсаторы.

Наоборот, в случае нелинейных нагрузок ток не пропорционален напряжению и колеблется в соответствии с импедансом переменной нагрузки .

Нелинейными нагрузками могут быть контроллеры двигателей, инверторы, сварочное оборудование, МРТ-сканеры, выпрямители, системы ИБП, компьютеры, принтеры, телевизоры и т. д.

К сожалению, нелинейные нагрузки потребляют токи резкими короткими импульсами. Эти импульсы искажают формы сигналов тока, которые, в свою очередь, генерируют гармоники , которые могут привести к проблемам с питанием. Проблемы с питанием могут повлиять как на оборудование системы распределения, так и на подключенные к нему нагрузки.

В некоторых странах, если на вашу сеть влияют гармоники, вам придется заплатить штрафов, которые будут добавлены к вашим счетам за электроэнергию .

Хороший сетевой анализатор легко предоставит вам дополнительную информацию о вашей сети и оценит гармонические искажения. Это поможет вам выбрать наиболее подходящее оборудование для ваших нужд.

Но как решить проблемы с питанием?

Линейные и нелинейные нагрузки требуют индивидуального подхода.

На самом деле линейные нагрузки довольствуются простым романтическим ужином (или стандартной конденсаторной батареей коррекции коэффициента мощности).

Напротив, нелинейные нагрузки требуют сложного обслуживания и требуют ресторана, отмеченного звездой Мишлен, чтобы быть счастливыми (т. е. использовать расстроенную панель коррекции коэффициента мощности с гармоническими реакторами).

Если вам нужно полностью избавиться от гармоник и сделать волновую форму идеальной и привлекательной, решением будет использование активного фильтра гармоник.

Обратите внимание, что в некоторых случаях ваша система может оказаться в ситуации, противоположной описанной в нашем предыдущем посте. Это означает, что у вас есть избыток емкостной нагрузки . В этом случае вам придется выбрать индуктивные компенсационные панели , оснащенные реакторами вместо конденсаторов.

Что такое Cos Phi (Cos φ) и коэффициент мощности (PF)?

Эти два параметра одновременно похожи и отличаются друг от друга. Фактически в сетях с линейными нагрузками 9Коэффициент мощности 0005 и cos (φ) соответствуют . Они указывают отношение между активной (рабочей или фактической) мощностью , измеряемой в кВт ( киловатт ) и полной мощностью , измеряемой в кВА ( киловольт-ампер ). Мы можем суммировать это с помощью следующей формулы:

Cos Phi (при 50 Гц) = Активная мощность (кВт) / Полная мощность (кВА) = Коэффициент мощности

Вы можете рассчитать полную мощность на , умножив В х А = кВА , и это соответствует количеству энергии, используемой для работы ваших машин и оборудования в течение определенного периода.

В сетях с нелинейными нагрузками ситуация немного сложнее, из-за наличия гармоник. Фактически, коэффициент мощности остается отношением кВт (активной мощности) к кВА (полной мощности) , но кВА теперь также имеет гармоническую составляющую .

Наконец, истинный коэффициент мощности (tPF) становится комбинация коэффициента мощности смещения (dPF) и коэффициента мощности искажения (hPF) . Смещение PF по-прежнему равно cos (φ), где (φ) представляет собой угол между основным током и напряжением .