табл.1. Показатели электрических нагрузок электроприемников
|
Формулы для расчета электрических величин.

Проводя диагностику и ремонт холодильников Стинол, мастер периодически сталкивается с необходимостью проводить
измерения электрических величин. По результатам измерения делаются выводы о работоспособности той или иной
детали электрооборудования холодильника.
На практике, рассматривая какую-либо электрическую нагрузку, полезно заранее знать, какое сопротивление
соответствует какой мощности и ток какой величины потечет через эту нагрузку при подаче на нее питающего
напряжения 220 Вольт. Если немного упростить теорию, все это не сложно вычислить, пользуясь формулами,
приведенными ниже.
Обозначения:
- I — Сила тока в цепи, единицы измерения - Амперы (А)
- U — Напряжение, единицы измерения - Вольты (В или V)
- R — Сопротивление нагрузки, единицы измерения — Омы (Ом или Ohm)
- P — Электрическая мощность нагрузки, единицы измерения — Ватты (Вт или W)
Эти электрические величины связаны друг с другом следующими формулами:
Электрооборудование холодильников Стинол рассчитано на питание от сети переменного тока напряжением 220 Вольт.
- I=220/R
- I=P/220
- R=220/I
- R=48400/P
- P=220·I
- P=48400/R
Важно! В цепях переменного тока данные формулы справедливы только для активной
нагрузки, сопротивление которой переменному току не зависит от его частоты. Для реактивных потребителей (емкости
и индуктивности) эти равенства выполняться уже не будут. А это значит, что, по большому счету, при ремонтах
холодильников Стинол всю эту математику мы можем применять только к нагревателям системы No Frost. А различные
электродвигатели (мотор-компрессор, вентилятор, микродвигатель таймера и т.п.), являясь нагрузкой реактивной
(индуктивной), автоматически из подобных рассчетов выпадают.
Во время работы удобно иметь под рукой табличку для быстрого взаимного пересчета электрической мощности, сопротивления и силы тока. Такая табличка представлена ниже. В свое время она была составлена мной для быстрого ориентирования в параметрах нагревателей оттайки различных импортных холодильников. Специалисту по ремонту холодильников Стинол она тоже может оказаться полезной.
Пользоваться таблицей достаточно просто:
- Измерив мультиметром сопротивление нагревателя, и найдя соответствующую строчку в таблице, сразу становится ясно, какой мощностью он обладает и какой ток потечет через него при подаче питающего напряжения 220 Вольт.
- Узнав при помощи токовых клещей, какой ток потребляет нагреватель, по таблице можно выяснить его сопротивление и мощность.
- Узнав по маркировке нагревателя его мощность, легко выяснить его сопротивление и ток.

|
Для напряжения 220 V (если ток переменный, то справедливо только для активной нагрузки) |
||
|---|---|---|
| Сила тока, А | Мощность, W | Сопротивление, Ом |
| 0.01 | 2.2 | 22k |
| 0.05 | 11 | 4.4k |
| 0.1 | 22 | 2.2k |
| 0.2 | 44 | 1.1k |
| 0.3 | 66 | 733 |
| 0.4 | 88 | 550 |
0. 5 5 |
110 | 440 |
| 0.6 | 132 | 366 |
| 0.7 | 154 | 314 |
| 0.8 | 176 | 275 |
| 0.9 | 198 | 244 |
| 1 | 220 | 220 |
| 1.1 | 242 | 200 |
| 1.2 | 264 | 183 |
| 1.3 | 286 | 169 |
| 1.4 | 308 | 157 |
1. 5 5 |
330 | 146 |
| 1.6 | 352 | 138 |
| 1.7 | 374 | 129 |
| 1.8 | 396 | 122 |
| 1.9 | 418 | 116 |
| 2 | 440 | 110 |
| 2.1 | 462 | 105 |
| 2.2 | 484 | 100 |
| 2.3 | 506 | 96 |
| 2.4 | 528 | 92 |
2. 5 5 |
550 | 88 |
| 2.6 | 572 | 85 |
| 2.7 | 594 | 81 |
| 2.8 | 616 | 79 |
| 2.9 | 638 | 76 |
| 3 | 660 | 73 |
| 3.1 | 682 | 71 |
| 3.2 | 704 | 69 |
Дополнительная информация по теме этой страницы есть в следующих статьях:
Запомнить эту страницу в:
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings. REQUIRED_FIELD}})
REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings. LANGUAGE}}
{{$select.selected.display}}
LANGUAGE}}
{{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Расчет на ударную нагрузку с учетом массы конструкции
Иногда этот запас может быть слишком большим и потому не совсем оправданным, так как приведет к перерасходу материалов, т. е. необоснованному завышению стоимости конструкции. Потому, если есть уверенность в своих силах и знаниях, то иногда имеет смысл пересчитать значение динамического коэффициента с учетом массы деформирующейся конструкции.
е. необоснованному завышению стоимости конструкции. Потому, если есть уверенность в своих силах и знаниях, то иногда имеет смысл пересчитать значение динамического коэффициента с учетом массы деформирующейся конструкции.
Как уже говорилось, удар — это достаточно сложное физическое явление, в результате которого происходит много различных процессов, в частности падающее тело в момент падения имеет импульс
p = mV (288.1)
где v — уже рассматривавшаяся нами скорость тела в момент касания с рассматриваемой конструкцией. При этом и упавший груз и рассматриваемая конструкция имеют некоторую массу. Из закона сохранения энергии и вытекающего из него закона сохранения импульсов вытекает следующее уравнение:
m1v1 + m2v2 = m1v’1 + m2v’2 (296.1.1)
где m1 — масса груза, m2 — масса рассматриваемой конструкции, v1 — скорость груза перед ударом, v’1 — скорость груза после удара, соответственно v2 — скорость рассматриваемой конструкции перед ударом, v’2— скорость рассматриваемой конструкции после удара.
Если скорость рассматриваемой конструкции до начала удара принять v2 = 0, то формула (288.11.2) преобразуется в
m1v1 = m1v’1 + m2v’2 (296.1.2)
Далее рассмотрим несколько граничных условий и промежуточных вариантов, характерных для столкновения тел:
1. Если масса рассматриваемой конструкции значительно меньше массы груза и для упрощения расчетов массой конструкции пренебречь, то
m1v1= m1v’1 (296.1.3)
Суть этой формулы в том, что при столкновении относительно тяжелого тела с относительно легким телом скорость движения тяжелого тела в момент столкновения практически не изменяется, что можно видеть и даже проверить самому, прыгая на батуте. Именно это допущение мы и использовали при расчете деформаций и динамических коэффициентов без учета массы деформирующегося тела.
2. Если масса падающего груза значительно меньше массы рассматриваемой конструкции, то формула (296.1.1) примет вид
m1v1 = — m1v’1 или v1 = — v’2 (296.1.4)
Суть этой формулы в том, что при столкновении очень легкого тела с очень тяжелым телом скорость движения тяжелого тела после столкновения практически не изменится, а вот легкое тело после столкновения начнет двигаться в противоположном направлении, проще говоря, отскочит от рассматриваемой конструкции, но в силу неизменного действия силы тяжести через некоторое время опять упадет на рассматриваемую конструкцию, снова отскочит и так будет продолжаться до тех пор, пока вся энергия не перейдет в указанные нами выше виды и легкое тело не упокоится с миром на поверхности тяжелого тела. Это можно наблюдать, роняя на пол теннисный или любой другой мяч.Тем не менее то, что легкое тело отскакивает от тяжелого почти с такой же скоростью (во всяком случае теоретически), означает, что на тяжелое тело действует такая же ударная сила, а значит деформируемую конструкцию все равно следует рассчитывать на действие ударной нагрузки и потому формула (288. 5.3), позволяющая определить максимальную деформацию в зависимости от линейной скорости и частоты колебаний, остается в силе.
5.3), позволяющая определить максимальную деформацию в зависимости от линейной скорости и частоты колебаний, остается в силе.
Если деформирующееся тело после столкновения движется по прямолинейной траектории (совершает поступательное движение) или по криволинейной траектории с радиусом, значительно превышающим размеры тела, то такое движение можно рассматривать как движение материальной точки, совпадающей с центром тяжести тела. Кроме того, чем больше радиус траектории, тем ближе криволинейное движение к прямолинейному по своим параметрам и вообще прямолинейное движение — это частный случай движения по криволинейной траектории с бесконечным радиусом.
Но если в качестве рассматриваемой конструкции выступает балка или плита, которая в результате удара прогибается, то такое движение никак нельзя назвать прямолинейным или вращательным относительно оси, расположенной на очень большом расстоянии, а потому масса не может рассматриваться, как одна из характеристик такого движения. Не является такое движение и вращательным относительно центра тяжести сечения. И потому момент инерции для описания такого движения также не подходит. А используется для корректного описания такого движения коэффициент жесткости с, учитывающий сложные и запутанные взаимоотношения между массой деформирующейся конструкции, длиной, моментом инерции поперечного сечения, и модулем упругости материала рассматриваемой конструкции.
Не является такое движение и вращательным относительно центра тяжести сечения. И потому момент инерции для описания такого движения также не подходит. А используется для корректного описания такого движения коэффициент жесткости с, учитывающий сложные и запутанные взаимоотношения между массой деформирующейся конструкции, длиной, моментом инерции поперечного сечения, и модулем упругости материала рассматриваемой конструкции.
Не смотря на столь припудренное определение коэффициента жесткости формула, позволяющая определить циклическую частоту, выглядит даже проще, чем при поступательном движении:
ω2 = с/m (296.2.1)
А при угловых колебаниях (вращении относительно центра тяжести):
ω2 = c/I (296.2.2)
Универсальность формулы (296.2.1) в том, что если колебания балки вызываются сосредоточенной нагрузкой, приложенной посредине пролета, при этом масса балки пренебрежимо мала по сравнению с массой груза, вызывающей деформацию, то исходя из формулы (288. 10.1) следует, что если
10.1) следует, что если
ω2 = Q/mfст (288.10.1)
то
сQ = Q/fст = 48EI/l3 (296.3.1)
и в итоге мы получаем ту же формулу (288.11.3) для определения динамического коэффициента.
А вот когда нужно определить коэффициент жесткости для балки, колеблющейся под действием нагрузки от собственного веса, то ситуация усложняется. Во-первых следует учитывать, что балка может иметь не постоянное по длине сечение и даже не постоянный модуль упругости. Но даже если сечение, определяющее значения момента инерции, и модуль упругости постоянны по длине, то все равно отсутствует сосредоточенная сила, которая может рассматриваться как ударная нагрузка, а есть только распределенная по длине балки масса. В таких случаях используется понятие приведенной массы.
Существует несколько методов учета этой приведенной массы: метод Рэлея, формула Граммеля, формула Донкерли, метод Ритца, метод Бубнова-Галеркина. Эти методы используют разные подходы и разные физические модели процессов, происходящих в процессе ударной деформации, а потому и результаты при использовании различных методов разные, впрочем разница не столь уж и существенна. Единственное, что все эти методы объединяет — это насыщенность дифференциальными уравнениями и интегралами, которые представляют определенный интерес для любителей высшей математики. Здесь же, оставаясь в формате справочника, отмечу лишь основную проблему, которая возникает, при переходе от распределенной массы к условно сосредоточенной.
Эти методы используют разные подходы и разные физические модели процессов, происходящих в процессе ударной деформации, а потому и результаты при использовании различных методов разные, впрочем разница не столь уж и существенна. Единственное, что все эти методы объединяет — это насыщенность дифференциальными уравнениями и интегралами, которые представляют определенный интерес для любителей высшей математики. Здесь же, оставаясь в формате справочника, отмечу лишь основную проблему, которая возникает, при переходе от распределенной массы к условно сосредоточенной.
Когда мы рассматривали возможные соотношения между сосредоточенной и равномерно распределенной нагрузкой, то выяснили, что момент от равномерно распределенной нагрузки, умноженной на длину балки (что и дает нам значение условно приведенной нагрузки), будет в два раза меньше, чем от сосредоточенной нагрузки, равной по значению условно приведенной нагрузке и приложенной посредине пролета. Таким образом мы определили коэффициент перехода γп = 2. Соответственно приведенный коэффициент при переходе от равномерно распределенной нагрузки к сосредоточенной будет равен:
Соответственно приведенный коэффициент при переходе от равномерно распределенной нагрузки к сосредоточенной будет равен:
kпр = 1/γ = 1/2 = 0.5 (296.4.1)
Однако прогиб от приведенной нагрузки будет не в 2, а приблизительно в 1.5 раза меньше, чем при сосредоточенной нагрузке (см. расчетные схемы для балок). Таким образом в этой ситуации некорректно применять один и тот же динамический коэффициент при определении прогиба, угла поворота поперечного сечения, нормальных и касательных напряжений. Между тем определяющими при расчете на ударные нагрузки являются нормальные напряжения, возникающие в поперечных сечениях под действием изгибающего момента, но расчет при этом производится в зависимости от значения прогиба. Чтобы с честью выйти из этой ситуации используют понятие приведенного прогиба, который имеет большее значение, чем прогиб при воздействии статической равномерно распределенной нагрузки и тогда:
fпр = fстkпр = Qпрl3/48EI = qlkпрl3/48EI = ql4/96EI (296. 5.1)
5.1)
где Qпр = ql = γFl — значение приведенной сосредоточенной силы, γ — плотность материала балки, F — площадь поперечного сечения.
Тогда условное значение коэффициента жесткости, необходимое для определения частоты колебаний, составит:
сq = ql/fпр = 96EI/l3 (296.3.2)
При таком подходе мы получаем максимально возможное значение приведенного прогиба по сравнению с вышеперечисленными методами, однако парадокс ситуации в том, что чем меньше статический прогиб, тем больше в итоге значение динамического коэффициента, а значит и меньше запас по прочности. Например, метод Рэлея приводит к следующему значению переходного коэффициента:
kРпр = β = 17/35 = 0.4857 (296.4.2)
и тогда
fРпр = 0.4857ql4/48EI = ql4/98.82EI (296. 5.2)
5.2)
соответственно
сРq = 98.82EI/l3(296.3.3)
Если рассматривать приведенный прогиб как сумму прогиба от равномерно распределенной нагрузки и производной этого прогиба (а производная от прогиба — это угол поворота), то:
спр =ql/fст + q/f’ст = 384EI/5l3 + 24EI/l3 = 100.8EI/l3 (296.3.4)
Как видим значения приведенных прогибов, полученные при разных способах определения, отличаются незначительно, максимальное расхождение составляет менее 5%. И не совсем понятно, зачем придумывать столько разных способов, чтобы вычислить максимальное значение приведенного прогиба, но напомню, что значение приведенного прогиба влияет на значение частоты колебаний, а когда частота свободных колебаний — колебаний груза, совпадает с частотой вынужденных колебаний — деформаций балки, то возникает резонанс, значительно увеличивающий амплитуду колебаний, что в итоге может привести к разрушению конструкции. На уроках физики изучение явления резонанса предваряется следующей байкой:
На уроках физики изучение явления резонанса предваряется следующей байкой:
Когда-то давным-давно рота солдат бодрым строевым шагом вступала в побежденный город по широкому и прочному мосту. Однако частота собственных (вынужденных) колебаний пролета моста совпала с частотой четко отбиваемого строевого шага (частотой свободных колебаний), возникло явление резонанса, пролет обвалился и рота победителей погибла под обломками моста, так и не успев собрать трофеи, точнее трофеи в том смысле, в каком это понятие использовали древние греки, буквально засыпали солдат. С тех солдатам строго настрого запрещено проходить строевым шагом по мостам, акведукам и прочим инженерным сооружениям, включая плиты перекрытия, в которых могут возникнуть вынужденные колебания. Тем не менее свои выводы из этой истории сделали и строители и потому при расчете конструкций на различные виды нагрузок учитывается как минимально возможное так и максимально возможное значение частоты колебаний.
При расчете на ударные нагрузки конструкций жилых помещений явление резонанса как правило не учитывается, потому что по большому счету максимальный прогиб от действия ударной силы — это и есть проявление резонанса. А так как в результате достаточно быстрого перераспределения энергии удара, колебания такой системы при любом соотношении масс являются быстро затухающими, то возникновение ударной силы, большей чем при первом столкновении, в моменты последующих возможных столкновений практически не возможно. Тем не менее ударные нагрузки, прикладываемые к конструкции с более-менее постоянной частотой мы можем наблюдать в обычной квартире при работе стиральной машины, работающей в режиме отжима. Самый простой способ максимально уменьшить ударные нагрузки от прыгающей по помещению стиральной машинки — это изменить количество оборотов при отжиме и у хороших стиральных машин-автоматов для этого есть специальный регулятор. Если же переключателя скоростей нет, то можно рассчитать перекрытие на дополнительную ударную нагрузку возникающую от прыгающей стиральной машины, руководствуясь приведенным выше принципом.
А так как в результате достаточно быстрого перераспределения энергии удара, колебания такой системы при любом соотношении масс являются быстро затухающими, то возникновение ударной силы, большей чем при первом столкновении, в моменты последующих возможных столкновений практически не возможно. Тем не менее ударные нагрузки, прикладываемые к конструкции с более-менее постоянной частотой мы можем наблюдать в обычной квартире при работе стиральной машины, работающей в режиме отжима. Самый простой способ максимально уменьшить ударные нагрузки от прыгающей по помещению стиральной машинки — это изменить количество оборотов при отжиме и у хороших стиральных машин-автоматов для этого есть специальный регулятор. Если же переключателя скоростей нет, то можно рассчитать перекрытие на дополнительную ударную нагрузку возникающую от прыгающей стиральной машины, руководствуясь приведенным выше принципом.
В обще случае определить значение коэффициента жесткости (когда это возможно), частоту и период колебаний можно по следующей таблице:
Таблица 1: Основные параметры упругих систем с одной степенью свободы
Если рассматривается случай приложения ударной нагрузки к изгибаемой конструкции, отличный от приведенных в таблице, то определить приближенное значение коэффициента жесткости можно по расчетным схемам для простых и статически не определимых балок. Приближенное потому, что при приложении сосредоточенной нагрузки не посредине пролета или при приложении не равномерно распределенной нагрузки колебания вряд ли будут гармоническими.
Приближенное потому, что при приложении сосредоточенной нагрузки не посредине пролета или при приложении не равномерно распределенной нагрузки колебания вряд ли будут гармоническими.
Таким образом формула для определения динамического коэффициента ударной нагрузки (288.11.3) при учете только массы деформирующейся конструкции примет вид
kд = 1 + √1 + 2h/fпр = 1 + √1 + 2h/(fстkпр) (296.7.1)
3. Если груз после падения продолжает движение вместе с рассматриваемой конструкцией, то формула (296.1.2) остается в силе
Это означает, что для определения максимального прогиба следует учитывать как массу падающего груза, так и параметры деформирующейся конструкции. Прогиб от действия сосредоточенной нагрузки, приложенной посредине балки, составляет fст = Ql3/48EI, прогиб от действия приведенной сосредоточенной нагрузки составляет fпр = kпрfст, таким образом суммарный прогиб составляет:
fсум = fст + fпр = (Q + qlkпр)l3/48EI = (1+ qlkпр/Q)Ql3/48EI = fст(1 + kпр(ql/Q) (296. 8.1)
8.1)
тогда значение динамического коэффициента ударной нагрузки с учетом масс обеих тел составит:
kд = 1 + √1 + 2h/fсум = 1 + √1 + 2h/(fст(1 +kпр(ql/Q)) (296.7.2)
Не смотря на кажущуюся сложность, все приведенные выше формулы определения динамического коэффициента максимально просты, так как основаны на простейшей физической модели процессов, происходящих при ударе. Между тем, как уже говорилось, процессы, происходящие в соударяемых телах, достаточно сложные. Да и падать на перекрытие могут не только твердые тела, но и жидкости в различной упаковке, сыпучие материалы (песок, цемент и различные сухие строительные смеси), ну и тем более человек. Особенность таких падений в том, что перечисленные вещества, а тем более человек, падая на поверхность, даже очень жесткую, очень редко от нее отскакивают. Происходит это потому, что у жидкостей, а тем более сыпучих материалов отсутствуют жесткие внутренние связи, характерные для твердых тел, а человек, приземляясь после прыжка, старается присесть и таким образом искусственно продлить время контакта, а значит и максимально уменьшить ударную силу. Это означает, что ударная сила в таких случаях будет меньше и в зависимости от множества различных факторов (включая ловкость, если речь идет о человеке), которые требуют отдельного учета, расчетное снижение скорости, может снижаться от 1.1. до нескольких десятков раз. В связи с этим из соображений упрощения расчетов и обеспечения дополнительной прочности такие тонкости поведения жидких сыпучих и человеческих тел можно не учитывать. Но опять же, если есть уверенность в понимании происходящих процессов и в своих силах, то
Это означает, что ударная сила в таких случаях будет меньше и в зависимости от множества различных факторов (включая ловкость, если речь идет о человеке), которые требуют отдельного учета, расчетное снижение скорости, может снижаться от 1.1. до нескольких десятков раз. В связи с этим из соображений упрощения расчетов и обеспечения дополнительной прочности такие тонкости поведения жидких сыпучих и человеческих тел можно не учитывать. Но опять же, если есть уверенность в понимании происходящих процессов и в своих силах, то
Для сыпучих материалов в зависимости от размера фракций и плотности упаковки можно применять понижающий коэффициент kп = 0.5-0.2 тогда формула (296.7.2) примет вид:
kд = 1 + √1 + 2hkп/fсум = 1 + √1 + 2h/(fст(1 +kпр(ql/Q)) (296.7.2)
Для человека упавшего головой на балку, тоже можно вычислить понижающий коэффициент в зависимости от наличия головного убора, пышности волос, толщины кожного и мышечного слоя, геометрии, жесткости и прочности черепа, но мой вам совет, не падайте головой на перекрытие, потому что в этом случае спасать придется уже не конструкцию перекрытия, а вас.
Пример расчета балки на ударную нагрузку с учетом масс балки и груза
А теперь посмотрим как изменится значение динамического коэффициента с учетом массы балки, на ранее рассматривавшемся примере. Напомню, рассматривается шарнирно закрепленная деревянная балка перекрытия длиной 4 м из древесины сечением 20х10 см. На средину балки с высоты 50 см падает гиря весом в 32 кг. Требуется определить прочность балки при ударной нагрузке с учетом массы балки.
1. При таком сечении и плотности древесины γ = 500 кг/м3 приведенная масса балки составит
ql = 500х0.2х0.1х4 = 40 кг
2. Прогиб балки при воздействии статической нагрузки от гравитационной массы гири мы уже определяли
fcт = Ql3/48EI = 32х4003/(48х100000х6666.667) = 0.064 см
где Е = 105 кгс/см2 — модуль упругости древесины, I = bh3/12 = 6666.667 см4 — момент инерции поперечного сечения.
3. Тогда значение динамического коэффициента составит
kд = 1 + √(1 + 2х50/0.064(1 + 0.5(40/32) = 32.02 (при использовании приведенного коэффициента 0.4875 значение динамического коэффициента составит 32.17)
напомню, значение динамического коэффициента без учета массы балки составляло 40.53, таким образом учет массы балки позволил уменьшить расчетное значение динамического коэффициента почти на треть.
4. Значение максимального изгибающего момента при таком динамическом коэффициенте составит
Мд = Qlkд/4 = 32х400х31.02/4 = 102464 кг·см
5. Тогда при расчетном сопротивлении R = 140 кг/см2 требуемый момент сопротивления составит
Wтр = М/R = 99279/140 = 731.9 см3
6. Момент сопротивления для балки сечением 20х10 см составит W = 2I/h = 6666.667/10 = 666.67см3 < Wтр = 731.9 см3.
Напомню, без учета массы балки требуемый момент сопротивления составлял 926. 4 см3.
4 см3.
Вывод: Не смотря на все наши старания балка под действием такой ударной нагрузки может разрушиться. Однако в данном случае мы совершенно не учитывали упругие свойства гири, полагая ее совершенно жесткой, а также то, что на балке перекрытия будут уложены как минимум доски пола (без досок балки перекрытия как-то теряют изначальный смысл). А это означает, что расчетную массу балки следует еще увеличить, а если еще учесть упругие свойства как гири, так и древесины, и вполне вероятное развитие местных неупругих деформаций, то у рассматриваемой балки большие шансы на выживание.
Как рассчитать время работы, мощность ИБП. Формулы расчета
Онлайн калькуляторы расчета параметров работы ИБП оперируют установленными значениями КПД инвертора и других коэффициентов – мощности нагрузки, глубины разряда, доступной емкости. Заложенные в программу данные могут не совпадать с реальными, в этом случае только результат самостоятельного расчета по формуле будет точным.
Расчет времени работы ИБП
Если требуется приблизительно оценить автономность бесперебойника в работе с конкретной нагрузкой при заданной емкости АКБ, можно воспользоваться упрощенной формулой:
T=C*U/P
T – расчетное время резерва (ч), C – суммарная емкость АКБ (Ач) (55 Ач, 75 Ач, 100 Ач и т.п.), U – суммарное напряжение АКБ (В) (12 В, 24 В или 48 В), P – полная мощность нагрузки (Вт) (100 Вт, 200 Вт, 1000 Вт и т.п.).
Пример: Мощность подключенной нагрузки к ИБП — 150 Вт (типичная для газового котла), емкость АКБ — 100 Ач, напряжение АКБ — 12 В. Ориентировочно ИБП проработает в режиме резерв следующие время:
Т=(100 Ач*12 В)/150 Вт = 8 ч.
T=C*(U/P*КПД)*Kр
КПД инвертора – паспортная величина, P – мощность нагрузки, U – напряжение АКБ, Kр – коэффициент разряда (глубина разярда) АКБ (0. 6 — 0.8).
6 — 0.8).
КПД инвертора в онлайн калькуляторах зачастую устанавливается 0.8, тогда как бесперебойники «Сибконтакт» демонстрируют 0.9.
Расчет мощности ИБП
Если мощность ИБП меньше суммарной нагрузки, тогда прибор сразу же отключится после запуска. Перед покупкой бесперебойника подсчитайте потребление всех устройств, которые будут от него запитаны. Найдите данные на корпусе или в техпаспорте изделий, затем сложите.
Для индуктивной нагрузки (аппараты с электродвигателями, люминесцентные лампы) обычно указывают полную мощность в вольт амперах (ВА). Если фигурируют ватты, надо рассчитать необходимую мощность ИБП с учетом реактивной составляющей:
P=Pa/cos φ
Здесь Pа – активная мощность (Вт), cos φ – коэффициент мощности (если неизвестен, примите равным 0.7).
Также учитывайте, что в технике с электродвигателями пусковые токи до пяти раз больше, чем в рабочем режиме: бытовой холодильник, например, потребляет в момент включения компрессора около киловатта. Приятная новость: подобным устройствам требуется синусоидальный ток, и все ИБП «Сибконтакт» выдают на выходе именно такую форму переменного напряжения.
Приятная новость: подобным устройствам требуется синусоидальный ток, и все ИБП «Сибконтакт» выдают на выходе именно такую форму переменного напряжения.
Расчет емкости батарей ИБП
После определения времени работы и мощности нагрузки проводится расчет необходимой емкости аккумуляторов ИБП по формуле:
С=(P*t)/U*Kр
P – мощность нагрузки, t – необходимое время резерва, U – напряжение АКБ, Kр – коэффициент разряда (глубина разярда) АКБ (0.6 — 0.8).
Помните, что емкость АКБ суммируется только при параллельном соединении. При последовательном подключении складывается вольтаж батарей, а емкость остается равной номинальному значению одного источника питания.
Все вышеприведенные формулы, в упрощенном виде, встроены в наш онлайн «КАЛЬКУЛЯТОР» (виджет). Меняя параметры, можно легко определить, например, время работы ИБП от аккумулятора или наоборот — емкость аккумулятора, для необходимого времени работы ИБП в режиме резерв.
Теперь пора перейти в интернет-магазин «Сибконтакт», где в наличии бесперебойники мощностью от 300 Вт, в том числе модели со сквозной нейтралью для газовых котлов.
Для серьезных задач подойдет UPS ИБП МИ3024 Offline номиналом 3,3 кВт, выдерживающий двойную нагрузку в течение пяти секунд.
Перейти в каталог ИБП
Перейти в каталог АКБ
Проблемы с блоком розжига газового котла в частном доме? Рекомендуем к прочтению статью — Ошибка на котле Е01
Если у Вас остались вопросы — сообщите нам. Мы подберем для Вас лучшее решение!
Расчетные нагрузки промышленных предприятий
3. Определение коэффициента максимума
При расчетах на стадии технического проекта или рабочих чертежей расчетные нагрузки определяются с учетом коэффициента максимума, величина которого зависит от коэффициента использования и эффективного числа электроприемников.
Под эффективным числом группы электроприемников с различной установленной мощностью и разными режимами работы понимается такое число приемников, одинаковых по мощности и однородных по режиму работы, которое обеспечивают ту же величину расчетной нагрузки, что и рассматриваемая группа различных по мощности и режиму работы электроприемников.
В общем случае эффективное число электроприемников может быть найдено из выражения
Эффективное число электроприемников может быть принято равным фактическому их числу в следующих случаях:
а) когда мощность всех приемников одинакова;
б) при коэффициенте использования Ки>0,8;
в) когда выполняются указанные в табл. 3-5 соотношения между коэффициентом использования и величиной отношения, равного:
где Ру.макс и Ру.мин — соответственно номинальные активные мощности наибольшего и наименьшего электроприемников в группе, квт.
При определении Ру.мин должны быть исключены наиболее мелкие электроприемники, суммарная мощность которых не превосходит 5% мощности всей группы приемников.
Когда указанные условия не выполняются, эффективное число электроприемников определяется в зависимости от величин Р*и n*, вычисляемых пo формулам (*—звездочки, поставленные под буквенными обозначениями, указывают на относительные величины).
где n — общее число электроприемников группы;
— сумма номинальных мощностей всей группы, квт;
— число приемников в группе, номинальная мощность каждого из которых больше или равна половине номинальной мощности наиболее мощного приемника в группе;
— сумма номинальных мощностей этих приемников, квт.
Мелкие электроприемники, суммарная мощность которых не превосходит 5% номинальной мощности всех электроприемников, при определении не учитываются.
В зависимости от величин р* и n* по табл. 3-6 находят величину относительного значения эффективного числа электроприемников:
и определяют эффективное число приемников умножением полученного значения на общее число электроприемников группы:
В зависимости от коэффициента использования Ки и эффективного числа приемников nэ по табл. 3-7 определяется коэффициент максимума Км.
3-7 определяется коэффициент максимума Км.
Величины расчетных активной и реактивной мощностей группы электроприемников определяется по формулам:
где Рсм — средняя активная мощность для группы электроприемников за наиболее нагруженную смену, кВт;
tgφ — соответствует характерному для данной группы электроприемников значению фазового угла в режиме максимальной активной мощности.
Полная расчетная мощность определяется из выражения
расчетный ток — по формуле
где U1 — номинальное напряжение сети, кв.
Коэффициент мощности при режиме расчетной нагрузки равен:
При определении эффективного числа электроприемников для большого числа питающих линий, нескольких трансформаторных пунктов, распределительных подстанций и т. п. допускается применять упрощенную методику расчета, которая заключается в следующем.
Для отдельных линий или подстанций, для которых ранее были определены величины номинальной мощности и эффективного числа электроприемников вычисляются мощности условных электроприемников по формуле
где Ру и nэ — соответственно номинальная мощность и эффективное число электроприемников рассматриваемой линии или подстанции.
При этом не учитывается нагрузка резервных электроприемников, ремонтных сварочных трансформаторов и других ремонтных электроприемников, пожарных насосов, а также электроприемников, работающих кратковременно (дренажные насосы, задвижки, вентили, щитовые затворы и т. п.). Нагрузка таких электроприемников учитывается только при расчете питающих эти приемники линий и линий, питающих силовые распределительные пункты, к которым они подключены.
Определение эффективного числа электроприемников, коэффициентов максимума и спроса для условных электроприемников, вычисленных по формуле (3-26), производится методом, изложенным выше для индивидуальных приемников.
При окончательном подсчете нагрузок должны быть учтены реактивные мощности присоединенных к сети батарей конденсаторов (мощности батарей статических конденсаторов учитываются со знаком «минус»), а также потери активной и реактивной мощности в понижающих трансформаторах.
Для электроприемников с малоизменяющейся во времени нагрузкой (насосы водоснабжения, вентиляторы, отопительные и нагревательные приборы, печи сопротивления и т. п.) коэффициент спроса может быть принят равным коэффициенту использования:
п.) коэффициент спроса может быть принят равным коэффициенту использования:
Кс=Ки (3-27)
Изложенный метод определения расчетных нагрузок рекомендуется применять на всех ступенях и для всех элементов системы электроснабжения промышленных предприятий без введения в расчеты понижающих коэффициентов. Допускается применение коэффициента участия в максимуме в пределах 0,9—0,95 в случаях, когда при определении нагрузок на высших ступенях системы электроснабжения можно ожидать несовпадения во времени максимально загруженных смен, а также при ориентировочных расчетах.
В табл. 3-8 дано число часов использования максимальной мощности для осветительной нагрузки промышленных предприятий.
Пример 3-1.
В отделении цеха промышленного предприятия установлена группа электродвигателей на номинальное напряжение 380 в с длительным режимом работы. По величине коэффициента использования электроприемники разбиваются на три подгруппы, для каждой из которых в табл. 3-9 указаны число и мощность двигателей, суммарная номинальная мощность, величины коэффициентов использования и мощности.
3-9 указаны число и мощность двигателей, суммарная номинальная мощность, величины коэффициентов использования и мощности.
Требуется определить расчетные нагрузки для всей группы электродвигателей отделения.
Удельная нагрузка — Энциклопедия по машиностроению XXL
Зная из опыта Ар, можно по формуле (8-8) определить V и далее G. В общем случае полученные зависимости позволяют провести качественно верный анализ влияния ряда факторов на скорость эжектируемого воздуха. Так, согласно (8-8) она увеличивается с ростом h, Gt и Gr/Q — удельной нагрузки канала. Увеличивающееся при этом сопротивление Ар влияет на и в обратную сторону, но Ар растет медленнее и и все же увеличивается. Опытные данные подтвердили справедливость этих положений. Для мелких частиц при прочих равных 252 [c.252]Согласно данным [Л. 64] установка на стенках канала проволочных спиралей приводит к увеличению времени пребывания и концентрации падающих частиц.
 Однако с увеличением удельной нагрузки Gt/Q распределение частиц становится все более неравномерным с максимумом по оси канала.
[c.254]
Однако с увеличением удельной нагрузки Gt/Q распределение частиц становится все более неравномерным с максимумом по оси канала.
[c.254]За расчетную нагрузку принимают максимальное значение удельной нагрузки, распределенной по линии контакта зубьев [c.108]
В косозубом зацеплении нагрузка распределяется на всю суммарную длину контактных линий 1, 2, 3. Удельная нагрузка уменьшается с увеличением суммарной длины контактных линий /j . С помощью рис. 8.26 нетрудно установить, что при е , равном целому числу, [c.126]
Расчет зубьев прямозубой конической передачи по напряжениям изгиба. Размеры поперечных сечений зуба конического колеса изменяются пропорционально расстоянию этих сечений от вершины конуса (рис. 8.32, а). Все поперечные сечения зуба геометрически подобны. При этом удельная нагрузка q распределяется неравномерно подлине зуба. Она изменяется в зависимости от деформации и жесткости зуба в различных сечениях. Можно доказать, что нагрузка q распределяется по закону треугольника, вершина которого совпадаете вершиной делительного конуса, и что напряжения изгиба одинаковы по всей длине зуба.
[c.132]
Можно доказать, что нагрузка q распределяется по закону треугольника, вершина которого совпадаете вершиной делительного конуса, и что напряжения изгиба одинаковы по всей длине зуба.
[c.132]
На основании формулы (8.41) можно отмстить, что приведенный радиус кривизны в различных сечениях зуба конического колеса изменяется пропорционально диаметрам этих сечений или расстоянию от вершины начального конуса. Ранее было сказано, что удельная нагрузка q также пропорциональна этим расстояниям. Следовательно, отношение постоянно для всех сечений зуба. При этом постоянными остаются и контактные напряжения по всей длине зуба, что позволяет производить расчет по любому сечению (в данном случае по среднему). Удельная нагрузка в этом сечении (см. рис. 8.32) [c.133]
Определение удельной нагрузки q и приведенного радиуса кривизны Рпр для зацепления Новикова значительно сложнее и здесь не рассматривается. [c.169]
По аналогии с косозубой передачей удельная нагрузка для червячных передач
[c. 181]
181]
Допускаемая удельная нагрузка [q в Мн/м [c.116]
Межосевое расстояние (из расчета по допускаемой удельной нагрузке на единицу ширины катка, так как материал обкладки одного из катков не следует закону Гука) [c.118]
Показатели нормы контакта зубьев в передаче. Для получения надежных зубчатых передач зубья парных зубчатых колес должны соприкасаться по всей длине контактных линий, В этом случае удельная нагрузка в зацеплении достаточно равномерно распределяется вдоль контактных линий исключается концентрация нагрузки, действующей на зубья, и напряжений в материале зубьев создаются условия для равномерной смазки зацепления и обеспечивается (наряду с другими мерами) расчетная изгибная и контактная долговечность зубьев передач. [c.200]
Среднетемпературное цианирование (800—840° С) используют для получения более глубокого диффузионного слоя, стойкого против износа при небольших удельных нагрузках.
 Продолжительность процесса от 5 до 90 мин, глубина слоя — 0,2—0,5 мм при этом цементация преобладает над азотированием.
[c.148]
Продолжительность процесса от 5 до 90 мин, глубина слоя — 0,2—0,5 мм при этом цементация преобладает над азотированием.
[c.148]Решение. I. По (табл. 7.1) принимаем коэффициент трения для пары чугун—фибра f = 0,2, допускаемую удельную нагрузку [9]=39 Н/мм (с. 130), коэффициент упругого скольжения = 0,02, коэффициент ширины роликов Ч л=0,5, коэффициент запаса сцепляемости Р=1,3. [c.133]
Решение. 1. Принимаем коэффициент трения пары чугун — прорезиненная ткань f=0,6 (см. табл. 7.I.), коэффициент запаса сцепляемости Р=1,5, допускаемую удельную нагрузку для прорезиненной ткани [ ] = 29,4 Н/мм (с. [c.135]
Малые скорости скольжения и небольшие удельные давления Кратковременный режим с постоянным или переменным направлением вращения вала. Малые скорости и большие удельные нагрузки Мало меняющиеся по величине и направлению усилия, нагрузка — большая и средняя Переменная нагрузка [c.308]
Ряс. 342. Давление в масляном слое при различных значениях удельной нагрузки к (экспериментальные данные)
[c.332]
342. Давление в масляном слое при различных значениях удельной нагрузки к (экспериментальные данные)
[c.332]
В выражении (114) ц — динамическая вязкость масла, кгс-с/м со — окружная скорость, с» к — удельная нагрузка на единицу несущей поверхности подшипника, кгс/.м / — относительный зазор (ф = А/с ). [c.336]
Если, например, возрастает удельная нагрузка, то характеристика режима падает, а с ней уменьшается и минимальная толщина масляного слоя подшипник приближается к режиму полужидкостного трения. Однако с понижением X одновременно падает коэффициент трения (см. рис. 360) и снижается тепловыделение. В результате повышается вязкость масла, отчего прежнее значение характеристики режима полностью или частично восстанавливается и подшипник переходит в состояние устойчивого равновесия. [c.352]
Пр 1 расчете подшипников из более прочных материалов (бронзы, алюминиевые сплавы, серебро) решающи.ми являются гидродинамика подшипника, его геометрические (с/, ф) п режимные (/. ) факторы, рациональный выбор которых позволяет довести удельные нагрузки до 150 — 300 кгс/см», а в отдельных случаях до 500 — 600 кге ехг.
[c.361]
) факторы, рациональный выбор которых позволяет довести удельные нагрузки до 150 — 300 кгс/см», а в отдельных случаях до 500 — 600 кге ехг.
[c.361]
В качестве критерия тепловой напряженности подшипников нередко применяют величину ки (произведение удельной нагрузки, кгс/см, на окружную скорость вала, м/с). Предельны.мн считаются значения кг = 400 -г 600. [c.361]
Таким образом, все факторы, рассмотренные в 8-2 и влияющие на истинную концентрацию падающего слоя, сказываются и на интенсивности его теплообмена. В частности, увеличение расхода и удельной нагрузки канала (массовой скорости частиц), а также уменьшение относительной длины канала и размера частиц способствуют усилению теплообмена. Для лучшего сравнения с флюидным потоком данные также обработаны в принятой автором манере Nun/N u = /(P). Оценка скорости и расхода газа по данным, приведенным в 8-2, позволила определить число Рейнольдса для газа, эжектируе-мого падающими частицами. Во всех случаях оказалось, что Reтечения газа. Для тех же условий, для которых получена зависимость (8-21), но с более значительной погрешностью, вызванной неточностью оценки расхода газа, получено Л. 96, 286]
[c.266]
Во всех случаях оказалось, что Reтечения газа. Для тех же условий, для которых получена зависимость (8-21), но с более значительной погрешностью, вызванной неточностью оценки расхода газа, получено Л. 96, 286]
[c.266]
Преимущество азо ированного слоя — в его более высокой износоустойчивости. Но азотирова ные детали значительно дороже, так как этот процесс более длительный, и для азотирования применяют дорогие легированные стали, Кроме того, ТОНКИ азотированный слой, в отличие от цементированного, может выдерживать меньшие удельные нагрузки. [c.335]
С увеличением удельной нагрузки коррозионный износ стали 1Х18Н9Т возрастает на воздухе в большей степени, чем в жидких средах. Снижение износа этой стали в жидких средах обусловлено тем, что эти среды служат смазкой. [c.339]
На рис. 8.7 изображен пример сжатия двух цилиндров с параллельными осями. До приложения удельной нагрузки q цилиндры соприкасались по линии. Под нагрузкой линейный контакт переходит в контакт по узкой площадке. При этом точки максимальных нормальиьгх напряжений располагаются на продольной оси симметрии контактной площадки. Значение этих напряжений вычисляют го формуле
[c.103]
Расчет прочност 1 зубьев по контактным напряжениям. Для косозубых передач удельная нагрузка с учетом формул (8.24) н (8.2G) д== ,Дн11 = РАнКнаЦЬ гаС05 а), где К На — коэффициент неравно.мерности нагрузки одновременно зацепляющихся пар зубьев — см. ниже. [c.128]
Для выбранной муфты необходимо выголнить проверку удельных нагрузок между дисками и произвести расчет механизма ее включения. Удельная нагрузка [c.193]
Решение. 1. По данным на с. 130 принимаем допускаемую удельную нагрузку [( ]=19,6 Н/мм, коэффициент трения чугун — кожа / = 0.3 (см. табл. 7.1). коэффициент запаса сценляемости 3=1,4, коэффициент ширины маховика Ч л = 0,2. [c.136]
Если этот крптери одинаков, то у всех геометрически подобных двигателей одинаковы термодинамический, механический и эффективный КПД (следовательно, н удельный расход топлива), тепловая напряженность (теплопереход на единицу охлаждающей поверхности), удельная мощность, напряжения от тазовых н Инерционных сил, удельные нагрузки на ПОДШИПНИКИ, конструкционная. масса двшателя (масса, отнесенная к сумме квадратов диа-мс1ра цилиндра).
[c.56]
масса двшателя (масса, отнесенная к сумме квадратов диа-мс1ра цилиндра).
[c.56]
Основной выигрыш в этом случае обусловлен уменьшением угла клиновидности сухарей вдвое по сравнению с конструкцией 6. Аналогичный результат можно получить и в конструкции б, уменьшив угол с 40° до 20°. Однако удельные нагрузки на поверхностях трения в это.м случае будут вдвое больше, чем в конструкЩ1и г.. [c.133]
Скос головки шатуна 5 сводит к минимуму протяженность неопертой поверхности днища и одновременно уменьшает изгиб поршневого пальца. Вместе с тем снижаются удельные нагрузки от газовых сил на рабочих поверхностях поршневого пальца. [c.564]
Удельная нагрузка Характеристика режима Число Зоммерфсльда [c.339]
Как ВИДНО ИЗ рис. 358, значения для подшипников малого диаметра д. = 204-30 мм) очень велики. Следовательно, такие подшипники могут надежно работать лишь при высоких характеристиках режима (большие частоты вращения, низкие удельные нагрузки). Как и для подшипников большого диаметра, целесообразно придерживаться умеренных значении отпосптсльното зазора (но не ниже ф = 0,001).
[c.350]
Как и для подшипников большого диаметра, целесообразно придерживаться умеренных значении отпосптсльното зазора (но не ниже ф = 0,001).
[c.350]
Коэффициент трения в области полужидкостной смазки уменьшается с увеличением X, т. е. для подшипника с заданной удельной нагрузкой II вязкосгью масла — с увеличением частоты вращения. Это означает, что по мере увеличения частоты вращения вал отходит от поверхности подшипника число соприкасающихся микронеровностей уменьшается. [c.351]
Коэффициент нагрузки, по сути, означает КПД. Это отношение фактических киловатт-часов, использованных за данный период, к общим возможных киловатт-часов, которые могли быть использованы за тот же период, на пиковом уровне кВт, установленном заказчиком в течение расчетного периода. Высокий коэффициент загрузки — это «хорошо», а низкий коэффициент загрузки — «плохо». Коэффициент нагрузки рассчитывается с использованием нескольких простых чисел из счета за электроэнергию. Требуемая информация:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Соотношение, которое выражает формула коэффициента нагрузки, представляет собой сравнение между фактических киловатт-часов, используемых с общими возможными киловатт-часами, которые может можно использовать на определенном уровне кВт. | кВтч——————————— = LF кВт x дней x 24 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
На диаграмме справа красный прямоугольник представляет общее возможное количество киловатт-часов, которое может быть использовано в зависимости от пикового потребления электроэнергии. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Концептуально управление спросом можно рассматривать как уменьшение общего размера коробки за счет уменьшения высоты. На рисунках ниже желтая линия — это предел потребления или уставка. Использование контроллера потребления Energy Sentry позволяет снизить пиковое потребление за счет управления нагрузкой и исходный пик использования энергии перераспределяется ниже предела.Дело не в изменении количества потребляемой электроэнергии, а в том, когда она используется. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Использование коэффициента нагрузки для определения предела нагрузкиЧтобы определить предел потребления кВт для желаемого процентного коэффициента нагрузки, возьмите фактическое количество кВтч, использованное домом в данном месяце, и разделите на 720 (общее количество часов в среднем 30-дневном месяце):
Если требуется коэффициент нагрузки 60%, выберите 4.
Если известна пиковая мощность и известна кВт-ч, коэффициент нагрузки можно найти, умножив кВт на общее количество часов и разделив фактические кВт-ч на это число. Например:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рекомендуемые пределы максимальной нагрузки (типичное жилое применение)
Примечание. Лимит спроса может быть выше или ниже в зависимости от индивидуального образа жизни или экстремальных погодных условий. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Расчет коэффициента нагрузки с учетом времени использованияЕсли вы работаете со ставками TOU, коэффициент загрузки необходимо рассчитывать другим способом. Нормы времени использования имеют отдельные значения времени пиковой и непиковой нагрузки, которые необходимо рассчитывать отдельно. Единственный вот изменения:
Если пиковые значения были разными между периодами включения и выключения, используйте соответствующие пиковые кВт и используйте расчет базового коэффициента нагрузки, приведенный выше. Если ставка TOU, с которой вы имеете дело, не учитывает спрос в периоды непиковой нагрузки, то в вычислении коэффициента нагрузки при непиковой нагрузке нет необходимости. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ПримерПредположим, вы находитесь в ситуации, когда:
Чтобы рассчитать коэффициент пиковой нагрузки, просто возьмите энергию, использованную во время пиковой нагрузки, и воспользуйтесь расчетом коэффициента нагрузки.Допустим, всего за время расчетный период. Предположим, что 15% или 600 кВт / ч использовались в пиковые часы с потребляемой мощностью 8 кВт. Коэффициент загрузки: 600LF = —————— = 68% 8 х 110 Таким образом, примерно две трети всей энергии (кВт / ч), которая может быть использована в течение расчетного периода, приходится на эти 22 пятичасовых периода. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Три процентных ноты:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Как рассчитать вес груза перед подъемом над головой
Один Самое первое, что вы должны сделать перед подъемом груза, — это определить общий вес груза. Это должно быть определено на ранних этапах планирования подъема, так как все остальное, что касается подвесного подъемника, должно учитывать вес груза, в том числе:
- Оборудование / тип крана, используемого для подъемника
- Тип подъемника подъемные стропы, такелажное оборудование и / или используемые устройства под крюком
- Тип строповой сцепки и угол стропы
Общий вес груза должен учитывать каждый элемент подъемного механизма, задействованный в подъемнике, включая крюк и все остальное, что ниже:
- Блок крюка
- Канаты
- Подъемные балки
- Скобы, подъемные кольца и другое оборудование
- Подъемные стропы
Существует множество различных методов, которые вы можете использовать для определения веса нагрузка, о которой мы поговорим более подробно в этой статье.
Простые методы определения веса груза
Есть много разных способов, которыми вы можете легко определить вес груза без каких-либо расчетов или использования специально разработанных датчиков веса или динамометров.
Посмотрите на нагрузку, чтобы увидеть, отмечен ли вес.
Нагрузка может быть указана с указанием веса производителем или может быть предварительно рассчитана и отмечена. Прежде чем выбирать подходящее подъемное и такелажное оборудование, обратите внимание на визуальные обозначения веса груза.
Знакомство с грузом
Если это груз, который вы регулярно поднимаете и перемещаете по своему объекту, например стальной рулон, связку труб или пиломатериалы, то вы уже знаете вес груза. Во многих случаях ваш мостовой кран, вероятно, был спроектирован с рабочим циклом и грузоподъемностью специально для этого повторяющегося подъема, поэтому вес груза учитывался при постройке крана.
См. Технические чертежи или планы проектирования
На распечатках продукта или разработанных чертежах груза может быть указан окончательный вес в собранном виде.
Просмотр коносамента или транспортной документации
Если груз был доставлен или транспортирован на ваш производственный объект или строительную площадку, в полученные вами транспортные документы должна быть указана информация о весе.
Используйте промышленные весы
Для небольших и легких нагрузок вы можете использовать промышленные напольные весы, которые обычно используются на производственных участках или в отделах отгрузки и приема на предприятии.
См. Спецификации производителя или данные каталога
Если груз представляет собой продукт или часть оборудования, вес груза может быть указан на:
- Документы, предоставленные производителем
- Информация на веб-сайте производителя или дистрибьютора
- Технические характеристики продукта в каталоге или брошюре о продукте
Расчет веса груза
Если информация о весе груза не предоставлена, вам нужно будет выполнить некоторые расчеты, чтобы определить вес груза, который вы собираетесь поднять. .В этом разделе мы предоставим вам некоторые базовые расчеты для расчета веса грузов разного размера из разных материалов.
.В этом разделе мы предоставим вам некоторые базовые расчеты для расчета веса грузов разного размера из разных материалов.
Шаг 1: Определите объем нагрузки
Прямоугольник / квадрат: Объем = Длина x Ширина x Высота
Полый цилиндр: Объем = 3,14 x Длина x Толщина стенки x (Диаметр — Толщина стенки )
Сложные формы: В некоторых случаях представьте, что весь объект заключен в прямоугольник, а затем вычислите объем этого прямоугольника.Или разделите объект на два или более прямоугольника меньшего размера, а затем вычислите вес каждой части и сложите их.
Шаг 2: Определите материал, который вы будете поднимать
Приведенную ниже таблицу можно использовать для приблизительных значений веса обычных нагрузок и материалов:
| Материал | фунтов / кубический фут | Материал | фунтов / кубический фут |
| Алюминий | 165 | Отливка из чугуна | 450 |
| Асбест | 153 | Свинец | 708 |
| Асфальт | Пиломатериал | 81 (Пихта)32 | |
| Латунь | 524 | Пиломатериалы (Дуб) | 62 |
| Кирпич | 120 | Пиломатериалы (RR Связи) | 50 |
| Бронза | 534 | Масло, моторное | 58 |
| Уголь | 56 | Бумага | 58 | 900 24
| Бетон | 150 | Портлендский цемент | 94 |
| Щебень | 95 | Речной песок | 120 |
| Дизель | 52 | Резина | 94 |
| Сухая земля (свободный) | 75 | Сталь | 480 |
| Бензин | 45 | Вода | 63 |
| Стекло | 162 | Цинк | 437 |
Шаг 3: Определите Вес объекта
Умножьте приблизительное количество фунтов на кубический фут материала на расчетный объем груза, чтобы получить вес объекта или груза.
Пример № 1: Алюминиевый блок
Вот как можно рассчитать вес нагрузки для алюминиевого блока длиной 6 футов, шириной 3 фута и высотой 4 фута:
Объем = Длина x Ширина x Высота
Объем = 6 футов x 3 фута x 4 фута
Объем = 72 кубических фута
Алюминий весит 165 фунтов на кубический фут (на основе чисел из таблицы выше). Основываясь на этой информации, вы должны выполнить следующий расчет:
Вес блока = 72 кубических фута x 165 фунтов на кубический фут
Вес блока = 11 880 фунтов./ 5,94 тонныПример № 2: Стальная труба
Вот как можно рассчитать вес нагрузки полой стальной трубы длиной 8 футов, с внешним диаметром 3 фута и толщиной стенки 1,5 дюйма:
Объем = 3,14 x Длина x Толщина стенки X (Диаметр — Толщина стенки)
Объем = 3,14 X 8 футов x 1,5 дюйма x (3 фута — 1,5 дюйма)
Преобразовать дюймы в футы (1,5 дюйма = 0,125 фута)
Объем = 3,14 x 8 футов x 0. 125 футов x (3 фута — 0,125 фута)
125 футов x (3 фута — 0,125 фута)
Объем = 3,14 x 8 футов x 0,125 фута x 2,875 футов
Объем = 9,03 кубических футов
Сталь весит 480 фунтов на кубический фут (на основе чисел из таблицы выше) . Основываясь на этой информации, вы должны выполнить следующий расчет:
Вес стальной трубы = 9,03 кубических футов x 480 фунтов на кубический фут
Вес стальной трубы = 4 334 фунта. / 2,17 тонныПример 3: Сложные формы
Вот как можно рассчитать нагрузочную массу объекта неправильной формы, сделанного из бетона.Сначала разделите объект на прямоугольники, а затем рассчитайте вес каждой секции по отдельности, а затем объедините их, как показано ниже:
Объем 1 (вверху) = 4 фута x 2 фута x 3 фута
Объем 1 = 24 кубических фута
Объем 2 (снизу) = 9 футов x 2 фута x 3 фута
Объем 2 = 54 кубических фута
Общий объем = Объем 1 (24 кубических фута) + Объем 2 (54 кубических фута)
Общий объем = 78 кубических футов
Бетон весит 150 фунтов на кубический фут (на основе чисел из таблицы выше). Основываясь на этой информации, вы должны выполнить следующий расчет:
Основываясь на этой информации, вы должны выполнить следующий расчет:
Сложная форма бетона = 78 кубических футов x 150 фунтов на кубический фут
Сложная форма бетона = 11 700 фунтов. / 5,85 тонныИспользование тензодатчиков или динамометров для определения веса груза
Кроме того, в оснастку могут быть включены другие устройства, которые обеспечат оператору считывание и определение веса груза, когда он немного приподнимается с платформы. земля.Эти устройства, называемые тензодатчиками или динамометрами, монтируются вместе с крюком крана, стропами и оборудованием. Затем нагрузка прикрепляется к датчику нагрузки, и датчик нагрузки вычисляет вес груза, измеряя силу, приложенную к нему с помощью тензодатчика, или гидравлическое или пневматическое давление внутри устройства.
Эти устройства могут отображать измеренный вес груза различными способами. Некоторые из них являются механическими с аналоговым дисплеем, на котором используются стрелка и циферблат — аналогично тому, как работают многие ванные или медицинские весы. Другие могут иметь цифровые дисплеи прямо на самом устройстве, а некоторые даже работают с портативными цифровыми устройствами или компьютерным программным обеспечением, чтобы отправлять показания оператору, который может выполнять удаленный мониторинг и диагностику кранового оборудования.
Другие могут иметь цифровые дисплеи прямо на самом устройстве, а некоторые даже работают с портативными цифровыми устройствами или компьютерным программным обеспечением, чтобы отправлять показания оператору, который может выполнять удаленный мониторинг и диагностику кранового оборудования.
Другой тип устройства для измерения веса — это грузозахватная скоба, которая, по сути, представляет собой полнофункциональную подъемную скобу со встроенной электроникой и микропроцессорами для определения веса груза, поднятого в воздух. Эти типы устройств также отправляют данные на портативное устройство или удаленную рабочую станцию.
Многие датчики веса и динамометры поставляются с датчиками перегрузки, которые предупреждают оператора, менеджеров по безопасности или другой назначенный персонал, если кран был перегружен. Перегрузка возникает, когда подъемник превышает номинальную грузоподъемность крана. Перегрузки запрещены в соответствии со стандартами OSHA и ASME B30, они могут вызвать перегрузку и повреждение кранового оборудования, что подвергнет опасности находящихся поблизости сотрудников в случае выхода крана из строя.
При использовании тензодатчиков или динамометров всегда обращайтесь к рекомендациям производителя по плановому обслуживанию и калибровке, чтобы убедиться, что ваше устройство соответствует требованиям и продолжает обеспечивать точные измерения.
В комплекте
Планирование подвесного подъема начинается с понимания веса груза, который вы планируете поднимать и перемещать. Все остальное должно встать на свои места, если вы будете следовать передовым методам подъема и такелажа и составить план подъема до того, как какой-либо груз будет поднят в воздух.
Некоторые из этих передовых методов такелажа включают:
- Всегда определяйте вес груза и учитывайте любые другие элементы, используемые ниже крюка, при расчете или определении общего веса груза.Сюда входят:
- Чан-стропы, канатные стропы и синтетические стропы
- Скобы, крюки, рым-болты, главные звенья и любое другое такелажное оборудование
- Подъемные балки, магниты, С-образные крюки, вакуумные подъемники или другое нижеследующее: крючки
- Определите стиль стропы, который вы будете использовать (цепь, трос или синтетический материал), и тип сцепки (вертикальный, корзина или колье).
 Рассчитайте угол стропы. Выберите правильное оборудование и стропы для подъемника в зависимости от номинальной и предельной рабочей нагрузки (WLL).
Рассчитайте угол стропы. Выберите правильное оборудование и стропы для подъемника в зависимости от номинальной и предельной рабочей нагрузки (WLL). - Осмотрите все такелажное оборудование перед любым подвесным подъемником. Любой предмет, который выглядит поврежденным, деформированным или имеет неправильный внешний вид, должен быть изъят из эксплуатации, и квалифицированный специалист может определить, можно ли вернуть оборудование в эксплуатацию или его следует вывести из эксплуатации и утилизировать.
- Надлежащее соединение такелажа и техника должны быть проверены, приподняв груз на несколько дюймов от земли, чтобы убедиться, что не происходит раскачивания, и что груз полностью закреплен, а центр тяжести учтен.
- Дополнительные факторы окружающей среды могут добавить сопротивление, влияющее на вес груза, и их необходимо учитывать. Некоторые примеры включают:
- Трение или сопротивление, вызванное поднятием груза с илистой поверхности, или грузом, который погружается в химикаты или другие жидкости и выходит из них
- Груз поднимается с наклонной поверхности
- Сильный ветер / порывы ветра
- Никогда не поднимайте груз над землей выше, чем необходимо, определяйте возможные препятствия и используйте слоган, когда это необходимо, для обеспечения дополнительного контроля нагрузки.

В Mazzella Companies мы можем предоставить консультации по подъему и такелажу, чтобы убедиться, что вы используете передовые методы такелажа, подъема и перемещения груза по вашему предприятию. Мы также предлагаем обучение в аудиториях для ваших сотрудников и продаем различные подъемные и такелажные изделия, в том числе:
- Мостовые краны
- Подъемники и детали подъемников
- Цепи из сплава, трос и синтетические стропы
- Такелажное оборудование
- Весоизмерительные ячейки и динамометры
Если вам нужна помощь в составлении плана подъема, требуется обучение ваших сотрудников такелажу или вы хотите запланировать оценку вашего такелажного оборудования и методов на месте, свяжитесь с нами сегодня, чтобы поговорить со специалистом по подъемным работам.
Подъем и оснастка
Имя Mazzella является синонимом качественных строп. Качественные стропы Mazzella включают цепи, тросы, нейлон, полиэстер, веревки и высококачественные синтетические стропы.
Мы также предоставляем сборные канаты — большие и малые. Мы производим мостовые тросы, крановые тросы, тросы для сталелитейных заводов и тысячи комплектов OEM. Также мы можем изготовить узлы со стандартной или нестандартной концевой арматурой. Также доступны специальные требования к испытаниям и допускам.
Mazzella также обладает одним из крупнейших в отрасли товарных запасов канатов, подъемников, деталей подъемников, съемников, оснастки и других связанных распределенных товаров.
Мы также проводим базовые тренинги по поднятию и монтажу на месте или онлайн!
Если вам требуется специальный курс обучения для соответствия требованиям OSHA, Mazzella может помочь вам в создании безопасного и надежного рабочего места.
Мы квалифицируем наших инструкторов, требуя от них прохождения внутренней программы обучения инструкторов (которая обучает применимым стандартам и методам обучения OSHA и ASME), обширного практического опыта и дополнительного обучения сторонних организаций, таких как Crosby, CM, Харрингтон, Горбель и Industrial Training International (ITI).
Позвоните нам по телефону 800.362.4601 или щелкните здесь, чтобы получить необходимые вам подъемные и такелажные изделия или пройти обучение!
Трос
Мы храним более 2 000 000 футов стального каната в различных местах… готовых к немедленной доставке! Мы обеспечиваем сборные стальные канаты и производим мостовые кабели, крановые кабели, кабели для сталелитейных заводов и тысячи сборок OEM.
Мы также можем изготовить узлы со стандартными или нестандартными концевыми соединениями. Также доступны специальные требования к испытаниям и допускам.
- Размеры от 1/4 ″ до 3 ″ в диаметре и от 9 до 52 мм в диаметре
- Для внутреннего и внешнего рынка
- На складе и готовы к отправке в тот же или следующий день из одного из наших многочисленных сервисных центров
Позвоните нам по телефону 800.362.4601 или щелкните здесь, если вам нужны изделия или сборки из троса!
Авторские права 2018. Компании Mazzella.
Расчеты оснастки и нагрузки: шаги и примеры — Видео и стенограмма урока
Углы и нагрузки стропов
После проверки веса груза следующим шагом будет расчет необходимой грузоподъемности.Номинальная грузоподъемность строп и скоб должна превышать вес поднимаемого груза.
Сила натяжения на опоре стропы зависит от угла стропы, поэтому силы на стропе необходимо определять для конкретного используемого угла стропы. Угол стропа — это внутренний угол стропы. По мере уменьшения этого угла нагрузка на опору стропы увеличивается.
Пример
Давайте рассмотрим два метода, используемых для расчета нагрузки на конкретную опору стропа.В одном методе используется диаграмма коэффициента угла стропы, в другом — отношение длины стропы к высоте.
Нагрузка на опору двух вертикальных строп составляет половину общей нагрузки на каждую стропу. Если вес груза составляет 1000 фунтов, нагрузка стропа для двух вертикальных строп составляет:
(1000 фунтов / 2) = 500 фунтов на каждую стропу.
По мере уменьшения угла стропы усилие на стропу увеличивается. Коэффициент нагрузки для угла стропа взят из диаграммы коэффициента нагрузки.
Допустим, две стропы поднимают груз весом 1000 фунтов под углом 45 градусов. Коэффициент нагрузки из таблицы для угла стропа 45 градусов составляет 1,414.
- Сила нагрузки стропа = (вес груза / 2) * коэффициент нагрузки
(1000 фунтов / 2) = 500 фунтов
1,414 * 500 фунтов = 707 фунтов (нагрузка на стропу)
Обратите внимание на увеличение нагрузки на стропу при уменьшении угла стропы.
Соотношение длины стропа к высоте
Если у вас нет диаграммы нагрузки, вы можете рассчитать коэффициент нагрузки стропа, используя отношение длины стропы к высоте стропа.В этом примере мы будем использовать стропу длиной 28 футов и высотой 20 футов. В этом случае коэффициент нагрузки стропа будет следующим:
28/20 = 1,4
После расчета силы нагрузки стропа вы можете сравнить ее с безопасной рабочей нагрузкой для стропа и связанного с ним такелажного оборудования. Безопасная рабочая нагрузка должна быть больше, чем сила нагрузки стропа. Две стропы на 500 фунтов не будут достаточно прочными, чтобы поднять 1000 фунтов, если угол стропы меньше 90 градусов.
Безопасная рабочая нагрузка должна быть больше, чем сила нагрузки стропа. Две стропы на 500 фунтов не будут достаточно прочными, чтобы поднять 1000 фунтов, если угол стропы меньше 90 градусов.
Резюме урока
Точный вес груза определяет характеристики оборудования, используемого в лифте.Основное оборудование, используемое в подъемнике, включает кран или подъемник, крюк крана, а также стропы и скобы, которые соединяют крюк с грузом.
Есть несколько источников для определения веса груза, в том числе:
- Штампованные или маркированные индикаторы веса
- Грузы, которые регулярно поднимаются, должны иметь известную массу груза
- Спроектированные отпечатки или планы дизайна
- Коносамент или товаросопроводительная документация
- Промышленные напольные весы
- Характеристики производителя
Вес груза = вес на единицу объема * общий объем
Грузоподъемность стропа и скоб должна превышать вес поднимаемого груза. Угол стропа — это внутренний угол стропы, и по мере его уменьшения нагрузка на опору стропы увеличивается.
Угол стропа — это внутренний угол стропы, и по мере его уменьшения нагрузка на опору стропы увеличивается.
Таблица коэффициента нагрузки показывает коэффициент нагрузки для соответствующих углов строп.
Сила нагрузки стропа = (вес / количество строп) * коэффициент нагрузки
Коэффициент нагрузки также можно рассчитать, разделив длину стропы на высоту стропа.
После расчета силы нагрузки стропа вы можете сравнить ее с безопасной рабочей нагрузкой для стропа и связанного с ним такелажного оборудования.Безопасная рабочая нагрузка должна быть больше, чем сила нагрузки стропа.
13 важнейших формул для переменных нагрузок, которые должен знать каждый энергетик
Электростанция обеспечивает электроэнергией большое количество потребительских нагрузок. Хотя потребительский спрос меняется со временем, это изменение нагрузки называется переменными нагрузками. Помня об этом изменении нагрузки, энергетик должен иметь дело с различными факторами, включая установку и обслуживание дополнительного оборудования, производственные затраты и использование электроэнергии. Вот 13 самых важных формул, которые вам следует запомнить.
Вот 13 самых важных формул, которые вам следует запомнить.
Средняя нагрузка (A.L)
Среднее количество единиц, генерируемых на электростанции за определенный промежуток времени, называется средними нагрузками. Мы можем представить себе среднюю нагрузку на день, неделю, месяц, год или десятилетие. Практически обычны среднесуточные, месячные и среднегодовые нагрузки.
Средняя дневная нагрузка = Единицы, генерируемые за день / 24 часа
Среднемесячная нагрузка = Единицы, генерируемые в месяц / 720 часов (часов в месяц)
Средняя годовая нагрузка = Единицы, произведенные в год / 8760 часов (часов в году)
Коэффициент нагрузки (LF)
Коэффициент нагрузки = средняя нагрузка / максимальная нагрузка
Средняя нагрузка — это среднее значение всех нагрузок, возникающих на электростанции за любой конкретный период времени.Принимая во внимание, что максимальная потребность — это самая высокая потребность в нагрузке, которая возникает в определенное время. Коэффициент загрузки — это отношение средней нагрузки к максимальной нагрузке за определенное время. Как и средняя нагрузка, коэффициент загрузки также зависит от времени, мы можем иметь дневной LF, ежемесячный LF или годовой LF. Мы можем умножить среднюю нагрузку на время для манипуляции сгенерированными блоками.
Коэффициент загрузки — это отношение средней нагрузки к максимальной нагрузке за определенное время. Как и средняя нагрузка, коэффициент загрузки также зависит от времени, мы можем иметь дневной LF, ежемесячный LF или годовой LF. Мы можем умножить среднюю нагрузку на время для манипуляции сгенерированными блоками.
LF = (AL * t) / (Макс. Потребность * t) = Единицы генерирования / (Макс. Потребность * t)
Генерируемые единицы
Часто требуется вычислить единицы, генерируемые на станции.Мы можем добиться этого с помощью LF и максимального спроса, манипулируя предыдущей формулой.
Сгенерированных единиц = LF * Максимальное потребление * время
Так как средняя нагрузка — это коэффициент нагрузки * Максимальное потребление, которое мы достигаем:
Сгенерированных единиц = Средняя нагрузка * время
Коэффициент разнесения (DF)
DF — это соотношение между суммой индивидуального максимального потребления, возникающего на электростанции, к максимальному спросу на электростанции.
DF = Сумма индивидуального максимального потребления / Макс.спрос на ТЭЦ
Поскольку сумма индивидуальных запросов всегда больше, чем максимальная потребность станции, коэффициент разнесения всегда больше 1.
Коэффициент мощности установки
Отношение фактически произведенной энергии к максимальной энергии, которая могла быть произведена на заводе.
Коэффициент мощности установки (PCF) = Фактическая произведенная энергия / Максимальная энергия, которая могла быть произведена
PCF = (Средняя потребность * время) / (Производительность предприятия / время)
PCF = Средняя потребность / Производительность
Резервная мощность
Дополнительная мощность, которая не требуется, но зарезервирована для будущих потребностей.
Резервная мощность = Производительность установки — максимальная потребность
Коэффициент использования завода
Это отношение фактических единиц, произведенных заводом, к общей мощности завода, умноженное на количество часов работы.
Математически,
Коэффициент использования установки = Единицы производительности установки в кВтч / (Производительность установки * Часы использования)
Давайте подведем итог формул:
Расчет нагрузок электродвигателей — Центр электротехники
В моем последнем посте я обсуждал, почему нам нужно определять нагрузки и КПД двигателя.В этом посте я хочу поделиться тем, как получить значение нагрузки двигателя, используя простую электрическую формулу расчета.
Прежде чем идти дальше, я хочу объяснить о мощности. Что такое мощность? Конечно, этот термин важен для нашей темы обсуждения. Мощность оценивается как энергия в электрической цепи.
Это комбинация силы тока и значения напряжения. Основная формула для расчета мощности — P (ватт) = I (ампер) x V (вольт). Мощность также измеряется в единицах лошадиных сил (л.с.). Для обычного преобразования электрической мощности в ватт используется 1 л. = 746 Вт.
Как рассчитать нагрузку на двигатель
Нагрузки электродвигателя рассчитываются исходя из мощности в кВт и полной номинальной нагрузки в кВт. Ниже приводится формула для расчета нагрузок двигателя.
Ниже приводится формула для расчета нагрузок двигателя.
Пример:
У нас есть 1 асинхронный двигатель мощностью 30 лошадиных сил (л. С.), Работающий с током 34,9 А для токовой нагрузки и 3-фазным напряжением 460 В, значение коэффициента мощности 0,75 и КПД двигателя 85%
ШАГ 1
По этой формуле определяем значение мощности в кВт (Пи).
ШАГ 2
Нам нужно определить полную номинальную нагрузку в кВт
ШАГ 3
Мы можем количественно оценить частичную нагрузку двигателя, сравнив измеренную входную мощность под нагрузкой с мощностью, необходимой, когда двигатель работает с номинальной мощностью, используя эту формулу.
Расчет: —
Первый шаг для определения фактического значения напряжения и силы тока, я предлагаю собрать данные измерений с двигателя, используя вольтметр и клещи на измерителе. Пример следующий: —
Пример следующий: —
а) НАПРЯЖЕНИЕ
В красный = 462 В V синий = 461 В V желтый = 460 В
В всего = (462 + 461 + 460) / 3 = 461 В
б) AMPERE
А красный = 34,5 А Синий = 33,8 А Желтый = 34,2 А
Итого = (34,5 + 33,8 + 34,2) / 3 = 34,1 А
c) Коэффициент мощности: 0,75
г) КПД двигателя: 85%
Формула 1:
Pi = (V xI x PF x 1.732) / 1000
Пи = (461 x 34,1 x 0,75 x 1,732) / 1000
Pi = 20,4 кВт
Формула 2
Pir = (л.с. x 0,7457) / КПД
Pir = (30 x 0,7457) / 0,85
Pir = 19 кВт
Формула 3
НАГРУЗКА = (Pi / Pir) x 100%
НАГРУЗКА = (20,4 / 19) x 100%
Выходная мощность как% от номинальной мощности = 107,4%
* Из этого примера значения мы можем определить нагрузку нашего электродвигателя в хорошем состоянии. Это 100% выходная мощность для привода оборудования. Это КПД, а не работа с перегрузкой.
Это 100% выходная мощность для привода оборудования. Это КПД, а не работа с перегрузкой.
Формула расчета циркулирующей нагрузки
Вот формула, которая позволяет рассчитать коэффициент циркуляционной нагрузки вокруг шаровой мельницы и гидроцилона как части контура измельчения.
Например, ваша шаровая мельница работает в замкнутом цикле с набором циклонов. В мельницу поступает измельченная руда. Плотность пульпы вокруг вашего циклона отбирается и известна за 8-часовую смену, что позволяет рассчитать соответствующие коэффициенты циркулирующей нагрузки и тоннаж циркулирующей нагрузки в тоннах / день или тоннах / час.
Это % твердых веществ / плотности на основе Метод расчета циркуляционной нагрузки , полученный для пульпы / суспензии вокруг вашего гидроциклона.
Справочник CytecЗачем нужна большая циркуляционная нагрузка:
Если требуется продукт более мелкого размера, чем определенный критический размер, производительность шаровой мельницы значительно увеличивается за счет использования ее в замкнутом цикле с классификатором, и это увеличение еще больше достигается за счет увеличения циркуляционной нагрузки между шаровой мельницей и классификатор (рис. 70). На практике циркулирующие нагрузки между шаровой мельницей и классификаторами редко составляют менее 200 процентов и часто превышают 700 процентов. На первый взгляд может показаться странным, что циркулирующая нагрузка между мельницей и классификатором, производящим, например, 100 тонн готовой продукции в день, может достигать 400 тонн и более, но это будет ясно из рисунка 71. Тенденция к использованию все более высоких циркуляционных нагрузок в схемах шаровых мельниц и классификаторов привела к определенным механическим требованиям к шаровым мельницам, классификаторам и вспомогательному оборудованию.
70). На практике циркулирующие нагрузки между шаровой мельницей и классификаторами редко составляют менее 200 процентов и часто превышают 700 процентов. На первый взгляд может показаться странным, что циркулирующая нагрузка между мельницей и классификатором, производящим, например, 100 тонн готовой продукции в день, может достигать 400 тонн и более, но это будет ясно из рисунка 71. Тенденция к использованию все более высоких циркуляционных нагрузок в схемах шаровых мельниц и классификаторов привела к определенным механическим требованиям к шаровым мельницам, классификаторам и вспомогательному оборудованию.
Артур Таггарт
Расчет циркуляционной нагрузки в шлифовальных контурах
Все, что вам нужно знать о предполагаемом коэффициенте нагрузки
Благодарим вас за проявленный интерес к плану Major Energy Select 12 — плану, который поощряет эффективных потребителей энергии по одним из лучших доступных тарифов. Сегодня потребители более осведомлены об энергии, чем когда-либо в прошлом. Если вы один из тех потребителей, которые заботятся об энергии, вам нужно больше узнать о коэффициенте нагрузки, связанной с вашим домом или бизнесом, и о том, какое отношение он имеет к тому, насколько эффективно вы используете энергию.
Что такое коэффициент нагрузки?
Коэффициент нагрузки — это показатель того, насколько эффективно используется энергия. Это фактическое количество энергии (киловатт-часы — кВт-ч), доставленное за определенный период времени, в отличие от общей возможной энергии (кВт-ч), которая может быть доставлена за тот же указанный период времени. Высокий коэффициент нагрузки указывает на то, что нагрузка (используемая энергия) использует электрическую систему более эффективно, тогда как потребители, которые недостаточно используют систему распределения электроэнергии, будут иметь низкий коэффициент нагрузки. Электроэнергетические компании должны обеспечивать электроэнергией всех в пределах своей зоны обслуживания, и они должны быть готовы поставлять электроэнергию, даже если все использовали максимально необходимое количество (пиковый спрос) в любой момент времени. Другими словами, коммунальному предприятию может не потребоваться фактически обеспечить это максимальное количество энергии, но у него должна быть возможность сделать это. Если им действительно нужно подавать электроэнергию в часы пик, это может быть дорого. Это просто спрос и предложение.
Электроэнергетические компании должны обеспечивать электроэнергией всех в пределах своей зоны обслуживания, и они должны быть готовы поставлять электроэнергию, даже если все использовали максимально необходимое количество (пиковый спрос) в любой момент времени. Другими словами, коммунальному предприятию может не потребоваться фактически обеспечить это максимальное количество энергии, но у него должна быть возможность сделать это. Если им действительно нужно подавать электроэнергию в часы пик, это может быть дорого. Это просто спрос и предложение.
Электроэнергия стоит дорого в пиковые периоды.Потребители, которые используют электроэнергию таким образом, чтобы уменьшить или сгладить эти пики, помогают снизить нагрузку на инфраструктуру электроснабжения. Это означает возможность более низких ставок для этих клиентов.
Коэффициент нагрузки — это число, которое дает вам представление о том, какой вы потребитель энергии; все необходимое для его расчета можно найти, посмотрев на счет за электроэнергию. Значение коэффициента нагрузки всегда будет меньше единицы. Меньшее число означает, что ваше общее потребление энергии далеко от вашего пикового спроса и что вы могли бы быть более эффективными в потреблении энергии.Чем ближе вы приближаетесь к 1 (или 100%), тем меньше пиков в способе потребления энергии и более эффективно вы потребляете электрическую энергию.
Значение коэффициента нагрузки всегда будет меньше единицы. Меньшее число означает, что ваше общее потребление энергии далеко от вашего пикового спроса и что вы могли бы быть более эффективными в потреблении энергии.Чем ближе вы приближаетесь к 1 (или 100%), тем меньше пиков в способе потребления энергии и более эффективно вы потребляете электрическую энергию.
Как рассчитывается коэффициент нагрузки?
Электроэнергия (спрос или мощность) Коэффициент нагрузки — это мера степени использования или эффективности использования электроэнергии. Это отношение общей энергии (кВт-ч), использованной в расчетном периоде, к возможной общей энергии, использованной в течение периода, если она используется при пиковом потреблении (кВт) в течение всего периода.Коэффициент нагрузки по запросу полезен при оценке преимуществ стратегии управления спросом и аккумулирования энергии от батарей.
Таким образом, Расчет коэффициента нагрузки спроса на электроэнергию составляет:
Коэффициент нагрузки по запросу = кВтч / кВт / час в период
Для расчета коэффициента нагрузки возьмите общее количество электроэнергии (кВт-ч), использованное в месяце, и разделите его на пиковое потребление (мощность) (кВт), затем разделите на количество дней в цикле выставления счетов, затем разделите на 24 часа в день. В результате получается соотношение между нулем и единицей.
В результате получается соотношение между нулем и единицей.
Пример расчета коэффициента нагрузки по запросу на электроэнергию
- Ежемесячное потребление энергии 2000 кВтч
- Месячная пиковая потребность в электроэнергии 35 кВт
- дней в месяце 30
- часов в сутки 24 дня
- Коэффициент мощности нагрузки = 2000/35/30 * 24 = 79,4% -> вы молодцы!
| Коэффициент нагрузки | > 0,75 | 0,50 — 0,75 | 0,35 — 0,50 | 0,20 — 0,35 | 0.10 -0,20 | <0,10 |
| Преимущества управления спросом | Ограниченная выгода | Возможная выгода | Да, зависит от возврата | Хороший потенциал | Отличный потенциал | Легкие деньги |
Если коэффициент нагрузки превышает 0,75, потребление электроэнергии достаточно эффективно.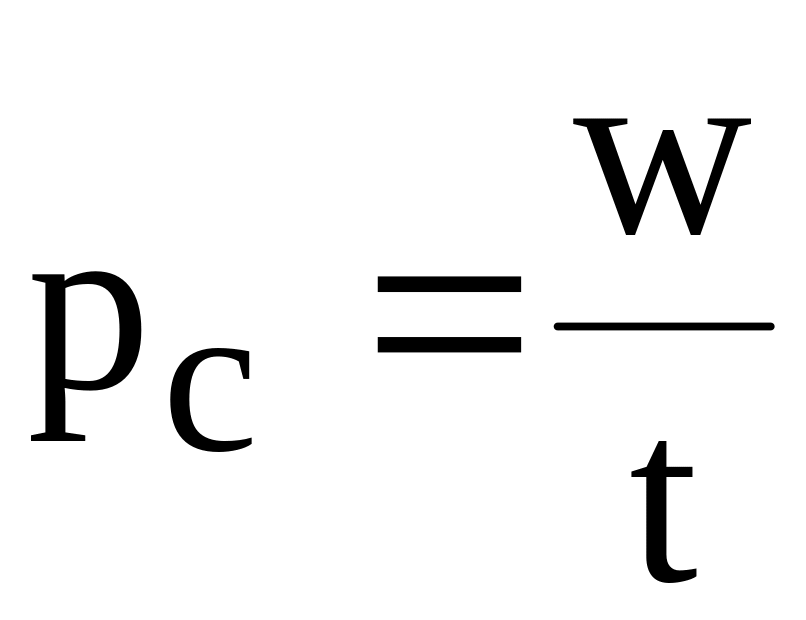 Если коэффициент загрузки ниже 0,5, у вас есть периоды очень высокого использования (спроса) и низкого коэффициента использования.Клиенты с низким коэффициентом нагрузки выиграют от системы контроля пикового потребления или от системы аккумулирования энергии от батареи, чтобы распределять потребление электроэнергии на более длительные интервалы времени и сглаживать пики.
Если коэффициент загрузки ниже 0,5, у вас есть периоды очень высокого использования (спроса) и низкого коэффициента использования.Клиенты с низким коэффициентом нагрузки выиграют от системы контроля пикового потребления или от системы аккумулирования энергии от батареи, чтобы распределять потребление электроэнергии на более длительные интервалы времени и сглаживать пики.
Низкие коэффициенты нагрузки, например, ниже 0,4, вносят значительный вклад в общий ежемесячный счет за электроэнергию в виде платы за потребление. Эти сборы за спрос указаны в счете как совпадающий спрос, спрос на оборудование и спрос, связанный с летним временем.
Как улучшить коэффициент нагрузки
Чем выше коэффициент загрузки, тем лучше, но как его приблизить к отметке 1? Повышение коэффициента загрузки в первую очередь связано с контролем пикового спроса.Снижение пикового спроса автоматически поможет увеличить процент загрузки.
Один из способов сделать это — уменьшить потребление энергии в часы пик.

 Низкий коэффициент загрузки означает
что вы используете электроэнергию неэффективно по сравнению с тем, чем вы могли бы быть, если бы контролировали свое пиковое потребление.
Низкий коэффициент загрузки означает
что вы используете электроэнергию неэффективно по сравнению с тем, чем вы могли бы быть, если бы контролировали свое пиковое потребление. Синяя область представляет фактически использованные киловатт-часы за месяц (дневной профиль показан для упрощения рисунка). Незаштрихованная область представляет собой потерянную мощность — область, где энергия могла быть использована, но не использовалась.Дело в том, что вы заплатили за емкость (спрос) всей коробки (плата за потребление), но не использовали большую ее часть. Все в незатененной области — это емкость, за которую вы заплатили, но не использовали.
Синяя область представляет фактически использованные киловатт-часы за месяц (дневной профиль показан для упрощения рисунка). Незаштрихованная область представляет собой потерянную мощность — область, где энергия могла быть использована, но не использовалась.Дело в том, что вы заплатили за емкость (спрос) всей коробки (плата за потребление), но не использовали большую ее часть. Все в незатененной области — это емкость, за которую вы заплатили, но не использовали. 16 (коэффициент нагрузки 100%) и разделите на 0,60.
16 (коэффициент нагрузки 100%) и разделите на 0,60. 5
5 5
5
