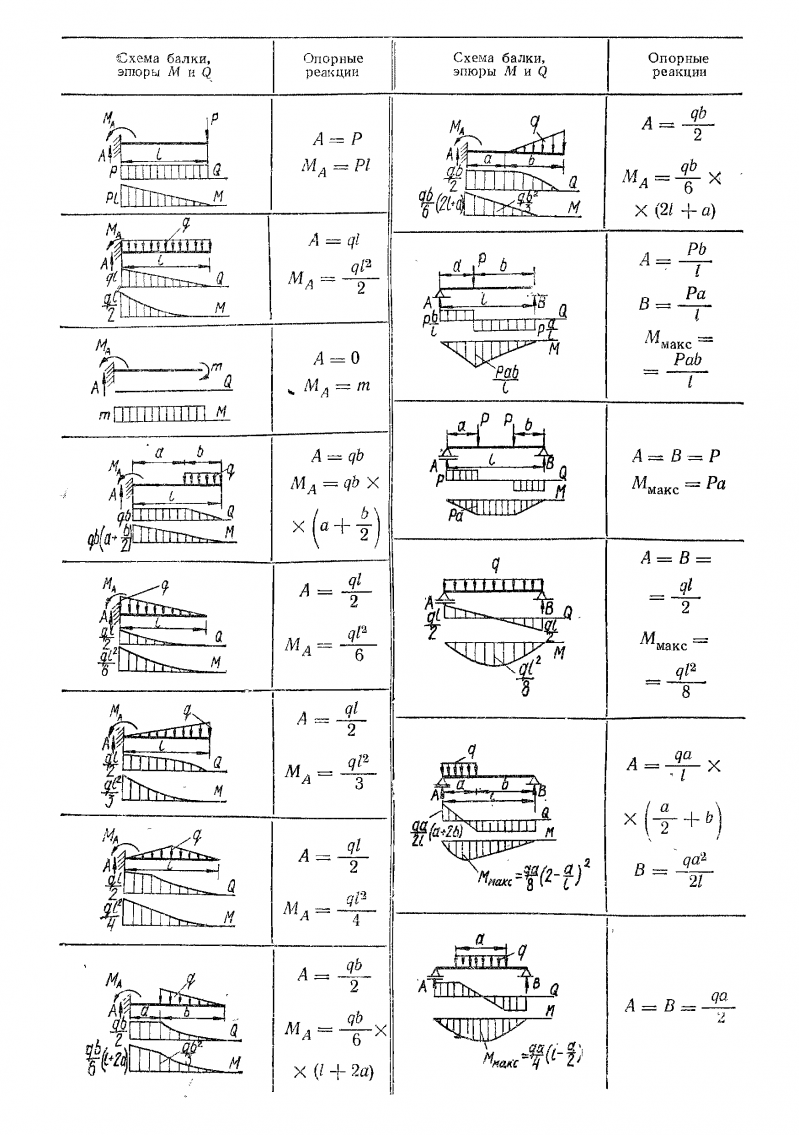
Защемленная по концам балка, нагруженная равномерно-распределенной нагрузкой
Цель: Нагружение защемленной по концам балки в одной плоскости без учета деформаций поперечного сдвига. Проверяются значения максимальных поперечного перемещения и изгибающих моментов.
Файл с исходными данными: 4_4.spr
Формулировка задачи: Защемленная по концам балка нагружается равномерно распределенной нагрузкой q. Определить максимальные поперечное перемещение w и изгибающие моменты М.
Ссылки: Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. — Киев: Наук. думка, 1988.
Исходные данные:
| E = 2.0·1011 Па | — модуль упругости, |
| μ = 0.3 | — коэффициент Пуассона, |
| l = 3 м | — длина балки; |
F = 14. | — площадь поперечного сечения; |
| I = 2.44·10-6 м4 | — момент инерции; |
| q = 10 кН/м | — значение нагрузки. |
Конечноэлементная модель: Расчетная схема плоская рама, 10 стержневых элементов типа 2, 11 узлов.
Результаты решения в SCAD
Эпюра изгибающего момента М (кН*м)
Значение поперечных перемещений w (мм).
Сравнение решений:
Параметр | Теория | SCAD | Отклонения, % | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Поперечное перемещение в середине пролета балки, мм | -4.32 | -4. Изгибающий момент и поперечная силаСодержание:Изгибающий момент и поперечная силаДавайте рассмотрим луч по желанию. Опорный конец (рис.61, а) подвергается воздействию вертикальной силы Pg, Pr, Pr. Предположим, что балка имеет симметричную продольную плоскость и на эту плоскость действует нагрузка. Затем, на основе симметрии, мы приходим к выводу, что изгиб происходит в одной плоскости.
Для исследования сил, возникающих в балке при изгибе, используйте уже использованный метод нахождения сил, возникающих в стержне при простом растяжении(Рис. 1).Представьте себе, что балка AB разрезана на 2 части сечением TP, взятым на любом расстоянии x от левой боковой опоры A (рис. При рассмотрении оставшейся левой балансировки балки (рис. 61.6) необходимо учитывать внутренние силы. Людмила Фирмаль Распределенные в сечении Абрамса, а также внешние силы, такие как нагрузка P и PJ и реакции. Представляет действие справа. Луч: слева. К 1 * Т 1 У-г-У7. 1. Так / Б * — Б-А;; Т /> Б) \ о Что?、- а. эээ… Диаграмма 61. Эти внутренние силы, вышеупомянутая внешняя сила Px, Pr n /?Он должен быть такого размера, чтобы он уравновешивался с R. Для последующего рассуждения полезно представить реальную систему внешних систем. Власть тебе.. Цервикальная эквивалентная система. Из статики нам известна система параллельных forces. It можно заменить на 1 силу, равную сумме алгебр.1 комплект питания плюс данный power. In в некоторых случаях сила может быть заменена. П пр-и/?Вертикальная сила<2, действие.
Таким образом, система внешних сил на левой стороне поперечного сечения МП может быть заменена статически эквивалентной системой, состоящей из боковой силы<2 и 1 пары сил м, действующих на плоскость поперечного сечения (рис.61, в).Сила, распределенная в поперечном сечении TP и представляющая собой действие правой стороны балки на левую сторону, должна быть такой, чтобы она уравновешивала изгибающий момент M и боковую силу<2. Например, рассмотрим равномерно нагруженную балку, показанную на Рис.1. 62, a. если нагрузка на единицу длины представлена d, то реакция в этом случае равна: Чтобы исследовать силы, распределенные по поперечному сечению mn, снова рассмотрим равновесие левой части балки. Если распределенная нагрузка действует на балку вместо сосредоточенной нагрузки, можно применить тот же вывод, что и в предыдущем случае. Людмила Фирмаль Внешние силы 4. 4. т и Это очень простое и удобное в использовании приложение. * Б. ’а / т 11111 и 111111 н. •1 Что же действует на эту часть луча-реакция/?И нагрузка равномерно распределяется по длине x. конечно, результат этой последней нагрузки будет равен dx. In вывод, алгебраическая сумма всех степеней y слева от раздела ТП, равный/?,- ЦТ. Алгебра рис. 62. Сумма всех моментов силы Реакция слева от секции Мп относительно центра тяжести этой секции, момент реакции/?, полученное вытягиванием момента результирующей распределенной нагрузки из x. момент распределенной нагрузки явно равен Х ОО * 4×2 * * 2 * Итак, для алгебраической суммы моментов выражение Все силы, действующие на левую сторону балки, действуют на плоскость поперечного сечения ТП、 -<7 * = <7(-5 — *)、(С. Пара равных сил М = /?, *- икс.) (СЗ)Уравнения©и (1) соответственно представляют боковые силы и изгибающие моменты поперечного сечения Мп. В приведенном выше примере рассматривалось равновесие на левой стороне балки. Рассматривая правую сторону балки, алгебраическая сумма сил на правой стороне сечения и алгебраическая сумма моментов одних и тех же сил будут одинаковыми 77. / 7 (- «л、 Л Что? W R —- ! г 1-1 у g-1 I£; і Рисунок 63. Количество ранее найденных но противоположных directions. Is это основано на том, что нагрузка, действующая на балку, действует вместе с реакцией? Должно быть zero. As в результате момент силы, действующей на левую сторону балки относительно центра тяжести сечения ТП, должен быть равен, но противоположен моменту для той же точки силы, действующей на правую сторону балки. Кроме того, алгебраическая сумма сил, действующих на левую сторону балки, должна быть равна, но противоположна алгебраической сумме сил, действующих на правую сторону. Смотрите также: Изгибающий момент и поперечная сила
Балка под действием изгибающего моментаБалка под действием изгибающего момента [c.94]
Принцип работы устройства заключается в следующем.  Вибратор /, возбуждаемый электрическими сигналами звуковой частоты, поступающими с генератора, передает поперечное усилие на консоль динамометрической балки 2 (которая связана с предварительным усилителем датчиков деформации 8), прикрепленной к исследуемой конструкции 5. В результате в месте присоединения балки к конструкции возникает изгибающий момент. Величина действующего на исследуемые конструкции момента фиксируется датчиками 3 и б деформации пограничного слоя балки вблизи ее корневого сечения. Под действием изгибающего момента в конструкции 5
[c.429] Вибратор /, возбуждаемый электрическими сигналами звуковой частоты, поступающими с генератора, передает поперечное усилие на консоль динамометрической балки 2 (которая связана с предварительным усилителем датчиков деформации 8), прикрепленной к исследуемой конструкции 5. В результате в месте присоединения балки к конструкции возникает изгибающий момент. Величина действующего на исследуемые конструкции момента фиксируется датчиками 3 и б деформации пограничного слоя балки вблизи ее корневого сечения. Под действием изгибающего момента в конструкции 5
[c.429]Пример 1.Паянтавровая балка работает под действием изгибающего момента, создаваемого поперечной силой Q = == 200 кН (рис. 26, п). Требуется определить значения касательных напряжений, возникающих в паяном шве. Материал балки СтЗ. Пайка выполнена припоем на железной основе, допускаемое напряжение прн срезе для паяного шва принимаем 108 МПа. [c.302] Наличие касательных напряжений в балке несколько искажает принятую нами раньше схему деформации балки. Потенциальную энергию от изгибающих моментов М , т.е. первое слагаемое в формуле (8.7.3), можно получить так же, как получена потенциальная энергия бруса при центральном растяжении сжатии в п. 4.7.1. Для этого рассмотрим элемент балки длиной dx. При его деформации под действием изгибающих моментов Mz ось бруса получит кривизну 1/р = Mz/EJz (см. формулу (8.3.1)), и поэтому правое сечение повернется относительно левого на угол da = dx/р (рис. 8.63). Если условно считать левое сечение неподвижным (т.е. вести рассуждения в системе координат, связанной с левым сечением), то при деформации элемента момент [c.231] Приме р 1. Балка находится под действием изгибающего момента в одной плоскости в данном сечении М [0,21]. Целевая функция — площадь поперечного сечения коробчатой балки (рис. 111.1.1) [c.339] Эта зависимость имеет один и тот же вид и при растяжении и при сжатии. Под действием изгибающего момента, вызванного силой Р (рис. 5-18), балка получит определенный прогиб/. Сжимающая сила N окажется приложенной эксцентрично к опасному сечению и вызовет дополнительный прогиб. 148 [c.148] Под действием изгибающего. момента, как уже было сказано выше, в каждой точке поперечного сечения балки возникнут напряжения а и, следовательно, на каждой элементарной площадке будет действовать усилие йЫ = айР. Так как рассматриваемая часть балки находится в равновесии, то система приложенных к ней сил должна удовлетворять шести уравнениям статики. [c.167] При анализе прогибов р (.v) балки под действием заданной распределенной нагрузки Р х) мы будем применять гипотезу Бернулли.  В соответствии с этим единственным обобщенным напряжением нужно считать изгибающий момент Q x), а соответствующей обобщенной деформацией — кривизну q x) = = — р» х). В г-м участке изгибающий момент и кривизна связаны зависимостью
[c.20] В соответствии с этим единственным обобщенным напряжением нужно считать изгибающий момент Q x), а соответствующей обобщенной деформацией — кривизну q x) = = — р» х). В г-м участке изгибающий момент и кривизна связаны зависимостью
[c.20]Для составления этой суммы показываем балку под действием каждой из нагрузок в отдельности и под каждой такой балкой строим эпюры изгибающего момента от нагрузки q на пролете iS (схема в)), от нагрузки q на консоли BD (схема г)), от лишней неизвестной D (схема d)) и от нагрузки силой Р =1, приложенной в точке D по направлению силы D (схема е)). На первых трех эпюрах указываем величины площадей эпюр и положение центров тяжести площадей, на четвертой же эпюре (е) —величины ординат Mq, приходящихся против центров тяжести площадей предыдущих эпюр. [c.197] Сила Р, действующая на простую балку, вызывает в сечении под грузом изгибающий момент (см. рис. 7.13) [c.599]
Рассмотрим балку, находящуюся в условиях плоского прямого изгиба под действием произвольных поперечных нагрузок в главной плоскости Оху (рис. 7.31, а). Рассечем балку на расстоянии л от ее левого конца и рассмотрим равновесие левой части. Влияние правой части в этом случае нужно заменить действием изгибающего момента и поперечной силы Qy в проведенном сечении (рис. 7.31,6). Изгибающий момент Мг в этом случае не является постоянным по величине, как это имело место при чистом изгибе, а изменяется по длине балки. Балка под действием осевой растягивающей нагрузки и изгибающего момента [c.97] Максимальный изгибающий момент, приложенный к балке под действием этой силы (при плече силы 70 см) 3780 кгс-см 371 нм [c.35] Для ТОГО чтобы получить основные уравнения неупругого изгиба, рассмотрим чистый изгиб балки под действием положительного изгибаюш его момента М (см. рис. 9.1, а). Изгибающие моменты [c.346] В качестве примера рассмотрим применение способа Верещагина для определения прогиба точки С (под силой Р ) балки, изображен ной ла рис. 16. 1Т,а при этом учтем действие изгибающих моментов и поперечных сил. [c.509] Предположим, что неразрезная балка рассчитана и известны величины опорных моментов. Возникает вопрос о том, как, зная эти моменты и внешнюю нагрузку, определить изгибающий момент в любом сечении балки. С. Н. Предтеченский [1.64] (1954) проанализировал влияние инерции вращения элементов балки на изгибающий момент. Рассмотрена свободно опертая балка под действием кратковременной равномерной симметрично распределенной нагрузки на средней части балки при нулевых начальных условиях. На конкретном примере показано, что влияние инерции вращения на величину максимального изгибающего момента в середине балки мало. [c.69] Пример Ш.З. На балку прямоугольного сечения при h = 35 см, Ь = = 20 см под углом Р = 8° к главной оси действует изгибающий момент М = == 10,9 т-м. Арматура 4 0 22 АП (/ = 15,2 см ) и 2 0 18 АП (/у = 5,1 см ) i a — 2600 кг/см бетон марки 300 i np = 155 кг/см . Выделим на участке, где нет сосредоточенных сил и моментов, малый элемент балки О О — Он находится в равновесии под действием внешней нагрузки, поперечных сил и изгибающих моментов в сечениях Oi и О2 (рис. 64, б). Поскольку в общем случае Q и УИ меняются вдоль оси балки, то в сечении Oi имеем Q (х) и М (х), а в сечении О2 имеем Q (х) + dQ и М (х) + dM. Для вывода, как всегда, изображаем их положительно направленными. Из условия равновесия выделенного элемента получим [c.54] Определяем опорные реакции и строим эпюры изгибающих моментов и поперечных сил. Разрезаем балку на три части в местах сопряжения ступеней. На рис. 290, б изображены отдельны части балки, находящиеся под действием внешних сил и внутренних усилий Q и М в местах разрезов. [c.300] Изгиб балки на двух опорах под действием равномерно распределенной нагрузки. На рис. 13.1.1, а показана консольная балка, на которую действует сила Р, приложенная под углом а к вертикальной оси у, создающая в произвольном сечении изгибающий момент, по абсолютному значению равный М=Рх. [c.222] Эпюры прогибов, перерезывающих сил и изгибающих моментов представлены на рис. 12.31. О поведении балки на упругом основании под действием сосредоточенной силы можно судить по приведенному простому решению для бесконечно длинной балки, если установить границы его применимости. Из решения (12.51) следует, что [c.272] При балке, жесткость которой невелика, влияние силы S на изгибающие моменты и прогибы балки может быть весьма существенным и пренебрегать им при расчете нельзя. В этом случае балку следует рассчитывать на продольно-поперечный изгиб, понимая под этим расчет на совместное действие изгиба и сжатия (или растяжения), выполняемый с учетом влияния осевой нагрузки (силы 5 ) на деформацию изгиба балки. Наибольший изгибающий момент М от статически действующей силы Р равен Р//4 он возникает в поперечном сечении балки под этой силой. [c.538] Части корпуса, обеспечивающие общую продольную крепость корабля, т. е. продольные связи корпуса, идущие непрерывно по всей длине или на значительной части длины его (стрингеры, наружная обшивка, внутреннее дно, палубы, продольные бимсы, продольные переборки) эти части корпуса, рассматриваемые совместно, представляют собой с точки зрения строительной механики составную балку, подверженную действию изгибающих моментов и срезывающих сил рассматриваемые же в отдельности, они представляют собой подкрепленные пластины и балки, подверженные растягивающим и сжимающим нагрузкам. 5) Части корпуса, обеспечивающие поперечную крепость корабля (поперечные переборки, палубы, поперечные бимсы, шпангоуты, днище). 6) Части корпуса, предназначенные для воспринятия различных местных или временных нагрузок (подкрепления) и передачи их на связи третьей категории (подкрепления под орудия, броню, рубки, машинные фундаменты, подкрепления для постановки в док и т. Положим, что балка изгибается двумя приложенными к ее концам парами сил (рис. 296), действующими в плоскости, проходящей через ее ось. При этом в поперечных сечениях балки возникнут только изгибающие моменты M , численно равные внешним моментам УИ, т. е. М =М. Как известно из предыдущего, такой изгиб называют чистым в поперечных сечениях балки возникают только нормальные напряжения. Установим зависимость между величинами этих нормальных напряжений и изгибающего момента. Выделим из балки по рис. 296 элемент abed, имеющий весьма малую длину в увеличенном масштабе этот элемент после деформации показан на рис. 297. Под действием приложенных парсил балка изогнется при этом первоначально прямая линия еп, представляющая собой проекцию нейтрального слоя на плоскость чертежа, обратится в некоторую кривую. Строим эпюру изгибающих мэтуггнтов. Напдег1ные опорные моменты откладываем от базы вверх (так как они отрицательны) под опорами. Ломаная штриховая линия тпрд (рис. 3.128, в) будет контуром эпюры моментов балки от действия опорных моментов. От наклонных прямых тп, пр и рд откладываем вниз ординаты эпюр моментов от нагрузки каждого пролета, рассматриваемого как простая балка. Таким образом, эпюры от опорных моментов и [c.344] J. Miklowitz [1.245] (1953) отметил, что в ряде случаев выгодно иметь дело с двумя уравнениями вида (2.5) и (2.6) относительно прогиба ио и угла поворота г)), а не с одним — вида (2.7) относительно w. Это упрощает интерпретацию формул для изгибающего момента и поперечной силы и, как следствие, запись граничных условий. В качестве примеров рассматриваются колебания бесконечной балки под действием поперечной сосредоточенной силы, полубесконечной балки, нагруженной сосредоточенным изгибающим моментом, и свободно опертой балки при действии поперечной сосредоточенной силы посредине. Изгибающий момент — балка — Большая Энциклопедия Нефти и Газа, статья, страница 1Изгибающий момент — балкаCтраница 1 Изгибающий момент балки определяется, считая ее свободно опертой по краям. [2] Изгибающий момент балки в сечении х равен сумме моментов сил Л и Р относительно центра тяжести названного сечения. [3] Максимальный изгибающий момент балки, свободно опертой на двух опорах и нагруженной силой Р посредине, равен Мх. [4] Отдельные линии осциллограммы обозначают: / — изгибающий момент балки моста в горизонтальной плоскости Ми г; 2 — то же в вертикальной плоскости Ми. [6] Приведенные материалы показывают, что, взяв изгибающие моменты балки постоянного сечения за координатные функции и проведя ортогонализацию, мы получаем распределение изгибающих моментов очень близким к фактическому. Тем же построением легко решается задача об изгибающем моменте балки для любого ее сечения. Изгибающим моментом балка или односторонним моментом для какого-нибудь сечения назы — вается общий момент относительно эгпаго сечения сил, расположенных по одну сторону от этого сечения. Так как балка находится в равновесии, то общий момент всех действующих на нее сил относительно любого сечения равен нулю; поэтому общий момент сил, расположенных по одну сторону сечения, равен по величине и противоположен по знаку общему моменту сил, расположенных по другую сторону сечения. Определим момент сил, расположенных, например, слева от сечения А ( черт. В предельном равновесии — непосредственно перед разрушением — изгибающие моменты балки находят статическим или кинематическим способом. [9] Следует отметить, что при точном расчете всей рамы изгибающий момент балки 6 будет SAfe5735 кГ — м, что опять указывает на хорошее совпадение обоих методов. [10] Все поперечные сечения ниже сечения IV — IV работают только на изгиб. Эпюра изгибающих моментов балки приведена на фиг. [11] Каждая сила, действующая на балку ( например, нагрузка балки, регкция опор), имеет момент относительно какого-нибудь поперечного сечения балки, равный произведению силы на расстояние точки приложения силы от данного сечения. Сумма М ( х) моментов всех сил, приложенных к части балки, расположенной по одну сторону от данного сечения, с абсциссой А, называется изгибающим моментом балки относительно данного сечения. Каждая сила, действующая на балку ( например, нагрузка балки, реакция опор), имеет момент относительно какого-нибудь поперечного сечения балки, равный произведению силы на расстояние точки приложения силы от данного сечения. Сумма М ( х) моментов всех сил, приложенных к части балки, расположенной по одну сторону от данного сечения, с абсциссой х, называется изгибающим моментом балки относительно данного сечения. В курсе сопротивления материалов доказывается, что изгибающий момент балки равен EJ / R, где Е — так называемый модуль упругости, зависящий от материала балки: J — момент инерции площади поперечного сечения балки относительно горизонтальной линии, проходящей через центр тяжести площади поперечного сечения; R — радиус кривизны оси изогнутой балки, который выражается формулой ( § 6, гл. [14] Каждая сила, действующая на балку ( например, нагрузка балки, реакция опор), имеет момент относительно какого-нибудь поперечного сечения балки, равный произведению силы на расстояние точки приложения силы от данного сечения. Страницы: 1 2 Правила знаков поперечных сил и изгибающих моментов (сопромат)Правила знаков для поперечных силВнешняя сила, действующая на отбрасываемую часть балки и стремящаяся повернуть ее относительно сечения по ходу часовой стрелки, входит в алгебраическую сумму для определения поперечной силы () со знаком плюс (рис. 7.5, а). Заметим, что положительная поперечная сила () «стремится вращать» любую из частей балки также по ходу часовой стрелки. Говоря простым языком: в сечении балки возникает поперечная сила, которую нужно определить и изобразить на эпюре поперечных сил. Чтобы правило знаков для поперечных сил выполнялось, нужно запомнить: Если поперечная сила возникает справа от сечения, она направлена вниз, а если поперечная сила возникает слева от сечения – вверх (рис. Поперечная сила является внутренней силой, поэтому поперечная сила противоположна равнодействующей внешних сил, действующих на рассматриваемую часть балки. Поэтому если внешняя сила P (рис. 7.5, а) направлена вниз, то интересующая поперечная сила, возникающая от действия силы P, направлена вверх (и наоборот). Значит, внутренняя сила положительна, если внешняя сила, породившая ее, направлена противоположно направлению поперечной силы по правилу знаков. Допустим, рассматривается правая часть балки (рис.7.5, а). Действует сила P, направленная вверх. По правилу, поперечная сила положительна, если направлена вниз (или внешняя сила P, породившая ее, направлена вверх). Правила знаков для изгибающих моментовПравила знаков для изгибающих моментов: внешняя нагрузка, приложенная к отбрасываемой части балки, создает момент относительно рассматриваемого сечения, стремящийся изогнуть отбрасываемую часть балки выпуклостью вниз, то этот момент входит в алгебраическую сумму для определения изгибающего момента () со знаком «плюс» (рис. По правилу знаков для изгибающих моментов, положительный изгибающий момент () «стремится изогнуть» любую из рассматриваемых частей балки тоже выпуклостью вниз. Кавычки использованы потому, что внутренние силовые факторы не являются активными силами и не могут вызывать деформацию балки. Для удобства определения знака изгибающего момента рекомендуется поперечное сечение балки мысленно представлять в виде неподвижной жесткой заделки. Иными словами: по правилу знаков изгибающий момент положителен, если «гнет балку» вверх, независимо от исследуемой части балки. Если в выбранном сечении результирующий момент всех внешних сил, порождающих изгибающий момент (является внутренней силой), направлен противоположно направлению изгибающего момента по правилу знаков, то изгибающий момент будет положительным. Допустим, рассматривается левая часть балки (рис. 7.5, б). Момент силы P относительно сечения направлен по часовой стрелке. По правилу знаков для изгибающих моментов для левой части балки изгибающий момент положителен, если направлен против часовой стрелки («гнет балку» вверх). Как рассчитать момент инерции балки?font-size:15px;} ]]>Как рассчитать момент инерции сечения балки (Второй момент области) Прежде чем мы найдем момент инерции (или второй момент области) сечения луча, его центроид (или центр масс) должен быть известен. Например, если момент инерции сечения относительно его горизонтали (XX) ось требовалась тогда вертикальная (и) сначала потребуется центроид (Пожалуйста, просмотрите наш учебник о том, как вычислить центр тяжести луча Раздел). Прежде чем мы начнем, если вы искали наш Калькулятор свободного момента инерции пожалуйста, нажмите на ссылку, чтобы узнать больше. Это вычислит центр тяжести, меня, и другие результаты и даже покажут вам пошаговые расчеты! Но сейчас, давайте посмотрим на пошаговое руководство и пример того, как рассчитать момент инерции: шаг 1: Сегментируйте сечение балки на частиПри расчете площади момента инерции, мы должны рассчитать момент инерции меньших сегментов. Нейтральная ось (Не Доступно) или горизонтальная ось ХХ находится в центре тяжести или центре масс. В нашем Centroid Tutorial, ранее было установлено, что центр тяжести этого участка 216.29 мм от нижней части секции. шаг 3: Рассчитать момент инерцииДля расчета общего момента инерции сечения нам нужно использовать “Теорема о параллельной оси”: Так как мы разделили его на три прямоугольные части, мы должны рассчитать момент инерции каждого из этих участков. Широко известно, что момент уравнения инерции прямоугольника относительно его оси центроида просто: Момент инерции других форм часто указывается на лицевой / оборотной стороне учебников или в этом руководстве. Теперь у нас есть вся информация, необходимая для использования “Теорема о параллельной оси” и найти общий момент инерции сечения двутавровой балки. В наш момент инерции пример: Итак, у нас есть руководство по расчету площади момента для сечений балок.. Этот результат имеет решающее значение в проектировании конструкций и является важным фактором в отклонении луча. Мы надеемся, что вам понравился урок, и с нетерпением ждем ваших комментариев.. БОНУС: Используя наш Калькулятор Момента ИнерцииАккаунт SkyCiv показывает полные расчеты момента инерции. Этот интерактивный модуль покажет вам пошаговые расчеты того, как найти момент инерции.: альтернативно, вы можете увидеть результаты нашего Калькулятор свободного момента инерции проверить свою работу. Это позволит вычислить все свойства вашего поперечного сечения и является полезным справочным материалом для расчета центроида. Калькулятор свободного момента инерции
DoITPoMS — Библиотека изгиба и кручения балок TLP Изгибающие моменты создаются поперечными нагрузками, приложенными к балкам. Уравновешивание внешнего и внутреннего моментов при изгибе консольной балки Следовательно, изгибающий момент M в нагруженной балке можно записать в виде \ [M = \ int {y (\ sigma dA)} \] Концепция кривизны балки, κ, является центральной для понимания изгиба балки. σ = E κ y Зависимость между радиусом кривизны R, кривизной балки κ и деформациями внутри балки, подверженной действию изгибающего момента.2} {\ rm {d}} A \] Единицы измерения I — м 4 . Значение I зависит исключительно от формы сечения балки. Щелкните здесь , чтобы увидеть, как I вычисляется для двух простых форм. Момент теперь можно записать как M = κ E I Эти уравнения позволяют рассчитать распределение кривизны по длине балки (т. Е. Ее форму) и распределение напряжений внутри нее для любого заданного набора приложенных сил. Эффективный подход к проектированию легких и жестких балок — сделать их полыми. Расчет второго момента площади для полых балок очень прост, поскольку он получается простым вычитанием I недостающего сечения из общего сечения.4}}} {{64}} \] предыдущая | следующий Консольные балки — моменты и прогибКонсольные балки — одиночная нагрузка на концеМаксимальная сила реакциина неподвижном конце может быть выражена как: R A = F (1a) где R A = сила реакции в A (Н, фунт) F = сила одностороннего действия в B (Н, фунт) Максимальный моментна неподвижном конце может быть выражается как M max = M A = — FL (1b) где M A = максимальный момент в A (Нм, Нмм, фунт-дюйм) L = длина балки (м, мм, дюйм) Максимальный прогибна конце консольной балки можно выразить как δ B = FL 3 / (3 EI) (1c) где δ B = максимальное отклонение в B (м, мм, дюйм) E = модуль упругости эластичность (Н / м 2 (Па), Н / мм 2 , фунт / дюйм 2 (psi)) I = момент инерции (м 4 , мм 4 , дюйм 4 ) b = длина между B и C (м, мм, дюйм) НапряжениеНапряжение в изгибающейся балке можно выразить как σ = y M / I ( 1d) где σ = напряжение (Па (Н / м 2 ), Н / мм 2 , psi) y = расстояние до точки от нейтральной оси (м, мм , дюйм) M = изгибающий момент (Нм, фунт-дюйм) I = момент инерции (м 4 , мм 4 , в 4 ) Максимальный момент консольной балки находится в фиксированной точке, а максимальное напряжение можно рассчитать, комбинируя 1b и 1d до σ max = y max FL / I (1e) Пример — консольная балка с одинарной нагрузкой на конце, метрические единицыМаксимальный момент на неподвижном конце UB 305 x 127 x 42 балка стальная полка консольная балка 5000 мм длинная, с моментом инерции 8196 см 4 (81960000 мм 4 ) , модуль упругости 200 ГПа (200000 Н / мм 2 ) и с одинарной нагрузкой 3000 Н в конце можно рассчитать как M max = (3000 Н) (5000 мм) = 1. = 1,5 10 4 Нм Максимальный прогиб на свободном конце можно рассчитать как δ B = (3000 Н) (5000 мм) 3 / (3 (2 10 5 Н / мм 2 ) (8,196 10 7 мм 4 )) = 7,6 мм Высота балки 300 мм и расстояние от крайней точки до нейтральной оси 150 мм .Максимальное напряжение в балке можно рассчитать как σ max = (150 мм) (3000 Н) (5000 мм) / ( 8,196 10 7 мм 4 ) = 27,4 (Н / мм 2 ) = 27,4 10 6 (Н / м 2 , Па) = 27,4 МПа Максимальное напряжение намного ниже предела прочности при растяжении прочность для большинства сталей. Консольная балка — одиночная нагрузкаМаксимальная сила реакциина неподвижном конце может быть выражена как: R A = F (2a) где R A = сила реакции в А (Н, фунт) F = сила одностороннего действия в В (Н, фунт) Максимальный моментна неподвижном конце может быть выражен как M max = M A = — F a (2b) где M A = максимальный момент в A (Н. a = длина между A и B (м, мм, дюйм) Максимальный прогибна конце консольной балки можно выразить как δ C = (F a 3 / (3 EI)) (1 + 3 b / 2 a) (2c) где δ C = максимальное отклонение в C (м, мм , дюйм) E = модуль упругости (Н / м 2 (Па), Н / мм 2 , фунт / дюйм 2 (psi)) I = момент инерции ( м 4 , мм 4 , дюйм 4 ) b = длина между B и C (м, мм, дюйм) Максимальный прогибпод действием единой силы может быть выраженным как δ B = F a 3 / (3 EI) (2d) где e δ B = максимальный прогиб в B (м, мм, дюйм) Максимальное напряжениеМаксимальное напряжение может быть вычислено путем объединения 1d и 2b до σ max = y max F a / I (2e) Консольная балка — Калькулятор одиночной нагрузки Универсальный калькулятор — будьте последовательны и используйте метрические значения на основе м или мм или британские значения на основе дюймов.
Консольная балка — равномерно распределенная нагрузкаМаксимальная реакцияна неподвижном конце может быть выражена как: R A = q L (3a) где R A = сила реакции в A (Н, фунт) q = равномерно распределенная нагрузка (Н / м, Н / м) мм, фунт / дюйм) L = длина консольной балки (м, мм, дюйм) Максимальный моментна фиксированном конце можно выразить как M A = — q L 2 /2 (3b) Максимальный прогибв конце можно выразить как δ B = q L 4 / (8 EI) (3c) где δ B = максимальное отклонение в B (м, мм, дюйм) Консольная балка — Калькулятор равномерной нагрузки Универсальный калькулятор — используйте метрические значения на основе м или мм или имперские значения на основе дюймов.
Более одной точечной нагрузки и / или равномерной нагрузки, действующей на консольную балкуЕсли на консольную балку действует более одной точечной нагрузки и / или равномерная нагрузка — результирующий максимальный момент на фиксированном конце A и результирующий максимальный прогиб на конце B может быть рассчитан путем суммирования максимального момента в A и максимального прогиба в B для каждой точки и / или равномерной нагрузки. Консольная балка — уменьшающаяся распределенная нагрузкаМаксимальная сила реакциина неподвижном конце может быть выражена как: R A = q L / 2 (4a) где R A = сила реакции в A (Н, фунт) q = уменьшающаяся распределенная нагрузка — максимальное значение при A — ноль при B (Н / м, фунт / фут) Максимальный моментпри фиксированный конец может быть выражен как M max = M A = — q L 2 /6 (4b) где M A = максимум момент в A (N. L = длина балки (м, мм, дюйм) Максимальный прогибна конце консольной балки можно выразить как δ B = q L 4 / (30 EI) (4c) где δ B = максимальный прогиб в B (м, мм, дюйм) E = модуль упругости ( Н / м 2 (Па), Н / мм 2 , фунт / дюйм 2 (psi)) I = момент инерции (м 4 , мм 4 , дюйм 4 ) Вставьте балки в модель Sketchup с помощью Engineering ToolBox Sketchup Extensionstatics — Как интерпретировать явные моменты в балках?Как интерпретировать такие моменты? 20 кН.Момент m называется «парой» или «парой силы». Пара сил создается равными и противоположными параллельными силами (результирующая сила = 0) вокруг точки в центре между ними. Пара вызывает чистое вращение без перевода. Пара имеет следующие объекты недвижимости:
ПРИЛОЖЕНИЕ Ниже приведены ответы на ваши конкретные вопросы. Они предполагают, что вы учитываете только требования статического равновесия для балки, потому что четвертое свойство применяется только к статическому анализу (например, установка суммы сил и моментов равной нулю для определения реакций на опорах). Для механики материаловедения расположение пары сил имеет решающее значение для определения изгибающих моментов и изгибающих напряжений. Здесь стрелка огибает точку на расстоянии 2 м от A. Значит ли это, что вокруг этой точки есть дополнительный момент? Да. Но вам не нужно принимать во внимание точку, где находится пара, из-за четвертого свойства. Вам нужно учитывать только расположение пары при определении изгибающих моментов и напряжений в балке, другими словами, для задач механики материалов. Для задач статики, где вы только пытаетесь определить реакции на опорах для статического равновесия, расположение пары не имеет значения. Но как этот момент влияет на момент, видимый из других точек, например, A? Или Б? Более конкретно, если бы я хотел сформировать уравнение моментного равновесия из A, я бы просто добавил / вычтет (в зависимости от моего определения положительного направления) 20 кНм из / в сумме моментов вокруг A?) И если бы я должен был сформировать моментное равновесие уравнения вокруг другой точки, например B, что мне тогда делать с 20 кНм? Если вы хотите суммировать моменты, относящиеся к A, вы можете представить себе пару, находящуюся в A, и просто добавить / вычесть это из других моментов относительно A. Если вы хотите суммировать моменты, относящиеся к B, вы можете представить себе пару, находящуюся в B, и просто прибавить / вычесть это из других моментов, связанных с B. В любом случае вы получите те же результаты. ПОМНИТЕ — Это относится только к требованиям статического равновесия. Когда вы анализируете изгибающие моменты и напряжения в балках, расположение пары имеет решающее значение. Кроме того, как такой момент может происходить в реальном мире? Это момент без силы или расстояния, просто момент.Как я мог произвести что-то подобное? Спасибо! Это не момент без силы. Это момент, вызванный двумя параллельными равными и противоположными силами. Итак, это момент без чистой силы. Подумайте о рулевом колесе вашей машины. Чтобы повернуть правую руку, вы прилагаете вертикальную силу вверх левой рукой и равную и параллельную вертикальную силу вниз правой рукой. Поскольку ваши силы равны, параллельны и противоположны, вы создаете пару моментов на колесе. Следующая ссылка с сайта MIT описывает пары более подробно и дает примеры (например, рулевое колесо), в том числе один, связанный с мостом. http://web.mit.edu/4.441/1_lectures/1_lecture12/1_lecture12.html Надеюсь, это поможет. Балка с простой опорой и моментомБалка с простой опорой и вычислителем момента для простой балки, на которую действует момент в центре, в конце или в любой промежуточной точке. Примечание. Используйте точку «.» как десятичный разделитель. Примечание *: M положительно по часовой стрелке, как показано на рисунке. Примечание **: Второй момент расчета площади несущих балок см. На странице » Калькуляторы сечений ».
Примечание *: R 1 и R 2 являются вертикальными концевыми реакциями слева и справа, соответственно, и положительными вверх.Поперечные силы и прогибы положительны в направлении вверх и отрицательны. в нисходящем направлении. Все моменты положительны при создании сжатия на верхней части поперечины балки. раздел. Все наклоны положительные, когда вверх и вправо. Примечание. Напряжения являются положительными числами, и это величины напряжений в луч. Он не делает различий между растяжением и сжатием конструкции. луч.Это различие зависит от того, с какой стороны нейтральной плоскости луча вход соответствует. Наклон Прогиб Момент Сила сдвига 7. 3: Изгибающие моменты и кривизна балки 3: Изгибающие моменты и кривизна балкиИзгибающие моменты создаются поперечными нагрузками, приложенными к балкам.Самый простой случай — консольная балка , широко распространенная на балконах, крыльях самолетов, трамплинах и т. Д. Изгибающий момент, действующий на секцию балки из-за приложенной поперечной силы, определяется произведением приложенной сила и ее расстояние от этой секции. Таким образом, он имеет единицы Н · м. Он уравновешивается внутренним моментом , возникающим из-за возникающих напряжений. Это получается путем суммирования всех внутренних моментов, действующих на отдельные элементы внутри секции.Они задаются силой, действующей на элемент (напряжение, умноженной на площадь элемента), умноженной на его расстояние от нейтральной оси, y . Уравновешивание внешнего и внутреннего моментов при изгибе консольной балки Следовательно, изгибающий момент M в нагруженной балке можно записать в виде \ [M = \ int y (\ sigma d A) \] Концепция кривизны балки, κ, является центральной для понимания изгиба балки. σ = E κ y Зависимость между радиусом кривизны R, кривизной балки κ и деформациями внутри балки, подверженной действию изгибающего момента.{4}} {64} \] Момент теперь можно записать как \ [M = \ каппа E I \] Эти уравнения позволяют рассчитать распределение кривизны по длине балки (т. Е. Ее форму) и распределение напряжений внутри нее для любого заданного набора приложенных сил. Следующее моделирование реализует эти уравнения для управляемой пользователем формы балки и набора сил. Конфигурации нагружения с трехточечным изгибом и четырехточечным изгибом в этой модели являются СИММЕТРИЧНЫМИ, с направленными вверх силами, обозначенными стрелками, за пределами направленной (ых) силы (-ей), обозначенных крючками Эффективный подход к проектированию легких и жестких балок — сделать их полыми. Схемы балок с простой опорой: артикулСхемы балок с простой опоройСодержаниеВведениеБалка с простой опорой — одна из самых простых конструкций. У него всего две опоры, по одной с каждой стороны. Одна — это опора с штифтами, а другая — роликовая опора. В этой конфигурации лучу запрещается любое вертикальное движение на обоих концах, в то время как он может свободно вращаться. Благодаря роликовому опору он также может расширяться или сжиматься в осевом направлении, хотя свободному горизонтальному перемещению препятствует другая опора. Удаление любой из опор при вставке внутреннего шарнира приведет к превращению балки с простой опорой в механизм, то есть без ограничений перемещается в одном или нескольких направлениях. Очевидно, это нежелательно для несущей конструкции. Следовательно, балка с простой опорой не обеспечивает избыточности в плане опор, и в случае локального отказа вся конструкция рухнет. Статический анализ — изгибающие моменты и поперечные силыОпределение опорных реакций — это только часть статического анализа конструкции. В большинстве случаев очень важно определить силы и моменты, возникающие внутри балки в результате приложенной нагрузки. Обычно для плоской конструкции, нагруженной в своей плоскости, могут возникать следующие внутренние воздействия:
Чтобы найти эти внутренние воздействия, при В любой конкретной точке конструкции необходимо выполнить разрез.Проще говоря, структура делится на две части в определенном месте, представляющем интерес.
На следующем рисунке проиллюстрирован разрез в произвольной точке свободно опертой балки. Выберем левую часть для работы. Неизвестные внутренние воздействия N, V и M были вставлены в разрез с их положительными направлениями. На данный момент примите показанные направления как правильные. Далее мы должны написать уравнения равновесия для левой части.A = 0 \ Rightarrow R_A 0 + M-V x = 0 Из первого уравнения мы получаем N = 0, что означает отсутствие осевой силы в определенной точке. Но поскольку эта точка случайна, можно утверждать, что вдоль пролета балки нет осевой силы. Нетрудно доказать, что, если отсутствует горизонтальная составляющая приложенных нагрузок, осевая сила в свободно опертой балке всегда равна нулю. Если отсутствует горизонтальная составляющая приложенных нагрузок, осевое усилие в балке с простой опорой всегда равно нулю. Из второго уравнения получаем: V = R_A. И подставляя V в третье уравнение, получаем: M = R_A x. Обычно нет необходимости проверять обе детали после разреза. Точечные силы и точечные моменты Определение поперечной силы и изгибающего момента в точках, где приложена сосредоточенная сила или изгибающий момент, требует некоторого дополнительного рассмотрения. Чтобы проиллюстрировать это, давайте рассмотрим следующую балку с простой опорой. Мы должны определить поперечную силу в точке приложения приложенной нагрузки. Таким образом, выполняется разрезание сечения слева от точки приложения. Так же выделяем левую часть. Равновесие сил на оси y становится: \ sum F_y = 0 \ Rightarrow R_A-V _ {\ mathrm {left}} = 0 \ Rightarrow V _ {\ mathrm {left}} = R_A Мы не включили сила F в равновесии, потому что разрез был сделан слева от точки приложения, таким образом, оставив F в правой части разреза.Теперь сделаем разрез немного правее силы F. Мы снова выбираем левую часть, но на этот раз сила включается. Равновесие принимает следующий вид: \ sum F_y = 0 \ Rightarrow R_A-F-V _ {\ mathrm {right}} = 0 \ Rightarrow V _ {\ mathrm {right}} = R_A-F Ясно, что: V _ {\ mathrm {left}} \ ne V _ {\ mathrm {right}}. Аналогичные соображения применимы, когда присутствует момент точки.Слева и справа от точки приложения результирующий изгибающий момент будет разным. Условные обозначения для изгибающих моментов и поперечных силЧто касается условных обозначений для внутренних сил и моментов при любом разрезе сечения, обычно принимаются следующие условные обозначения:
Эти правила хотя и не являются обязательными, но скорее установлены. Другой набор правил, если его последовательно соблюдать, также даст правильные результаты. Пример 1: внутренние воздействия в разрезе поперечного сечения балки с простой опорой
Опорные реакции Прежде чем приступить к нахождению внутренних сил и моментов, мы должны определить опорные реакции для данной конструкции . И путем подстановки R_B в первое уравнение находим: R_A + {wL \ over2} -wL = 0 \ Rightarrow R_A = {wL \ over2} Нахождение внутреннего действия в среднем пролете Шаг 1. Делаем разрез посередине балки, и выбираем правую часть. Шаг 2. Помещаем внутренние силы и моменты в разрез с их положительными направлениями. M — изгибающий момент, (V \) — поперечная сила, N — осевая сила.Обратите внимание, что даже несмотря на то, что вычисление N не требуется, и мы можем не включать его в равновесие без вреда, в более общем случае такое упущение приведет к неверным результатам. Шаг 3. Обеспечиваем равновесие вырезанной детали. Перед написанием уравнений заменим распределенную нагрузку эквивалентной точечной нагрузкой. Он должен иметь величину wL / 2 и точку приложения в середине детали, то есть на четверть длины от конца A. Уравнения равновесия: \ sum F_x = 0 \ Rightarrow N = 0 \ sum F_y = 0 \ Rightarrow {wL \ over2} — {wL \ over2} -V = 0 \ \ circlearrowleft \ sum M ^ {A} = 0 \ Rightarrow {wL \ over2} 0- {wL \ over2} {L \ over4} -V {L \ over2} + N \ times0 + M = 0 Шаг 4. Определение изгибающего момента и поперечной силы как функции расстояния x Чтобы найти соотношение между внутренними силами или моментами в зависимости от расстояния x, все, что нам нужно сделать, это разрезать на этом расстоянии x, с левого конца. Порядок остается прежним. Мы выбираем левую часть выреза и вводим неизвестные величины как M (x для изгибающего момента, V (x) для поперечной силы и N (x) для осевой силы. Также мы заменяем наложенные на вырезанную часть , распределенная нагрузка с эквивалентной точечной нагрузкой.2 \ справа) Диаграмма изгибающего момента и диаграмма поперечных сил Знание внутренних сил и моментов в определенной точке полезно, но не может дать полного представления о том, что происходит во всей конструкции. Чтобы получить эту информацию, необходимо сделать большое количество разрезов по всей конструкции. Таким образом можно определить критические точки в конструкции, в которых изгибающий момент, или поперечная сила, или осевая сила достигают своих пиковых значений. В этом контексте очень полезно проиллюстрировать, как изгибающие моменты меняются внутри конструкции.Диаграмма изгибающего момента, или сокращенно BMD, представляет собой диаграмму, нанесенную поверх конструкции, которая отображает значение изгибающего момента в любой точке. Точно так же диаграмма поперечных сил, или SFD, отображает значение поперечной силы в любой точке конструкции, а диаграмма осевых сил, или AFD, отображает значение осевой силы. Чтобы построить любую из этих диаграмм, мы должны предпочтительно знать аналитическое выражение (я) соответствующей величины (например, изгибающий момент для BMD) вдоль конструктивного элемента (ей).Для балки с опорой на опору такие аналитические выражения довольно легко вычислить, как показано в последнем примере. Пример 2: BMD и SFD балки с простой опорой
Из решения предыдущего примера мы нашли аналитические выражения поперечной силы и изгибающего момента в зависимости от расстояния x от левого конца. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 {2}}{24}. \]
{2}}{24}. \]
 , равная алгебраической сумме внешних сил, распределяется Поперечное сечение расположено на левой стороне ТП и называется поперечной силой по сечению т. пара сил м относительно центра тяжести этого сечения, равная алгебраической сумме моментов внешних сил, расположенных на левой стороне поперечного сечения Мп, называется изгибающими моментами сечения Мп.
, равная алгебраической сумме внешних сил, распределяется Поперечное сечение расположено на левой стороне ТП и называется поперечной силой по сечению т. пара сил м относительно центра тяжести этого сечения, равная алгебраической сумме моментов внешних сил, расположенных на левой стороне поперечного сечения Мп, называется изгибающими моментами сечения Мп. (Рис. 62, 6).
(Рис. 62, 6). )
) силы справа дают моменты против часовой стрелки. 63, а. таким образом, можно видеть, что направление момента таково, что луч изгибается с нисходящей выпуклостью. Если изгибающие моменты сечений mn и mn отрицательные, то балка изгибается вверх, как показано на рисунке. 63.6.Поэтому в разрезе балки、
силы справа дают моменты против часовой стрелки. 63, а. таким образом, можно видеть, что направление момента таково, что луч изгибается с нисходящей выпуклостью. Если изгибающие моменты сечений mn и mn отрицательные, то балка изгибается вверх, как показано на рисунке. 63.6.Поэтому в разрезе балки、 Удобный графический интерфейс. Считает любые схемы.
Удобный графический интерфейс. Считает любые схемы.

 Мы считали, что под действием изгибающих моментов поперечные сечения, оставаясь
[c.254]
Мы считали, что под действием изгибающих моментов поперечные сечения, оставаясь
[c.254] Балка изгибается под действием изгибающего момента М, причем возникает напряжение, максимальное значение которого равно 75 кГ/см . Определить, чему равен изгибающий момент М.
[c.384]
Балка изгибается под действием изгибающего момента М, причем возникает напряжение, максимальное значение которого равно 75 кГ/см . Определить, чему равен изгибающий момент М.
[c.384] 117. Цилиндрическая балка под действием крутящего ЛТ] и изгибающего M моментов (М = Му + М,к).
117. Цилиндрическая балка под действием крутящего ЛТ] и изгибающего M моментов (М = Му + М,к).
 Так как изгибающий момент согласно (7.14) связан с нормальными напряжениями а = С , то нормальные напряжения в продольных волок-
[c.136]
Так как изгибающий момент согласно (7.14) связан с нормальными напряжениями а = С , то нормальные напряжения в продольных волок-
[c.136] Рассмотрим п-й пролет неразрезной балки, находящийся под действием опорных моментов УИ 1 и М и внешней нагрузки (рис. 11.36,а). Окончательная эпюра в этом пролете представляет собой сумму трех эпюр две от моментов и Л1 и третья М°п от внешней нагрузки (рис. 11.36,6).
[c.360]
Рассмотрим п-й пролет неразрезной балки, находящийся под действием опорных моментов УИ 1 и М и внешней нагрузки (рис. 11.36,а). Окончательная эпюра в этом пролете представляет собой сумму трех эпюр две от моментов и Л1 и третья М°п от внешней нагрузки (рис. 11.36,6).
[c.360] [c.149]
[c.149] Примем функцию напряжений в этой задаче в виде (7.28). Изгибающий момент и перерезывающая сила в произвольном сечении равны (рис. 7.3, а)
[c.142]
Примем функцию напряжений в этой задаче в виде (7.28). Изгибающий момент и перерезывающая сила в произвольном сечении равны (рис. 7.3, а)
[c.142] [c.498]
[c.498] п.). 7) Части корпуса, служащие для увеличения устойчивости листов и балок (набор днища и палуб, обеспечивающий устойчивость наружной обшивки и настилки палуб поперечный набор, увеличивающий устойчивость стрингеров и пр.). 8) Части корпуса, служащие для соединения листов и профилей, идущих на постройку (заклепочные соединения) заклепочные соединения корпуса входят в состав связей всех предыдущих категорий и помимо общей теории их рассматриваются каждый раз отдельно при расчете этих связей. Из приведенного разделения частей корпуса по характеру их работы на различные категории видно, что в судовом корпусе нет строгого разделения функций,выполняемых отдельными связями его, что и является отличительным свойством этой конструкции в ряду других инженерных сооружений напр, наружная обшивка днища д. б. отнесена к связям всех пяти первых категорий она воспринимает давление воды, служит нижним пояскомг у стрингеров и шпангоутов и т. о. принимает участие в работе связей второй категории, является подкрепленной пластиной (днищем) уравновешивЕ ющей реакции противоположных бортов, является главной связью в обеспечении общей продольной и поперечной крепости корабля.
п.). 7) Части корпуса, служащие для увеличения устойчивости листов и балок (набор днища и палуб, обеспечивающий устойчивость наружной обшивки и настилки палуб поперечный набор, увеличивающий устойчивость стрингеров и пр.). 8) Части корпуса, служащие для соединения листов и профилей, идущих на постройку (заклепочные соединения) заклепочные соединения корпуса входят в состав связей всех предыдущих категорий и помимо общей теории их рассматриваются каждый раз отдельно при расчете этих связей. Из приведенного разделения частей корпуса по характеру их работы на различные категории видно, что в судовом корпусе нет строгого разделения функций,выполняемых отдельными связями его, что и является отличительным свойством этой конструкции в ряду других инженерных сооружений напр, наружная обшивка днища д. б. отнесена к связям всех пяти первых категорий она воспринимает давление воды, служит нижним пояскомг у стрингеров и шпангоутов и т. о. принимает участие в работе связей второй категории, является подкрепленной пластиной (днищем) уравновешивЕ ющей реакции противоположных бортов, является главной связью в обеспечении общей продольной и поперечной крепости корабля. Другой особенностью конструкции судового корпуса является обилие в этой конструкции частей, работающих на продольный изгиб, т. е. частей, требующих проверки и обеспечения их устойчивости эта особенность конструкции кор-
[c.98]
Другой особенностью конструкции судового корпуса является обилие в этой конструкции частей, работающих на продольный изгиб, т. е. частей, требующих проверки и обеспечения их устойчивости эта особенность конструкции кор-
[c.98] [c.285]
[c.285] [c.58]
[c.58] Естественно, что и прогибы, определенные по этим изгибающим моментам, также должны быть близки к их точным значениям; поэтому, вычислив кинетическую и потенциальную энергию для выбранных — таким образом прогибов и изгибающих моментов, мы должны получить очень близкие к истинным значения частот колебаний.
[7]
Естественно, что и прогибы, определенные по этим изгибающим моментам, также должны быть близки к их точным значениям; поэтому, вычислив кинетическую и потенциальную энергию для выбранных — таким образом прогибов и изгибающих моментов, мы должны получить очень близкие к истинным значения частот колебаний.
[7] [8]
[8] [12]
[12] Сумма М ( х) моментов всех сил, приложенных к части балки, расположенной по одну сторону от данного сечения, с абсциссой х, называется изгибающим моментом балки относительно данного сечения.
[15]
Сумма М ( х) моментов всех сил, приложенных к части балки, расположенной по одну сторону от данного сечения, с абсциссой х, называется изгибающим моментом балки относительно данного сечения.
[15] 7.5, а).
7.5, а). 7.5, б).
7.5, б). Значит, изгибающий момент будет положительным (сумма моментов внешних сил и изгибающий момент по правилу знаков противоположно направлены).
Значит, изгибающий момент будет положительным (сумма моментов внешних сил и изгибающий момент по правилу знаков противоположно направлены). Попробуйте разбить их на простые прямоугольные секции. Например, рассмотрите раздел I-луча ниже, который также был показан в нашем Centroid Tutorial. Мы решили разделить этот раздел на 3 прямоугольные сегменты:
Попробуйте разбить их на простые прямоугольные секции. Например, рассмотрите раздел I-луча ниже, который также был показан в нашем Centroid Tutorial. Мы решили разделить этот раздел на 3 прямоугольные сегменты: момент инерции формы. Однако прямоугольная форма очень распространена для секций балки, так что, наверное, стоит запомнить.
момент инерции формы. Однако прямоугольная форма очень распространена для секций балки, так что, наверное, стоит запомнить. , Площадь, и момент инерции секций вашей балки!
, Площадь, и момент инерции секций вашей балки! Самый простой случай — консольная балка , широко распространенная на балконах, крыльях самолетов, трамплинах и т. Д. Изгибающий момент, действующий на секцию балки из-за приложенной поперечной силы, определяется произведением приложенной сила и ее расстояние от этой секции. Таким образом, он имеет единицы Н · м. Он уравновешивается внутренним моментом , возникающим из-за возникающих напряжений. Это получается путем суммирования всех внутренних моментов, действующих на отдельные элементы внутри секции.Они задаются силой, действующей на элемент (напряжение, умноженной на площадь элемента), умноженной на его расстояние от нейтральной оси, y .
Самый простой случай — консольная балка , широко распространенная на балконах, крыльях самолетов, трамплинах и т. Д. Изгибающий момент, действующий на секцию балки из-за приложенной поперечной силы, определяется произведением приложенной сила и ее расстояние от этой секции. Таким образом, он имеет единицы Н · м. Он уравновешивается внутренним моментом , возникающим из-за возникающих напряжений. Это получается путем суммирования всех внутренних моментов, действующих на отдельные элементы внутри секции.Они задаются силой, действующей на элемент (напряжение, умноженной на площадь элемента), умноженной на его расстояние от нейтральной оси, y . Рисунок ниже, который теперь относится к сплошной балке, а не к полой опоре, показанной в предыдущем разделе, показывает, что осевая деформация, ε , задается соотношением y / R . Эквивалентно 1 / R («кривизна», κ) равна градиенту осевой деформации по толщине. Отсюда следует, что осевое напряжение на расстоянии y от нейтральной оси балки равно
Рисунок ниже, который теперь относится к сплошной балке, а не к полой опоре, показанной в предыдущем разделе, показывает, что осевая деформация, ε , задается соотношением y / R . Эквивалентно 1 / R («кривизна», κ) равна градиенту осевой деформации по толщине. Отсюда следует, что осевое напряжение на расстоянии y от нейтральной оси балки равно Следующее моделирование реализует эти уравнения для управляемой пользователем формы балки и набора сил. Конфигурации нагружения с трехточечным изгибом и четырехточечным изгибом в этой модели являются СИММЕТРИЧНЫМИ, с направленными вверх силами, обозначенными стрелками, за пределами направленной (ых) силы (-ей), обозначенных крючками
Следующее моделирование реализует эти уравнения для управляемой пользователем формы балки и набора сил. Конфигурации нагружения с трехточечным изгибом и четырехточечным изгибом в этой модели являются СИММЕТРИЧНЫМИ, с направленными вверх силами, обозначенными стрелками, за пределами направленной (ых) силы (-ей), обозначенных крючками 5 10 7 Нмм
5 10 7 Нмм  m, N.mm, lb.in)
m, N.mm, lb.in)  Стандартные значения в миллиметрах.
Стандартные значения в миллиметрах. Стандартные значения в миллиметрах.
Стандартные значения в миллиметрах.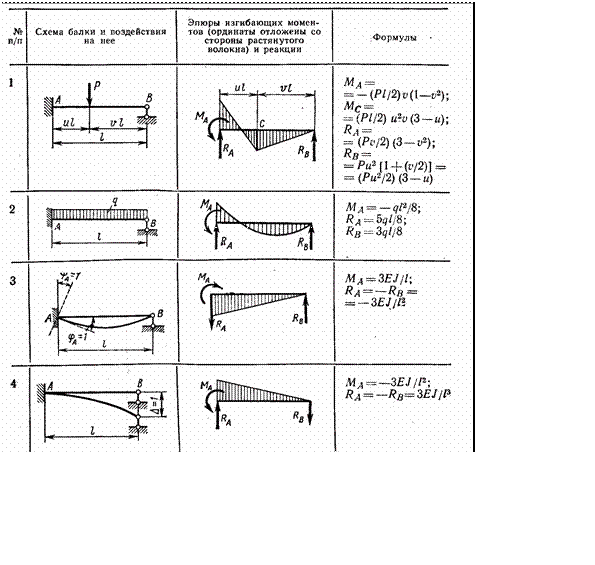 м, Нмм, фунт-дюйм)
м, Нмм, фунт-дюйм) 


 То есть вы создаете крутящий момент (момент) относительно центра рулевого колеса без какой-либо чистой силы на колесо.
То есть вы создаете крутящий момент (момент) относительно центра рулевого колеса без какой-либо чистой силы на колесо. ]
] ]
] Рисунок ниже, который теперь относится к сплошной балке, а не к полой опоре, показанной в предыдущем разделе, показывает, что осевая деформация, ε , задается соотношением y / R . Эквивалентно 1 / R («кривизна», κ) равна градиенту осевой деформации по толщине. Отсюда следует, что осевое напряжение на расстоянии y от нейтральной оси балки равно
Рисунок ниже, который теперь относится к сплошной балке, а не к полой опоре, показанной в предыдущем разделе, показывает, что осевая деформация, ε , задается соотношением y / R . Эквивалентно 1 / R («кривизна», κ) равна градиенту осевой деформации по толщине. Отсюда следует, что осевое напряжение на расстоянии y от нейтральной оси балки равно {4}} {64} \]
{4}} {64} \] Структуры такого типа, которые не обеспечивают избыточности, называются структурами критических или детерминант .Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией .
Структуры такого типа, которые не обеспечивают избыточности, называются структурами критических или детерминант .Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией . Затем, применяя уравнения равновесия к любой из двух частей, можно определить внутренние действия. Процедуру можно описать следующими шагами:
Затем, применяя уравнения равновесия к любой из двух частей, можно определить внутренние действия. Процедуру можно описать следующими шагами: Позже мы более подробно остановимся на конвенции о позитивных направлениях.
Позже мы более подробно остановимся на конвенции о позитивных направлениях. В частности, в месте приложения точечной нагрузки результирующая сила сдвига отличается слева и справа от точки приложения.
В частности, в месте приложения точечной нагрузки результирующая сила сдвига отличается слева и справа от точки приложения. Поэтому в таких случаях важно, чтобы уточнить сторону точки приложения, мы оцениваем поперечную силу сдвига, влево или вправо.
Поэтому в таких случаях важно, чтобы уточнить сторону точки приложения, мы оцениваем поперечную силу сдвига, влево или вправо. 2 \ over2} + R_B L = 0 \ Rightarrow R_B = {wL \ over2}
2 \ over2} + R_B L = 0 \ Rightarrow R_B = {wL \ over2} 2 \ over8}
2 \ over8}
