Теория рядов

Теория рядов

Теория рядов. Воробьев Н. Н. 4 изд., перераб. и доп., Наука, Главная редакция физико-математической литературы, М., 1979, — 408 с. В книге излагаются основы теории числовых рядов и функциональных рядов, в том числе степенных рядов и рядов Фурье. Первая часть курса составлена в точном соответствии с разделом «Ряды» программы по высшей математике для инженерно-технических специальностей высших учебных заведений. Ее можно использовать не только как учебное пособие для слушателей курса лекций, но и при самостоятельной работе над предметом. Вторая часть представляет собой цикл очерков, посвященных более глубоким вопросам теории рядов, Оглавление ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ Часть I ГЛАВА 1. ПРОГРЕССИИ § 2. Геометрические прогрессии § 3. Бесконечные прогрессии; их сходимость и расходимость § 4. Элементарные преобразования прогрессий § 5. Функциональные прогрессии: область сходимости; равномерная сходимость § 6. Почленное интегрирование прогрессий § 7. Почленное дифференцирование прогрессий § 8. Прогрессии с комплексными членами ГЛАВА 2. ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ. ОСНОВНЫЕ ТЕОРЕМЫ О СХОДИМОСТИ § 2. Определение числового ряда и его сходимости § 3. Остаток ряда § 4. Принцип сходимости Коши § 5. Критерий Коши сходимости рядов § 6. Необходимый признак сходимости ряда § 7. Желательность систематической теории § 8. Свойства сходящихся рядов, подобные свойствам сумм § 9. Дальнейшие свойства рядов ГЛАВА 3. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ § 1. Признаки сходимости рядов § 2. Признаки сравнения § 3. Интегральный признак сходимости Маклорена — Коши § 4. Применения интегрального признака сходимости § 5. Сравнительная оценка различных признаков сходимости § 6. Признак сходимости Даламбера § 7. Признак сходимости Коши § 8. Чувствительность признаков сходимости Даламбера и Коши ГЛАВА 4. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ § 2. Абсолютная сходимость и расходимость § 3. Возможность переставлять члены в абсолютно сходящихся рядах § 4. Условно сходящиеся знакопеременные ряды § 5. Умножение абсолютно сходящихся рядов § 6. Признак сходимости Лейбница § 7. Существенность условий признака сходимости Лейбница ГЛАВА 5. ФУНКЦИОНАЛЬНЫЕ РЯДЫ § 2. Область сходимости функционального ряда § 3. Сходимость последовательности функций. Основные определения § 4. Предел последовательности непрерывных функций § 5. Переход к пределу под знаком интеграла § 6. Переход к пределу под знаком производной § 7. Определение равномерной сходимости функционального ряда и признак Вейерштрасса § 8. Непрерывность суммы равномерно сходящегося ряда с непрерывными членами § 9. Почленное интегрирование функциональных рядов § 10. Почленное дифференцирование функциональных рядов ГЛАВА 6. СТЕПЕННЫЕ РЯДЫ. ОБЩИЕ ВОПРОСЫ § 2. Теорема Абеля § 3. Круг сходимости ряда § 4. Вещественный степенной ряд и его интервал сходимости § 5. Равномерная сходимость ряда в круге его сходимости § 6. Вещественные ряды § 7. Комплексные ряды § 8. Разложение функций в степенные ряды § 9. Формула Тейлора § 10. Ряды Тейлора и Маклорена ГЛАВА 7. СТЕПЕННЫЕ РЯДЫ. ПРИМЕРЫ И ПРИЛОЖЕНИЯ § 2. Разложения в ряды Маклорена гиперболических функций ch x и sh x § 3. Разложения в ряды Маклорена тригонометрических функций cos x и sin x § 4. Показательная функция с комплексным значением показателя § 5. Формулы Эйлера § 6. Тригонометрические функции от комплексного значения аргумента § 7. Гиперболические функции от комплексного значения аргумента § 8. Вычисление значений функций при помощи ряда Маклорена § 9. Биномиальный ряд § 10. Приложения биномиального ряда § 11. Разложение в ряд Маклорена логарифмической функции § 12. Приближенное вычисление определенных интегралов при помощи степенных рядов § 13. Приближенное интегрирование дифференциальных уравнений при помощи степенных рядов ГЛАВА 8. ОРТОГОНАЛЬНЫЕ И ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ § 2. Векторы и функции § 3. Нормированные и ортогональные функции § 4. Нормированные и ортогональные системы функций § 5. Нормировка систем функций § 6. Разложение по системам функций ГЛАВА 9. РЯДЫ ФУРЬЕ § 1. Ряды и коэффициенты Фурье § 2. Условия Дирихле и теорема о разложении функции в ряд Фурье § 3. Разложение периодических функций в ряд Фурье § 4. Физическое истолкование разложения функции в тригонометрический ряд Фурье § 5. Разложение функции f(x) = x § 6. Сдвиг сегмента разложения § 7. Изменение длины сегмента разложения § 8. Четные и нечетные функции § 9. Разложение четной функции в ряд Фурье § 10. Разложение нечетной функции в ряд Фурье § 11. Разложение ряд Фурье функций на сегменте от 0 до пи § 12. Комплексная форма записи ряда Фурье § 13. Разложение в комплексный ряд Фурье § 14. Характер сходимости рядов Фурье ГЛАВА 10. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ С ЗАКРЕПЛЕННЫМИ КОНЦАМИ § 2. Начальные и граничные условия § 3. Метод разделения переменных § 4. Использование граничных условий. Собственные функции и собственные значения § 5. Использование начальных условий ГЛАВА 11. ИНТЕГРАЛ ФУРЬЕ § 1. Представление функций интегралом Фурье § 2. Простейшие достаточные условия представимости функции интегралом Фурье § 3. Интеграл Фурье для четных функций § 4. Интеграл Фурье для нечетных функций § 5. Комплексная форма интеграла Фурье § 6. Понятие о преобразовании Фурье § 7. Косинус-преобразование Фурье § 8. Синус-преобразование Фурье § 9. Спектральная функция Часть II § 1. Признак сходимости Куммера § 2. Признак сходимости Раабе § 3. Признак сходимости Бертрана § 4. Признак сходимости Гаусса § 5. Сходимость знакопеременных рядов § 6. Признак сходимости Дирихле ГЛАВА 13. ДВОЙНЫЕ РЯДЫ § 1. Определение двойного ряда § 2. Сходимость двойных рядов § 3. Критерии сходимости двойных рядов. Теорема Маркова § 4. Свойства двойных рядов и признаки сходимости § 5. Абсолютная сходимость двойных рядов § 6. Двойные функциональные ряды § 7. Двойные степенные ряды § 8. Разложение функций двух переменных в двойные ряды Тейлора и Маклорена § 9. Ортогональные и ортонормальные системы функций от двух переменных § 10. Двойные ряды Фурье ГЛАВА 14. СУММИРОВАНИЕ СХОДЯЩИХСЯ РЯДОВ § 2. Линейные преобразования рядов § 3. Теорема Абеля и почленное дифференцирование и интегрирование рядов § 4. Последовательности разностей § 5. Преобразование рядов по Эйлеру § 6. Преобразование рядов по Куммеру ГЛАВА 15. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ § 1. Расходящиеся геометрические прогрессии § 2. Суммирующие функции § 3. Суммирование по Пуассону — Абелю § 4. Линейность и регулярность суммирования по Пуассону — Абелю § 5. Суммируемость рядов по Пуассону — Абелю и их абсолютная сходимость § 6. Теорема Таубера § 7. Суммирование по Чезаро § 8. Соотношение между сходимостью по Чезаро и по Пуассону — Абелю § 9. Суммирование по Эйлеру ГЛАВА 16. СХОДИМОСТЬ РЯДОВ ФУРЬЕ § 2. Исследование двух интегралов § 3. Исследование одного класса интегралов § 4. Доказательство теоремы Дирихле § 5. Теорема Фурье § 6. Коэффициенты Фурье разрывных функций § 7. Скорость сходимости рядов Фурье § 8. Улучшение сходимости рядов Фурье по методу выделения особенностей § 9. О равномерной сходимости рядов Фурье § 10. Неравномерная сходимость последовательностей непрерывных функций § 11. Поведение рядов Фурье функций в точках их разрыва. Явление Гиббса § 12. Экстремальное свойство сумм Фурье § 13. Суммирование рядов Фурье по Чезаро. Теорема Фейера § 14. Равенство Парсеваля § 15. Теорема Вейерштрасса ГЛАВА 17. ПРИМЕНЕНИЕ РЯДОВ ФУРЬЕ В ТЕОРИИ ИЗГИБА БАЛОК § 2. Изгиб балки § 3. Свободно опертая балка § 4. Первая возможность ограничиться двукратным дифференцированием § 5. Случай сосредоточенной нагрузки § 6. Прогиб балки от распределенной нагрузки § 7. Прогиб от сосредоточенного момента § 8. Статически неопределимая балка § 9. Сложный изгиб балки § 10. Балка на упругом основании § 11. Вторая возможность ограничиться двукратным дифференцированием. Потенциальная энергия изгиба балки § 12. Потенциальная энергия изгиба балки в случае нескольких нагрузок § 13. Функции прогиба с ортогональными вторыми производными § 14. Свободно опертая нагруженная балка § 15. Работа продольных сил при сложном изгибе балки § 16. Общий случай изгиба балки § 17. Общий случай изгиба свободно опертой балки § 18. Изгиб симметрично нагруженной балки, жестко заделанной по концам § 19. 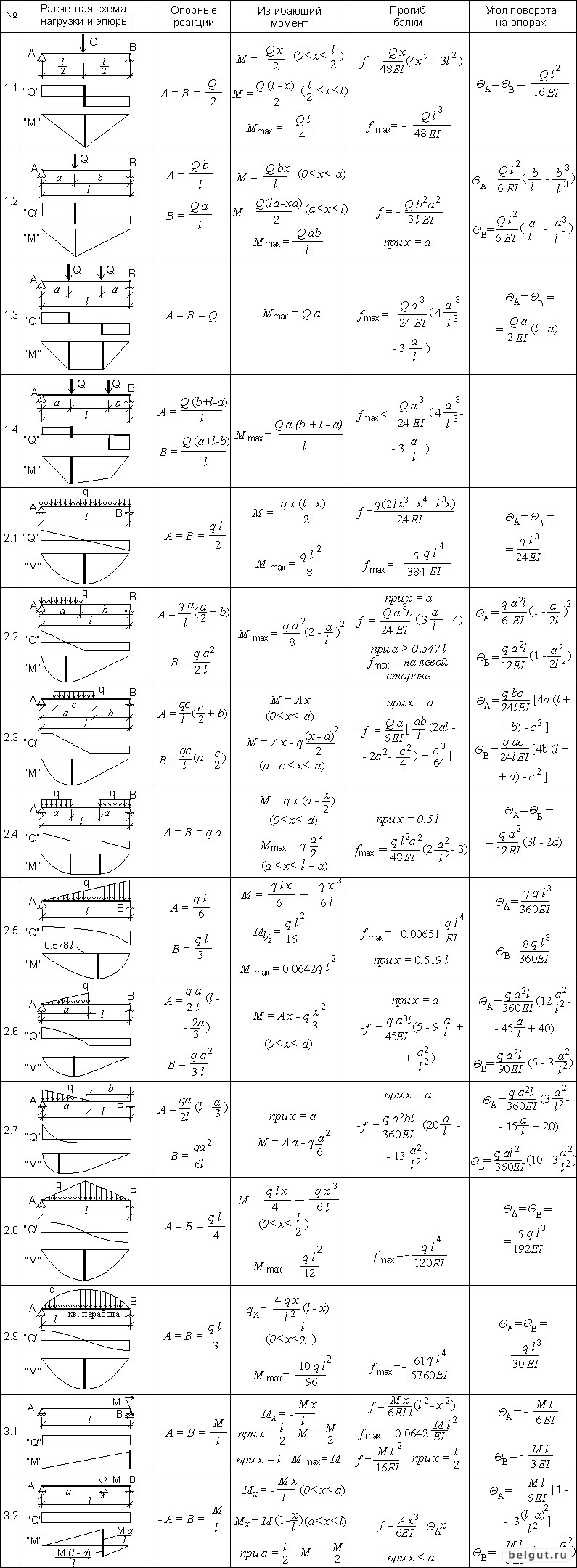Функция прогиба симметрично загруженной балки с жестко заделанными концами

Просто поддерживаемая балка: 9 важных фактов —

Просто поддерживаемое определение луча

Балка с простой опорой — это балка, у которой один конец обычно шарнирно закреплен, а другой конец имеет опору ролика. Таким образом, из-за шарнирных опор ограничение смещения в (x, y) будет, а из-за роликовых опор будет предотвращено концевое смещение в направлении y, и они будут свободно перемещаться параллельно оси балки.

Просто поддерживаемая диаграмма тела без луча.

Схема свободного тела балки приведена ниже, на которой точечная нагрузка действует на расстоянии «p» от левого конца балки.Схема свободного тела для SSB

Опертые граничные условия Beam и формула

Оценка сил реакции, действующих на балку, с использованием условий равновесия 

Фх + Фу = 0

Для вертикального равновесия

Fy = RA + RB – W = 0

Момент об А равен 0 в стандартных обозначениях.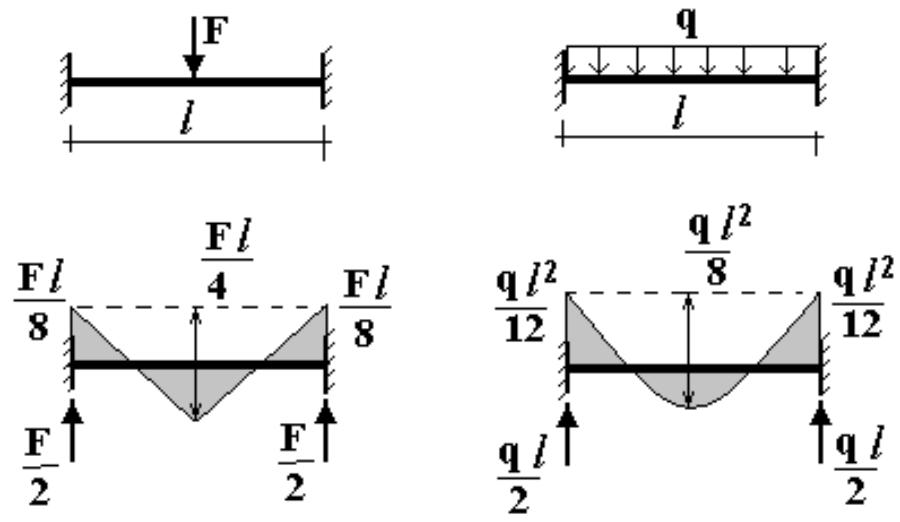

Rb = Wp/л

Из приведенного выше уравнения

RA + Wp/L = W

Пусть XX будет пересечением на расстоянии x от конечной точки, обозначенной A.

Принимая во внимание стандартное знаковое соглашение, мы можем вычислить поперечную силу в точке A, как показано на рисунке.

Сила сдвига в точке A,

Va = Ra = wq/л

Сдвигающая сила в области XX равна

Vx = RA – W = Wq/L – W

Сила сдвига в точке B составляет 

Vb = -Wp/л

Это доказывает, что поперечная сила остается постоянной между точками приложения точечных нагрузок.

Применяя стандартные правила изгибающего момента, изгибающий момент по часовой стрелке от левого конца балки принимается как + ve, а изгибающий момент против часовой стрелки считается как -ve соответственно.

• BM в точке A = 0.
• BM в точке C = -R_A p ………………………… [поскольку момент направлен против часовой стрелки, изгибающий момент выходит как отрицательный]

• BM в точке C выглядит следующим образом
• BM = -Wpq/л

• BM в точке B = 0.

Сила сдвига и диаграмма изгибающего момента

Просто поддерживаемый изгибающий момент балки для равномерно распределенной нагрузки как функция от x.

Ниже приведена балка с простой опорой и равномерно распределенной нагрузкой, приложенной по всему пролету.

SSB с UDL

Регион XX — это любой регион на расстоянии x от A.

Результирующая эквивалентная нагрузка, действующая на балку из-за равномерной нагрузки, может быть рассчитана следующим образом:

Ф = Л * Ф

F = fL

Эквивалентная точечная нагрузка fL действующий в середине пролета. т.е. при L / 2

Оценка сил реакции, действующих на балку, с использованием условий равновесия 

Fx = 0 = Fy = 0

Для вертикального равновесия

Фу = 0

Ra + Rb = fL

принимая стандартные соглашения о знаках, мы можем написать

Л/2 – Р = 0

Из приведенного выше уравнения

РА + эт/2

Согласно стандартному соглашению Знаков, поперечная сила в точке A будет.

Va = Ra = FL/2

Сила сдвига при C

Vc = Ra – fL/2

Сдвигающая сила в области XX равна

Vx = RA – fx = fL/2 – fx

Сила сдвига в точке B

Vb = -fL/2

Для диаграммы изгибающего момента мы можем найти это, приняв стандартные обозначения.

• BM в точке A = 0.

• BM в точке X находится
• B.Mx = MA – Fx/2 = -fx/2

• BM в точке B = 0.

Таким образом, изгибающий момент можно записать в виде

B.Mx = fx/2

Случай I. Для балки с простой опорой и сосредоточенной нагрузкой F, действующей в центре балки.

Ниже представлена ​​диаграмма свободного тела для стальной балки с простой опорой, несущей сосредоточенную нагрузку (F) = 90 кН, действующую в точке C. Теперь вычислите уклон в точке A и максимальный прогиб. если I = 922 см⁴, E = 210 Гигапаскаль, L = 10 метров.

Решения:

FBD. Ниже приведен пример.

Схема свободного тела для SSB с сосредоточенной точечной нагрузкой

Наклон в конце балки:

dy/dx = FL/16E

Для стальной балки с простой опорой, несущей сосредоточенную нагрузку в центре, максимальное отклонение составляет,

Ymax = FL/48 EI

Ymax = 90 х 10 х 3 = 1. 01 м

Случай II: Для балки с простой опорой, имеющей нагрузку на расстоянии «на» от опоры A.

Для этого случая действующая нагрузка (F) = 90 кН в точке C. Затем вычислите наклон в точках A и B и максимальный прогиб, если I = 922 см.⁴, E = 210 Гигапаскаль, L = 10 метров, a = 7 метров, b = 3 метра.

Итак,

Наклон на торцевой опоре А балки,

θ = Fb(L2 – b2) = 0.211

Наклон в конце опоры B балки,

θ = Fb (l2 – B2) (6 LE) = 0.276 рад

Уравнение дает максимальный прогиб,

Ymax = Fb (3L – 4b) 48EI

Таблица уклонов и прогибов для стандартных случаев нагружения:

Уклон и прогиб в балке с простой опорой при равномерно распределенной нагрузке дома

Пусть вес W₁ действующий на расстоянии а от Конца A и W₂ действующий на расстоянии b от конца A.

UDL, применяемый ко всей балке, не требует какой-либо специальной обработки, связанной с скобками Маколея или условиями Маколея. Имейте в виду, что термины Маколея интегрированы по отношению к себе. В приведенном выше случае (xa), если результат окажется отрицательным, его следует проигнорировать. Подстановка конечных условий даст стандартные значения интегрирования и, следовательно, требуемые значения уклона и отклонения.

В этом случае UDL начинается в точке B, уравнение изгибающего момента модифицируется, и член равномерно распределенной нагрузки становится членами скобки Маколея.

Наблюдения и советы этой статьи мы подготовили на основании опыта команды Изгибающий момент уравнение для описанного выше случая приведено ниже.

EI (dy/dx) = Rax – w(xa) – W1 (xa) – W2 (xb)

Интегрируя получаем,

EI (dy/dx) = Ra (x2/2) – frac w(xa) (6) – W1 (xa) – W1 (xb)

Отклонение балки с простой опорой как функция от x для распределенной нагрузки [треугольная нагрузка]

Ниже приведена балка с простой опорой пролета L, подверженная треугольной нагрузке, и уравнение уклона и изгибающего момента, полученное с использованием методологии двойного интегрирования, выглядит следующим образом.

Для симметричной нагрузки каждая реакция опоры принимает на себя половину общей нагрузки, а реакция на опору равна wL / 4, и с учетом момента в точке, которая находится на расстоянии x от опоры A, рассчитывается как.

M = wL/4x – wx/L – x/3 = w (12L) (3L – 4x)

Использование diffⁿ-уравнение кривой.

двойным интегрированием мы можем найти как.

EI (dy/dx) = w/12L (3L x 2x 2) (-x) + C1

положив x = 0, y = 0 в уравнение [2],

C2 = 0

Для симметричной нагрузки наклон при 0.5 л равен нулю.

 Таким образом, наклон = 0 при x = L / 2,

0 = с 12 л (3 л x L2 – L4 +C1)

Подставляя значения констант C₂ и C₁ мы получаем,

EI (dy/dx) = w 12L (3L) (2) – 5wl/192

Самый большой прогиб находится в центре балки. т.е. на L / 2.

Ely = w/12L (3L x 2L x 3) (2 x 8) / l5 (5 x 32) (192)

Оценка уклона на L = 7 м и отклонения по заданным данным: I = 922 см⁴ , E = 220 ГПа, L = 10 м, w = 15 Нм

Из приведенных выше уравнений: при x = 7 м,

EI (dy/dx) = w (12L) (3L x 2x x 2) – x4 – 5wl/192

используя уравнение [4]

Эли = – зл/120

220 х 10 х 922 = 6.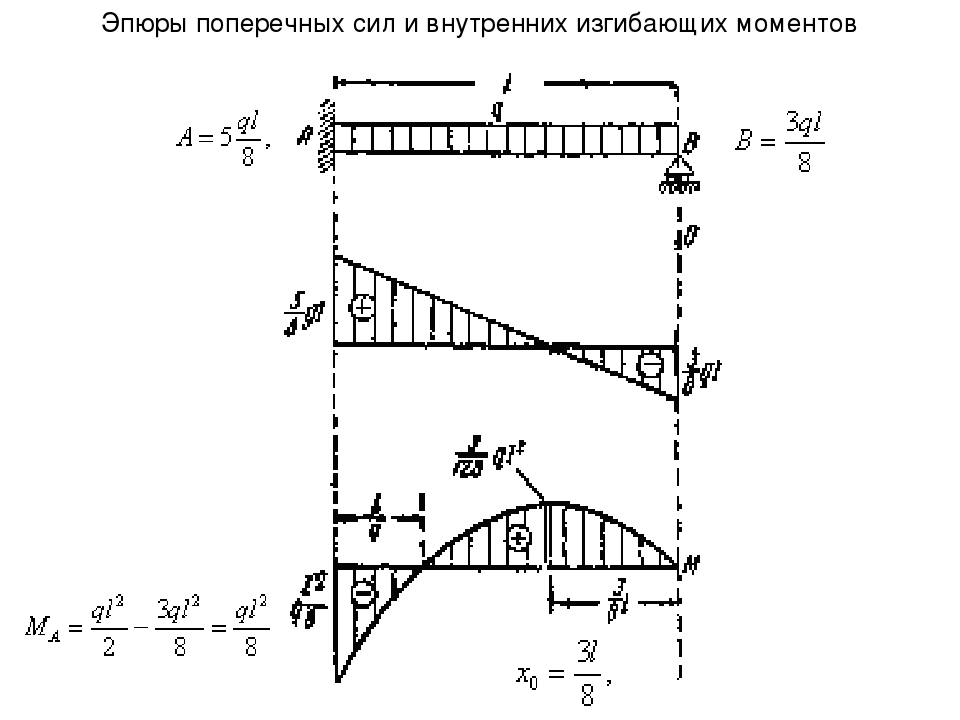 16 х 10^-4 m

Отрицательный знак означает отклонение вниз.

Балка с простой опорой подвергается различным нагрузкам, вызывающим изгибающее напряжение.

Ниже приведен пример стальной балки с простой опорой, несущей точечную нагрузку, и опоры в этой балке опираются на штифт на одном конце, а на другом конце — роликовая опора. Эта балка имеет следующий заданный материал и данные о загрузке.

нагрузка, показанная на рисунке ниже, составляет F = 80 кН. L = 10 м, E = 210 ГПа, I = 972 см⁴, d = 80 мм

Оценка сил реакции, действующих на балку, с использованием условий равновесия 

Fx = 0; Фу = 0

Для вертикального равновесия

Fy = 0 (Ra + Rb – 80000 = 0)

Момент относительно A, момент по часовой стрелке + ve и момент против часовой стрелки принимают как -ve, мы можем рассчитать как.

80000 х 4 – Рб х 10 = 0

Рб = 32000Н

Положив значение R_B в уравнении [1].

РА + 32000 = 80000

Ra = 48000

Пусть XX будет интересующим сечением на расстоянии x от конечной точки A, поэтому поперечная сила в точке A будет.

ВА = РА = 48000 Н

Сдвигающая сила в области XX равна

Vx = RA – F = Fb/L – F

Сила сдвига в точке B составляет 

Vb = -Fa/L = -32000

Это доказывает, что поперечная сила остается постоянной между точками приложения точечных нагрузок.

Применяя стандартные правила изгибающего момента, изгибающий момент по часовой стрелке от левого конца балки принимается как положительный. Изгибающий момент против часовой стрелки принимается отрицательным.

• Изгибающий момент при A = 0
• Изгибающий момент при C = -R_A a ………………………… [поскольку момент направлен против часовой стрелки, изгибающий момент выходит как отрицательный]

• Изгибающий момент в точке C составляет
• ВМ = -80000 х 4 х 6/4 = -192000 Нм

• Изгибающий момент при B = 0

Уравнение Эйлера-Бернулли для изгибающего момента дается формулой

M/I = σy = E/R

M = нанесенный BM над поперечным сечением балки.

I = момент инерции 2-го участка.

σ = изгиб, вызванный напряжением.

y = нормальное расстояние между нейтральной осью балки и желаемым элементом.

E = модуль Юнга в МПа

R = радиус кривизны в мм

Таким образом, изгибающее напряжение в балке

σb = Mmax / y = 7.90

Знать об отклонении балки и Консольная балка другую статью нажмите ниже.

Engineering at Alberta Courses » Распределенные нагрузки

В действительности любая сила, приложенная к телу, распределяется по площади, то есть распределенная нагрузка или давление. Распределенная нагрузка может быть упрощена (или смоделирована) как сосредоточенная сила, когда площадь контакта относительно мала и упрощение не влияет на внешние эффекты (например, деформацию). В этом случае нагрузка на тело называется сосредоточенной нагрузкой . Например, силы реакции земли на шины автомобиля можно рассматривать как сосредоточенные нагрузки на силы (рис.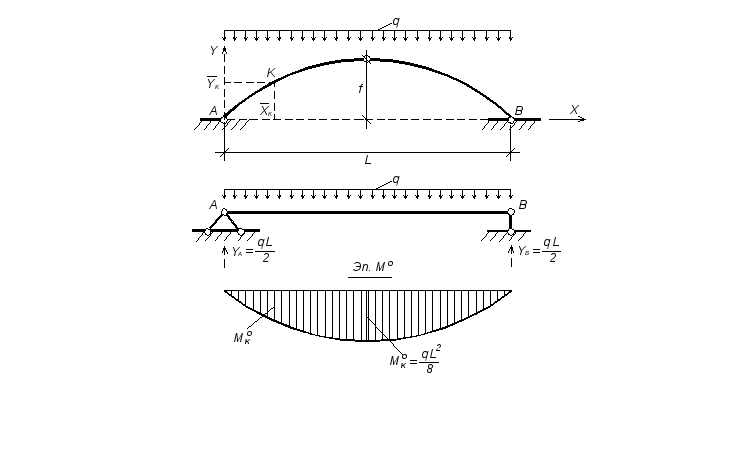 3.32). Другой пример — нагрузка человека, идущего по канату (рис. 3.32). Если мы рассматриваем веревку как тело, вес человека, приложенный к веревке через подошвы ног человека, является нагрузкой на веревку. Силы на веревке можно рассматривать как сосредоточенные силы, поскольку площадь контакта между подошвой каждой ноги и веревкой мала.

Рис. 3.32 Примеры сосредоточенных нагрузок.

Однако во многих случаях следует учитывать непрерывное распределение сил на теле. Непрерывно распределенная внешняя сила называется распределенной нагрузкой . Например, вес кучи снега на крыше распределяется по площади крыши (рис. 3.33). Это означает, что на каждую единицу площади приходится какая-то часть общего веса снежной массы на крыше.

Рис. 3.33 Распределение веса кучи снега на крыше.

Распределенная нагрузка по площади имеет направление и величину. Направление распределенной нагрузки по площади может различаться в разных точках и показано маленькими стрелками по площади. Величина распределенной нагрузки описывается ее интенсивностью , определяемой как силы на единицу площади , или давления . В единицах СИ распределенная нагрузка имеет единицу ньютона на квадратный метр , определяемую как Паскаль , .

В качестве примера рассмотрим твердый ящик, опирающийся на часть поверхности стола (рис. 3.34). Вес ящика, передаваемый на стол через основание ящика, соприкасающееся со столом, представляет собой распределенную нагрузку на стол. Эта нагрузка равна , равномерно распределенной по на столе, как показано на рис. 3.34. Интенсивность нагрузки равна , где — вес ящика, — площадь основания, соприкасающегося со столом. Обратите внимание, что, .

Рис. 3.34 Равномерное распределение веса твердого ящика по площади стола.

Равномерная интенсивность . Говорят, что распределенная нагрузка с постоянной интенсивностью по площади имеет равномерную интенсивность. Соответственно, равномерная нагрузка или равномерно распределенная нагрузка имеют одно и то же значение.

По аналогии с весовой нагрузкой коробки на поверхность величина полной (результирующей) силы, оказываемой однородной нагрузкой на площадь, равна .

Контекст: распределенные нагрузки

• Хотя многие нагрузки можно идеализировать как силу, действующую в одной точке, во многих случаях инженеры используют распределенные нагрузки при проектировании.
• Распределенные нагрузки могут представлять собой либо давление (например, фунты на квадратный дюйм, килопаскали), либо «линейную нагрузку» (например, килоньютоны на метр). Нагрузки от давления обычно используются для проектирования широких элементов, таких как плиты и стены, а линейные нагрузки используются для проектирования узких элементов, таких как балки.
• Инженеры используют распределенные нагрузки для учета собственного веса элементов (например, балок, плит, окон, подпорных стен), нагрузок окружающей среды (например, ветра и снега) и внутренних давлений (например, баллоны под давлением) в конструкциях.
• Инженеры также используют распределенные нагрузки для проектирования конструкций, где точное распределение сил неизвестно. Например, инженеры не могут предсказать, как люди расставляют мебель и насколько тяжела их мебель, но, используя исторические данные об условиях проживания, они могут предположить, что ежедневное давление людей и мебели в жилых домах составляет 1,9 кПа (~40 фунтов на квадратный метр). фут), когда они проектируют эти типы структур.

Области применения: В каких ситуациях инженеры рассматривают распределенные нагрузки?

До сих пор в этом тексте мы фокусировались на сосредоточенных силах (или «точечных силах»). На самом деле ни одна сила не действует в одной точке (обсуждается в разделе 3.1), но предположение о том, что силы действуют в одной точке, подходит для многих ситуаций, которые рассматривают инженеры.

Тем не менее, во многих ситуациях инженерам необходимо учитывать распределенные нагрузки. Например, чтобы гарантировать, что крыша здания на рис. 3.35а не рухнет под тяжестью снега, инженеры должны учитывать ожидаемую глубину и плотность снега на крыше как давление. Они могут определить наихудшую глубину снега на основе климатических данных за десятилетия, которые публикуются федеральным правительством для каждого города в Канаде. Те же проблемы (хотя и труднее увидеть) возникают с ветром, который может толкать или тянуть объекты.

Рис. 3.35 Типичные ситуации, когда инженеры рассматривают распределенные нагрузки (а) снег на крыше здания (б) открытые бетонные плиты перекрытия в строящейся башне кондоминиума. (Фото Д. Томлинсона)

Еще одним источником распределенных нагрузок является фактический вес самой конструкции. Железобетонные перекрытия жилых домов (рис. 3.35b) обычно имеют толщину около 200 мм, что соответствует давлению от 4,5 до 5,0 килопаскалей (кН/м ² ), что более чем в два раза превышает ожидаемые нагрузки, которые испытывают жильцы квартир (и их вещи) были бы.

ПРИМЕР 3.5.1

Цилиндр лежит на столе и его основание имеет диаметр .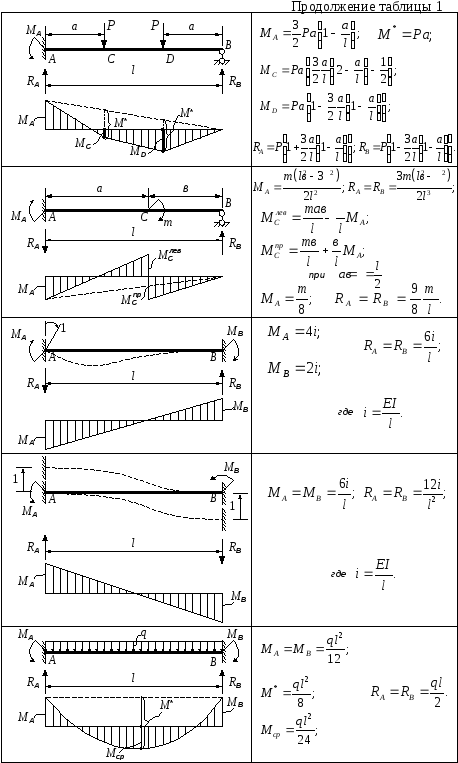 Вес цилиндра передается на поверхность стола через основание цилиндра и создает равномерно распределенную нагрузку с интенсивностью . Вычислите вес цилиндра.

РАСТВОР

Распределенная нагрузка не обязательно распределяется по плоской поверхности. Например, нагрузка от давления внутри цилиндра под давлением (равномерно) распределяется по внутренней поверхности цилиндра (рис. 3.36).

Рис. 3.36. Равномерное распределение давления внутри цилиндра на неровной поверхности.

Как правило, интенсивность нагрузки варьируется в зависимости от области распространения. Например, напор воды (интенсивность водной нагрузки) над плотиной изменяется с глубиной воды (рис. 3.37а), или распределение веса книг на полке может иметь разную интенсивность по полке (рис. 3.37б). ).

Рис. 3.37 (а) Напор воды (интенсивность водной нагрузки) над плотиной, (б) распределение веса книг на полке.

Математически интенсивность нагрузки зависит от положения , на площади. Следовательно, интенсивность может быть определена функцией по точкам области.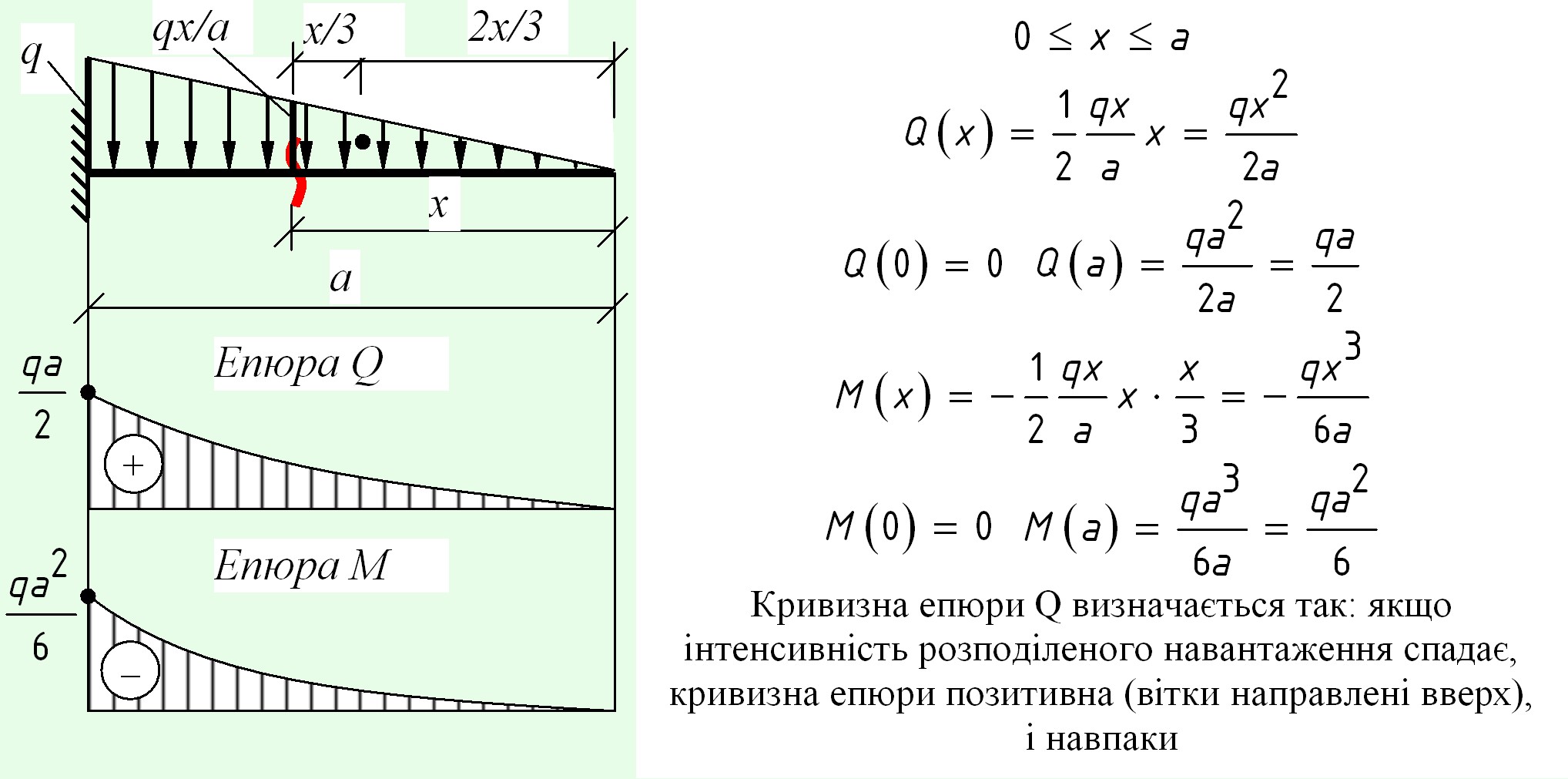 Эту функцию можно построить в трех измерениях, если считать, что точки распределенной области расположены на осях x и y , а значения интенсивности расположены на оси z .

В этой книге особый тип распределенной нагрузки, известный как распределенная нагрузка вдоль линии или оси считается. Реальные нагрузки во многих задачах инженерной практики моделируются или близко представляются этим типом нагрузки.

Распределенная нагрузка вдоль оси

Распределенная нагрузка по площади может изменяться только в одном направлении или оси и быть постоянной в другом направлении. Рассмотрим распределенную нагрузку по верхней поверхности прямоугольной пластины, как показано на рис. 3.38. Декартова система координат размещена на пластине так, чтобы ее начало , располагалось на одном конце пластины, а точка 9Ось 0027 x проходит по центральной линии ширины пластины (ось y параллельна ширине пластины). Интенсивность нагрузки является функцией x и y по площади пластины.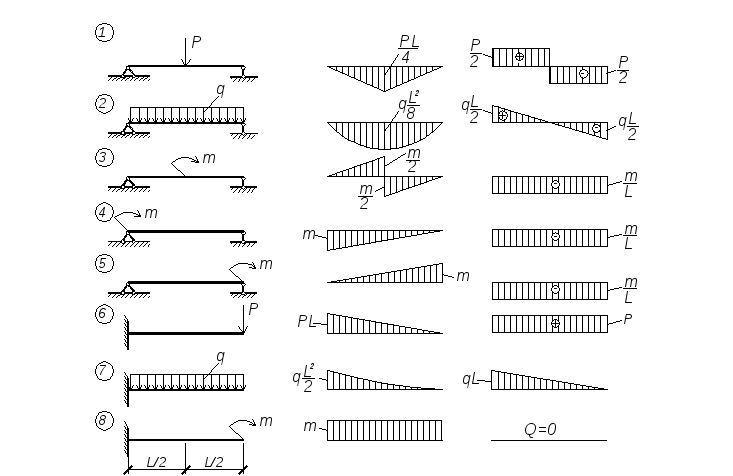

Рис. 3.38 Распределенная нагрузка по верхней поверхности прямоугольной пластины.

В этом случае интенсивность нагрузки постоянна вдоль оси y . Следовательно, интенсивность зависит только от x и может быть описана функцией x как . Более удобно определить функцию интенсивности, которая описывает нагрузку на единицу длины вместо единицы площади, записав . Единицей в системе СИ является ньютон на метр, . Нагрузка, описываемая , приложена вдоль оси х (рис. 3.39а). Двумерное представление рис. 3.39а, как показано на рис. 3.39б, достаточно для большинства анализов.

Рис. 3.39 Распределенная нагрузка на единицу длины по центральной линии прямоугольной пластины.

Во многих инженерных задачах нам нужно найти приблизительное значение ​. Здесь приведен один пример для пояснения концепции нагрузки на единицу длины.

ПРИМЕР 3.5.2

На фотографии Обед на вершине небоскреба (1932 г.) показаны одиннадцать рабочих-металлургов, сидящих на балке.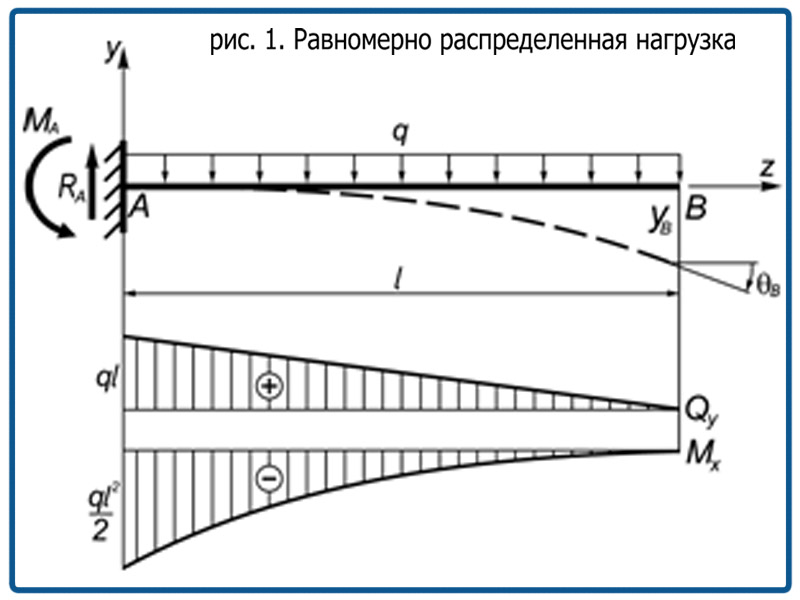 Если принять среднюю массу каждого человека, определить их весовую нагрузку, распределенную по длине (оси) балки. Предположим, что длина балки, над которой сидят люди, равна .

Изображение из Википедии.

РЕШЕНИЕ

Общий вес, который нужно распределить по оси балки, равен . Таким образом,

постоянны по длине, как показано на рисунке ниже.

Упрощение распределенной нагрузки вдоль оси

Во многих задачах, таких как равновесие твердых тел (раздел 5.2) или расчет опорной реакции, распределенная нагрузка может быть представлена ​​сосредоточенной нагрузкой, по соображениям простоты, без изменения ее эффектов при расчете. Эквивалентная система распределенной нагрузки, показанная на рис. 3.40, состоит из равнодействующей силы в определенном месте. Эквивалентная система получается на основе упрощения копланарной системы сил до равнодействующей силы (см. раздел 3.4.2 и пример 3.4.5).

Рис. 3.40 Распределенная нагрузка и предполагаемая эквивалентная система.

Во многих задачах форма функции интенсивности нагрузки проста и легко вычислима. На рис. 3.41 показаны результирующая сила и два обычных распределения нагрузки.

Рис. 3.41 Два простых распределения нагрузки и положения их равнодействующих сил.

Величина равнодействующей силы представляет собой площадь под функцией интенсивности и является координатой центроида формы площади под функцией интенсивности. В следующих параграфах показаны общие расчеты и . Студентам рекомендуется читать их после приобретения твердых знаний в области исчисления.

Для определения величины равнодействующей силы общая длина распределенной нагрузки делится на равновеликие элементы (отрезки) длиной (рис. 3.42). Если достаточно мала, то почти однородна по элементу и, следовательно, величина силы по элементу равна . Величина примерно определяется суммированием как

   

Точное значение получается, если количество делений, , увеличить до бесконечности,

   

ведет к

(3,27)  

Рис. 3.42 Деление оси нагрузки на n элементов.

Геометрическая интерпретация этого интеграла есть площадь, , под функцией интенсивности нагрузки ,

(3,28)  

где – элемент площади, как показано на рис. 3.43.

Рис. 3.43 Геометрическая интерпретация интегралов.

Расположение определяется путем приравнивания моментов сил относительно точки в двух системах (рис. 3.40). Точка для расчета моментов может быть где угодно на x , однако обычно выбирают любой конец длины, по которому распределяется нагрузка. Выбираем точку, расположенную в начале координат оси х (рис. 3.40). Приравнивание моментов двух систем записывается как

.

   

, что становится эквивалентным следующему интегралу:

   

и (по уравнению 3.27) приводит к

(3,29)  

Учитывая геометрический смысл этого интегрирования (рис. 3.43), запишем уравнение 3,29как,

(3,30)  

, который можно рассматривать как геометрическую интерпретацию уравнения.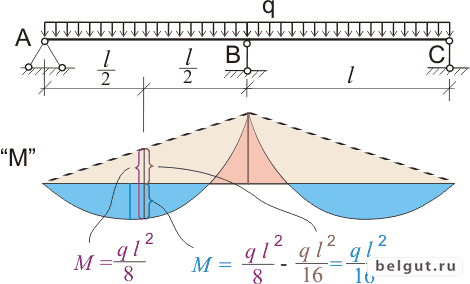 3.29. Точка, связанная с координатой, представляет собой геометрические свойства формы области под диаграммой (графиком) функции интенсивности нагрузки. Это называется координатой центроида формы области. Концепция центроида будет представлена ​​в разделе 9.3.

Видео

Просто поддерживаемая балка – формулы моментов и поперечных сил, обусловленных различными нагрузками

Последнее обновление: 30 апреля 2023 г.

Расчет изгибающих моментов и поперечных сил в балках для различных сценариев нагружения, вероятно, является одной из задач проектирования конструкций, которыми мы постоянно занимаемся. наша учеба, а также карьера позже.

Хотя очень важно знать, как получить и рассчитать внутренние силы, чем дальше мы продвигаемся в наших исследованиях, тем больше мы можем использовать формулы момента балки и сдвига.

В этом посте мы покажем наиболее важные и простые формулы для свободно опертых балок из-за различных сценариев нагрузки, таких как линейные нагрузки UDL, точечные нагрузки и треугольные нагрузки.

Все будет показано и объяснено на примерах.

Теперь, прежде чем мы начнем, всегда помните, что единицей измерения изгибающего момента является килоньютон-метр [$kNm$] и килоньютон [$kN$] для поперечной силы в Европе.

А теперь приступим.

1. Свободно опертая балка – формулы равномерно распределенной линейной нагрузки (UDL) 92$

Перерезывающие силы на опорах

$V_{a} = -V_b = 1/2 \cdot q \cdot l$

Силы реакции

$R_a = R_b = 1/2 \cdot q \cdot l$

Эти формулы также можно рассчитать вручную. Ознакомьтесь с этой статьей, если вы хотите подробно узнать, как рассчитать изгибающие моменты, поперечные силы и силы реакции вручную.

2. Свободно опертая балка – равномерно распределенная нагрузка (UDL) в середине пролета (формулы)

Диаграмма изгибающего момента и поперечной силы | Свободно поддерживаемая балка с равномерно распределенной линейной нагрузкой (UDL) в середине пролета. 92} \cdot (c+\frac{b}{2})\cdot (a+\frac{b}{2})\cdot (l- \frac{b}{2})$

, если $x = a + \frac{b\cdot (c + \frac{b}{2})}{l}$

Перерезывающие усилия на опорах

$V_{a} = q \cdot b \cdot \frac{c + \ frac{b}{2}}{l}$

$V_{b} = -q \cdot b \cdot \frac{a + \frac{b}{2}}{l}$

Силы реакции

$R_{a} = q \cdot b \cdot \frac{c + \frac{b}{2}}{l}$

$R_{b} = q \cdot b \cdot \frac{a + \frac{b}{2}}{l}$

3. Свободно опертая балка – Равномерно распределенная нагрузка (РНД) на 1 опоре (формулы) 92$

, если $x = a \cdot (1-  \frac{a}{2l})$

Перерезывающие усилия на опорах

$V_{a} = q \cdot a \cdot (1-\frac{ a}{2l})$

$V_{b} = -q \cdot a \cdot \frac{a}{2l}$

Силы реакции

$R_{a} = q \cdot a \cdot ( 1-\frac{a}{2l})$

$R_{b} = q \cdot a \cdot \frac{a}{2l}$

4. Свободно опертая балка – точечная нагрузка в середине пролета (формулы)

Диаграмма изгибающего момента и поперечной силы | Просто поддерживаемая балка с точечной нагрузкой в ​​середине пролета.

Изгибающий момент

$M(x) = 1/2 \cdot Q \cdot x$, если x < l/2

$M(x) = 1/2 \cdot Q \cdot (l- x)$, если x > l/2

Максимальный изгибающий момент

$M_{max} = 1/4 \cdot Q \cdot l$

Перерезывающие усилия на опорах

$V_{a} = 1/2 \cdot Q$

$V_{b} = -1/2 \cdot Q$

Силы реакции

$R_{a} = 1/2 \cdot Q$

$R_{b} = 1/2 \cdot Q$

5. Свободно опертая балка – точечная нагрузка не в середине пролета (формулы)

Диаграмма изгибающего момента и поперечной силы | Свободно опертая балка с точечной нагрузкой не в середине пролета.

Изгибающий момент

$M(x) = Q \cdot b \cdot \frac{x}{l}$, если x < a

$M(x) = Q \cdot a \cdot \frac{l-x}{ l}$, если x > a

Максимальный изгибающий момент

$M_{max} = Q \cdot \frac{a\cdot b}{l}$

Поперечные силы на опорах

$V_{a} = Q \cdot \frac{b}{l}$

$V_{b} = -Q \cdot \frac{a}{l}$

Силы реакции

$R_{a} = Q \cdot \frac{ b}{l}$

$R_{b} = Q \cdot \frac{a}{l}$

6.

Свободно опертая балка – 2 Точечные нагрузки – равномерно распределены (формулы) Диаграмма изгибающего момента и поперечной силы | Просто поддерживаемая балка с равномерно распределенными 2-точечными нагрузками.

Изгибающий момент

$M(x) = Q \cdot x$, если x < a

Максимальный изгибающий момент

$M_{max} = Q \cdot a$

Перерезывающие силы на опорах

$V_{a } = Q$

$V_{b} = -Q$

Силы реакции

$R_{a} = Q$

$R_{b} = Q$

7. Свободно опертая балка – 3 точечные нагрузки – равномерно распределены (формулы)

Диаграмма изгибающего момента и поперечной силы | Просто поддерживаемая балка с равномерно распределенными 3-точечными нагрузками.

Изгибающий момент

$M(x) = 3/2 Q \cdot x$, если x < l/4

Максимальный изгибающий момент

$M_{max} = 1/2 \cdot Q \cdot l$

Перерезывающие усилия на опорах

$V_{a} = 3/2 \cdot Q$

$V_{b} = -3/2 \cdot Q$

Силы реакции

$R_{a} = 3/2 \cdot Q$

$R_{b} = 3/2 \cdot Q$

8.

Свободно опертая балка – 2 точечные нагрузки – неравномерно распределенные (формулы) Диаграмма изгибающего момента и поперечной силы | Просто поддерживаемая балка с 2 точечными нагрузками, распределенными неравномерно.

Изгибающий момент M1

$M = \frac{Q}{l} \cdot (l – a + b) \cdot a$ макс. момент, если a>b

Макс. изгибающий момент M2 (макс. момент, если a

$M_{max} = \frac{Q}{l} \cdot (l – b + a) \cdot b$  

Перерезывающие усилия на опорах

$V_{a} = \frac{Q}{l } \cdot (l – a + b)$

$V_{b} = -\frac{Q}{l} \cdot (l – b + a)$

Силы реакции

$R_{a} = \frac{Q}{l} \cdot (l – a + b)$

$R_{b} = \frac{Q}{l} \cdot (l – b + a)$ 92$ в точке $x = \frac{1}{\sqrt{3}}\cdot l $

Сдвиговые усилия на опорах

$V_{a} = \frac{1}{6} \cdot q \cdot l $

$V_{b} = -\frac{1}{3} \cdot q \cdot l$

Силы реакции

$R_{a} = \frac{1}{6} \cdot q \cdot l$

$R_{b} = \frac{1}{3} \cdot q \cdot l$

10.