Типовые эпюры. Консольная балка | buildingbook.ru

Эпюра — это график, который показывает напряжения в элементе.

На основе эпюры мы можем проверить прочность элемента, подобрать нужный профиль.

В этой статье мы рассмотрим наиболее распространенные эпюры консольных балок, встречающихся в строительстве.

Типовые эпюры для однопролетной шарнирно-опертой балки можно посмотреть в статье Типовые эпюры. Однопролетная шарнирно-опертая балка.

Рассматривать будем только эпюры Q (поперечная сила), M (изгибающий момент).

Хочу отметить интересный момент, эпюра изгибающих моментов у строителей откладывается в сторону растягивающихся волокон, а у машиностроителей в сторону сжатых. Это не является ошибкой ни в каком из случаев, просто разные методы построения. Мы будем рассматривать построение эпюр как это делают строители.

Типовые эпюры консольной балки

В консольной балке один конец жестко закреплен, другой висит в воздухе.

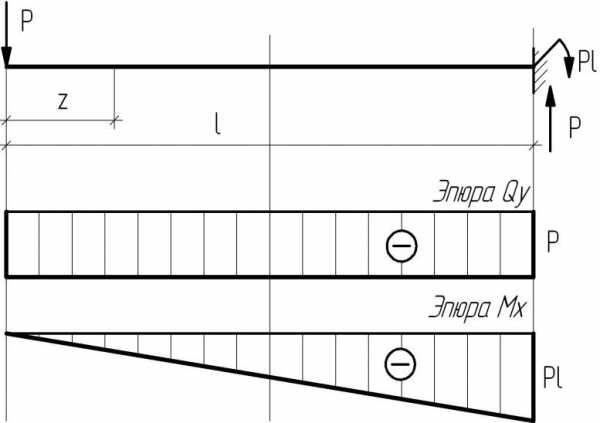
Сила приложена в конце балки

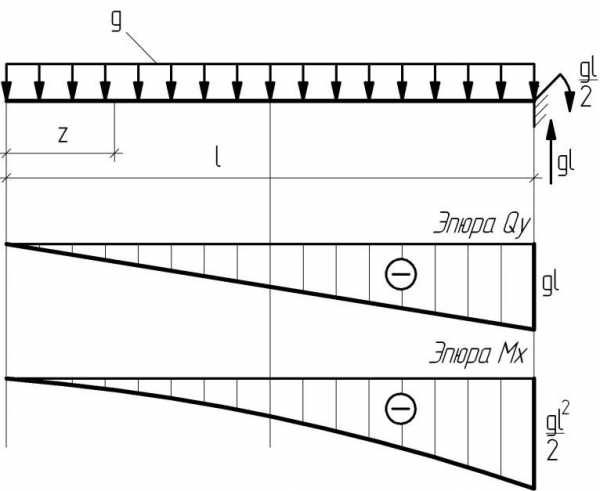
Равномерно-распределенная нагрузка

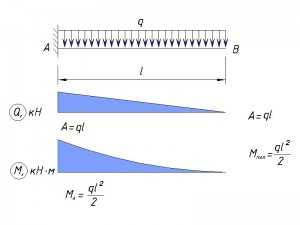
Равномерно-распределенная нагрузка, приложенная не по всей длине консоли

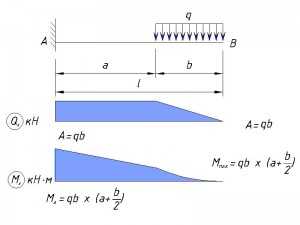
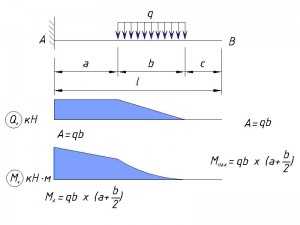
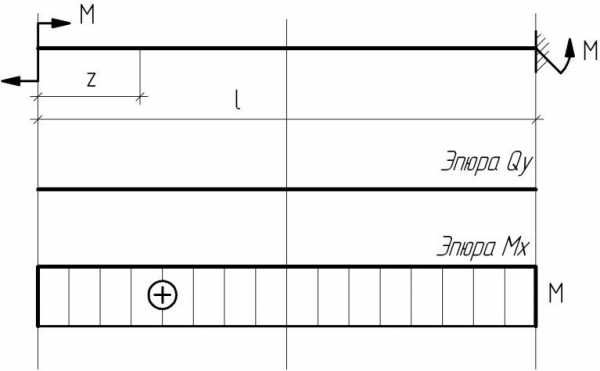
Момент приложен в конце консоли

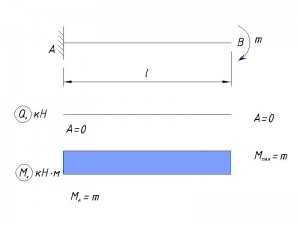
Переменная нагрузка по всей длине консоли

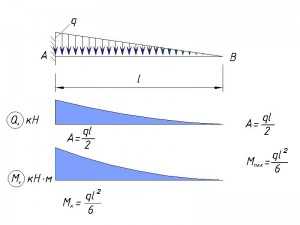
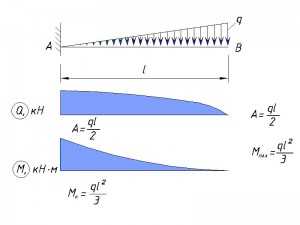
Переменная нагрузка, приложенная не по всей длине консоли

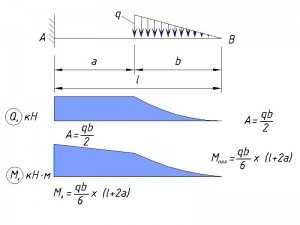
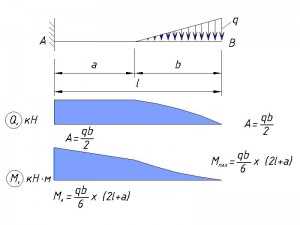
buildingbook.ru

Расчетные схемы для балок. Расчёт шарнирно-консольных балок на постоянную и подвижную нагрузки

Балка — это стержень или брус, работающий преимущественно на изгиб. Статически определимые балки разделяются на следующие типы (рис. 1.8):

простые балки — балки на двух опорах по концам;

консольные — балки на двух опорах со свешивающимися концами или консолями;

консоли — балки, защемлённые одним концом;

шарнирно-консольные балки, составленные из двух или нескольких последовательно расположенных балок, концы которых связаны между собой шарнирами.

Рис. 1.8. Различные типы балок: а – простая балка; б – консольная балка; в – консоль; г – шарнирно-консольная балка

Расстановка шарниров в многопролётной балке должна быть произведена так, чтобы она была статически определимой и геометрически неизменяемой:

в каждом пролёте должно быть размещено не более двух шарниров;

пролёты с двумя шарнирами должны быть размещены не менее чем через пролёт;

пролёты с одним шарниром могут следовать один за другим, если в системе есть одна неподвижная балка.

Консоль, простая балка и балка с консолями — это геометрически неизменяемые и статически определимые системы.

Длина консоли называется вылетом консоли, а длина простой балки – пролётом.

1.6. Порядок расчёта шарнирно-консольных балок

Подсчитывают степень свободы системы.

Проводят анализ геометрической неизменяемости системы. Изображают схему взаимодействия элементов шарнирно-консольной балки, то есть поэтажную схему, для чего мысленно разъединяют элементы балки, разделив их на основные или главные, которые могут самостоятельно воспринимать внешнюю нагрузку, и второстепенные или присоединённые, которые не могут работать самостоятельно, а должны опираться на основные балки в соответствии с рисунком 9.

Аналитический расчёт шарнирно-консольных балок начинают со второстепенной балки самого верхнего этажа. Построив для верхней балки эпюры изгибающихся моментов и поперечных сил, прикладывают реакцию опоры на нижележащую балку с обратным направлением и рассчитывают её. Последней рассчитывается опорная балка.

Признаки основной и второстепенной частей:

если разрушается основная часть, то разрушается вся система;

при разрушении второстепенной части, основная или главная остаётся без изменения.

Рис. 1.9. Поэтажные схемы шарнирно-консольных балок

Контрольные вопросы

Почему недопустимы системы, близкие к мгновенно изменяемым?

Для чего проводится кинематический анализ систем?

Как проверить статическую определимость и геометрическую неизменяемость многопролетной статически определимой балки?

2. Расчёт сооружений на подвижную нагрузку

При расчёте сооружения на подвижную нагрузку: движущийся поезд, автомобиль – пользуются линиями влияния (лв).

Линия влияния – это график, показывающий закон изменения того или иного усилия: реакции, момента, поперечной силы – в определённом или фиксированном сечении сооружения при перемещении по его длине груза F=1.

Ордината линии влияния показывает величину усилия, для которого построена ЛВ, когда груз F=1 стоит над этой ординатой на сооружении.

Ординаты линий влияния R и Q безразмерны, а линии влияния М выражаются в метрах.

Сравнение линий влияния и эпюр какого-либо усилия J приведены в табл. 2.1.

Таблица 2.1

Сравнение линии влияния и эпюр

Для расчета балок первым делом необходимо определить усилия, возникающие в конструкциях. В данном разделе показано, как находить усилия, опорные реакции, прогибы и углы поворота в различных изгибаемых конструкциях. Для самых распространенных из них вы можете воспользоваться онлайн расчетом. Для редких — приведены все формулы определения необходимых значений.

Онлайн расчет балки на двух опорах (калькулятор).

Оранжевые ячейки — максимальные значения.

Онлайн расчет консольной балки (калькулятор).

Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.

Синие ячейки — ввод данных. (Белые ячейки — ввод координаты для определения промежуточного итога).

Зеленые ячейки — расчетные, промежуточный итог.

Оранжевые ячейки — максимальные значения.

Расчет однопролетной балки на двух шарнирных опорах.

Рис.1 Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке

Рис.2 Расчет балки на двух шарнирных опорах при двух с

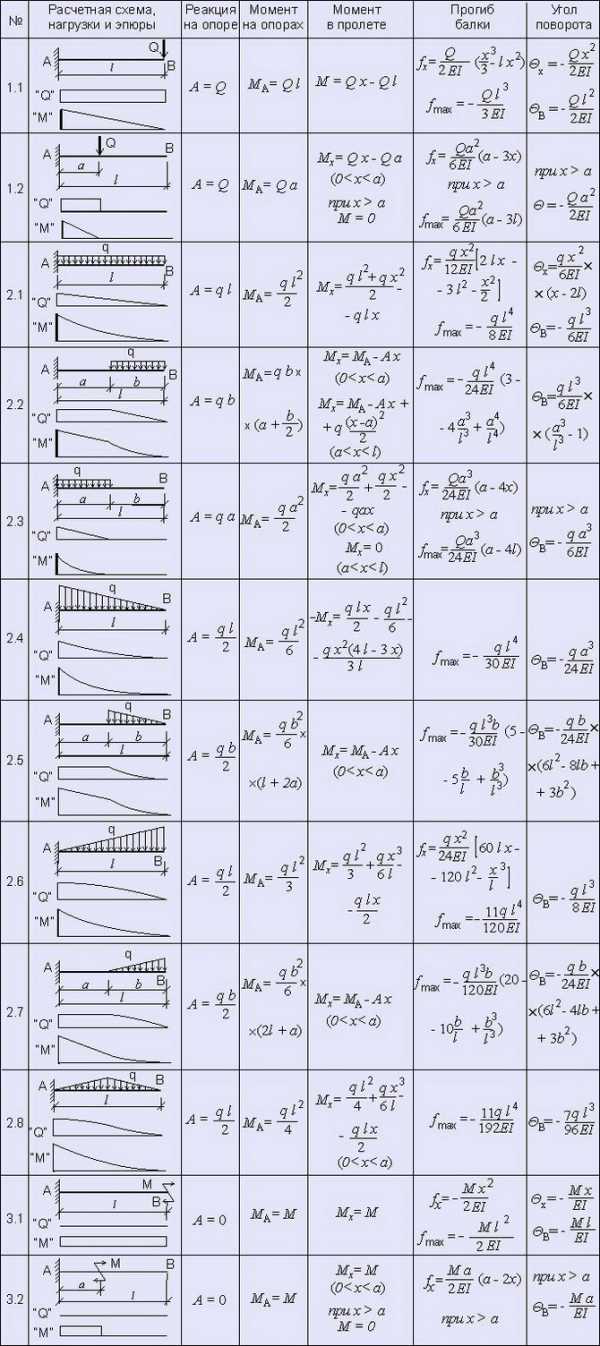
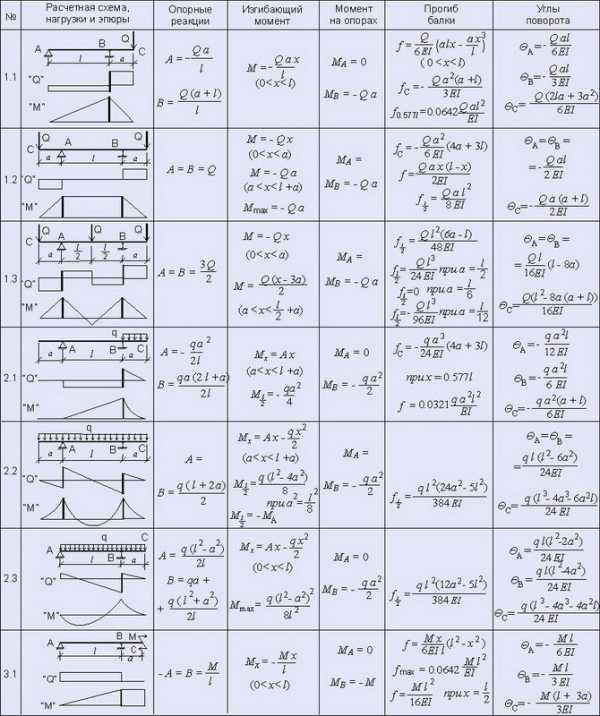
Представлены расчетные схемы, различные виды действующих нагрузок, эпюры сил, отображающие характер изменения касательных напряжений, эпюры изгибающих моментов, отображающие характер изменения нормальных напряжений, возникающих в поперечном сечении балки, а также формулы для определения опорных реакций, действующего изгибающего момента, максимального изгибающего момента, формулы для определения прогиба балки на расстоянии х от начала балки и формулы для определения максимального прогиба балки, а также формулы для определения тангенса угла поворота поперечного сечения на опорах и на концах — для консольных балок. Классификация производилась не по действующим нагрузкам, а по виду опор балки. В данном разделе представлены статически определимые балки. Ось х , относительно которой производятся расчеты изгибающего момента и прогиба, соответствует продольной оси, проходящей через центр тяжести поперечных сечений балки. Значение момента инерции I следует определять относительно оси z . Если в таблицах отсутствует формула для определения прогиба на каком-то из участков балки (из-за чрезмерной длины формулы), то опять же ее можно вывести, дважды должным образом проинтегрировав уравнение изгибающего момента, разделив результат на EI и добавив к этому результат интегрирования угла поворота. В общем виде уравнение для определения углов поворота выглядит так: θ х = — θ A + Мх/EI + Ax 2 /2EI — qx 3 /6ЕI например, для шарнирной балки, к которой приложена сосредоточенная нагрузка (таблица 1, №1.1, момент и распределенная нагрузка осутствуют) на участке от начала балки до точки приложения силы (0 θ х = — θ A + Ax 2 /2EI = — Ql 2 /16EI + Qx 2 /4EI = Q(4x 2 — l 2)/16EI Соответственно в общем виде уравнение для определения прогиба выглядит так: f х = — θ A x + Мх 2 /2EI + Ax 3 /6EI — qx 4 /24ЕI для той же шарнирной балки на участке от начала балки до точки приложения силы (0 f х = — θ A x + Ax 3 /6EI = — Ql 2 x/16EI + Qx 3 /12EI = Qx(4x 2 — 3l 2)/48EI На участке от точки приложения силы до конца балки (l/2 f х = — θ A x + Ax 3 /6EI — Q(x — l/2) 3 /6EI Эпюры углов поворота и прогибов поперечного сечения по длине балки не приводятся. Если в формуле прогиба есть знак минус, то это значит, что балка прогибается вниз (что в общем-то логично), а если быть более точным, то центр тяжести поперечного сечения смещается вниз по оси у . Представленные расчетные схемы позволяют рассчитать балку практически при любом возможном виде нагрузки. Если на балку действует несколько различных нагрузок, то можно производить отдельный расчет для каждой схемы загружения, а затем полученные результаты сложить (с учетом знаков). Это правило называется принципом суперпозиции и в некоторых случаях значительно упрощает общий расчет, а также экономит уйму времени на поиск в сети подходящей расчетной схемы. 1. БАЛКА НА ДВУХ ШАРНИРНЫХ ОПОРАХ 2. КОНСОЛЬНАЯ БАЛКА 3. БАЛКА НА ШАРНИРНЫХ ОПОРАХ С КОНСОЛЯМИ Расчетные схемы для статически неопределимых балок .

stroyew.ru

Определение опорных реакций в заделке консольной балки

Задача

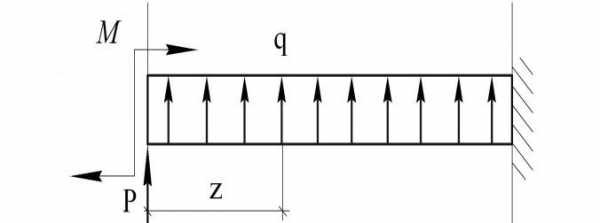
Консольная балка, нагружена сосредоточенными силой F и моментом m, а также равномерно распределенной нагрузкой q. Определить величину и направление опорных реакций в жесткой заделке.

Пример решения

В данном случае имеет место случай плоского поперечного изгиба, поэтому реакции, очевидно, также будут располагаться исключительно в плоскости чертежа.

Для удобства обозначим характерные сечения балки точками A, B, C и D и установим систему координат с началом в т. A

Как известно заделка препятствует одновременно перемещению и вращению балки, поэтому в защемлении возникнут сила R и момент M.

Не зная истинного направления, направим их произвольно, например: реакцию R направим вверх, а опорный момент M против хода часовой стрелки

Для определения неизвестных усилий запишем уравнения равновесия системы (уравнения статики):

Правила знаков для сил и моментов.

из первого уравнения определяем опорную силу

из второго — момент в заделке

Положительный знак найденных реакций показывает, что произвольно выбранное их направление оказалось правильным.

В качестве проверки полученных данных запишем уравнение суммы моментов относительно любой другой точки балки, например точки D:

Ноль говорит о том, что опорные реакции определены верно.

Другие примеры решения задач >

isopromat.ru

Задача 4. Проверочный расчёт консольной балки Условие задачи

Для стальной двутавровой балки (см. рис. 4.2, а) известна внешняя нагрузка, размер сечения и длина балки даны в табл. 4.1.

Требуется:

1. Построить эпюры внутренних усилий: поперечной силы Q_y и изгибающего момента М_x.

2. Проверить прочность балки, используя условие прочности по нормальным напряжениям. Принять допускаемое напряжение [σ] = 200 МПа.

3. Принимая схему балки как схему мостовой балки подъёмного крана, найти наибольшее нормальное напряжение σ_max, возникающее при торможении, при котором за счёт сил инерции угол наклона нагрузки составил 10⁰ к вертикали.

Теоретические основы решения

Изгиб  это часто встречаемый вид деформации прямолинейных элементов машин, механизмов и строительных конструкций, и поэтому плоский изгиб является важнейшим разделом сопротивления материалов, и ему уделяется большое внимание.

а
б

Рис. 4.1

При расчёте прямолинейные элементы изображают в виде прямого бруса (рис. 4.1). Рассмотрим нагрузку (рис. 4.1, а) в вертикальной плоскости бруса, совпадающей с его главной плоскостью инерции. Пусть действуют сосредоточенная сила Р, момент М и распределённая нагрузка интенсивности q. Деформация бруса выглядит как искривление (изгибание) бруса в плоскости нагрузки (рис. 4.1, б). При этом наблюдается следующая картина деформирования продольных волокон: имеем растяжение продольных волокон с одной стороны от продольной оси бруса и сжатие с другой, а продольная ось лишь искривилась, и поэтому она называется нейтральной осью. Такой вид деформации носит название плоский изгиб, а брус, получающий изгиб, называют балкой. Итак, если воздействие нагрузки происходит в плоскости, перпендикулярной продольной оси бруса и проходящей через главную ось инерции сечения, то имеем плоский изгиб.

Рассмотрим расчёт балки для общего случая нагружения при плоском изгибе (рис. 4.2): при наличии распределённой нагрузки, сосредоточенной силы и сосредоточенного момента. Направление нагрузок считаем положительным, если нагрузка отгибает балку к верху и вызывает растяжение нижних волокон.

Для расчёта балки необходимо знать внутренние усилия, вычисление которых производится методом сечений по правилу РОЗУ (рис 4.2). Последовательно выполняются следующие действия:

1) разрезать балку на две части;

2) отбросить одну из частей;

3) заменить воздействие отброшенной части на оставленную внутренними усилиями;

4) уравновесить внешнюю нагрузку и внутренние усилия.

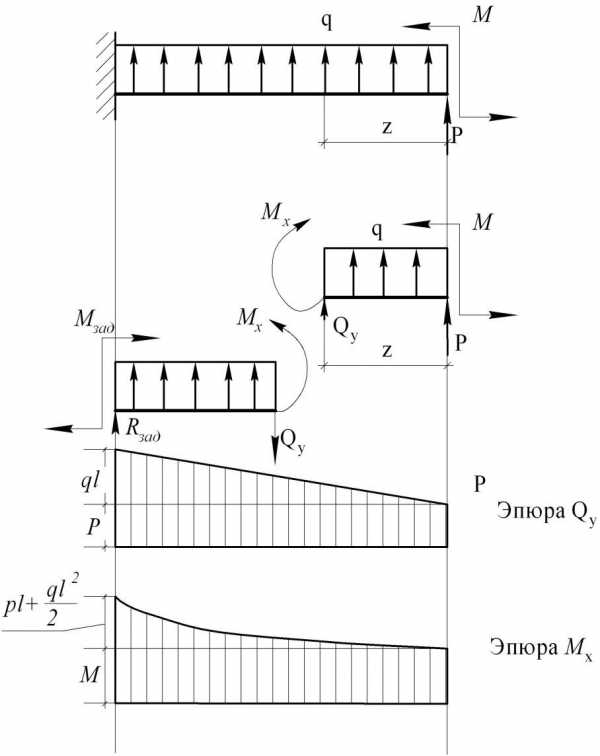
Рассмотрим эту методику на примере консольной балки (рис 4.2, а). Так как схема нагружения не изменяется по всей длине консоли, то имеем один грузовой участок, и достаточно рассмотреть один разрез балки на две части. На схеме балки покажем положение разреза координатой z (рис. 4.2, а).

Далее нужно рассмотреть одну из частей: либо левую, либо правую. На рис 4.2, б изображены обе части. Из них для расчёта левой части нужны значения опорных реактивных усилий R_зад и М_зад, возникающих в заделке, так как реактивные воздействия  часть внешней нагрузки, а в расчёт правой эти усилия не войдут, поскольку они не действуют на неё. Поэтому проще рассматривать правую часть, т. е. внутренние усилия в консольных балках лучше вычислять со свободного края. Итак, рассмотрим отсечённую правую часть длиною z. Сечение с координатой z называют текущим сечением.

Имеем 0 ≤ z ≤ l. В текущем сечении отсечённой части покажем внутренние усилия: поперечную силу Q_y и изгибающий момент M_x, причём строго определённого направления.

а б в д

Рис. 4.2

При изображении Q_y и M_x нужно пользоваться общепринятым правилом знаков: сила Q_y положительна, если вектор силы вращает оставленную часть по часовой стрелке; момент M_x положителен, если растягивает нижние волокна (рис. 4.3).

Сила Qy > 0 Момент Мх> 0

Рис. 4.3

Остановимся на составлении уравнений равновесия. Оставленная часть балки нагружена в одной и той же плоскости внешней нагрузкой и внутренними усилиями Q_y и M_x. Имеем плоскую систему сил, для которой существуют три уравнения равновесия; в плоской системе координат (у, z) они имеют вид:

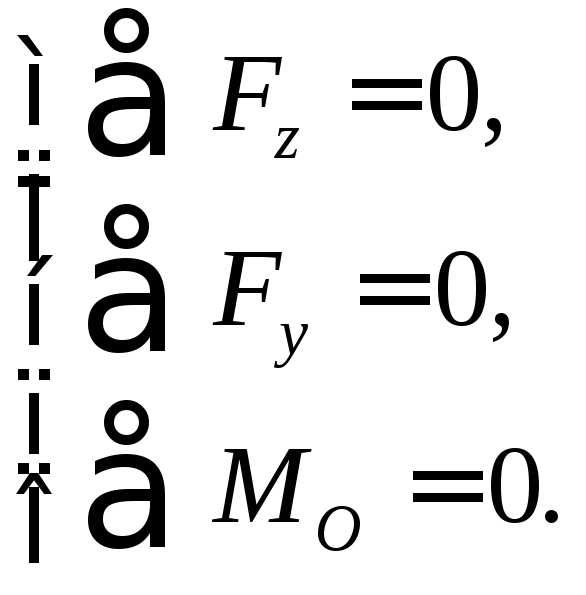
Заметим, что за точку О здесь удобнее взять центр тяжести текущего сечения.

При плоском изгибе отсутствуют продольные воздействия вдоль оси балки (вдоль оси z), и первое уравнение превращается в тождество 0=0, поэтому при расчёте балок оставляют лишь два уравнения:

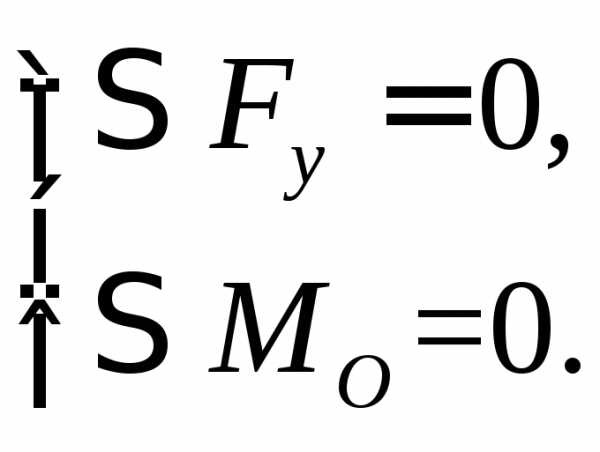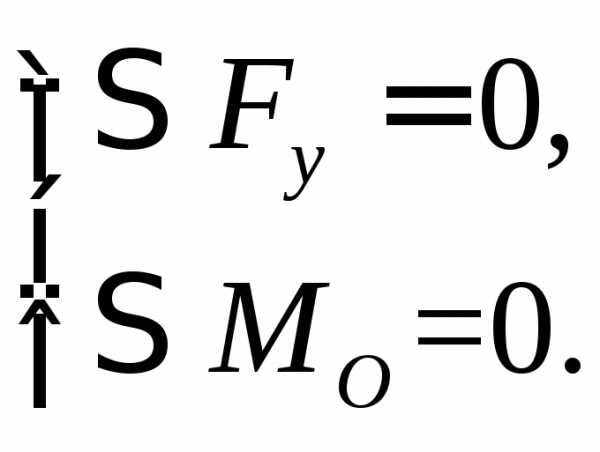. (4.1)

Запишем уравнения (4.1) для отсечённой левой части рассматриваемой консоли:

, ,

из которых получаем выражения:

, . (4.2)

Выражения (4.2) представляют по сути формулы для сил Q_y и моментов М_x, в них входят все виды нагрузок, и при подстановке в эти формулы значений реальных нагрузок получаем значения Q_y и М_x для реальной балки. По (4.2) видно, что в общем случае для силы Q_y имеем линейную зависимость, а для моментов М_x  криволинейную. Заметим, что между Q_y и M_x существует соотношение, которое известно как теорема Д.И. Журавского: если взять производные от функции M_x по z и от функции Q_y по z, то получим

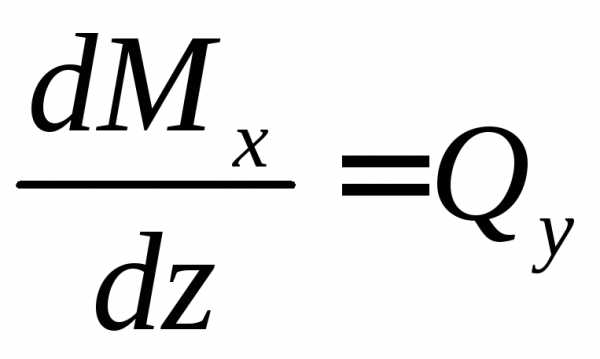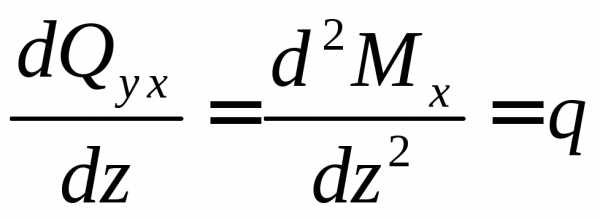, . (4.3)

Вычислим значения Q_y и М_x в начале балки (при z = 0) и в конце (при z = l). Получим граничные значения Q_y и М_x:

при z=0 Q_y=,;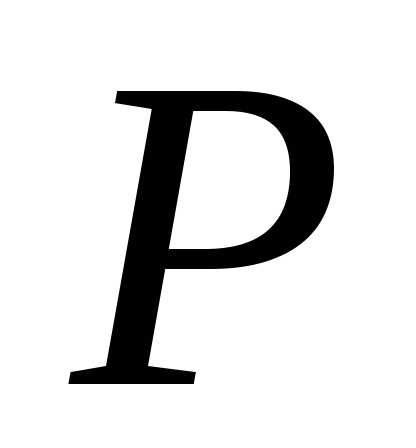

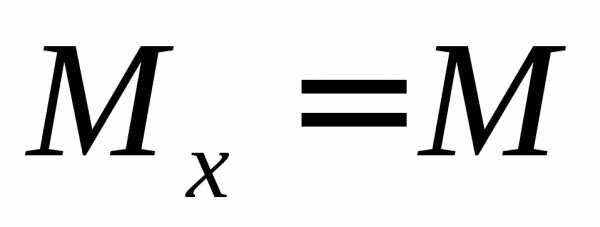при z=l Q_y =,.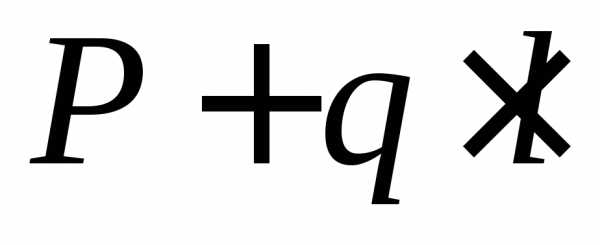

Значения сил Q_y и моментов М_x изменяются вдоль балки, для выбора максимальных значений Q_y и M_x (т.е. расчётных значений) изображают графики их изменения вдоль балки, которые называются эпюрами поперечных сил Q_y и изгибающих моментов M_x (рис 4.2). Построение эпюр проводят, используя найденные значения Q_y и М_x. Для этого отложим эти значения от базисной линии (эта линия, проведённая под балкой параллельно оси балки). Далее проводим наклонную прямую для Q_y и параболу для М_x.

На рис. 4.4 приведены эпюры поперечных сил Q_y и изгибающих моментов M_x в консольной балке отдельно от сосредоточенной силы, сосредоточенного момента и от распределённой нагрузки, которые хорошо показывают зависимость линий эпюр от вида нагрузки.

При расчётах элементов машин и механизмов положительные моменты откладываются вверх от базисной линии, с этой стороны расположены сжатые волокна, поэтому говорят, что эпюру изгибающих моментов строят со стороны сжатых волокон. Для строительных конструкций построение эпюр обычно выполняют на растянутых волокнах. Этот факт связан с использованием графоаналитических методов расчёта, т. е. исторически закрепилось построение на растянутых волокнах. Знак момента на эпюре обычно не ставится, так как для описания прочности используется модуль момента, а не его направление.

От изгибающих моментов M_x в сечении балки возникают нормальные напряжения σ, от поперечных сил Q_y ─ касательные напряжения τ. Решающее влияние на прочность балок имеют нормальные напряжения, поэтому составляют условие прочности по нормальным напряжениям:

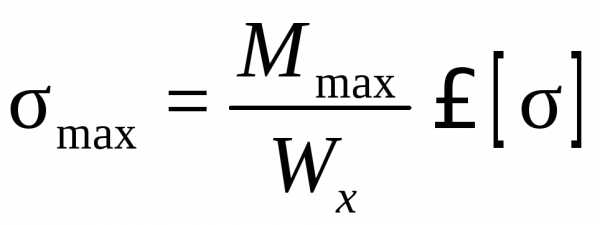, (4.4)

где σ_max  максимальное напряжение в опасном сечении балки, в котором модуль изгибающего момента M_x принимает максимальное значение M_max, значение момента M_max называют расчётным; 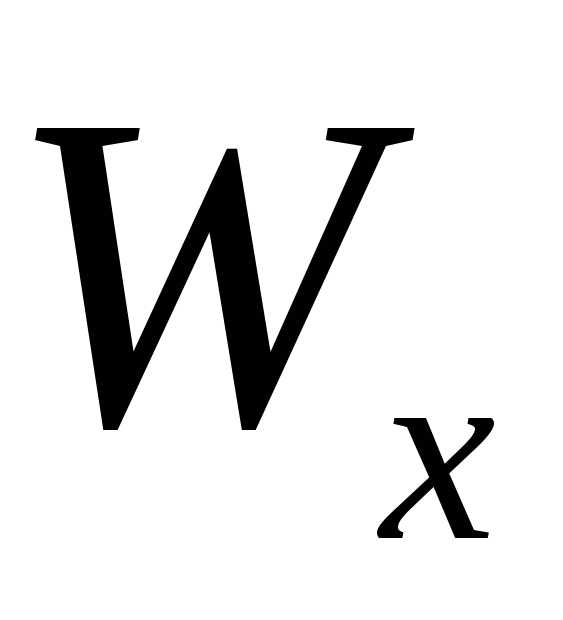осевой момент сопротивления сечения, 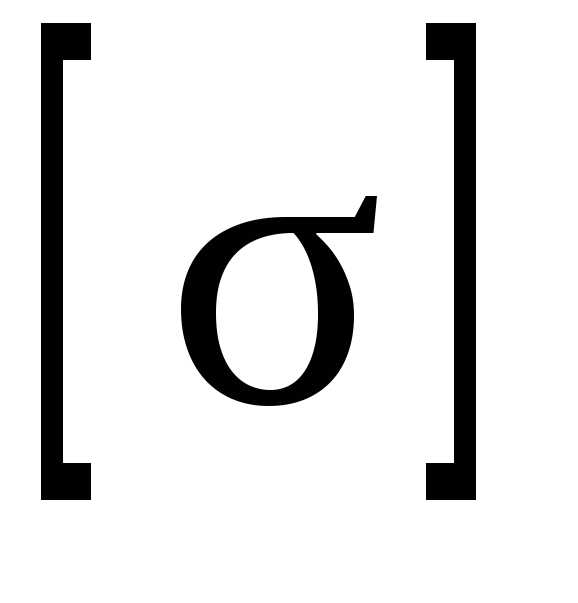 допускаемое напряжение для материала балки.

Согласно с видом деформирования при изгибе балки (рис. 4.1) со стороны растянутых волокон возникают растягивающие напряжения, со стороны сжатых волокон  сжимающие, и те и другие принимают наибольшее значение в крайних верхних и нижних точках сечения. Поэтому, если материал балки одинаково хорошо сопротивляется растяжению и сжатию, используют сечения, симметричные по высоте: прямоугольник, двутавр, швеллеры, круг и др. (рис. 4.5). Для симметричных сечений эпюра напряжений σ по высоте сечения линейна и симметрична.

Балка 1	В текущем сечении z Qy=0, Mx=M=const
Балка 2	В текущем сечении z Qy=—P=const, Mx= —P·z. При z=0 Mx=0, при z=l Mx=-P·l.
Балка3	В текущем сечении z Qy=—q·z, Mx=—q·z2/2. При z=0 Qy=0, Mx=0; при z=l Qy=—q·l, Mx=- q·l2/2.

Рис. 4.4

Рис. 4.5

По условию прочности (4.4) можно выполнять следующие три вида расчётов:

проектный, когда определяют требуемые размеры поперечного сечения балки;

проверочный, при котором вычисляют напряжения и сравнивают с допускаемыми;

определение нагрузочной способности, когда находят допускаемые значения внешней нагрузки.

studfiles.net

Расчет реакций опор в жесткой заделке консольной балки

Задача

Рассчитать величину и направление опорных реакций в жесткой заделке консольной балки нагруженной заданной системой внешних нагрузок.

Пример решения

Покажем значения нагрузок и продольные размеры балки, обозначим ее характерные сечения буквами A, B и C.

В случае плоского поперечного изгиба в жесткой заделке консольной балки могут иметь место только две опорные реакции:

На данном этапе решения задачи эти реакции можно направить в любую сторону.

Определим величину, а заодно и истинное направление опорных реакций.

Зададим систему координат y-z.

Для нахождения двух реакций нам понадобятся два уравнения равновесия.

Балка не перемещается вверх-вниз, поэтому сумма проекций всех сил на ось y должна равняться нулю.

Проецируя все силы на ось y получаем первое уравнение:

∑F(y)=0=-R-q∙1+F

Правило знаков для проекций сил.

Откуда находим величину реакции R

R=-q∙1+F=-100∙1+40=-60кН

Знак «-» в ответе говорит о том, что реальное направление реакции R противоположно выбранному вначале.

Поэтому изменим направление силы и соответственно ее знак на противоположные.

Второе уравнение статики получим из условия, что балка не вращается, так как сумма моментов приложенных к ней тоже равнв нулю.

Запишем уравнение суммы моментов, например, относительно точки A:

∑m_A=0=M-m+q∙1∙(0,5+0,5)-F(0,5+1)

Правило знаков для моментов.

Отсюда находим опорный момент M

M=m-q+F∙1,5=70-100+40∙1,5=30кНм

Положительный результат показывает, что выбранное наугад направление момента М оказалось верным, то есть перенаправлять его не нужно.

Полученные значения опорных реакций можно легко проверить.

Для этого запишем уравнение суммы моментов относительно точки B или C:

∑m_B=M+R∙0,5-m+q∙1∙0,5-F∙1

и подставив в него полученные значения, мы должны получить сумму равную нулю

∑m_B=30+60∙0,5-70+100∙1∙0,5-40∙1=0

Так и есть! Значит опорные реакции определены верно.

Рекомендуем посмотреть видеоурок решения этой задачи.

Другие примеры решения задач >

isopromat.ru

6.3. Пример расчета консольной балки на прочность по нормальным напряжениям Пример

Для заданной балки (рис. 6.3) из условия прочности по нормальным напряжениям определить размеры различных по форме поперечных сечений: двутавра, прямоугольника (с соотношением сторон 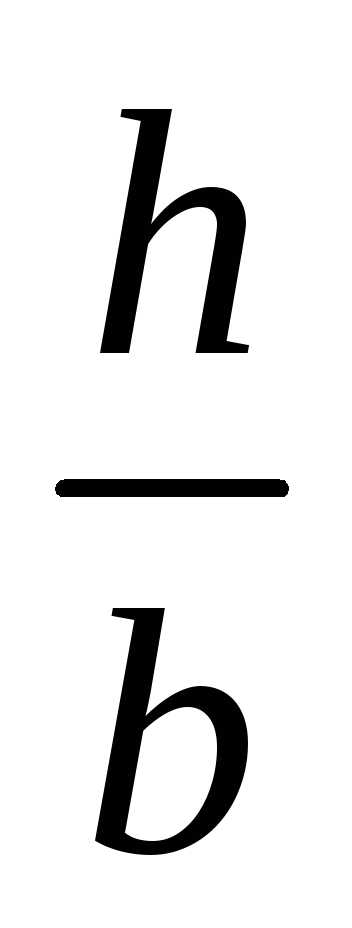= 1,8), квадрата, круга, кольца (при 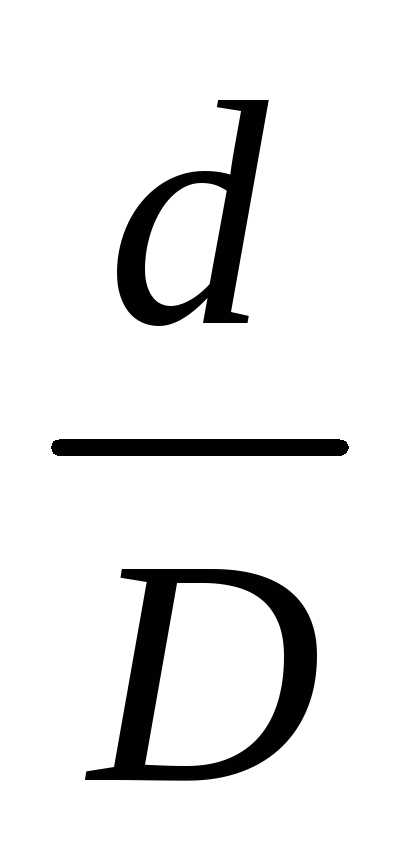= = 0,8) и оценить их рациональность.

a = 1,0 м, b = 1,4 м, F = 18 кН, q = 20 кH/м, М = 16 кHм, [] = 160 МПа.

Решение

Составить уравнения поперечных сил и изгибающих моментов по участкам и построить их эпюры.

Запишем уравнения статики и определим опорные реакции:

: ;

;

: ;;

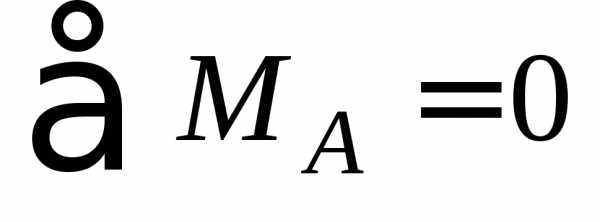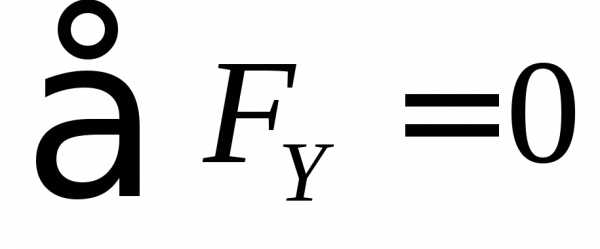Проверка: :.

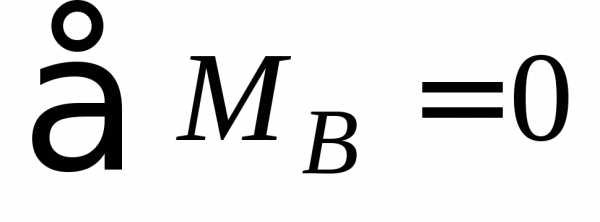Выражения для внутренних усилий Q_у, М_х получим с помощью метода сечений. Поперечная сила в произвольном сечении балки равна алгебраической сумме внешних сил, приложенных по одну сторону от сечения. При этом поперечная сила считается положительной, если равнодействующая внешних сил слева от сечения направлена вверх, а справа – вниз, т.е. стремится сдвинуть левую отсеченную часть балки относительно правой вверх.

Изгибающий момент в сечении балки равен алгебраической сумме моментов относительно данного сечения всех внешних сил, приложенных к отсеченной части. Момент считается положительным, если сжатые волокна находятся в верхней части сечения балки.

На рис. 6.3, а показаны выделенные участки балки. Запишем для каждого из них выражения внутренних усилий и найдем их значения на границах участков.

1. м.

; ;.

; ;

.

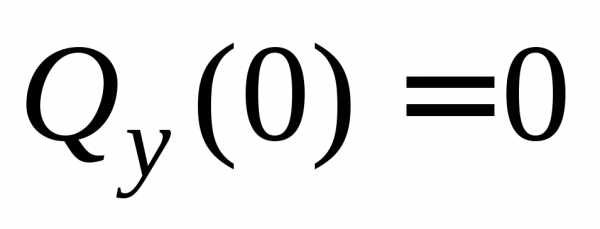2. м.

;

; ;.

3. м.

.

; ;

.

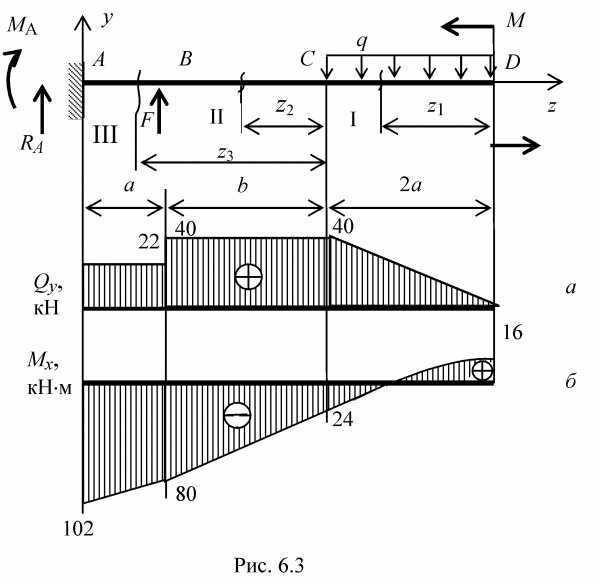
Рис. 6.3

Построение эпюр Q_у, М_х проводится по участкам на основе полученных уравнений. Положительные значения ординат откладываются выше оси, отрицательные – ниже. На первом участке поперечная сила линейно зависит от координаты, возрастая от нуля в начале участка до 40 кH в конце. Эпюра Q_у на этом участке ограничена отрезком прямой, проходящей через указанные значения. Изгибающий момент имеет на данном участке уравнение квадратной параболы с вершиной в сечении z₁= 0, т.е. там, где равна нулю поперечная сила, являющаяся производной от М_х по координате z. Эпюра изгибающего момента ограничена кривой второго порядка, проходящей через точки с координатами 16 кHм и –24 кHм, соответственно на правой и левой границах участка. Парабола имеет выпуклость, направленную навстречу распределенной нагрузке.

На втором и третьем участках поперечная сила имеет постоянные значения, соответственно 40 кH и 22 кH. Изгибающий момент меняется по линейному закону – эпюра М_х ограничена на участках отрезками прямых, проходящих через точки с ординатами –24 кHм, –80 кHм на втором и –80 кHм, –102 кHм на третьем участках. Результаты построения эпюр Q_у, М_х приведены на рис. 6.3.

Наиболее опасным является сечение А, в котором изгибающий момент достигает наибольшего по модулю значения .

Произвести проверку с помощью дифференциальных зависимостей.

Построение эпюры проводится в соответствии с формулой (6.1) на основе известных дифференциальных зависимостей между Q_у, М_х и интенсивностью распределенной нагрузки q.

В нашем случае на первый участок действует распределенная нагрузка q = const, следовательно, поперечная сила должна быть линейной функцией координаты z₁, а изгибающий момент должен меняться по закону квадратной параболы. Эпюра изгибающих моментов не имеет экстремумов, поскольку эпюра ее производной Q_у не пересекает ось (исключением является сечение D). Второй и третий участки свободны от распределенной нагрузки, т.е. производная функции Q_у тождественно равна нулю, следовательно, сама поперечная сила должна быть постоянна в границах каждого участка, а эпюра изгибающего момента описывается прямой наклонной линией.

В тех сечениях, где балка нагружена сосредоточенными внешними силами, на эпюре Q_у должно скачком меняться значение ординаты на величину этой силы с учетом ее направления. В нашем случае это происходит в сечении А, где возникает реакция R_А, и в сечении В, где приложена нагрузка F. На эпюре М_х аналогичные скачки имеют место в сечениях А и D, где действуют сосредоточенные внешние моменты. Анализируя все перечисленное, делаем вывод о правильности построения эпюр.

Подобрать размеры указанных выше сечений из условия прочности по нормальным напряжениям.

Из условия прочности при изгибе 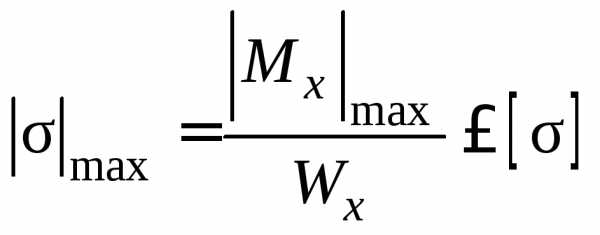определим требуемое значение момента сопротивления сечения балки:

.

Определим размеры указанных сечений, обеспечивающие прочность балки.

1. Подбираем по ГОСТ 8239–72 номер двутавра, момент сопротивления которого наиболее близок к расчетному. В данном случае подходит двутавр № 36, у которого W_x = 743,0 см³, площадь сечения А = 61,9 см².

Определим наибольшее значение возникающих при этом напряжений:

.

2. Определяем размеры прямоугольного сечения с отношением сторон 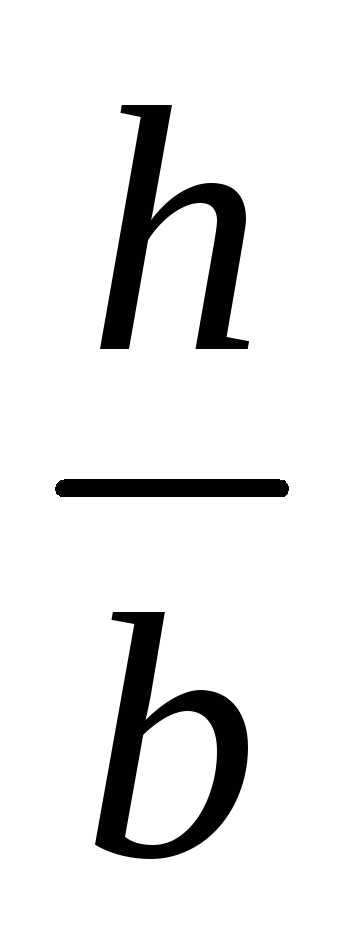= 1,8.

;

;

.

Окончательно выбираем размер по ГОСТ 6636–69: b = 110 мм, А = bh = 217,810^–4 м².

Вычисляем наибольшее напряжение:

.

3. Определяем размер квадратного сечения.

; ;.

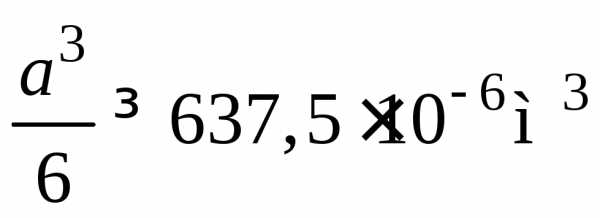Окончательно: а = 160 мм, А = a² = 25610^–4 м².

Определяем наибольшее напряжение:

.

4. Определяем размеры круглого сечения.

; ;

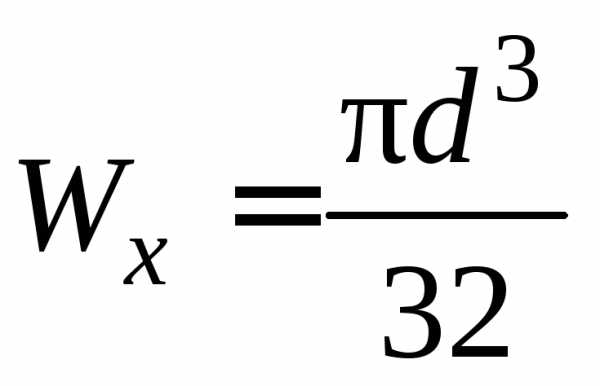Принимаем по ГОСТу d = 200 мм, площадь сечения .

Определим наибольшее напряжение:

.

5. Определяем размеры кольцевого сечения с отношением внутреннего и внешнего диаметров .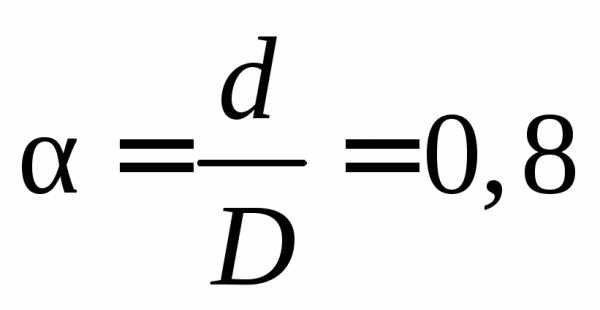

; ;.

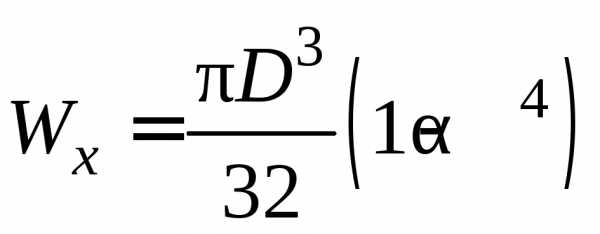Принимаем D = 250 мм, d = 200 мм.

Площадь сечения .

Вычисляем наибольшее напряжение:

.

Оценить рациональность подобранных сечений.

1. Двутавр: .

2. Прямоугольник: .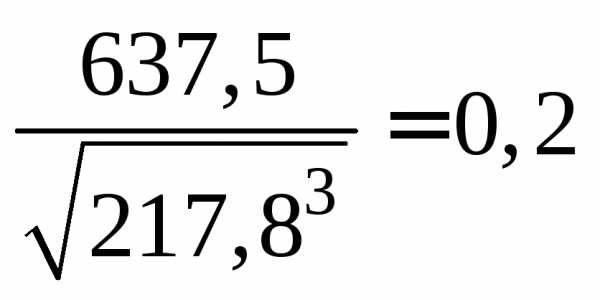

3. Квадрат: .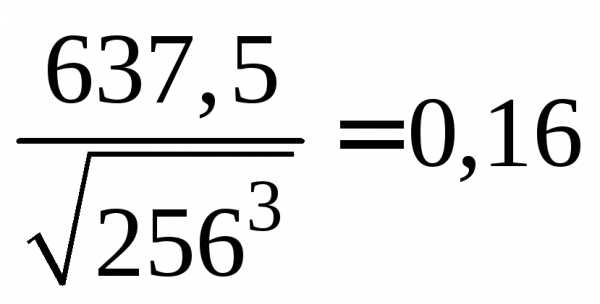

4. Круг: .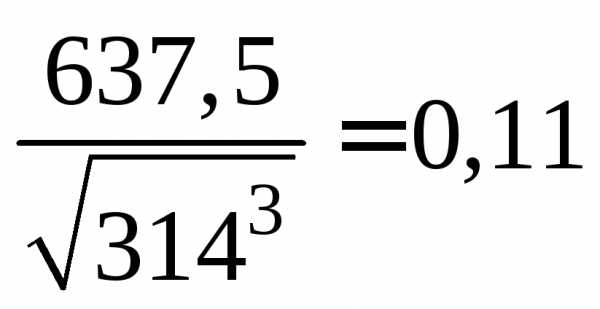

5. Кольцевое сечение: .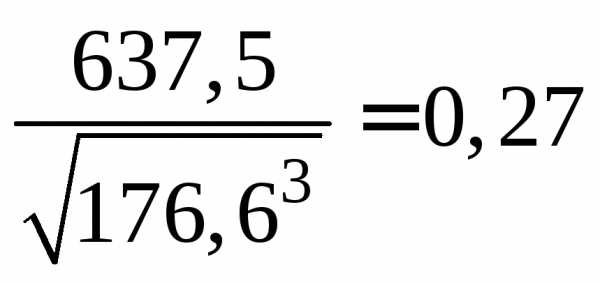

Как видим, наиболее рациональными при изгибе являются тонкостенные сечения, двутавр, кольцевое сечение.

Построить эпюру нормальных напряжений в опасном сечении (для двутавра, кольца).

Напряжения в опасном сечении меняются по линейному закону

,

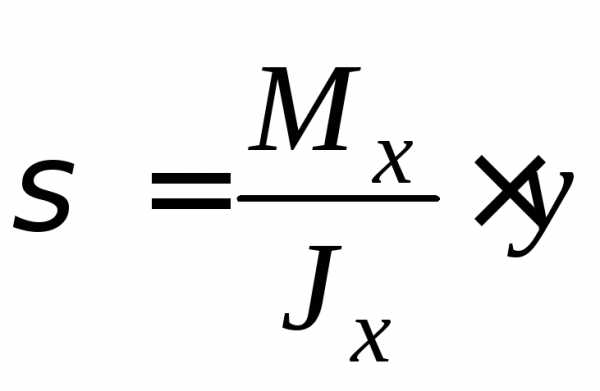достигая максимума в наиболее удаленных от оси точках.

На рис. 6.4 показаны эпюры напряжений для указанных сечений.

6.4. Пример расчета на прочность двутавровой балки по нормальным и касательным напряжениям. Расчет по теориям прочности

Пример

Для заданной стальной балки (рис. 6.5) из условия прочности подобрать номер двутавра по ГОСТ 8239–72 и произвести полную проверку прочности.

а = 0,4 м, b = 0,6 м, l = 2,4 м, F = 150 кH, q = 200 кH/м, М = 20 кHм, [] = 160 MПа, [] = 0,6·[] = 96 МПа.

studfiles.net

Проверка на прочность консольной балки

Проверим на прочность консольную балку, закрепленную в жесткой заделке.

Приложим к балке систему внешних нагрузок:

Укажем величину заданных усилий и продольные размеры участков балки.

Это расчетная схема для решения задачи.

Проверим эту балку на прочность при следующих данных:

Прежде чем приступить к решению проанализируем задачу.

Чтобы проверить балку на прочность надо определить величину максимальных напряжений σ_max в ее сечениях и сравнить их с допустимыми [σ].

В случае если максимальные напряжения окажутся меньше, либо равны допустимым (т.е. σ_max≤[σ]) прочность балки будет обеспечена.

Если же найденные напряжения превысят величину допустимых (т.е. σ_max>[σ]) значит балка не прочная.

Условие прочности при плоском поперечном изгибе:

Здесь
M_x – внутренний изгибающий момент,
W_x – осевой момент сопротивления сечения балки.

У балки постоянного сечения, форма и размеры сечения одинаковы по всей ее длине, следовательно, W_x=const.

Тогда очевидно, что наибольшими напряжения окажутся в сечении, где будет максимальный изгибающий момент M_x.

Определить максимальный изгибающий момент M_{x max} в балке можно только по его эпюре.

Для построения эпюр сначала надо определить опорные реакции.

Ниже приведены ссылки на каждый этап решения данной задачи.

Порядок проверки балки на прочность при изгибе:

isopromat.ru