9 важных факторов, связанных с ним
- Определение изгибающего момента
- Уравнение изгибающего момента
- Связь между интенсивностью нагрузки, поперечной силой и изгибающим моментом
- Единица измерения изгибающего момента
- Изгибающий момент балки
- Соглашение о знаках изгибающего момента
- Диаграмма усилия сдвига и изгибающего момента
- Типы опор и нагрузок
- Вопрос и ответ
Уравнение изгибающего моментаВ механике твердого тела изгибающий момент представляет собой реакцию, возникающую внутри элемента конструкции, когда к нему прикладывается внешняя сила или момент, вызывающие изгиб элемента. Самым передовым, стандартным и простейшим элементом конструкции, подверженным изгибающим моментам, является балка. Если момент, приложенный к балке, пытается изогнуть балку в плоскости стержня, это называется изгибающим моментом.
В случае простого изгиба, если изгибающий момент применяется к определенному поперечному сечению, возникающие напряжения называются изгибающим или изгибающим напряжением. Он изменяется линейно от нейтральной оси по поперечному сечению балки.
Алгебраическая сумма моментов по конкретному поперечному сечению балки, возникающих из-за моментов по часовой или против часовой стрелки, называется изгибающим моментом в этой точке.
Пусть W — вектор силы, действующий в точке A тела. Момент этой силы относительно реперной точки (O) определяется как
M = W xp
Где M = Момент вектор, р = вектор положения от опорной точки (О) до точки приложения силы А. символ обозначает векторное произведение. легко вычислить момент силы вокруг оси, которая проходит через опорную точку O. Если единичный вектор вдоль оси равен «i», момент силы вокруг оси определяется как
M = я. (Вт xp)
где [.]представляют собой точечное произведение вектора.
Соотношения: Пусть f = интенсивность нагрузки
Q = поперечная сила
M = изгибающий момент
Скорость изменения поперечной силы даст интенсивность распределенной нагрузки.
Скорость изменения изгибающего момента даст силу сдвига только в этой точке.
Единица измерения изгибающего моментаИзгибающий момент имеет единицу, аналогичную паре как Нм.
Изгибающий момент балкиПредполагая, что балка AB определенной длины подвержена изгибающему моменту M, Если верхнее волокно балки, то есть выше нейтральной оси, находится в состоянии сжатия, это называется положительным изгибающим моментом или прогибающим изгибающим моментом. Точно так же, если верхнее волокно балки, то есть выше нейтральной оси, находится в напряжении, это называется отрицательным изгибающим моментом или изгибающим моментом изгиба.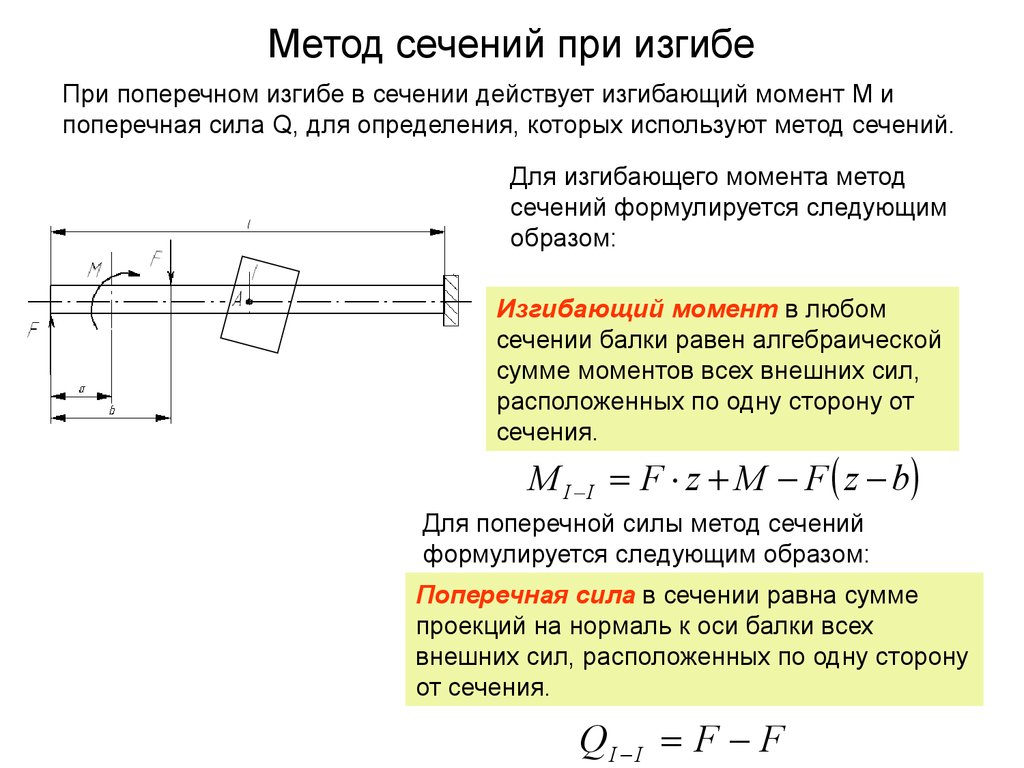 Провисание и заедание балки
Провисание и заедание балки
При определении максимального изгибающего момента, вытяжки и BMD соблюдается соглашение о конкретных знаках.
- Если мы начнем вычислять изгибающий момент с правая сторона или правый конец луч, Момент по часовой стрелке принимается как отрицательный Противодействующий момент принимается как Положительно.
- Если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный, и Момент против часовой стрелки принимается как Negative.
- Если мы начнем вычислять поперечную силу с правая сторона или правый конец луч, Сила, действующая вверх принимается как Отрицательный Сила, действующая вниз принимается как Положительно.
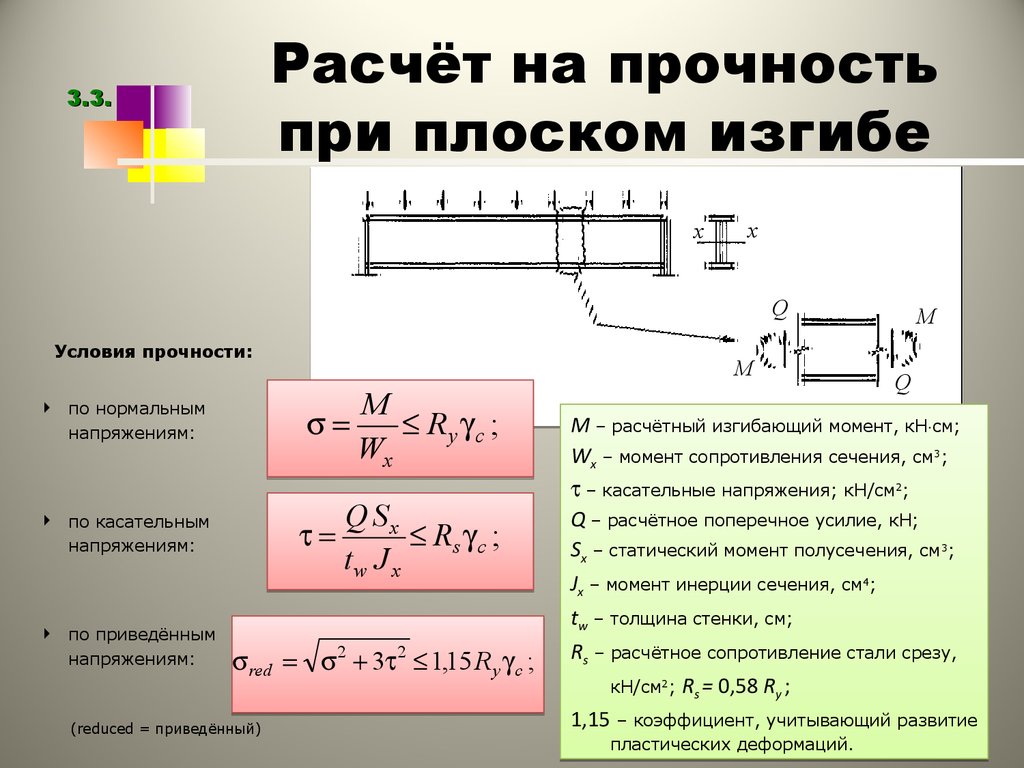
- Если мы начнем вычислять поперечную силу с Левая сторона или левый конец балки, Сила, действующая вверх принимается как Положительный, и Сила, действующая вниз принимается как Negative.
Сдвигающая сила представляет собой алгебраическую сумму сил, параллельных поперечному сечению по конкретному поперечному сечению балки, возникающих из-за сил действия и противодействия. Сила сдвига пытается срезать поперечное сечение балки перпендикулярно оси балки, и из-за этого развитое распределение напряжения сдвига является параболическим по отношению к нейтральной оси балки. Изгибающий момент представляет собой сумму моментов в определенном поперечном сечении балки, обусловленных моментами по часовой стрелке и против часовой стрелки. Это пытается изогнуть балку в плоскости элемента, и из-за передачи его по поперечному сечению балки распределение развиваемого изгибающего напряжения является линейным относительно нейтральной оси балки.
Диаграмма усилия сдвига — это графическое изображение изменения поперечной силы в поперечном сечении по длине балки. С помощью диаграммы силы сдвига мы можем определить критические секции, подверженные сдвигу, и внести поправки в конструкцию, чтобы избежать разрушения.
Кроме того, Диаграмма изгибающего момента — графическое представление изменения изгибающего момента в поперечном сечении по длине балки. С помощью диаграммы B. M мы можем определить критические секции, подлежащие изгибу, и внести изменения в конструкцию, чтобы избежать отказа. При построении диаграммы поперечных сил [SFD], при построении диаграммы изгибающих моментов [BMD] происходит резкое повышение или резкое падение из-за точечной нагрузки, действующей на балку; происходит внезапный подъем или резкое падение из-за воздействия пар на балку.
Типы опор и нагрузокФиксированная поддержка: Он может предложить три реакции в плоскости элемента (1 горизонтальная реакция, 1 вертикальная реакция, 1 моментная реакция).
Поддержка контактов: Он может предложить две реакции в плоскости элемента (1 горизонтальная реакция, 1 вертикальная реакция).
Роликовая опора: Он может предложить только одну реакцию в плоскости члена (1 вертикальная реакция).
Концентрированная или точечная нагрузка: При этом вся интенсивность нагрузки ограничена конечной площадью или точкой.
Равномерно распределенная нагрузка [UDL]: При этом вся интенсивность нагрузки постоянна по длине балки.
Равномерно изменяющаяся нагрузка [UVL]: При этом вся интенсивность нагрузки изменяется линейно по длине балки.Типы опор и нагрузок
Диаграмма усилия сдвига и диаграмма изгибающего момента только для балки, несущей точечную нагрузку.Учитывайте только опорную балку, показанную на рисунке ниже, несущую только точечные нагрузки. В балке с простой опорой один конец опирается на штифт, а другой конец — на роликовую опору.
Значение реакции в точках A и B можно рассчитать, применяя условия равновесия
Для вертикального равновесия
RA + RB=Ф…………[1]
Принимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.
ДалекоB*L=0
RB=Фа/л
Ставя ценность RB в [1] получаем
RA =FRB
RA =F – Фа/л
RA =F(La)/L=Fb/L
Таким образом, РA =Fb/L
Пусть XX — интересующий участок на расстоянии x от конца A.
В соответствии с обсуждавшимся ранее соглашением о знаках, если мы начнем вычислять поперечную силу с Левая сторона или левый конец балки, Сила, действующая вверх принимается как Положительный, и Сила, действующая вниз принимается как Negative.
Сила сдвига в точке А
Мы знаем, что поперечная сила остается постоянной между точками приложения точечных нагрузок.
Сила сдвига при C
СФ=РA=Fb/L
Сдвигающая сила в области XX равна
СФ=РA-F
СФ=Фб/Л-Ф
=F(бл)/л
SF=-Fa/L
Сила сдвига в точке B
СФ=РB=-Фа/л
Для диаграммы изгибающего момента, если мы начнем расчет BM с Левая сторона или левый конец балки, Момент по часовой стрелке воспринимается как положительный. Момент против часовой стрелки принимается как Negative.
- при A = 0
- при B = 0
- в C
BMC=-RA*a
BMC=-Fb/L*a
BMC=-Fab/лДиаграмма поперечной силы и изгибающего момента для Просто поддерживаемый луч с точечной нагрузкой
Сдвигающая сила [SFD] и диаграмма изгибающего момента [BMD] только для консольной балки с равномерно распределенной нагрузкой (UDL).
Рассмотрим только консольную балку, показанную на рисунке ниже UDL. В консольной балке один конец зафиксирован, а другой конец может двигаться.
Консольная балка подвергается равномерно распределенной нагрузкеРезультирующая нагрузка, действующая на балку из-за UDL, может быть определена как
W = Площадь прямоугольника
Ш = Д * ш
W = wL
Эквивалентная точечная нагрузка wL будет действовать в центре луча. т.е. при L / 2
Диаграмма свободного тела луча становитсяСхема свободного тела балки
Значение реакции в точке А можно рассчитать, применив условия равновесия.
Для горизонтального равновесия
ΣFx=0
RHA=0
Для вертикального равновесия
ΣFy=0
RVA-wL=0
RVA=wL
Принимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.
шл*л/2-мA=0
MA=wL2/2
Пусть XX — интересующий участок на расстоянии x от свободного конца.
В соответствии с обсуждавшимся ранее соглашением о знаках, если мы начнем вычислять поперечную силу с Левая сторона или левый конец балки, Сила, действующая вверх принимается как Положительный, и Сила, действующая вниз принимается как Negative.
Сила сдвига в точке A составляет
SFA=RVA=wL
в районе ХХ
SFX=RVA-w[Lx]
SFX=wL-wL+wx=wx
Сила сдвига в точке B составляет
СФ=РVA-wL
SFB=wL-wL=0
Значения силы сдвига в точках A и B показывают, что сила сдвига изменяется линейно от фиксированного конца к свободному концу.
Для BMD, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный и Момент против часовой стрелки принимается как Negative.
BM в A
BMA=MA=wL2 /2
BM в X
BMX=[МA-w][Lx]2/2
BMX=wL2 /2-ш(Дх)2 /2
BMX=wx(Lx/2)
BM в B
BMB=MA-wL2 /2
BMB=wL2/2- л2/ 2 = 0Диаграмма SFD и BMD для консольная балка с равномерно распределенной нагрузкой
4-точечная диаграмма изгибающего момента и уравненияРассмотрим балку с простой опорой, у которой две равные нагрузки W действуют на расстоянии a от обоих концов.FBD для 4-точечной диаграммы изгиба
Значение реакции в точках A и B можно рассчитать, применив условия равновесия.
Для вертикального равновесия
RA + RB=2Вт…………[1]
Принимая момент относительно A, положительный момент по часовой стрелке и отрицательный момент против часовой стрелки.
Ва+В[Ла]=РBL
RB=W
Из [1] получаем
RA =2W-W=W
Согласно описанному ранее соглашению о знаках, если мы начинаем вычислять поперечную силу с левой стороны или с левого конца балки, сила, действующая вверх, принимается как положительная, а сила, действующая вниз, принимается как отрицательная. Для построения диаграммы BMD, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный и Момент против часовой стрелки принимается как Negative.
Для построения диаграммы BMD, если мы начнем вычислять изгибающий момент с Левая сторона или левый конец балки, Момент по часовой стрелке принимается как Положительный и Момент против часовой стрелки принимается как Negative.
Сила сдвига в точке A составляет
SFA =RA =W
Сила сдвига в C составляет
SFC=W
Сила сдвига в D составляет
SFD=0
Сила сдвига в точке B составляет
SFB=0-W=-W
Для диаграммы изгибающего момента
Б. M при A = 0
B. M в C
BMC=RA*a
BMC=Ва
BM в D
BMD=WL-Wa-WL+2Wa
BMD=Ва
B. M при B = 0
Диаграммы SFD и BMD для 4-точечной диаграммы изгибаВ.1) В чем разница между моментом и изгибающим моментом?Ответ: Момент можно определить как произведение силы и длины линии, проходящей через точку опоры и перпендикулярной силе. Изгибающий момент — это реакция, возникающая внутри элемента конструкции, когда к нему прикладывается внешняя сила или момент, вызывающие изгиб элемента.
Изгибающий момент — это реакция, возникающая внутри элемента конструкции, когда к нему прикладывается внешняя сила или момент, вызывающие изгиб элемента.
Ответ: Диаграмма изгибающего момента — Графическое изображение изменения BM по поперечному сечению по длине балки. С помощью этой схемы мы можем определить критические участки, подлежащие изгибу, и внести изменения в конструкцию, чтобы избежать сбоев.
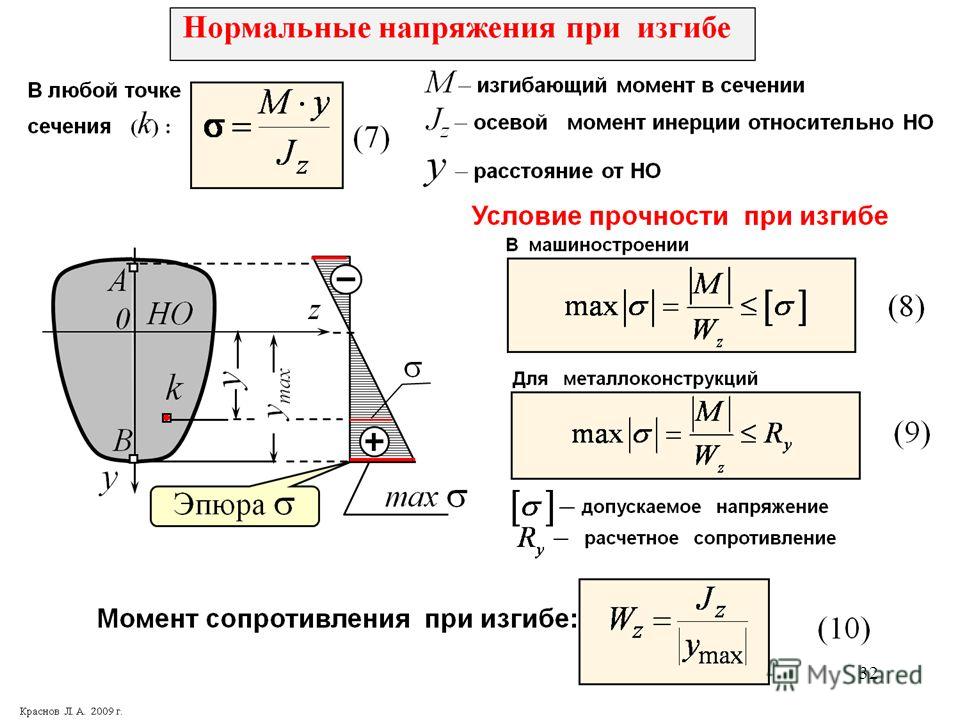
В.3) Какова формула напряжения изгиба?Ответ: изгиб Напряжение можно определить как сопротивление, вызванное изгибающим моментом или двумя равными и противоположными парами в плоскости элемента. Его формула дается
M/I=σ/y=E/R
Где M = приложенный изгибающий момент по поперечному сечению балки.
I = Второй момент инерции площади
σ = изгибное напряжение, вызванное в стержне
y = расстояние по вертикали между нейтральной осью луча и желаемым волокном или элементом в мм
E = модуль Юнга в МПа
R = радиус кривизны в мм
Знать о прочности материала нажмите здесь.
ОглавлениеПРЕДИСЛОВИЕОСНОВЫ РАСЧЕТА НА ПРОЧНОСТЬ НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ РАСТЯЖЕНИЕ И СЖАТИЕ ИЗГИБ СРЕЗ И СМЯТИЕ КРУЧЕНИЕ КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ НАПРЯЖЕННО-ДЕФОРМИРОВАННЫЕ СОСТОЯНИЯ Глава 2. МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ И ОЦЕНКА ПРОЧНОСТИ ДЕТАЛЕЙ СВОЙСТВА ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ СВОЙСТВА ПРИ ВЫСОКИХ И НИЗКИХ ТЕМПЕРАТУРАХ СВОЙСТВА ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ МАЛОЦИКЛОВАЯ И ТЕРМИЧЕСКАЯ ПРОЧНОСТЬ ПРОЧНОСТЬ ПРИ НАЛИЧИИ ТРЕЩИН РАЗРУШЕНИЯ И ИЗЛОМЫ ОЦЕНКА ПРОЧНОСТИ ЗАПАСЫ ПРОЧНОСТИ ПРИ СТАТИЧЕСКИХ НАПРЯЖЕНИЯХ ЗАПАСЫ ПРОЧНОСТИ ПО НЕСУЩЕЙ СПОСОБНОСТИ ЗАПАСЫ ПРОЧНОСТИ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ ЗАПАСЫ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ ЗАПАСЫ ВЫНОСЛИВОСТИ ПРИ РАБОТЕ НА РАЗЛИЧНЫХ РЕЖИМАХ РАСЧЕТЫ НА ПРОЧНОСТЬ МАТЕРИАЛЫ, ПОКРЫТИЯ И КОНТРОЛЬ КРЕПЕЖНЫХ ДЕТАЛЕЙ УПРОЩЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ РАСЧЕТ НАПРЯЖЕНИЙ КРУЧЕНИЯ ВЫБОР ПРЕДВАРИТЕЛЬНОЙ ЗАТЯЖКИ РАСПРЕДЕЛЕНИЕ НАГРУЗКИ ПО ВИТКАМ РЕЗЬБЫ И КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В СОЕДИНЕНИЯХ ПРОЧНОСТЬ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ Глава 4.  ФЛАНЦЕВЫЕ СОЕДИНЕНИЯ ФЛАНЦЕВЫЕ СОЕДИНЕНИЯТИПЫ ФЛАНЦЕВЫХ СОЕДИНЕНИЙ УТОЧНЕННЫЙ РАСЧЕТ СОЕДИНЕНИЙ С НЕКОНТАКТИРУЮЩИМИ ФЛАНЦАМИ НАПРЯЖЕННОЕ СОСТОЯНИЕ ФЛАНЦА И ТРУБЫ Глава 5. ШПОНОЧНЫЕ И ШЛИЦЕВЫЕ СОЕДИНЕНИЯ ШЛИЦЕВЫЕ СОЕДИНЕНИЯ РАСЧЕТ ШЛИЦЕВЫХ СОЕДИНЕНИЙ НА ПРОЧНОСТЬ ИЗНАШИВАНИЕ СОЕДИНЕНИЙ Глава 6. СОЕДИНЕНИЯ ДЕТАЛЕЙ С ГАРАНТИРОВАННЫМ НАТЯГОМ РАСЧЕТНЫЙ И ПОТРЕБНЫЙ НАТЯГИ Глава 7. СВАРНЫЕ И ПАЯНЫЕ СОЕДИНЕНИЯ КОНТРОЛЬ КАЧЕСТВА СВАРНЫХ СОЕДИНЕНИЙ РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ ПРИ ПОСТОЯННЫХ НАГРУЗКАХ ВЛИЯНИЕ ОСНОВНЫХ КОНСТРУКТИВНЫХ И ТЕХНОЛОГИЧЕСКИХ ФАКТОРОВ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ ПАЯНЫЕ СОЕДИНЕНИЯ Глава 8. ВАЛЫ КОНСТРУКТИВНЫЕ ФОРМЫ И МАТЕРИАЛЫ ВАЛОВ ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ НАГРУЗКИ НА ВАЛЫ И РАСЧЕТНЫЕ СХЕМЫ РАСЧЕТ СТАТИЧЕСКОЙ ПРОЧНОСТИ, ЖЕСТКОСТИ И УСТОЙЧИВОСТИ ВАЛОВ РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ РАСЧЕТ НА КОЛЕБАНИЯ КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ Глава 9. 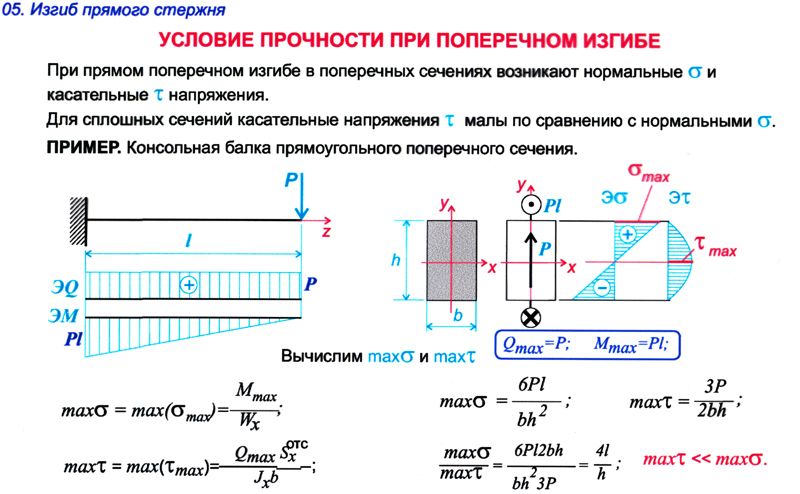 ПОДШИПНИКИ КАЧЕНИЯ ПОДШИПНИКИ КАЧЕНИЯОСНОВНЫЕ КОНСТРУКЦИИ И ХАРАКТЕРИСТИКИ ГЕОМЕТРИЧЕСКИЕ, КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ В ПОДШИПНИКАХ КАЧЕНИЯ ГРУЗОПОДЪЕМНОСТЬ И РАСЧЕТ ПОДШИПНИКОВ ЭКВИВАЛЕНТНАЯ НАГРУЗКА И РАСЧЕТ ДОЛГОВЕЧНОСТИ ПОДШИПНИКОВ СМАЗЫВАНИЕ ПОДШИПНИКОВ НЕКОТОРЫЕ ПРИЧИНЫ ПРЕЖДЕВРЕМЕННОГО ВЫХОДА ИЗ СТРОЯ ПОДШИПНИКОВ КАЧЕНИЯ И МЕТОДЫ ИХ ПРЕДОТВРАЩЕНИЯ Глава 10. ПРУЖИНЫ ВИТЫЕ ПРУЖИНЫ РАСЧЕТ ВИТЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН РАСЧЕТ НА СТАТИЧЕСКУЮ ПРОЧНОСТЬ РАСЧЕТ НА СОПРОТИВЛЕНИЕ УСТАЛОСТИ РАСЧЕТ НА УДАРНУЮ НАГРУЗКУ ТАРЕЛЬЧАТЫЕ ПРУЖИНЫ ПРОРЕЗНЫЕ ПРУЖИНЫ КОЛЬЦЕВЫЕ ПРУЖИНЫ КОЛЬЦЕВЫЕ ВОЛНИСТЫЕ ПРУЖИНЫ РЕЗИНОВЫЕ УПРУГИЕ ЭЛЕМЕНТЫ Глава 11. ЗУБЧАТЫЕ ПЕРЕДАЧИ УПРОЩЕННЫЙ РАСЧЕТ НА ПРОЧНОСТЬ ПРЯМЫХ ЗУБЬЕВ СТРУКТУРА РАСЧЕТНЫХ ФОРМУЛ ПО ГОСТ 21354—87 НАГРУЗКИ, ДЕЙСТВУЮЩИЕ НА ЗУБ РАСЧЕТ ЗУБЬЕВ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ РАСЧЕТ НА КОНТАКТНУЮ ВЫНОСЛИВОСТЬ АКТИВНЫХ ПОВЕРХНОСТЕЙ ЗУБЬЕВ РАБОТА ПЕРЕДАЧ ПРИ РАЗЛИЧНЫХ РЕЖИМАХ ОСОБЕННОСТИ РАСЧЕТА ПЕРЕДАЧ С КОСЫМИ, ШЕВРОННЫМИ, КОНИЧЕСКИМИ ЗУБЬЯМИ И ПЕРЕДАЧ М. 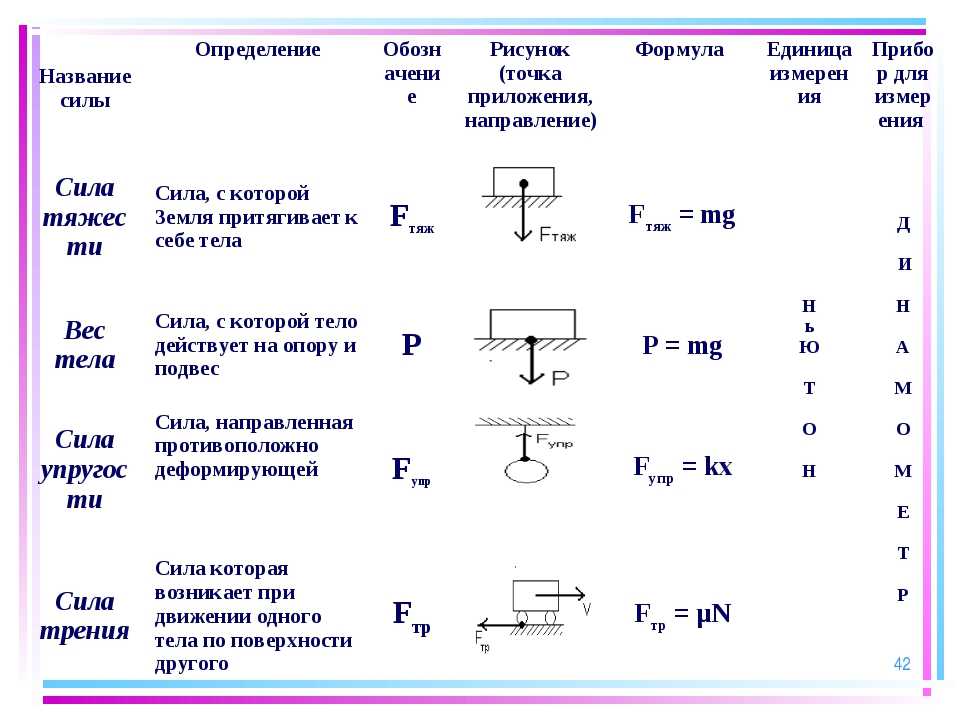 Л. НОВИКОВА Л. НОВИКОВАКОНСТРУКЦИИ ПЕРЕДАЧ И МАТЕРИАЛЫ РАСЧЕТ ПЕРЕДАЧ Глава 13. РЕМЕННЫЕ ПЕРЕДАЧИ МЕХАНИКА РЕМЕННОЙ ПЕРЕДАЧИ РАСЧЕТ РЕМЕННЫХ ПЕРЕДАЧ ПЕРЕДАЧИ С ЗУБЧАТЫМИ РЕМНЯМИ ПОРЯДОК РАСЧЕТА И ПРОЕКТИРОВАНИЯ РЕМЕННЫХ ПЕРЕДАЧ Глава 14. ЦЕПНЫЕ ПЕРЕДАЧИ СИЛЫ В ПЕРЕДАЧЕ ВЫБОР ОСНОВНЫХ ПАРАМЕТРОВ ПЕРЕДАЧИ НЕСУЩАЯ СПОСОБНОСТЬ ПЕРЕДАЧИ ОСОБЕННОСТИ ПРОЕКТИРОВАНИЯ И ЭКСПЛУАТАЦИИ ПЕРЕДАЧ ПОРЯДОК РАСЧЕТА ПЕРЕДАЧИ Глава 15. РАСЧЕТ ДЕТАЛЕЙ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ РАСЧЕТ КОЛЕНЧАТЫХ ВАЛОВ РАСЧЕТ ШАТУНОВ РАСЧЕТ ПОРШНЕВОГО ПАЛЬЦА РАСЧЕТ ПОРШНЕВЫХ КОЛЕЦ РАСЧЕТ ДНИЩА ПОРШНЯ ПРОЧНОСТЬ ЭЛЕМЕНТОВ КОРПУСА РАСЧЕТ КЛАПАННЫХ ПРУЖИН Глава 16. РАСЧЕТ ДЕТАЛЕЙ ТУРБОМАШИН РАСЧЕТ ЛОПАТОК НА ИЗГИБ ЗАПАС ПРОЧНОСТИ ПРОФИЛЬНОЙ ЧАСТИ ЛОПАТКИ РАВНОПРОЧНЫЕ ЛОПАТКИ ОХЛАЖДАЕМЫЕ ЛОПАТКИ ИЗГИБНЫЕ КОЛЕБАНИЯ ЛОПАТОК ЗАКРУЧЕННЫЕ ЛОПАТКИ ШАРНИРНЫЕ ЛОПАТКИ БАНДАЖИРОВАННЫЕ ЛОПАТКИ РАСЧЕТ ЗАМКОВ ЛОПАТОК ВИБРАЦИЯ ЛОПАТОК РАСЧЕТ ДИСКОВ.  НАПРЯЖЕНИЯ НА КОНТУРЕ НАПРЯЖЕНИЯ НА КОНТУРЕЗАПАСЫ ПРОЧНОСТИ ДИСКА ПРОФИЛИРОВАНИЕ РАВНОПРОЧНЫХ ДИСКОВ ОСНОВНЫЕ УРАВНЕНИЯ ПРИ РАСЧЕТЕ ДИСКОВ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПОСТОЯННОЙ ТОЛЩИНЫ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ДИСКЕ ПЕРЕМЕННОЙ ТОЛЩИНЫ ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ ПЕРЕРЕЗЫВАЮЩАЯ СИЛА И ИЗГИБАЮЩИЙ МОМЕНТ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ ПРИ ИЗГИБЕ УПРУГАЯ ЛИНИЯ СТЕРЖНЯ ОПРЕДЕЛЕНИЕ ПРОГИБОВ С ПОМОЩЬЮ ИНТЕГРАЛА МОРА ПРОГИБЫ И УГЛЫ ПОВОРОТА В СТЕРЖНЕ ПЕРЕМЕННОГО СЕЧЕНИЯ ИЗГИБ СТЕРЖНЯ С УЧЕТОМ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ Глава 18. КРУЧЕНИЕ СТЕРЖНЕЙ СТЕРЖЕНЬ С ЭЛЛИПТИЧЕСКИМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ СТЕРЖНИ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ И ТОНКОСТЕННЫЕ РАСПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ УЧЕТ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ ТРУБЧАТЫЕ СТЕРЖНИ Глаза 19. РАСЧЕТ КОЛЕЦ ПЛОСКАЯ ДЕФОРМАЦИЯ КОЛЕЦ ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КОЛЕЦ ТАБЛИЦЫ ДЛЯ РАСЧЕТА КРИТИЧЕСКОЙ НАГРУЗКИ ВЛИЯНИЕ НАЧАЛЬНОГО ПРОГИБА И ВНЕЦЕНТРЕННОГО ПРИЛОЖЕНИЯ СИЛЫ НА ВЫПУЧИВАНИЕ СТЕРЖНЯ РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ ВЫПУЧИВАНИЕ СТЕРЖНЯ ПРИ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ ДИНАМИЧЕСКИЙ АНАЛИЗ УСТОЙЧИВОСТИ.  ДЕЙСТВИЕ СЛЕДЯЩИХ НАГРУЗОК ДЕЙСТВИЕ СЛЕДЯЩИХ НАГРУЗОКПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАГРЕВЕ ПОТЕРЯ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ СКРУЧИВАНИИ Глава 21. КОЛЕБАНИЯ УПРУГИХ СИСТЕМ МЕТОД ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ СИСТЕМЫ МЕТОДОМ ДИНАМИЧЕСКИХ ЖЕСТКОСТЕЙ КРУТИЛЬНЫЕ КОЛЕБАНИЯ ИЗГИБНЫЕ КОЛЕБАНИЯ ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ НЕКОТОРЫХ ДИНАМИЧЕСКИХ СИСТЕМ Глава 22. КРИТИЧЕСКИЕ ЧАСТОТЫ ВРАЩЕНИЯ ВАЛОВ ВАЛ С НЕСКОЛЬКИМИ ДИСКАМИ ВАЛ С НЕПРЕРЫВНО РАСПРЕДЕЛЕННЫМИ МАССАМИ Глава 23. РАСЧЕТ ПЛАСТИНОК ПРОРЫВНЫЕ МЕМБРАНЫ ПРЯМОУГОЛЬНЫЕ ПЛАСТИНКИ Глава 24. РАСЧЕТ НА ПРОЧНОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК РАСЧЕТ ДЛИННЫХ ОБОЛОЧЕК РАСЧЕТ КОРОТКИХ ОБОЛОЧЕК ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ОБОЛОЧКЕ Глава 25. УСТОЙЧИВОСТЬ ПЛАСТИНОК, КОЛЕЦ И ОБОЛОЧЕК УСТОЙЧИВОСТЬ ПЛАСТИНОК УСТОЙЧИВОСТЬ КОЛЕЦ УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК УСТОЙЧИВОСТЬ КОНИЧЕСКИХ ОБОЛОЧЕК УСТОЙЧИВОСТЬ СФЕРИЧЕСКИХ И ЭЛЛИПСОИДАЛЬНЫХ ОБОЛОЧЕК УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК ПРИ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЯХ УСТОЙЧИВОСТЬ АНИЗОТРОПНЫХ ОБОЛОЧЕК УСТОЙЧИВОСТЬ ПОДКРЕПЛЕННЫХ ОБОЛОЧЕК Глава 26.  ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙВАРИАЦИОННО-РАЗНОСТНЫЙ МЕТОД МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ ДИНАМИЧЕСКИЕ РАСЧЕТЫ Глава 27. РАСЧЕТ КОНСТРУКЦИЙ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ УРАВНЕНИЯ ПЛАСТИЧНОСТИ РАСЧЕТ КОНСТРУКЦИЙ НА ПРОЧНОСТЬ С УЧЕТОМ ПЛАСТИЧНОСТИ И ПОЛЗУЧЕСТИ (ПРОСТОЕ НАГРУЖЕНИЕ) РАСЧЕТ НА ПРОЧНОСТЬ КОНСТРУКЦИЙ ПРИ СЛОЖНОМ НАГРУЖЕНИИ Глава 28. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В ДЕТАЛЯХ МАШИН КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ОКОЛО ОТВЕРСТИЙ КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ПЛОСКИХ И ОСЕСИММЕТРИЧНЫХ ВЫТОЧКАХ И ГАЛТЕЛЯХ КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В УСЛОВИЯХ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ И ПОЛЗУЧЕСТИ КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ЭЛЕМЕНТАХ КОНСТРУКЦИЙ Глава 29. КОНТАКТНЫЕ ЗАДАЧИ КОНТАКТ ДЕТАЛЕЙ ПРОСТОЙ ФОРМЫ КОНСТРУКЦИОННЫЕ КОНТАКТНЫЕ ЗАДАЧИ ОБЩИЙ МЕТОД РЕШЕНИЯ КОНСТРУКЦИОННЫХ КОНТАКТНЫХ ЗАДАЧ ОЦЕНКА ПРОЧНОСТИ И НАДЕЖНОСТИ Глава 30. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ КРИТЕРИИ ДЛИТЕЛЬНОЙ И МАЛОЦИКЛОВОЙ ПРОЧНОСТИ Глава 31.  РАСЧЕТ НА УСТАЛОСТЬ РАСЧЕТ НА УСТАЛОСТЬОСНОВНЫЕ ЗАКОНОМЕРНОСТИ СОПРОТИВЛЕНИЯ УСТАЛОСТИ ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ УСЛОВИЯ СОПРОТИВЛЕНИЯ УСТАЛОСТИ ОПРЕДЕЛЕНИЕ ЗАПАСОВ ПРОЧНОСТИ ПРИ УСТАЛОСТИ СТАТИСТИЧЕСКИЕ МОДЕЛИ УСТАЛОСТИ Глава 32. ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ И ЗАПАСЫ ПРОЧНОСТИ ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ ВЕРОЯТНОСТЬ РАЗРУШЕНИЯ ПРИ ПРОИЗВОЛЬНЫХ ЗАКОНАХ РАСПРЕДЕЛЕНИЯ НАПРЯЖЕНИЙ И ПРЕДЕЛОВ ПРОЧНОСТИ СТАТИСТИЧЕСКИЕ ЗАПАСЫ ПРОЧНОСТИ Глава 33. ЭЛЕМЕНТЫ ТЕОРИИ НАДЕЖНОСТИ ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ И ИНТЕНСИВНОСТЬ ОТКАЗОВ ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ НАДЕЖНОСТИ ОБЩАЯ ЗАКОНОМЕРНОСТЬ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ ОТКАЗОВ ПО ВРЕМЕНИ НАРАБОТКИ ПРОГНОЗИРУЕМАЯ ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН НАДЕЖНОСТИ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ РАСПРЕДЕЛЕНИЕ ВЕЙБУЛЛА ДЛЯ ВРЕМЕНИ БЕЗОТКАЗНОЙ РАБОТЫ НАДЕЖНОСТЬ СИСТЕМЫ ПОСЛЕДОВАТЕЛЬНЫХ ЭЛЕМЕНТОВ НАДЕЖНОСТЬ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ ЭЛЕМЕНТОВ АНАЛИЗ НАДЕЖНОСТИ СИСТЕМЫ С НЕСКОЛЬКИМИ ПАРАЛЛЕЛЬНО РАБОТАЮЩИМИ ЭЛЕМЕНТАМИ КОЛИЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ Глава 34.  ТЕХНОЛОГИЧЕСКИЕ МЕТОДЫ ПОВЫШЕНИЯ ДОЛГОВЕЧНОСТИ ДЕТАЛЕЙ МАШИН ТЕХНОЛОГИЧЕСКИЕ МЕТОДЫ ПОВЫШЕНИЯ ДОЛГОВЕЧНОСТИ ДЕТАЛЕЙ МАШИНУПРОЧНЕНИЕ ДЕТАЛЕЙ МАШИН ПОВЕРХНОСТНЫМ ПЛАСТИЧЕСКИМ ДЕФОРМИРОВАНИЕМ ТЕРМИЧЕСКАЯ И ХИМИКОТЕРМИЧЕСКАЯ ОБРАБОТКА ОПРЕДЕЛЕНИЕ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ Глава 35. ОСНОВЫ ТЕОРИИ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ ВЕРОЯТНОСТНЫЕ МЕТОДЫ РАСПОЗНАВАНИЯ МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ ПРИ НАЛИЧИИ ЗОНЫ НЕОПРЕДЕЛЕННОСТИ МЕТРИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ МЕТОД РАЗДЕЛЕНИЯ В ПРОСТРАНСТВЕ ПРИЗНАКОВ ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ Глава 36. ОСНОВЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ ОБЩИЕ ПРИНЦИПЫ СОЗДАНИЯ СИСТЕМ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ ЦЕЛИ И МЕТОДЫ ОПТИМИЗАЦИИ СПИСОК ЛИТЕРАТУРЫ |
Изгибающий момент — определение, формула, примеры, диаграмма
Серия испытаний
Автор: Айна Парашер|Обновлено: 13 октября 2022 г. в конструктивном элементе. Это отклонение может быть положительным или отрицательным. Обычно это называется изгибом, а эффект, создаваемый приложенной силой, известен как изгибающий момент . Изгибающий момент также зависит от направления приложения напряжения.
Изгибающий момент также зависит от направления приложения напряжения.
В этой статье мы собираемся узнать, что такое изгибающий момент и какой тип изгибающего момента возникает в стандартном случае структурного поперечного сечения или условий нагрузки. Эти стандартные случаи основаны на типе опоры элемента конструкции или направлении нагрузки. 1. Формула изгибающего момента0020
Читать статью полностью
Формула изгибающего момента
Изгибающий момент представляет собой алгебраическую сумму приложенной нагрузки на заданном расстоянии от исходной точки. Изгибающие моменты также будут вызваны суммой приложенных моментов от опорной точки. Изгибающий момент является важной частью программы GATE CE. Как правило, момент, вызывающий изгиб элемента конструкции, называется изгибающим моментом.
Прочность материала, структурный анализ, железобетон и анализ стали используют уравнение изгибающего момента. В уравнении изгибающего момента изгибающий момент имеет соотношение:
В уравнении изгибающего момента изгибающий момент имеет соотношение:
M/I = f/y = E/R
Где;
- M = изгибающий момент, I = момент инерции
- f = напряжение при изгибе
- y = расстояние от центра тяжести внешнего волокна
- E = модуль упругости
- R = радиус кривизны
Загрузить формулы для GATE Civil Engineering — Fluid Mechanics
Диаграмма изгибающего момента
Расчет изгибающего момента выполняется для различных условий опоры, таких как свободно опертая, консольная опора, опорная консольная опора, выступающая опора или сплошная опора с различной нагрузкой комбинации, такие как точечная нагрузка, равномерная нагрузка, постепенно меняющаяся нагрузка или прямой момент. Диаграмма изгибающего момента различных объектов задается на экзамене GATE; поэтому рекомендуется изучить этот раздел с особой тщательностью.
Основным принципом определения изгибающего момента является приложенная нагрузка или сила, умноженная на расстояние от контрольной точки на пролете элемента конструкции.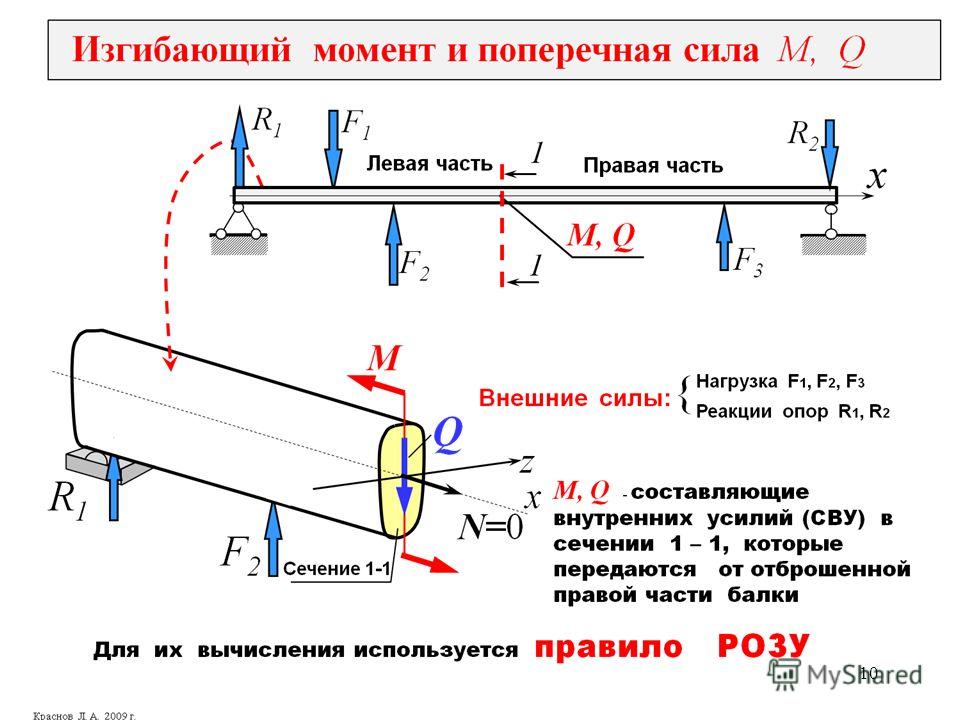
Загрузить формулы для GATE Civil Engineering — Environmental Engineering
Примеры изгибающего момента
Свободно опертая балка имеет точечную нагрузку в середине пролета. Изгибающий момент можно определить как центральную точечную нагрузку P, деленную на опору как 0,5P; это значение известно как реакция поддержки. Мы знаем, что длина пролета равна L. Мы знаем, что значение изгибающего момента равно нулю как на шарнирной опоре, так и просто на опоре. Мы получили максимальный изгибающий момент в центре пролета. Таким образом, реакция опоры умножается на половину длины пролета. Таким образом, я получил изгибающий момент в центре как 0,25PL. По схеме мы видим это-
Стандартные случаи изгибающего момента
Мы знаем, что изгибающий момент может быть получен из приложенной нагрузки и заданного расстояния. В опросном листе GATE можно увидеть различные вопросы, основанные на MCQ. Как правило, некоторые случаи выводятся для стандартизации, эти стандартные случаи создаются как эталонные варианты, и мы можем спроектировать элемент конструкции, просто изменив условия нагрузки и размеры пролета. Некоторые из них
Некоторые из них
С.НО. | Стандартные чехлы | Максимальный момент изгиба | |
1. | , если просто поддерживаемый блок, несущий нагрузку в центральной точке As W W W. Span Span . WL/4 | ||
2. | Если свободно опертая балка несет равномерно распределенную нагрузку W (Н/м) с пролетом L. | WL/4xL/2 | |
3. | If a simply supported beam carrying a uniformly distributed load as W (KN) with span L. | WL/8 | |
4. | Если внецентренная точечная нагрузка на балку на расстоянии «а» от левой опоры и расстоянии «b» от правой опоры, когда общая длина пролета составляет L. | Если свободно опертая балка с пролетом L несет двухточечную нагрузку на расстоянии L/3 от обеих опор. | WL/3 |
6. | Если свободно опертая балка воспринимает момент M на расстоянии «a» от левой опоры или на расстоянии «b» от правой опоры с пролет L стержня | Положительный максимальный момент = +Mb/L Отрицательный максимальный момент = -Mb/L | |
7. | . Проще говоря, пучка переносит U.V.L при нуле на левой поддержке и W на правой поддержке со SPAN L. | WL/6XL/2 | |
8. | |||
8. | |||
В центре = WL/8 На опоре = WL/8 на пролете L. | в центре = WL/12xl/2 AT Support = WL/6xl/2 | ||
10. | AISTER, который несет U.V. опора = WL/15xL/2 At W опора нагрузки = WL/10xL/2 | ||
11. | Консольная балка, несущая точечную нагрузку на свободном конце с пролетом L. |
Некоторые важные определения
- В точке на балке, где поперечная сила меняет знак, эта точка называется положением максимального изгибающего момента.
- В точке изменения изгибающего момента известна точка обратного изгиба.
- В пролете, где значение поперечной силы полностью равно нулю, а постоянный изгибающий момент называется чистым изгибающим пролетом.
Часто задаваемые вопросы по изгибающему моменту
Что вызывает эффект изгибающего момента в элементах конструкции?
Изгибающий момент — это сопротивление вращению элемента, вызванное приложением нагрузки к конструкции на расстоянии от исходной точки. Приложенный момент зависит от интенсивности нагрузки, характера нагрузки и расстояния от точки отсчета, а тип опоры оказывает влияние на изгибающий момент.
Что такое положительный изгибающий момент и отрицательный изгибающий момент?
Изгибающий момент классифицируется по двум параметрам: положительный и отрицательный.
 Когда все нагрузки отклоняют конструкцию вниз, это называется положительным изгибающим моментом или моментом провисания. Когда все нагрузки отклоняют конструкцию вверх, это называется отрицательным изгибающим моментом или изгибающим моментом.
Когда все нагрузки отклоняют конструкцию вниз, это называется положительным изгибающим моментом или моментом провисания. Когда все нагрузки отклоняют конструкцию вверх, это называется отрицательным изгибающим моментом или изгибающим моментом.Как поперечная сила связана с изгибающим моментом?
Сила сдвига — это результирующая сила, действующая на опору из-за всей приложенной силы. Сила сдвига может быть обозначена как V. Но изгибающий момент является производной от силы сдвига, как в терминах M. Другими словами, изгибающий момент равен dv/dx.
Что такое контрафлексура?
При приложении нагрузки по всему пролету неподвижной балки изгибающий момент меняет знак с положительного на отрицательный или с отрицательного на положительный. В той точке, где изменяется изгибающий момент, знак называется точкой обратного изгиба.
Как модуль упругости влияет на изгибающий момент?
Мы знаем, что изгибающий момент прямо пропорционален модулю упругости в уравнении изгибающего момента (M/I = f/y = E/R).
 Когда материал имеет большой прогиб из-за высокого модуля упругости, изгибающий момент также велик для этого материала. Следовательно, можно сказать, что изгибающий момент зависит от модуля упругости.
Когда материал имеет большой прогиб из-за высокого модуля упругости, изгибающий момент также велик для этого материала. Следовательно, можно сказать, что изгибающий момент зависит от модуля упругости.
ESE & GATE CE
Civil Engg.GATEGATE CEESE CEESEBARC CEAFCAT CE
Избранные статьи
Следите за последними обновлениями
Наши приложения
- BYJU’S Exam Prep: приложение для подготовки к экзамену 900 Ltd.Windsor IT Park, Tower — A, 2nd Floor,
- 1. Положительная поперечная сила:
- Результирующая сила, перпендикулярная оси сечения балки с правой стороны находится в направлении вниз, а левая сторона секции — в направлении вверх.
- 2. Отрицательная поперечная сила:
- Результирующая сила, перпендикулярная оси балочного элемента на правой стороне секции, которая направлена вниз, а левая сторона секции направлена вверх. .
- 1. Изгиб BM :
- Тенденция BM в сечении выше центральной линии, когда балка изгибается.
 Знак считается отрицательным. В результате нижняя грань балки сжимается, а верхняя – растягивается.
Знак считается отрицательным. В результате нижняя грань балки сжимается, а верхняя – растягивается. - 2. Провисание BM :
- Тенденция BM в сечении, когда балка изгибается так, чтобы образовалась вогнутость над осевой линией. Симптом считается положительным. В результате нижняя грань балки растягивается, а верхняя сжимается.
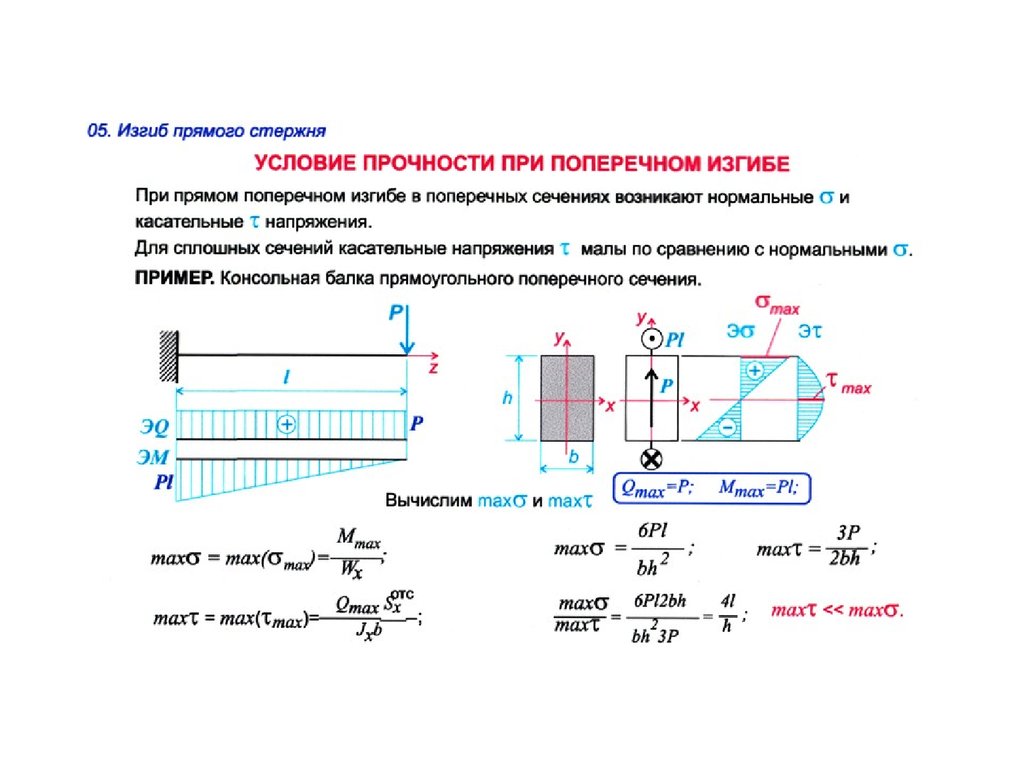
- Рассчитайте поперечную силу и изгибающий момент для балки, подвергаемой сосредоточенной нагрузке, затем начертите диаграмму поперечной силы (SFD) и диаграмму изгибающего момента (BMD).
Sector 125, Noida,
Uttar Pradesh 201303
Схема поперечной силы и изгибающего момента и примеры
Маянк Панчал Гражданское строительство
Сила сдвига (SF) Алгебраическая сумма неуравновешенных вертикальных сил с левой или правой стороны сечения называется силой сдвига. Сила, приложенная к единице площади элемента.
Сила, приложенная к единице площади элемента.
Шариковая сила – это сила в балке, действующая перпендикулярно ее продольной оси.
Изгибающий момент (BM)Алгебраическая сумма моментов с левой или правой стороны сечения называется изгибающим моментом.
Единица Н·м и кН·м
Условные обозначения для сдвигаРазница между силой сдвига и изгибающим моментом
| Диаграмма сдвига | Диаграмма момента |
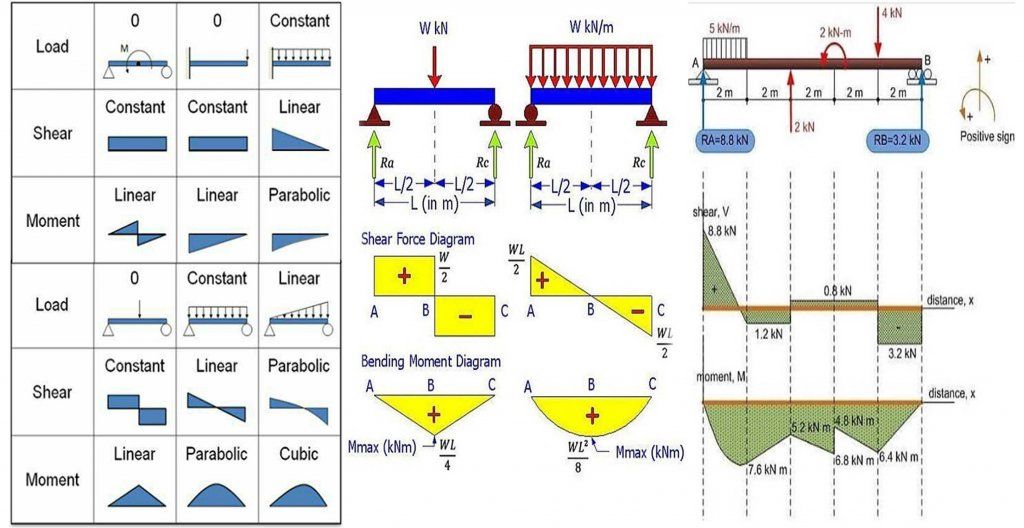
1. Диаграмма моментов представляет собой прямую наклонную линию для расстояний вдоль балки без приложенной нагрузки. 2. Udl приводит к параболической кривой на диаграмме моментов. 3. Максимальные/минимальные значения момента возникают там, где линия сдвига пересекает ноль. 4. Момент в любой точке балки равен площади под диаграммой сдвига до этой точки: M = V dx |
SFD и BMD
Из обсуждений видно, что на сечении нагруженной балки можно визуализировать две внутренние силы, а именно изгибающий момент и поперечную сила.
Также следует понимать, что величина изгибающего момента и поперечной силы различна для различных поперечных сечений балки. Диаграмма, изображающая изменение изгибающего момента и поперечной силы на балке, называется диаграммой изгибающего момента [BMD] и диаграммой поперечной силы [SFD].
Variation of shear force and bending moment diagrams
| Point load | UDL | UVL | |
| Shear force | Constant | Linear | Parabolic |
| Bending Moment | Linear | Параболический | Кубический |
Читайте также: Что такое проектирование конструкций, Какова область применения проектирования конструкций?
Примеры диаграмм поперечной силы и изгибающего момента: В случае простого изгиба, если изгибающий момент применяется к определенному поперечному сечению, возникающие напряжения называются изгибающим или изгибающим напряжением. Он изменяется линейно от нейтральной оси по поперечному сечению балки.
В случае простого изгиба, если изгибающий момент применяется к определенному поперечному сечению, возникающие напряжения называются изгибающим или изгибающим напряжением. Он изменяется линейно от нейтральной оси по поперечному сечению балки.

 WL
WL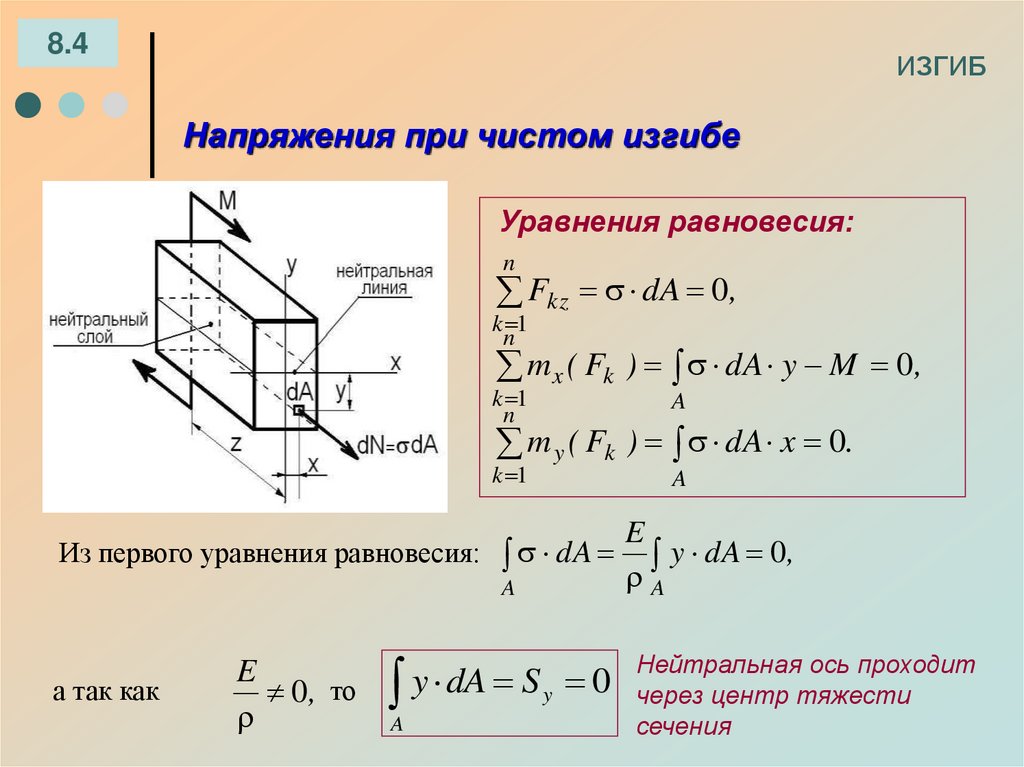 Наклон линии равен величине сдвига
Наклон линии равен величине сдвига