Балка 35К1 — вес, характеристики, размеры » Металлобазы.ру

Выбор металлопрокатаАрматураБалка двутавроваяКатанкаКвадратКругЛентаЛистПолосаПроволокаСеткаТруба профильнаяТруба круглаяТруба чугуннаяУголокШвеллерШестигранникШпунтТипРазмер

По всей РоссииСанкт-Петербург

Двутавровая балка 35К входит в серию колонных двутавров, горячекатаной группы.

• Стандарт: ГОСТ Р 57837;
• Вес погонного метра: 109,10 кг;
• Площадь поперечного сечения (F_n): 139,03 cm²;
• Ближайшие по параметрам колонные двутавры: 35К1,5, 35К2, 35К3, 35К4, 35К5, 35К6, 35К7, 35К8.

Размеры профиля

Участок профиля	Значение
Высота двутавра (h):	342,0 mm
Ширина полки (b):	348,0 mm
Толщина стенки (s ):	10,0 mm
Толщина полки (t):	15,0 mm
Высота стенки двутавра (hw):	312,0 mm
Свес полки (bw):	169,00 mm
Радиус сопряжения (r):	20,0 mm
Величины и значения в осях
Величины профиля в оси X	Значение
Момент инерции (Ix):	31 247,91 cm4
Момент сопротивления (Wx):	1 827,40 cm3
Статический момент полусечения (Sx):	1 001,17 cm3
Радиус инерции (ix):	149,92 mm
Величины профиля в оси Y	Значение
Момент инерции (Iy):	10 542,21 cm4
Момент сопротивления (Wy):	605,87 cm3
Статический момент полусечения (Sy):	459,67 cm3
Радиус инерции (iy):	87,08 mm

Название серии: Колонные двутавры. Принадлежность профиля к колонной серии отражается в номере двутавра наличием буквы К.

Двутавровые профили серии К (по ГОСТ Р 57837) состоят из 89-ти типоразмеров, разделенных на 6 размерных рядов. Двутавровая балка 35К является сорок пятым типоразмером из 89-ти в серии К (по ГОСТ Р 57837), и первым в своём размерном ряду.

Кроме двутавров серии К, в государственном стандарте качества ГОСТ Р 57837 присутствуют следующие серии:

• Свайные двутавры — серия С;
• Балочные нормальные двутавры — серия Б;
• Балочные широкополочные двутавры — серия Ш;
• Дополнительные балочные двутавры — серия ДБ;
• Дополнительные колонные двутавры — серия ДК.

---

Указанные данные двутавра 35К1 соответствуют регламентирующему стандарту качества ГОСТ Р 57837 Двутавры стальные горячекатаные с параллельными гранями полок.

Геометрические характеристики плоского поперечного сечения 3 элемента (двутавр, полоса, уголок) 025

Рис. 1

Дано схему поперечного сечения, составленную из трех элементов (рис. 1). Определить геометрические характеристики составного сечения. Площадь, центр тяжести, положение главных осей, главные моменты инерции, главные радиусы инерции, главные моменты сопротивления и построить эллипс инерции. План выполнения задачи: 1) Геометрические характеристики элементов сечения. 2) Положение центра тяжести сечения. 3) Моменты инерции относительно центральных осей. 4) Положение главных осей. 5) Определение главных моментов инерции. 6) Главные радиусы инерции. 7) Определение главных моментов сопротивления.

1) Выписываем из таблицы сортамента (ГОСТ 8239-72 и ГОСТ 8509-86) необходимые геометрические характеристики для двутавра, уголка и вычисляем по формулам прямоугольника:

 

а) Двутавр №27

см 2, см 4, см 4, см, см.

 

б) Полоса (прямоугольник) 260Х12

 

см 2, см 4, см 4,

 

в) Уголок 80Х6

см 2, см 4, см 4, см 4, см, см.

 

2) Определяем положение центра тяжести сечения относительно начальных осей (осей полосы)

На отдельном листе бумаги в масштабе чертим схему поперечного сечения (рис. 2) и указываем положение центральных осей каждого элемента. Выполняем привязку (указываем расстояния) центров тяжести каждого элемента относительно начальных осей

Координаты центров тяжести элементов в осях

см,

см,

см,

см.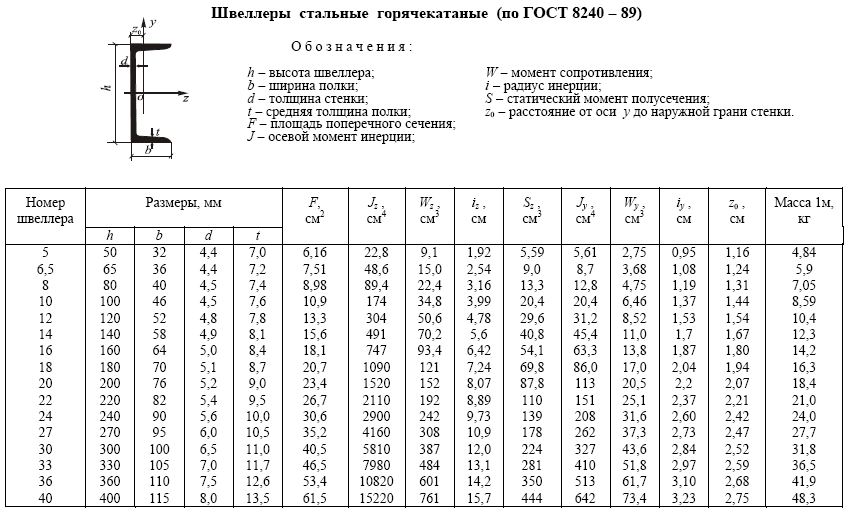

Рис. 2

Площадь поперечного сечения:

см ²,

Координаты центра тяжести сечения:

см,

см.

Откладываем на рисунке координаты и с учетом знаков, обозначаем положение центра тяжести (точка С) и проводим центральные оси

Контролируем достоверность определения положения центра тяжести сложного сечения. Для этого вычисляем координаты центров тяжести элементов сечения в координатных осях и (расстояния между собственными центральными осями отдельных элементов и центральными осями сечения):

см, см, см.

см, см, см.

и статические моменты площади сечения относительно центральных осей:

см ³,

погрешность:

см

3,

погрешность:

3) На основании формул параллельного перехода вычисляем моменты инерции сечения относительно центральных осей и

— осевые

см ⁴,

см ⁴,

— центробежный

см ⁴.

4) Определяем положение главных центральных осей инерции:

Отсюда

На рисунке откладываем положительный угол против часовой стрелки и чертим главные центральные оси инерции (рис. 3).

5) Для определения величин главных центральных моментов инерции используем три вида формул.

а)

см ⁴,

см ⁴,

Для проверки правильности нахождения главных моментов инерции, определяем центробежный момент инерции относительно главных осей:

,

погрешность:

б)

см ⁴,

см ⁴,

в)

.

Поскольку , то

см ⁴,

см ⁴.

Проверяем условие инвариантности осевых моментов инерции:

см ⁴,

см ⁴.

6) Вычисляем главные радиусы инерции:

см,

см,

и строим эллипс инерции (рис. 3). Определяем графически радиусы инерции относительно осей

см, см.

Вычисляем моменты инерции относительно этих осей:

см ⁴,

см ⁴,

и сравниваем с ранее вычисленными значениями:

см ⁴, см ⁴.

7) Определяем главные моменты сопротивления и

Наиболее удаленной точкой от оси является точка а от оси — точка Измеряя на рисунке расстояния до этих точек от соответствующих главных осей, находим: см, см.

Проверяем по формулам:

см,

см.

Главные моменты сопротивления:

см ³,

см ³.

Рис. 3

Понравилась статья! Поддержи проект! Ставь ЛАЙК!

Момент инерции двутавровой балки

Момент инерции объекта является выражением тенденции этого объекта сопротивляться угловому ускорению, т. е. вращению. Момент инерции широко используется в технике как конструкционный параметр. При проектировании конструкции инженер будет использовать момент инерции для оптимизации конструкции по отношению к ожидаемым нагрузкам.

Двутавровая балка является обычным элементом конструкции, и расчет ее момента инерции можно разбить на три конкретных этапа, как показано ниже.

Момент инерции двутавровой балки

Первым шагом для расчета момента инерции двутавровой балки является разделение балки на более мелкие части. В этом случае балка делится на три секции, как показано на рисунке ниже:

Момент инерции балки можно рассчитать, определив отдельные моменты инерции трех сегментов.

Найти нейтральную ось

Момент инерции будет относительно нейтральной оси, проходящей через центр масс. На приведенном выше рисунке отмечена нейтральная ось, а положение центра масс можно рассчитать следующим образом:

, где Y _i — центр масс отдельного прямоугольника, в единицах СИ, равных м, а A _i — площадь отдельного прямоугольника, в единицах СИ, равных м ² . В случае двутавровой балки i составляет от 1 до 3.

Расчет момента инерции

Теорема о параллельных осях используется для определения полного момента инерции двутавровой балки следующим образом:

где момент инерции отдельного прямоугольника в единицах СИ м ⁴ и d _i — расстояние от центра тяжести отдельного прямоугольника до центра тяжести двутавровой балки в единицах СИ, равных м.

Отдельные моменты инерции рассчитываются для прямоугольников по следующей формуле:

где b — основание прямоугольника, а h — высота прямоугольника, оба значения выражены в единицах СИ, равных м.

Момент инерции относительно оси Y

Как правило, двутавровые балки проектируются симметричными относительно оси Y. То есть момент инерции двутавровой балки относительно оси Y равен центру балки.

Пример момента инерции двутавровой балки

Следующая двутавровая балка используется в качестве примера для расчета момента инерции:

Сегмент балки

Вышеупомянутая балка разделена на три секции: зеленую, желтую и синюю. , которые обозначены разделами 1, 2 и 3 соответственно.

Найти нейтральную ось

Нейтральная ось проходит через центр масс, который рассчитывается следующим образом:

Расчет моментов инерции

Отдельные моменты инерции трех сегментов рассчитываются с использованием формулы момента инерции для прямоугольника:

Применение теоремы о параллельной оси

Для каждого сегмента применяется теорема о параллельной оси:

Сумма отдельных моментов инерции

Суммирование отдельных моментов инерции трех секций:

Применение момента инерции двутавровых балок

Двутавровые балки являются общими элементами инженерных конструкций. Они используются не только как компоненты инженерных проектов, но также могут использоваться в качестве элементов моделирования для предварительного проектирования таких вещей, как крылья самолета. Хотя большинство двутавровых балок имеют симметричную компоновку, балка может быть асимметричной относительно оси x, как в предыдущем примере. Для двутавровой балки, которая является симметричной, момент инерции относительно оси x будет расположен в физическом центре балки, аналогично моменту инерции относительно оси y, как обсуждалось ранее.

Момент инерции площади — типичные поперечные сечения I

Момент инерции площади или Момент инерции площади — , также известный как Второй момент площади — I , является свойством формы, которое используется прогнозировать прогиб, изгиб и напряжение в балках.

Момент инерции площади — Британские единицы

• дюймов ⁴

Момент инерции площади — Метрические единицы

• мм ⁴
• см ⁴
• м ^{4 9 0026}

Перевод единиц измерения

• 1 см ⁴ = 10 ^-8 м ⁴ = 10 ⁴ мм ⁴
• 1 дюйм ⁴ = 4,16×10 ⁵ мм ⁴ = 41,6 см ⁴

Единицы инерции

9240 см ⁴ можно преобразовать в мм ⁴ путем умножения на 10 ⁴

90 002 (9240 см ⁴ ) 10 ⁴ = 9,24 10 ⁷ мм ⁴

Момент инерции площади (момент инерции для площади или второй момент площади)

для изгиба вокруг оси x можно выразить как

I _х = ∫ у ² dA                        (1)

где

I _x = момент инерции площади относительно оси x ( м ⁴ , мм ⁴ , дюймы ⁴ )

y = расстояние по перпендикуляру от оси x до элемента dA (м, мм, дюймов )

дА = площадь элемента ( м ² , мм ² , дюймов ² )

Момент инерции при изгибе вокруг оси Y можно выразить как

I _y = ∫ x ² dA                      (2)

где

I _y = момент инерции площади относительно оси y ( м 9002 5 4 , мм ⁴ , дюймы ⁴ )

x = перпендикулярное расстояние от оси y до элемента dA (м, мм, дюймов ) 9 0092

Площадь Момент инерции для типичных поперечных сечений I

• Момент инерции площади для типичных сечений II

Сплошное квадратное сечение

Момент инерции площади для сплошного квадратного сечения можно рассчитать как

I _x  = a ⁴  / 12                     (2)

где

a = сторона (мм, м , дюйм. .)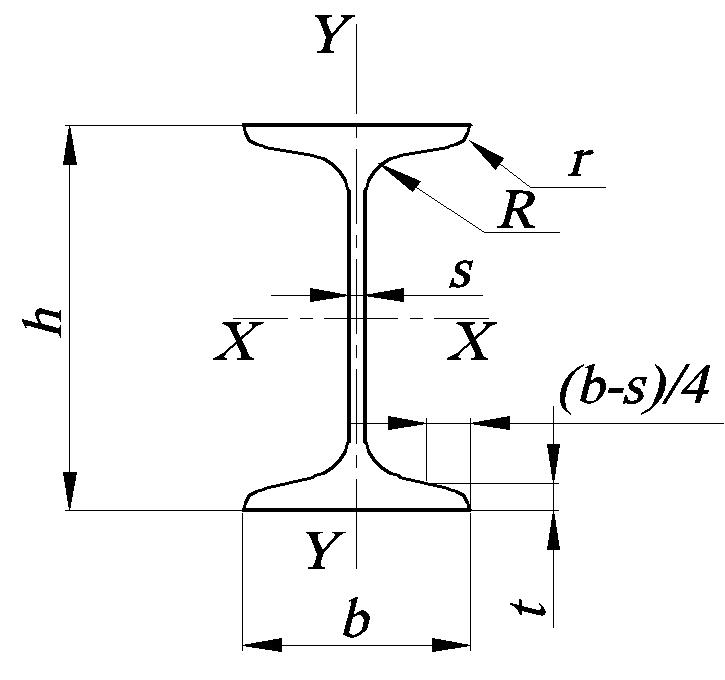

 

I _y  = a ⁴  / 12                       (2b)

Сплошное прямоугольное сечение

Момент инерции площади для прямоугольного сечения можно рассчитать как

9 0002 I _x = b h ³ / 12                        (3)

где

b = ширина

h = высота

 

I _y  = b ³ h / 12                           (3b)

Сплошное круглое сечение

Момент инерции площади для твердого цилиндрического сечения можно рассчитать как ⁴ / 64                        (4)

где

r = радиус

d = диаметр 9 0092

 

I _y  = π r ⁴  / 4

    = π d ⁴  / 64                             (4b)

Полое цилиндрическое сечение

Момент инерции площади для полого цилиндрического сечения можно рассчитать как

I _x = π (d _o ⁴ — d _i ⁴ ) / 64                            (5)

где

d _o = наружный диаметр цилиндра

d _i = внутренний диаметр цилиндра 5 4  — d _i ⁴ ) / 64                        (5b)

Квадратное сечение — диагональные моменты

Моменты инерции площади диагонали квадратного сечения можно рассчитать как

I _x = I _y = a ⁴ / 12                   (6)

Прямоугольное сечение – Моменты площади на любой линии, проходящей через центр тяжести

Прямоугольное сечение и площадь момента на линии, проходящей через центр тяжести, можно рассчитать как

I _x = (b h / 12) (h ² cos ² a + b ² sin ² a)                  (7)

Симметричная форма

Площадь Момент инерции для симметричного сечения может вычисляется как

I _x = (a h ³ / 12) + (b / 12) (H ³ — h ³ )                      (8)

I _у = (а ³ h / 12) + (b ³ / 12) (H — h)                      (8b)

Несимметричная форма

Площадь Момент инерции для сечения несимметричной формы можно рассчитать как

I _x = (1 / 3) (B y _b ³ — В ₁ h _b ³ + b y _t ³ — b1 h _t ³ )                              (9) 90 020

• Момент инерции площади для типичных сечений II

Момент инерции площади в зависимости от Полярный момент инерции против момента инерции

• «Момент инерции площади» — это свойство формы, которое используется для прогнозирования прогиба, изгиба и напряжения в балках.