Определение перемещений. Метод начальных параметров

Метод начальных параметров (или по универсальным формулам прогибов и углов поворота сечений)

где у₀и φ₀ – начальные параметры, то есть прогиб и угол поворота в начале координат, которые определяются из условий закрепления балки:

Порядок определения перемещений по универсальным формулам:

1. Определить все опорные реакции.
2. Поместить начало координат обязательно в крайнее сечение балки (левое или правое).
3. Ось у направить вверх, ось z — вдоль балки.
4. Найти начальные параметры из условий закрепления балки (возможные случаи показаны выше).
5. Зная начальные параметры у₀ и φ₀, по универсальным формулам определить интересующие нас перемещения.

При использовании универсальных формул необходимо выполнять следующие требования:

а) В универсальные формулы включать только те внешние силы, которые действуют между началом координат (т.0) и сечением, в котором определяются перемещения. Следует помнить, что опорные реакции – тоже внешние силы.

б) Каждая внешняя сила (М_i, F_i, q_i) вводится со знаком изгибающего момента, который эта сила вызывает в сечении, где определяется перемещение.

 Задача 

Найти прогиб конца консоли.

Решение

1. Задаемся направлениями опорной реакции А и реактивного момента в заделке М_А и составляем уравнения статики:

(1) ,

откуда А = q·2 + F = 10·2 + 20 = 40кН,

(2) ,

откуда  

2. Помещаем начало координат в заделку (т. 0).
3. Ось у направляем вверх, ось z – вдоль балки (вправо).
4. Формулируем условия закрепления балки при выбранном расположении начала координат:

при z = 0:  у_А = 0    (1)

φ_А= 0    (2).

Реализуем эти условия с помощью универсальных формул:

(1):  0=ЕIу₀,  откуда у₀=0,

(2):  0=ЕIφ₀,  откуда φ₀=0.

5. Учитывая найденные значения у₀ и φ₀, с помощью формулы прогибов найдём прогиб конца консоли:

при z = 4м

Знак «плюс» результата говорит о том, что прогиб конца консоли происходит в положительном направлении оси у, то есть вверх.

Для получения численного значения прогиба результат следует разделить на изгибную жёсткость балки ЕI, то есть

 

Метод начальных параметров решение и примеры задач по сопромату

Содержание:

1. Пример решения задачи 3.1.
2. Пример решения задачи 3.2.

Метод непосредственного интегрирования, рассмотренный ранее, удобен при определении углов поворота и прогибов сечений балки, когда число участков балки незначительно (один-два). При интегрировании приближенного дифференциального уравнения изогнутой оси балки каждый участок дает две постоянных интегрирования т. е. при числе участков балки имеем постоянных интегрирования.

При числе участков более двух удобнее пользоваться универсальным уравнением упругой линии, вывод которого приводится ниже.

Число постоянных интегрирования можно свести к двум при любом количестве участков балки, если при составлении и интегрировании дифференциальных уравнений соблюдать следующие правила.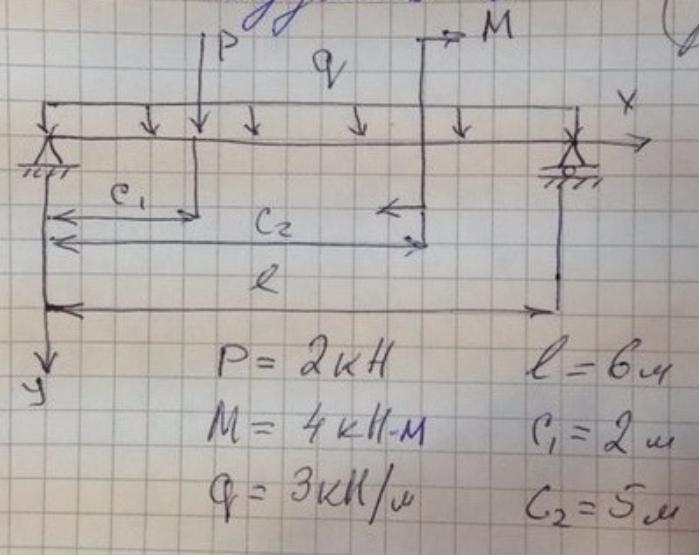

• Начало координат для рассматриваемой балки выбирается в крайних левой или правой точках и считается постоянным для всех участков балки.

• Уравнения для изгибающих моментов составляются при рассмотрении всех участков балки, в зависимости от того, где выбрано начало координат: слева или справа от сечения.

• Если в каком-либо сечении балки действует сосредоточенный момент то он вводится в выражение изгибающего момента с сомножителем равным единице ( — расстояние от начала координат до точки приложения сосредоточенного момента).

• При действии на каком-либо участке балки распределенной нагрузки ее необходимо продолжить до конца балки и ввести точно такую же компенсирующую нагрузку, используя аксиому статики о присоединении или отбрасывании взаимно уравновешенных сил.

• Интегрирование дифференциальных уравнений производить без раскрытия скобок.

Используя эти правила, составим приближенное дифференциальное уравнение упругой линии пятого участка балки, представленной на рис. 3.1, проинтегрируем его дважды. Для удобства рассуждений все нагрузки, приложенные к балке, приняты такими, что создают положительные изгибающие моменты. Изгибающий момент для пятого участка равен:

Тогда дифференциальное уравнение примет вид

где момент, создаваемый компенсирующей нагрузкой момент создаваемый треугольной нагрузкой Интегрируем уравнение (3.1) дважды:

Момент от треугольной нагрузки находится следующим образом

Интегрируем уравнение (3.1) дважды

Возможно вам будут полезны данные страницы:

Расчет фермы: примеры с решением

Олег македонский решение задач по сопромату

Расчет рамы по сопромату примеры и решения

Задачи на сжатие и растяжение по сопромату примеры и решения

Если внимательно рассмотреть рис. 3.1, то можно убедиться, что для четвертого участка балки дифференциальное уравнение упругой линии будет таким же, как и для пятого участка, только оно не будет содержать моменты, действующие на пятом участке:

Интегрируем это уравнение дважды:

Имея уравнения (а), (б), (в) и (г), можно доказать, что при соблюдении правил составления дифференциальных уравнений упругой линии и их интегрировании постоянные интегрирования для всех участков будут одинаковыми.

Рассматривая уравнения (а) и (в) при и считая участки плавно сопрягающимися, видим, что К равенству можно прийти, приравняв правые части уравнений (а) и (в). Аналогично, рассмотрев уравнения (б) и (г), получим

Переходя последовательно от четвертого участка к третьему, а затем ко второму и первому, и рассматривая смежные участки при равенстве можно убедиться, что постоянные интегрирования т. е. они равны друг другу.

Геометрический смысл постоянных интегрирования можно установить при рассмотрении уравнений углов поворота и прогибов для первого участка балки. Для первого участка балки имеем

Здесь — угол поворота сечения и его прогиб в начале координат соответственно. Их принято называть начальными параметрами. Тогда уравнение прогибов для пятого участка примет вид

Уравнение (3.3) принято называть универсальным уравнением упругой линии, так как оно может применяться при любых расчетных схемах балок.

В обобщенном виде универсальное уравнение упругой линии можно представить следующим образом: где — статические начальные параметры (момент и реакция в заделке).

При необходимости определения углов поворота сечений методом начальных параметров уравнение (3.4) нужно продифференцировать, тогда получим Прежде чем пользоваться уравнениями (3.4) и (3.5), т. е. находить перемещения методом начальных параметров, необходимо найти начальные параметры

Статические начальные параметры находятся обычным способом уравнениями статики. Начальные же параметры определяются по граничным условиям.

1. Если в начале координат балка имеет заделку (рис. 3.2), то и равны нулю, так как в заделке нет ни прогиба, ни угла поворота сечения. Балка содержит статические начальные параметры в виде опорного момента в заделке и реакции

2. Балка опирается на две опоры (рис. 3.3), при этом слева от опоры нет консоли. Для рассматриваемой балки граничными условиями будут значения — точки, прогибы в которых заведомо равны нулю. При т. е. первый начальный параметр равен нулю. При имеем

Из этого уравнения найдем второй начальный параметр. 1. Если двухопорная балка имеет на левой и на правой опорах консоли (рис. 3.4), то по граничным условиям составляют два уравнения упругой линии для рассматриваемой балки. Решая эту систему, находят начальные параметры. При

Решая совместно уравнения (ж) и (з), находят которые входят в уравнение прогибов.

В случае действия на каком-либо участке балки треугольной нагрузки, так же как и равномерно распределенной нагрузки, она должна быть продолжена до конца балки, при этом вводится ее компенсирующая нагрузка (рис.

3.5, а, б) или только компенсирующая нагрузка (рис. 3.5, в, г).

Пример решения задачи 3.1.

На консольную балку (рис. 3.6) длиной действует сосредоточенная сила Определить методом начальных параметров угол поворота и прогиб в точке приложения силы

Решение

Начало координат принимаем в точке . Ось направляем вправо, ось — вверх. Поскольку в начале координат имеем заделку, начальные параметры равны нулю, т.е. сечение балки в точке не имеет ни прогиба, ни угла поворота. Но в точке будут действовать реакция и опорный момент, т.е. балка содержит статические начальные параметры. Находим их:

Рассекаем балку сечением и составляем уравнение упругой линии, используя метод начальных параметров. Слева от сечения действуют только поэтому уравнение имеет вид Подставляя значения получаем

Прогиб в точке найдется при

Угол поворота сечения в точке найдем из уравнения предварительно продифференцировав его:

Пример решения задачи 3.

2.

Достроить эпюры прогибов и углов поворота для двутавровой балки № 30, если

Решение

Определим опорные реакции

Выбрав начало координат в крайней левой точке балки, составляем уравнение изгибающих моментов для наиболее удаленного от начала координат участка балки:

Подставляем в дифференциальное уравнение упругой линии:

Полученное уравнение дважды проинтегрируем:

В уравнения (а) и (б) вошли начальные параметры Найдем их, используя граничные условия рассматриваемой балки.

Если задать то мы попадем в левую опору Как известно, в опоре нет прогиба, поэтому уравнение (б) можно записать в следующем виде:

Вторым граничным условием для этой балки будет значение В этом случае уравнение (б) запишется как

Решая совместно уравнения (в) и (г), находим начальные параметры и

Уравнения для определения перемещений (а) и (б) будут следующими:

Пользуясь этими уравнениями, построим по участкам эпюру углов поворотов сечений и эпюру прогибов балки:

Для участка 1

При

Для участка 2

Для участка 1 имеем

Эпюры представлены на рис 3. 7 г,д соответственно

Метод вариации параметров

Эта страница посвящена дифференциальным уравнениям второго порядка такого типа:

d ² y dx ² + P(x) dy dx 9001 2 + Q(х)у = f(x)

, где P(x), Q(x) и f(x) — функции от x.

Сначала прочтите Введение в дифференциальные уравнения второго порядка, там показано, как решить более простой «однородный» случай, когда f(x)=0

Два метода

Существует два основных метода решения уравнений, подобных

.

d ² y dx ² + P(x) dy dx + Q(x)y = f (х)

Неопределенные коэффициенты, которые работают только тогда, когда f(x) является полиномом, экспонентой, синусом, косинусом или их линейной комбинацией.

Изменение параметров (которое мы узнаем здесь), которое работает с широким спектром функций, но немного неудобно в использовании.

Изменение параметров

Для простоты рассмотрим только корпус:

d ² y dx ² + p dy dx + qy = f(x)

где p и q — константы, а f(x) — ненулевая функция от x.

Можно найти полное решение такого уравнения комбинируя два типа раствора:

1. Общее решение однородное уравнение d ² y dx ² + p dy dx + qy = 0
2. Частные растворы неоднородное уравнение d ² y dx ² + p dy dx + qy = ф(х)

Обратите внимание, что f(x) может быть отдельной функцией или суммой двух или более функции.

Как только мы нашли общее решение и все частные решения, то окончательное полное решение находится путем сложения всех решения вместе.

Этот метод основан на интеграции.

Проблема с этим методом заключается в том, что, хотя он может дать решение, в некоторых случаях решение приходится оставлять в виде интеграла.

Начните с общего решения

В разделе «Введение в дифференциальные уравнения второго порядка» мы научимся находить общее решение.

В основном мы берем уравнение

d ² y dx ² + p dy дх + ку = 0

и привести его к «характеристическому уравнению»:

г ² + пр + кв = 0

Квадратное уравнение, имеющее три возможных типа решения в зависимости от дискриминанта p ² − 4q . Когда p ² − 4q равно

положительный получаем два действительных корня, и решение

y = Ae ^{r ₁ x} + Be ^{r ₂ x}

ноль получаем один реальный корень, а решение

у = Ae ^rx + Bxe ^rx

минус получаем два комплексных корня r ₁ = v + wi и r ₂ = v − wi , и решение

y = e ^vx ( Ccos(wx) + iDsin(wx))

Фундаментальные решения уравнения

Во всех трех вышеприведенных случаях «у» состоит из двух частей:

• y = Ae ^{r ₁ x} + Be ^{r ₂ x} изготовлен из y ₁ = Ae ^{r ₁ x} и y ₂ = Be ^{r ₂ x}
• y = Ae ^rx + Bxe ^rx состоит из y ₁ = Ae ^rx и y ₂ = Bxe ^rx
• y = e ^vx ( Ccos(wx) + iDsin(wx)) состоит из y ₁ = e ^vx Ccos(wx) и y ₂ = e ^vx iDsin(wx)

y ₁ и y ₂ известны как фундаментальные решения уравнения

И y ₁ и y ₂ считаются линейно равными независимым , потому что ни одна из функций не является постоянным кратным другой.

Вронскиан

Когда у ₁ и у ₂ два основных решения однородного уравнения

d ² y dx ² + p dy dx + qy = 0

, то вронскиан W(y ₁ , y ₂ ) является определителем матрицы

   

Так

Вт(у ₁ , у ₂ ) = у ₁ у ₂ ‘ − у ₂ у ₁ ‘

Вронскиан назван в честь польского математика и философ Юзеф Хене-Вронский (1776−1853).

Поскольку y ₁ и y ₂ линейно независимы, значение вронскиана не может быть равно нулю.

Особое решение

Используя вронскиан, теперь мы можем найти частное решение дифференциального уравнения

d ² y dx ² + p dy dx + qy = f(x)

по формуле:

y _p (x) = −y ₁ (x)∫ y ₂ (x)f(x) W(y ₁ , y _{2 9015 3 )} дх + y ₂ (x)∫ y ₁ (x)f(x) W(y ₁ , y ₂ ) dx

Пример 1: решить

d ² y dx ² − 3 dy dx + 2y = e ^3x

1. Найдите общее решение d ² y dx ² − 3 dy dx + 2y = 0

Характеристическое уравнение: r ² − 3r + 2 = 0

Коэффициент: (r − 1)(r − 2) = 0

r = 1 или 2

Таким образом, общее решение дифференциального уравнения равно y = Ae ^x + Be ^2x

Таким образом, в этом случае фундаментальные решения и их производные составляют:

у ₁ (х) = е ^х

у ₁ ‘(х) = е ^х

у ₂ (х) = е ^2х

у ₂ ‘(х) = 2e ^2x

2. Найдите Вронскиан:

W(y ₁ , y ₂ ) = y ₁ y ₂ ‘ − y ₂ y ₁ ‘ = 2e ^3x − e ^3x = e ^3x

3. Найдите частное решение по формуле: 9004 4

у _р (х) = — у ₁ (x)∫ y ₂ (x)f(x) W(y ₁ , y ₂ ) dx + y ₂ (x)∫ y ₁ (x)f(x) W(y ₁ , y ₂ ) dx

4. Сначала решаем интегралы:

∫ y ₂ (x)f(x) W(y ₁ , y ₂ ) dx

= ∫ e ^2x e ^3x e ^3x dx

= ∫e ^2x dx

= 1 2e ^2x

Итак:

−y ₁ (x)∫ y 901 52 2 (х)f(х) Ш(у ₁ , у ₂ ) дх = -(e ^x )( 1 2e ^2x ) = − 1 2e ^3x

А также:

∫ y ₁ (x)f(x) W(y ₁ , у ₂ ) дх

= ∫ e ^x e ^3x e ^3x dx

= ∫e ^x dx

= e ^x

Итак:

y ₂ (x)∫ y 9015 2 1 (х)f(х) Ш(у ₁ , у ₂ ) дх = (e ^2x )(e ^x ) = e ^3x

Наконец:

y _p (x) = −y ₁ (х)∫ у ₂ (х )f(x) W(y ₁ , y ₂ ) dx + у ₂ (x)∫ y ₁ (x)f(x) W(y ₁ , y ₂ ) dx

= − 9 0005 1 2e ^3x + e ^3x

= 1 2e ^3x

и полное решение дифференциального уравнения d ² y dx ^{2 900 07} − 3 dy dx + 2y = e ^3x is

y = Ae ^x + Be ^2x + 1 2e ^3x

Это выглядит так (примеры значений A и B):

Пример 2.

Решите d ² y dx ² − y = 2x ² − x − 3 1. Найдите общее раствор d ² y dx ² — у = 0

Характеристическое уравнение: r ² − 1 = 0

Коэффициент: (r − 1)(r + 1) = 0

r = 1 или −1

Таким образом, общее решение дифференциального уравнения имеет вид у = Ае ^x +Be ^−x

Таким образом, в этом случае фундаментальные решения и их производные: ‘(х) = е ^x

y ₂ (x) = e ^−x

y ₂ ‘(x) = −e ^−x

2. Найдите вронскиан:

W(y ₁ , у ₂ ) = у ₁ у ₂ ‘ − у ₂ у ₁ ‘ = −e ^x e ^-x — e ^x e ^-x = -2

3. Найдите частное решение по формуле:

y _p (х) = -y ₁ (x)∫ y ₂ (x)f(x) W(y ₁ , y ₂ ) dx + y ₂ (x)∫ y ₁ (x)f(x) W(y ₁ , y ₂ ) dx

4. Решите интегралы:

Каждый интегралов можно получить с помощью интеграции по частям дважды:

∫ y ₂ (x)f(x) W(y ₁ , y ₂ ) dx

= ∫ e ^−x (2x ² −x−3) −2 dx

= − 1 2 ∫(2x ² −x−3)e ^−x dx

= − 1 2[ −(2x ^{2 9000 7 −x−3)e −x + ∫(4x−1)e −x dx ]}

= − 1 2[ −(2x ² −x−3)e ^−x − (4x − 1)e ^{−x 9000 7 + ∫4e −x дх ]}

= − 1 2[ −(2x ² −x−3)e ^−x − (4x − 1)e ^−x − 4e ^−x ]

9 0002 = и ^−x 2[ 2x ² − x − 3 + 4x −1 + 4 ]

= e ^−x 2[ 2x ² + 3x ]

Итак:

−y ₁ (x)∫ y ₂ (x)f(x) W(y ₁ , y ₂ ) dx = (−e ^x )[ e ^−x 2( 2x ² + 3x )] = − 1 2(2x ² + 3x)

А это:

∫ y 9015 2 1 (х)f(х) Вт(у ₁ , у ₂ ) дх

= ∫ e ^x (2x ² −x−3) −2 dx

= − 1 2 ∫(2x ² −x−3)e ^× dx

= − 1 2[ (2x ² − х-3)е ^х — ∫( 4x−1)e ^x dx ]

= — 1 2[ (2x ² -x-3)e ​​ ^x — (4x — 1)e ^x + ∫4e ^x dx ]

= — 1 2[ (2x ² -x-3)e ​​ ^x — (4x — 1)e ^x + 4e ^x ]

= −е ^х 2[ 2x ² — x — 3 — 4x + 1 + 4 ]

= — e ^x 2[ 2x ² — 5x + 2 ]
 

9 0002 Итак:

у ₂ ( х)∫ у ₁ (х)f(х) Вт(у ₁ , у ₂ ) дх = (е ^{— х} )[ — е ^х 2( 2x ² — 5x + 2 ) ] = — 1 2( 2x ² − 5x + 2 )  

Наконец:

y _p (x) = −y ₁ (x)∫ 90 005 г ₂ (х)ф(х) W(у ₁ , у ₂ ) дх + y ₂ (x)∫ y ₁ (x)f(x) W(y ₁ , y ₂ ) dx

= − 1 2( 2x ² + 3x ) − 1 2( 2x ² − 5x + 2 ) 

= − 1 2( 4x ² − 2x + 2 )

= −2x ² + x − 1

и полное решение дифференциального уравнения d ² y dx ² 9001 2 — у = 2х ² — х — 3 равно

y = Ae ^x + Be ^−x − 2x ² + x − 1

(Это тот же ответ, который мы получили в Примере 1 на странице Метод неопределенных коэффициентов. )

Пример 3: решить

d ² y dx ² − 6 dy dx + 9y = 1 9000 8 x 1. Найдите общее решение d ² y dx ² − 6 dy dx + 9y = 0

Уравнение характеристики: r ² − 6r + 9 = 0

Коэффициент: (r − 3)(r − 3) = 0

r = 3

Таким образом, общее решение дифференциального уравнения имеет вид y = Ae ^3x + Bxe ^3x

Таким образом, в этом случае фундаментальные решения и их производные таковы: 0006 3x

у ₂ (x) = xe ^3x

y ₂ ‘(x) = (3x + 1)e ^3x

2. Найдите вронскиан:

W(y ₁ , y ₂ ) = y ₁ y ₂ ‘ − y ₂ y ₁ ‘ = (3x + 1)e ^3x e ^3x — 3xe ^3x e ^3x = e ^6x

0152 1 (х)∫ у ₂ (x)f(x) W(y ₁ , y ₂ ) дх + y ₂ (x)∫ y ₁ (x)f(x) W(y ₁ , y ₂ ) dx

4. Решите интегралы:

∫ y ₂ (x)f(x) W(y ₁ , y ₂ ) dx

= ∫ (xe ^3x )x ⁻¹ e ^6x dx (Примечание: 1 x = x 900 06 −1 )

= ∫e ^−3x dx

= − 1 3e ^−3x

Итак:

−y ₁ (x)∫ y ₂ (x)f(x) W( у ₁ , у ₂ ) дх = -(e ^3x )(- 1 3e ^-3x ) = 1 3

А это:

∫ y ₁ (x)f(x) W(y ₁ , у ₂ ) дх

= ∫ e ^3x x ⁻¹ e ^6x дх

= ∫e ^-3x x ^-1 dx

Это нельзя проинтегрировать, так что это пример, где ответ оставить в виде интеграла.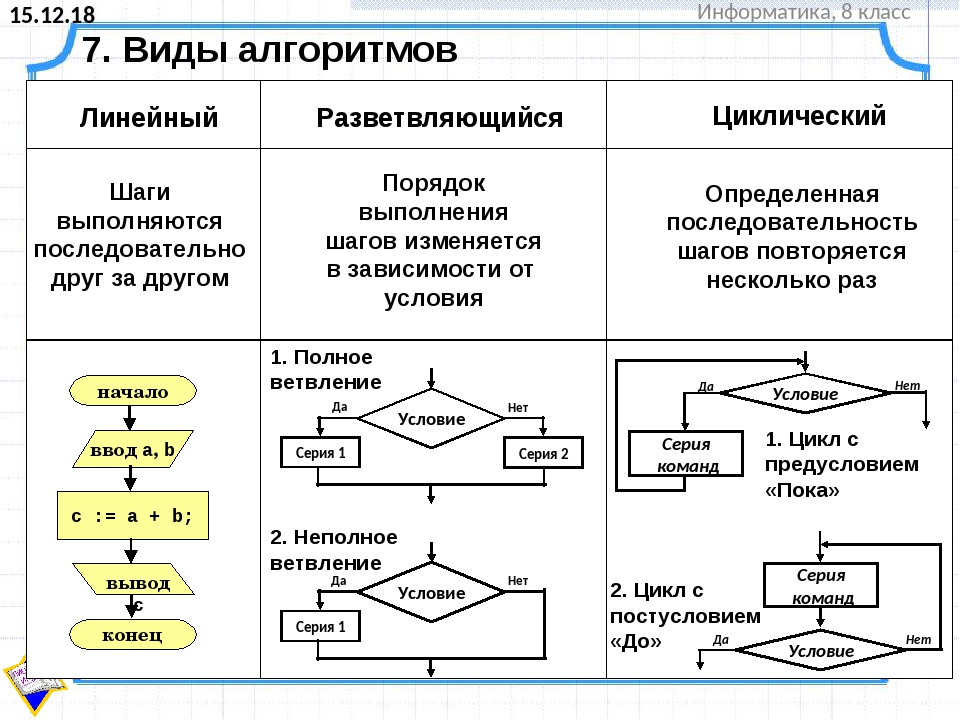

Итак:

y ₂ (x)∫ y ₁ (x)f(x) W(y ₁ , y _{2 901 53 )} дх = ( xe ^3x )( ∫e ^−3x x ⁻¹ dx ) = xe ^3x ∫e ^−3x x ⁻¹ dx

Наконец:

y _p (x) = −y ₁ (x)∫ y ₂ (x)f(x) W(y ₁ , y ₂ ) дх + y ₂ (x)∫ y ₁ (x)f(x) W(y ₁ , y ₂ ) dx

= 1 3 + xe ^3x ∫ e ^−3x x ⁻¹ dx

Таким образом, полное решение дифференциального уравнения день dx + 9y = 1 x is

y = Ae ^3x + Bxe ^3x + 1 3 + xe ^3x ∫e ^−3x x ⁻¹ dx

Пример 4 (более сложный пример): решить

d ² y dx ² − 6 dy dx + 13y = 195cos(4x)

В этом примере используется следующая тригонометрическая тождества

sin ² (θ) + cos ² (θ) = 1

sin⁡(θ ± φ) = sin(θ)cos(φ) ± cos(θ)sin(φ)

cos⁡(θ ± φ) = cos(θ)cos (φ) sin(θ)sin(φ)

sin(θ)cos(φ) = 1 2 [sin⁡(θ + φ) + sin⁡(θ − φ)]
cos(θ)cos(φ) = 1 2 [cos⁡(θ − φ) + cos⁡(θ + φ)]

1. Найдите общее решение задачи дх + 13у = 0

Уравнение характеристики: r ² − 6r + 13 = 0

Используйте квадратное уравнение формула

х = −b ± √(b ² − 4ac) 2a

с a = 1, b = −6 и c = 13

Итак:

r = −(−6) ± √[(−6) ² − 4(1 ) (13)]. 09 2

= 6 ± 4i 2

= 3 ± 2i

Итак, α = 3 и β = 2

⇒ y = e ^3x [Acos(2x) + iBsin(2x)]

Таким образом, в этом случае мы имеем:

y ₁ (x) = e ^3x cos(2x)

y ₁ ‘(x) = e 9000 6 3x [3cos( 2x) − 2sin(2x)]

y ₂ (x) = e ^3x sin(2x)

y ₂ ‘(x) = e ^3x [3sin( 2x) + 2cos(2x )]

2. Найдите вронскиан:

W(y ₁ , y ₂ ) = y ₁ y ₂ ‘ − y ₂ y ₁ ‘

= e ^6x cos(2x)[3sin(2x) + 2cos(2x)] — e ^6x sin(2x)[ 3cos(2x) − 2sin(2x)]

= e ^6x [3cos(2x)sin(2x) +2cos ² (2x) − 3sin(2x)cos(2x) + 2sin ² (2x)]

9 0002 =2e ^6x

3. Найдите частное решение по формуле:

y _p (x) = −y ₁ (x)∫ y 9 0152 2 (х)ф(х ) Вт(у ₁ , у ₂ ) дх + y ₂ (x)∫ y ₁ (x)f(x) W(y ₁ , y ₂ ) dx

4. Решите интегралы:

∫ y ₂ (x)f(x) W(y ₁ , y ₂ ) dx

= ∫ e ^3x sin⁡(2x)[195cos⁡(4x)] 2e ^6x dx

= 195 2 ∫e ^−3x sin(2x)cos(4x)dx

= 195 4 ∫e ^−3x [sin(6x) − sin(2x)]dx    …  (1)

В этом случае интегрировать пока не будем по причинам, которые стать понятным в одно мгновение.

Другой интеграл:

∫ y ₁ (x)f(x) W(y ₁ , y ₂ ) dx 9 0003

= ∫ e ^3x cos(2x )[195cos(4x)] 2e ^6x dx

= 195 2 ∫e ^−3x cos(2x)cos(4x)dx

= 195 4 ∫e ^−3x [cos (6x) + cos(2x)]dx    . ..  (2)

  
Из уравнений (1) и (2) видно, что существует четыре очень похожих интегрирования, которые нам нужно выполнить:

I ₁ = ∫e ^−3x sin(6x)dx
I ₂ = ∫e ^{−3 х} sin(2x)dx
I ₃ = ∫e ^−3x cos(6x)dx
I ₄ = ∫e ^−3x cos(2x)dx

Каждый из них можно получить, дважды используя Интегрирование по частям, но есть способ проще:

I ₁ = ∫e ^−3x sin(6x)dx = − 1 6 e ^−3x cos(6x) − 3 6 ∫e ^−3x cos(6x)dx = − 1 6 e ^−3x cos(6x) − 1 2 I ₃

⇒ 2 I ₁ + I ₃ = − 1 3e 9000 6 −3x cos(6x) …  (3)

I ₂ = ∫e ^−3x sin(2x)dx = − 1 2 e ^−3x cos(2x) − 3 2∫e ^−3x cos(2x)dx = − 1 2e ^−3x cos(2x) − 3 2 I ₄

⇒ 2 I ₂ + 3 I ₄ = − e ^−3x cos(2x) . ..  (4)

I ₃ = ∫e ^−3x cos(6x)dx = 1 6 e ^−3x sin(6x) + 3 6 ∫e ^−3x sin(6x)dx = 1 6 e ^−3x sin(6x) + 1 2 I ₁
⇒ 2 I ₃ − I ₁ = 1 3e ^−3x sin(6x) …  (5)
I ₄ = ∫e ^−3x cos(2x)dx = 1 2 e ^−3x sin(2x) + 3 2∫e ^−3x sin(2x)dx = 1 2e ^−3x sin(2x) + 3 2 I ₂

⇒ 2 I 90 152 4 − 3 I ₂ = e ^−3x sin(2x) …  (6)

Решить уравнения (3) и (5) одновременно:

2 I ₁ + I ₃ = − 1 3e 9000 6 −3x cos(6x) . ..  (3)

2 I ₃ − I ₁ = 1 3e ^−3x sin(6x) …  (5)

Умножьте уравнение (5) на 2 и сложите их (слагаемое I ₁ нейтрализует):

⇒ 5 I ₃  = − 1 3e ^−3x cos(6x) + 2 3e ^−3x sin(6x)

            = 1 3e 90 006 −3x [2sin(6x) − cos(6x)]

⇒ I ₃  = 1 15e ^−3x [2sin(6x) − cos(6x)]

Умножить уравнение (3) на 2 и вычесть (слагаемое I ₃ нейтрализует):

⇒ 5 I ₁  = − 2 3e ^−3x cos(6x) − 1 3e ^−3x sin(6x)

            = − 1 3e ^−3x [2cos(6x) + sin(6x)]

⇒ I ₁  = − 1 15e ^−3x [2cos(6x) + sin(6x)]

Решить уравнения (4) и (6) одновременно: 0007 cos(2x)    . . . (4)

2 I ₄ − 3 I ₂ = e ^−3x sin(2x)    …  (6)

Умножьте уравнение (4) на 3 и уравнение (6) на 2 и добавьте (член I ₂ нейтрализует ):

⇒ 13 I ₄  = − 3e ^−3x cos(2x) + 2e ^−3x sin(2x)

            =e ^−3x [2sin(2x) − 3 cos(2x)]

⇒ I ₄  = 1 13e ^−3x [2sin(2x) − 3cos(2x)]

Умножьте уравнение (4) на 2 и уравнение (6) на 3 и вычтите (слагаемое I ₄ нейтрализует):

⇒ 13 I ₂  = − 2e ^−3x cos(2x) − 3e ^−3x sin(2x)

            =− e ^−3x [2cos(2x) + 3 sin(2x)]

⇒ I ₂  = − 1 13e ^−3x [2cos (2 раза) + 3sin(2x)]

Подставить в (1) и (2):

∫ y ₂ (x)f(x) W(y ₁ , y ₂ ) dx

= 195 90 008 4∫e ^−3x [sin(6x) − sin(2x)]dx   . .. (1)  

= 195 4[ − 1 15e ^−3x [2cos(6x) + sin(6x)] − [− 1 13e ^−3x [2cos(2x) + 3sin(2x)]]]

= e ^−3x 4[−13(2cos(6x)+sin(6x))+15(2 cos⁡(2x)+3sin(2x))]

∫ y ₁ (x)f(x) W(y ₁ , y ₂ ) dx

= 195 4 ∫e ^−3x [cos(6x) + cos(2x)]dx    …  (2)

= 195 4[ 1 15e ^−3x [2sin(6x) − cos(6x)] + 1 13e ^−3x [2sin(2x) − 3cos(2x)]]

= e ^−3x 4[13(2sin(6x) − cos(6x)) + 15(2sin⁡(2x) − 3cos(2x))]

Итак, y _p (x) = −y ₁ (x)∫ y ₂ (x)f(x) W(y ₁ , y ₂ ) dx + y ₂ (x)∫ y ₁ (x)f(x) W(y ₁ , y ₂ ) dx

= − e ^3x cos(2x) e ^−3x 4[−13(2cos(6x)+sin(6x)) + 15(2 cos⁡(2x)+3sin(2x))] + e ^3x sin(2x) e ^−3x 4[13(2sin(6x) − cos(6x)) + 15(2sin⁡(2x) − 3cos(2x))]

= − 1 4cos(2x) [−13(2cos(6x) − sin(6x)) + 15(2 cos⁡(2x) + 3sin(2x))] + 1 4 sin⁡(2x)[13(2sin(6x) − cos(6x)) + 15(2 sin⁡ (2 раза) — 3cos(2x))]  

= 1 4[26cos(2x)cos(6x) + 13cos(2x)sin(6x) − 30cos ² (2x) − 45cos(2x)sin(2x) + 26sin(2x)sin(6x) − 13sin(2x)cos(6x) + 30sin ² (2x) − 45sin(2x)cos(2x)]

= 1 4[26[cos(2x)cos(6x) + sin(2x)sin(6x)] + 13[cos(2x)sin(6x) − sin(2x)cos(6x)] − 30[cos ² (2 раза) − sin ² (2x)] − 45[cos(2x)sin(2x) + sin(2x)cos(2x)]]

= 1 4[26cos(4x) + 13sin(4x) − 30cos(4x) − 45sin(4x)]

= 1 4[−4cos(4x) − 32sin(4x)]

= −cos⁡(4x) − 8 sin⁡(4x)

Итак, полное решение дифференциального уравнения 195cos(4x) равно

y = e ^3x (Acos(2x) + iBsin(2x)) — потому что (4x) — 8sin (4x)

 

9529, 9530, 9531, 9532, 9533, 9534, 9535, 9536, 9537, 9538

задач с начальным значением | Исчисление II

Результаты обучения

• Определение задачи с начальным значением
• Определите, является ли данная функция решением дифференциального уравнения или задачи с начальными значениями

Обычно данное дифференциальное уравнение имеет бесконечное число решений, поэтому естественно спросить, какое из них мы хотим использовать. Чтобы выбрать одно решение, необходимо больше информации. Некоторая конкретная информация, которая может быть полезна, — это начальное значение, представляющее собой упорядоченную пару, которая используется для поиска конкретного решения. 9{t},y\влево(0\вправо)=3[/латекс].

 

Показать решение

Посмотрите следующее видео, чтобы увидеть работающее решение примера: Проверка решения задачи с начальным значением ручном углу видеодисплея. На YouTube видео начнется с той же начальной точки, что и этот клип, но будет воспроизводиться до самого конца. 9{x}[/latex], а второй частью было начальное значение [latex]y\left(0\right)=3[/latex]. Эти два уравнения вместе образуют начальную задачу.

В целом то же самое. Начальная задача будет состоять из двух частей: дифференциального уравнения и начального условия. Дифференциальное уравнение имеет семейство решений, а начальное условие определяет значение [latex]C[/latex]. Семейство решений дифференциального уравнения в примере задается как [latex]y=2{e}^{-2t}+C{e}^{t}[/latex].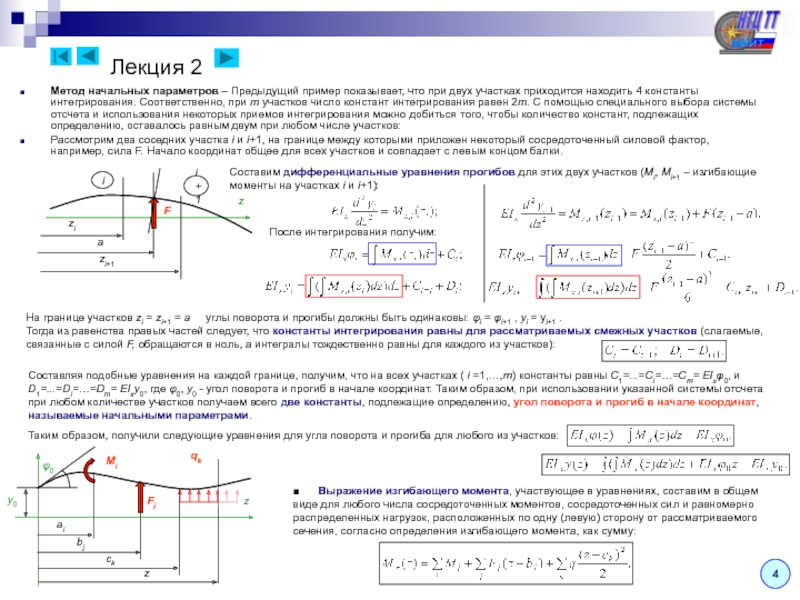 {t}[/latex] помечено. 9{2}-4,y\влево(0\вправо)=5[/латекс].

 

Показать решение

Посмотрите следующее видео, чтобы увидеть работающее решение примера: Проверка решения задачи с начальным значением ручном углу видеодисплея. На YouTube видео начнется с той же начальной точки, что и этот клип, но будет воспроизводиться до самого конца. 9{x},y\влево(0\вправо)=8[/латекс].

 

Показать решение

В физических и инженерных приложениях мы часто рассматриваем силы, действующие на объект, и используем эту информацию для понимания результирующего движения, которое может произойти. Например, если мы начнем с объекта на поверхности Земли, основной силой, действующей на этот объект, будет гравитация. Физики и инженеры могут использовать эту информацию вместе со вторым законом движения Ньютона (в форме уравнения [латекс]F=ma[/латекс], где [латекс]F[/латекс] представляет собой силу, [латекс]м[/латекс] представляет массу, а [латекс]а[/латекс] представляет собой ускорение), чтобы вывести уравнение, которое можно решить. {\prime}\left(t\right)[/latex]. Однако эта сила должна быть равна силе тяжести, действующей на объект, которая (опять же с использованием второго закона Ньютона) определяется формулой [latex]{F}_{g}=\text{-}mg[/latex], так как эта сила направлена ​​вниз. Следовательно, мы получаем уравнение [латекс]F={F}_{g}[/латекс], которое становится [/латекс]. Деление обеих частей уравнения на [latex]m[/latex] дает уравнение 9{\ простое число} \ влево (т \ вправо) = \ текст {-} г [/ латекс].

 

Обратите внимание, что это дифференциальное уравнение остается неизменным независимо от массы объекта.

Теперь нам нужно начальное значение. Поскольку мы ищем скорость, в контексте задачи имеет смысл предположить, что мы знаем начальную скорость или скорость в момент времени [latex]t=0[/latex]. Это обозначается как [латекс]v\left(0\right)={v}_{0}[/latex].

Пример: Скорость движущегося бейсбольного мяча

Бейсбольный мяч брошен вверх с высоты [латекс]3[/латекс] метров над поверхностью Земли с начальной скоростью [латекс]10\текст{м/с}[/ латекс], и единственная сила, действующая на него, — сила тяжести. Мяч имеет массу [латекс]0,15\текст{кг}[/латекс] на поверхности Земли.

1. Найдите скорость [латекс]v\влево(t\вправо)[/латекс] бейсбольного мяча в момент времени [латекс]t[/латекс].
2. Какова его скорость через [latex]2[/latex] секунды?

Показать раствор

попробуй

Предположим, что камень падает из состояния покоя с высоты [латекс]100[/латекс] метров, и единственная сила, действующая на него, — сила тяжести. Найдите уравнение для зависимости скорости [латекс]v\влево(t\вправо)[/латекс] от времени, измеряемой в метрах в секунду.

Показать решение 9{\ простое число} \ влево (т \ вправо) = v \ влево (т \ вправо), s \ влево (0 \ вправо) = {s} _ {0} [/ латекс].

 

Если функция скорости известна, то можно найти и функцию положения.

Пример: высота движущегося бейсбольного мяча

Бейсбольный мяч брошен вверх с высоты [латекс]3[/латекс] метров над поверхностью Земли с начальной скоростью [латекс]10\текст{м/с}[/ латекс], и единственная сила, действующая на него, — сила тяжести.