Лекции краткий курс Сопромат Иовенко 2011

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет»

КРАТКИЙ КУРС ЛЕКЦИЙ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ

Хабаровск Издательство ТОГУ

2011

УДК 539.3.(076)

Краткий курс лекций по сопротивлению материалов для студентов заочного факультета и заочного факультета ускоренного обучения / Сост. В. В. Иовенко. – Хабаровск: изд-во ТОГУ, 2011. – 100 с.

Лекции составлены на кафедре «Механика деформируемого твердого тела». Составлены для студентов заочного факультета и заочного факультета ускоренного обучения.

Печатается в соответствии с решениями кафедры «Механика деформируемого твердого тела» и методического совета заочного факультета.

Главный редактор Л. А. Суевалова

Редактор О. В. Астафьеваа

Компьютерная верстка В. В. Иовенко

Подписано в печать	. Формат 60×84 1/16.
Бумага писчая. Гарнитура «Таймс». Печать офсетная. Усл. печ. л.			.
Уч.-изд. л. . Тираж	экз. Заказ	.

Издательство Тихоокеанского государственного университета. 680035, Хабаровск, ул. Тихоокеанская, 136.

Отдел оперативной полиграфии издательства Тихоокеанского государственного университета. 680035, Хабаровск, ул. Тихоокеанская, 136.

Издательство ТОГУ, 2011

Оглавление
Лекция 1. Введение. Задачи курса. Понятие о расчетной схеме.	7c
Лекция 2. Внутренние силовые факторы. Метод сечений.
Напряжения, перемещения и деформации.	7c
Лекция 3. Растяжение. Построение эпюр продольных сил.
Напряжения и деформации.	12c
Лекция 4. Опытное изучение свойств материалов.	7c
Лекция 5. Понятие о напряженном состоянии в точке.
Чистый сдвиг.	8c
Лекция 6. Геометрические характеристики плоских сечений	8c
Лекция 7. Кручение стержней круглого профиля. Построение эпюр
крутящих моментов. Напряжения и деформации	10c
Лекция 8. Прямой (плоский) изгиб. Построение эпюр
поперечных сил и изгибающих моментов.
Напряжения и деформации.	21с
Лекция 9. Определение перемещений при изгибе.	8с
Лекция 10. Продольный изгиб прямого стержня	11с
Всего	99с

1

Лекция № 1

Введение. Задачи курса. Понятие о расчетной схеме

Введение.

Сопротивление материалов – это наука о прочности, жесткости и устойчивости отдельных элементов конструкций, сооружений и машин.

Методами сопротивления материалов ведутся практические расчеты и определяются необходимые (надежные) размеры деталей элементов инже- нерных конструкций.

Основные положения сопротивления материалов опираются на законы и теоремы механики и в первую очередь на законы статики, без знания которых изучение данного предмета становится практически невозможным.

В отличие от теоретической механики, сопротивление материалов рас- сматривает задачи, где наиболее существенными являются свойства деформи- руемых тел, а законы движения тела, как жесткого целого, не только отступают на второй план, но в ряде случаев являются попросту не существенными.

Начало науки о сопротивлении материалов обычно связывают с именем знаменитого физика, математика и астронома Галилео Галилея. В 1660 году Р. Гук сформулировал закон, устанавливающий связь между нагрузкой и дефор- мацией. В XVIII веке необходимо отметить работы Л. Эйлера по устойчивости конструкций. XIX и XX века являются временем наиболее интенсивного развития науки в связи с общим бурным ростом строительства и промышлен- ного производства при безусловно огромном вкладе ученых – механиков России.

Сопротивление материалов – одна из сложных дисциплин, занятия по этому курсу должны обязательно сопровождаться составлением конспекта и решением задач.

Совершенно необходимо научиться решать задачи самостоятельно. Следует также научиться делать выводы формул. При этом необходимо обращать особое внимание на физическую сущность явления и на те допуще- ния и ограничения, которые делаются в процессе выводов.

Задачи курса.

Первую задачу курса сопротивления материалов составляет изложение методов расчета элементов конструкций на прочность. Под прочностью мы будем понимать способность нагруженной конструкций сопротивляться разру- шению.

Вторую задачу курса сопротивления материалов составляет изложение методов расчета элементов конструкций на жесткость, т. е. способность элемента конструкции сопротивляться деформациям.

И, наконец, изложение методов расчета элемента конструкции на устой- чивость составляет третью задачу курса. Понятие устойчивости может быть сформулировано следующим образом: равновесие элемента устойчиво, если малому изменению нагрузки соответствует малое изменение деформаций, и

2

равновесие неустойчивое, если ограниченный рост нагрузки сопровождается неограниченным ростом деформаций.

При выполнении указанных видов расчета необходимо стремиться к максимальной экономии материала, т. е. к достаточным, но не завышенным раз- мерам деталей машин и механизмов.

Таким образом, сопротивление материалов имеет целью создать практи- чески приемлемые, простые приемы расчета типичных, наиболее часто встреча- ющихся элементов конструкций.

Понятие о расчетной схеме.

Необходимость довести решение каждой практической задачи до некото- рого числового результата заставляет в сопротивлении материалов прибегать к упрощающим гипотезам – т. е. предположениям, которые оправдываются в дальнейшем путем сопоставления расчетных данных с экспериментом.

Таким образом, приступая к расчету конструкции, следует прежде всего установить, что в данном случае является существенным и что не существенно.

Необходимо, как говорят, произвести схематизацию объекта конструк- ции (рис. 1.1), т. е. отбросить все те факторы, которые не могут сколько-нибудь заметным образом повлиять на работу системы в целом.

Реальная конструкция

Производится схематизация по…

материалу опорам

геометрии нагрузке

и т. д.

Принимаются…

принцип

независимости действия сил

гипотеза плос- ких сечений

принцип Сен-Венана

гипотеза об от- сутствии началь- ных напряжений

и другие

Расчетная схема

Рис.

1.1

Такого рода упрощения задачи совершенно необходимы, так как решение с полным учетом всех свойств реального объекта является принципиально невозможным в силу их очевидной неисчерпаемости.

3

Реальный объект, освобожденный от несущественных признаков, носит название расчетной схемы.

Схематически процесс получения расчетной схемы показан на рис. 1.1. Остановимся подробнее на отдельных этапах процесса превращения реальной конструкции в расчетную схему.

Cхематизация по материалу.

Будем считать, что материал рассчитываемой конструкции однороден, т.е. его свойства не зависят от величины выделенного из тела объема.

Вводится понятие сплошности среды, как среды, непрерывно заполняющей отведенный ей объем. Вследствие чего к сплошной среде может быть применен анализ бесконечно малых.

Эти положения позволяют не принимать во внимание дискретную, атомистическую структуру вещества. Они применяются даже при расчете конструкций из такого неоднородного материала, как бетон.

Материал изотропен, т.е. обладает во всех направлениях одинаковыми свойствами. Это предпосылка используется при решении большинства задач сопротивления материалов, хотя для некоторых материалов (дерево, железо- бетон, медь, пластмассы и др.) она весьма условна.

Материалы, свойства которых в разных направлениях различны,

называются анизотропными.

Материал конструкции обладает свойством идеальной упругости, т.е. способностью полностью восстанавливать первоначальные форму и размеры тела после снятия внешней нагрузки.

Эта предпосылка справедлива лишь при напряжениях, не превышающих для данного материала определенной, постоянной величины, называемой

пределом упругости.

Предпосылка об идеальной упругости материала используется при решении большинства задач сопротивления материалов.

Cхематизация по геометрии отдельных элементов конструкции.

Основное внимание в сопротивлении материалов уделяется изучению брусьев, являющихся наиболее распространенным элементом многих конст- рукций.

Брусом называется элемент, длина которого значительно больше его поперечных размеров.

Осью бруса называется линия, соединяющая центры тяжести его поперечных сечений.

Плоская фигура, имеющая свой центр тяжести на оси и нормальная к ней, называется его поперечным сечением.

Брус с прямолинейной осью часто называют стержнем (рис. 1.2, а). Элемент конструкции, длина и ширина которого во много раз превы-

шают его толщину, называется оболочкой (рис. 1.2, б).

Геометрическое место точек, равноудаленных от наружной и внутренней поверхностей оболочки, называется срединной поверхностью.

4

Оболочка, срединная поверхность которой представляет собой плос- кость, называется пластинкой (рис. 1.2, в).

Элемент конструкции, размеры которого во всех направлениях мало отличаются друг от друга (например, сплошная опора моста), называется

массивным телом (рис. 1.2, г ).

Методы расчета пластинок, оболочек и массивов рассматриваются в курсе «Прикладная теория упругости».

а б

Рис. 1.2

Cхематизация по опорным устройствам.

Для прикрепления сооружения к основанию служат опоры, обеспечи- вающие неподвижность опорных точек конструкции. Обычно в сопротивлении материалов рассматривают три основных типа опор: шарнирно подвижная опора, шарнирно неподвижная опора и жесткое защемление.

На рис. 1.3, а изображена простейшая схема устройства шарнирно подвижной опоры, а на рис. 1.3, б – ее условное изображение. Подвижная опора допускает вращение вокруг оси, проходящей через центр шарнира k опоры, и поступательное перемещение по линии kl. В шарнирно подвижной опоре возникает реакция Rk , нормальная к направлению перемещения катков.

Шарнирно неподвижная опора (рис. 1.3, в) обеспечивает вращение верхнего балансира K вокруг оси, проходящей через центр шарнира k, и не допускает линейных перемещений. В расчетной схеме она представляется двумя опорными стержнями (рис. 1.3, г ). В шарнирно неподвижной опоре возникает наклонная реакция, вертикальная и горизонтальная составляющие которой ( Rk и H k ) показаны на рис. 1.3, г .

Жесткое защемление (рис. 1.3, д, е, з) не допускает каких либо линей- ных перемещений и поворота. В защемлении возникают две составляющие Rk ,

5

H k и реактивный момент M k (рис. 1.3, е). Жесткое защемление эквивалентно

трем опорным стержням –		рис. 1.3, з).
а	F	в	F	д	F
		K
		k			F
k					H k
	F		F		k
б		г		е	M k
k	l	k			Rk
		H k
				з
	R	Rk
	k

Рис. 1.3

Cхематизация по нагрузке.

Распределенные нагрузки могут быть поверхностными (давление ветра, воды на стенку) или объемными (сила тяжести, силы инерции). Если давление

q1 ( Нм2 ) передается на элемент конструкции через площадку, размеры которой очень малы по сравнению с размерами всего элемента ( a << L ), то его на основании принципа Сен-Венана (см. ниже) можно привести к

сосредоточенной силе F (рис. 1.4).

q1				q	2

L1

a

с

b

L

F = q a b

q3 =

q2

c b

= q2

b

c

1

L1 + a 2

L

с

Рис. 1.4

Сосредоточенная сила F измеряется в ньютонах ( Н ), килоньютонах ( кН ). Подобным образом вводятся понятия сосредоточенных изгибающих и крутящих моментов.

6

Если давление q2 ( Нм2 ) передается на элемент конструкции через площадку, размеры которой сравнимы с размерами всего элемента ( c < L ), то его представляют в виде распределенной или погонной нагрузки q3 с размер-

ностью Нм (рис. 1.4).

На расчетной схеме вместо бруса изображается его ось.

Нагрузки, распределенные по линии и сосредоточенные в точках, реально не существуют. Их можно получить лишь в результате схематизации реальных нагрузок, распределенных по объему (объемных сил) или по поверхности.

Нагрузки различаются не только по способу их приложения (распре- деленные и сосредоточенные), но также по длительности действия (постоянные и временные) и характеру воздействия на конструкцию (статические и динамические).

Постоянные нагрузки (например, собственный вес конструкции) дейст- вуют на протяжении всего периода эксплуатации конструкции.

Временные нагрузки (например, вес поезда) действуют в течение ограни- ченного промежутка времени.

Статическими называются нагрузки, которые изменяют свою величину или точку приложения (или направление) с очень небольшой скоростью, так что возникающими при этом ускорениями можно пренебречь.

Если ускорения значительны и нагрузка изменяется во времени с большой скоростью, то мы имеем дело с динамической нагрузкой. Действие таких нагрузок сопровождается возникновением колебаний сооружений. При этом, согласно второму закону Ньютона, возникают силы инерции, пропор- циональные массам и ускорениям, которыми при расчете пренебречь нельзя.

Временная нагрузка может сохранять более или менее постоянную величину в течение всего периода ее действия, а может непрерывно изменяться по некоторому закону; в последнем случае она называется переменной нагрузкой.

Если переменная нагрузка изменяется по циклическому (повторяюще- муся) закону, то она называется циклической.

В заключение отметим, что если для одного объекта может быть предло- жено несколько расчетных схем, то, с другой стороны, одной расчетной схеме может быть поставлено в соответствие много различных реальных объектов.

Последнее обстоятельство является весьма важным, так как исследуя не- которую схему, можно получить решение целого конкретных задач, сводящих- ся к данной схеме.

Основные принципы и гипотезы сопротивления материалов

Принцип независимости действия сил гласит, что результат действия на тело системы сил равен сумме результатов воздействия тех же сил, прилагае- мых к телу последовательно и в любом порядке.

7

Например, прогиб w конца бруса (рис. 1.5) от нагрузок F	и F равен
1	2

сумме прогибов w и w от действия каждой нагрузки в отдельности, т. е.

1 2

w = w + w .

1 2

F	F						F					F
1	2						1					2
					w						w						w
							1										2

Рис. 1.5

Он применим к деформируемым телам лишь тогда, когда перемещения точек приложения сил, являющиеся результатом деформации тела, во-первых малы по сравнению с размерами тела и во-вторых линейно зависят от действу-

ющих сил (закон Гука).

Закон Гука используется при решении большинства задач сопротивления материалов.

На основании принципа Сен-Венана в точках тела, достаточно удаленных от мест приложения нагрузок, величина внутренних сил весьма мало зависит от конкретного способа приложения этих нагрузок, а зависит только от ее стати- ческого эквивалента (рис. 1.6).

Этот принцип во многих случаях позволяет производить замену одной системы сил другой системой, статически эквивалентной, что позволяет часто значительно упростить расчет.

Под внутренними силами будем понимать изменение взаимодействия между частицами материала, вызванное внешней нагрузкой.

		F = ∫ q dA
q		y
	y	A
σ = F A		σ = F A

Рис.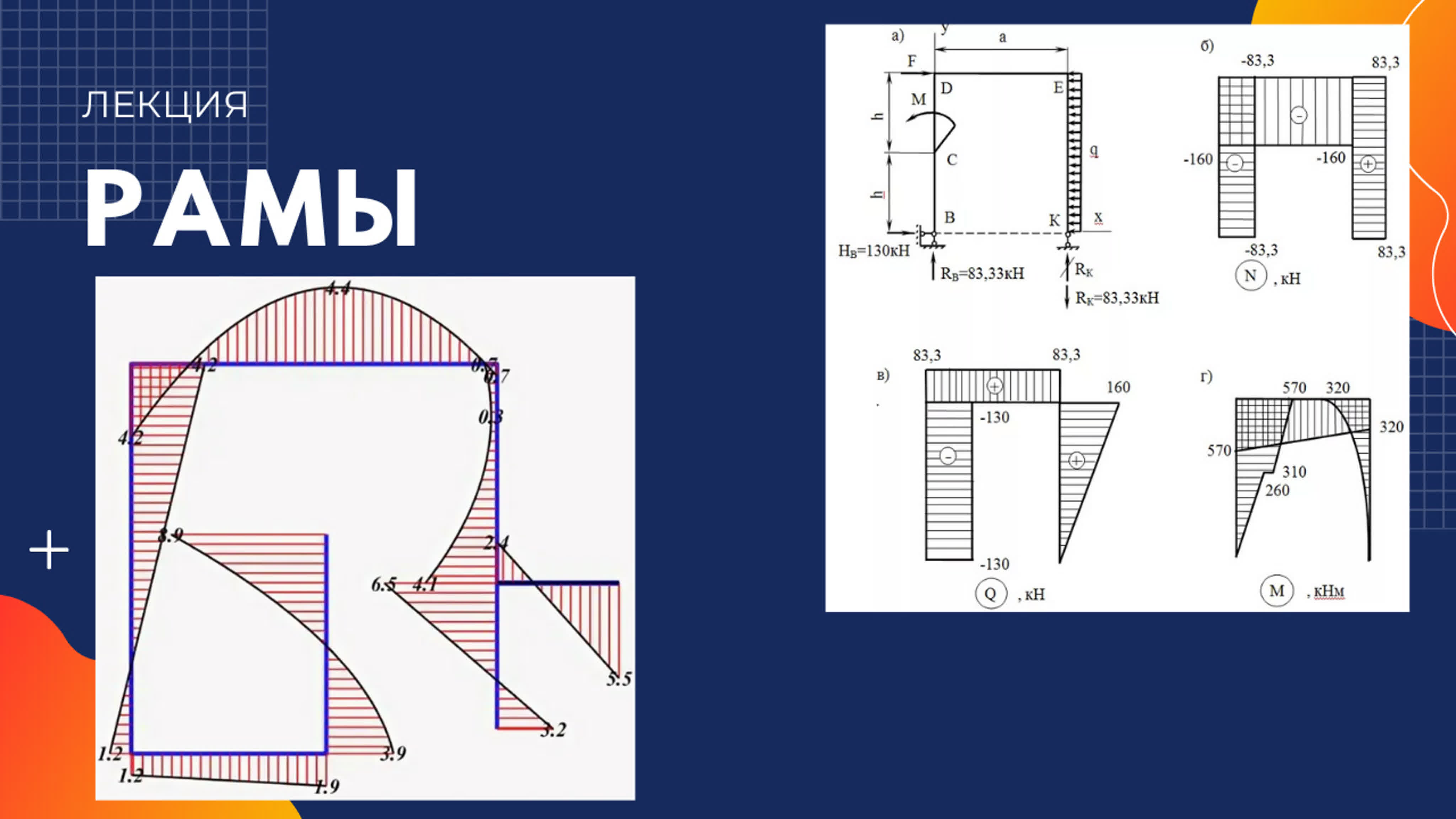 1.6

Гипотеза плоских сечений предполагает, что сечение, плоское и перпен- дикулярное к продольной оси до деформации, остается таким же и после де- формации (рис. 1.7).

F

90O

90O

n

n

Рис. 1.7

Эта предпосылка впервые была введена Бернулли. Она играет исключительно важную роль в сопротивлении материалов и используется при

Лекция-беседа В.И. Федосьева «Сопротивление материалов, теория упругости и прочее…»

Что такое сопротивление материалов? Ответ на этот вопрос дается на первых страницах каждого учебника по сопротивлению материалов. Сопротивление материалов — наука о прочности. Она учит рассчитывать инженерные конструкции и определять их надежные размеры.

Такое определение является традиционным, и оно, конечно; правильное, но вместе с тем — не совсем полное, да и не совсем точное. Расчеты инженерных конструкций, действительно, строятся прежде всего на основе методов сопротивления материалов. Вместе с тем на практике само понятие расчета имеет более широкое содержание, чем то, которое в него порой вкладывается.

Рассчитать конструкцию это значит дать оценку ее прочности. В сопротивлении материалов эта задача не решается. Сопротивление материалов еще не дает расчета конструкции. Оно дает только теоретические основы для ведения этих расчетов.

Каждый инженерный расчет, да и не только расчет, а вообще исследование в области технических наук, включает в себя, как известно, следующие три этапа:
I. Идеализация объекта. На этом этапе рассматривается реальная конструкция и выделяются те ее особенности, которые являются наиболее существенными для рассматриваемой задачи. В результате получаем расчетную схему.
II. Анализ расчетной схемы. Здесь при помощи средств теории выясняются закономерности расчетной схемы, отвечающей реальной конструкции.
III. Обратный переход от расчетной схемы к реальной конструкции и формулировка практических выводов, ради которых было предпринято ее исследование.

Содержание сопротивления материалов относится в основном к этапу II. В сопротивлении материалов излагаются приемы анализа типичных расчетных схем и даются методы определения напряжений и перемещений в балках, трубах, тонкостенных сосудах, методы раскрытия статической неопределимости стержневых систем и т. д. и т. п. Словом, рассматриваются все те расчетные схемы, которые являются практически общими для большей части инженерных конструкций. Что же касается выбора расчетной схемы и оценки надежности самой конструкции, то об этих вопросах в сопротивлении материалов лишь упоминается, но ответа на них в конечном итоге не дается. Да это и понятно. Многообразие современных инженерных задач столь велико, что в пределах одной дисциплины невозможно изложить специфические особенности прочностных расчетов по всем разделам техники. В связи с этим возникает необходимость создания специальных дисциплин, дополняющих сопротивление материалов для каждого инженерного направления.

Расчетные схемы, выходящие за рамки общетехнических и свойственные только конкретно взятой области техники, рассматриваются в разделах инженерной механики, название которых начинается со слов «Строительная механика…», например, строительная механика сооружений, строительная механика сварных конструкций, строительная механика корабля, самолета и т. д. Эти дисциплины посвящены в основном развитию эффективных методов анализа специфических расчетных схем. Так, например, в строительной механике самолета рассматриваются вопросы устойчивости пластин, подкрепленных оболочек и других тонкостенных элементов. В строительной механике сооружений большое место занимают специальные вопросы раскрытия статической неопределимости рам и стержневых систем. Словом, строительная механика любого профиля может рассматриваться как специализированное сопротивление материалов, изложенное в духе определенной отрасли техники.

Вопросы о выборе расчетной схемы (этап I), а также оценки коэффициентов безопасности и прочности конструкции (этап III) наиболее полно излагаются в технических
дисциплинах, название которых начинается со слова «прочность…»: прочность строительных сооружений, прочность корабля, прочность самолета и т. д.

Уместно заметить, что учебных курсов и монографий по этим дисциплинам создано очень немного. Объясняется это прежде всего сложностью вопроса. Курс прочности, в отличие от строительной механики, представляет собой взаимопроникающее единство расчетно-теоретического аппарата, особенностей конструкции, технологических и эксплуатационных условий. Правильное сочетание этих вопросов предъявляет к труду автора очень высокие требования, выполнение которых далеко не всегда под силу даже авторскому коллективу.

Большую роль играет также и элемент ответственности. Ясно, что общие суждения, связанные с подсчетом напряжений, с определенными математическими оценками, в частности, с возможностью пренебречь теми или иными слагаемыми в расчетных формулах, по сути говоря, ко многому не обязывают. Даже в том случае, когда они сомнительны, их легко оправдать (как это часто и делается) выражениями: «положим, что», «можно принять» и т. п. Все погрешности, допущенные в подобного рода анализе, могут быть в дальнейшем при практических расчетах перекрыты запасом прочности, а наиболее грубые — выявлены на стадии предварительных испытаний конструкции.
Что же касается назначения коэффициента запаса (или коэффициента безопасности), то всякие рекомендации в этой части являются достаточно ответственными. Для того чтобы их дать, надо учитывать и современный уровень производства, и опыт, который накоплен в области создания и эксплуатации подобных конструкций, и те последствия, которые влечет за собой выход из строя рассматриваемого узла, и многие другие обстоятельства.

Наконец, в вопросах создания курсов прочности большую роль играет скоротечность тех изменений, которые претерпевают некоторые разделы техники. Поэтому курс прочности быстро устаревает, в то время как курс строительной механики в ряде случаев живет десятилетиями.

Итак, сопротивление материалов представляет собой азбуку и грамматику расчетов на прочность. Это — введение в высокое общество прикладных наук прочностного цикла, дающих углубленную проработку вопросов, связанных с конкретными техническими направлениями. Границы  между этими направлениями не являются строгими. Многие пути исследований пересекаются, многие идут параллельно. Бывает, что некоторые разделы строительной механики после надлежащей проработки приобретают достаточную общность и занимают прочное место в курсе сопротивления материалов. Так, в частности, исследования по статике тонкостенных стержней, проводившиеся в свое время для целей расчета авиационных и некоторых строительных конструкций, в последнее время стали включаться в курс сопротивления материалов.

И сопротивление материалов, и строительная механика и прочность конструкций развиваются не изолированно от других дисциплин. И наиболее тесно они связаны с теорией упругости. Влияние этой науки на развитие прочностного цикла механики носит принципиальный характер.

Порой приходится слышать, что основное различие между сопротивлением материалов и теорией упругости сводится к точности применяемых методов. С одной стороны,— прикладная дисциплина «сопротивление материалов», использующая правдоподобные, но недоказанные гипотезы и упрощающие приемы. С другой,— строгая математическая наука, теория упругости, отрицающая недоказанные положения и дающая «точное» решение задач.

Такое сравнение является не только упрощенным, но даже неверным по существу.
Сопротивление материалов и теория упругости имеют в конечном счете общие цели, и там и здесь используются и приближенные методы и упрощающие приемы. Различие заключается в круге рассматриваемых задач и в глубине их проработки, хотя, конечно, вопросы простоты и практически необходимой точности играют не последнюю роль.

Как было уже сказано, при решении задач сопротивления материалов расчетная схема считается заданной. Таким образом, этап I из рассмотрения исключается. Тем не менее, приступая к решению любой задачи, мы должны помнить, что этот этап существует, что он был пройден до этого кем-то другим, что рассматриваемая расчетная схема получена как результат пренебрежения целым рядом особенностей реального объекта. Следовательно, анализ расчетной схемы должен быть проведен в пределах той точности, которая уже заложена выбором расчетной схемы.

Мы обычно не знаем, какие пренебрежения были сделаны при идеализации конструкции. Схема, предложенная к анализу, может быть и очень грубой и очень точной. Но во всяком случае известно, что имеющиеся в ней погрешности не могут быть меньше определенного реального минимума. Этот уровень погрешностей связан со многими факторами. Сюда входит и неоднородность материала, и отклонения действительной зависимости  от идеальной пропорциональности, т. е. от закона Гука и особенности наложения связей и многое другое.

При решении задач сопротивления материалов всегда уместно спросить, как та или иная нагрузка может быть реализована, как обеспечить практически выполнение заданных граничных условий. Если они точно не могут быть выполнены, то сколь велика возникающая погрешность.

В сопротивлении материалов не выполняется также и этап III, и вопрос о расчете конструкции еще не получает своего решения. Но существование этого этапа, как и этапа I, налагает также свой отпечаток на характер проводимого анализа. Это сказывается хотя бы уже в том, что в задачу сопротивления материалов, кроме определения напряжений, входит определение коэффициента запаса (по пределу прочности, либо по разрушающим нагрузкам) или определение запаса циклической прочности. Решение тем самым подводится вплотную к заключительному этапу расчета конструкции.

Таким образом, анализ в сопротивлении материалов выглядит как средство для решения более широкой задачи — задачи расчета конструкции.

Для теории упругости такого рода подчиненность аналитического аппарата практическим целям не характерна. Теория упругости не скована необходимостью дать краткую сводку рекомендаций к расчету. Это позволяет провести более углубленную проработку не только конкретных задач, но в первую очередь — общих задач и методов.
Из сказанного не следует, конечно, что результаты, полученные методами теории упругости, не могут без надлежащей обработки получить практического применения. В тех случаях, когда решение получено в достаточно простой и общей форме, оно сразу может быть включено в арсенал средств практических расчетов. Достаточно вспомнить такие классические задачи теории упругости, как контактная задача, нашедшая прямое приложение, хотя бы в расчете шариковых подшипников, как задача о кручении призматического бруса или задача определения местных напряжений вблизи отверстий и выточек и многие другие.

Теория упругости богата не только множеством решенных задач. Трудами Пуассона, Сен-Венана, Клебша созданы основы механики деформируемых систем и заложены принципы, соблюдение которых стало нормой во всех дисциплинах, прямо или косвенно связанных с вопросами прочности.

Когда мы пользуемся, например, технической теорией изгиба балок, мы часто забываем, что ее достоверность обеспечена многочисленными исследованиями, проведенными методами теории упругости. Именно эти исследования дают нам ориентировку в таких вопросах, как пренебрежение вторичными напряжениями, как применимость или неприменимость гипотезы плоских сечений, да и во многих других. Теория упругости, таким образом, не только обогащает сопротивление материалов новыми задачами и новыми постановками проблемы, но, образно говоря, «обеспечивает тылы» в тех простейших методах, которыми мы пользуемся повседневно.

Можно смело сказать: не будь теории упругости, сопротивление материалов напоминало бы удручающий свод прочностных нормативов. Так, кстати, и было до тех пор, пока в преподавании сопротивления материалов игнорировались достижения теории упругости.

Еще до 1929 г. появлялись в свет издания курса П. К. Худякова, в которых в полной мере проявился полурецептурный характер расчетов на прочность. И это было в то время, когда теория упругости уже достигла основных позиций, а С. П. Тимошенко создал основы современного курса сопротивления материалов.

Таким образом, сопротивление материалов и теория упругости могут рассматриваться как единое целое, и если случается услышать пожелания «о сближении» этих наук, то это следует понимать только как необходимость более глубокого овладения всеми достижениями современной науки в области теории деформируемых твердых тел.

Среди наук, занимающихся этими вопросами, за последние десятилетия возникли и развились новые дисциплины, родственные сопротивлению материалов, такие как теория пластичности и теория ползучести. Они значительно обогащают аппарат, используемый инженером-исследователем и открывают перед ним новые возможности в выборе более точных расчетных схем, в которых учитывалось бы и наличие пластических деформаций, и влияние фактора времени.

Таким образом, дисциплин, занимающихся вопросами механики деформируемых тел, очень много. По степени теоретичности и прикладной направленности они образуют целую гамму оттенков. Среди этих дисциплин сопротивление материалов занимает одно из основных мест.

Методы сопротивления материалов не остаются неизменными. Они непрерывно развиваются и совершенствуются.

На заре развития науки о прочности все внимание было обращено на способность материала сопротивляться действующим нагрузкам. Термин «сопротивление материалов» тогда еще можно было понимать буквально. Постепенное внедрение в расчетную практику многообразных приемов анализа сделало это невозможным. От времен «младенчества» сохранилось только название.

Если проследить за эволюцией сопротивления материалов за последние 40 лет, то легко заметить общую тенденцию, направленную к переходу от решения задач строительного профиля к более общему машиностроительному. Сопротивление материалов заметно обогатилось, стало многообразнее и насыщеннее. В него вошли вопросы усталостной прочности и динамики. В современных учебных курсах нашли свое отражение теории пластичности и ползучести. Введены основные задачи теории пластин и оболочек, анализ которых прежде традиционно относился к теории упругости. В ближайшее время следует ожидать внедрения в сопротивление материалов некоторых элементов нелинейной теории упругих систем.

Наряду с появлением новых в курсе происходит отмирание некоторых устаревших разделов. Так исчезли графические и графоаналитические методы построения упругой линии. В настоящее время они повсеместно заменяются численными методами, которые вообще приобрели доминирующее значение в связи с развитием электронной вычислительной техники. Отбрасываются некоторые устаревшие трактовки и углубляется изложение.

Изучая курс сопротивления материалов, следует помнить, что изложенные в нем истины не являются незыблемыми, что они тесно связаны с общим техническим и научным прогрессом и являются прямым его отражением.

ГУМ-RED-LINE — Выставки

Выставки

Фарид Богдалов Девятая волна05 июля — 31 августа 2023

Прошедшие выставки

ПахомЛеса цветов дю…28 февраля — 16 апреля 2 023

Андрей ЛюблинскийКто они?»09 сентября — 16 декабря 2022

ВДШ 2022Выставка достижений современных художников22 апреля — 21 июня 2022

Школа «Инженеры искусства»: Далекий баланс17 с сентябрь 2021 — 31 марта 2022

Николай ПолисскийРусская древность21 июля — 12 сентября 2021

Красный сад01 июля — 12 сентября 2021

Серж ГоловачСопромат от Головача38 апреля — 14 июля 2021

Чжан ХуаньЛюбовь как Мудрость09 февраля — 08 апреля 2021

9 0004 Евгений ГранильщиковОбстоятельства непреодолимого времени06 ноября 2020 — 29 января 2021

Тело как медиа — Мастерская Оли Кройтор23 сентября — 26 октября 2020

Николай ФилатовПоловецкие танцы10 сентября — 28 октября 2020

Международный фестиваль современного искусства 2020 EverArt Weekend03 июля — 05 июля 2020

Семен ФайбисовичНовый Мир12 марта — 01 сентября 2020

Серия прямых трансляций с артистами18 апреля — 18 мая 2020

Аристарх ЧернышевMetaConsumer23 декабря 2022 — 20 февраля 2023 9 0003 Art Consulting ArtIQ Lectures11 февраля — 14 мая 2020

Fashion to Know Project Lectures03 марта — 23 апреля 2020

Тело как медиа — Мастерская Оли Кройтор26 февраля — 25 марта 2020

(Pro к) Тип. Выставка Марии и Александра Погоржельских06 февраля — 10 марта 2020

Арт-баттл: Орлицкий против Тузова24 января — 04 февраля 2020

Да светит вам счастливая звезда19 декабря 2019 — 20 января 2020

Утилизируй или умри21 ноября — 17 декабря 2019 900 03 Гоша ОстрецовПокорители Солнца22 октября — 17 ноября 2019

Максимальный уровень существования династии Тотибадзе26 сентября — 18 октября 2019

Философия общей цели. Глоссарий.05 сентября — 24 сентября 2019

Философский проект общей цели. Космосков. Гостиный Двор05 сентября — 08 сентября 2019

Превью 5-й Уральской индустриальной биеннале современного искусства07 августа — 04 сентября 2019

Олег КуликБезответственная живопись28 июня — 04 августа 2019

ГУМ Red LineВыставка современного искусства13 апреля — 28 мая 201 9

Одна семья13 апреля — 28 мая 2019

ГУМ-RED-LINE — События

Фарид Богдалов. Девятый вал

Прошедшие мероприятия

Торжественное открытие выставки Фарида Богдалова «Девятый вал»4 июля 2023
19:00

Пахом. Цветы дю…

Прошедшие мероприятия

Экскурсия с куратором выставки Михаилом Сидлиным19 марта 2023
17:00

ВДШ 2022. Выставка достижений современных художников

Прошедшие мероприятия

Экскурсия с куратором выставки Мариной Федоровской2 8 мая 2022
17:00

Экскурсия с куратором выставки Мариной Федоровской29 апреля 2022
19:00

Школа «Инженеры искусства»: Запредельное равновесие

Прошедшие мероприятия

Встреча с художниками Школы искусств Инженеры Инал Савченков и Франц Родвальт16 января 2022
19:00

Экскурсия с кураторами выставки Николаем Маргиевым и Екатериной Юшкевич30 ноября 2021
17:00

Artist-talk с художниками Школы инженеров искусств Иналом Савченковым и Францем Родвалтом19 ноября 2021
19:00

Премьера фильма Федора Курёхина с художниками и кураторами выставки Школа «Инженеры искусства»: Далекий баланс.18 ноября 2021
19:00

Экскурсия с куратором выставки Николаем Маргиевым8 октября 2021
19:00

Николай Полисский. Русская Старина

Прошедшие события

Паблик Арт. Современный. Действительный. Жизненно важный? Круглый стол. Часть проекта ГУМ-Red-Line «Красный сад». Финишаж.9 сентября 2021
19:00

Красный сад

Прошедшие мероприятия

Экскурсии на выставку ГУМ-Red-Line x Архстояние «Красный сад»3 июля 2021
18:00

9 0002 Серж Головач. Сопромат Головача

Прошедшие мероприятия

Публичная лекция «Прозрачность в современном искусстве» с Сергеем Хачатуровым26 мая 2021
18:00

СОРПОМАТ ГОЛОВАЧ Экскурсии по выставке с Сержем Головачем25 мая 2021
16:00

Чжан Хуан. Любовь как мудрость

Прошедшие события

Public talk Дмитрия Озеркова4 апреля 2021
14:00

Public talk Чжан Хуан. Любовь как мудрость3 марта 2021
12:00

Торжественное открытие выставки Чжан Хуан. Любовь как мудрость8 февраля 2021
19:00

Евгений Гранильщиков. Обстоятельства непреодолимого времени

Прошлые события

Разговор художника с Евгением Гранильщиковым. Закрытие выставки.29 января 2021

Фестиваль российского видеоарта14 января 2021

Пятичасовое чаепитие Семейный набор. Новогодняя вечеринка в стиле домашнего посиделки.20 декабря 2020
17:00

Экскурсия с куратором выставки Мариной Федоровской18 декабря 2020
18:00

Лекция Евгения Гранильщикова. Монтаж и метод куратора Карины Караевой.11 декабря 2020
16:00

Public talk Кино VS Видео. Евгений Гранильщиков7 декабря 2020
16:00

Экскурсия с куратором выставки Мариной Федоровской21 ноября 2020
16:00

Public talk Фарфоровая революция14 ноября 2020
16:00

Индивидуальные экскурсии по выставке с художником Евгением Граном ilshchikov11 ноября 2020

Торжественное открытие выставки Евгения Гранильщикова «Обстоятельства непреодолимого времени»5 ноября 2020
19:00

Тело как медиа — Мастерская Оли Кройтор

Прошедшие мероприятия

Мастер-классы аспирантов28 октября 2020 г.
19:00

Николай Филатов. Половецкие танцы

Прошедшие мероприятия

Гастроли выставки «Половецкие танцы Николая Филатова»17 октября 2020
16:00

Торжественное открытие выставки «Половецкие танцы Николая Филатова» 9 сентября 2020
19: 00

Международный фестиваль современного искусства. 2020 EverArt Weekend

Прошедшие мероприятия

Посещение мастерской художника: Возвращение в «Новый мир» паблик 4 июля 2020
15:00

Семен Файбисович. Новый мир

Прошедшие мероприятия

Посещение мастерской художника: Возвращение в «Новый мир» паблик4 июля 2020
15:00

Семен Файбисович в программе «Первоисточник», Радио Культура.10 апреля 2020
09:50

Public talk с Семеном Файбисовичем.2 апреля 2020
16:00

Технологии реализации идей. Хронотип картины. Public talk.26 марта 2020
19:00

Встреча с Семеном Файбисовичем. Преобразования. От реализма к абстракции.21 марта 2020
16:00

Кураторские экскурсии27 августа 2020
20:00

Торжественное открытие выставки Семена Файбисовича «Новый мир»22 марта 2020
19:00

Онлайн-трансляции с художниками Серия 9 0003

Прошедшие события

Прямая трансляция с Айдан Салаховой16 мая 2020
20:00

Прямая трансляция с Олегом Шапиро и Екатериной Ковбашиной14 мая 2020
17:00

Прямая трансляция с Сергеем Бра tkov6 мая 2020
20:00

Прямая трансляция с Павлом Пепперштейном4 мая 2020
20:00

Прямой эфир с Георгием Тотибадзе1 мая 2020
20:00

Прямой эфир с Ириной Кориной29 апреля 2020
20:00

Прямой эфир с Таней Пионикер27 апреля 2020
20:00

Прямая трансляция с Гошей Острецовым24 апреля 2020
20:00

Прямая трансляция с Арт-группой АЕС+Ф22 апреля 2020
20:00

Прямая трансляция с Владимиром Дубо ssarsky20 апреля 2020
20:00

Прямая трансляция с Александром Виноградовым и Марией Погоржельской18 апреля 2020
16:00

Аристарх Чернышев. MetaConsumer

Прошедшие события

Экскурсия с художником выставки Аристархом Чернышевым22 января 2023
18:00

Экскурсия с художником выставки Аристархом Чернышевым21 января 2023
18:00

Торжественное открытие выставки Аристарха Чернышева «МетаПотребитель»22 декабря 2022
19:00

Арт-консалтинг ArtIQ Лекции

Прошедшие мероприятия

Онлайн-лекция «Самые нашумевшие аукционные продажи»14 мая 2020
19:00

Онлайн-лекция «Искусство в дизайне интерьера»30 апреля 2020
19:00

Как создать коллекцию произведений искусства? Онлайн-лекция23 апреля 2020
19:00

Ярмарки и биеннале современного искусства онлайн-лекция16 апреля 2020
19:00

Онлайн-конференция «Самые влиятельные художники в современном искусстве»9 апреля 2020
19:00

90 004 Лекция «Кто создает тренды в современном искусстве»11 февраля 2020
19:30

Проект Fashion to Know Лекции

Прошедшие события

Лекция. Разнообразие в моде: история, тренды, кейсы23 апреля 2020
19:00

Лекция. Коллаборации моды и искусства. Как модные бренды меняют мир искусства21 апреля 2020
19:00

Лекция. Бельгийская мода: Дрис Ван Нотен14 апреля 2020
19:00

Лекция. Бельгийская мода: Раф Симонс7 апреля 2020
19:00

Лекция: DIOR & HERMÈS: кто сегодня у руля модных домов31 марта 2020
19:00

Лекция: Почему в моде так много искусства: от классики до современности19 марта 2020
19:00

Лекция: Назад в 90-е: любимые кутюрье 1990-х и их влияние на моду18 марта 2020
19:00 900 03 Лекция: Устойчивое развитие в индустрии моды или Модная экология5 марта 2020
19:00

Лекция: CHANEL & FENDI: кто сегодня у руля модных домов3 марта 2020
19:00

(Proto)Type. Выставка Марии и Александра Погоржельских

Прошедшие мероприятия

Public-Talk с Годфруа де Вирье из Hermès4 марта 2020
16:00

Дискуссия с Марией и Александром Погоржельскими8 февраля 2020
18:30

Кураторский тур Татьяна Мартьянова8 февраля 2020
12:30

Кураторская экскурсия Татьяны Мартьяновой7 февраля 2020
19:30

Торжественное открытие выставки (Proto)Type Марии и Александра Погоржельских6 февраля 2020
19:00

Арт-баттл: Орлицкий vs. Тузов

Прошедшие мероприятия

Кураторский тур31 января 2020
19:00

Арт-баттл: Орлицкий против Тузова24 января 2020
19:00

Пусть тебе светит счастливая звезда

Прошедшие мероприятия

Лекция: Гороскопы в современном искусстве.20 января 2020
20:00

Кураторские экскурсии20 января 2020
19:00

Торжественное открытие выставки «Пусть тебе светит счастливая звезда».19 декабрь 2019
19:00

Переработай или умри

Прошлые события

Вечер с Маргаритой Пушкиной10 декабря 2019
19:00

Мастер-класс Джексона де Виля: Радости апсайклинга8 декабря 2019
18:30

Public Talk Нелли Недре: Переработка в модной индустрии: Как мода решает проблему переработки.5 декабря 2019
19:00

DOCA-talk: Лекция художников Ирины Кориной и Аристарха Чернышева5 декабря 2019
15:00

Кураторские экскурсии27 ноября 2019 9 0075 18:00

Торжественное открытие выставки Recycle or Die21 ноября 2019
19:00

Гоша Острецов. Покорители Солнца

Прошедшие мероприятия

Мастер-класс Гоши Острецова для детей9 ноября 2019

Дока-беседа с художником Гошей Острецовым: Покорение Солнца сегодня31 октября 2019
15:30

9 0004 Покорители Солнца – Открытие персональной выставки Гоши Острецова22 октября 2019
19:00

Династия Тотибадзе. Максимальный уровень пропитания

Прошедшие события

Династия Тотибадзе Выставка Вернисаж. Максимальный уровень жизнеобеспечения26 сентября 2019
19:00

Философия общей цели. Глоссарий.

Прошедшие мероприятия

Благотворительный аукцион в поддержку Фонда современного искусства Cosmoscow.2224 сентября 2019
19:00

Открытие Common Goal Philosophy. Глоссарий выставки.11 сентября 2019
19:00

Философский проект Common Goal. Космосков. Гостиный Двор

Прошедшие мероприятия

Благотворительный аукцион в поддержку Фонда современного искусства Cosmoscow.24 сентября 2019
19:00

ДРАМ Премьера фильма7 сентября 2019
20:00

Фуршет для участников и гостей Cosmoscow6 сентября 2019
20:30

Вернисаж Cosmoscow 5 сентября 2019
20:00

Пресс-конференция: Философский проект «Единая цель» на Cosmoscow.