Определение неизвестного момента при кручении

Задача

Вал нагружен скручивающими моментами. Определить величину и направление неизвестного уравновешивающего момента M₂ (рис. 1), если M₁=30кНм, M₃=44кНм, M₄=6кНм

рис. 1

Пример решения

Величина и направление неизвестного скручивающего момента M₂ определяется из условия неподвижности вала.

Конечно на самом деле вал при работе вращается, собственно для этого он и предназназначен — вращаясь передавать крутящий момент.

Но в сопротивлении материалов, при расчетах валов, часть крутящего момента необходимая для вращения вала отбрасывается, и учитываются только моменты деформирующие (скручивающие) вал.

Таким образом будем полагать что рассматриваемый вал не вращается. Для этого должно выполняться следующее условие: сумма крутящих моментов относительно продольной оси вала должна быть равна нулю

Для составления уравнения равновесия зададим произвольным образом направление искомого крутящего момента M

рис. 2

Запишем уравнение равновесия вала относительно продольной оси z, при этом моменты вращающие вал в одну сторону запишем со знаком «+», а моменты обратного направления соответственно со знаком «-«:

отсюда следует, что

Знак «-» в результате показывает, что реальное направление крутящего момента M₂ противоположно ранее выбранному, т.е. в данном случае момент M₂ направлен против хода часовой стрелки и равен 8кНм.

Проверить себя можно сложив отдельно величины крутящих моментов направленных по ходу часовой стрелки и моментов обратного направления. Эти суммы должны получиться одинаковыми.

Другие примеры решения задач >

isopromat.ru

8.3. Изгиб с кручением

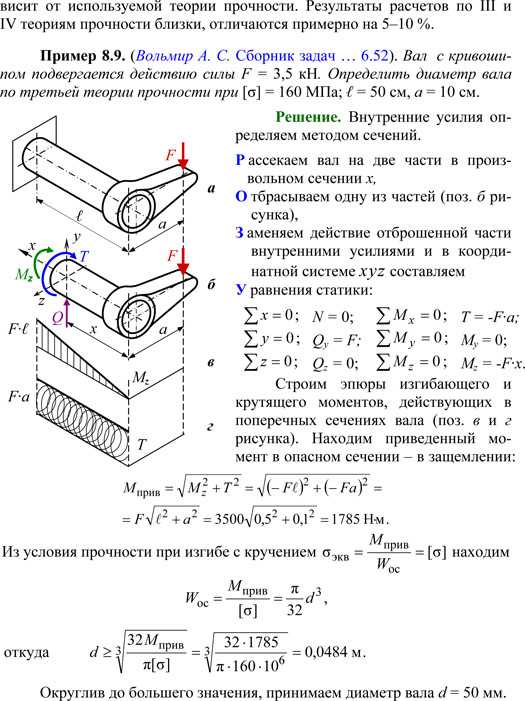
8.3. ИЗГИБ С КРУЧЕНИЕМ

Изгиб с кручением – вид сложного сопротивления, при котором в поперечном сечении бруса возникают изгибающие и крутящий моменты. Рассмотрим случай, при котором внешние силы располагаются в плоскости поперечного сечения, но не пересекают геометрическую ось х (рис. 8.12, а). Силу F разложим на ее составляющие Fz, Fy. Методом сечений определим внутренние усилия в произвольном сечении х (рис. 8.12, б). Спроецировав все силы на координатные оси и составив уравнения моментов относительно координатных осей, найдем внутренние усилия. Из шести внутренних усилий не равно нулю пять. На выделенном элементе В (рис. 8.12, б) показаны действующие по его граням напряжения (рис. 8.13, а). От поперечных сил и крутящего момента возникают касательные напряжения τQy, τQz, τT. От изгибающих мо- ментов – нормальные напряжения σ′ и σ″. Для длинных валов и балок (ℓ > 10 d) влиянием поперечных сил часто пренебрегают. Таким образом, учитывают только три момента: крутящий и два изгибающих. От них возникают три напряжения: одно касательное и два нормальных (рис. 8.13, б). Расчет на прочность при изгибе с кручением Из рисунка 8.13, б следует, что в произвольном сечении возникает плоское напряженное состояние Рис. 8.12. Определение внутренних усилий при изгибе с кручением Рис. 8.13. Анализ напряженного состояния Как при изгибе, так и при кручении круглого сечения опасными являются точки на периферии. Для круга и кольца Условие прочности для пластичных материалов по III теории прочности (наибольших касательных напряжений): σэкв = σ1 − σ3 ≤ [σ] Поскольку для круглого и кольцевого сечений не существует точки, одинаково удаленной от обеих осей инерции z, y, то используют результирующий момент – геометрическую сумму векторов изгибающих моментов относительно осей z, y: Условие прочности при совместном действии изгиба и кручения: σ=≤[σ] Мприв – приведенный момент, действие которого эквивалентно совместному действию My, Mz, T в соответствии с используемыми теориями прочности. По III теории прочности (наибольших касательных напряжений) Приведенного момента в действительности не существует, изобразить его нельзя, вектора он не имеет. Величина приведенного момента зависит от используемой теории прочности. Результаты расчетов по III и IV теориям прочности близки, отличаются примерно на 5–10 %. Пример 8.9. (Вольмир А. С. Сборник задач … 6.52). Вал с кривошипом подвергается действию силы F = 3,5 кН. Определить диаметр вала по третьей теории прочности при [σ] = 160 МПа; ℓ = 50 см, а = 10 см. Решение. Внутренние усилия определяем методом сечений. Рассекаем вал на две части в произвольном сечении х, Отбрасываем одну из частей (поз. б рисунка), Заменяем действие отброшенной части внутренними усилиями и в координатной системе xyz составляем У равнения статики: Строим эпюры изгибающего и крутящего моментов, действующих в поперечных сечениях вала (поз. в и г рисунка). Находим приведенный момент в опасном сечении – в защемлении: Из условия прочности при изгибе с кручением σ [σ] Округлив до большего значения, принимаем диаметр вала d = 50 мм.

dx-dy.ru