Коэффициент вариации прочности бетона
Главная » Статьи » Коэффициент вариации прочности бетона
Коэффициент вариации прочности бетона и его определение
Коэффициент вариации прочности бетона – это показатель, применяемый для контроля качества при изготовлении бетонных смесей. Наряду со средней прочностью в партии, этот показатель является одним из важнейших и характеризует однородность бетонной смеси.
Однородность бетонной смеси является залогом ее качества и прочности. Наличие коэффициента вариации прочности в паспорте указывает на то, что на заводе ведется статистический контроль прочности бетона. Как правило, средние значения этого показателя для тяжелого и легкого видов бетона составляют 6-10%. При этом согласно нормативам (СНиП 52-01-2003 «Бетонные и железобетонные конструкции. Основные положения») удовлетворительной считается технология, при которой коэффициент вариации равен 13,5%.
Определяется коэффициент вариации плотности бетона как отношение среднеквадратического отклонения к средней прочности бетона в партии.
Таким образом, чем он ниже, тем однороднее смесь, а, следовательно, тем выше ее качество. Низкий коэффициент вариации говорит о налаженности технологии, поэтому снижение данного показателя позволяет производителю уменьшить затраты на производство. Однако если в паспорте указано слишком низкое значение этого показателя (3-5%), это должно насторожить, так как, скорее всего, оно не соответствует действительности.
Определение коэффициента вариации прочности бетона
Определение коэффициента вариации прочности бетона (Vm) в партии согласно ГОСТ 10180-90 «Бетоны. Методы определения прочности по контрольным образцам» производится следующим образом:
- Для начала необходимо вычислить среднеквадратическое отклонение прочности бетона в партии (Sm).
- Затем следует вычислить среднюю прочность бетона в партии (Rm). Она определяется как среднее арифметическое единичных значений прочности бетона (n), при этом их число не должно быть ниже 30.
- После этого вычисляется отношение Sm к Rn, которое и будет равно коэффициенту вариации в партии.
Для того чтобы рассчитать средний коэффициент вариации для всех партий (Vn), необходимо вычислить отношение суммы произведений значений Vm и n к общему числу единичных значений прочности.
Таким образом, коэффициент вариации прочности бетона показывает отношение среднеквадратического отклонения к математическому ожиданию. Другими словами он отображает отличие максимальных и минимальных значений прочности от среднего показателя, то есть характеризует степень надежности технологии производства бетонной смеси.
szbeton.ru
Коэффициент вариации прочности бетона
. контакты 8 929 943 69 68 http://vk.com/club23595476 .. Уже кроме лаборатории и делать наверное не умею ничего. Выучила уже сама человек 10 с нуля, приятно когда тех, кого ты учил добиваются хороших результатов. Ирина
Ну вот наш блог развивается и всем миром мы приведем расчеты коэффициента вариации прочности бетона в порядок ,может быть в расчетах коэффициента вариации прочности и есть какие то неточности,но я точно знаю ,что работа по расчету коэффициента вариации прочности бетона выполнялась достаточно профессионально и все расчеты переданы моему блогу безвозмездно.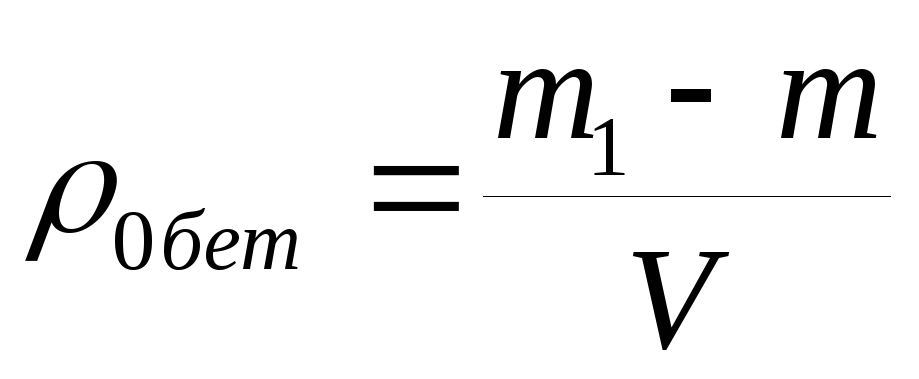
Мне не сказали ,
-Ой у меня все в автокаде ,я не могу дать вам документы ,
мне не сказали ,
— пусть заплатят мы научим ,почему мы будем учить бесплатно
мне не сказали
ой ну вот так нужно оформлять но я не могу вам дать в екселе это же я делал ,я только показать могу (это на курсах)
-Мне не сказали ой я через месяц сделаю и вам отправлю ,ой я занят .
Вот первое что попалось под руку раз и на электронке .
Как определить коэффициент вариации прочности бетона
Первое что попалось под руку это расчет коэффицента вариации бетона по сх В ,хорошее попадание почти в 10.Я благодарна Ирине за профессионализм ,умения и открытость .Нас уже сообщество собирается ,сообщество людей знающих и умеющих иногда незнающих но мыслящих ,не продающих знания а …И господа если вы желаете воспользоваться на информацией с блога не забывайте ставить ссылку потому что скопировать все невозможно .А блог создавался для строительной лаборатории и может быть кто-нибудь что-нибудь для себя полезное найдет .
И еще всегда просматривайте страницу оформление актов испытаний ,там будут загружаться файлы в формате ексель ,пока все так на одной странице может однажды мы все это разделим .Все расчеты по коэффициенту вариации прочности бетона т.е пример расчета коэффициента вариации по всем схемам контроля в отдельной рубрике .Мы продвигаемся с технологиям…..CALS-технология оценки качества
| СТАТИСТИЧЕСКИЙ КОНТРОЛЬРасчет внутрисерийного коэфф вариации | |||||||||
| И ОЦЕНКА ПРОЧНОСТИ БЕТОНА | |||||||||
| по ГОСТ Р 53231-2008 “Бетоны. Правила контроля и оценки прочности” (схема В) | |||||||||
| в промежуточном (и проектном )возрасте | |||||||||
| монолитные конструкции | |||||||||
| Объект: | |||||||||
| Организация-изготовитель: | |||||||||
| Потребитель: | |||||||||
1. Основные положения: | |||||||||
| 1.1.Номер карты подбора состава: | |||||||||
| 1.2. Проектный класс бетона: | В25 F 200 W6 | ||||||||
| 1.3. Контролируемый период: | 27.09.2009 | ||||||||
| 1.3. Контролируемый возраст конструкций: | промежуточный (проектный) | ||||||||
| 1.3. Партия конструкций: | одна конструкция, группа конструкций каждого вида. | ||||||||
| 1.3. Число участков испытаний в партии: | |||||||||
| 1.3.1 | для плоских конструкций (стены, перекрытия, фудаментные плиты) ? 3 измерений. | ||||||||
| 1.3.2 | для линейных вертикальных конструкций (колонны, пилоны) ? 6 измерений. | ||||||||
| 1.3.3 | для линейных горизонтальных конструкций (балки, ригели) ? 3 измерений на захватку или 1 на 4м длины | ||||||||
| 1.3. Число участков измерений на каждом контролируемом участке по ГОСТ 22690-88 или ГОСТ 17624: | |||||||||
1. 3. Общее число участков испытаний в партии для оценки класса бетона: | |||||||||
| 1.3.1 | для одной конструкции ? 6 измерений. | ||||||||
| 1.3.1 | для группы конструкций ? 20 измерений. | ||||||||
| 1.3. Единичное значение прочности: | |||||||||
| 1.4.Промежуточный возраст бетона: | |||||||||
| 1.5. Класс бетона в промежуточном возрасте : | |||||||||
| 2. Средства измерения: | |||||||||
| Прибор неразрушающего контроля ОНИКС-2.51, №зав | |||||||||
| Дата поверки: 5.02 2009 г.; Дата следующей поверки: 5.02.2010 г. | |||||||||
| 3. Дополнительные сведения: | |||||||||
| 2.1. Бетон изготавлен в соответствии с ГОСТ 26633-91 “Бетоны тяжелые и мелкозернистые. Технические | |||||||||
| условия.” | |||||||||
2.2.Прочность бетона определяена по ГОСТ 22690-88 “Бетоны. Определение прочности методами | |||||||||
| неразрушающего контроля”. Метод: (ударный импульс + упругий отскок). | |||||||||
| 2.4.Морозостойкость бетона определяена по ГОСТ 10060.2-95 “Бетоны. Ускоренные методы определения | |||||||||
| морозостойкости при многократном замораживании и оттаивании” – Протокол испытания №2 от 4.06.2009г. | |||||||||
| (в контрольных образцах-кубах) | |||||||||
| |||||||||
| водонепроницаемости.” – Протокол испытания №4 от 5.05.2009г. | |||||||||
| 2.6. Исходные материалы: | Т а б л и ц а 1 | ||||||||
| Наименование материала | Производитель материала | ||||||||
| Цемент: | |||||||||
| Щебень: | |||||||||
| Песок: | |||||||||
| Добавка: | |||||||||
3. Приемка бетона: | |||||||||
| 3.1. Предварительная оценка прочности бетона представлена в табл. 2, 3 | Копия Ведомость испытаний бетона для градуировочной зависимости | ||||||||
| 3.2. Окончательная приемка партий бетона представлена втабл. 4. | 3. Схема В – 2011- |
xn--90afcnmwva.xn--p1ai
Коэффициент вариации прочности бетона
То, что для частных нужд многие хозяева предпочитают изготовить бетон самостоятельно, а не приобретать заводской, ни для кого не секрет. Кустарное производство бетона – это норма и, в принципе, ничего плохого в этом нет, ведь человек строит дом только для себя, значит, он сам несет ответственность за прочность материалов и сооружения в целом.
Нормативные документы
Не так обстоят дела с государственным строительством. Тут уже приходится считаться с нормативными документами и использовать материалы только соответствующего качества, изготовленные по заводской технологии с учетом всех теоретических и практических рекомендаций.
Ведь в таких случаях строят не для одного человека, а для великого множества людей, и не на один год, а на десятилетия и даже на века.
Стандартные требования к качеству бетона для конструкций различного назначения и методам проверки можно найти в специальной литературе или в государственных стандартах.
Что такое коэффициент прочности
Одним из самых распространенных методов, определяющих прочность бетона, является измерение коэффициента вариации прочности бетона. Этот показатель измеряется в процентах и характеризует однородность бетонной смеси. Обозначается он латинскими литерами Vn.
Однородность – это важный показатель, ведь если бетон неоднородный, то и плотность его будет неравномерная, что в процессе эксплуатации может привести к повреждению или разрушению конструкции.
Как проходят испытания вариаций
Для определения коэффициента вариации прочности бетона проводят последовательные испытания 30 образцов бетона одной марки. Так определяют коэффициент одной партии.
Таких партий за определенный период времени изучается некоторое количество, а потом вычисляется средний показатель на основании коэффициентов всех изученных партий.
Обычно срок, за который определяется коэффициент вариации прочности определенной марки бетона и классификации бетона, составляет от 1 до 8 недель. Этот показатель является важным критерием при определении качества бетона и надежности технологий его производства. Чем ниже этот показатель, тем стабильнее и надежнее технология производства бетона, и исходя из этого, выбирается и марка бетона для фундамента дома.
Надо сказать, что необходимая прочность бетона достигается не сразу, полная его прочность достигается после 28 дней твердения. Самое интенсивное твердение достигается в первые 5-7 дней после его заливки. За это время достигается 70-процентная прочность бетона, поэтому так важно знать график набора прочности бетона.
График набора прочности бетона определенной марки демонстрирует скорость затвердевания бетона при разных температурах, диапазон составляет от 30℃ до 80℃.
Прочность на графике обозначена процентами.
Видео в этой статье покажет, как работает специальный прибор для измерения прочности бетона, и не только прочности.
dom-fundament.ru
Опасный бетон
Дело в том, что железобетон является композиционным материалом, представляющим собой успешное сочетание двух разнородных материалов – арматурной стали и бетона, которые эффективно дополняют и поддерживают друг друга. Арматурная сталь противостоит растягивающим напряжениям, а бетон отвечает за сжимающие, обеспечивает жесткость конструкции и защиту стали от коррозии.
В случае если конструкция грамотно спроектирована и качество бетона в полной мере соответствует проектному, – за безопасность можно не беспокоиться. Нельзя сказать, что качество бетона ухудшается повсеместно. Крупные объединения производителей товарного бетона и целый ряд заводов железобетонных изделий до сих пор выдают бетон гарантированного качества.
Ухудшение качества цемента и труднообъяснимые скачки его характеристик они либо компенсируют увеличением расхода цемента, либо подстраховываются завышенным коэффициентом вариации. Бетону подавляющего большинства этих предприятий доверять можно.О целом ряде мелких предприятий, которые производят товарный бетон в Санкт-Петербурге и Ленинградской области, таких слов не скажешь. И дело тут, как правило, в низкой технической грамотности инженерно-технического персонала. После того как строители перешли от марок бетона к классам по прочности, первое время повсеместно использовался нормативный коэффициент вариации прочности бетона. Классы бетона можно было пересчитать в марки и, наоборот, по специальной формуле, либо по таблице, приведенных в ГОСТ [1].
В настоящее время нормативный коэффициент вариации прочности 13,5% практически не применяется, так как большинство современных предприятий имеет оборудование, которое обеспечивает большую точность. В соответствии с ГОСТ [2] предприятие – производитель бетона само назначает коэффициент вариации прочности, в зависимости от ее фактической однородности за анализируемый период.
А вот производится это назначение в соответствии с данными фактического контроля прочности или путем принятия административного решения зависит от позиции руководства предприятия.
Снижение коэффициента вариации прочности бетона приводит к уменьшению требуемой прочности. Это позволяет экономить цемент, но влечет за собой увеличение ответственности за постоянный контроль всех изменяющихся от партии к партии качественных характеристик компонентов бетонной смеси. Большинство крупных объединений производителей товарного бетона и заводов сборных железобетонных конструкций, понимая всю меру ответственности, подстраховывается и назначает коэффициенты вариации прочности близкие к нормативному. При этом многие из них работают на современном оборудовании и имеют все необходимые средства контроля качества. Проблемы с качеством бетонной смеси у таких предприятий бывают крайне редко.
На бетонных заводах, которые выпускают бетонные смеси с низким коэффициентом вариации прочности (8%, 6%, а иногда и еще меньше), такие проблемы возникают значительно чаще.
Дело в том, что строители при контроле качества бетона на строительной площадке ориентируются на значение требуемой прочности, указанное в документе о качестве бетонной смеси. Не все из них знают, что требуемая прочность это не средняя прочность для соответствующего класса бетона, а минимально допустимая прочность, но если фактические данные оказываются ниже этой величины, беспокоиться начинают почти все. Было бы не так страшно, если бы проблемы заключались только в этом. В некоторых случаях в документе о качестве бетонной смеси указывается требуемая прочность, величина которой меньше, чем класс бетона!
Между тем, для расчета требуемой прочности не нужно ни знаний высшей математики, ни высшего технического образования. Это простое арифметическое действие. Значение требуемой прочности получают умножением класса бетона по прочности на коэффициент требуемой прочности (Кт), взятый из таблицы ГОСТ [2]. Фрагмент этой таблицы представлен ниже.
Для определения требуемой прочности нужно просто умножить класс бетона на коэффициент требуемой прочности из правого столбца, расположенный в той строке, где находится коэффициент вариации, принятый для данного бетона.
Ошибиться практически невозможно. После того, как один раз увидел эту таблицу, становится понятно, что требуемая прочность всегда больше, чем класс бетона.
Тем не менее, подобные ошибки случаются. И не во всех случаях имеется уверенность, что это была именно ошибка. Ниже представлены два фрагмента из наиболее одиозных документов по контролю качества бетонной смеси, произведенной в январе текущего года.
Дата отправки бетонной смеси 11.01.11
Класс (марка) бетона по прочности на сжатие в возрасте 28 суток В25
Другие показатели качества:
Коэффициент вариации прочности бетона 8%
Требуемая прочность бетона 16,4 МПа
Дата отправки бетонной смеси 18.01.11
Класс (марка) бетона по прочности на сжатие в возрасте 28 суток В25
Другие показатели качества:
Коэффициент вариации прочности бетона 8%
Требуемая прочность бетона 16,4 МПа
Еще страшнее, когда подобные цифры фигурируют не в документах на смесь, а в протоколах испытаний образцов.
По закону, в таком случае конструкции не должны быть приняты заказчиком, но этим дело заканчивается достаточно редко. Снижение фактического класса бетона на один – два МПа против заложенного в проекте не критично, но аналогичное уменьшение его в полтора – два раза, – это уже запредельно много. И может быть приведено в соответствие только путем демонтажа конструкции, либо применения целого комплекса трудоемких и дорогостоящих мероприятий по усилению несущей способности.
Зимнее бетонирование конструкций – это отдельная песня. Есть определенные виды конструкций, как правило, массивных, которые, наоборот, рекомендуется бетонировать только в зимнее время. Все остальные конструкции зимой надо утеплять или греть. Получается это далеко не всегда. Нам приносили керны, выбуренные из конструкций, забетонированных при отрицательных температурах воздуха. Верхний слой бетона, граничащий с утеплителем или теплым помещением, производил благоприятное впечатление, но буквально через несколько сантиметров начинался замороженный бетон, который после оттаивания разваливался на отдельные фрагменты.
www.vestnik.info
1. ОБЩИЕ ПОЛОЖЕНИЯ
Министерство образования и науки РФ Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования «Сибирская государственная автомобильно-дорожная академия (СибАДИ)»
Кафедра «Строительные материалы и специальные технологии»
ПОДБОР СОСТАВА ТЯЖЕЛОГО
ЦЕМЕНТНОГО БЕТОНА
ДЛЯ КОНСТРУКЦИЙ МОСТОВ
Методические указания к лабораторной работе
Составитель В.
Д. Галдина
Омск
СибАДИ
2015
УДК 666. 97 ББК 38. 331
Рецензент канд. техн. наук, доц. В.Е. Русанов (ФГБОУ ВПО «СибАДИ»)
Работа утверждена редакционно-издательским советом СибАДИ в качестве методических указаний.
Подбор состава тяжелого цементного бетона для конструкций мостов :
методические указания к лабораторной работе / сост. В.Д. Галдина. – Омск :
СибАДИ, 2015. – 40 с.
ISBN 978-5-93204-831-3
Приведены порядок определения однородности прочности бетона и требуемой прочности бетона; требования к исходным материалам для бетона; методика подбора состава тяжелого цементного бетона технологическим методом; методика определения водонепроницаемости бетона; пример подбора состава бетона; правила техники безопасности при выполнении лабораторной работы; приложения со справочными таблицами; библиографический список.
При составлении методических указаний использованы действующие нормативно-технические документы.
Рекомендованы для студентов специальности «Строительство, эксплуатация, восстановление и техническое прикрытие автомобильных дорог, мостов и тоннелей» и направления «Строительство» профиль «Мосты и транспортные тоннели» при проведении лабораторных работ по дисциплине «Материаловедение и технология конструкционных материалов».
УДК 666. 97 ББК 38. 331
ISBN 978-5-93204-831-3 | © ФГБОУ ВПО «СибАДИ», 2015 |
2
ВВЕДЕНИЕ
Мосты относятся к сложным транспортным сооружениям, к которым предъявляются повышенные требования по долговечности и надежности. Их срок эксплуатации определяется долговечностью применяемых конструкционных материалов (бетона, железобетона, углеродистой стали). Мостовые конструкции подвергаются значительным вибрационным нагрузкам, интенсивному увлажнению, воздействию атмосферных факторов (перепады температур, повышенная влажность, агрессивные газовые выбросы автомобилей и др.). Поэтому к бетонам для строительства мостов предъявляются требования по прочности на сжатие, маркам по морозостойкости и водонепроницае-
мости [1, 2].
Целью лабораторной работы является ознакомление студентов с методикой подбора состава тяжелого цементного бетона, используемого для изготовления конструкций мостов.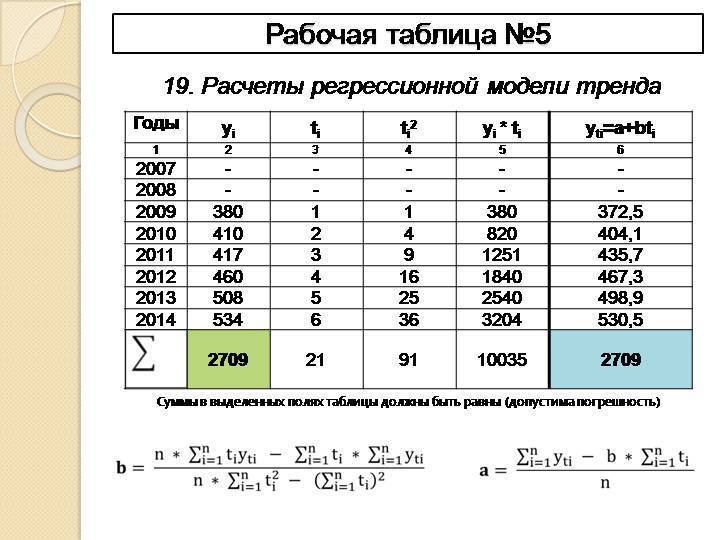
Лабораторную работу предусмотрено выполнять в течение трех занятий (12 ч). На предыдущих занятиях должны быть испытаны заполнители и цемент.
На первом занятии (4 ч) составляется задание на подбор состава бетона и подбирается номинальный состав бетона технологическим методом с принятым средним значением соотношения между песком
ищебнем. На втором занятии (4 ч) выполняются следующие работы:
1)изготовление бетонной смеси расчетного состава, определение ее удобоукладываемости, при необходимости корректировка состава, изготовление контрольных образцов;
2)расчет двух дополнительных составов смесей с увеличенным
иуменьшенным значением водоцементного отношения по сравнению с расчетным, изготовление бетонных смесей и контрольных образцов. Образцы до испытания хранят в нормальных условиях [3, 4].
На третьем занятии (4 ч) определяются плотность, водонепроницаемость и прочность бетона по контрольным образцам, анализируются результаты испытаний, полученные на трех занятиях, предлагается уточненный состав бетона.
При выполнении лабораторной работы рекомендуется пользоваться также методическими указаниями «Подбор состава тяжелого цементного бетона» [3].
Справочные таблицы, используемые при подборе состава бетона, даны в прил. 1, пример оформления таблиц по лабораторной работе – в прил. 2.
3
Защита лабораторной работы проводится путем устного или письменного опроса по контрольным вопросам.
1.1.Подбор состава бетона включает в себя определение номинального состава, расчет и корректировку рабочего состава. Подбор номинального состава бетона должен выполняться по утвержденному заданию в соответствии с ГОСТ 27006 [5].
1.2.Задание на подбор состава бетона должно быть составлено для конструкций конкретной номенклатуры, изготавливаемых по определенной технологии из бетона одного вида и качества.
В задании указываются:
— нормируемые показатели качества бетона в соответствии с техническими требованиями стандартов или с проектной документацией: класс прочности бетона на сжатие, марки по морозостойкости и водонепроницаемости;
— показатели качества бетонной смеси (подвижность или жесткость), длительность и режимы твердения бетона;
— показатель однородности бетона по прочности – коэффициент вариации прочности, а также соответствующая ему требуемая прочность, планируемые на предстоящий период;
— ограничения по составу бетона (расход цемента, объем вовлеченного воздуха, водоцементное отношение) и применению материалов для его приготовления, установленные нормативно-технической и технологической документацией (вид, марка и класс цемента, вид химических добавок, вид и качество крупного и мелкого заполнителей).
1.3.Согласно СП 35.13330.2011, для конструкций мостов следует применять тяжелый бетон классов по прочности на сжатие В20;
В22,5; В25; В27,5; В30; В35; В40; В45; В50; В55 и В60. Класс прочно-
сти бетона на сжатие назначается с учетом вида конструкции, армирования и условий работы (табл. П.1.1).
1.4.Марки по морозостойкости и водонепроницаемости бетона назначаются в зависимости от климатических условий зоны строительства, расположения и вида конструкции (табл. П.1.2).
1.5.При приготовлении бетонов следует выполнять нормативные требования к минимальному и максимальному расходам цемента
иводоцементному отношению.
4
Минимальный расход цемента в зависимости от расположения конструкций из бетона составляет, кг/м3:
-нижеглубиныпромерзания или возможногоразмывадна–230;
-в подводной и надводной (надземной) частях сооружения–260;
-впределахпеременногоуровняводыилипромерзаниягрунта–290;
-в мостовом полотне – 290.
Максимальный расход цемента зависит от класса прочности бетона и составляет, кг/м3:
•до класса В35 включительно – 450;
•В40 – 500; В 45 и выше – 550.
Водоцементное отношение В/Ц должно быть: в бетонах подземной зоны – не более 0,65; в бетонах подводной зоны – не более 0,60.
В бетонах с добавками, в том числе расположенных в зоне переменного уровня воды, водоцементное отношение следует принимать по табл. 1.
Таблица 1
Водоцементное отношение в бетонах в зависимости от вида конструкции и марки по морозостойкости
Вид конструкции | Марки по морозостойкости |
| ||
| F100 | F200 |
| F300 |
Железобетонные и тонкостенные |
|
|
|
|
бетонные толщиной менее 0,5 м | — | 0,50 |
| 0,45 |
Бетонные массивные | 0,60 | 0,55 |
| 0,47 |
|
|
|
|
|
Бетонные облицовки | — | — |
| 0,47 |
|
|
|
|
|
1.
6.Подвижность и жесткость бетонной смеси устанавливают для виброуплотняемых смесей по СНиП 3.09.01–85* [6] и уточняют в зависимости от характера и размеров конструкции, степени армирования, способа транспортировки и интенсивности уплотнения смеси
(табл. П.1.3).
1.7.Наибольшая крупность заполнителей в зависимости от видов бетонируемых элементов назначается по табл. П.1.4.
5
2.ОПРЕДЕЛЕНИЕ ТРЕБУЕМОЙ ПРОЧНОСТИ БЕТОНА
2.1.Для нормирования прочности бетона используют стандартную характеристику, которая гарантирует получение бетона заданной прочности с учетом возможных ее колебаний. Такой характеристикой является класс бетона по прочности.
Класс бетона по прочности на сжатие В – это гарантирован-
ная прочность бетона с учетом его неоднородности, принимаемая с обеспеченностью 0,95. Обеспеченность 0,95 означает, что установленная классом прочность будет обеспечиваться в 95 % случаях из 100 % и только в 5 % случаях можно ожидать ее невыполнения.
Нормируемая прочность бетона Внорм = В – прочность бетона
впроектном возрасте или ее доля в промежуточном возрасте, установленная в нормативном или техническом документе, по которому изготавливают бетонную смесь, готовую к применению (БСГ), или конструкцию.
2.2.В качестве характеристик однородности бетона по прочности, используемых для определения требуемой прочности бетона RТ, вычисляют коэффициенты вариации прочности бетона.
Требуемая прочность бетона RТ – минимально допустимое среднее значение прочности бетона в контролируемых партиях БСГ или конструкций, соответствующее нормируемой прочности бетона при ее фактической однородности.
2.3.Контроль и оценку прочности бетона на предприятиях, производящих БСГ, сборные, сборно-монолитные и монолитные бетонные и железобетонные конструкции, проводят по ГОСТ 18105 [7] статистическими методами с учетом характеристик однородности бетона по прочности в течение анализируемого периода.
Анализируемый период – период времени, за который вычисляют среднее значение коэффициента вариации прочности бетона для партий БСГ или конструкций, изготовленных за этот период.
За анализируемый период определяют:
— фактическую прочность бетона Rm и текущий коэффициент вариации прочности бетона Vm в каждой партии;
— средний коэффициент вариации прочности бетона за анализи-
руемый период Vm ;
— требуемую прочность бетона RТ для следующего контролируемого периода и проводят оценку прочности бетона каждой партии, изготовленной в контролируемом периоде.
6
Контролируемый период – период времени, в течение которого требуемая прочность бетона принимается постоянной в соответствии
скоэффициентом вариации за предыдущий анализируемый период.
2.4.Продолжительность анализируемого периода для определения характеристик однородности бетона по прочности устанавливают от одной недели до трех месяцев. Число единичных значений прочности бетона в течение этого периода должно быть не менее 30.
2.5.Фактическую прочность бетона Rm в партии, МПа, рассчитывают по формуле
n
Ri
R |
| i 1 | , | (1) |
| ||||
m |
| n |
| |
где Rm – фактическое значение прочности бетона в партии, МПа; Ri – единичное значение прочности бетона, МПа; n – общее число единичных значений прочности бетона в партии.
За единичное значение прочности бетона по образцам принимают среднюю прочность серий образцов, изготовленных из одной пробы бетонной смеси, для контроля одного вида нормируемой прочности.
2.6. Среднеквадратическое отклонение прочности бетона в партии Sm рассчитывают по формуле
n
(Ri Rm)2
Sm | i 1 |
| . | (2) |
|
| |||
|
| n 1 |
| |
При числе единичных значений прочности бетона в партии от двух до шести значение среднеквадратического отклонения Sm допускается рассчитывать по формуле
Sm = Wm/α, | (3) |
где Sm – среднеквадратическое отклонение, МПа; Wm = (Rmax – Rmin) – pазмах прочности бетона в партии, МПа; Rmin и Rmax – минимальное и максимальное значения прочности бетона в партии, МПа; α – коэффициент, принимаемый по табл.
2.
7
Значения коэффициента α |
|
| Таблица 2 | ||||
|
|
|
| ||||
|
|
|
|
|
|
|
|
Число единичных значений n | 2 | 3 |
| 4 | 5 |
| 6 |
Коэффициент α | 1,13 | 1,69 |
| 2,06 | 2,33 |
| 2,50 |
2.7. Текущий коэффициент вариации прочности бетона Vm в партии бетонной смеси или конструкций определяют по формуле
V |
| Sm | 100. | (4) |
| ||||
m |
| R |
| |
|
| m |
| |
2.8. Среднее значение коэффициента вариации прочности бетона Vm за анализируемый период рассчитывают по формуле
n Vmi ni
V | i 1 |
| , | (5) |
| n | |||
m |
|
| ||
ni
i 1
где Vmi – коэффициент вариации прочности бетона в каждой i-й пар-
тии; ni – число единичных значений прочности бетона в каждой i-й
n
партии; ni – общее число единичных значений прочности бетона
i 1
за анализируемый период.
2.9. Требуемую прочность бетона каждого вида для БСГ и сборных конструкций рассчитывают по формуле
RТ = КТ ∙Внорм, | (6) |
где RТ – требуемая прочность бетона, МПа; КТ – коэффициент требуемой прочности, принимаемый для тяжелых бетонов (кроме ячеистого и массивного гидротехнического) по табл. 3 в зависимости от
среднего коэффициента вариации Vm за анализируемый период; Внорм – нормируемая прочность бетона, МПа.
2.10. В начальный период производства, когда недостаточно данных для определения характеристик однородности бетона по прочности, требуемую прочность рассчитывают по формуле (6).
8
Z-4: Среднее значение, стандартное отклонение и коэффициент вариации
Не попадайтесь в ловушку, когда говорите о CV или путаете STD с SD. Вы знаете, что они имеют в виду, когда говорят о подлости? Это хлеб с маслом статистические расчеты. Убедитесь, что вы делаете их правильно.
EdD Доцент
Научная программа клинической лаборатории Университет Луисвилля
Луисвилл, Кентукки
Июнь 1999
- Среднее или среднее
- Стандартное отклонение
- Степени свободы
- Дисперсия
- Нормальное распределение
- Коэффициент вариации
- Альтернативные формулы
- Ссылки
- Упражнения для самооценки
- Об авторе
Многие из терминов, рассматриваемых в этом уроке, также встречаются в уроках по основам контроля качества, которые размещены на этом веб-сайте. Настоятельно рекомендуется изучать эти уроки онлайн или в печатном виде[1]. Однако важность этого текущего урока заключается в процессе. Урок устанавливает образец, которому нужно следовать на следующих уроках.
Среднее или среднее
Простейшей статистикой является среднее или среднее. Много лет назад, когда лаборатории только начинали анализировать контрольные образцы, было легко рассчитать среднее значение и использовать это значение в качестве «целевого значения», которое необходимо было достичь.
Например, для следующих десяти анализов контрольного материала — 90, 91, 89, 84, 88, 93, 80, 90, 85, 87 — среднее значение Xbar составляет 877/10 или 87,7. [Термин Xbar относится к символу, имеющему черту или черту над X, однако мы будем использовать этот термин вместо символа в тексте этих уроков, потому что его легче представить.]
Среднее значение характеризует «центральную тенденцию» или «местоположение» данных. Хотя среднее значение является наиболее вероятным наблюдаемым значением, многие фактические значения отличаются от среднего. При анализе контрольных материалов очевидно, что технологи не будут получать среднее значение каждый раз при анализе контроля. Наблюдаемые значения будут показывать дисперсию или распределение относительно среднего значения, и это распределение необходимо охарактеризовать, чтобы установить диапазон приемлемых контрольных значений.
Стандартное отклонение
Разброс значений относительно среднего предсказуем и может быть охарактеризован математически с помощью ряда манипуляций, как показано ниже, где отдельные значения x показаны в столбце A.
| Столбец A | Колонна В | Колонна С |
| Значение X | Значение X-Xbar | (X-Xbar) 2 |
| 90 | 90 — 87,7 = 2,30 | (2,30) 2 = 5,29 |
| 91 | 91 — 87,7 = 3,30 | (3,30) 2 = 10,89 |
| 89 | 89 — 87,7 = 1,30 | (1,30) 2 = 1,69 |
| 84 | 84 — 87,7 = -3,70 | (-3,70) 2 = 13,69 |
| 88 | 88 — 87,7 = 0,30 | (0,30) 2 = 0,09 |
| 93 | 93 — 87,7 = 5,30 | (5,30) 2 = 28,09 |
| 80 | 80 — 87,7 = -7,70 | (-7,70) 2 = 59,29 |
| 90 | 90 — 87,7 = 2,30 | (2,30) 2 = 5,29 |
| 85 | 85 — 87,7 = -2,70 | (-2,70) 2 = 7,29 |
| 87 | 87 — 87,7 = -0,70 | (-0,70) 2 = 0,49 |
| Х = 877 | (Х-Хбар) = 0 | (X-Xбар)² = 132,10 |
- Первая математическая операция заключается в суммировании () отдельных точек и вычислении среднего значения, которое равно 877, деленному на 10, или 87,7 в этом примере.
- Вторая манипуляция заключается в вычитании среднего значения из каждого контрольного значения, как показано в столбце B. Этот термин, отображаемый как значение X — Xbar, называется показателем различия. Как видно здесь, индивидуальные оценки различий могут быть положительными или отрицательными, а сумма оценок различий всегда равна нулю.
- Третья манипуляция заключается в том, чтобы возвести в квадрат оценку разности, чтобы сделать все термины положительными, как показано в столбце C.
- Затем суммируются квадраты разностей.
- Наконец, предсказуемую дисперсию или стандартное отклонение (SD или s) можно рассчитать следующим образом:
= [132,10/(10-1)]1/2 = 3,83
Степени свободы
Член «n-1» в приведенном выше выражении представляет степеней свободы (df). В произвольной интерпретации термин «степени свободы» указывает, сколько свободы или независимости имеется в группе чисел.
Например, если вам нужно просуммировать четыре числа, чтобы получить сумму, у вас есть свобода выбора любых чисел, которые вам нравятся. Однако, если сумма четырех чисел установлена равной 92, выбор первых 3 чисел достаточно свободен (при условии, что они являются младшими числами), но последний выбор ограничен условием, что сумма должна равняться 92. Например, если первые три выбранных наугад числа равны 28, 18 и 36, эти числа в сумме дают 82, что на 10 меньше цели. Для последнего числа нет свободы выбора. Нужно выбрать число 10, чтобы в сумме получилось 92. Таким образом, степени свободы были ограничены 1, и осталось только n-1 степеней свободы. В формуле SD степени свободы равны n минус 1, поскольку среднее значение данных уже рассчитано (что накладывает одно условие или ограничение на набор данных).
Дисперсия
Другим статистическим термином, связанным с распределением, является дисперсия, которая представляет собой квадрат стандартного отклонения (дисперсия = SD²).
SD может быть как положительным, так и отрицательным по значению, поскольку он рассчитывается как квадратный корень, который может быть как положительным, так и отрицательным. Возводя SD в квадрат, проблема знаков устраняется. Одним из распространенных применений дисперсии является ее использование в F-тесте для сравнения дисперсии двух методов и определения наличия статистически значимой разницы в неточности между методами.
Однако во многих случаях предпочтение отдается стандартному отклонению, поскольку оно выражается в тех же единицах концентрации, что и данные. Используя стандартное отклонение, можно предсказать диапазон контрольных значений, которые следует соблюдать, если метод остается стабильным. Как обсуждалось в одном из предыдущих уроков, лаборанты часто используют стандартное отклонение для наложения «ворот» на ожидаемое нормальное распределение контрольных значений.
Нормальное или гауссово распределение
Традиционно после обсуждения среднего значения, стандартного отклонения, степеней свободы и дисперсии следующим шагом было описание нормального распределения (полигона частот) с точки зрения «ворот» стандартного отклонения.
» Рисунок здесь представляет частотное распределение большого набора лабораторных значений, полученных при измерении одного контрольного материала. Это распределение имеет вид нормальной кривой. Обратите внимание, что «ворота», состоящие из ±1SD, составляют 68% распределения или 68% площади под кривой, ±2SD составляют 95% и ±3SD составляют >99%. При ±2SD 95 % распределения находится внутри «ворот», 2,5 % распределения — в нижнем или левом хвосте и столько же (2,5 %) — в верхнем хвосте. Некоторые авторы называют этот многоугольник кривой ошибки, чтобы проиллюстрировать, что небольшие ошибки от среднего значения происходят чаще, чем большие. Другие авторы называют эту кривую распределением вероятностей.
Коэффициент вариации
Еще один способ описания вариации теста — расчет коэффициента вариации, или CV. CV выражает вариацию в процентах от среднего значения и рассчитывается следующим образом:
CV% = (SD/Xbar)100
В лаборатории предпочтительным является CV, когда SD увеличивается пропорционально концентрации.
Например, данные повторного эксперимента могут показать стандартное отклонение 4 единицы при концентрации 100 единиц и стандартное отклонение 8 единиц при концентрации 200 единиц. CV составляет 4,0% на обоих уровнях, и CV более полезен, чем стандартное отклонение, для описания эффективности метода при промежуточных концентрациях. Однако не все тесты демонстрируют неточность, постоянную с точки зрения CV. Для некоторых испытаний стандартное отклонение может быть постоянным в пределах аналитического диапазона.
Резюме также дает общее «ощущение» эффективности метода. CV 5 % или менее обычно дают нам ощущение хорошей эффективности метода, тогда как CV 10 % и выше звучат плохо. Тем не менее, вы должны внимательно посмотреть на среднее значение, прежде чем оценивать CV. При очень низких концентрациях CV может быть высоким, а при высоких концентрациях CV может быть низким. Например, тест на билирубин со стандартным отклонением 0,1 мг/дл при среднем значении 0,5 мг/дл имеет коэффициент вариации 20%, в то время как стандартное отклонение 1,0 мг/дл при концентрации 20 мг/дл соответствует коэффициенту вариации.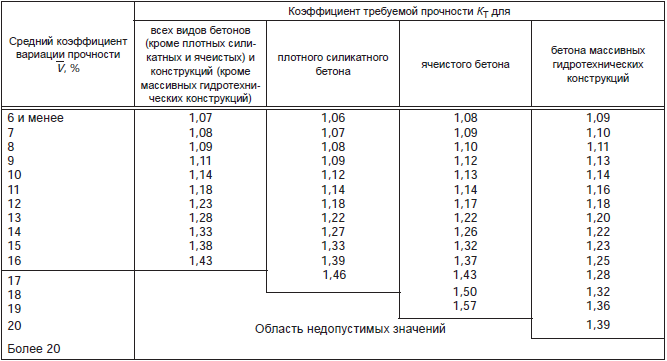
5,0%.
Альтернативные формулы
Уроки по основным методам контроля качества охватывают те же термины (см. Контроль качества — расчеты данных), но используют другую форму уравнения для расчета кумулятивных или текущих средних значений и стандартных отклонений. Руководящие принципы в литературе рекомендуют использовать кумулятивные средние и стандартные отклонения при расчете контрольных пределов [2-4], поэтому важно уметь выполнять эти расчеты.
Суммарное среднее может быть выражено как Xbar = (x i ) t / n t , что похоже на предыдущий средний член, за исключением индексов «t», которые относятся к данным за разные периоды времени. Идея состоит в том, чтобы добавить x i и n членов из групп данных, чтобы вычислить среднее значение объединенных групп.
Совокупное стандартное отклонение, или среднее стандартное отклонение для партии, может быть выражено следующим образом:
Это уравнение выглядит совершенно иначе, чем предыдущее уравнение в этом уроке, но на самом деле оно эквивалентно.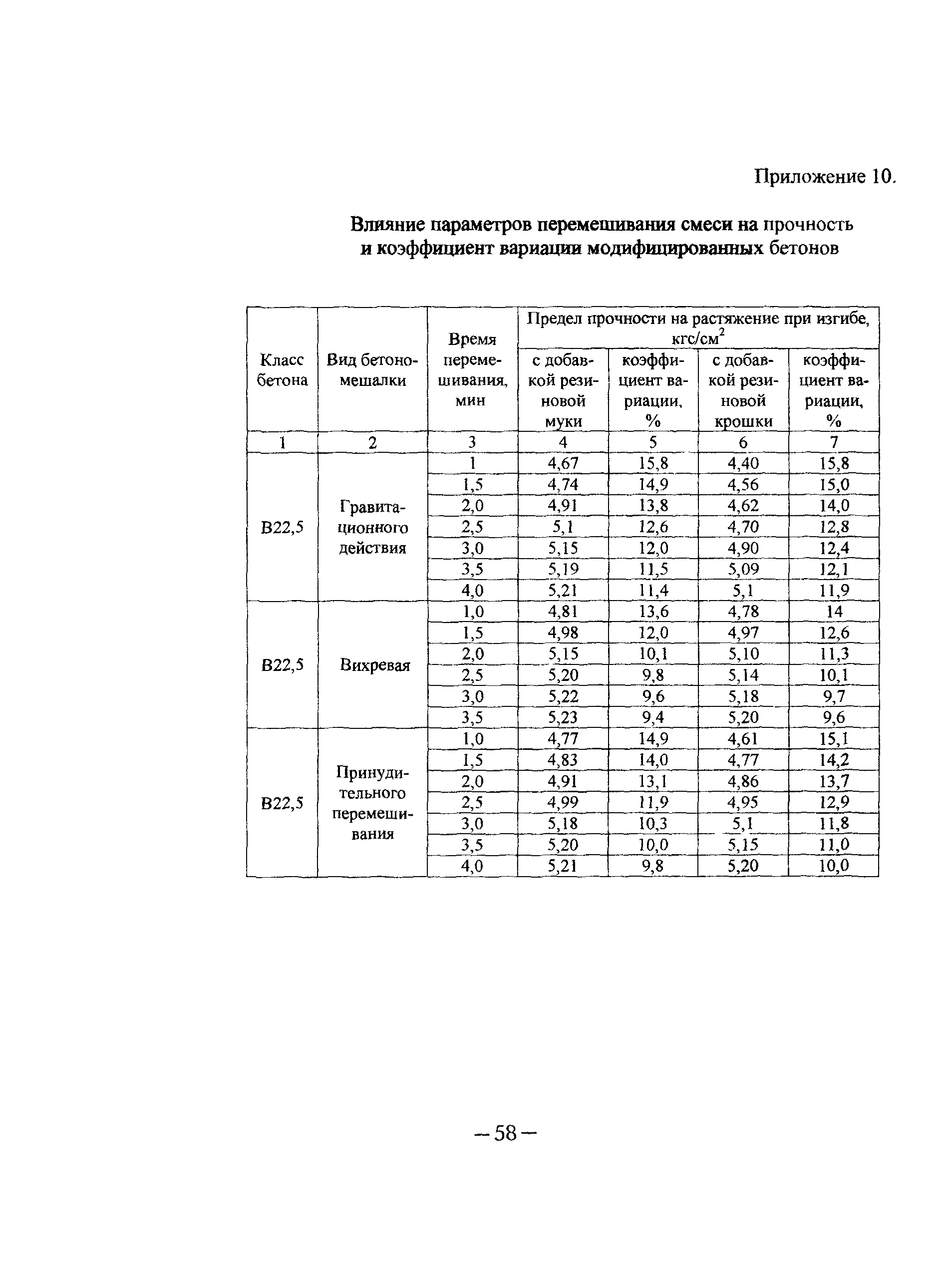
Формула кумулятивного стандартного отклонения получена из формулы стандартного отклонения, называемой формулой сырой оценки. Вместо того, чтобы сначала вычислять среднее значение или Xbar, Raw Score Формула вычисляет Xbar внутри знака квадратного корня.
Часто при чтении статистики может встречаться незнакомая формула. Вы должны понимать, что математика в статистике часто бывает избыточной. Каждая процедура основывается на предыдущей процедуре. Формулы, которые кажутся другими, получены в результате математических манипуляций со стандартными выражениями, с которыми вы часто уже знакомы.
Ссылки
- Вестгард Д.О., Барри, П.Л., Куам Э.Ф. Основные практики контроля качества: Обучение статистическому контролю качества для лабораторий здравоохранения. Мэдисон, Висконсин: Westgard Quality Corporation, 19 лет.98.
- Вестгард Дж. О., Барри П. Л., Хант М. Р., Грот Т. Многоуровневая диаграмма Шухарта для контроля качества в клинической химии. Clin Chem 1981; 27:493-501.
- Вестгард Дж.О., Клее Г.Г. Управление качеством. Глава 17 в Учебнике Tietz по клинической химии, 3-е изд., Burtis and Ashwood, eds. Филадельфия, Пенсильвания: Сондерс, 1999. .
- Документ NCCLS C24-A2. Статистический контроль качества количественных измерений: Принципы и определения. Национальный комитет клинических лабораторных стандартов, Уэйн, Пенсильвания, 19 лет.99.
Clin Chem 1981; 27:493-501.Упражнения для самооценки
- Вручную рассчитайте среднее значение, SD и CV для следующих данных: 44, 47, 48, 43, 48.
- Используйте калькулятор SD для расчета среднего, SD и CV для следующих данных: 203, 202, 204, 201, 197, 200, 198, 196, 206, 198, 196, 192, 205, 190, 207, 198 , 201, 195, 209, 186.
- Если приведенные выше данные относятся к контрольному материалу холестерина, рассчитайте контрольные пределы, которые содержали бы 95% ожидаемых значений.
- Если контрольные пределы (или SD «ворота») были установлены как среднее +/- 2,5 SD, какой процент контрольных значений, как ожидается, превысит эти пределы? [Подсказка: вам нужно найти таблицу площадей под нормальной кривой. ]
- Опишите, как рассчитать совокупные контрольные пределы.
- (Необязательно) Покажите эквивалентность обычной формулы SD и формулы Raw Score. [Совет: начните с обычной формулы, замените Xbar суммирующим членом, умножьте обе части на n/n, затем переставьте.]
]Об авторе: Маделон Ф. Зейди
Маделон Ф. Зейди является доцентом Университета Луисвилля, Школы смежных медицинских наук, клинической лабораторной научной программы, и имеет более чем 30-летний опыт преподавания. Она имеет степени бакалавра, магистра и доктора философии Университета Луисвилля, прошла другие курсы повышения квалификации в Школе медицины и Школе образования, а также курсы повышения квалификации по статистике. Она является зарегистрированным MT (ASCP) и сертифицированным CLS (NCA) и работала неполный рабочий день в качестве технолога на стенде в течение 14 лет. Она является членом: Американского общества клинических лабораторных исследований, Общества клинических лабораторных исследований штата Кентукки, Американской ассоциации исследований в области образования и Национальной ассоциации преподавателей естественных наук.
Областями ее преподавания являются клиническая химия и статистика. Областями ее исследований являются метапознание и теория обучения.
ЧТО ТАКОЕ СТАНДАРТНОЕ ОТКЛОНЕНИЕ И КАК ЕГО РАССЧИТАТЬ НА ПРИМЕРЕ РАСЧЕТА
by Suryakanta
Что такое стандартное отклонение?Когда повторные измерения дают разные результаты, мы хотим знать, насколько широко разбросаны показания. Разброс значений говорит нам кое-что о неопределенности измерения. Зная, насколько велик этот разброс, мы можем начать судить о качестве измерения или набора измерений.
Обычный способ количественной оценки разброса – стандартное отклонение. Стандартное отклонение набора чисел говорит нам о том, насколько отдельные показания обычно отличаются от среднего значения набора.
Математически стандартное отклонение выражается как среднеквадратичное отклонение всех результатов.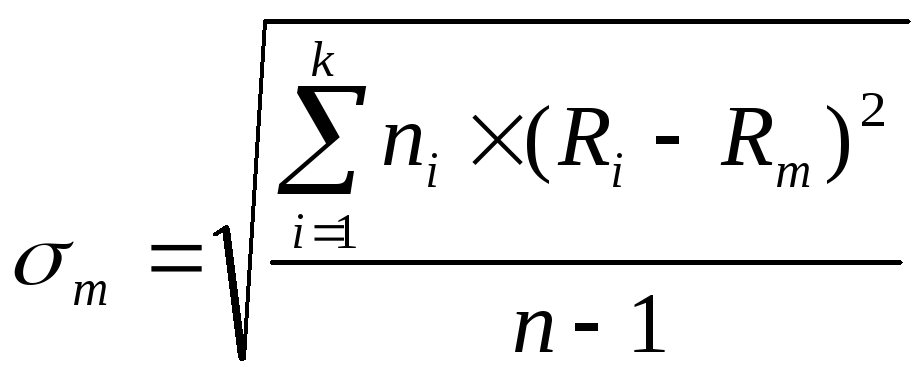
Это обозначается σ.
Стандартное отклонение будет меньше, если контроль качества на объекте лучше, и большая часть результатов испытаний будет сгруппирована вокруг среднего значения. Если контроль качества плохой, результаты теста будут сильно отличаться от среднего значения, и, следовательно, стандартное отклонение будет выше.
Кривая нормального распределения Пример расчета стандартного отклонения для набора из 20 результатов испытаний бетонного куба
| Номер образца | Прочность на раздавливание ( x ) МПа | Средняя прочность μ=∑x/n | Отклонение( x- μ ) | Квадрат отклонения (x- мк) 2 |
| 1 | 43 | 40.2 | +2,8 | 7,84 |
| 2 | 48 | +7,8 | 60,84 | |
| 3 | 40 | -0,2 | 0,04 | |
| 4 | 38 | -2,2 | 4,84 | |
| 5 | 36 | -4,2 | 16,64 | |
| 6 | 39 | -1,2 | 1,44 | |
| 7 | 42 | +1,8 | 3,24 | |
| 8 | 45 | +4,8 | 23. |