Коэффициент расширения: Коэффициент расширения: что такое, для чего нужен и как рассчитать

Коэффициент расширения: что такое, для чего нужен и как рассчитать

Коэффициент расширения: что такое, для чего нужен и как рассчитать | Глоссарий компании «Техноформ»8 (800) 550-83-25

Пн.-Пт., 9:00 — 18:00

Вход

Регистрация

Когда твердое тело и жидкость нагреваются, их температура повышается. Это приводит к тому, что в определенной мере увеличивается их объем при повышении температуры с каждым градусом. Свойство, которое характеризует отношение температуры и объема, называется коэффициентом расширения. У разных веществ коэффициент имеет разное значение, также может меняться у одного вещества в зависимости от того, какую оно имеет температуру. Принцип используется в работе термометров и других инструментов, используемых для измерения температуры.

Что такое тепловое расширение?

Тепловым расширение принято считать способность тел к расширению, когда они нагреваются. Это означает, что при повышении температуры изменяются их линейные и объемные размеры. Когда происходит охлаждение тела, процесс будет обратным – объем уменьшается.

Для чего нужен коэффициент?

Коэффициент теплового расширения описывает, как изменяется размер объекта, когда происходит повышение его температуры. В зависимости от конкретного использования, коэффициент расширения может быть линейный или объемный. Если тело твердое, требуется узнать изменение его длины или конкретной области, поэтому применяется коэффициент линейного расширения. Для жидкостей и газов используется только температурное расширение, коэффициент линейного теплового расширения для них не подходит, потому что приобретают форму емкости, в которой находятся.

Коэффициент объемного теплового расширения показывает, какое относительное изменение объема тела при постоянном давлении и изменении его температуры на 1 градус. Выражается формулой:

Коэффициент линейного теплового расширения показывает относительное изменение длины тела, когда происходит его нагревание.

Выражается формулой:

Коэффициент линейного теплового расширения может иметь разные значения, если направления измерений будут разными.

Теоретически рассчитать коэффициент линейного объема можно, зная коэффициент объемного расширения (α V ≈ 3 α L).

При нагревании некоторых материалов происходит их сжатие, а не расширение. У них коэффициент расширения (линейный) будет иметь отрицательное значение, к примеру, вода (коэффициент расширения с отрицательным значением при температуре 0-3,984 °С).

Особенности измерения

Тепловое расширение тел, независимо от их фазового состояния, измеряется дилатометром. Принцип действия практически всех приборов основан на измерении сдвигов (малых и сверхмалых), которые возникают вследствие изменения размеров тела относительно шкалы дилатометра. Прибор позволяет определить коэффициент теплового расширения даже в тех случаях, когда смещения микроскопические.

Сегодня существуют такие типы приборов:

  • оптико-механические;
  • емкостные;
  • индукционные;
  • интерференционные;
  • рентгеновские;
  • радиорезонансные и др.

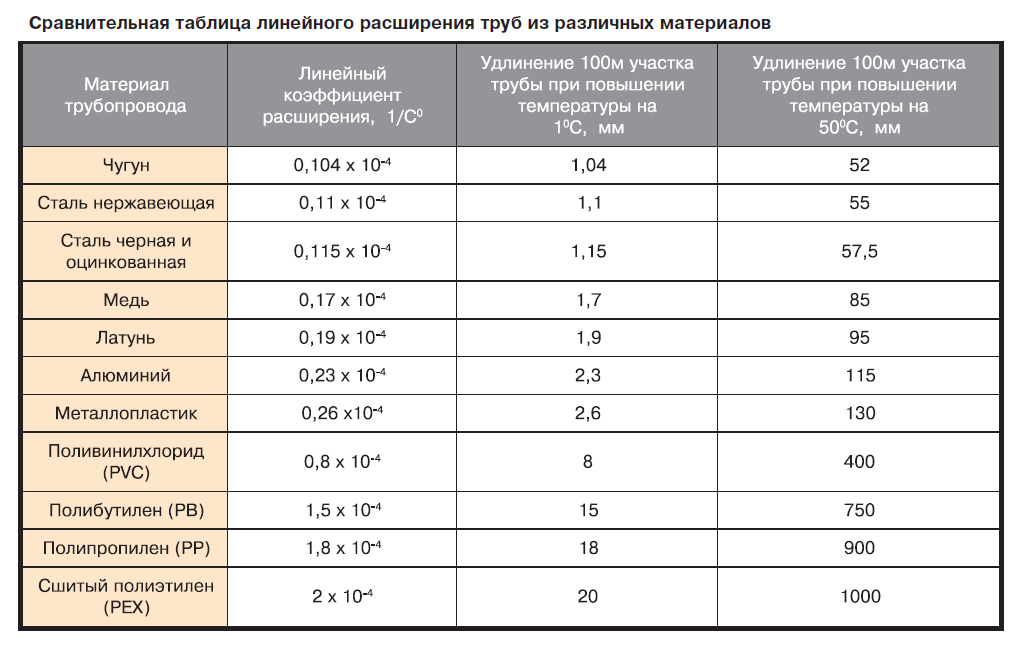
Чаще всего используются тепловые дилатометры, которые позволяют определять объемное и линейное расширение, происходящее под воздействием температуры.

Регистрация на сайте

Регистрация на сайте — процедура, необходимая только партнерам компании.
Зарегистрированным партнерам открывается доступ к закрытому разделу сайта — загрузки.

Ваша заявка

Ваша заявка

Ваша заявка

Коэффициент расширения теплоносителя пропиленгликоля | teplonositeli-pro.ru

Под коэффициентом теплового расширения любого тела понимают физическую величину, которая характеризует относительное изменение его объёма или линейных размеров при изменении (увеличении) температуры на 1К (˚С) при постоянном давлении. На практике более заметно расширение либо уменьшение объёма на примере жидкостей при их нагреве либо охлаждении, соответственно, по сравнению с твёрдыми телами. Изменение объёма обозначается показателем в виде коэффициента объёмного расширения: β = 1/V, К-1 (˚С-1).

Поскольку пропиленгликоль не может использоваться в чистом виде в качестве теплоносителя (состава низкозамерзающего всесезонного), ввиду его повышенной вязкости и коррозионной активности по отношению к металлам и сплавам, правильнее говорить о применении его водных растворах различной концентрации, в которые вводится пакет антикоррозионных присадок.

Водопропиленгликолевые составы низкозамерзающие всесезонные или жидкости охлаждающие для теплообменных систем относятся к одной из наиболее востребованной группе теплообменных жидкостей (после воды), применяемых в отопительной аппаратуре. Это обусловлено их довольно низкой температурой начала кристаллизации, что позволяет применять их и в зимний период (отопительный сезон).

К тому же они не столь токсичны как растворы этиленгликоля и не наносят вреда окружающей среде, хотя и обладают свойствами присущими гликолям. При низких отрицательных температурах окружающего воздуха они не переходят в твёрдую структуру льда (как это происходит с водой) и сохраняют работоспособность теплообменных систем.

Для чего необходимо знать коэффициент расширения?

Большинство автономных систем теплоснабжения спроектированы для применения воды, либо иногда — составов низкозамерзающих всесезонных, в качестве теплоносителя. Поэтому при расчётах и выборе аппаратов системы теплообмена (расширительной ёмкости) для них, учитываются и физические параметры.

Но если в качестве альтернативы будет использоваться не обычная техническая вода, нужно учитывать, что коэффициент расширения теплоносителя на основе пропиленгликоля (антифриза) будет другим. Его вычисляют для внесения необходимых корректировок, проверки соответствия объёма емкости расширительного бака.

Использование антифриза может привести к «завоздушиванию» отопительной системы. Этот процесс – результат более высокого (если сравнивать с водой) коэффициента температурного расширения теплоносителя на основе пропиленгликоля. В итоге объёма емкости расширительного бака оказывается недостаточно для его заполнения. Поэтому излишки антифриза при нагреве его до рабочей температуры (обычно это около 85 °C) сбрасываются путем слива через предохраняющий клапан.

После снижения тепловой нагрузки требуется подпитка системы теплообмена рабочей средой. Для этого используется вода, в которой содержатся растворённый воздух, который выделяется из жидкой фазы в результате нагрева. Все это провоцирует образование воздушных пробок, вызывающих серьезные аварии в системе отопления и поломки отдельной аппаратуры. На практике этот процесс хорошо демонстрируется во время эксплуатации двигателей внутреннего сгорания автотранспортной техники, когда система их охлаждения не обеспечивает нормальной работы и начинает «закипать».

Зависимость величины коэффициента расширения от температуры

Величина коэффициента объёмного теплового расширения теплоносителей на базе водных растворов пропиленгликоля зависит не только от его концентрации (содержании) в растворе, но и от температурного диапазона системы теплообмена в которой применяется теплоноситель. Существуют материалы и диапазоны температур, даже для воды когда, в узком интервале температур от 0˚С до + 4˚С, величина коэффициента отрицательная. Рассматриваемый коэффициент для теплоносителей на основе пропиленгликоля увеличивается с ростом температуры. Конкретные величины коэффициента объёмного расширения и динамику его увеличения при повышении температур для антифризов можно найти в справочной литературе.

Теплоноситель, в основе которого содержится пропиленгликоль, имеет значительно больший коэффициент расширения при нагреве, по сравнению с водой, поэтому рекомендуется подбирать бак для такой системы отопления большего объема. В отличие от воды, теплоемкость такого теплоносителя меньше на 15%. Это приводит к ухудшению условий теплообмена и требует монтажа дополнительных радиаторов, обладающих максимальной мощностью.

Кроме теплового расширения в результате нагрева, в теплоносителе на базе пропиленгликоля могут происходить необратимые изменения его химического состава в результате перегрева. Поэтому допускать повышение температуры антифриза до максимальных показателей не рекомендуется. Для объектов, где в отопительных системах требуется применение теплоносителей на основе водных растворов пропиленгликоля, гарантирующих экологическую безопасность, можно приобрести такую продукцию у компании «Савиа», которая занимается производством теплоносителей широкой номенклатуры. {\deg f}$. Вложение коэффициентов берет некоторый вход $r(x)$, уменьшает его по модулю $f(x)$, чтобы получить уникального представителя $r(x)$ в пределах $\mathbb{Z}[x] + \langle f(x )\rangle$ (это единственный представитель степени $< \deg f$), а затем считывает коэффициенты этого единственного представителя как вектор. Это означает, что норма, с которой вы работаете, определена таким образом, что различие между "$r(x)$ полиномом" и "$\vec r$ вектором" намеренно очень мало.

Откуда такое количество?

Он по существу определен, поскольку требуемое соотношение $\lVert g(x)h(x)\rVert \not\leq \lVert g(x)\rVert\lVert h(x)\rVert$ не выполняется, где $ \lVert\cdot\rVert$ — норма, индуцированная на $R$ вложением коэффициентов. Можно определить коэффициент расширения таким образом, чтобы выполнялась приблизительная версия этого неравенства, т.е. \rВерт$. Если вы рассматриваете это как цель его определения, должно быть относительно ясно, почему коэффициент расширения принимает именно такое определение, какое он дает.

Что касается того, почему мы хотим, чтобы выражение, подобное этому, выполнялось, вы должны рассматривать его как похожее на «мультипликативную» версию неравенства треугольника. По сути, при работе с нормой некоторой алгебраической структуры все работает намного лучше, если ваша норма «уважает» вашу алгебраическую структуру. Для колец это означает, что норма является субаддитивной (также известной как удовлетворяющая неравенству треугольника) и субмультипликативной (то есть удовлетворяет $\lVert g(x)h(x)\rVert \leq \lVert g(x)\ rVert \lVert h(x)\rVert$), или даже «приблизительно» (скажем, до «коэффициента выдумки» $\gamma$).

Какие результаты мы знаем об этом?

Есть некоторые общие результаты, ограничивающие его (которые обсуждаются в связанной статье), но многие авторы больше не работают с ним, потому что есть «лучший» способ определить норму на $\mathbb{Z}[x ]/(f(x))$, что напрямую приводит к субмультипликативным конструкциям без необходимости вводить «коэффициент выдумки» (что, по сути, и делает коэффициент расширения).

См. раздел 4.3.3 обзора Piekert A Decade of Lattice Cryptography 9.0004 для подробностей. Норма, определяемая с использованием коэффициента расширения, часто называется вложением коэффициентов, норма, которая по умолчанию является субмультипликативной, часто называется вложением Минковского или каноническим вложением.

Обратите внимание, что каноническое вложение имеет и другие преимущества помимо анализа выражений — оно соответствует вычислению многочлена по ряду точек, т.е. операции типа «Преобразование Фурье». Хотя вычисление этого представления менее эффективно, чем простое считывание коэффициентов некоторого полинома, после его вычисления вы получаете определенные вычислительные преимущества (более быстрые алгоритмы умножения).

Как рассчитывается для разных колец, а может даже модулей?

Это вычислено для нескольких примеров в этой статье, но по большей части я думаю, что ответ «нет». Оно было вычислено для ряда «общих» колец, если вы хотите его использовать (включая некоторые общие результаты — см. статью), но многие авторы просто используют вложение Минковского, что позволяет обойти проблему принуждения определенной нормы к быть субмультипликативным.

Обратите внимание, что такие вещи, как коэффициент расширения, могут отображаться в других областях, «смежных с решеткой». Например, в этой недавней статье авторам необходимо определить/проанализировать аналогичные величины для версии решетчатой ​​криптографии «больших целых чисел» (см. эту статью, чтобы узнать, почему она так называется). Конечно, возможно, что это указание на то, что для анализа используется «неправильная норма», и если бы люди могли просто найти «правильную норму», им не нужно было бы определять коэффициент расширения (возможно, именно это и произошло). для норм на $\mathbb{Z}[x]/(f(x))$). Время покажет.

Измерение коэффициента расширения и искажения для микроскопии расширения с использованием изолированных почечных клубочков в качестве ориентиров

Сохранить цитату в файл

Формат: Резюме (текст)PubMedPMIDAbstract (текст)CSV

Добавить в коллекции

  • Создать новую коллекцию
  • Добавить в существующую коллекцию
Назовите свою коллекцию:

Имя должно содержать менее 100 символов

Выберите коллекцию:

Не удалось загрузить вашу коллекцию из-за ошибки
Повторите попытку

Добавить в мою библиографию

  • Моя библиография

Не удалось загрузить делегатов из-за ошибки
Повторите попытку

Ваш сохраненный поиск

Название сохраненного поиска:

Условия поиска:

Тестовые условия поиска

Электронная почта: (изменить)

Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый рабочий день

Который день? ВоскресеньеПонедельникВторникСредаЧетвергПятницаСуббота

Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed

Отправить максимум: 1 штука5 штук10 штук20 штук50 штук100 штук200 штук

Отправить, даже если нет новых результатов

Необязательный текст в электронном письме:

Создайте файл для внешнего программного обеспечения для управления цитированием

Полнотекстовые ссылки

Уайли

Полнотекстовые ссылки

. 2021 июль;14(7):e202100001.

doi: 10.1002/jbio.202100001. Epub 2021 27 апр.

Чен Чжу 1 2 , Айдонг Ван 3 , Лили Чен 3 , Ляншэн Го 3 , Цзяцзя Е 1 4

, Цилинь Чен 5 , Ци Ван 1 2 , Гоцзя Яо 1 4 , Цинь Ся 1 4 , Тянью Цай 1 4 , Цзяюнь Го 6 , Чжэньюй Ян 6 , Чжэнлун Сунь 6 , Ювэй Сюй 7 , Гоюань Лу 7 , Цзэсинь Чжан 1 8 , Цзинъюань Цао 9 , Ин Лю 10 , Хуэйчжун Сюй 1 4

Принадлежности

  • 1 Институт перспективных исследований Университета Сучжоу, Сучжоу, Китай.
  • 2 Факультет оптоэлектронных наук и инженерии Университета Сучжоу, Сучжоу, Китай.
  • 3 Вторая дочерняя больница Университета Сучжоу, Сучжоу, Китай.
  • 4 Школа физических наук и технологий Университета Сучжоу, Сучжоу, Китай.
  • 5 Детская больница Чунцинского медицинского университета, Чунцин, Китай.
  • 6 Сучжоуский институт биомедицинской инженерии и технологии Китайской академии наук, Сучжоу, Китай.
  • 7 Первая дочерняя больница Университета Сучжоу, Сучжоу, Китай.
  • 8 Колледж химии, химической инженерии и материаловедения Университета Сучжоу, Сучжоу, Китай.
  • 9 Отделение нефрологии, Народная больница Тайчжоу, Пятая дочерняя больница Университета Наньтун, Тайчжоу, Китай.
  • 10 Институт педиатрических исследований, Детская больница Университета Сучжоу, Сучжоу, Китай.
  • PMID: 33856738
  • DOI: 10.1002/jbio.202100001

Чэнь Чжу и др. J Биофотоника. 2021 9 июля0005 . 2021 июль;14(7):e202100001.

doi: 10.1002/jbio.202100001. Epub 2021 27 апр.

Авторы

Чен Чжу 1 2 , Айдонг Ван 3 , Лили Чен 3 , Ляншэн Го 3 , Цзяцзя Е 1 4 , Цилинь Чен 5 , Ци Ван 1 2 , Гоцзя Яо 1 4 , Цинь Ся 1 4 , Тяньюй Цай 1 4 , Цзяюнь Го 6 , Чжэньюй Ян 6 , Чжэнлун Сунь 6 , Ювэй Сюй 7 , Гоюань Лу 7 , Цзэсинь Чжан 1 8 , Цзинъюань Цао 9 , Ин Лю 10 , Хуэйчжун Сюй 1 4

Принадлежности

  • 1 Институт перспективных исследований Университета Сучжоу, Сучжоу, Китай.
  • 2 Факультет оптоэлектроники и инженерии Университета Сучжоу, Сучжоу, Китай.
  • 3 Вторая дочерняя больница Университета Сучжоу, Сучжоу, Китай.
  • 4 Школа физических наук и технологий Университета Сучжоу, Сучжоу, Китай.
  • 5 Детская больница Чунцинского медицинского университета, Чунцин, Китай.
  • 6 Сучжоуский институт биомедицинской инженерии и технологии Китайской академии наук, Сучжоу, Китай.
  • 7 Первая дочерняя больница Университета Сучжоу, Сучжоу, Китай.
  • 8 Колледж химии, химической инженерии и материаловедения Университета Сучжоу, Сучжоу, Китай.
  • 9 Отделение нефрологии, Народная больница Тайчжоу, Пятая дочерняя больница Университета Наньтун, Тайчжоу, Китай.
  • 10 Институт педиатрических исследований, Детская больница Университета Сучжоу, Сучжоу, Китай.
  • PMID: 33856738
  • DOI: 10.1002/jbio.202100001

Абстрактный

Расширительная микроскопия позволила получить изображения биологических образцов со сверхвысоким разрешением. Точное измерение коэффициента расширения и искажения обычно требует локализации и визуализации одной и той же интересующей области в образце до и после расширения, что часто требует много времени. Здесь мы представляем удобный метод для перемещения, используя изолированные клубочки свиньи в качестве ориентиров во время расширения. После тепловой денатурации и расщепления протеиназой К клубочки демонстрируют коэффициент расширения от 3,5 до 4 (всего на 7-16% меньше, чем гидрогель), и от 1% до 2% относительного искажения. Из-за подходящего размера от 100 до 300 мкм расположение клубочка в образце видно глазу, а его детальная форма требует только светлопольной микроскопии. Для коэффициентов расширения от 3 до 10 область вблизи клубочка может быть легко повторно идентифицирована, что иногда позволяет количественно определить коэффициент расширения и искажение в светлом поле без флуоресцентных меток.

Ключевые слова: коэффициент расширения; микроскопия расширения; клубочек; супер разрешение.

© 2021 Wiley-VCH GmbH.

Похожие статьи

  • Микроскопия расширения с терморегулируемым коэффициентом расширения с использованием термочувствительных биообразцов-гидрогелевых гибридов.

    Кан С, Пак С, Сонг Х, Чхве Д, Пак ХЭ, Ан БХ, Ким Си, Ли Ю. Кан С и др. Интерфейсы приложений ACS. 2021 23 июн;13(24):28962-28974. doi: 10.1021/acsami.1c07592. Epub 2021 10 июня. Интерфейсы приложений ACS. 2021. PMID: 34107679

  • Визуализация с молекулярным разрешением с помощью микроскопии локализации одной молекулы после мечения (Ex-SMLM).

    Цветтлер Ф.У., Рейнхард С., Гамбаротто Д., Белл ТДМ, Амель В., Гишар П., Зауэр М. Цветтлер Ф.У. и соавт. Нац коммун. 2020 7 июля; 11 (1): 3388. doi: 10.1038/s41467-020-17086-8. Нац коммун. 2020. PMID: 32636396 Бесплатная статья ЧВК.

  • Выявление наноструктур в ткани головного мозга путем расщепления белков с помощью итеративной микроскопии расширения.

    Саркар Д., Канг Дж., Васси А.Т., Шредер М.Э., Пэн З., Тарр Т.Б., Танг А.Х., Нидерст Э.Д., Янг Дж.З., Су Х., Парк Д., Инь П., Цай Л.Х., Бланпьед Т.А., Бойден Э.С. Саркар Д. и др. Нат Биомед Инж. 2022 сен;6(9):1057-1073. doi: 10.1038/s41551-022-00912-3. Epub 2022 авг 29. Нат Биомед Инж. 2022. PMID: 36038771 Бесплатная статья ЧВК.

  • Расширительная микроскопия: масштабируемая и удобная микроскопия сверхвысокого разрешения.

    Тилберг П.В., Чен Ф. Тилберг П.В. и соавт. Annu Rev Cell Dev Biol. 2019 6 октября; 35: 683-701. doi: 10.1146/annurev-cellbio-100818-125320. Epub 2019 19 августа. Annu Rev Cell Dev Biol. 2019. PMID: 31424964 Обзор.

  • Введение в методологию расширительной микроскопии.

    Фолкнер Э.Л., Томас С.Г., Нили Р.К. Фолкнер Э.Л. и др. Int J Biochem Cell Biol. 2020 июль; 124:105764. doi: 10.1016/j.biocel.2020.105764. Эпаб 2020 12 мая. Int J Biochem Cell Biol. 2020. PMID: 32407880 Обзор.

Посмотреть все похожие статьи

Рекомендации

ССЫЛКИ
    1. Ф. Хуанг, Г. Сиринакис, Э. С. Аллгейер, Л. К. Шредер, В. К. Дуим, Э. Б. Кроманн, Т. Фан, Ф. Э. Ривера-Молина, Дж. Р. Майерс, И. Ирнов, М. Лессард, Ю. Чжан, М. А. Гендель, К. Джейкобс -Вагнер, С. П. Ласк, Дж. Э. Ротман, Д. Тоомре, М. Дж. Бут, Дж. Беверсдорф, Cell 2016, 166 (4), 1028.
    1. F.